Prediction of Compressive Behavior of Laser-Powder-Bed Fusion-Processed TPMS Lattices by Regression Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. TPMS Lattice Structure Design
2.2. Additive Manufacturing of the TPMS Lattice Structures
2.3. Compression Test
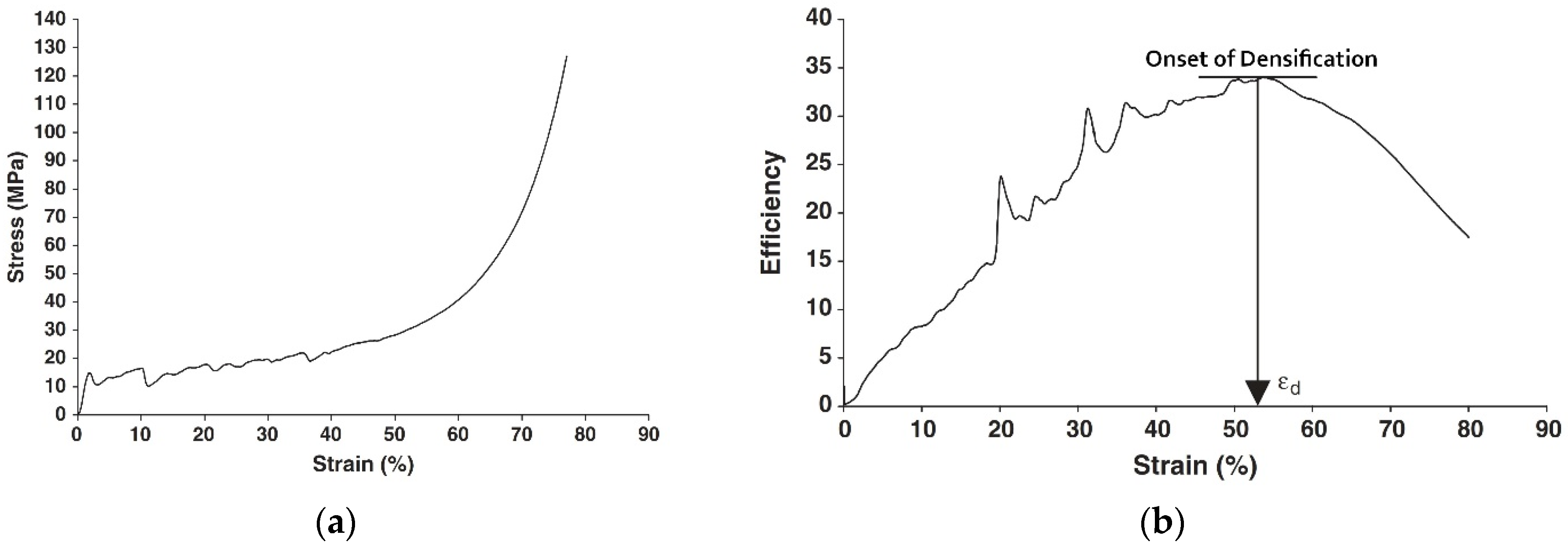
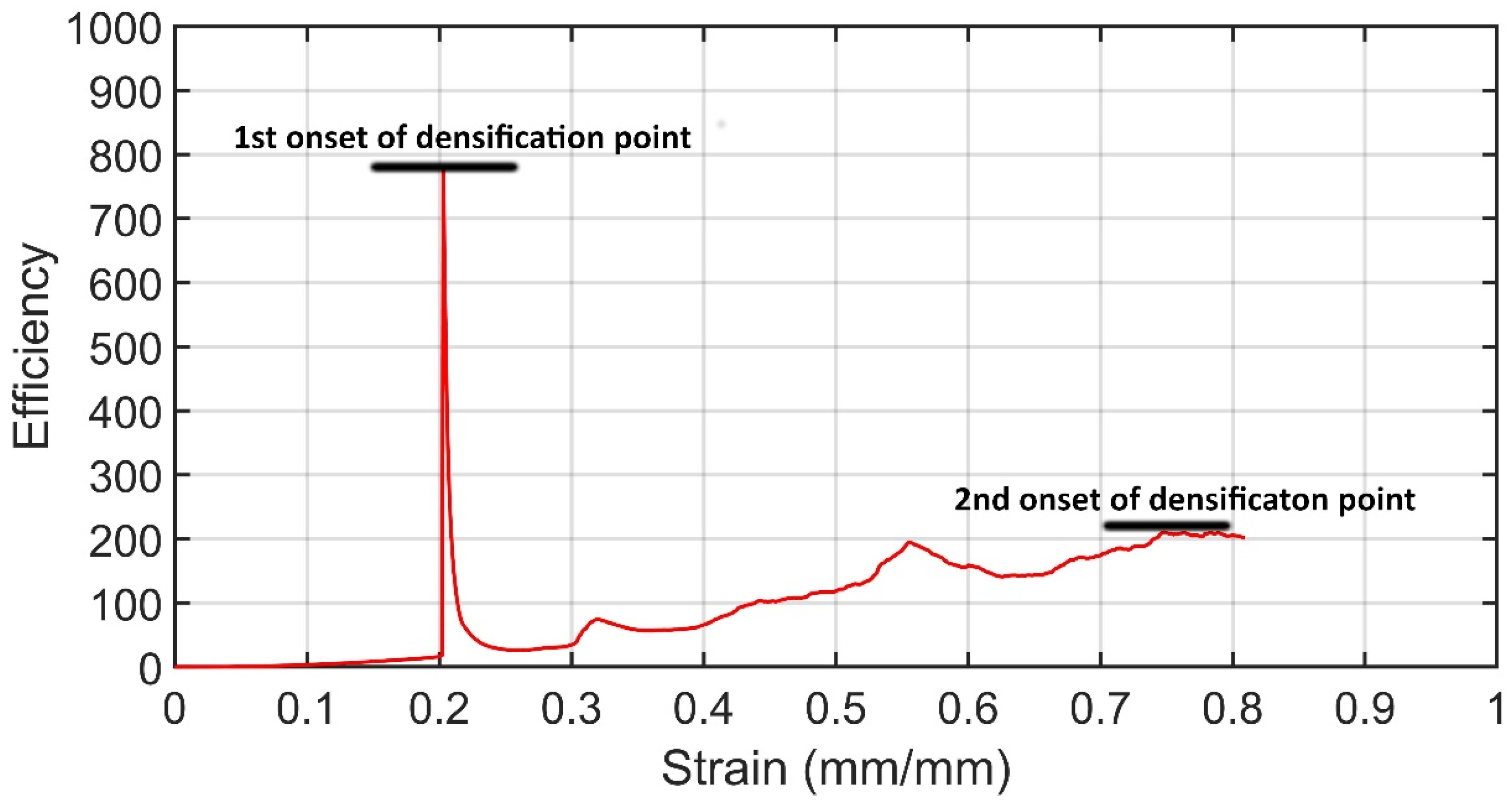
2.4. Compression and Energy Absorption Indicators
3. Results and Discussions
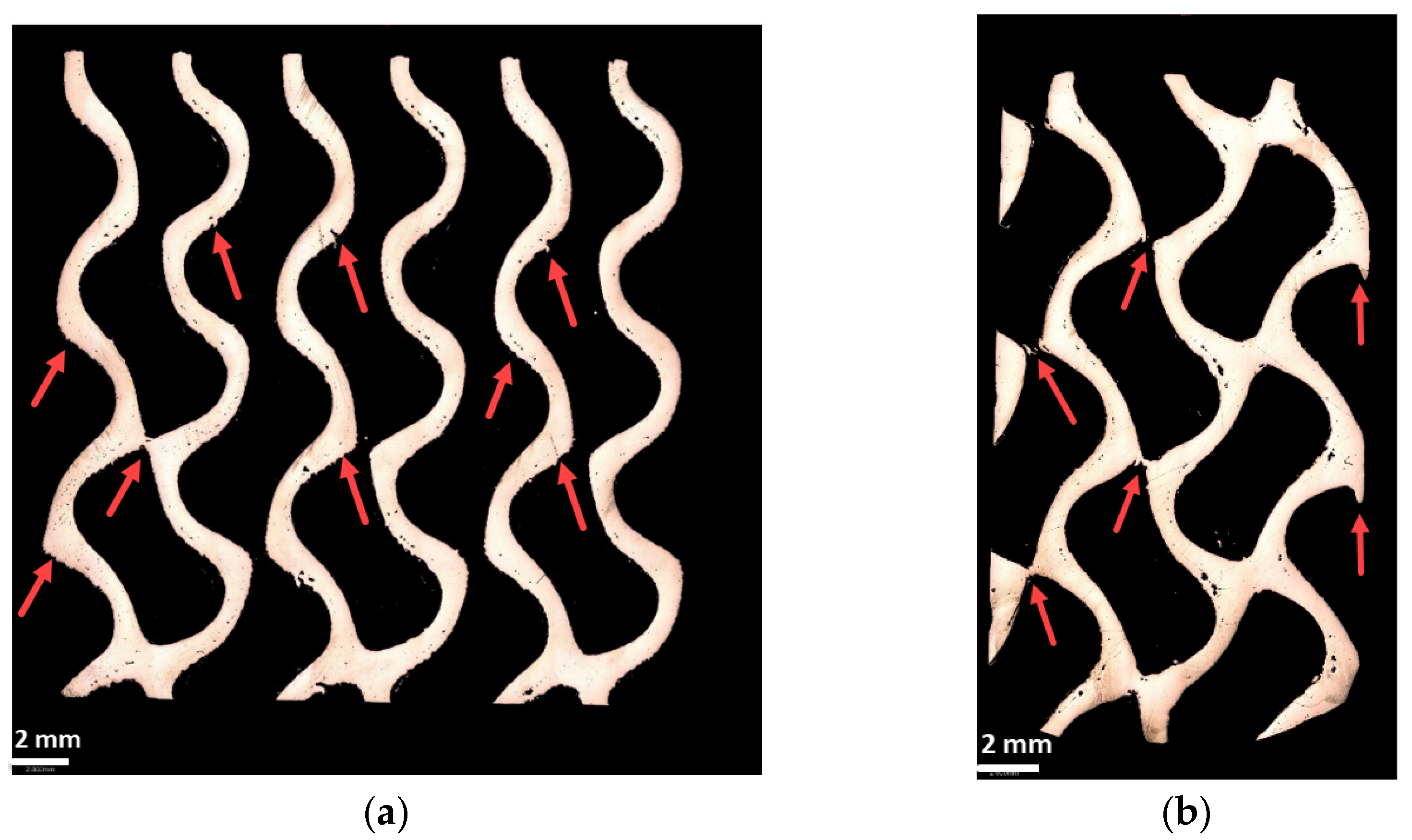
3.1. Manufacturing and Inspection Results
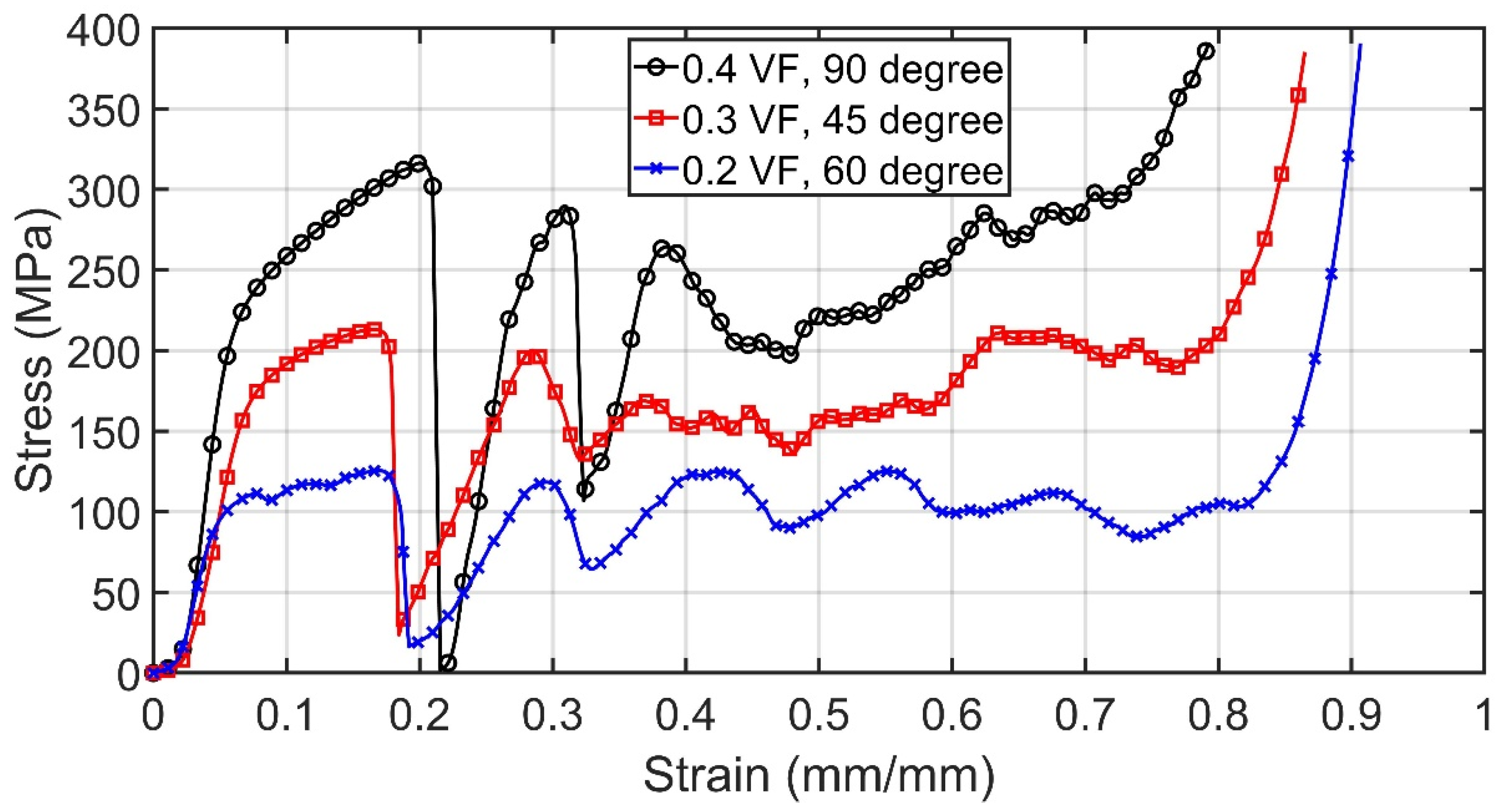
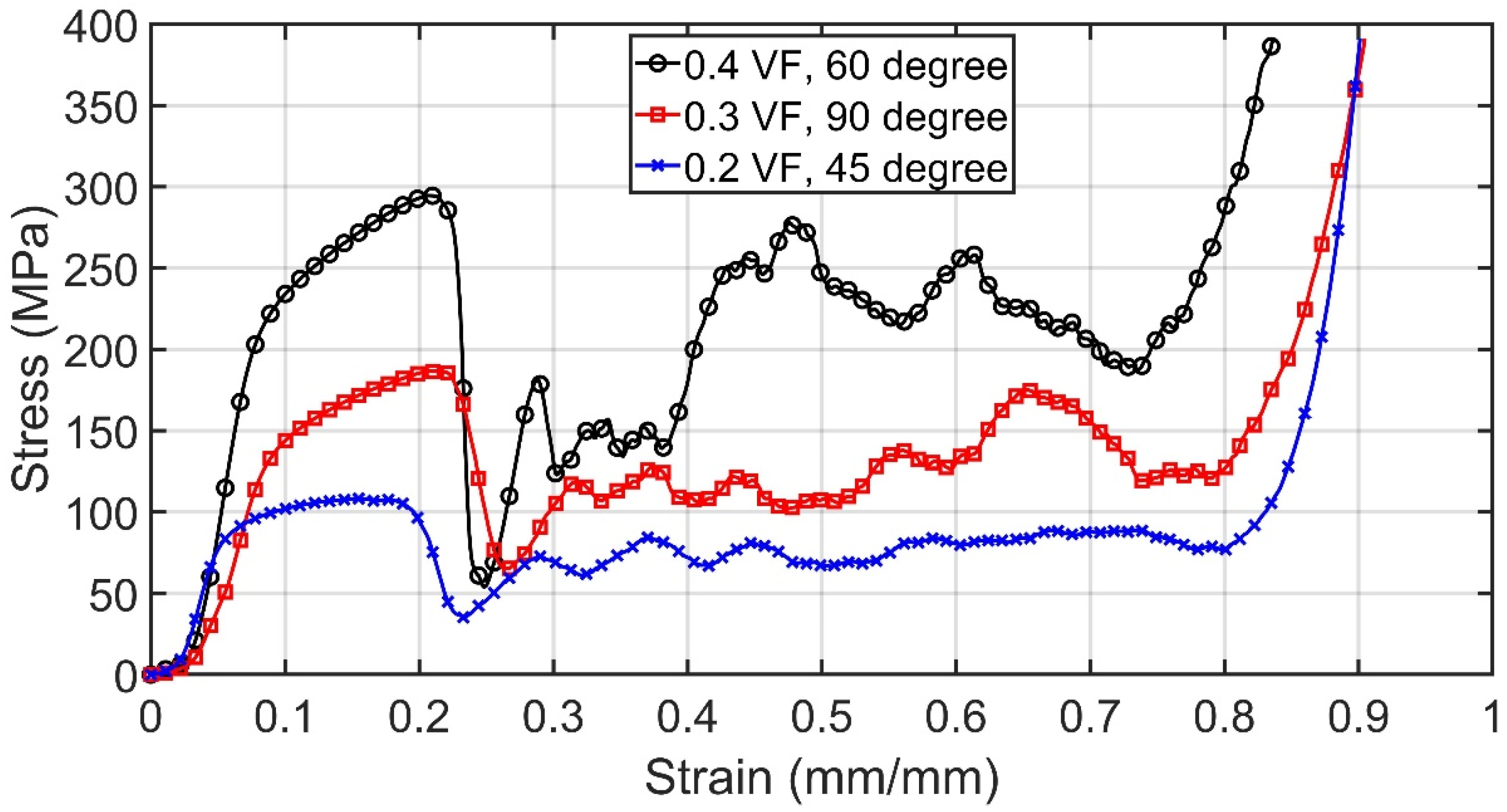
3.2. Compression Test Results
3.3. Regression Analysis Results
3.4. Validation Study Results
4. Conclusions
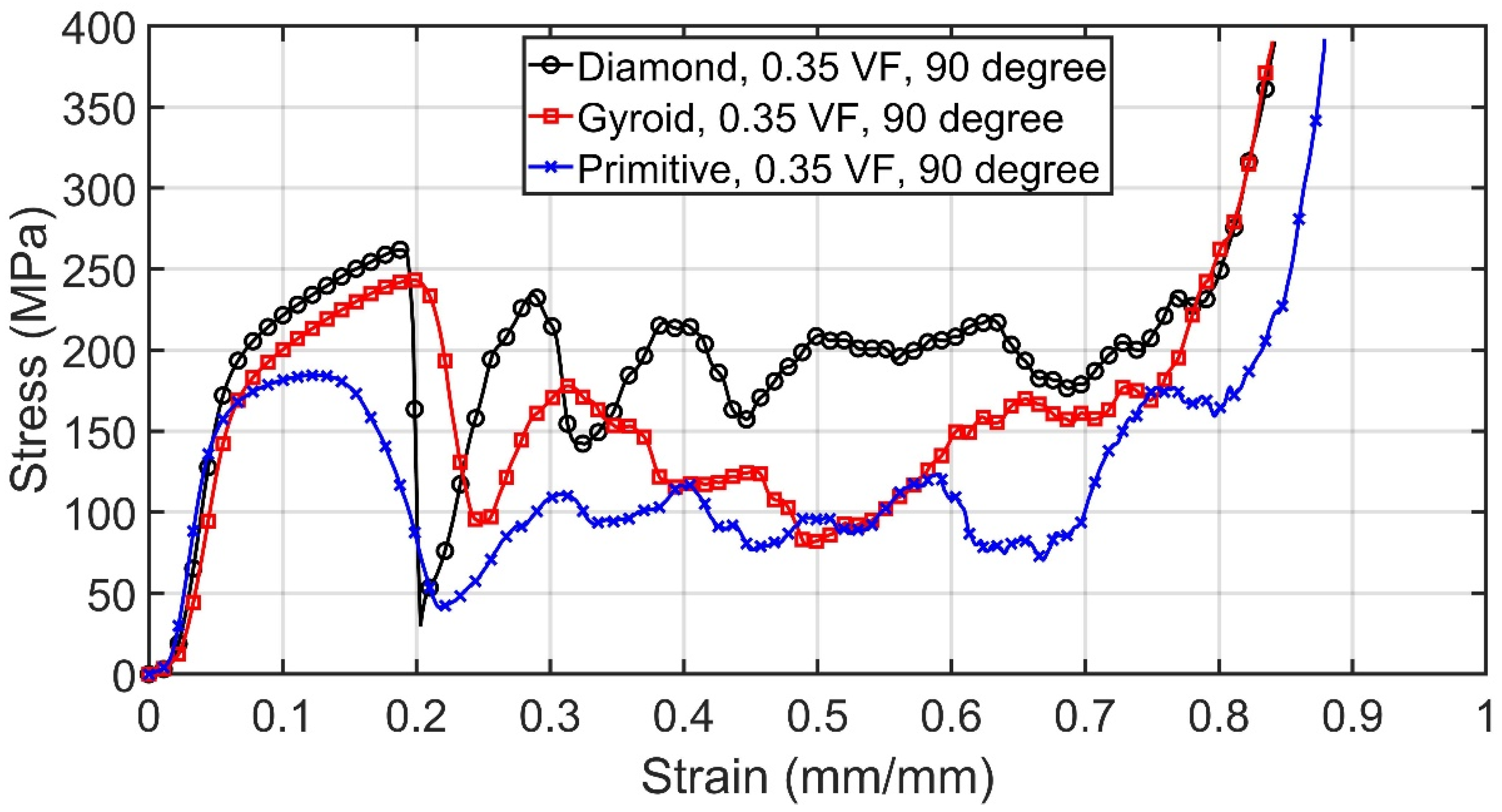
- All specimens (gyroid, diamond, and primitive) showed similar compressive behaviors. There was a rapid decrease in stress at the onset of yielding and stress fluctuated at the plateau regime. These fluctuations increased at higher volume fraction values.
- Diamond specimens outperformed in terms of yield stress and specific energy absorption when compared with gyroid and primitive specimens. This makes diamond structures good candidates for applications where higher strains are needed before plastic deformations [9].
- Regression analysis and related equations can be used for predicting mass, yield stress, elastic modulus, specific energy absorption, and the onset of densification values of TPMS specimens with intermediate volume fraction values. The present study showed that mass, yield stress, elastic modulus, specific energy absorption, and the onset of densification of TPMS lattices can be predicted with an error value less than 1.4%, 7.1%, 19.04%, 21.6%, and 13.4%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xi, H.; Zhou, Z.; Zhang, H.; Huang, S.; Xiao, H. Multi-morphology TPMS structures with multi-stage yield stress platform and multi-level energy absorption: Design, manufacturing, and mechanical properties. Eng. Struct. 2023, 294, 116733. [Google Scholar] [CrossRef]
- Bouakaz, I.; Dehkord, E.S.; Meille, S.; Schrijnemakers, A.; Boschini, F.; Preux, N.; Hocquet, S.; Geris, L.; Nolens, G.; Grossin, D.; et al. 3D printed triply periodic minimal surfaces calcium phosphate bone substitute: The effect of porosity design on mechanical properties. Ceram. Int. 2024, 50, 2623–2636. [Google Scholar] [CrossRef]
- Sauermoser-Yri, M.; Veldurthi, N.; Wölfle, C.H.; Svartvatn, P.J.; Hoem, S.O.F.; Lid, M.J.; Bock, R.; Palko, J.W.; Torgersen, J. On the porosity-dependent permeability and conductivity of triply periodic minimal surface based porous media. J. Mater. Res. Technol. 2023, 27, 585–599. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brant, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108–137. [Google Scholar] [CrossRef]
- Sefene, E.M. State-of-the-art of selective laser melting process: A comprehensive review. J. Manuf. Syst. 2022, 63, 250–274. [Google Scholar] [CrossRef]
- Gülcan, O.; Günaydın, K.; Çelik, A.; Yasa, E. Mechanical properties of laser powder bed fusion produced overhang parts with different support geometries: An experimental study. Prog. Addit. Manuf. 2023. [CrossRef]
- Gong, G.; Ye, J.; Chi, Y.; Zhao, Z.; Wang, Z.; Xia, G.; Du, X.; Tian, H.; Yu, H.; Chen, C. Research status of laser additive manufacturing for metal: A review. J. Mater. Res. Technol. 2021, 15, 855–884. [Google Scholar] [CrossRef]
- Zheng, X.; Fu, Z.; Du, K.; Wang, C.; Yi, Y. Minimal surface designs for porous materials: From microstructures to mechanical properties. J. Mater. Sci. 2018, 53, 10194–10208. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Yu, S.; Sun, J.; Bai, J. Investigation of functionally graded TPMS structures fabricated by additive manufacturing. Mater. Des. 2019, 182, 108021. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Borovinsek, M.; Krstulovic-Opara, L.; Rowshan, R.; Vesenjak, M.; Ren, Z. Development of novel hybrid TPMS cellular lattices and their mechanical characterization. J. Mater. Res. Technol. 2021, 15, 1318–1329. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Krstulović-Opara, L.; Rowshan, R.; Abu Al-Rub, R.K.; Vesenjak, M.; Ren, Z. Quasi-static and dynamic compressive behaviour of sheet TPMS cellular structures. Compos. Struct. 2021, 266, 113801. [Google Scholar] [CrossRef]
- Sokollu, B.; Gulcan, O.; Konukseven, E.I. Mechanical properties comparison of strut-based and triply periodic minimal surface lattice structures produced by electron beam melting. Addit. Manuf. 2022, 60, 103199. [Google Scholar]
- Gülcan, O.; Simsek, U.; Cokgunlu, O.; Özdemir, M.; Şendur, P.; Yapici, G.G. Effect of build parameters on the compressive behavior of additive manufactured CoCrMo lattice parts based on experimental design. Metals 2022, 12, 1104. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Al Mahri, S.; Santiago, R.; Lee, D.W.; Ramos, H.; Alabdouli, H.; Alteneiji, M.; Guan, Z.; Cantwell, W.; Alves, M. Evaluation of the dynamic response of triply periodic minimal surfaces subjected to high strain-rate compression. Addit. Manuf. 2021, 46, 102220. [Google Scholar]
- Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Babamiri, B.B.; Hazel, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical characterisation and numerical modelling of tpms-based gyroid and diamond Ti6Al4V scaffolds for bone implants: An integrated approach for translational consideration. Bioengineering 2022, 9, 504. [Google Scholar] [CrossRef]
- Teng, F.; Sun, Y.; Guo, S.; Gao, B.; Yu, G. Topological and mechanical properties of different lattice structures based on additive manufacturing. Micromachines 2022, 13, 1017. [Google Scholar] [CrossRef]
- Li, Z.; Nie, Y.; Liu, B.; Kuai, Z.; Zhao, M.; Liu, F. Mechanical properties of AlSi10Mg lattice structures fabricated by selective laser melting. Mater. Des. 2020, 192, 108709. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.-W.; Rowshan, R.; Abu Al-Rub, R.K. Functionally graded and multi-morphology sheet TPMS lattices: Design, manufacturing, and mechanical properties. J. Mech. Behav. Biomed. Mater. 2020, 102, 103520. [Google Scholar] [CrossRef]
- Available online: https://www.oraibkhitan.com/mslattice/ (accessed on 30 January 2023).
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive strain at the onset of the densification of cellular solids. J. Cell Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Günaydın, K.; Eren, Z.; Kazancı, Z.; Scarpa, F.; Grande, A.M.; Türkmen, H.S. In-plane compression behavior of anti-tetrachiral and re-entrant lattices. Smart Mater. Struct. 2019, 28, 115028. [Google Scholar] [CrossRef]
- Feng, G.; Wang, J.; Li, X.; Xiao, L.; Song, W. Mechanical behavior of Ti–6Al–4V lattice-walled tubes under uniaxial compression. Def. Technol. 2022, 18, 1124–1138. [Google Scholar] [CrossRef]
- Liu, J.; Guo, K.; Sun, J.; Sun, Q.; Wang, L.; Li, H. Compressive behavior and vibration-damping properties of porous Ti-6Al-4V alloy manufactured by laser powder bed fusion. J. Manuf. Process 2021, 66, 1–10. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Liu, F.; Li, Z.; Ma, Z.; Ren, Z. Mechanical and energy absorption characteristics of additively manufactured functionally graded sheet lattice structures with minimal surfaces. Int. J. Mech. Sci. 2020, 167, 105262. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Bubb, S.L.; Young, P.; Raymont, D. Evaluation of light-weight AlSi10Mg periodic cellular lattice structures fabricated via direct metal laser sintering. J. Mater. Process Technol. 2014, 4, 856–864. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Y.; Wang, D.; Xiao, Z.; Song, C.; Weng, C. Effect of heat treatment on the microstructure and mechanical properties of Ti6Al4V gradient structures manufactured by selective laser melting. Mater. Sci. Eng. A 2018, 736, 288–297. [Google Scholar] [CrossRef]
- Sun, Q.; Sun, J.; Guo, K.; Wang, L. Compressive mechanical properties and energy absorption characteristics of SLM fabricated Ti6Al4V triply periodic minimal surface cellular structures. Mech. Mater. 2022, 166, 104241. [Google Scholar] [CrossRef]
- Ran, Q.; Yang, W.; Hu, Y.; Shen, X.; Yu, Y.; Xiang, Y.; Cai, K. Osteogenesis of 3D printed porous Ti6Al4V implants with different pore sizes. J. Mech. Behav. Biomed. Mater. 2018, 84, 1–11. [Google Scholar] [CrossRef]
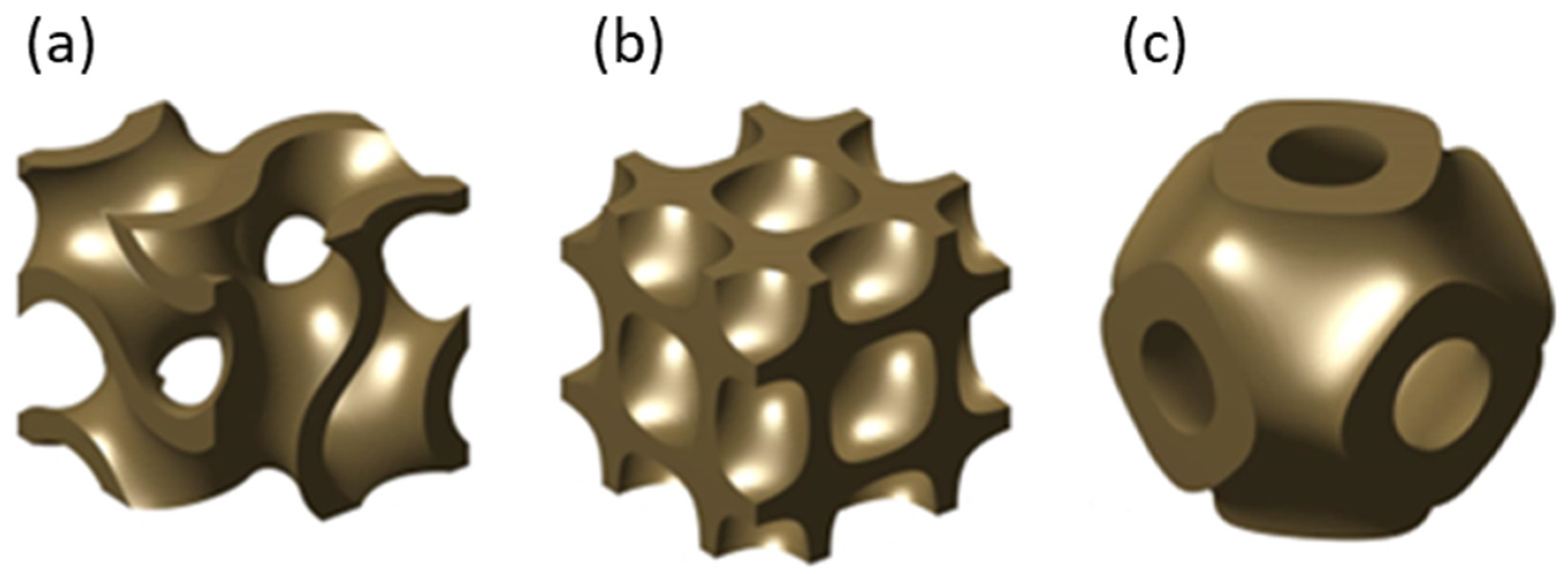



| TPMS Type | Mathematical Equations |
|---|---|
| Diamond | U = sin(kxx)sin(kyy)sin(kzz) + sin(kxx)cos(kyy)cos(kzz) + cos(kxx)sin(kyy)cos(kzz) + cos(kxx)cos(kyy)sin(kzz) − t |
| Gyroid | U = cos(kxx)sin(kyy) + cos(kyy)sin(kzz) + cos(kzz)sin(kxx) − t |
| Primitive | U = cos(x) + cos(y) + cos(z) − t |
| ki = 2πni/Li, where ki: k value in x, y, and z directions, ni: number of unit cells in x, y, and z directions, and Li: outer dimension of structure in x, y, and z directions. t: variable used to alter relative density. U: represents isosurface boundary between solid and void sections and needs to be zero to generate TPMS lattices. | |
| Specimen No | Build Orientation (°) | Volume Fraction | TPMS Type |
|---|---|---|---|
| 1 | 45 | 0.2 | Gyroid |
| 2 | 60 | 0.2 | Diamond |
| 3 | 90 | 0.2 | Primitive |
| 4 | 45 | 0.3 | Diamond |
| 5 | 60 | 0.3 | Primitive |
| 6 | 90 | 0.3 | Gyroid |
| 7 | 45 | 0.4 | Primitive |
| 8 | 60 | 0.4 | Gyroid |
| 9 | 90 | 0.4 | Diamond |
| Specimen No | Yield Stress (MPa) | Elastic Modulus (GPa) | Mass (g) | Specific Energy Absorption (J/g) | Onset of Densification (mm/mm) |
|---|---|---|---|---|---|
| 1 | 70.9 ± 1.4 | 2.87 ± 0.06 | 54.3 ± 1.1 | 35.8 ± 0.7 | 0.815 ± 0.016 |
| 2 | 88.4 ± 1.8 | 3.57 ± 0.07 | 54.9 ± 1.1 | 42.5 ± 0.9 | 0.745 ± 0.015 |
| 3 | 55.5 ± 1.1 | 2.06 ± 0.04 | 53.1 ± 1.1 | 19.7 ± 0.4 | 0.757 ± 0.015 |
| 4 | 170.5 ± 3.4 | 3.80 ± 0.08 | 80.7 ± 1.6 | 49.7 ± 1.0 | 0.772 ± 0.015 |
| 5 | 123.7 ± 2.5 | 3.20 ± 0.06 | 80.2 ± 1.6 | 26.5 ± 0.5 | 0.744 ± 0.015 |
| 6 | 144.9 ± 2.9 | 2.94 ± 0.06 | 80.6 ± 1.6 | 39.6 ± 0.8 | 0.792 ± 0.016 |
| 7 | 186.1 ± 3.7 | 7.67 ± 0.15 | 108.7 ± 2.2 | 40.6 ± 0.8 | 0.806 ± 0.016 |
| 8 | 197.0 ± 3.9 | 5.63 ± 0.11 | 106.8 ± 2.1 | 38.0 ± 0.8 | 0.705 ± 0.014 |
| 9 | 204.0 ± 4.1 | 6.74 ± 0.14 | 107.9 ± 2.2 | 52.3 ± 1.1 | 0.758 ± 0.015 |
| Strain (mm/mm) | Gyroid | Diamond | Primitive |
|---|---|---|---|
| 0 |  |  |  |
| 0.2 |  |  |  |
| 0.4 |  |  |  |
| 0.6 |  |  |  |
| 0.8 |  |  |  |
| Design Output | TPMS Type | Build Orientation | Equation |
|---|---|---|---|
| Mass (g) | Gyroid | 45° | 3.32 + 245.7xVF + 47.17xVF2 |
| Gyroid | 60° | 8.07 + 228.0xVF + 47.17xVF2 | |
| Gyroid | 90° | 2.55 + 246.0xVF + 47.17xVF2 | |
| Diamond | 45° | 2.70 + 245.7xVF + 47.17xVF2 | |
| Diamond | 60° | 7.45 + 228.0xVF + 47.17xVF2 | |
| Diamond | 90° | 1.93 + 246.0xVF + 47.17xVF2 | |
| Primitive | 45° | 2.83 + 245.7xVF + 47.17xVF2 | |
| Primitive | 60° | 7.58 + 228.0xVF + 47.17xVF2 | |
| Primitive | 90° | 2.06 + 246.0xVF + 47.17xVF2 | |
| Yield Stress (MPa) | Gyroid | 45° | −168.7 + 1453xVF − 1272xVF2 |
| Gyroid | 60° | −157.8 + 1396xVF − 1272xVF2 | |
| Gyroid | 90° | −131.3 + 1302xVF − 1272xVF2 | |
| Diamond | 45° | −150.8 + 1453xVF − 1272xVF2 | |
| Diamond | 60° | −139.9 + 1396xVF − 1272xVF2 | |
| Diamond | 90° | −113.3 + 1302xVF − 1272xVF2 | |
| Primitive | 45° | −191.4 + 1453xVF − 1272xVF2 | |
| Primitive | 60° | −180.5 + 1396xVF − 1272xVF2 | |
| Primitive | 90° | −154.0 + 1302xVF − 1272xVF2 | |
| Elastic Modulus (GPa) | Gyroid | 45° | 9.66 − 62.8xVF + 144.3xVF2 |
| Gyroid | 60° | 13.07 − 76.3xVF + 144.3xVF2 | |
| Gyroid | 90° | 8.84 − 63.0xVF + 144.3xVF2 | |
| Diamond | 45° | 9.65 − 62.8xVF + 144.3xVF2 | |
| Diamond | 60° | 13.06 − 76.3xVF + 144.3xVF2 | |
| Diamond | 90° | 8.83 − 63.0xVF + 144.3xVF2 | |
| Primitive | 45° | 9.70 − 62.8xVF + 144.3xVF2 | |
| Primitive | 60° | 13.11 − 76.3xVF + 144.3xVF2 | |
| Primitive | 90° | 8.88 − 63.0xVF + 144.3xVF2 | |
| Specific Energy Absorption (J/g) | Gyroid | 45° | 15.7 + 109.3xVF − 45.33xVF2 |
| Gyroid | 60° | 32.8 + 31.0xVF − 45.33xVF2 | |
| Gyroid | 90° | 11.8 + 106.2xVF − 45.33xVF2 | |
| Diamond | 45° | 21.0 + 109.3xVF − 45.33xVF2 | |
| Diamond | 60° | 38.1 + 31.0xVF − 45.33xVF2 | |
| Diamond | 90° | 17.1 + 106.2xVF − 45.33xVF2 | |
| Primitive | 45° | 4.1 + 109.3xVF − 45.33xVF2 | |
| Primitive | 60° | 21.2 + 31.0xVF − 45.33xVF2 | |
| Primitive | 90° | 0.2 + 106.2xVF − 45.33xVF2 | |
| Onset of Densification (mm/mm) | Gyroid | 45° | 0.774 + 0.307xVF − 0.5xVF2 |
| Gyroid | 60° | 0.842 − 0.143xVF − 0.5xVF2 | |
| Gyroid | 90° | 0.688 + 0.497xVF − 0.5xVF2 | |
| Diamond | 45° | 0.725 + 0.307xVF − 0.5xVF2 | |
| Diamond | 60° | 0.794 − 0.143xVF − 0.5xVF2 | |
| Diamond | 90° | 0.639 + 0.497xVF − 0.5xVF2 | |
| Primitive | 45° | 0.763 + 0.307xVF − 0.5xVF2 | |
| Primitive | 60° | 0.832 − 0.143xVF − 0.5xVF2 | |
| Primitive | 90° | 0.678 + 0.497xVF − 0.5xVF2 |
| Design Output | TPMS Type | Predicted | Tested | Error (%) |
|---|---|---|---|---|
| Mass (g) | Gyroid | 94.4 ± 1.9 | 93.8 ± 1.9 | 0.7 |
| Diamond | 93.8 ± 1.9 | 95.1 ± 1.9 | 1.4 | |
| Primitive | 93.9 ± 1.9 | 93.9 ± 1.9 | 0.1 | |
| Yield Stress (MPa) | Gyroid | 168.6 ± 3.4 | 157.4 ± 3.2 | 7.1 |
| Diamond | 186.6 ± 3.7 | 176.2 ± 3.5 | 5.9 | |
| Primitive | 145.9 ± 2.9 | 141.7 ± 2.8 | 2.9 | |
| Elastic Modulus (GPa) | Gyroid | 4.48 ± 0.09 | 5.14 ± 0.10 | 12.9 |
| Diamond | 4.47 ± 0.09 | 5.52 ± 0.11 | 19.1 | |
| Primitive | 4.52 ± 0.09 | 5.00 ± 0.10 | 9.7 | |
| Specific Energy Absorption (J/g) | Gyroid | 43.5 ± 0.9 | 39.9 ± 0.8 | 8.9 |
| Diamond | 38.4 ± 0.8 | 47.0 ± 0.9 | 18.4 | |
| Primitive | 31.9 ± 0.6 | 26.20 ± 0.52 | 21.6 | |
| Onset of Densification (mm/mm) | Gyroid | 0.80 ± 0.02 | 0.74 ± 0.02 | 8.6 |
| Diamond | 0.75 ± 0.02 | 0.75 ± 0.02 | 0.0 | |
| Primitive | 0.79 ± 0.02 | 0.70 ± 0.01 | 13.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şimşek, U.; Gülcan, O.; Günaydın, K.; Tamer, A. Prediction of Compressive Behavior of Laser-Powder-Bed Fusion-Processed TPMS Lattices by Regression Analysis. J. Manuf. Mater. Process. 2024, 8, 16. https://doi.org/10.3390/jmmp8010016
Şimşek U, Gülcan O, Günaydın K, Tamer A. Prediction of Compressive Behavior of Laser-Powder-Bed Fusion-Processed TPMS Lattices by Regression Analysis. Journal of Manufacturing and Materials Processing. 2024; 8(1):16. https://doi.org/10.3390/jmmp8010016
Chicago/Turabian StyleŞimşek, Uğur, Orhan Gülcan, Kadir Günaydın, and Aykut Tamer. 2024. "Prediction of Compressive Behavior of Laser-Powder-Bed Fusion-Processed TPMS Lattices by Regression Analysis" Journal of Manufacturing and Materials Processing 8, no. 1: 16. https://doi.org/10.3390/jmmp8010016
APA StyleŞimşek, U., Gülcan, O., Günaydın, K., & Tamer, A. (2024). Prediction of Compressive Behavior of Laser-Powder-Bed Fusion-Processed TPMS Lattices by Regression Analysis. Journal of Manufacturing and Materials Processing, 8(1), 16. https://doi.org/10.3390/jmmp8010016









