Abstract
Arc additive manufacturing (AAM) has the advantages of fast deposition speed and good surfacing quality. It is a promising additive manufacturing (AM) method. However, arc additive manufacturing is difficult to use widely in industry due to its poor deformation, microstructure, and mechanical properties. Since the mechanical properties of materials can be greatly improved by rolling, a method for configuration synthesis of the side-rolling mechanism by using metamorphic mechanism theory is presented in this paper. Firstly, by analyzing the operational demands of the side-rolling mechanism, we obtained the motion cycle diagram for the metamorphic mechanism in addition to the corresponding equivalent resistance gradient matrix. Secondly, according to the motion cycle diagram and equivalent resistance gradient matrix of the metamorphic mechanism, the structure and constraint form of the metamorphic joints were established, and the relationship between the force variation and the structure and the constraint form of the metamorphic joints was also obtained. Then, the structures of all 12 corresponding constrained metamorphic mechanisms were synthesized. Ultimately, one among the twelve mechanisms was chosen as the side-rolling metamorphic mechanism. The topological transformation of its working configuration was examined. The results confirmed the feasibility and practicality of the proposed structural synthesis method in this study.
1. Introduction
AM [1], also called 3D printing [2], has a high profile within the industry and the wider public. Several AM methods have been developed to fabricate metal parts, such as 3D welding [3], selective laser melting [4], selected laser sintering [5], laser-engineered net shaping [6], direct metal deposition [7], laminated object manufacturing [8], and electron beam melting [9,10]. An important aspect that is often overlooked is that material properties may be lower than those of conventional forged products, which may limit the applicability of the AM processes. In addition, the residual stress and deformation can be very serious, which may lead to parts being out of the tolerance range, affecting performance. In the field of welding, rolling is a very effective method to reduce residual stress and deformation [11]. Recently, this concept has been used by two organizations to manufacture components: One was adopted by Colegrove et al. [12] at Cranfield University in the UK. When the material is cooled to near-ambient temperature, it is applied between the passes of the additive manufacturing test block. This technique was applied to an AM wall between passes, where the material cooled to near-ambient temperature. The other example is that of Zhang et al. [13] from Huazhong University of Science and Technology, who adopted hybrid deposition and micro-rolling (HDMR) [14] technology, which is directly applied behind the deposition welding torch. Their purpose was to improve the microstructure and texture [15,16], properties [17], geometric structure [18], and residual stress and deformation of AM components [19]. Since the mechanical properties of materials can be greatly improved by rolling, a method for configuration synthesis of the side-rolling mechanism by using metamorphic mechanism theory is presented in this paper.
The metamorphic mechanism was discovered in the study of reconfigurable mechanisms in 1996 and was proposed as a new mechanism at the 25th American Society of Mechanical Engineers (ASME) Biannual Conference on Mechanism and Robotics in 1998 [20]. The configuration switching of the metamorphic mechanism is realized by switching the motion states of the metamorphic joints [21]. The proposal of a metamorphic mechanism brings vitality to traditional mechanism science [22]. At present, the comprehensive research on the configuration of metamorphic mechanisms pays more attention to the source metamorphic mechanisms and their topological transformation [23,24,25]. However, starting from the same source metamorphic mechanism, research on the accessory form/structure of the metamorphic joints and their corresponding metamorphic configurations is rare.
This study embraces the concept of active–passive compound drive [26,27], employing a driving methodology that amalgamates an active motor with passive components. According to the special operation and technical background of side rolling, it comprehensively considers the requirements of multi-degrees of freedom, underactuated operation, specific movement requirements, and special operating conditions. A two-degree-of-freedom (2-DOF) metamorphic mechanism was designed based on the principles of metamorphosis, with the intention to function as a side-rolling metamorphic mechanism.
The innovations of this paper include the following:
- Under drive, the side-rolling mechanism adopts the principle of metamorphic transformation, and only one drive can be realized when unilaterally rolling, which simplifies the driving and control system and increases the practicability;
- A method of configuration synthesis of the side-rolling metamorphic mechanism is herein proposed. By establishing the configuration matrix of the side-rolling metamorphic mechanism, all 12 structural forms of constraint metamorphic motion pairs and their corresponding theoretical configurations of the metamorphic mechanism are summarized. According to the principle of high reliability and simple structure, one of them is selected as the side-rolling metamorphic mechanism;
- The method of composite manufacturing and constant pressure control is used in the forming process of the additive material. In addition to making the side roll and the welding gun move synchronously, the side roll applies the rated rolling force to the weld bead, and the constant pressure control method is also used so that the mechanism can react and adjust in time under the condition of overload, so the mechanism can work smoothly.
The rest of this paper is organized as follows: In Section 2, the design of a 2-DOF planar-constrained metamorphic mechanism according to the special task requirements of the side-rolling mechanism is described. Section 3 introduces the metamorphic mode of the metamorphic mechanism, the structure and constraint form of the metamorphic joint, the equivalent resistance gradient sketch of metamorphic joints, and the structural topology matrixes of the metamorphic mechanism. In Section 4, the selection of the metamorphic mechanism is introduced, and its working configuration is analyzed. In Section 5, combined with the rolling target, the key structural parameters of the side-rolled metamorphic mechanism are determined, and the kinematic analysis and dynamic simulation of the mechanism are carried out. Finally, Section 6 concludes this paper and gives an outlook for our future work.
2. Materials and Methods
In this paper, a design method of a side-rolling mechanism is proposed by combining the design idea of an underactuated mechanism and a metamorphic mechanism, and its flow diagram is shown in Figure 1. An underactuated mechanism is defined as one in which the number of actuators is fewer than the degrees of freedom [28]. Firstly, the motion requirements and working conditions of the side-rolling mechanism were briefly introduced, and a 2-DOF planar constraint mechanism was designed. Then, we used the motion cycle diagram to describe the working-state transition of the 2-DOF planar constraint metamorphic mechanism and obtain the equivalent resistance gradient sketch. The equivalent resistance matrix was used to describe the equivalent resistance gradient sketch. By analyzing the relationship between the constraining configurations of metamorphic joints and the corresponding resistance matrices, we established the structural topology matrix of the constrained metamorphic mechanism.
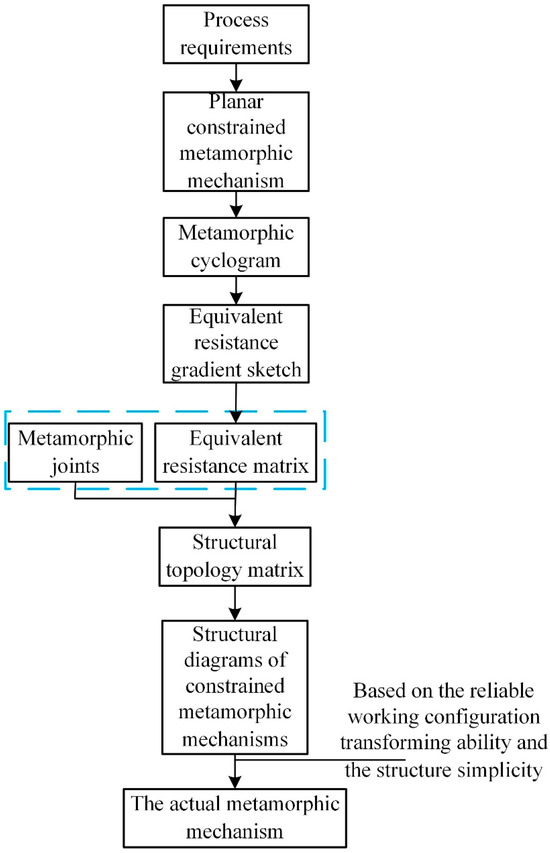
Figure 1.
Designing a lateral-rolling mechanism inspired by metamorphic principle.
Finally, according to the structural topological matrix, a variety of corresponding constrained metamorphic mechanisms were designed to satisfy the side-rolling operation. Based on the reliability of configuration conversion and the simplicity of the structure, the final metamorphic mechanism was selected.
2.1. Functional Requirements
In line with the functional requirements of the mechanism, the lateral-rolling mechanism proposed in this study possesses a 2-DOF metamorphic mechanism. When the mechanism starts to move, the two links adjacent to the spring are fixed together under the constraint of the spring. At this time, the number of links in the mechanism changes, and the mechanism is one degree of freedom. When one of the links adjacent to the spring and the frame becomes one, the other link breaks free from the constraint of the spring force and starts to move; at this time, the mechanism also has a degree of freedom. Due to the special operating conditions, it is required to reduce the weight of the drive and simplify the control system. Therefore, only one actuator is used in the 2-DOF-constrained metamorphic mechanism.
2.2. The Design of the Metamorphic Mechanism for Side Rolling
Nine structural forms of extended class II Assur groups were proposed in the reference [25], and the composition principle of constrained metamorphic mechanism based on extended Assur groups was also proposed. According to the kinematic requirements and operating conditions, a metamorphic mechanism with 2-DOF and two rotationally constrained metamorphic joints were designed, as shown in Figure 2. The mechanism consists of an extended Assur group (RRRR) successively connected to the driving link and the frame, where A, B, C, D, and E are the serial numbers of the joints in the mechanism.
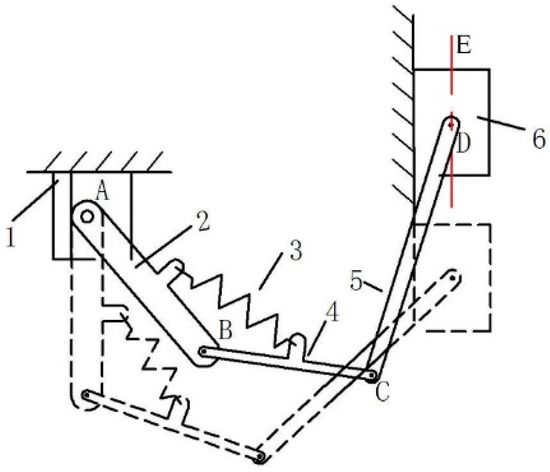
Figure 2.
Assembly drawing of the planar-constrained metamorphic mechanism with two degrees of freedom. 1, frame; 2, link 2; 3, spring; 4, link 4; 5, link 5; 6, drive link.
We assume that the horizontal axis represents the driver’s displacement (either the turning angle or the moving distance) and that the vertical axis denotes the operational states of the joints (where it signifies the revolute joint or denotes the prismatic joint) during the corresponding operational stages [29]. Then, the working-state transition of the metamorphic mechanism can be described by the motion cycle diagram, as shown in Figure 3 [30].
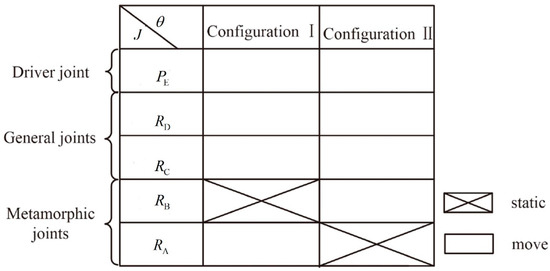
Figure 3.
Chart illustrating the motion cycle of constrained metamorphic mechanisms.
The figure shows the driving link moving along the screw under the drive of the motor and the different working states of all the moving joints in different working stages. When working in configuration I, there is no relative rotation between the two connected links at point B due to the effect of spring preload and geometric position constraints. When working in configuration II, becomes a part of the frame, and the link will overcome the resistance of spring 3 and start to rotate around the joint .
3. The Structural Topology Matrix of the Side-Rolling Metamorphic Mechanism
The main task of the design of the metamorphic mechanism is the design of the metamorphic joint. The metamorphic mode realizes the conversion between configurations by metamorphic joint, and the design of the metamorphic joint is the basis of the configuration synthesis of the metamorphic mechanism.
3.1. The Mode of the Metamorphic Process Used by the Metamorphic Mechanism
There are three main modes of metamorphic transformation. The first is the combination and separation of components in the mechanism. The second is that the properties of the components in the mechanism change; for example, the switch between rigidity and flexibility can be realized by changing the material of the components. The third is that the number and attributes of metamorphic joints in the mechanism change.
3.2. Constrained Metamorphic Joints
Reference [30] offers a comprehensive overview of various metamorphic kinematic joints and delineates the relationships among the variations exhibited by their components, as illustrated in Figure 4.
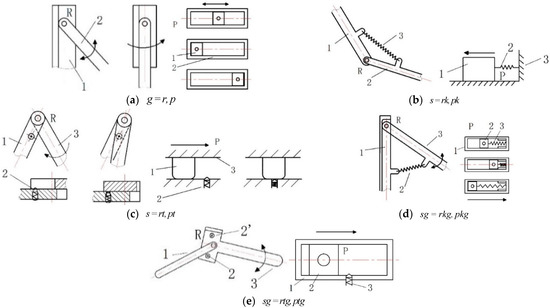
Figure 4.
Several types of metamorphic kinematic joints.
Figure 4a illustrates a metamorphic kinematic joints constrained geometrically and featuring mechanical hard stops. Figure 4b,c display metamorphic kinematic joints constrained by force, specifically governed by spring force control. Figure 4d,e depict metamorphic kinematic joints subject to both geometric and force constraints.
3.3. The Gradient of Equivalent Resistance for the Constrained Metamorphic Joints
In the operation of the metamorphic mechanism, each configuration is associated with a specific metamorphic joints that engages in relative movement, while the remaining metamorphic joints stay fixed. Utilizing the equivalent resistance gradient model outlined in Figure 3 and detailed in reference [31], we present the equivalent resistance gradient diagram for a 2-DOF metamorphic mechanism in Figure 5. The term denotes the equivalent resistance gradient coefficient, defined as the ratio between the constraint force exerted by the metamorphic joint and the actual force encountered during the specific working configuration; signifies the angle of rotation or displacement [30].
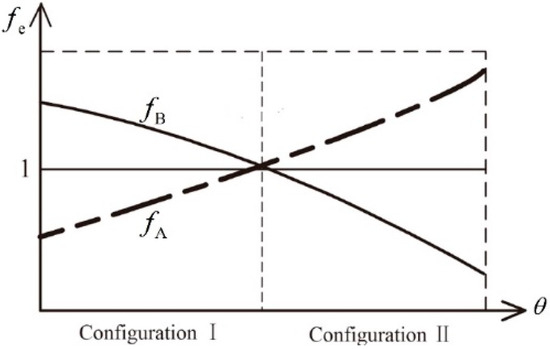
Figure 5.
Equivalent resistance gradient sketch of the metamorphic mechanism.
The equivalent resistance gradient sketch for metamorphic joints can be represented by a matrix, specifically the equivalent resistance matrix [30]. Here, the working configurations are depicted in the matrix’s columns, while the rows display the constrained states of metamorphic joints under various working configurations, with indicating that metamorphic joint remains constrained and 0 signifying that joint continues to function.
As in (1), is , and is ; they are constrained.
3.4. The Structural Topology Matrix of the Metamorphic Mechanism
To build the connection between constrained structures of metamorphic joints and their equivalent resistance matrixes corresponding with working stages, the structural topology matrix of constrained metamorphic mechanism and the constrained structures matrix of constrained metamorphic joints are built:
In matrix C, the columns correspond to the working configurations, and the rows correspond to the constrained structures matrix of metamorphic joints [30]. When compared to the constrained structures depicted in the rows of (2) from Figure 4, the matrix for the constrained structures of metamorphic joints can be inferred:
By substituting Equation (3) into Equation (2), we obtain the structural topology matrix for the constrained metamorphic mechanism:
According to (4), twelve structural topology matrices can be derived:
- , , , , , , , , , , , .
There are twelve constrained structures of metamorphic joints for metamorphic mechanisms, which theoretically can result in the design of twelve corresponding constrained metamorphic mechanism configurations to meet the lateral-rolling operations.
4. Analysis of Structural Design and Operational Configurations for Side-Rolling Constrained Metamorphic Mechanisms
4.1. Structural Diagram of the Constrained Metamorphic Mechanism
According to Equation (4), the structural diagrams of 12 kinds of side-rolling constrained metamorphic mechanisms are shown in Figure 6.
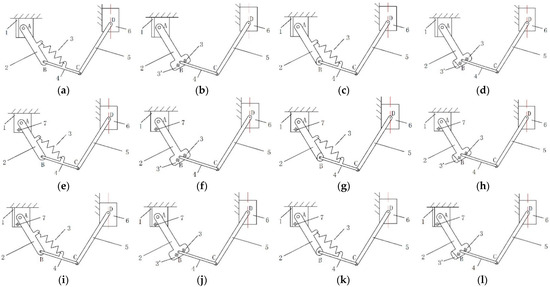
Figure 6.
Structural diagrams of side rolling constrained metamorphic mechanisms.
4.2. Design and Topological Transformation of Constrained Metamorphic Mechanism for Side Rolling
The selection of the structure for the side-rolling mechanism hinges on the reliability of the ability to transform the working configuration and the structural simplicity. Guided by this rationale, both mechanisms shown in Figure 6c and Figure 6d can achieve a reliable metamorphic process at joint B. The mechanism shown in Figure 6c was selected as the actual side-rolling metamorphic mechanism given that its joint exhibits greater simplicity compared to that depicted in Figure 6d.
As shown in Figure 6a,b, there are only spring force constraints but no geometric constraints at the joint of the mechanism, which deselects them. Since the form combinations of the metamorphic joints at joint A controlled by the spring force are not as reliable as that of Figure 6c in the configuration transformation, the mechanisms of Figure 6e–h were not considered. When it comes to Figure 6i–l, the structural simplicity of joint is not as good as that of Figure 6c, and they were not considered for selection.
The mechanism in Figure 6c was selected as the actual metamorphic mechanism for side rolling. The joint has a spring force constraint and geometric constraint, while the joint A has a geometric constraint. Considering the symmetrical operation of the actual mechanism, the actual side-rolling mechanism was finally designed, and the motion diagram of the mechanism is shown in Figure 7. The lateral-rolling mechanism is a planar seven-link mechanism, which consists of two parts: One part is a Class II link group composed of link 7 and slider 8; the other part is the side-rolling metamorphic mechanism as shown in Figure 6c, which is a five-link mechanism composed of link 2, link 4, link 5, driving link 6, and frame 1 in the x-y plane. The slider moves horizontally along the guide rail.
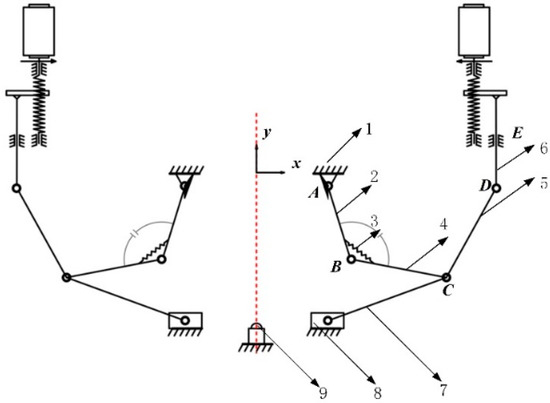
Figure 7.
Schematic diagram of double-sided rolling metamorphic mechanism. 1, frame; 2, link 2; 3, spring; 4, link 4; 5, link 5; 6, drive link; 7, link 7; 8, side-rolling slider; 9, substrate and weld bead.
4.3. Analysis of Working Configuration of Mechanism for Side Rolling
The side-rolling mechanism is driven by a drive motor, and the power is transmitted through the ball screw pair, driving the drive link to linear motion.
When in the working configuration I, as shown in Figure 7, there is no relative rotation between link 2 and link 4 at the joint due to the action of spring preload and geometric position constraints; at this time, the link , link 5, the driving link 6, and the frame 1 constitute a four-link mechanism. In this configuration, the degree of freedom of the mechanism is one. As the driving link moves down under the drive of the motor, the slider moves towards the weld bead.
When in working configuration II, as shown in Figure 8, link 2 becomes a part of the frame due to the constraints of the geometric limit at the frame, and link 4 will overcome the resistance of spring 3 and begin to rotate at the joint ; at this time, the link , link 5, the driving link 6, and the frame 1 constitute a four-link mechanism. In this configuration, the degree of freedom of the mechanism is one. As the driving link moves down under the drive of the motor, the slider moves towards the weld bead, making contact with the weld at some point and rolling against the pass.
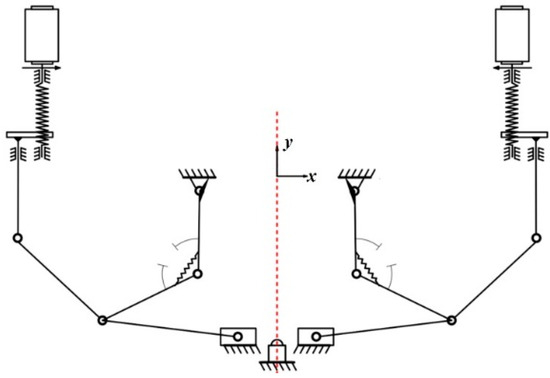
Figure 8.
Work-phase configuration when link 2 is constrained by geometric constraints.
5. Evaluations and Results
In this section, we detail how the specific structure size of the metamorphic mechanism of side rolling was determined first. Then, the kinematic analysis of the two configurations of the mechanism was carried out. Finally, Solidworks software 2022 was used to model and assemble the side-rolling metamorphic mechanism, and the mechanism was imported into Adams software 2019 for dynamic simulation, which verified the effectiveness of the design theory and method proposed in this paper.
5.1. A Dimensional Parameter of the Mechanism for Side Rolling
Taking the compactness of the metamorphic mechanism as the design basis, the key structural parameters of the side-rolling mechanism were preliminarily determined as shown in Table 1. In addition, the three-dimensional model of the side-rolling mechanism is shown in Figure 9. The optimization process for the mechanism’s dimensional parameters is thoroughly detailed in reference [32] and thus will not be reiterated herein. An objective function approach was employed with the aim of minimizing the motor torque subject to the specified rolling force.

Table 1.
Structural parameters of the side-rolling metamorphic mechanism.
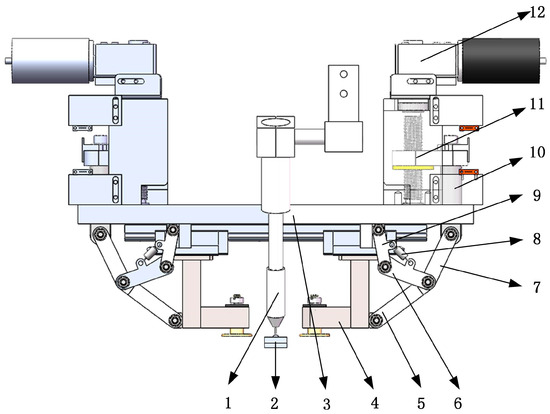
Figure 9.
Schematic diagram of double-sided rolling metamorphic mechanism. 1, welding gun; 2, substrate and weld bead; 3, frame; 4, side-rolling slider; 5, link 4; 6, link 2; 7, link 3; 8, spring; 9, link 1; 10, drive link; 11, ball screw pair; 12, drive motor.
5.2. Position Analysis of Metamorphic Mechanism for Side Rolling
The side-rolling metamorphic mechanism is composed of two symmetrical planar five-link mechanisms, so only one-half of it needs to be analyzed; for example, we can analyze the right half. To analyze the movement of the side-rolling metamorphic mechanism in the moving process, the states of the moving phase are divided into configuration I and configuration II. The commonly used kinematics analysis methods include the vector method, matrix method, spinor method, and influence coefficient method. For the planar mechanism, the vector method is more suitable, so this paper adopts the vector method for kinematics analysis.
5.2.1. Kinematics Modelling in Configuration I
As shown in Figure 10, a plane coordinate system of working configuration I was established with the lower end face of the slider, the central axis along the guide rail as the axis, and the central axis of the driving link as the axis. The and axes intersect at . The active link is simplified as a slider, its downward movement speed is , and the motion law of the slider is , where is a fixed value, which is the initial position of the slider. represents the link length, i.e., . represents the angle between the positive direction of the axis and . The angle is positive in the counterclockwise direction and negative in the clockwise direction. When the mechanism remains in the configuration I, the degree of freedom of the mechanism is one. , , and are known; is the input parameter; , , , and are unknown; and the angle between and is relatively fixed, in which case .
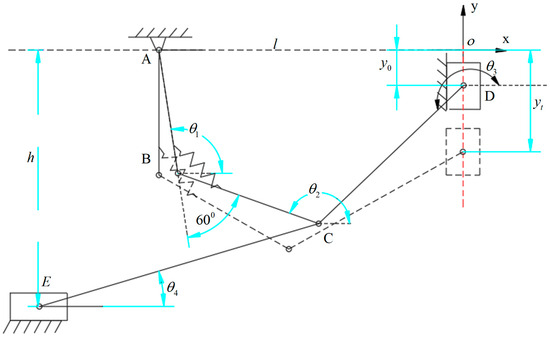
Figure 10.
Schematic diagram of the right half of the side-rolling metamorphic mechanism in configuration I.
The module lengths of , , , , , and are, respectively, , , , , , and . For closed-loop , the closed-loop vector equation can be obtained:
It is derived from Euler’s equations:
Subtracting from (6) gives the following:
The following can be can be solved from (7):
In the equation above, the following is true:
We substitute Equation (8) into Equation (6) to obtain the following:
For closed-loop , the closed-loop vector equation can be obtained:
It is derived from Euler’s equations:
The following can be solved from (11):
5.2.2. Kinematics Modelling in Configuration II
As shown in Figure 11, when the mechanism remains in configuration II, due to the geometric limit, becomes a part of the frame, and . When the mechanism is kept in configuration II, the degree of freedom of the mechanism is one. , , and are known; is the input parameter; , , and are unknown.
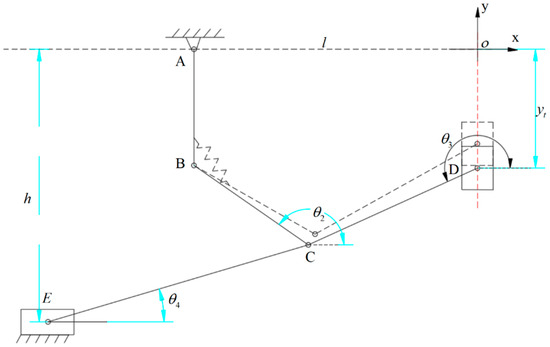
Figure 11.
Schematic diagram of the right half of the side-rolling metamorphic mechanism in configuration II.
For closed-loop , the closed-loop vector equation can be obtained:
It is derived from Euler’s equations:
Subtracting from (14) yields the following:
The following can be solved from (15):
In the equation above, the following is true:
We substitute Equation (16) into Equation (14) to obtain the following:
For closed-loop , the closed-loop vector equation can be obtained:
It is derived from Euler’s equations:
The following can be solved from (19):
According to Equations (5)–(20), the relationship between and is shown in Figure 12. The value of the key kinematic parameters is listed in Table 2.
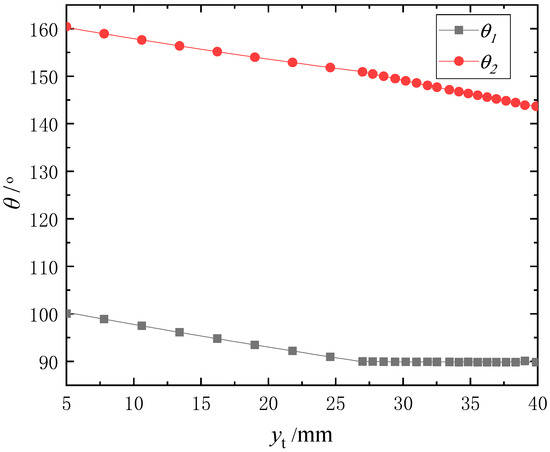
Figure 12.
The correlation of and in two different configurations.

Table 2.
The crucial kinematic parameters transitioning from configuration I to configuration II.
5.3. Dynamic Simulation and Experimental Verification of side-Rolling Metamorphic Mechanism
In this section, we describe how the three-dimensional model of the lateral-rolling mechanism was established by using Solidworks software 2022, and the kinematics simulation of the full configuration of the lateral-rolling mechanism was carried out to provide a basis for experimental verification.
The whole working process of the side-rolling mechanism is shown in Figure 13. When working, the drive motor is driven by the ball screw pair to drive the drive link to linear movement. Figure 13a shows the configuration I. At this point, and are held together by a spring and geometric limit. Figure 13b shows the switch between configurations in which contacts the geometric limit on the frame and becomes part of the frame. Figure 13c shows the configuration II. At this time, with the movement of the driving link, begins to rotate around the joint between and after overcoming the spring resistance, thereby driving to further move and pushing the side-rolling slider to further move.
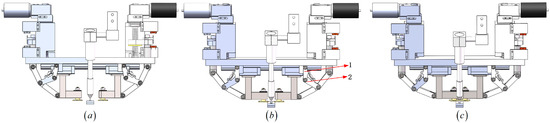
Figure 13.
The whole working process of the side-rolling mechanism: (a) configuration I; (b) switching position between configurations; (c) configuration II.
In the above part, we mainly analyzed the motion of the mechanism in SolidWorks software 2022 without considering the forces related to the motion of the mechanism. For the whole mechanism, since there is no other load except gravity and the self-locking property of the ball screw, all members of the mechanism are considered to be in force balance at any moment in configuration I to configuration II. Due to the symmetry of the side-rolling mechanism, we only needed to study the right part of the mechanism when conducting the dynamics simulation in Adams software. To improve the stability of the flexible system, we determined the stiffness of the spring should be appropriately increased. The spring stiffness was 6.77 N/mm, and the original length was 41.5 mm; the driving rod speed mm/s was used as the driving force for dynamic simulation. The parameters of the spring are shown in Table 3.

Table 3.
The spring parameters.
The variation of the spring force during the whole movement of the mechanism is shown in Figure 14. It can be seen from the figure that the value of spring force gradually increased linearly from t = 21.3 s, indicating that the elastic body began to stretch, and the movement of the mechanism conformed to the predetermined scheme.
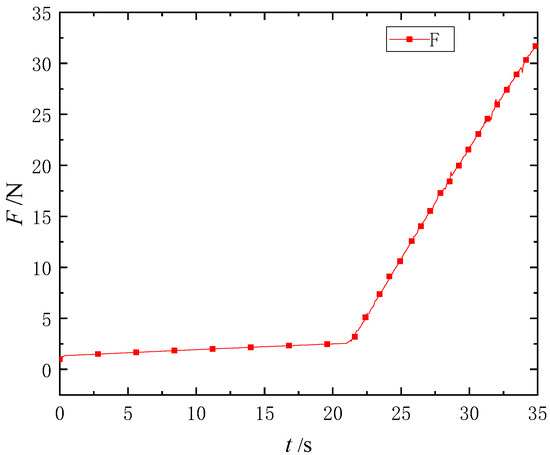
Figure 14.
The variation of spring force during the whole movement of the mechanism.
In reality, to acquire the rolling force in real time, a pressure sensor was installed on the side-rolling slider, as shown in Figure 15a. Through the sensor feedback rolling force parameters, the rolling process constant-pressure closed-loop control was realized. The target load of rolling was set on the upper computer, and the rolling quantity of molten deposit was obtained by controlling the rolling force. According to the technical indicators, installation size, operating environment, and other factors, the NTJH-10 micro-pressure sensor was selected. The pressure sensor adopted a miniature load pressure sensor, as shown in Figure 15b; the range of the sensor is 0.1~30 kN, and the specific parameters are shown in the following Table 4. The substrate material used in this study is low-carbon steel Q235, with the selected wire material being a 1.2 mm diameter welding wire ER50-6. Based on the lateral-rolling mechanism designed in this paper, a lateral rolling force of 3000 N was applied to the side of the formed weld bead. To verify the effectiveness of the rolling mechanism, comparative experiments were conducted between free fusion and lateral-rolling processes, focusing primarily on comparisons in terms of morphology and mechanical properties: (1) As shown in Figure 16, the weld seam sides produced by the direct lateral-rolling process were greater even compared to those produced by free fusion welding. (2) In terms of mechanical properties, the average tensile strength of the specimens formed by free fusion was 507 Mpa, while that of the specimens formed by direct lateral rolling was 578 Mpa, marking a 14% improvement over the free fusion process. The experimental results indicate that this study has both theoretical and practical implications for the engineering application of arc additive manufacturing technology.
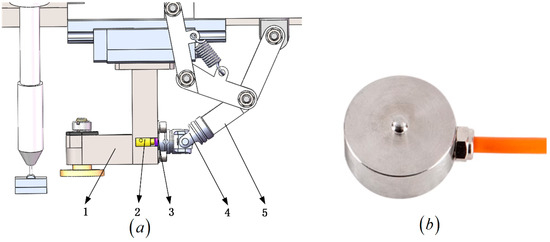
Figure 15.
Pressure sensor installation drawing. (a) 1, side-rolling slider; 2, pressure sensor; 3, pressure sensor pressing block; 4, universal joint; 5, link. (b) The miniature load pressure sensor.

Table 4.
The miniature load pressure sensor parameter table.

Figure 16.
The morphologies of the two processes are compared as follows: (a) free deposition forming pass; (b) the side of the pass is rolled.
6. Conclusions
This study focuses on the implementation of the auxiliary lateral-rolling process in arc additive manufacturing, incorporating the principles of planar mechanism design, and it proposes a comprehensive strategy for configuring the lateral-rolling mechanism. The research findings and conclusions are as follows:
- A comprehensive configuration approach for underactuated side-rolling metamorphic mechanisms is herein presented. This was achieved through the creation of a configuration matrix for the lateral-rolling mechanism. From a comprehensive analysis, the structural forms of all 12 constrained metamorphic joints were derived, along with their corresponding 12 theoretical mechanism configurations. Considering the reliability of structural transformation capability and structural simplicity, one type was selected as the side-rolling metamorphic mechanism;
- A kinematic analysis was conducted on both configurations of the mechanism. Using SolidWorks software 2022, a 3D model of the lateral-rolling mechanism was constructed. Furthermore, a kinematic simulation was executed on the complete configuration of the lateral-rolling mechanism. Finally, a dynamic simulation of the mechanism was conducted using Adams software 2019. The accuracy of the mechanism’s motion was validated via the spring force process;
- The performance of the rolling mechanism was evaluated through comparative experiments between free fusion and lateral-rolling processes, focusing particularly on morphological and mechanical aspects. Experimental results showed that the weld beads generated by the upright lateral rolling process exhibited smoother surfaces than those produced by the free fusion process. Regarding mechanical properties, a significant difference was observed: The average tensile strength of samples formed by the free fusion process was 507 Mpa, whereas that of samples formed by the upright lateral-rolling process was 578 Mpa, representing a 14% increase in strength in comparison with the free fusion method.
This paper focuses exclusively on the structural synthesis and design of a two-degree-of-freedom (2-DOF) constrained metamorphic mechanism. It provides a novel approach to designing lateral-rolling mechanisms and lays out new insights for the analysis and design of subsequent multi-degrees-of-freedom (multi-DOF) metamorphic mechanisms.
The primary limitations of this study stem from the limited number of components considered. Future research is imperative for metamorphic mechanisms with a larger number of components and degrees of freedom. Additionally, it is necessary to expand the innovative design methods of the metamorphic mechanism, which could be utilized in the design research of limb rehabilitation robots.
Author Contributions
Conceptualization, L.S.; methodology, L.S.; software, L.S.; validation, Y.W.; formal analysis, L.S.; investigation, L.S.; resources, H.Z.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, L.S. and Y.W.; visualization, L.S.; supervision, H.Z.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hubei Science and Technology Innovation Talent Plan, grant number 2023DJC053.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mueller, B. Additive manufacturing technologies-rapid prototyping to direct digital manufacturing. Assem. Autom. 2012, 32. [Google Scholar] [CrossRef]
- Sachs, E.; Cima, M.; Williams, P.; Brancazio, D.; Cornie, J. Three-dimensional printing: Rapid tooling and prototypes directly from a CAD Model. J. Manuf. Sci. Eng. 1992, 114, 481–488. [Google Scholar] [CrossRef]
- Petrik, J.; Sydow, B.; Bambach, M. Beyond parabolic weld bead models: AI-based 3D reconstruction of weld beads under transient conditions in wire-arc additive manufacturing. J. Mater. Process. Technol. 2022, 302, 117457. [Google Scholar] [CrossRef]
- Pelevin, I.A.; Ozherelkov, D.Y.; Chernyshikhin, S.V.; Nalivaiko, A.Y.; Gromov, A.A.; Chzhan, V.B.; Tereshi-na, I.S. Selective laser melting of Nd-Fe-B: Single track study. Mater. Lett. 2022, 315, 131947. [Google Scholar] [CrossRef]
- Lupone, F.; Padovano, E.; Casamento, F.; Badini, C. Process Phenomena and Material Properties in Selective Laser Sintering of Polymers: A Review. Materials 2022, 15, 183. [Google Scholar] [CrossRef]
- Durejko, T.; Łazńska, M. Characterization of Cobalt-Based Stellite 6 Alloy Coating Fabricated by Laser-Engineered Net Shaping (LENS). Materials 2021, 14, 7442. [Google Scholar] [CrossRef]
- Kumar, S.P.; Elangovan, S.; Mohanraj, R.; Narayanan, V.S. Significance of continuous wave and pulsed wave laser in direct metal deposition. Mater. Today Proc. 2021, 46, 8086–8096. [Google Scholar] [CrossRef]
- Flora, F.; Pinto, F.; Meo, M. Manufacturing and characterisation of a new thermal pre-stressed carbon fibre-reinforced lattice core for sandwich panels. J. Compos. Mater. 2022, 56, 1233–1254. [Google Scholar] [CrossRef]
- Cormier, D.; Harrysson, O.; West, H. Characterization of H13 steel produced via electron beam melting. Rapid Prototyp. J. 2003, 10, 35–41. [Google Scholar] [CrossRef]
- Heinl, P.; Müller, L.; Körner, C.; Singer, R.F.; Müller, F.A. Cellular Ti–6Al–4V structures with interconnected macro porosity for bone implants fabricated by selective electron beam melting. Acta Biomater. 2008, 4, 1536–1544. [Google Scholar] [CrossRef]
- Coules, H.E.; Colegrove, P.; Cozzolino, L.D.; Wen, S.W.; Kelleher, J.F. High pressure rolling of low carbon steel weld seams: Part 2–Roller geometry and residual stress. Sci. Technol. Weld. Join. 2013, 18, 84–90. [Google Scholar] [CrossRef]
- Colegrove, P.A.; Coules, H.E.; Fairman, J.; Martina, F.; Kashoob, T.; Mamash, H.; Cozzolino, L.D. Microstructure and residual stress improvement in wire and arc additively manufactured parts through high-pressure rolling. J. Mater. Process. Technol. 2013, 213, 1782–1791. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Wang, G.; Zhang, Y. Hybrid direct manufacturing method of metallic parts using deposition and micro continuous rolling. Rapid Prototyp. J. 2013, 19, 387–394. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.; Wang, G.; Bai, X.; Fu, Y.; Zhao, J. Simulation of microstructure evolution during hybrid deposition and micro-rolling process. J. Mater. Sci. 2016, 51, 6735–6749. [Google Scholar] [CrossRef]
- Donoghue, J.; Antonysamy, A.A.; Martina, F.; Colegrove, P.A.; Williams, S.W.; Prangnell, P.B. The effectiveness of combining rolling deformation with Wire-Arc Additive Manufacture on β-grain refinement and texture modification in Ti–6Al–4V. Mater. Charact. 2016, 114, 103–114. [Google Scholar] [CrossRef]
- Martina, F.; Colegrove, P.A.; Williams, S.W.; Meyer, J. Microstructure of interpass rolled wire+ arc additive manufacturing Ti-6Al-4V components. Metall. Mater. Trans. A 2015, 46, 6103–6118. [Google Scholar] [CrossRef]
- Martina, F. Investigation of Methods to Manipulate Geometry, Microstructure and Mechanical Properties in Titanium Large Scale Wire + Arc Additive Manufacturing. PhD Thesis, Cranfield University, Cranfield, UK, 2014. [Google Scholar]
- Xie, Y.; Zhang, H.; Zhou, F. Improvement in geometrical accuracy and mechanical property for arc-based additive manufacturing using metamorphic rolling mechanism. J. Manuf. Sci. Eng. 2016, 138, 111002. [Google Scholar] [CrossRef]
- Martina, F.; Roy, M.J.; Szost, B.A.; Terzi, S.; Colegrove, P.A.; Williams, S.W.; Hofmann, M. Residual stress of as-deposited and rolled wire+ arc additive manufacturing Ti–6Al–4V components. Mater. Sci. Technol. 2016, 32, 1439–1448. [Google Scholar] [CrossRef]
- Dai, J.S.; Rees Jones, J. Mobility in metamorphic mechanisms of foldable/erectable kinds. J. Mech. Des. 1999, 121, 375–382. [Google Scholar] [CrossRef]
- Dai, J.S.; Zhang, Q.X. Metamorphic mechanisms and their configuration models. J. Mech. Eng. 2000, 13, 212–218. [Google Scholar] [CrossRef]
- Yan, H.S.; Kuo, C.H. Topological representations and characteristics of variable kinematic joints. J. Mech. Des. 2006, 128, 384–391. [Google Scholar] [CrossRef]
- Li, S.J.; Dai, J.S. The equivalent resistance gradient model of metamorphic mechanisms and the design approach. In Advances in Reconfigurable Mechanisms and Robots I; Springer: London, UK, 2012; pp. 53–62. [Google Scholar]
- Li, S.J. Structure of metamorphic mechanisms based on augmented Assur groups. J. Mech. Eng. 2010, 46, 31004. [Google Scholar] [CrossRef]
- Li, S.J.; Dai, J. Topological representation of planar mechanisms based on Assur group elements. J. Mech. Eng. 2011, 47, 8–13. [Google Scholar] [CrossRef]
- Liu, F.; He, G.; Lu, Z. Research and design of a novel tendon driven underactuated multi-fingered hand. J. Mech. Eng. 2014, 50, 53–59. [Google Scholar] [CrossRef]
- Chu, Z.Y.; Lei, Y.A. Parameters matching of an active-passive composite driver deployable manipulator for a space probe. Acta Aeronaut. Astronaut. Sin. 2014, 33, 268–278. [Google Scholar]
- Sun, L.L.; Zhang, H.O.; Lin, H.; Pan, W.J. Design and Research of an Underactuated Manipulator Based on the Metamorphic Mechanism. Sensors 2022, 22, 4766. [Google Scholar] [CrossRef] [PubMed]
- Li, S.J.; Wang, H.G.; Dai, J.S. The Equivalent Resistance Gradient Model of Metamorphic Mechanisms and the Design Method. J. Mech. Eng. 2014, 50, 18–23. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, H.G.; Li, S.J. Structural synthesis for broken strands repair operation metamorphic mechanism of EHV transmission lines. J. Vibroeng. 2014, 16, 2768–2778. [Google Scholar]
- Li, S.J.; Wang, H.; Meng, Q.; Dai, J.S. Task-based structure synthesis of source metamorphic mechanisms and constrained forms of metamorphic joints. Mech. Mach. Theory 2016, 96, 334–345. [Google Scholar] [CrossRef]
- Sun, L.L.; Zhang, H.O. Dynamic simulation and optimal design of side rolling cellular mechanism. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).