Hot-Air Contactless Single-Point Incremental Forming
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of the Contactless Incremental Point Forming
2.2. Nozzle Design and Manufacturing
2.3. Sheet Material
2.4. Process Parameters
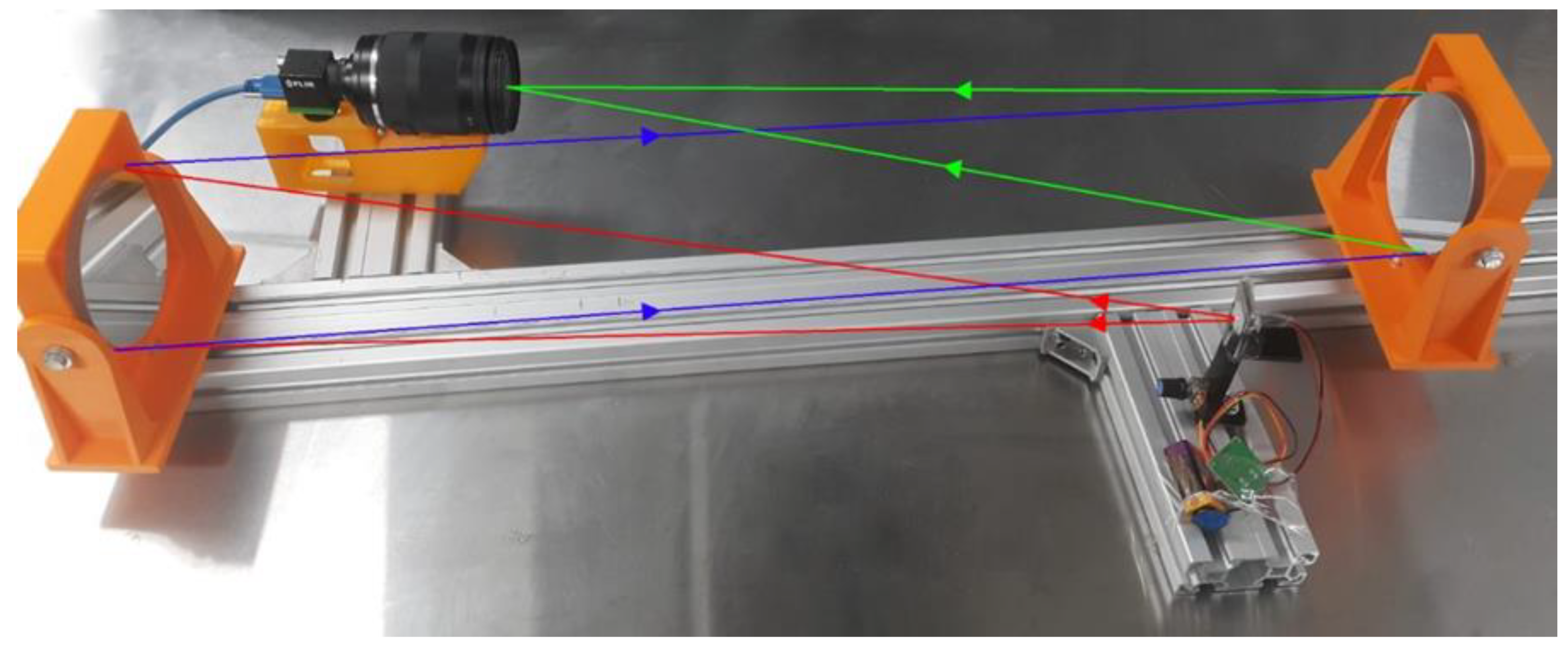
2.5. Visualization of the Air Flow
3. Results and Discussion
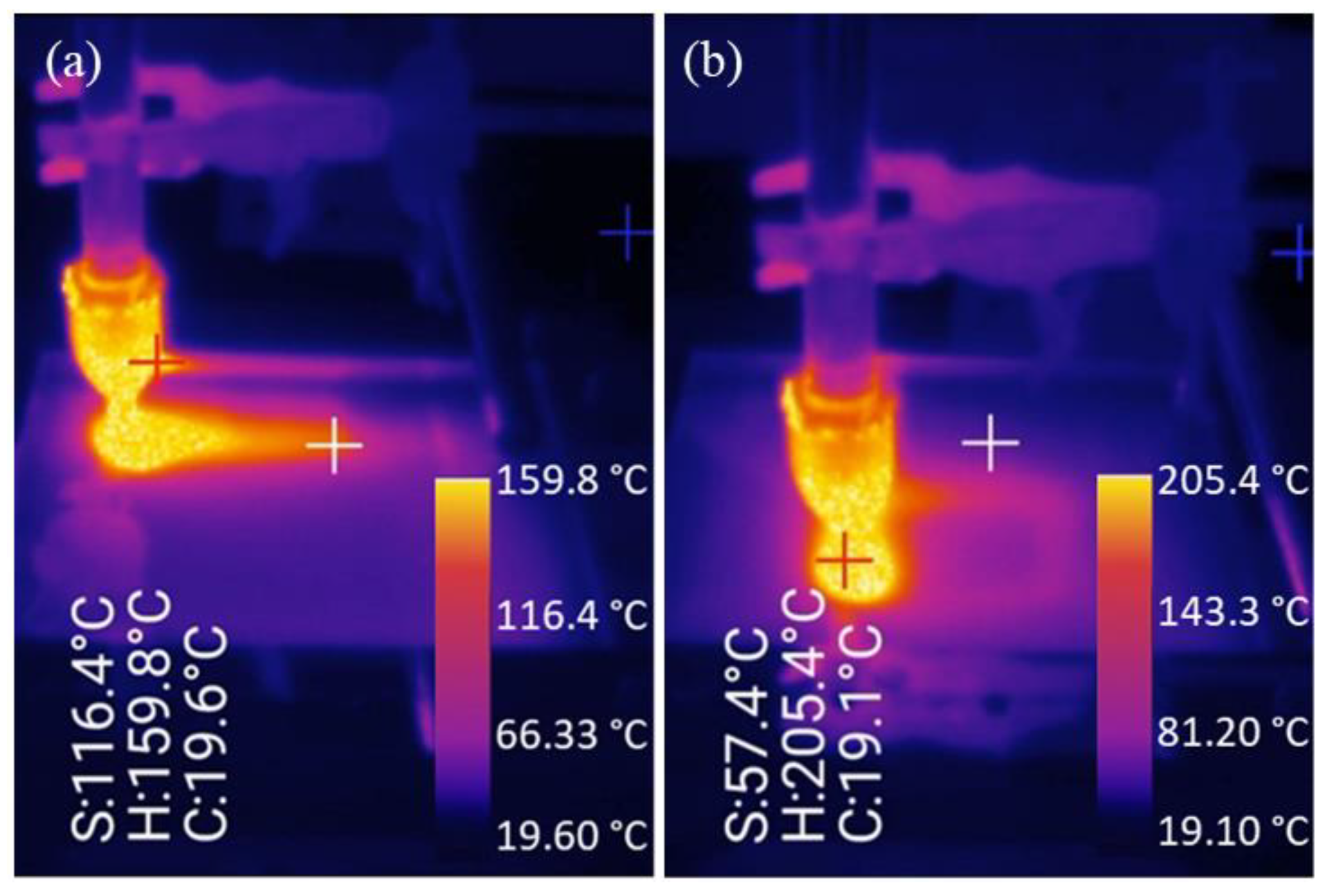
3.1. Forming Force and Air Thermal Flow
3.2. Geometric Profile of the PC Workpiece
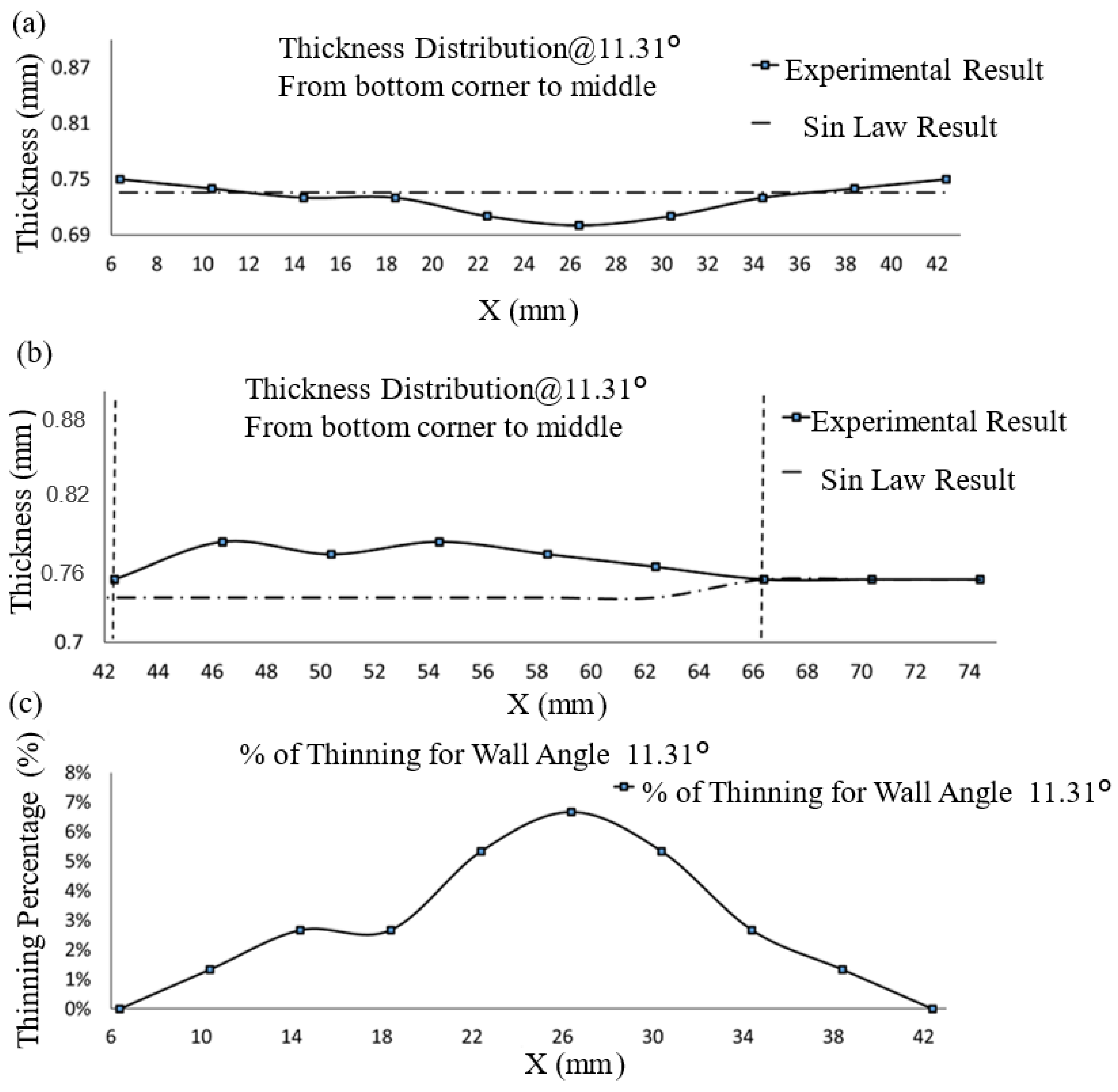
3.3. Thickness Distribution
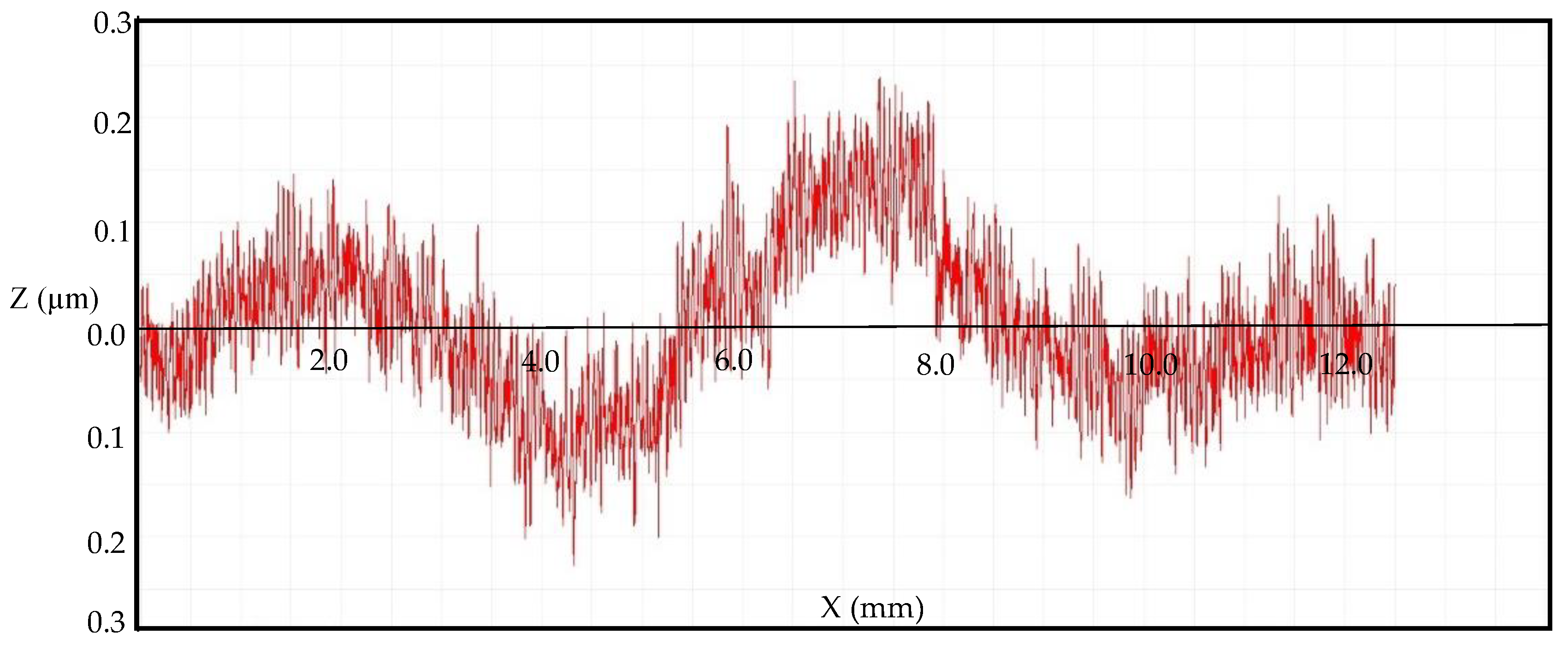
3.4. Surface Roughness
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pratheesh Kumar, S.; Elangovan, S.; Mohanraj, R.; Naveen Anthuvan, R.; Nithin, V. Development of Flexible Mechanism for Two-Point Incremental Forming. In Advances in Forming, Machining and Automation: Select Proceedings of AIMTDR 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 37–46. [Google Scholar]
- Zhou, C.; Zhang, F.; Wei, B.; Lin, Y.; He, K.; Du, R. Digital twin–based stamping system for incremental bending. Int. J. Adv. Manuf. Technol. 2021, 116, 389–401. [Google Scholar] [CrossRef]
- Leszak, E. Apparatus and Process for Incremental Dieless Forming. U.S. Patent No 3,342,051, 19 September 1967. [Google Scholar]
- Mohanraj, R.; Elangovan, S. Incremental sheet metal forming of Ti–6Al–4V alloy for aerospace application. Trans. Can. Soc. Mech. Eng. 2019, 44, 56–64. [Google Scholar] [CrossRef]
- Li, W.; Attallah, M.M.; Essa, K. Experimental and numerical investigations on the process quality and microstructure during induction heating assisted incremental forming of Ti-6Al-4V sheet. J. Mater. Process. Technol. 2022, 299, 117323. [Google Scholar] [CrossRef]
- Pandre, S.; Morchhale, A.; Kotkunde, N.; Kurra, S. Processing of DP590 steel using single point incremental forming for automotive applications. Mater. Manuf. Process. 2021, 36, 1658–1666. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, Y.; Xu, C.; Liu, Y.; Ghafoor, S.; Li, F. Incremental sheet forming towards biomedical implants: A review. J. Mater. Res. Technol. 2020, 9, 7225–7251. [Google Scholar] [CrossRef]
- Essa, K.; Hartley, P. An assessment of various process strategies for improving precision in single point incremental forming. Int. J. Mater. Form. 2011, 4, 401–412. [Google Scholar] [CrossRef]
- Grimm, T.J.; Parvathy, G.V.; Mears, L. Single Point Incremental Forming Springback Reduction Using Edge Stiffener. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, 16–19 November 2020; p. V02AT02A022. [Google Scholar]
- Van Viet, M.; Thinh, N.T.; Van Sy, L. Effect of Lubrication on Deforming the Aluminum Sheet with Two Points Incremental Forming Technology. In Proceedings of the 2nd Annual International Conference on Material, Machines and Methods for Sustainable Development (MMMS2020), Nha Trang, Vietnam, 12–15 November 2020; pp. 975–982. [Google Scholar]
- Sieczkarek, P.; Wernicke, S.; Gies, S.; Tekkaya, A.; Krebs, E.; Wiederkehr, P.; Biermann, D.; Tillmann, W.; Stangier, D. Wear behavior of tribologically optimized tool surfaces for incremental forming processes. Tribol. Int. 2016, 104, 64–72. [Google Scholar] [CrossRef]
- Murugesan, M.; Yu, J.-H.; Jung, K.-S.; Cho, S.-M.; Bhandari, K.S.; Lee, C.-W. Optimization of forming parameters in incremental sheet forming of AA3003-H18 sheets using Taguchi method. Materials 2022, 15, 1458. [Google Scholar] [CrossRef]
- Zavala, J.M.D.; Martínez-Romero, O.; Elías-Zúñiga, A.; Gutiérrez, H.M.L.; Vega, A.E.-d.l.; Taha-Tijerina, J. Study of friction and wear effects in aluminum parts manufactured via single point incremental forming process using petroleum and vegetable oil-based lubricants. Materials 2021, 14, 3973. [Google Scholar] [CrossRef]
- Li, W.; Essa, K.; Li, S. A novel tool to enhance the lubricant efficiency on induction heat-assisted incremental sheet forming of Ti-6Al-4 V sheets. Int. J. Adv. Manuf. Technol. 2022, 120, 8239–8257. [Google Scholar] [CrossRef]
- Li, W.; Shu, C.; Hassan, A.; Attallah, M.M.; Essa, K. Application of machine learning on tool path optimisation and cooling lubricant in induction heating-assisted single point incremental sheet forming of Ti-6Al-4V sheets. Int. J. Adv. Manuf. Technol. 2022, 123, 821–838. [Google Scholar] [CrossRef]
- Hassan, M.; Hussain, G.; Wei, H.; Qadeer, A.; AlKahtani, M. Progress on single-point incremental forming of polymers. Int. J. Adv. Manuf. Technol. 2021, 114, 1–26. [Google Scholar] [CrossRef]
- Zhu, H.; Ou, H.; Popov, A. Incremental sheet forming of thermoplastics: A review. Int. J. Adv. Manuf. Technol. 2020, 111, 565–587. [Google Scholar] [CrossRef]
- Roşca, N.A.; Oleksik, M. Simulation of the Single Point Incremental Forming of Polyamide and Polyethylene Sheets. MATEC Web Conf. 2019, 290, 03014. [Google Scholar] [CrossRef]
- Durante, M.; Formisano, A.; Lambiase, F. Formability of polycarbonate sheets in single-point incremental forming. Int. J. Adv. Manuf. Technol. 2019, 102, 2049–2062. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Li, X.; Xu, D.; Shao, Y.; Attallah, M.M.; Essa, K. Crystal plasticity model of induction heating-assisted incremental sheet forming with recrystallisation simulation in cellular automata. Int. J. Adv. Manuf. Technol. 2022, 123, 903–925. [Google Scholar] [CrossRef]
- Li, W.; Attallah, M.M.; Essa, K. Heat-assisted incremental sheet forming for high-strength materials—A review. Int. J. Adv. Manuf. Technol. 2023, 124, 2011–2036. [Google Scholar] [CrossRef]
- Ambrogio, G.; Gagliardi, F.; Conte, R.; Russo, P. Feasibility analysis of hot incremental sheet forming process on thermoplastics. Int. J. Adv. Manuf. Technol. 2019, 102, 937–947. [Google Scholar] [CrossRef]
- Conte, R.; Gagliardi, F.; Ambrogio, G.; Filice, F.; Russo, P. Performance analysis of the incremental sheet forming on PMMA using a combined chemical and mechanical approach. In Proceedings of the AIP Conference Proceedings, Dublin, Ireland, 26–28 April 2017. [Google Scholar]
- Okada, M.; Kato, T.; Otsu, M.; Tanaka, H.; Miura, T. Development of optical-heating-assisted incremental forming method for carbon fiber reinforced thermoplastic sheet—Forming characteristics in simple spot-forming and two-dimensional sheet-fed forming. J. Mater. Process. Technol. 2018, 256, 145–153. [Google Scholar] [CrossRef]
- Sridhar, R.; Rajenthirakumar, D. Polymer sheet hot incremental forming-an innovative polymer forming approach. Polym. Polym. Compos. 2016, 24, 447–454. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.A. Spring back analysis in incremental forming of polypropylene sheet: An experimental study. J. Mech. Sci. Technol. 2018, 32, 4859–4869. [Google Scholar] [CrossRef]
- Bagudanch, I.; Lozano-Sánchez, L.M.; Puigpinós, L.; Sabater, M.; Elizalde, L.E.; Elías-Zúñiga, A.; Garcia-Romeu, M.L. Manufacturing of polymeric biocompatible cranial geometry by single point incremental forming. Procedia Eng. 2015, 132, 267–273. [Google Scholar] [CrossRef]
- Sabater, M.; Garcia-Romeu, M.L.; Vives-Mestres, M.; Ferrer, I.; Bagudanch, I. Process parameter effects on biocompatible thermoplastic sheets produced by incremental forming. Materials 2018, 11, 1377. [Google Scholar] [CrossRef] [PubMed]
- Thangavel, K.; Duraiswamy, R.; Nagarajan, S.; Ramasamy, S. Influence of roller ball tool in single point incremental forming of polymers. Teh. Vjesn. 2019, 26, 171–176. [Google Scholar]
- Medina-Sánchez, G.; Torres-Jimenez, E.; Lopez-Garcia, R.; Dorado-Vicente, R.; Cazalla-Moral, R. Temperature influence on single point incremental forming of PVC parts. Procedia Manuf. 2017, 13, 335–342. [Google Scholar] [CrossRef]
- Miroir, M.; Laniel, R.; Brient, A.; Kerbrat, O. Water jet incremental sheet metal forming: A critical state-of-the-art review and a proposal for technological windows. Int. J. Adv. Manuf. Technol. 2022, 119, 4159–4175. [Google Scholar] [CrossRef]
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Adharapurapu, R.R. Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: Characterization and modeling of the compressive yield stress. Int. J. Solids Struct. 2006, 43, 2318–2335. [Google Scholar] [CrossRef]
- Dar, U.A.; Zhang, W.; Xu, Y.; Wang, J. Thermal and strain rate sensitive compressive behavior of polycarbonate polymer-experimental and constitutive analysis. J. Polym. Res. 2014, 21, 519. [Google Scholar] [CrossRef]
- Kaessinger, J.C.; Kors, K.C.; Lum, J.S.; Dillon, H.E.; Mayer, S.K. Utilizing Schlieren imaging to visualize heat transfer studies. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; p. V005T005A033. [Google Scholar]
- Borboni, A.; De Santis, D. Large deflection of a non-linear, elastic, asymmetric Ludwick cantilever beam subjected to horizontal force, vertical force and bending torque at the free end. Meccanica 2014, 49, 1327–1336. [Google Scholar] [CrossRef]
- Archansdran, S.; Shaari, M.; Rosly, M. Characterization of double layer IPMC bending actuation. ARPN J. Eng. Appl. Sci. 2016, 11, 6536. [Google Scholar]
- Cao, T.; Lu, B.; Xu, D.; Zhang, H.; Chen, J.; Long, H.; Cao, J. An efficient method for thickness prediction in multi-pass incremental sheet forming. Int. J. Adv. Manuf. Technol. 2015, 77, 469–483. [Google Scholar] [CrossRef]
- Limpadapun, K.; Kesvarakul, R. An investigation of thickness distribution in Single-Point incremental forming with different forming parameter in Hot-dipped zinc-coated cold-rolled steel. Mater. Today Proc. 2020, 33, 1988–1992. [Google Scholar] [CrossRef]
- Hussain, G.; Gao, L. A novel method to test the thinning limits of sheet metals in negative incremental forming. Int. J. Mach. Tools Manuf. 2007, 47, 419–435. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Xu, D.K.; Chen, J.; Ai, S.; Long, H.; Ou, H.; Cao, J. Investigation of material deformation mechanism in double side incremental sheet forming. Int. J. Mach. Tools Manuf. 2015, 93, 37–48. [Google Scholar] [CrossRef]
- Tolipov, A.; Elghawail, A.; Abosaf, M.; Pham, D.; Hassanin, H.; Essa, K. Multipoint forming using mesh-type elastic cushion: Modelling and experimentation. Int. J. Adv. Manuf. Technol. 2019, 103, 2079–2090. [Google Scholar] [CrossRef]
- Abe, Y.; Mori, K.-i.; Ito, T. Plate forging of drawn cup with flange including thickening of corners. Manuf. Rev. 2014, 1, 16. [Google Scholar] [CrossRef][Green Version]
- Abd Ali, R.; Chen, W.; Al-Furjan, M.; Jin, X.; Wang, Z. Experimental investigation and optimal prediction of maximum forming angle and surface roughness of an Al/SUS bimetal sheet in an incremental forming process using machine learning. Materials 2019, 12, 4150. [Google Scholar] [CrossRef]






| Thickness | 0.75 (mm) |
| Density | 1.2 (g/cm) |
| Young’s modulus | 2.3 (Gpa) |
| Yield stress | 60 (Mpa) |
| Poisson’s ratio | 0.38 |
| Maximum elongation | 110% |
| Thermal conductivity | 0.2 (W/m.°C) |
| Air pressure | 1 (bar) |
| Air temperature | 160 (°C) |
| Nozzle speed | 750 (mm/min) |
| Initial gap | 6 (mm) |
| Step-down | mm) |
| Sample No | Ra (µm) | Rq (µm) | Rz (µm) | Rt (µm) |
|---|---|---|---|---|
| As-received | 0.0796 | 0.0846 | 0.1938 | 0.2441 |
| Experimental (top) | 0.4543 | 0.4722 | 0.5508 | 1.5403 |
| Experimental (middle) | 0.1310 | 0.1490 | 0.5470 | 1.5228 |
| Experimental (bottom) | 0.2761 | 0.3067 | 0.6521 | 1.3956 |
| Average | 0.2871 | 0.3093 | 0.5833 | 1.486 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almadani, M.; Guner, A.; Hassanin, H.; Essa, K. Hot-Air Contactless Single-Point Incremental Forming. J. Manuf. Mater. Process. 2023, 7, 179. https://doi.org/10.3390/jmmp7050179
Almadani M, Guner A, Hassanin H, Essa K. Hot-Air Contactless Single-Point Incremental Forming. Journal of Manufacturing and Materials Processing. 2023; 7(5):179. https://doi.org/10.3390/jmmp7050179
Chicago/Turabian StyleAlmadani, Mohammad, Ahmet Guner, Hany Hassanin, and Khamis Essa. 2023. "Hot-Air Contactless Single-Point Incremental Forming" Journal of Manufacturing and Materials Processing 7, no. 5: 179. https://doi.org/10.3390/jmmp7050179
APA StyleAlmadani, M., Guner, A., Hassanin, H., & Essa, K. (2023). Hot-Air Contactless Single-Point Incremental Forming. Journal of Manufacturing and Materials Processing, 7(5), 179. https://doi.org/10.3390/jmmp7050179









