Influence of the Pore Radius on the Penetration Depth of Inks in Binder Jetting—A Modification of the Washburn Equation
Abstract
:1. Introduction
1.1. Washburn Equation
1.2. Pore Radius
2. Hypothesis
- the contact regions in the powder bed and their resulting capillary pressure, and
- their spatial distribution within the powder bed.
3. Methodology and Modeling Approach
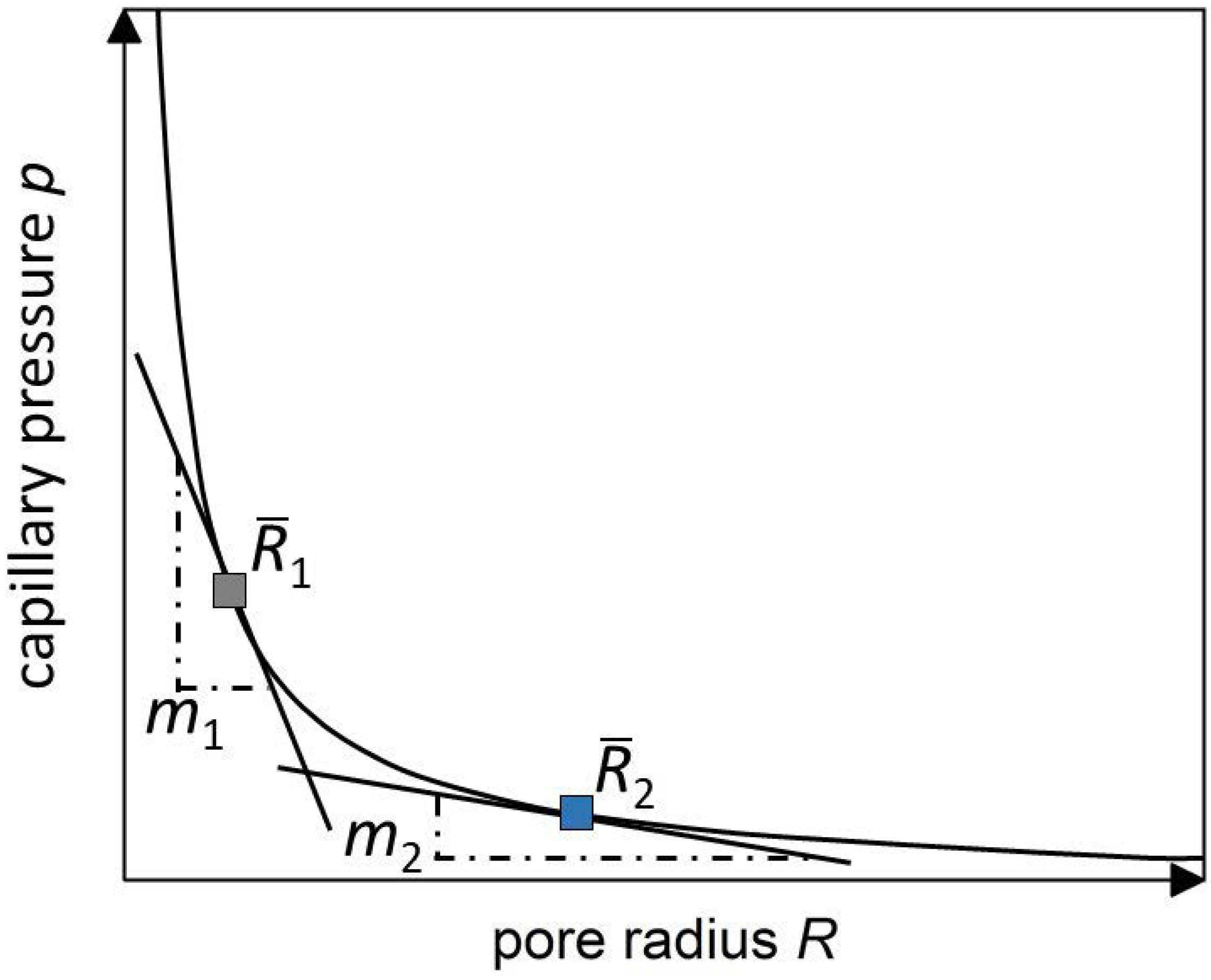
3.1. Critical Radius
3.2. Weighting of the Volume Fraction
3.3. Weighting of the Capillary Pressure
3.4. Determination of the Weighted Radius
4. Materials and Methods
4.1. Preparation and Characterization of the Ink
4.2. Characterization of the Powder
4.3. Powder–Ink Interaction: Contact Angle and Penetration Time
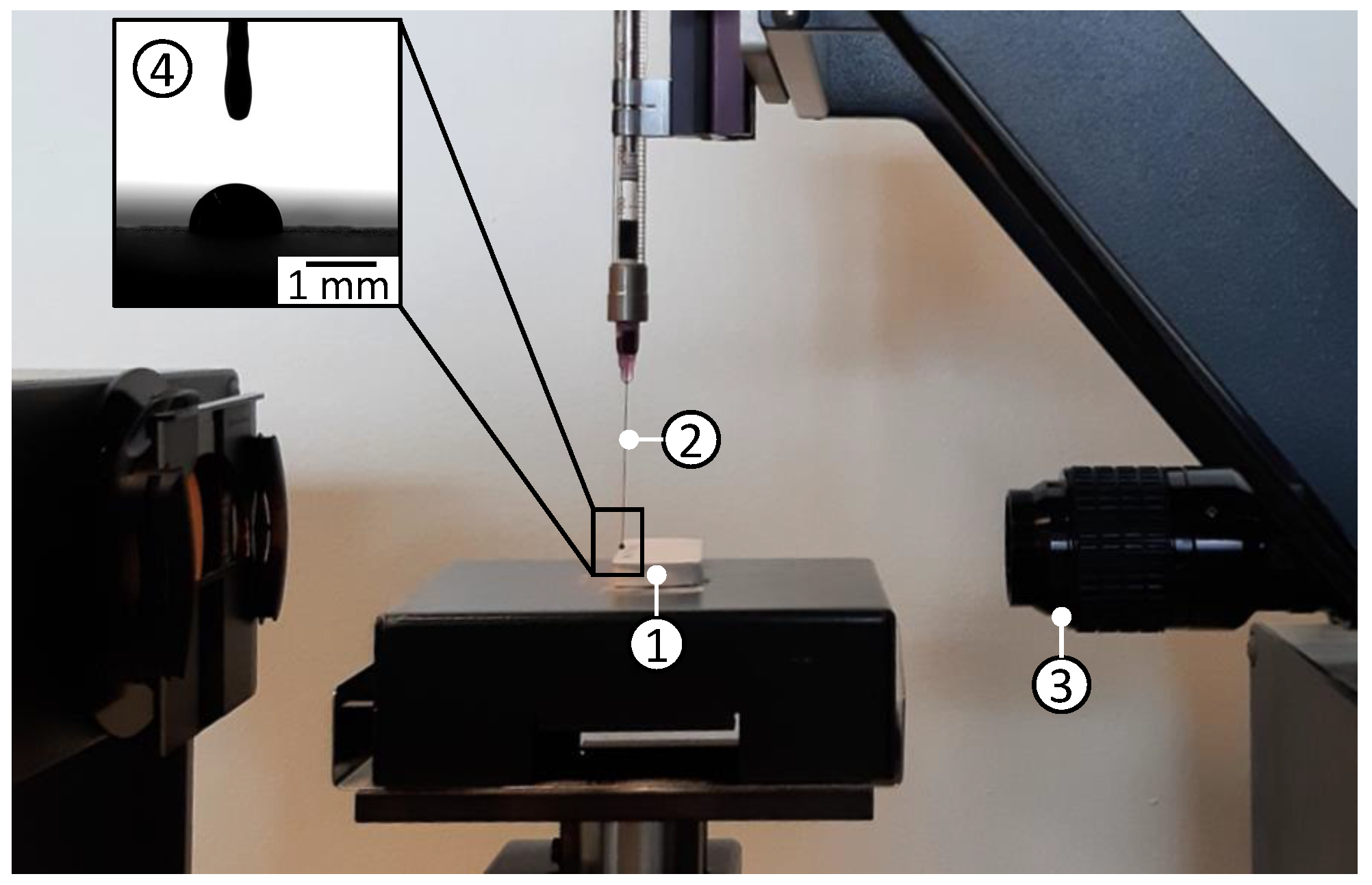
4.4. Measurement of the Penetration Depth
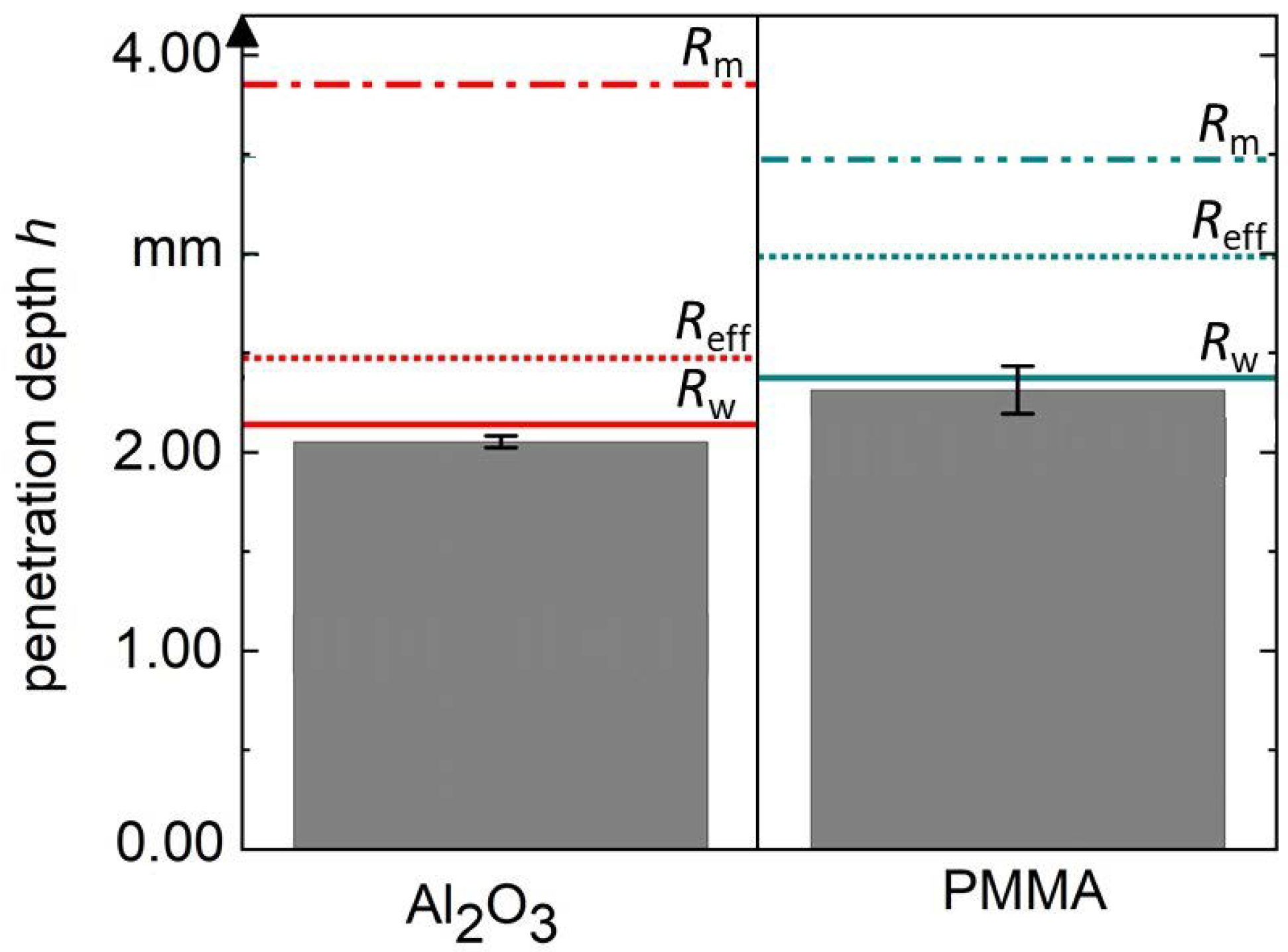
5. Validation, Results, and Discussion
6. Conclusions
- A weighting of the pore radius according to the volume distribution and the acting capillary pressure was shown to be advantageous.
- The validation with two powders showed that the measured penetration depth can be reproduced very well by the calculation with . The calculation is independent of the shape of the particle size distribution, since is based on the effective porosity and the of the particle size distribution.
- Estimating the penetration depth with equations from the literature that are based on the Sauter diameter are only useful for mono-modal narrow pore size distributions that are not oversized. For wider distributions, the estimation with the Sauter diameter no longer reflects the effective porosity in the powder bed. The use of the mean pore radius is not suitable for a calculation of the penetration depth.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
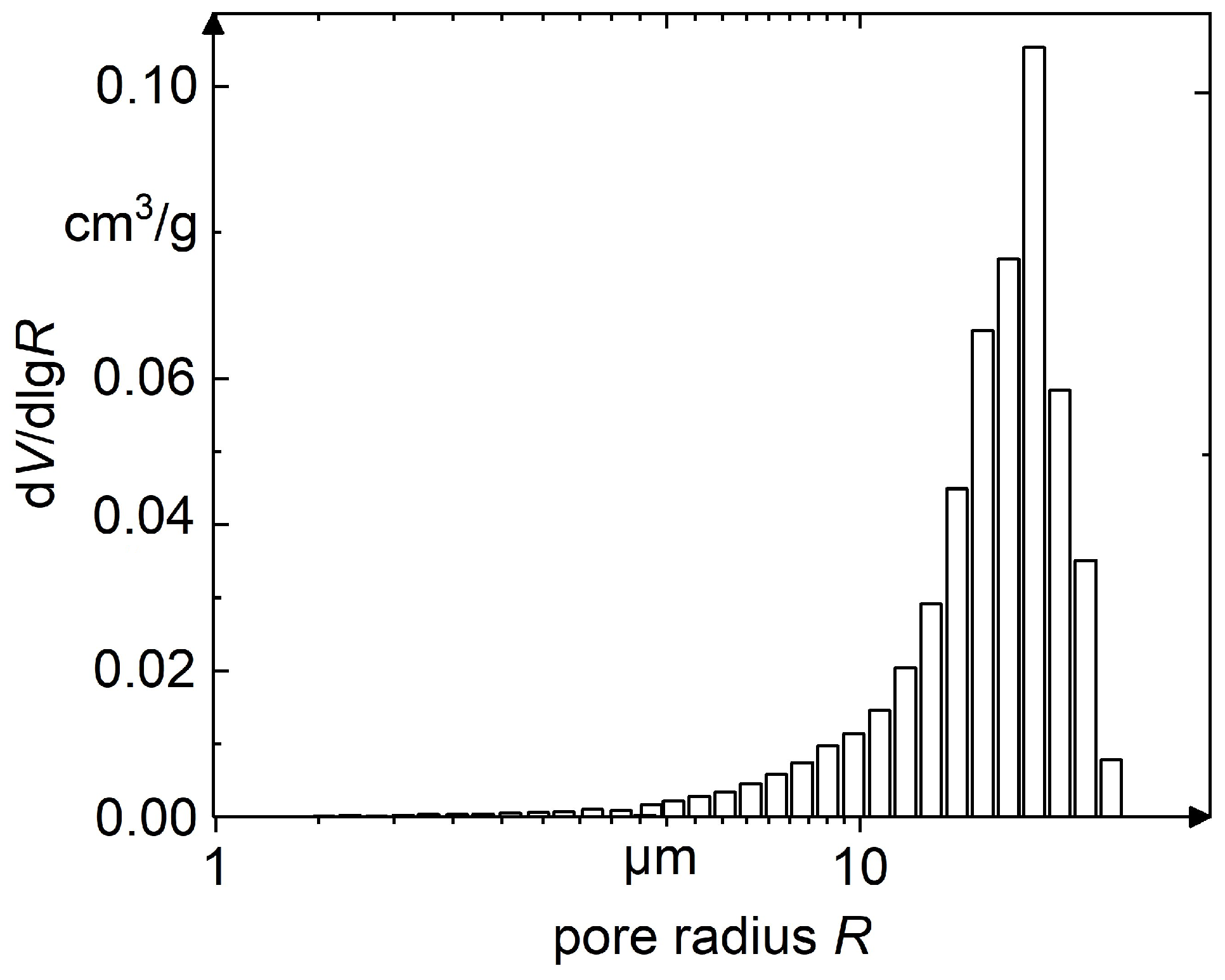

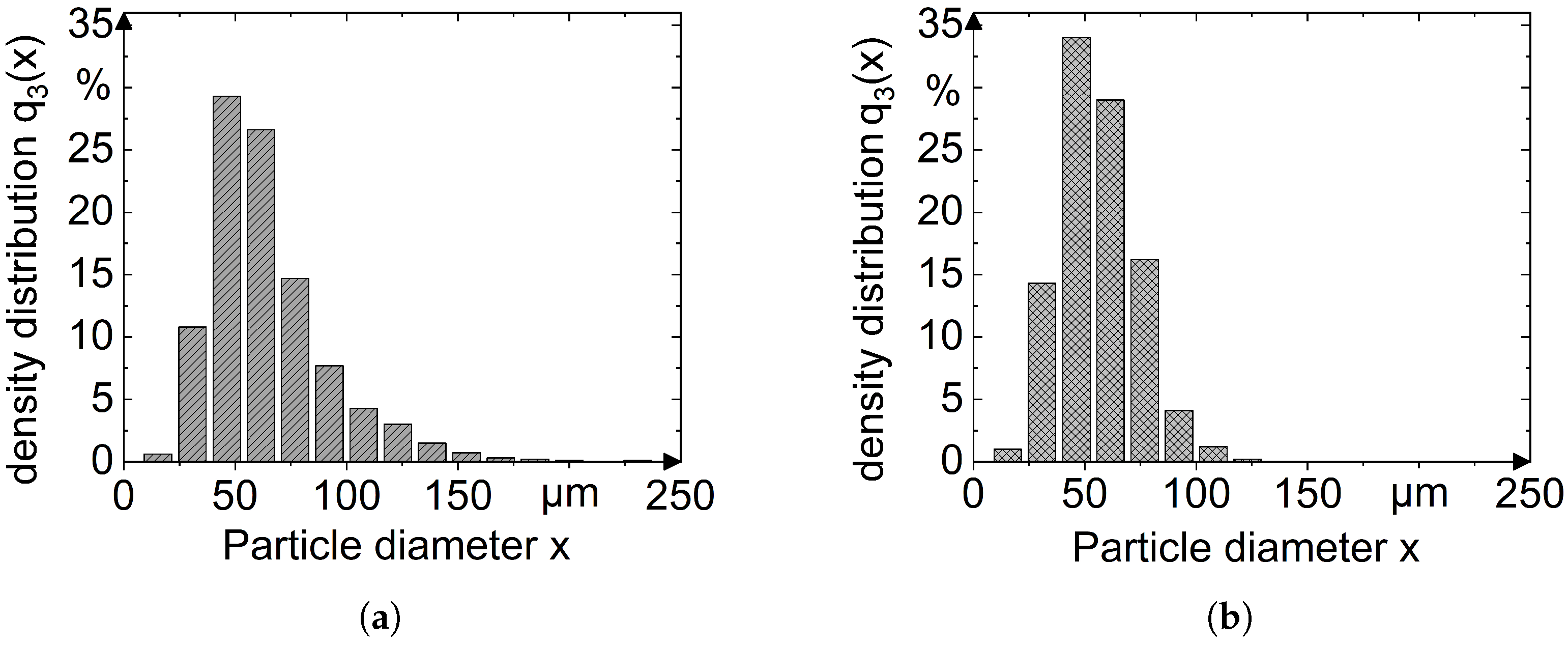
References
- Günther, D.; Heymel, B.; Franz Günther, J.; Ederer, I. Continuous 3D-printing for additive manufacturing. Rapid Prototyp. J. 2014, 20, 320–327. [Google Scholar] [CrossRef]
- Barui, S.; Ding, H.; Wang, Z.; Zhao, H.; Marathe, S.; Mirihanage, W.; Basu, B.; Derby, B. Probing Ink-Powder Interactions during 3D Binder Jet Printing Using Time-Resolved X-ray Imaging. ACS Appl. Mater. Interfaces 2020, 12, 34254–34264. [Google Scholar] [CrossRef]
- Bai, Y.; Wall, C.; Pham, H.; Esker, A.; Williams, C.B. Characterizing Binder–Powder Interaction in Binder Jetting Additive Manufacturing Via Sessile Drop Goniometry. J. Manuf. Sci. Eng. 2019, 141, 4041624. [Google Scholar] [CrossRef]
- Wudy, K.; Drummer, D. Infiltration Behavior of Thermosets for Use in a Combined Selective Laser Sintering Process of Polymers. JOM 2019, 71, 920–927. [Google Scholar] [CrossRef]
- Baek, S.; Jeong, S.; Seo, J.; Lee, S.; Park, S.; Choi, J.; Jeong, H.; Sung, Y. Effects of Tube Radius and Surface Tension on Capillary Rise Dynamics of Water/Butanol Mixtures. Appl. Sci. 2021, 11, 3533. [Google Scholar] [CrossRef]
- Breitwieser, M.; Viaene, D. Capillary Pressure in Wound Dressings. 2021. Available online: https://www.imeter.de/120VACUTEX2020eng (accessed on 5 September 2022).
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Bouchard, D.J.; Chandra, S. Infiltration of impacting droplets into porous substrates. Exp. Fluids 2020, 61, 235. [Google Scholar] [CrossRef]
- Popovich, L.L.; Feke, D.L.; Manas-Zloczower, I. Influence of physical and interfacial characteristics on the wetting and spreading of fluids on powders. Powder Technol. 1999, 104, 68–74. [Google Scholar] [CrossRef]
- Hapgood, K.P.; Litster, J.D.; Biggs, S.R.; Howes, T. Drop penetration into porous powder beds. J. Colloid Interface Sci. 2002, 253, 353–366. [Google Scholar] [CrossRef]
- Zhang, J.; Tuohey, J.; Amini, N.; Morton, D.A.; Hapgood, K.P. Liquid imbibition into 3D printed porous substrates. Chem. Eng. Sci. 2021, 245, 116967. [Google Scholar] [CrossRef]
- Holman, R.K.; Cima, M.J.; Uhland, S.A.; Sachs, E. Spreading and infiltration of inkjet-printed polymer solution droplets on a porous substrate. J. Colloid Interface Sci. 2002, 249, 432–440. [Google Scholar] [CrossRef]
- Kowalczuk, P.B.; Drzymala, J. Physical meaning of the Sauter mean diameter of spherical particulate matter. Part. Sci. Technol. 2016, 34, 645–647. [Google Scholar] [CrossRef]
- Miyanaji, H.; Zhang, S.; Yang, L. A new physics-based model for equilibrium saturation determination in binder jetting additive manufacturing process. Int. J. Mach. Tools Manuf. 2018, 124, 1–11. [Google Scholar] [CrossRef]
- Lian, G.; Seville, J. The capillary bridge between two spheres: New closed-form equations in a two century old problem. Adv. Colloid Interface Sci. 2016, 227, 53–62. [Google Scholar] [CrossRef]
- Dörmann, M.; Schmid, H.J. Simulation of Capillary Bridges between Particles. Procedia Eng. 2015, 102, 14–23. [Google Scholar] [CrossRef]
- Scheel, M.; Seemann, R.; Brinkmann, M.; Di Michiel, M.; Sheppard, A.; Breidenbach, B.; Herminghaus, S. Morphological clues to wet granular pile stability. Nat. Mater. 2008, 7, 189–193. [Google Scholar] [CrossRef]
- Hassanizadeh, S.M.; Gray, W.G. Thermodynamic Basis of Capillary Pressure in Porous Media. Water Resour. Res. 1993, 29, 3389–3405. [Google Scholar] [CrossRef]
- Lehmann, M.; Kolb, C.G.; Klinger, F.; Zaeh, M.F. Preparation, characterization, and monitoring of an aqueous graphite ink for use in binder jetting. Mater. Des. 2021, 207, 109871. [Google Scholar] [CrossRef]
- Polsakiewicz, D.A.; Kollenberg, W. Highly loaded alumina inks for use in a piezoelectric print head. Mater. Und Werkst. 2011, 42, 812–819. [Google Scholar] [CrossRef]
- Kolb, C.G.; Lehmann, M.; Lindemann, J.L.; Bachmann, A.; Zaeh, M.F. Improving the Dispersion Behavior of Organic Components in Water-Based Electrode Dispersions for Inkjet Printing Processes. Appl. Sci. 2021, 11, 2242. [Google Scholar] [CrossRef]
- Traube, J. Ueber die Capillaritaetsconstanten organischer Stoffe in waesserigen Loesungen. Justus Liebig’s Ann. Chem. 1891, 265, 27–55. [Google Scholar] [CrossRef]
- Muster, T.H.; Prestidge, C.A. Application of time-dependent sessile drop contact angles on compacts to characterise the surface energetics of sulfathiazole crystals. Int. J. Pharm. 2002, 234, 43–54. [Google Scholar] [CrossRef]
- Danilov, V.E.; Korolev, E.V.; Ayzenshtadt, A.M. Measuring the Contact Angles of Powders by the Sessile Drop Method. Inorg. Mater. Appl. Res. 2021, 12, 794–798. [Google Scholar] [CrossRef]
- Bacelos, M.S.; Passos, M.L.; Freire, J.T. Effect of interparticle forces on the conical spouted bed behavior of wet particles with size distribution. Powder Technol. 2007, 174, 114–126. [Google Scholar] [CrossRef]
- Bai, Y.; Wagner, G.; Williams, C.B. Effect of particle size distribution on powder packing and sintering in binder jetting additive manufacturing of metals. J. Manuf. Sci. Eng. 2017, 139. [Google Scholar] [CrossRef]
- De Lazzer, A.; Dreyer, M.; Rath, H. Particle-surface capillary forces. Langmuir 1999, 15, 4551–4559. [Google Scholar] [CrossRef]

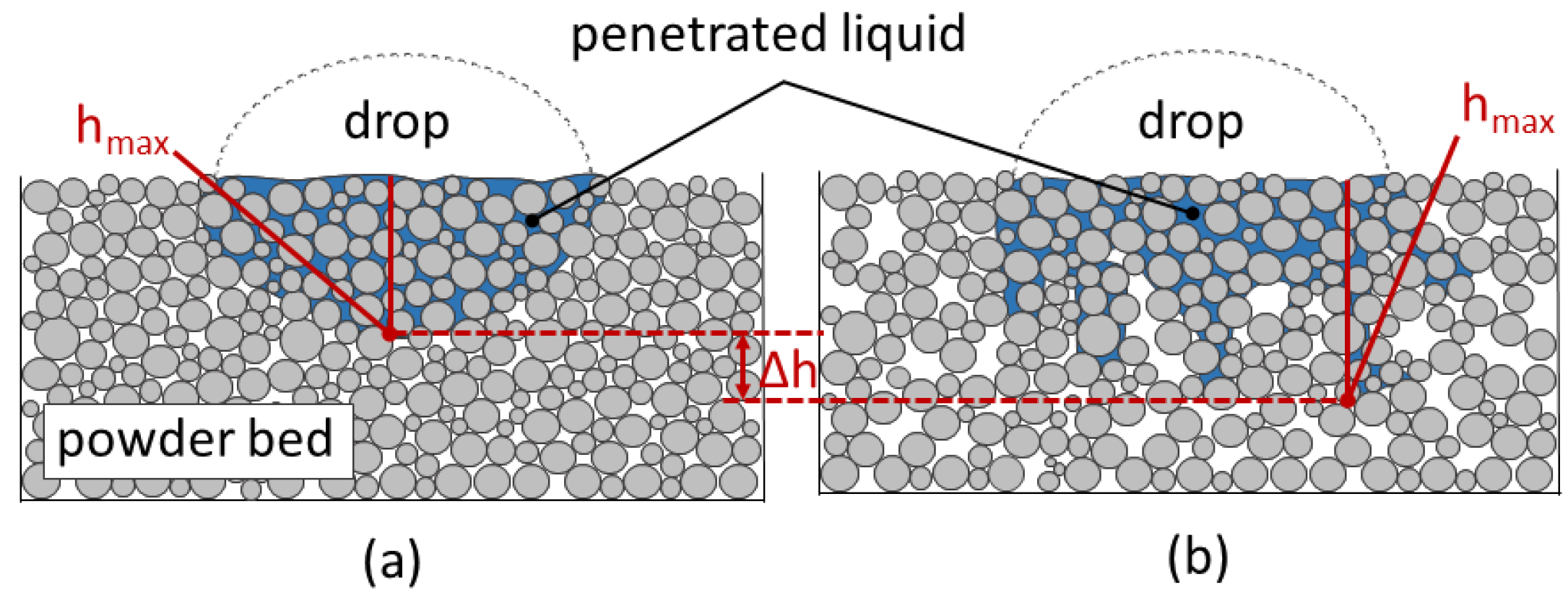
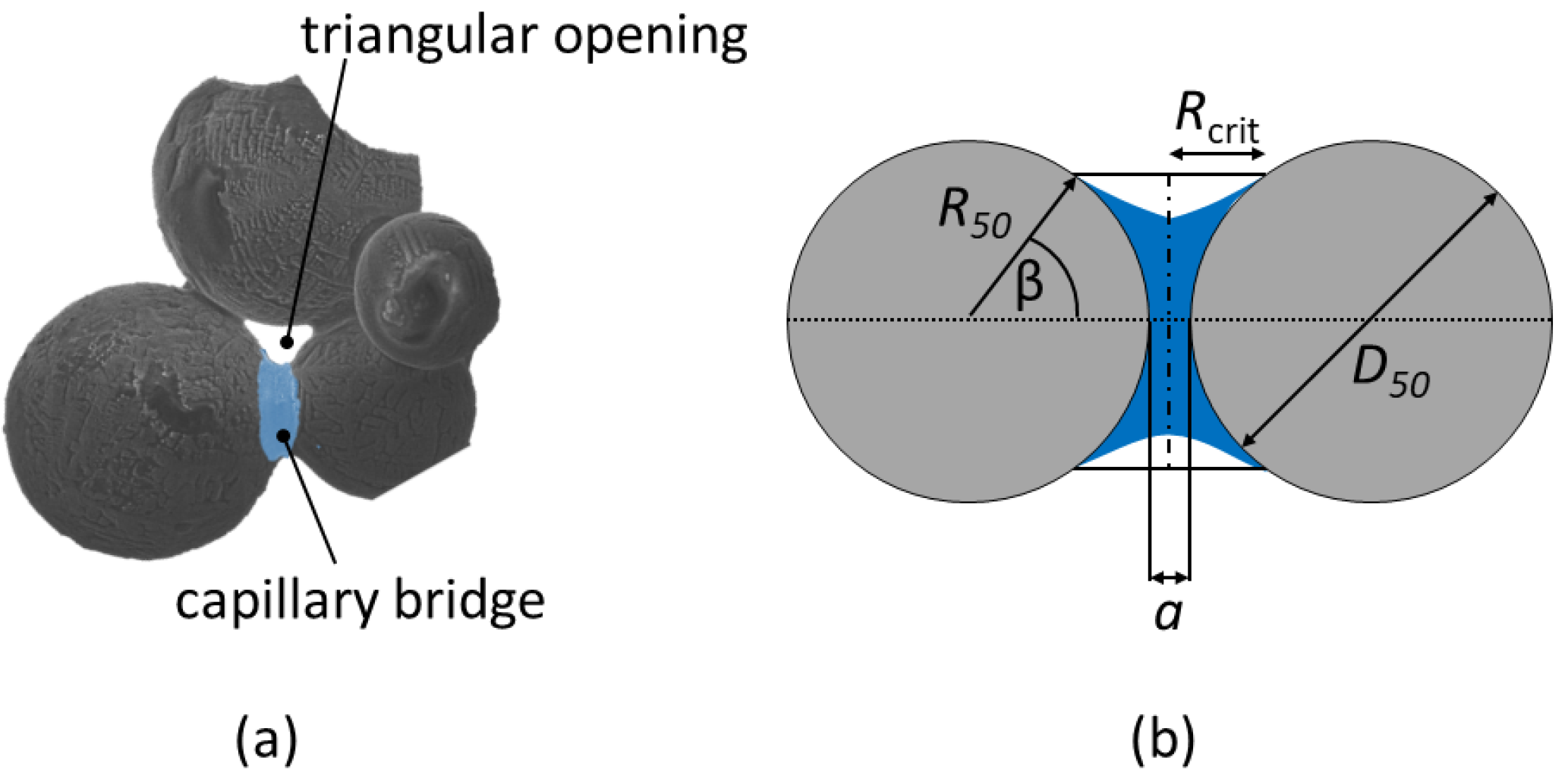

| Powder | t | ||||||
|---|---|---|---|---|---|---|---|
| in | in mN/m | in mPas | in s | - | in µm | in µm | |
| Al2O3 | 40.39 | 33.20 | 8.72 | 1.56 | 0.40 | 12.28 | 46.54 |
| PMMA | 53.58 | 33.20 | 8.72 | 1.21 | 0.45 | 23.65 | 50.50 |
| Powder | in µm | in µm | in µm | in µm | in µm | in µm | in µm | [12] in µm | [2] in µm | [17] in ° | - | - | - | - |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al2O3 | 3.37 | 23.27 | 2.03 | 0.79 | 6.68 | 3.26 | 0.78 | 6.56 | 2.71 | 30 | 0.58 | 0.42 | 0.99 | 0.01 |
| PMMA | 3.39 | 25.25 | 4.15 | 1.53 | 7.23 | 6.52 | 1.77 | 8.87 | 6.54 | 30 | 0.12 | 0.88 | 0.96 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehmann, M.; Panzer, H.; Kolb, C.G.; Zaeh, M.F. Influence of the Pore Radius on the Penetration Depth of Inks in Binder Jetting—A Modification of the Washburn Equation. J. Manuf. Mater. Process. 2022, 6, 101. https://doi.org/10.3390/jmmp6050101
Lehmann M, Panzer H, Kolb CG, Zaeh MF. Influence of the Pore Radius on the Penetration Depth of Inks in Binder Jetting—A Modification of the Washburn Equation. Journal of Manufacturing and Materials Processing. 2022; 6(5):101. https://doi.org/10.3390/jmmp6050101
Chicago/Turabian StyleLehmann, Maja, Hannes Panzer, Cara G. Kolb, and Michael F. Zaeh. 2022. "Influence of the Pore Radius on the Penetration Depth of Inks in Binder Jetting—A Modification of the Washburn Equation" Journal of Manufacturing and Materials Processing 6, no. 5: 101. https://doi.org/10.3390/jmmp6050101
APA StyleLehmann, M., Panzer, H., Kolb, C. G., & Zaeh, M. F. (2022). Influence of the Pore Radius on the Penetration Depth of Inks in Binder Jetting—A Modification of the Washburn Equation. Journal of Manufacturing and Materials Processing, 6(5), 101. https://doi.org/10.3390/jmmp6050101






