Multi-Scale Modeling of Residual Stresses Evolution in Laser Powder Bed Fusion of Inconel 625
Abstract
:1. Introduction
- Multi-scale modeling, including single track, multi-track layer, and part scale models;
- Comparing different volumetric heat sources with optical penetration;
- A proper powder material model is used to calculate the temperature-dependent thermal conductivity incorporating the solid conductivity, the nitrogen gas conductivity, and the inter-particle radiation;
- The Marangoni effects inside the melt pool by calculating the Marangoni number and its equivalent thermal conductivity;
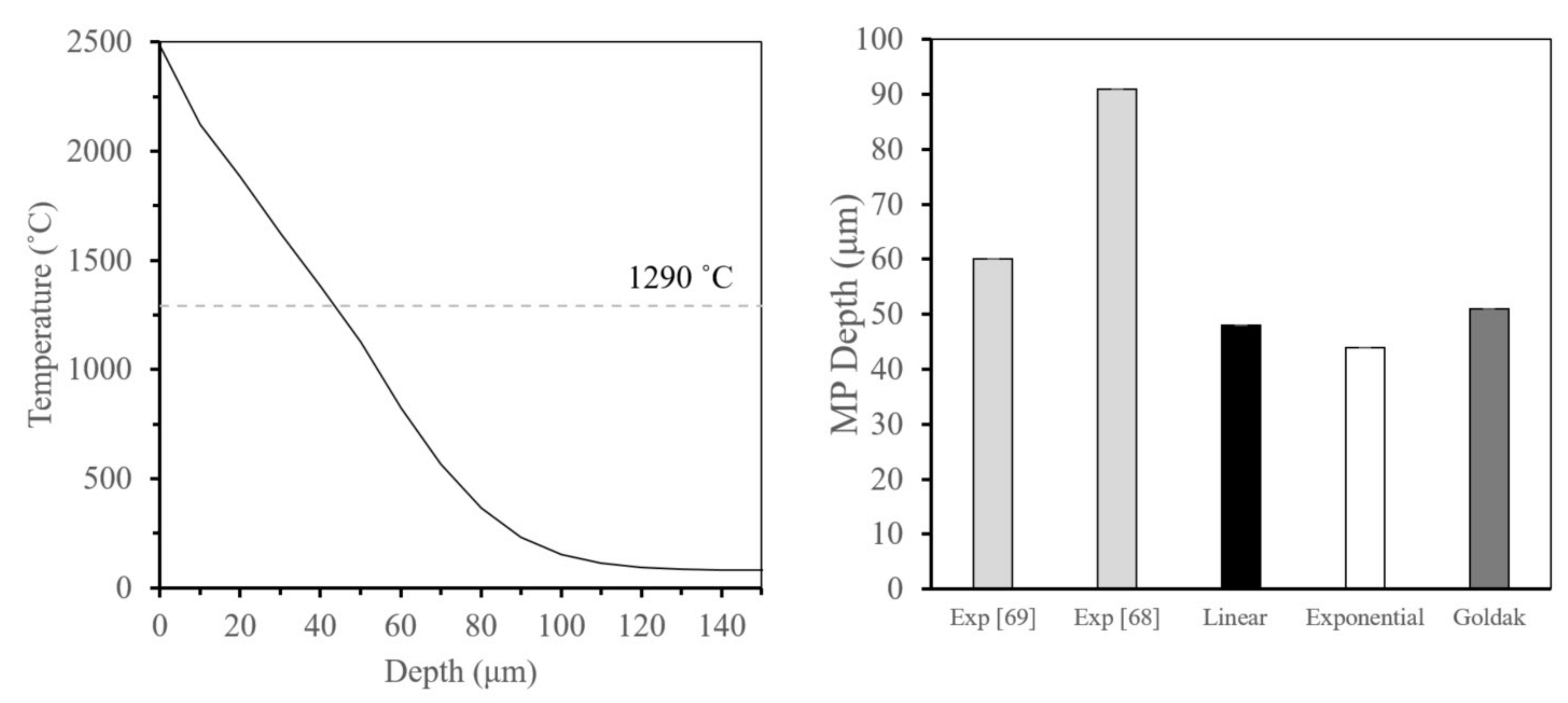
- Validation of the melt pool dimensions for single tracks with the literature;
- Experimental temperature measurement using a two-color pyrometer to validate the temperature from the multi-track layer model;
- In-depth RS profile measurement using XRD to validate the part scale model RS predictions;
- Study the effect of process parameters on thermal history, temperature gradients, CR, and their subsequent impact on the formation of RS.
2. Model Setup
2.1. Transient Thermal Model
2.2. Boundary Conditions
2.2.1. Heat Flux Boundary Condition
2.2.2. Convection Boundary Condition
2.2.3. Radiation Boundary Condition
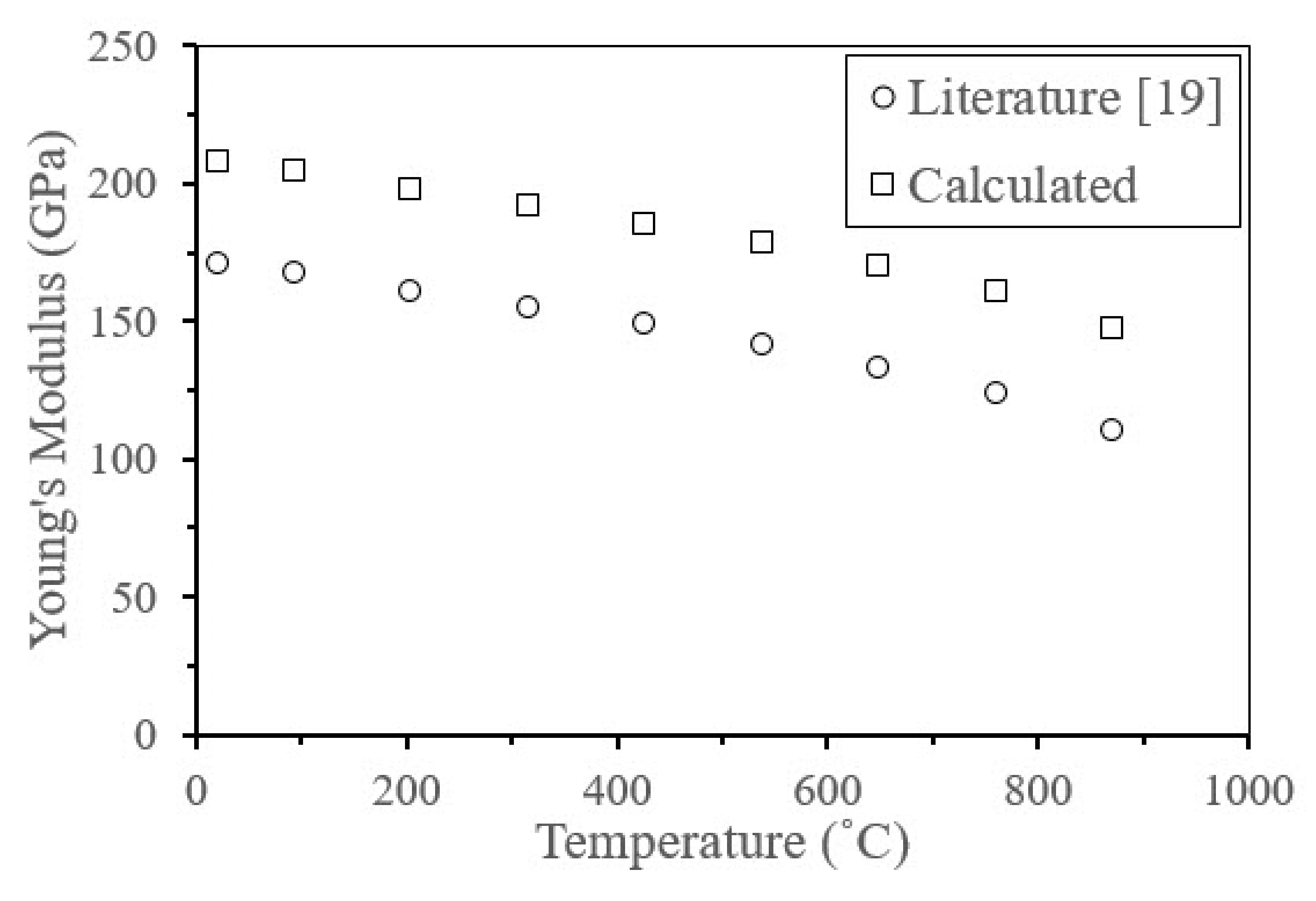
2.3. Material Model
2.4. Heat Source Modeling
2.5. Melt Pool Modeling
2.6. Modeling Approach
2.6.1. Single-Track Model
2.6.2. Multi-Track Model
2.6.3. Multi-Layer Model
3. Experimental Validation
3.1. Laser Absorptivity Measurement
3.2. Single Track Validation
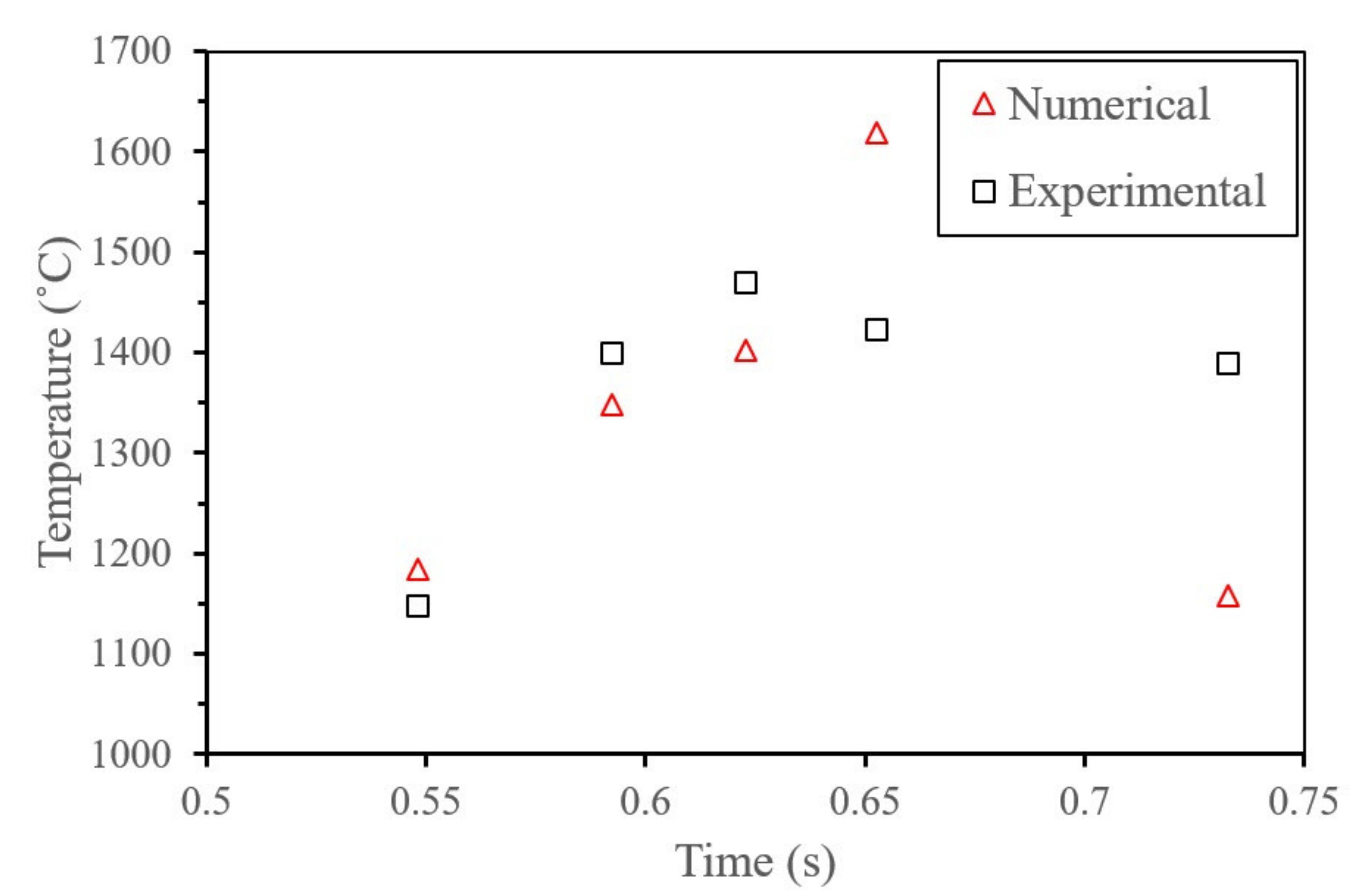
3.3. Multi-Track Temperature Measurement
3.4. Residual Stresses Measurements
4. Results
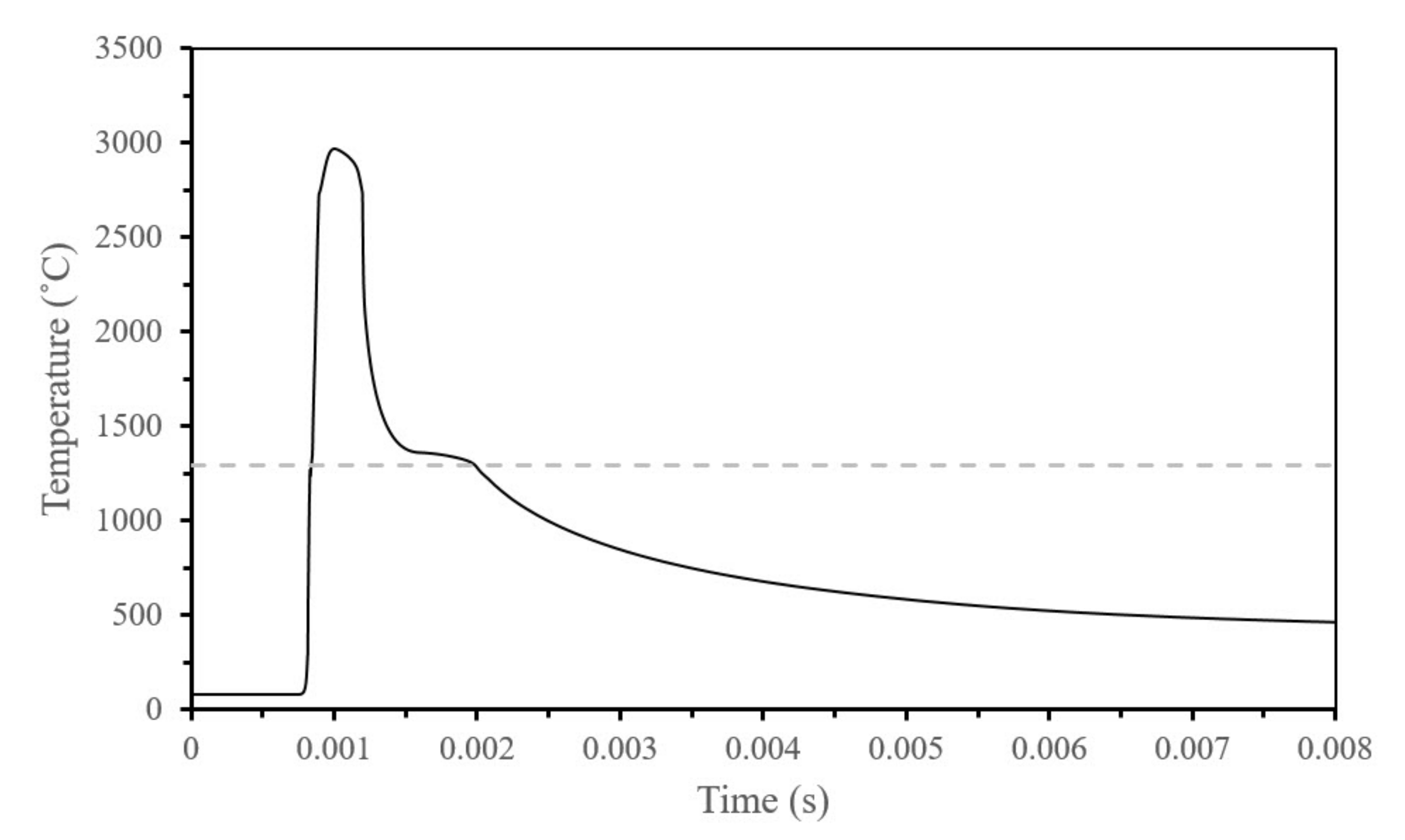
4.1. Single Tracks
4.2. Multi-Track Model
4.2.1. Temperature Validation and Evolution
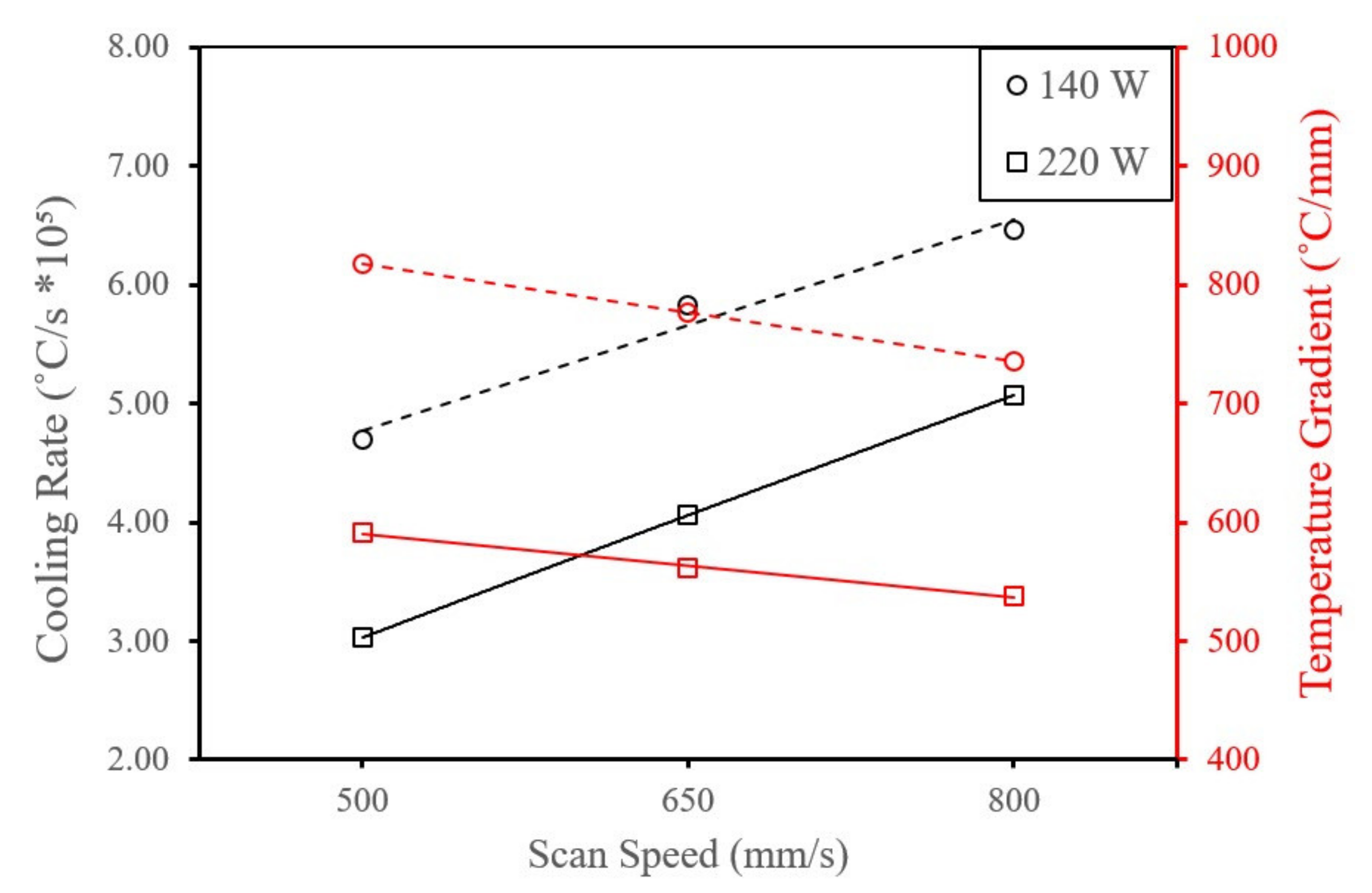
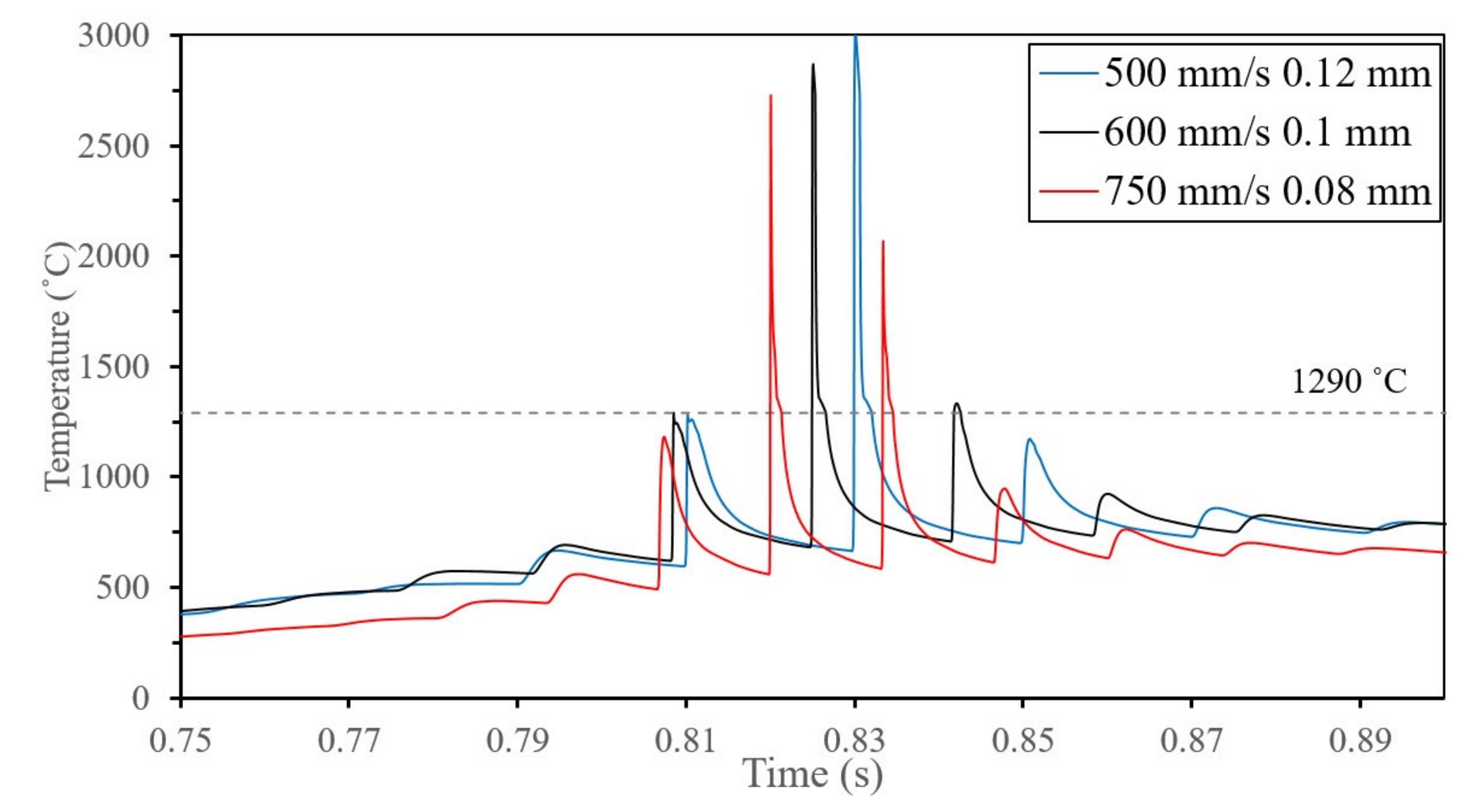
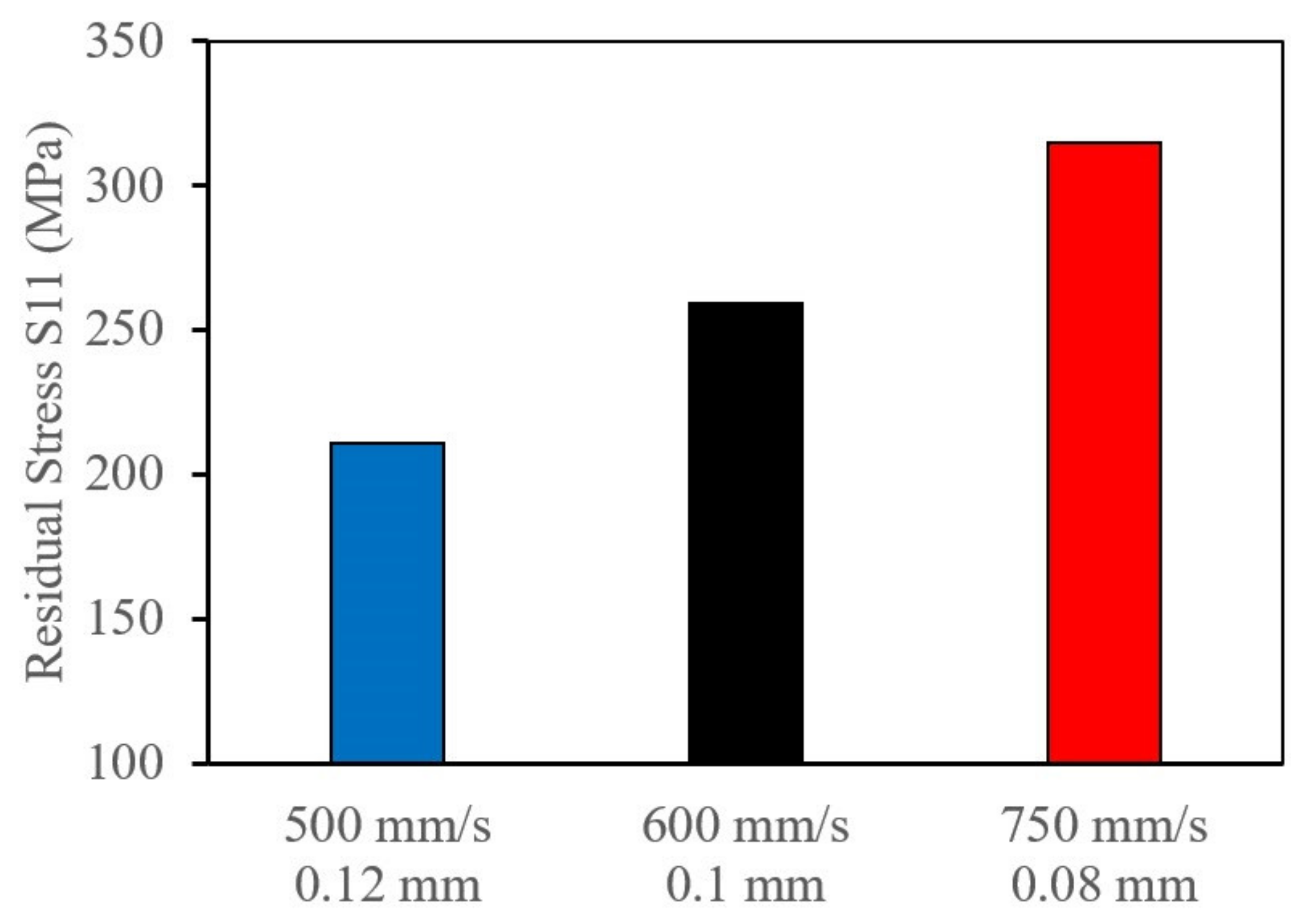
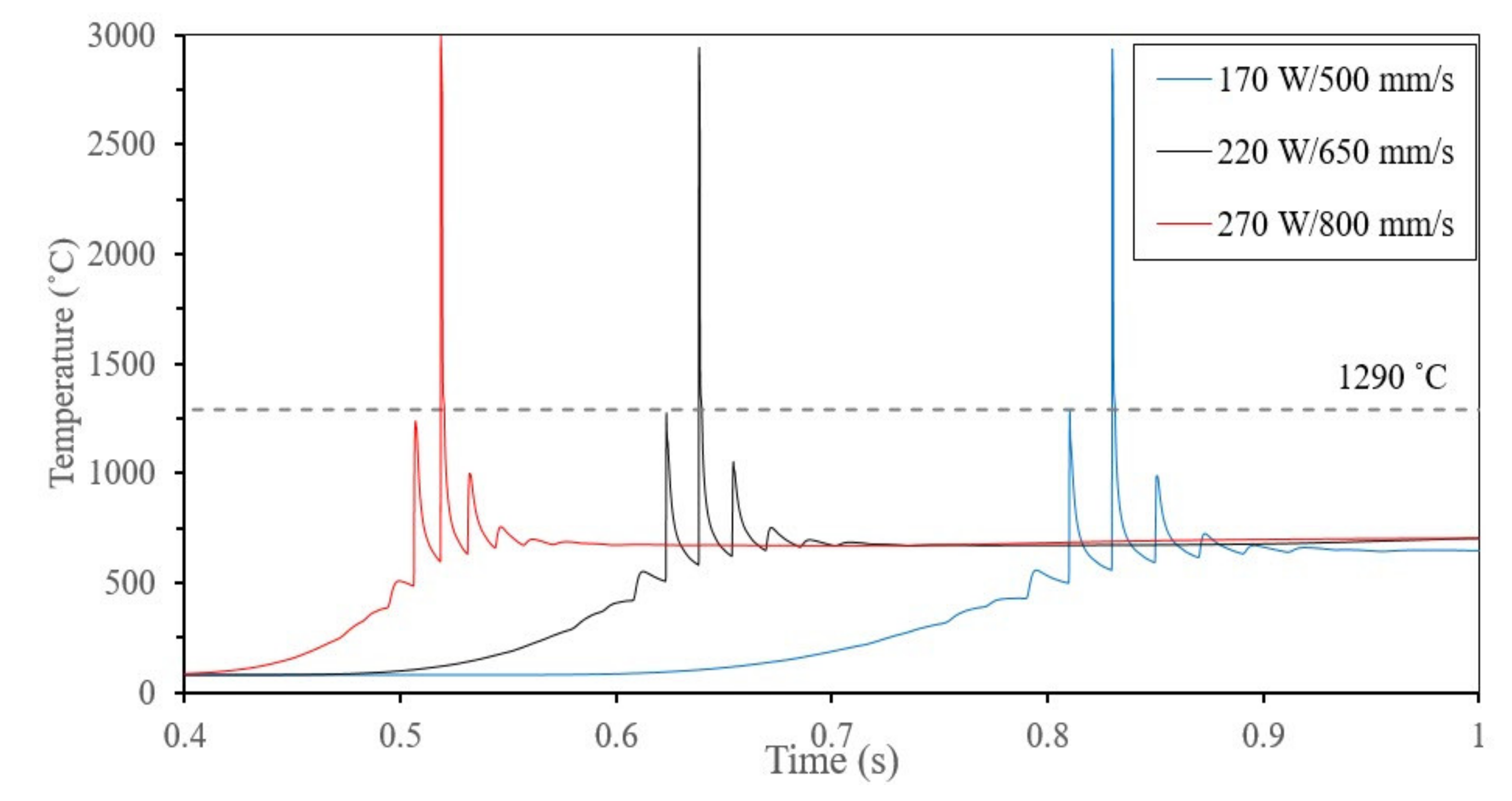
4.2.2. Effect of Scan Speed on RS
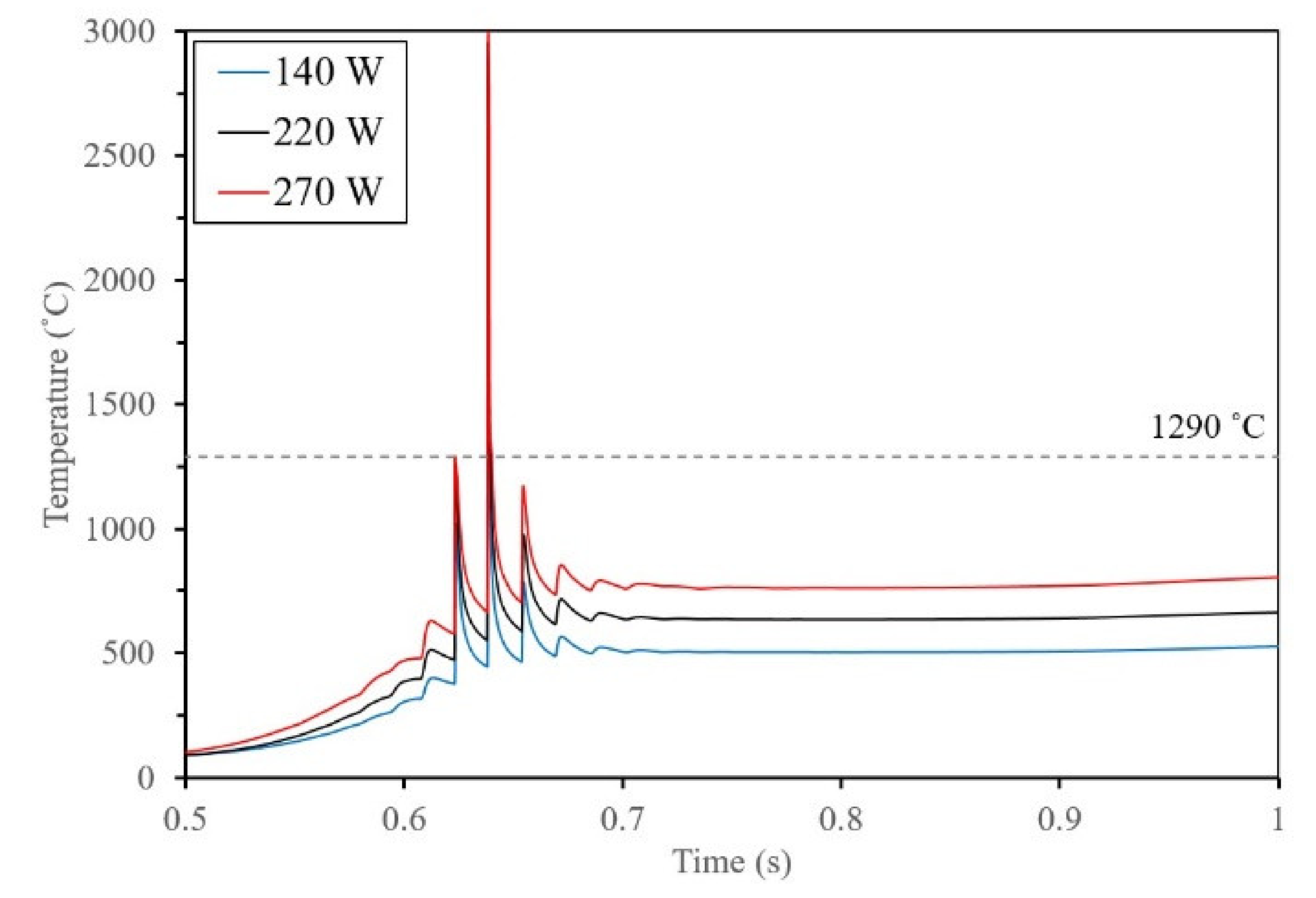
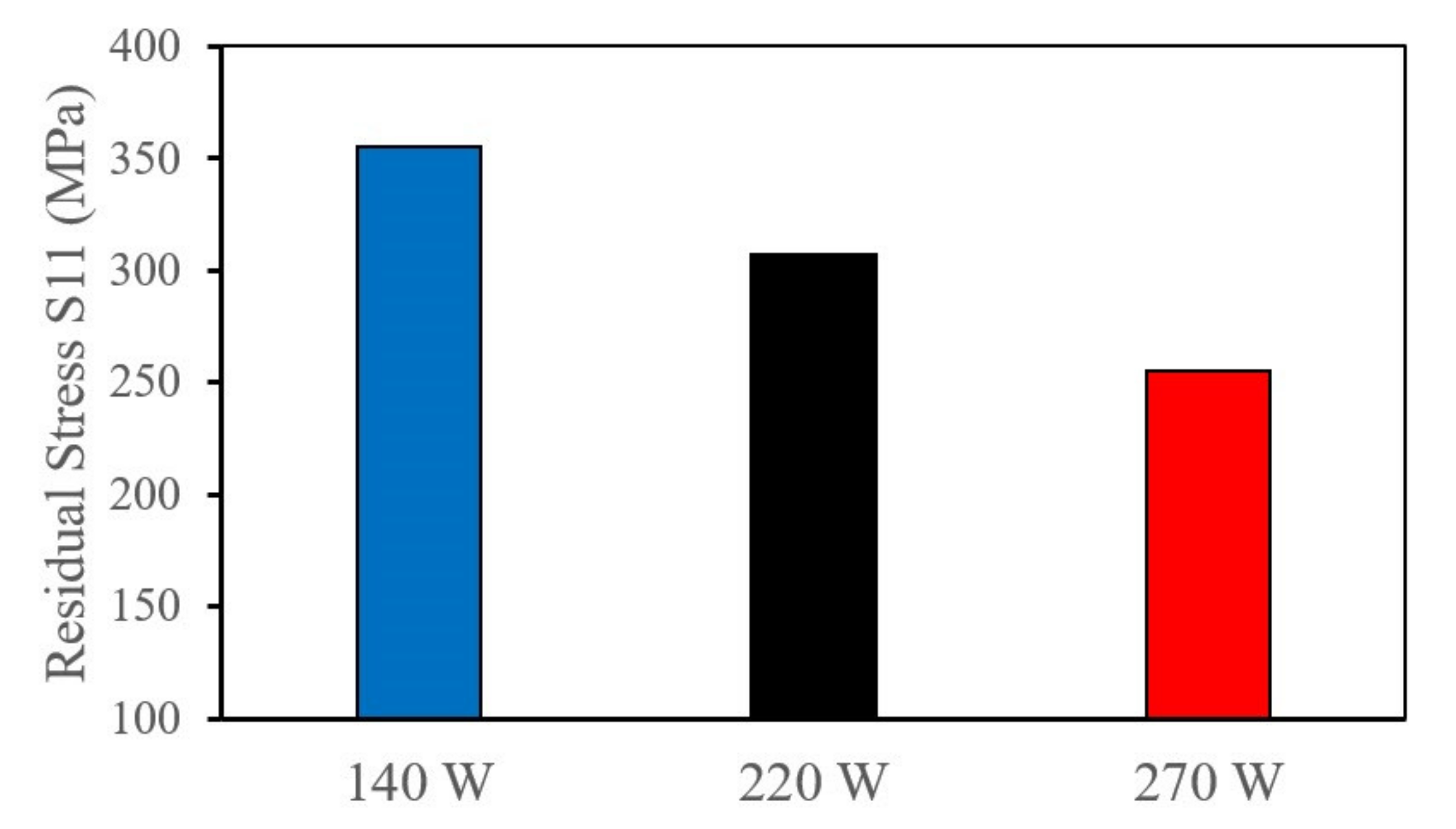
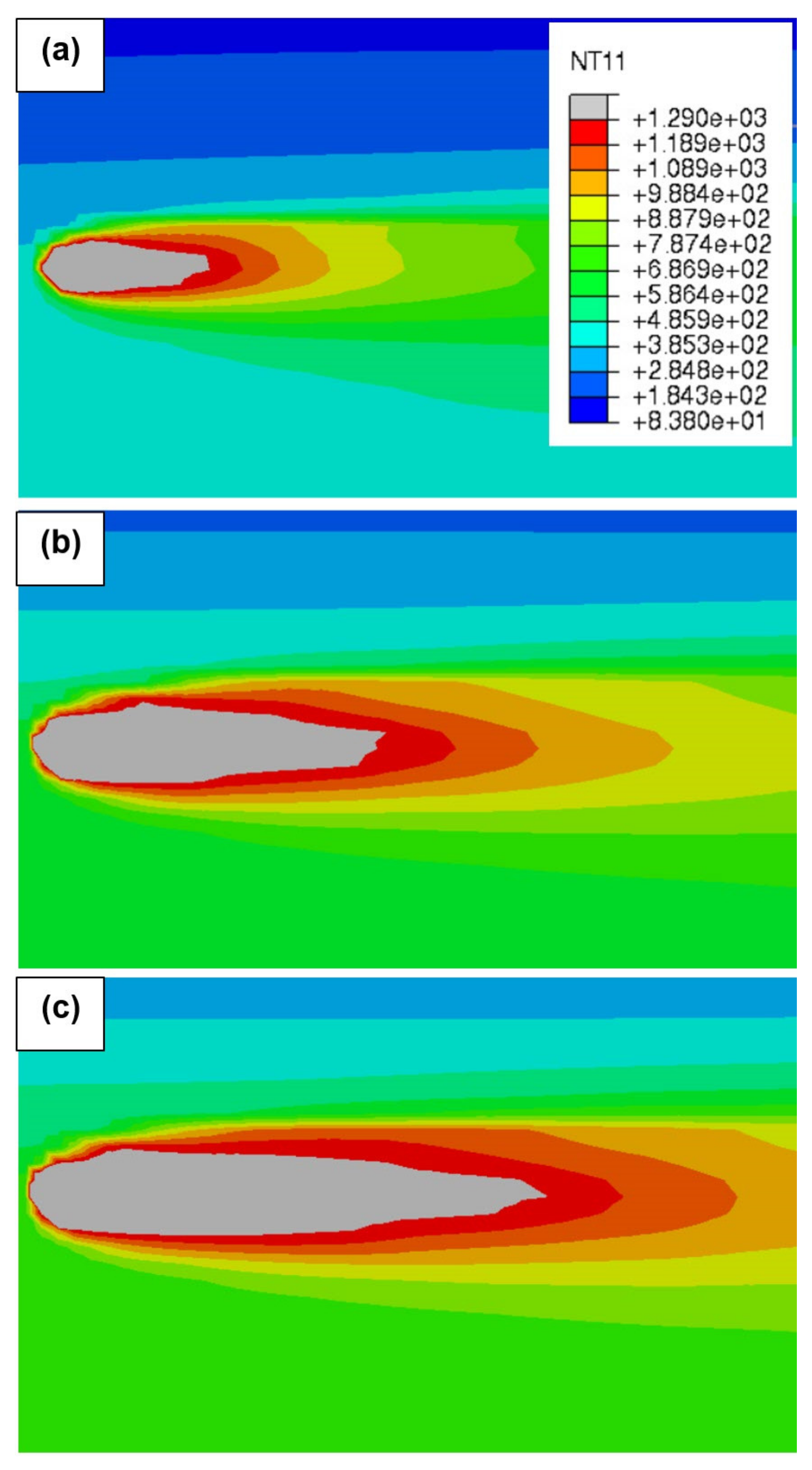
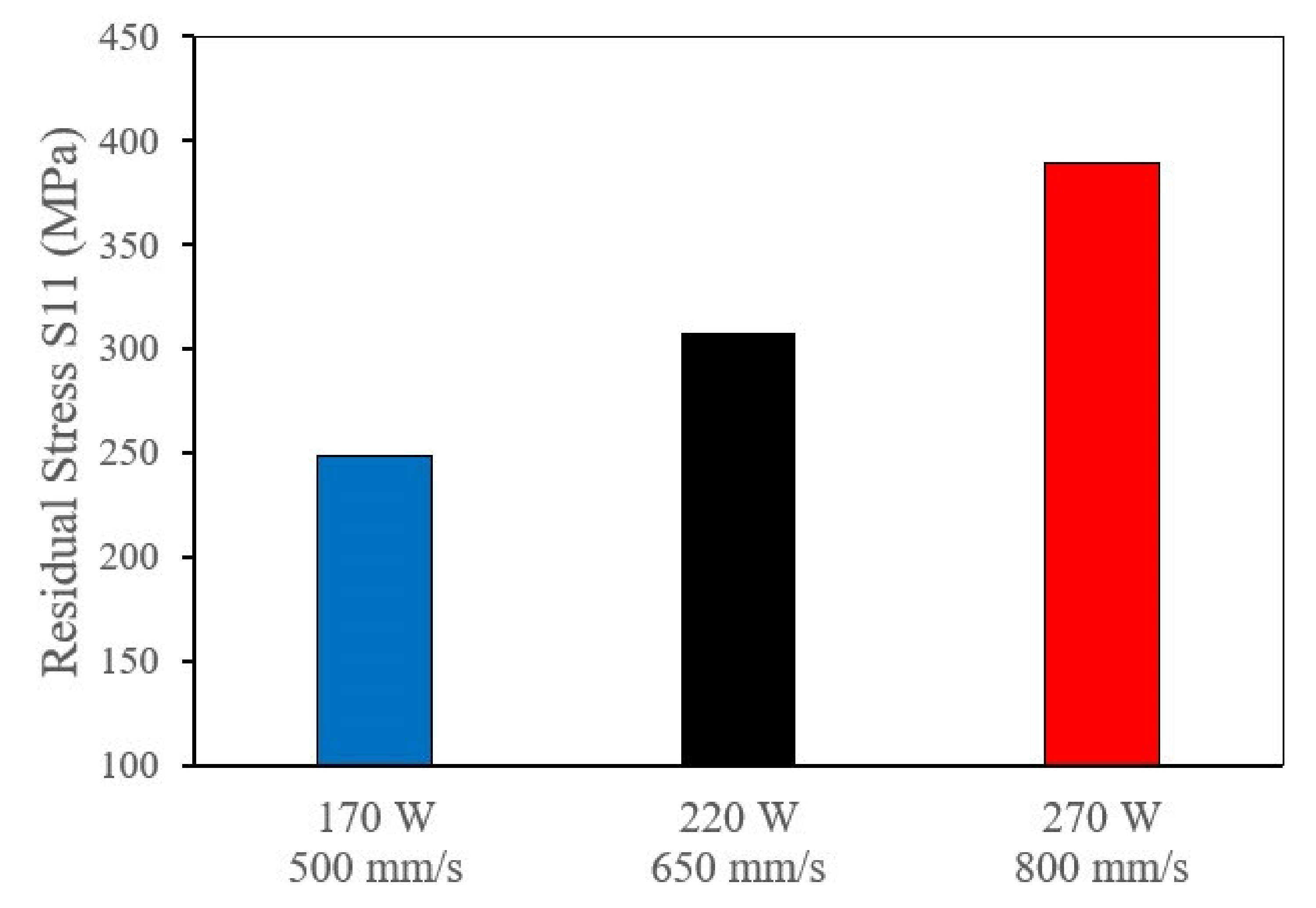
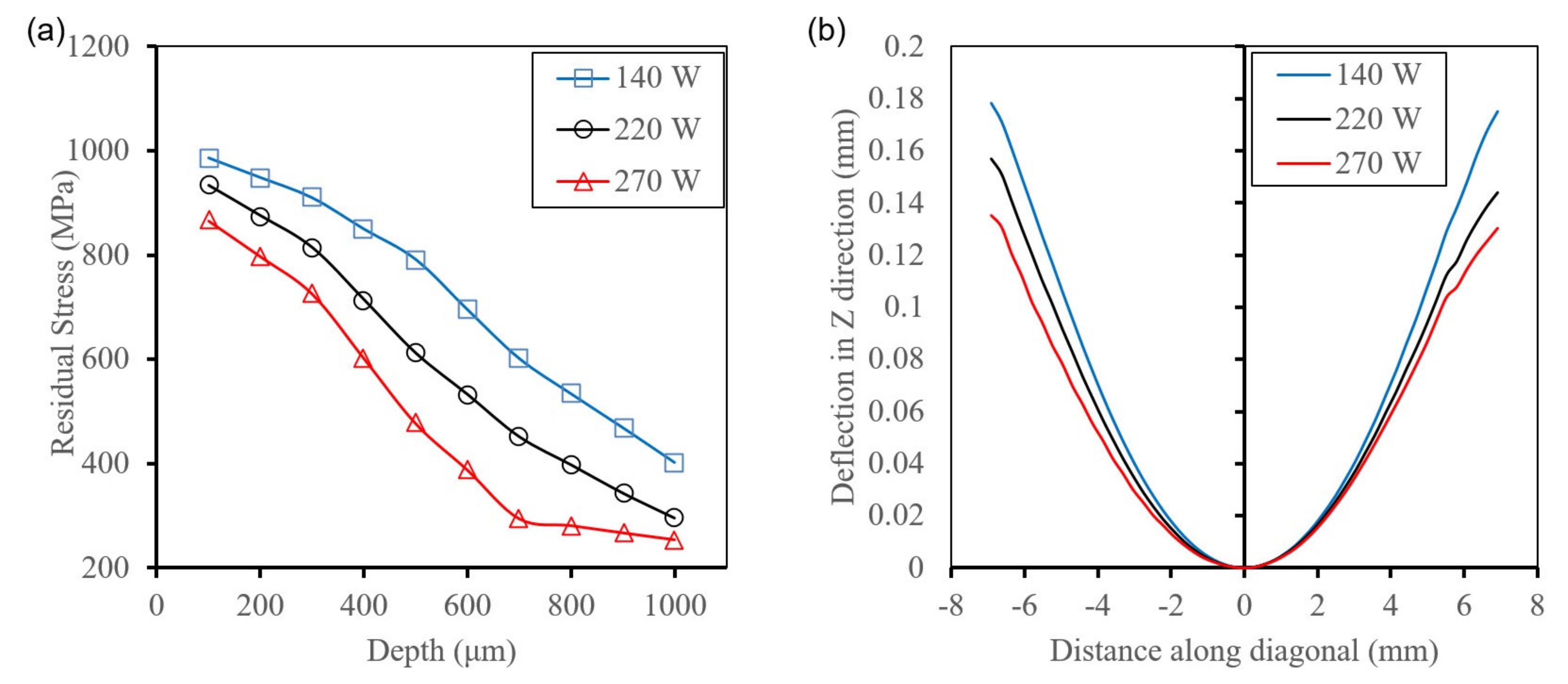
4.2.3. Effect of Laser Power on RS
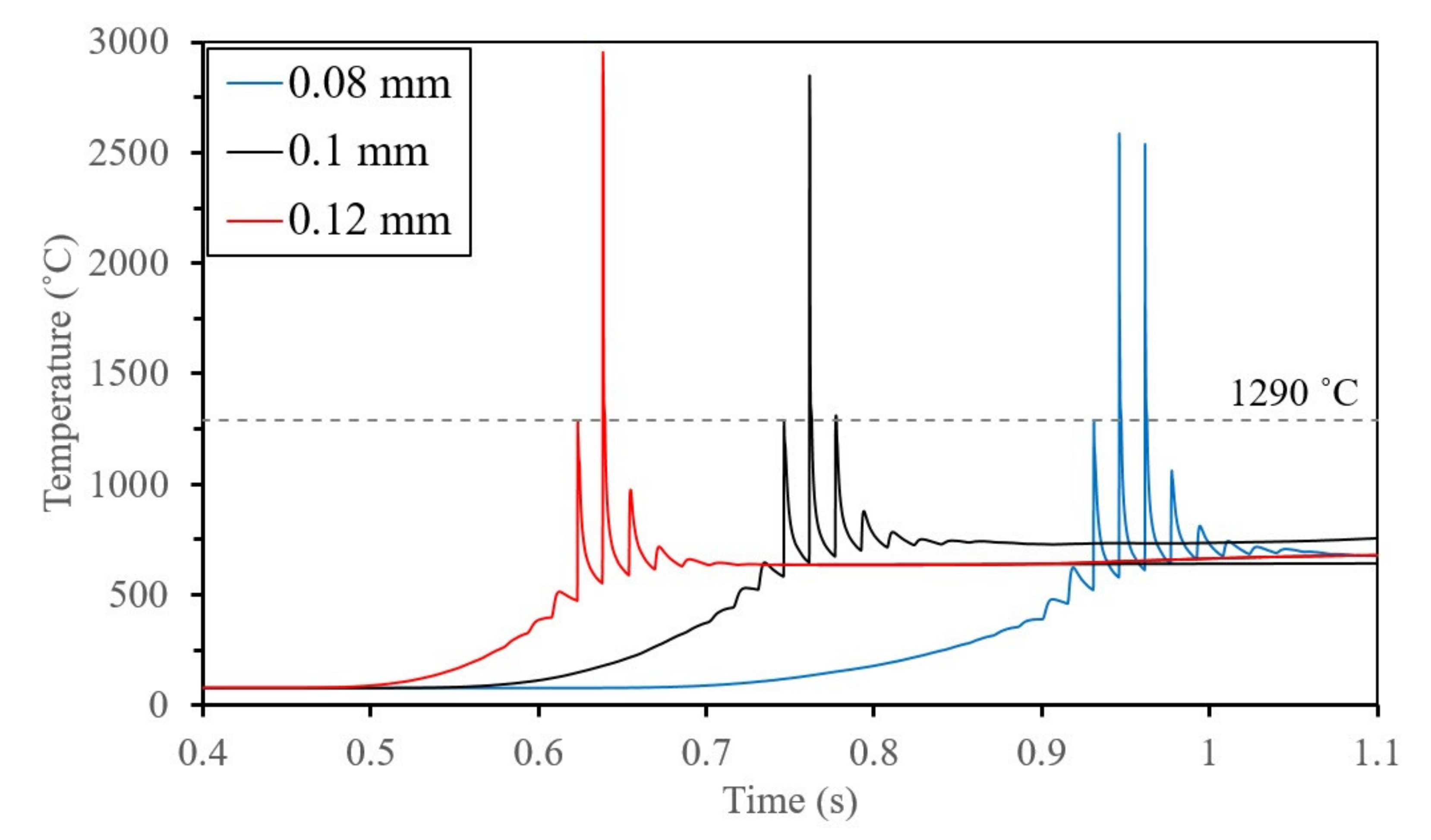
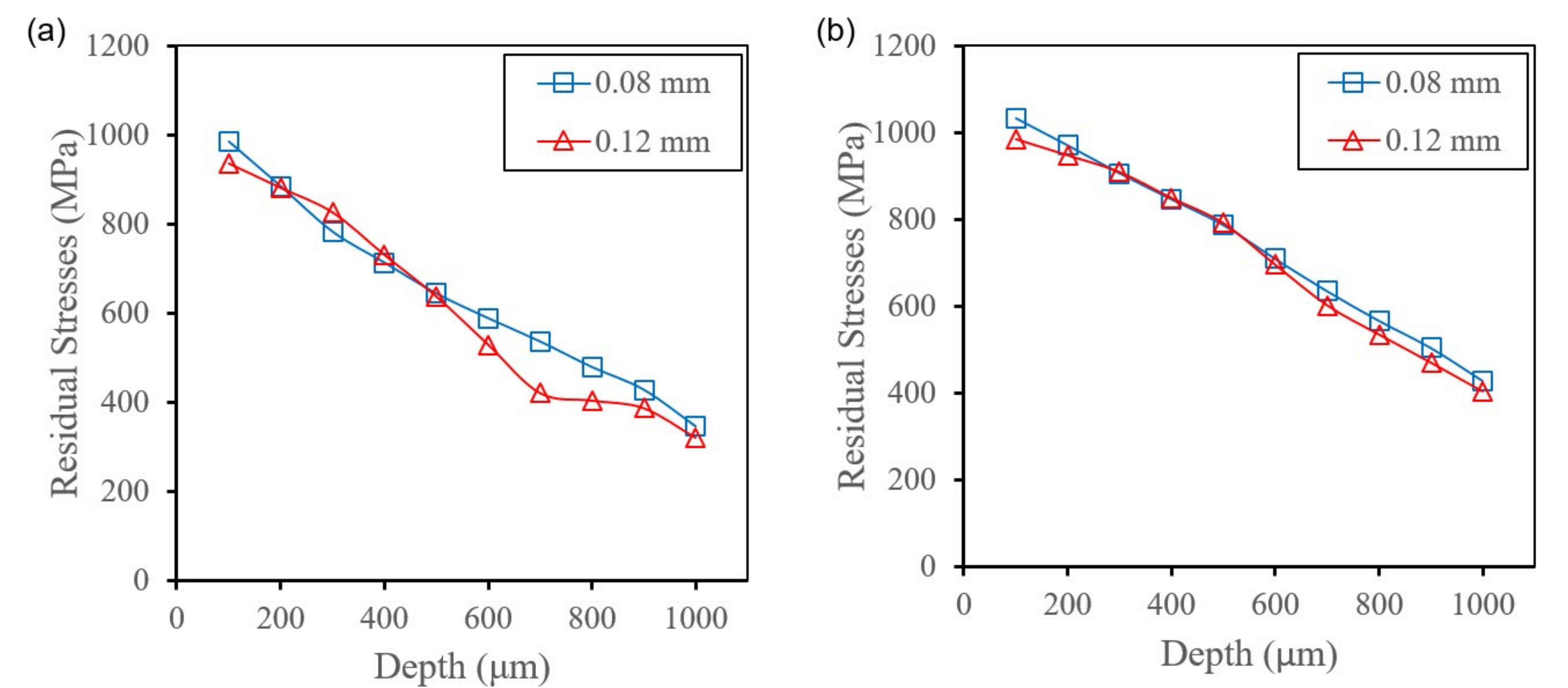
4.2.4. Effect of Hatch Spacing on RS
4.2.5. Effect of Same Energy Density
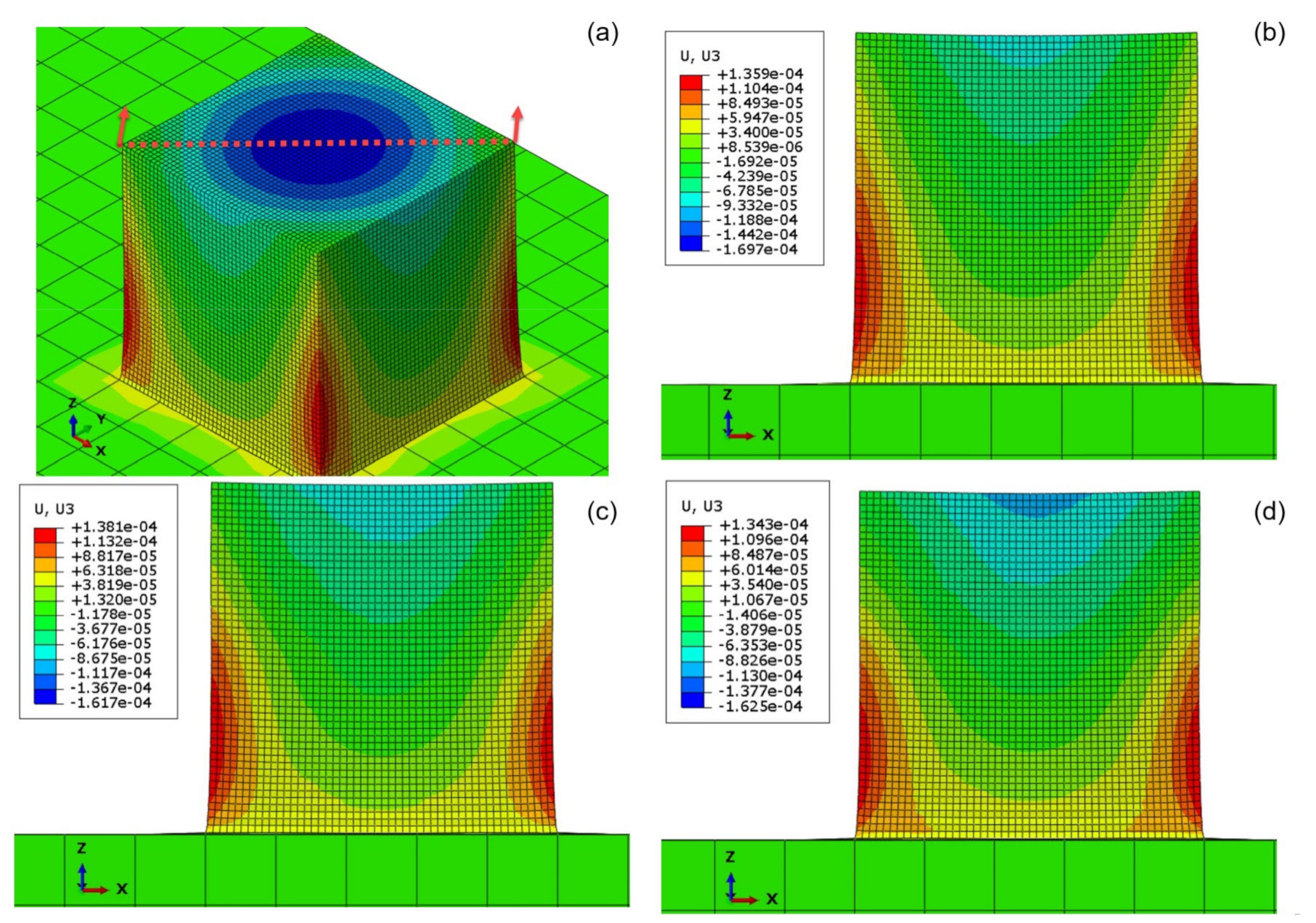
4.3. Part Scale Model
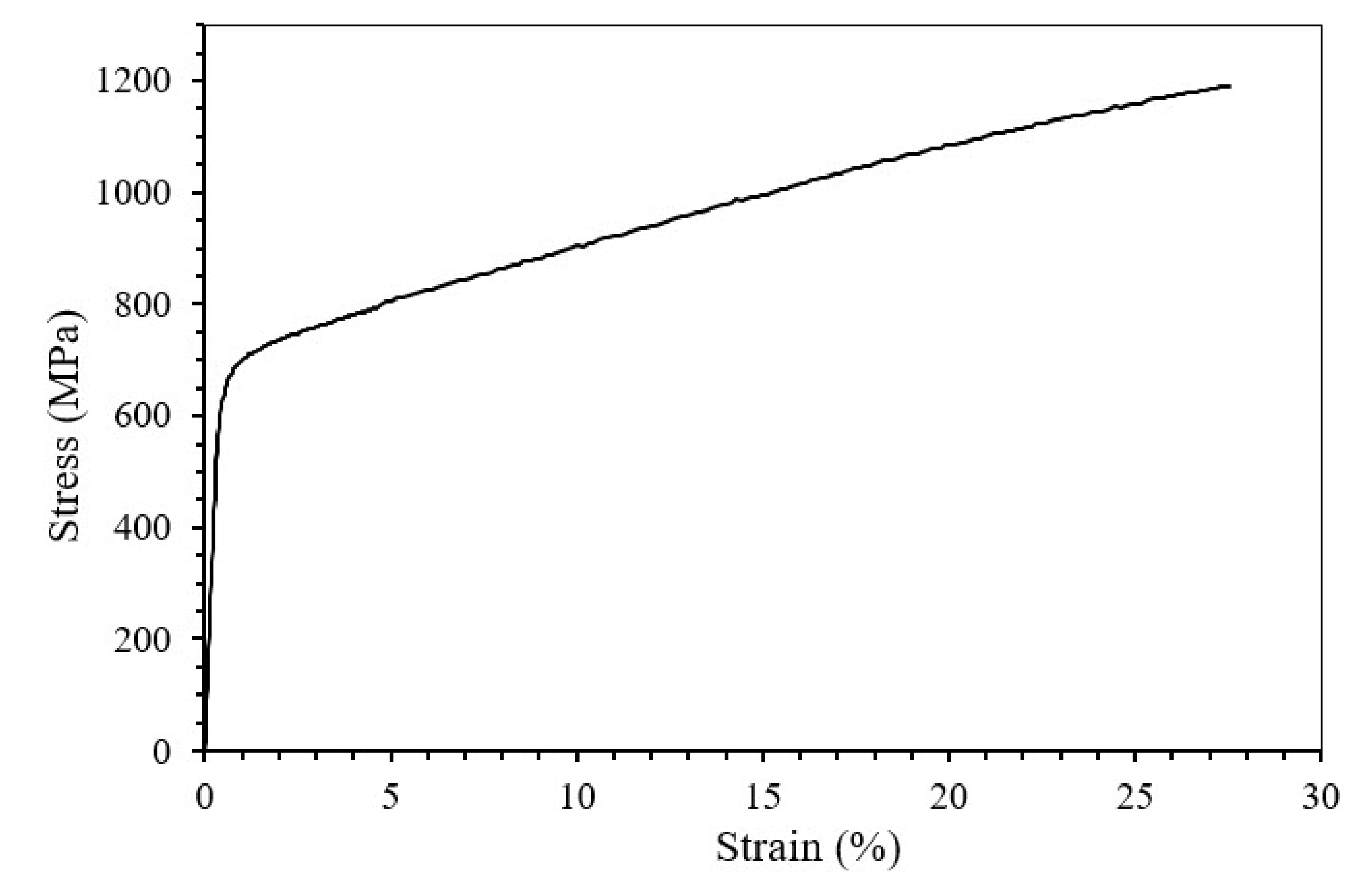
4.3.1. Tensile Test
4.3.2. Numerical Results
5. Conclusions
- The exponential decay volumetric heat source, with an artificial increase in thermal conductivity to account for the Marangoni effects, resulted in the best prediction of melt pool dimensions.
- The maximum residual stress is generated along the laser scan direction, governed by the temperature gradient and cooling rate in the hatch direction.
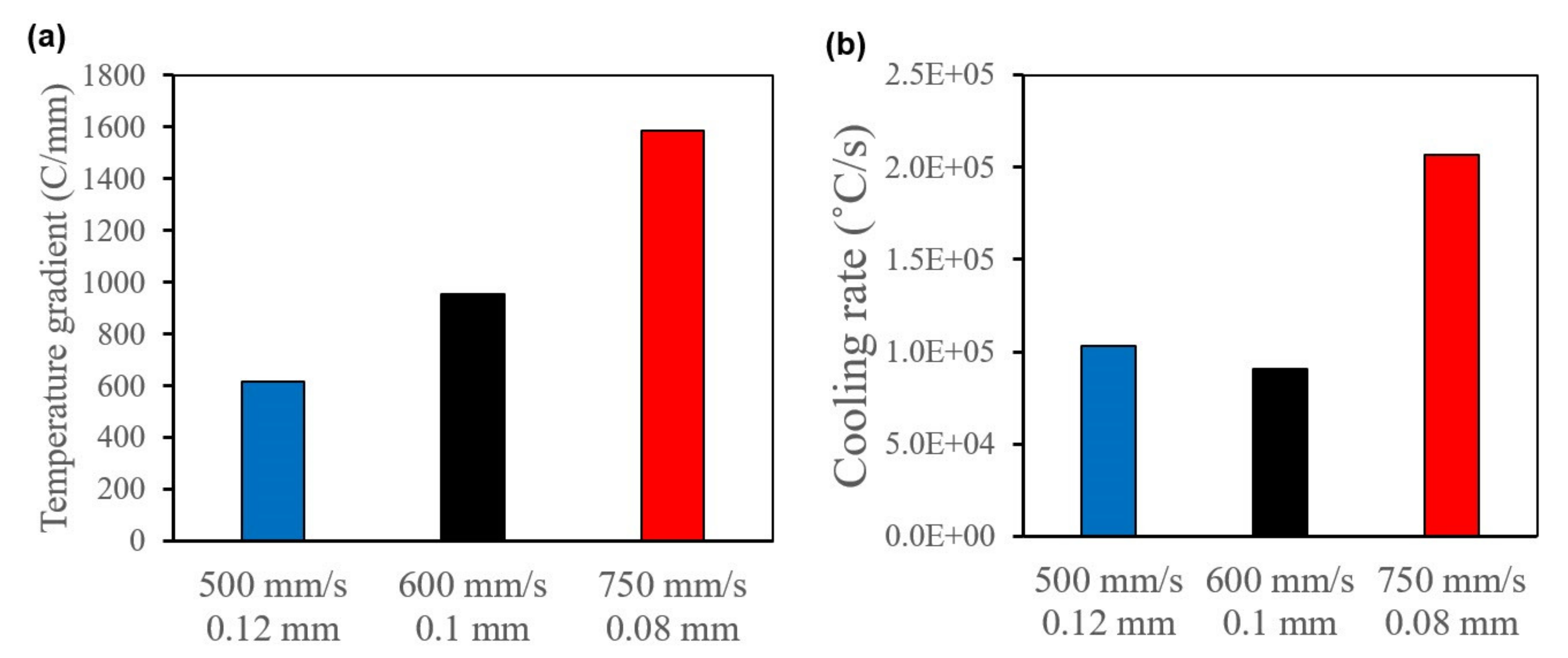
- Increasing the scan speed resulted in an increase in the surface tensile residual stress due to the increase in the temperature gradient.
- The surface tensile residual stress decreases with the increase in hatch spacing.
- At the same energy density, the thermal stresses are mostly affected by the scan speed, laser power, and hatch spacing.
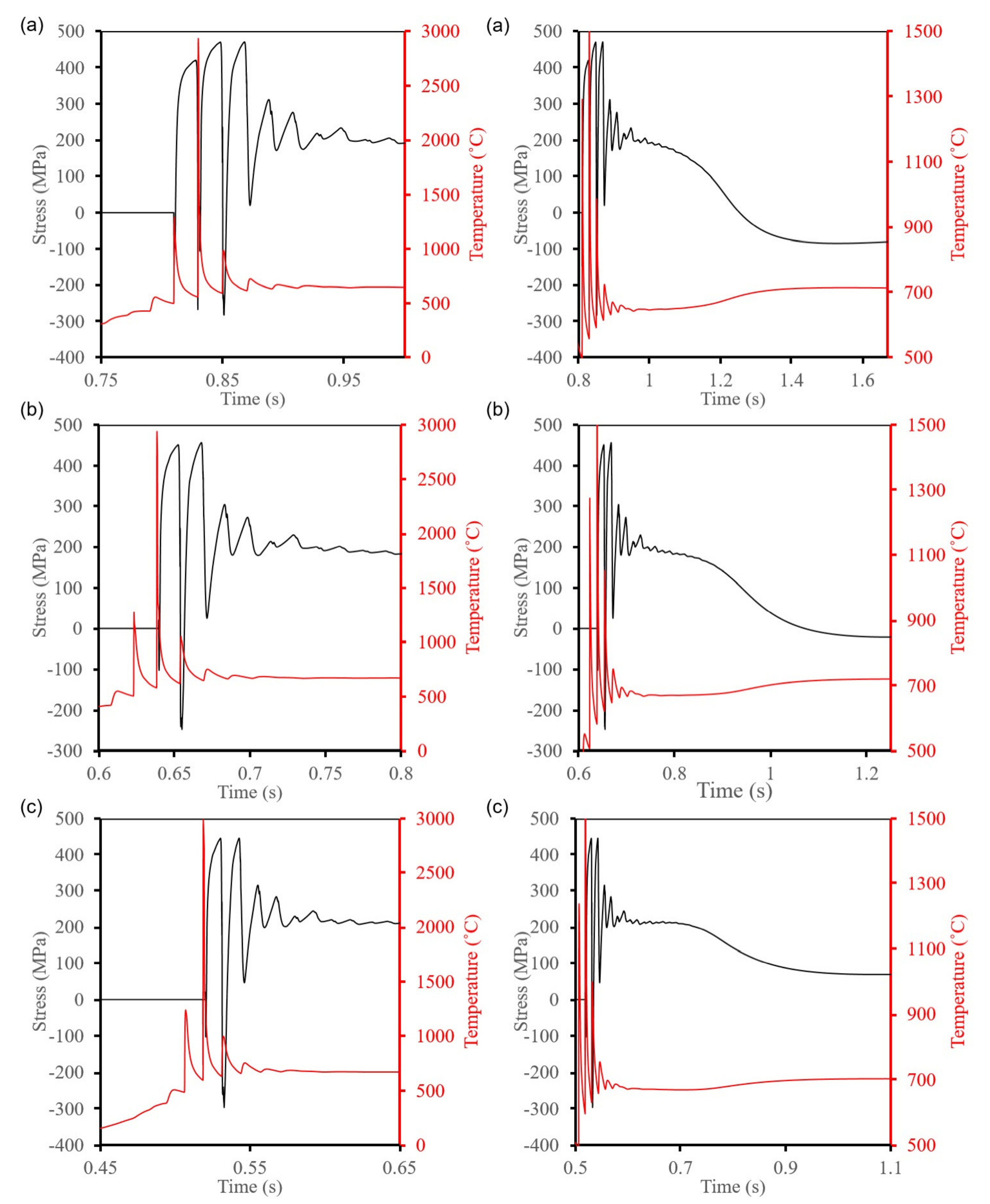
- Although the high cooling rate will increase the strain rate experienced by the material, the evolution of the stresses is mainly dominated by the temperature gradient.
- The cyclic temperature governs the final state of the stress during the non-linear phase and the cooling rate during the linear phase.
- In-depth residual stresses on a part scale and the top surface deflection exhibit the same trend, where increasing the laser power lowers the residual stresses.
- Increasing the scan speed increases the in-depth residual stresses as well as the top surface deflection.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ISO/ASTM52900-15, Standard Terminology for Additive Manufacturing—General Principles—Terminology; ASTM International: West Conshohocken, PA, USA. 2015. Available online: www.astm.org (accessed on 1 September 2021).
- DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.M.; Wilson-Heid, A.D.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Armillotta, A.; Baraggi, R.; Fasoli, S. SLM tooling for die casting with conformal cooling channels. Int. J. Adv. Manuf. Technol. 2014, 71, 573–583. [Google Scholar] [CrossRef] [Green Version]
- Dehoff, R.; Duty, C.; Peter, W.; Yamamoto, Y.; Chen, W.; Blue, C.; Tallman, C. Case study: Additive manufacturing of aerospace brackets. Adv. Mater. Process. 2013, 171, 19–23. [Google Scholar]
- Huang, R.; Riddle, M.; Graziano, D.; Warren, J.; Das, S.; Nimbalkar, S.; Cresko, J.; Masanet, E. Energy and emissions saving potential of additive manufacturing: The case of lightweight aircraft components. J. Clean. Prod. 2016, 135, 1559–1570. [Google Scholar] [CrossRef] [Green Version]
- Leal, R.; Barreiros, F.; Alves, L.; Romeiro, F.; Vasco, J.; Santos, M.; Marto, C. Additive manufacturing tooling for the automotive industry. Int. J. Adv. Manuf. Technol. 2017, 92, 1671–1676. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.; Bai, Q. Defect formation mechanisms in selective laser melting: A review. Chin. J. Mech. Eng. 2017, 30, 515–527. [Google Scholar] [CrossRef] [Green Version]
- Piscopo, G.; Salmi, A.; Atzeni, E. On the quality of unsupported overhangs produced by laser powder bed fusion. Int. J. Manuf. Res. 2019, 14, 198–216. [Google Scholar] [CrossRef] [Green Version]
- Balbaa, M.; Ghasemi, A.; Fereiduni, E.; Elbestawi, M.; Jadhav, S.; Kruth, J.-P. Role of powder particle size on laser powder bed fusion processability of AlSi10Mg alloy. Addit. Manuf. 2020, 37, 101630. [Google Scholar] [CrossRef]
- Criales, L.E.; Arısoy, Y.M.; Lane, B.; Moylan, S.; Donmez, A.; Özel, T. Laser powder bed fusion of nickel alloy 625: Experimental investigations of effects of process parameters on melt pool size and shape with spatter analysis. Int. J. Mach. Tools Manuf. 2017, 121, 22–36. [Google Scholar] [CrossRef]
- Maamoun, A.H.; Xue, Y.F.; Elbestawi, M.A.; Veldhuis, S.C. Effect of selective laser melting process parameters on the quality of al alloy parts: Powder characterization, density, surface roughness, and dimensional accuracy. Materials 2018, 11, 2343. [Google Scholar] [CrossRef] [Green Version]
- Narvan, M.; Al-Rubaie, K.S.; Elbestawi, M. Process-structure-property relationships of AISI H13 tool steel processed with selective laser melting. Materials 2019, 12, 2284. [Google Scholar] [CrossRef] [Green Version]
- Sealy, M.P.; Madireddy, G.; Williams, R.E.; Rao, P.; Toursangsaraki, M. Hybrid processes in additive manufacturing. J. Manuf. Sci. Eng. 2018, 140, 060801. [Google Scholar] [CrossRef]
- Han, S.; Salvatore, F.; Rech, J.; Bajolet, J. Abrasive flow machining (AFM) finishing of conformal cooling channels created by selective laser melting (SLM). Precis. Eng. 2020, 64, 20–33. [Google Scholar] [CrossRef]
- Kruth, J.-P.; Deckers, J.; Yasa, E.; Wauthlé, R. Assessing and comparing influencing factors of residual stresses in selective laser melting using a novel analysis method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 980–991. [Google Scholar] [CrossRef]
- Narvan, M.; Ghasemi, A.; Fereiduni, E.; Kendrish, S.; Elbestawi, M. Part deflection and residual stresses in laser powder bed fusion of H13 tool steel. Mater. Des. 2021, 204, 109659. [Google Scholar] [CrossRef]
- Yang, Y.; Allen, M.; London, T.; Oancea, V. Residual strain predictions for a powder bed fusion Inconel 625 single cantilever part. Integr. Mater. Manuf. Innov. 2019, 8, 294–304. [Google Scholar] [CrossRef] [Green Version]
- Simson, T.; Emmel, A.; Dwars, A.; Böhm, J. Residual stress measurements on AISI 316L samples manufactured by selective laser melting. Addit. Manuf. 2017, 17, 183–189. [Google Scholar] [CrossRef]
- Kruth, J.-P.; Mercelis, P.; Van Vaerenbergh, J.; Froyen, L.; Rombouts, M. Binding mechanisms in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2005, 11, 26–36. [Google Scholar] [CrossRef] [Green Version]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Fu, C.; Guo, Y. 3-dimensional finite element modeling of selective laser melting Ti-6Al-4V alloy. In Proceedings of the 25th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 4–6 August 2014. [Google Scholar]
- Roberts, I.; Wang, C.; Esterlein, R.; Stanford, M.; Mynors, D. A three-dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. Int. J. Mach. Tools Manuf. 2009, 49, 916–923. [Google Scholar] [CrossRef]
- Dong, L.; Makradi, A.; Ahzi, S.; Remond, Y. Three-dimensional transient finite element analysis of the selective laser sintering process. J. Mater. Process. Technol. 2009, 209, 700–706. [Google Scholar] [CrossRef]
- Dong, L.; Correia, J.; Barth, N.; Ahzi, S. Finite element simulations of temperature distribution and of densification of a titanium powder during metal laser sintering. Addit. Manuf. 2017, 13, 37–48. [Google Scholar] [CrossRef]
- Andreotta, R.; Ladani, L.; Brindley, W. Finite element simulation of laser additive melting and solidification of Inconel 718 with experimentally tested thermal properties. Finite Elem. Anal. Des. 2017, 135, 36–43. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Mukherjee, T.; Wei, H.; De, A.; DebRoy, T. Heat and fluid flow in additive manufacturing—Part I: Modeling of powder bed fusion. Comput. Mater. Sci. 2018, 150, 304–313. [Google Scholar] [CrossRef] [Green Version]
- Robichaud, J.; Vincent, T.; Schultheis, B.; Chaudhary, A. Integrated computational materials engineering to predict melt-pool dimensions and 3D grain structures for selective laser melting of Inconel 625. Integr. Mater. Manuf. Innov. 2019, 8, 305–317. [Google Scholar] [CrossRef]
- Xia, M.; Gu, D.; Yu, G.; Dai, D.; Chen, H.; Shi, Q. Influence of hatch spacing on heat and mass transfer, thermodynamics and laser processability during additive manufacturing of Inconel 718 alloy. Int. J. Mach. Tools Manuf. 2016, 109, 147–157. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Jagdale, V.; Srinivasan, G.; El-Wardany, T.; Michaleris, P. Thermal modeling of Inconel 718 processed with powder bed fusion and experimental validation using in situ measurements. Addit. Manuf. 2016, 11, 7–15. [Google Scholar] [CrossRef]
- Criales, L.E.; Arısoy, Y.M.; Lane, B.; Moylan, S.; Donmez, A.; Özel, T. Predictive modeling and optimization of multi-track processing for laser powder bed fusion of nickel alloy 625. Addit. Manuf. 2017, 13, 14–36. [Google Scholar] [CrossRef]
- Masoomi, M.; Thompson, S.M.; Shamsaei, N. Laser powder bed fusion of Ti-6Al-4V parts: Thermal modeling and mechanical implications. Int. J. Mach. Tools Manuf. 2017, 118, 73–90. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Yin, J.; Zhu, H.; Xiao, Z.; Zhang, L.; Zeng, X. Effect of overlap rate and pattern on residual stress in selective laser melting. Int. J. Mach. Tools Manuf. 2019, 145, 103433. [Google Scholar] [CrossRef]
- Olleak, A.; Xi, Z. Efficient lpbf process simulation using finite element modeling with adaptive remeshing for distortions and residual stresses prediction. Manuf. Lett. 2020, 24, 140–144. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, X.; Hayduke, D.; Liu, J.; Cheng, L.; Oskin, J.; Whitmore, R.; To, A.C. An inherent strain based multiscale modeling framework for simulating part-scale residual deformation for direct metal laser sintering. Addit. Manuf. 2019, 28, 406–418. [Google Scholar] [CrossRef]
- Gouge, M.; Denlinger, E.; Irwin, J.; Li, C.; Michaleris, P. Experimental validation of thermo-mechanical part-scale modeling for laser powder bed fusion processes. Addit. Manuf. 2019, 29, 100771. [Google Scholar] [CrossRef]
- Turner, J.A.; Babu, S.S.; Blue, C. Advanced Simulation for Additive Manufacturing: Meeting Challenges through Collaboration. 2015. Available online: https://info.ornl.gov/sites/publications/files/Pub56487.pdf (accessed on 1 September 2021).
- Lavery, N.P.; Brown, S.G.; Sienz, J.; Cherry, J.; Belblidia, F. A review of computational modelling of additive layer manufacturing—Multi-scale and multi-physics. Sustain. Des. Manuf. 2014, 651, 673. [Google Scholar]
- Mirkoohi, E.; Ning, J.; Bocchini, P.; Fergani, O.; Chiang, K.-N.; Liang, S.Y. Thermal modeling of temperature distribution in metal additive manufacturing considering effects of build layers, latent heat, and temperature-sensitivity of material properties. J. Manuf. Mater. Process. 2018, 2, 63. [Google Scholar] [CrossRef] [Green Version]
- Neiva, E.; Chiumenti, M.; Cervera, M.; Salsi, E.; Piscopo, G.; Badia, S.; Martín, A.F.; Chen, Z.; Lee, C.; Davies, C. Numerical modelling of heat transfer and experimental validation in powder-bed fusion with the virtual domain approximation. Finite Elem. Anal. Des. 2020, 168, 103343. [Google Scholar] [CrossRef]
- Criales, L.E.; Arısoy, Y.M.; Özel, T. Sensitivity analysis of material and process parameters in finite element modeling of selective laser melting of Inconel 625. Int. J. Adv. Manuf. Technol. 2016, 86, 2653–2666. [Google Scholar] [CrossRef]
- Gan, Z.; Lian, Y.; Lin, S.E.; Jones, K.K.; Liu, W.K.; Wagner, G.J. Benchmark study of thermal behavior, surface topography, and dendritic microstructure in selective laser melting of Inconel 625. Integr. Mater. Manuf. Innov. 2019, 8, 178–193. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, L.; Tan, L.; Bai, P.; Li, J.; Wu, L.; Liao, H.; Cheng, Y. Simulation of stress field during the selective laser melting process of the nickel-based superalloy, GH4169. Materials 2018, 11, 1525. [Google Scholar] [CrossRef] [Green Version]
- Heeling, T.; Cloots, M.; Wegener, K. Melt pool simulation for the evaluation of process parameters in selective laser melting. Addit. Manuf. 2017, 14, 116–125. [Google Scholar] [CrossRef]
- Xiao, Z.; Chen, C.; Zhu, H.; Hu, Z.; Nagarajan, B.; Guo, L.; Zeng, X. Study of residual stress in selective laser melting of Ti6Al4V. Mater. Des. 2020, 193, 108846. [Google Scholar] [CrossRef]
- Churchill, S.W. A comprehensive correlating equation for forced convection from flat plates. AIChE J. 1976, 22, 264–268. [Google Scholar] [CrossRef]
- Sih, S.S.; Barlow, J.W. Emissivity of powder beds. In Proceedings of the 1995 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 1995. [Google Scholar]
- Sih, S.S.; Barlow, J.W. The prediction of the emissivity and thermal conductivity of powder beds. Part. Sci. Technol. 2004, 22, 427–440. [Google Scholar] [CrossRef]
- Heugenhauser, S.; Kaschnitz, E. Density and thermal expansion of the nickel-based superalloy INCONEL 625 in the solid and liquid states. High Temp.—High Press. 2019, 48, 381–393. [Google Scholar] [CrossRef]
- Balbaa, M.; Elbestawi, M.; McIsaac, J. An experimental investigation of surface integrity in selective laser melting of Inconel 625. Int. J. Adv. Manuf. Technol. 2019, 104, 3511–3529. [Google Scholar] [CrossRef]
- Zimina, N.; Fomicheva, I. Thermal accommodation in the gas-metal system. 3. Nitrogen. Zhurnal Fizicheskoi Khimii 1992, 66, 3184–3190. [Google Scholar]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Fischer, P.; Romano, V.; Weber, H.-P.; Karapatis, N.; Boillat, E.; Glardon, R. Sintering of commercially pure titanium powder with a Nd: YAG laser source. Acta Materialia 2003, 51, 1651–1662. [Google Scholar] [CrossRef]
- Markl, M.; Körner, C. Multiscale modeling of powder bed–based additive manufacturing. Annu. Rev. Mater. Res. 2016, 46, 93–123. [Google Scholar] [CrossRef]
- Zhao, Y.; Koizumi, Y.; Aoyagi, K.; Wei, D.; Yamanaka, K.; Chiba, A. Molten pool behavior and effect of fluid flow on solidification conditions in selective electron beam melting (SEBM) of a biomedical Co-Cr-Mo alloy. Addit. Manuf. 2019, 26, 202–214. [Google Scholar] [CrossRef]
- Miyata, Y.; Okugawa, M.; Koizumi, Y.; Nakano, T. Inverse columnar-equiaxed transition (CET) in 304 and 316L stainless steels melt by electron beam for additive manufacturing (AM). Crystals 2021, 11, 856. [Google Scholar] [CrossRef]
- Ladani, L.; Romano, J.; Brindley, W.; Burlatsky, S. Effective liquid conductivity for improved simulation of thermal transport in laser beam melting powder bed technology. Addit. Manuf. 2017, 14, 13–23. [Google Scholar] [CrossRef]
- Van Elsen, M.; Al-Bender, F.; Kruth, J.P. Application of dimensional analysis to selective laser melting. Rapid Prototyp. J. 2008, 14, 15–22. [Google Scholar] [CrossRef]
- Piscopo, G.; Atzeni, E.; Salmi, A. A hybrid modeling of the physics-driven evolution of material addition and track generation in laser powder directed energy deposition. Materials 2019, 12, 2819. [Google Scholar] [CrossRef] [Green Version]
- Abaqus User’s Manual. Available online: https://www.3ds.com/products-services/simulia/support/documentation (accessed on 1 September 2021).
- Song, X.; Feih, S.; Zhai, W.; Sun, C.-N.; Li, F.; Maiti, R.; Wei, J.; Yang, Y.; Oancea, V.; Brandt, L.R. Advances in additive manufacturing process simulation: Residual stresses and distortion predictions in complex metallic components. Mater. Des. 2020, 193, 108779. [Google Scholar] [CrossRef]
- Simulia. Abaqus 6.19 User’s Manual; Simulia: Johnston, RI, USA, 2019. [Google Scholar]
- Special Metals, Inconel Alloy 625. Available online: https://www.specialmetals.com/assets/smc/documents/alloys/inconel/inconel-alloy-625.pdf (accessed on 1 September 2021).
- Johnson, G.R. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Lotfi, M.; Jahanbakhsh, M.; Farid, A.A. Wear estimation of ceramic and coated carbide tools in turning of Inconel 625: 3D FE analysis. Tribol. Int. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- ASTM E8/E8M-21, Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2021.
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Lane, B.; Heigel, J.; Ricker, R.; Zhirnov, I.; Khromschenko, V.; Weaver, J.; Phan, T.; Stoudt, M.; Mekhontsev, S.; Levine, L. Measurements of melt pool geometry and cooling rates of individual laser traces on IN625 bare plates. Integr. Mater. Manuf. Innov. 2020, 9, 16–32. [Google Scholar] [CrossRef]
- Dilip, J.; Anam, M.A.; Pal, D.; Stucker, B. A short study on the fabrication of single track deposits in SLM and characterization. In Proceedings of the 2016 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Rezaeifar, H.; Elbestawi, M. On-line melt pool temperature control in L-PBF additive manufacturing. Int. J. Adv. Manuf. Technol. 2021, 112, 2789–2804. [Google Scholar] [CrossRef]
- Li, S.; Xiao, H.; Liu, K.; Xiao, W.; Li, Y.; Han, X.; Mazumder, J.; Song, L. Melt-pool motion, temperature variation and dendritic morphology of Inconel 718 during pulsed-and continuous-wave laser additive manufacturing: A comparative study. Mater. Des. 2017, 119, 351–360. [Google Scholar] [CrossRef]
- Schajer, G.S. Practical Residual Stress Measurement Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Balbaa, M.; Mekhiel, S.; Elbestawi, M.; McIsaac, J. On selective laser melting of Inconel 718: Densification, surface roughness, and residual stresses. Mater. Des. 2020, 193, 108818. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J.-P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Katayama, S. Handbook of Laser Welding Technologies; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
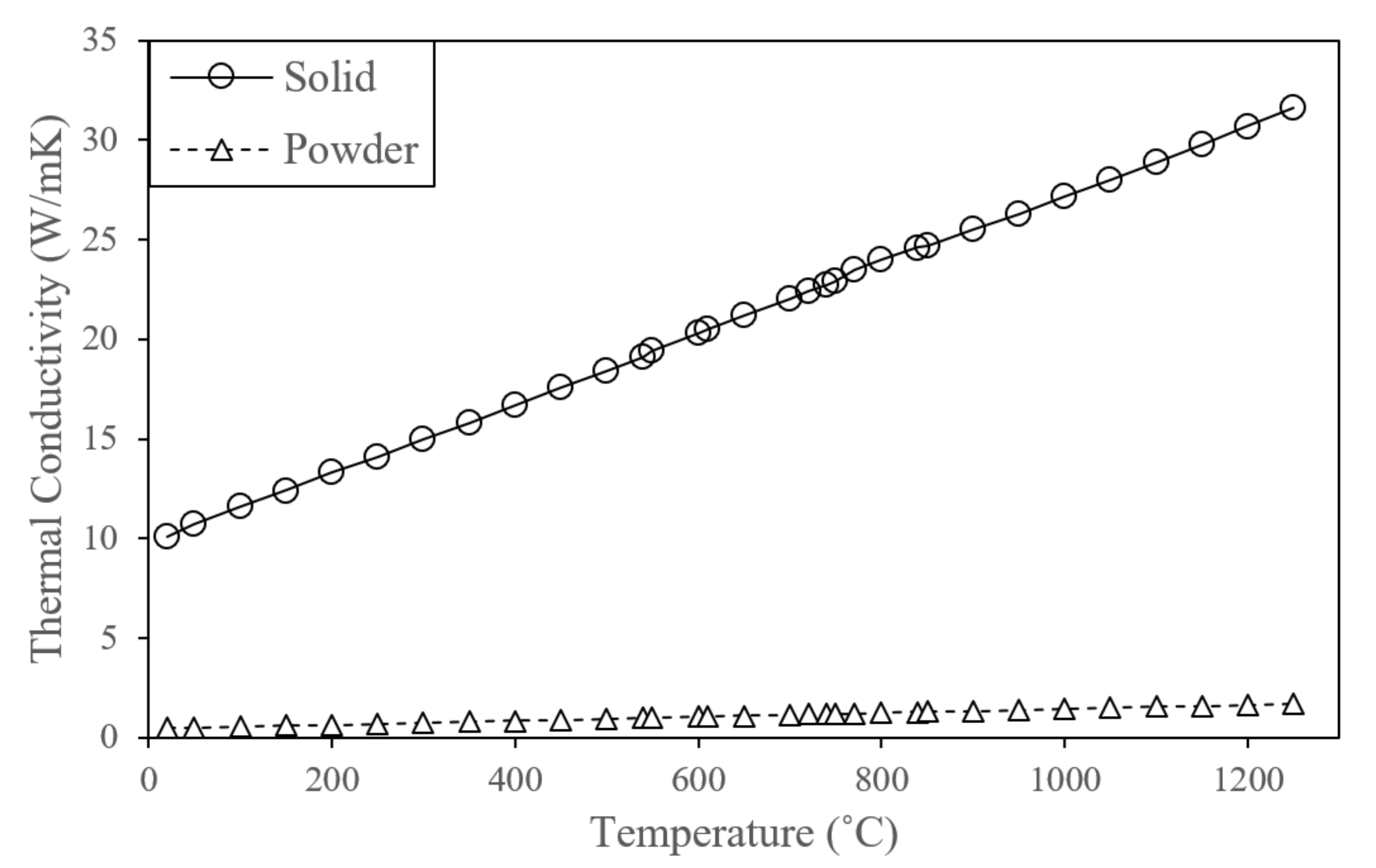

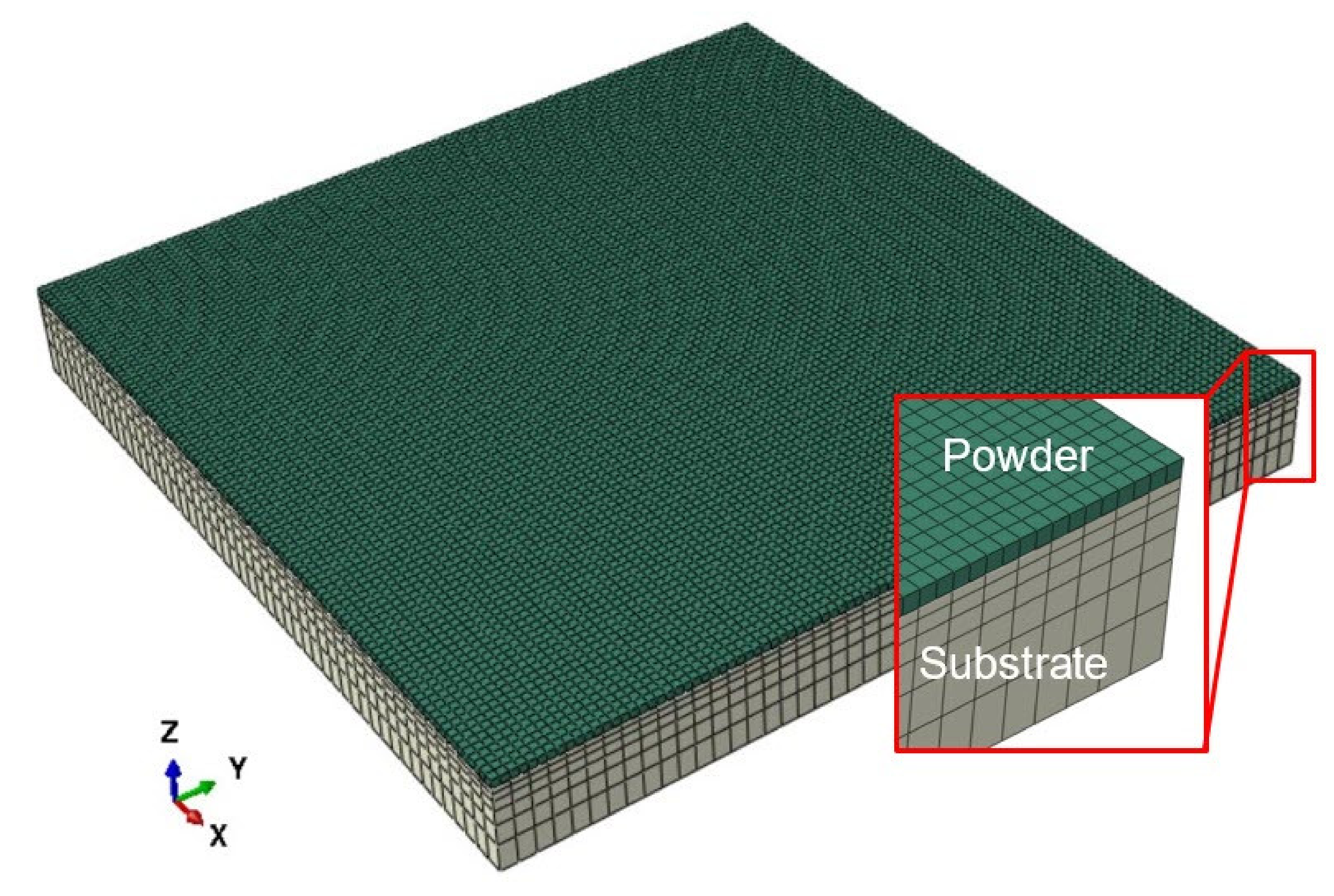

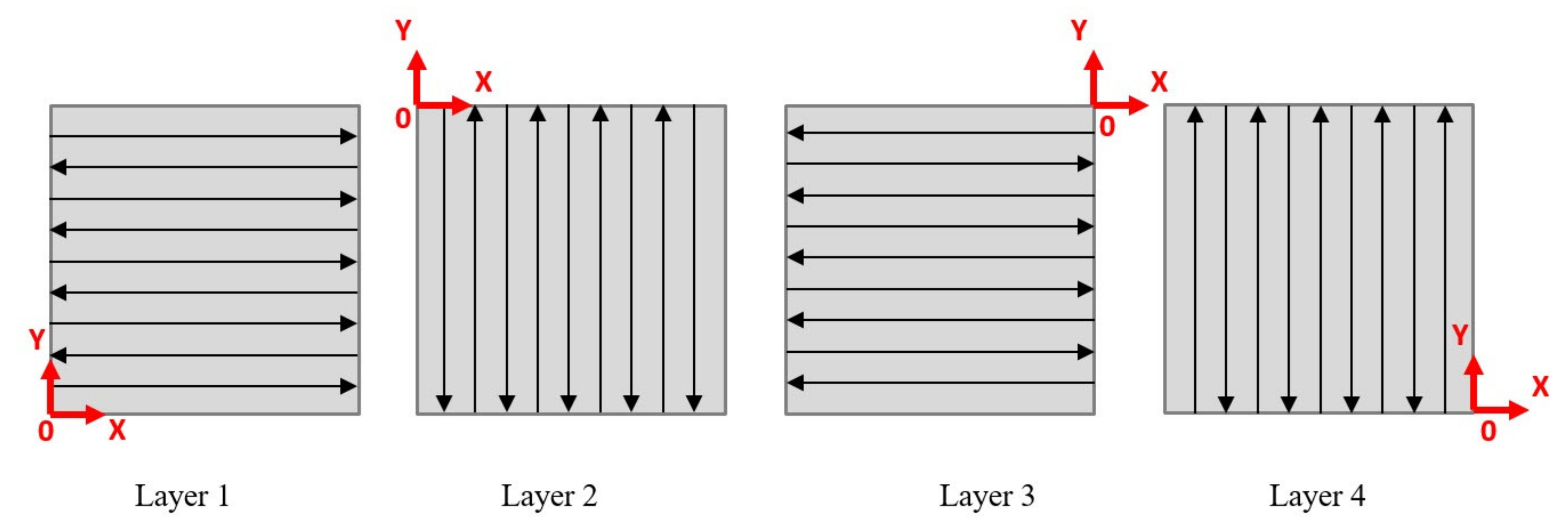

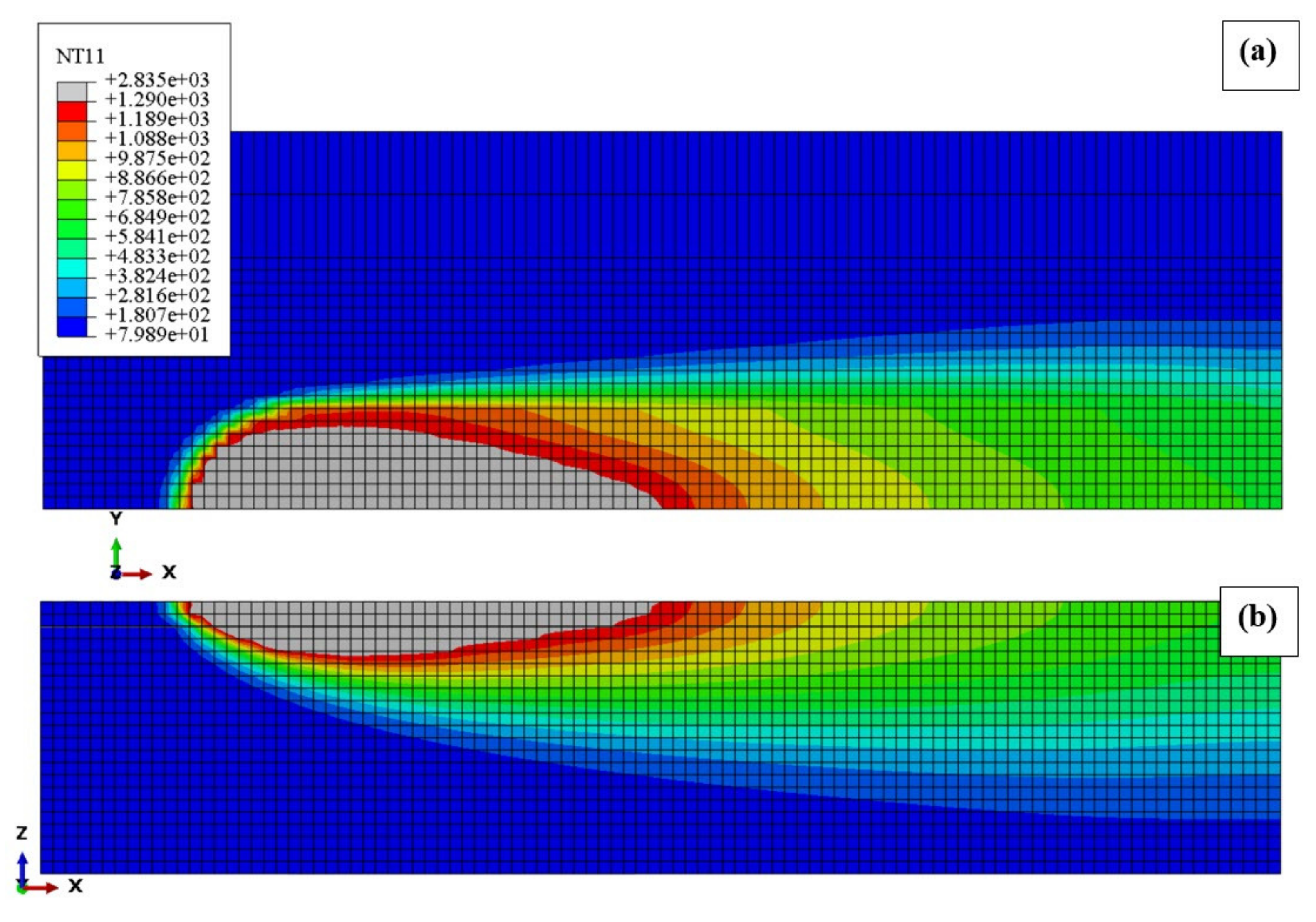



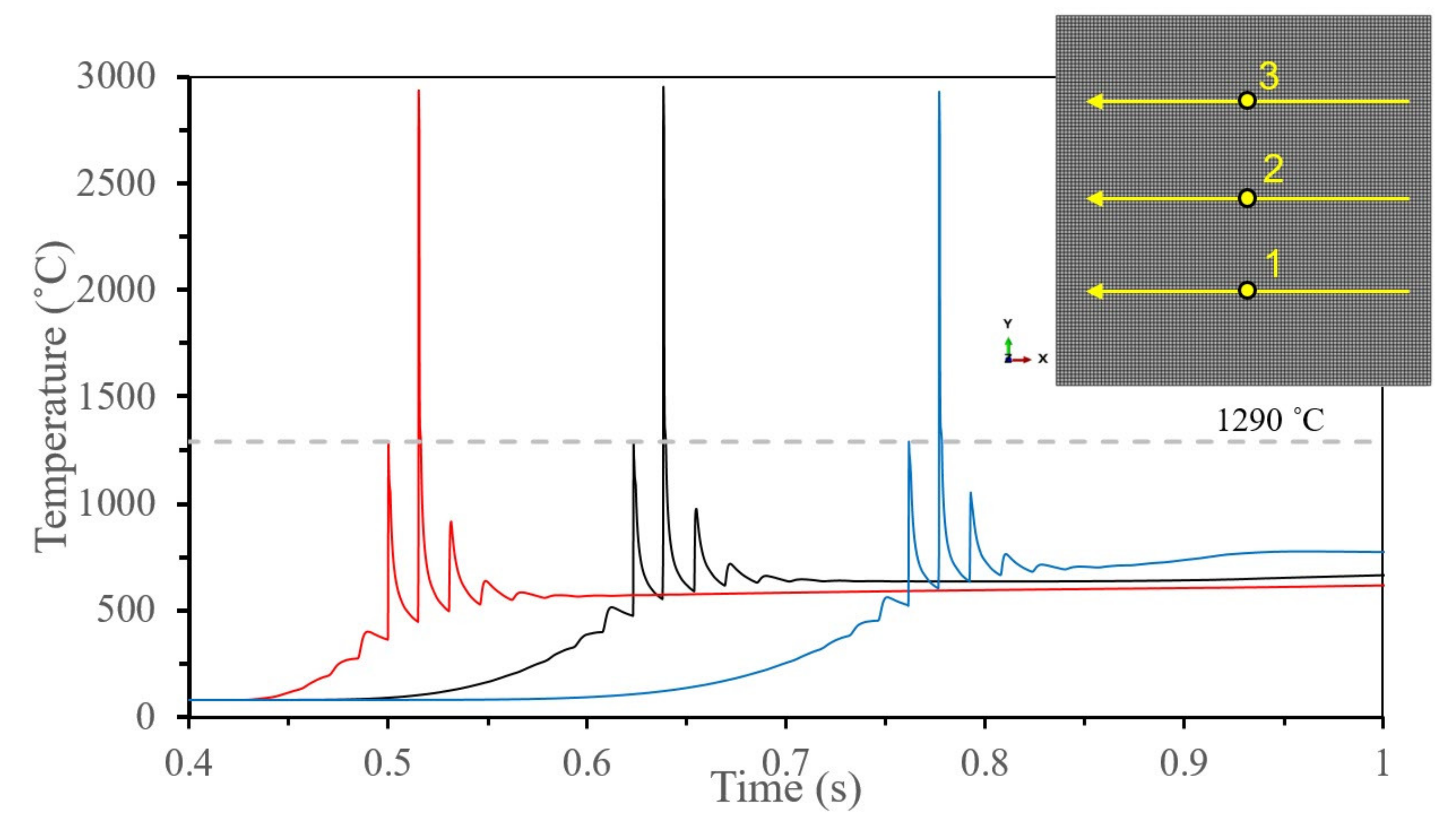
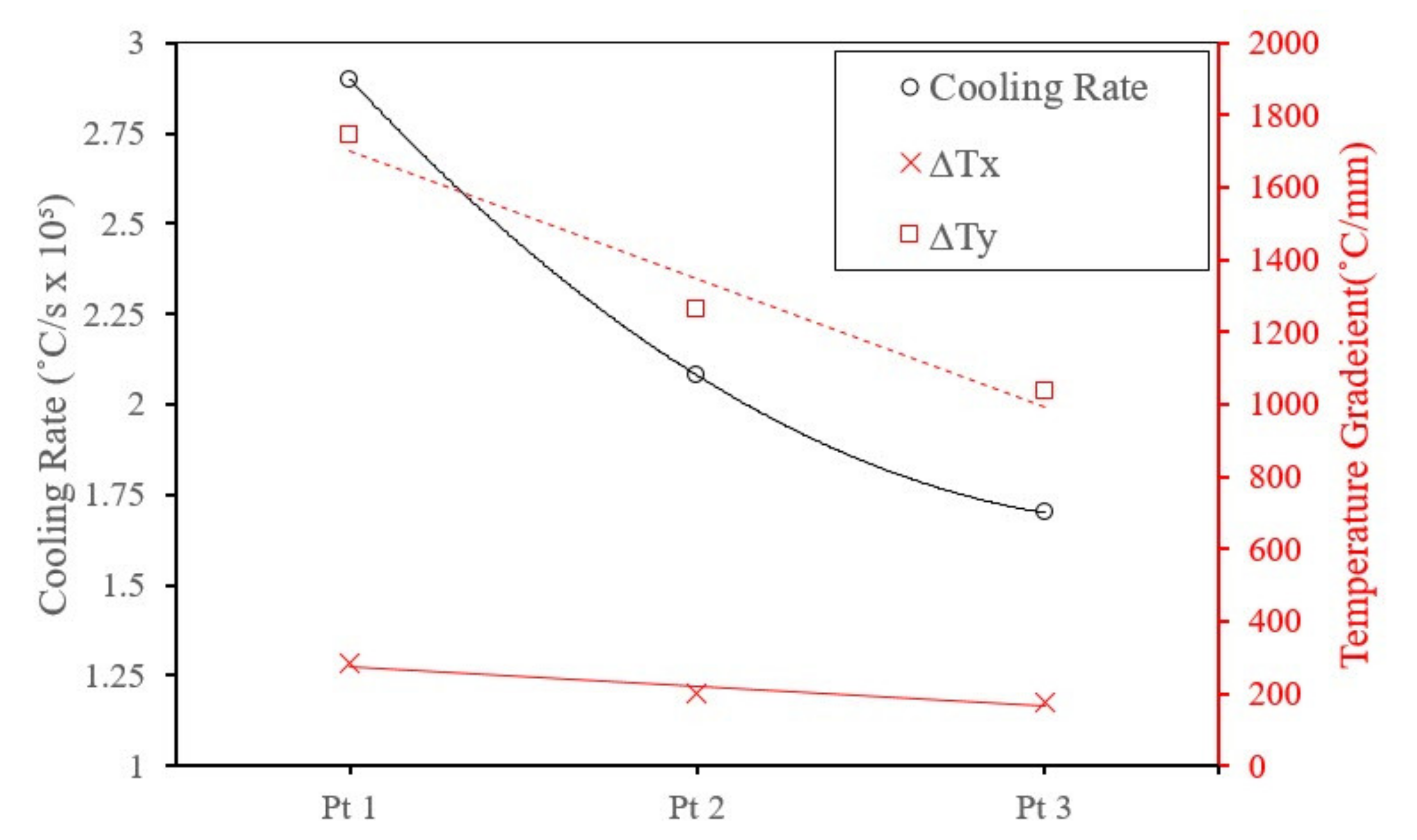
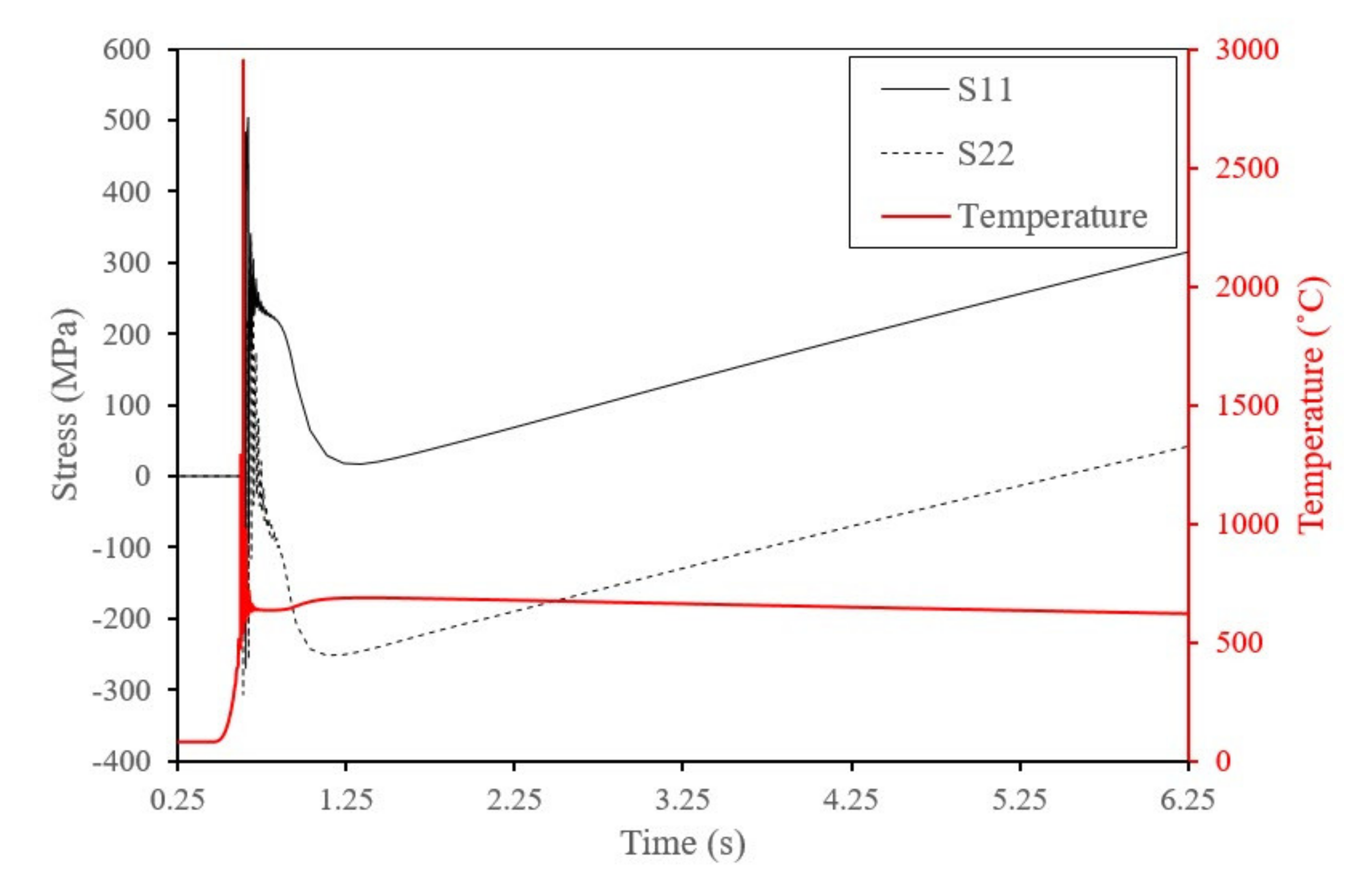
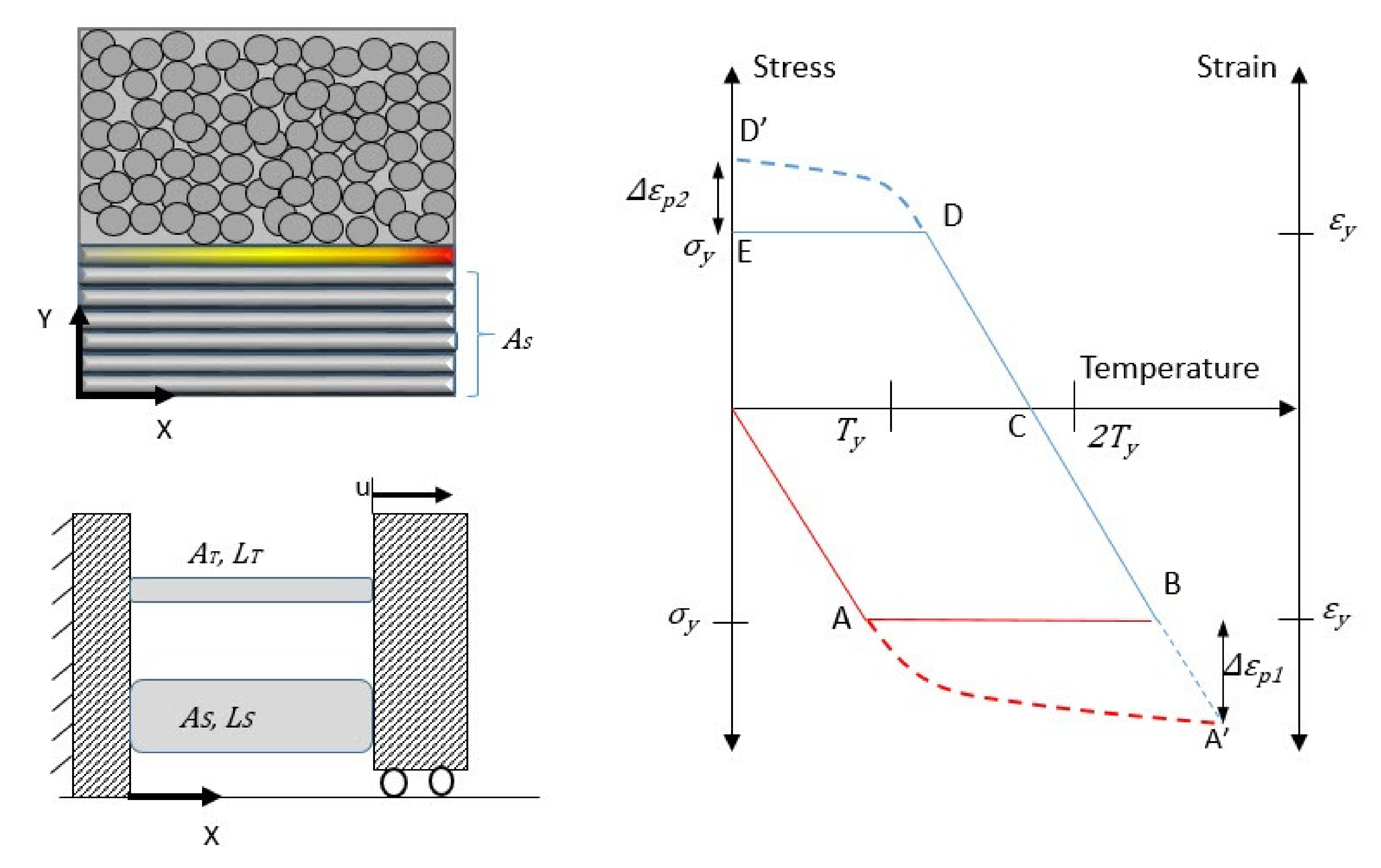

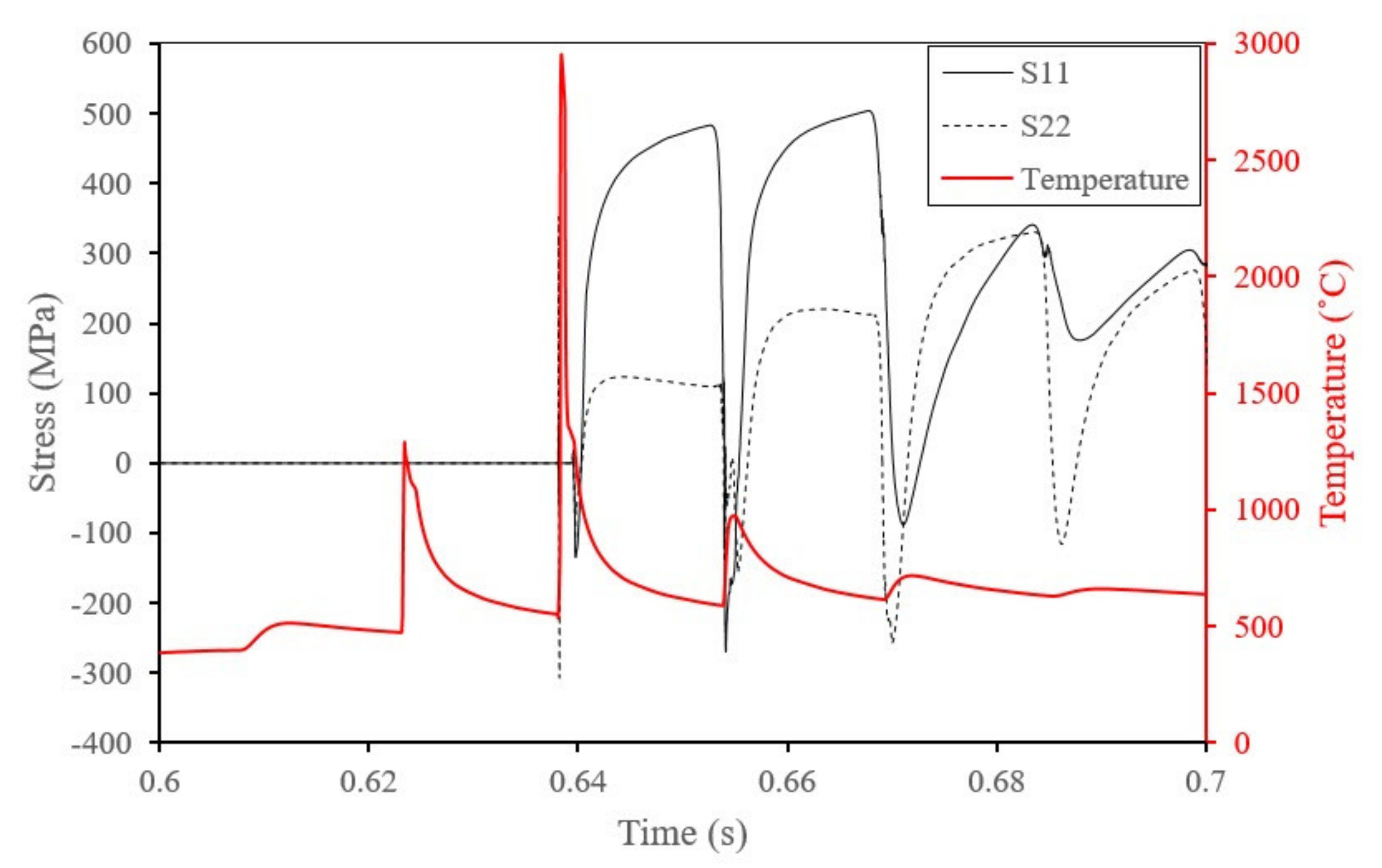

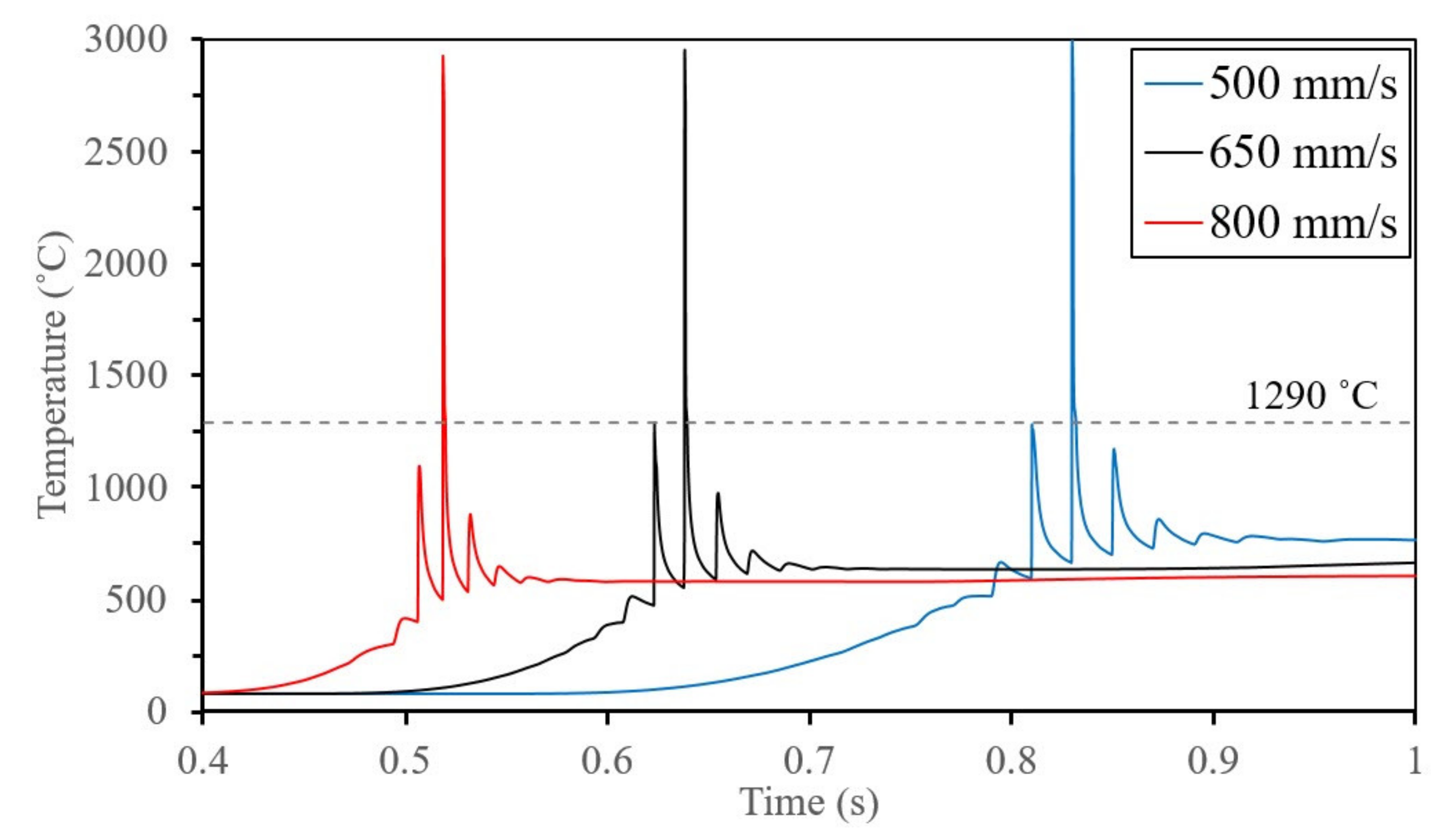
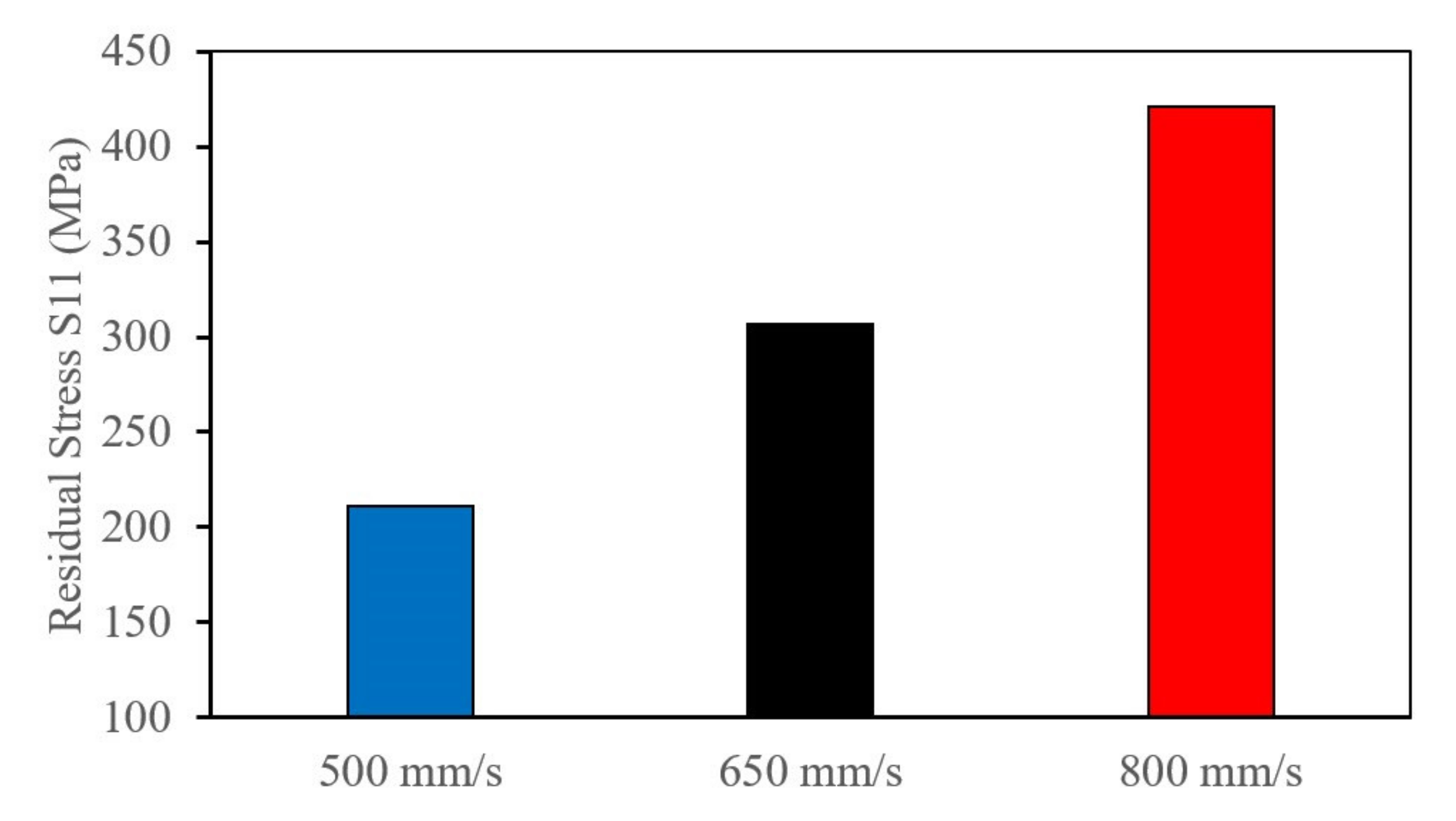









| Property | Units | Ref. | |
|---|---|---|---|
| 10.1–31.6 | W/m∙K | [49] | |
| 8453–7925 | Kg/m3 | [49] | |
| 419–657 | J/kg∙K | [49] | |
| 30.078 | W/m∙K | [42] | |
| 709.25 | J/kg∙K | [42] | |
| 1563 | K | [42] | |
| 1623 | K | [42] | |
| 3000 | K | [42] | |
| 290 | kJ/kg∙K | [42] | |
| 640 | kJ/kg∙K | [28] | |
| Dynamics viscosity (μ) | Pa∙s | [42] | |
| N∙m/K | [28] | ||
| 27 | μm | [50] | |
| Powder bed porosity (φ) | 0.4 | - | - |
| Emissivity (e) | 0.4 | - | [42] |
| 0.02604–0.0947 | W/m∙K | [51] | |
| 313 | K | - | |
| Particle Size Distribution | OPD |
|---|---|
| −20 μm | 20 μm |
| −75 μm | 200 μm |
| Parameter | Levels |
|---|---|
| Power (W) | 140, 220, 270 |
| Scan speed (mm/s) | 500, 650, 800 |
| Hatch spacing (mm) | 0.08, 0.1, 0.12 |
| Parameter | Value |
|---|---|
| A (MPa) | 558 |
| B (MPa) | 2201.3 |
| n | 0.8 |
| C | 0.000209 |
| m | 1.146 |
| Tm (°C) | 1290 |
| Tr (°C) | 20 |
| 1670 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balbaa, M.; Elbestawi, M. Multi-Scale Modeling of Residual Stresses Evolution in Laser Powder Bed Fusion of Inconel 625. J. Manuf. Mater. Process. 2022, 6, 2. https://doi.org/10.3390/jmmp6010002
Balbaa M, Elbestawi M. Multi-Scale Modeling of Residual Stresses Evolution in Laser Powder Bed Fusion of Inconel 625. Journal of Manufacturing and Materials Processing. 2022; 6(1):2. https://doi.org/10.3390/jmmp6010002
Chicago/Turabian StyleBalbaa, Mohamed, and Mohamed Elbestawi. 2022. "Multi-Scale Modeling of Residual Stresses Evolution in Laser Powder Bed Fusion of Inconel 625" Journal of Manufacturing and Materials Processing 6, no. 1: 2. https://doi.org/10.3390/jmmp6010002
APA StyleBalbaa, M., & Elbestawi, M. (2022). Multi-Scale Modeling of Residual Stresses Evolution in Laser Powder Bed Fusion of Inconel 625. Journal of Manufacturing and Materials Processing, 6(1), 2. https://doi.org/10.3390/jmmp6010002







