Investigation of the Influence of Tool Rake Angles on Machining of Inconel 718
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Properties and Workpiece
2.2. Experiment and Investigation Setup
3. Numerical Prediction of Cutting Force and Temperature
4. Results
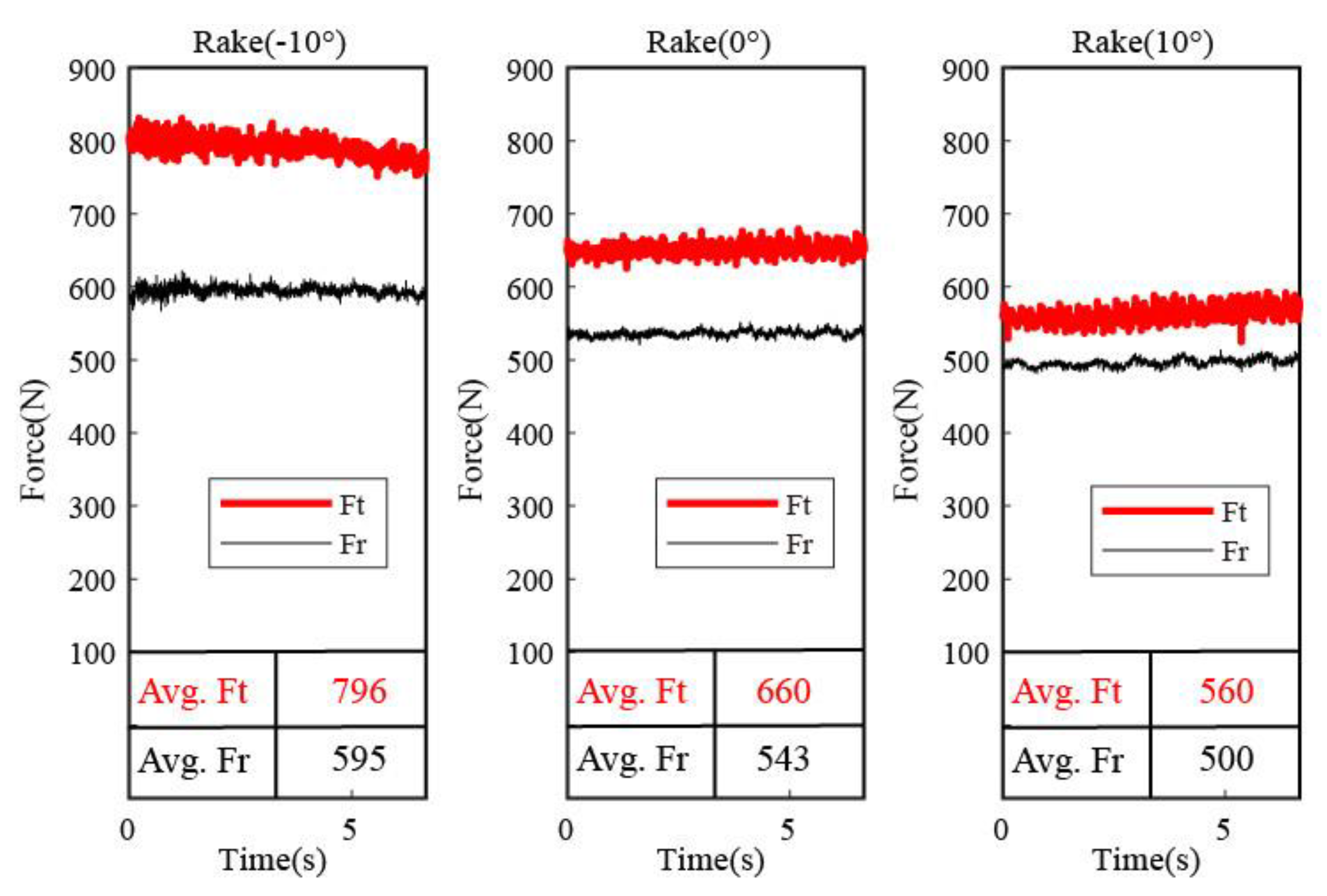
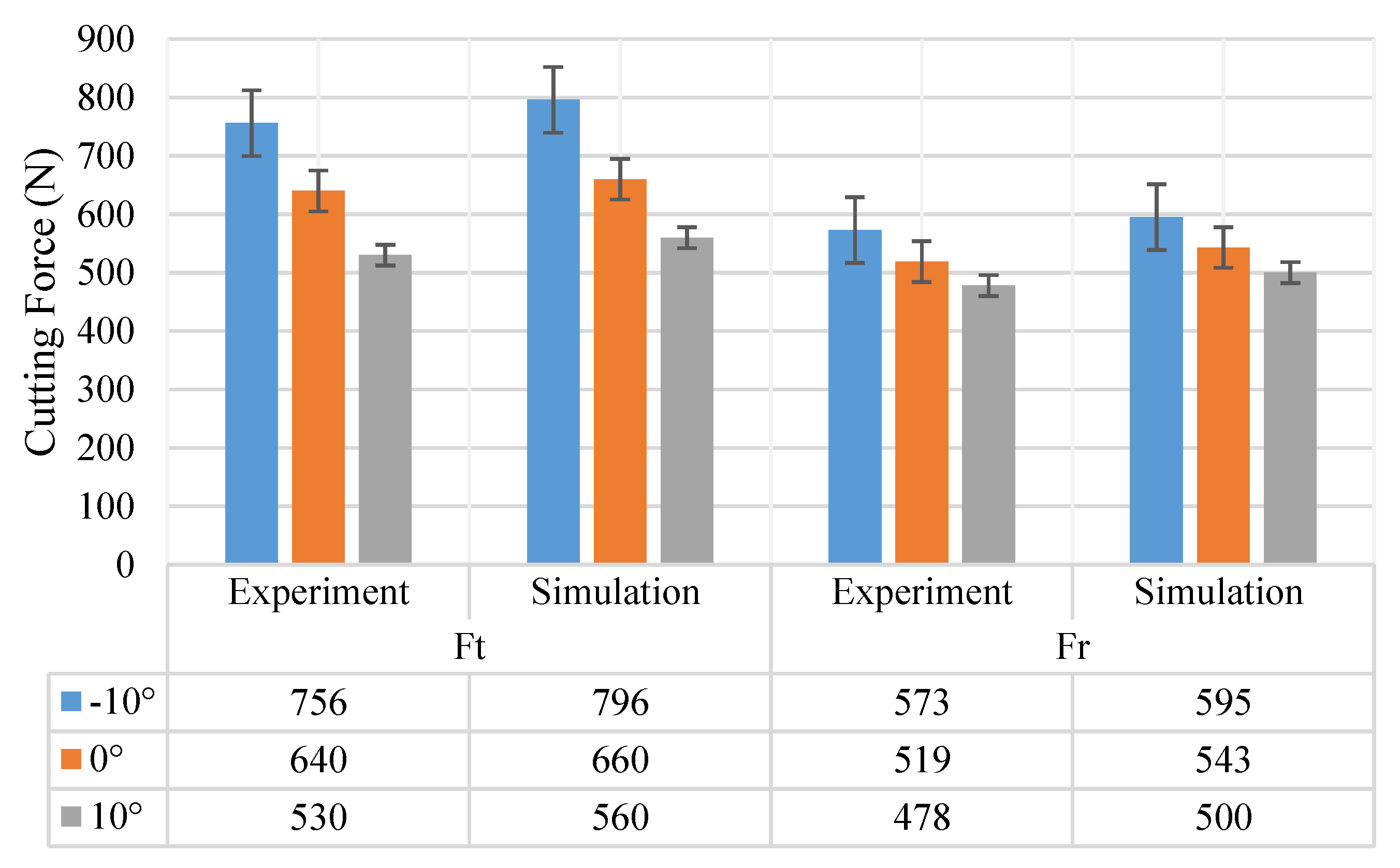
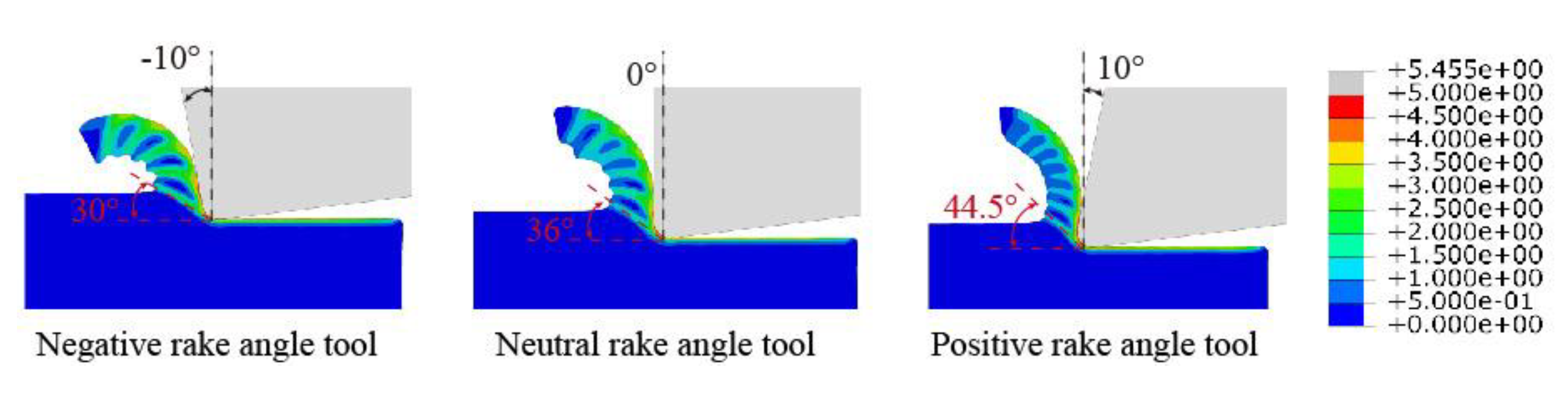
4.1. Influence of Tool Rake Angles on Cutting Force Variation
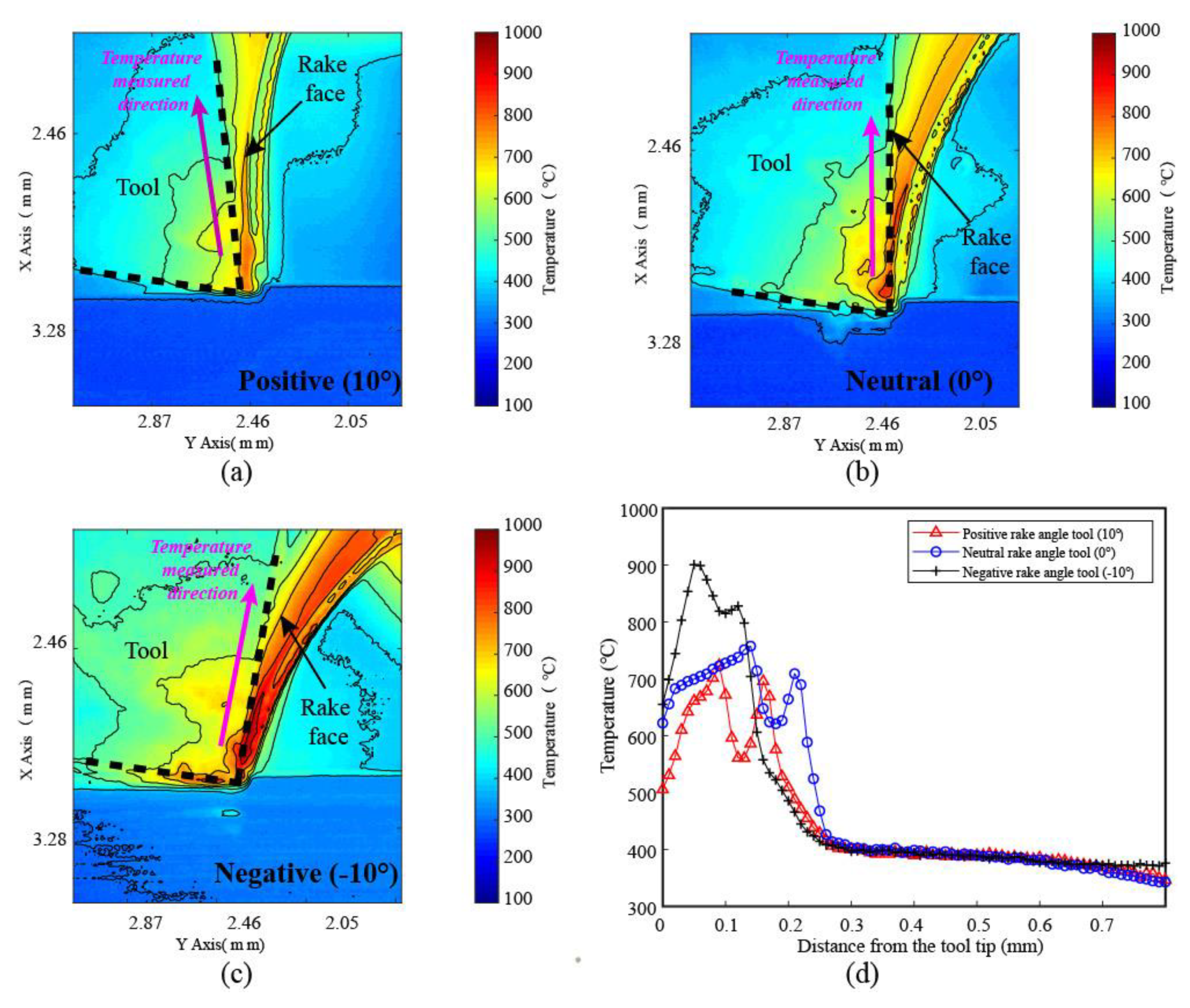
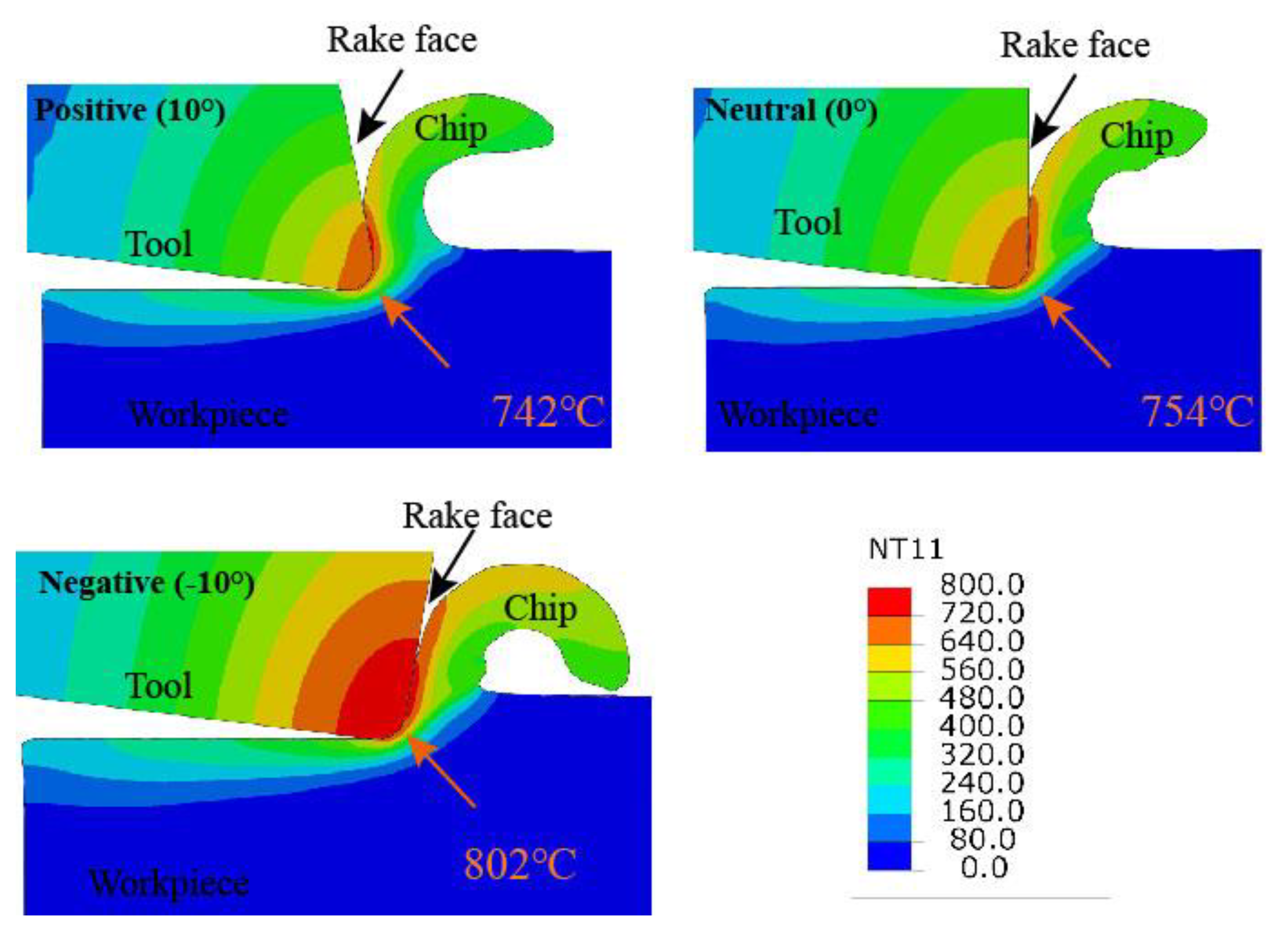
4.2. Temperature Distribution Gradient in Cutting Process
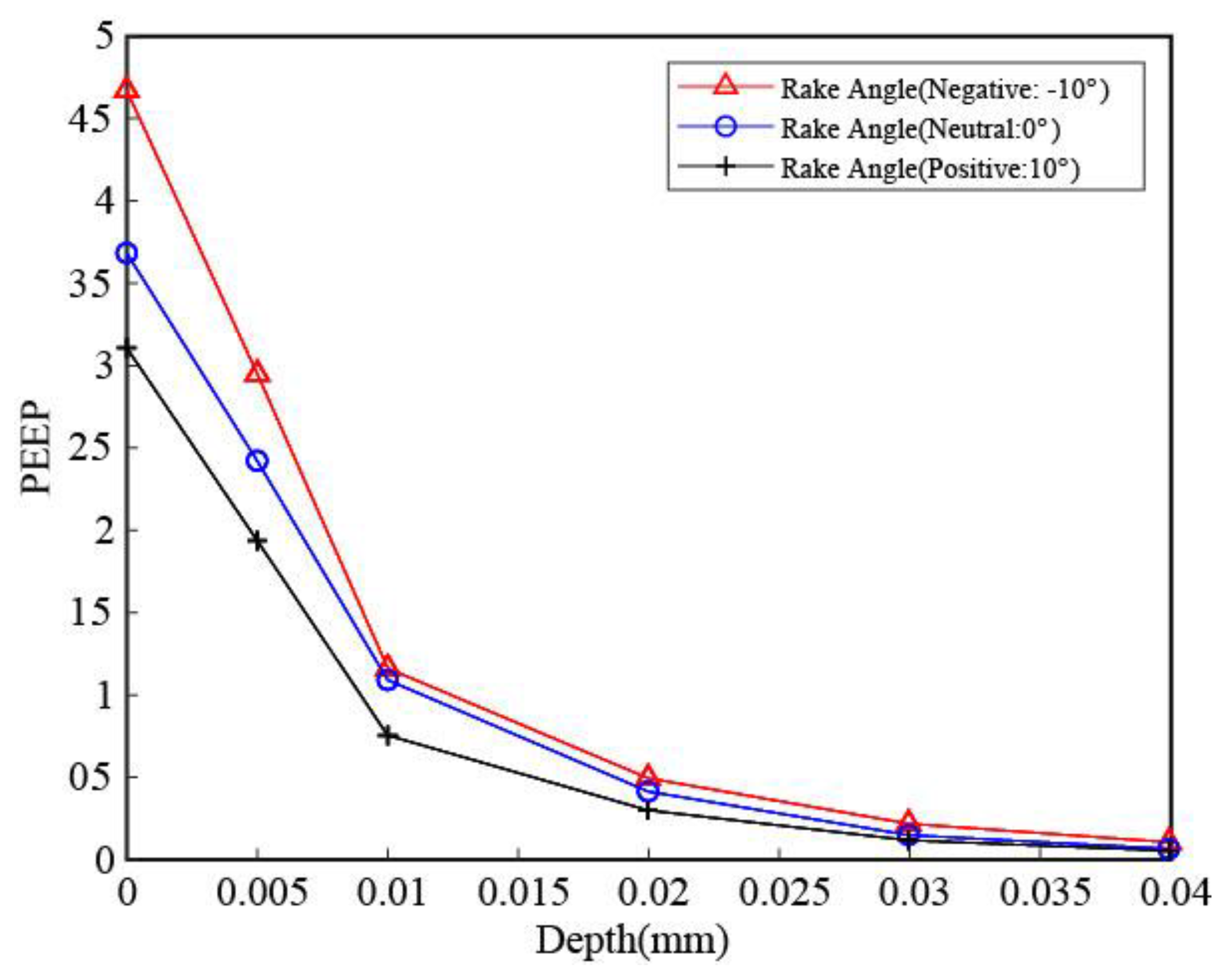
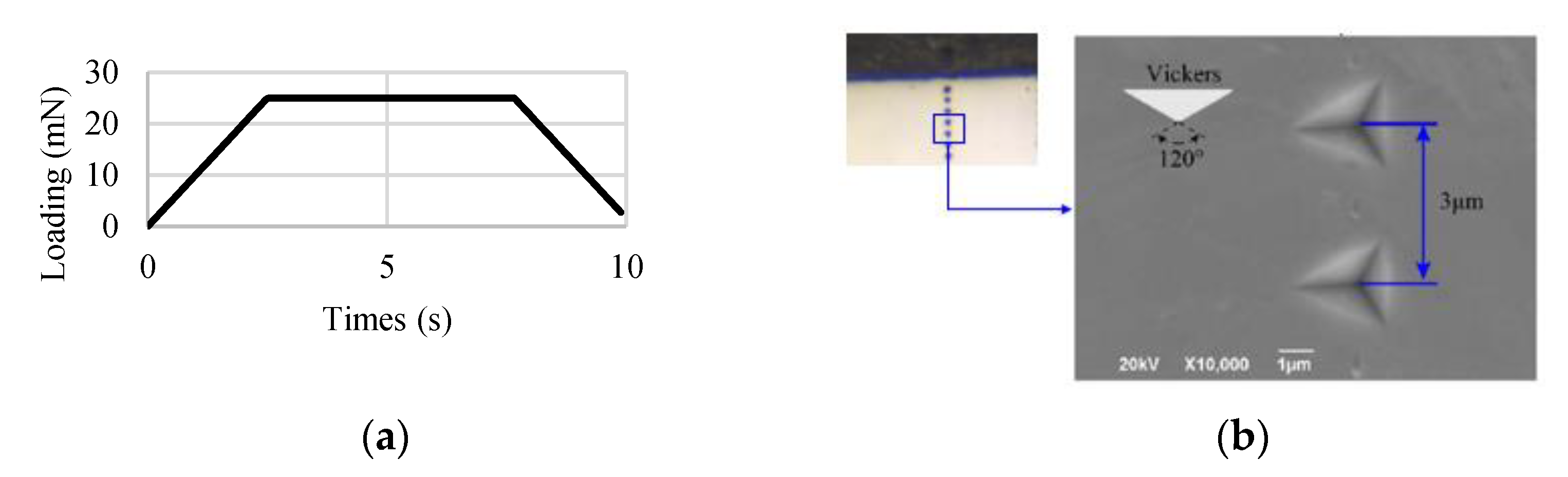
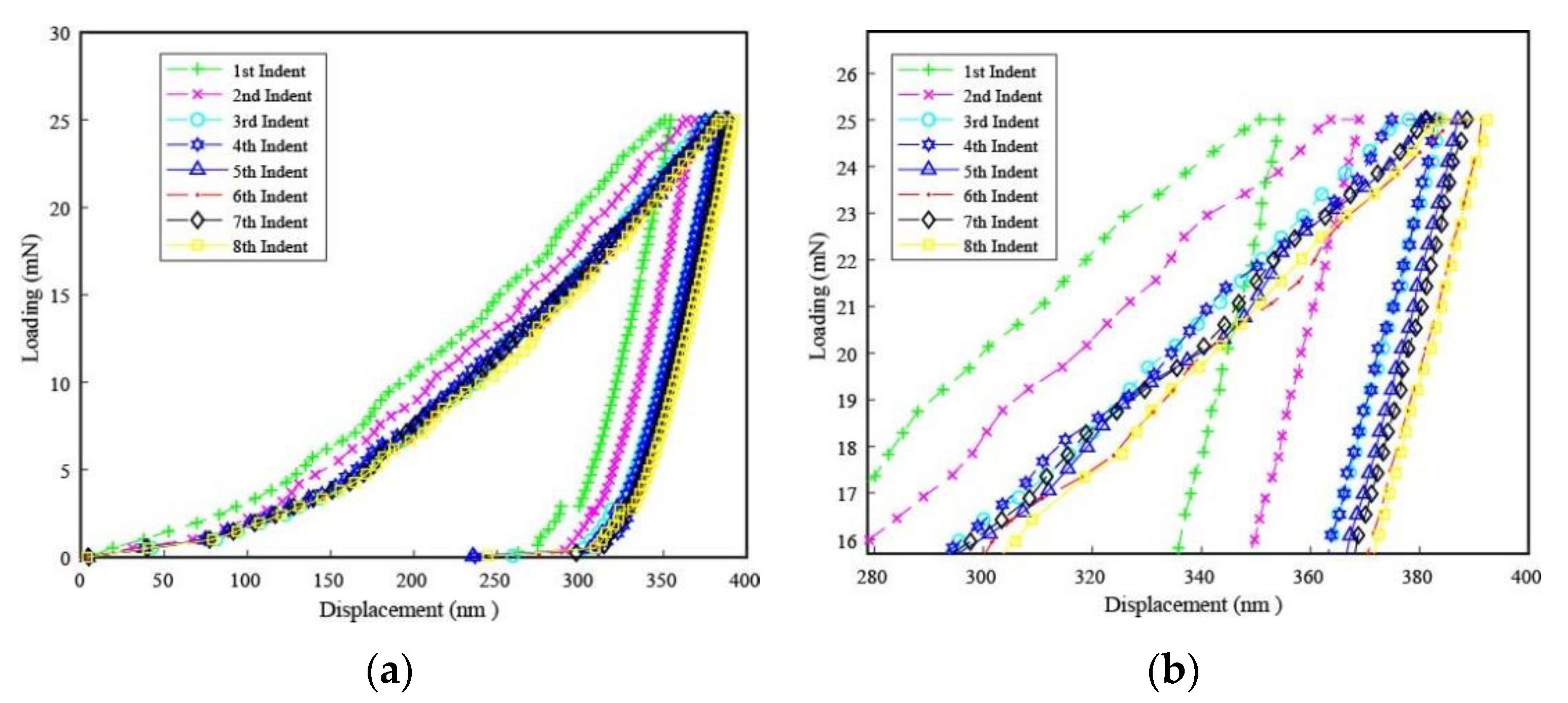
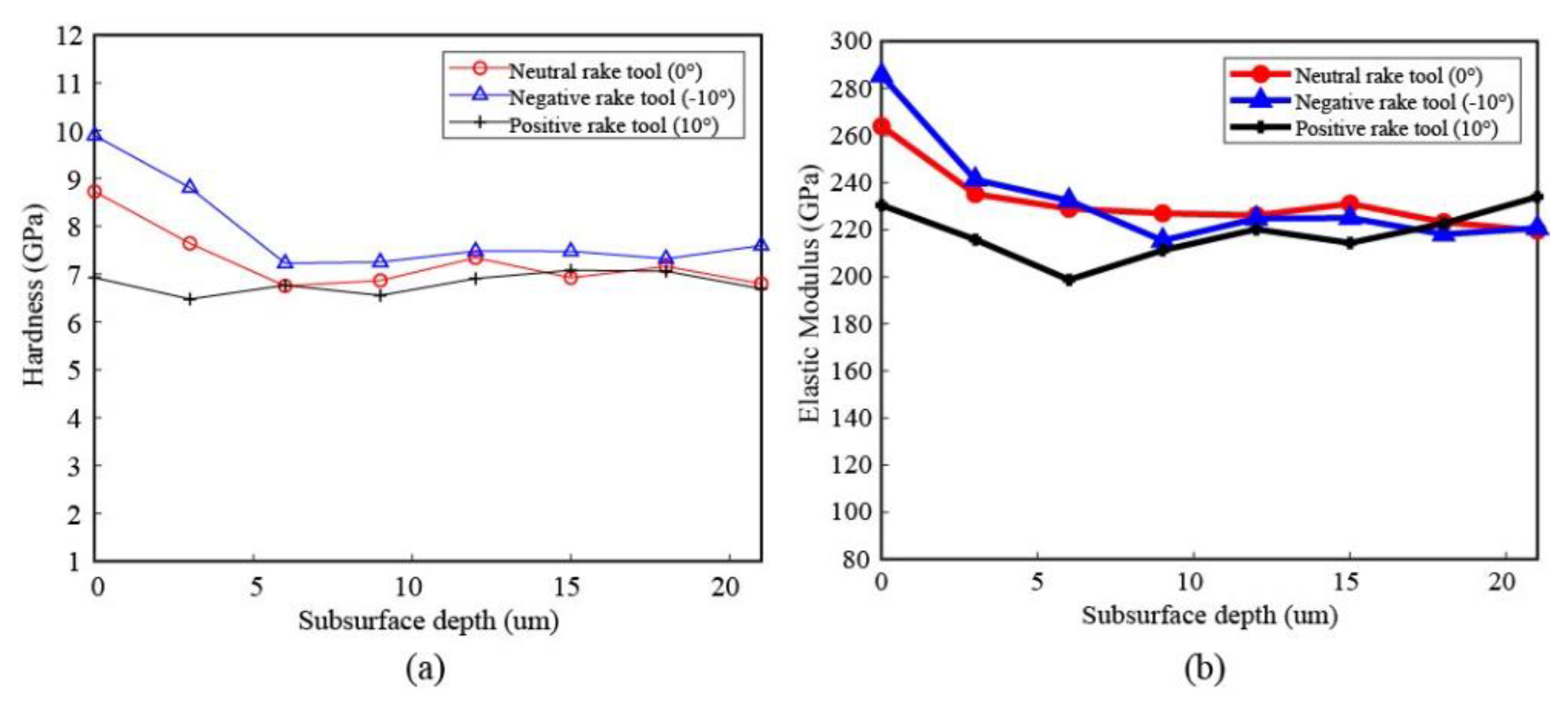
4.3. Subsurface Deformation and Its Mechanical Properties
5. Conclusions
- (1)
- In the comparison of different rake angles, the smallest cutting force and largest shear angles in the cutting process are found. The results have clearly emphasized that the rake angle plays significant roles in determining the cutting force by influencing the rake angles during cutting processes. The increasing of rake angles has a tendency to decrease the cutting force during the machining of Inconel 718, which is consistent with the former observation, and the numerical simulation presents a good coherence with the experimental analysis;
- (2)
- It is clear that the rake angle variation has led to a difference in the thermal map distribution in several presented cutting scenarios, and the negative tool has the trend to increase the cutting temperature. However, it is also worth noting that the temperature in the rake face does not decrease monotonically but achieves another temperature summit in a small distance from the tool tip, which is a clear indication of the reason for crater wear, which has been widely observed;
- (3)
- With respect to the surface integrity, the smallest deformation depth is no doubt found for the workpiece generated from positive rake angle tools, and there is no white layer observed when comparing with the neutral and negative rake angle tools, where a clear white layer over 1 μm is noticed. In addition, the mechanical property investigation shows that the strain hardening effect is also the smallest in the subsurface of the workpiece machined from positive rake angle tools, which can be validated from the non-varied hardness and elastic modulus.
Author Contributions
Funding
Conflicts of Interest
References
- Miller, S. Advanced materials mean advanced engines. Interdiscip. Sci. Rev. 1995, 20, 117–129. [Google Scholar]
- Xu, D.; Liao, Z.; Axinte, D.; Hardy, M. A novel method to continuously map the surface integrity and cutting mechanism transition in various cutting conditions. Int. J. Mach. Tools Manuf. 2020, 151, 103529. [Google Scholar] [CrossRef]
- Shang, Z.; Liao, Z.; Sarasua, J.A.; Billingham, J.; Axinte, D. On modelling of laser assisted machining: Forward and inverse problems for heat placement control. Int. J. Mach. Tools Manuf. 2019, 138, 36–50. [Google Scholar] [CrossRef] [Green Version]
- M’Saoubi, R.; Axinte, D.; Soo, S.L.; Nobel, C.; Attia, H.; Kappmeyer, G.; Engin, S.; Sim, W.-M. High performance cutting of advanced aerospace alloys and composite materials. CIRP Ann. Technol. 2015, 64, 557–580. [Google Scholar] [CrossRef]
- de Garmo, E.P.; Black, J.T.; Kohser, R.A.; Klamecki, B.E. Materials and Process in Manufacturing; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Shizuka, H.; Sakai, K.; Yang, H.; Sonoda, K.; Nagare, T.; Kurebayashi, Y.; Hayakawa, K. Difficult cutting property of NiTi alloy and its mechanism. J. Manuf. Mater. Process. 2020, 4, 124. [Google Scholar]
- Shintani, K.; Kato, H.; Fujimura, Y.; Yamamoto, A.; Maeda, T. Cutting performance of CBN tools in machining of nickel based superalloy. Seimitsu Kogaku Kaishi 1992, 58, 1685–1690. [Google Scholar]
- Bushlya, V.; Zhou, J.; Ståhl, J.-E. Effect of cutting conditions on machinability of superalloy Inconel 718 during high speed turning with coated and uncoated PCBN tools. Procedia CIRP 2012, 3, 370–375. [Google Scholar] [CrossRef] [Green Version]
- Ezugwu, E.O.; Bonney, J.; Yamane, Y. An overview of the machinability of aeroengine alloys. J. Mater. Process. Technol. 2003, 134, 233–253. [Google Scholar] [CrossRef]
- Ezugwu, E.O. Key improvements in the machining of difficult-to-cut aerospace superalloys. Int. J. Mach. Tools Manuf. 2005, 45, 1353–1367. [Google Scholar] [CrossRef]
- Ulutan, D.; Ozel, T. Machining induced surface integrity in titanium and nickel alloys: A review. Int. J. Mach. Tools Manuf. 2011, 51, 250–280. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, B. State-of-the-art of surface integrity induced by tool wear effects in machining process of titanium and nickel alloys: A review. Meas. J. Int. Meas. Confed. 2019, 132, 150–181. [Google Scholar] [CrossRef]
- Jawahir, I.S.; Brinksmeier, E.; M’saoubi, R.; Aspinwall, D.K.; Outeiro, J.C.; Meyer, D.; Umbrello, D.; Jayal, A.D. Surface integrity in material removal processes: Recent advances. CIRP Ann. Technol. 2011, 60, 603–626. [Google Scholar] [CrossRef]
- Liao, Z.; la Monaca, A.; Murray, J.; Speidel, A.; Ushmaev, D.; Clare, A.; Axinte, D.; M’Saoubi, R. Surface integrity in metal machining-Part I: Fundamentals of surface characteristics and formation mechanisms. Int. J. Mach. Tools Manuf. 2020, 162, 103687. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Z.; Persson, H.; Peng, R.L.; M’Saoubi, R.; Gustasson, D. Comparative assessment of the surface integrity of AD730® and IN718 superalloys in high-speed turning with a CBN tool. J. Manuf. Mater. Process. 2019, 3, 73. [Google Scholar] [CrossRef] [Green Version]
- Wolf, T.; Iovkov, I.; Biermann, D. Influence of a Discontinuous Process Strategy on Microstructure and Microhardness in Drilling Inconel 718. J. Manuf. Mater. Process. 2021, 5, 43. [Google Scholar]
- Ozel, T.; Llanos, I.; Soriano, J.; Arrazola, P.-J. 3D finite element modelling of chip formation process for machining Inconel 718: Comparison of FE software predictions. Mach. Sci. Technol. 2011, 15, 21–46. [Google Scholar] [CrossRef]
- Pu, Z.; Umbrello, D.; Dillon, O.W., Jr.; Jawahir, I.S. Finite element simulation of residual stresses in cryogenic machining of AZ31B Mg alloy. Procedia CIRP 2014, 13, 282–287. [Google Scholar] [CrossRef] [Green Version]
- Ducobu, F.; Rivière-Lorphèvre, E.; Filippi, E. Numerical contribution to the comprehension of saw-toothed Ti6Al4V chip formation in orthogonal cutting. Int. J. Mech. Sci. 2014, 81, 77–87. [Google Scholar] [CrossRef]
- Calamaz, M.; Coupard, D.; Girot, F. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2008, 48, 275–288. [Google Scholar] [CrossRef] [Green Version]
- Nasr, M.N.A.; Ng, E.-G.; Elbestawi, M.A. A modified time-efficient FE approach for predicting machining-induced residual stresses. Finite Elem. Anal. Des. 2008, 44, 149–161. [Google Scholar]
- Nasr, M.N.A.; Ng, E.-G.; Elbestawi, M.A. Modelling the effects of tool-edge radius on residual stresses when orthogonal cutting AISI 316L. Int. J. Mach. Tools Manuf. 2007, 47, 401–411. [Google Scholar] [CrossRef]
- Liu, Y.; Agmell, M.; Xu, D.; Ahadi, A.; Stahl, J.E.; Zhou, J. Numerical contribution to segmented chip effect on residual stress distribution in orthogonal cutting of Inconel 718. Int. J. Adv. Manuf. Technol. 2020, 109, 993–1005. [Google Scholar] [CrossRef]
- Xu, D.; Liao, Z.; Axinte, D.; Sarasua, J.A.; M’Saoubi, R.; Wretland, A. Investigation of surface integrity in laser-assisted machining of nickel based superalloy. Mater. Des. 2020, 194, 108851. [Google Scholar] [CrossRef]
- Thakur, D.G.; Ramamoorthy, B.; Vijayaraghavan, L. Study on the machinability characteristics of superalloy Inconel 718 during high speed turning. Mater. Des. 2009, 30, 1718–1725. [Google Scholar] [CrossRef]
- Ducobu, F.; Rivière-Lorphèvre, E.; Filippi, E. Application of the Coupled Eulerian-Lagrangian (CEL) method to the modeling of orthogonal cutting. Eur. J. Mech. A/Solids. 2016, 59, 58–66. [Google Scholar] [CrossRef]
- Arrazola, P.-J.; Aristimuno, P.; Soler, D.; Childs, T. Metal cutting experiments and modelling for improved determination of chip/tool contact temperature by infrared thermography. CIRP Ann. 2015, 64, 57–60. [Google Scholar] [CrossRef]
- Agmell, M.; Bushlya, V.; M’Saoubi, R.; Gutnichenko, O.; Zaporozhets, O.; Laakso, S.V.A.; Ståhl, J.-E. Investigation of mechanical and thermal loads in pcBN tooling during machining of Inconel 718. Int. J. Adv. Manuf. Technol. 2020, 107, 1451–1462. [Google Scholar] [CrossRef] [Green Version]
- Ducobu, F.; Rivière-Lorphèvre, E.; Filippi, E. Mesh influence in orthogonal cutting modelling with the Coupled Eulerian-Lagrangian (CEL) method. Eur. J. Mech. A/Solids. 2017, 65, 324–335. [Google Scholar] [CrossRef]
- Chen, L.; Mi, G.; Zhang, X.; Wang, C. Numerical and experimental investigation on microstructure and residual stress of multi-pass hybrid laser-arc welded 316L steel. Mater. Des. 2019, 168, 107653. [Google Scholar] [CrossRef]
- Sartori, E. Convection coefficient equations for forced air flow over flat surfaces. Sol. Energy 2006, 80, 1063–1071. [Google Scholar] [CrossRef]
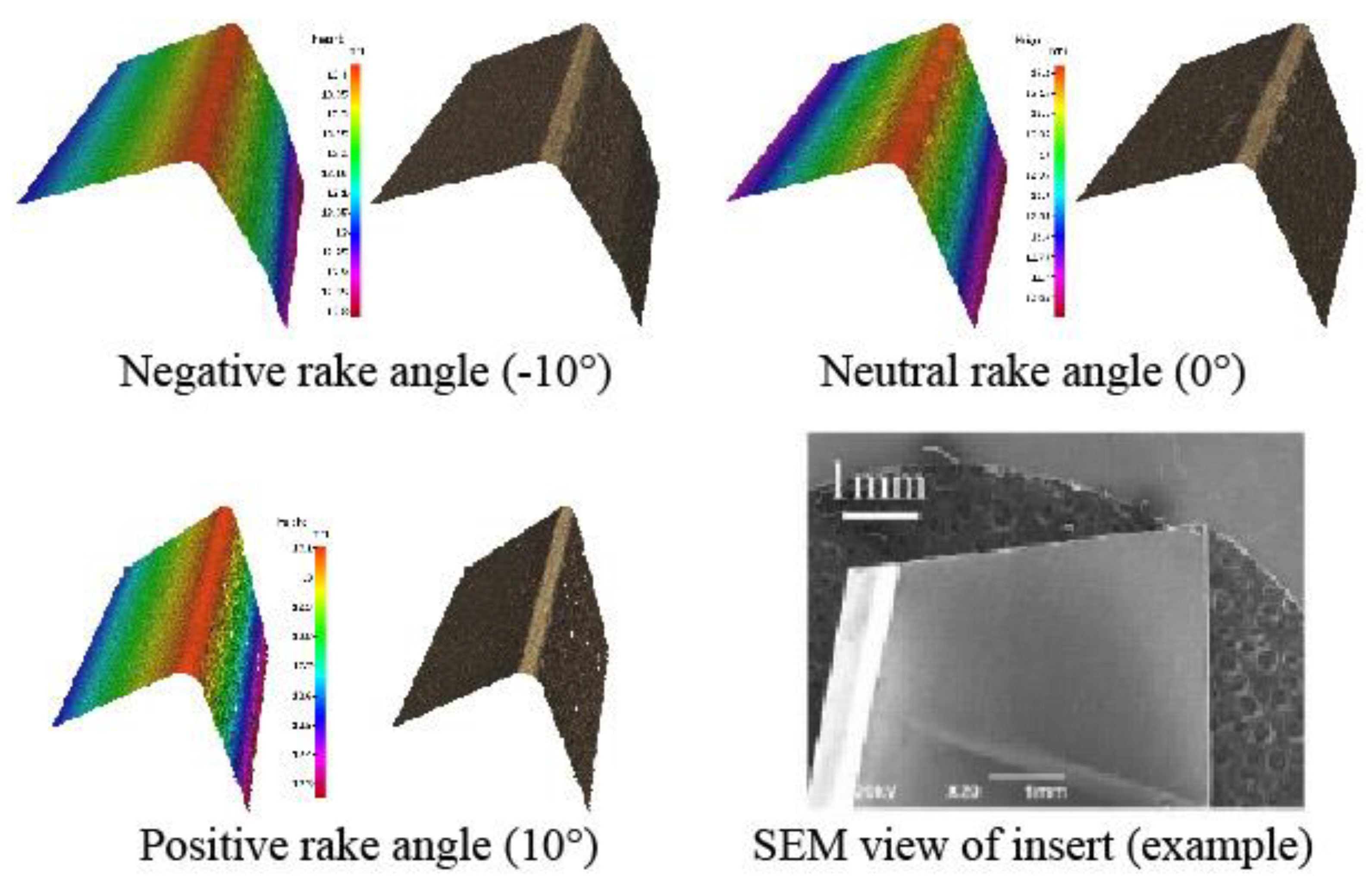
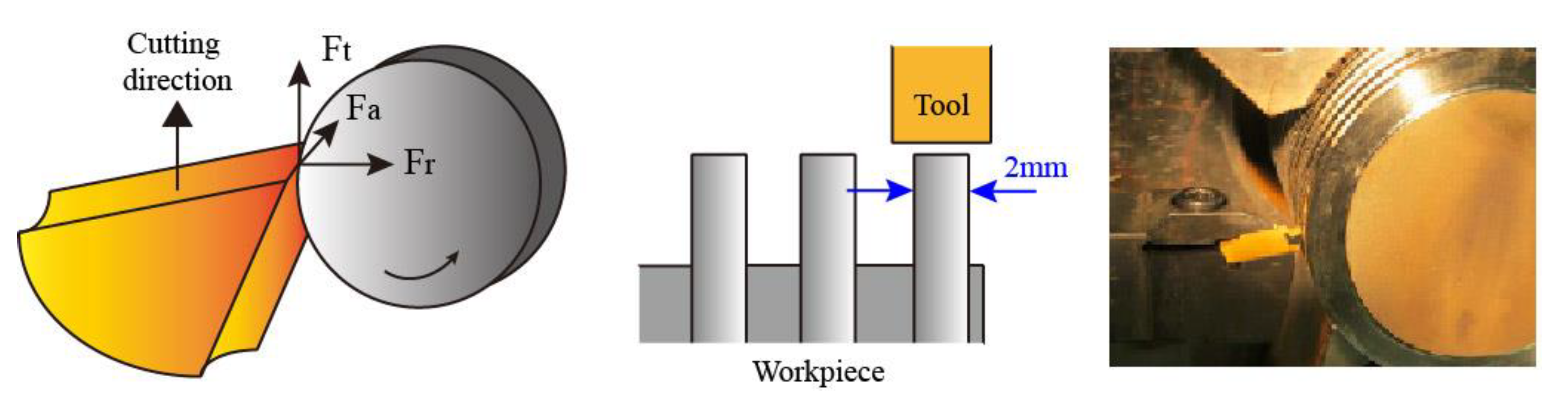
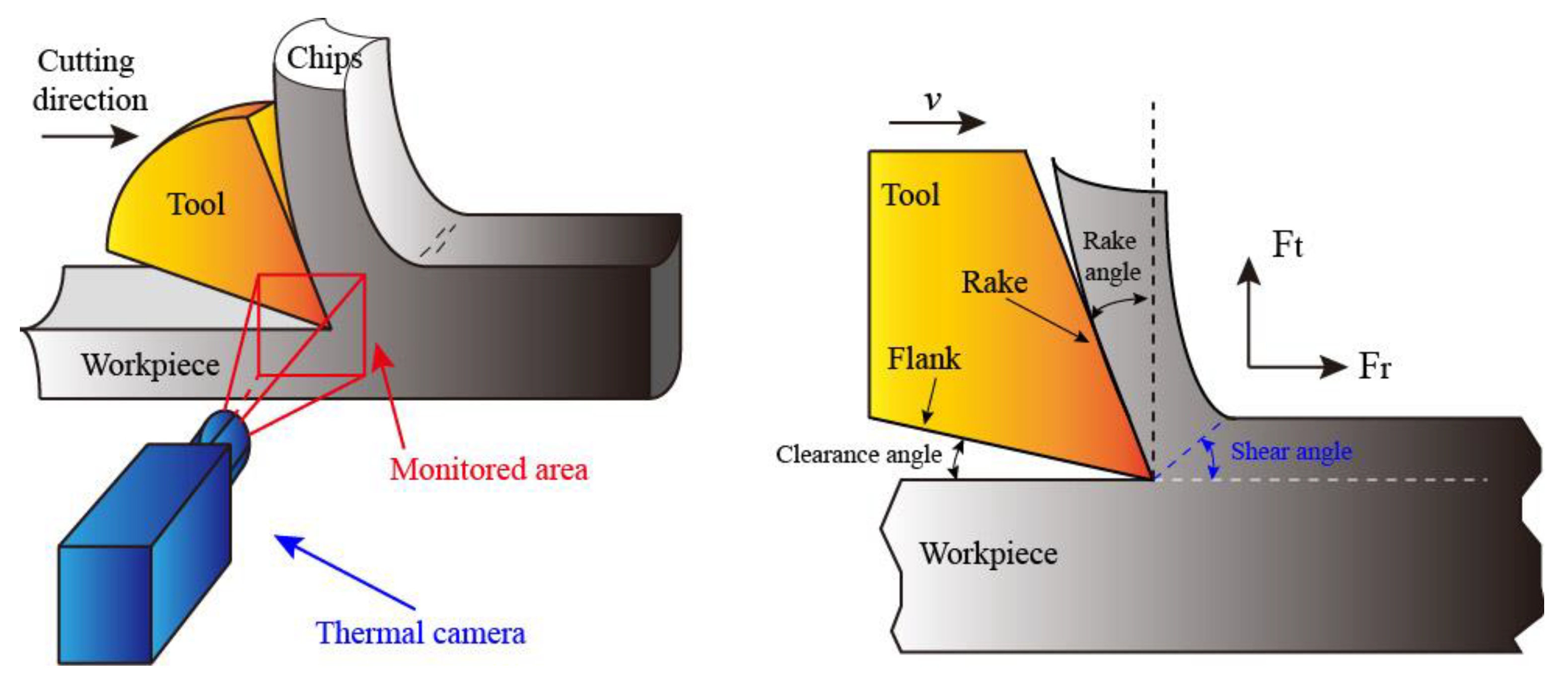
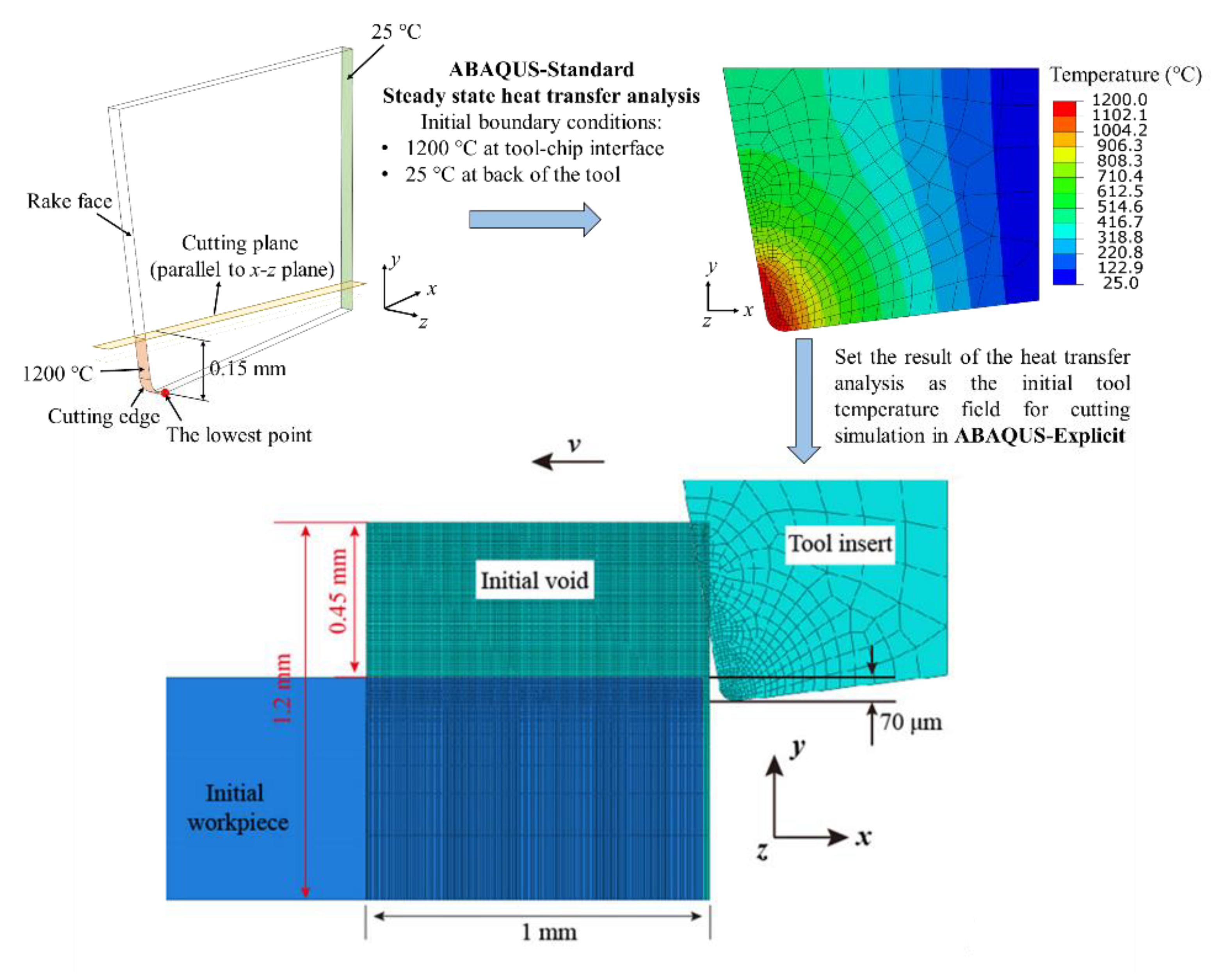

| Ti | Cr | Cu | Mo | Nb | Ni | Co | Mn | Al | Fe |
| 1.05 | 18.50 | 0.21 | 3.10 | 4.95 | 52.18 | 0.76 | 0.17 | 0.41 | Balance |
| Properties | Workpiece (Inconel 718) | Tool (Uncoated Cemented Carbide) | |||
|---|---|---|---|---|---|
| Thermal conductivity (W/m °C) | 12 (20 °C) 24 (900 °C) | 82 | |||
| Density (kg/m3) | 8221 | 14860 | |||
| Young’s modulus E (GPa) | 212 | 600 | |||
| Poisson’s ratio v | 0.294 | 0.2 | |||
| Expansion (°C−1) | 1.2 × 10−5 (20 °C) 1.7× 10−5 (900 °C) | 5.2 | |||
| Inelastic heat fraction | 0.9 | - | |||
| Specific heat (J/Kg °C) | 440 (20 °C) | 249.8 | |||
| 680 (900 °C) | |||||
| Troom (°C) | 25 | 25 | |||
| Tmelt (°C) | 1344 | - | |||
| VB | - | 200 um | |||
| Johnson–Cook constants | A (Mpa) | B (Mpa) | C | n | m |
| (Inconel 718) | 1377 | 1243.5 | 0.0045 | 0.6767 | 1.2 |
| Test | Rake Angle (°) | Edge Radius (um) | Vc (m/min) | Depth of Cut (mm) | Cutting Width (mm) |
|---|---|---|---|---|---|
| 1 | −10 | 45 | 50 | 0.07 | 2 |
| 2 | 0 | 45 | 50 | 0.07 | 2 |
| 3 | 10 | 45 | 50 | 0.07 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Ding, L.; Liu, Y.; Zhou, J.; Liao, Z. Investigation of the Influence of Tool Rake Angles on Machining of Inconel 718. J. Manuf. Mater. Process. 2021, 5, 100. https://doi.org/10.3390/jmmp5030100
Xu D, Ding L, Liu Y, Zhou J, Liao Z. Investigation of the Influence of Tool Rake Angles on Machining of Inconel 718. Journal of Manufacturing and Materials Processing. 2021; 5(3):100. https://doi.org/10.3390/jmmp5030100
Chicago/Turabian StyleXu, Dongdong, Liang Ding, Yang Liu, Jinming Zhou, and Zhirong Liao. 2021. "Investigation of the Influence of Tool Rake Angles on Machining of Inconel 718" Journal of Manufacturing and Materials Processing 5, no. 3: 100. https://doi.org/10.3390/jmmp5030100
APA StyleXu, D., Ding, L., Liu, Y., Zhou, J., & Liao, Z. (2021). Investigation of the Influence of Tool Rake Angles on Machining of Inconel 718. Journal of Manufacturing and Materials Processing, 5(3), 100. https://doi.org/10.3390/jmmp5030100







