Abstract
Milling tools with a large length–diameter ratio are widely applied in machining structural features with deep depth. However, their high dynamic flexibility gives rise to chatter vibrations, which results in poor surface finish, reduced productivity, and even tool damage. With a passive tuned mass damper (TMD) embedded inside the arbor, a large length–diameter ratio milling tool with chatter-resistance ability was developed. By modeling the milling tool as a continuous beam, the tool-tip frequency response function (FRF) of the milling tool with TMD was derived using receptance coupling substructure analysis (RCSA), and the gyroscopic effect of the rotating tool was incorporated. The TMD parameters were optimized numerically with the consideration of mounting position based on the maximum cutting stability criterion, followed by the simulation of the effectiveness of the optimized and detuned TMD. With the tool-tip FRF obtained, the chatter stability of the milling process was predicted. Tap tests showed that the TMD was able to increase the minimum real part of the FRF by 79.3%. The stability lobe diagram (SLD) was predicted, and the minimum critical depth of cut in milling operations was enhanced from 0.10 to 0.46 mm.
1. Introduction
Regenerative chatter stems from the self-excited vibration of the machining system and limits the productivity and surface finish quality. A considerable amount of research has been done toward chatter suppression or avoidance during the past years. In addition to chatter avoidance by cutting parameter selection based on a stability lobe diagram (SLD) [,,], there are generally two ways to mitigate undesirable vibrations during the machining processes: namely, improving the dynamics of the spindle-holder-tool system [,,], and enhancing the stiffness of the workpiece [,,]. Among these studies, the tuned mass damper (TMD) has demonstrated its effectiveness and superiority for attenuating machining vibrations []. Although various TMD types have been proposed, the single-degree-of-freedom (SDOF) TMD is predominantly employed for chatter suppression in practice, owing to its low cost and easily implemented structure [].
With the TMD embedded inside the tool, flexible vibrations caused by the cutting tool can be absorbed and dissipated effectively with slight structural change, e.g., the Sandvik silent tool series. Tewani et al. studied the milling chatter suppression of a boring bar using an active TMD, which is actuated by a piezoelectric actuator []. Moradi et al. implemented two TMDs into the extension part of the milling tool for suppressing the in-plane lateral chatter vibrations []. Miguélez et al. [] and Rubio et al. [] investigated the parameter optimization of a TMD embedded in boring bars for chatter mitigation. With an SDOF TMD embedded inside, a milling tool with a high length–diameter ratio was developed by Yang et al., which has 75% less vibration amplitude than that without a TMD []. Furthermore, the authors integrated a three-element type vibration absorber into a slender turning cutting tool, which reduces 87.1% of the amplitude of the dominant mode []. Yadav et al. optimized the parameters of a TMD embedded in a boring bar for enhancing the critical depth of cut [].
Accurate dynamic modeling of the machining system plays a critical role in the design of TMDs. Although an SDOF model of a milling tool is simple and desirable for efficient TMD design, neglecting the TMD location relative to the tool-tip during dynamic modeling may result in the inaccurate parameter design of TMDs []. An effective solution to this problem is using receptance coupling substructure analysis (RCSA), which models the dynamics of each substructure at different positions and couples them to obtain the overall system dynamics, instead of using a simplified SDOF model. Schmitz and Donaldson first proposed the RCSA to determine the endpoint of the frequency response functions (FRFs) by combining receptance of multiple components through boundary coupling []. Afterward, researchers modeled spindle-holder-tool assembly using RCSA to obtain the tool-point FRF for chatter stability prediction [,,].
Moreover, the dynamics of the milling tool vary with the change of rotating speed. Therefore, a more accurate dynamic model can be derived by considering the gyroscopic effect of the rotating tool. Based on the finite element method (FEM), the element matrices of the rotating Timoshenko beam were given by Nelson []. Afterward, several analytical modeling methods for rotary rotor systems were proposed in addition to the FEM. Lee et al. studied the forced response of an undamped rotating shaft by employing a modal analysis technique, with the consideration of the rotary inertia and gyroscopic effects []. Using the Timoshenko beam model incorporating the gyroscopic effect, Özşahin et al. presented analytical modeling for asymmetric multi-segment rotor-bearing systems []. Similarly, Lu et al. performed analytical modeling of the micro-milling system considering the centrifugal force and gyroscopic effect induced by the high rotation speed [].
The current work implements a passive TMD in a milling tool with a large length–diameter ratio for chatter mitigation. Dynamic modeling of the milling tool embedded with a TMD was carried out using a continuous analytical model, with the effect of TMD location relative to the tool tip incorporated. The TMD parameters were then optimized, considering the spindle rotation. The rest of this paper is organized as follows. Section 2 gives the structural design and dynamic modeling of the milling tool embedded with a TMD. Numerical parameter optimization and simulation of the proposed milling tool are performed in Section 3. In Section 4, tap tests are carried out, and the cutting SLD is simulated to predict the practical performance of the proposed chatter-resistance milling tool.
2. Structural Design and Dynamic Modeling
2.1. Structural Design
The chatter vibration arises from the flexibility of the arbor with a large length–diameter ratio. Since it is impractical to realize a TMD at the tool tip, a TMD is embedded inside the tool arbor. Figure 1 shows the milling bar of the developed chatter-resistance milling tool, in addition to a Sandvik face milling cutter head (R245-050Q22-12 M). The milling bar is composed of an adaptor, a cutter connector, and a hollow arbor embedded with the TMD. The cutter and TMD are designed with symmetrical structures to avoid the mass imbalance that causes centrifugal forces, as it results in tool-tip runout and has a negative influence on cutting stability. The damping of the TMD is provided by hard polyurethane rubber (HPU) to generate a considerable amount of damping.
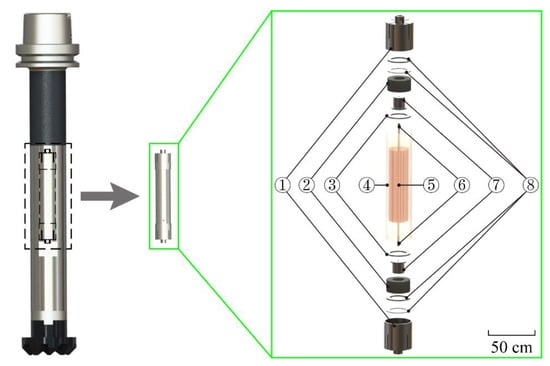
Figure 1.
The milling tool embedded with a tuned mass damper (TMD). 1—end cover; 2—damping element; 3 and 8—gasket; 4—shell; 5—mass block; 6—steel rod; 7—support block.
2.2. Dynamics of the Rotating Milling Tool with Embedded TMD
In order to obtain the tool-tip dynamics for cutting stability prediction, dynamic modeling of the milling tool embedded with a TMD is performed in this section. The schematic of the milling tool coupled with the TMD is shown in Figure 2. The TMD is attached with the milling tool at the midpoint of the arbor. It should be noted that ineffective parameter design of the TMD or inaccurate prediction of cutting stability may be caused if the milling tool is simplified as an SDOF model at the coupling position, which neglects the difference between the coupling position and tool-tip point in the dynamic model. Therefore, the current study employs a continuous model and predicts the tool-tip dynamics using receptance coupling substructure analysis (RCSA), with the effect of the rotating tool considered.
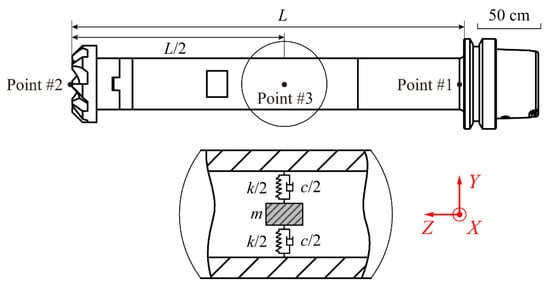
Figure 2.
Schematic of the coupling subsystems.
As the modeling accuracy could be further enhanced by considering the gyroscopic effect, the rotating Timoshenko beam model is employed to obtain the dynamics of the milling tool. For a beam element rotating at the speed of Ω, the governing equations for backward motion (l = b) are given as follows []
where
z is the axial displacement; x and y are the transverse displacements; θy and θx are the rotation angles about the y and x axes, respectively. I is the second moment of area, and A is the area of the cross-section. ρ represents the density, E denotes Young’s modulus, G is the shear modulus, and κ is the shear coefficient. The general solution of Equation (1) gives the dynamic transverse deflection and bending rotation at the tool tip, as written in Equation (5).
The coefficients in Equation (5) are given as
Combining Equation (5) with the boundary conditions of free-free beams, a characteristic equation is obtained as Equation (7).
where
For forward modes (l = f), Equation (11) becomes
Therefore, the rth solution of Equaiton (7) is obtained as ωr, as well as the corresponding αr and βr. After substituting the coefficients into Equations (5) and (6), the FRFs are given by modal superposition method as
γ is the solid damping factor. The subscript i and j represent the measured and impact point, respectively.
Next, the tool-tip FRF is calculated by using receptance coupling substructure analysis (RCSA). Therefore, the FRF matrix of the spindle-holder-tool (SHT) system, αSHT, is derived as
where
KSH is the coupling stiffness matrix between the holder and milling tool, and it is given as
kx, cx, kθy, and cθy are identified using the experimental tool-tip FRF of the idle milling tool along the feed direction [], as listed in Table 1.

Table 1.
Identified coupling stiffness.
With the TMD embedded inside the tool arbor, the suppressed tool-tip FRF, H22D (ω), is obtained as Equation (17), which will be employed as the objective function in Section 3 for determining the optimum TMD parameters.
where k* = k + jωc; m is the mass of the TMD. H23SHT and H33SHT are the cross and direct FRFs at point #3, which are given as Equaitons (18) and (19), according to [] and [], respectively.
3. Numerical Simulation and TMD Optimization
3.1. Simulation of the Rotating Milling Tool without TMD
Based on the above model, the predicted tool-tip FRFs (H22SHT) of the idle milling tool in the frequency range of 10–500 Hz are shown in Figure 3, and the experimental FRF, whose frequency resolution is 1 Hz, is also presented for comparison purposes. It is found that the predicted FRF fits well with the experimental result. Consequently, the FRFs of the milling tool at different spindle speeds are simulated (Figure 4). It can be seen that four vibration modes appear within the frequency range of 0–10,000 Hz. Meanwhile, the rotation of the milling tool has a limited effect on the low-order vibration modes compared to the high-order modes. Specifically, the gyroscopic effect leads to the separation of the 2nd, 3rd, and 4th modes in the rotary status, and each mode is divided into a forward mode and a backward mode. As the spindle speed increases, the separated two modes deviate from each other. Furthermore, caused by the bending of the tool and spindle system, the 1st mode at 250 Hz has the maximum vibration amplitude and therefore dominates the cutting stability. Although the gyroscopic effect seems to have little influence on the 1st mode, its effect on other modes is unneglectable and further affects the critical depth of cut during milling operations [].
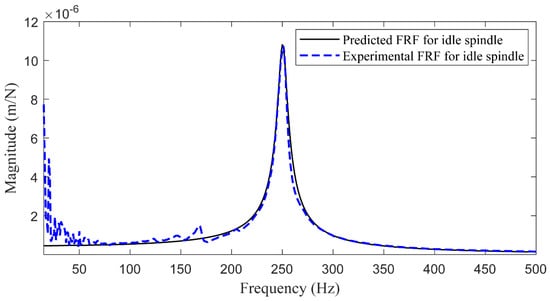
Figure 3.
The predicted and experimental tool-tip frequency response functions (FRFs) of the dominant mode.
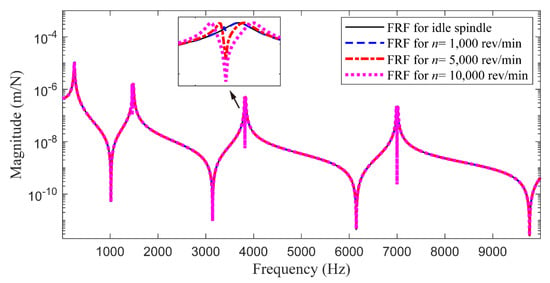
Figure 4.
The tool-tip FRFs of the idle and rotating milling tool.
3.2. Optimization and Simulation of the Rotating Milling Tool with TMD
Numerical optimization is carried out to increase the critical depth of cut during the cutting processes. The damper mass md of the TMD is selected as 0.3 kg, which is 2.5% of the equivalent mass of the target mode. The undamped tool-tip FRF H22SHT is substituted by the predicted FRF at the spindle speed n = 5000 rev/min, and the frequency range of interest is set as 0–10,000 Hz. Based on the maximum machining stability criterion [], the TMD parameters are determined for increasing the negative real part of the target mode at 250 Hz. Due to the difficulty in obtaining the optimum values using analytical methods for systems with damping, a numerical algorithm is employed, and the optimization problem is presented in Equaiton (20). It should be noted that the current study employs the continuous model considering the TMD mounting position and the gyroscopic effect based on different optimization criterion, compared to the previous study [].
where βd = ωd/ωT is the frequency ratio, and ζd stands for the damping ratio. ωd denotes the frequency of the TMD, while ωT is the frequency of the target mode.
Let the mass ratio μd = md/mT; md and mT are the TMD mass and the equivalent mass of the target mode. Using the minimax algorithm [], the optimum TMD parameters are converged. Figure 5 shows the optimum frequency ratio βd and damping ratio ζd with varying mass ratio μd. It demonstrates that the optimum βd increases with μd ascending from 0.2% to 2.2%, and βd decreases when μd continues rising. Meanwhile, a positive correlation between the optimum ζd and μd is observed. Therefore, a large μd should be avoided due to the large needed viscous damping and the limited mounting space inside the arbor.
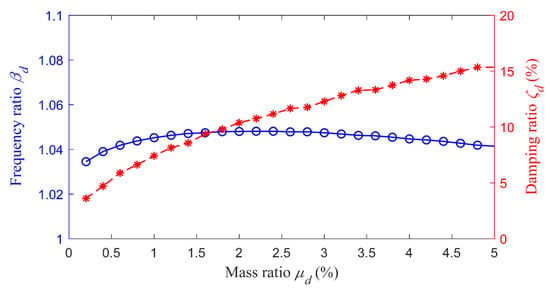
Figure 5.
Optimum parameters versus different mass ratios.
In order to achieve a better trade-off between desirable effectiveness and compact structure, μd is selected as 2.5%. According to Figure 5, the corresponding βd and ζd are obtained as 1.05 and 11.43%, respectively. They are employed to guide the experimental tuning of the TMD for achieving optimum performance.
When the TMD is optimally tuned based on the converged value given in Figure 5, the tool-tip FRF of the milling tool is plotted in Figure 6. The minimum real part of the tool-tip FRF is enhanced by 79.5% with the utilization of TMD, compared to that without TMD. Meanwhile, the FRF with TMD optimized based on the identified modal parameters of the target mode in [] is presented, in which the effect of background modes is neglected. It can be observed that a 12.4% greater increase of the minimum real part is achieved by using the method proposed in the current study, compared to the method using the discrete model.
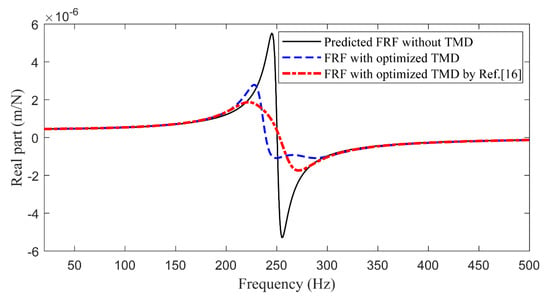
Figure 6.
The predicted tool-tip FRFs of the milling tool with TMD optimized by the current study and [].
In order to examine the TMD’s performance when detuning occurs due to the unavoidable manufacturing and tuning errors, a robustness analysis of the TMD’s performance against its parameter variation is simulated. βd and ζd are tuned to deviate from the optimum values, and it is assumed that βd and ζd detune independently within the range of −30% to 30%. Figure 7 shows that the performance of the TMD significantly deteriorates as βd deviates from the optimum value, while the minimum negative real part of the tool-tip FRF is less sensitive to damping ratio uncertainties. Moreover, it is observed that when βd is tuned away from its optimum, the negative real part enhances with the increase of ζd. In contrast, the increased ζd results in the reduction of the negative real part of FRF for optimally tuned βd. Furthermore, the TMD achieves the worst performance when βd and ζd deviate −30% from the optimum values, and the minimum real part is increased by 29.0% more than that without TMD. As the minimum real part can still be enhanced even when the TMD parameters deviate from the optimum values by 30%, the proposed milling tool with TMD is expected to have an effective chatter-resistance ability in practical milling operations.
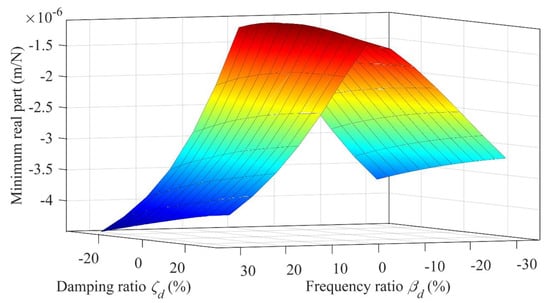
Figure 7.
The influence of TMD parameter deviation on the negative real part of the tool-tip FRF.
4. Performance Validation
4.1. Tap Tests
Tap tests were first carried out to examine the optimization strategy and the effectiveness of the TMD in improving the frequency response at tool-tip. The frequency of the TMD was tuned to the optimum value, according to Section 3.1. With an overhang of 310 mm, the milling tool embedded with TMD was clamped on the tool holder of the milling machine XKR50A, as shown in Figure 8.

Figure 8.
The experimental setup.
An impact hammer (PCB 086C03) was utilized to impact the tool-tip (point #2), and a miniature accelerometer (KISTLER 8778A500) was used to measure the excited vibration signal at tool-tip. The data were then collected by a data acquisition card (National Instrument 9233) and analyzed by the CutPro software. After performing fast Fourier transformation (FFT), the experimental FRFs were obtained with a frequency resolution of 1 Hz.
Figure 9 shows the measured FRFs of the milling tool without and with the optimally tuned TMD along the feed direction, and the predicted result is also plotted for comparison purposes. It is found that the minimum negative real part of the tool-tip FRF is raised by 79.3% after employing the TMD, which demonstrates the TMD is capable of increasing a significant amount of the minimum negative real part of the FRF, therefore the cutting stability. Nevertheless, 0.2% less enhancement of the minimum real part is observed compared to that of the predicted FRF, which is attributed to the unavoidable manufacturing and tuning errors of the TMD, in addition to background noises. Meanwhile, the damping ratio of HPU adopted for the TMD is identified as 7.97%, which is 3.46% less than the optimum value. As the damping value is hard to adjust continuously, the difference between the practical damping and the optimum value also contributes to the deviation between the predicted and experimental results. Therefore, the performance of the TMD on cutting stability can be further enhanced by employing materials whose damping ratio is more close to the optimum value.
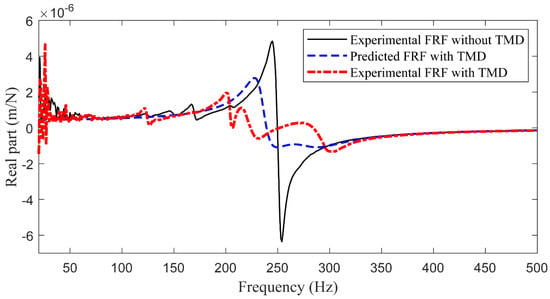
Figure 9.
The predicted and experimental tool-tip FRFs of the milling tool embedded with TMD.
4.2. Cutting Stability Prediction
Next, the effectiveness of TMD in chatter suppression was investigated by cutting stability prediction. With the gyroscopic effect of the rotating milling tool considered, the stability lobs of the cutting process without and with optimized TMD were simulated numerically. As the flexibility of the workpiece was much less than that of the tool, the workpiece was assumed to be rigid.
After identifying the cutting force coefficients using Altintas’s method [], the SLDs were calculated for slotting processes on the material aluminum 7075-T6. The predicted FRF with TMD when n = 5000 rev/min was utilized for SLD prediction (Figure 4). The SLDs for the milling tool without and with TMD are shown in Figure 10. For the milling tool without TMD, the minimum critical depth of cut was predominantly attributed to the mode at 250 Hz, and it was enhanced from 0.10 to 0.46 mm with the utilization of TMD. Meanwhile, as the dominant mode of the milling tool was split into two modes when employing the TMD, the minimum stable cutting depth was determined by the modes at 228 Hz and 266 Hz for the milling tool with TMD.
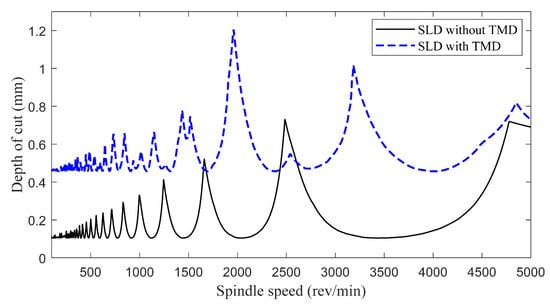
Figure 10.
The SLDs of the milling tool without and with TMD.
5. Conclusions
The current study highlights a practical optimization and tuning routine of a TMD embedded in a milling tool with a large length–diameter ratio for suppressing machining chatter. In order to achieve an accurate TMD parameter design, dynamic modeling of the chatter-resistance milling tool was carried out by using RCSA, and the effect of TMD location relative to the tool-tip was incorporated. The parameters of the embedded TMD were optimized, considering the gyroscopic effect under rotary status.
Simulations show that the gyroscopic effect had little influence on the 1st mode of the milling tool but separated high-order modes into two peaks. The minimum real part of the tool-tip FRF could be increased by 79.5% after employing the optimized TMD. Compared to the previous study that optimized a TMD using the identified modal parameters of the target mode [], the current study employed a continuous model considering TMD mounting position and the gyroscopic effect, which led to a 12.4% greater increase of the minimum real part. Meanwhile, the performance of the optimally tuned and detuned TMD was numerically evaluated. It indicated that a 29.0% enhancement of the minimum real part of the FRF was still achieved, even with a 30% deviation of the optimum TMD parameters. However, a slight experimental tuning of the embedded TMD is desirable to achieve the optimum damping performance under different spindle speeds.
Tap tests were carried out to evaluate the improvement on tool-tip dynamics by the embedded TMD, and cutting stability of the milling tool with TMD was validated by cutting stability prediction. It was demonstrated by tap tests that the TMD can achieve a 79.3% increase of the minimum real part of the tool-tip FRF, which validates the theoretical model and the optimization strategy. Meanwhile, the predicted SLD showed that the minimum critical depth of cut is increased by around three- to fourfold (from 0.10 to 0.46 mm) after implementing the TMD into the milling tool.
As the damping of TMDs is fixed by employing commercial damping material, the performance of TMDs is restricted and could be further improved by employing tunable damping modules. Cutting experiments would be performed in future works to validate the practical effectiveness of the optimized TMD. Meanwhile, the unavoidable imbalance of milling tools or TMDs could result in a centrifugal force that also affects the structural dynamics. Therefore, efforts should be devoted to further investigate the effect of structural imbalance, in order to realize a more effective TMD optimization and more accurate cutting stability prediction.
Author Contributions
Formal analysis, W.M.; funding acquisition, J.Y.; project administration, Y.Y.; software, Y.W.; supervision, J.Y. and Y.Y.; writing–original draft, W.M.; writing–review and editing, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 91960108, 91748205 and 51675032).
Data Availability Statement
Data is contained within the article or supplementary material.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780511843723. [Google Scholar]
- Altintas, Y.; Weck, M. Chatter stability of metal cutting and grinding. CIRP Ann. Manuf. Technol. 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Houck, L.; Schmitz, T.L.; Scott Smith, K. A tuned holder for increased boring bar dynamic stiffness. J. Manuf. Process. 2011, 13, 24–29. [Google Scholar] [CrossRef]
- Burtscher, J.; Fleischer, J. Adaptive tuned mass damper with variable mass for chatter avoidance. CIRP Ann. Manuf. Technol. 2017, 66, 397–400. [Google Scholar] [CrossRef]
- Gibbons, T.J.; Ozturk, E.; Xu, L.; Sims, N.D. Chatter avoidance via structural modification of tool-holder geometry. Int. J. Mach. Tools Manuf. 2020, 150. [Google Scholar] [CrossRef]
- Munoa, J.; Iglesias, A.; Olarra, A.; Dombovari, Z.; Zatarain, M.; Stepan, G. Design of self-tuneable mass damper for modular fixturing systems. CIRP Ann. Manuf. Technol. 2016, 65, 389–392. [Google Scholar] [CrossRef]
- Fan, W.; Zheng, L.; Ji, W.; Zhao, X.; Wang, L.; Yang, Y. Eddy current-based vibration suppression for finish machining of assembly interfaces of large aircraft vertical tail. J. Manuf. Sci. Eng. Trans. ASME 2019, 141. [Google Scholar] [CrossRef]
- Wan, M.; Liang, X.Y.; Yang, Y.; Zhang, W.H. Suppressing vibrations in milling-trimming process of the plate-like workpiece by optimizing the location of vibration absorber. J. Mater. Process. Technol. 2020, 278. [Google Scholar] [CrossRef]
- Yang, Y.; Muñoa, J.; Altintas, Y. Optimization of multiple tuned mass dampers to suppress machine tool chatter. Int. J. Mach. Tools Manuf. 2010, 50, 834–842. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. Manuf. Technol. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Tewani, S.G.; Rouch, K.E.; Walcott, B.L. A study of cutting process stability of a boring bar with active dynamic absorber. Int. J. Mach. Tools Manuf. 1995, 35, 91–108. [Google Scholar] [CrossRef]
- Moradi, H.; Bakhtiari-Nejad, F.; Movahhedy, M.R.; Vossoughi, G. Stability improvement and regenerative chatter suppression in nonlinear milling process via tunable vibration absorber. J. Sound Vib. 2012, 331, 4668–4690. [Google Scholar] [CrossRef]
- Miguélez, M.H.; Rubio, L.; Loya, J.A.; Fernández-Sáez, J. Improvement of chatter stability in boring operations with passive vibration absorbers. Int. J. Mech. Sci. 2010, 52, 1376–1384. [Google Scholar] [CrossRef]
- Rubio, L.; Loya, J.A.; Miguélez, M.H.; Fernández-Sáez, J. Optimization of passive vibration absorbers to reduce chatter in boring. Mech. Syst. Signal Process. 2013, 41, 691–704. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Liu, Q. Design of a milling cutter with large length–diameter ratio based on embedded passive damper. JVC J. Vib. Control 2019, 25, 506–516. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, H.; Ma, W.; Liu, Q. Design of a turning cutting tool with large length–diameter ratio based on three-element type vibration absorber. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 1032–1043. [Google Scholar] [CrossRef]
- Yadav, A.; Talaviya, D.; Bansal, A.; Law, M. Design of chatter-resistant damped boring bars using a receptance coupling approach. J. Manuf. Mater. Process. 2020, 4, 53. [Google Scholar] [CrossRef]
- Bansal, A.; Law, M. A receptance coupling approach to optimally tune and place absorbers on boring bars for chatter suppression. Procedia CIRP 2018, 77, 167–170. [Google Scholar] [CrossRef]
- Schmitz, T.L. Predicting high-speed machining dynamics by substructure analysis. CIRP Ann. Manuf. Technol. 2000, 49, 303–308. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Duncan, G.S. Three-component receptance coupling substructure analysis for tool point dynamics prediction. J. Manuf. Sci. Eng. Trans. ASME 2005, 127, 781–790. [Google Scholar] [CrossRef]
- Ertürk, A.; Özgüven, H.N.; Budak, E. Analytical modeling of spindle-tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF. Int. J. Mach. Tools Manuf. 2006, 46, 1901–1912. [Google Scholar] [CrossRef]
- Filiz, S.; Cheng, C.H.; Powell, K.B.; Schmitz, T.L.; Ozdoganlar, O.B. An improved tool-holder model for RCSA tool-point frequency response prediction. Precis. Eng. 2009, 33, 26–36. [Google Scholar] [CrossRef]
- Nelson, H.D. A finite rotating shaft element using Timoshenko beam theory. J. Mech. Des. Trans. ASME 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Lee, C.W.; Katz, R.; Ulsoy, A.G.; Scott, R.A. Modal analysis of a distributed parameter rotating shaft. J. Sound Vib. 1988, 122, 119–130. [Google Scholar] [CrossRef]
- Özşahin, O.; Özgüven, H.N.; Budak, E. Analytical modeling of asymmetric multi-segment rotor—Bearing systems with Timoshenko beam model including gyroscopic moments. Comput. Struct. 2014, 144, 119–126. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Z.; Liu, S.; Yang, K.; Feng, Y.; Liang, S.Y. Chatter stability of micro-milling by considering the centrifugal force and gyroscopic effect of the spindle. J. Manuf. Sci. Eng. Trans. ASME 2019, 141. [Google Scholar] [CrossRef]
- Ji, Y.; Bi, Q.; Zhang, S.; Wang, Y. A new receptance coupling substructure analysis methodology to predict tool tip dynamics. Int. J. Mach. Tools Manuf. 2018, 126, 18–26. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Smith, K.S. Machining Dynamics: Frequency Response to Improved Productivity; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 9780387096445. [Google Scholar]
- Jin, X.; Altintas, Y. Chatter stability model of micro-milling with process damping. J. Manuf. Sci. Eng. Trans. ASME 2013, 135. [Google Scholar] [CrossRef]
- Sims, N.D. Vibration absorbers for chatter suppression: A new analytical tuning methodology. J. Sound Vib. 2007, 301, 592–607. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S.A. Minimax optimization of multi-degree-of-freedom tuned-mass dampers. J. Sound Vib. 2004, 272, 893–908. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).