Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Background of Surrogate Modeling
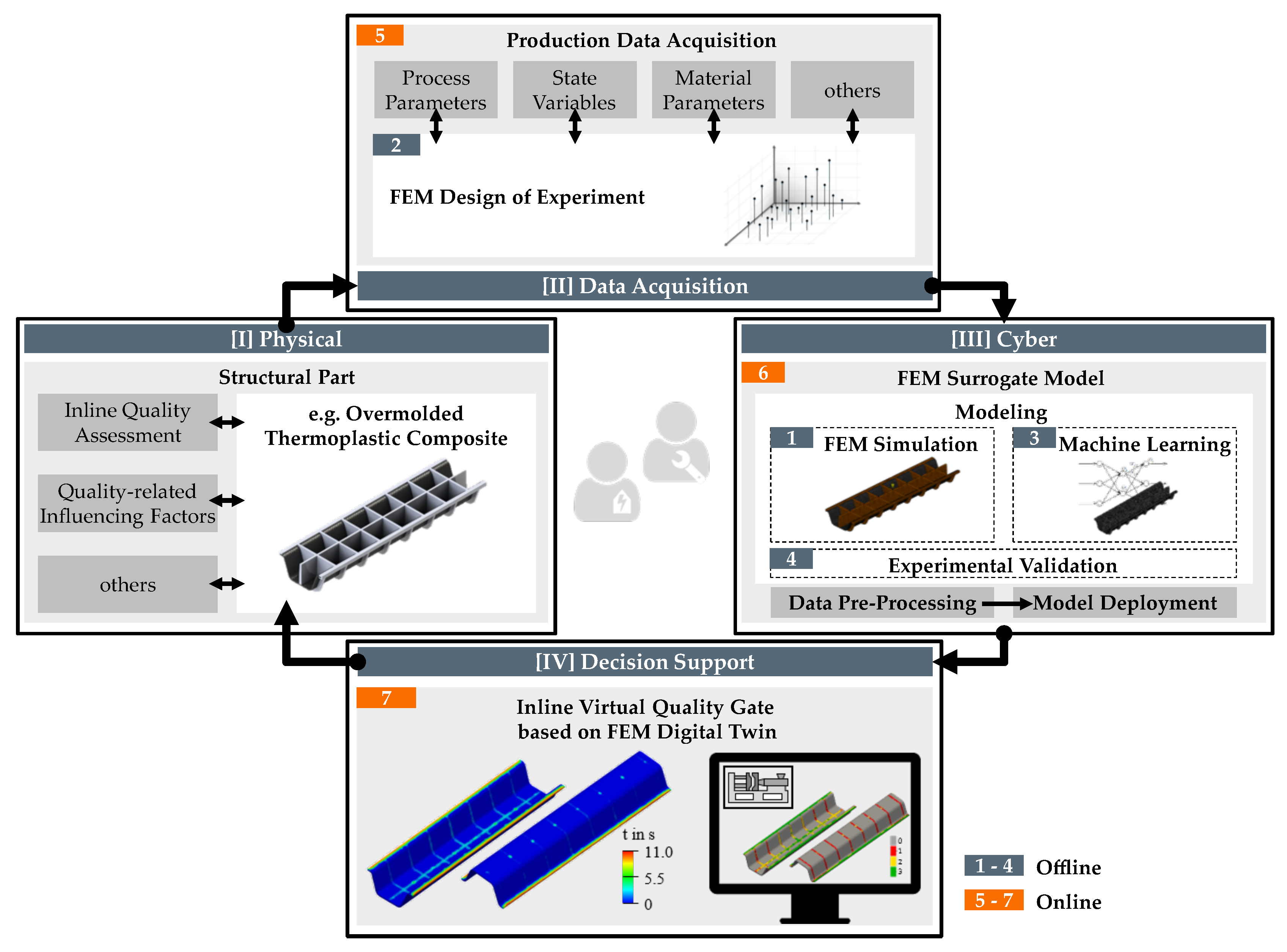
2.2. Physics-Based Digital Twin Based on Simulation Surrogate Modeling
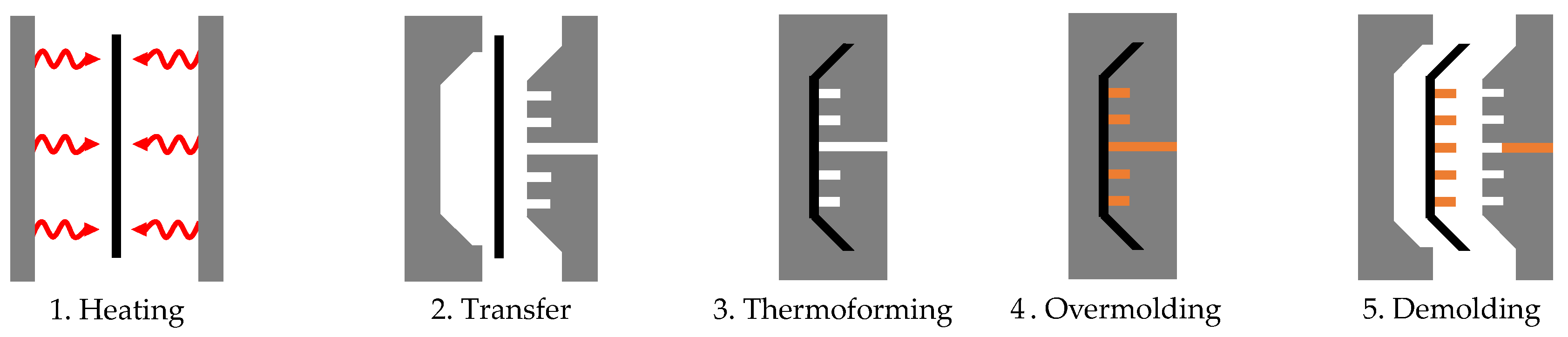
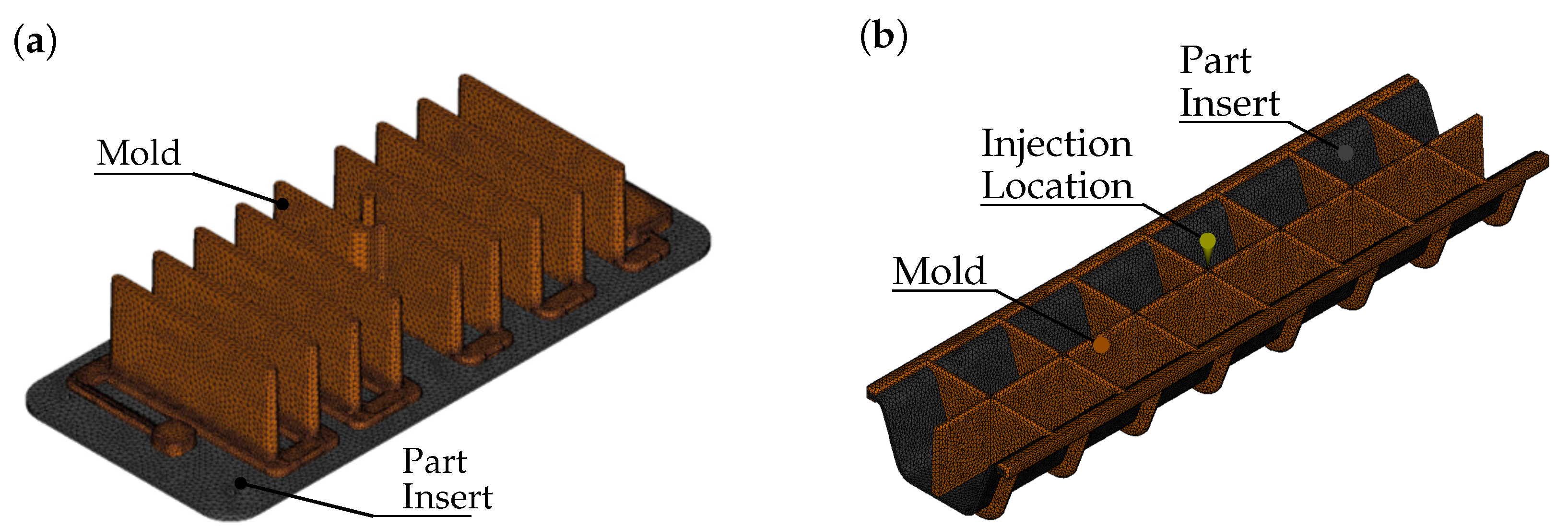
2.3. Geometry and Simulation Model
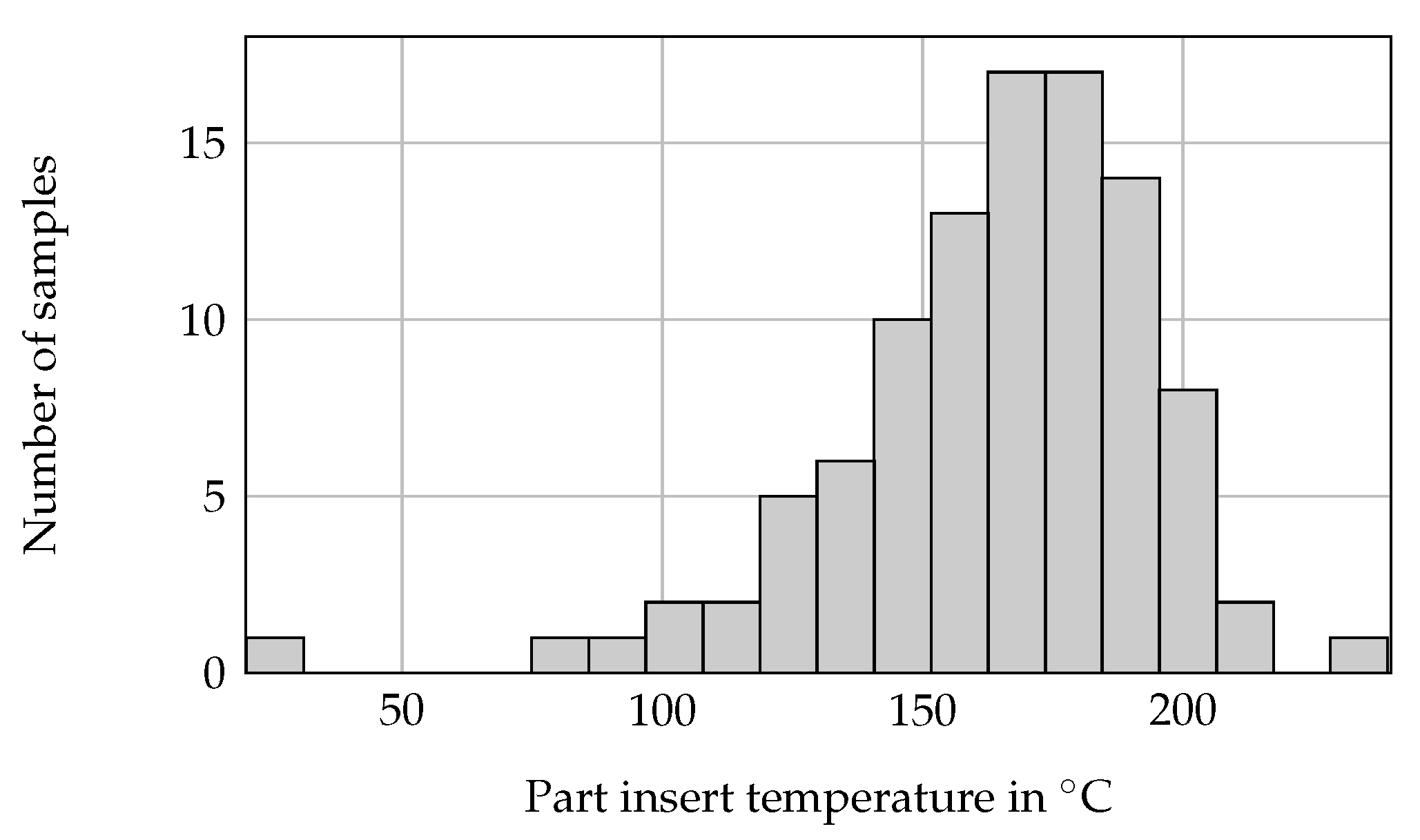
2.4. Sampling Strategy
2.5. Experimental Cross Tension Tests
2.6. Surrogate Modeling
3. Results and Discussion
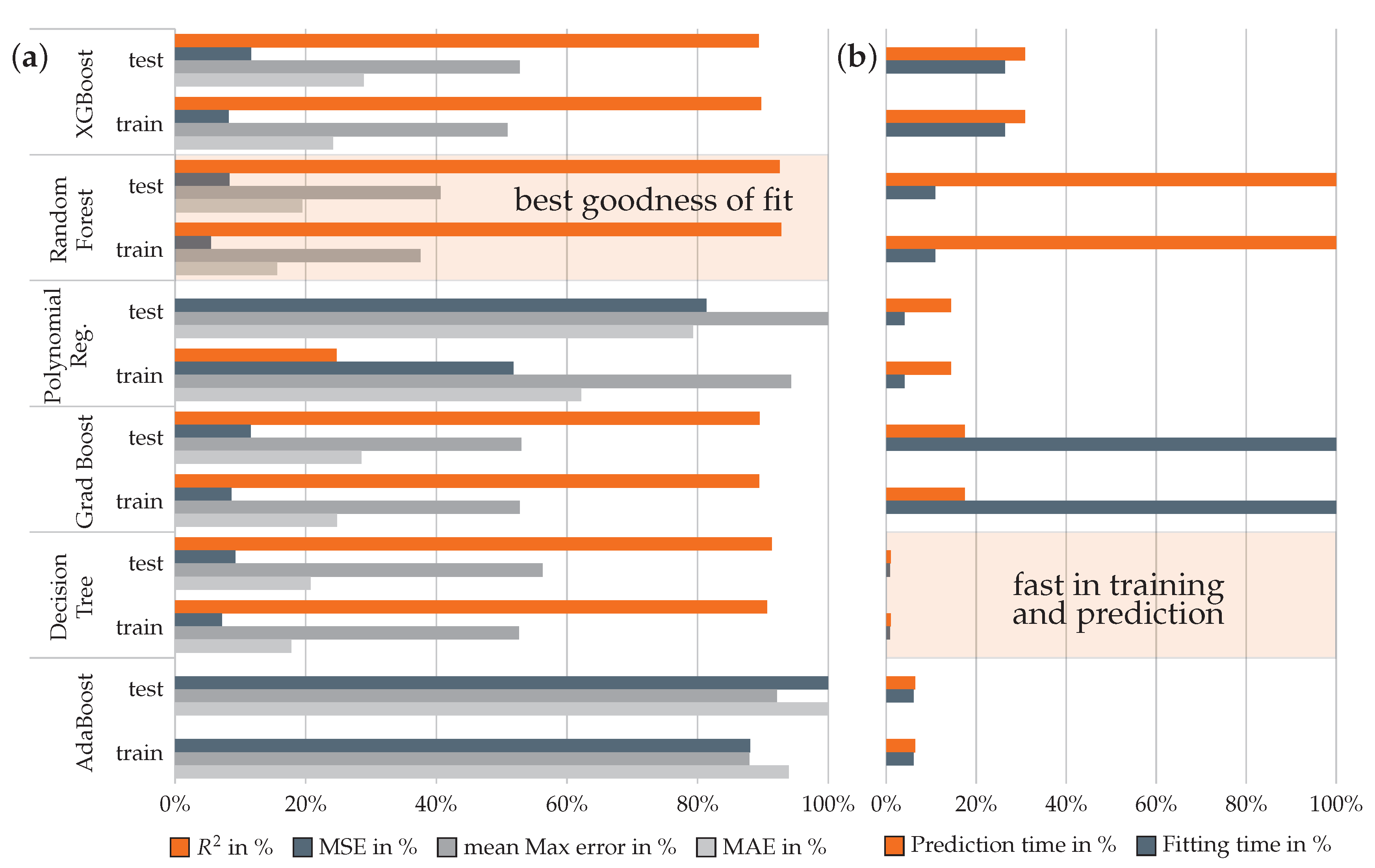
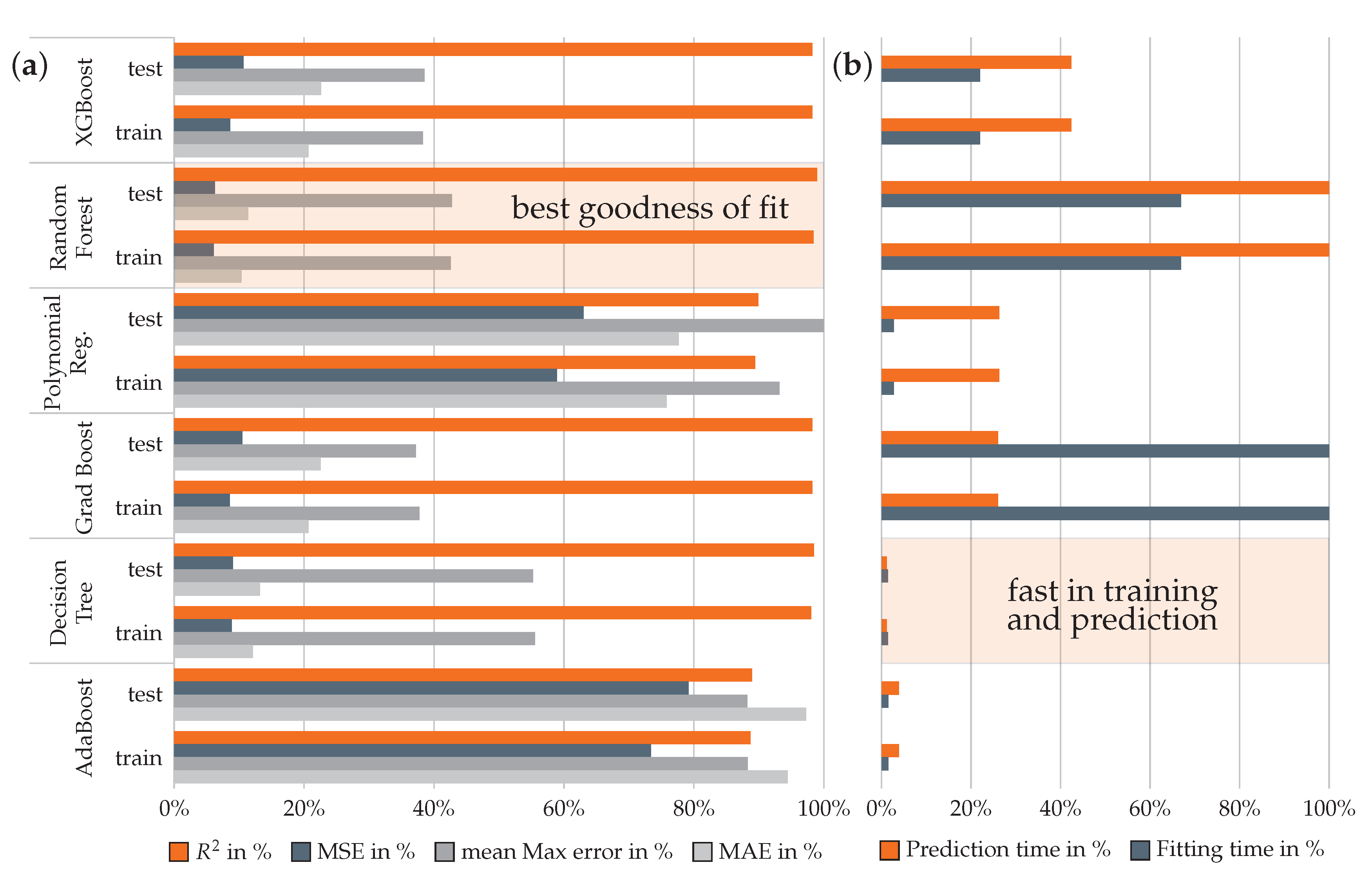
3.1. Evaluation of Surrogate Models for the Rib Structure
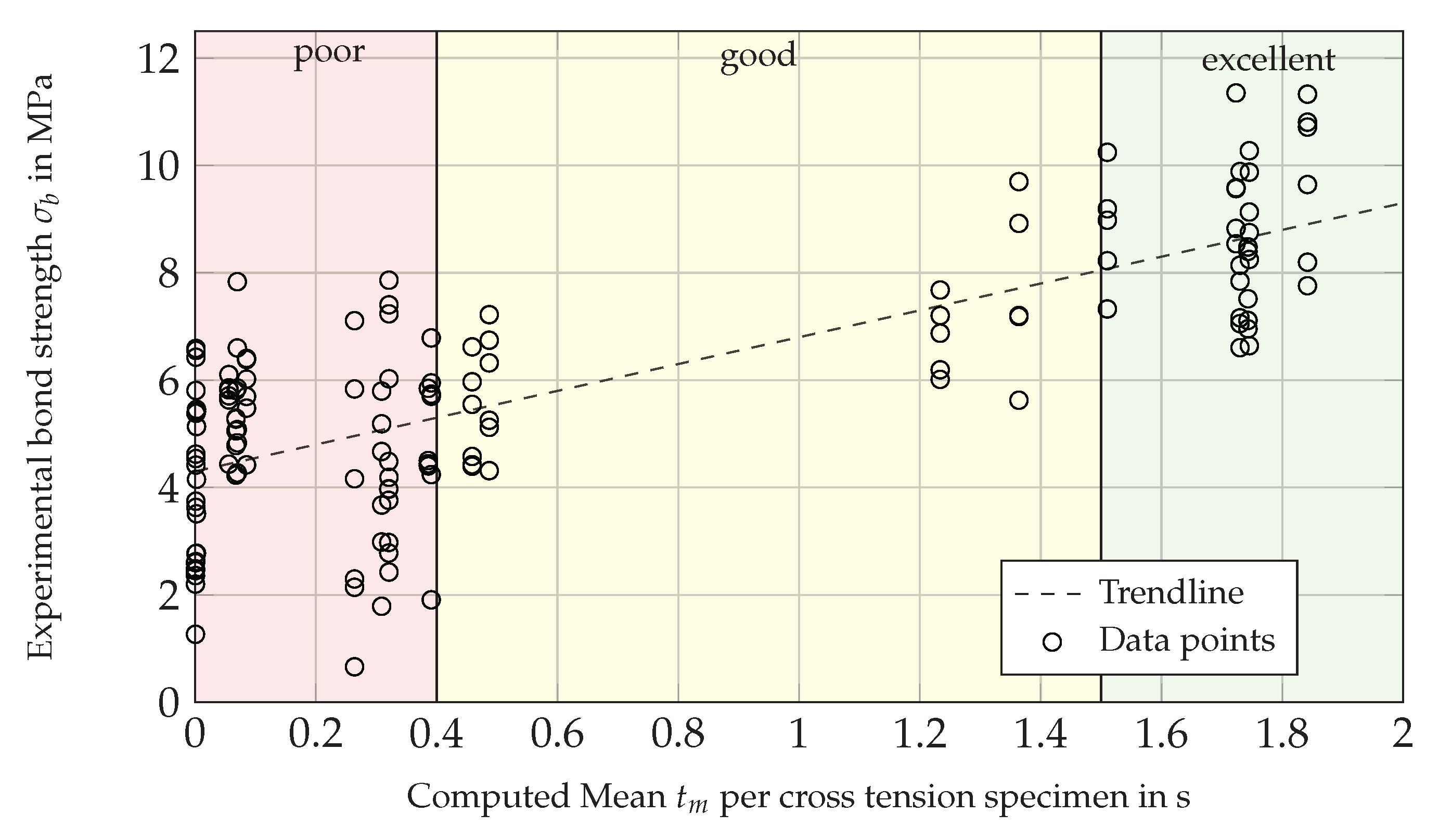
3.2. Experimental Results of Cross Tension Testing
3.3. Case Study of Virtual Demonstrator Structure
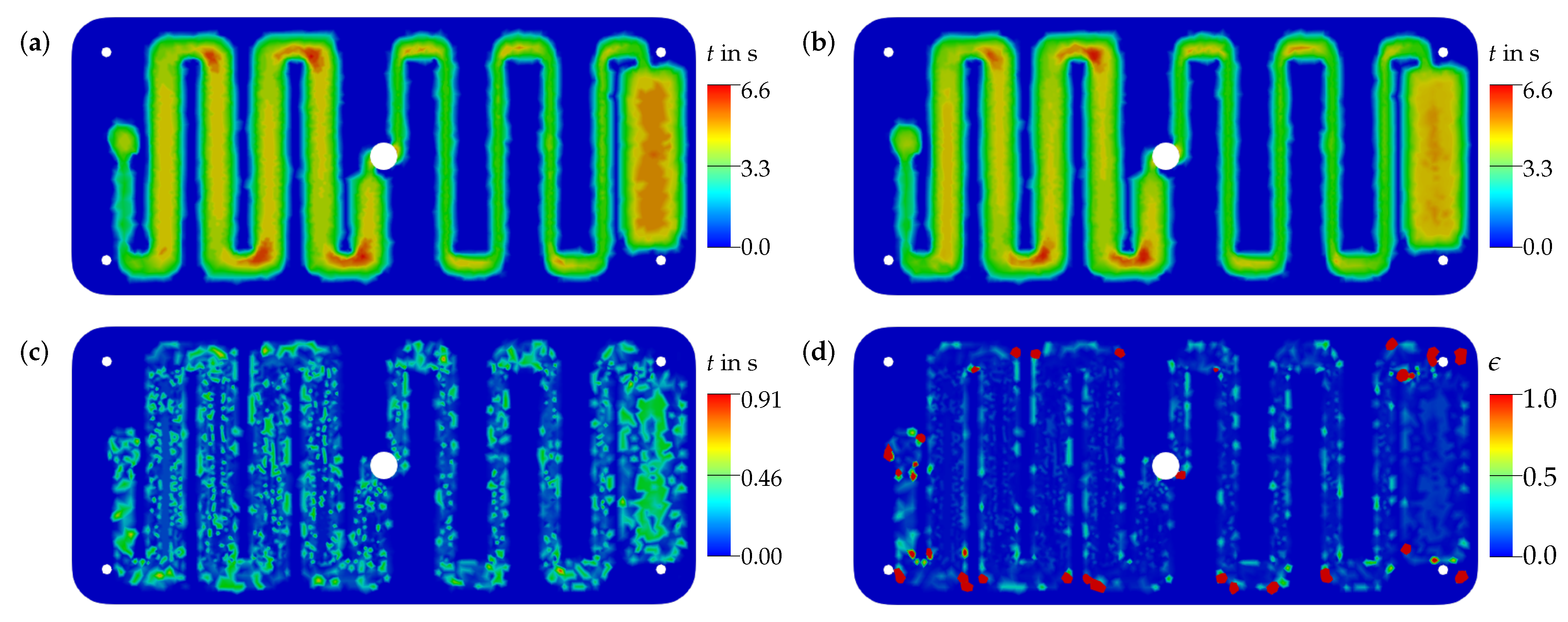
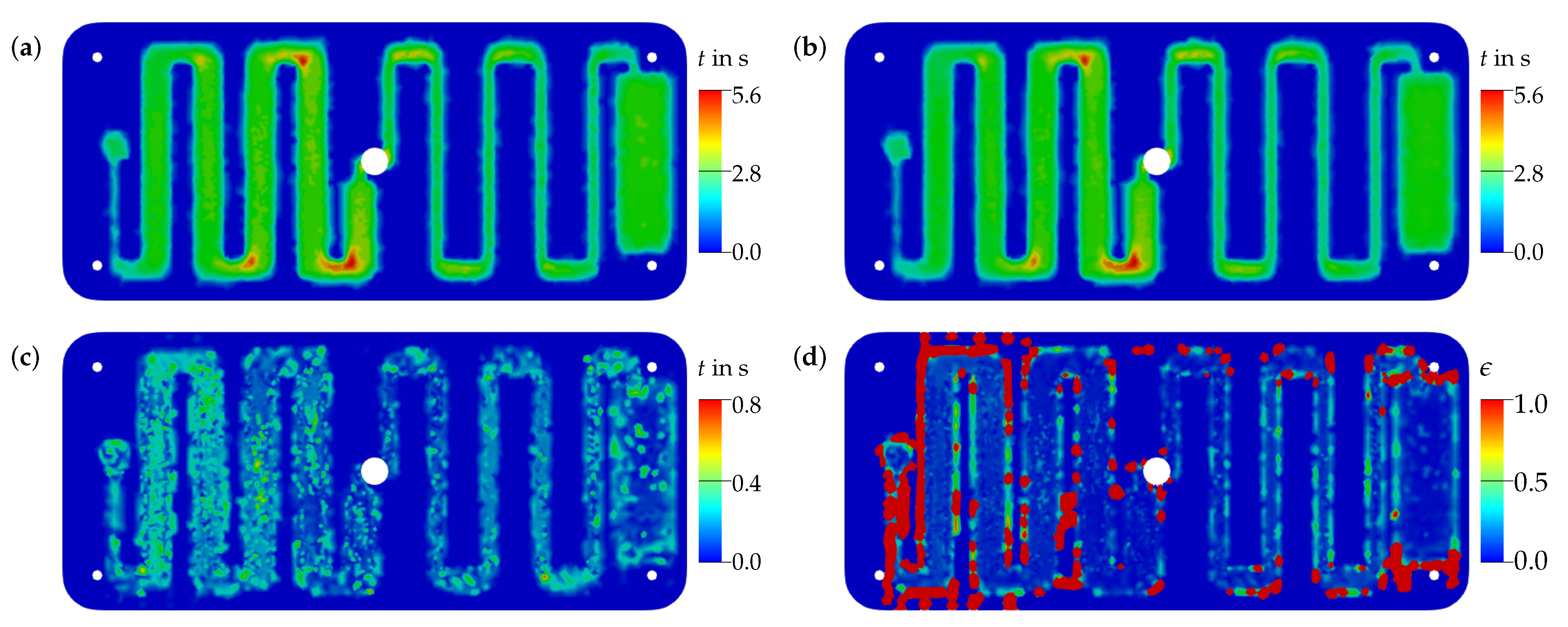
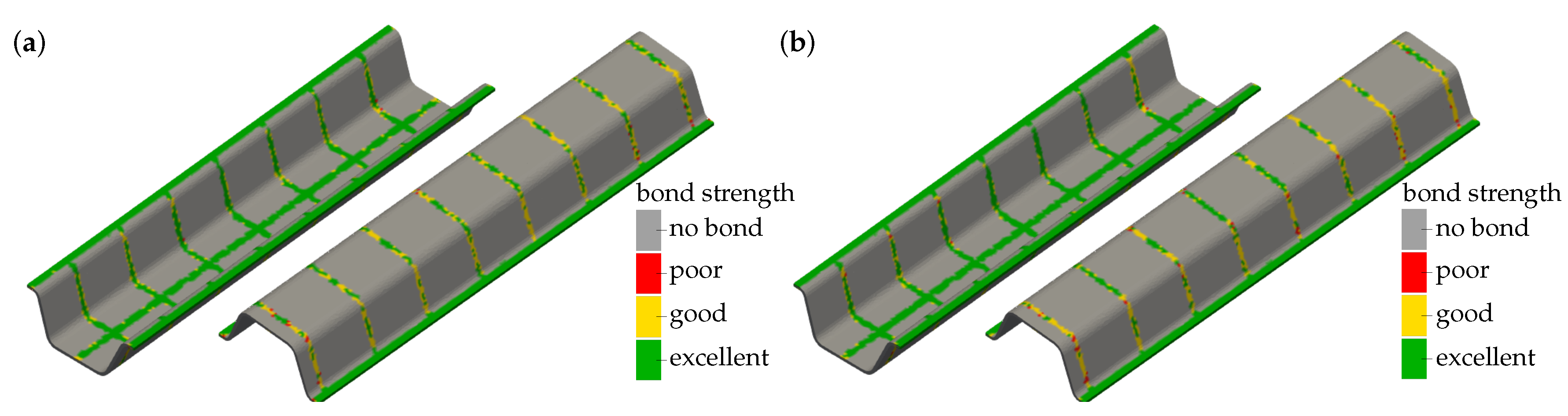
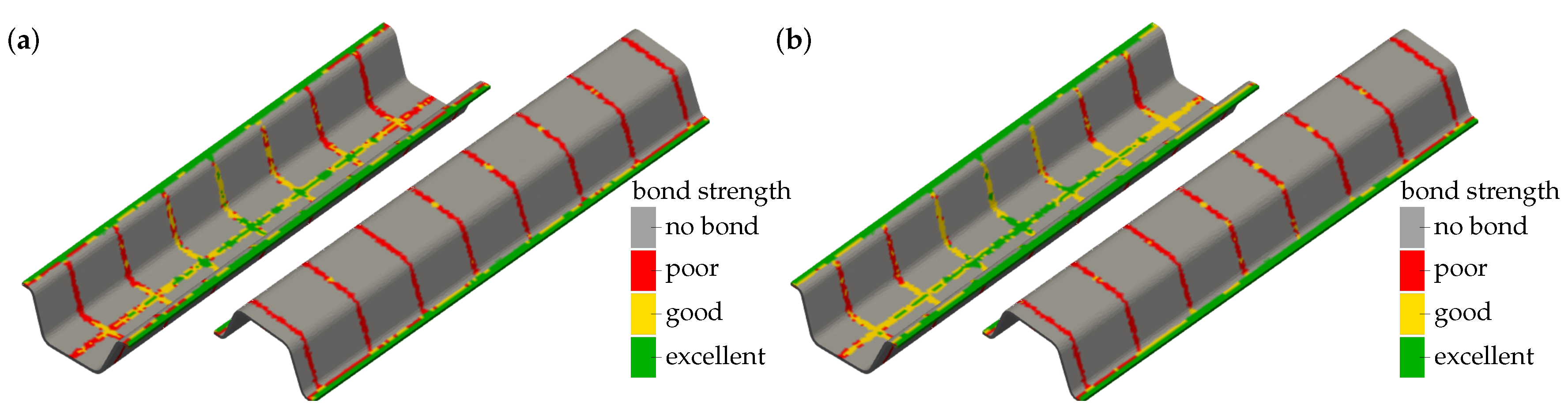
3.3.1. Evaluation of Surrogate Models
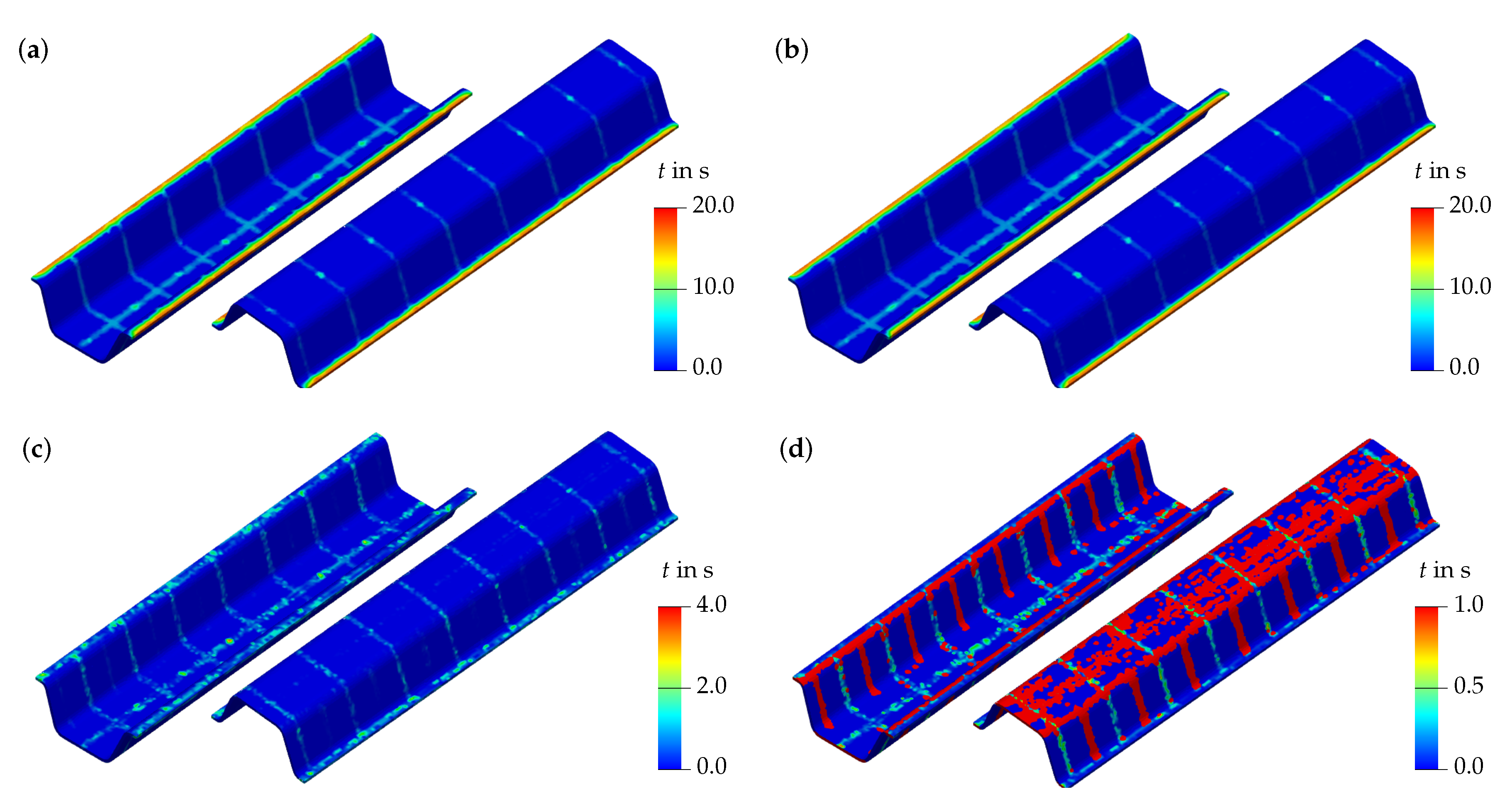
3.3.2. Transfer to a Quality Prediction System
4. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Fleischer, J.; Nieschlag, J. Introduction to CFRP-metal hybrids for lightweight structures. Prod. Eng. 2018, 12, 109–111. [Google Scholar] [CrossRef]
- Modler, N.; Adam, F.; Maaß, J.; Kellner, P.; Knothe, P.; Geuther, M.; Irmler, C. Intrinsic Lightweight Steel-Composite Hybrids for Structural Components. Mater. Sci. Forum 2015, 825–826, 401–408. [Google Scholar] [CrossRef]
- Mallick, P.K. Thermoplastics and thermoplastic–matrix composites for lightweight automotive structures. In Materials, Design and Manufacturing for Lightweight Vehicles: Woodhead Publishing Series in Composites Science and Engineering; Mallick, P.K., Ed.; Woodhead Publishing: Sawston, UK, 2010; pp. 174–207. [Google Scholar] [CrossRef]
- Liebsch, A.; Kupfer, R.; Krahl, M.; Haider, D.R.; Koshukow, W.; Gude, M. Adhesion studies of thermoplastic fibre-plastic composite hybrid components—Part 1: Thermoplastic-thermoplastic-composites. In Proceedings of the Hybrid Materials and Structure, Bremen, Germany, 18–19 April 2018. [Google Scholar]
- Liebsch, A.; Koshukow, W.; Gebauer, J.; Kupfer, R.; Gude, M. Overmoulding of consolidated fibre-reinforced thermoplastics—Increasing the bonding strength by physical surface pre-treatments. Procedia CIRP 2019, 85, 212–217. [Google Scholar] [CrossRef]
- Valverde, M.A.; Kupfer, R.; Wollmann, T.; Kawashita, L.F.; Gude, M.; Hallett, S.R. Influence of component design on features and properties in thermoplastic overmoulded composites. Compos. Part A Appl. Sci. Manuf. 2020, 132, 105823. [Google Scholar] [CrossRef]
- Bouwman, M.; Donderwinkel, T.; Krämer, E.; Wijskamp, S.; Costa, S.F. Overmoulding—An Integrated Design Approach for Dimensional Accuracy and Strength of Structural Parts. In Proceedings of the 3rd Annual Composites and Advanced Materials Expo, CAMX, ITHEC Proceedings, Anaheim, CA, USA, 26–29 September 2016. [Google Scholar]
- Akkerman, R.; Bouwman, M.; Wijskamp, S. Analysis of the Thermoplastic Composite Overmolding Process: Interface Strength. Front. Mater. 2020, 7. [Google Scholar] [CrossRef]
- Hürkamp, A.; Dér, A.; Gellrich, S.; Ossowski, T.; Lorenz, R.; Behrens, B.A.; Herrmann, C.; Dröder, K.; Thiede, S. Integrated Computational Product and Production Engineering for Multi-Material Lightweight Structures. Int. J. Adv. Manuf. Technol. 2020. [Google Scholar] [CrossRef]
- Görthofer, J.; Meyer, N.; Pallicity, T.D.; Schöttl, L.; Trauth, A.; Schemmann, M.; Hohberg, M.; Pinter, P.; Elsner, P.; Henning, F.; et al. Motivating the development of a virtual process chain for sheet molding compound composites. PAMM 2019, 19, e201900124. [Google Scholar] [CrossRef]
- Hieber, C.A.; Shen, S.F. A finite-element/finite-difference simulation of the injection-molding filling process. J. Non Fluid Mech. 1980, 7, 1–32. [Google Scholar] [CrossRef]
- Austin, C. Improving the Design of Injection Molds and Parts Using Computer Simulation of Plastic Flow. In International Pacific Conference on Automotive Engineering; SAE International: Warrendale, PA, USA, 1981. [Google Scholar] [CrossRef]
- Azaiez, J.; Chiba, K.; Chinesta, F.; Poitou, A. State-of-the-Art on numerical simulation of fiber-reinforced thermoplastic forming processes. Arch. Comput. Methods Eng. 2002, 9, 141–198. [Google Scholar] [CrossRef]
- Gellrich, S.; Filz, M.A.; Wölper, J.; Herrmann, C.; Thiede, S. DATA MINING APPLICATIONS IN MANUFACTURING OF LIGHTWEIGHT STRUCTURES. In Technologies for Economical and Functional Lightweight Design; Dröder, K., Vietor, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 15–27. [Google Scholar]
- Biehl, S.; Rumposch, C.; Paetsch, N.; Bräuer, G.; Weise, D.; Scholz, P.; Landgrebe, D. Multifunctional thin film sensor system as monitoring system in production. Microsyst. Technol. 2016, 22, 1757–1765. [Google Scholar] [CrossRef]
- Gellrich, S.; Beganovic, T.; Mattheus, A.; Herrmann, C.; Thiede, S. Feature Selection Based on Visual Analytics for Quality Prediction in Aluminium Die Casting. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki-Espoo, Finland, 22–25 July 2019; pp. 66–72. [Google Scholar] [CrossRef]
- Lee, J.; Noh, S.D.; Kim, H.J.; Kang, Y.S. Implementation of Cyber-Physical Production Systems for Quality Prediction and Operation Control in Metal Casting. Sensors 2018, 18, 1428. [Google Scholar] [CrossRef] [PubMed]
- García, V.; Sánchez, J.S.; Rodríguez-Picón, L.A.; Méndez-González, L.C.; de Jesús Ochoa-Domínguez, H. Using regression models for predicting the product quality in a tubing extrusion process. J. Intell. Manuf. 2019, 30, 2535–2544. [Google Scholar] [CrossRef]
- Gao, R.X.; Tang, X.; Gordon, G.; Kazmer, D.O. Online product quality monitoring through in-process measurement. CIRP Ann. 2014, 63, 493–496. [Google Scholar] [CrossRef]
- Zambal, S.; Eitzinger, C.; Clarke, M.; Klintworth, J.; Mechin, P. A digital twin for composite parts manufacturing: Effects of defects analysis based on manufacturing data. In Proceedings of the 2018 IEEE 16th International Conference on Industrial Informatics (INDIN), Porto, Portugal, 18–20 July 2018; pp. 803–808. [Google Scholar] [CrossRef]
- Chinesta, F.; Cueto, E.; Abisset-Chavanne, E.; Duval, J.L.; Khaldi, F.E. Virtual, Digital and Hybrid Twins: A New Paradigm in Data-Based Engineering and Engineered Data. Arch. Comput. Methods Eng. 2018. [Google Scholar] [CrossRef]
- Hürkamp, A.; Lorenz, R.; Behrens, B.A.; Dröder, K. Computational Manufacturing for Multi-Material Lightweight Parts. Procedia CIRP 2019, 85, 102–107. [Google Scholar] [CrossRef]
- Han, Z.H.; Zhang, K.S. Surrogate-Based Optimization. In Real-World Applications of Genetic Algorithms; Roeva, O., Ed.; InTech Open Access Publisher: London, UK, 2012. [Google Scholar]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15. [Google Scholar] [CrossRef]
- Pfrommer, J.; Zimmerling, C.; Liu, J.; Kärger, L.; Henning, F.; Beyerer, J. Optimisation of manufacturing process parameters using deep neural networks as surrogate models. Procedia CIRP 2018, 72, 426–431. [Google Scholar] [CrossRef]
- Thiede, S.; Juraschek, M.; Herrmann, C. Implementing Cyber-physical Production Systems in Learning Factories. Procedia CIRP 2016, 54, 7–12. [Google Scholar] [CrossRef]
- Kang, H.S.; Lee, J.Y.; Choi, S.; Kim, H.; Park, J.H.; Son, J.Y.; Kim, B.H.; Noh, S.D. Smart manufacturing: Past research, present findings, and future directions. Int. J. Precis. Eng.-Manuf. Technol. 2016, 3, 111–128. [Google Scholar] [CrossRef]
- Emilsson, E.; Dahllöf, L.; Söderman, M.L. Plastics in Passenger Cars: A Comparison over Types and Time; IVL Swedish Environmental Research Institute: Stockholm, Sweden, 2019. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Autodesk, Inc. Moldflow Insight; Autodesk, Inc.: Mill Valley, CA, USA, 2017. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
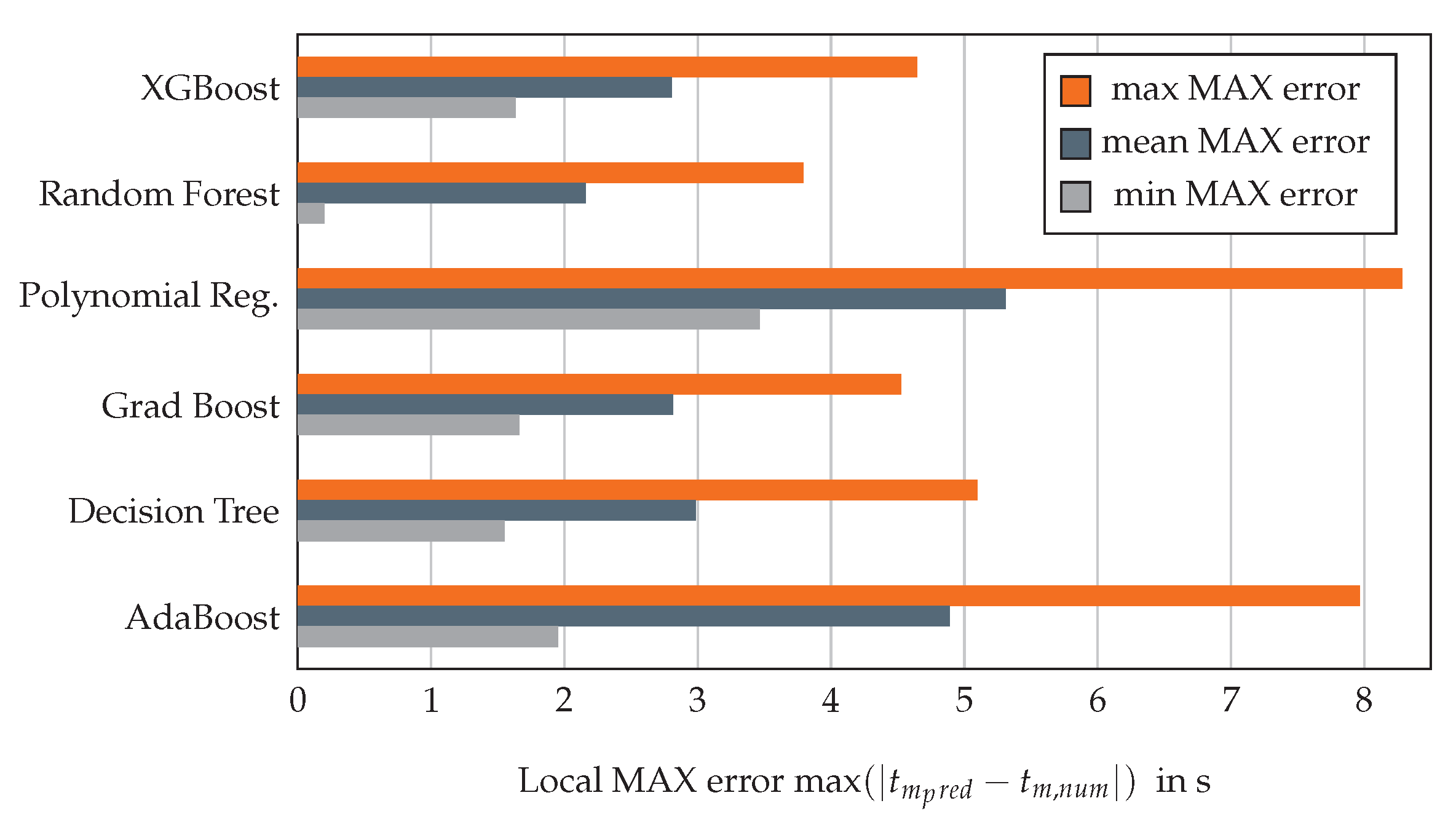

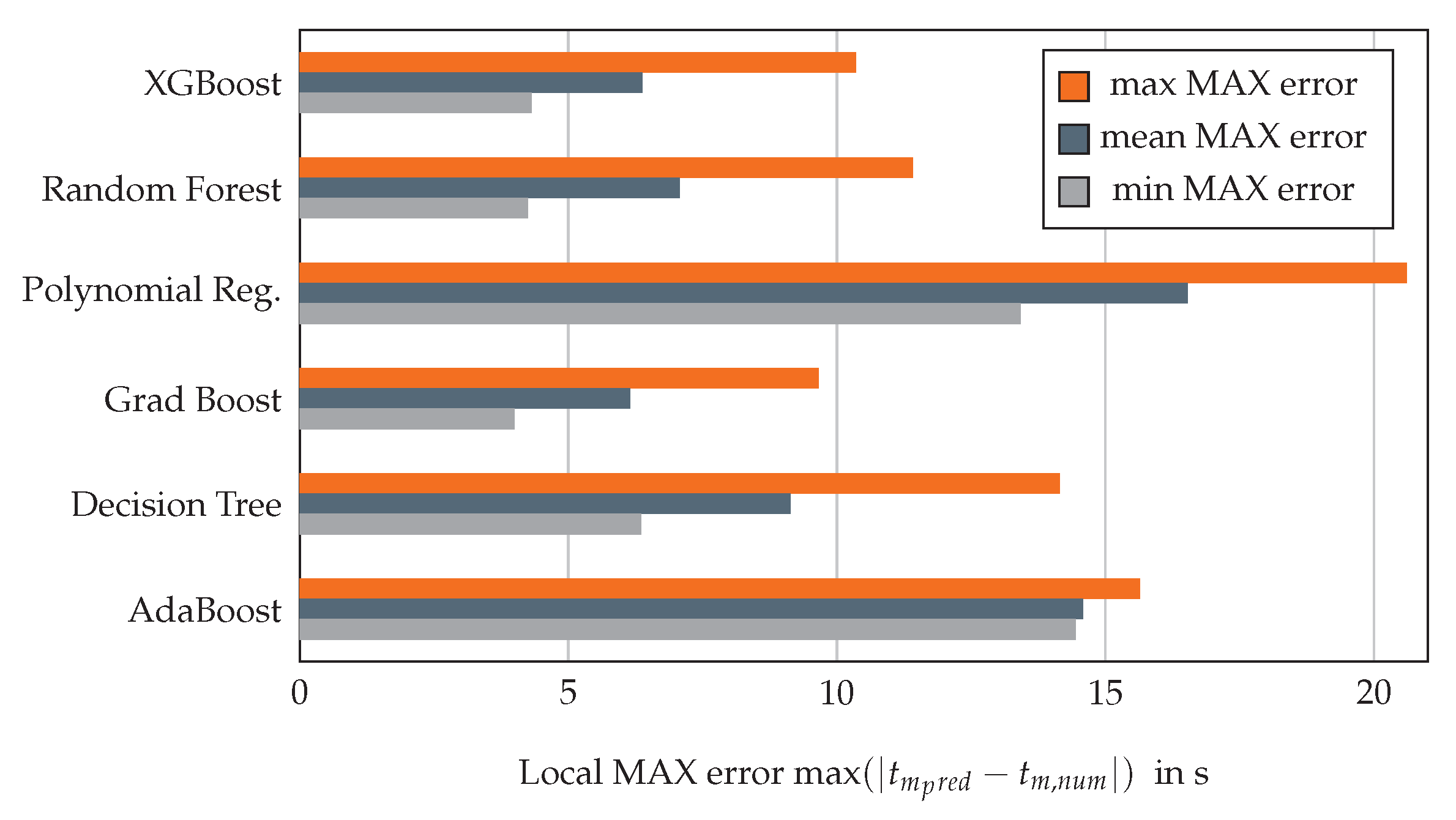
| Process Parameter | Min. Value | Max. Value | Distribution |
|---|---|---|---|
| Part insert temperature in °C | 20 | 240 | Modified Log-normal |
| Mold temperature in °C | 30 | 80 | uniform |
| Flow rate in cm/s | 10 | 100 | uniform |
| Process Parameter | Min. Value | Max. Value |
|---|---|---|
| Part insert temperature in °C | 50 | 160 |
| Melt temperature in °C | 240 | 240 |
| Mold temperature in °C | 50 | 80 |
| Packing pressure in MPa | 60 | 90 |
| Flow rate in cm/s | 50 | 100 |
| Method | Hyperparameters | Variation Range | # Steps | Best Parameters Rib Structure | Best Parameters Demonstrator |
|---|---|---|---|---|---|
| XGBoost | Learning rate | 0.1–1 | 10 | 0.7 | 0.4 |
| # Estimators | 10–500 | 7 | 500 | 500 | |
| Random Forest | Max depth | 10–70 | 4 | 50 | 70 |
| Min samples leaf | 1–10 | 5 | 1 | 1 | |
| # Estimators | 10–500 | 9 | 100 | 500 | |
| Polyn. Regr. | Degree | 1–7 | 7 | 4 | 4 |
| Grad Boost | Learning rate | 0.1–1 | 10 | 0.7 | 0.4 |
| # Estimators | 10–500 | 7 | 500 | 500 | |
| Decision Tree | Max depth | 1–None | 7 | None | 200 |
| Min samples leaf | 1–10 | 10 | 6 | 3 | |
| AdaBoost | Learning rate | 0.1–1 | 10 | 0.7 | 1 |
| # Estimators | 10–100 | 7 | 30 | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hürkamp, A.; Gellrich, S.; Ossowski, T.; Beuscher, J.; Thiede, S.; Herrmann, C.; Dröder, K. Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites. J. Manuf. Mater. Process. 2020, 4, 92. https://doi.org/10.3390/jmmp4030092
Hürkamp A, Gellrich S, Ossowski T, Beuscher J, Thiede S, Herrmann C, Dröder K. Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites. Journal of Manufacturing and Materials Processing. 2020; 4(3):92. https://doi.org/10.3390/jmmp4030092
Chicago/Turabian StyleHürkamp, André, Sebastian Gellrich, Tim Ossowski, Jan Beuscher, Sebastian Thiede, Christoph Herrmann, and Klaus Dröder. 2020. "Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites" Journal of Manufacturing and Materials Processing 4, no. 3: 92. https://doi.org/10.3390/jmmp4030092
APA StyleHürkamp, A., Gellrich, S., Ossowski, T., Beuscher, J., Thiede, S., Herrmann, C., & Dröder, K. (2020). Combining Simulation and Machine Learning as Digital Twin for the Manufacturing of Overmolded Thermoplastic Composites. Journal of Manufacturing and Materials Processing, 4(3), 92. https://doi.org/10.3390/jmmp4030092








