Learning-Based Prediction of Pose-Dependent Dynamics
Abstract
1. Introduction
2. Technological Investigation
3. Geometric Physically-Based Simulation of Milling Processes
4. Fitting of Parameter Values of Compliance Models
5. ML Methods for Predicting Pose-Dependent Dynamics of Milling Processes
6. Results
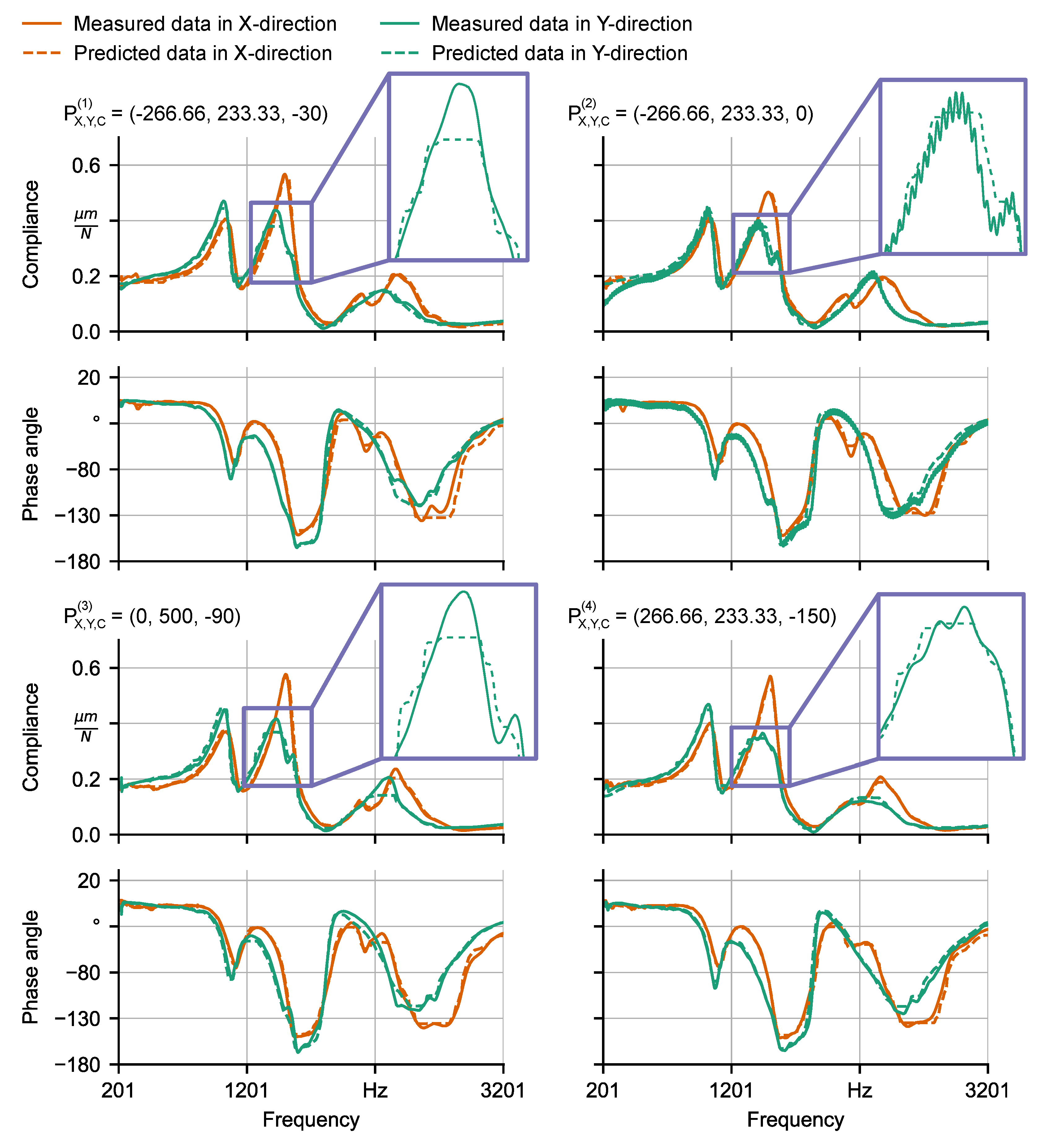
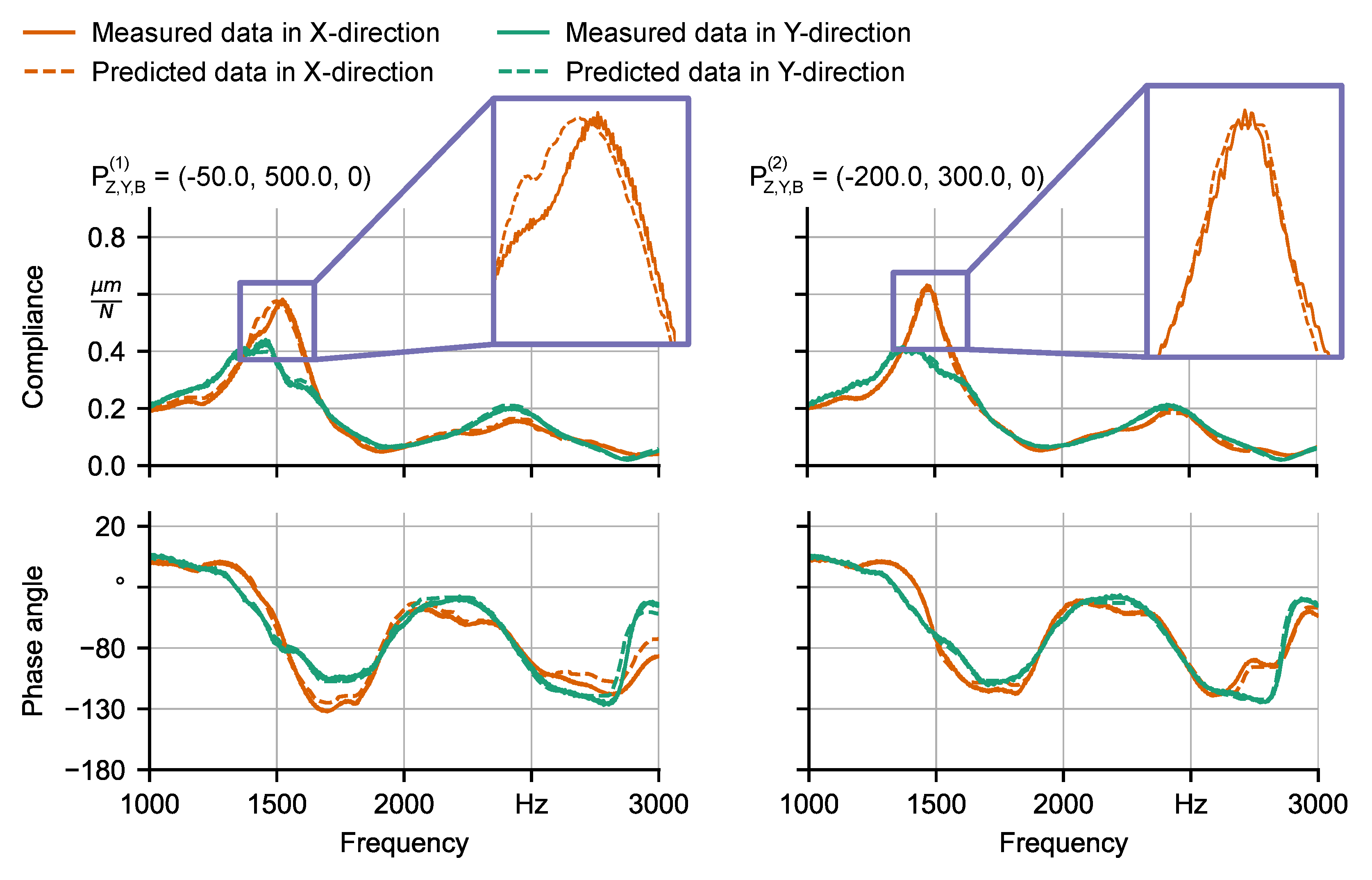
6.1. Learning of FRFs
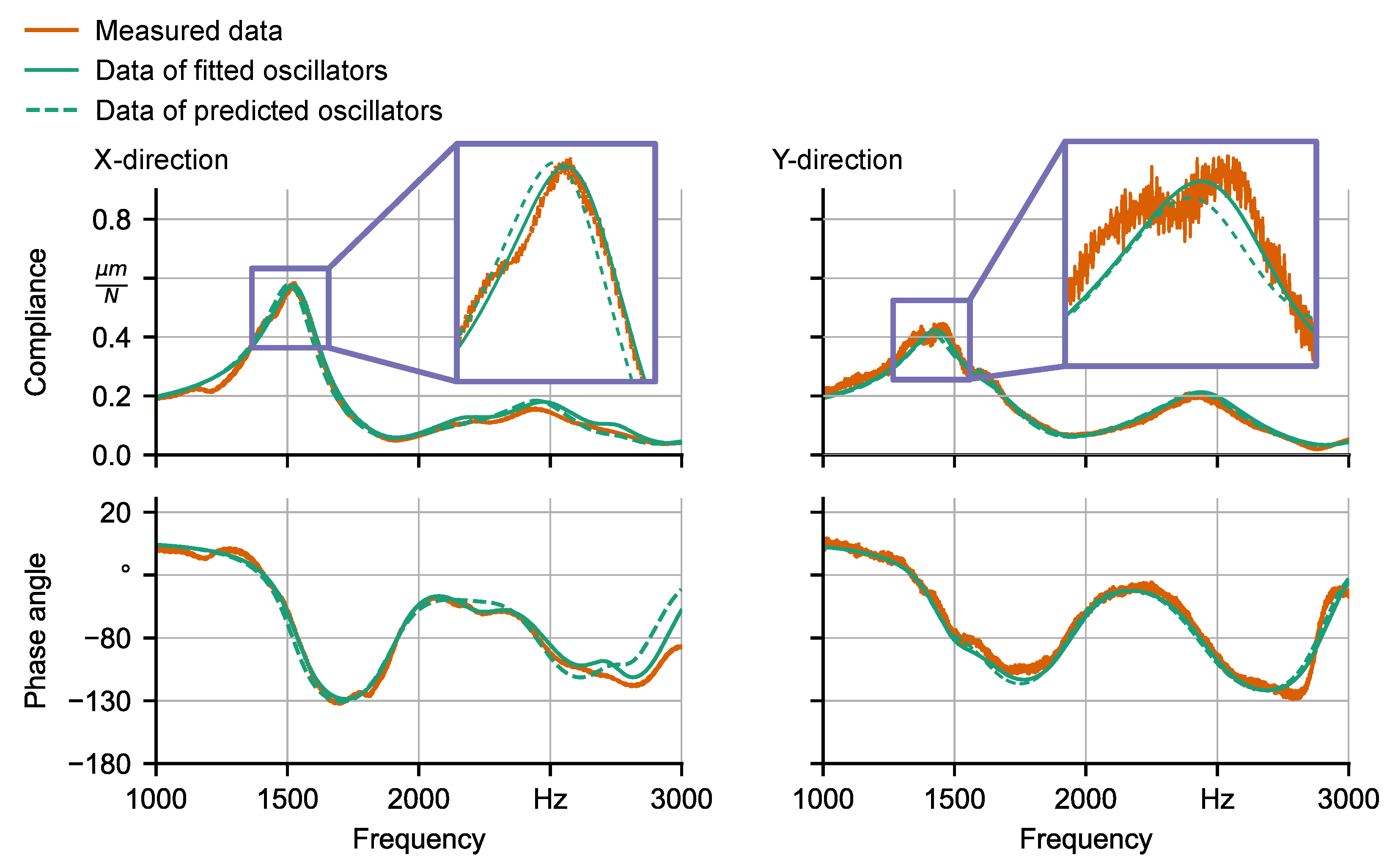
6.2. Learning of Oscillator Parameter Values
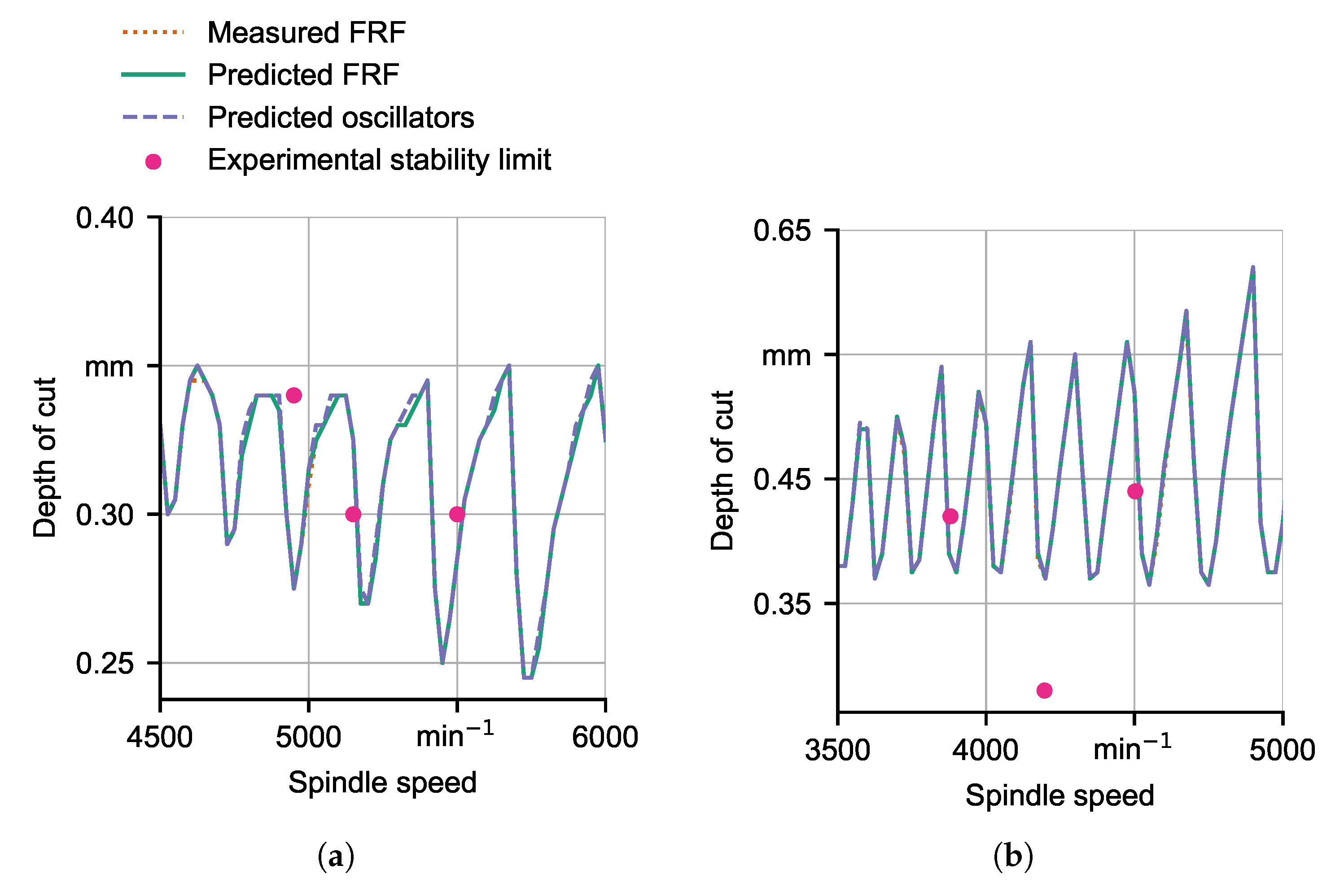
6.3. Comparison between SLDs
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Biermann, D.; Kersting, P.; Surmann, T. A general approach to simulating workpiece vibrations during five-axis milling of turbine blades. CIRP Ann. 2010, 59, 125–128. [Google Scholar] [CrossRef]
- Wiederkehr, P.; Siebrecht, T. Virtual Machining: Capabilities and Challenges of Process Simulations in the Aerospace Industry. Procedia Manuf. 2016, 6, 80–87. [Google Scholar] [CrossRef]
- Ismail, F.; Bastami, A. Improving Stability of Slender End Mills Against Chatter. J. Eng. Ind. 1986, 108, 264–268. [Google Scholar] [CrossRef]
- Tlusty, J.; Smith, S.; Winfough, W. Techniques for the Use of Long Slender End Mills in High-speed Milling. CIRP Ann. 1996, 45, 393–396. [Google Scholar] [CrossRef]
- Davies, M.; Dutterer, B.; Pratt, J.; Schaut, A.; Bryan, J. On the Dynamics of High-Speed Milling with Long, Slender Endmills. CIRP Ann. 1998, 47, 55–60. [Google Scholar] [CrossRef]
- De Aguiar, M.M.; Diniz, A.E.; Pederiva, R. Correlating surface roughness, tool wear and tool vibration in the milling process of hardened steel using long slender tools. Int. J. Mach. Tools Manuf. 2013, 68, 1–10. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Kiss, A.K.; Hajdu, D.; Bachrathy, D.; Stepan, G. Operational stability prediction in milling based on impact tests. Mech. Syst. Signal Process. 2018, 103, 327–339. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Altintas, Y.; Kersting, P.; Biermann, D.; Budak, E.; Denkena, B.; Lazoglu, I. Virtual process systems for part machining operations. CIRP Ann. 2014, 63, 585–605. [Google Scholar] [CrossRef]
- Baumann, J.; Siebrecht, T.; Wiederkehr, P. Modelling the Dynamic Behavior of a Machine Tool Considering the Tool-position-dependent Change of Modal Parameters in a Geometric-kinematic Simulation System. Procedia CIRP 2017, 62, 351–356. [Google Scholar] [CrossRef]
- Surmann, T.; Biermann, D.; Kehl, G. Oscillator model of machine tools for the simulation of self excited vibrations in machining processes. In Proceedings of the 1st International Conference on Process Machine Interactions (PMI 2008), Hannover, Germany, 3–4 September 2008; pp. 23–29. [Google Scholar]
- Law, M. Position-Dependent Dynamics and Stability of Machine Tools. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2013. [Google Scholar]
- Brecher, C.; Altstädter, H.; Daniels, M. Axis position dependent dynamics of multi-axis milling machines. In Proceedings of the 15th CIRP Conference on Modelling of Machining Operations, Karlsruhe, Germany, 11–12 June 2015; Volume 31, pp. 508–514. [Google Scholar] [CrossRef]
- Law, M.; Altintas, Y.; Phani, A.S. Rapid evaluation and optimization of machine tools with position-dependent stability. Int. J. Mach. Tools Manuf. 2013, 68, 81–90. [Google Scholar] [CrossRef]
- Kono, D.; Moriya, Y.; Matsubara, A. Influence of rotary axis on tool-workpiece loop compliance for five-axis machine tools. Precis. Eng. 2017, 49, 278–286. [Google Scholar] [CrossRef]
- Budak, E.; Ozturk, E.; Tunc, L. Modeling and simulation of 5-axis milling processes. CIRP Ann. 2009, 58, 347–350. [Google Scholar] [CrossRef]
- Shamoto, E.; Akazawa, K. Analytical prediction of chatter stability in ball end milling with tool inclination. CIRP Ann. 2009, 58, 351–354. [Google Scholar] [CrossRef]
- Du, C.; Lu, D.; Zhang, J.; Zhang, H.; Zhao, W. Pose-dependent dynamic modeling and analysis of Bi-rotary milling head. In Proceedings of the ASME 11th 2016 International Manufacturing Science and Engineering Conference, Blacksburg, VA, USA, 1–27 June 2016; The American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Du, C.; Zhang, J.; Lu, D.; Zhang, H.; Zhao, W. A parametric modeling method for the pose-dependent dynamics of bi-rotary milling head. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 232, 797–815. [Google Scholar] [CrossRef]
- Chao, S.; Altintas, Y. Chatter free tool orientation in 5-axis ball-end milling. Int. J. Mach. Tools Manuf. 2016, 106, 89–97. [Google Scholar] [CrossRef]
- Siebrecht, T.; Odendahl, S.; Hense, R.; Kersting, P. Interpolation method for the oscillator-based modeling of workpiece vibrations. In Proceedings of the 3th CIRP International Conference on High Performance Cutting; Byrne, G., Ed.; CIRP: Paris, France, 2008. [Google Scholar]
- Deris, A.; Zain, A.; Sallehuddin, R. Overview of Support Vector Machine in Modeling Machining Performances. Procedia Eng. 2011, 24, 308–312. [Google Scholar] [CrossRef]
- Al-Zubaidi, S.; Ghani, J.; Haron, C. Application of ANN in Milling Process: A Review. Model. Simul. Eng. 2011, 2011, 696275. [Google Scholar] [CrossRef]
- Wuest, T.; Weimer, D.; Irgens, C.; Thoben, K.D. Machine learning in manufacturing: Advantages, challenges, and applications. Prod. Manuf. Res. 2016, 4, 23–45. [Google Scholar] [CrossRef]
- Tandon, V.; El-Mounayri, H. A Novel Artificial Neural Networks Force Model for End Milling. Int. J. Adv. Manuf. Technol. 2001, 18, 693–700. [Google Scholar] [CrossRef]
- Briceno, J.F.; El-Mounayri, H.; Mukhopadhyay, S. Selecting an artificial neural network for efficient modeling and accurate simulation of the milling process. Int. J. Mach. Tools Manuf. 2002, 42, 663–674. [Google Scholar] [CrossRef]
- Aykut, Ş.; Gölcü, M.; Semiz, S.; Ergür, H. Modeling of cutting forces as function of cutting parameters for face milling of satellite 6 using an artificial neural network. J. Mater. Process. Technol. 2007, 190, 199–203. [Google Scholar] [CrossRef]
- Sheikh-Ahmad, J.; Twomey, J.; Kalla, D.; Lodhia, P. Multiple regression and committee neural network force prediction models in milling frp. Mach. Sci. Technol. 2007, 11, 391–412. [Google Scholar] [CrossRef]
- Palani, S.; Natarajan, U. Prediction of surface roughness in CNC end milling by machine vision system using artificial neural network based on 2D Fourier transform. Int. J. Adv. Manuf. Technol. 2011, 54, 1033–1042. [Google Scholar] [CrossRef]
- Mahesh, G.; Devadasan, S. Prediction of surface roughness of end milling operation using genetic algorithm. Int. J. Adv. Manuf. Technol. 2014, 77, 369–381. [Google Scholar] [CrossRef]
- Nguyen, T.T. Prediction and optimization of machining energy, surface roughness, and production rate in SKD61 milling. Measurement 2019, 136, 525–544. [Google Scholar] [CrossRef]
- Lamraoui, M.; Barakat, M.; Thomas, M.; Badaoui, M.E. Chatter detection in milling machines by neural network classification and feature selection. J. Vib. Control 2015, 21, 1251–1266. [Google Scholar] [CrossRef]
- Chen, Y.; Li, H.; Jing, X.; Hou, L.; Bu, X. Intelligent chatter detection using image features and support vector machine. Int. J. Adv. Manuf. Technol. 2019, 102, 1433–1442. [Google Scholar]
- Friedrich, J.; Hinze, C.; Renner, A.; Verl, A.; Lechler, A. Estimation of stability lobe diagrams in milling with continuous learning algorithms. Robot. Comput. Integr. Manuf. 2017, 43, 124–134, Special Issue: Extended Papers Selected from FAIM 2014. [Google Scholar] [CrossRef]
- Denkena, B.; Bergmann, B.; Reimer, S. Analysis of different machine learning algorithms to learn stability lobe diagrams. Procedia CIRP 2020, 88, 282–287. [Google Scholar] [CrossRef]
- Chen, G.; Li, Y.; Liu, X. Pose-dependent tool tip dynamics prediction using transfer learning. Int. J. Mach. Tools Manuf. 2019, 137, 30–41. [Google Scholar] [CrossRef]
- Tangjitsitcharoen, S.; Saksri, T.; Ratanakuakangwan, S. Advance in chatter detection in ball end milling process by utilizing wavelet transform. J. Intell. Manuf. 2015, 26, 485–499. [Google Scholar]
- Yao, Z.; Mei, D.; Chen, Z. On-line chatter detection and identification based on wavelet and support vector machine. J. Mater. Process. Technol. 2010, 210, 713–719. [Google Scholar]
- Cao, H.; Lei, Y.; He, Z. Chatter identification in end milling process using wavelet packets and Hilbert–Huang transform. Int. J. Mach. Tools Manuf. 2013, 69, 11–19. [Google Scholar]
- Sun, Y.; Xiong, Z. An optimal weighted wavelet packet entropy method with application to real-time chatter detection. IEEE/ASME Trans. Mechatron. 2016, 21, 2004–2014. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Ngui, W.K.; Leong, M.S.; Hee, L.M.; Abdelrhman, A.M. Wavelet Analysis: Mother Wavelet Selection Methods. Adv. Manuf. Mech. Eng. 2013, 393, 953–958. [Google Scholar]
- Blackman, R.B.; Tukey, J.W. The Measurement of Power Spectra from the Point of View of Communications Engineering—Part I. Bell Syst. Tech. J. 1958, 37, 185–282. [Google Scholar] [CrossRef]
- Denkena, B.; Schmidt, C. Experimental investigation and simulation of machining thin-walled workpieces. Prod. Eng. 2007, 1, 343–350. [Google Scholar] [CrossRef]
- Wöste, F.; Siebrecht, T.; Fast, M.; Wiederkehr, P. Geometric Physically-Based and Numerical Simulation of NC-Grinding Processes for the Calculation of Process Forces. Procedia CIRP 2019, 86, 133–138. [Google Scholar]
- Joliet, R.; Kansteiner, M.; Kersting, P. A process Model for Force-controlled Honing Simulations. Procedia CIRP 2015, 28, 46–51. [Google Scholar] [CrossRef]
- Delbrügger, T.; Meißner, M.; Wirtz, A.; Biermann, D.; Myrzik, J.; Rossmann, J.; Wiederkehr, P. Multi-Level Simulation Concept for Multi-Disciplinary Analysis and Optimization of Production Systems. Int. J. Adv. Manuf. Technol. 2019, 103, 3993–4012. [Google Scholar]
- Foley, J.D.; van Dam, A.; Feiner, S.K.; Hughes, J.F. Computer Graphics: Principles and Practice, 2nd ed.; Reprinted with Corrections; Addison-Wesley Publishing Company, Inc.: Boston, MA, USA, 1997. [Google Scholar]
- Odendahl, S.; Kersting, P. Higher Efficiency Modeling of Surface Location Errors by Using a Multi-scale Milling Simulation. Procedia CIRP 2013, 9, 18–22. [Google Scholar] [CrossRef]
- Kienzle, O. Die Bestimmung von Kräften und Leistungen an spanenden Werkzeugen und Werkzeugmaschinen. VDI-Z 1952, 94, 299–305. [Google Scholar]
- Surmann, T.; Biermann, D. The effect of tool vibrations on the flank surface created by peripheral milling. CIRP Ann. 2008, 57, 375–378. [Google Scholar] [CrossRef]
- Freiburg, D.; Hense, R.; Kersting, P.; Biermann, D. Determination of Force Parameters for Milling Simulations by Combining Optimization and Simulation Techniques. J. Manuf. Sci. Eng. 2016, 138, 044502-1–044502-6. [Google Scholar] [CrossRef]
- Surmann, T.; Enk, D. Simulation of milling tool vibration trajectories along changing engagement conditions. Int. J. Mach. Tools Manuf. 2007, 47, 1442–1448. [Google Scholar] [CrossRef]
- Gulsen, M.; Smith, A.E.; Tate, D.M. A genetic algorithm approach to curve fitting. Int. J. Prod. Res. 1995, 33, 1911–1923. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L.M. Genetic algorithms: A survey. Computer 1994, 27, 17–26. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Rencher, A.C.; Christensen, W.F. Methods of Multivariate Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural Networks and the Bias/Variance Dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar]
- Sollich, P.; Krogh, A. Learning with ensembles: How overfitting can be useful. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1996; pp. 190–196. [Google Scholar]
- Ueda, N.; Nakano, R. Generalization error of ensemble estimators. In Proceedings of the International Conference on Neural Networks (ICNN’96), Washington, DC, USA, 2–7 June 1996; Volume 1, pp. 90–95. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’16, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Dombovari, Z.; Sanz-Calle, M.; Zatarain, M. The Basics of Time-Domain-Based Milling Stability Prediction Using Frequency Response Function. J. Manuf. Mater. Process. 2020, 4, 72. [Google Scholar] [CrossRef]
- Hess, S.; Finkeldey, F.; Wiederkehr, P. Elaborated Analysis of Force Model Parameters in Milling Simulations with Respect to Tool State Variations. Procedia CIRP 2016, 55, 83–88. [Google Scholar] [CrossRef][Green Version]
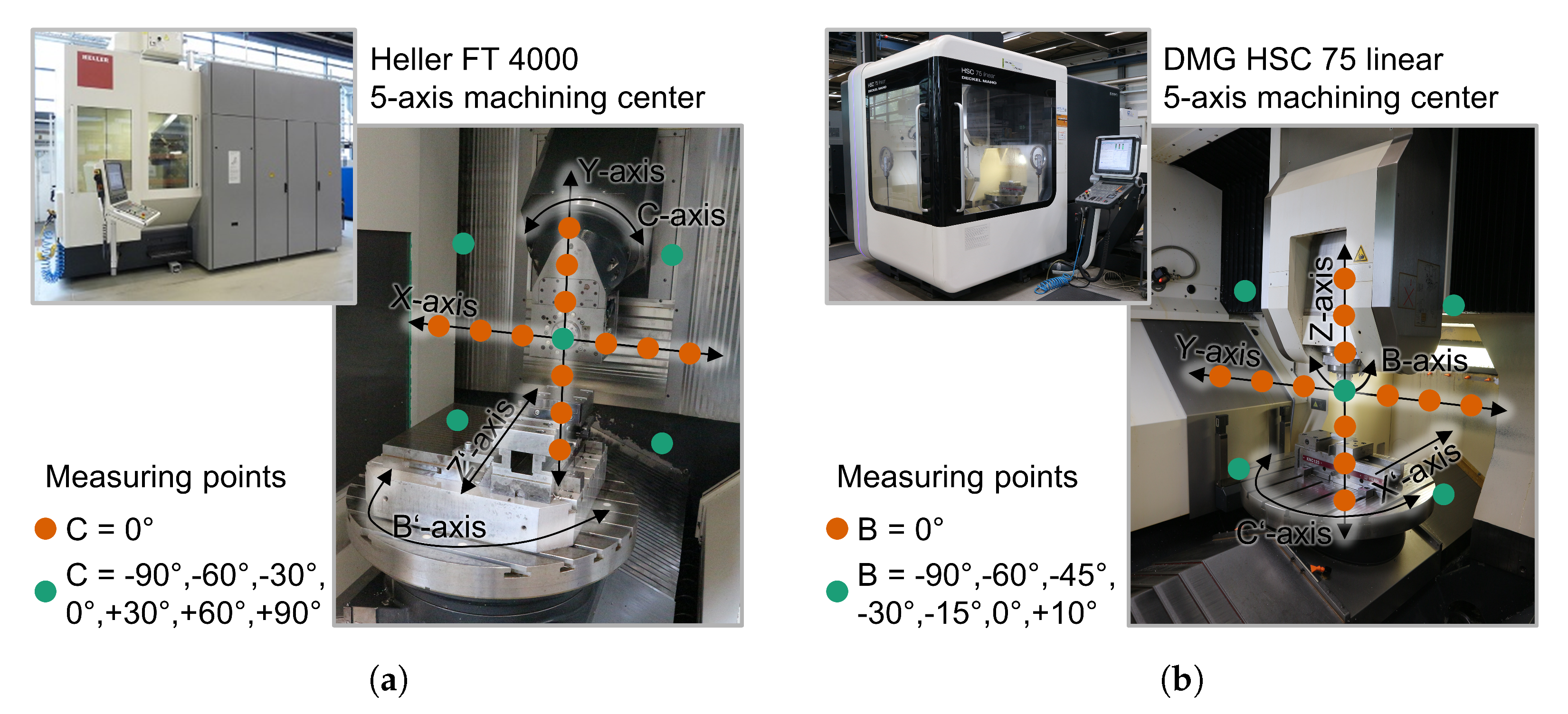
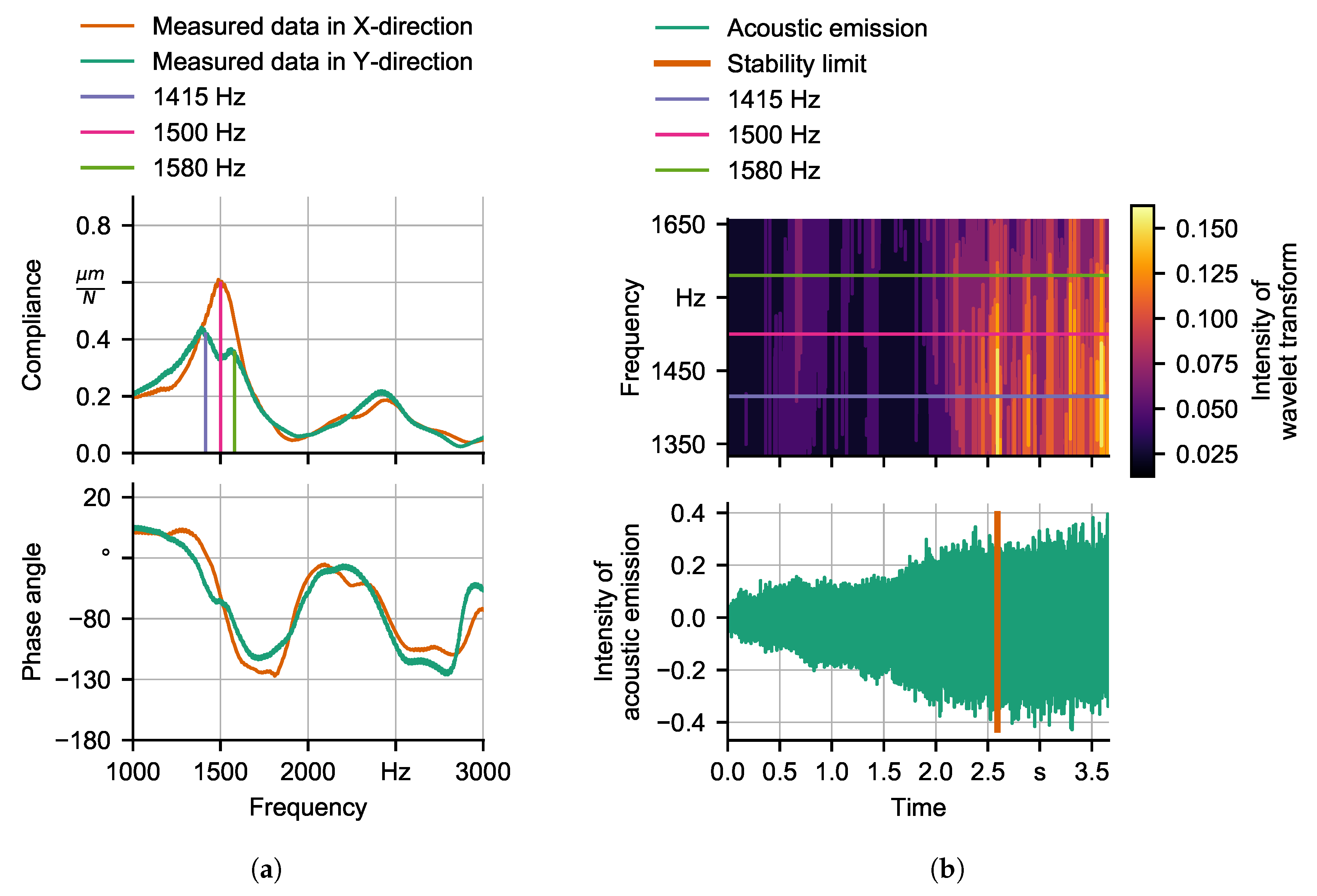
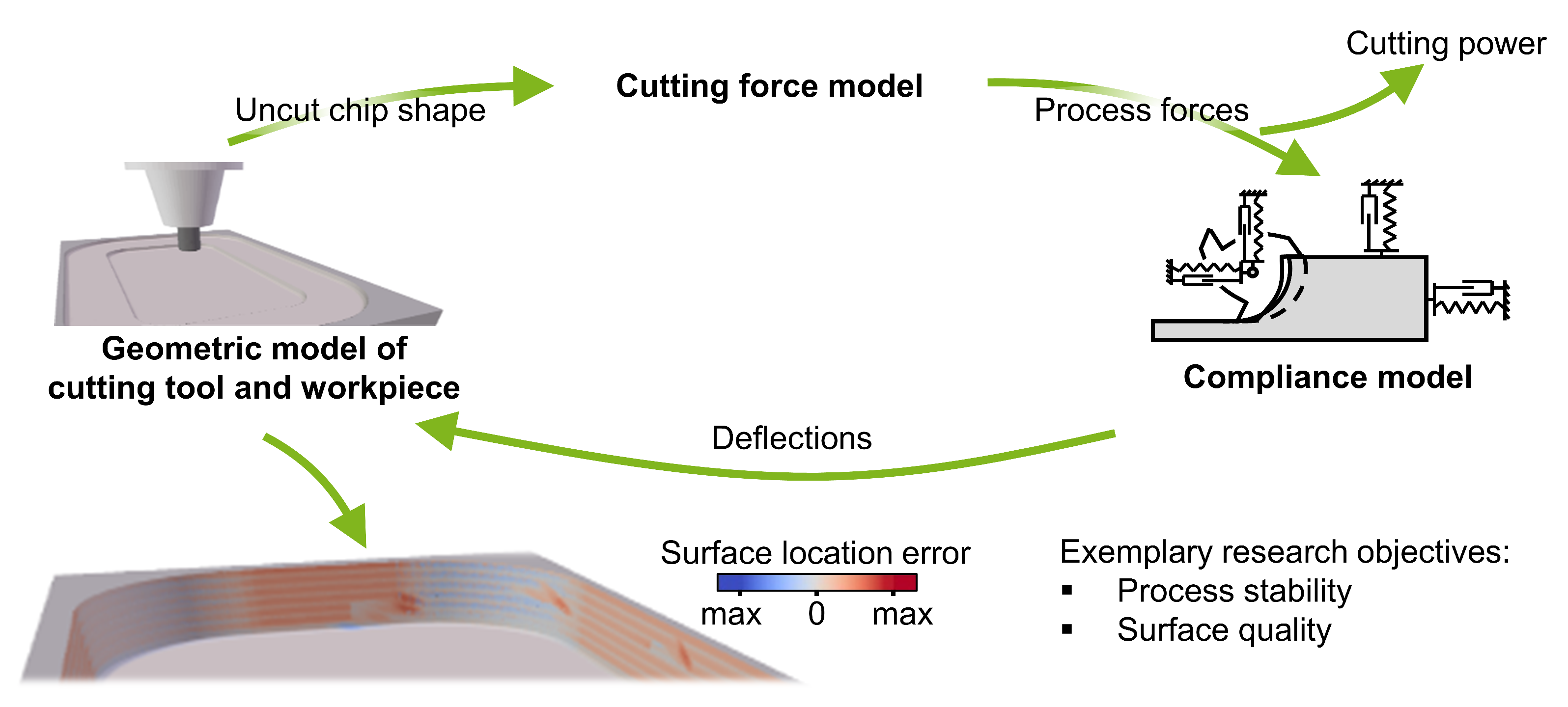
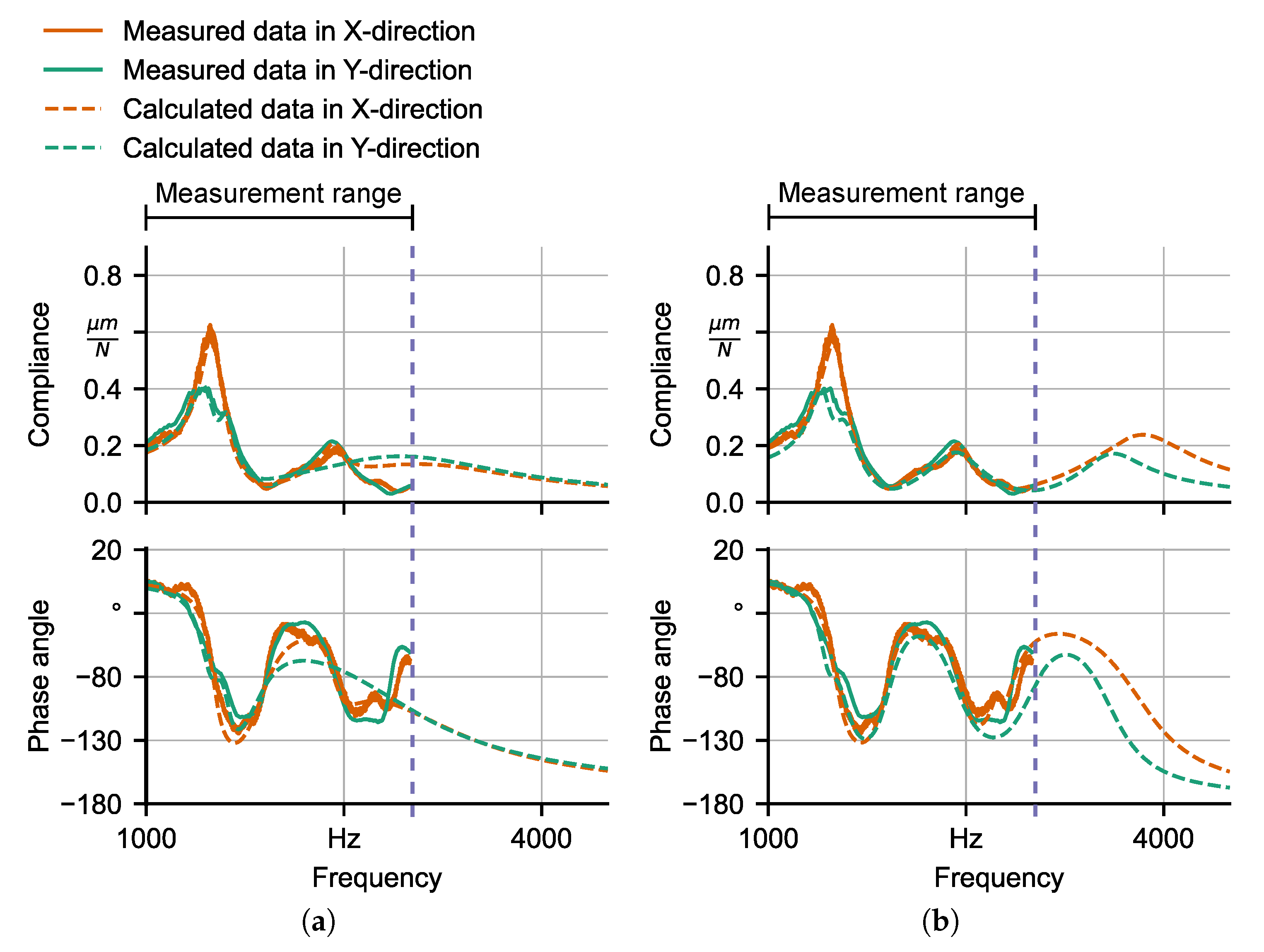
| Machine Tool | M1 | M2 | ||
|---|---|---|---|---|
| Range of investigated axis positions | X | mm to mm | Y | 0 mm to mm |
| Y | to | Z | to 0 | |
| C | to | B | to |
| Tool Diameter | Workpiece Material | Spindle Speed | Depth of Cut | Radial Immersion | Inclination Angle |
|---|---|---|---|---|---|
| 10 mm | ASP 2012 (58 HRC) | mm | 100% | , , |
| Inclination Angle () | (N mm ) | (N mm ) | (N mm ) | |||
|---|---|---|---|---|---|---|
| 8745 | 337 | |||||
| 7333 | 436 | |||||
| 6651 | 612 |
| Method | Machine Tool | Test Angle () | RMSE (N/m) Amplitude X-direction | RMSE (N/m) Amplitude Y-Direction | RMSE () Phase X-Direction | RMSE () Phase Y-Direction |
|---|---|---|---|---|---|---|
| Naïve linear interpolation | 0.02 ± 0.01 | 0.01 ± 0.01 | 6.15 ± 4.39 | 7.57 ± 6.08 | ||
| 0.02 ± 0.01 | 0.01 ± 0.01 | 7.95 ± 5.75 | 5.75 ± 4.44 | |||
| 0.02 ± 0.02 | 0.02 ± 0.01 | 7.25 ± 4.98 | 7.57 ± 5.39 | |||
| Random | 0.02 ± 0.01 | 0.02 ± 0.02 | 5.47 ± 3.94 | 8.91 ± 6.69 | ||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 4.30 ± 3.05 | 6.73 ± 5.24 | |||
| 0.02 ± 0.01 | 0.01 ± 0.01 | 5.61 ± 3.75 | 4.85 ± 3.55 | |||
| 0.02 ± 0.02 | 0.01 ± 0.01 | 7.34 ± 5.17 | 3.90 ± 2.75 | |||
| Random | 0.02 ± 0.02 | 0.01 ± 0.01 | 7.16 ± 4.84 | 5.64 ± 4.29 | ||
| Elastic net | 0.11 ± 0.07 | 0.09 ± 0.06 | 38.28 ± 23.04 | 42.37 ± 24.80 | ||
| 0.11 ± 0.07 | 0.09 ± 0.06 | 38.66 ± 22.34 | 43.62 ± 25.41 | |||
| 0.10 ± 0.07 | 0.09 ± 0.06 | 38.83 ± 21.71 | 42.70 ± 25.08 | |||
| Random | 0.11 ± 0.08 | 0.10 ± 0.06 | 38.55 ± 23.25 | 42.05 ± 25.21 | ||
| 0.11 ± 0.08 | 0.08 ± 0.05 | 31.22 ± 17.09 | 30.50 ± 13.37 | |||
| 0.11 ± 0.08 | 0.08 ± 0.05 | 31.55 ± 17.46 | 30.24 ± 13.46 | |||
| 0.12 ± 0.08 | 0.08 ± 0.04 | 31.91 ± 17.39 | 30.17 ± 12.97 | |||
| Random | 0.14 ± 0.10 | 0.10 ± 0.06 | 31.48 ± 16.93 | 29.52 ± 13.05 | ||
| RF | 0.01 ± 0.01 | 0.01 ± 0.01 | 5.07 ± 3.67 | 6.01 ± 4.99 | ||
| 0.02 ± 0.01 | 0.01 ± 0.01 | 5.46 ± 3.94 | 5.07 ± 3.87 | |||
| 0.02 ± 0.01 | 0.01 ± 0.01 | 5.80 ± 3.85 | 6.34 ± 4.51 | |||
| Random | 0.01 ± 0.01 | 0.01 ± 0.01 | 4.53 ± 3.39 | 5.71 ± 4.42 | ||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 3.28 ± 2.29 | 4.67 ± 3.46 | |||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 3.83 ± 2.58 | 5.57 ± 4.14 | |||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 2.58 ± 1.72 | 3.08 ± 2.15 | |||
| Random | 0.02 ± 0.01 | 0.01 ± 0.01 | 5.64 ± 3.67 | 4.32 ± 3.09 | ||
| XGBoost | 0.01 ± 0.01 | 0.01 ± 0.01 | 4.22 ± 2.86 | 6.31 ± 5.05 | ||
| 0.02 ± 0.01 | 0.01 ± 0.01 | 5.23 ± 3.72 | 4.96 ± 3.91 | |||
| 0.02 ± 0.01 | 0.01 ± 0.01 | 5.35 ± 3.58 | 5.34 ± 3.73 | |||
| Random | 0.01 ± 0.01 | 0.01 ± 0.01 | 4.54 ± 3.37 | 6.03 ± 4.62 | ||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 2.85 ± 2.06 | 4.17 ± 3.09 | |||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 3.77 ± 2.58 | 4.60 ± 3.28 | |||
| 0.01 ± 0.01 | 0.01 ± 0.01 | 2.05 ± 1.29 | 2.89 ± 1.92 | |||
| Random | 0.02 ± 0.02 | 0.01 ± 0.01 | 5.48 ± 3.60 | 4.41 ± 3.18 |
| Method | Machine Tool | Test Angle () | RMSE (Hz) Mean Frequency | RMSE (1/s) Mean Damping Constant | RMSE (kg) Mean Mass |
|---|---|---|---|---|---|
| Naïve linear interpolation | 31.71 ± 7.54 | 108.22 ± 15.15 | 0.09 ± 0.04 | ||
| 27.91 ± 7.16 | 126.09 ± 21.63 | 0.16 ± 0.10 | |||
| 25.00 ± 6.15 | 79.63 ± 18.88 | 0.06 ± 0.01 | |||
| Random | 22.80 9.13 | 124.43 36.97 | 0.09 0.01 | ||
| 9.95 ± 4.20 | 252.86 ± 58.68 | 0.92 ± 0.19 | |||
| 12.06 ± 3.67 | 329.58 ± 5.40 | 1.35 ± 0.24 | |||
| 12.96 ± 3.26 | 399.25 ± 64.87 | 1.28 ± 0.29 | |||
| Random | 23.17 ± 20.93 | 376.27 ± 456.82 | 0.90 ± 1.15 | ||
| Elastic net | 24.35 ± 6.63 | 117.18 ± 45.63 | 0.07 ± 0.03 | ||
| 22.78 ± 6.15 | 86.06 ± 38.50 | 0.05 ± 0.02 | |||
| 23.49 ± 5.96 | 93.34 ± 28.51 | 0.04 ± 0.02 | |||
| Random | 27.83 ± 8.44 | 89.37 ± 18.93 | 0.07 ± 0.04 | ||
| 9.04 ± 3.32 | 200.36 ± 50.46 | 0.65 ± 0.13 | |||
| 9.94 ± 1.48 | 158.15 ± 42.03 | 0.51 ± 0.26 | |||
| 8.98 ± 3.41 | 146.53 ± 32.06 | 0.35 ± 0.14 | |||
| Random | 22.65 ± 19.65 | 292.88 ± 363.70 | 0.77 ± 0.67 | ||
| RF | 23.90 ± 6.46 | 106.38 ± 45.23 | 0.06 ± 0.02 | ||
| 23.30 ± 6.95 | 80.51 ± 33.53 | 0.05 ± 0.02 | |||
| 23.40 ± 5.99 | 90.22 ± 30.91 | 0.04 ± 0.02 | |||
| Random | 27.54 ± 9.05 | 90.25 ± 18.57 | 0.06 ± 0.04 | ||
| 7.56 ± 3.47 | 68.75 ± 23.22 | 0.23 ± 0.11 | |||
| 10.30 ± 2.54 | 79.31 ± 24.98 | 0.27 ± 0.14 | |||
| 9.28 ± 4.46 | 86.67 ± 38.51 | 0.23 ± 0.14 | |||
| Random | 21.05 ± 20.21 | 387.27 ± 344.32 | 1.04 ± 0.78 | ||
| XGBoost | 24.28 ± 8.00 | 94.68 ± 40.28 | 0.05 ± 0.02 | ||
| 23.77 ± 4.80 | 107.50 ± 46.74 | 0.04 ± 0.02 | |||
| 24.05 ± 5.47 | 98.15 ± 29.58 | 0.05 ± 0.02 | |||
| Random | 27.27 ± 10.44 | 83.01 ± 19.11 | 0.07 ± 0.04 | ||
| 7.70 ± 2.84 | 71.17 ± 32.38 | 0.25 ± 0.18 | |||
| 11.45 ± 3.45 | 85.40 ± 34.32 | 0.33 ± 0.14 | |||
| 8.74 ± 3.69 | 87.39 ± 52.48 | 0.43 ± 0.17 | |||
| Random | 21.49 ± 21.05 | 435.98 ± 447.16 | 1.22 ± 1.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finkeldey, F.; Wirtz, A.; Merhofe, T.; Wiederkehr, P. Learning-Based Prediction of Pose-Dependent Dynamics. J. Manuf. Mater. Process. 2020, 4, 85. https://doi.org/10.3390/jmmp4030085
Finkeldey F, Wirtz A, Merhofe T, Wiederkehr P. Learning-Based Prediction of Pose-Dependent Dynamics. Journal of Manufacturing and Materials Processing. 2020; 4(3):85. https://doi.org/10.3390/jmmp4030085
Chicago/Turabian StyleFinkeldey, Felix, Andreas Wirtz, Torben Merhofe, and Petra Wiederkehr. 2020. "Learning-Based Prediction of Pose-Dependent Dynamics" Journal of Manufacturing and Materials Processing 4, no. 3: 85. https://doi.org/10.3390/jmmp4030085
APA StyleFinkeldey, F., Wirtz, A., Merhofe, T., & Wiederkehr, P. (2020). Learning-Based Prediction of Pose-Dependent Dynamics. Journal of Manufacturing and Materials Processing, 4(3), 85. https://doi.org/10.3390/jmmp4030085





