Relative Density of SLM-Produced Aluminum Alloy Parts: Interpretation of Results
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. SLM Process
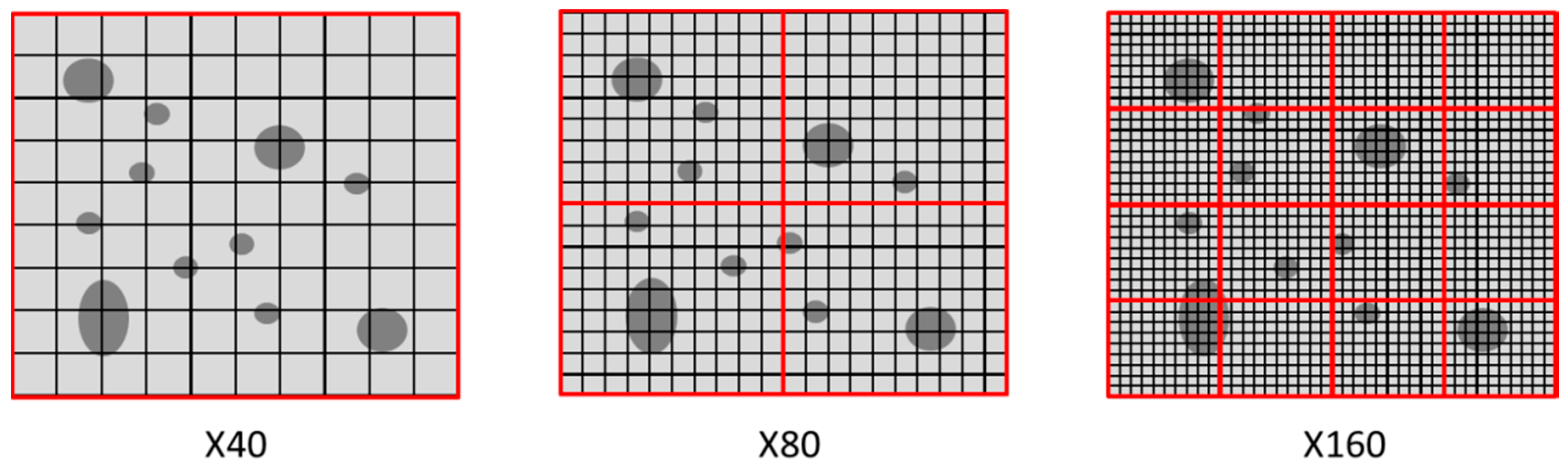
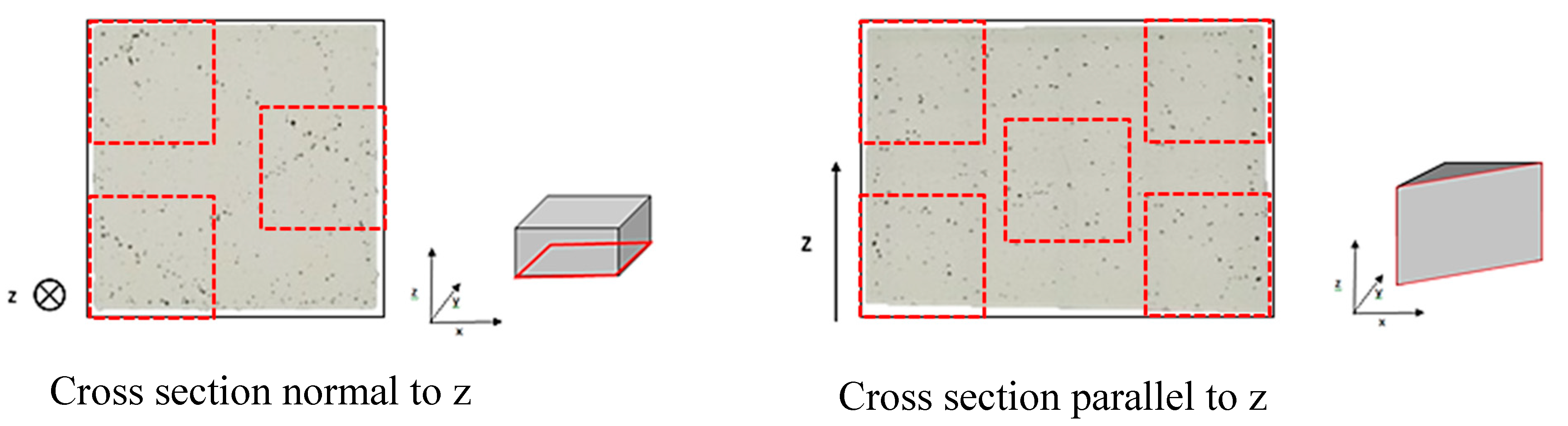
2.3. Micrographic Image Analysis
2.4. Tomography
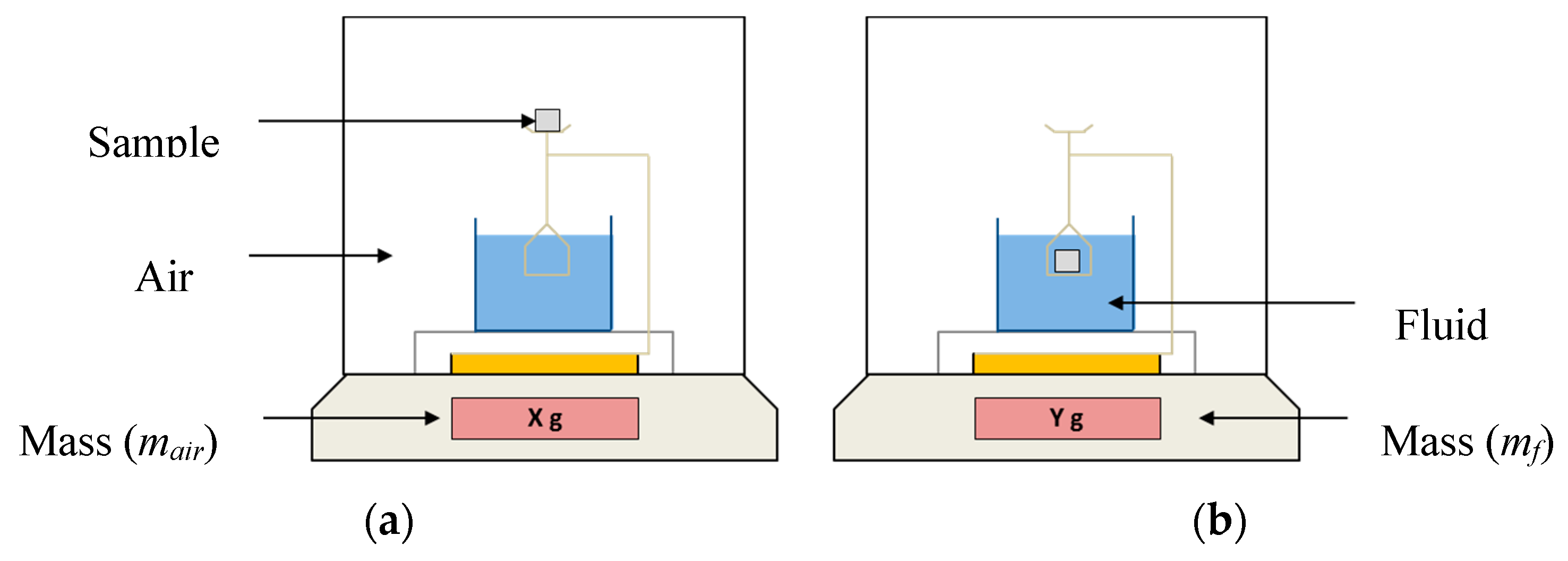
2.5. Archimedes Method
2.6. Helium Pycnometer
3. Results and Discussion
3.1. Estimation of Relative Density by Image Analysis
3.1.1. Influence of Magnification
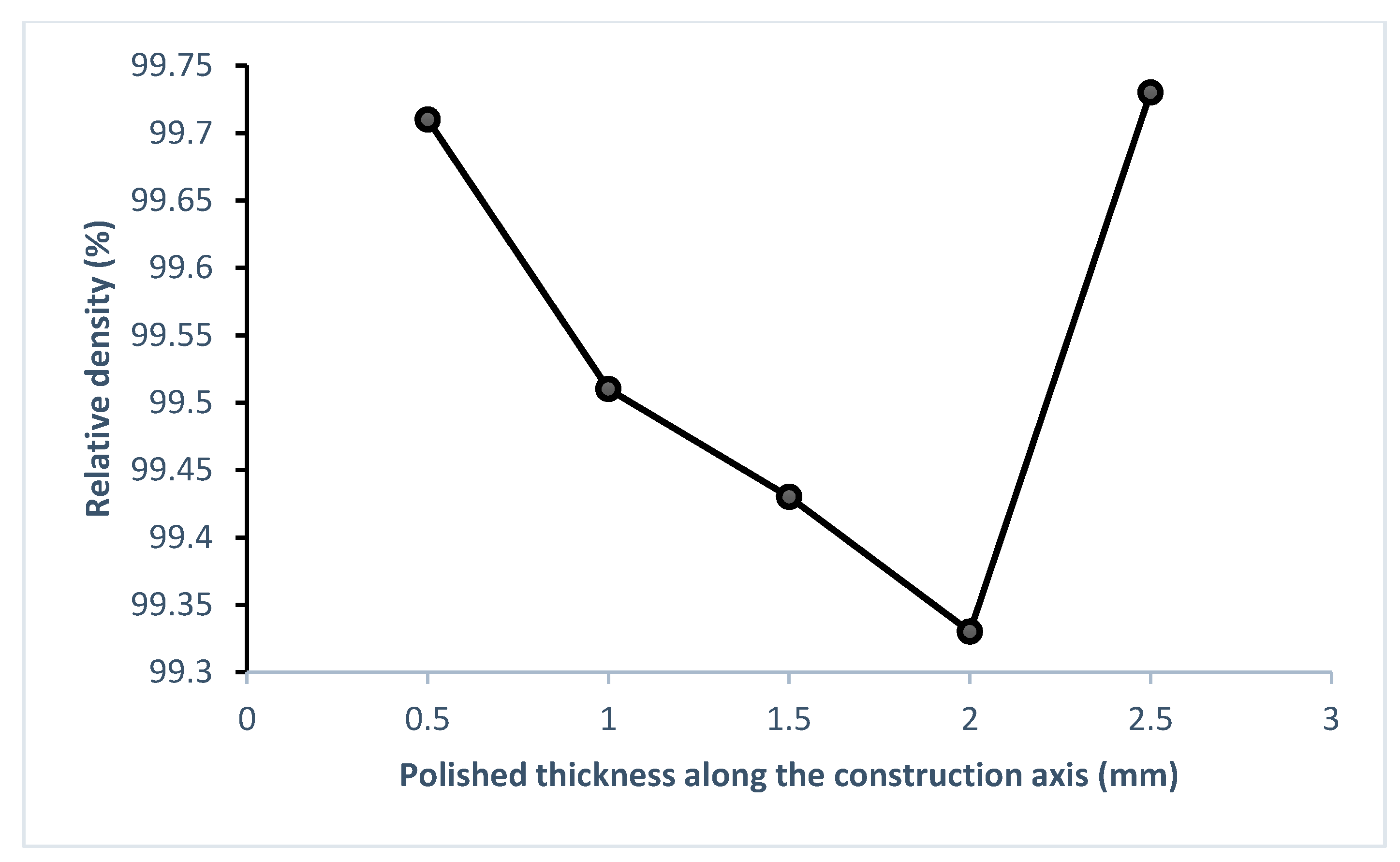
3.1.2. Representativeness of the Surface Observed
3.2. Measuring Relative Density Using Archimedes Method
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Frazier, W.E. Metal Additive Manufacturing: A Review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Galy, C.; Le Guen, E.; Lacoste, E.; Arvieu, C. Main defects observed in aluminum alloy parts produced by SLM: From causes to consequences. Addit. Manuf. 2018, 22, 165–175. [Google Scholar] [CrossRef]
- Sun, S.; Zheng, L.; Liu, Y.; Liu, J.; Zhang, H. Characterisation of Al-Fe-V-Si heat-resistant aluminum alloy components fabricated by selective laser melting. J. Mater. Res. 2015, 30, 1661–1669. [Google Scholar] [CrossRef]
- Leung, C.L.A.; Marussi, S.; Towrie, M.; Atwood, R.C.; Withers, P.J.; Lee, P.D. The effect of powder oxidation on defect formation in laser additive manufacturing. Acta Mater. 2019, 166, 294–305. [Google Scholar] [CrossRef]
- Wang, D.; Wu, S.; Fu, F.; Mai, S.; Yang, Y.; Liu, Y.; Song, C. Mechanisms and characteristics of spatter generation in SLM processing and its effect on the properties. Mater. Des. 2017, 117, 121–130. [Google Scholar] [CrossRef]
- Anwar, A.B.; Pham, Q.-C. Selective laser melting of AlSi10Mg: Effects of scan direction, part placement and inert gas flow velocity on tensile strength. J. Mater. Process. Technol. 2017, 240, 388–396. [Google Scholar] [CrossRef]
- Kimura, T.; Nakamoto, T. Microstructures and mechanical properties of A356 (AlSi7Mg0.3) aluminum alloy fabricated by selective laser melting. Mater. Des. 2016, 89, 1294–1301. [Google Scholar] [CrossRef]
- Spierings, A.B.; Schneider, M.; Eggenberger, R. Comparison of density measurement techniques for additive manufactured metallic parts. Rapid Prototyp. J. 2011, 17, 380–386. [Google Scholar] [CrossRef]
- de Terris, T.; Andreau, O.; Peyre, P.; Adamski, F.; Koutiri, I.; Gorny, C.; Dupuy, C. Optimization and comparison of porosity rate measurement methods of Selective Laser Melted metallic parts. Addit. Manuf. 2019, 28, 802–813. [Google Scholar] [CrossRef]
- Wang, P.; Tan, X.; He, C.; Ling Sharon Nai, M.; Huang, R.; Beng Tor, S.; Wei, J. Scanning optical microscopy for porosity quantification of additively manufactured components. Addit. Manuf. 2018, 21, 350–358. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Corfield, M.R.; Tuck, C.; Clare, A.T.; Leach, R.K.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Quantification and characterisation of porosity in selectively laser melted Al–Si10–Mg using X-ray computed tomography. Mater. Charact. 2016, 111, 193–204. [Google Scholar]
- Simchi, A. Direct laser sintering of metal powders: Mechanism, kinetics and microstructural features. Mater. Sci. Eng. A 2006, 428, 148–158. [Google Scholar] [CrossRef]
- Turner, R.P.; Panwisawas, C.; Lu, Y.; Dhiman, I.; Basoalto, H.C.; Brooks, J.W. Neutron tomography methods applied to a nickel-based superalloy additive manufacture build. Mater. Lett. 2018, 230, 109–112. [Google Scholar] [CrossRef]
- du Plessis, A. Effects of process parameters on porosity in laser powder bed fusion revealed by X-ray tomography. Addit. Manuf. 2018, 30. [Google Scholar] [CrossRef]
- Casalino, G.; Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D. Experimental investigation and statistical optimisation ofthe selective laser melting process of amaraging steel. Opt. Laser Technol. 2015, 65, 151–158. [Google Scholar] [CrossRef]
- Obaton, A.-F.; Lê, M.-Q.; Prezza, V.; Marlot, D.; Delvart, P.; Huskic, A.; Senck, S.; Mahé, E.; Cayron, C. Investigation of new volumetric non-destructive techniques to characterise additive manufacturing parts. Weld. World 2018, 62, 1049–1057. [Google Scholar] [CrossRef]
- Bai, S.; Perevoshchikova, N.; Sha, Y.; Wu, X. The Effects of Selective Laser Melting Process Parameters on Relative Density of the AlSi10Mg Parts and Suitable Procedures of the Archimedes Method. Appl. Sci. 2019, 9, 583. [Google Scholar] [CrossRef]
- ASM specialty handbook. Aluminum and Aluminum Alloys, 6th ed.; ASM International: Cleveland, OH, USA, 2007; p. 720. [Google Scholar]




| Chemical Composition | Al | Si | Mg | Fe | Cu | Mn | Zn | Ti | Ag | B | Other |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AlSi7Mg0.6 foundry alloy (Wt %) [ASM, 1993] | remainder | 6.5–7.5 | 0.21 | 0.15 | 0.03 | 0.1 | 0.07 | 0.10–0.18 | 0.1 | ||
| AlSi7Mg0.6 powder (Wt %) | remainder | 7.2 | 0.65 | 0.14 | <0.01 | <0.005 | <0.002 | <0.005 | 0.1 | ||
| AM205 powder (Wt %) | remainder | <0.10 | 0.20–0.33 | <0.08 | 4.2–5.0 | 3.0–3.85 | 0.6–0.9 | 1.25–1.55 | <0.17 |
| Alloy | Power W | Laser Spot Scan Rate mm·s−1 | Scan Spacing mm | Energy Density J·mm−3 |
|---|---|---|---|---|
| AlSi7Mg0.6 | 350 | 1150 | 0.272 | 22.38 |
| AlSi7Mg0.6 | 350 | 1150 | 0.221 | 27.54 |
| AlSi7Mg0.6 | 350 | 1150 | 0.145 | 41.98 |
| AlSi7Mg0.6 | 350 | 1150 | 0.119 | 51.15 |
| AlSi7Mg0.6 | 350 | 1150 | 0.068 | 89.51 |
| AM205 | 105 | 675 | 0.18 | 17.28 |
| AM205 | 400 | 1000 | 0.27 | 29.63 |
| AM205 | 225 | 625 | 0.18 | 40 |
| AM205 | 400 | 1000 | 0.09 | 88.89 |
| AM205 | 175 | 350 | 0.09 | 111.11 |
| Magnification | X 40 | X 80 | X 200 |
|---|---|---|---|
| Number of images needed to reconstruct the zone | 1 | 4 | 30 |
| Average relative density of the zone | 99.17% | 99.14% | 99.00% |
| Energy Density (J·mm−3) | Relative Density with Foundry ρtheoretical | Relative Density with Powder ρtheoretical | Standard Deviation σ (Foundry) |
|---|---|---|---|
| 22.38 | 95.53 | 96.25 | 0.2 |
| 27.54 | 97.31 | 98.05 | 0.17 |
| 42.12 | 97.98 | 98.71 | 0.008 |
| 51.15 | 98.10 | 98.84 | 0.004 |
| 89.51 | 98.20 | 98.94 | 0.03 |
| Energy Density (J·mm−3) | Relative Density with Foundry ρtheoretical | Relative Density with Powder ρtheoretical | Standard Deviation σ (Foundry) |
|---|---|---|---|
| 17.09 | 87.72 | 88.33 | 0.25 |
| 29.63 | 98.53 | 99.21 | 0.006 |
| 40.00 | 99.26 | 99.95 | 0.007 |
| 88.89 | 99.58 | 100.27 | 0.014 |
| 111.11 | 99.70 | 100.40 | 0.008 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arvieu, C.; Galy, C.; Le Guen, E.; Lacoste, E. Relative Density of SLM-Produced Aluminum Alloy Parts: Interpretation of Results. J. Manuf. Mater. Process. 2020, 4, 83. https://doi.org/10.3390/jmmp4030083
Arvieu C, Galy C, Le Guen E, Lacoste E. Relative Density of SLM-Produced Aluminum Alloy Parts: Interpretation of Results. Journal of Manufacturing and Materials Processing. 2020; 4(3):83. https://doi.org/10.3390/jmmp4030083
Chicago/Turabian StyleArvieu, Corinne, Cassiopée Galy, Emilie Le Guen, and Eric Lacoste. 2020. "Relative Density of SLM-Produced Aluminum Alloy Parts: Interpretation of Results" Journal of Manufacturing and Materials Processing 4, no. 3: 83. https://doi.org/10.3390/jmmp4030083
APA StyleArvieu, C., Galy, C., Le Guen, E., & Lacoste, E. (2020). Relative Density of SLM-Produced Aluminum Alloy Parts: Interpretation of Results. Journal of Manufacturing and Materials Processing, 4(3), 83. https://doi.org/10.3390/jmmp4030083




