In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation
Abstract
1. Introduction
2. Materials and Methods
2.1. Blade Profile—Test Case
2.2. Analytical Approach
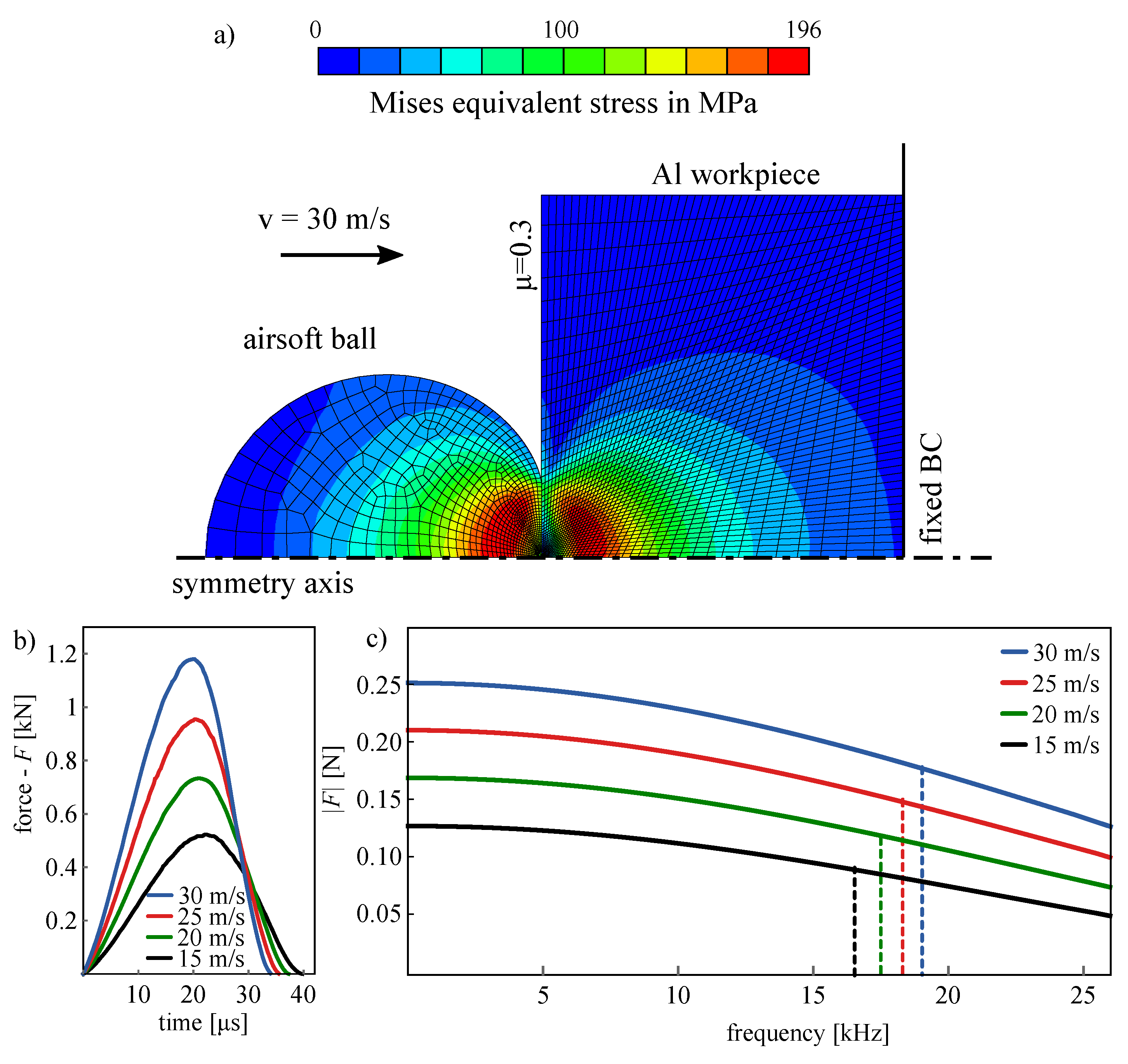
2.3. FEA Analysis
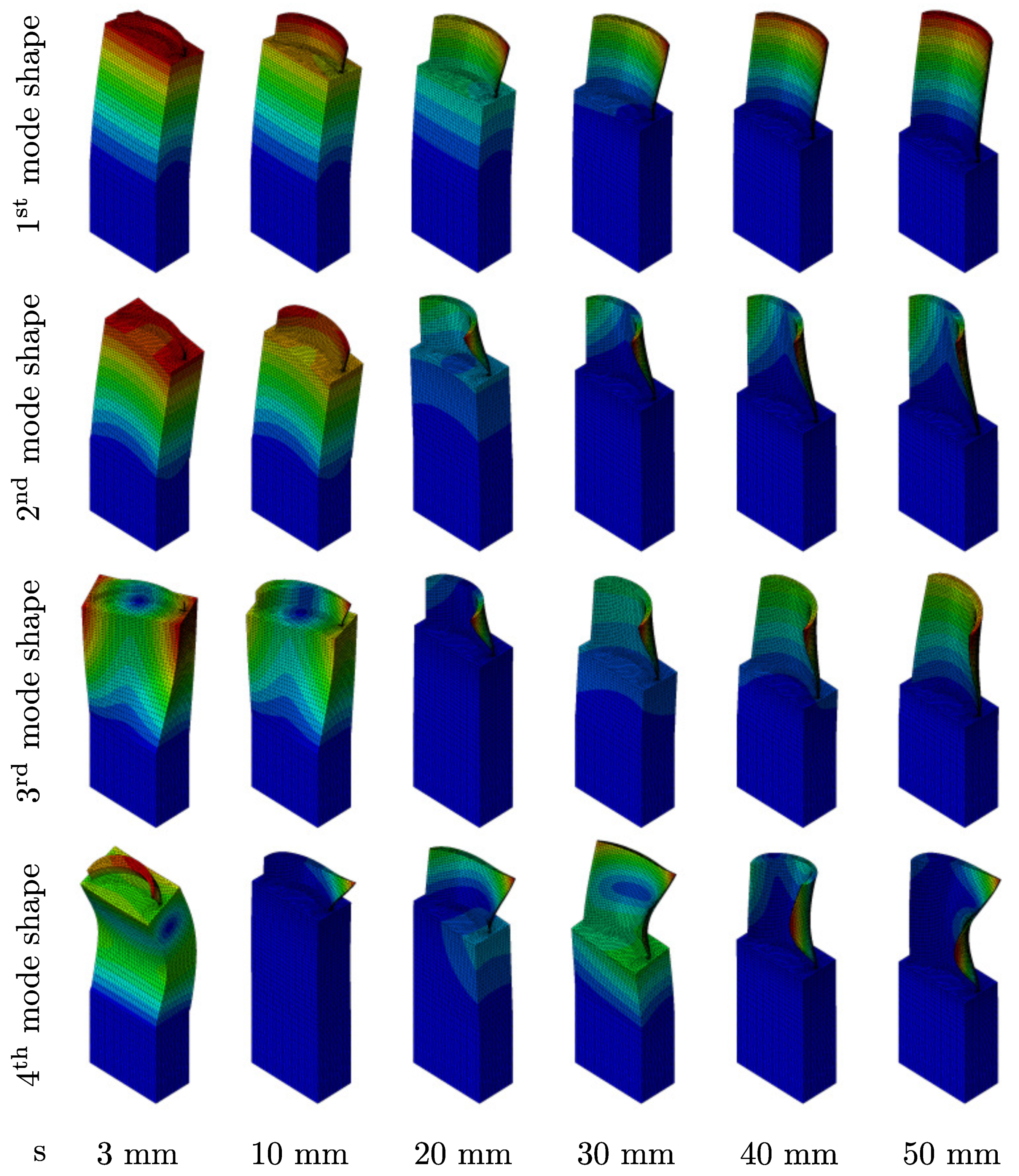
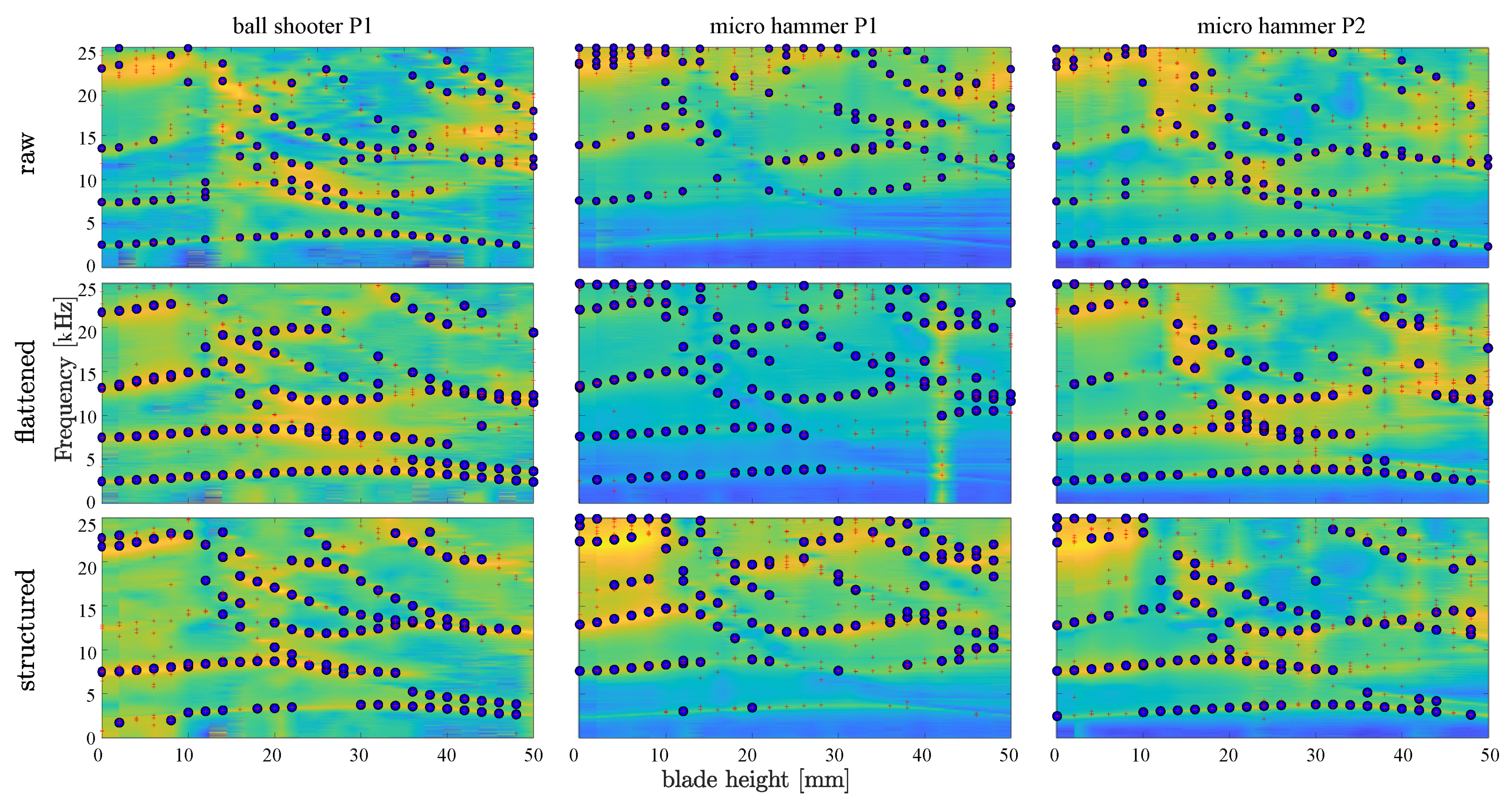
3. Results
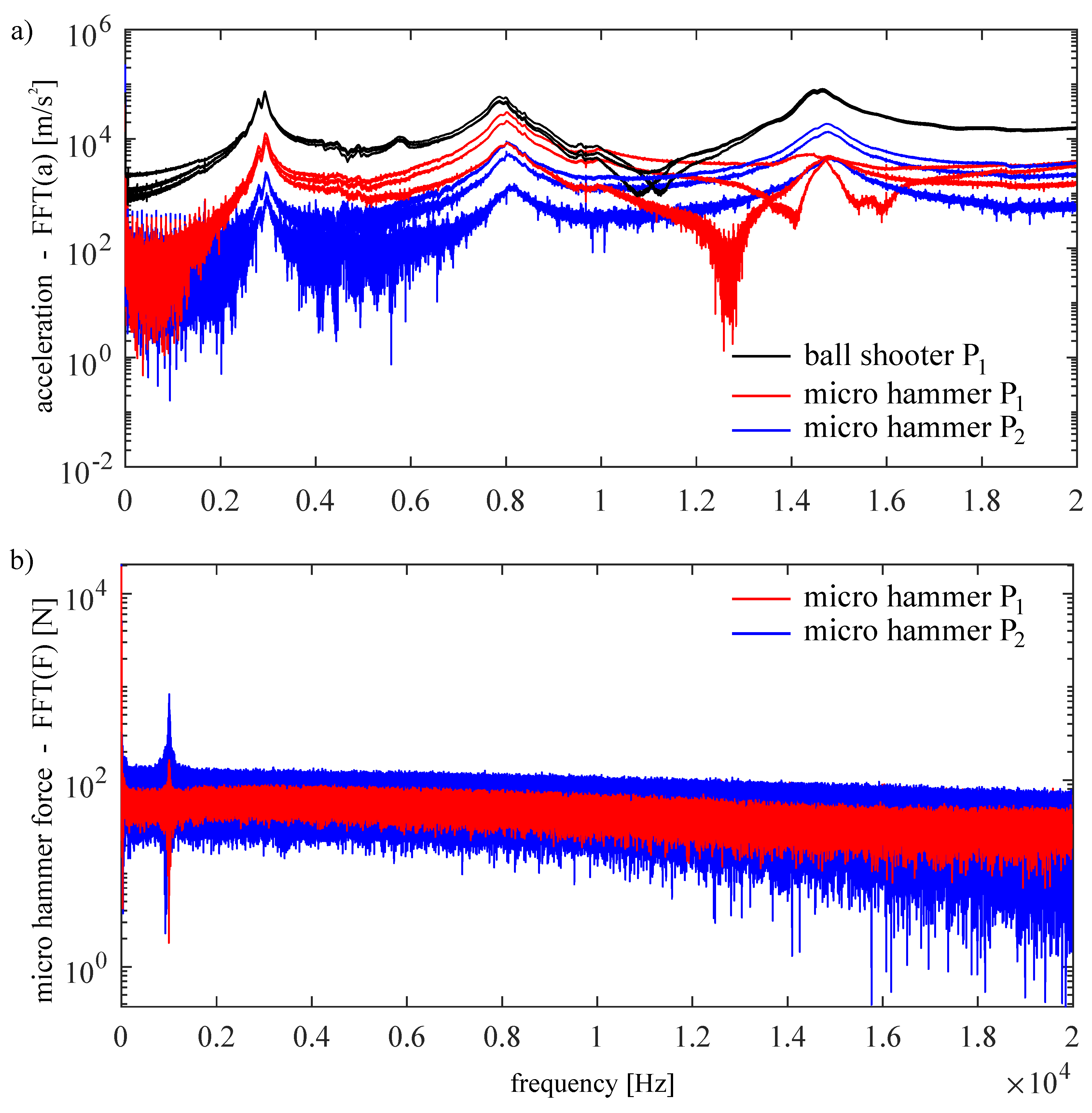
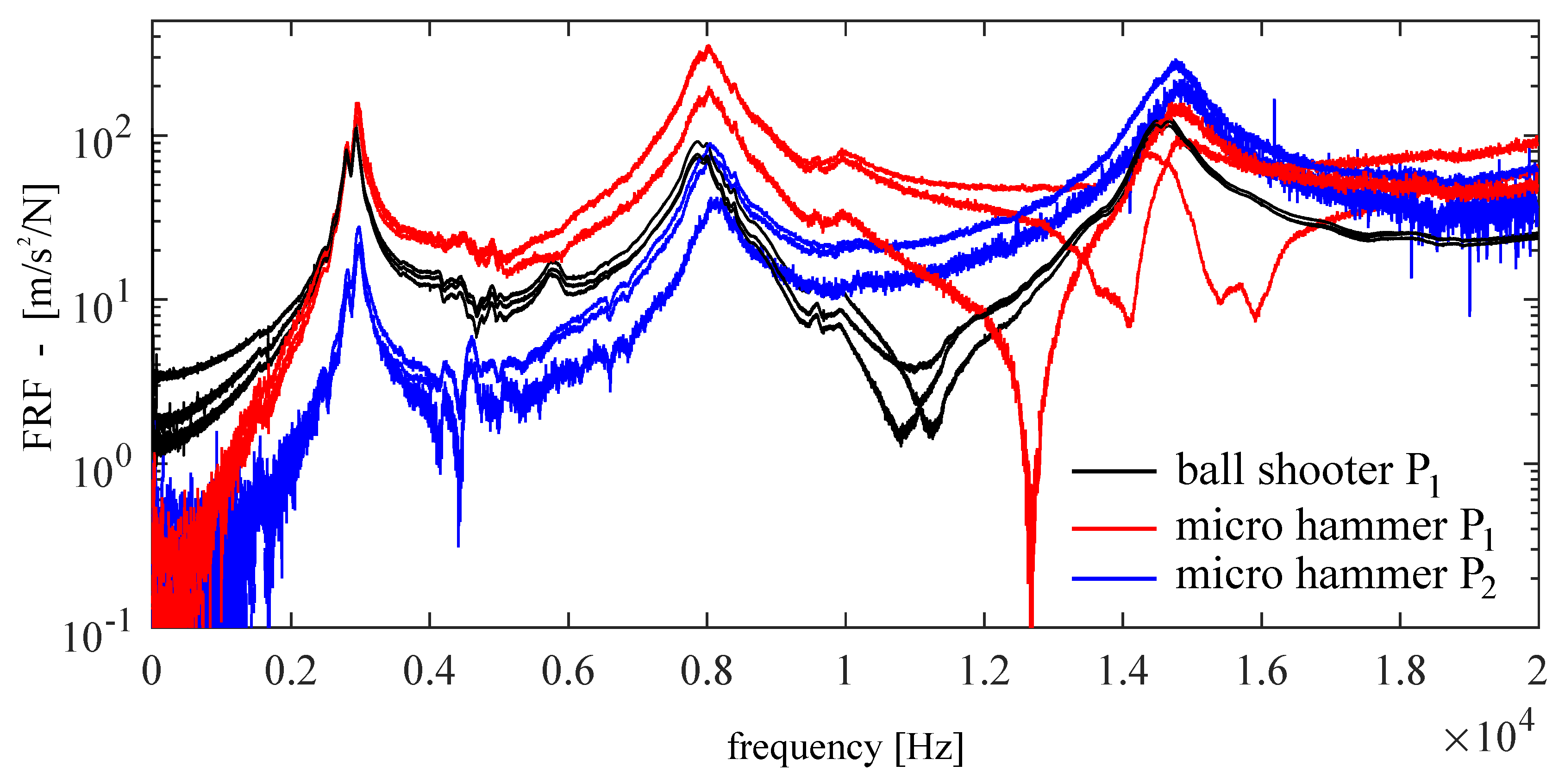
3.1. Measurement
3.1.1. Impulse Excitation with a Ball Shooter
3.1.2. Analysis of Impact Spectrum with Finite Element Simulations
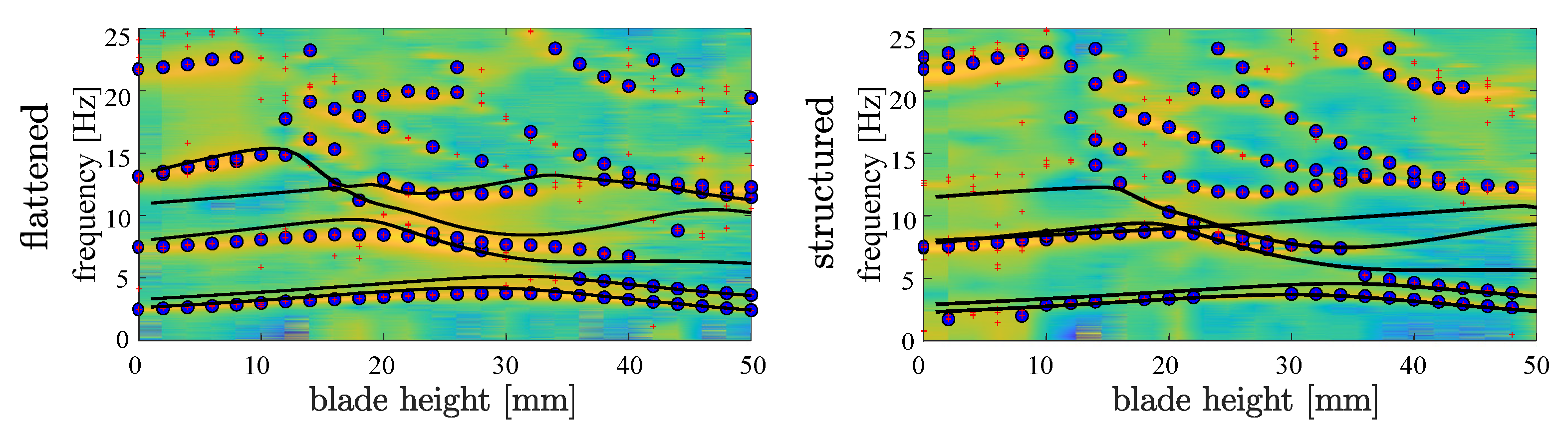
3.2. Measured Impulse Responses
3.3. Improved FE Model
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tlusty, J.; Spacek, L. Self-excited Vibrations on Machine Tools; Nakl. CSAV: Prague, Czech Republic, 1954. [Google Scholar]
- Tobias, S. Machine-tool Vibration; Blackie: London, UK, 1965. [Google Scholar]
- Altintas, Y. Manufacturing Automation—Metal Cutting Mechanics, Machine Tool Vibrations and CNC Design, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Altintas, Y.; Stépán, G.; Merdol, D.; Dombóvári, Z. Chatter stability of milling in frequency and discrete time domain. Cirp J. Manuf. Sci. Technol. 2008, 1, 35–44. [Google Scholar] [CrossRef]
- Yadav, A.; Talaviya, D.; Bansal, A.; Law, M. Design of Chatter-Resistant Damped Boring Bars Using a Receptance Coupling Approach. J. Manuf. Mater. Process. 2020, 4, 53. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Cao, L.; Huang, T.; Shi, D.; Zhang, X.M.; Ding, H. Active chatter suppression in low immersion intermittent milling process. J. Manuf. Sci. Eng. 2020, 1–21. [Google Scholar] [CrossRef]
- Cherukuri, H.; Perez-Bernabeu, E.; Selles, M.; Schmitz, T. Machining chatter prediction using a data learning model. J. Manuf. Mater. Process. 2019, 3, 45. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Mann, B.P. Closed-form solutions for surface location error in milling. Int. J. Mach. Tools Manuf. 2006, 46, 1369–1377. [Google Scholar] [CrossRef]
- Siddhpura, M.; Paurobally, R. A review of chatter vibration research in turning. Int. J. Mach. Tools Manuf. 2012, 61, 27–47. [Google Scholar] [CrossRef]
- Kayhan, M.; Budak, E. An experimental investigation of chatter effects on tool life. Proc. Inst. Mech. Eng. Part J. Eng. Manuf. 2009, 223, 1455–1463. [Google Scholar] [CrossRef]
- Zapata, R.; DeMarco, C.; Schmitz, T. The Milling Dynamics “Super Diagram”: Combining Stability and Surface Location Error. In Proceedings of the American Society for Precision Engineering Annual Meeting, ASPE 2009, Monterey, CA, USA, 4–9 October 2009. [Google Scholar]
- Caixu, Y.; Haining, G.; Xianli, L.; Liang, S.Y.; Lihui, W. A review of chatter vibration research in milling. Chin. J. Aeronaut. 2019, 32, 215–242. [Google Scholar]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Clancy, B.E.; Shin, Y.C. A comprehensive chatter prediction model for face turning operation including tool wear effect. Int. J. Mach. Tools Manuf. 2002, 42, 1035–1044. [Google Scholar] [CrossRef]
- Tyler, C.T.; Schmitz, T.L. Analytical process damping stability prediction. J. Manuf. Process. 2013, 15, 69–76. [Google Scholar] [CrossRef]
- Altintas, Y.; Eynian, M.; Onozuka, H. Identification of dynamic cutting force coefficients and chatter stability with process damping. CIRP Ann. 2008, 57, 371–374. [Google Scholar] [CrossRef]
- Budak, E.; Tunc, L.T. Identification and modeling of process damping in turning and milling using a new approach. CIRP Ann. 2010, 59, 403–408. [Google Scholar] [CrossRef]
- Bravo, U.; Altuzarra, O.; de Lacalle, L.L.; Sánchez, J.; Campa, F. Stability limits of milling considering the flexibility of the workpiece and the machine. Int. J. Mach. Tools Manuf. 2005, 45, 1669–1680. [Google Scholar] [CrossRef]
- Thevenot, V.; Arnaud, L.; Dessein, G.; Cazenave–Larroche, G. Influence of Material Removal on the Dynamic Behavior of Thin-walled Structures in Peripheral Milling. Mach. Sci. Technol. 2006, 10, 275–287. [Google Scholar] [CrossRef]
- Denkena, B.; Schmidt, C. Experimental investigation and simulation of machining thin-walled workpieces. Prod. Eng. 2007, 1, 343–350. [Google Scholar] [CrossRef]
- Otto, A.; Khasawneh, F.A.; Radons, G. Position-dependent stability analysis of turning with tool and workpiece compliance. Int. J. Adv. Manuf. Technol. 2015, 79, 1453–1463. [Google Scholar] [CrossRef]
- Stepan, G.; Beri, B.; Miklos, A.; Wohlfart, R.; Bachrathy, D.; Porempovics, G.; Toth, A.; Takacs, D. On stability of emulated turning processes in HIL environment. CIRP Ann. 2019, 68, 405–408. [Google Scholar] [CrossRef]
- Budak, E.; Tunc, L.; Alan, S.; Özgüven, H.N. Prediction of workpiece dynamics and its effects on chatter stability in milling. CIRP Ann. 2012, 61, 339–342. [Google Scholar] [CrossRef]
- Seguy, S.; Dessein, G.; Arnaud, L. Surface roughness variation of thin wall milling, related to modal interactions. Int. J. Mach. Tools Manuf. 2008, 48, 261–274. [Google Scholar] [CrossRef]
- Li, Z.L.; Tuysuz, O.; Zhu, L.M.; Altintas, Y. Surface form error prediction in five-axis flank milling of thin-walled parts. Int. J. Mach. Tools Manuf. 2018, 128, 21–32. [Google Scholar] [CrossRef]
- Song, Q.; Ai, X.; Tang, W. Prediction of simultaneous dynamic stability limit of time–variable parameters system in thin-walled workpiece high-speed milling processes. Int. J. Adv. Manuf. Technol. 2011, 55, 883–889. [Google Scholar] [CrossRef]
- Stepan, G.; Kiss, A.K.; Ghalamchi, B.; Sopanen, J.; Bachrathy, D. Chatter avoidance in cutting highly flexible workpieces. CIRP Ann. 2017, 66, 377–380. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Frequency Domain Updating of Thin-Walled Workpiece Dynamics Using Reduced Order Substructuring Method in Machining. J. Manuf. Sci. Eng. 2017, 139, 071013. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Time-domain modeling of varying dynamic characteristics in thin-wall machining using perturbation and reduced-order substructuring methods. J. Manuf. Sci. Eng. 2018, 140, 011015. [Google Scholar] [CrossRef]
- Wan, M.; Dang, X.B.; Zhang, W.H.; Yang, Y. Optimization and improvement of stable processing condition by attaching additional masses for milling of thin-walled workpiece. Mech. Syst. Signal Process. 2018, 103, 196–215. [Google Scholar] [CrossRef]
- Kiss, A.K.; Hajdu, D.; Bachrathy, D.; Stepan, G. Operational stability prediction in milling based on impact tests. Mech. Syst. Signal Process. 2018, 103, 327–339. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing, Theory, Practice, and Application, 2nd ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Takács, D.; Wohlfart, R.; Miklós, Á.; Krajnyák, G.; Tóth, A.; Stépán, G. Ball shooting tests for identification of modal parameter variation in rotating main spindles. Procedia CIRP 2018, 77, 481–484. [Google Scholar] [CrossRef]
- Berezvai, S.; Kossa, A.; Bachrathy, D.; Stepan, G. Numerical and experimental investigation of the applicability of pellet impacts for impulse excitation. Int. J. Impact Eng. 2018, 115, 19–31. [Google Scholar] [CrossRef]
- Kruth, J.P.; Liu, A.M.M.; Vanherck, P.; Lauwers, B. A strategy for selection of optimal cutting parameter in high-speed milling to avoid chatter vibration. Int. J. Prod. Eng. Comput. 2002, 4, 35–42. [Google Scholar]
- Reith, M.J.; Stépán, G. Optimization of material removal rate for orthogonal cutting with vibration limits. Period. Polytech. Mech. Eng. 2012, 56, 91–97. [Google Scholar] [CrossRef][Green Version]
- Eksioglu, C.; Kilic, Z.; Altintas, Y. Discrete-time prediction of chatter stability, cutting forces, and surface location errors in flexible milling systems. J. Manuf. Sci. Eng. 2012, 134, 061006. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; Waveland Press: Long Grove, IL, USA, 2010. [Google Scholar]
- Kiss, A.K.; Bachrathy, D.; Stepan, G. Effects of varying dynamics of flexible workpieces in milling operations. J. Manuf. Sci. Eng. 2020, 142, 011005. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2009. [Google Scholar]
- Wiederkehr, P.; Wilck, I.; Siebrecht, T. Determination of the dynamic behaviour of micro-milling tools at higher spindle speeds using ball-shooting tests for the application in process simulations. CIRP Ann. 2020, 69, 97–100. [Google Scholar] [CrossRef]
- Dombovari, Z. Dominant modal decomposition method. J. Sound Vib. 2017, 392, 56–69. [Google Scholar] [CrossRef]


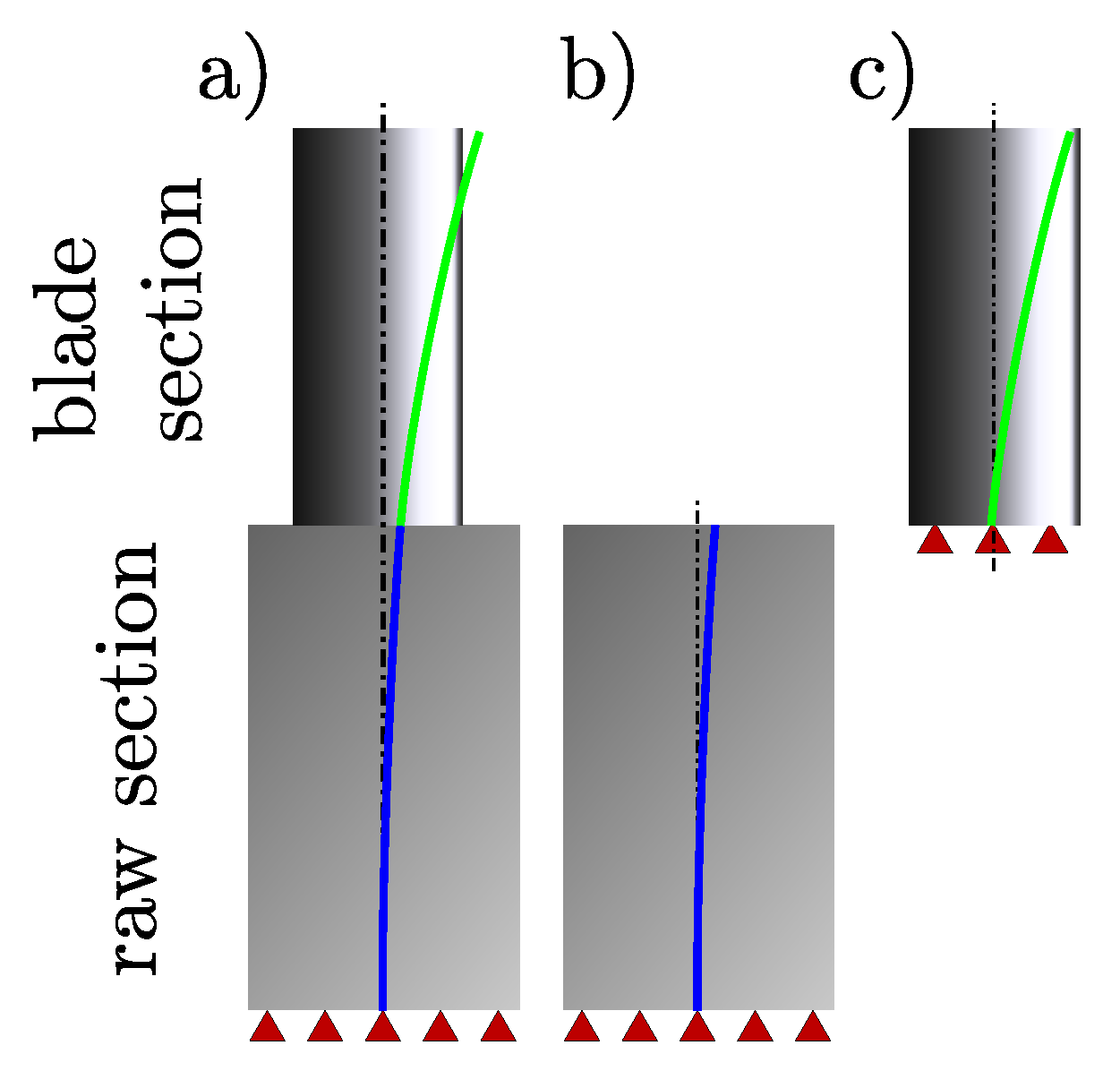
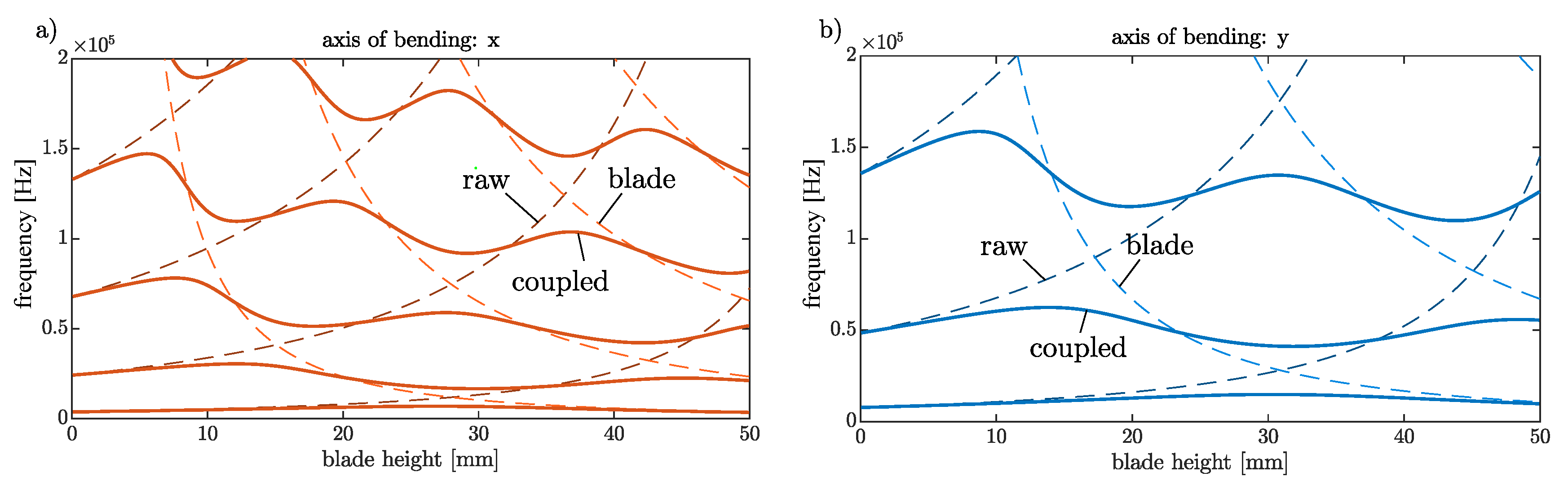
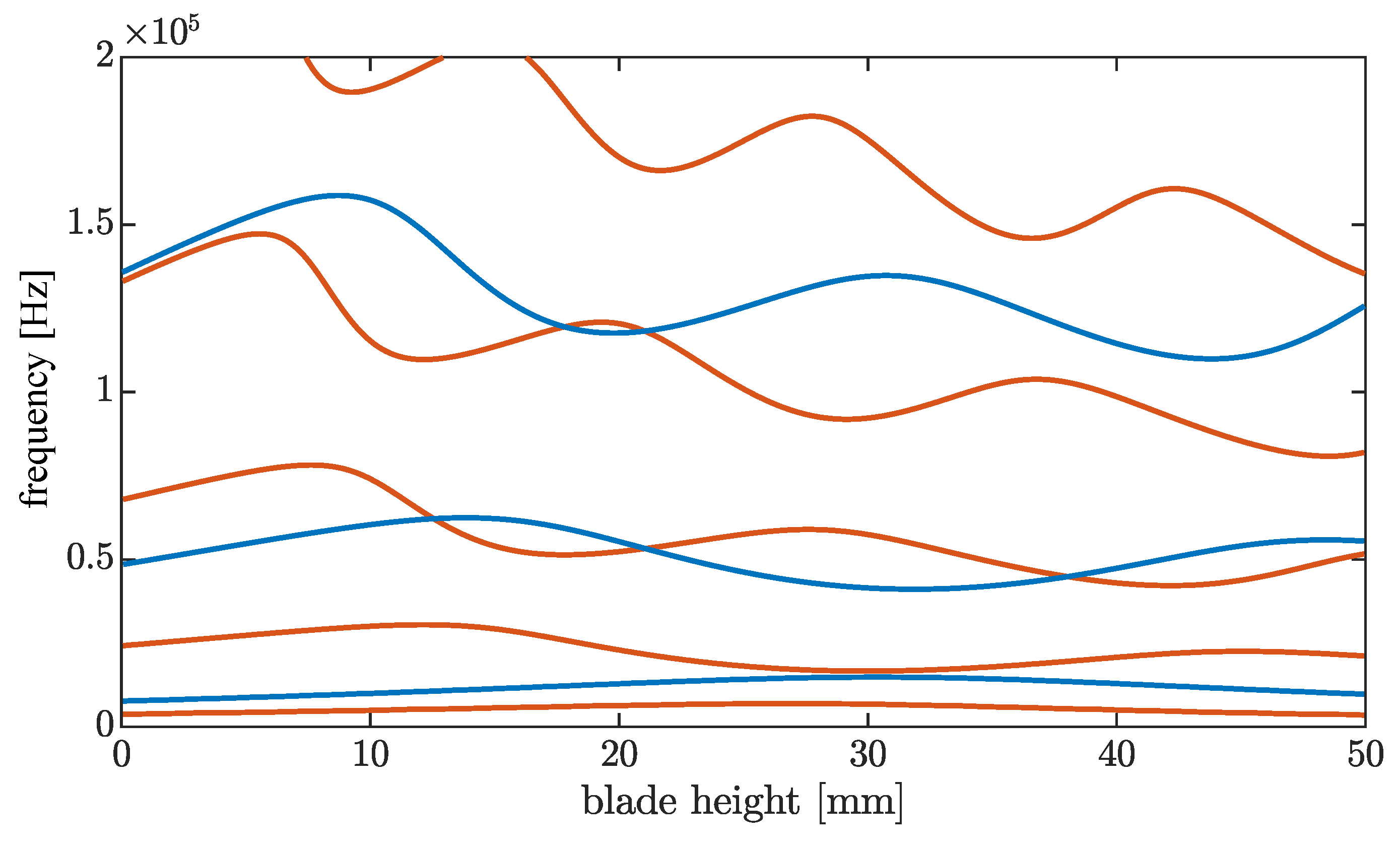
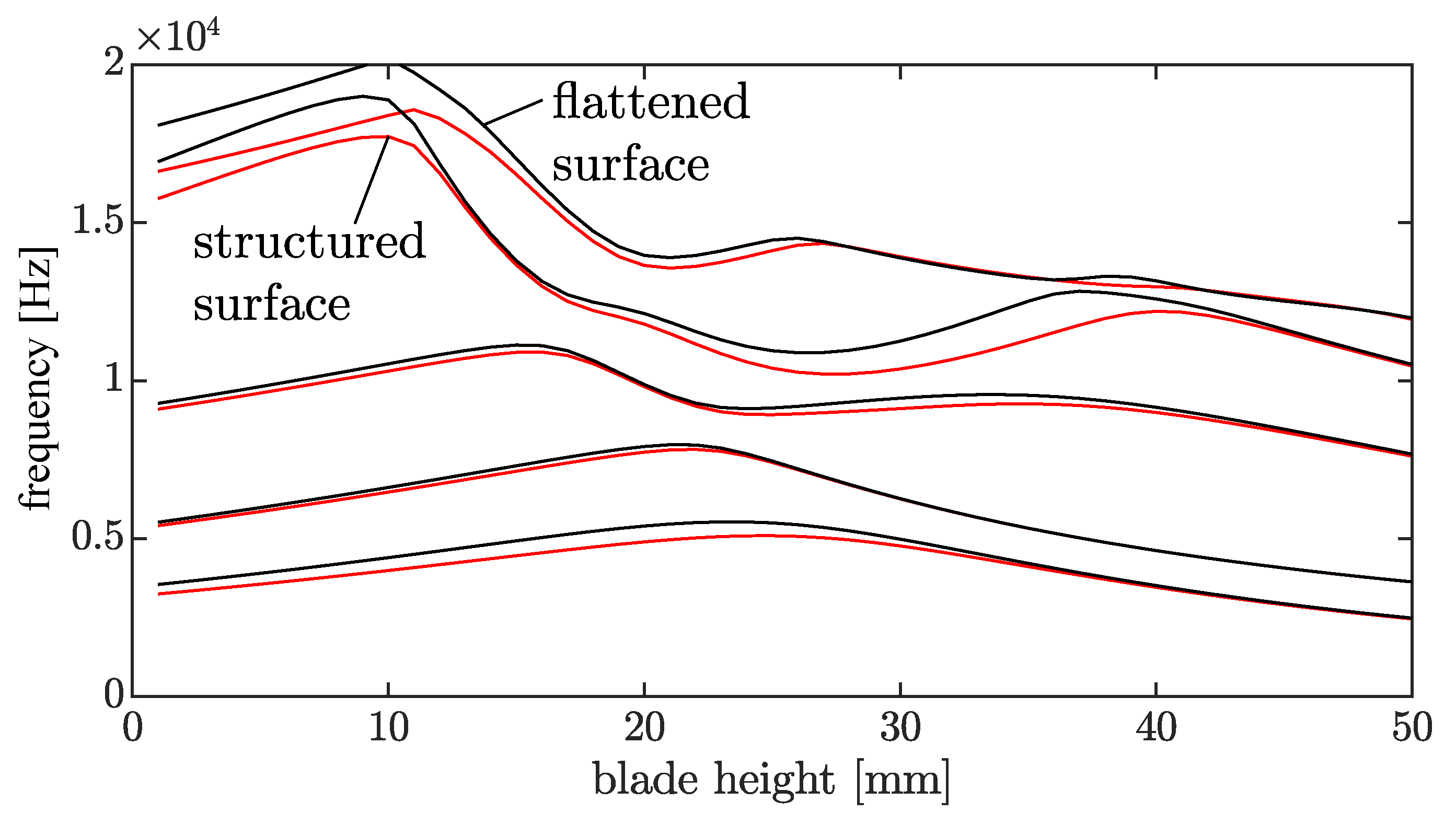


| Name | Unit | Value |
|---|---|---|
| Density | kg/m | 2700 |
| Young’s modulus | GPa | 70 |
| Poisson’s ratio | 1 | 0.35 |
| Name | Unit | Raw Secion | Blade Secion |
|---|---|---|---|
| Area | mm | 800 | 137.7 |
| second moment of area to axis x | mm | 26,666 | 1500 |
| second moment of area to axis y | mm | 106,666 | 12,330 |
| Parameter | Unit | Airsoft Ball | Wall |
|---|---|---|---|
| Density | [kg/m] | 3900 | 2700 |
| Elastic modulus | [GPa] | 2.31 | 70 |
| Poisson’s ratio | [1] | 0.25 | 0.35 |
| Initial yield stress | [MPa] | 23.71 | 324 |
| Plastic hardening | [MPa] | 1659.72 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachrathy, D.; Kiss, A.K.; Kossa, A.; Berezvai, S.; Hajdu, D.; Stepan, G. In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation. J. Manuf. Mater. Process. 2020, 4, 78. https://doi.org/10.3390/jmmp4030078
Bachrathy D, Kiss AK, Kossa A, Berezvai S, Hajdu D, Stepan G. In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation. Journal of Manufacturing and Materials Processing. 2020; 4(3):78. https://doi.org/10.3390/jmmp4030078
Chicago/Turabian StyleBachrathy, Daniel, Adam K. Kiss, Attila Kossa, Szabolcs Berezvai, David Hajdu, and Gabor Stepan. 2020. "In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation" Journal of Manufacturing and Materials Processing 4, no. 3: 78. https://doi.org/10.3390/jmmp4030078
APA StyleBachrathy, D., Kiss, A. K., Kossa, A., Berezvai, S., Hajdu, D., & Stepan, G. (2020). In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation. Journal of Manufacturing and Materials Processing, 4(3), 78. https://doi.org/10.3390/jmmp4030078





