Investigation and Modeling of the Preheating Effects on Precipitation and Hot Flow Behavior for Forming High Strength AA7075 at Elevated Temperatures
Abstract
1. Introduction
2. Materials and Methods
3. Unified Constitutive Modeling and Calibration
3.1. Modeling of Precipitation during Heating
3.2. Modeling of Hot Deformation
3.3. Modeling Calibration
4. Results and Discussions
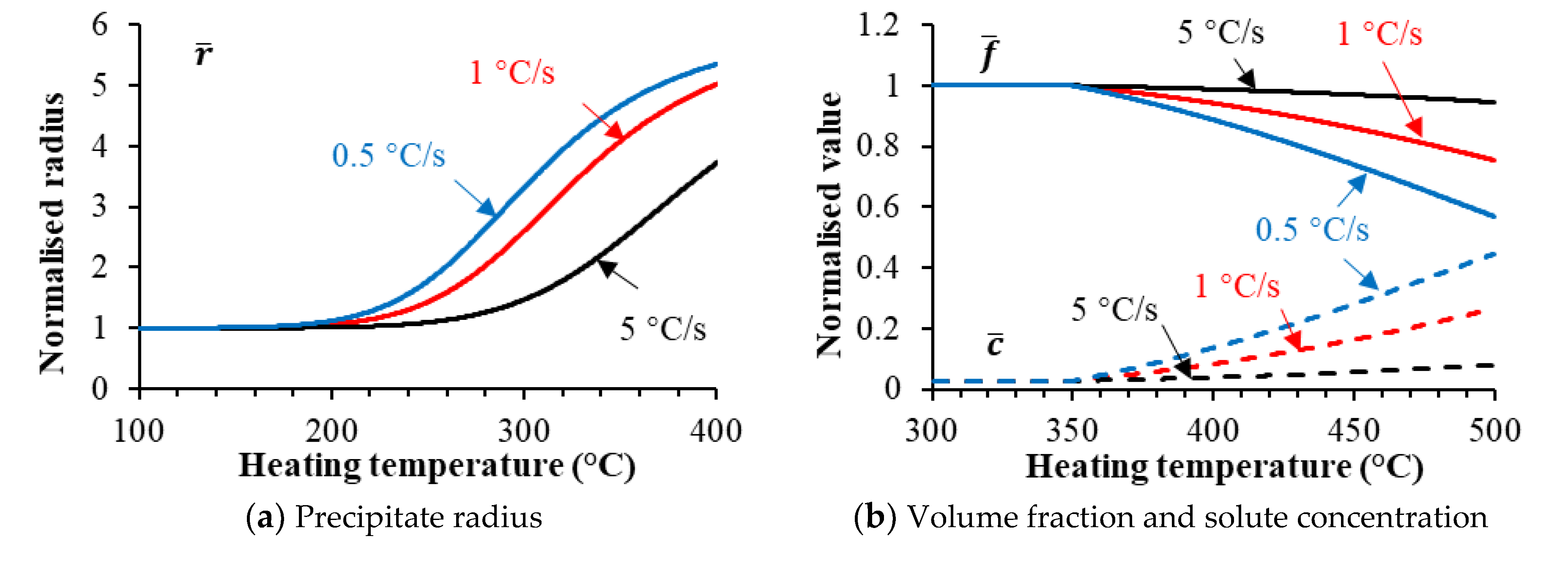
4.1. Microstructure Evolution
4.2. Effects of Preheating on Strength
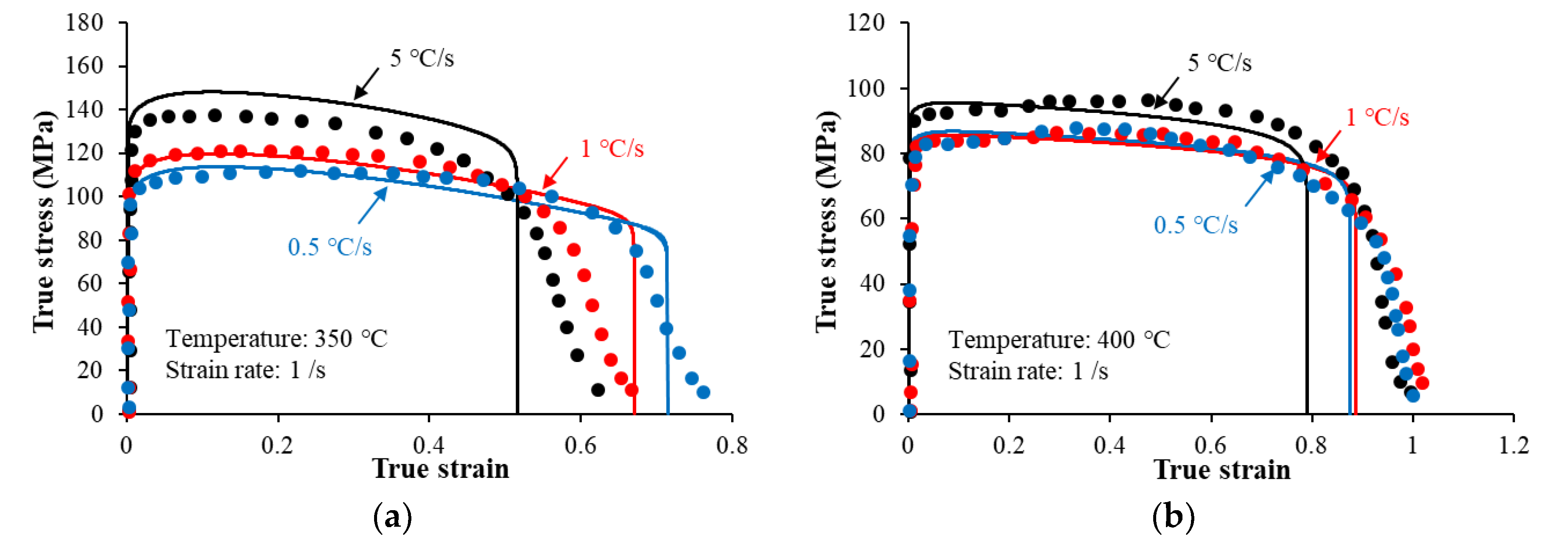
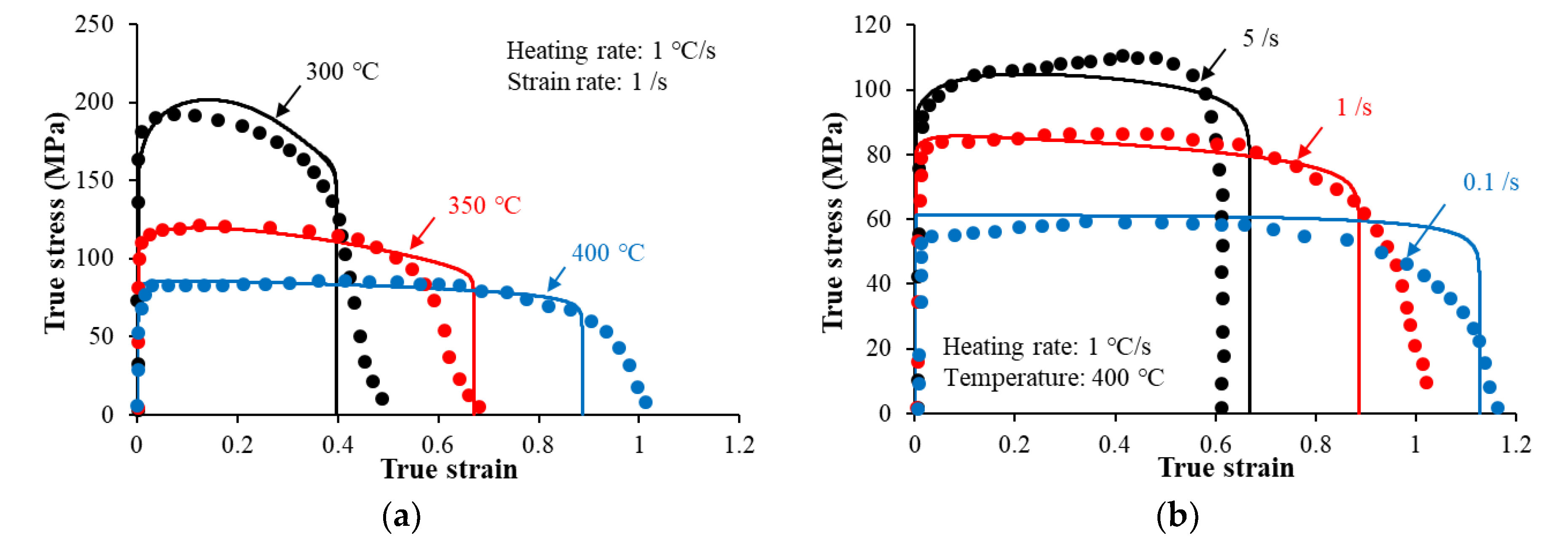
4.3. Effects of Preheating on Hot Flow Behavior
4.4. Model Verification
5. Conclusions
- (1)
- The precipitate coarsening and dissolution of AA7050-T6 during heating were considered in the unified constitutive model, enabling appropriate predictions of the heating rate effects on both the strength and hot flow behaviors of the alloy.
- (2)
- Increasing the target heating temperature leads to a rapid reduction in the post-forming hardness followed by a slight increase, due to the coarsening and subsequent dissolution of the precipitates. A higher heating rate results in delayed hardness reduction due to the shortened heating time.
- (3)
- An increase in the heating rate from 0.5 °C/s to 5 °C/s increased the flow stress levels, from 100 MPa to 130 MPa at 350 °C and from 80 to 90 MPa at 400 °C. This is attributed to the coarsening of the precipitates during heating prior to the deformation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, K.; Politis, D.; Wang, L.; Lin, J. A review on forming techniques for manufacturing lightweight complex—Shaped aluminium panel components. Int. J. Light. Mater. Manuf. 2018, 1, 55–80. [Google Scholar] [CrossRef]
- Zheng, K.; Lee, J.; Xiao, W.; Wang, B.; Lin, J. Experimental Investigations of the In-Die Quenching Efficiency and Die Surface Temperature of Hot Stamping Aluminium Alloys. Metals 2018, 8, 231. [Google Scholar] [CrossRef]
- Hirsch, J.; Hirsch, J. Recent development in aluminium for automotive applications. Trans. Nonferrous Met. Soc. China 2014, 24, 1995–2002. [Google Scholar] [CrossRef]
- Palumbo, G.; Piccininni, A.; Guglielmi, P.; Spina, R.; Tricarico, L.; Sorgente, D.; Russello, G.; Vitrano, A.; Franco, A.L. Warm Forming of an AA5754 Component for Railway Vehicle Applications. Procedia Eng. 2017, 183, 351–356. [Google Scholar] [CrossRef]
- Mohamed, M.S.; Foster, A.D.; Lin, J.; Balint, D.S.; Dean, T.A. Investigation of deformation and failure features in hot stamping of AA6082: Experimentation and modelling. Int. J. Mach. Tools Manuf. 2012, 53, 27–38. [Google Scholar] [CrossRef]
- Zheng, K.; Dong, Y.; Zheng, J.-H.; Foster, A.; Lin, J.; Dong, H.; Dean, T.A. The effect of hot form quench (HFQ®) conditions on precipitation and mechanical properties of aluminium alloys. Mater. Sci. Eng. A 2019, 761, 138017. [Google Scholar] [CrossRef]
- El Fakir, O.; Wang, L.; Balint, D.; Dear, J.P.; Lin, J.; Dean, T.A. Numerical study of the solution heat treatment, forming, and in-die quenching (HFQ) process on AA5754. Int. J. Mach. Tools Manuf. 2014, 87, 39–48. [Google Scholar] [CrossRef]
- Toros, S.; Ozturk, F.; Kacar, I. Review of warm forming of aluminum–magnesium alloys. J. Mater. Process. Technol. 2008, 207, 1–12. [Google Scholar] [CrossRef]
- Krajewski, P.E.; Schroth, J.G. Overview of quick plastic forming technology. Mater. Sci. Forum 2007, 551, 3–12. [Google Scholar] [CrossRef]
- Zheng, K.; Dong, Y.; Zheng, D.; Lin, J.; Dean, T.A. An experimental investigation on the deformation and post-formed strength of heat-treatable aluminium alloys using different elevated temperature forming processes. J. Mater. Process. Technol. 2019, 268, 87–96. [Google Scholar] [CrossRef]
- Wang, H.; Luo, Y.; Friedman, P.; Chen, M.-H.; Gao, L. Warm forming behavior of high strength aluminum alloy AA7075. Trans. Nonferrous Met. Soc. China 2012, 22, 1–7. [Google Scholar] [CrossRef]
- Huo, W.; Hou, L.; Zhang, Y.; Zhang, J. Warm formability and post-forming microstructure/property of high-strength AA 7075-T6 Al alloy. Mater. Sci. Eng. A 2016, 675, 44–54. [Google Scholar] [CrossRef]
- Maeno, T.; Mori, K.-I.; Yachi, R. Hot stamping of high-strength aluminium alloy aircraft parts using quick heating. CIRP Ann. 2017, 66, 269–272. [Google Scholar] [CrossRef]
- Zhang, Q.; Luan, X.; Dhawan, S.; Politis, D.J.; Du, Q.; Fu, M.; Wang, K.; Gharbi, M.M.; Wang, L. Development of the post-form strength prediction model for a high-strength 6xxx aluminium alloy with pre-existing precipitates and residual dislocations. Int. J. Plast. 2019, 119, 230–248. [Google Scholar] [CrossRef]
- Priya, P.; Johnson, D.R.; Krane, M.J. Precipitation during cooling of 7XXX aluminum alloys. Comput. Mater. Sci. 2017, 139, 273–284. [Google Scholar] [CrossRef]
- Lloyd, D.J.; Chaturvedi, M.C. A calorimetric study of aluminium alloy AA-7075. J. Mater. Sci. 1982, 17, 1819–1824. [Google Scholar] [CrossRef]
- Nicolas, M.; Deschamps, A. Characterisation and modelling of precipitate evolution in an Al–Zn–Mg alloy during non-isothermal heat treatments. Acta Mater. 2003, 51, 6077–6094. [Google Scholar] [CrossRef]
- Zheng, J.-H.; Lin, J.; Lee, J.; Pan, R.; Li, C.; Davies, C.M. A novel constitutive model for multi-step stress relaxation ageing of a pre-strained 7xxx series alloy. Int. J. Plast. 2018, 106, 31–47. [Google Scholar] [CrossRef]
- Milkereit, B.; Schick, C.; Keßler, O.; Osten, J. Dissolution and precipitation behaviour during continuous heating of Al–Mg–Si Alloys in a wide range of heating rates. Materials 2015, 8, 2830–2848. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Lin, J.; Yang, Y.-L.; Rong, Q.; Huang, B.-M.; Chung, T.-F.; Tsao, C.-S.; Yang, J.-R.; Balint, D.S. A unified constitutive model for asymmetric tension and compression creep-ageing behaviour of naturally aged Al-Cu-Li alloy. Int. J. Plast. 2017, 89, 130–149. [Google Scholar] [CrossRef]
- Shercliff, H.; Ashby, M. A process model for age hardening of aluminium alloys—I. The model. Acta Met. Mater. 1990, 38, 1789–1802. [Google Scholar] [CrossRef]
- Lin, J.; Dean, T. Modelling of microstructure evolution in hot forming using unified constitutive equations. J. Mater. Process. Technol. 2005, 167, 354–362. [Google Scholar] [CrossRef]
- Lin, J. A set of unified constitutive equations for modelling microstructure evolution in hot deformation. J. Mater. Process. Technol. 2003, 143, 281–285. [Google Scholar] [CrossRef]
- Ji, H.; Liu, J.; Wang, B.; Tang, X.; Lin, J.; Huo, Y. Microstructure evolution and constitutive equations for the high-temperature deformation of 5Cr21Mn9Ni4N heat-resistant steel. J. Alloys Compd. 2017, 693, 674–687. [Google Scholar] [CrossRef]
- Alabort, E.; Putman, D.; Reed, R. Superplasticity in Ti–6Al–4V: Characterisation, modelling and applications. Acta Mater. 2015, 95, 428–442. [Google Scholar] [CrossRef]
- Lin, J.; Yang, J. GA-based multiple objective optimisation for determining viscoplastic constitutive equations for superplastic alloys. Int. J. Plast. 1999, 15, 1181–1196. [Google Scholar] [CrossRef]
- Cao, J.; Lin, J. A study on formulation of objective functions for determining material models. Int. J. Mech. Sci. 2008, 50, 193–204. [Google Scholar] [CrossRef]
- Li, N.; Sun, C.; Guo, N.; Mohamed, M.; Lin, J.; Matsumoto, T.; Liu, C. Experimental investigation of boron steel at hot stamping conditions. J. Mater. Process. Technol. 2016, 228, 2–10. [Google Scholar] [CrossRef]
- Li, G.-F.; Zhang, X.; Li, P.-H.; You, J.-H. Effects of retrogression heating rate on microstructures and mechanical properties of aluminum alloy 7050. Trans. Nonferrous Met. Soc. China 2010, 20, 935–941. [Google Scholar] [CrossRef]
- Buha, J.; Lumley, R.; Crosky, A. Secondary ageing in an aluminium alloy 7050. Mater. Sci. Eng. A 2008, 492, 1–10. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, B.; Wu, Y.; Yang, X. Constitutive modeling of flow behavior and microstructure evolution of AA7075 in hot tensile deformation. Mater. Sci. Eng. A 2018, 712, 704–713. [Google Scholar] [CrossRef]
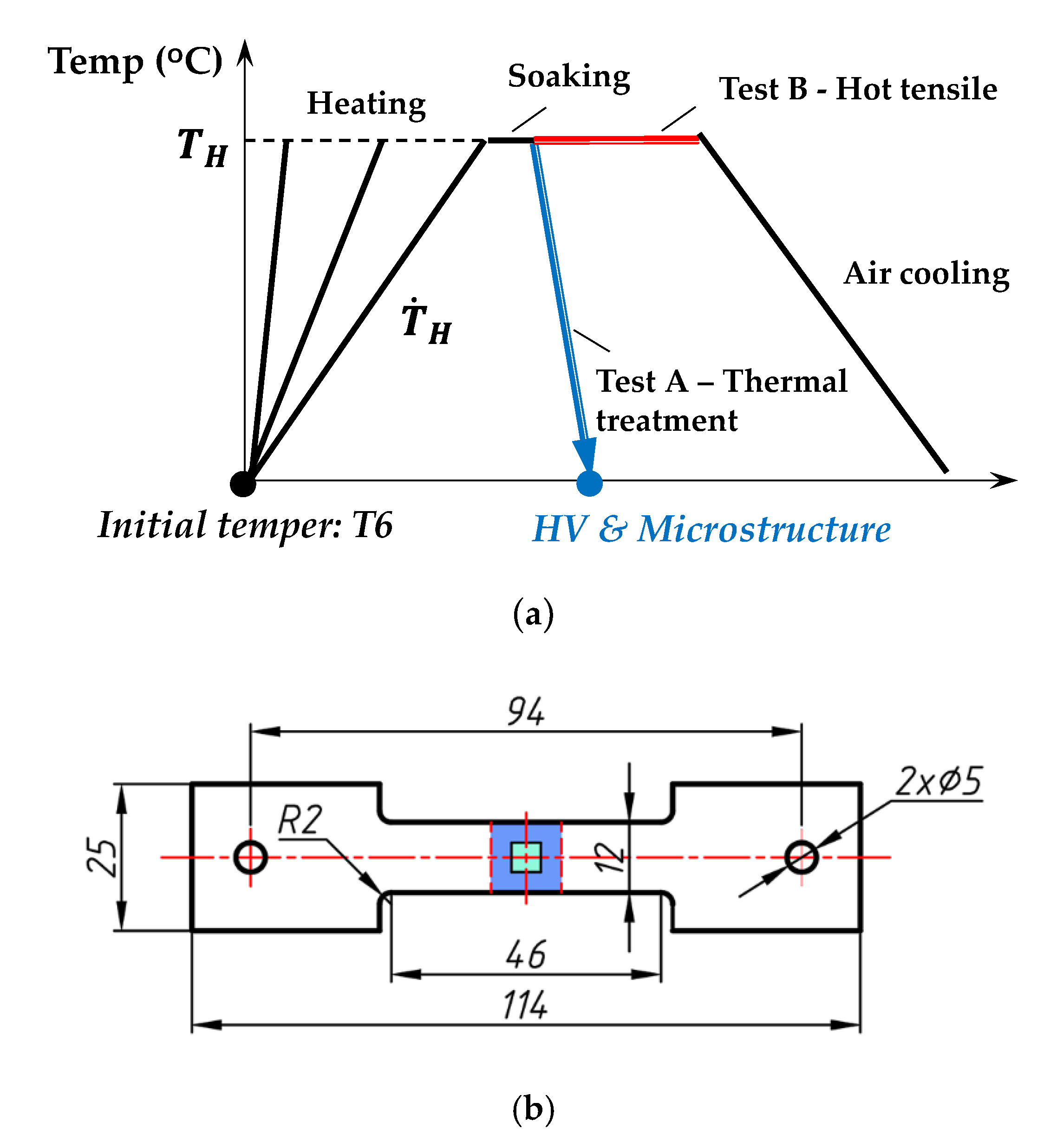
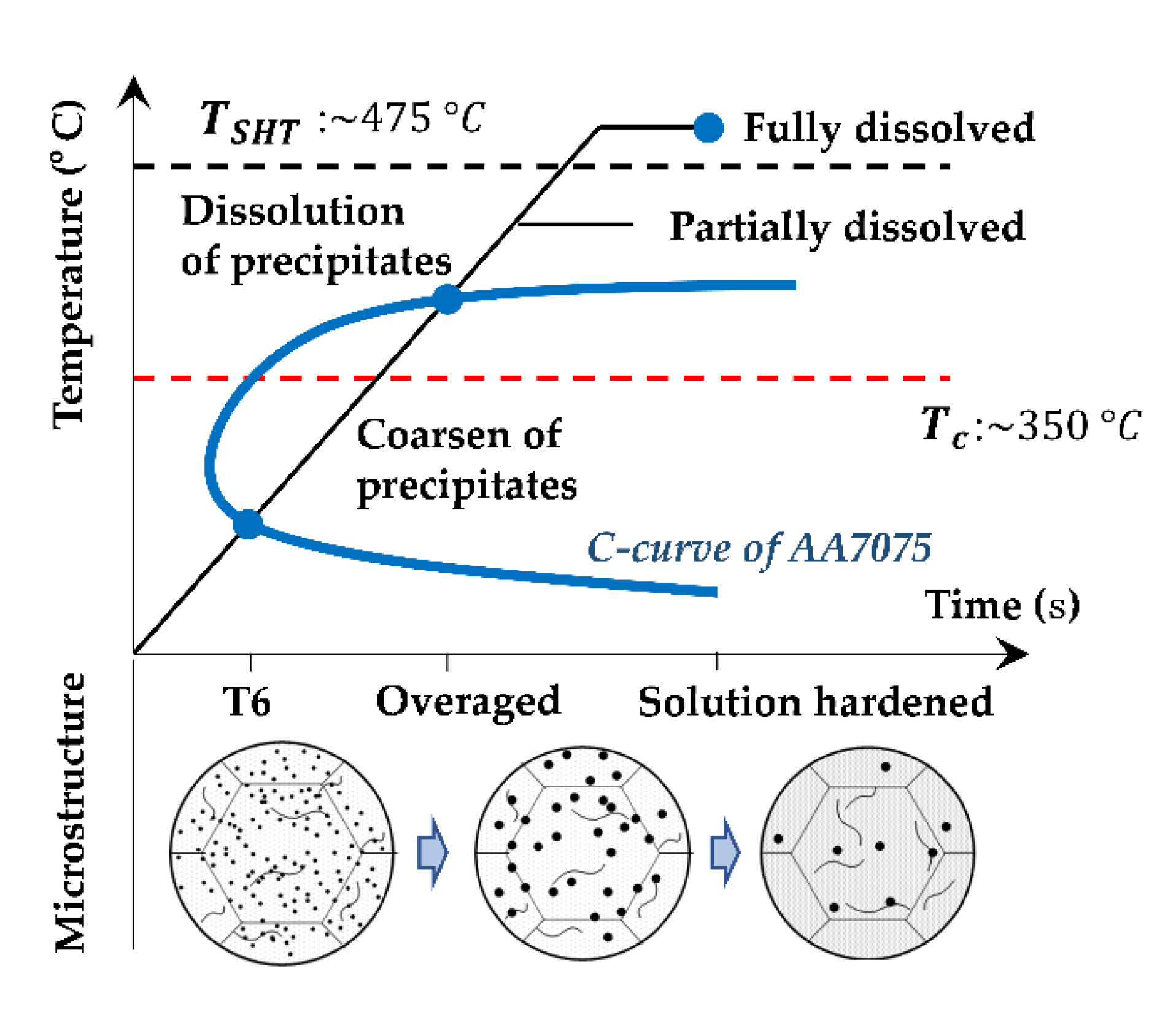

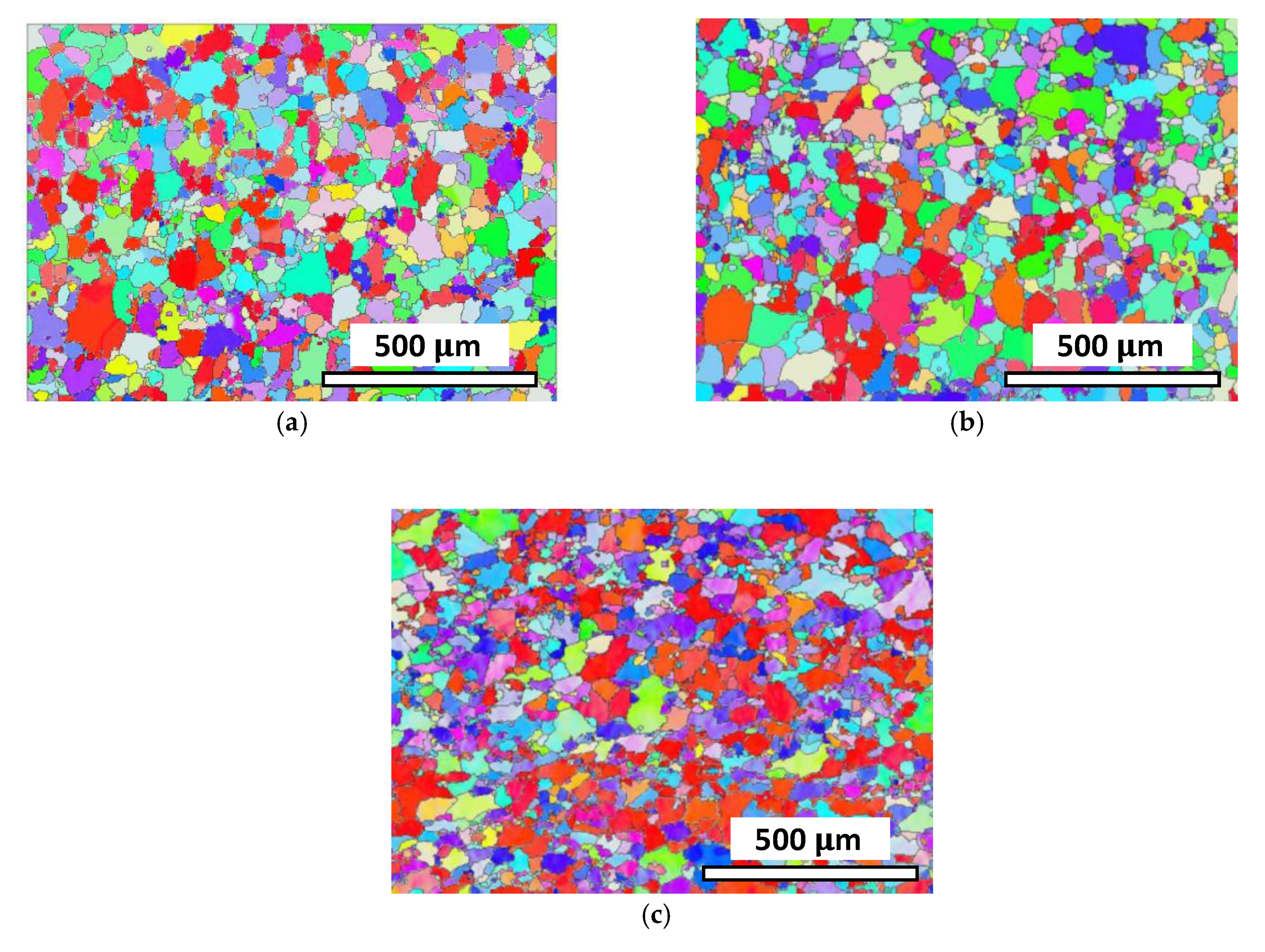
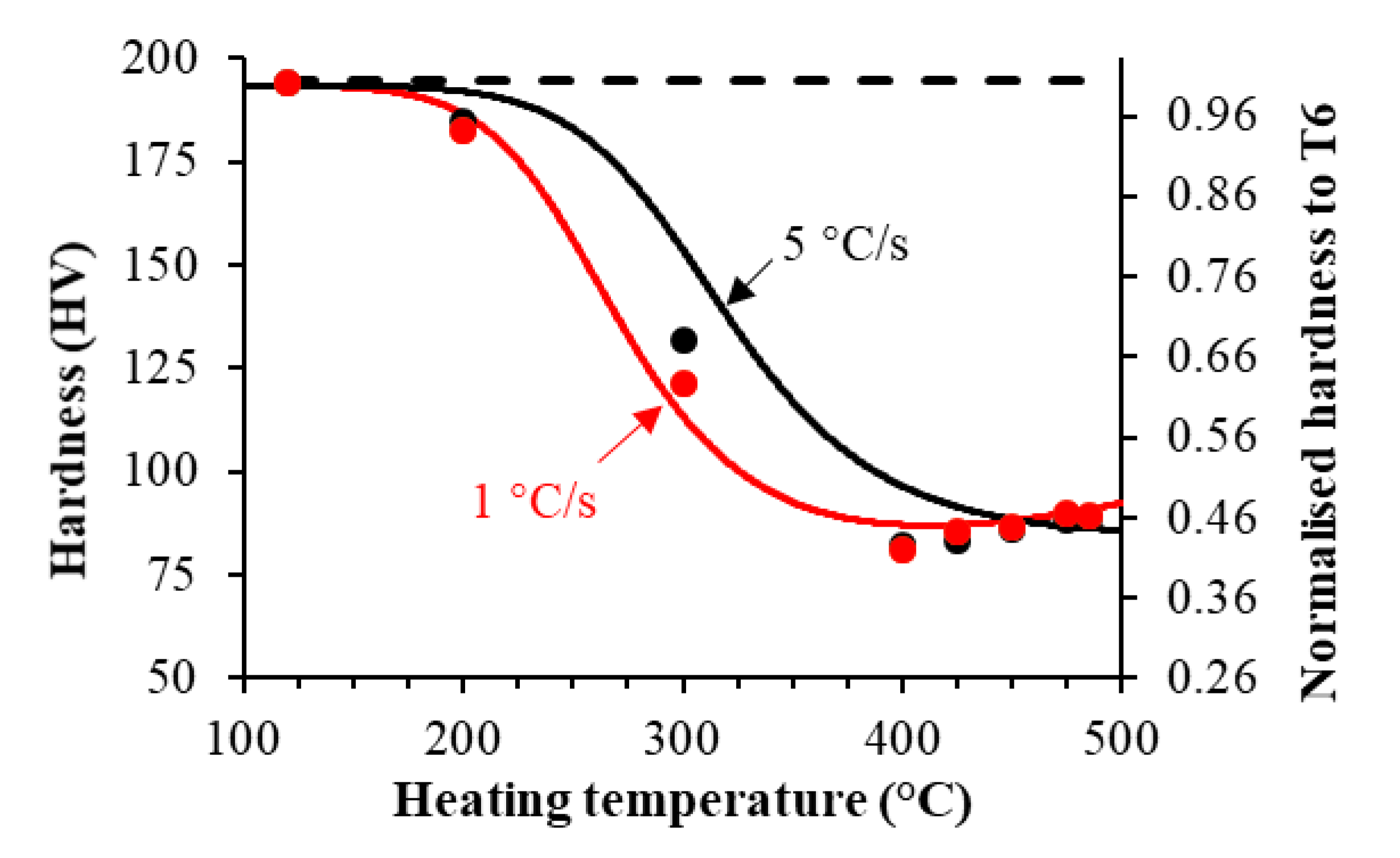
| Zn | Mg | Cu | Si | Fe | Mn | Cr | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| 5.1–6.1 | 2.1–2.9 | 1.2–2.0 | 0.4 | 0.5 | 0.3 | 0.18–0.28 | 0.2 | Balanced |
| Test Conditions | |||
|---|---|---|---|
| Heating Rate (°C/s) | Heating Temperature (°C) | Strain Rate (1/s) | |
| Hardness test | 1, 5 | 120, 200, 300, 350, 400, 425, 450, 485 | - |
| Hot uniaxial tensile test | 0.5, 1, 5 | 300, 350, 400 | 0.1, 1, 5 |
| As-Received | As-Heated | As-Heated and Strained | ||
|---|---|---|---|---|
| 1 °C/s, 300 °C | 1 °C/s, 400 °C | 1 °C/s, 400 °C + ε:0.3 | ||
| TEM | √① | √② | √③ | |
| EBSD | √④ | √⑤ | √⑥ | |
| (-) | (-) | (-) | (kJ/mol) | (-) | (kJ/mol) | (MPa) |
| 1.2 × 104 | 1.5 | 6.0 | 76.5 | 4.5 × 10−1 | 32.0 | 968.1 |
| (kJ/mol) | (MPa) | (MPa) | (MPa) | (-) | (-) | (-) |
| 2.6 × 10−3 | 452.7 | 2.2 × 10−3 | 304.7 | 4.6 × 10−3 | 0.1 | 0.8 |
| (-) | (MPa) | (J/mol) | (-) | (J/mol) | (MPa) | (J/mol) | (-) | (J/mol) | (s−1) |
| 0.3 | 0.236 | 23,368 | −0.37 | 11,567 | 0.0036 | 48,322 | 18.21 | 4093.3 | 2784 |
| (J/mol) | (-) | (s−1) | (-) | (MPa) | (J/mol) | (s−1) | (J/mol) | (-) | (-) |
| 29,514 | 0.1 | 60.0 | 1.1 | 1.7 × 10−7 | 58,716 | 1.4 × 10−5 | 41,173 | 1.5 | 0.97 |
| (-) | (-) | (-) | (J/mol) | (-) | (J/mol) | (-) | (J/mol) | (MPa) | (J/mol) |
| 0.58 | −0.01 | 2.55 × 10-2 | 20,959 | 0.57 | 20,470 | 2.05 | 3776.3 | 3369 | 12,596 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, K.; Li, Y.; Yang, S.; Fu, K.; Zheng, J.; He, Z.; Yuan, S. Investigation and Modeling of the Preheating Effects on Precipitation and Hot Flow Behavior for Forming High Strength AA7075 at Elevated Temperatures. J. Manuf. Mater. Process. 2020, 4, 76. https://doi.org/10.3390/jmmp4030076
Zheng K, Li Y, Yang S, Fu K, Zheng J, He Z, Yuan S. Investigation and Modeling of the Preheating Effects on Precipitation and Hot Flow Behavior for Forming High Strength AA7075 at Elevated Temperatures. Journal of Manufacturing and Materials Processing. 2020; 4(3):76. https://doi.org/10.3390/jmmp4030076
Chicago/Turabian StyleZheng, Kailun, Yong Li, Song Yang, Kunning Fu, Jinghua Zheng, Zhubin He, and Shijian Yuan. 2020. "Investigation and Modeling of the Preheating Effects on Precipitation and Hot Flow Behavior for Forming High Strength AA7075 at Elevated Temperatures" Journal of Manufacturing and Materials Processing 4, no. 3: 76. https://doi.org/10.3390/jmmp4030076
APA StyleZheng, K., Li, Y., Yang, S., Fu, K., Zheng, J., He, Z., & Yuan, S. (2020). Investigation and Modeling of the Preheating Effects on Precipitation and Hot Flow Behavior for Forming High Strength AA7075 at Elevated Temperatures. Journal of Manufacturing and Materials Processing, 4(3), 76. https://doi.org/10.3390/jmmp4030076





