Predicting the Ultimate Tensile Strength of Friction Stir Welds Using Gaussian Process Regression
Abstract
1. Introduction
- Due to the flexibility in modeling, since GPR is a non-parametric method [9].
- Due to the possibility of quantifying uncertainties for the prediction, which can be a great benefit for safety-critical applications [9].
- Since Verma et al. [8] compared the performance of the GPR to predict the ultimate tensile strength based on the process parameters with the multi-linear regression and support vector machines—the GPR led to the best results.
2. Materials and Methods
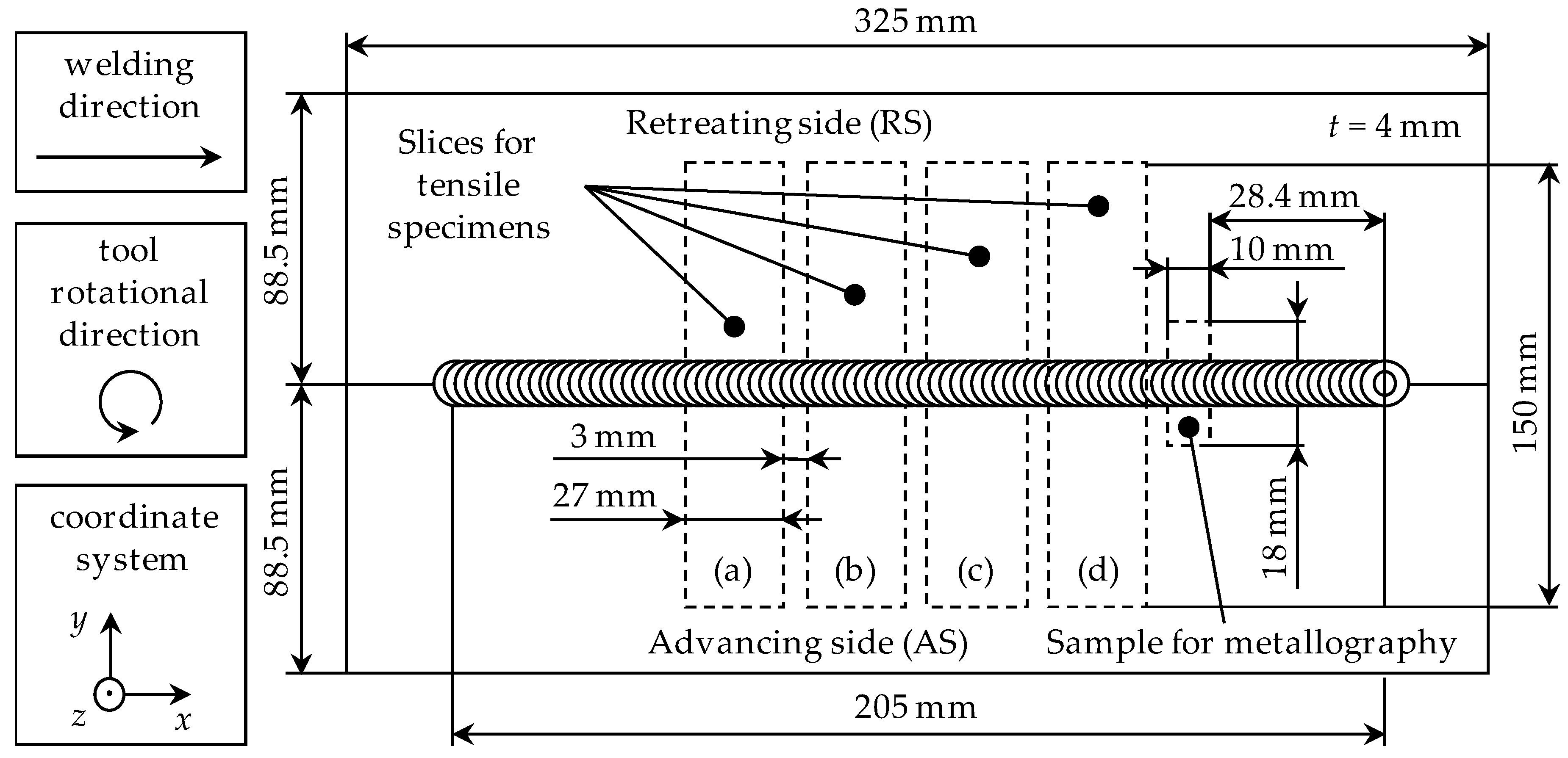
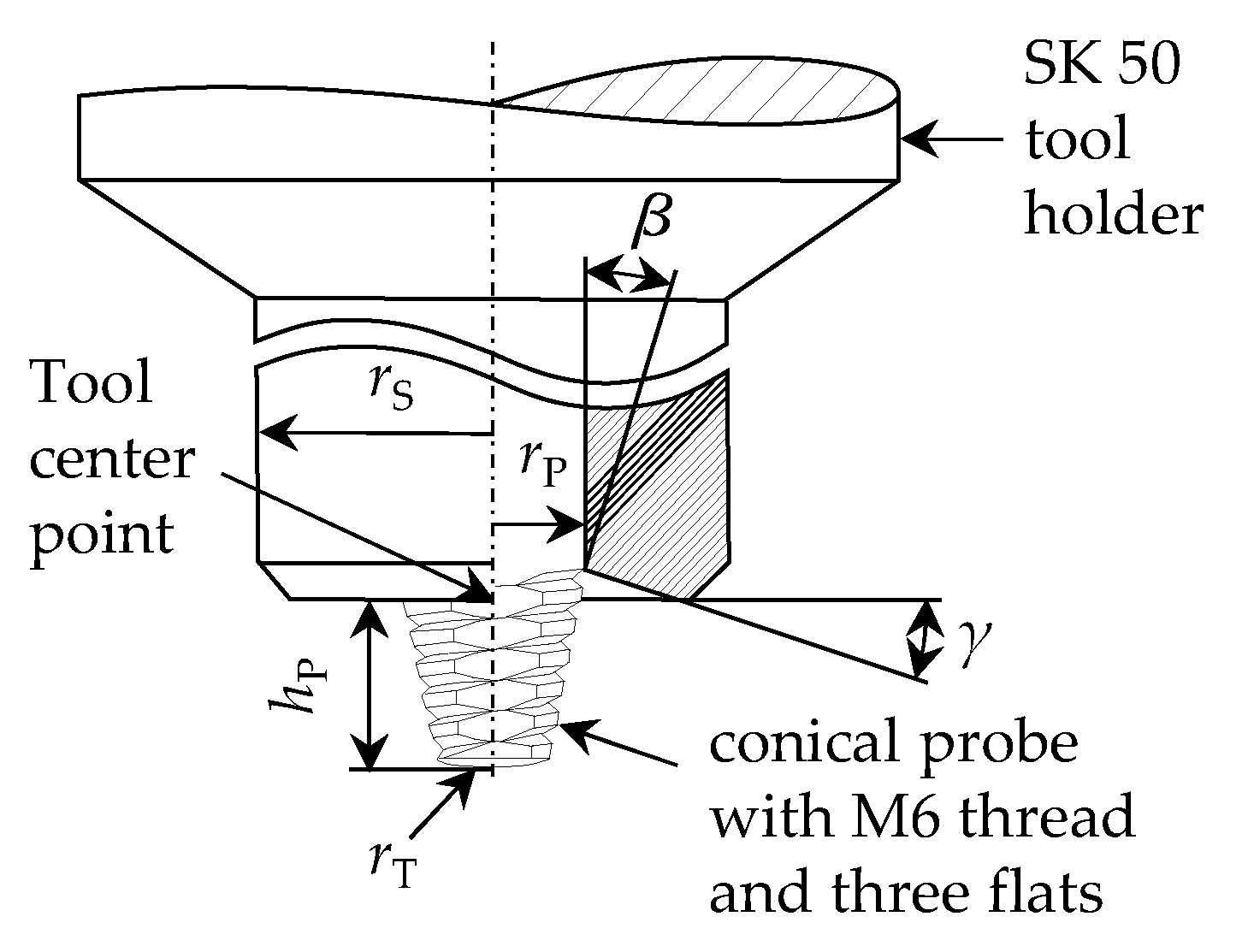
2.1. Welding Experiments
2.2. Application of the Gaussian Process Regression
3. Results
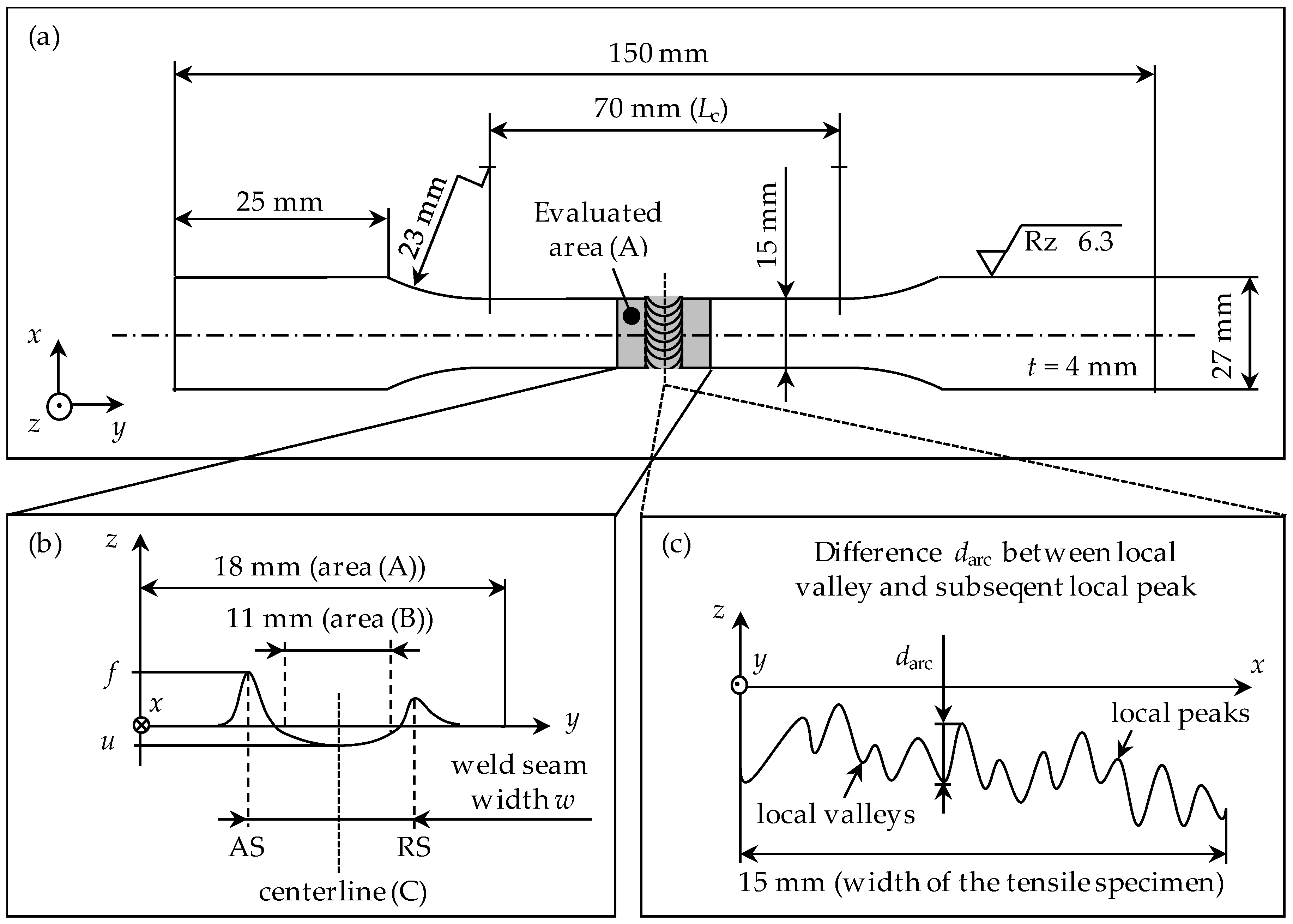
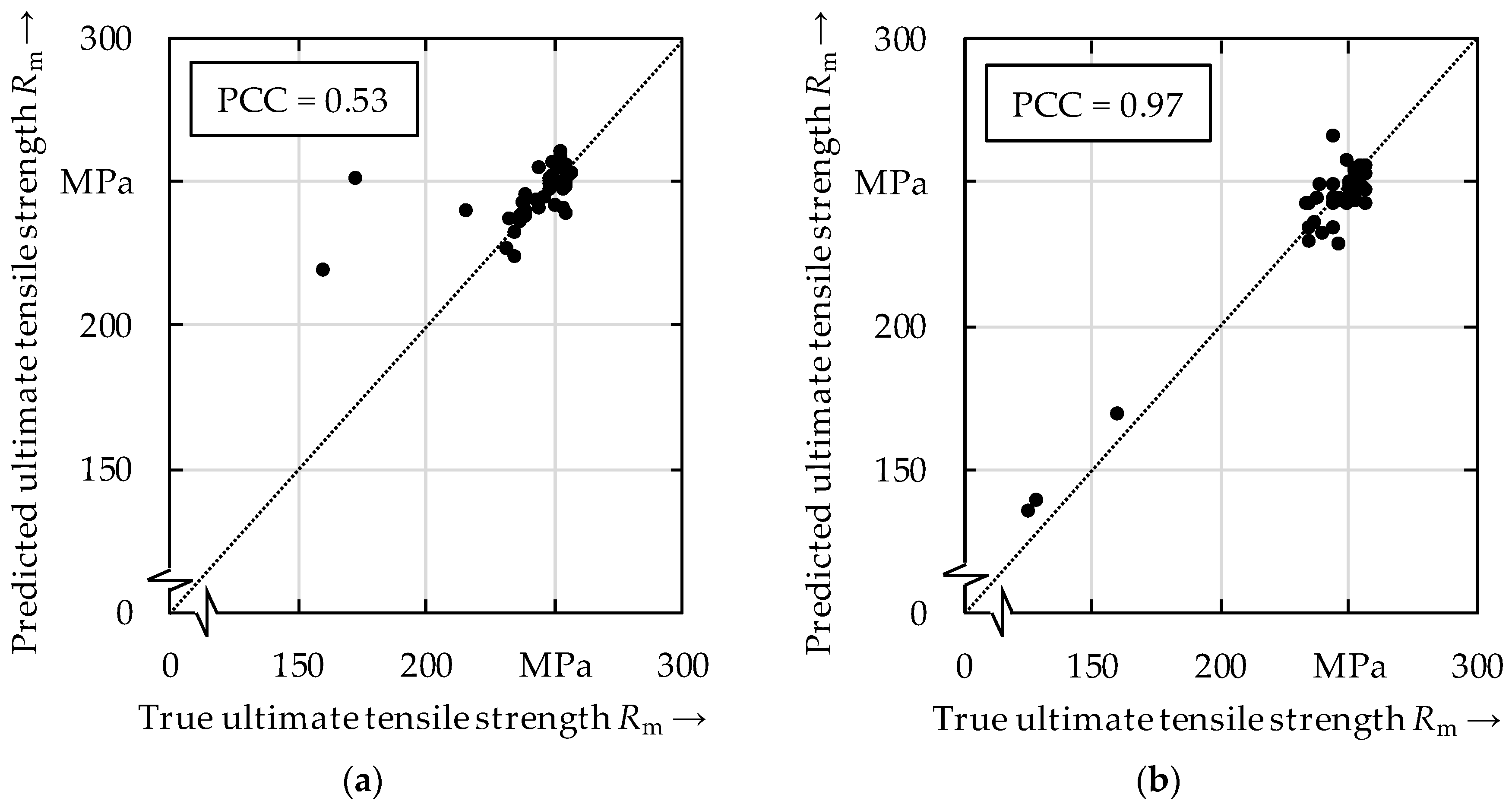
3.1. Prediction of the Ultimate Tensile Strength Using Surface Topography Data
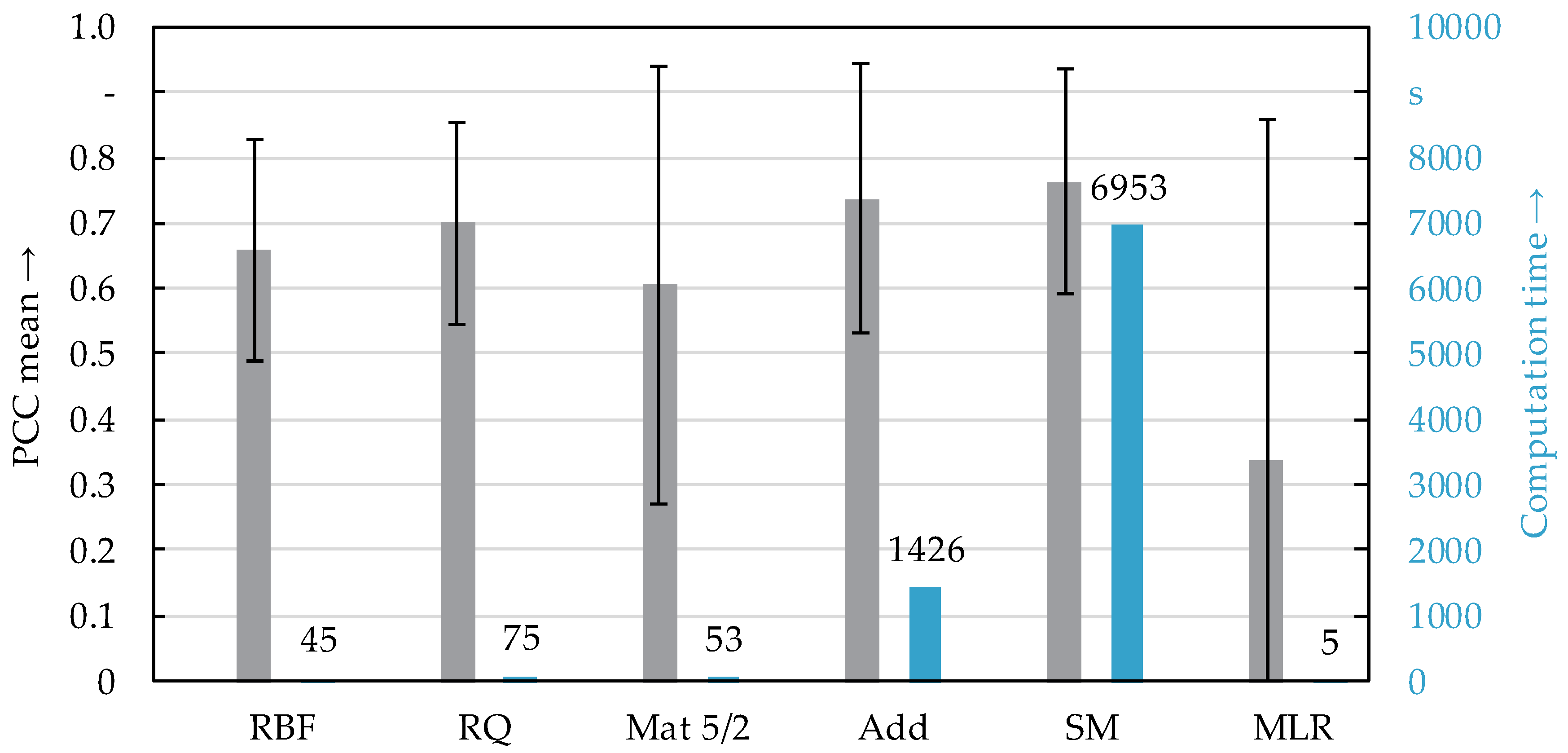
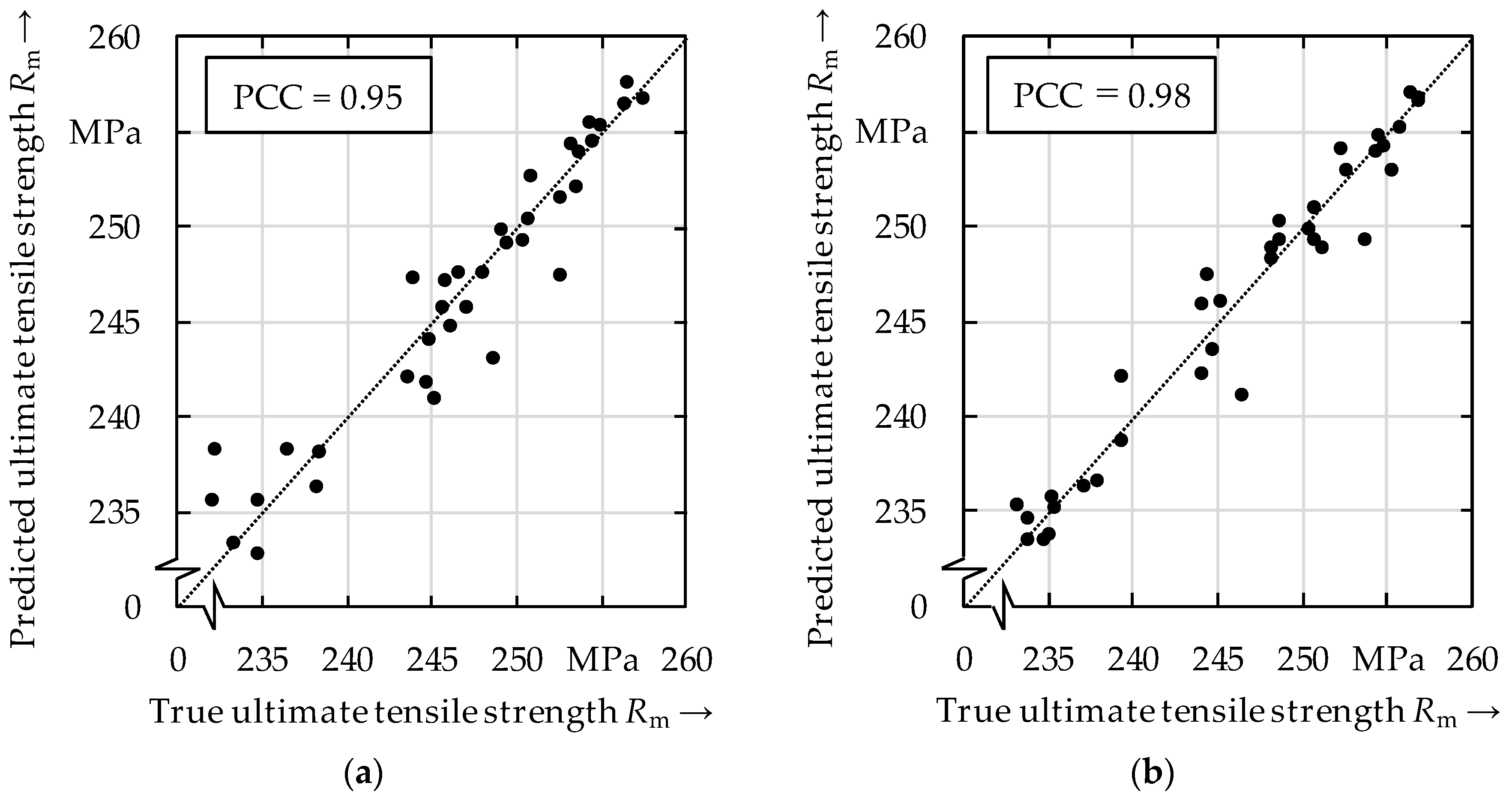
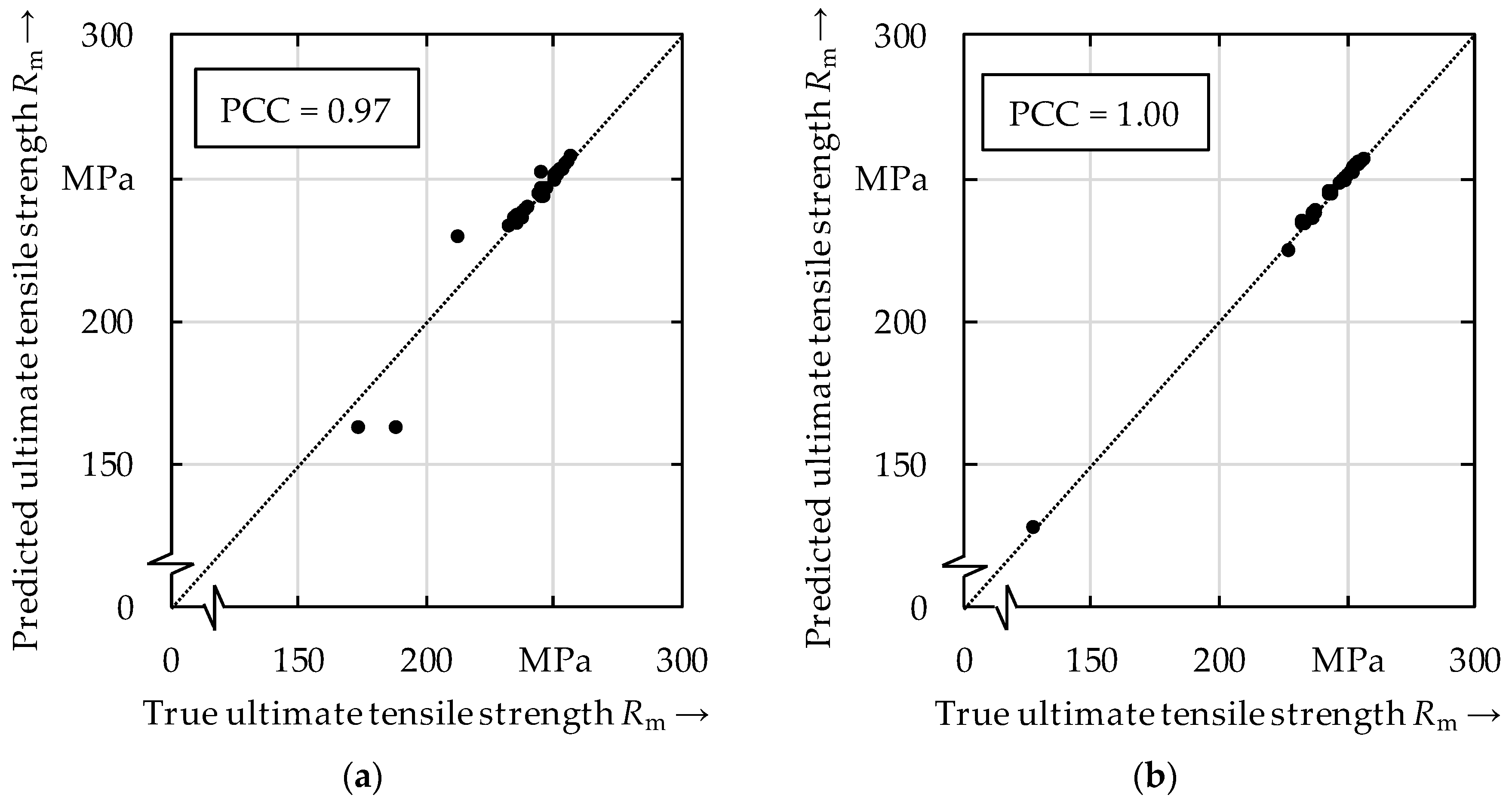
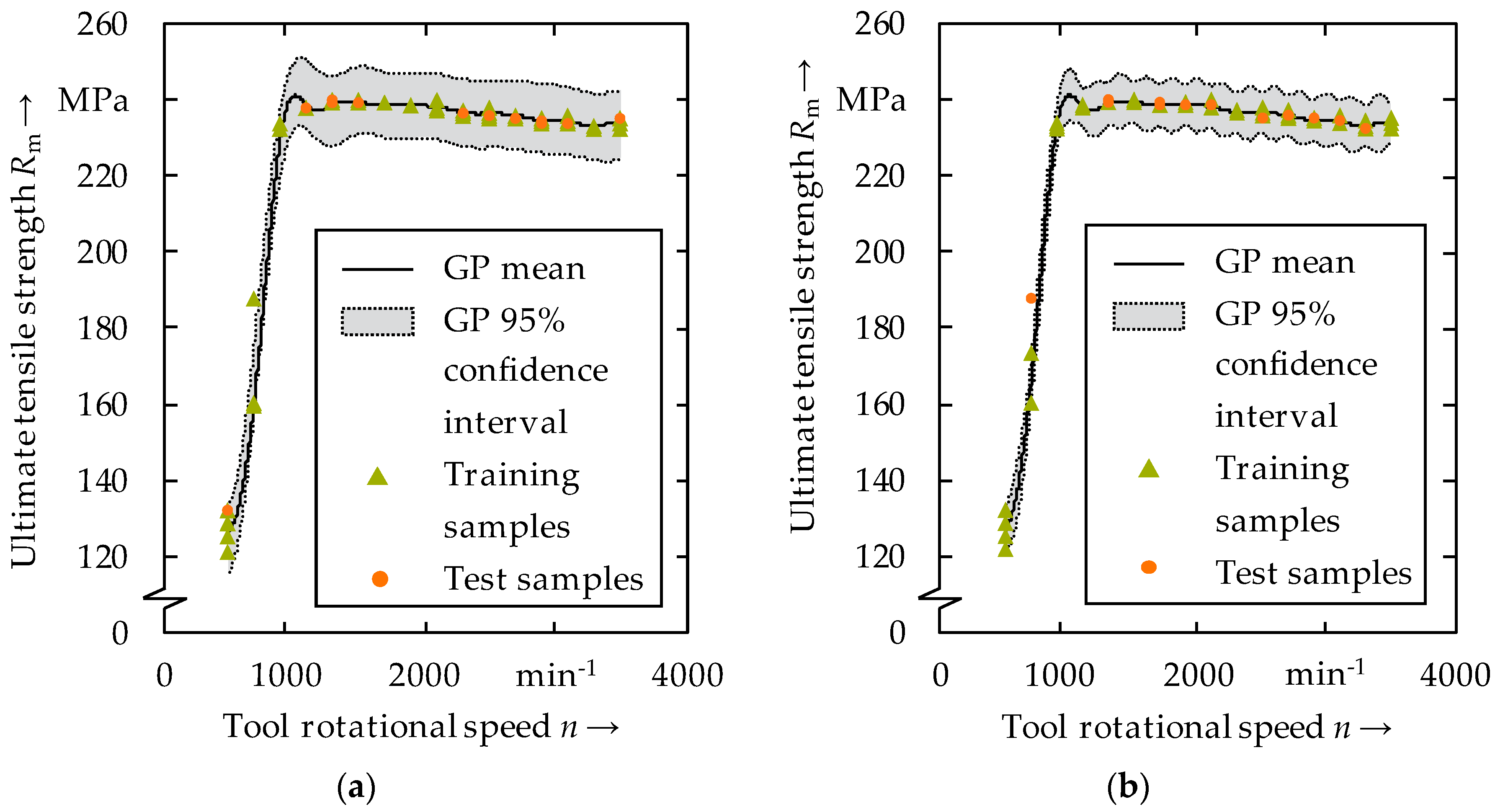
3.2. Predicting Ultimate Tensile Strength Using Process Variables
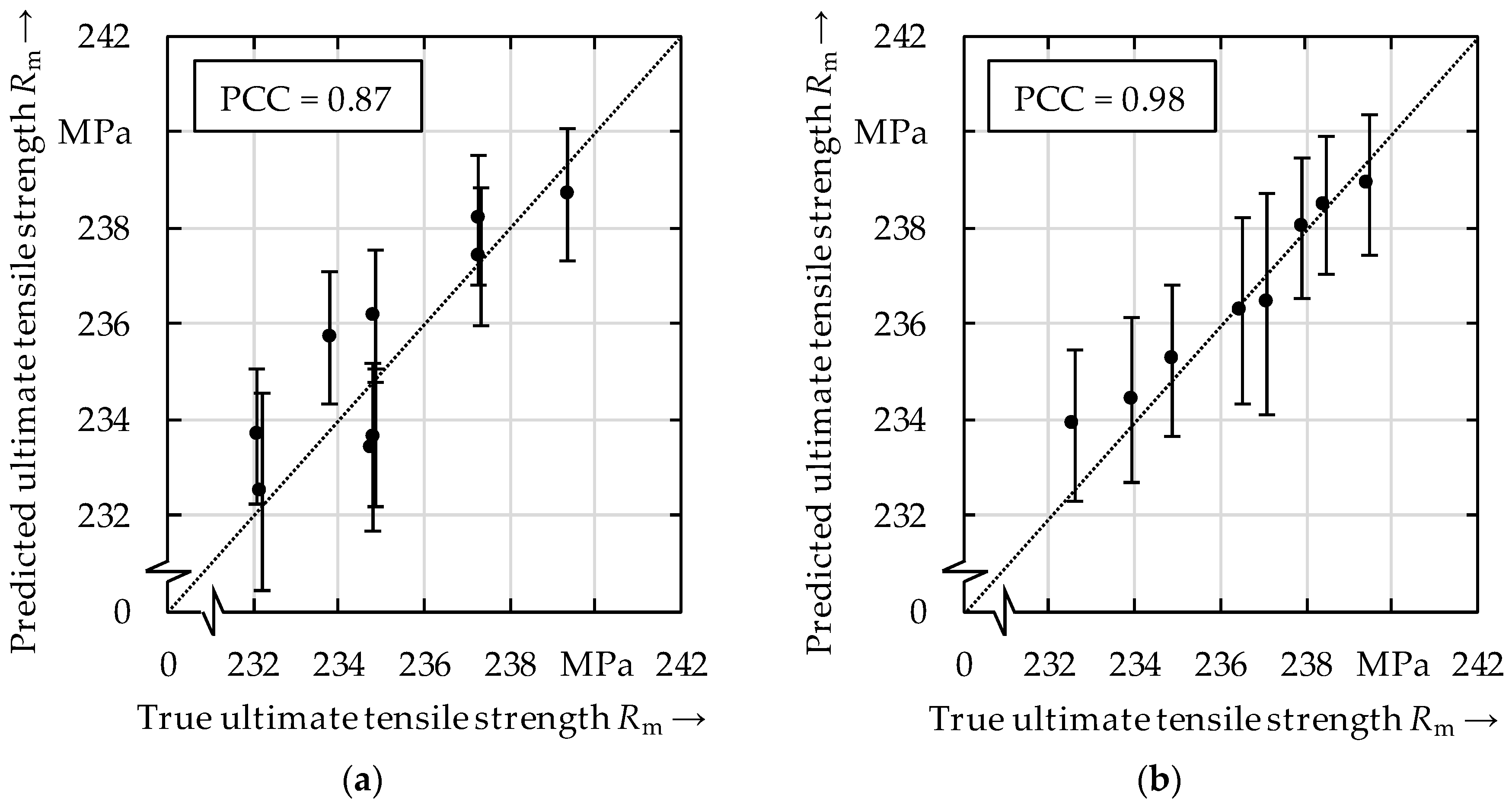
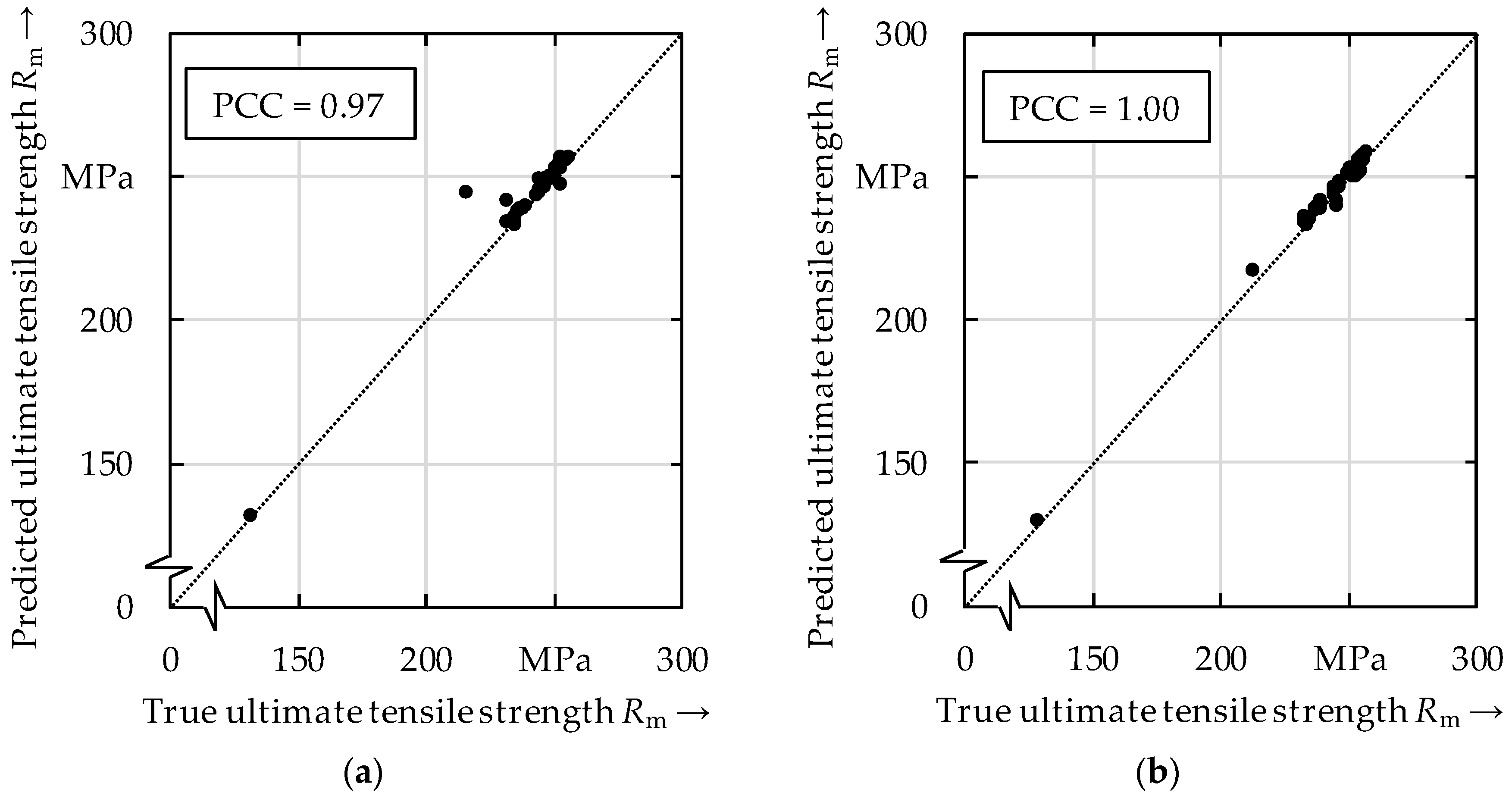
3.3. Predicting the Ultimate Tensile Strength Using Process Parameters
4. Discussion
5. Conclusions
- The Gaussian process regression is a powerful approach to non-destructively predict ultimate tensile strength through data evaluation. The uncertainty of the prediction can be quantified, and a confidence interval can be specified within which the ultimate tensile strength is located with a certain probability.
- It is possible to predict the ultimate tensile strength of friction stir welds by evaluating the surface topography through Gaussian process regression. This is especially valid for low welding speeds and when extremely low or high tool rotational speeds are not employed.
- The correlation coefficients for the prediction of the ultimate tensile strength by using the process variables or the process parameters were even higher compared to when using the surface topography data as inputs to the model.
- The differences in the PCCs for the various covariance functions used were low. However, when using the data from all investigated welding speeds, the spectral mixture covariance function according to Wilson et al. [19], always yielded the best results.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Experimental Plan
| vs = 500 mm/min | vs = 1000 mm/min | vs = 1500 mm/min | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. no. | n min−1 | n/vs mm−1 | MPa | Exp. no. | n min−1 | n/vs mm−1 | MPa | Exp. no. | n min−1 | n/vs mm−1 | MPa | ||
| 1 | 500 | 1.0 | 127 | 17 | 1100 | 1.1 | 245 | 37 | 1500 | 1.0 | 252 | ||
| 2 | 700 | 1.4 | 170 | 18 | 1300 | 1.3 | 247 | 38 | 1700 | 1.1 | 255 | ||
| 3 | 900 | 1.8 | 233 | 19 | 1500 | 1.5 | 248 | 39 | 1900 | 1.3 | 255 | ||
| 4 | 1100 | 2.2 | 238 | 20 | 1700 | 1.7 | 249 | 40 | 2100 | 1.4 | 254 | ||
| 5 | 1300 | 2.6 | 239 | 21 | 1900 | 1.9 | 250 | 41 | 2300 | 1.5 | 255 | ||
| 6 | 1500 | 3.0 | 239 | 22 | 2100 | 2.1 | 250 | 42 | 2500 | 1.7 | 256 | ||
| 7 | 1700 | 3.4 | 239 | 23 | 2300 | 2.3 | 251 | 43 | 2700 | 1.8 | 257 | ||
| 8 | 1900 | 3.8 | 238 | 24 | 2500 | 2.5 | 250 | 44 | 2900 | 1.9 | 257 | ||
| 9 | 2100 | 4.2 | 238 | 25 | 2700 | 2.7 | 249 | 45 | 3100 | 2.1 | 257 | ||
| 10 | 2300 | 4.6 | 236 | 26 | 2900 | 2.9 | 251 | 46 | 3300 | 2.2 | 255 | ||
| 11 | 2500 | 5.0 | 236 | 27 | 3100 | 3.1 | 249 | 47 | 3500 | 2.3 | 253 | ||
| 12 | 2700 | 5.4 | 236 | 28 | 3300 | 3.3 | 246 | 48 | 3700 | 2.5 | 254 | ||
| 13 | 2900 | 5.8 | 234 | 29 | 3500 | 3.5 | 246 | 49 | 3900 | 2.6 | 253 | ||
| 14 | 3100 | 6.2 | 234 | 30 | 3700 | 3.7 | 245 | 50 | 4100 | 2.7 | 250 | ||
| 15 | 3300 | 6.6 | 233 | 31 | 3900 | 3.9 | 244 | 51 | 4300 | 2.9 | 251 | ||
| 16 | 3500 | 7.0 | 234 | 32 | 4100 | 4.1 | 244 | 52 | 4500 | 3.0 | 253 | ||
| Average: | 225 | 33 | 4300 | 4.3 | 247 | 53 | 4700 | 3.1 | 253 | ||||
| 34 | 4500 | 4.5 | 245 | 54 | 4900 | 3.3 | 248 | ||||||
| 35 | 4700 | 4.7 | 236 | Average: | 254 | ||||||||
| 36 | 4900 | 4.9 | 225 | ||||||||||
| Average: | 246 | ||||||||||||
Appendix B. Fundamentals of the Gaussian Process Regression
References
- Colligan, K.J. The friction stir welding process: An Overview. In Friction Stir Welding—From Basics to Applications; Lohwasser, D., Chen, Z., Eds.; Woodhead Publishing Limited and CRC Press LLC: Cambridge, UK, 2010; pp. 15–41. ISBN 978-1-84569-450-0. [Google Scholar]
- Thomas, W.M.; Nicholas, E.D.; Needham, J.C.; Murch, M.G.; Temple-Smith, P.; Dawes, C.J. Improvements Relating to Friction Welding. European Patent Specifications 0 615 480 B1, 8 November 1995. [Google Scholar]
- Taheri, H.; Kilpatrick, M.; Norvalls, M.; Harper, W.J.; Koester, L.W.; Bigelow, T.; Bond, L.J. Investigation of Nondestructive Testing Methods for Friction Stir Welding. Metals 2019, 9, 624. [Google Scholar] [CrossRef]
- Sagar, S.P.; Miyasaka, C.; Ghosh, M.; Tittmann, B.R. NDE of friction stir welds of Al alloys using high-frequency acoustic microscopy. Nondestruct. Test. Eval. 2012, 27, 375–389. [Google Scholar] [CrossRef]
- Mishra, D.; Roy, R.B.; Dutta, S.; Pal, S.K.; Chakravarty, D. A review on sensor based monitoring and control of friction stir welding process and a roadmap to Industry 4.0. J. Manuf. Process. 2018, 36, 373–397. [Google Scholar] [CrossRef]
- Yunus, M.; Alsoufi, M.S. Mathematical Modelling of a Friction Stir Welding Process to Predict the Joint Strength of Two Dissimilar Aluminium Alloys Using Experimental Data and Genetic Programming. Model. Simul. Eng. 2018, 1–18. [Google Scholar] [CrossRef]
- Pathak, M.; Jaiswal, D. Applications of Artificial Neural Networks in Friction Stir Welding: A Review. Int. J. Technol. Explor. Learn. 2014, 3, 513–517. [Google Scholar]
- Verma, S.; Gupta, M.; Misra, J.P. Performance evaluation of friction stir welding using machine learning approaches. MethodsX 2018, 5, 1048–1058. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 026218253X. [Google Scholar]
- Schoelkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002; ISBN 9780262194754. [Google Scholar]
- Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression. Models, Methods and Applications; Springer: Dordrecht, The Netherlands, 2013; ISBN 978-3-642-34333-9. [Google Scholar]
- Üstün, B.; Melssen, W.J.; Buydens, L.M.C. Facilitating the application of Support Vector Regression by using a universal Pearson VII function based kernel. Chemom. Intell. Lab. Syst. 2006, 81, 29–40. [Google Scholar] [CrossRef]
- Zuo, L.; Zuo, D.; Zhu, Y.; Wang, H. Effect of process parameters on surface topography of friction stir welding. Int. J. Adv. Manuf. Technol. 2018, 98, 1807–1816. [Google Scholar] [CrossRef]
- Huang, W.; Kovacevic, R. A laser-based vision system for weld quality inspection. Sensors 2011, 11, 506–521. [Google Scholar] [CrossRef] [PubMed]
- Hartl, R.; Bachmann, A.; Liebl, S.; Zens, A.; Zaeh, M.F. Automated surface inspection of friction stir welds by means of structured light projection. In Proceedings of the 21st Chemnitz Seminar on Materials Engineering, Chemnitz, Germany, 6–7 March 2019; 2019; p. 12035. [Google Scholar] [CrossRef]
- Hartl, R.; Praehofer, B.; Zaeh, M.F. Prediction of the surface quality of friction stir welds by the analysis of process data using Artificial Neural Networks. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 732–751. [Google Scholar] [CrossRef]
- Hartl, R.; Vieltorf, F.; Zaeh, M.F. Correlations between the Surface Topography and Mechanical Properties of Friction Stir Welds. Metals 2020, 10, 890. [Google Scholar] [CrossRef]
- Duvenaud, D.; Nickisch, H.; Rasmussen, C.E. Additive Gaussian Processes. In Advances in Neural Information Processing Systems 24, Neural Information Processing Systems 2011 (NIPS 2011), Granada Congress and Exhibition Centre, Granada, Spain, 12–17 December 2011; Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.W., Eds.; Neural Information Processing Systems Foundation: La Jolla, CA, USA, 2011. [Google Scholar]
- Wilson, A.G.; Adams, R.P. Gaussian Process Kernels for Pattern Discovery and Extrapolation. In International Conference on Machine Learning (ICML), JMLR W&CP 28(3), Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June, 2013; Dasgupta, S., McAllester, D., Eds.; International Machine Learning Society: Princeton, NJ, USA, 2013; pp. 1067–1075. [Google Scholar]
- Hesse, W. Key to Aluminum Alloys, 12th ed.; fully revised; Beuth Verlag GmbH: Berlin, Germany; Wien, Austria; Zürich, Switzerland, 2016; ISBN 978-3-410-26873-4. [Google Scholar]
- Krutzlinger, M.; Bachmann, A.; Wirth, F.X.; Roth, A.; Sünger, S.; Pieczona, S.J.; Zaeh, M.F. Implementierung Einer Messsensorik in ein Fräsbearbeitungszentrum zur Ermittlung Der Prozesskräfte und des Prozessmoments Beim Rührreibschweißen (Translated Title: “Implementation of a measuring system in a milling machining center to determine the process forces and the process torque during friction stir welding”). In DVS Congress 2015, Proceedings of the Große Schweißtechnische Tagung, Nuremberg, Germany, 15–17 September 2015; DVS—German Welding Society, Ed.; DVS Media: Duesseldorf, Germany, 2015; pp. 209–214. ISBN 9783945023464. [Google Scholar]
- Costanzi, G.; Bachmann, A.; Zaeh, M.F. Entwicklung eines FSW-Spezialwerkzeugs zur Messung der Schweißtemperatur (Translated title: “Development of a FSW special tool for measuring the welding temperature”). In DVS Congress 2017, Proceedings of the DVS Congress, Duesseldorf, Germany, 26–29 September 2017; DVS—German Welding Society, Ed.; DVS Media GmbH: Duesseldorf, Germany, 2017; pp. 119–125. ISBN 9783961440085. [Google Scholar]
- Bachmann, A.; Krutzlinger, M.; Zaeh, M.F. Influence of the welding temperature and the welding speed on the mechanical properties of friction stir welds in EN AW-2219-T87. In Proceedings of the 20th Chemnitz Seminar on Materials Engineering, Chemnitz, Germany, 14–15 March 2018. [Google Scholar] [CrossRef]
- Richter, B. Robot-based Friction Stir Welding for E-mobility and General Applications. Biul. Inst. Spaw. W Gliwicach 2017, 5, 103–110. [Google Scholar] [CrossRef]
- German Institute for Standardization. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters; Beuth Verlag GmbH: Berlin, Germany, 2012; DIN EN ISO 25178-2. [Google Scholar]
- Brenner, P.; Kostron, H. Über die Vergütung der Aluminium-Magnesium-Silizium-Legierungen (Translated title: “On the tempering of aluminium-magnesium-silicon alloys”). Z. Metallkde. 1939, 31, 89–97. [Google Scholar]
- German Institute for Standardization. Testing of Metallic Materials—Tensile Test Pieces; Beuth Verlag GmbH: Berlin, Germany, 2016; DIN 50125. [Google Scholar]
- German Institute for Standardization. Destructive Tests on Welds in Metallic Materials—Transverse Tensile Test; Beuth Verlag GmbH: Berlin, Germany, 2013; DIN EN ISO 4136. [Google Scholar]
- German Institute for Standardization. Metallic Materials—Tensile Testing—Part. 1: Method of Test at Room Temperature; Beuth Verlag GmbH: Berlin, Germany, 2017; DIN EN ISO 6892-1. [Google Scholar]
- Vander Voort, G.F. Metallography and Microstructures, 9th ed.; ASM International: Almere, The Netherlands, 2004; ISBN 978-0871707062. [Google Scholar]
- Haerdle, W.; Klinke, S.; Roenz, B. Introduction to Statistics. Using Interactive MM*Stat. Elements; Springer: Cham, Switzerland, 2015; ISBN 9783319177045. [Google Scholar]
- Bachmann, A.; Gigl, T.; Hugenschmidt, C.P.; Zaeh, M.F. Characterization of the microstructure in friction stir welds of EN AW-2219 using coincident Doppler-broadening spectroscopy. Mater. Charact. 2019, 149, 143–152. [Google Scholar] [CrossRef]
- Whitley, E.; Ball, J. Statistics review 2: Samples and populations. Crit. Care 2002, 6, 143–148. [Google Scholar] [CrossRef] [PubMed]
- SheffieldML. Available online: https://github.com/SheffieldML/GPy/blob/40137cc8f7e0794bff55639ec55d4884c72e86b5/GPy/kern/src/coregionalize.py (accessed on 24 March 2020).
- Duvenaud, D. Automatic Model Construction with Gaussian Processes. Doctoral Thesis, University of Cambridge, Cambridge, UK, 2014. [Google Scholar] [CrossRef]
| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Others |
|---|---|---|---|---|---|---|---|---|
| 0.90 | 0.42 | 0.10 | 0.44 | 0.70 | 0.03 | 0.13 | 0.03 | max. 0.05 |
| Geometry Feature | Value |
|---|---|
| Probe radius rP | 3 mm |
| Shoulder radius rS | 7 mm |
| Conical probe angle β | 10° |
| Probe length hP | 3.75 mm |
| Probe tip radius rT | 10 mm |
| Concave shoulder angle γ | 10° |
| Surface Feature | Key Indicator 1 | Key Indicator 2 |
|---|---|---|
| Flash formation | Mean flash height fm | Standard deviation of the flash height Sf |
| Seam underfill | Mean seam underfill um | Standard deviation of the seam underfill Su |
| Weld seam width | Standard deviation of the weld seam width Sw | - |
| Arc texture formation | Ratio between the counted and the theoretical number of local valleys and peaks along the weld centerline rarc | Standard deviation of the differences between the local valleys and the subsequent local peaks along the weld centerline Sd |
| Surface galling | Peak material volume Vmp | - |
| Welding Speed vs | 500 mm/min | 1000 mm/min | 1500 mm/min | All Data |
|---|---|---|---|---|
| PCC mean | 0.87 | 0.79 | 0.80 | 0.76 |
| PCC standard deviation | 0.15 | 0.23 | 0.05 | 0.17 |
| Best covariance function | Add | SM | Mat 5/2 | SM |
| Computation time in s | 152 | 1130 | 1017 | 6953 |
| Welding Speed vs | 500 mm/min | 1000 mm/min | 1500 mm/min | All Data |
|---|---|---|---|---|
| PCC mean | 0.94 | 0.93 | 0.83 | 0.96 |
| PCC standard deviation | 0.05 | 0.03 | 0.11 | 0.01 |
| Best covariance function | Mat 5/2 | Add | Add | SM |
| Computation time in s | 28 | 203 | 179 | 4879 |
| Welding Speed vs | 500 mm/min | 1000 mm/min | 1500 mm/min | All Data |
|---|---|---|---|---|
| PCC mean | 0.99 | 0.91 | 0.93 | 0.99 |
| PCC standard deviation | 0.02 | 0.08 | 0.06 | 0.01 |
| Best covariance function | Mat 5/2 | RQ | Mat 5/2 | SM |
| Computation time in s | 27 | 32 | 30 | 6374 |
| Welding Speed vs | 500 mm/min | 1000 mm/min | 1500 mm/min | All Data |
|---|---|---|---|---|
| PCC mean | 1.00 | 0.88 | 0.94 | 0.99 |
| PCC standard deviation | 0.00 | 0.12 | 0.05 | 0.01 |
| Best covariance function | RBF | SM | RQ | SM |
| Computation time in s | 625 | 807 | 23 | 5761 |
| Input Variable | Surface Topography | Process Variables | Process Parameters |
|---|---|---|---|
| PCC mean | 0.76 | 0.99 | 0.99 |
| PCC standard deviation | 0.17 | 0.01 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartl, R.; Vieltorf, F.; Benker, M.; Zaeh, M.F. Predicting the Ultimate Tensile Strength of Friction Stir Welds Using Gaussian Process Regression. J. Manuf. Mater. Process. 2020, 4, 75. https://doi.org/10.3390/jmmp4030075
Hartl R, Vieltorf F, Benker M, Zaeh MF. Predicting the Ultimate Tensile Strength of Friction Stir Welds Using Gaussian Process Regression. Journal of Manufacturing and Materials Processing. 2020; 4(3):75. https://doi.org/10.3390/jmmp4030075
Chicago/Turabian StyleHartl, Roman, Fabian Vieltorf, Maximilian Benker, and Michael F. Zaeh. 2020. "Predicting the Ultimate Tensile Strength of Friction Stir Welds Using Gaussian Process Regression" Journal of Manufacturing and Materials Processing 4, no. 3: 75. https://doi.org/10.3390/jmmp4030075
APA StyleHartl, R., Vieltorf, F., Benker, M., & Zaeh, M. F. (2020). Predicting the Ultimate Tensile Strength of Friction Stir Welds Using Gaussian Process Regression. Journal of Manufacturing and Materials Processing, 4(3), 75. https://doi.org/10.3390/jmmp4030075





