1. Introduction
Machining operations are used to produce shapes or surface characteristics for a product. Some common conventional machining operations are turning, boring, drilling, reaming, milling, and tapping. Conditions for machining operations were chosen based on geometry and surface finish requirements rather than profit when costs were comparatively low on labor, resource, machines, and tools. However, nowadays, many researchers proposed optimizing machining parameters to maximize profit when using expensive modern machine tools.
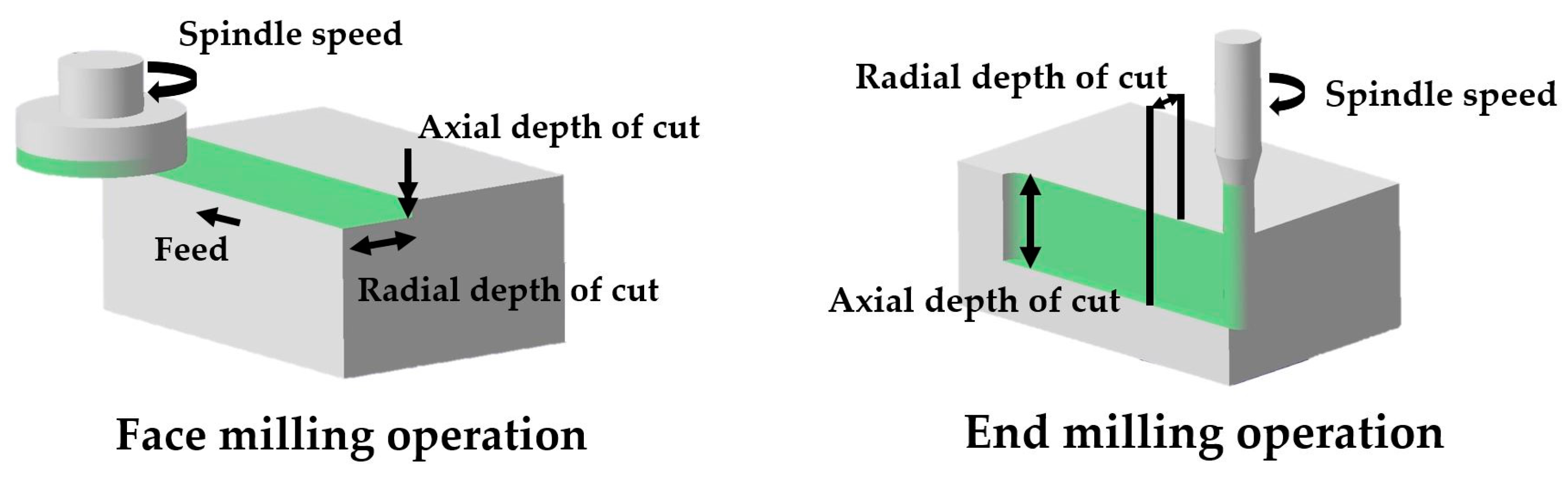
Milling processes have rotating cutters to make specific shapes or surface characteristics by eliminating material from the workpiece. There are two basic milling operations, as shown in
Figure 1, namely peripheral (end) milling and face milling. Peripheral milling is usually used for profiling or slotting works, and face milling is required for making flat surfaces of a workpiece [
1]. Milling processes were used to test an optimization method in this study.
There are many ways to optimize the machining process, such as minimizing production unit time, minimizing production cost, or maximizing profit.
Karandikar and Kurfess [
2] used machining costs to optimize milling operations based on tool life. They described an approach for experimental design for tool life testing and machining cost optimization using surrogate modeling and the value of information method. They found that the proposed approach can be utilized in an industrial setting without explicitly modeling tool life, and it is better in predicting tool life than the traditional statistical design of experiments such as factorial designs and central composite design.
Li et al. [
3] examined energy saving for multi-objective machining with consideration of the energy consumption by optimizing machining parameters for the cutting process. They defined a relationship between cutting parameters and energy consumption in the machining process. They analyzed the energy consumption and production rate with sets of optimized and unoptimized cutting parameters for different objectives. They found that the objectives of low consumed energy and high production rate can be obtained simultaneously by optimizing cutting parameters.
Chen et al. [
4] were able to optimize machining parameters with a reduction in energy consumption and production time for the face milling process. They presented an integrated approach for minimizing the energy footprint and production time by optimizing cutting tools and cutting parameters. Three energy footprint-aware optimization models were used to demonstrate the necessity of the integrated approach. In model 1, the cutting tool-related parameters were preset according to the machining handbook. In model 2, the cutting tool-related parameters were optimized through the Cuckoo algorithm with feasible cutting parameters. In model 3, the integrated optimization of the cutting tool and parameters was used. When the energy footprint of each model was compared, the integrated approach achieved the most energy-efficient footprint. Therefore, they found that it is necessary to optimize the cutting tool and cutting parameters in an integrated manner.
Faisal and Kumar [
5] researched the optimization of machining process parameters in Electric Discharge Machining (EDM) by using the Particle Swarm Optimization (PSO) and Biogeography-Based Optimization (BBO) techniques. The PSO technique took initialization with a population of random solutions and then updating the generations to achieve an optimal solution. The BBO technique optimizes a function stochastically and iteratively. They found that the BBO method improved the material removal rate and reduced surface roughness.
Abbas et al. [
6] researched surface roughness optimization of AZ61 magnesium alloy finish turning by using a novel Edgeworth–Pareto optimization of an Artificial Neural Network (ANN). Cutting parameters were optimized for minimum surface roughness. When they compared the theoretical and experimental results, the reliability of ±1.35% was achieved.
An approach for maximizing the profit of CNC milling operations was proposed by Tolouei and Bidhendi [
7] without exceeding constraints, such as maximum machine power and maximum cutting forces, for each milling operation. Tolouei and Bidhendi [
7] suggested using empirical and mechanistic functions to estimate the profit of CNC milling operations.
The profit for CNC milling operations generally consists of production cost, production time, and the sale price of a product. The production cost per part is made up of several components, including raw material cost, overhead cost, tool changing cost, machining cost, and setup cost. Setup, material, and overhead costs are not dependent on the selection of machining parameters. Machining cost tends to decrease with increasing cutting speed, while tool changing cost tends to increase with higher cutting speeds. Even though low cutting speeds and feed tend to increase tool life, they will produce a rough surface finish [
8].
Production time per part is made up of several components, including machining time, tool changing time, and setup time. Contrary to the production cost, machining time decreases with increasing cutting speeds and feed, but this results in increasing tool wear. However, gains in the material removal rate with increased cutting speeds, feed, and depth of cut are accompanied by decreasing tool life [
9]. Kant and Sangwan [
10] investigated the effect of cutting speeds and feed. They observed that cutting forces and vibrations decrease with high cutting speeds, but high feed causes vibration and heat generation. Therefore, determining the proper cutting speed and feed was the most crucial issue in this paper.
As shown in
Figure 1, feed is the distance machined by a tool at each revolution of a tool during the machining operation. The depth of cut is defined as the thickness of metal removed from a workpiece through the radial or axial direction [
11]. The rotational speed of the spindle determines the cutting speed, which can be expressed as the tangential speed of a cutting tool, regardless of machining operation. Since the optimum depth of cut is dependent on the interaction between the cutting tool, the geometry of the product, and workpiece material, it is usually a fixed value and not a candidate for optimization. Therefore, the cutting speed and feed were considered machining parameters in this study [
1].
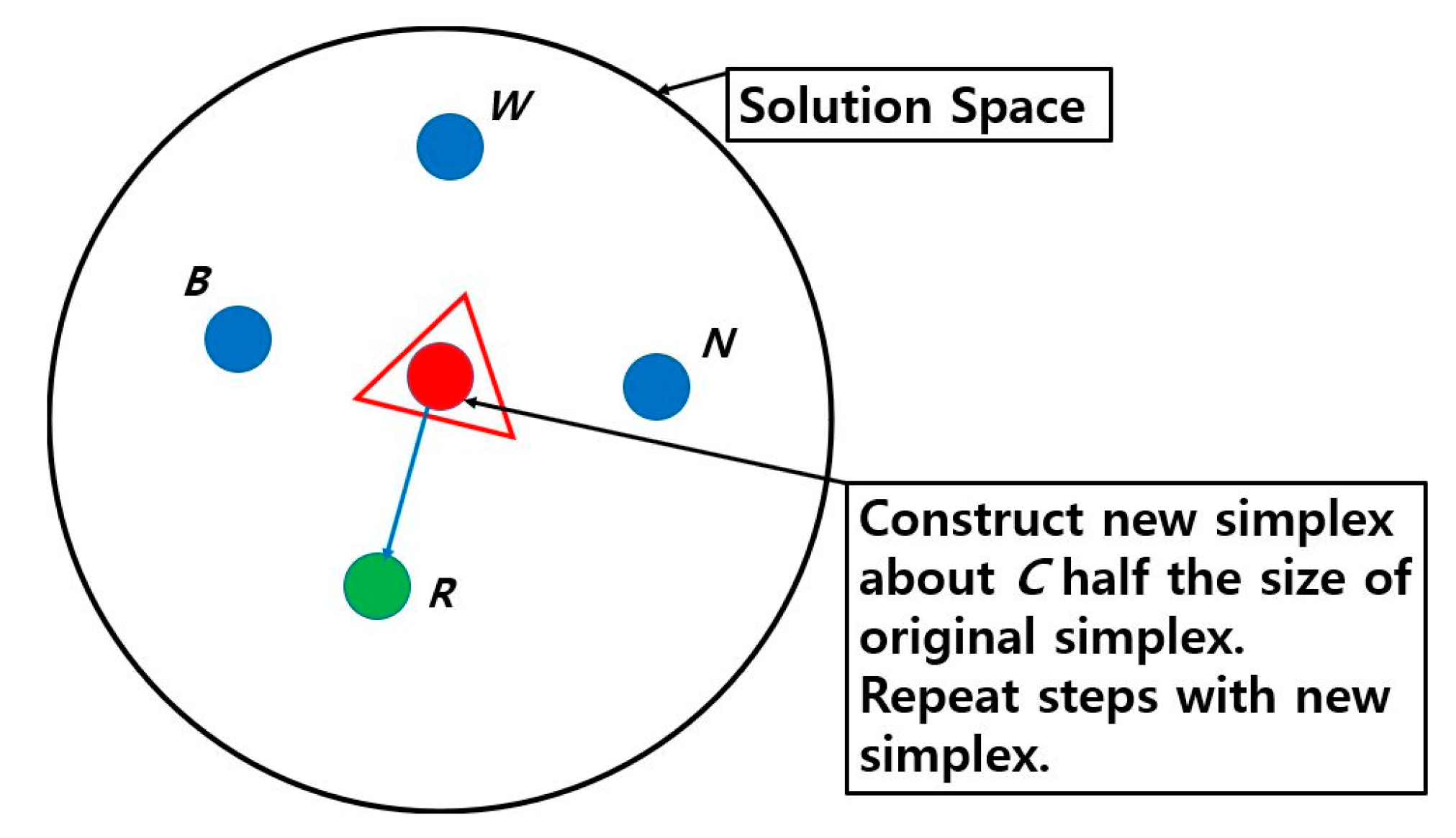
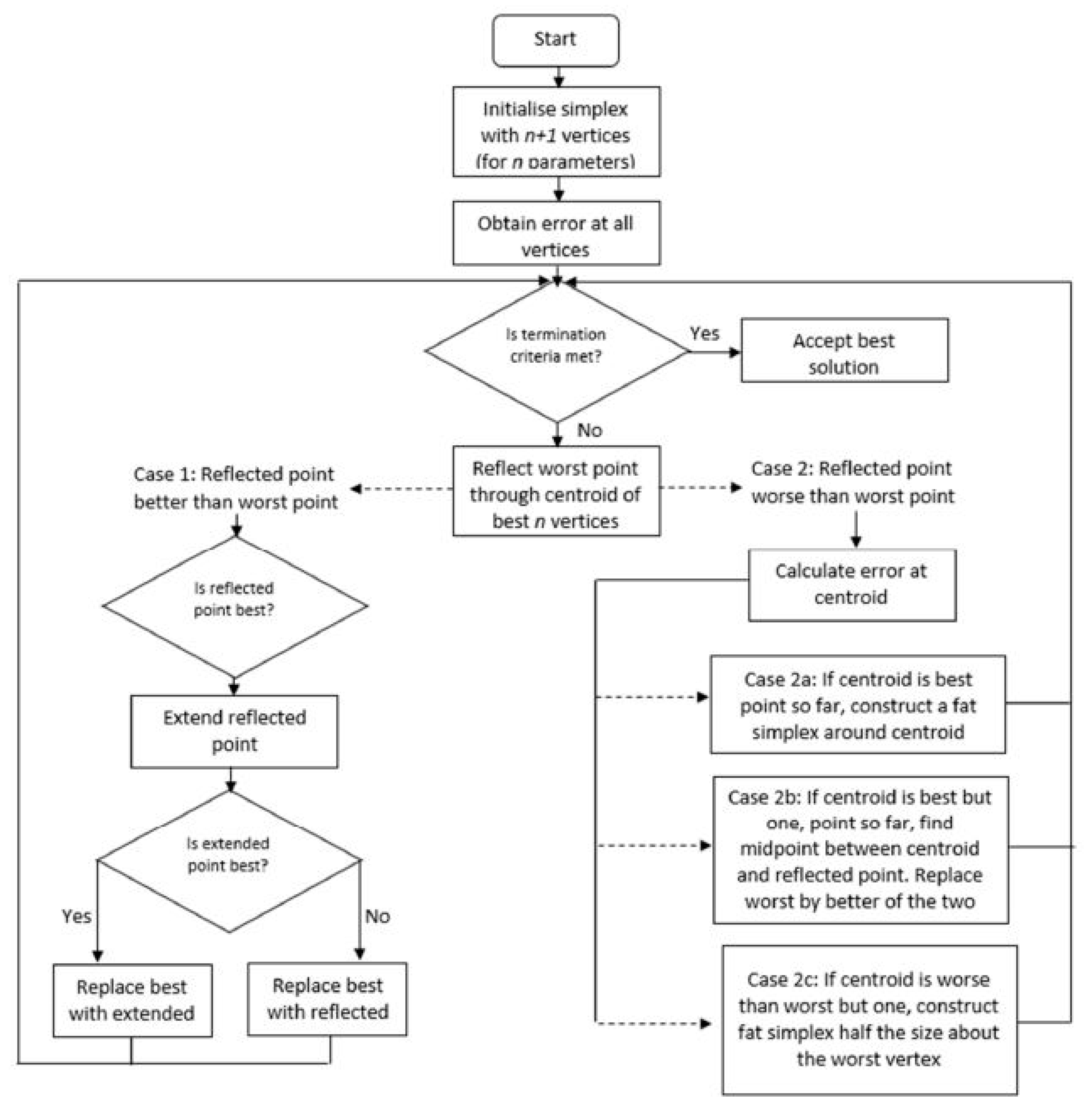
The optimization of CNC machining processes using machine learning and numerical algorithms is a key way to eliminate unnecessary testing, and it will result in saving time, material wastage, and effort. We expect that the Nelder–Mead Simplex method, when applied to optimize machining parameters of the CNC milling operation, will yield a higher profit accurately and rapidly.
3. Results
To illustrate how profit, unit cost, and unit time are affected by the cutting speed, we verified the model using a feed of 0.3 (mm/tooth). The objective function was considered for face milling, corner milling, pocket, and two slot millings suggested by the case study. Specific constant values suggested by the case study, such as travel length, cutting tool type, and labor cost, were utilized.
Figure 5 shows the relationship between unit cost, profit, and unit time as a function of the cutting speed for all five milling operations assuming a constant feed was used. It was observed that the maximum profit and corresponding minimum unit cost was obtained at a cutting speed of approximately 26 m/min, whereas unit production time seems to plateau at approximately 9 min, corresponding to a cutting speed of 15 m/min.
Optimum Parameters by the Nelder–Mead Simplex Method
To determine the efficiency of the Nelder–Mead method in solving the range of possible cutting speeds and feed, we examined each operation of the case study separately. As shown in
Figure 6, optimum machining parameters of the step milling listed in
Table 5 were found at iteration 52, when the initial cutting speed and feed listed in
Table 5 were used.
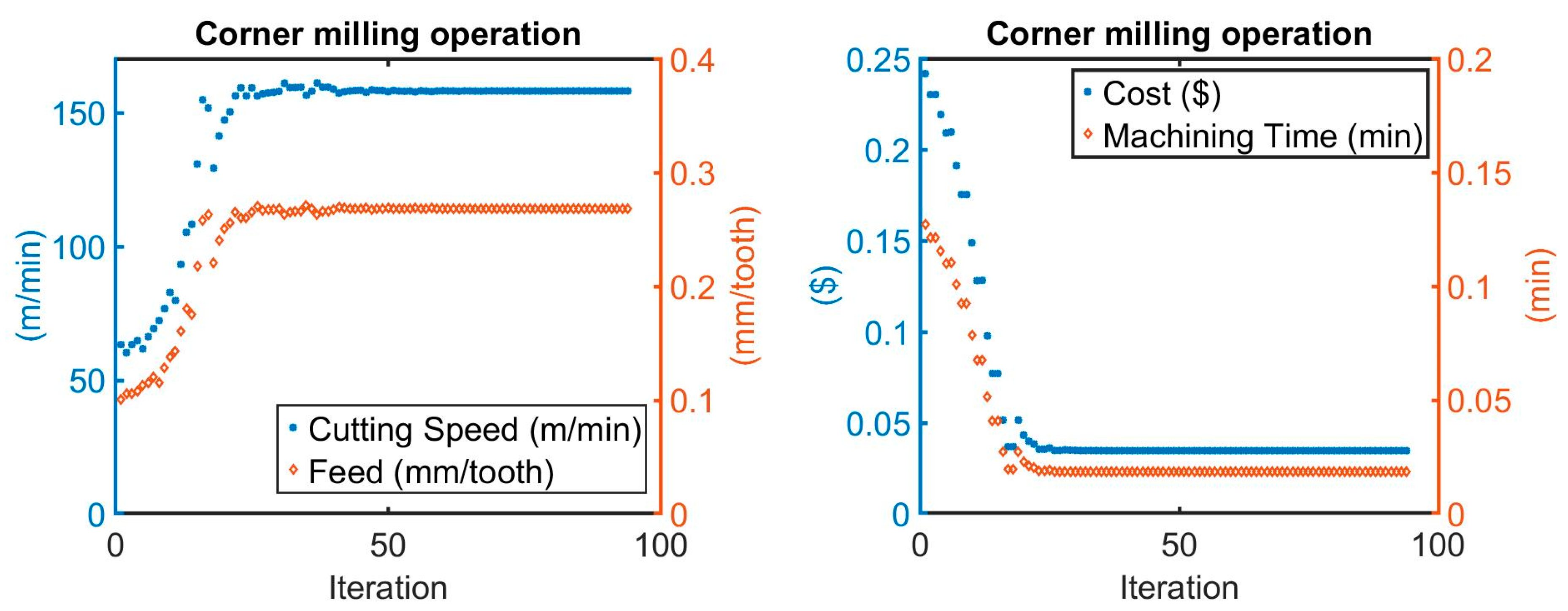
As shown in
Figure 7, optimum machining parameters of the corner milling listed in
Table 6 were found at iteration 54, when the initial cutting speed and feed listed in
Table 6 were used.
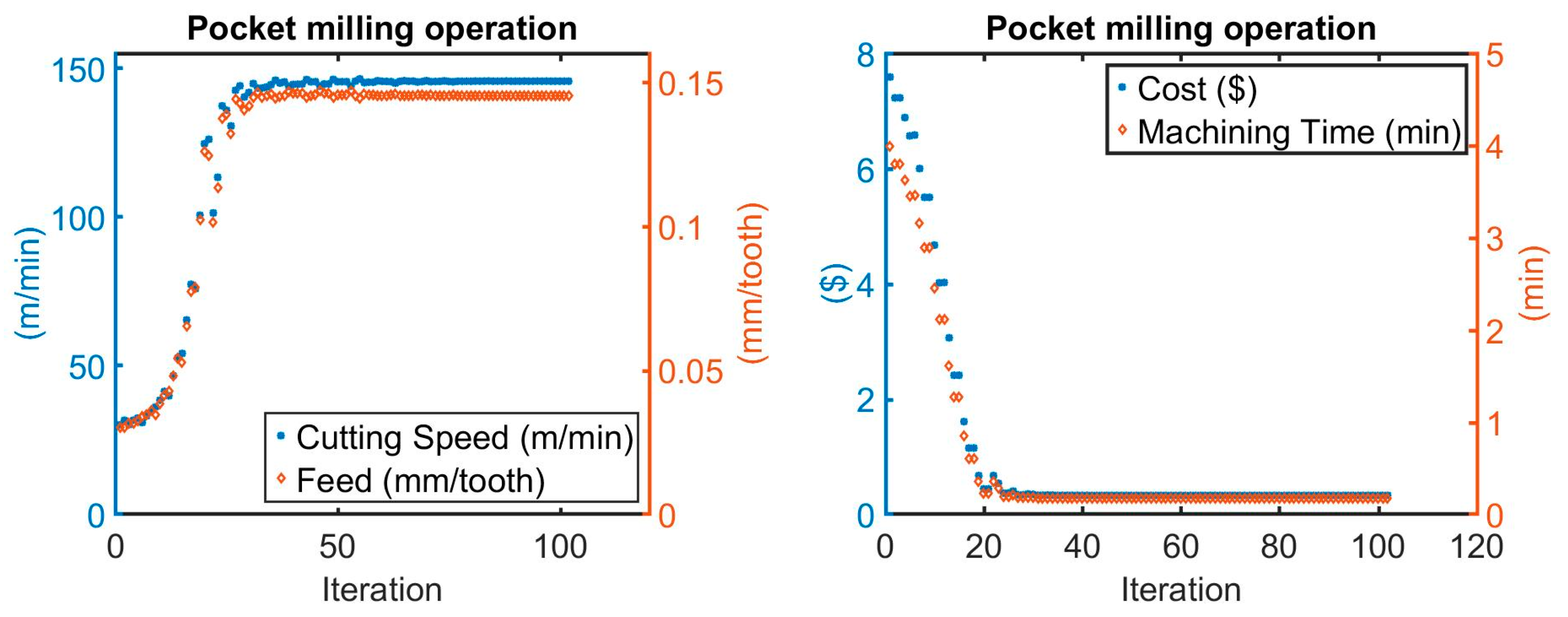
Figure 8 shows the optimum machining parameters of the pocket milling parameters using the initial condition as listed in
Table 7.
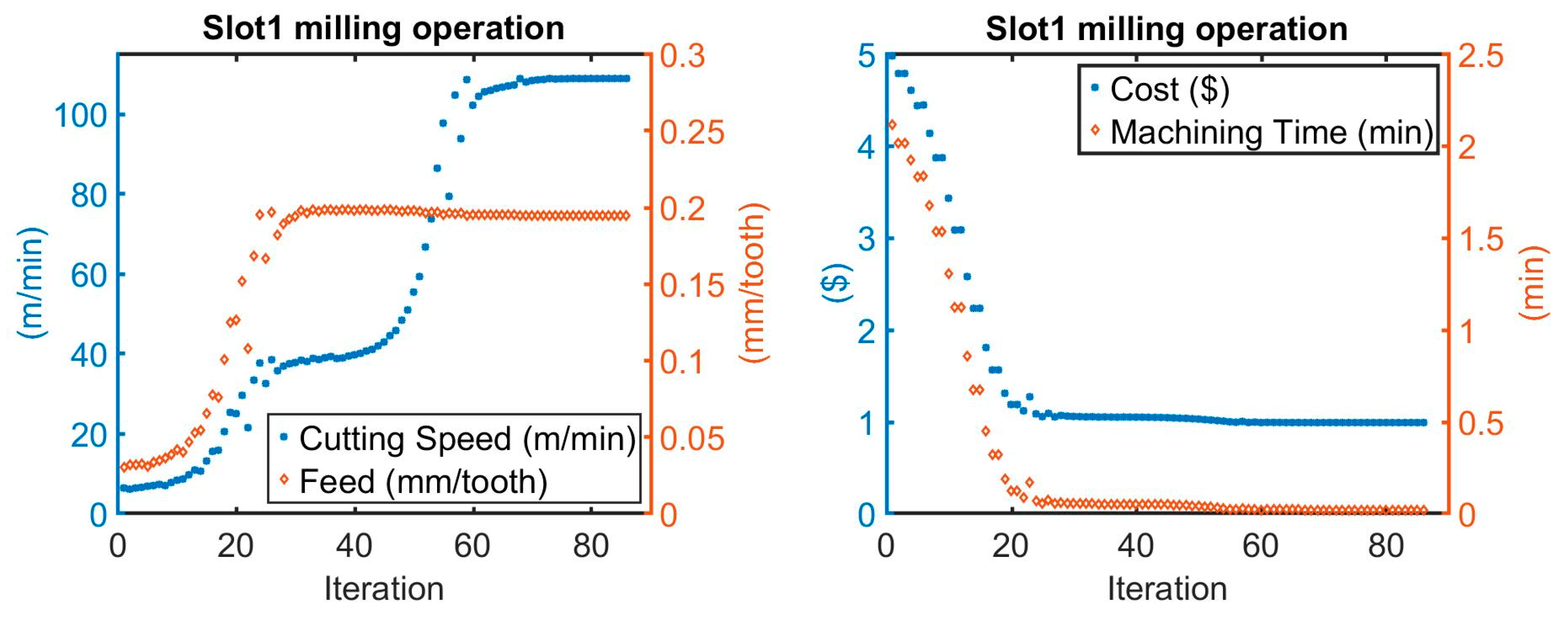
Figure 9 and
Figure 10 show the optimum machining parameters of the slot1 milling and slot2 milling, whereas
Table 8 and
Table 9 list the optimized parameters with the initial cutting speed and feed. In general, we observed that the convergence of a solution is possible with less than sixty iterations.
4. Discussion
Table 10 summarizes the optimized machining cost and time for the operations used to produce the model part. Using the results in
Table 10, we determined the final unit production time, unit cost, and profit as shown in
Table 11.
Constraint values of the maximum machine power are listed in
Table 2. Power consumption for all machining operations should not exceed 8.5 kW to meet maximum machine power proposed by Tolouei and Bidhendi [
7]. Constraint values of surface finish requirements are listed in
Table 3, and surface finish requirements for all machining operations should be satisfied. Lastly, the cutting forces should not exceed the permitted cutting forces listed in
Table 3. Optimized power consumption, surface finish, and cutting forces using Nelder–Mead methods are listed in
Table 12. It should be noted that the optimum process parameters met specific constraint values by Tolouei and Bidhendi [
7].
In this paper, the Nelder–Mead simplex method was used to find the maximum profit of milling operations by identifying optimum process parameters without violating any constraints. We compared the profit derived in this study with previous studies, as shown in
Table 13, and we found that the Nelder–Mead Method was able to produce a higher profit.
Even though the profit found by Abhishek [
13], using the Genetic Algorithm, is higher than the Nelder–Mead simplex method, it should be noted that Abhishek arrived at an optimum feed of 0.264 (mm/tooth) for face milling. However, the surface finish requirement of 2 (μm) would limit the feed to be less than 0.079 (mm/tooth). Therefore, we arrived at a better solution while meeting the constraints and objective function suggested by Tolouei and Bidhendi. Finally, the Nelder–Mead simplex method not only improves production profit, but it will also increase productivity by eliminating unnecessary testing.