Characterization of Thermomechanical Boundary Conditions of a Martensitic Steel for a FAST Forming Process
Abstract
1. Introduction
2. Experimental Procedures
2.1. Heat Transfer Test
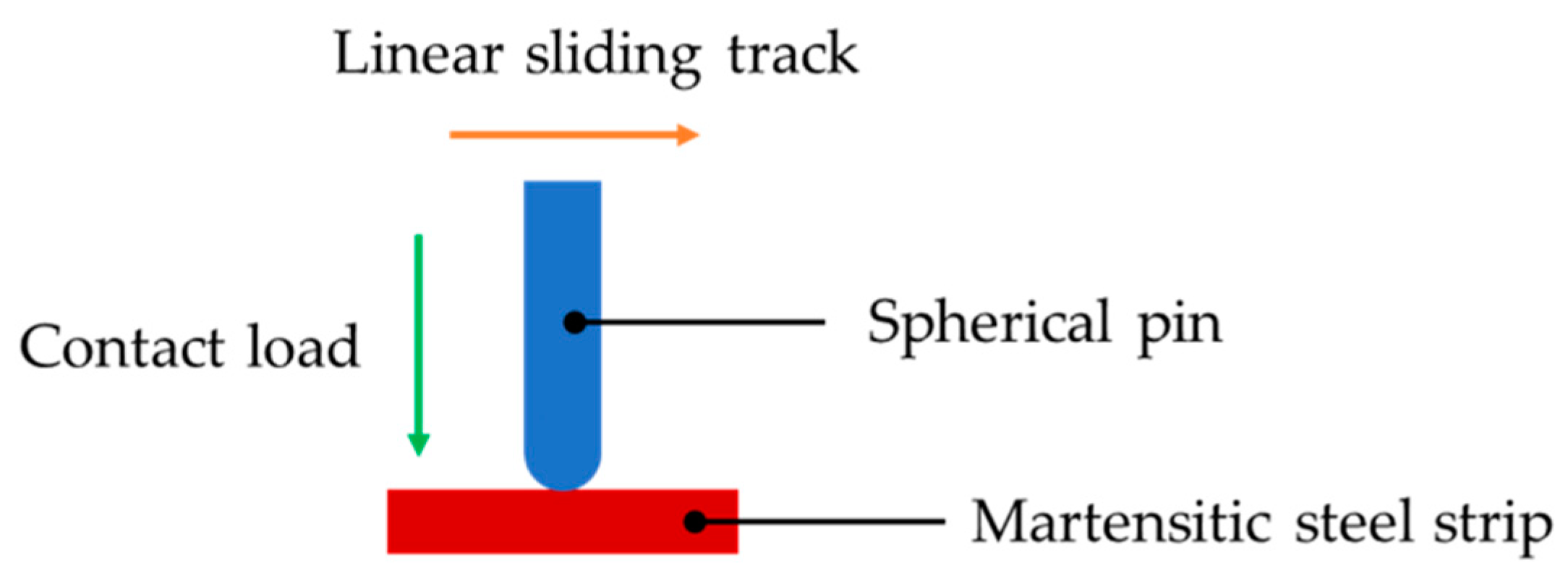
2.2. Friction Test
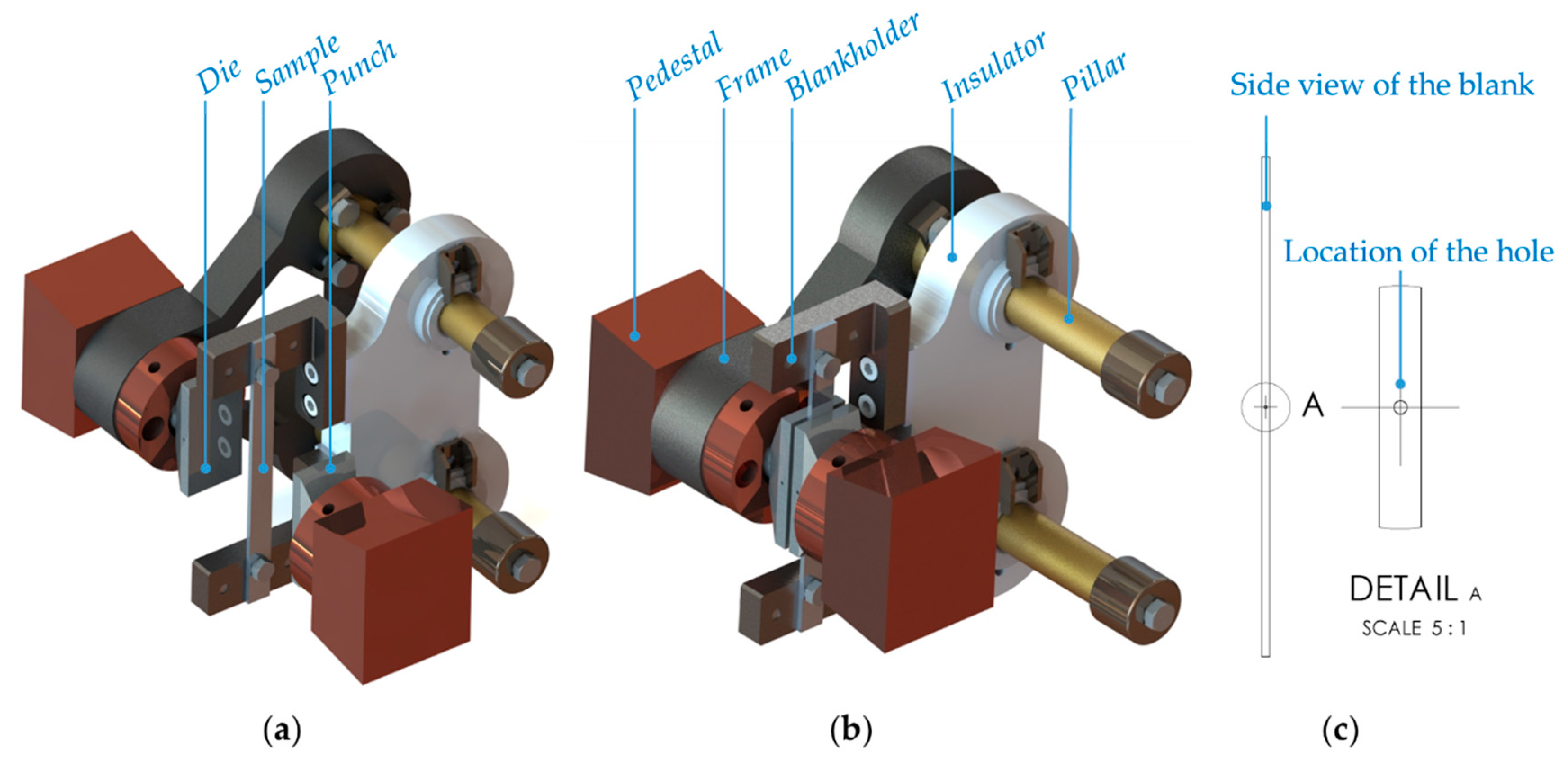
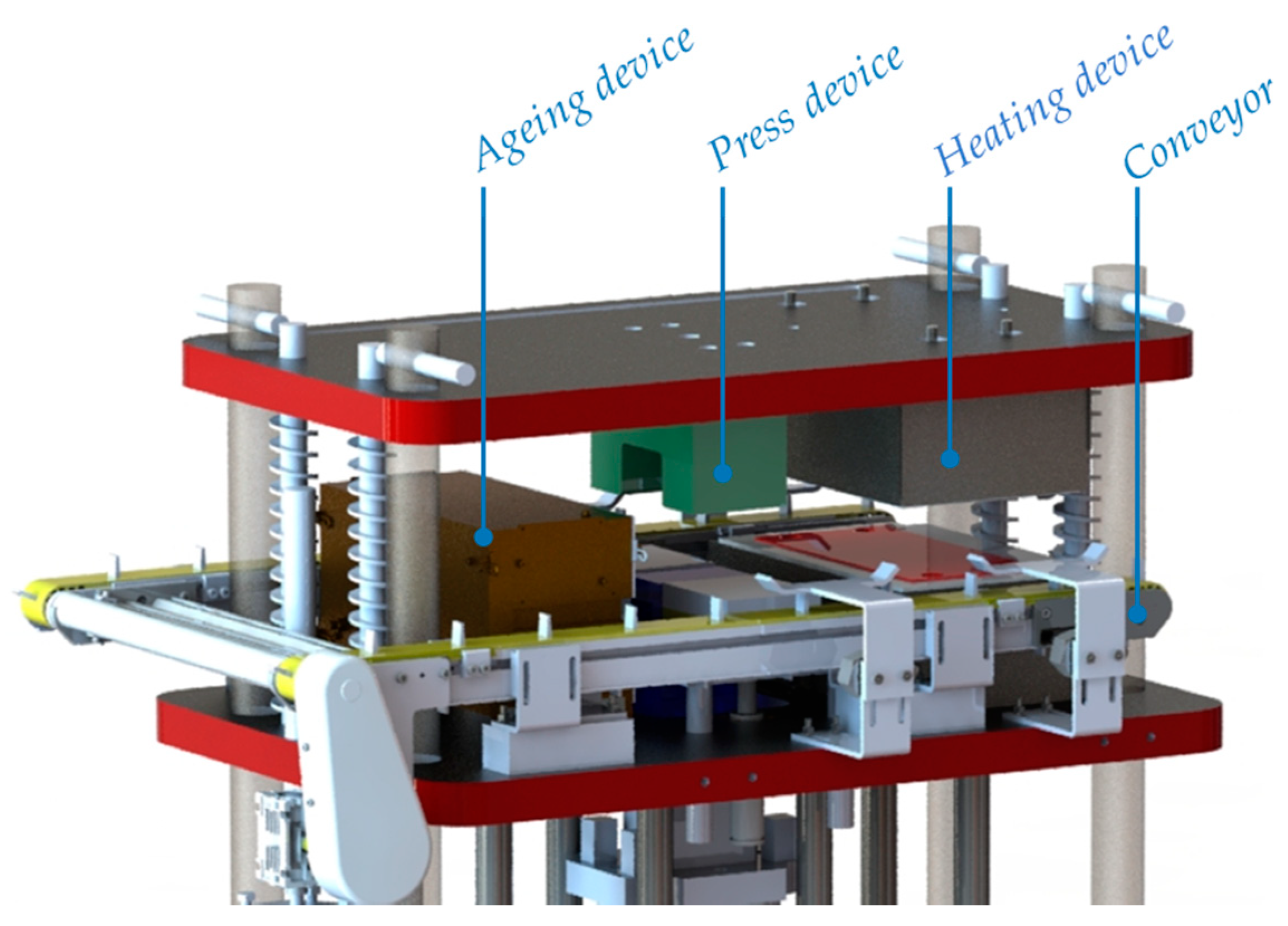
2.3. Forming Test
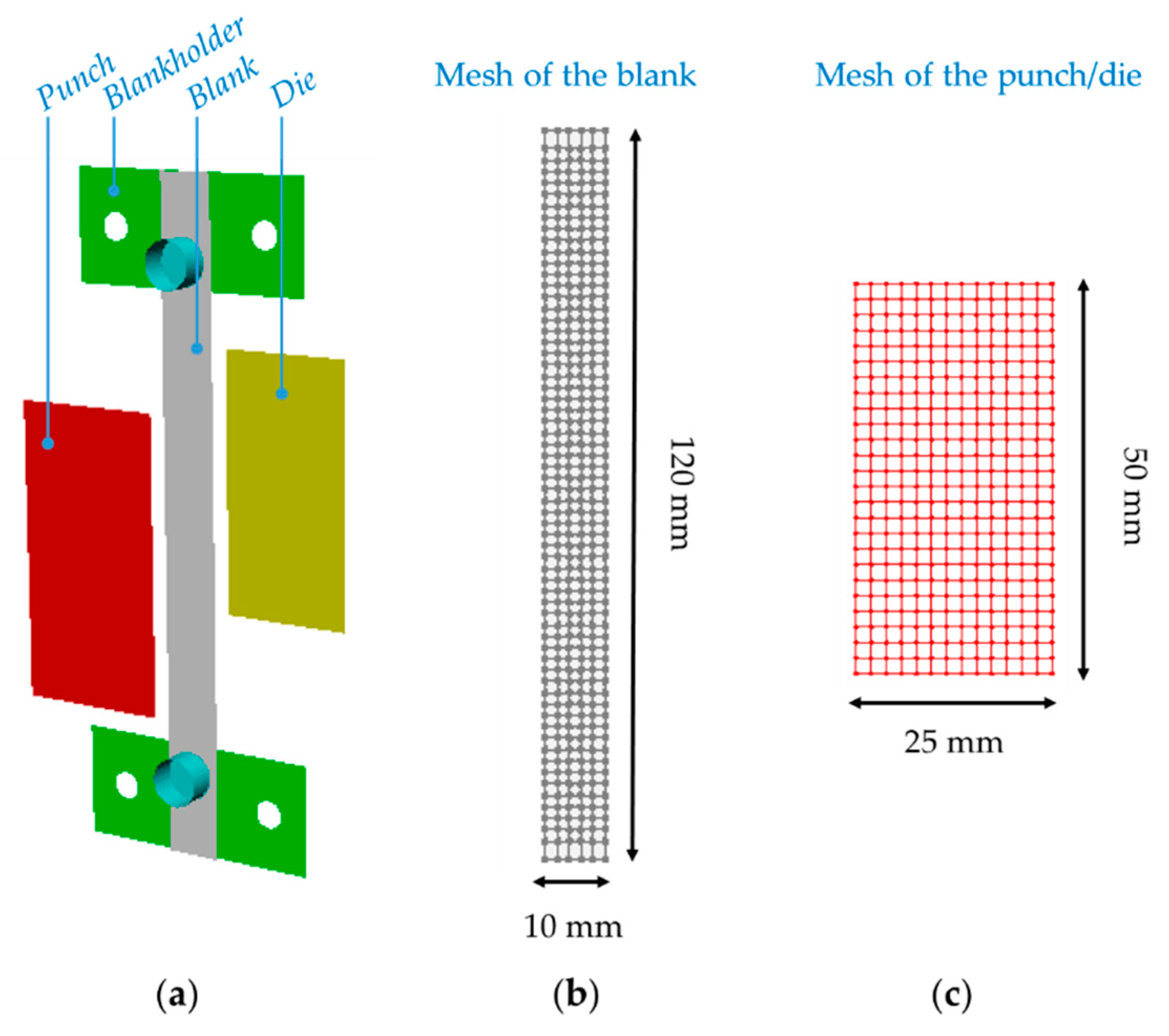
3. FE Simulation
3.1. Characterization of the IHTC by Using an Inverse Technique
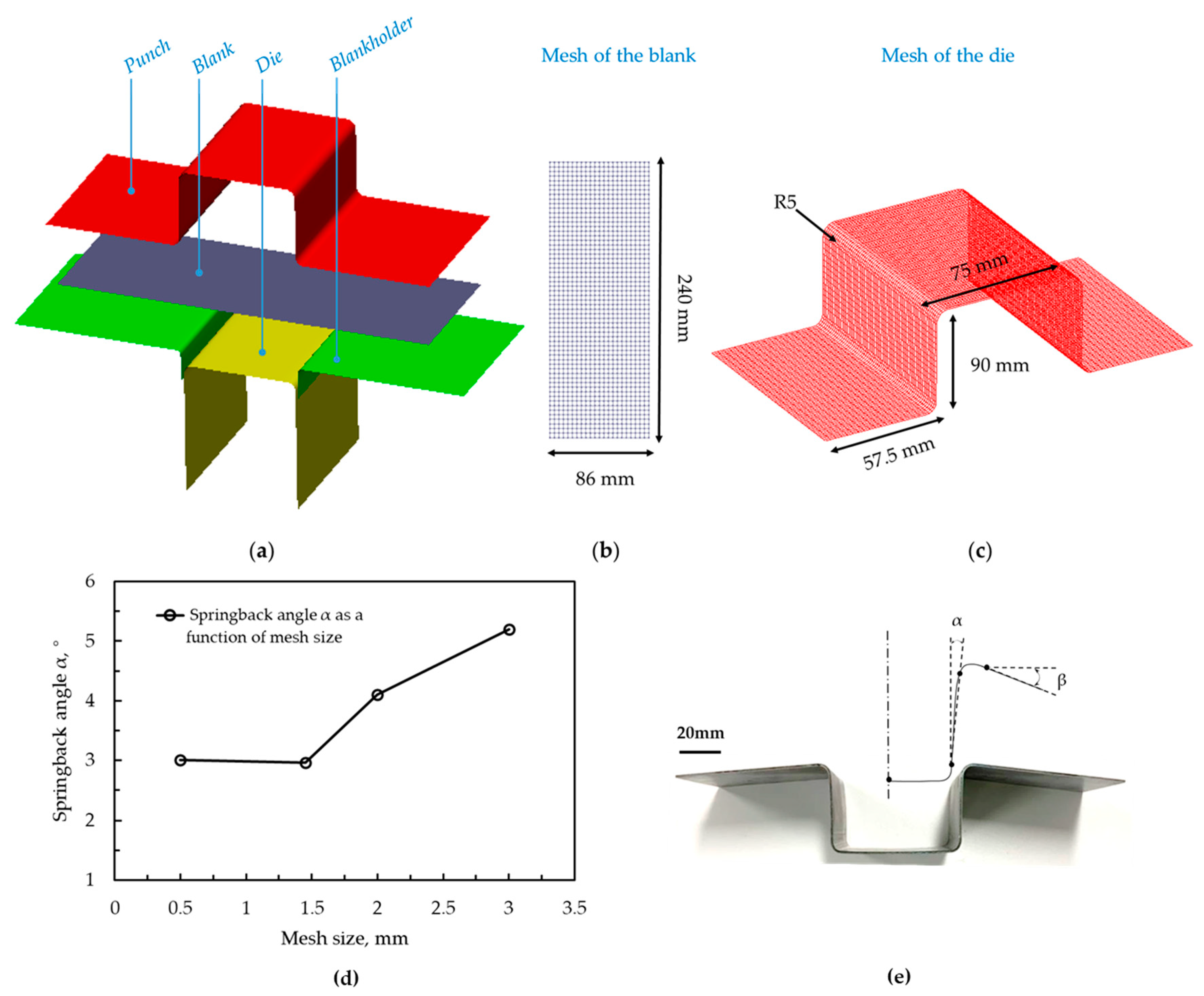
3.2. FE Simulation of a FAST Forming Process
4. Mechanism-Based Models for the Thermomechanical Boundary Conditions
4.1. IHTC Model between Martensitic Steel and P20 Steel
4.2. Friction Coefficient Model between Martensitic Steel and P20 Steel
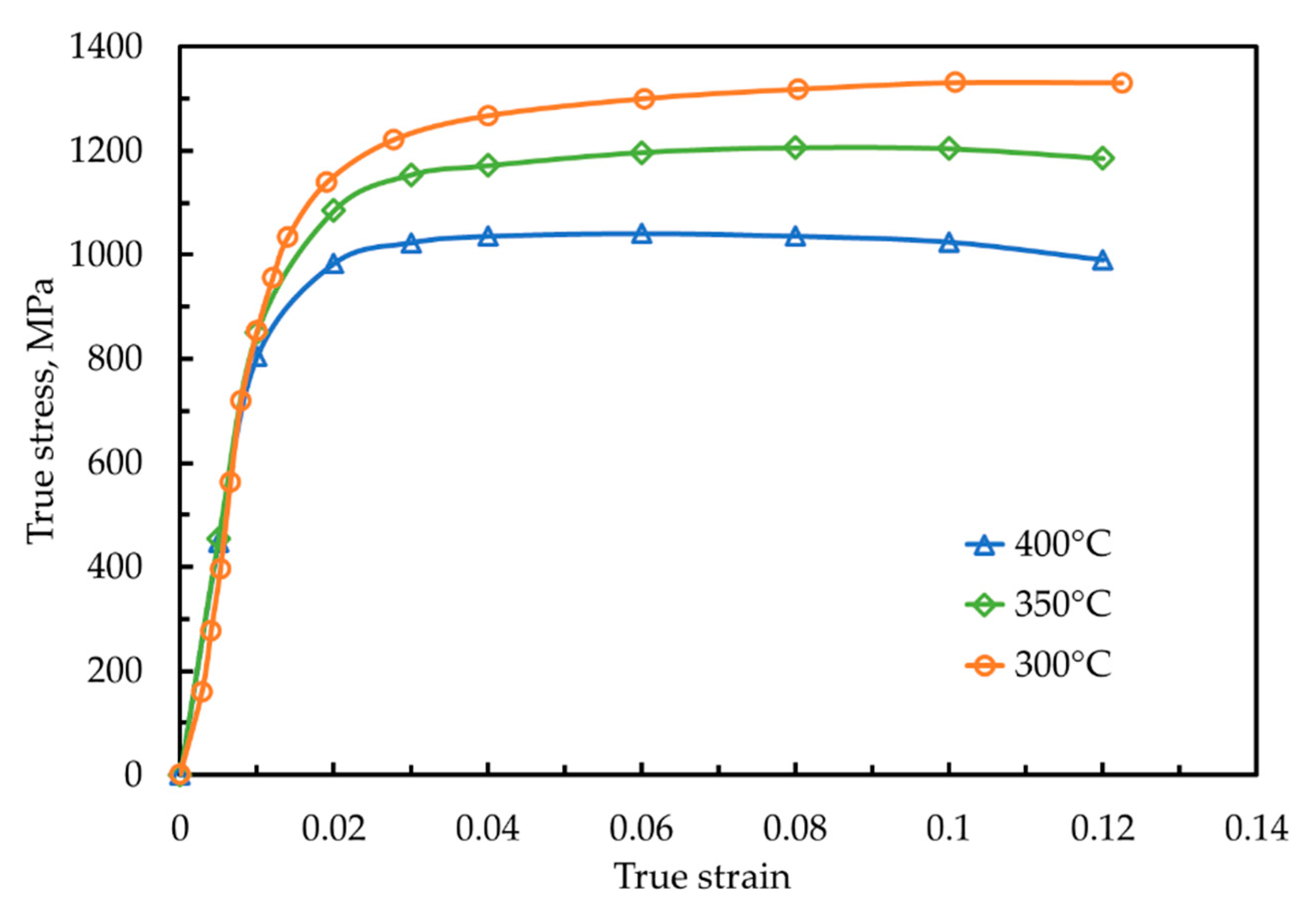
5. Results and Discussion
5.1. Thermomechanical Boundary Conditions of Martensitic Steel
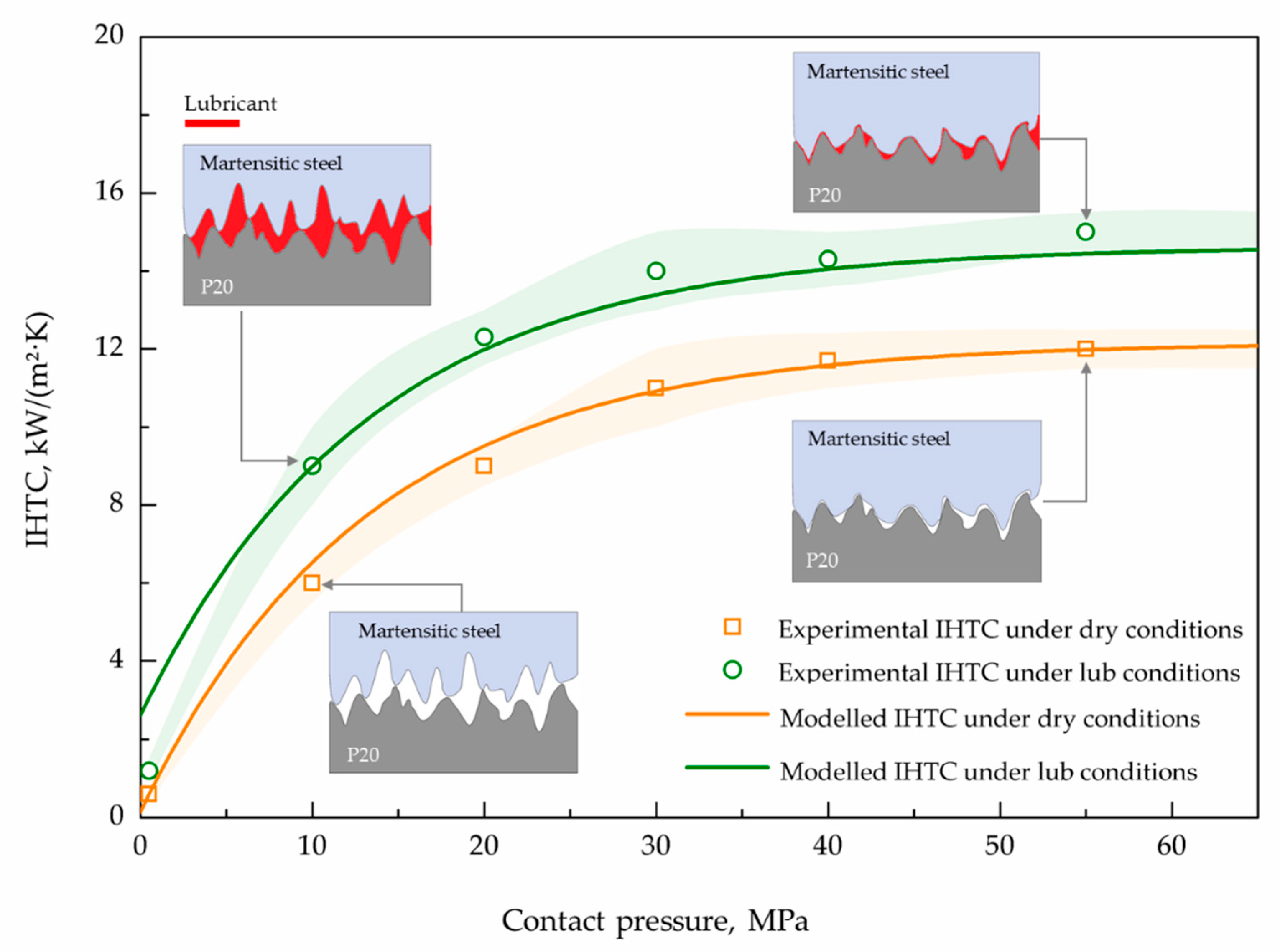
5.1.1. IHTC between Martensitic Steel and P20 Steel
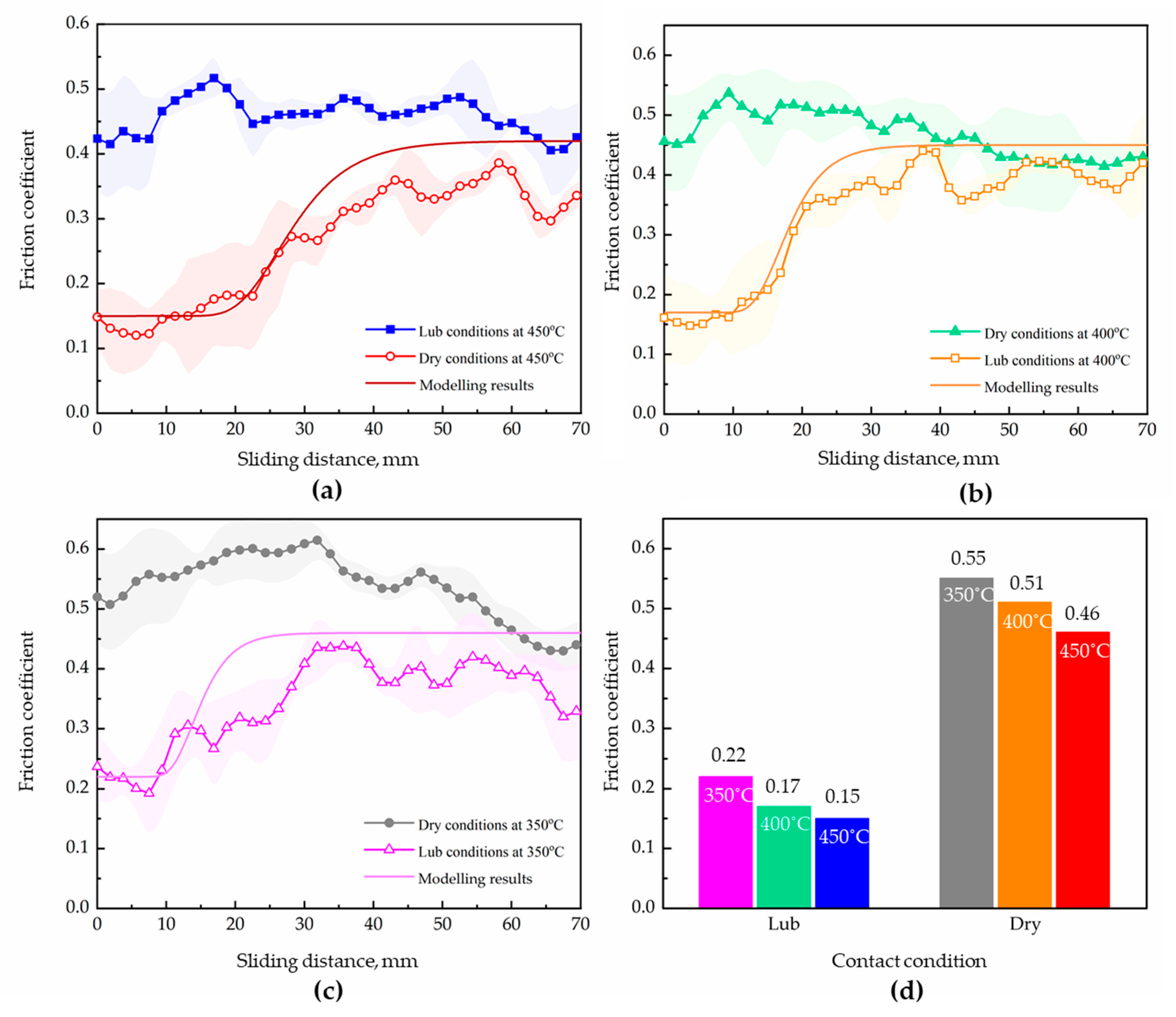
5.1.2. Friction Coefficient between Martensitic Steel and P20 Steel
5.2. Experimental Validation
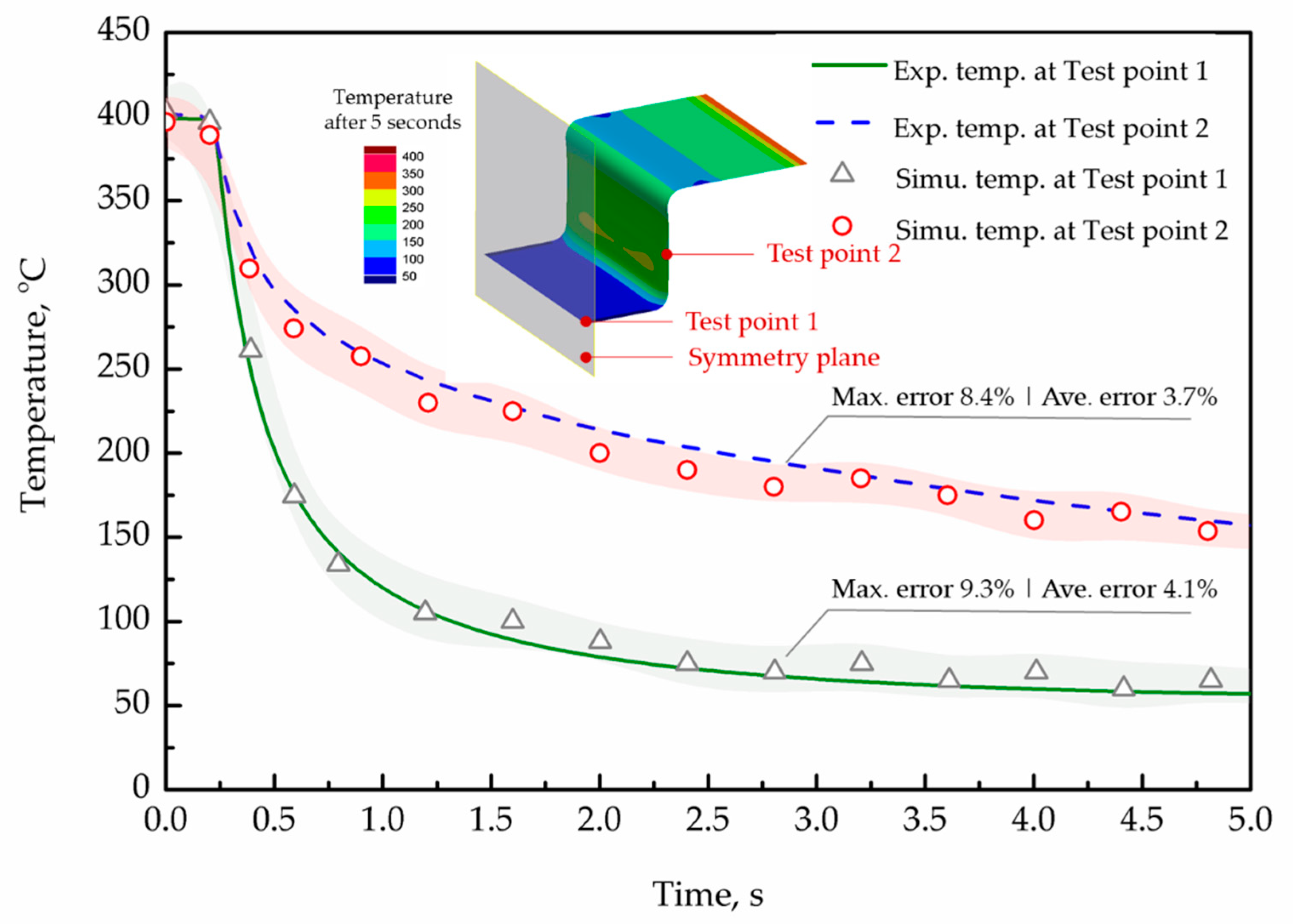
5.2.1. Temperature Evolution
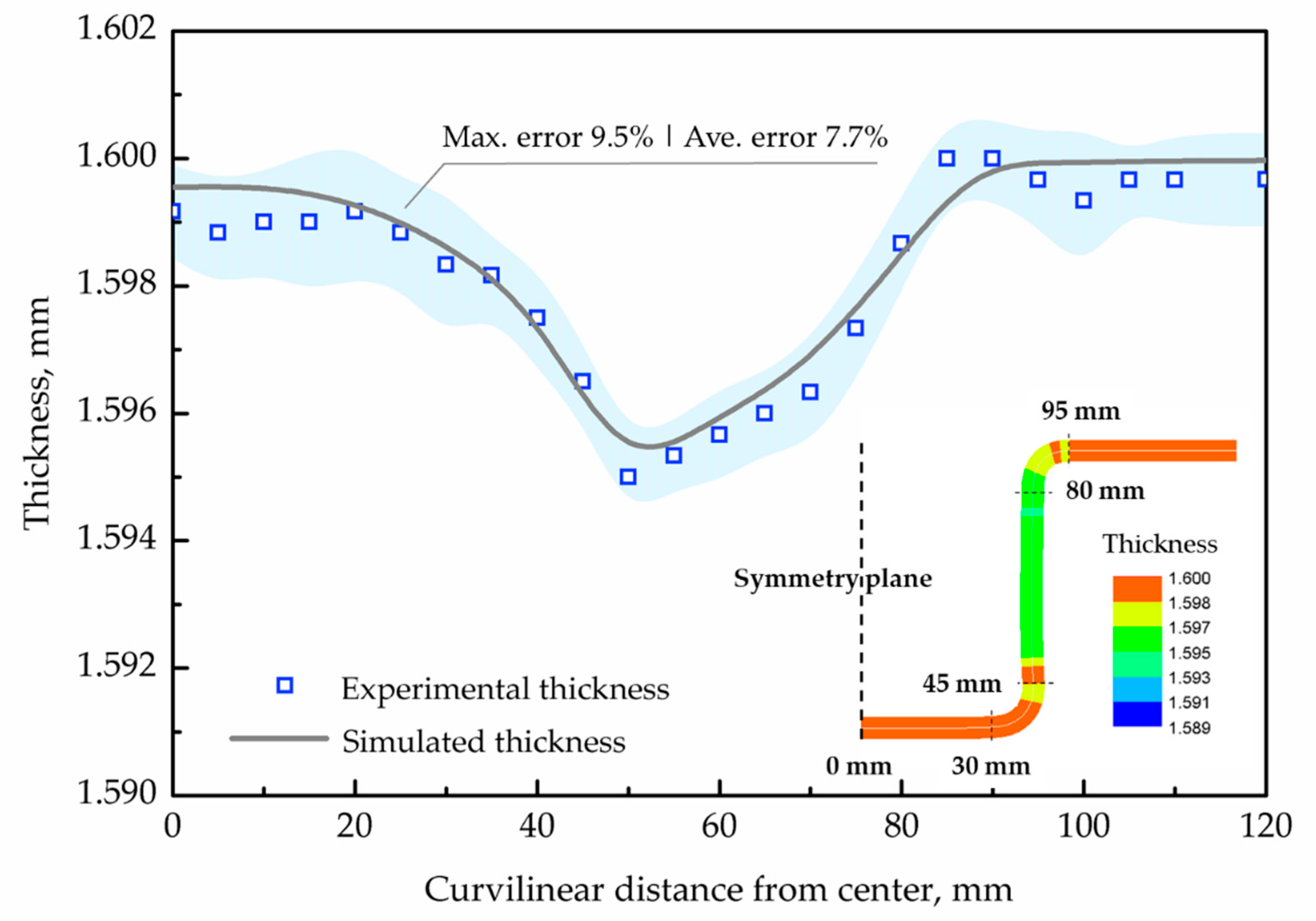
5.2.2. Thickness Distribution
5.2.3. Springback
6. Conclusions
- The IHTC for the martensitic steel rapidly increased at the initial stage and reached a stable value after 40 MPa, for either the dry or lubricated-contact conditions. The application of the graphite lubricant could increase the IHTC by 43% on average.
- The friction coefficient for the martensitic steel was identified at elevated temperatures, from 350 °C to 450 °C, for both dry- and lubricated-contact conditions, showing that the friction coefficient slightly decreased with increasing temperature, and was significantly decreased by the application of the graphite lubricant.
- Mechanism-based IHTC and friction coefficient models for the martensitic steel were developed to predict the IHTC at a range of pressures, as well as the friction coefficient at a range of sliding distances and temperatures for dry- and lubricated-contact conditions.
- The agreements between the experimentally-measured and FE-simulated temperature evolutions, thickness distributions and springback of the U-shaped components achieved close agreement, with an error of less than 10%, verifying the characterized thermomechanical boundary conditions and developed models of the martensitic steel.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mori, K.; Maki, S.; Tanak, Y. Warm and hot stamping of ultra high tensile strength steel sheets using resistance heating. CIRP Ann. Manuf. Technol. 2005, 54, 209–212. [Google Scholar] [CrossRef]
- El Fakir, O.; Wang, L.; Balint, D.; Dear, J.P.; Lin, J.; Dean, T.A. Experimental and numerical studies of the solution heat treatment, forming, and in-die quenching (HFQ) process on AA5754. Int. J. Mach. Tools Manuf. 2014, 87, 39–48. [Google Scholar] [CrossRef]
- Maeno, T.; Tomobe, M.; Mori, K.; Ikeda, Y. Hot stamping of titanium alloy sheets using partial contact heating. Procedia Manuf. 2018, 15, 1149–1155. [Google Scholar] [CrossRef]
- Karbasian, H.; Tekkaya, A.E. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Wang, L.; El Fakir, O.; Sun, Y.; Ji, K.; Luan, X.; Cai, Z.; Liu, X. A Method of Forming Parts from Sheet Metal. International Patent No. WO2019/038556, 28 Feburary 2019. [Google Scholar]
- Wang, Z.; Wang, K.; Liu, Y.; Zhu, B.; Zhang, Y.; Li, S. Multi-scale simulation for hot stamping quenching & partitioning process of high-strength steel. J. Mater. Process. Technol. 2019, 269, 150–162. [Google Scholar]
- Wang, A.; El Fakir, O.; Liu, J.; Zhang, Q.; Zheng, Y.; Wang, L. Multi-objective finite element simulations of a sheet metal-forming process via a cloud-based platform. Int. J. Adv. Manuf. Technol. 2018, 100, 2753–2765. [Google Scholar] [CrossRef]
- Mu, Y.; Simonetto, E.; Scagnolari, M.; Ghiotti, A. Wear in hot stamping by partition heating. J. Manuf. Mater. Process. 2020, 4, 18. [Google Scholar] [CrossRef]
- Kim, H.S.; Koç, M. Numerical investigations on springback characteristics of aluminum sheet metal alloys in warm forming conditions. J. Mater. Process. Technol. 2008, 204, 370–383. [Google Scholar] [CrossRef]
- Hardell, J.; Kassfeldt, E.; Prakash, B. Friction and wear behaviour of high strength boron steel at elevated temperatures of up to 800 °C. Wear 2008, 264, 788–799. [Google Scholar] [CrossRef]
- Hardell, J.; Prakash, B. High-temperature friction and wear behaviour of different tool steels during sliding against Al-Si-coated high-strength steel. Tribol. Int. 2008, 41, 663–671. [Google Scholar] [CrossRef]
- Karupannasamy, D.K.; Hol, J.; de Rooij, M.B.; Meinders, T.; Schipper, D.J. A friction model for loading and reloading effects in deep drawing processes. Wear 2014, 318, 27–39. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, L.; Politis, D.J.; Masen, M.A. Development of an interactive friction model for the prediction of lubricant breakdown behaviour during sliding wear. Tribol. Int. 2017, 110, 370–377. [Google Scholar] [CrossRef]
- Liu, X.; El Fakir, O.; Zheng, Y.; Gharbi, M.M.; Wang, L. Effect of tool coatings on the interfacial heat transfer coefficient in hot stamping of aluminium alloys under variable contact pressure conditions. Int. J. Heat Mass Transf. 2019, 137, 74–83. [Google Scholar] [CrossRef]
- Bai, Q.; Lin, J.; Zhan, L.; Dean, T.A.; Balint, D.S.; Zhang, Z. An efficient closed-form method for determining interfacial heat transfer coefficient in metal forming. Int. J. Mach. Tools Manuf. 2012, 56, 102–110. [Google Scholar] [CrossRef]
- Hu, P.; Ying, L.; Li, Y.; Liao, Z. Effect of oxide scale on temperature-dependent interfacial heat transfer in hot stamping process. J. Mater. Process. Technol. 2013, 213, 1475–1483. [Google Scholar] [CrossRef]
- Zhang, Q.; Luan, X.; Dhawan, S.; Politis, D.J.; Du, Q.; Fu, M.W.; Wang, K.; Gharbi, M.M.; Wang, L. Development of the post-form strength prediction model for a high-strength 6xxx aluminium alloy with pre-existing precipitates and residual dislocations. Int. J. Plast. 2019, 119, 230–248. [Google Scholar] [CrossRef]
- Merklein, M.; Lechler, J. Determination of material and process characteristics for hot stamping processes of quenchenable ultra high strength steels with respect to a FE-based process design. Sae Int. J. Mater. Manuf. 2008, 1, 411–426. [Google Scholar] [CrossRef]
- Venezuela, J.; Liu, Q.; Zhang, M.; Zhou, Q.; Atrens, A. The influence of hydrogen on the mechanical and fracture properties of some martensitic advanced high strength steels studied using the linearly increasing stress test. Corros. Sci. 2015, 99, 98–117. [Google Scholar] [CrossRef]
- Deole, A.D.; Barnett, M.R.; Weiss, M. The numerical prediction of ductile fracture of martensitic steel in roll forming. Int. J. Solids Struct. 2018, 144–145, 20–31. [Google Scholar] [CrossRef]
- Soyarslan, C.; Malekipour Gharbi, M.; Tekkaya, A.E. A combined experimental-numerical investigation of ductile fracture in bending of a class of ferritic-martensitic steel. Int. J. Solids Struct. 2012, 49, 1608–1626. [Google Scholar] [CrossRef]
- Godin, H.; Mithieux, J.D.; Parrens, C.; Badinier, G.; Sennour, M.; Gourgues-Lorenzon, A.F. Effects of cooling path and resulting microstructure on the impact toughness of a hot stamping martensitic stainless steel. Mater. Sci. Eng. A 2019, 742, 597–607. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, K.; Politis, D.J.; Chen, G.; Wang, L. An experimental investigation on the ductility and post-form strength of a martensitic steel in a novel warm stamping process. J. Mater. Process. Tech. 2020, 275, 116387. [Google Scholar] [CrossRef]
- Yang, X.; Liu, X.; Liu, H.; Politis, D.J.; Wang, L. An interactive friction model for predicting friction evolution and lubricant breakdown behaviour under varying contact conditions. Tribol. Int. 2020. under review. [Google Scholar]
- Luan, X.; Zhang, Q.L.; Fakir, O.E.; Wang, L.L.; Gharbi, M.M. Uni-Form: A Pilot Production Line for Hot/wArm Sheet Metal Forming Integrated in a Cloud Based Smartforming Platform. In Proceedings of the 3rd International Conference on Advanced High Strength Steel and Press Hardening, Xi’an, China, 25–27 August 2016. [Google Scholar]
- ESI-group. Pam-Stamp 2015.1 User’s Guide; ESI Group: Paris, France, 2015. [Google Scholar]
- Liu, X.; El Fakir, O.; Cai, Z.; Gharbi, M.M.; Dalkaya, B. Development of an interfacial heat transfer coefficient model for the hot and warm aluminium stamping processes under different initial blank temperature conditions. J. Mater. Process. Technol. 2019, 273, 116245. [Google Scholar] [CrossRef]
- Liu, X.; Kopec, M.; El Fakir, O.; Qu, H.; Wang, Y.; Wang, L.; Li, Z. Characterisation of the interfacial heat transfer coefficient in hot stamping of titanium alloys. Int. Commun. Heat Mass Transf. 2020, 113, 104535. [Google Scholar] [CrossRef]
- Ghiotti, A.; Bruschi, S.; Medea, F. Wear onset in hot stamping of aluminium alloys sheets. Wear 2017, 376–377, 484–495. [Google Scholar] [CrossRef]
- Ma, G.; Wang, L.; Gao, H.; Zhang, J.; Reddyhoff, T. The friction coefficient evolution of a TiN coated contact during sliding wear. Appl. Surf. Sci. 2015, 345, 109–115. [Google Scholar] [CrossRef]
- Azushima, A.; Uda, K.; Yanagida, A. Friction behavior of aluminum-coated 22MnB5 in hot stamping under dry and lubricated conditions. J. Mater. Process. Technol. 2012, 212, 1014–1021. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Hsu, T.-C.; Huang, X.-B. A realistic friction model for computer simulation of sheet metal forming processes. J. Eng. Ind. 1995, 117, 202–209. [Google Scholar] [CrossRef]
- Wang, A.; Zhong, K.; El Fakir, O.; Liu, J.; Sun, C.; Wang, L.L.; Lin, J.; Dean, T.A. Springback analysis of AA5754 after hot stamping: Experiments and FE modelling. Int. J. Adv. Manuf. Technol. 2017, 89, 1339–1352. [Google Scholar] [CrossRef]

| Non-Alloy Martensitic Steel | ||||||||||
| Element | C | Si | Mn | P | S | Al | Ti+Nb | Cr+Mo | B | Fe |
| Wt % | 0.25 | 0.8 | 2.5 | 0.06 | 0.015 | 0.015–2.0 | 0.25 | 1.2 | 0.005 | Bal. |
| AISI P20 Tool Steel | ||||||||||
| Element | C | Cr | Mn | Mo | Ni | Si | S | Fe | ||
| Wt % | 0.37 | 2.0 | 1.4 | 0.2 | 1 | 0.3 | 0.01 | Bal. | ||
| Heat Transfer | Pressure | Temperature | Lubricant | Purpose |
| 0.5–50 MPa | 400 °C | None | Effect of pressure on the interfacial heat transfer coefficient | |
| 0.5–50 MPa | 400 °C | Graphite | Effect of lubricant on the interfacial heat transfer coefficient | |
| Friction | Load | Temperature | Lubricant | Purpose |
| 5 N | 350–450 °C | None | Effect of temp. on the friction | |
| 5 N | 350–450 °C | Graphite | Effect of lubricant on the friction |
| Material | Elastic Modulus | Density | Thermal Conductivity | Specific Heat | Expansion Coefficient |
|---|---|---|---|---|---|
| MS | 210 GPa | 7780 kg/m3 | 24.5 kW/(m·K) | 431 J/(kg·K) | 11.1 μm/(m·K) |
| P20 | 205 GPa | 7850 kg/m3 | 31.5 kW/(m·K) | 473 J/(kg·K) | 12.8 μm/(m·K) |
| Constant | ha | σU | γ | δl | |||
| Unit | kW/(m2·K) | MPa | μm−1 | μm | - | - | - |
| Value | 0.15 | 90 | 0.15 | 20 | 4.2·10−4 | 6.8 | 9.8·10−5 |
| Constant | μl0 | μd0 | Ql | Qd | R0 | ||
| Unit | - | - | J/mol | J/mol | J/(mol·K) | - | - |
| Value | 0.0133 | 0.1532 | 14,432 | 6650.7 | 8.31 | 57.25 | 0.61 |
| Constant | c | n1 | n2 | n3 | η0 | Qη | |
| Unit | kg/(mm2·s) | - | - | - | mm2/s | J/mol | mm/s |
| Value | 90 | 0.74 | 2.99 | 0.08 | 6.04·10−4 | 3433.6 | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yang, X.; Sun, Y.; Politis, D.J.; Mori, K.-i.; Wang, L. Characterization of Thermomechanical Boundary Conditions of a Martensitic Steel for a FAST Forming Process. J. Manuf. Mater. Process. 2020, 4, 57. https://doi.org/10.3390/jmmp4020057
Liu X, Yang X, Sun Y, Politis DJ, Mori K-i, Wang L. Characterization of Thermomechanical Boundary Conditions of a Martensitic Steel for a FAST Forming Process. Journal of Manufacturing and Materials Processing. 2020; 4(2):57. https://doi.org/10.3390/jmmp4020057
Chicago/Turabian StyleLiu, Xiaochuan, Xiao Yang, Yuhao Sun, Denis J. Politis, Ken-ichiro Mori, and Liliang Wang. 2020. "Characterization of Thermomechanical Boundary Conditions of a Martensitic Steel for a FAST Forming Process" Journal of Manufacturing and Materials Processing 4, no. 2: 57. https://doi.org/10.3390/jmmp4020057
APA StyleLiu, X., Yang, X., Sun, Y., Politis, D. J., Mori, K.-i., & Wang, L. (2020). Characterization of Thermomechanical Boundary Conditions of a Martensitic Steel for a FAST Forming Process. Journal of Manufacturing and Materials Processing, 4(2), 57. https://doi.org/10.3390/jmmp4020057








