Evaluation of Prediction Accuracy for Anisotropic Yield Functions Using Cruciform Hole Expansion Test
Abstract
1. Introduction
2. Anisotropic Yield Functions
- Hill 1948 [1]: this is the most popular anisotropic yield function especially in the car manufacturing industry because of its simplicity. For calibration of this yield function, the results of uniaxial tensile tests in three directions are required. Usually, parameters are identified from the flow stress in the rolling direction (RD) and Lankford coefficients (r-values) in three directions.
- YLD2000-2D [2]: this is a widely used yield function and is implemented in the several commercial finite element (FE) simulation software tools. In the case of face-centered cubic lattice metal, such as aluminum alloy, it is recommended that the order is set to 8 [14]. To calibrate this yield function, the flow stresses and r-values at 0°, 45°, and 90° with respect to the RD, the equi-biaxial stress value, and the strain increment direction at the equi-biaxial stress state are used.
- Vegter [15]: this yield function is defined in the principal stress space. In addition to the uniaxial tensile tests in five or more directions and a material test of the equi-biaxial stress state, plane-strain tensile tests are required in five or more directions. The Vegter model can consider the results of many material tests, but it requires substantial effort to determine all input variables, and it is difficult to conduct pure plane-strain tensile test.
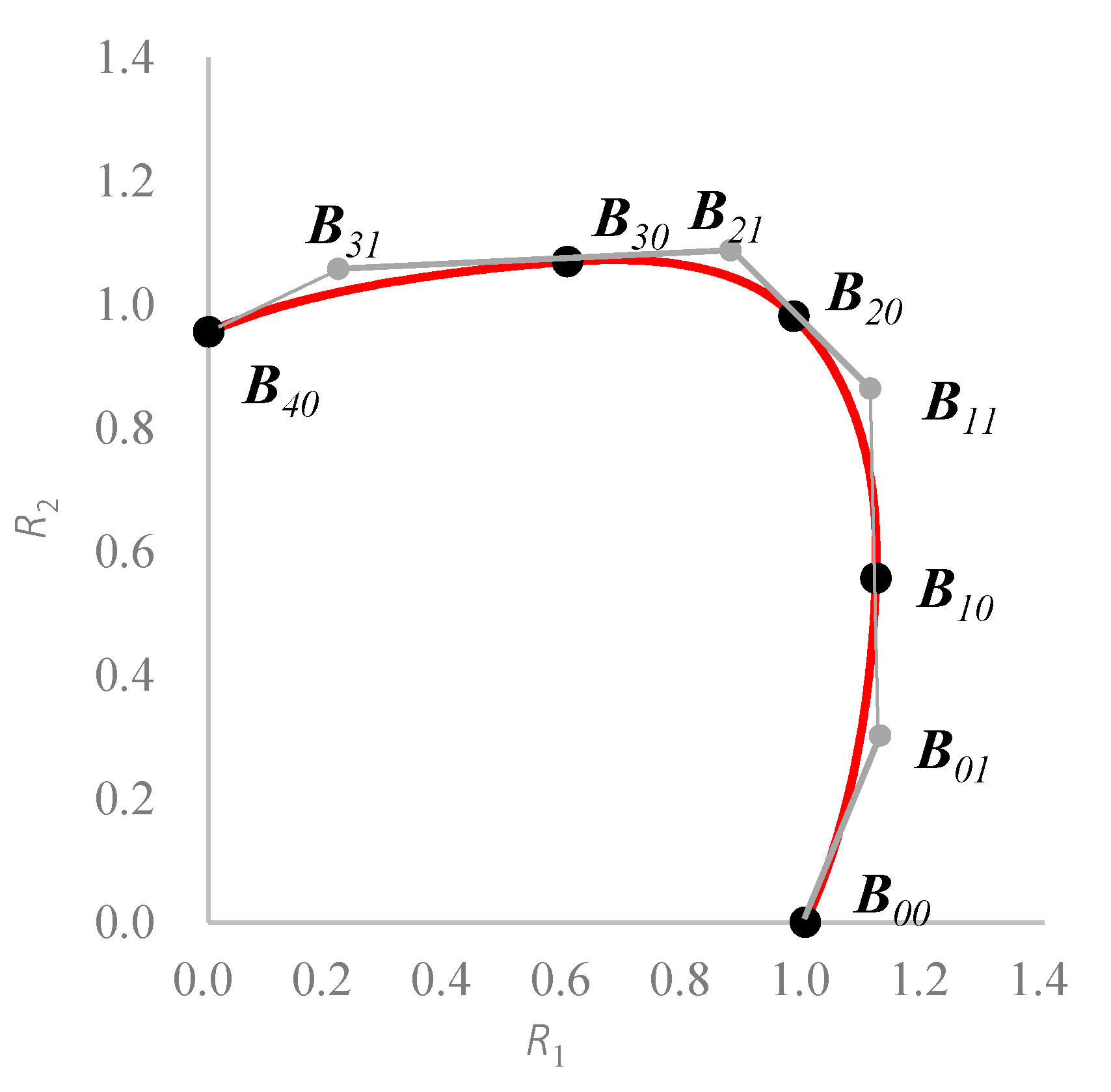
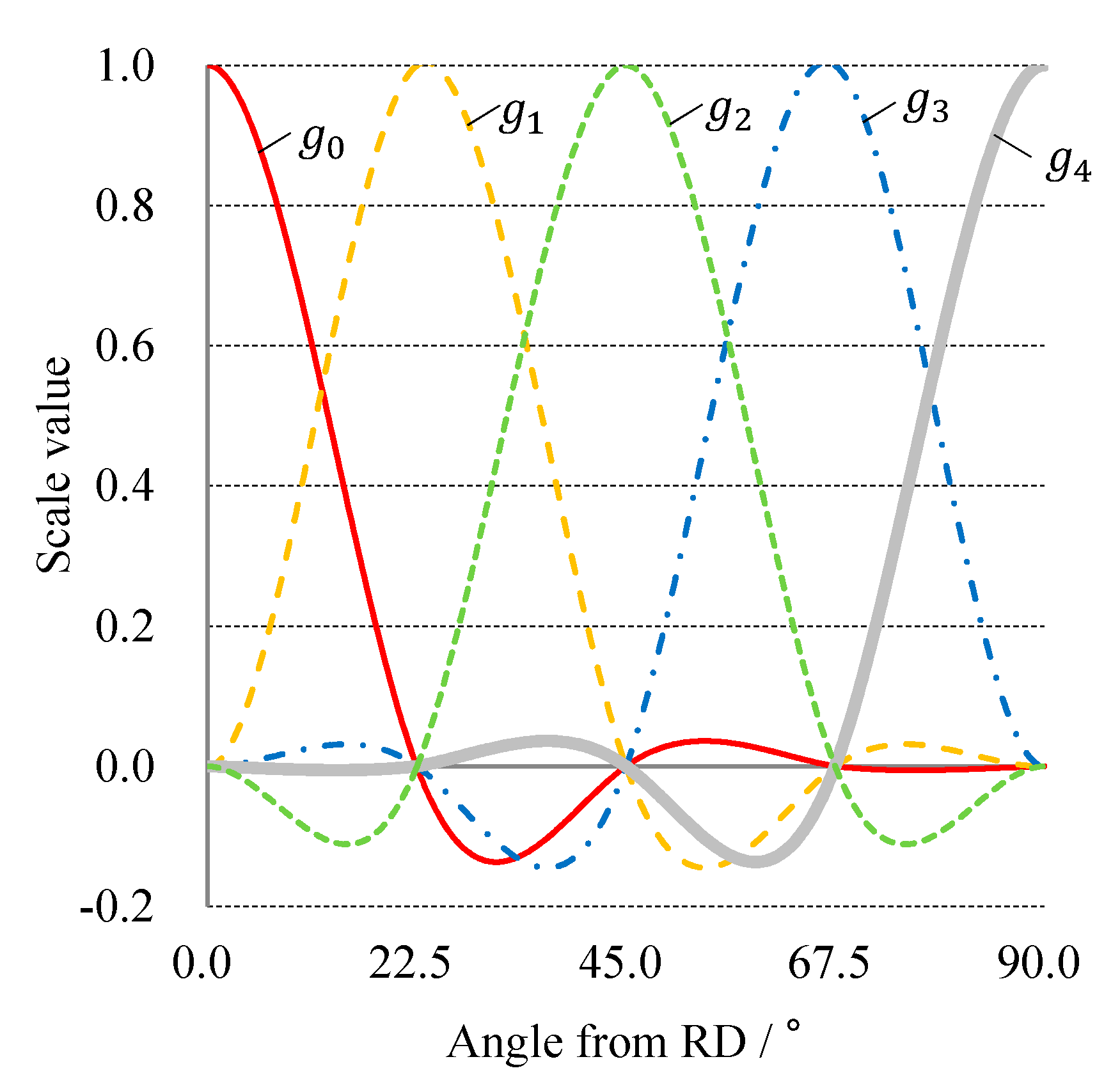
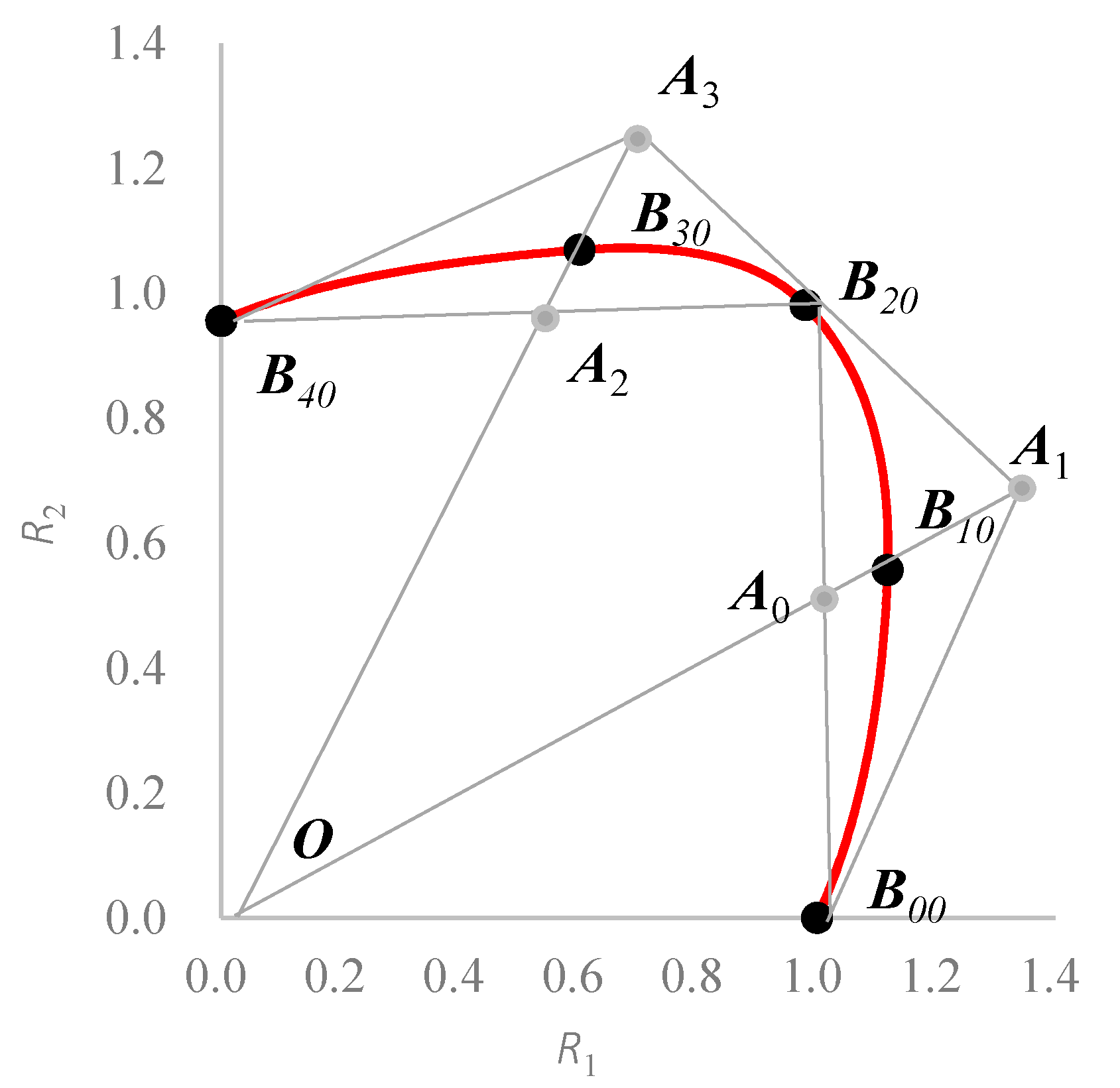
3. Spline Yield Function
4. Calibration of Spline Yield Function
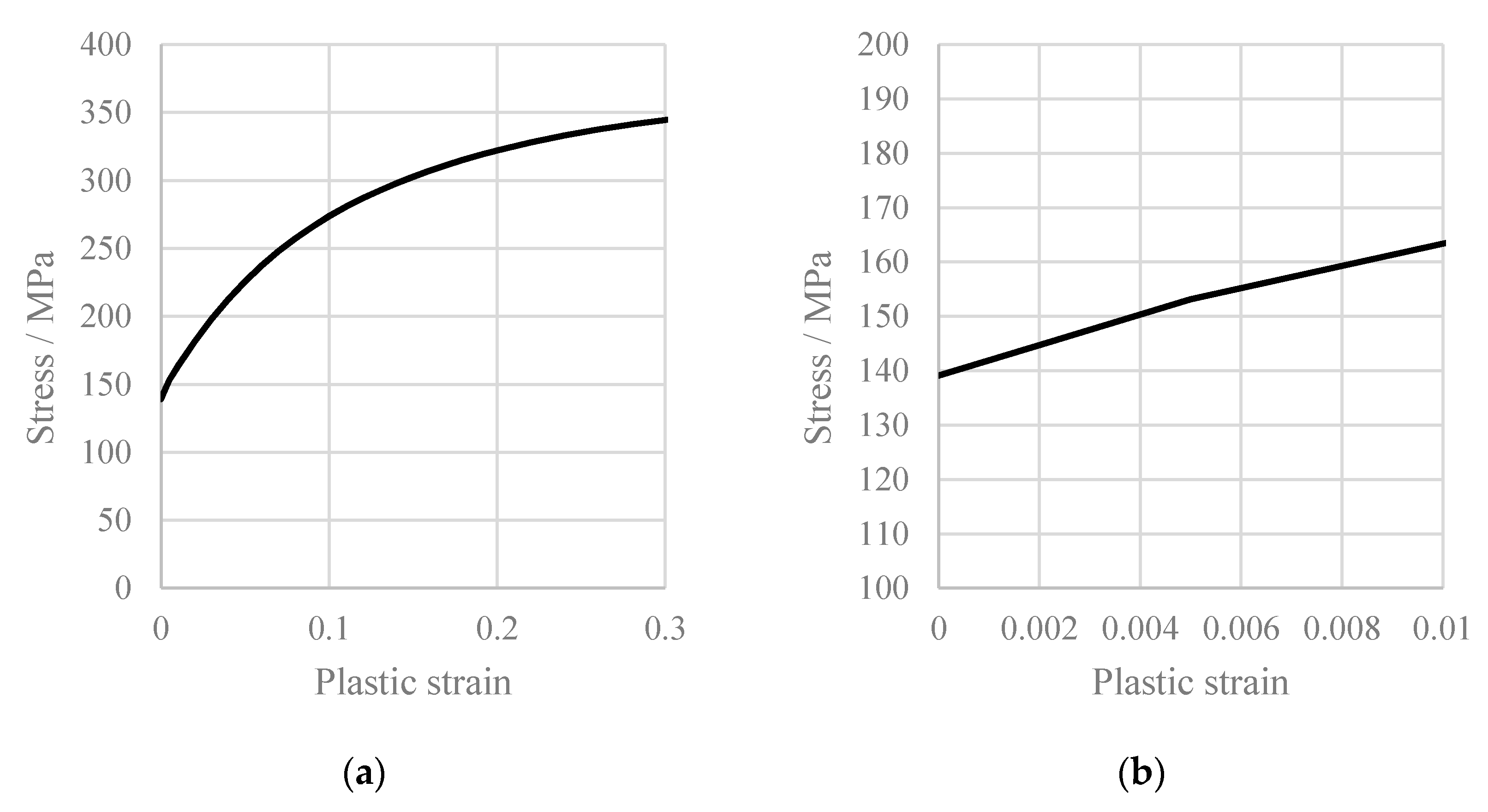
4.1. Uniaxial Tensile Tests
4.2. Bulge Tests
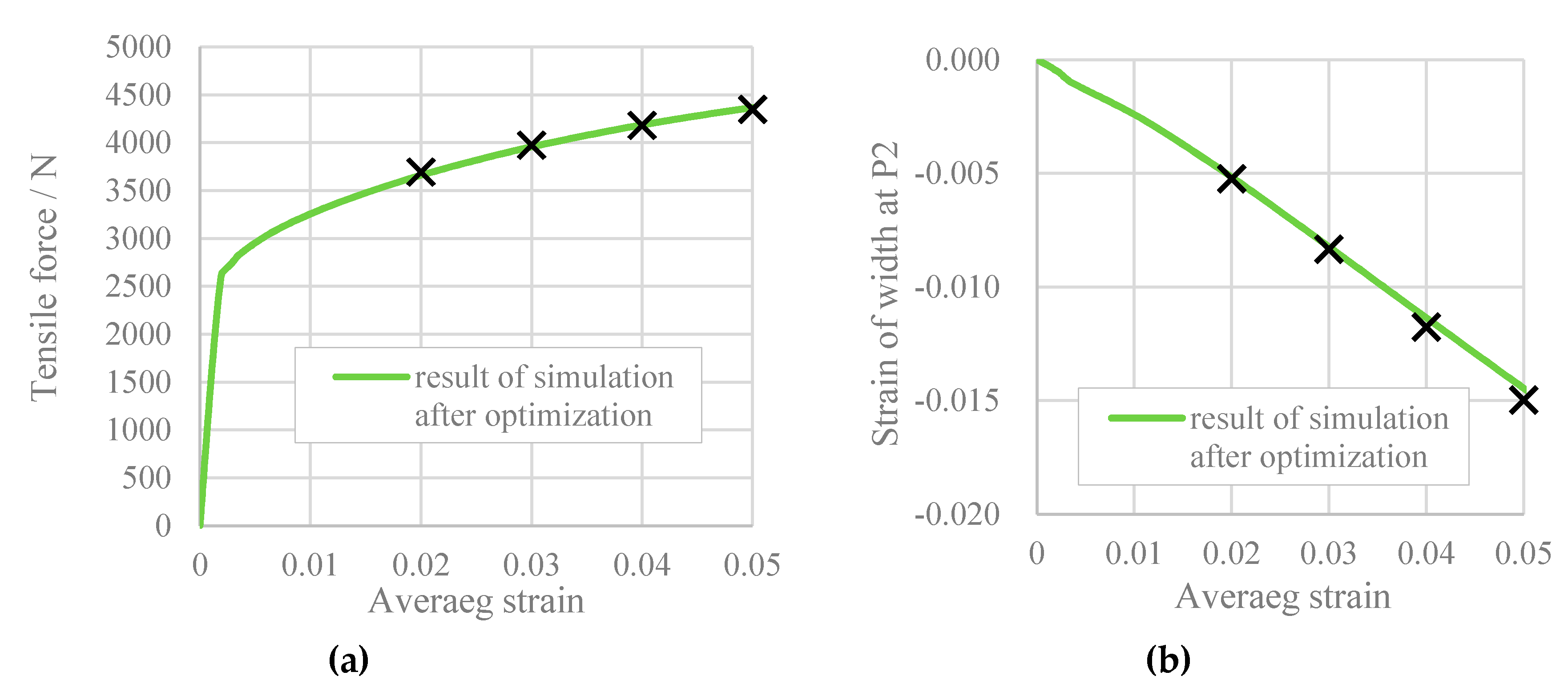
4.3. Pseudo Plane Strain Tensile Tests
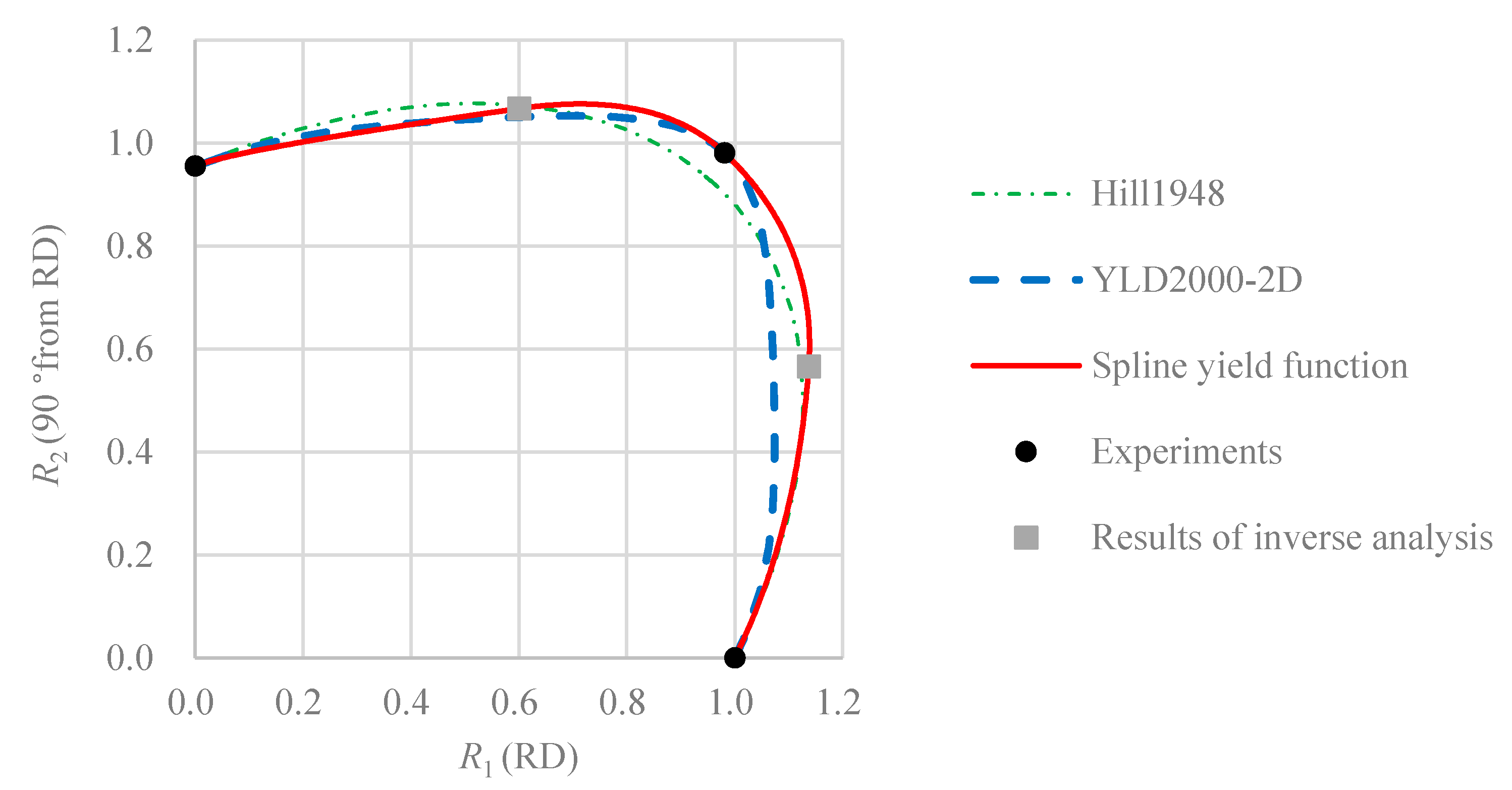
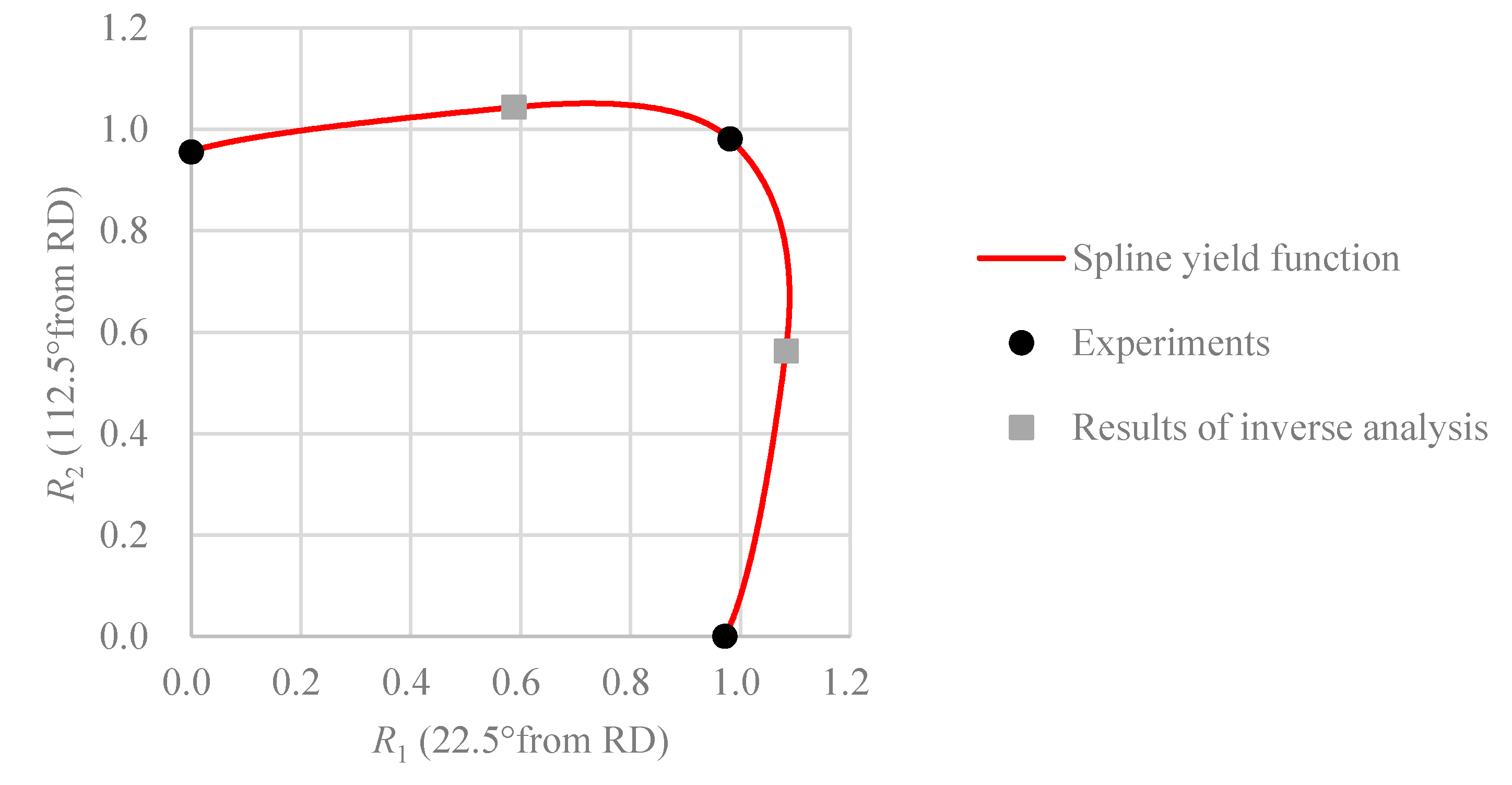
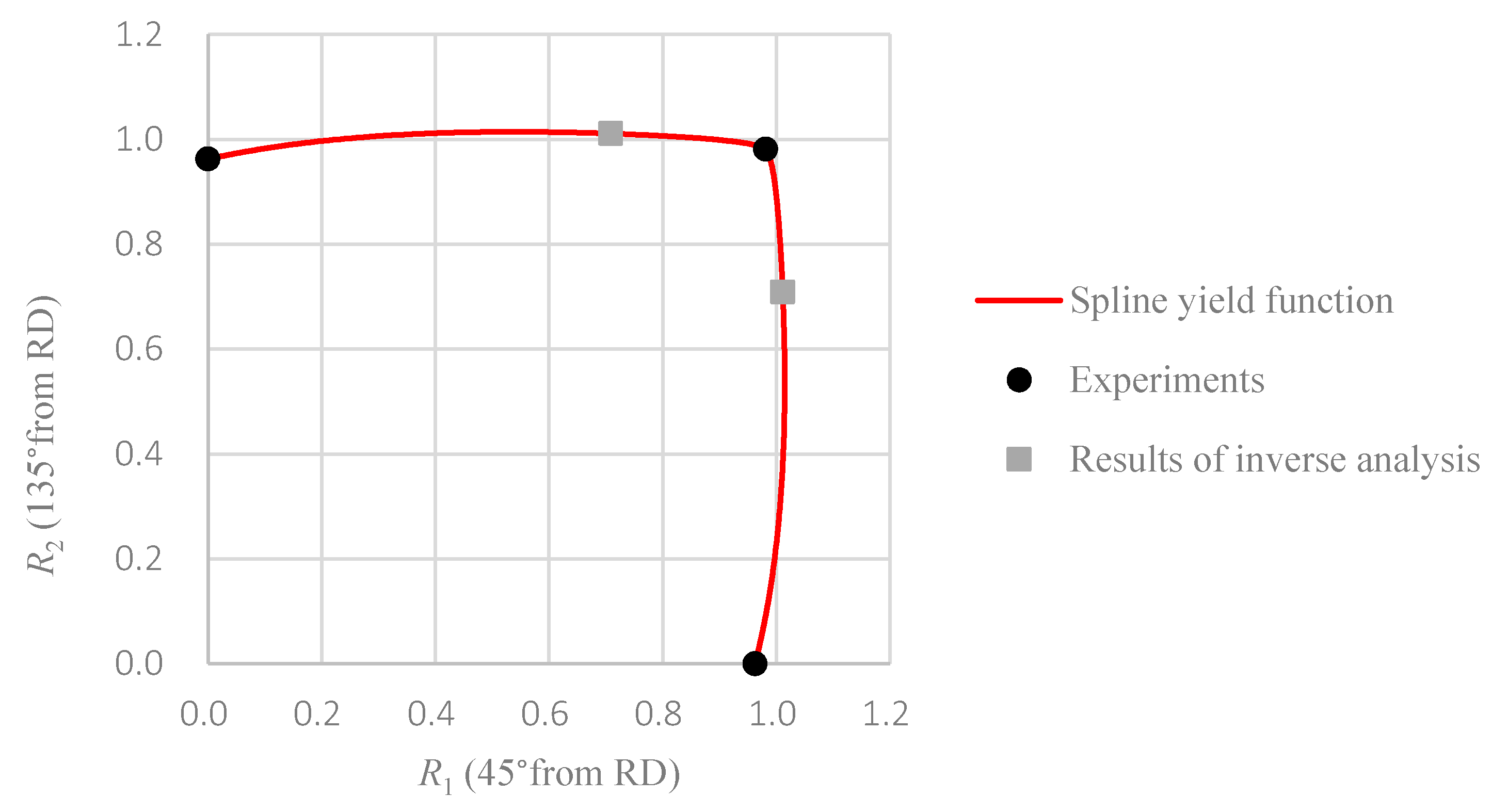
4.4. Comparison of the Equi-Plastic Work Surface Shape
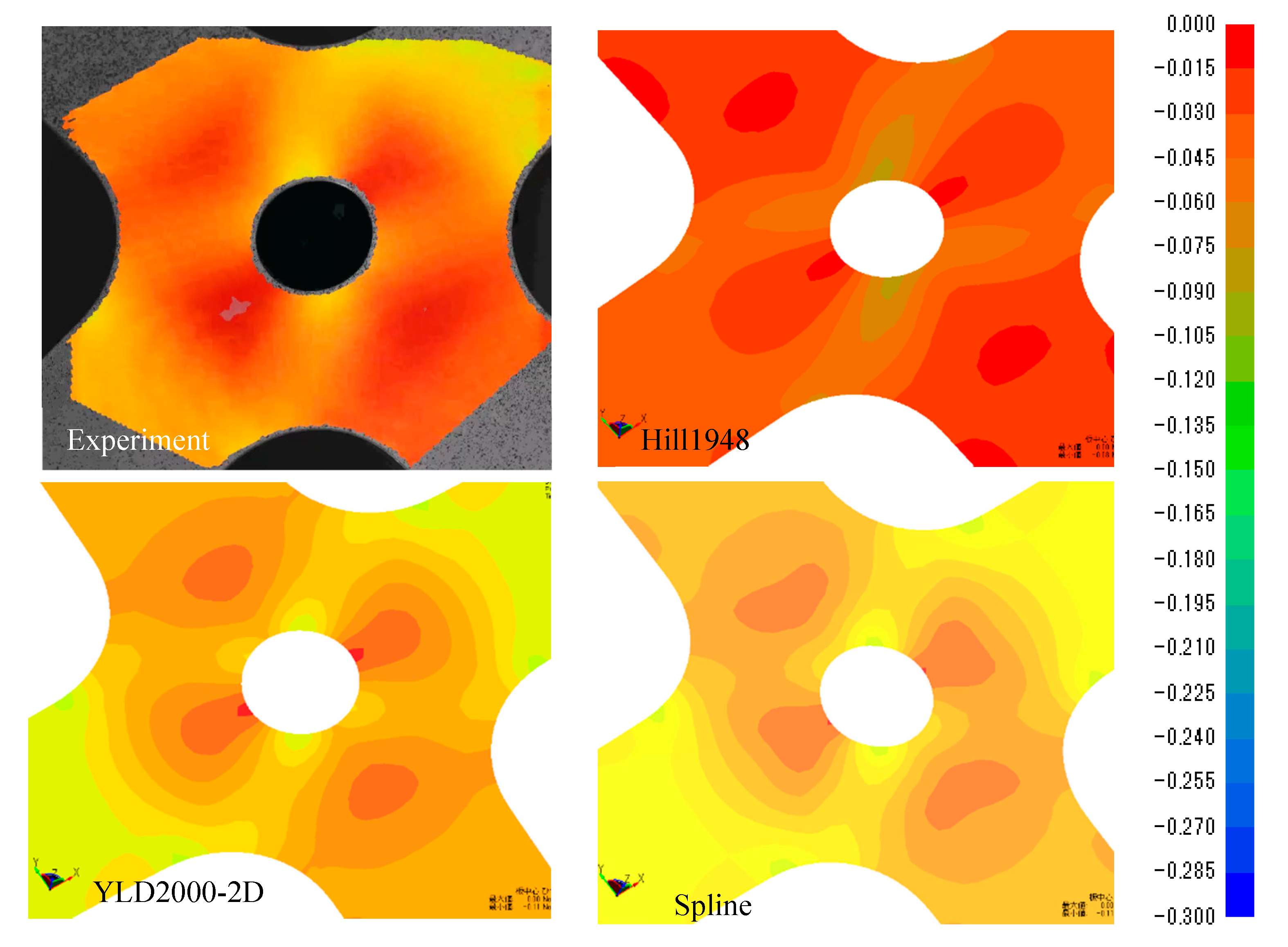
5. Evaluation of Anisotropic Yield Functions
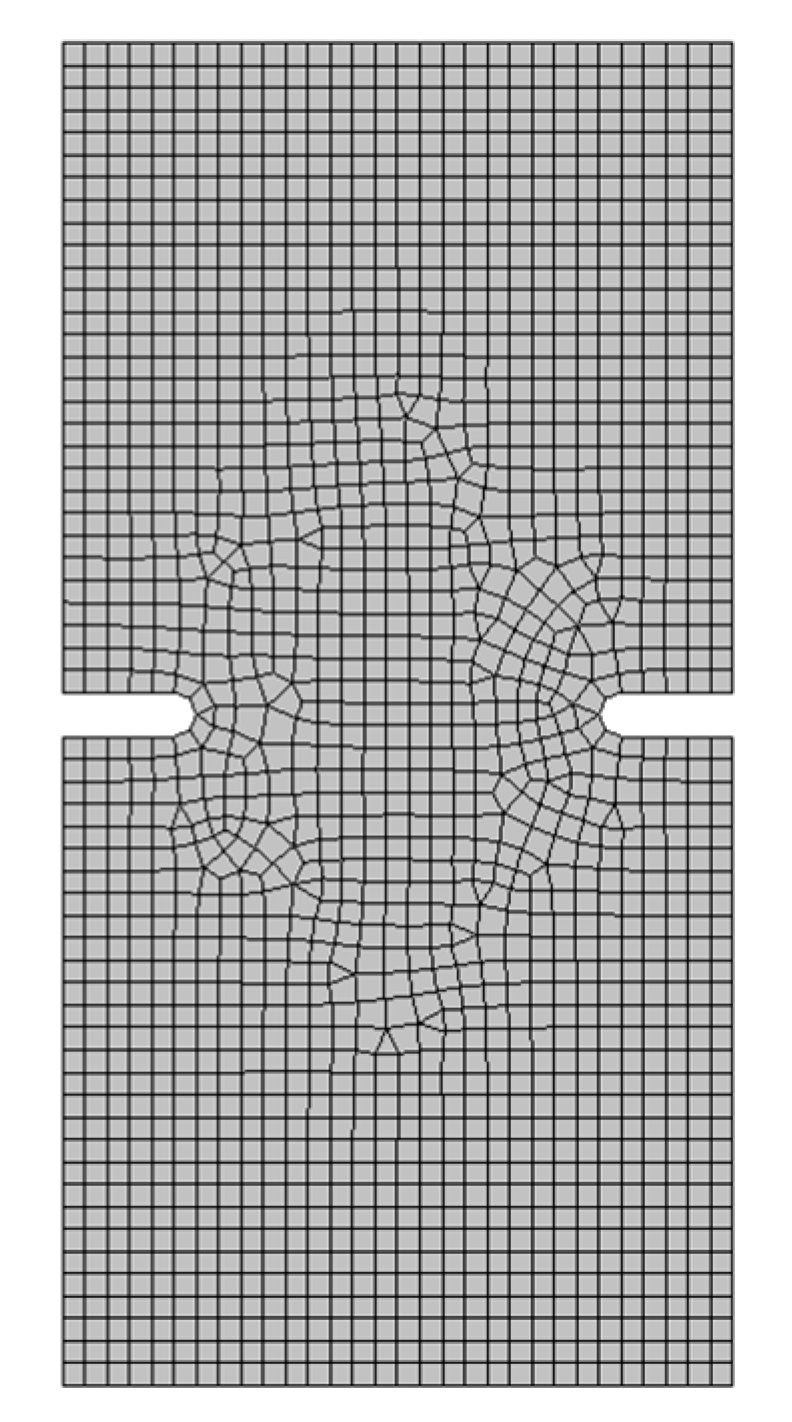
5.1. Experiment
5.2. Numerical Analysis
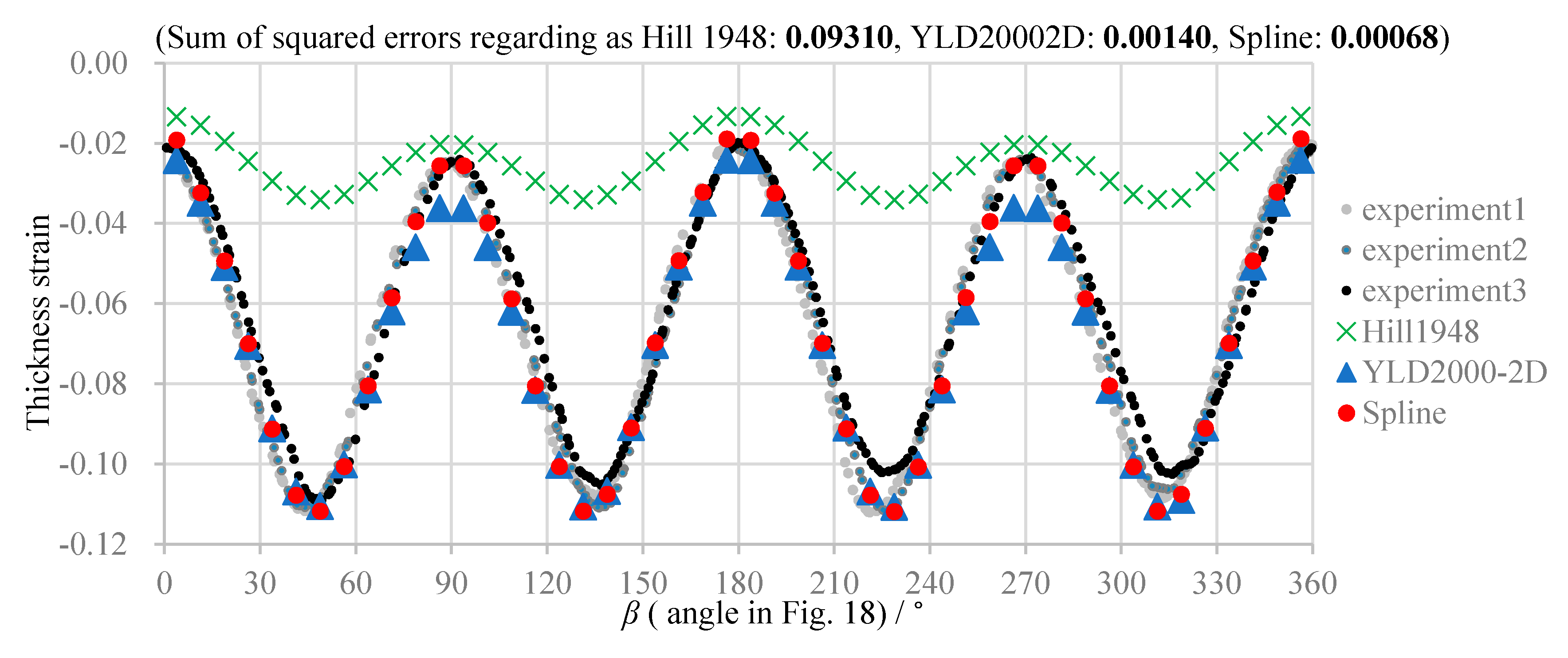
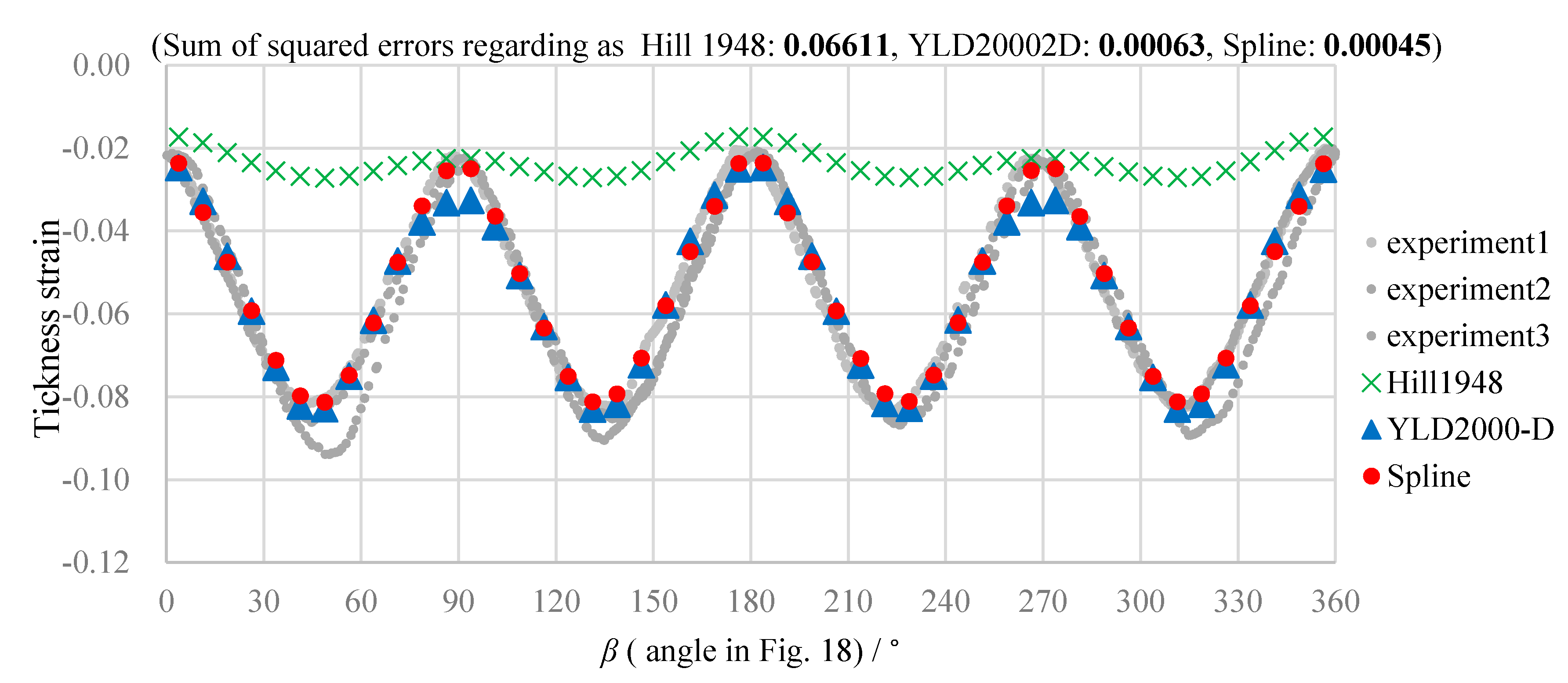
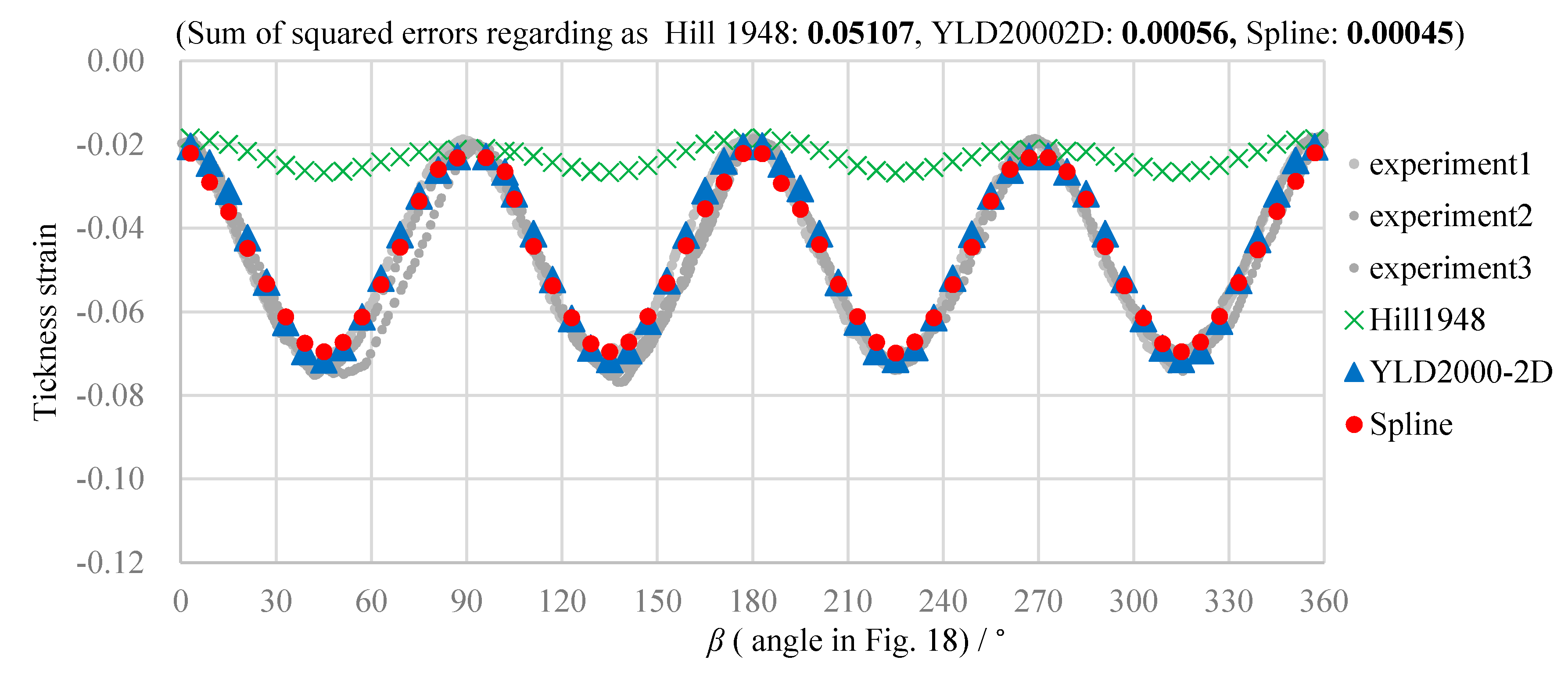
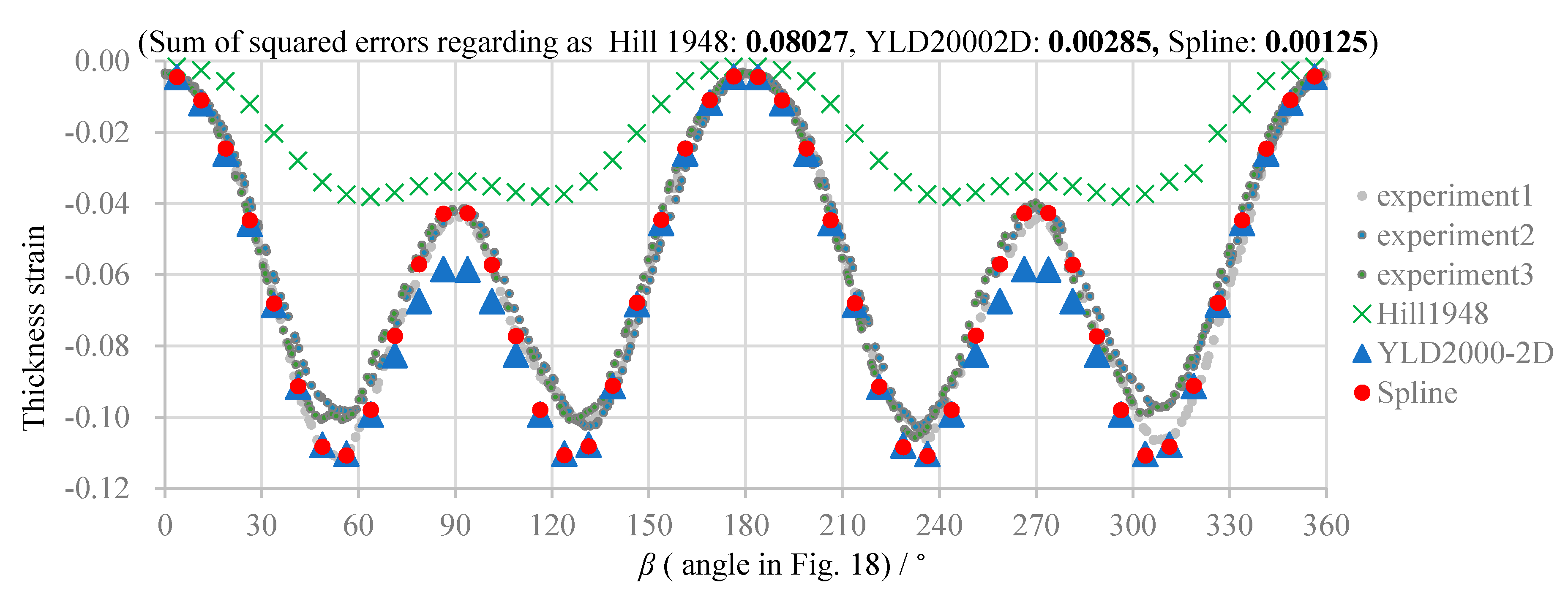
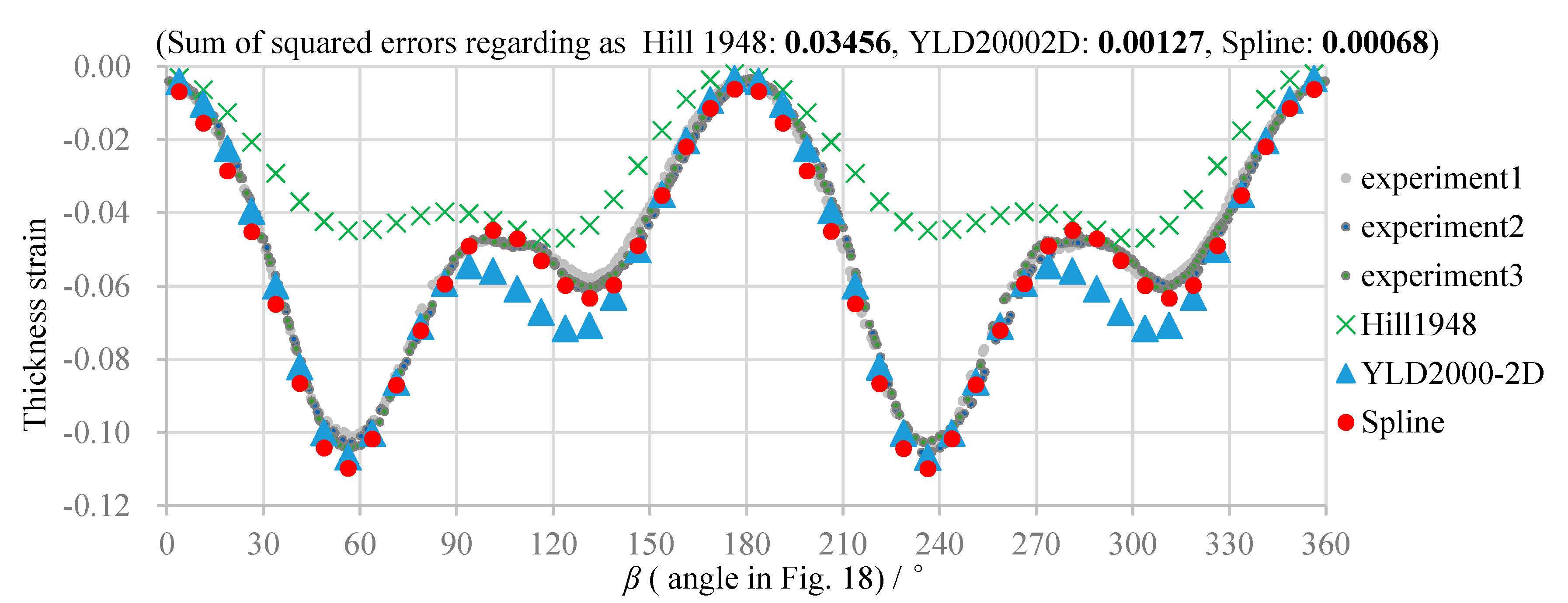
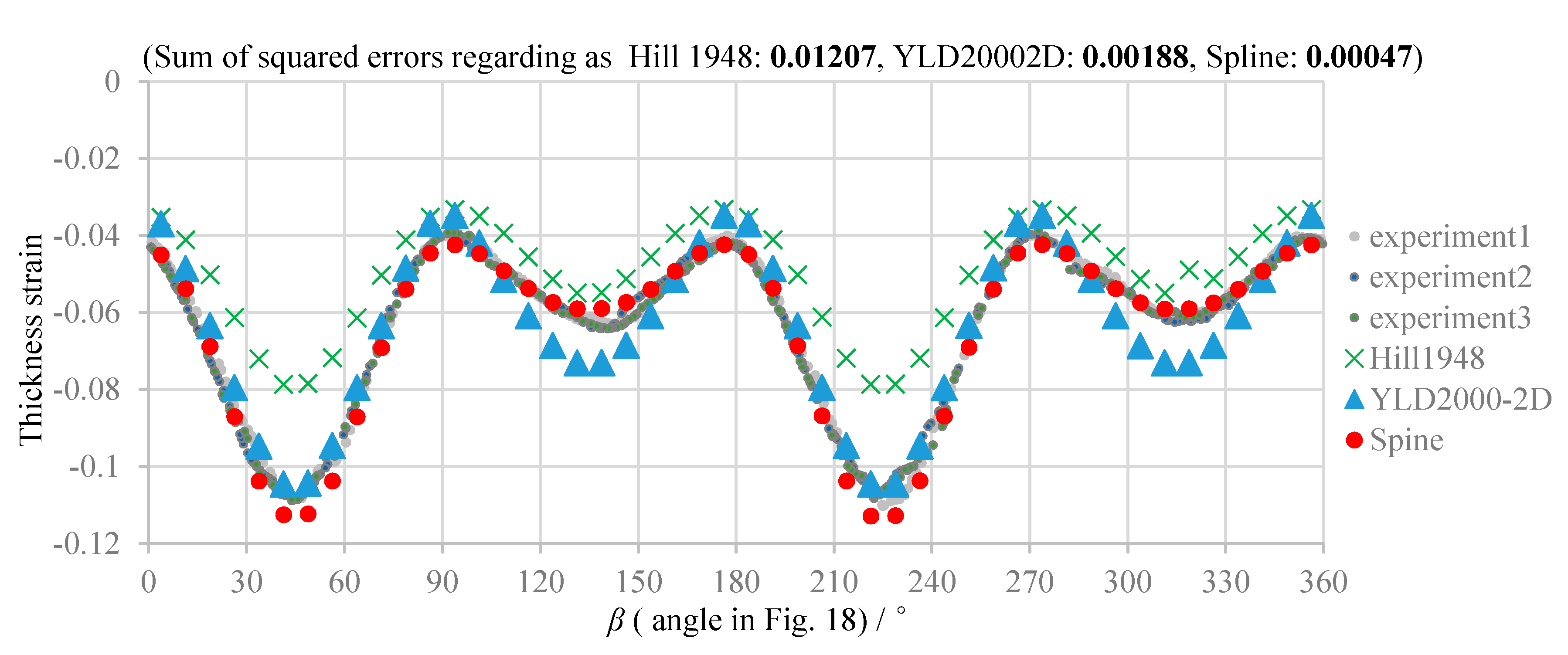
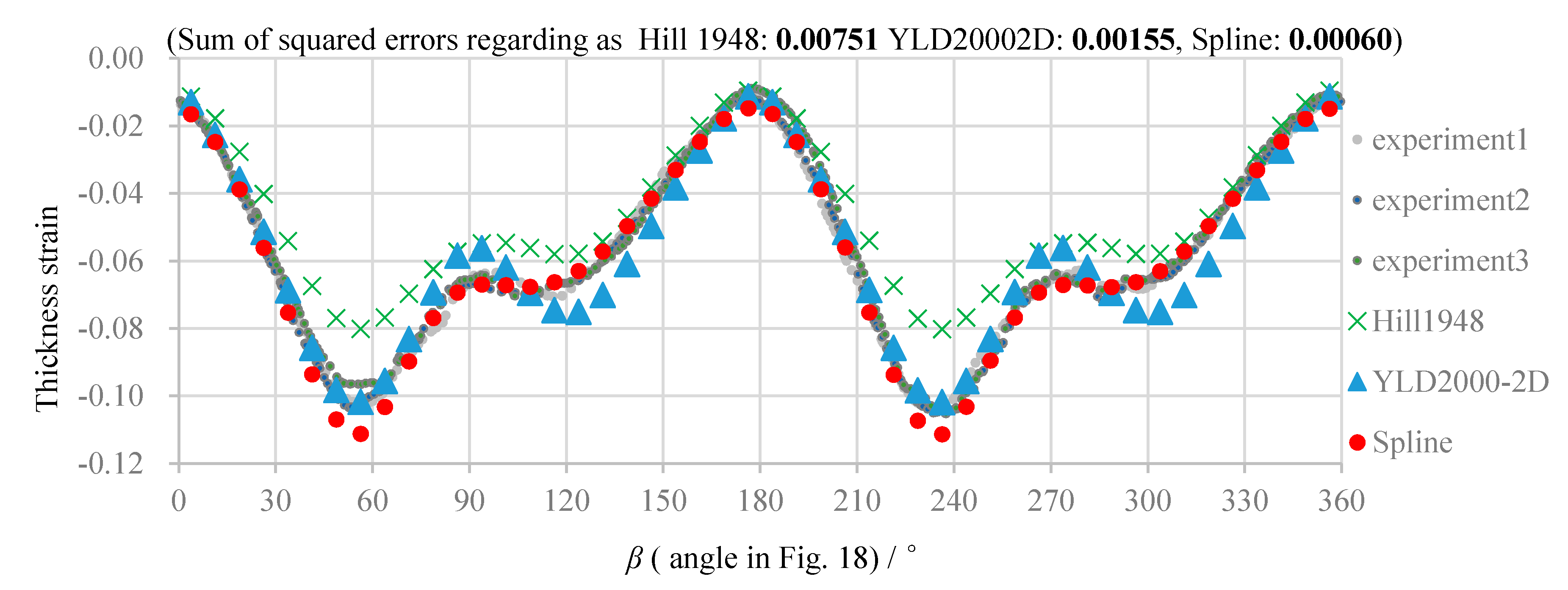
5.3. Comparison of Numerical and Experimental Results
6. Concluding Remarks
- A method for determining the parameters of the spline yield function has been developed, which includes a pseudo plane strain stress test by using inverse analysis.
- For the evaluation of the prediction accuracy of the yield function, an in-plane cruciform tensile test was conducted. This kind of test is appropriate, because it is frictionless and free of bending.
- The experimental and simulation results reveal high prediction accuracy of the spline yield function. Hence, the validity of the method for parameter determination is verified.
- The spline yield function is the most accurate model for all considered conditions of the evaluation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. 1948, 193, 281–297. [Google Scholar]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.H.; Chu, E. Plane stress yield function for aluminum alloy sheets—Part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Tsutamori, H.; Iizuka, E.; Amaishi, T.; Sato, K.; Ogihara, Y.; Miyamoto, J. Plane Stress Yield Function Described by 3rd-degree Spline Curves Considering Differential Work Hardening. J. Jpn. Soc. Technol. Plast. 2016, 657–662, 245–251. (In Japanese) [Google Scholar] [CrossRef]
- Iizuka, E.; Hashimoto, K.; Kuwabara, T. Effects of anisotropic yield functions on the accuracy of forming simulations of hole expansion. Procedia Eng. 2014, 81, 2433–2438. [Google Scholar] [CrossRef]
- Panich, S.; Uthaisangsuk, V.; Suranuntchai, S.; Jirathearanat, S. Anisotropic Plastic Behavior of TRIP 780 Steel Sheet in Hole Expansion Test. Key Eng. Mater. 2012, 504–506, 89–94. [Google Scholar] [CrossRef]
- Kuwabara, T.; Mori, T.; Asano, M.; Hakoyama, T.; Barlat, F. Material modeling of 6016-O and 6016-T4 aluminum alloy sheets and application to hole expansion forming simulation. Int. J. Plast. 2017, 93, 164–186. [Google Scholar] [CrossRef]
- Kuwabara, T.; Hashimoto, K.; Iizuka, E.; Yoon, J.W. Effect of anisotropic yield functions on the accuracy of hole expansion simulations. J. Mater. Process. Technol. 2011, 211, 475–481. [Google Scholar] [CrossRef]
- Hol, J.; Alfaro MV, C.; Rooij, M.B.; Meinders, T. Advanced friction modeling for sheet metal forming. Wear 2012, 286–287, 66–78. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Wang, Z.; Hua, M.; Wei, X. A study on variable friction model in sheet metal forming with advanced high strength steels. Tribol. Int. 2016, 93, 17–28. [Google Scholar] [CrossRef]
- Hashimoto, K.; Isogai, E.; Yoshida, T.; Kuriyama, Y.; Ito, K. Finite Element Analysis of Sheet Metal Forming Taking Account of Nonlinear Friction Model—Assessment of Sheet Formability by Nonlinear Friction Model III. J. Jpn. Soc. Technol. Plast. 2007, 549–573, 995–999. (In Japanese) [Google Scholar]
- Kuwabara, T.; Ichikawa, K. Hale Expansion Simulation Considering the Differential Hardening of a Sheet Metal. Rom. J. Technol. Sci. 2015, 60, 63–81. [Google Scholar]
- Suzuki, T.; Okamura, K.; Capilla, G.; Hamasaki, H.; Yoshida, F. Effect of anisotropy evolution on circular and oval hole expansion behavior of high-strength steel sheets. Int. J. Mech. Sci. 2018, 146–147, 556–570. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, K.; Fujiwara, K. Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain. Int. J. Plast. 2002, 18, 633–659. [Google Scholar] [CrossRef]
- Logan, R.W.; Hosford, W.F. Upper-Bound Anisotropic yield Locus Calculations Assuming <1 1 1 >—Pencil Glide. Int. J. Mech. Sci. 1980, 22, 419–430. [Google Scholar] [CrossRef]
- Vegter, H.; Boogaard, A.H. A plane stress yield function for anisotropic sheet material by interpolation of biaxial stress states. Int. J. Plast. 2006, 22, 557–580. [Google Scholar] [CrossRef]
- Amaishi, T.; Tsutamori, H.; Iizuka, I.; Sato, K.; Ogihara, Y.; Matsui, Y. A Yield Function for Anisotropic Sheet Material Described by 3rd-Degree Spline Curve and its Applications. Key Eng. Mater. 2017, 725, 653–658. [Google Scholar] [CrossRef]
- Amaishi, T.; Tsutamori, H.; Nishiwaki, T.; Kimoto, T. A Plane Stress Yield Function by Multi-Segment Third Order Beézier curves. Key Eng. Mater. 2018, 794, 163–168. [Google Scholar] [CrossRef]
- Brünig, M.; Brenner, D.; Gerke, S. Stress state dependence of ductile damage and fracture behavior: Experiments and numerical simulations. Eng. Fract. Mech. 2015, 141, 152–169. [Google Scholar] [CrossRef]
- Bathe, K.J.; Dvorkin, E.N. A four-node plate bending element based on Mindlin/Reissner plate theory and a mixed interpolation. Int. J. Numer. Method Eng. 1985, 21, 367–383. [Google Scholar] [CrossRef]
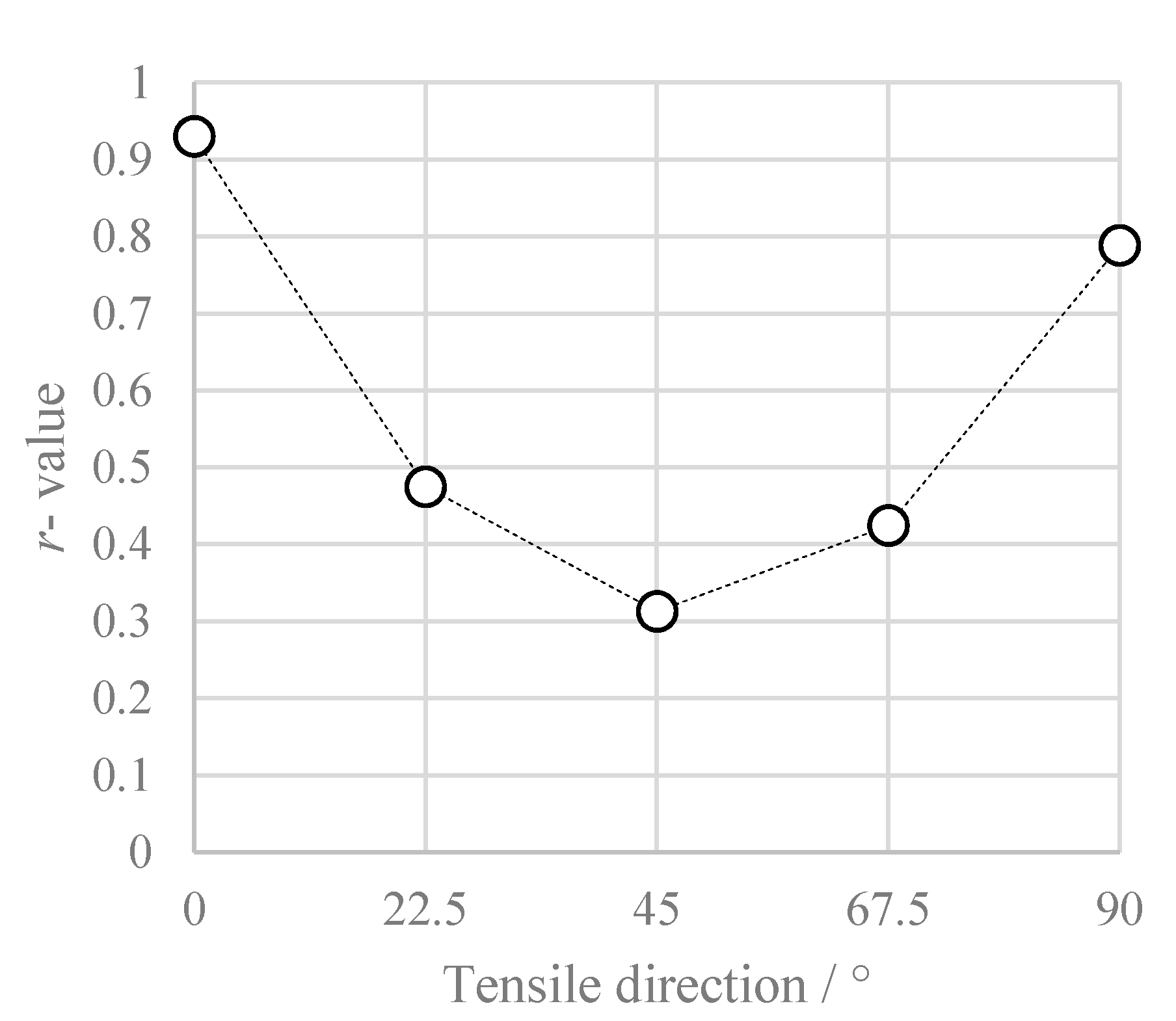


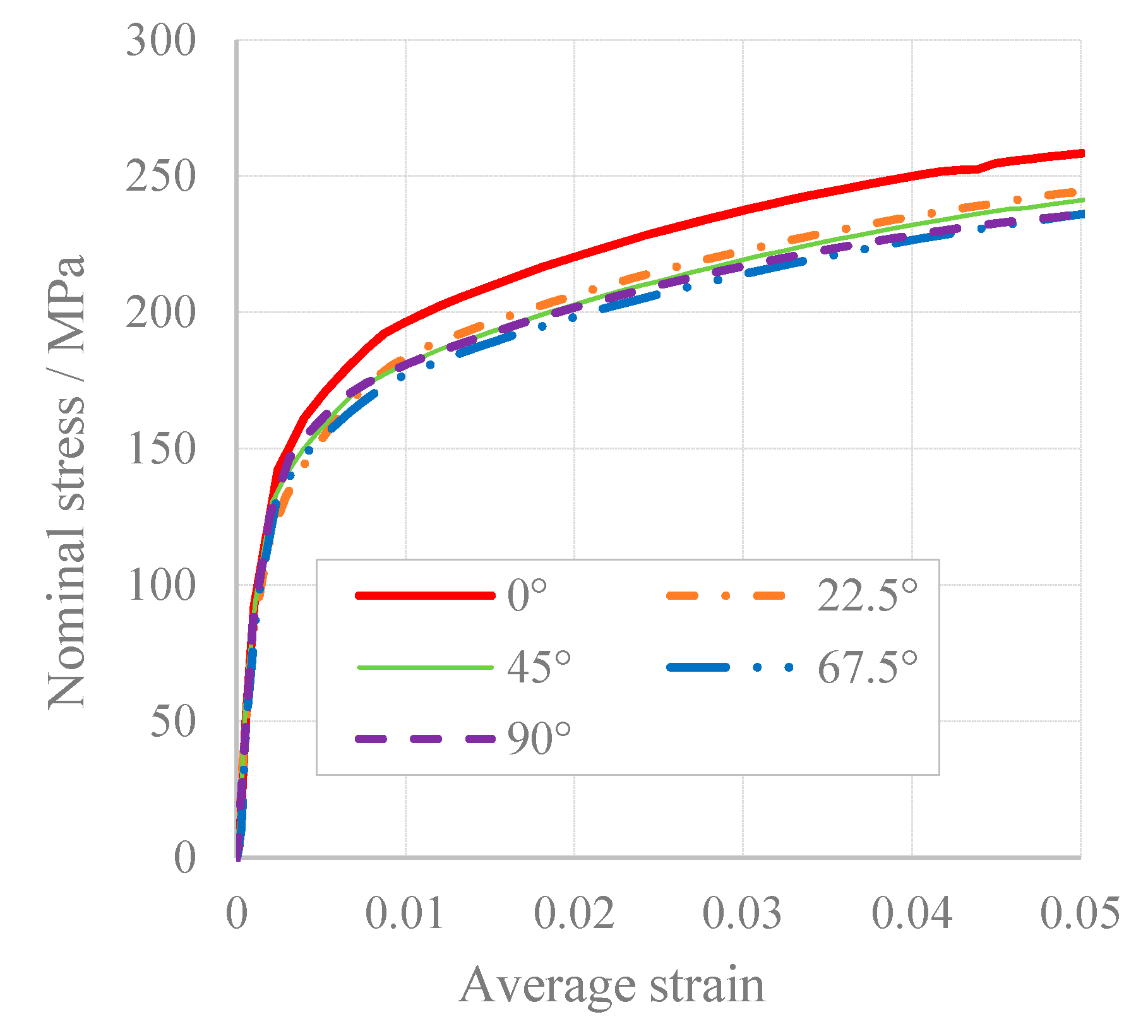
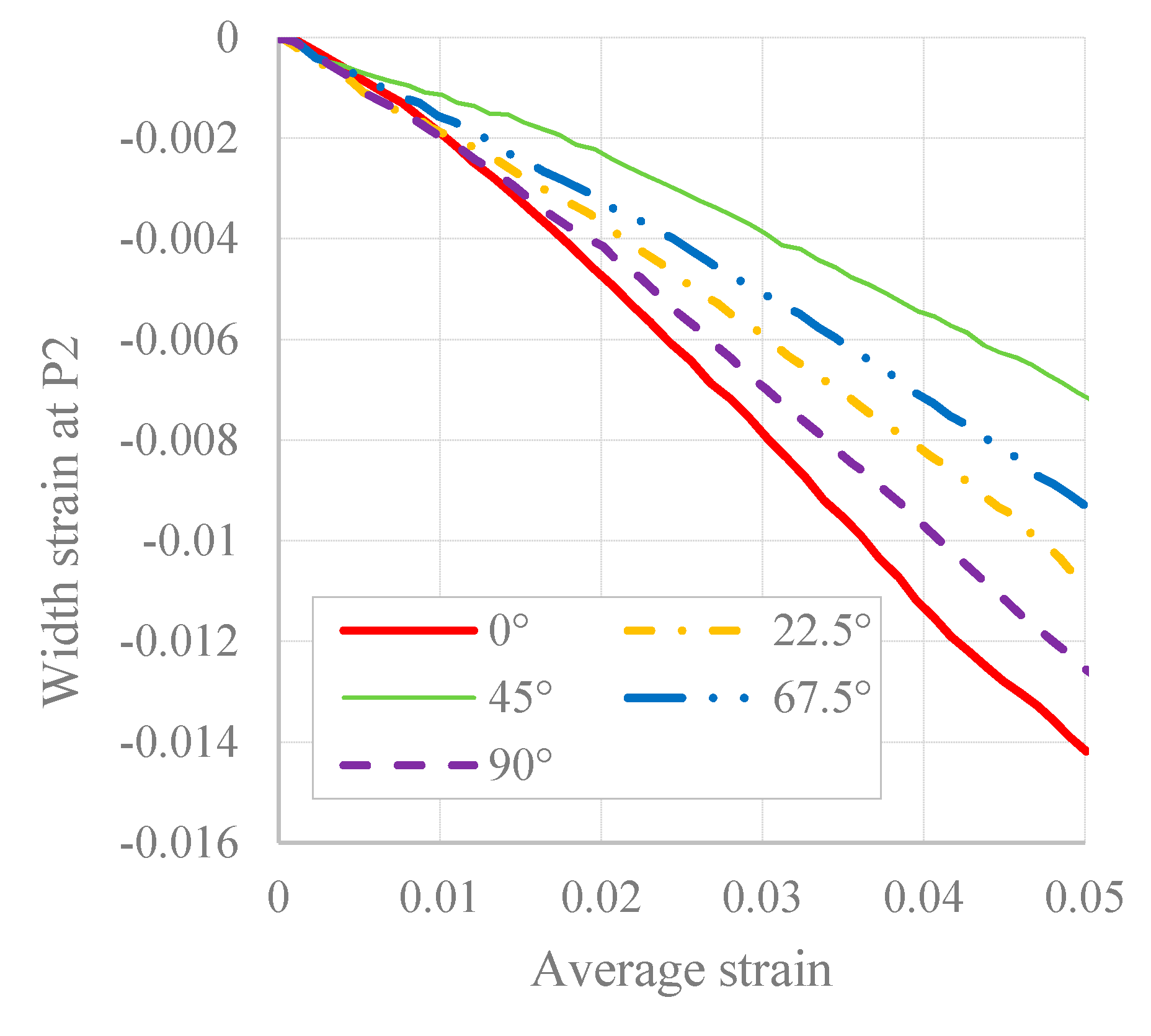





| Tensile Direction/° | Yield Strength (0.2%)/MPa | Tensile Strength/MPa | r (εp = 0.05) | Normalized Stress (εp = 0.05) | |
|---|---|---|---|---|---|
| 0 | 144.15 | 262.66 | 0.930 | 0.909 | 1.000 |
| 22.5 | 140.82 | 256.55 | 0.475 | 0.487 | 0.972 |
| 45 | 140.37 | 254.88 | 0.313 | 0.310 | 0.962 |
| 67.5 | 137.42 | 250.07 | 0.424 | 0.418 | 0.956 |
| 90 | 137.30 | 251.32 | 0.788 | 0.736 | 0.980 |
| Normalized Stress (εp = 0.05) | |
|---|---|
| 0.981 | 1.005 |
| k | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Angle from RD/° | 0 | 22.5 | 45 | 67.5 | 90 |
| pk | 0.458 | 0.337 | 0.200 | 0.260 | 0.342 |
| qk | 0.328 | 0.289 | 0.283 | 0.276 | 0.238 |
| Type of Experiment | α/° (Angle between Horizontal Arm and RD) | Displacement Ratio | Number of Repetitions |
|---|---|---|---|
| A | 0.0 | 1:1 | 3 |
| B | 0.0 | 2:1 | 3 |
| C | 22.5 | 1:1 | 3 |
| D | 22.5 | 2:1 | 3 |
| E | 45.0 | 1:1 | 3 |
| F | 45.0 | 2:1 | 3 |
| m | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.9760 | 1.0367 | 0.9459 | 1.0400 | 1.0166 | 1.0553 | 0.9083 | 1.1948 | 8 |
| Hill 1948 | YLD2000-2D | Spline Yield Function | |
|---|---|---|---|
| Average of sum of squared errors between experimental averages and simulation results for 3 circles of 6 conditions in Table 4 | 0.03032 | 0.00114 | 0.00063 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsutamori, H.; Amaishi, T.; Chorman, R.R.; Eder, M.; Vitzthum, S.; Volk, W. Evaluation of Prediction Accuracy for Anisotropic Yield Functions Using Cruciform Hole Expansion Test. J. Manuf. Mater. Process. 2020, 4, 43. https://doi.org/10.3390/jmmp4020043
Tsutamori H, Amaishi T, Chorman RR, Eder M, Vitzthum S, Volk W. Evaluation of Prediction Accuracy for Anisotropic Yield Functions Using Cruciform Hole Expansion Test. Journal of Manufacturing and Materials Processing. 2020; 4(2):43. https://doi.org/10.3390/jmmp4020043
Chicago/Turabian StyleTsutamori, Hideo, Toshiro Amaishi, Ray Rizaldi Chorman, Matthias Eder, Simon Vitzthum, and Wolfram Volk. 2020. "Evaluation of Prediction Accuracy for Anisotropic Yield Functions Using Cruciform Hole Expansion Test" Journal of Manufacturing and Materials Processing 4, no. 2: 43. https://doi.org/10.3390/jmmp4020043
APA StyleTsutamori, H., Amaishi, T., Chorman, R. R., Eder, M., Vitzthum, S., & Volk, W. (2020). Evaluation of Prediction Accuracy for Anisotropic Yield Functions Using Cruciform Hole Expansion Test. Journal of Manufacturing and Materials Processing, 4(2), 43. https://doi.org/10.3390/jmmp4020043




