Using the Segmented Iterative Learning Control Method to Generate Volumetric Error-Compensated Part Programs for Three-Axis CNC Milling Machine Tools
Abstract
1. Introduction
2. Introduction to Experimental System and Architecture
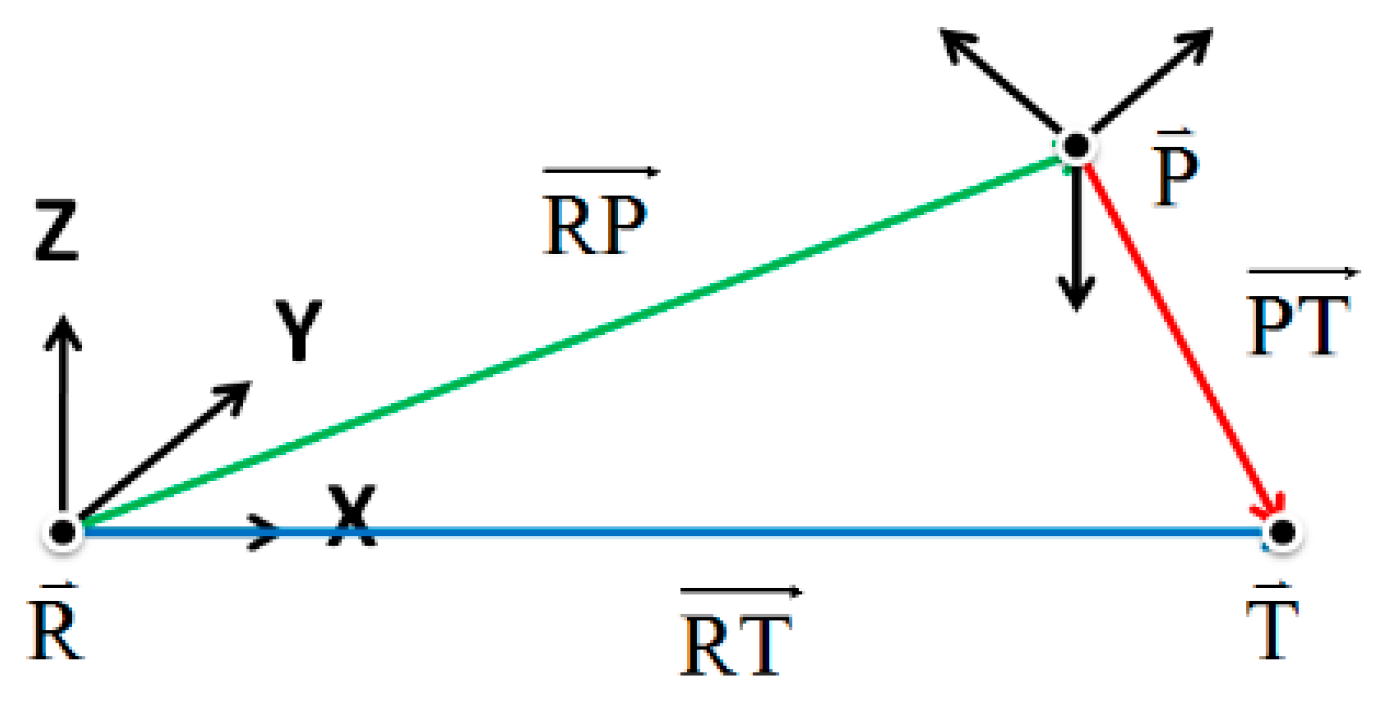
3. Volumetric Error Calculation and Compensation
- (S1)
- The tool moving direction from position R to position T (direction of vector) determines the load of the table of the forward volumetric errors or table of the reverse volumetric errors.
- (S2)
- The volumetric error vector (=) of the tool moves from position R to position T and is calculated by the loaded table of the volumetric errors.
- (S3)
- The tool moving T position and the calculated volumetric error vector are added up to generate the volumetric error-compensated position .
- The compensation and calculation of Equation (2) only consider the error compensation of target position T, while the position error compensation of a tool moving from R to T is not considered. In other words, the position accuracy of the tool moving process cannot be guaranteed.
- The compensation and calculation of Equation (2) disregard the effect of the volumetric error of the machine tool when the tool moves from position R to position . In other words, the actual position of the tool cannot be guaranteed, and the target position to be reached has position error.
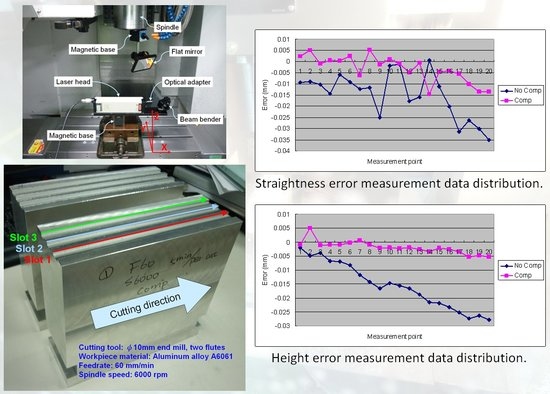
4. CNC Volumetric Error Compensation Experiment Results and Discussion
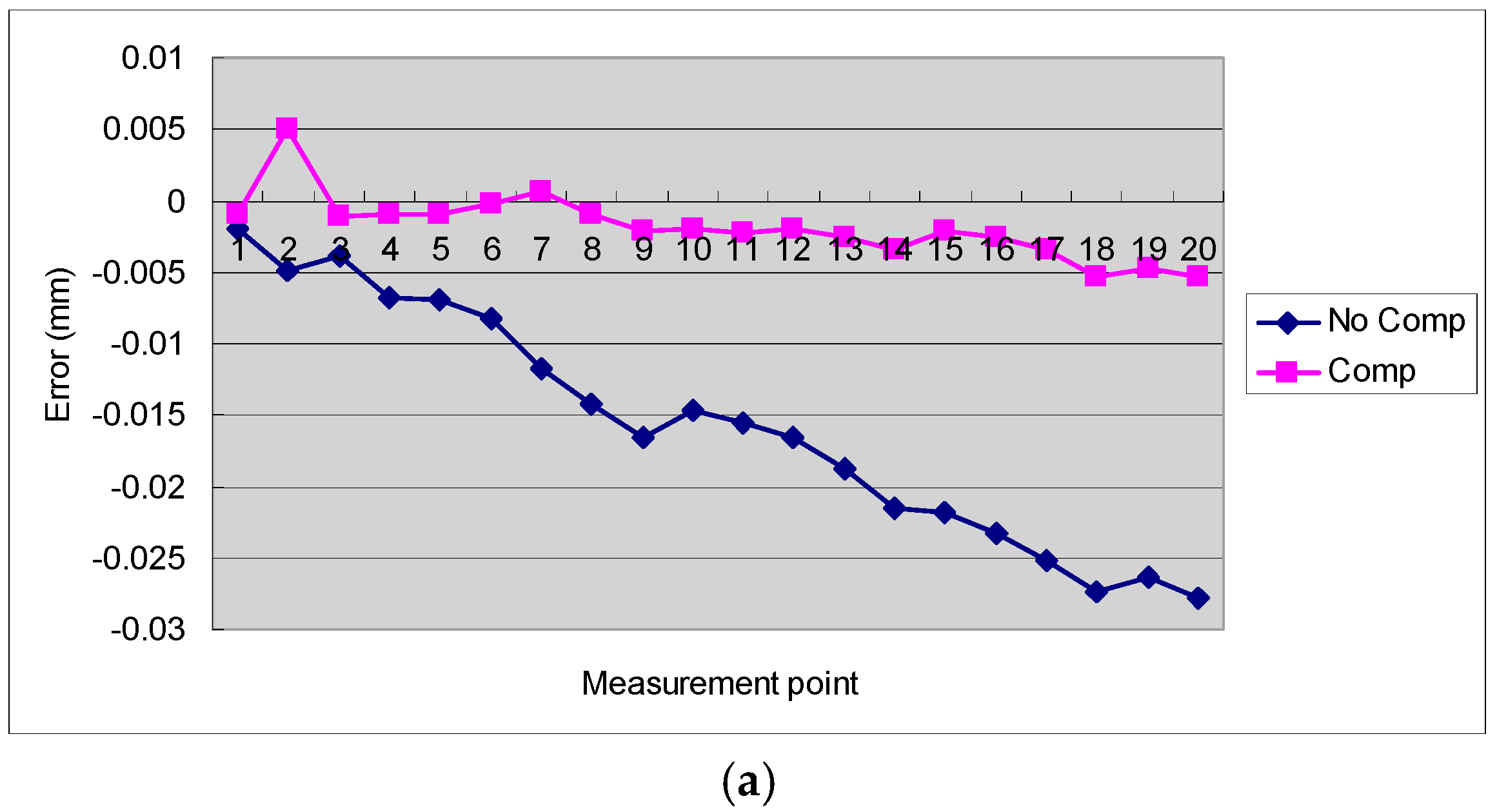
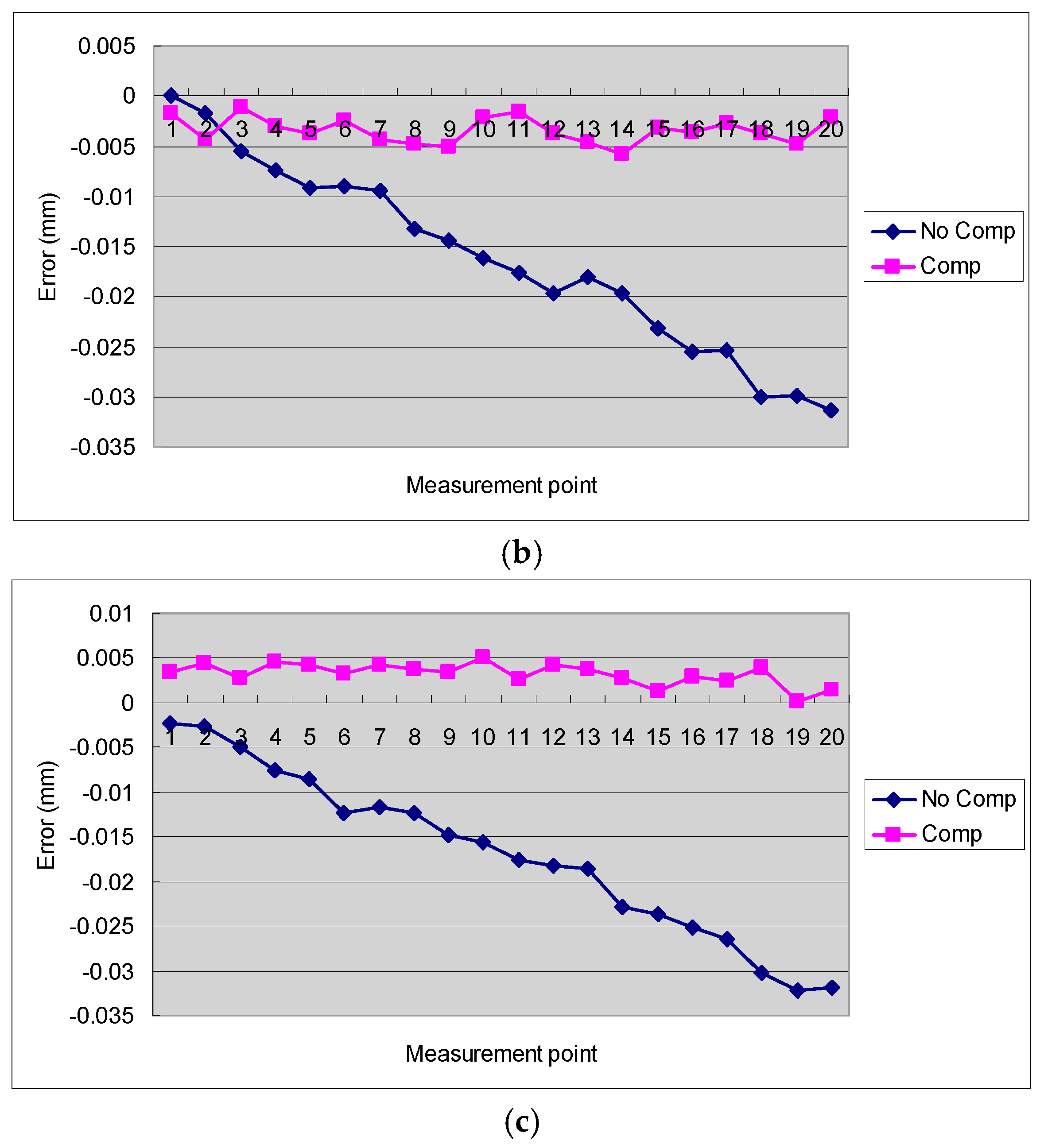
4.1. Simulation Results and Discussion
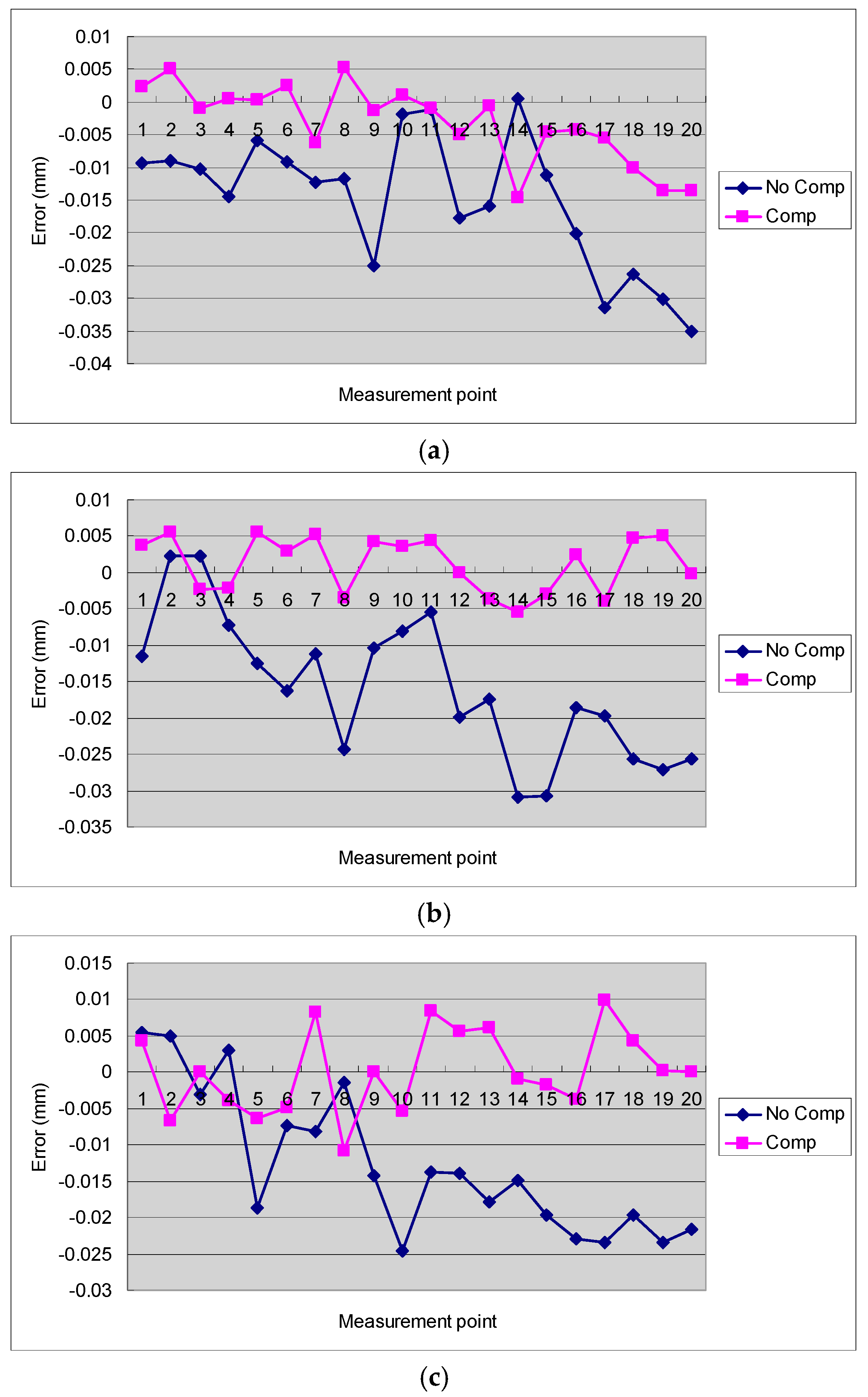
4.2. Discussion of the Results of Cutting Tests
5. Conclusions
- The volumetric error of the working volume of the three-axis CNC milling machine tool strongly influences the geometric dimension accuracy of the workpiece. The volumetric error compensation therefore becomes an issue that high-precision mechanical parts manufacturers must consider.
- Existing part-program modification methods only consider the compensation of the position of a single block of a part program but neglect the movement bias induced by volumetric error in the tool moving process, which leads to limited volumetric error compensation effect.
- In this study, the position of a single block of a part program was segmented, and volumetric error compensation was implemented for the tool moving position in each segment to generate a part program with multiple compensated blocks. The proposed compensation method can effectively compensate for volumetric errors in the tool moving process.
- In addition, this study used the ILC concept and referred to the present compensated tool path and volumetric error induced by the compensated tool path to calculate the next compensated tool path. Therefore, the optimum compensated tool path can be obtained by the iterative computation of the compensated tool path.
- To validate the effect of the proposed segmented volumetric error compensation, the measured and established table of volumetric errors was used for path simulation and cutting tests. Both the simulation and experimental results prove the feasibility of using the ILC method for the segmented modification of the volumetric error-compensated tool path.
- Several cutting tests were performed on a three-axis CNC milling machine tool. The experimental results showed that the average rate of improvement of the straightness error of the proposed volumetric error compensation method is higher than 60% while the rate of improvement of the height error is higher than 80%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zou, X.; Zhao, X.; Li, G.; Li, Z.; Sun, T. Sensitivity analysis using a variance-based method for a three-axis diamond turning machine. Int. J. Adv. Manuf. Technol. 2017, 92, 4429–4443. [Google Scholar] [CrossRef]
- Wang, Z.; Maropoulos, P.G. Real-time laser tracker compensation of a 3-axis positioning system—Dynamic accuracy characterization. Int. J. Adv. Manuf. Technol. 2016, 84, 1413–1420. [Google Scholar] [CrossRef]
- Uekita, M.; Takaya, Y. On-machine dimensional measurement of large parts by compensating for volumetric errors of machine tools. Precis. Eng. 2016, 43, 200–210. [Google Scholar] [CrossRef]
- Wang, K.; Sheng, X.; Kang, R. Volumetric error modelling, measurement, and compensation for an integrated measurement-processing machine tool. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 2477–2486. [Google Scholar] [CrossRef]
- Fletcher, S.; Postlethwaite, S.R.; Ford, D.G. Volumetric compensation through the machine controller. Laser Metrol. Mach. Perform. V 2001, 34, 321–330. [Google Scholar]
- Li, D.; Feng, P.; Zhang, J.; Yu, D.; Wu, Z. An identification method for key geometric errors of machine tool based on matrix differential and experimental test. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 3141–3155. [Google Scholar] [CrossRef]
- Okafor, A.C.; Ertekin, Y.M. Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics. Int. J. Mach. Tools Manuf. 2000, 40, 1199–1213. [Google Scholar] [CrossRef]
- Chen, J.S.; Kou, T.W.; Chiou, S.H. Geometric error calibration of multi-axis machines using an auto-alignment laser interferometer. Precis. Eng. 1999, 23, 243–252. [Google Scholar] [CrossRef]
- Knapp, W.; Matthias, E. Test of the three-dimensional uncertainty of machine tools and measuring machines and its relation to the machine errors. CIRP Ann. Manuf. Technol. 1983, 32, 459–464. [Google Scholar] [CrossRef]
- Ni, J.; Wu, S.M. On-line measurement technique for machine volumetric error compensation. J. Eng. Ind. Trans. ASME 1993, 115, 85–92. [Google Scholar] [CrossRef]
- Ibaraki, S.; Knapp, W. Indirect measurement of volumetric accuracy for three-axis and five-axis machine tools: A review. Int. J. Autom. Technol. 2012, 6, 110–124. [Google Scholar] [CrossRef]
- Majda, P. Modeling of geometric errors of linear guideway and their influence on joint kinematic error in machine tools. Precis. Eng. 2012, 36, 369–378. [Google Scholar] [CrossRef]
- He, Z.; Fu, J.; Yao, X.; Qian, W. Volumetric error identification for CNC machine tool based on multi-body system and vector diagonal measurement. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 3345–3349. [Google Scholar]
- Jung, J.H.; Choi, J.P.; Lee, S.J. Machining accuracy enhancement by compensating for volumetric errors of a machine tool and on-machine measurement. J. Mater. Process. Technol. 2006, 174, 56–66. [Google Scholar] [CrossRef]
- Ahn, K.G.; Min, B.K.; Pasek, Z.J. Modeling and compensation of geometric errors in simultaneous cutting using a multi-spindle machine tool. Int. J. Adv. Manuf. Technol. 2006, 29, 929–939. [Google Scholar] [CrossRef]
- Yang, S.H.; Kim, K.H.; Park, Y.K.; Lee, S.G. Error analysis and compensation for the volumetric errors of a vertical machining centre using a hemispherical helix ball bar test. Int. J. Adv. Manuf. Technol. 2004, 23, 495–500. [Google Scholar] [CrossRef]
- Xiang, S.; Yang, J.; Fan, K.; Lu, H. Multi-machine tools volumetric error generalized modeling and ethernetbased compensation technique. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 870–882. [Google Scholar] [CrossRef]
- Holub, M.; Blecha, P.; Bradac, F.; Kana, R. Volumetric compensation of three-axis vertical machining centre. MM Sci. J. 2015, 2015, 677–681. [Google Scholar] [CrossRef]
- Holub, M.; Vetiska, J.; Bradac, F.; Vala, M. Application on-the-fly measurement of CNC machine tools. MM Sci. J. 2017, 2017, 2085–2089. [Google Scholar] [CrossRef]
- Gomez-Acedo, E.; Olarra, A.; Orive, J.; Lopez De La Calle, L.N. Methodology for the design of a thermal distortion compensation for large machine tools based in state-space representation with Kalman filter. Int. J. Mach. Tools Manuf. 2013, 75, 100–108. [Google Scholar] [CrossRef]
- Gomez-Acedo, E.; Olarra, A.; Zubieta, M.; Kortaberria, G.; Ariznabarreta, E.; López de Lacalle, L.N. Method for measuring thermal distortion in large machine tools by means of laser multilateration. Int. J. Adv. Manuf. Technol. 2015, 80, 523–534. [Google Scholar] [CrossRef]
- López De Lacalle, L.N.; Lamikiz, A.; Ocerin, O.; Díez, D.; Maidagan, E. The Denavit and Hartenberg approach applied to evaluate the consequences in the tool tip position of geometrical errors in five-axis milling centres. Int. J. Adv. Manuf. Technol. 2008, 37, 122–139. [Google Scholar] [CrossRef]
- Díaz-Tena, E.; Ugalde, U.; López De Lacalle, L.N.; De La Iglesia, A.; Calleja, A.; Campa, F.J. Propagation of assembly errors in multitasking machines by the homogenous matrix method. Int. J. Adv. Manuf. Technol. 2013, 68, 149–164. [Google Scholar] [CrossRef]
- Shen, H.; Fu, J.; He, Y.; Yao, X. On-line asynchronous compensation methods for static/quasi-static error implemented on CNC machine tools. Int. J. Mach. Tools Manuf. 2012, 60, 14–26. [Google Scholar] [CrossRef]
- Wang, J.; Guo, J. Research on volumetric error compensation for NC machine tool based on laser tracker measurement. Sci. China Technol. Sci. 2012, 55, 3000–3009. [Google Scholar] [CrossRef]
- Vahebi Nojedeh, M.; Habibi, M.; Arezoo, B. Tool path accuracy enhancement through geometrical error compensation. Int. J. Mach. Tools Manuf. 2011, 51, 439–449. [Google Scholar] [CrossRef]
- Wang, S.M.; Lin, J.J. On-machine volumetric-error measurement and compensation methods for micro machine tools. Int. J. Precis. Eng. Manuf. 2013, 14, 989–994. [Google Scholar] [CrossRef]
- Eskandari, S.; Arezoo, B.; Abdullah, A. Positional, geometrical, and thermal errors compensation by tool path modification using three methods of regression, neural networks, and fuzzy logic. Int. J. Adv. Manuf. Technol. 2013, 65, 1635–1649. [Google Scholar] [CrossRef]
- Sun, S.H.; Lee, E.S.; Sohn, J.W. Enhancement of geometric accuracy via an intermediate geometrical feedback scheme. J. Manuf. Syst. 1999, 18, 12–21. [Google Scholar]
- Lee, E.S.; Suh, S.H.; Shon, J.W. A comprehensive method for calibration of volumetric positioning accuracy of CNC-machines. Int. J. Adv. Manuf. Technol. 1998, 14, 43–49. [Google Scholar] [CrossRef]
- Kiridena, V.S.B.; Ferreira, P.M. Computational approaches to compensating quasistatic errors of three-axis machining centers. Int. J. Mach. Tools Manuf. 1994, 34, 127–145. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, Z.; Yamazaki, K. Machine tool component error extraction and error compensation by incorporating statistical analysis. Int. J. Mach. Tools Manuf. 2010, 50, 798–806. [Google Scholar] [CrossRef]
- Lee, J.H.; Liu, Y.; Yang, S.H. Accuracy improvement of miniaturized machine tool: Geometric error modeling and compensation. Int. J. Mach. Tools Manuf. 2006, 46, 1508–1516. [Google Scholar] [CrossRef]
- Wang, C. Laser vector measurement technique for the determination and compensation of volumetric positioning errors. Part I: Basic theory. Rev. Sci. Instrum. 2000, 71, 3933–3937. [Google Scholar] [CrossRef]
- Janeczko, J.; Griffin, B.; Wang, C. Laser vector measurement technique for the determination and compensation of volumetric position errors. Part II: Experimental verification. Rev. Sci. Instrum. 2000, 71, 3938–3941. [Google Scholar] [CrossRef]
- Fanuc. Fanuc User’s Manual: Common to Lathe System/Machining Center System; Fanuc Corporation: Yamanashi Prefecture, Japan, 2004; Volume B-63944EN/02. [Google Scholar]
- Spong, M.K.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Uchiyama, M. Formation of high speed motion pattern of mechanical arm by trial. Trans. Soc. Instrum. Control Eng. 1978, 14, 706–712. [Google Scholar] [CrossRef]
- Kim, D.-I.; Kim, S. On iterative learning control algorithm for industrial robots and CNC machine tools. In Proceedings of the IECON’93 19th Annual Conference of IEEE Industrial Electronics, Maui, HI, USA, 15–19 November 1993; pp. 601–606. [Google Scholar]
- Kim, D.I.; Kim, S. An iterative learning control method with application for CNC machine tools. IEEE Trans. Ind. Appl. 1996, 32, 66–72. [Google Scholar] [CrossRef]
- Arimoto, S.; Kawamura, S.; Miyazaki, F. Bettering operation of robots by learning. J. Robot. Syst. 1984, 1, 123–140. [Google Scholar] [CrossRef]
- Arimoto, S.; Naniwa, T.; Suzuki, H. Robustness of P-type learning control with a forgetting factor for robotic motions. In Proceedings of the IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 2640–2645. [Google Scholar]
- Bien, Z.; Huh, K.M. Higher-order iterative learning control algorithm. IEEE Proc. D Control Theory Appl. 1989, 136, 105–112. [Google Scholar] [CrossRef]


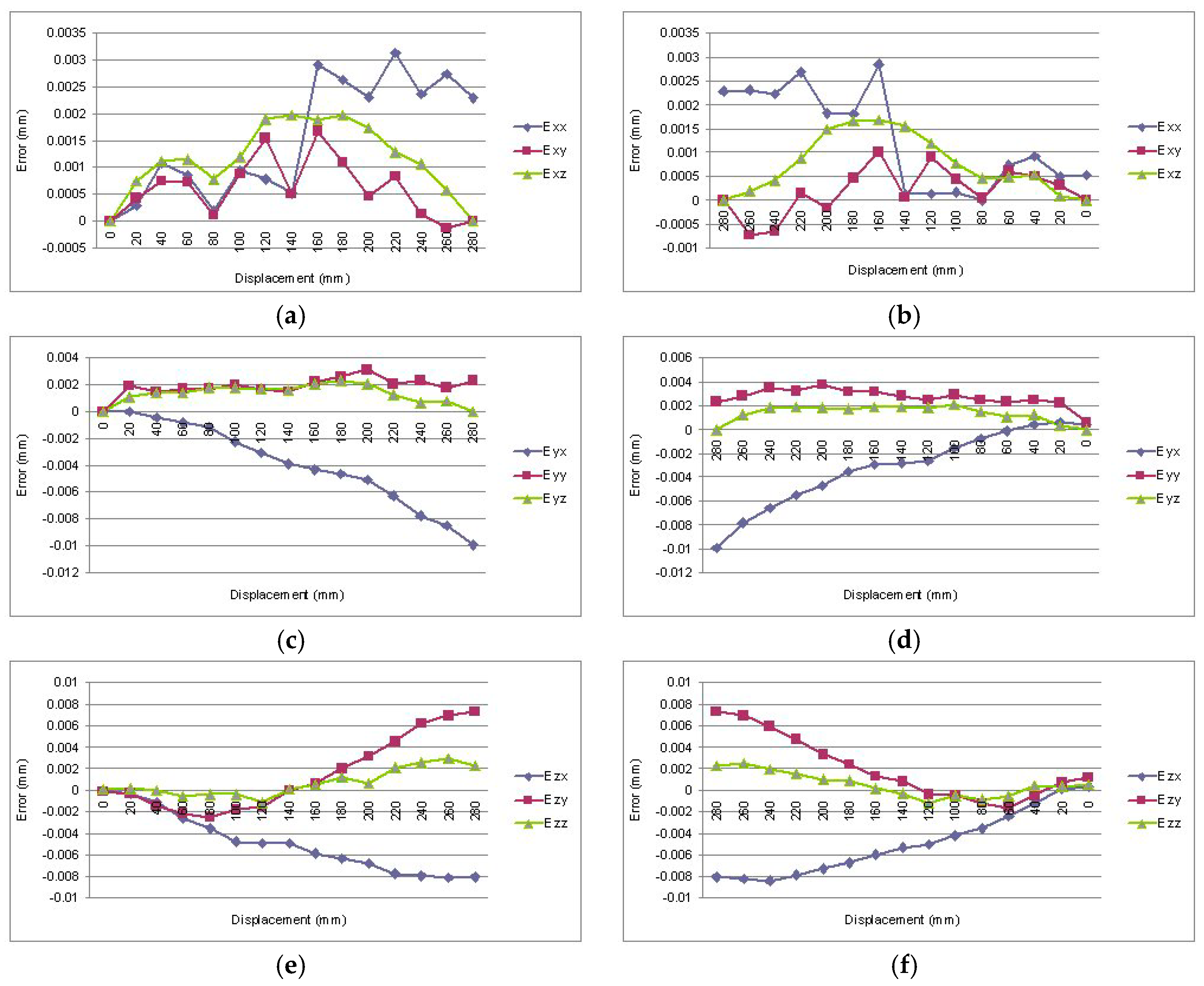
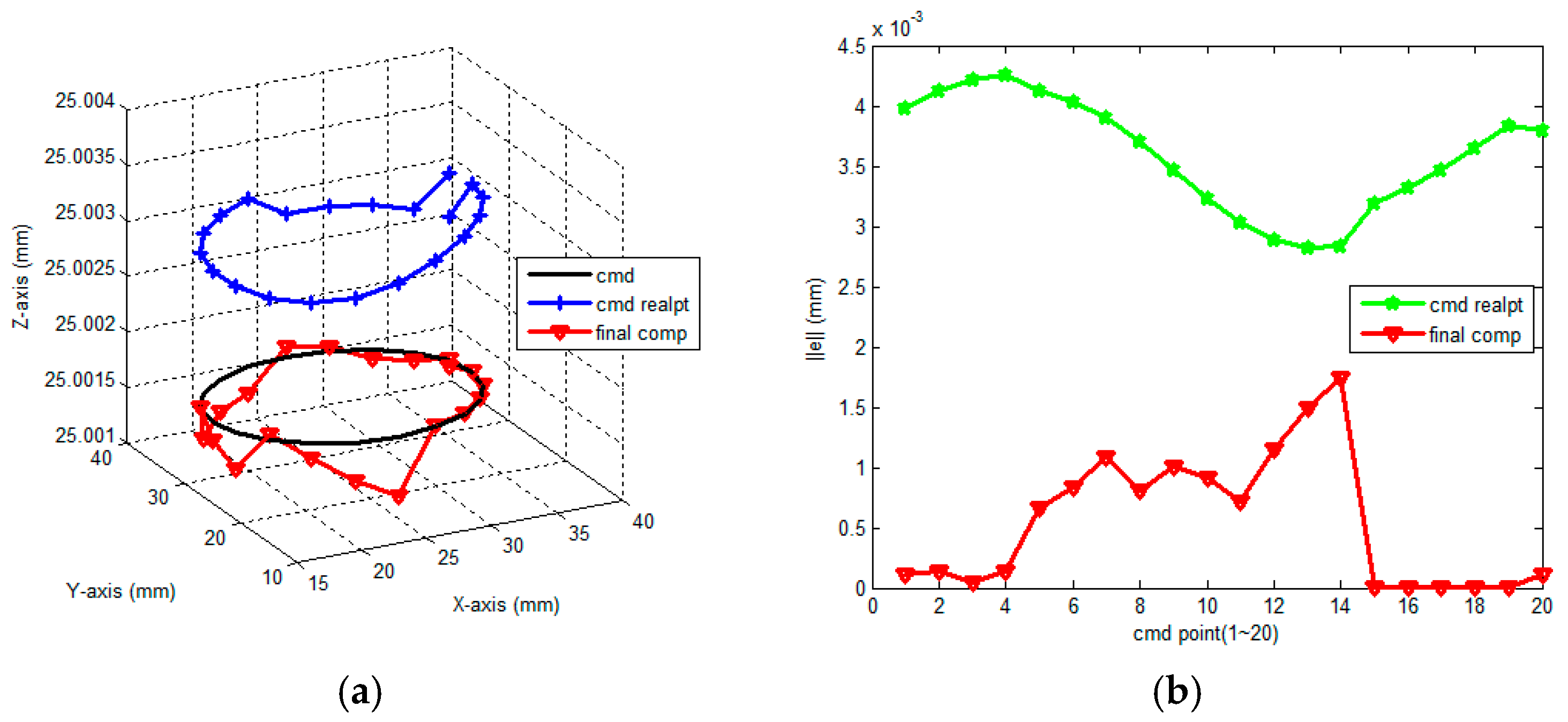
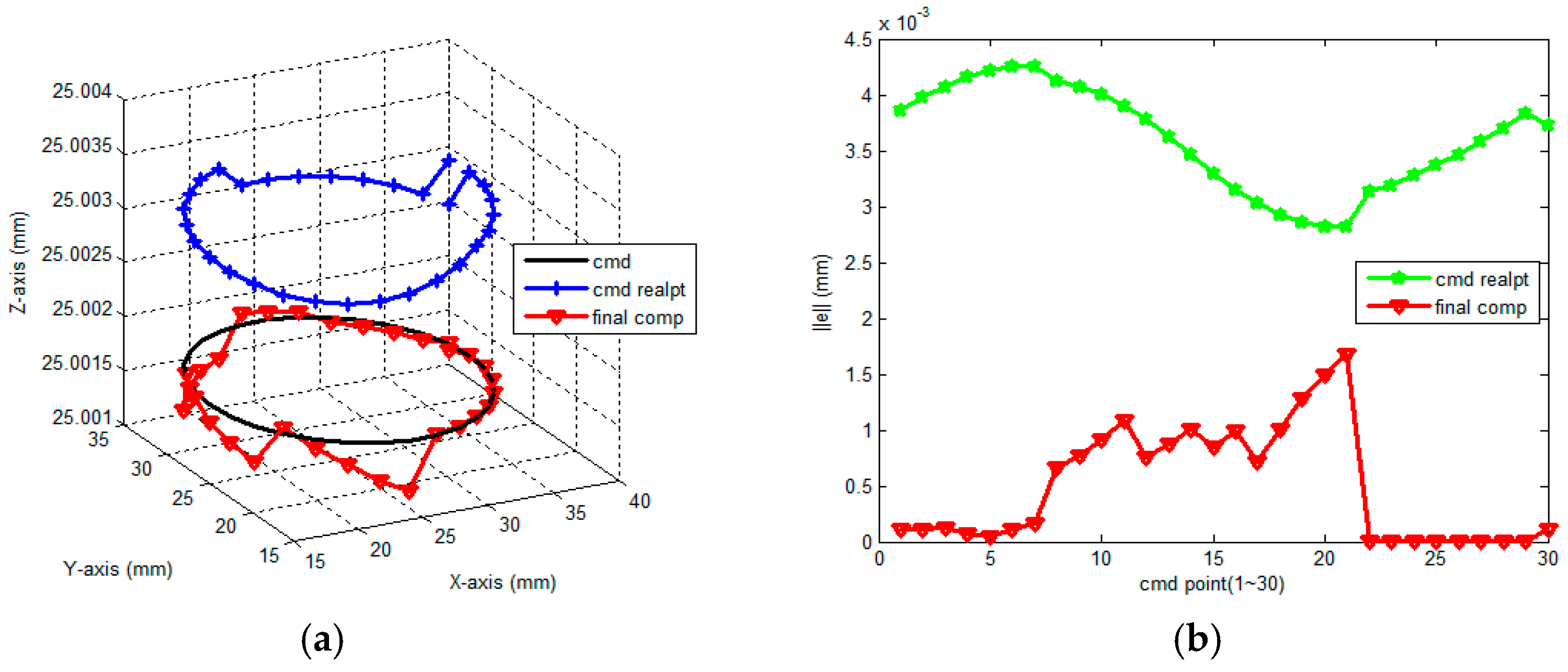
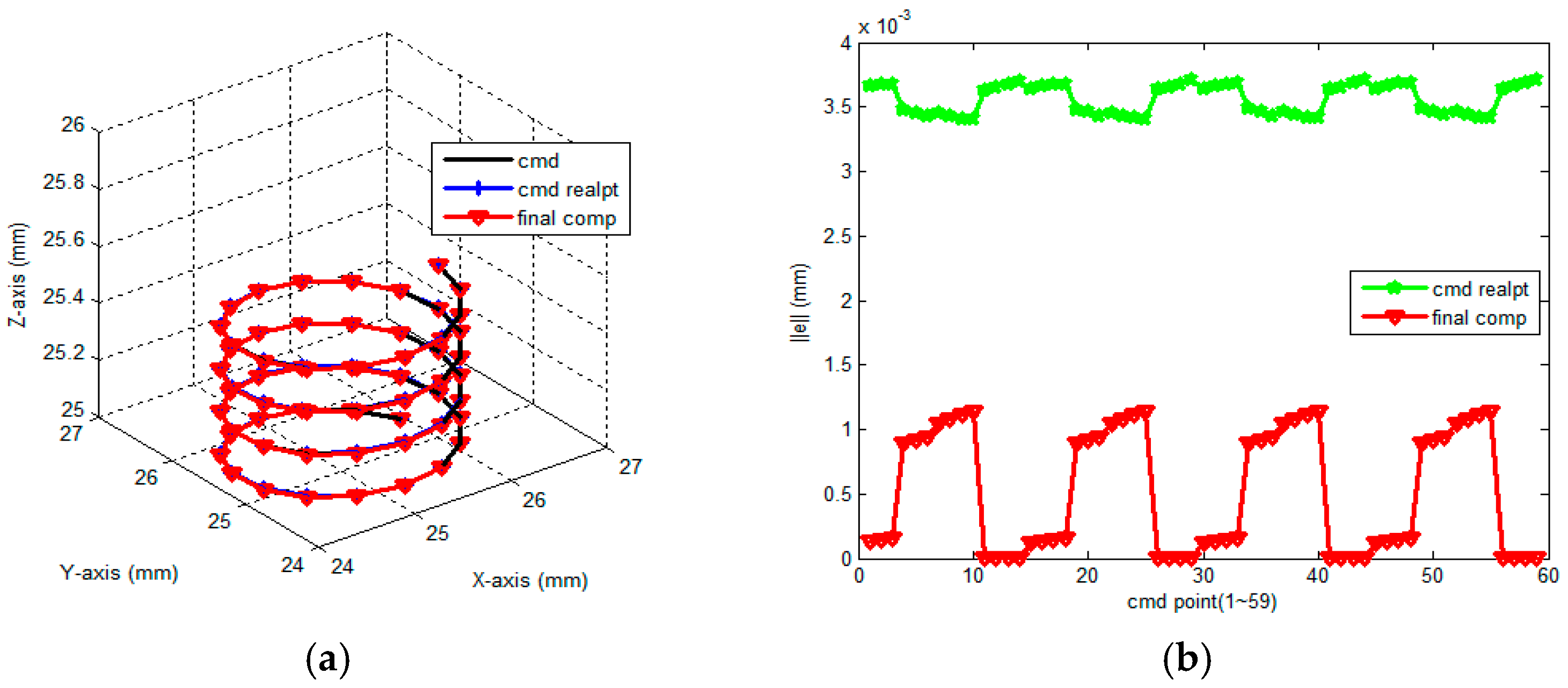

| Tool Moving Path | Circular 20 Segments | Circular 30 Segments | Spiral 60 Segments |
|---|---|---|---|
| Euclidean norm root-mean-square value of position errors of the segmented tool moving path (μm) | |||
| Volumetric error (before ILC compensation) | 3.39 | 3.41 | 3.31 |
| ILC compensation (after ILC compensation) | 0.77 | 0.72 | 0.71 |
| Rate of improvement (%) | 77.28 | 78.89 | 78.55 |
| Slot Number | 1 | 2 | 3 |
|---|---|---|---|
| Straightness error root-mean-square value comparison (unit: mm) | |||
| Without compensation | 0.0179 | 0.0186 | 0.0160 |
| With ILC compensation | 0.0067 | 0.0039 | 0.0056 |
| Rate of improvement (%) | 62.57 | 79.03 | 65.00 |
| Height error root-mean-square value comparison (unit: mm) | |||
| Without compensation | 0.0177 | 0.0187 | 0.0193 |
| With ILC compensation | 0.0029 | 0.0037 | 0.0035 |
| Rate of improvement (%) | 83.62 | 80.21 | 81.87 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.-C.; Yeh, S.-S. Using the Segmented Iterative Learning Control Method to Generate Volumetric Error-Compensated Part Programs for Three-Axis CNC Milling Machine Tools. J. Manuf. Mater. Process. 2018, 2, 53. https://doi.org/10.3390/jmmp2030053
Lu Y-C, Yeh S-S. Using the Segmented Iterative Learning Control Method to Generate Volumetric Error-Compensated Part Programs for Three-Axis CNC Milling Machine Tools. Journal of Manufacturing and Materials Processing. 2018; 2(3):53. https://doi.org/10.3390/jmmp2030053
Chicago/Turabian StyleLu, Ying-Chen, and Syh-Shiuh Yeh. 2018. "Using the Segmented Iterative Learning Control Method to Generate Volumetric Error-Compensated Part Programs for Three-Axis CNC Milling Machine Tools" Journal of Manufacturing and Materials Processing 2, no. 3: 53. https://doi.org/10.3390/jmmp2030053
APA StyleLu, Y.-C., & Yeh, S.-S. (2018). Using the Segmented Iterative Learning Control Method to Generate Volumetric Error-Compensated Part Programs for Three-Axis CNC Milling Machine Tools. Journal of Manufacturing and Materials Processing, 2(3), 53. https://doi.org/10.3390/jmmp2030053