Numerical and Experimental Analysis of the Gear Size Influence on Density Variations and Distortions during the Manufacturing of PM Gears with an Innovative Powder Processing Route Incorporating HIP
Abstract
1. Introduction
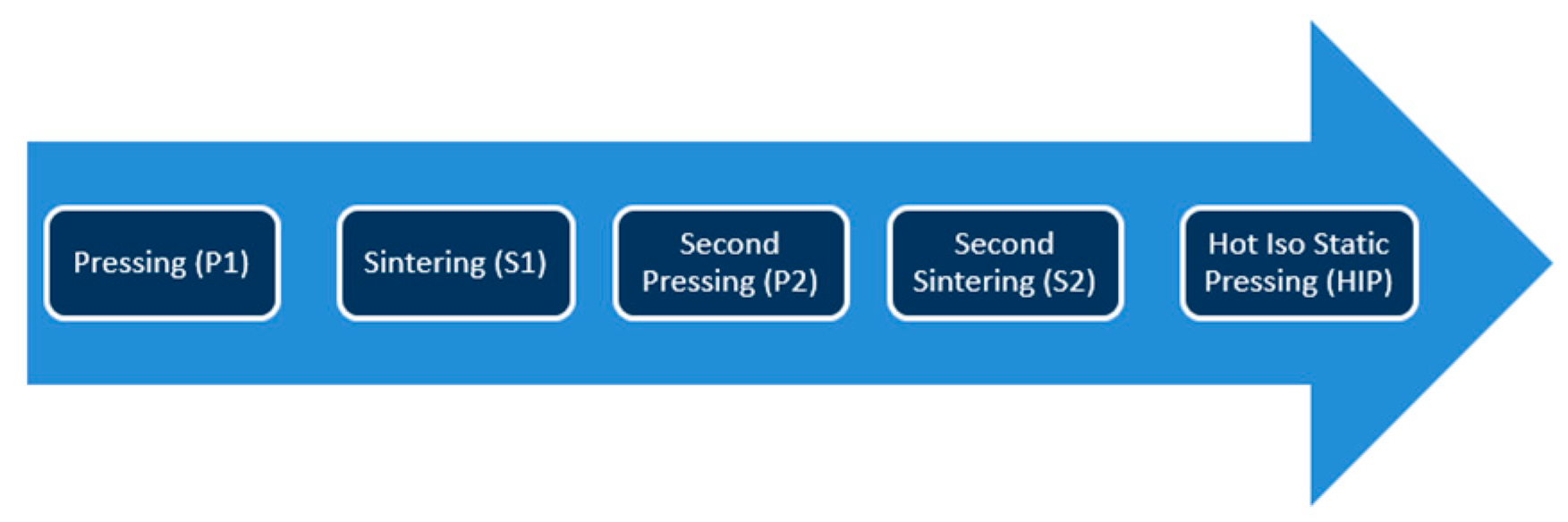
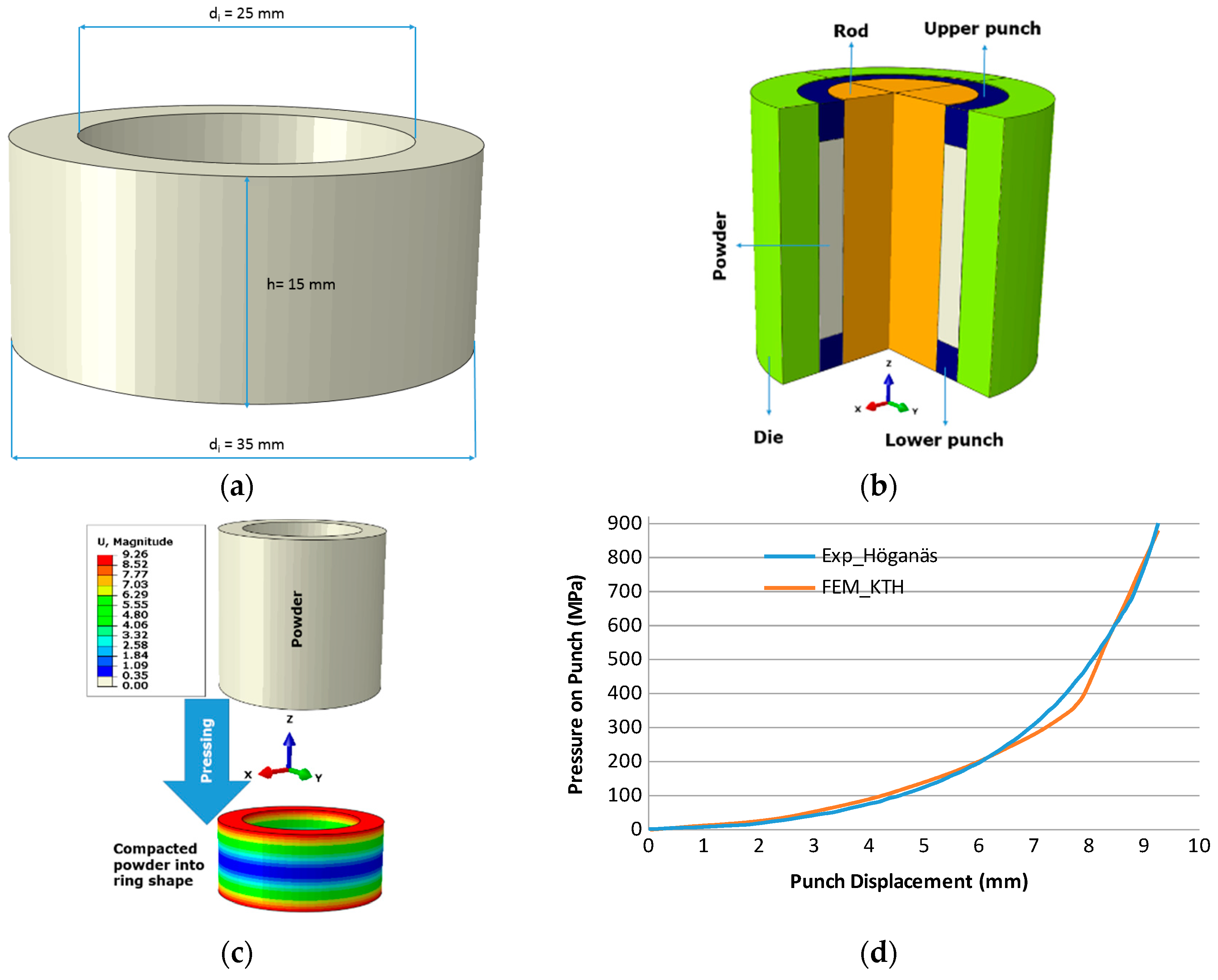
2. Experimental Procedure
3. Numerical Simulation
3.1. Material Models
Material Model Parameters
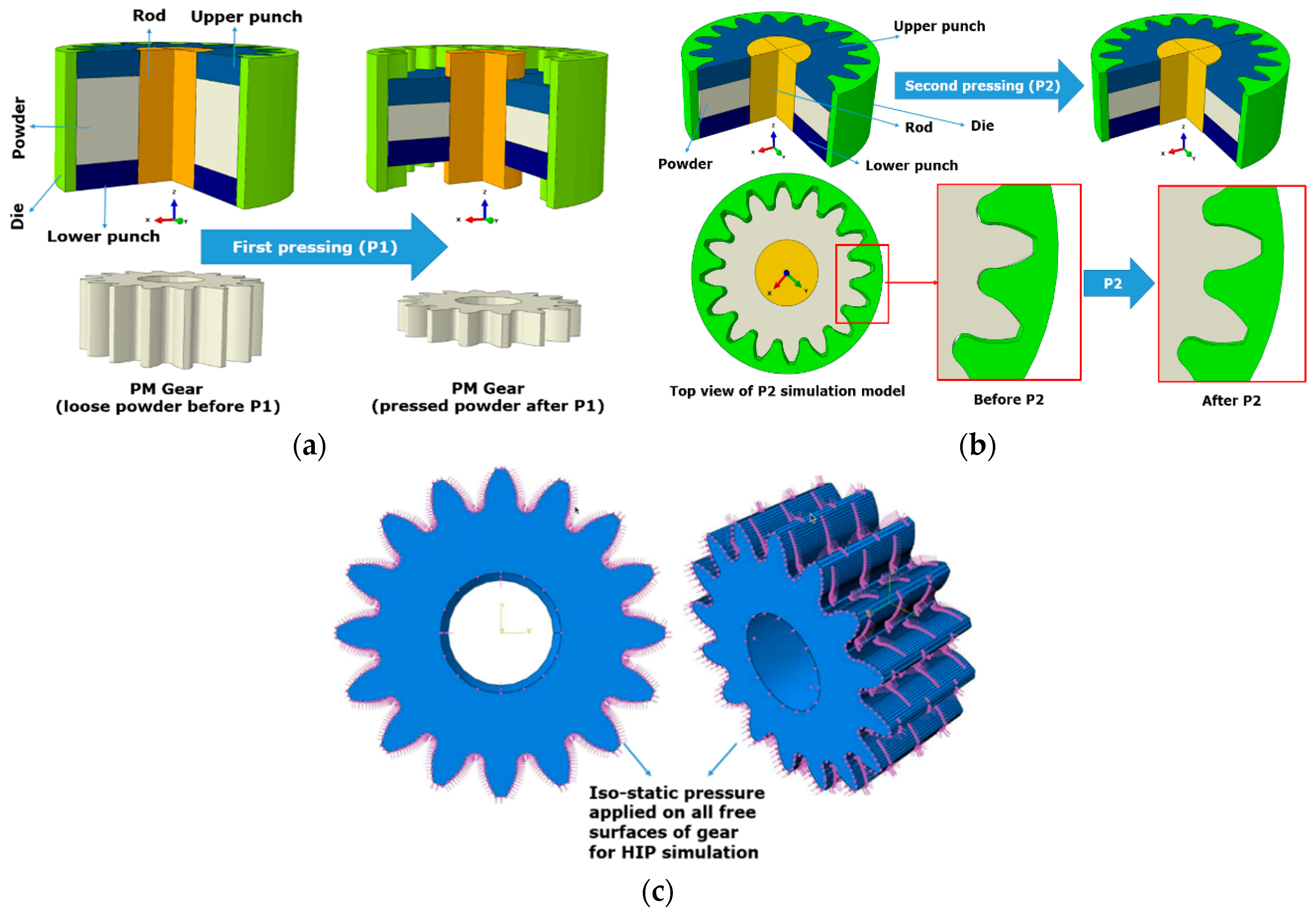
3.2. Geometrical Modelling
3.3. Friction
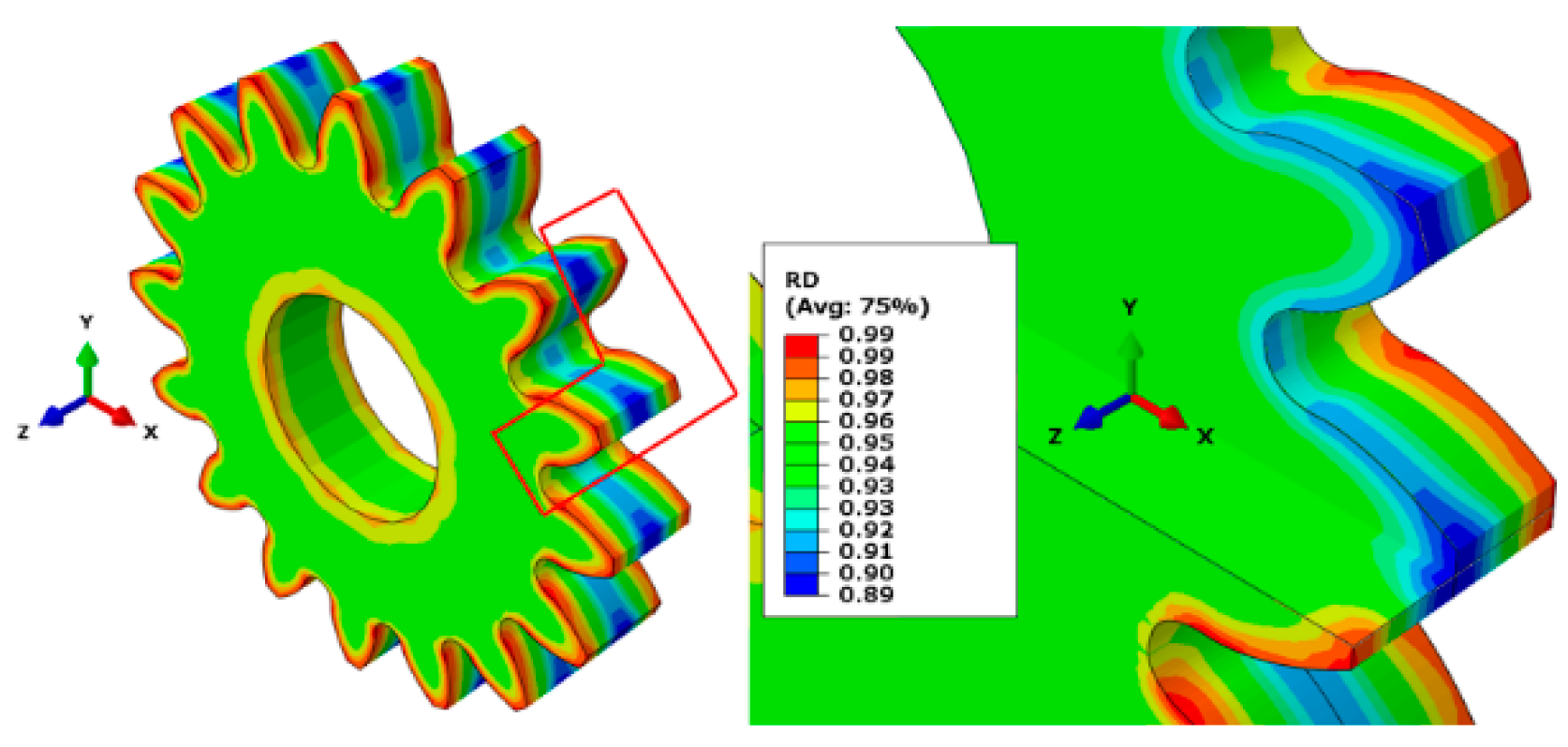
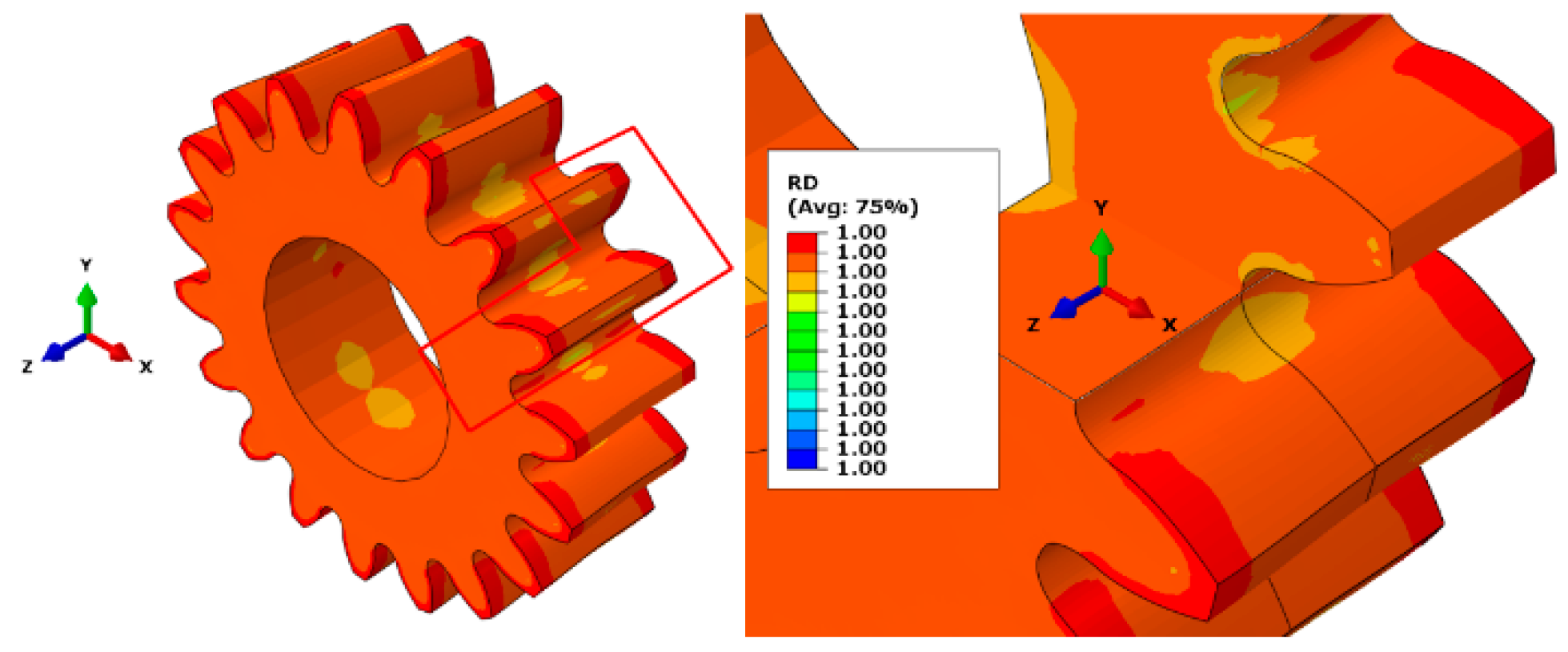
4. Results
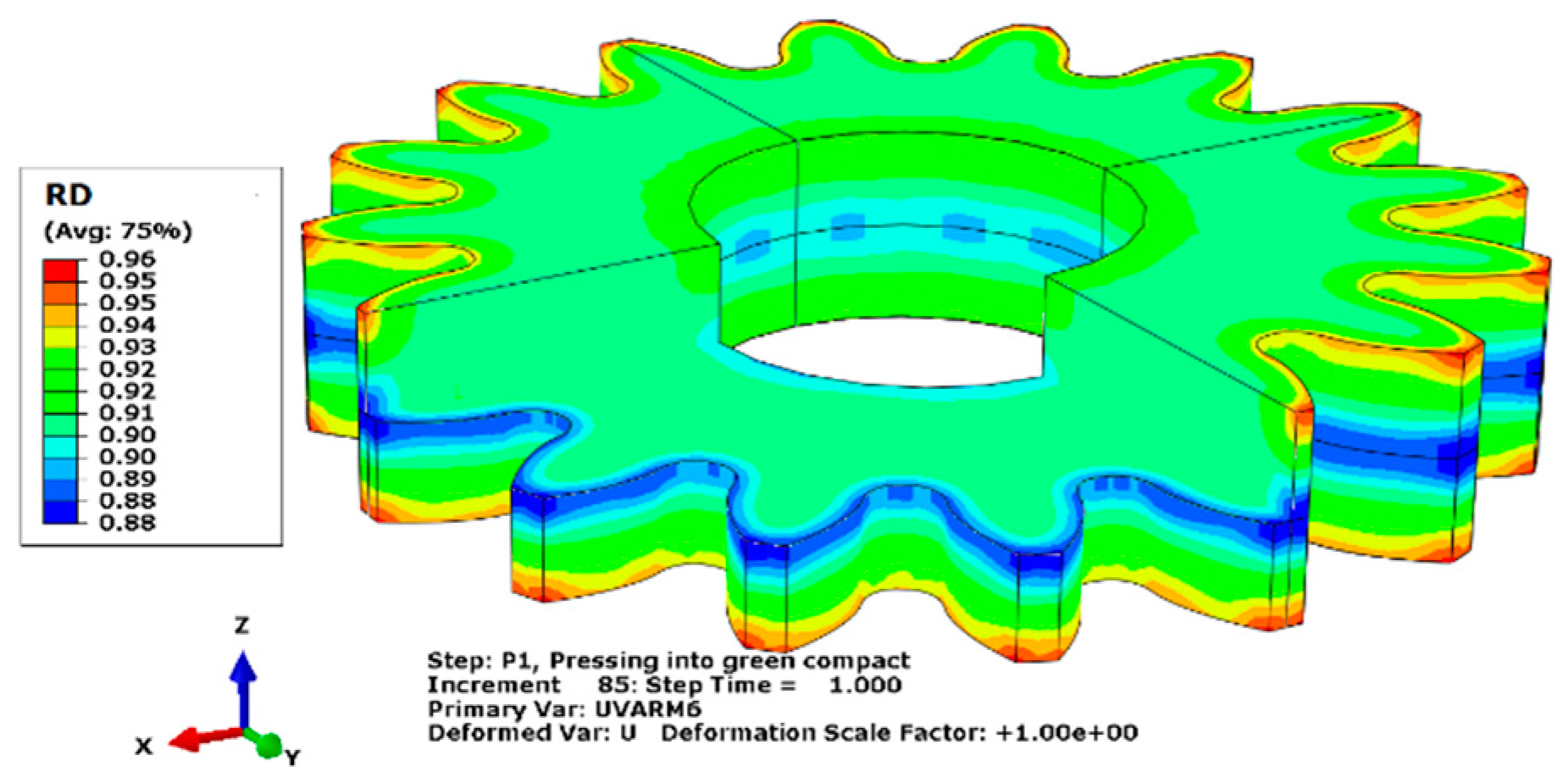
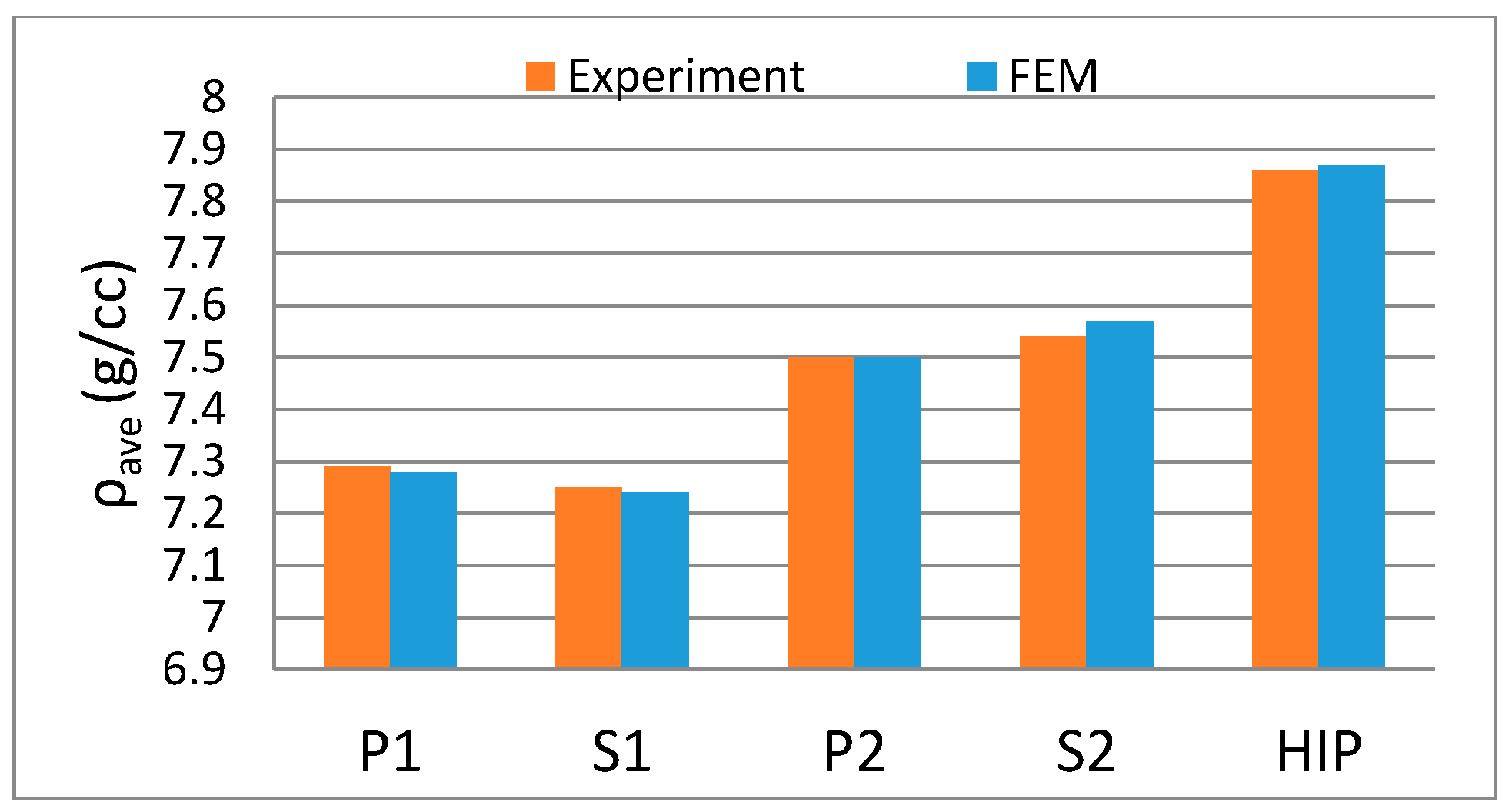
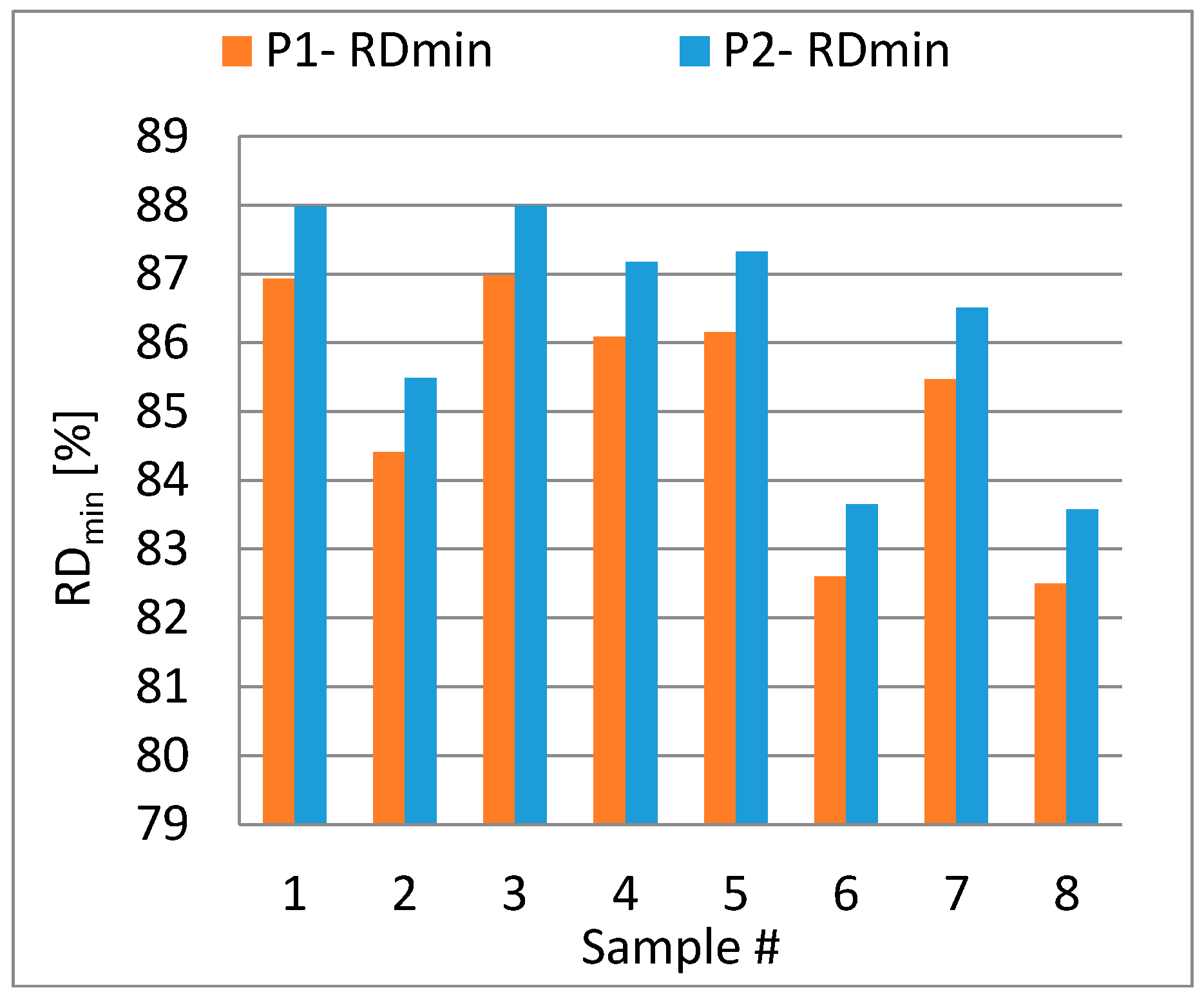
4.1. Average Density Results
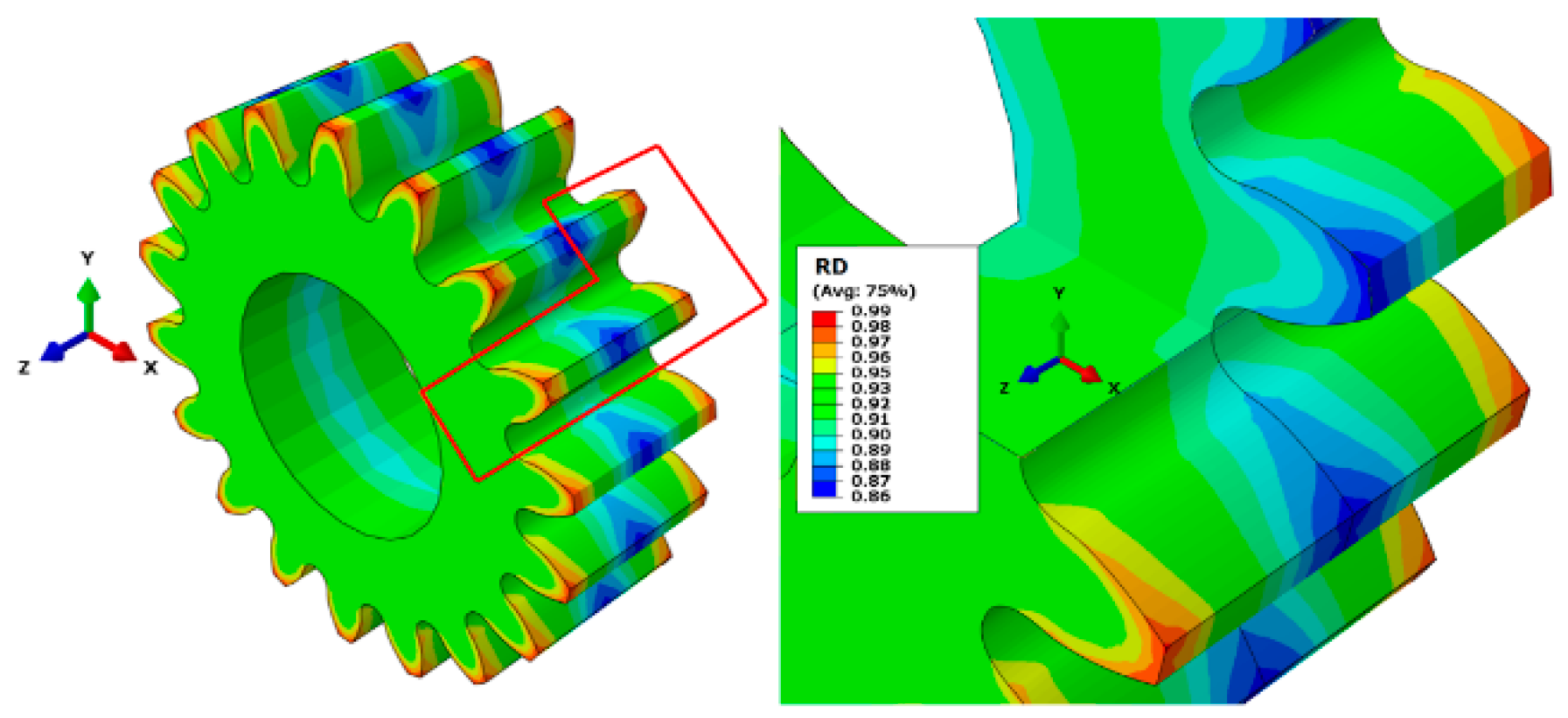
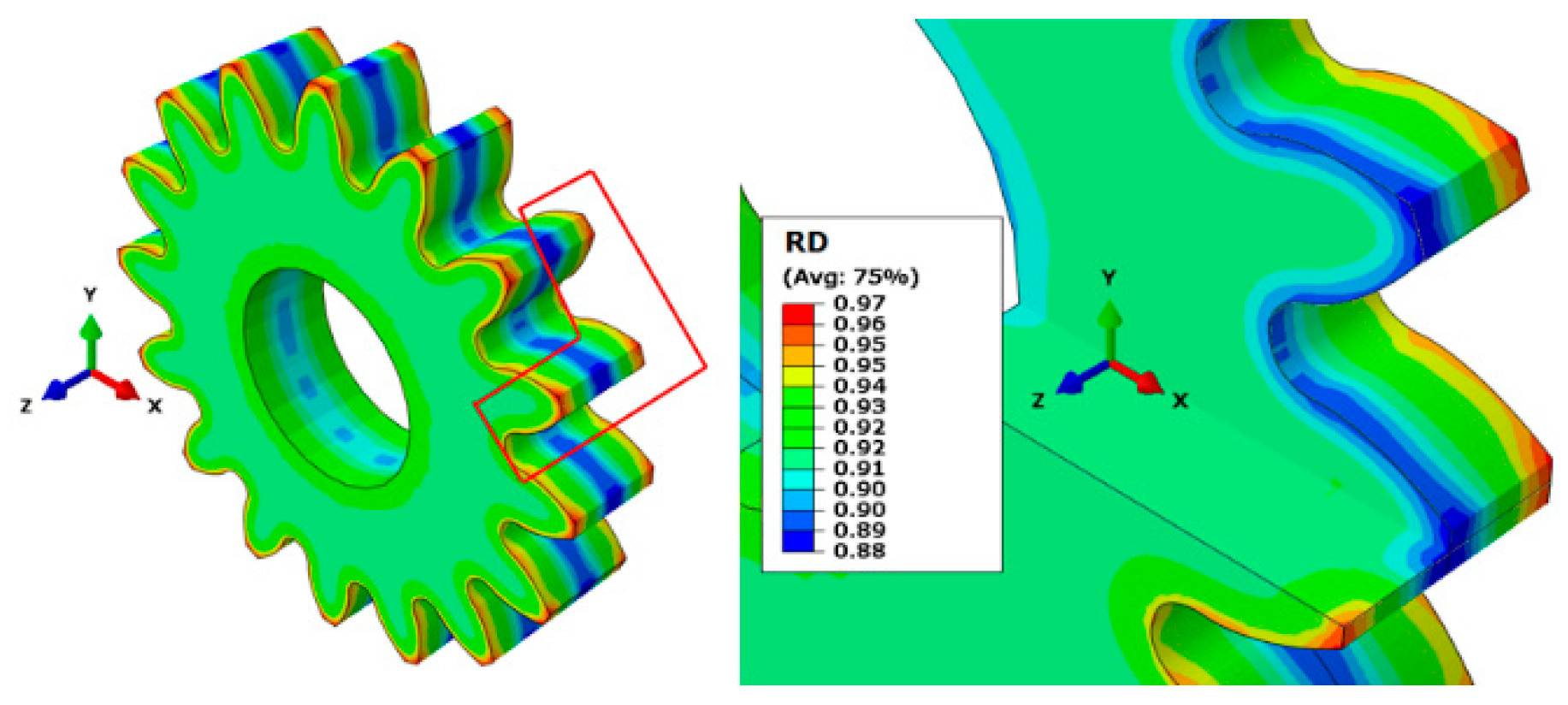
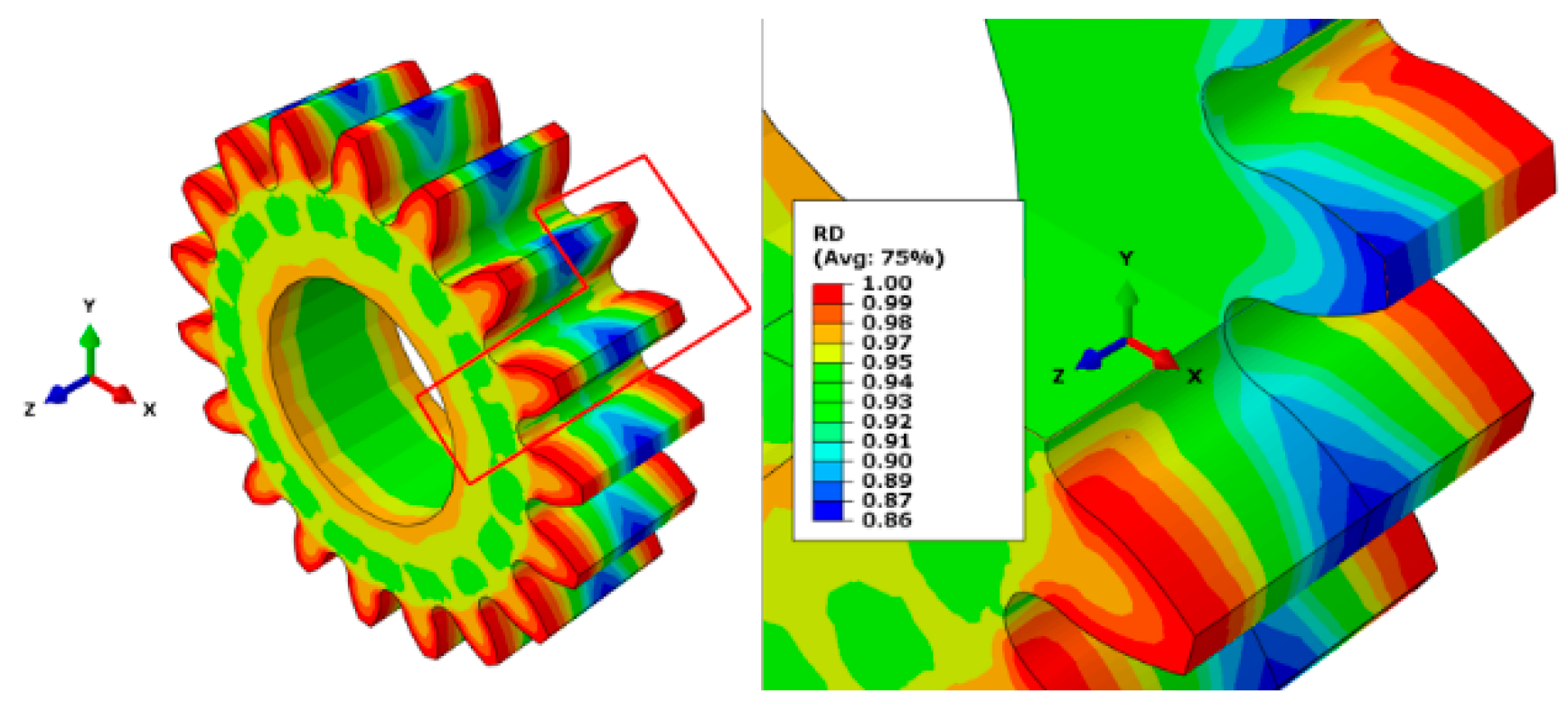
4.2. Geometrical Results
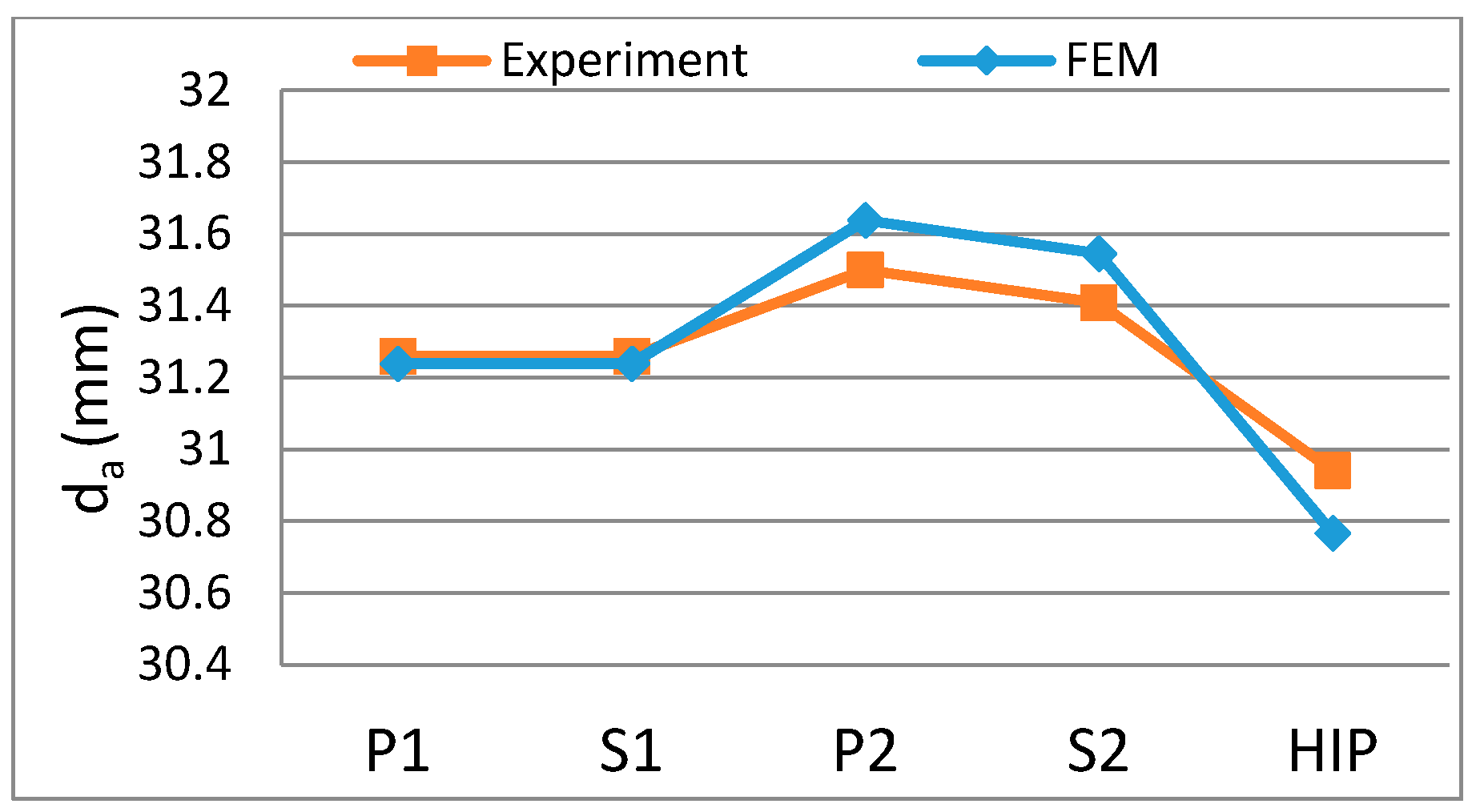
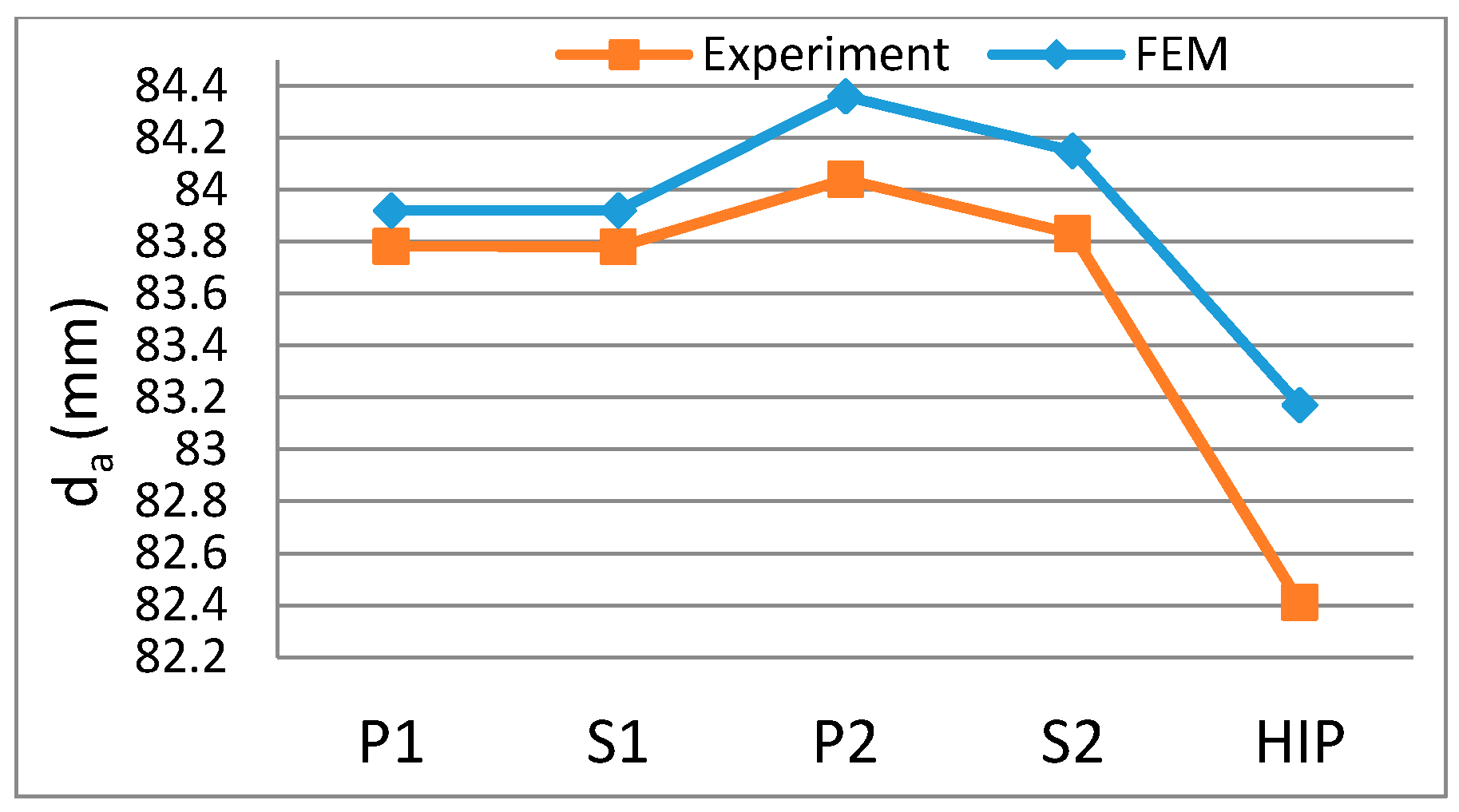
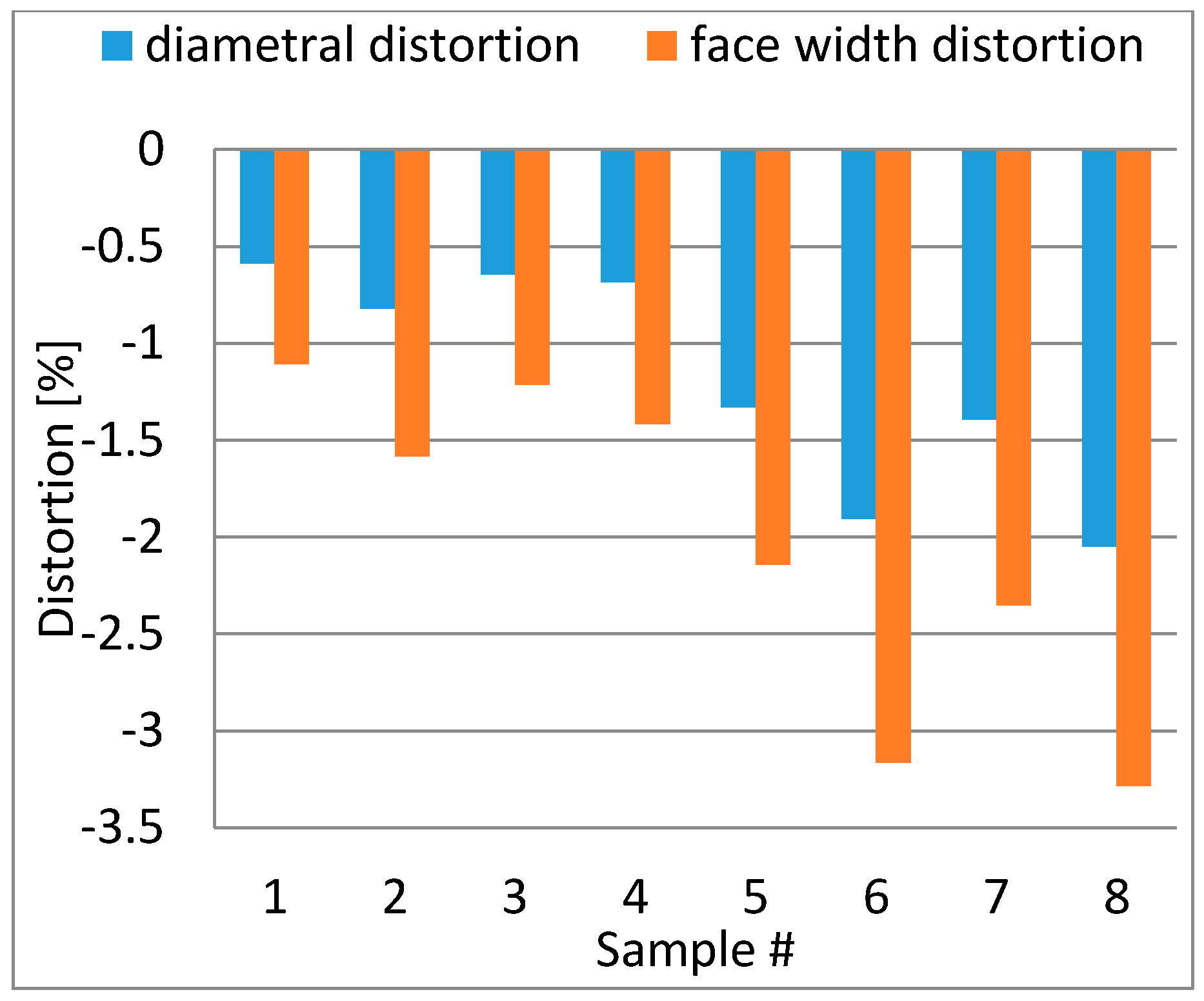
4.2.1. Addendum Diameter Variations
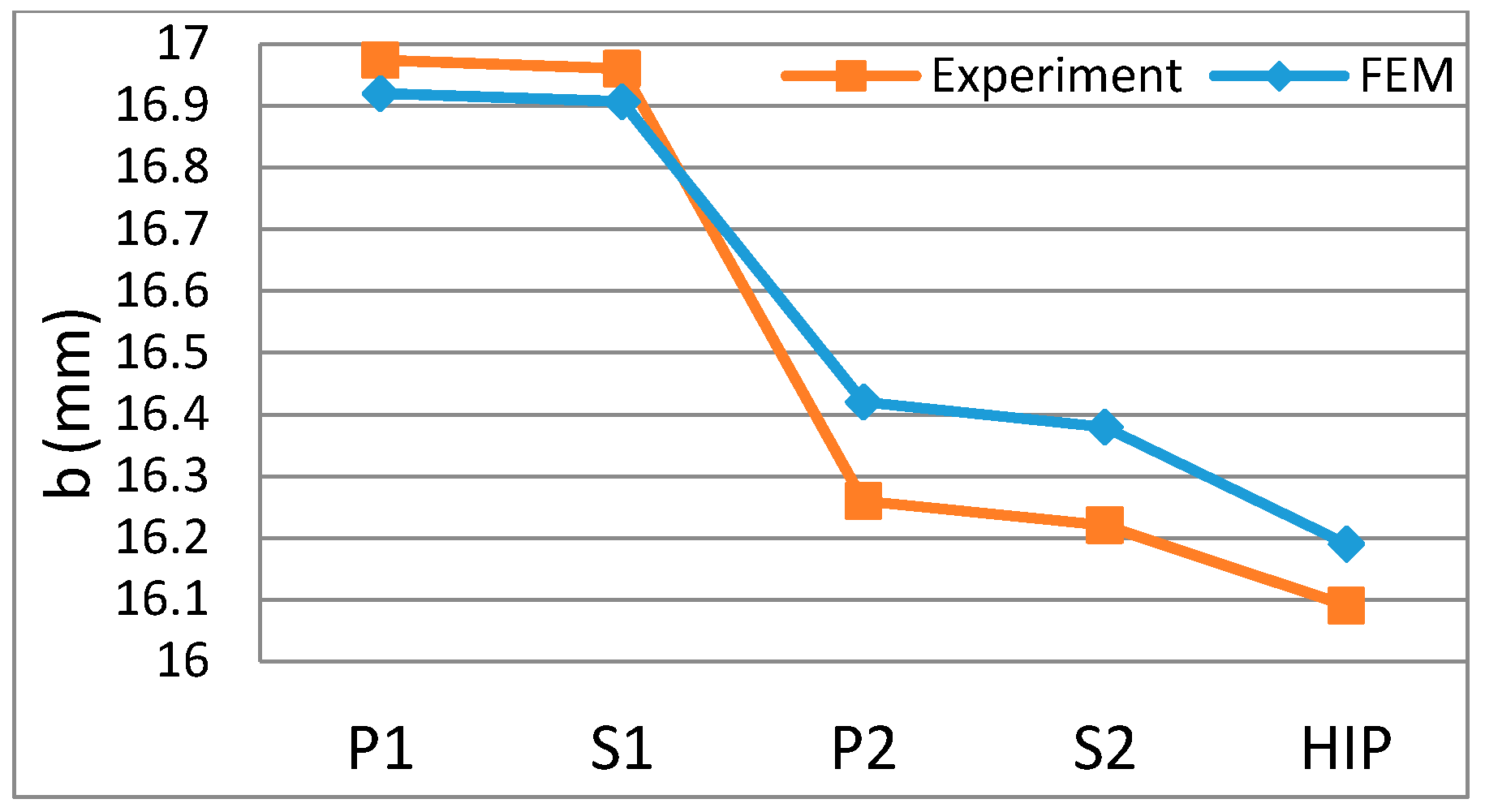
4.2.2. Face Width Variations
4.3. Validation of Numerical Simulation
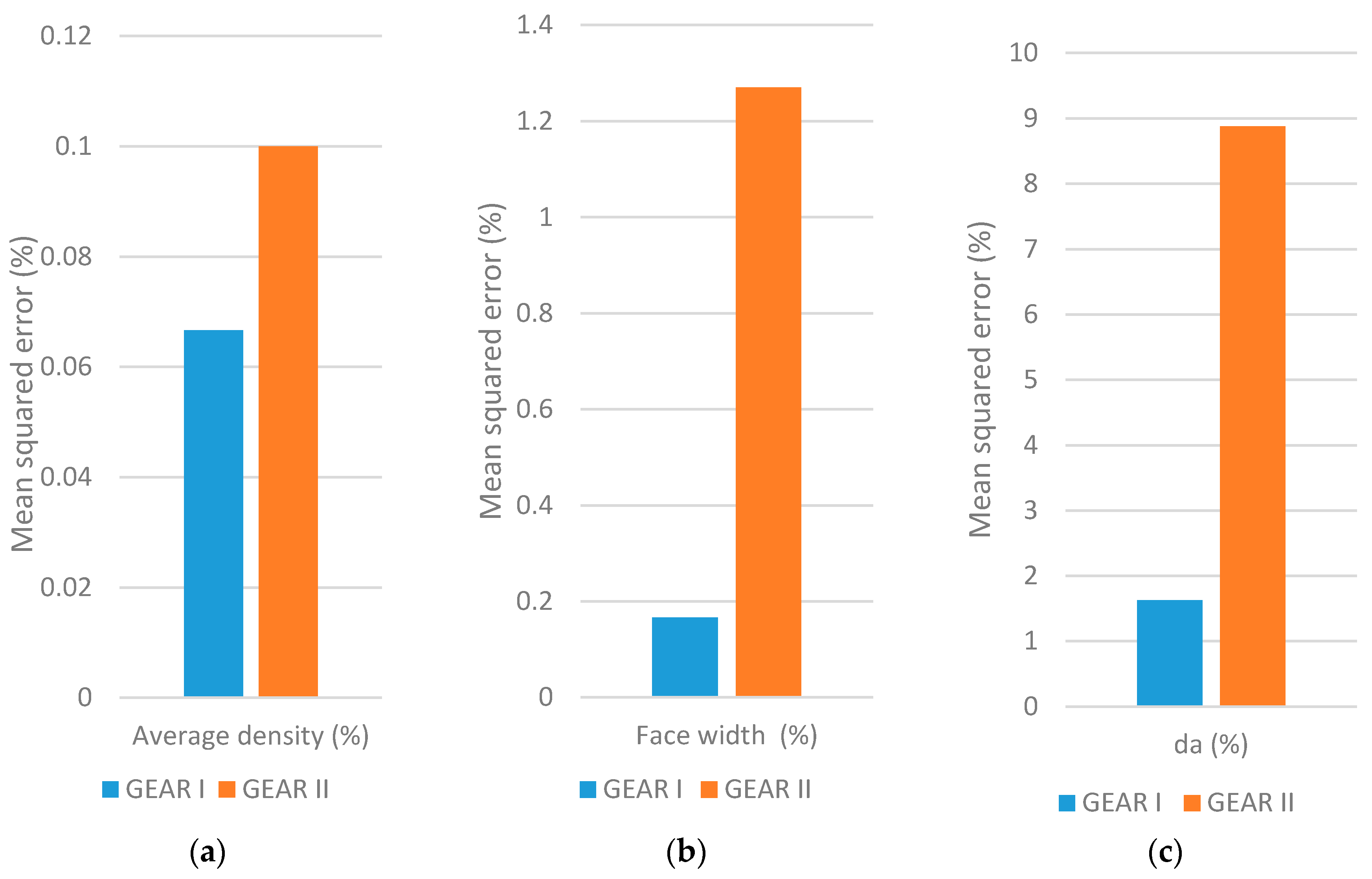
4.4. Analysis on the Gear Size Influences
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flodin, A.; Karlsson, P. Automotive transmission design using full potential of powder metal. In Proceedings of the PM2012, Yokohama, Japan, 14–18 October 2012; pp. 15–18. [Google Scholar]
- Capus, J. Industry Roadmap update from MPIF. Met. Powder Rep. 2012, 67, 10–11. [Google Scholar] [CrossRef]
- Capus, J.M. Surface-densified PM gears: New hope in new transmissions. Met. Powder Rep. 2006, 61, 18–21. [Google Scholar] [CrossRef]
- Cedergren, J.; Melin, S.; Lidström, P. Numerical investigation of Powder Metallurgy manufactured gear wheels subjected to fatigue loading. Powder Technol. 2005, 160, 161–169. [Google Scholar] [CrossRef]
- Glodež, S.; Šori, M. Bending Fatigue Analysis of PM Gears. Key Eng. Mater. 2017, 754, 299–302. [Google Scholar] [CrossRef]
- Klocke, F.; Gorgels, C.; Kauffmann, P. Challenges of Surface Densification of PM Gears by Rolling. In Advances in Powder Metallurgy and Particulate Materials, Proceedings of the 2008 World Congress on Powder Metallurgy & Particulate Materials, Washington, DC, USA, 8–12 June 2008; Metal Powder Industries Federation: Princeton, NJ, USA, 2008. [Google Scholar]
- Klocke, F.; Gorgels, C.; Kauffmann, P.; Gräser, E. Influencing Densification of PM Gears. In Future Trends in Production Engineering; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Klocke, F.; Schröder, T.; Kauffmann, P. Fundamental study of surface densification of PM gears by rolling using FE analysis. Prod. Eng. 2007, 1, 113–120. [Google Scholar] [CrossRef]
- Strondl, A.; Khodaee, A.; Sundaram, M.V.; Andersson, M.; Melander, A.; Heikkilä, I.; Miedzinski, A.; Nyborg, L.; Ahlfors, M. Innovative Powder Based Manufacturing of High Performance Gears. In Proceedings of the European PM Conference Proceedings, European Congress and Exhibition on Powder Metallurgy, Hamburg, Germany, 9–13 October 2016; The European Powder Metallurgy Association: Shrewsbury, UK, 2016; pp. 1–6. [Google Scholar]
- Flodin, A.; Andersson, M.; Miedzinski, A. Full density powder metal components through Hot Isostatic Pressing. Met. Powder Rep. 2017, 72, 107–110. [Google Scholar] [CrossRef]
- Sundaram, M.V. Processing Methods for Reaching Full Density Powder Metallurgical Materials. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2017. [Google Scholar]
- ElRakayby, H.; Kim, H.; Hong, S.; Kim, K. An investigation of densification behavior of nickel alloy powder during hot isostatic pressing. Adv. Powder Technol. 2015, 26, 1314–1318. [Google Scholar] [CrossRef]
- Van Nguyen, C.; Bezold, A.; Broeckmann, C. Anisotropic shrinkage during hip of encapsulated powder. J. Mater. Process. Technol. 2015, 226, 134–145. [Google Scholar] [CrossRef]
- Van Nguyen, C.; Deng, Y.; Bezold, A.; Broeckmann, C. A combined model to simulate the powder densification and shape changes during hot isostatic pressing. Comput. Methods Appl. Mech. Eng. 2017, 315, 302–315. [Google Scholar] [CrossRef]
- Khodaee, A.; Melander, A. Evaluation of effects of geometrical parameters on density distribution in compaction of PM gears. In Proceedings of the 20th International ESAFORM Conference on Material Forming (ESAFORM 2017), Dublin, Ireland, 26–28 April 2017; American Institute of Physics (AIP): College Park, MD, USA, 2017. [Google Scholar]
- Höganäs, A.B. Material and Powder Properties Handbook. 2018. Available online: https://www.hoganas.com/globalassets/uploaded-files/handbooks/handbook-1-material_and_powder_properties_december_2013_0674hog-interactive.pdf (accessed on 3 July 2018).
- Dlapka, M.; Danninger, H.; Gierl, C.; Lindqvist, B. Defining the pores in PM components. Met. Powder Rep. 2010, 65, 30–33. [Google Scholar] [CrossRef]
- Essa, K.; Jamshidi, P.; Zou, J.; Attallah, M.M.; Hassanin, H. Porosity control in 316L stainless steel using cold and hot isostatic pressing. Mater. Des. 2018, 138, 21–29. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS Documentation; Dassault Systèmes: Providence, RI, USA, 2011. [Google Scholar]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Wagle, G.S. Die Compaction Simulation: Simplifying the Application of a Complex Constitutive Model Using Numerical and Physical Experiments. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2006. [Google Scholar]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Bourih, A.; Kaddouri, W.; Kanit, T.; Madani, S.; Imad, A. Effective yield surface of porous media with random overlapping identical spherical voids. J. Mater. Res. Technol. 2018, 7, 103–117. [Google Scholar] [CrossRef]
- Slimane, A.; Bouchouicha, B.; Benguediab, M.; Slimane, S.A. Parametric study of the ductile damage by the Gurson–Tvergaard–Needleman model of structures in carbon steel A48-AP. J. Mater. Res. Technol. 2015, 4, 217–223. [Google Scholar] [CrossRef]
- Cochran, W.G.; Cox, G.M. Experimental Designs; Willey and Sons: Hoboken, NJ, USA, 1950. [Google Scholar]





| Material Cohesion [MPa] | Angle of Friction [°] | Cap Eccentricity [-] | Initial Yield Surface Position [MPa] | Transition Surface Radius [-] | Flow Stress Ratio [-] |
|---|---|---|---|---|---|
| 0.059 | 70.55 | 0.5 | 0.01 | 0.01 | 1 |
| q1 [-] | q2 [-] | q3 [-] |
|---|---|---|
| 1 | 1 | 1 |
| Process | Modification Factor [%] |
|---|---|
| S1 | −0.69 |
| S2 | +0.50 |
| Coefficients | Standard Error | t Stat | p-Value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept | 86.431 | 1.115 | 77.497 | 0.000 | 83.564 | 89.298 |
| b | −0.225 | 0.045 | −4.958 | 0.004 | −0.342 | −0.108 |
| mn | 1.184 | 0.300 | 3.953 | 0.011 | 0.414 | 1.954 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodaee, A.; Melander, A. Numerical and Experimental Analysis of the Gear Size Influence on Density Variations and Distortions during the Manufacturing of PM Gears with an Innovative Powder Processing Route Incorporating HIP. J. Manuf. Mater. Process. 2018, 2, 49. https://doi.org/10.3390/jmmp2030049
Khodaee A, Melander A. Numerical and Experimental Analysis of the Gear Size Influence on Density Variations and Distortions during the Manufacturing of PM Gears with an Innovative Powder Processing Route Incorporating HIP. Journal of Manufacturing and Materials Processing. 2018; 2(3):49. https://doi.org/10.3390/jmmp2030049
Chicago/Turabian StyleKhodaee, Alireza, and Arne Melander. 2018. "Numerical and Experimental Analysis of the Gear Size Influence on Density Variations and Distortions during the Manufacturing of PM Gears with an Innovative Powder Processing Route Incorporating HIP" Journal of Manufacturing and Materials Processing 2, no. 3: 49. https://doi.org/10.3390/jmmp2030049
APA StyleKhodaee, A., & Melander, A. (2018). Numerical and Experimental Analysis of the Gear Size Influence on Density Variations and Distortions during the Manufacturing of PM Gears with an Innovative Powder Processing Route Incorporating HIP. Journal of Manufacturing and Materials Processing, 2(3), 49. https://doi.org/10.3390/jmmp2030049




