Prediction of Temperature Distribution in Orthogonal Machining Based on the Mechanics of the Cutting Process Using a Constitutive Model
Abstract
1. Introduction
1.1. Johnson–Cook Constitutive Model
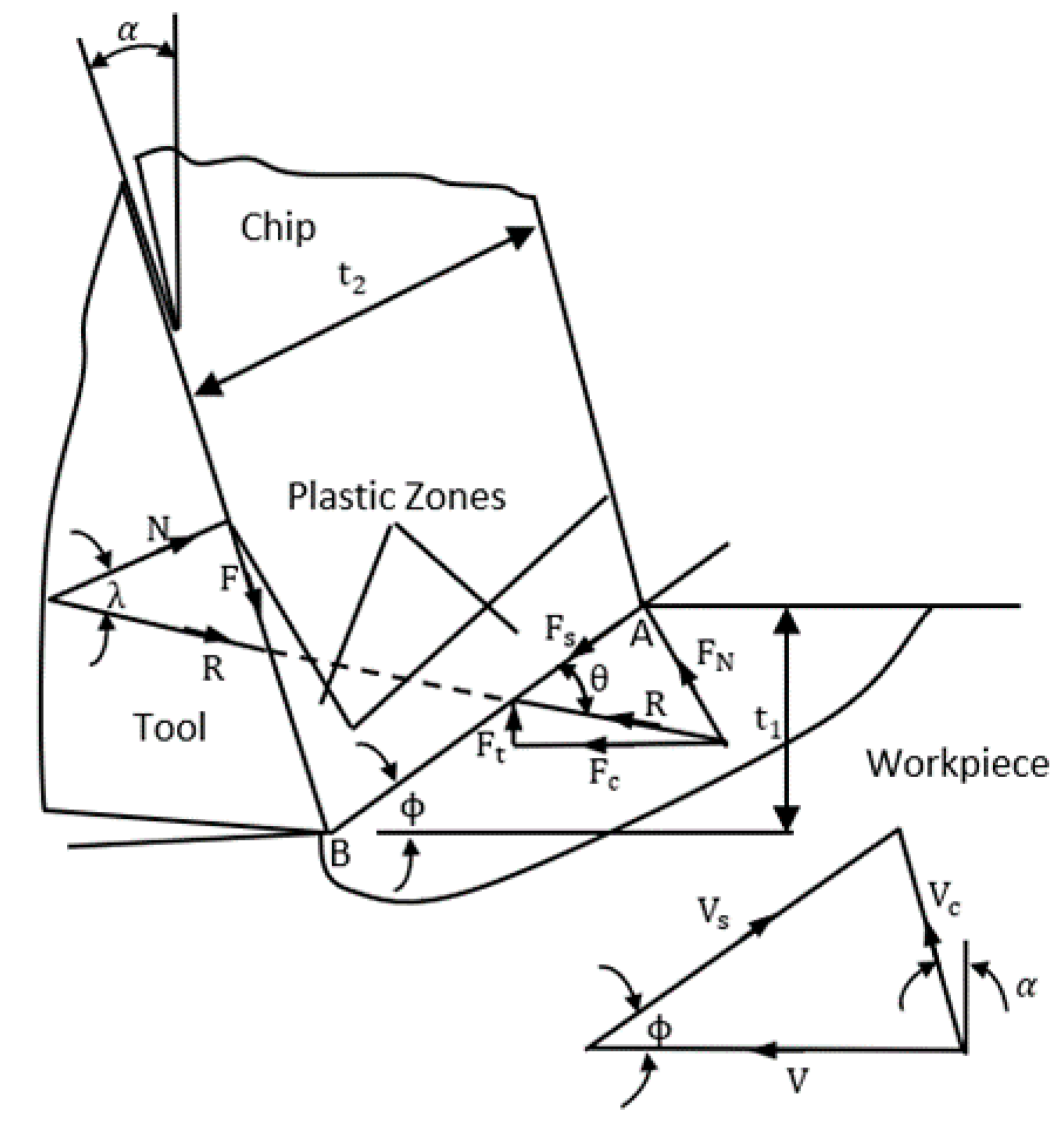
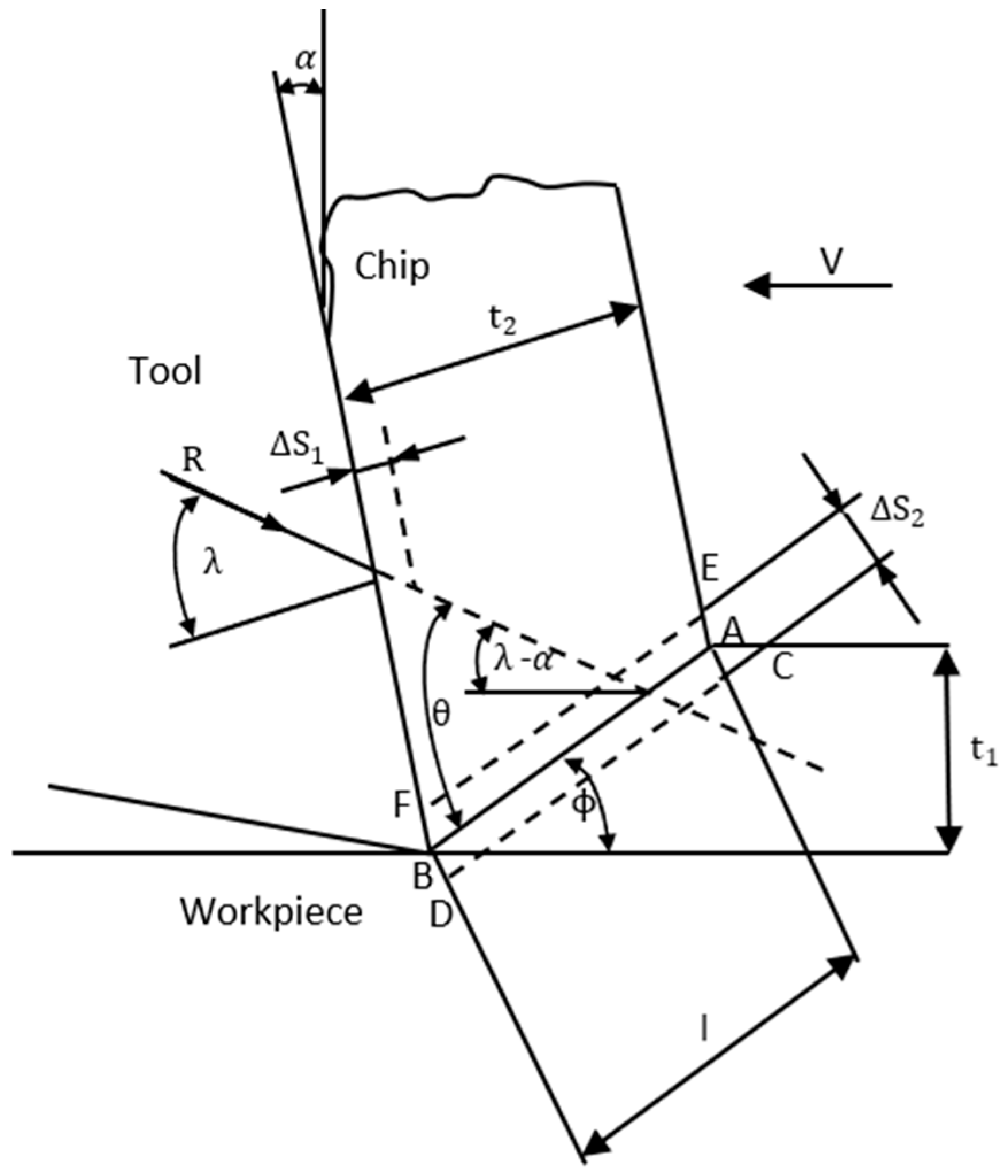
1.2. Chip Formation Model
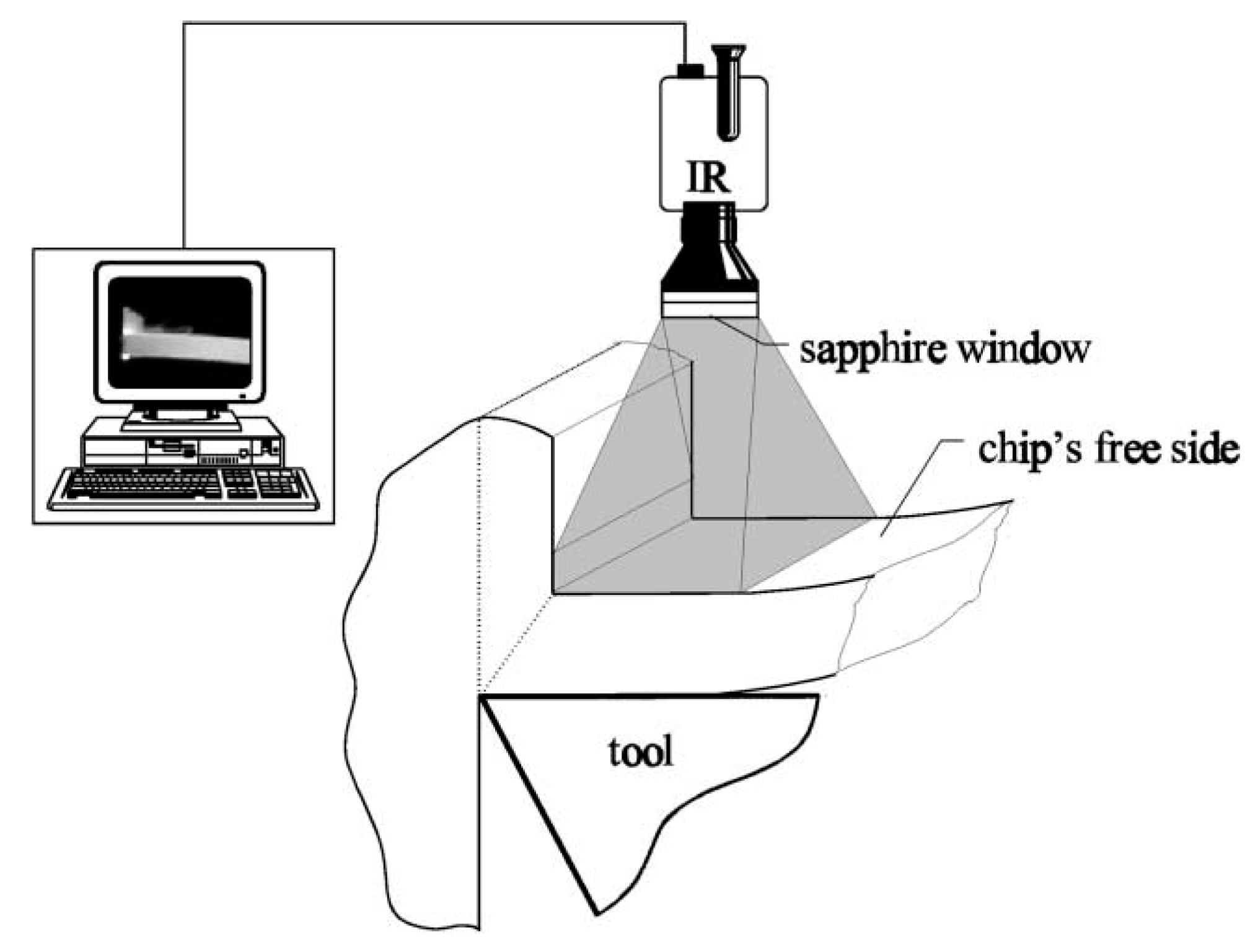
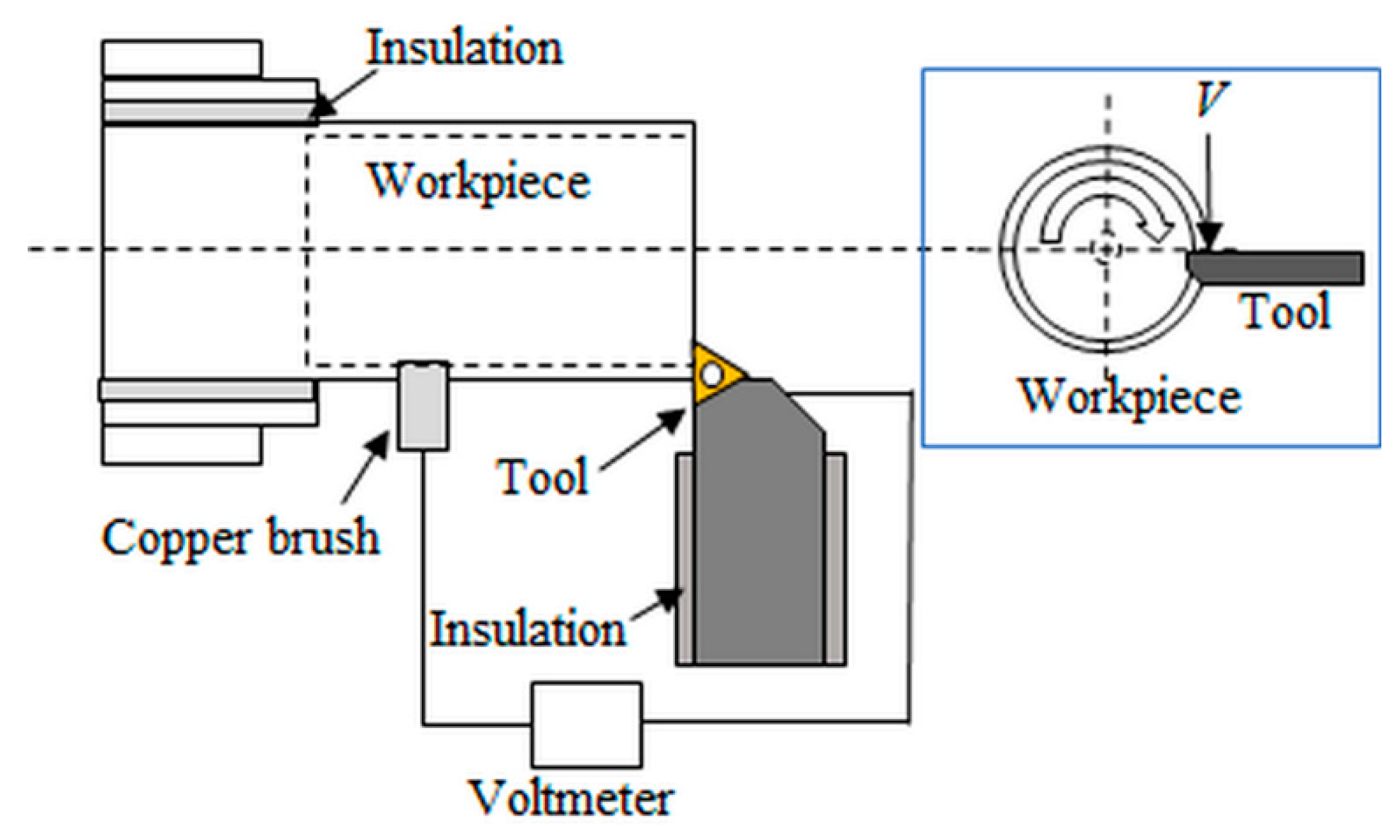
1.3. Experimental Measurements
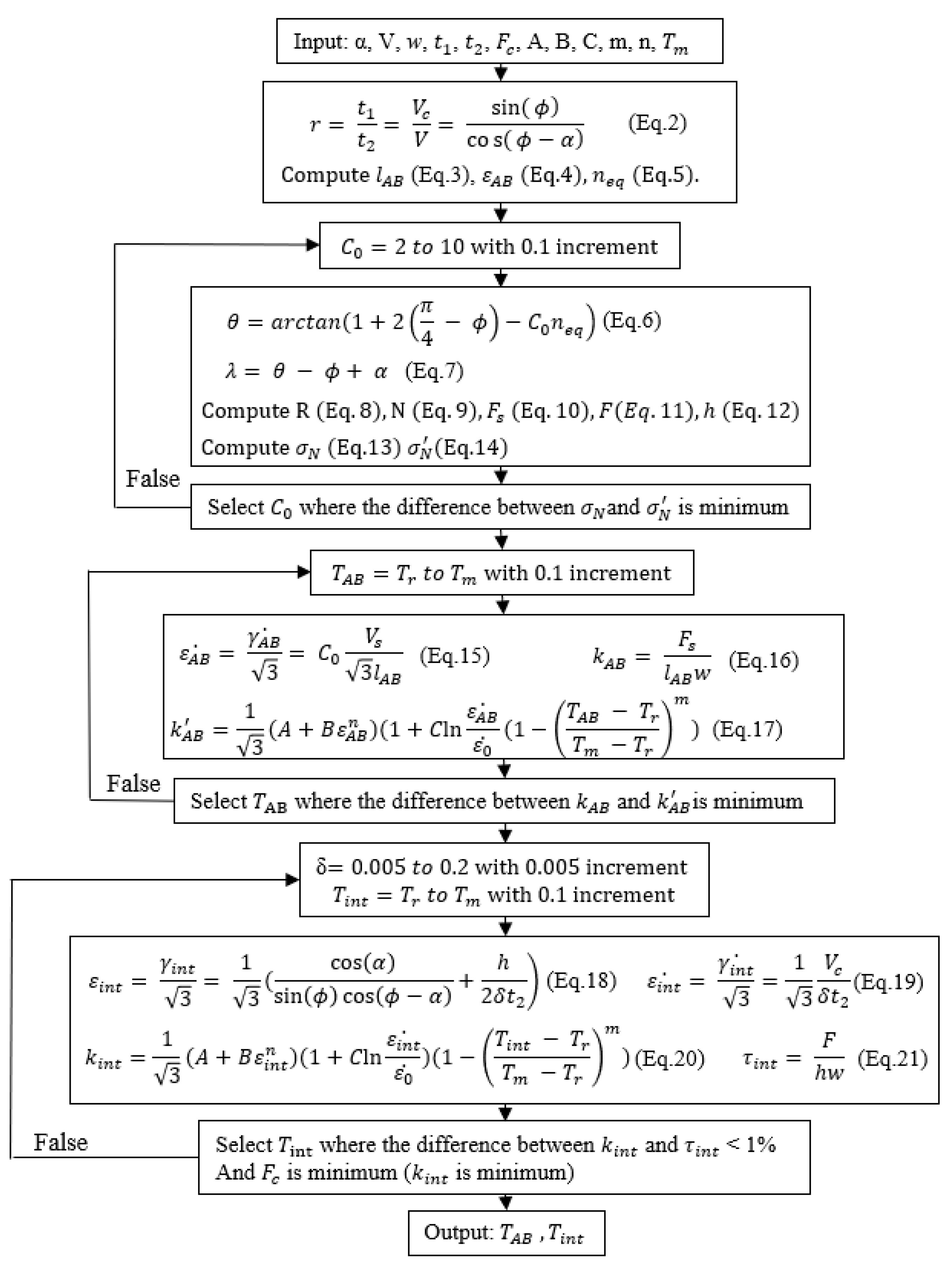
2. Methodology and Validation
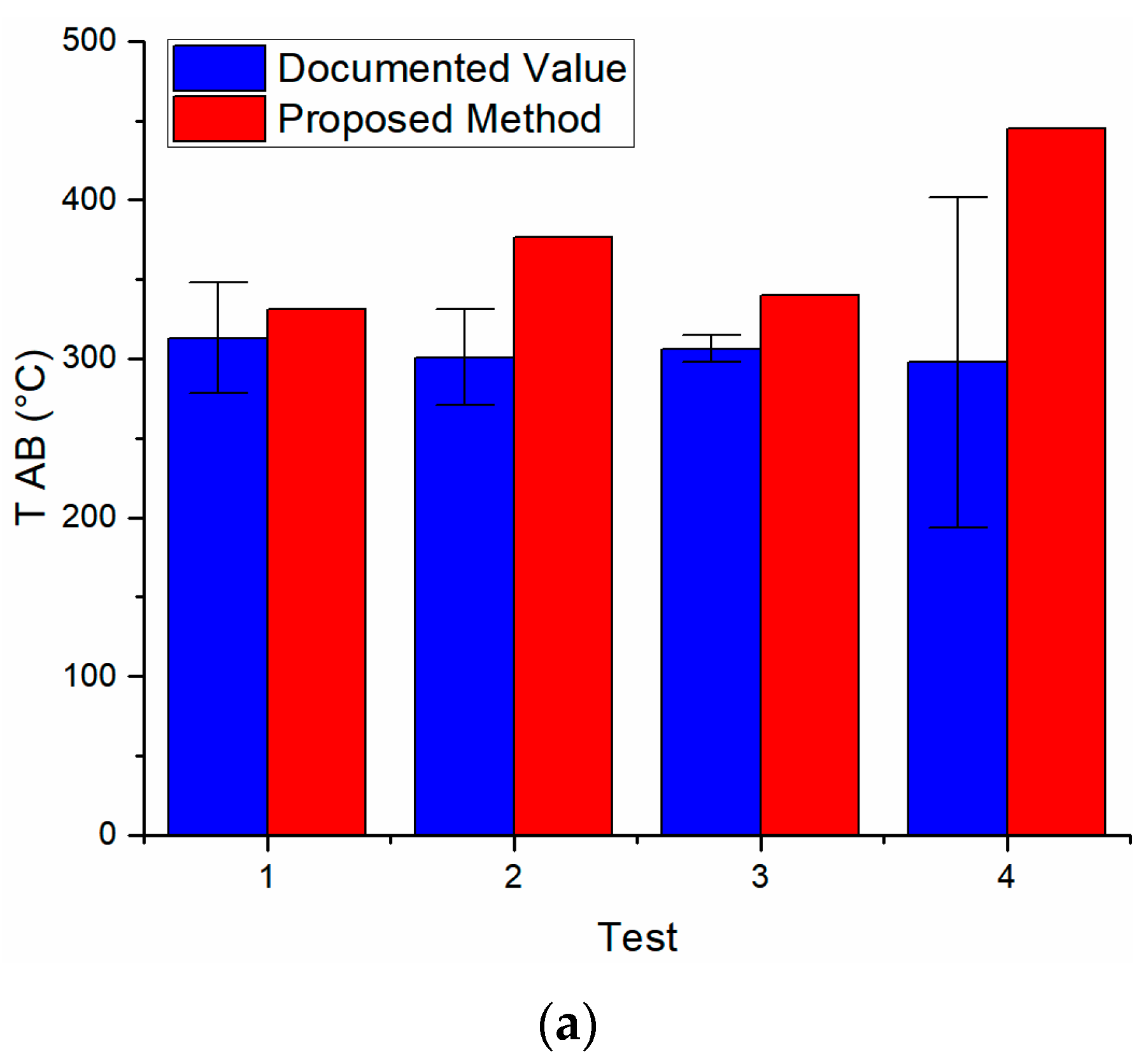
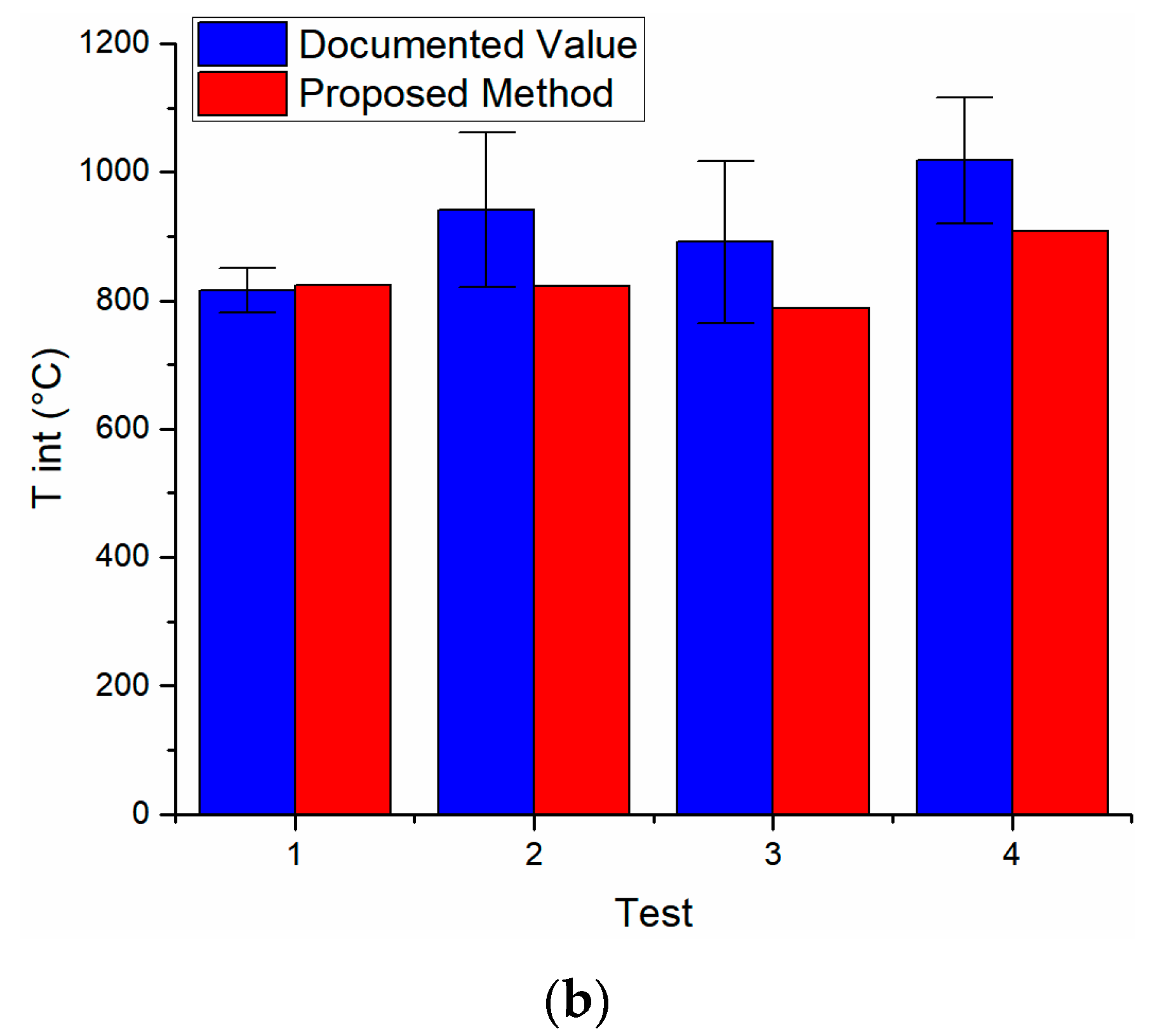
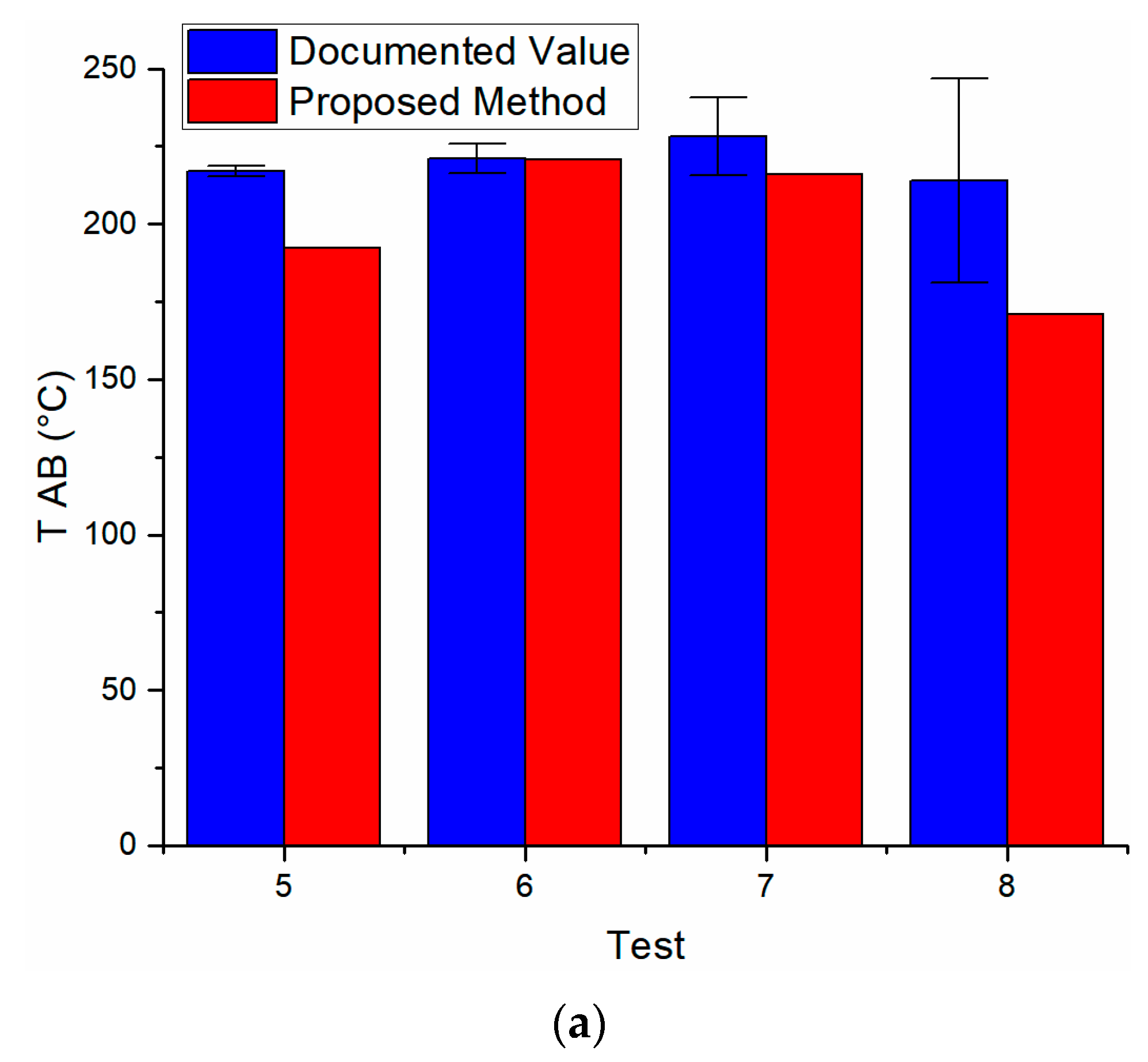
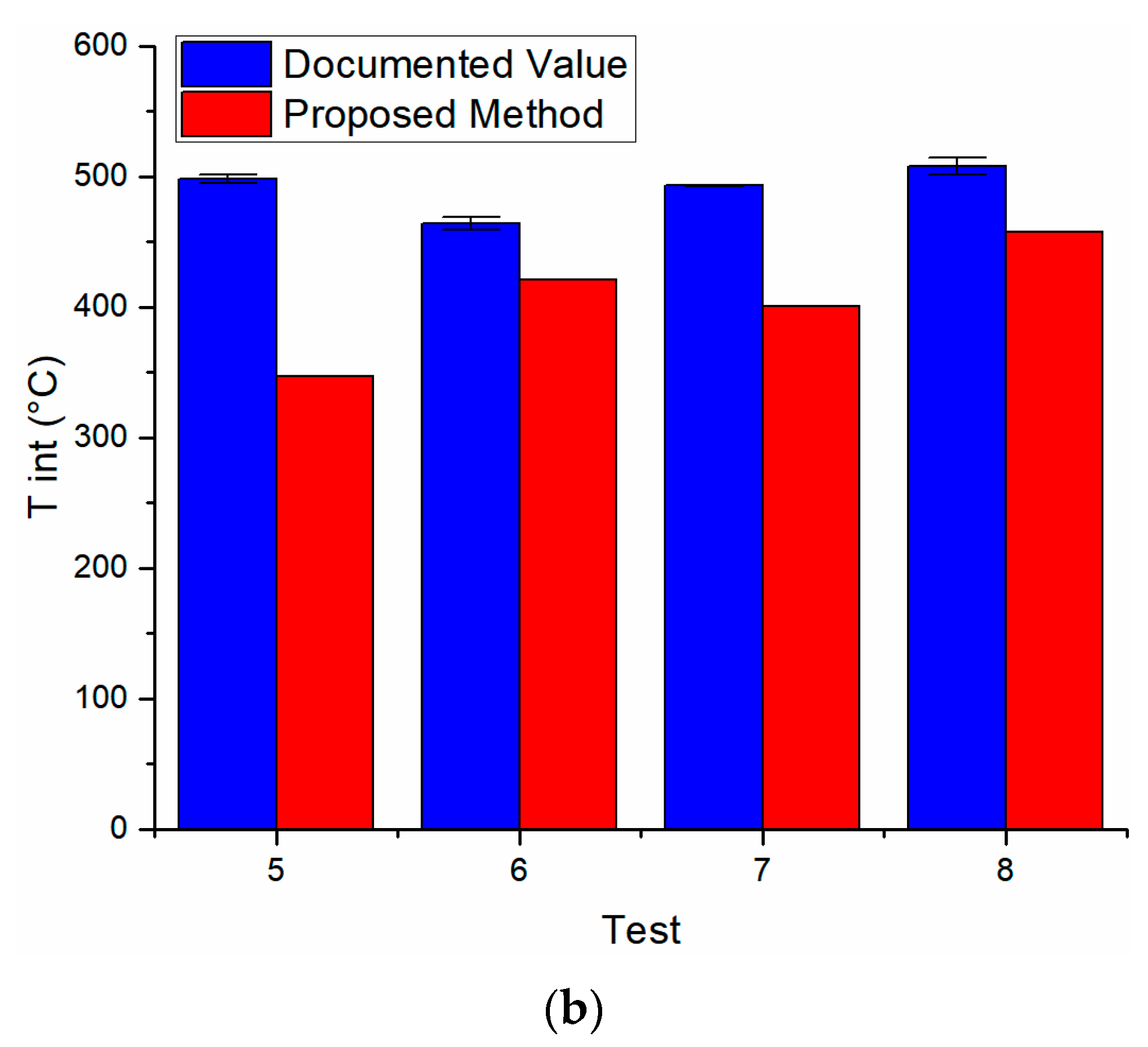
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | yield strength in the J–C model |
| B | strength coefficient in the J–C model |
| C | strain rate constants in the J–C model |
| m | thermal softening coefficient in the J–C model |
| n | strain hardening coefficient in the J–C model |
| melting temperature of the materials | |
| reference temperature | |
| temperature | |
| cutting force | |
| thrust force | |
| shear force on the primary shear plane AB | |
| normal force on the primary shear plane AB | |
| F | shear force on the tool–chip interface |
| N | normal force on the tool–chip interface |
| R | resultant force |
| h | tool–chip contact length |
| length of the primary shear zone AB | |
| t1 | cutting depth |
| t2 | chip thickness |
| w | width of cut |
| cutting velocity | |
| chip velocity | |
| shear velocity | |
| α | rake angle |
| ϕ | shear angle |
| λ | friction angle at the tool–chip interface |
| θ | the angle between the resultant force R and the primary shear plane AB |
| Oxley constants (the ratio of the shear plane length to the thickness of the PSZ) | |
| strain rate constant (and the ratio of the thickness of the SSZ to the chip thickness) | |
| strain hardening constant | |
| strain on shear plane AB | |
| strain rate on shear plane AB | |
| strain at the tool–chip interface | |
| strain rate at the tool–chip interface | |
| reference strain rate | |
| material flow stress on shear plane AB (calculated using the J–C model) | |
| shear stress at the tool–chip interface (calculated using the chip formation model) | |
| shear stress at the tool–chip interface (calculated using the J–C model) | |
| normal stress at the tool–chip interface (calculated using the chip formation model) | |
| normal stress at the tool–chip interface (calculated using the J–C model) | |
| heat partition ratio in calculated temperature in the PSZ |
Appendix A
References
- Stephenson, D.A.; Ali, A. Tool temperatures in interrupted metal cutting. J. Eng. Ind. 1992, 114, 127–136. [Google Scholar] [CrossRef]
- Lezanski, P.; Shaw, M.C. Tool face temperatures in high speed milling. J. Eng. Ind. 1990, 112, 132–135. [Google Scholar] [CrossRef]
- Yashiro, T.; Ogawa, T.; Sasahara, H. Temperature measurement of cutting tool and machined surface layer in milling of CFRP. Int. J. Mach. Tools Manuf. 2013, 70, 63–69. [Google Scholar] [CrossRef]
- Kitagawa, T.; Kubo, A.; Maekawa, K. Temperature and wear of cutting tools in high-speed machining of Inconel 718 and Ti6Al6V2Sn. Wear 1997, 202, 142–148. [Google Scholar] [CrossRef]
- Chen, W.C.; Tsao, C.C.; Liang, P.W. Determination of temperature distributions on the rake face of cutting tools using a remote method. Int. Commun. Heat Mass Transf. 1997, 24, 161–170. [Google Scholar] [CrossRef]
- O’sullivan, D.; Cotterell, M. Temperature measurement in single point turning. J. Mater. Process. Technol. 2001, 118, 301–318. [Google Scholar] [CrossRef]
- Jaspers, S.P.; Dautzenberg, J.H. Material behaviour in metal cutting: Strains, strain rates and temperatures in chip formation. J. Mater. Process. Technol. 2002, 121, 123–135. [Google Scholar] [CrossRef]
- Lin, J.; Lee, S.L.; Weng, C.I. Estimation of cutting temperature in high speed machining. J. Mater. Process. Technol. 1992, 114, 289–296. [Google Scholar] [CrossRef]
- Sutter, G.; Faure, L.; Molinari, A.; Ranc, N.; Pina, V. An experimental technique for the measurement of temperature fields for the orthogonal cutting in high speed machining. Int. J. Mach. Tools Manuf. 2003, 43, 671–678. [Google Scholar] [CrossRef]
- Wright, P.K. Correlation of tempering effects with temperature distribution in steel cutting tools. J. Eng. Ind. 1978, 100, 131–136. [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, K.; Watanabe, Y.; Hiraiwa, Y. Measurement of temperature distribution within tool using powders of constant melting point. J. Eng. Ind. 1976, 98, 607–613. [Google Scholar] [CrossRef]
- Dawson, P.R.; Malkin, S. Inclined moving heat source model for calculating metal cutting temperatures. J. Eng. Ind. 1984, 106, 179–186. [Google Scholar] [CrossRef]
- Kim, K.W.; Sins, H.C. Development of a thermo-viscoplastic cutting model using finite element method. Int. J. Mach. Tools Manuf. 1996, 36, 379–397. [Google Scholar] [CrossRef]
- Moriwaki, T.; Sugimura, N.; Luan, S. Combined stress, material flow and heat analysis of orthogonal micromachining of copper. CIRP Ann. Manuf. Technol. 1993, 42, 75–78. [Google Scholar] [CrossRef]
- Lei, S.; Shin, Y.C.; Incropera, F.P. Thermo-mechanical modeling of orthogonal machining process by finite element analysis. Int. J. Mach. Tools Manuf. 1999, 39, 731–750. [Google Scholar] [CrossRef]
- Levy, E.K.; Tsai, C.L.; Groover, M.P. Analytical investigation of the effect of tool wear on the temperature variations in a metal cutting tool. J. Eng. Ind. 1976, 98, 251–257. [Google Scholar] [CrossRef]
- Chan, C.L.; Chandra, A. A boundary element method analysis of the thermal aspects of metal cutting processes. J. Eng. Ind. 1991, 113, 311–319. [Google Scholar] [CrossRef]
- Umbrello, D.; Filice, L.; Rizzuti, S.; Micari, F.; Settineri, L. On the effectiveness of finite element simulation of orthogonal cutting with particular reference to temperature prediction. J. Mater. Process. Technol. 2007, 189, 284–291. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, C.M. A study of cutting force and preheating-temperature prediction for laser-assisted milling of Inconel 718 and AISI 1045 steel. Int. J. Heat Mass Transf. 2014, 71, 264–274. [Google Scholar] [CrossRef]
- Yang, J.; Sun, S.; Brandt, M.; Yan, W. Experimental investigation and 3D finite element prediction of the heat affected zone during laser assisted machining of Ti6Al4V alloy. J. Mater. Process. Technol. 2010, 210, 2215–2222. [Google Scholar] [CrossRef]
- Özel, T.; Zeren, E. Finite element modeling the influence of edge roundness on the stress and temperature fields induced by high-speed machining. Int. J. Adv. Manuf. Technol. 2007, 35, 255–267. [Google Scholar] [CrossRef]
- Attia, M.H.; Kops, L. A new approach to cutting temperature prediction considering the thermal constriction phenomenon in multi-layer coated tools. CIRP Ann. Manuf. Technol. 2004, 53, 47–52. [Google Scholar] [CrossRef]
- Wiener, J.H. Shear-plane temperature distribution in orthogonal cutting. Trans. ASME 1955, 77, 1331–1341. [Google Scholar]
- Boothroyd, G. Fundamentals of Metal Machining and Machine Tools; Scripta Book Company: Washington, DC, USA, 1975; ISBN 9780070064980. [Google Scholar]
- Radulescu, R.; Kapoor, S.G. An analytical model for prediction of tool temperature fields during continuous and interrupted cutting. J. Eng. Ind. 1994, 116, 135–143. [Google Scholar] [CrossRef]
- Stephenson, D.A.; Jen, T.C.; Lavine, A.S. Cutting tool temperatures in contour turning: Transient analysis and experimental verification. J. Manuf. Sci. Eng. 1997, 119, 494–501. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part III: Temperature rise distribution due to the combined effects of shear plane heat source and the tool–chip interface frictional heat source. Int. J. Mech. Sci. 2001, 43, 89–107. [Google Scholar] [CrossRef]
- Hahn, R.S. On the temperature developed at the shear plane in the metal cutting process. J. Appl. Mech. Trans. ASME 1951, 18, 661–666. [Google Scholar]
- Jaeger, C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959; ISBN 9780198533689. [Google Scholar]
- Huang, Y.; Liang, S.Y. Cutting forces modeling considering the effect of tool thermal property—Application to CBN hard turning. Int. J. Mach. Tools Manuf. 2003, 43, 307–315. [Google Scholar] [CrossRef]
- Li, K.M.; Liang, S.Y. Modeling of cutting forces in near dry machining under tool wear effect. Int. J. Mach. Tools Manuf. 2007, 47, 1292–1301. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, S.Y. Cutting temperature modeling based on non-uniform heat intensity and partition ratio. Mach. Sci. Technol. 2005, 9, 301–323. [Google Scholar] [CrossRef]
- Korkut, I.; Acır, A.; Boy, M. Application of regression and artificial neural network analysis in modelling of tool–chip interface temperature in machining. Exp. Syst. Appl. 2011, 38, 11651–11656. [Google Scholar] [CrossRef]
- Oxley, P.L.B. The Mechanics of Machining: An Analytical Approach to Assessing Machinability; Ellis Horwood Ltd.: Chichester, UK, 1989; ISBN 0745800076. [Google Scholar]
- Calculating the shear angle in orthogonal metal cutting from fundamental stress-strain-strain rate properties of the work material. Available online: https://dspace.lib.cranfield.ac.uk/handle/1826/12577 (accessed on 23 April 2018).
- Ivester, R.W.; Kennedy, M.; Davies, M.; Stevenson, R.; Thiele, J.; Furness, R.; Athavale, S. Assessment of machining models: Progress report. Mach. Sci. Technol. 2000, 4, 511–538. [Google Scholar] [CrossRef]
- Adibi-Sedeh, A.H.; Madhavan, V.; Bahr, B. Extension of Oxley’s analysis of machining to use different material models. J. Manuf. Sci. Eng. 2003, 125, 656–666. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Response surface and neural network based predictive models of cutting temperature in hard turning. J. Adv. Res. 2016, 7, 1035–1044. [Google Scholar] [CrossRef] [PubMed]
- M’saoubi, R.; Chandrasekaran, H. Investigation of the effects of tool micro-geometry and coating on tool temperature during orthogonal turning of quenched and tempered steel. Int. J. Mach. Tools Manuf. 2004, 44, 213–224. [Google Scholar] [CrossRef]
- Jaspers, S.P.; Dautzenberg, J.H. Material behaviour in conditions similar to metal cutting: Flow stress in the primary shear zone. J. Mater. Process. Technol. 2002, 122, 322–330. [Google Scholar] [CrossRef]
- Karpat, Y.; Özel, T. Predictive analytical and thermal modeling of orthogonal cutting process—Part I: Predictions of tool forces, stresses, and temperature distributions. J. Manuf. Sci. Eng. 2006, 128, 435–444. [Google Scholar] [CrossRef]
- Aydın, M. Cutting temperature analysis considering the improved Oxley’s predictive machining theory. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 2435–2448. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, J.; Gan, Y.; Li, B.; Fang, N. Improvement of algorithm and prediction precision of an extended Oxley’s theoretical model. Int. J. Adv. Manuf. Technol. 2015, 77, 1–3. [Google Scholar] [CrossRef]
- Ning, J.; Liang, S.Y. Model-driven determination of Johnson-Cook material constants using temperature and force measurements. Int. J. Adv. Manuf. Technol. 2018, 1–8. [Google Scholar] [CrossRef]
- Umbrello, D.; M’saoubi, R.; Outeiro, J.C. The influence of Johnson–Cook material constants on finite element simulation of machining of AISI 316L steel. Int. J. Mach. Tools Manuf. 2007, 47, 462–570. [Google Scholar] [CrossRef]
- Ducobu, F.; Rivière-Lorphèvre, E.; Filippi, E. On the importance of the choice of the parameters of the Johnson-Cook constitutive model and their influence on the results of a Ti6Al4V orthogonal cutting model. Int. J. Mech. Sci. 2017, 122, 143–155. [Google Scholar] [CrossRef]
| Materials | A (MPa) | B (MPa) | C | m | n | (°C) | (°C) | |
|---|---|---|---|---|---|---|---|---|
| ASIS 1045 Steel [40] | 553.1 | 600.8 | 0.0134 | 1 | 0.234 | 1 | 1460 | 25 |
| Al 6082-T6 Aluminum [37] | 250 | 243.6 | 0.00747 | 1.31 | 0.17 | 1 | 582 | 25 |
| Material | Test | α (degs) | V (m/min) | w (mm) | (mm) | (mm) | Fc (N) | Ft (N) |
|---|---|---|---|---|---|---|---|---|
| AISI 1045 Steel | 1 | 5 | 200 | 1.6 | 0.15 | 0.424 | 583 | 402 |
| [36] | 2 | 5 | 200 | 1.6 | 0.30 | 0.734 | 976 | 493 |
| 3 | 5 | 300 | 1.6 | 0.15 | 0.389 | 539 | 326 | |
| 4 | 5 | 300 | 1.6 | 0.30 | 0.709 | 888 | 406 | |
| Al 6082-T6 Aluminum | 5 | 8 | 120 | 3.0 | 0.20 | 0.52 * | 552 | 384 |
| [37] | 6 | 8 | 240 | 3.0 | 0.40 | 0.76 * | 795 | 300 |
| 7 | 8 | 360 | 3.0 | 0.20 | 0.44 * | 456 | 204 | |
| 8 | 8 | 360 | 3.0 | 0.40 | 0.64 * | 768 | 276 |
| Test | (°C) R | (°C) | (°C) R | (°C) | ϕ (degs) | δ | |
|---|---|---|---|---|---|---|---|
| 1 | 313.12 | 330.97 | 815.74 | 823.23 | 19.14 | 5.45 | 0.05 |
| 2 | 300.77 | 376.61 | 941.15 | 822.37 | 22.00 | 5.10 | 0.16 |
| 3 | 306.30 | 340.01 | 891.20 | 787.49 | 20.76 | 5.25 | 0.13 |
| 4 | 297.80 | 445.07 | 1018.00 | 908.47 | 22.78 | 5.00 | 0.10 |
| 5 | 217.00 | 192.40 | 498.00 | 346.80 | 20.76 | 7.58 | 0.14 |
| 6 | 221.00 | 220.64 | 464.00 | 421.35 | 20.02 | 6.33 | 0.17 |
| 7 | 228.00 | 216.01 | 493.00 | 400.90 | 24.39 | 6.90 | 0.06 |
| 8 | 198.00 | 171.00 | 508.00 | 457.72 | 31.67 | 5.72 | 0.08 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, J.; Liang, S.Y. Prediction of Temperature Distribution in Orthogonal Machining Based on the Mechanics of the Cutting Process Using a Constitutive Model. J. Manuf. Mater. Process. 2018, 2, 37. https://doi.org/10.3390/jmmp2020037
Ning J, Liang SY. Prediction of Temperature Distribution in Orthogonal Machining Based on the Mechanics of the Cutting Process Using a Constitutive Model. Journal of Manufacturing and Materials Processing. 2018; 2(2):37. https://doi.org/10.3390/jmmp2020037
Chicago/Turabian StyleNing, Jinqiang, and Steven Y. Liang. 2018. "Prediction of Temperature Distribution in Orthogonal Machining Based on the Mechanics of the Cutting Process Using a Constitutive Model" Journal of Manufacturing and Materials Processing 2, no. 2: 37. https://doi.org/10.3390/jmmp2020037
APA StyleNing, J., & Liang, S. Y. (2018). Prediction of Temperature Distribution in Orthogonal Machining Based on the Mechanics of the Cutting Process Using a Constitutive Model. Journal of Manufacturing and Materials Processing, 2(2), 37. https://doi.org/10.3390/jmmp2020037






