Application of Finite Element Method to Analyze the Influences of Process Parameters on the Cut Surface in Fine Blanking Processes by Using Clearance-Dependent Critical Fracture Criteria
Abstract
:1. Introduction
2. Ductile Fracture Criteria and Determination of Critical Fracture Criteria, (C)
2.1. Ductile Fracture Criteria
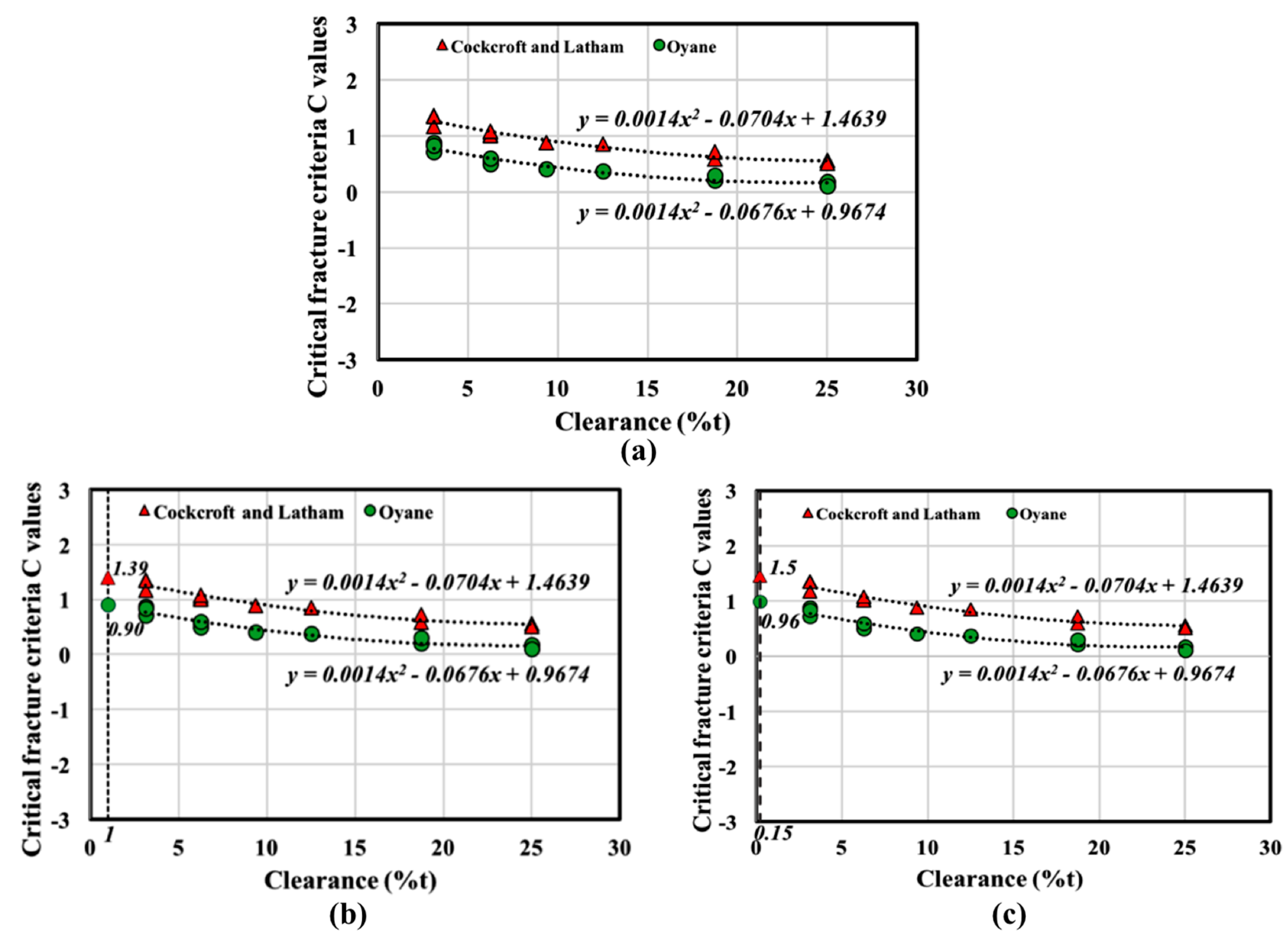
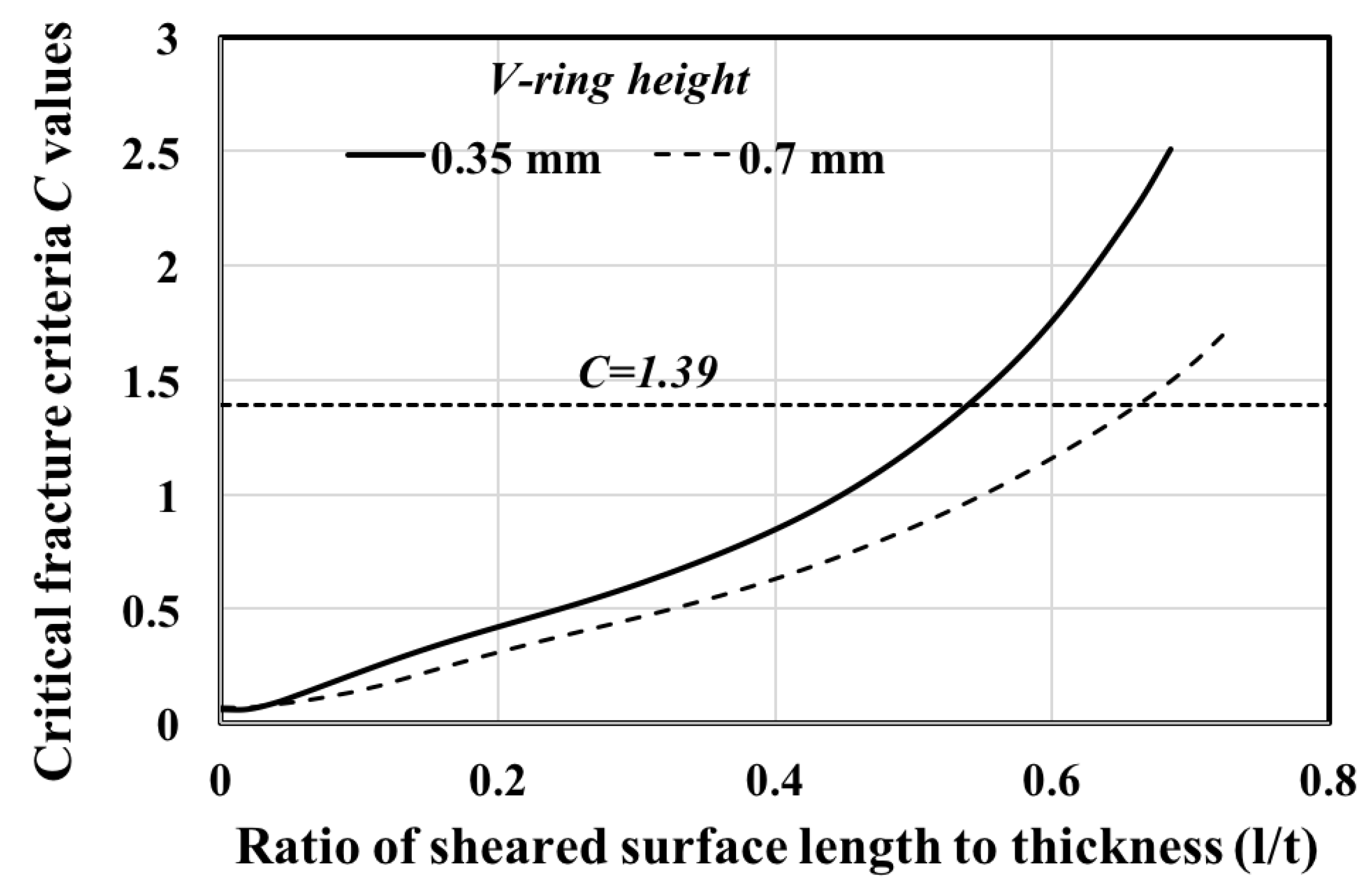
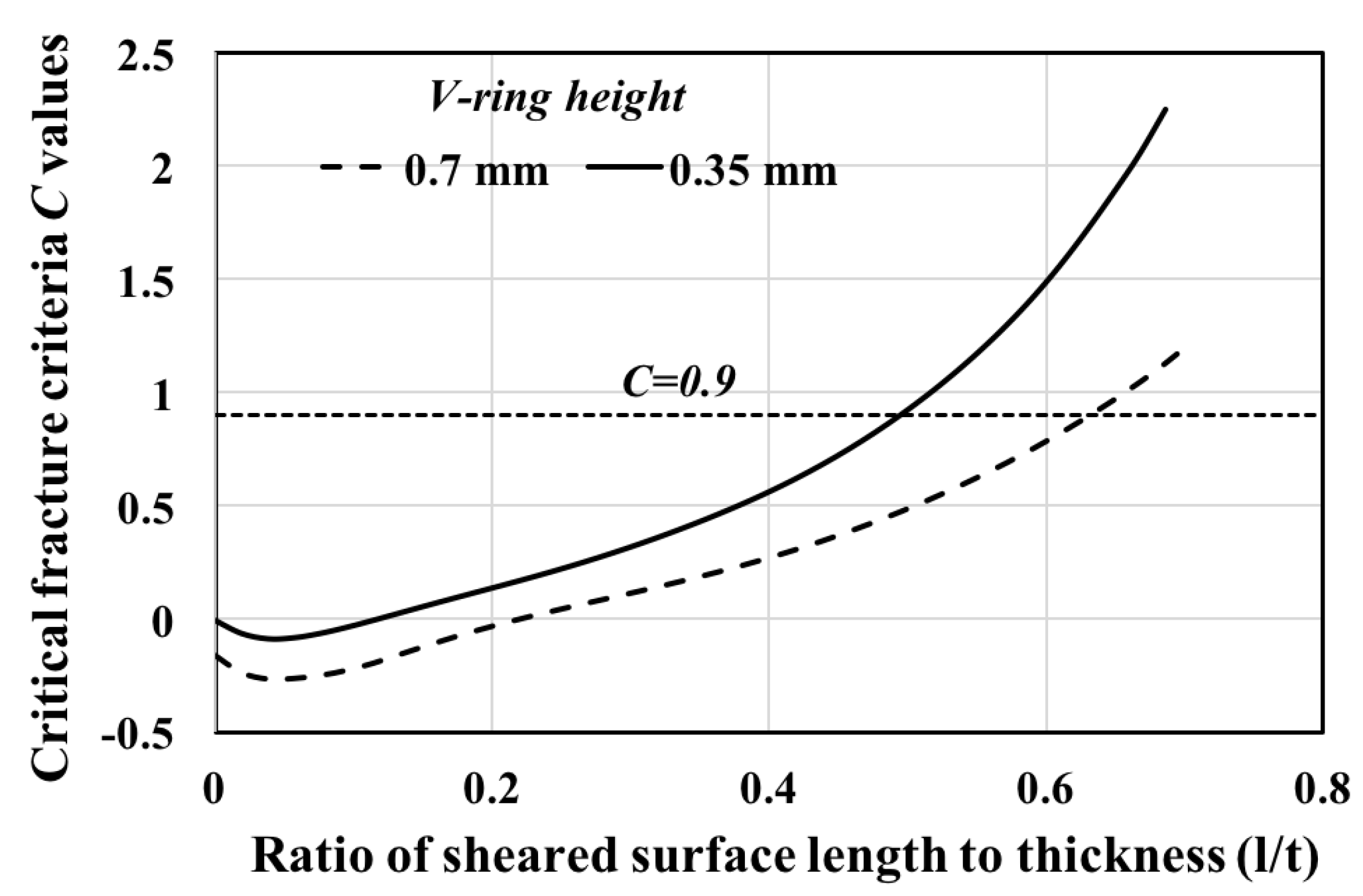
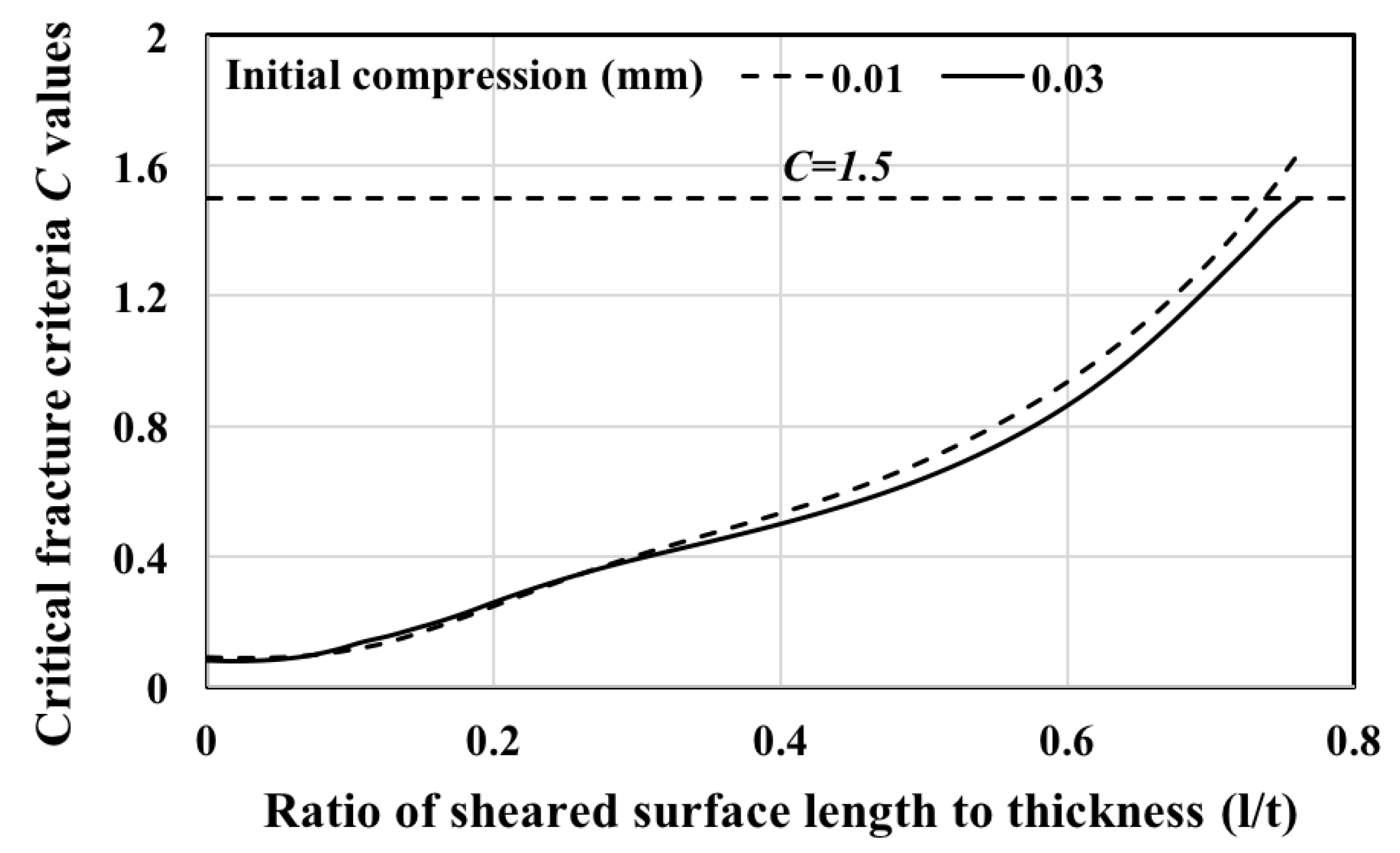
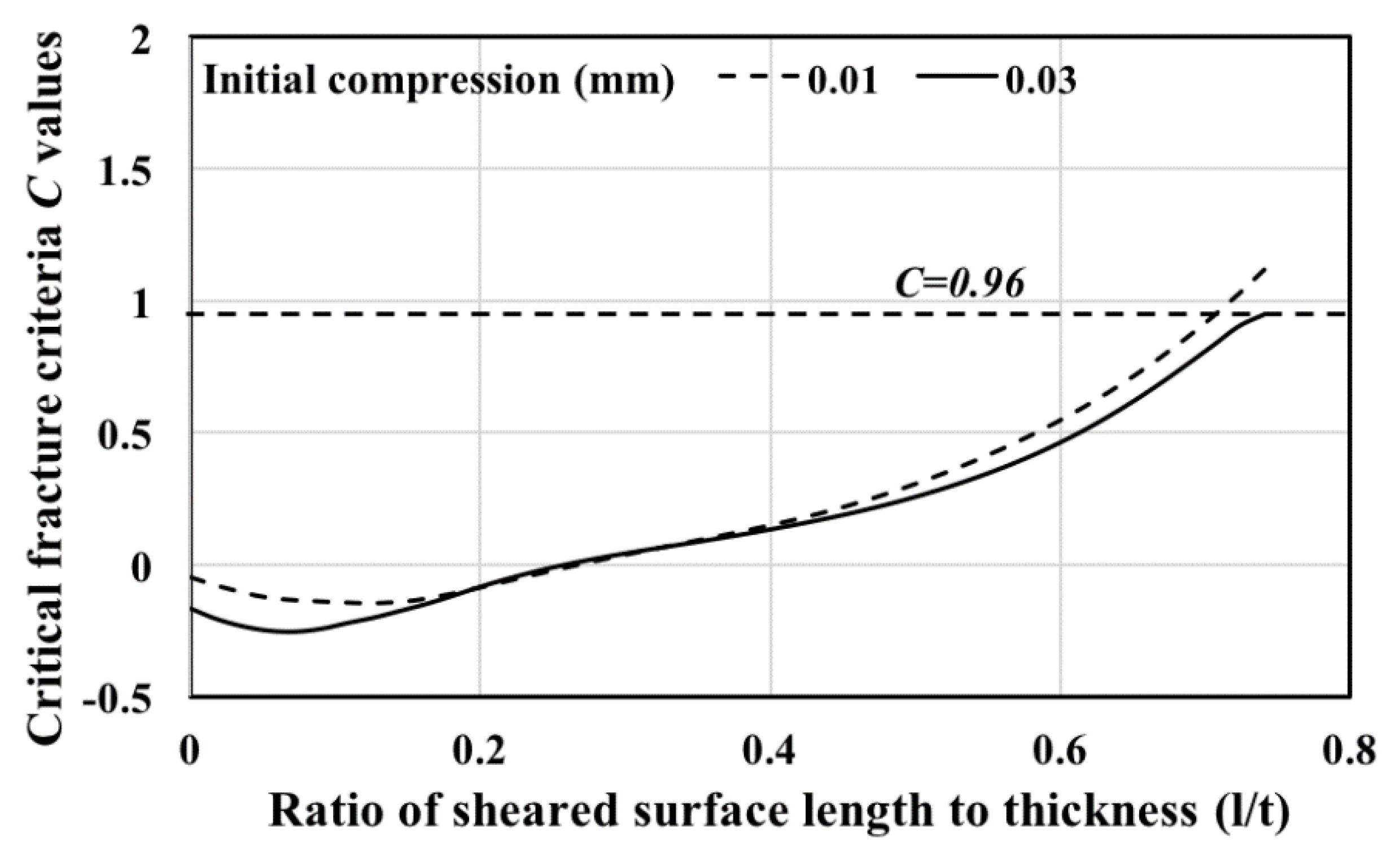
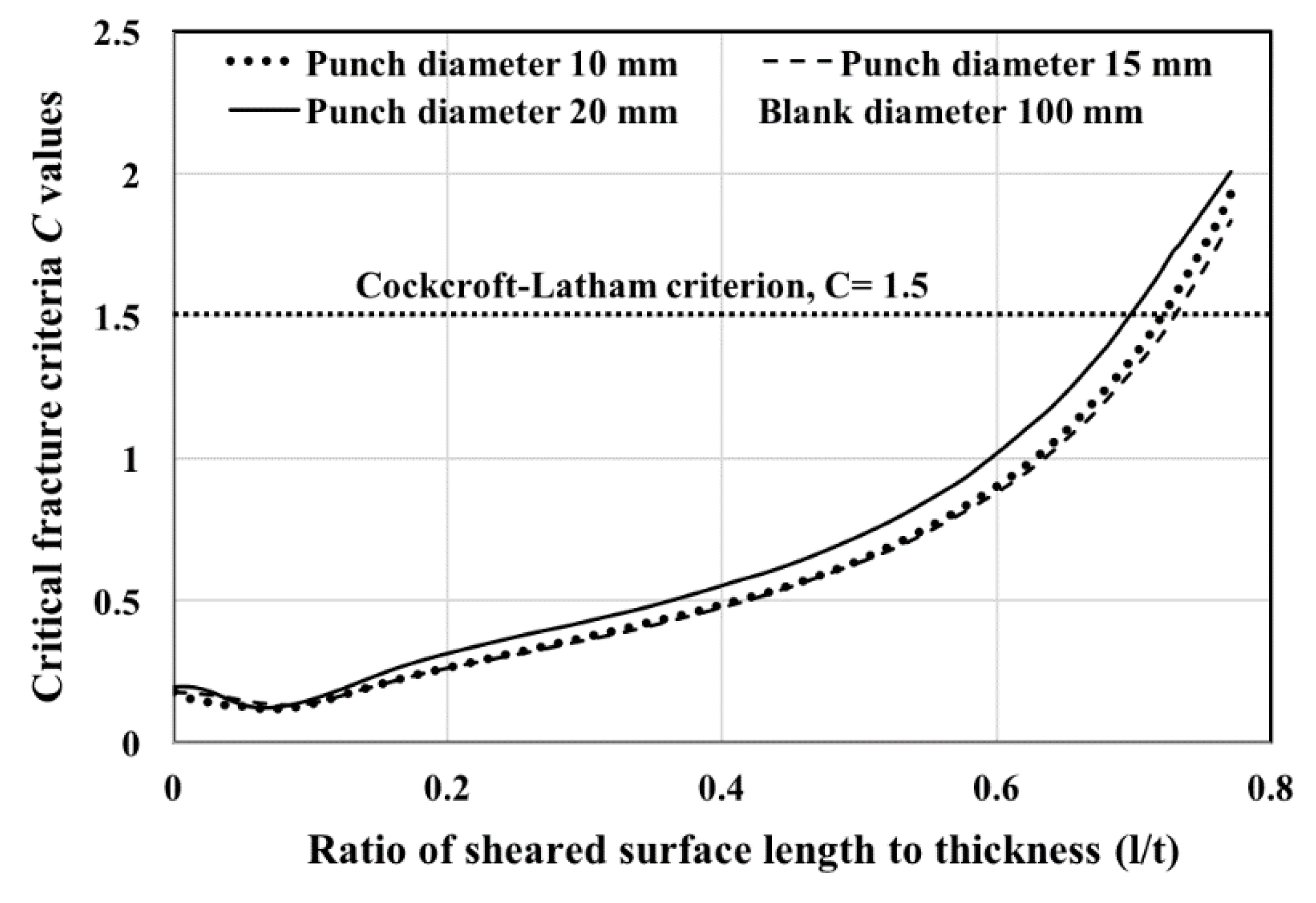
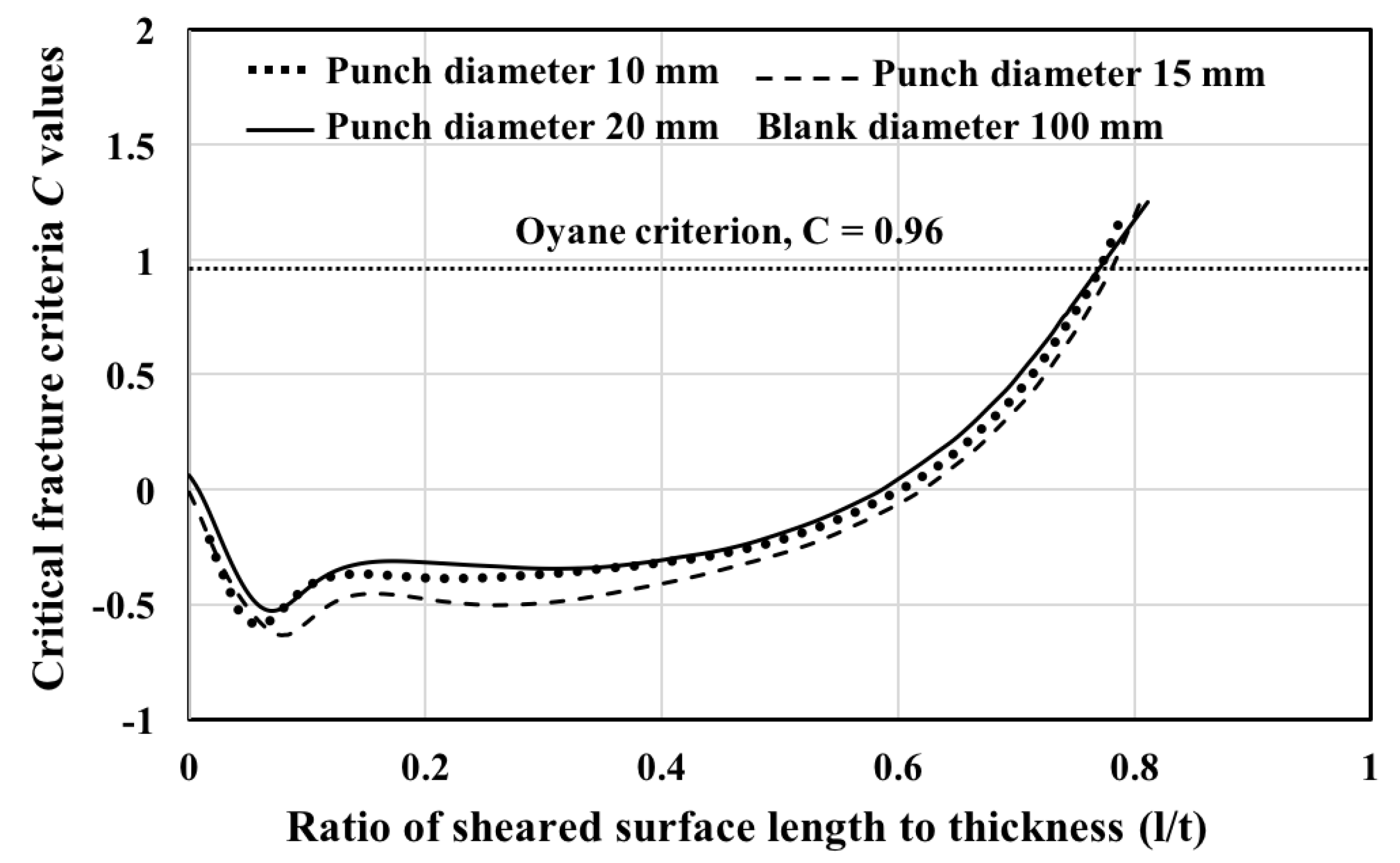
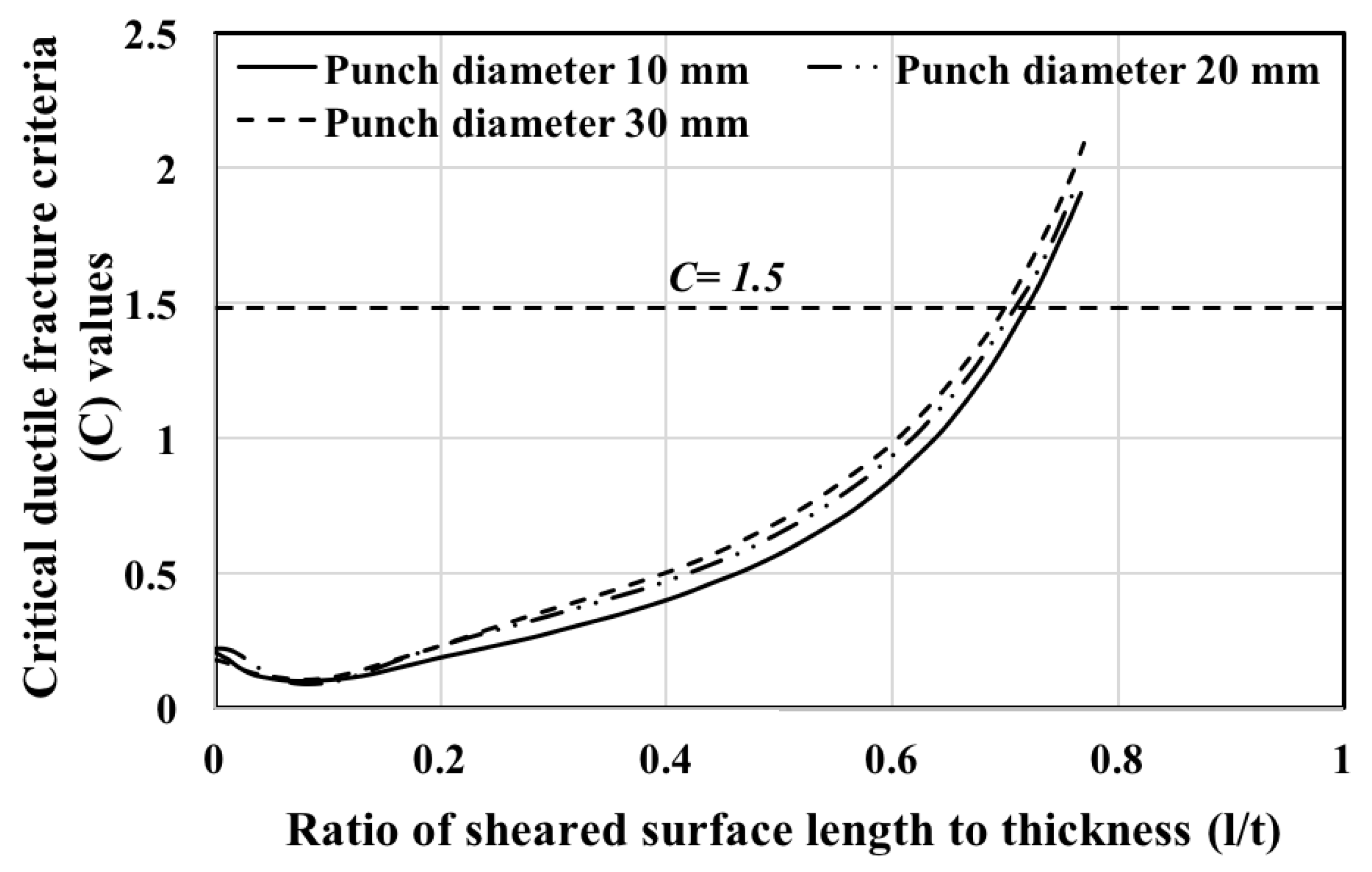
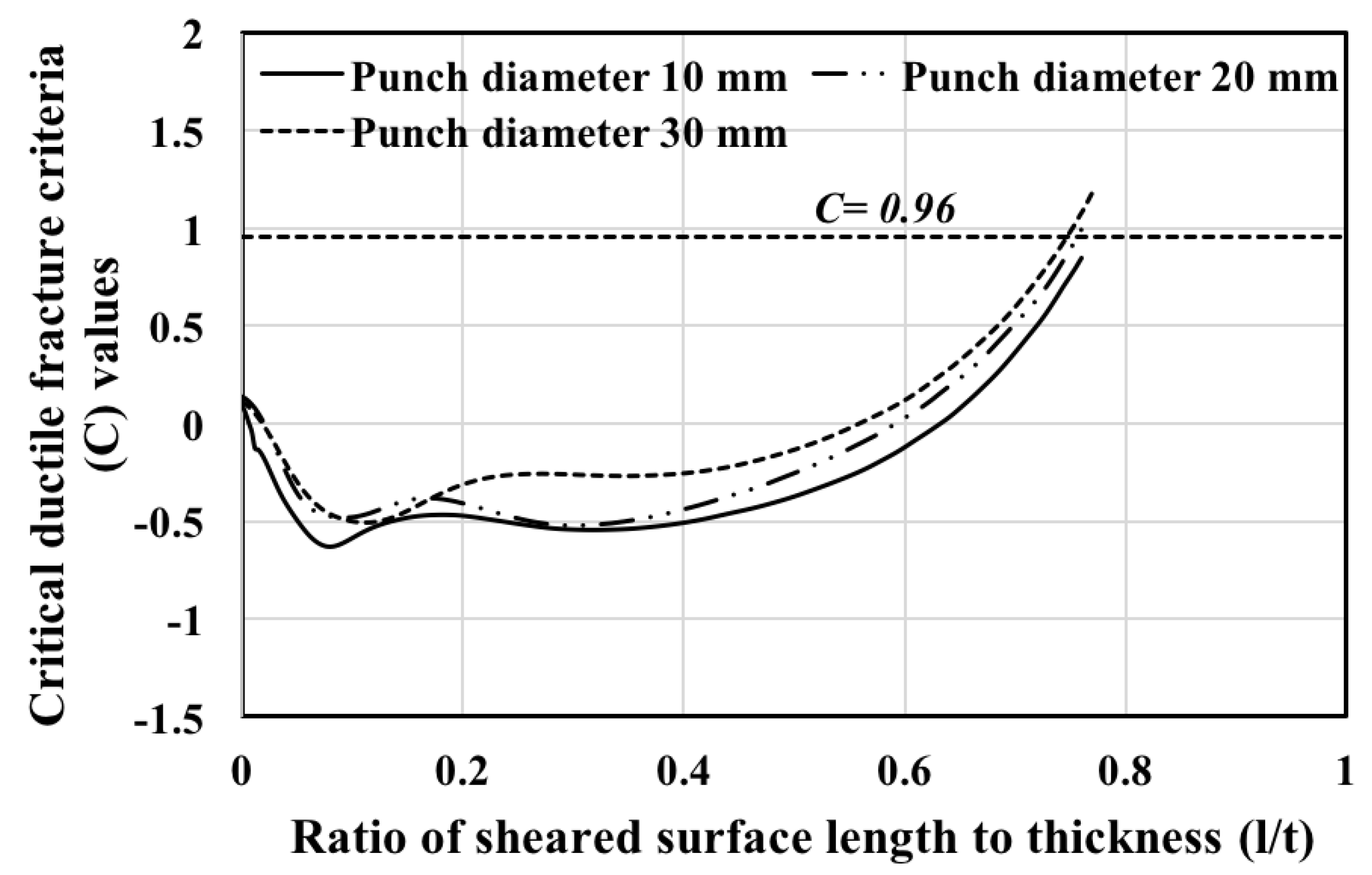
2.2. Determination of Critical Fracture Criteria, (C)
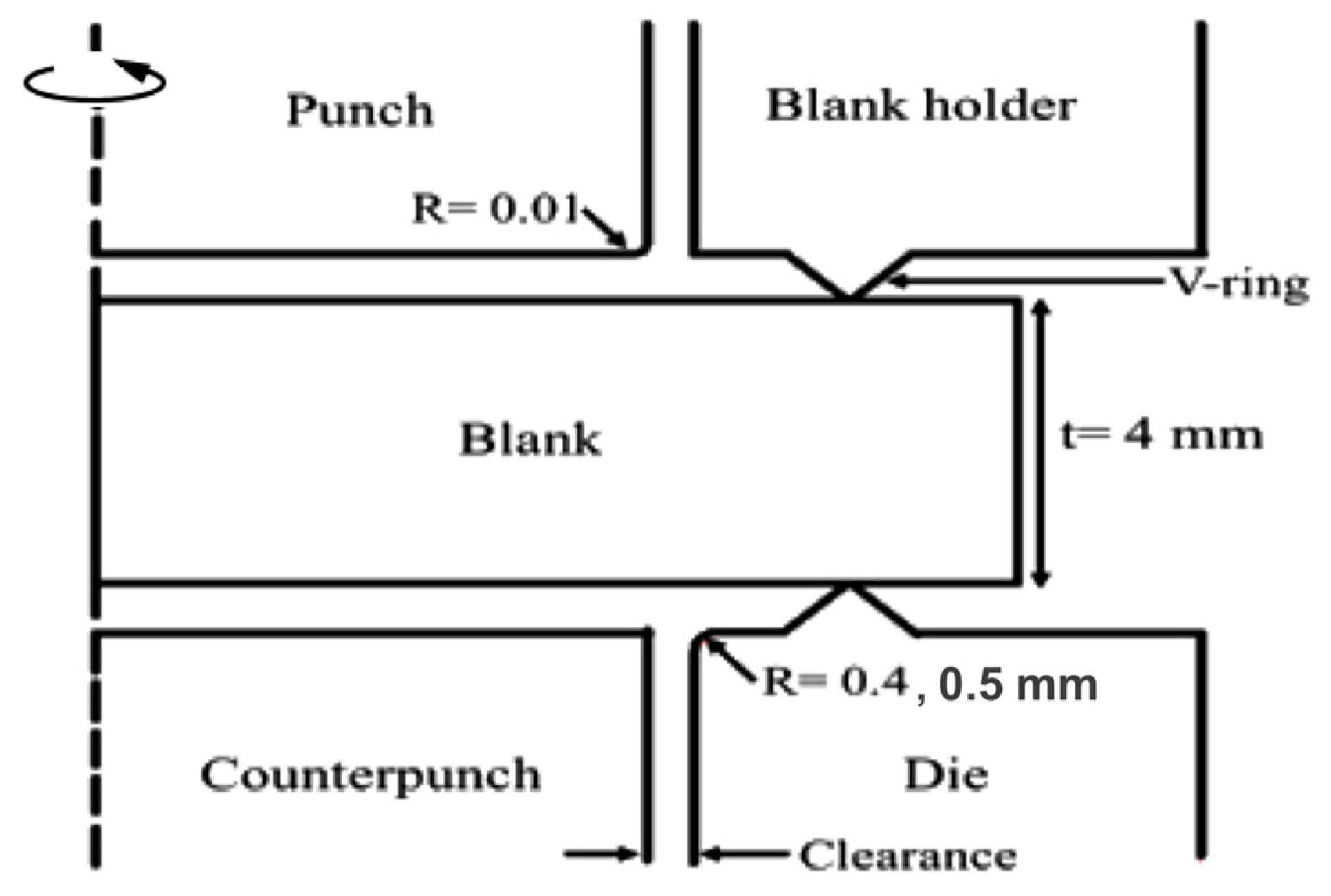
3. Finite-Element Analysis of Fine Blanking Processes
4. Results and Discussion
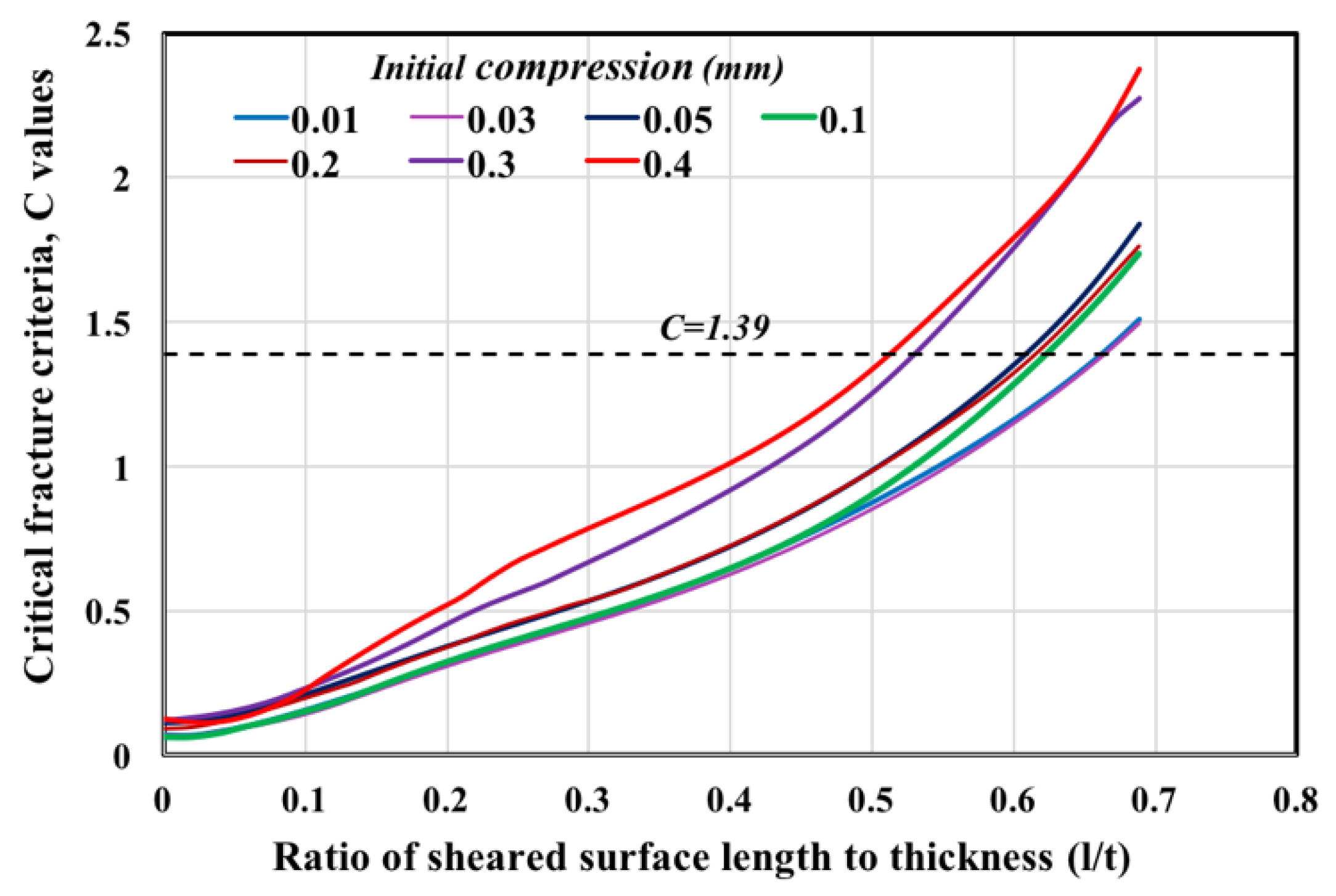
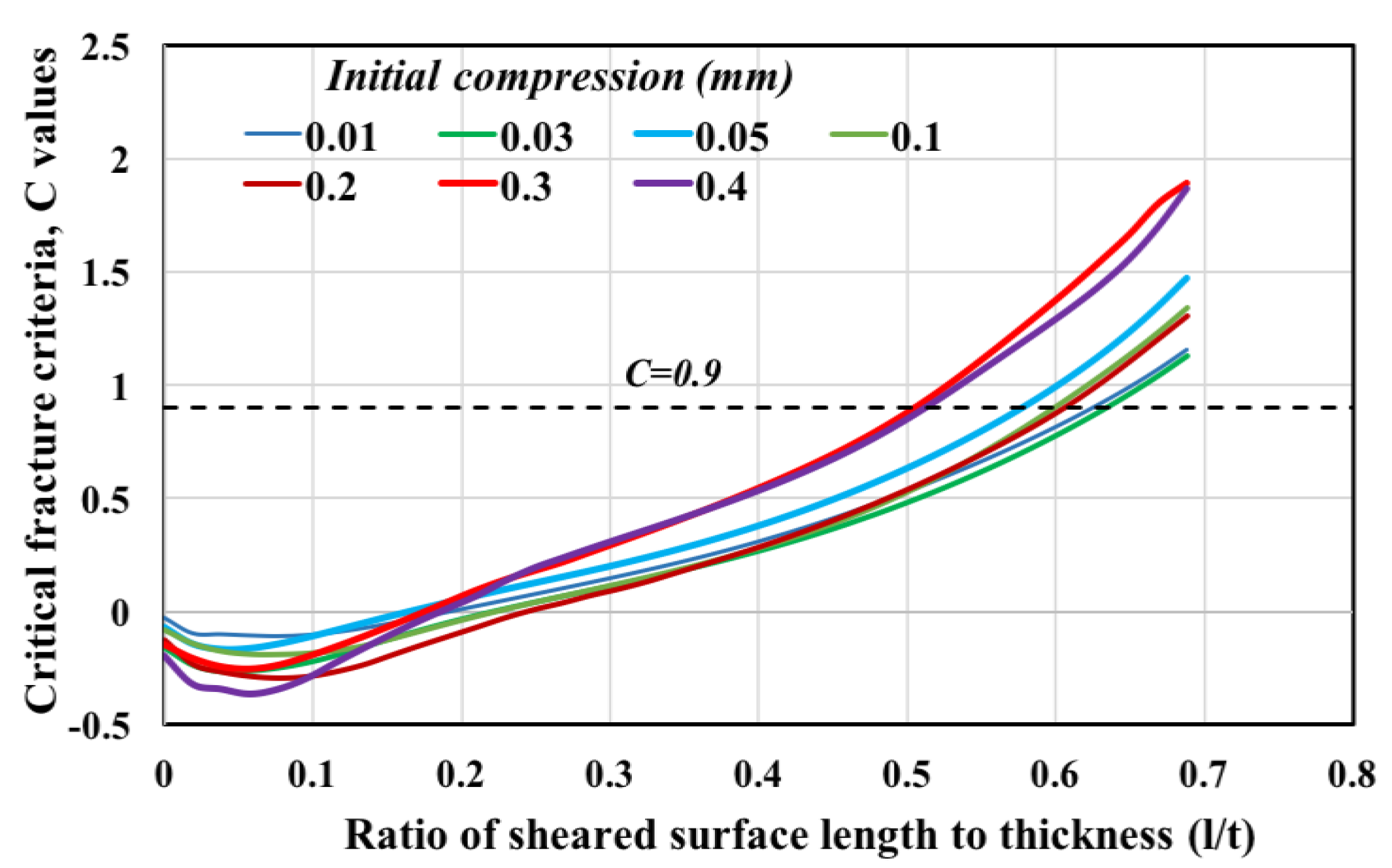
4.1. Effect of Initial Compression on the Sheared Surface Length
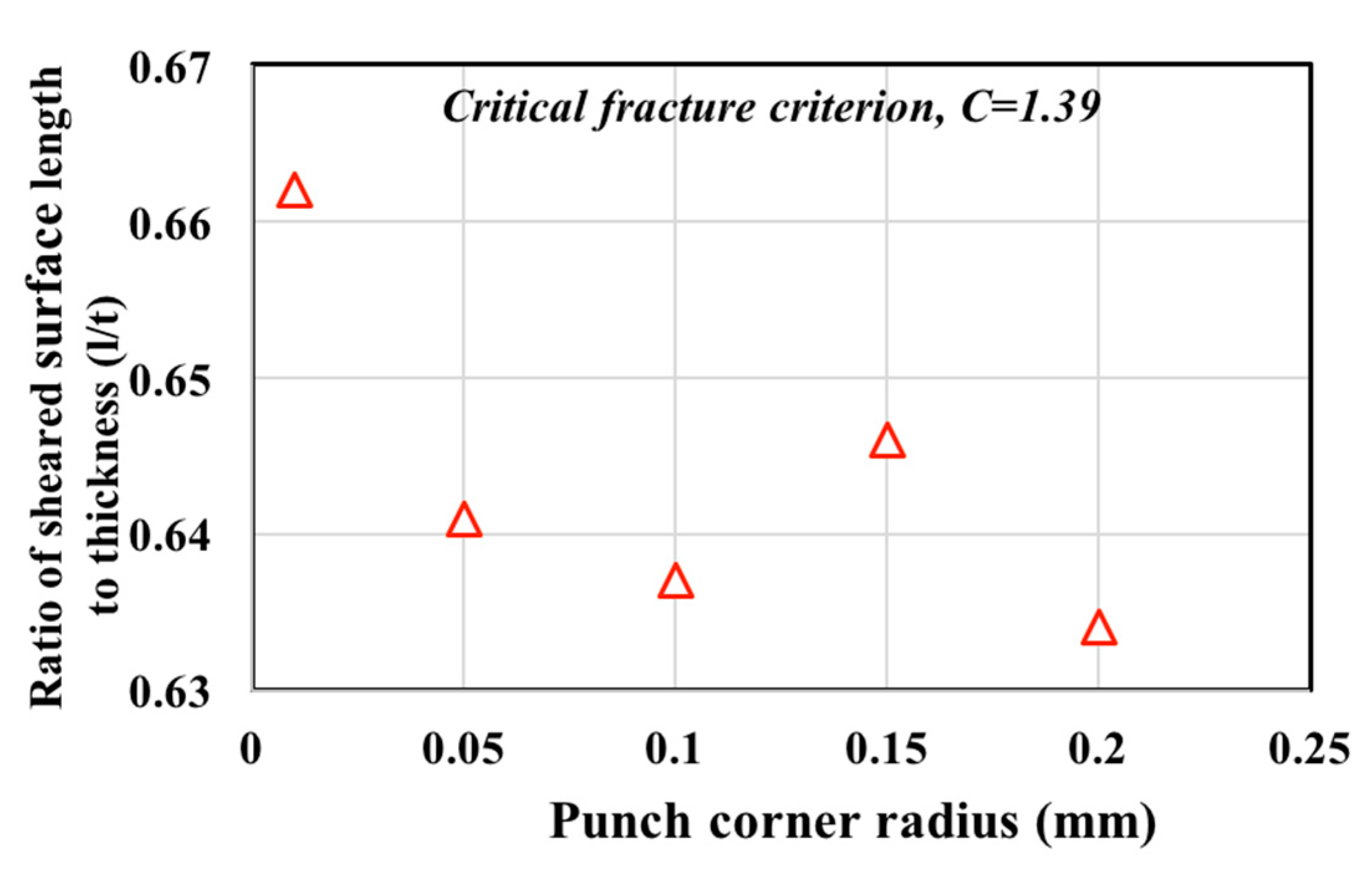
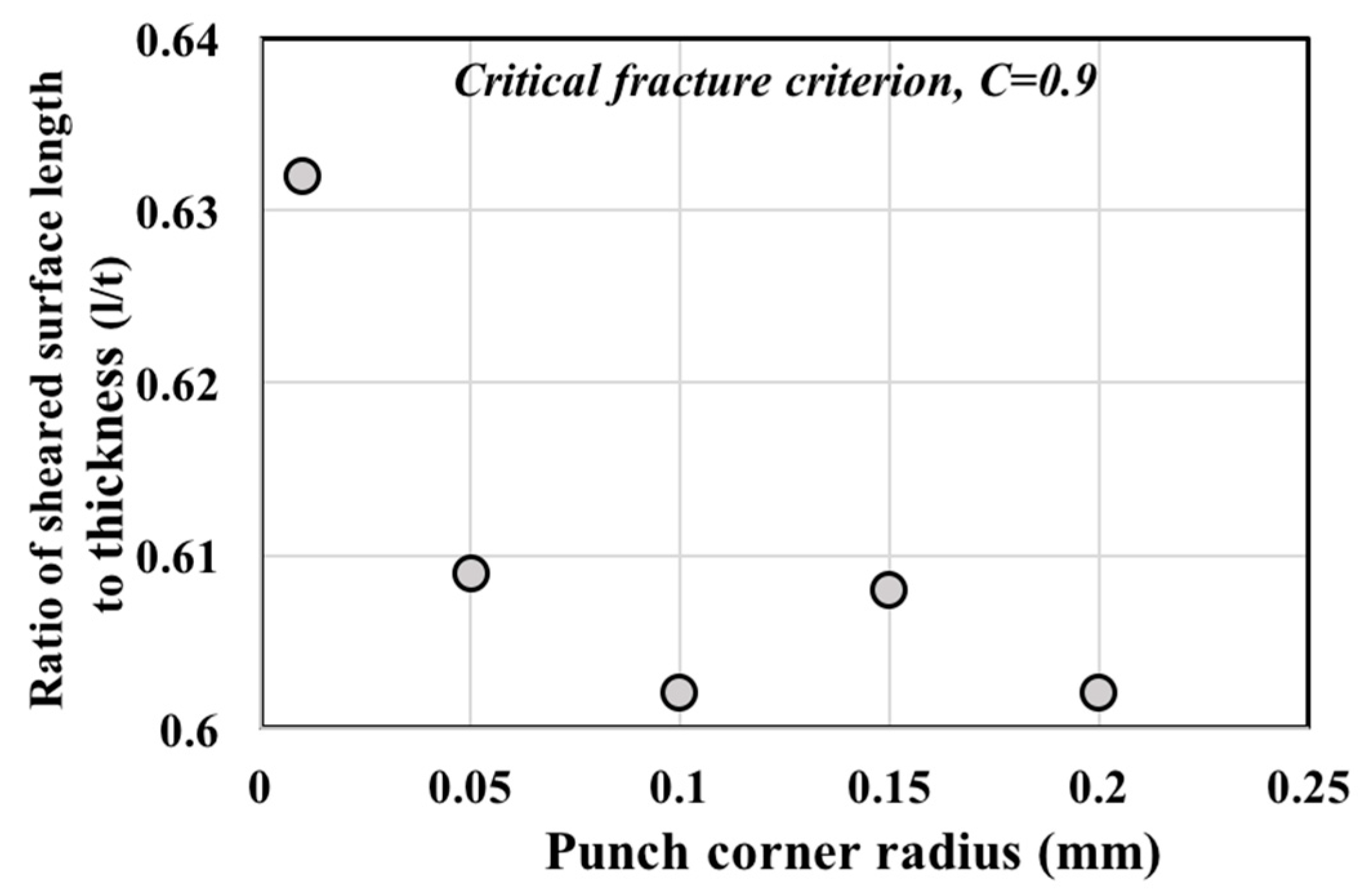
4.2. Effect of Punch Corner Radius on the Cut Surface
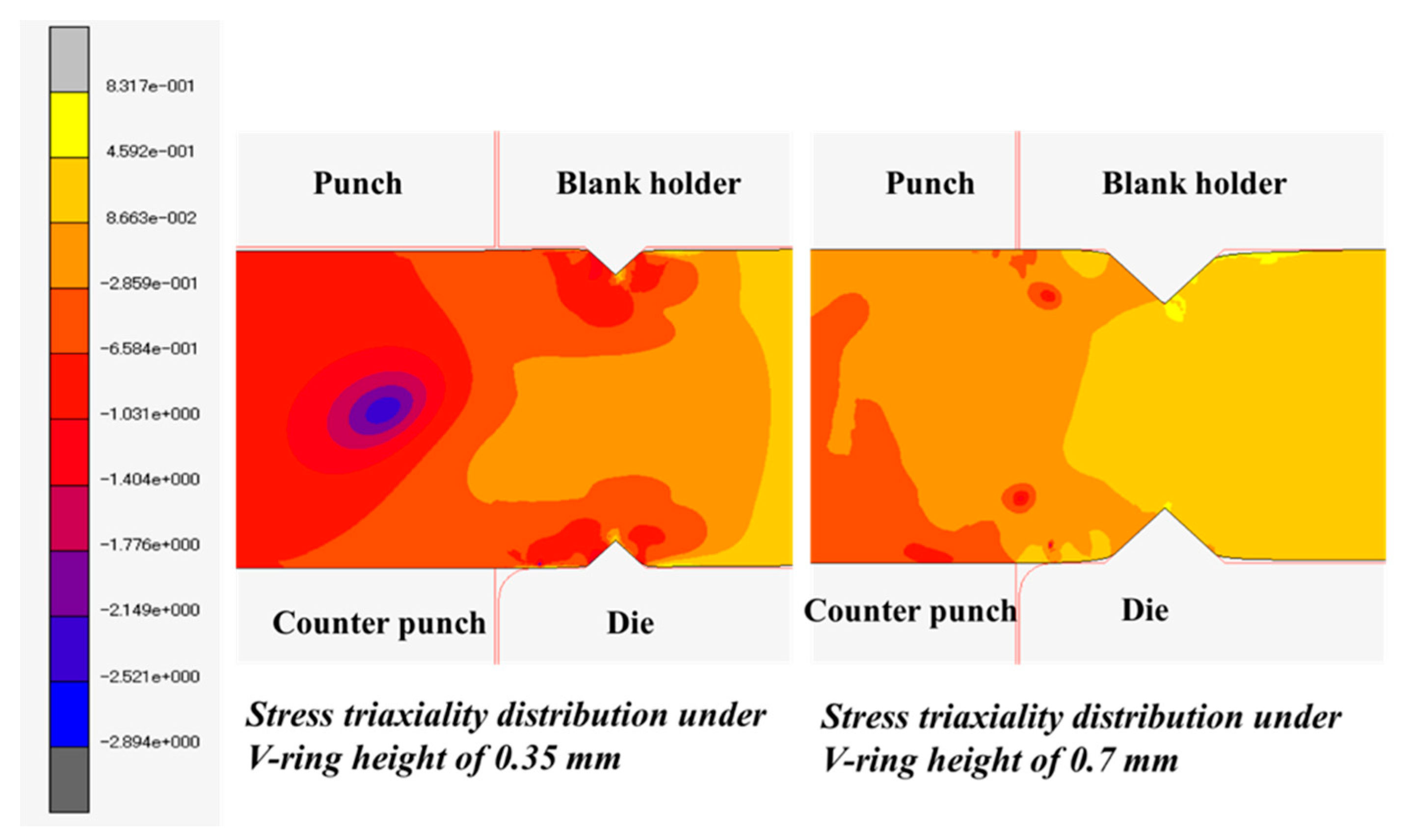
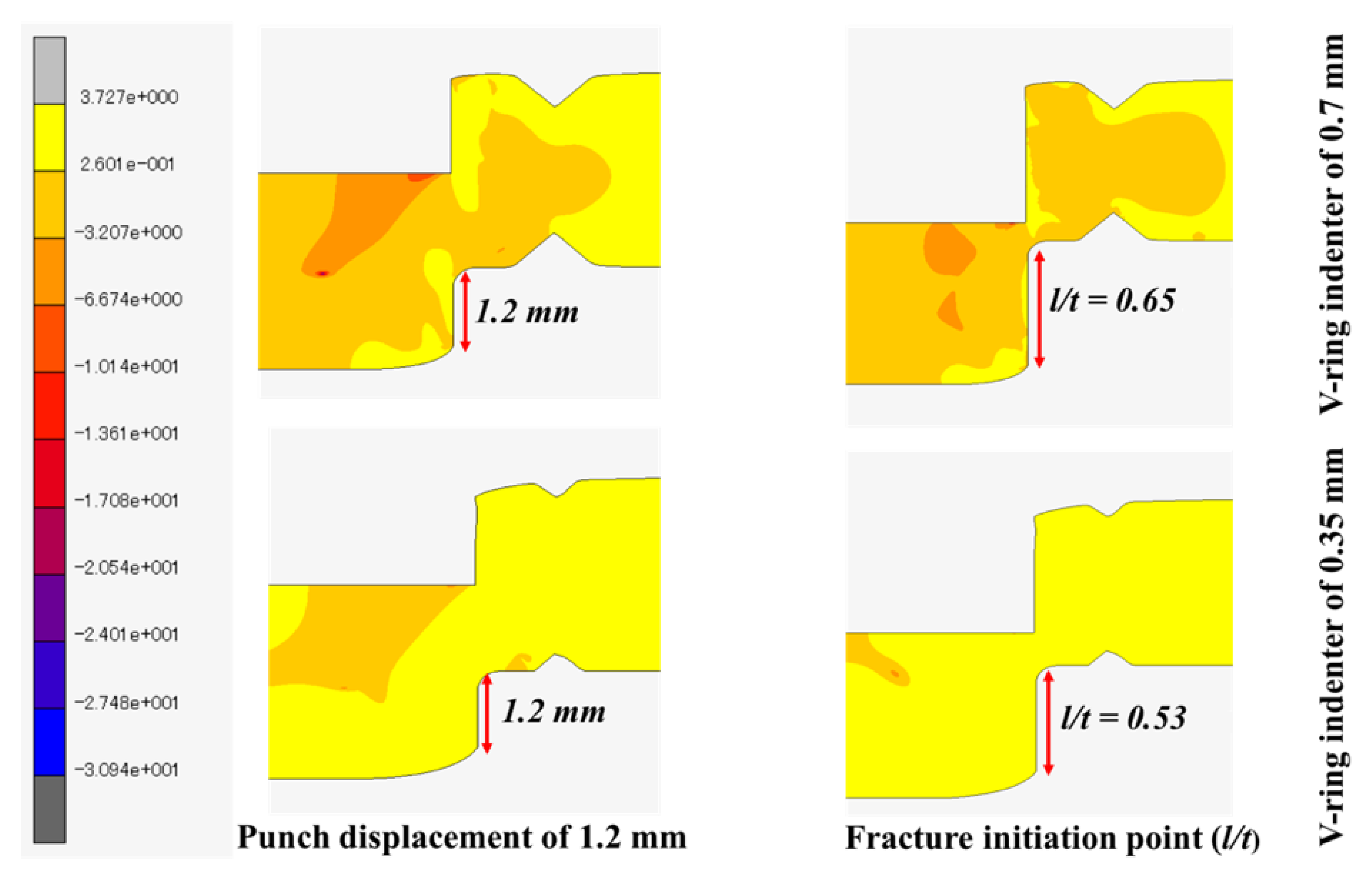
4.3. Effect of V-Ring Indenter on the Cut Surface
4.4. Effect of Stress Triaxiality
4.5. Selection of Optimized Parameters for Fine Blanking Process
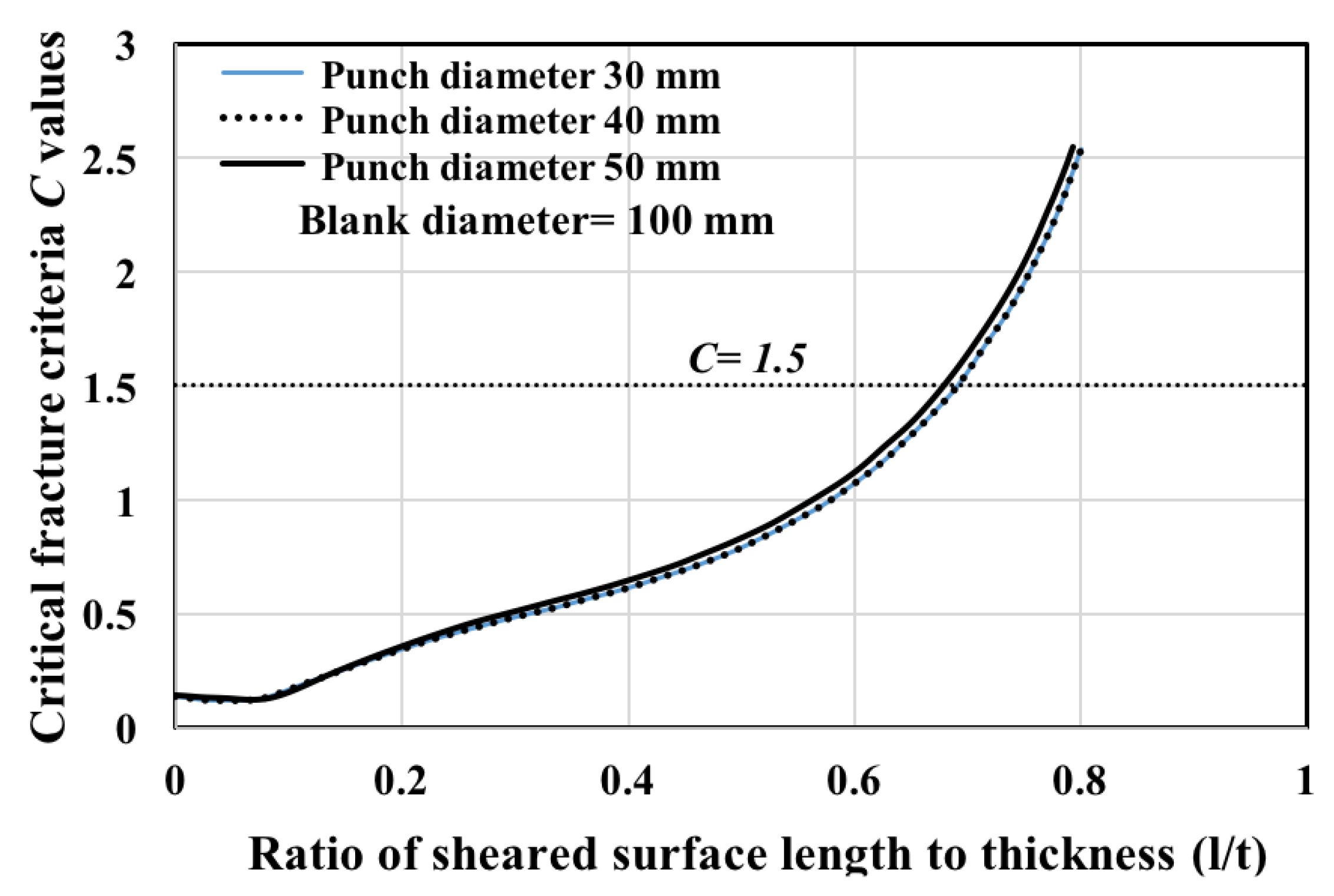
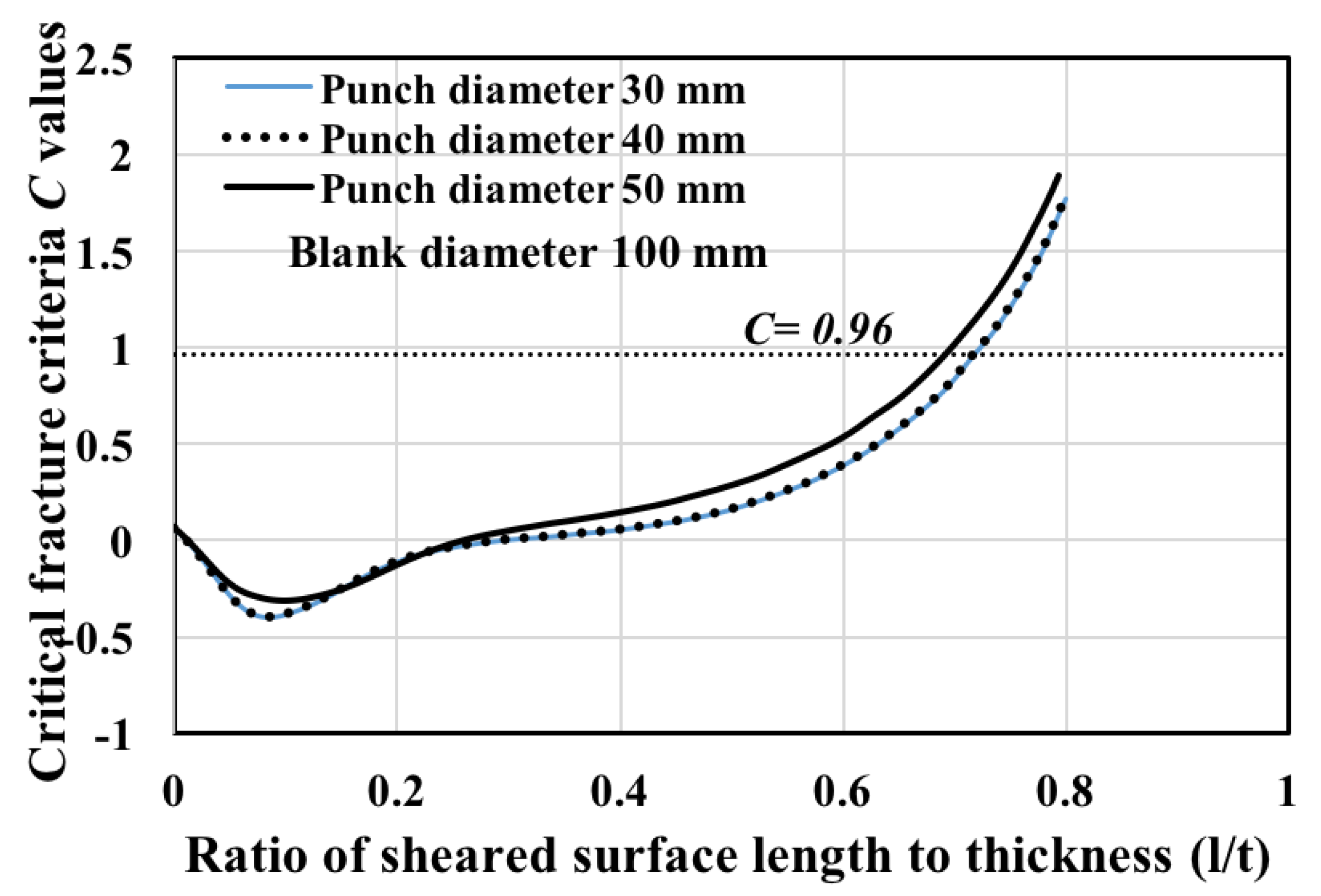
4.6. Verification of the Optimized Parameters
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhao, Z.; Zhuang, X.; Xie, X. An improved ductile fracture criterion for fine blanking process. J. Shanghai Jiaotong Univ. 2008, 13, 702–706. [Google Scholar] [CrossRef]
- Hambli, R. Finite element simulation of fine blanking processes using a pressure dependent damage model. J. Mater. Process. Tech. 2001, 116, 252–264. [Google Scholar] [CrossRef]
- Kwak, T.S.; Kim, Y.J.; Bae, W.B. Finite element analysis on the effect of die clearance on shear planes in fine blanking. J. Mater. Process. Tech. 2002, 130–131, 462–468. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Y. Fine-blanking process simulation by rigid viscous-plastic FEM coupled with void damage. J. Finite Elem. Anal. Des. 2003, 39, 457–472. [Google Scholar] [CrossRef]
- Thipprakmas, S. Finite element analysis of V-ring indenter mechanism in fine blanking process. J. Mater. Des. 2008. [Google Scholar] [CrossRef]
- Tanaka, T.; Hagihara, S.; Tadano, Y.; Yoshimura, S.; Inada, T.; Mori, T.; Fuchiwaki, K. Analysis of shear droop on cut surface of high-strength steel in fine blanking process. Mater. Trans. JSTP 2011, 52, 447–451. [Google Scholar] [CrossRef]
- Liu, Y.; Hua, L.; Mao, H.; Feng, W. Finite element simulation of effect of part shape on forming quality in fine blanking process. Procedia Eng. 2014, 81, 1108–1113. [Google Scholar] [CrossRef]
- Meng, B.; Fu, M.W.; Fu, C.M.; Chen, K.S. Ductile fracture and deformation behavior in progressive micro-forming. J. Mater. Des. 2015, 83, 14–25. [Google Scholar]
- Wang, J.P. A novel fine blanking approach. Int. J. Adv. Manuf. Technol. 2015, 78, 1015–1019. [Google Scholar] [CrossRef]
- Mao, H.; Zhou, F.; Liu, Y.; Hua, L. Numerical and experimental investigation of the discontinuous dot indenter in the fine blanking process. J. Manuf. Process. 2016, 24, 90–99. [Google Scholar] [CrossRef]
- Tang, B.; Liu, Y.; Mao, H. Investigation of a novel modified die design for fine-blanking process to reduce the die-roll size. Proc. Eng. 2017, 20, 1546–1551. [Google Scholar] [CrossRef]
- Voigt, H.; Trauth, D.; Feuerhack, A.; Mattfeld, P.; Klocke, F. Dependencies of the die-roll height during fine blanking of case hardening steel 16MnCr5 V-ring using a nesting strategy. Int. J. Adv. Manuf. Technol. 2018, 95, 3083–3091. [Google Scholar] [CrossRef]
- Luo, C.; Chen, Z.; Zhou, K.; Yang, X.; Zhang, X. A novel method to significantly decrease the die roll during fine blanking process with verification by simulation and experiments. J. Mater. Process. Tech. 2017, 250, 254–260. [Google Scholar] [CrossRef]
- Yoshida, Y.; Ishikawa, T. Determination of ductile damage parameters by notched plate tensile test using image analysis. J. Mater. Res. Innov. 2011, 15, s422–s425. [Google Scholar] [CrossRef]
- Phyo, W.M.; Hagihara, S.; Tanaka, T.; Taketomi, S.; Tadano, Y. Determination of the values of critical ductile fracture criteria to predict fracture initiation in punching processes. J. Manuf. Mater. Process. 2017, 1, 12. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D.J. Ductility and workability of metals. J. Inst. Metals 1968, 96, 33–39. [Google Scholar]
- Oyane, M.; Sato, T.; Okimoto, K.; Shima, S. Criteria for ductile fracture and their applications. J. Mech. Work. Tech. 1980, 4, 65–81. [Google Scholar] [CrossRef]
- Pacas, I.; Hernandez, R.; Casellas, D.; Valls, I. Strategies to increase the tool performance in punching operations of UHSS. In Proceedings of the 50th Anniversary Conference (IDDRG), Graz, Austria, 31 May–2 June 2010; pp. 325–334. [Google Scholar]
- Kwak, T.S.; Kim, Y.J.; Seo, M.K.; Bae, W.B. The effective of V-ring indenter on the sheared surface in the fine blanking process of pawl. J. Mater. Process. Tech. 2003, 143–144, 656–661. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mach. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
| Flow Stress (MPa) | 154 | 182 | 201.7 | 218 | 232.0 | 244.6 | 255.3 | 264.7 | 273.1 | 280.7 | 287.6 | 294 | 296.6 |
| Plastic Strain | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.1 | 0.11 | 0.114 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wai Myint, P.; Hagihara, S.; Tanaka, T.; Taketomi, S.; Tadano, Y. Application of Finite Element Method to Analyze the Influences of Process Parameters on the Cut Surface in Fine Blanking Processes by Using Clearance-Dependent Critical Fracture Criteria. J. Manuf. Mater. Process. 2018, 2, 26. https://doi.org/10.3390/jmmp2020026
Wai Myint P, Hagihara S, Tanaka T, Taketomi S, Tadano Y. Application of Finite Element Method to Analyze the Influences of Process Parameters on the Cut Surface in Fine Blanking Processes by Using Clearance-Dependent Critical Fracture Criteria. Journal of Manufacturing and Materials Processing. 2018; 2(2):26. https://doi.org/10.3390/jmmp2020026
Chicago/Turabian StyleWai Myint, Phyo, Seiya Hagihara, Toru Tanaka, Shinya Taketomi, and Yuichi Tadano. 2018. "Application of Finite Element Method to Analyze the Influences of Process Parameters on the Cut Surface in Fine Blanking Processes by Using Clearance-Dependent Critical Fracture Criteria" Journal of Manufacturing and Materials Processing 2, no. 2: 26. https://doi.org/10.3390/jmmp2020026





