A DRL Framework for Autonomous Pursuit-Evasion: From Multi-Spacecraft to Multi-Drone Scenarios

Highlights

What are the main findings?

• A single, generalizable DRL framework is proposed for autonomous pursuit-evasion that is successfully validated across both multi-spacecraft and multi-drone scenarios.
• A novel prediction-based reward function combined with curriculum learning significantly improves performance, achieving a 90.7% success rate and superior robustness under perturbations.

What is the implication of the main finding?

• The framework demonstrates adaptability to complex environments, including scenarios with larger team sizes (3-vs.-1) and static obstacles, highlighting its potential for real-world applications.
• The transferable nature of the prediction-based reward offers a practical methodology for overcoming sparse reward challenges in other complex aerospace tasks, such as spacecraft on-orbit servicing and mission-oriented UAV applications.

Abstract

To address the challenges of autonomous pursuit-evasion in aerospace, particularly in achieving cross-domain generalizability and handling complex terminal constraints, this paper proposes a generalizable deep reinforcement learning (DRL) framework. The core of the method is a self-play Proximal Policy Optimization (PPO) architecture enhanced by two key innovations. First, a dynamics-agnostic curriculum learning (CL) strategy is employed to accelerate training and enhance policy robustness by structuring the learning process from simple to complex. Second, a transferable prediction-based reward function is designed to provide dense, forward-looking guidance, utilizing forward-state projection to effectively satisfy mission-specific terminal conditions. Comprehensive simulations were conducted in both multi-spacecraft and multi-drone scenarios. In the primary spacecraft validation, the proposed method achieved a 90.7% success rate, significantly outperforming baseline algorithms like traditional PPO and Soft Actor-Critic (SAC). Furthermore, it demonstrated superior robustness, with a performance drop of only 8.3% under stochastic perturbations, a stark contrast to the over 18% degradation seen in baseline methods. The successful application in a multi-drone scenario, including an obstacle-rich environment, confirms the framework’s potential as a unified and robust solution for diverse autonomous adversarial systems.

1. Introduction

With the rapid advancement of autonomous systems, the complexity and dynamism of operational environments, both in space and in the air, have increased significantly. In the space domain, next-generation intelligent spacecraft are being developed for complex tasks like on-orbit servicing, debris removal, and close-proximity inspection [1,2,3]. Similarly, in the aerial domain, autonomous unmanned aerial vehicles (UAVs or drones) are becoming ubiquitous in surveillance, package delivery, and mission-oriented applications. The pursuit-evasion game is a fundamental challenge that spans both domains. It is a dynamic and adversarial scenario where agents must make real-time decisions to achieve conflicting objectives [4]. For these critical encounters, traditional ground-based or pre-programmed decision-making approaches are often inadequate. Consequently, developing robust autonomous decision-making strategies has become a critical research focus, with deep reinforcement learning emerging as a powerful paradigm for learning optimal policies in uncertain and adversarial settings [5].

Orbital and aerial pursuit-evasion games represent a canonical two-agent (or multi-agent) decision-making process with competing goals. Unlike standard trajectory planning where future states can be predetermined, these games involve strategic interactions where each agent’s optimal move is contingent on its opponent’s anticipated actions. This interdependency means neither the pursuer nor the evader can pre-calculate a fixed optimal trajectory, necessitating adaptive strategies that can respond to an intelligent adversary in real time [6,7]. Traditional methods for solving such problems primarily fall into two categories: model-based differential game theory and data-driven reinforcement learning.

In model-based methods, differential game theory and optimal control principles are leveraged to compute Nash equilibrium strategies for both the pursuer and the evader. The pursuit-evasion problem is often formulated as a two-player zero-sum game, where the Hamilton–Jacobi–Isaacs (HJI) equation describes the optimal strategies for both agents [8,9]. However, in most practical scenarios, these equations lack analytical solutions and must be solved numerically using techniques such as the shooting method, pseudo-spectral methods, or collocation techniques [10]. In [11], a pseudo-spectral optimal control approach was proposed to solve spacecraft pursuit-evasion problems, but its computational cost remains a challenge for real-time applications. Similarly, in [12], high-thrust impulsive maneuvers were incorporated into pursuit-evasion scenarios, significantly increasing the problem’s complexity due to discrete thrust applications. However, these model-based methods often struggle with high computational costs and the inability to adapt to complex, dynamic, and uncertain environments.

Recent advancements in artificial intelligence have established reinforcement learning as a powerful framework for addressing complex decision-making challenges within uncertain and adversarial environments [13]. RL enables autonomous agents to learn through interactions with their environment, optimizing their strategies via reward-based feedback. This capability renders RL particularly well-suited for highly dynamic and time-sensitive adversarial tasks [14,15]. In particular, actor–critic RL architectures, such as Trust Region Policy Optimization (TRPO) and Proximal Policy Optimization (PPO), have demonstrated superior performance in high-dimensional control problems, achieving a balance between exploration and exploitation while ensuring stable learning convergence [16,17]. The application of DRL to aerospace pursuit-evasion has become an active area of research, with studies exploring near-optimal interception strategies, two-stage pursuit missions, and intelligent maneuvers for hypersonic vehicles [18,19,20].

Despite these advancements, a review of the current literature reveals several key research gaps that motivate this work. First, the challenge of generalizability is evident, as many existing RL applications focus on specific domains, such as planetary landing or orbital transfers, without emphasizing the transferability of the core decision-making architecture [21,22,23]. Few studies have proposed a unified framework applicable to pursuit-evasion games in both space and aerial contexts. Second, many approaches struggle to effectively address complex, state-dependent terminal constraints. This is often due to the difficulty in designing a reward function that effectively guides agents toward these specific conditions, with many relying on simple distance-based rewards that can lead to suboptimal or myopic strategies [24]. To highlight how the proposed framework addresses these gaps in relation to recent works, a methodological comparison is provided in

Table 1. Methodological comparison with recent works.

Study	Method and Domain	Distinction from the Proposed Approach
Zhang et al. [4]	MADDPG for Multi-UAV Air Combat	Focuses on online planning; the proposed framework emphasizes cross-domain generalizability and utilizes a more stable on-policy algorithm (PPO).
Yu et al. [8]	Hybrid SAC + HJI for Spacecraft	Combines RL with complex differential game models. The presented approach is a pure, end-to-end DRL solution.
Zhao et al. [7]	PRD-MADDPG for Spacecraft	Employs a specific reward decomposition method. The current work introduces a novel prediction-based reward and a curriculum learning strategy.
Chen et al. [25]	DRL with Luring Strategy for Incomplete Information Scenarios	Focuses on complex information structures (e.g., luring, partial observability). The proposed framework focuses on generalizability and robustness under full observability.

.

Motivated by these challenges, the primary objective of this paper is to develop and validate a single, unified DRL framework that is both effective and generalizable for autonomous pursuit-evasion tasks across different domains. Specifically, this work aims to (1) design a modular architecture that can seamlessly transition from multi-spacecraft to multi-drone scenarios; (2) introduce a training methodology that accelerates learning and enhances policy robustness; and (3) create a reward mechanism capable of handling complex, state-dependent terminal constraints that are common in aerospace missions.

To achieve these objectives, a generalizable DRL-based framework is developed in this paper. The method’s robustness and versatility are demonstrated in both a challenging multi-spacecraft orbital scenario and a multi-drone aerial scenario. The main contributions of this paper are threefold:

• A generalizable DRL framework is proposed for autonomous pursuit-evasion, with its modularity demonstrated across both multi-spacecraft and multi-drone domains, directly addressing the challenge of generalizability.
• A dynamics-agnostic curriculum learning strategy is integrated to improve the training efficiency and robustness of the learned policies, providing an effective training methodology for complex adversarial games.
• A transferable prediction-based reward function is designed to effectively handle complex, state-dependent terminal constraints, a common challenge in aerospace missions.

The remainder of this paper is structured as follows. Section 2 details the problem formulation. Section 3 presents the proposed DRL framework, including the CL strategy and reward design. Section 4 provides a comprehensive experimental validation, and Section 5 concludes the paper.

2. Problem Definition

This section formulates the pursuit-evasion problem using a multi-spacecraft orbital game as the primary case for validation. While the dynamics are specific to the space domain, the general structure of the game, constraints, and objectives are analogous to those in aerial drone scenarios.

2.1. Orbital Game Dynamics Modeling

Orbital maneuvering games refer to dynamic interactions between two or more spacecraft within the gravitational field of celestial bodies. These interactions are governed by orbital dynamics constraints, with each spacecraft pursuing its own objectives within its allowable control capabilities and available information.

This study focuses on local orbital maneuvering games within geosynchronous orbit (GEO), where the pursuit-evasion dynamics occur over a distance of thousands of kilometers. Specifically, a multi-spacecraft orbital pursuit-evasion scenario involving n homogeneous active spacecraft (pursuers) and a single non-cooperative target (evader) is investigated. The pursuers, initially located at a distance of m km from the target, aim to intercept it within the capture zone, potentially establishing a safe approach corridor for subsequent operations. Meanwhile, the target seeks to evade capture while remaining within l km of its initial orbital position [26].

The orbital pursuit task is considered successful when any pursuer enters the capture zone at the terminal time $t_f$. To describe the geometry of the engagement, a relative orbital coordinate system is first established. Its origin is a virtual reference point located on a circular geostationary orbit (GEO), which serves as the center of the relative motion frame. This reference point defines the nominal orbit, while the target (evader) as well as the pursuers maneuver relative to this frame. The relative orbital coordinate system is defined following the traditional Hill’s frame, which is aligned with the RSW coordinate system described in Ref. [27] (p. 389). Specifically, the axes are defined as follows: the $x_o$ (S) axis points along the orbital velocity direction (along-track), the $z_o$ (R) axis points from the spacecraft to the Earth’s center (radial), and the $y_o$ (W) axis completes the right-hand system, pointing along the orbital angular momentum direction (cross-track). This definition ensures consistency with the Clohessy–Wiltshire equations in Equation (1) and with the state transition matrix adopted later in this work. The state of a spacecraft is thus described by its relative position ${\mathbf{r}}_i\left(k\right)={[x_i\left(k\right),y_i\left(k\right),z_i\left(k\right)]}^{\top }$ and velocity ${\mathbf{v}}_i\left(k\right)={[{\dot{x}}_i\left(k\right),{\dot{y}}_i\left(k\right),{\dot{z}}_i\left(k\right)]}^{\top }$.

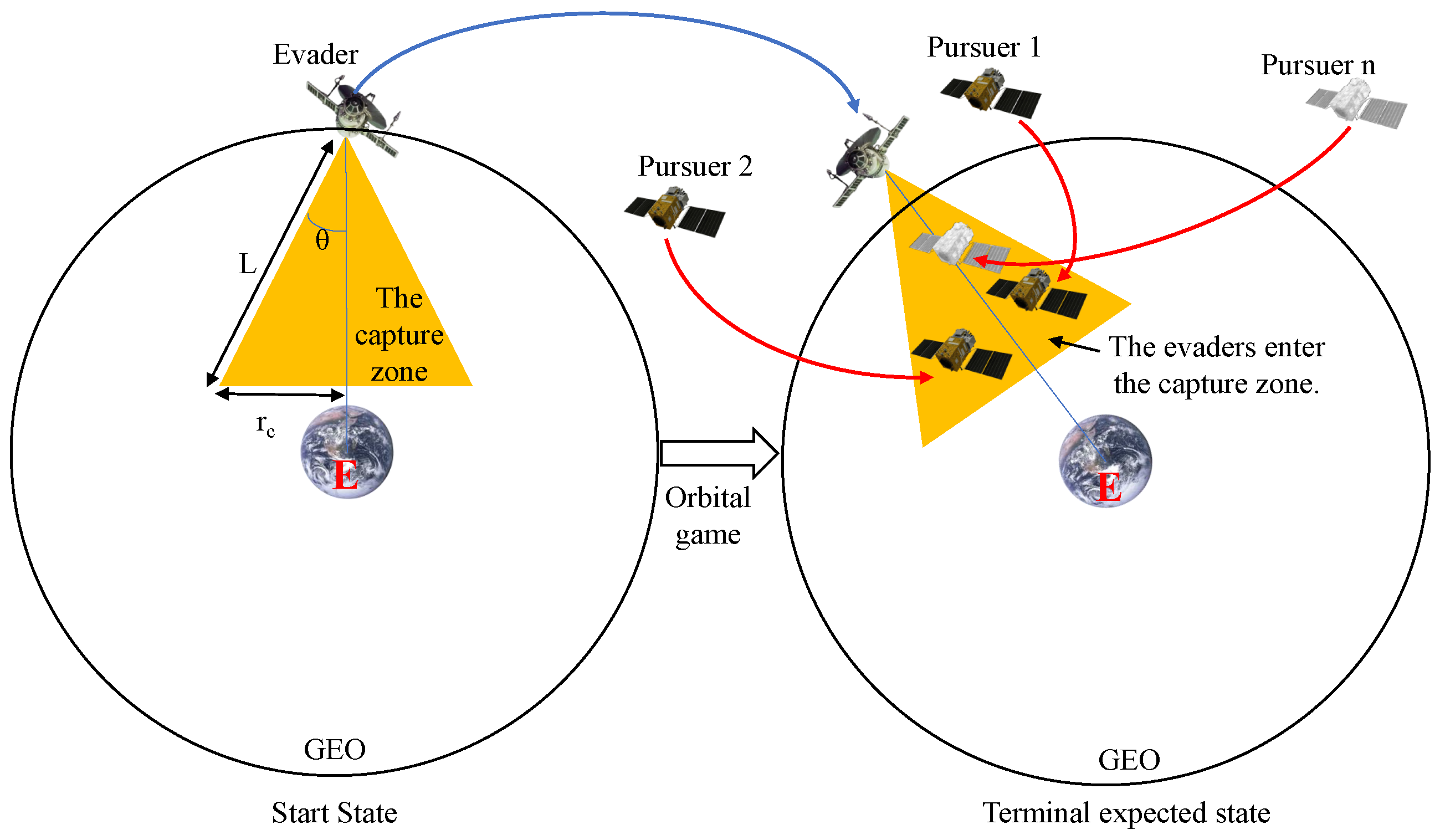
With the reference frame defined, the capture zone can be described as a cone-shaped region with a fixed generatrix length, L, and a half-opening angle, $\theta$. The apex of the cone is located at the target’s position [28]. The central axis of this cone is fixed along the positive z-axis of the evader’s relative orbital frame. This orientation, which directs the approach path towards the Earth (i.e., from the zenith direction), is representative of specific mission profiles. For instance, in missions involving Earth observation or remote sensing, a pursuer might need to maintain a nadir-pointing instrument orientation during its final approach to collect data on the target against the background of the Earth. This geometry is therefore adopted to reflect such operational constraints. The cone maintains this orientation relative to the evader’s frame throughout the engagement. The schematic diagram of this orbital maneuvering game is shown in Figure 1.

In this study, the game is formulated within a discrete-time framework where control actions are modeled as impulsive thrusts applied at fixed decision intervals. This modeling choice is a pragmatic necessity driven by the need for computational tractability in a complex, game-theoretic reinforcement learning context. While deterministic optimal control methods often handle continuous-thrust profiles, such approaches are typically intractable for real-time, multi-agent strategic decision-making. By discretizing the control actions, the problem’s complexity is significantly reduced, making it amenable to solution via DRL algorithms like PPO. This abstraction allows the focus to shift from low-level continuous trajectory optimization to the high-level strategic interactions, which is the core of the pursuit-evasion game.

The relative motion between spacecraft is governed by nonlinear dynamics. To provide a challenging and realistic testbed for the DRL agents, a high-fidelity nonlinear model of relative orbital motion is used as the simulation environment in this study. All agent interactions and trajectories are propagated by numerically integrating the full nonlinear equations of motion derived from the two-body problem.

For the agent’s internal model, however, particularly for the prediction-based reward function, which requires rapid state projections, a linearized approximation is necessary for computational tractability. The well-known Clohessy–Wiltshire (CW) equations are employed for this purpose. The form of the equations presented below is specific to the coordinate system defined above and is consistent with authoritative sources [27,29,30]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\ddot{x}-2\omega \dot{y}-3{\omega }^{2}x=0\\ \ddot{y}+2\omega \dot{x}=0\\ \ddot{z}+{\omega }^{2}z=0\end{array}\right.\end{array}$$

(1)

where $\omega$ is the mean orbital motion. It is crucial to note that this linearized model is used exclusively by the agent for its internal reward calculation. In contrast, its actual movement within the simulation is governed by the high-fidelity nonlinear dynamics. This creates a realistic model mismatch that adds to the complexity of the learning task and tests the robustness of the learned policy. From the CW equations, the natural acceleration vector ${\mathbf{a}}_i\left(k\right)$ under the linearized model at time step k is given by

$${\mathbf{a}}_i\left(k\right)={[2\omega {\dot{y}}_i\left(k\right)+3{\omega }^2{x}_i\left(k\right),-2\omega {\dot{x}}_i\left(k\right),-{\omega }^2{z}_i\left(k\right)]}^{\top }.$$

(2)

Maneuvers are executed as impulsive thrusts, $∆{\mathbf{v}}_i\left(k\right)$, at discrete time steps $T_d$. The state propagation between maneuvers is then calculated as

$$\begin{array}{cc}\hfill {\mathbf{r}}_i(k+1)& ={\mathbf{r}}_i\left(k\right)+{\mathbf{v}}_i\left(k\right)T_d+{\displaystyle \frac{1}{2}}{\mathbf{a}}_i\left(k\right)T_d^2,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathbf{v}}_i(k+1)& ={\mathbf{v}}_i\left(k\right)+{\mathbf{a}}_i\left(k\right)T_d+∆{\mathbf{v}}_i\left(k\right).\hfill \end{array}$$

(4)

The state propagation equations above represent the Euler integration based on the linearized dynamics and are used internally by the agent for its predictions. This does not represent the high-fidelity propagation used in the main simulation environment.

2.2. Design of Constraints

To ensure the realism and practicality of the multi-agent maneuvering problem, a set of constraints are incorporated into the decision-making and training process. These constraints, including input saturation, terminal conditions, and collision avoidance, are fundamental to real-world scenarios in both the space and aerial domains.

To reflect realistic actuator limitations, the velocity increment that can be applied at each decision step is constrained. This input saturation is described as

$$\parallel ∆{\mathbf{v}}_i\left(k\right)\parallel \le ∆v_{max}$$

(5)

where $\parallel ∆{\mathbf{v}}_i\left(k\right)\parallel$ is the magnitude of the velocity increment for spacecraft i at step k and $∆v_{max}$ is the maximum allowable impulse magnitude per step.

The terminal conditions for a successful pursuit at time $t_f$ are defined by both distance and angle constraints within the capture cone:

$$\parallel {\mathbf{r}}_{tp}\parallel \le L\mathrm{and}\angle ({\mathbf{r}}_{tp},\mathbf{u})\le \theta$$

(6)

where ${\mathbf{r}}_{tp}$ is the vector from the evader to the pursuer and $\mathbf{u}$ is the cone’s central axis (defined as the positive z-axis in our setup). The specific values for L and $\theta$ are mission-dependent. For long-range GEO scenarios, they define a relatively large ’approach corridor’ rather than a precise docking port, as will be detailed in the simulation setup. The evader’s objective is to violate at least one of these conditions at $t_f$.

The constraints of the evader aim to violate either condition to achieve escape. The constraints of the pursuer and the evader at terminal time $t_f$ are depicted as in Figure 2.

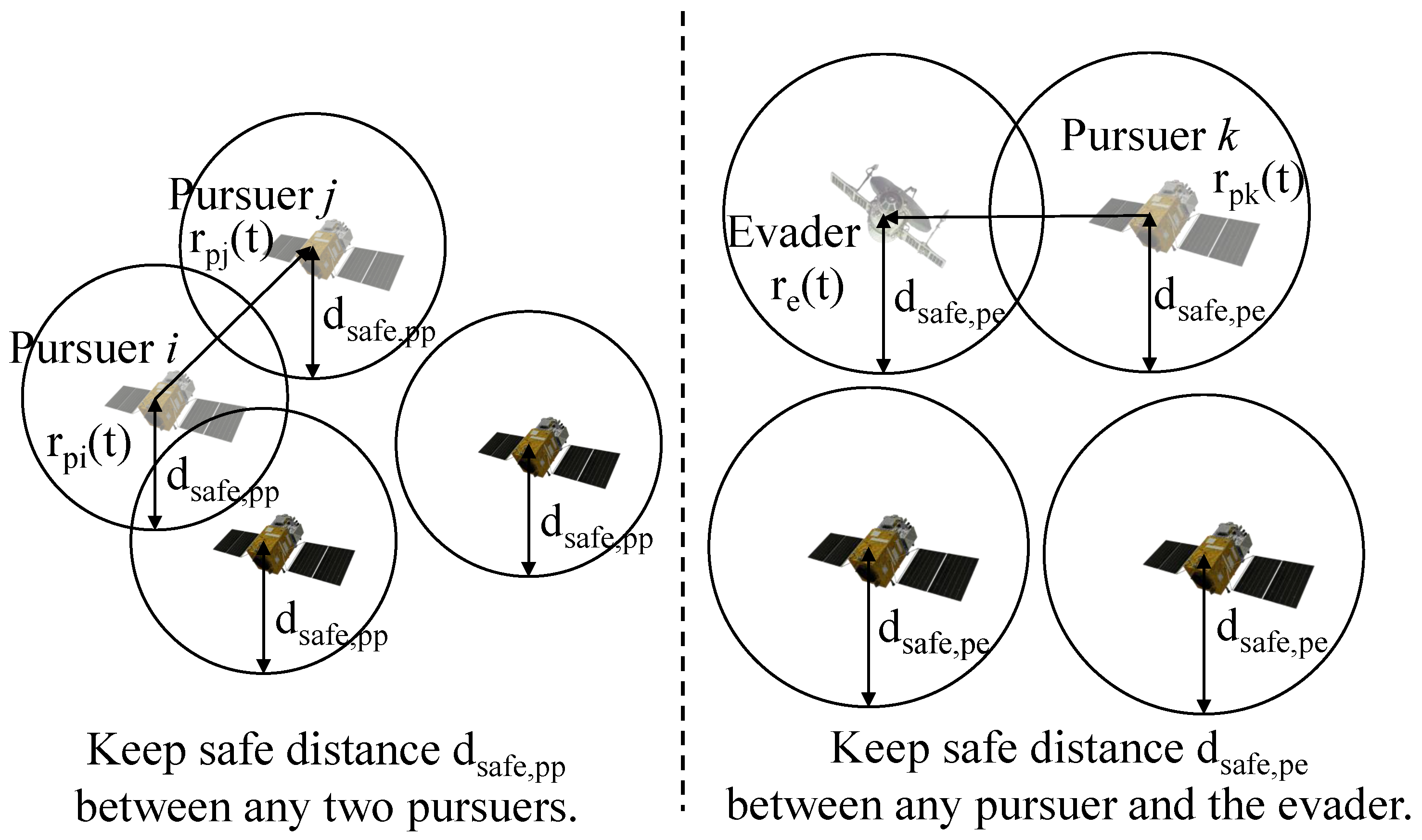
Furthermore, to ensure safe operations and prevent mission failure due to collisions, safety distance constraints can be described as in [31]:

$$\left\{\begin{array}{cccc}\hfill & ∥{\mathbf{r}}_{p_i}\left(t\right)-{\mathbf{r}}_{p_j}\left(t\right)∥\ge d_{\mathrm{safe},\mathrm{pp}},\hfill & \hfill & \forall i,j\in \{1,\dots ,n\},i\ne j\hfill \\ \hfill & ∥{\mathbf{r}}_{p_k}\left(t\right)-{\mathbf{r}}_e\left(t\right)∥\ge d_{\mathrm{safe},\mathrm{pe}},\hfill & \hfill & \forall k\in \{1,\dots ,n\}\hfill \end{array}\right.$$

(7)

where ${\mathbf{r}}_{p_i}\left(t\right)$, ${\mathbf{r}}_{p_j}\left(t\right)$, and ${\mathbf{r}}_{p_k}\left(t\right)$ denote the positions of pursuer i, pursuer j, and pursuer k at time t, and ${\mathbf{r}}_e\left(t\right)$ denotes the position of the evader. The parameters $d_{\mathrm{safe},\mathrm{pp}}$ and $d_{\mathrm{safe},\mathrm{pe}}$ represent the minimum safe separation distance between any two pursuers and between any pursuer and the evader, respectively.

As shown in Figure 3, the constraint defines the safety distance around each spacecraft to prevent collisions.

3. Track Game Decision Method Based on PPO

This section details the proposed DRL framework. The core of the method is a self-play training architecture where pursuer and evader agents concurrently learn and evolve their strategies. Proximal Policy Optimization (PPO) was selected as the learning algorithm due to its balance of sample efficiency and stable convergence, a critical feature for adversarial multi-agent training. Unlike more complex algorithms such as Soft Actor–Critic (SAC) or off-policy methods like Deep Q-Networks (DQN), PPO’s clipped surrogate objective provides robust performance with simpler implementation [32]. The framework integrates PPO with two key innovations: a curriculum learning strategy and a prediction-based reward function, which are detailed below.

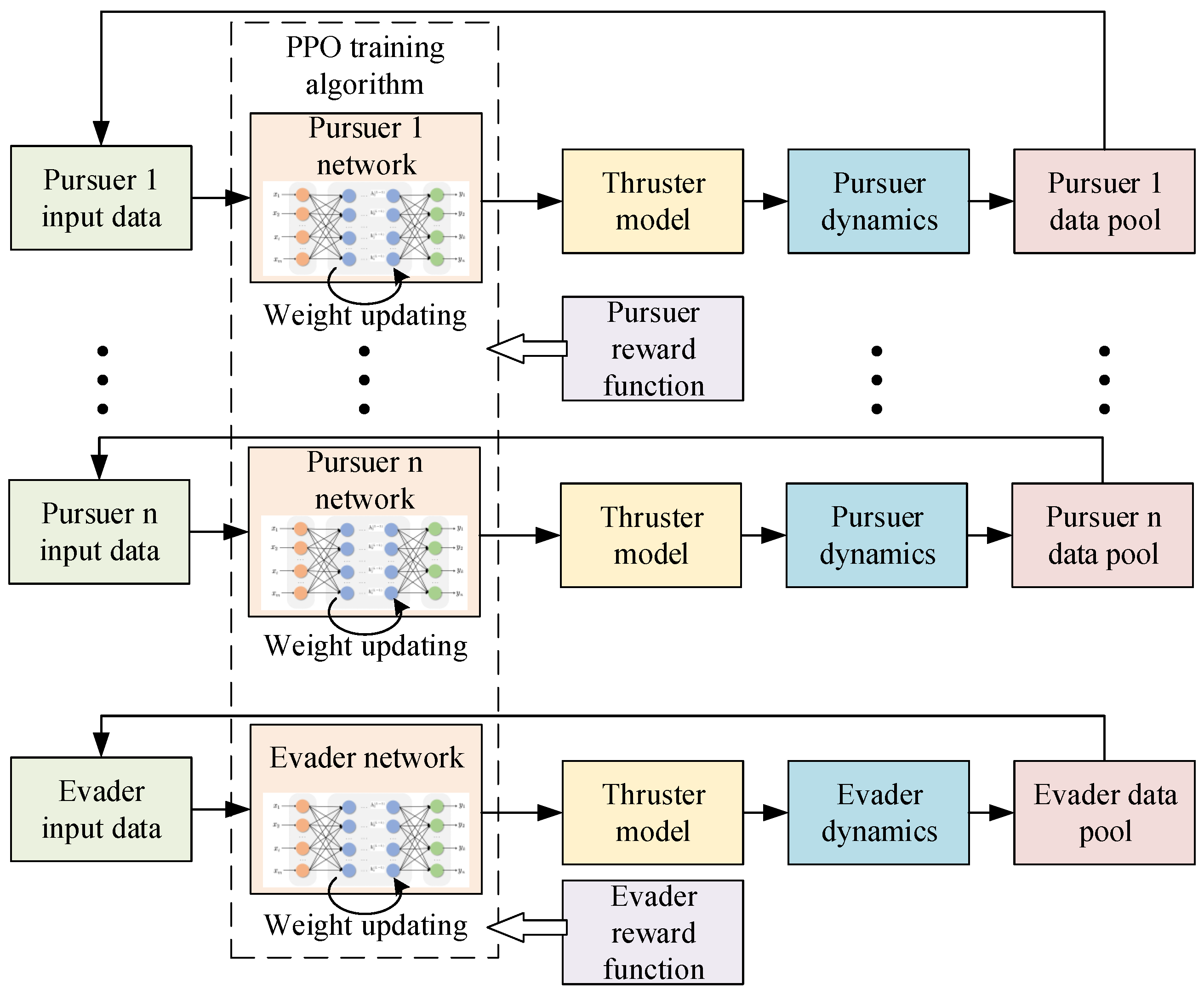
3.1. Self-Play Training Architecture

A self-play training strategy is employed to develop the agents’ policies. In this architecture, both the pursuer and evader agents are trained simultaneously, continuously competing against each other. This adversarial process allows each agent’s policy, represented by a neural network, to improve iteratively in response to the evolving strategy of its opponent.

The decision-making process for each agent is as follows. At each time step, the agent receives a state observation from the environment. This state is then fed into its policy network. The network outputs a continuous action vector, which directly represents the impulsive thrust command (i.e., the velocity increment $∆\mathbf{v}$) to be applied. The environment executes this action, transitions to a new state, and returns a reward signal. This entire interaction loop is depicted in Figure 4, which illustrates the overall training architecture. This framework naturally extends to multi-agent scenarios, facilitating either cooperative or competitive behaviors.

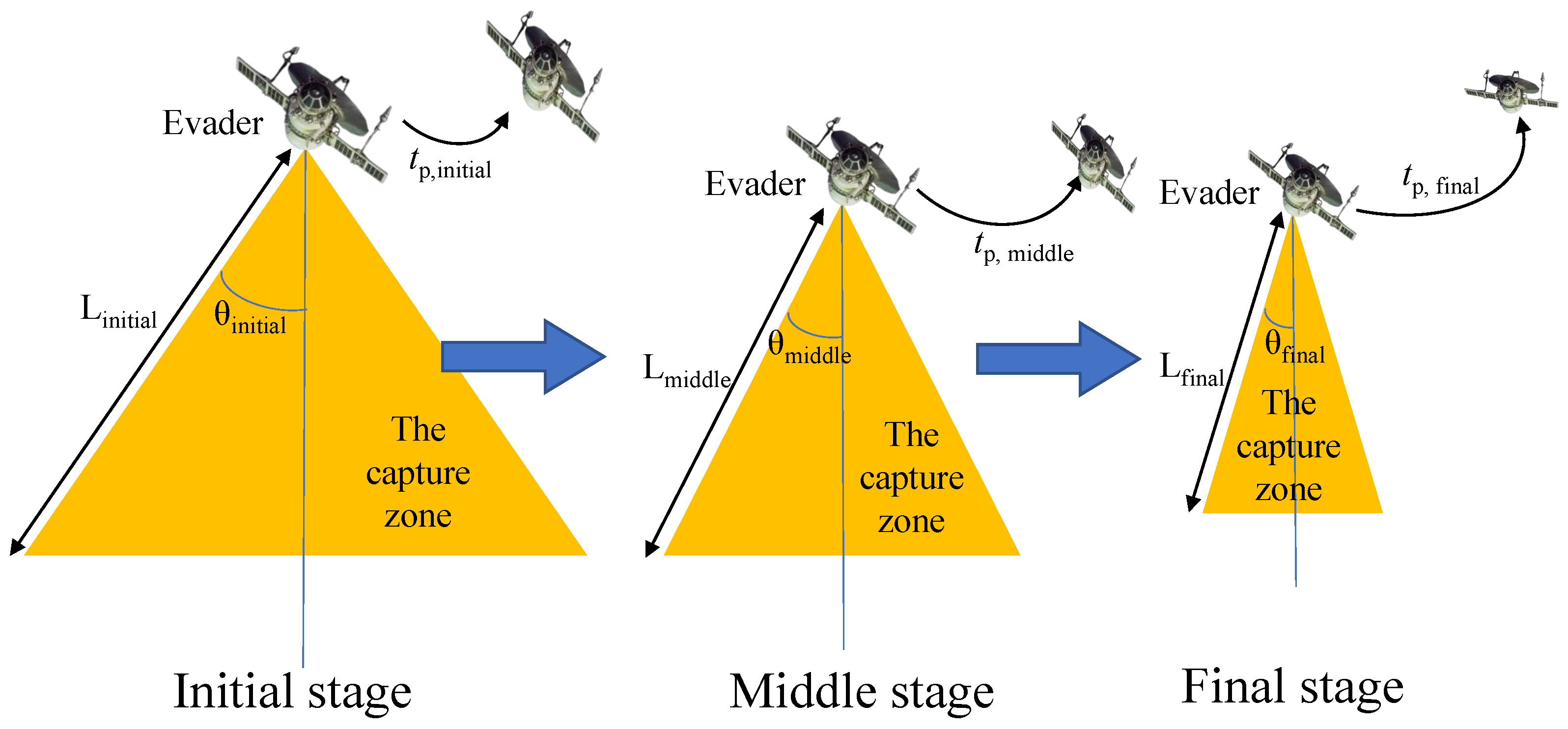
3.2. Curriculum Learning for Enhanced Training

To accelerate learning and improve policy robustness, a curriculum learning (CL) strategy is implemented. This approach is dynamics-agnostic and structures the training process by initially presenting the agents with a simplified task. The task difficulty is then gradually increased over the course of the training [33].

The core principle of this CL strategy is to treat the terminal capture conditions not as fixed constraints during training but as adjustable parameters of the learning problem itself. This addresses the challenge of sparse rewards in complex tasks. By starting with a large, easy-to-achieve capture zone (i.e., lenient terminal conditions), agents can more frequently receive positive rewards and learn a basic, viable policy. As training progresses, the capture zone is progressively tightened. This process forces the agents to refine their strategies from coarse maneuvering to precise targeting. It is important to note that this is a training methodology; the final, trained policy is evaluated against the original, fixed mission constraints.

In this work, the curriculum is implemented by dynamically adjusting three key parameters as a function of the training episode number. The concept of progressively tightening goal-related parameters is a common technique in CL for control tasks [34]. The generatrix length L and the half-opening angle $\theta$ of the capture cone are gradually reduced, as illustrated in Figure 5.

The generatrix length L is updated as

$$L\left(episode\right)=L_{\mathrm{initial}}-{\displaystyle \frac{L_{\mathrm{initial}}-L_{\mathrm{final}}}{N}}·episode$$

(8)

where $L_{\mathrm{initial}}$ is the initial generatrix length, $L_{\mathrm{final}}$ is the final generatrix length, N is the total number of training episodes, and $episode$ is the current training episode number.

Similarly, the capture cone half-opening angle $\theta$ is updated as

$$\theta \left(episode\right)={\theta }_{\mathrm{initial}}-{\displaystyle \frac{{\theta }_{\mathrm{initial}}-{\theta }_{\mathrm{final}}}{N}}·episode$$

(9)

where ${\theta }_{\mathrm{initial}}$ is the initial half-opening angle and ${\theta }_{\mathrm{final}}$ is the desired final half-opening angle.

Furthermore, the curriculum extends to the prediction horizon, $t_p$, used within the terminal prediction reward. This parameter defines the duration over which the future state is predicted to assess capturability with respect to the current $L\left(episode\right)$ and $\theta \left(episode\right)$. The prediction horizon $t_p$ is also dynamically adjusted as

$$t_p\left(episode\right)=t_{p,\mathrm{initial}}+{\displaystyle \frac{t_{p,\mathrm{final}}-t_{p,\mathrm{initial}}}{N}}·episode$$

(10)

where $t_{p,\mathrm{initial}}$ is the initial short prediction horizon and $t_{p,\mathrm{final}}$ is the final longer prediction horizon. This progressive extension of $t_p$ encourages the development of more far-sighted strategies.

3.3. PPO Algorithm Design

PPO is an actor–critic algorithm that optimizes the policy and value functions concurrently. It employs two neural networks: a policy network (the actor, ${\pi }_{\omega }$) that maps states to action probabilities and a value network (the critic) that estimates the state-value function. The state-value function, denoted as $V_{\omega }\left(s_t\right)$, is trained to approximate the expected return (cumulative discounted reward) from a given state $s_t$. Mathematically, the value function under a policy $\pi$ is defined as in [35]:

$$V_{\pi }\left(s\right)={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s\right]$$

(11)

where $\gamma$ is the discount factor and R is the reward at each time step. In our implementation, the value network with parameters $\omega$ approximates this function, i.e., $V_{\omega }\left(s_t\right)\approx V_{{\pi }_{\omega }}\left(s_t\right)$. This value serves as a crucial baseline to reduce the variance of policy gradient estimations.

The PPO algorithm optimizes a clipped surrogate objective. The overall loss function, which is a composite of policy loss, value loss, and an entropy bonus, is defined as [32]:

$$L_t^{\mathrm{Total}}\left(\omega \right)={\mathbb{E}}_t\left[L_t^{\mathrm{CLIP}}\left(\omega \right)-c_1{L}_t^{\mathrm{VF}}\left(\omega \right)+c_{2}S\left[{\pi }_{\omega }\right]\left(s_t\right)\right]$$

(12)

where ${\mathbb{E}}_t$ indicates the expectation over a batch of samples, $c_1$ and $c_2$ are weighting coefficients, and S denotes an entropy bonus to encourage exploration.

The core of PPO is the clipped surrogate objective for the policy, $L_t^{\mathrm{CLIP}}\left(\omega \right)$, which is given by

$$L_t^{\mathrm{CLIP}}\left(\omega \right)={\mathbb{E}}_t\left[min(r_t\left(\omega \right){\widehat{A}}_t,\mathrm{clip}(r_t\left(\omega \right),1-ϵ,1+ϵ){\widehat{A}}_t)\right]$$

(13)

where $r_t\left(\omega \right)={\displaystyle \frac{{\pi }_{\omega }\left(a_t\right|s_t)}{{\pi }_{{\omega }_{\mathrm{old}}}\left(a_t\right|s_t)}}$ is the probability ratio between the new and old policies and $ϵ$ is a hyperparameter for the clipping range.

The advantage function, ${\widehat{A}}_t$, quantifies how much better an action is than the average action at a state. It is computed using Generalized Advantage Estimation (GAE) [36]:

$${\widehat{A}}_t=\sum _{l=0}^{T-1}{\left(\gamma \lambda \right)}^l{\delta }_{t+l},\mathrm{where}{\delta }_t=r_t+\gamma V_{\omega }\left(s_{t+1}\right)-V_{\omega }\left(s_t\right)$$

(14)

Here, $\gamma$ is the discount factor, $\lambda$ is the GAE parameter, and ${\delta }_t$ is the Temporal-Difference (TD) error.

The value function loss, $L_t^{\mathrm{VF}}\left(\omega \right)$, is typically a squared-error loss:

$$L_t^{\mathrm{VF}}\left(\omega \right)={\mathbb{E}}_t\left[{\left(R_t-V_{\omega }\left(s_t\right)\right)}^2\right]$$

(15)

where $R_t$ is the actual return calculated from the trajectory. The network parameters $\omega$ are updated using gradient-based optimization on $L_t^{\mathrm{Total}}$.

The specific steps of the PPO-based self-play training with curriculum learning are depicted in Algorithm 1.

Algorithm 1 PPO-based Self-Play Training with Curriculum Learning

1: Input: Initial policy parameters ${\omega }_p,{\omega }_e$; value function parameters; curriculum learning parameters 2: Output: Trained policy networks ${\pi }_{{\omega }_p}$ and ${\pi }_{{\omega }_e}$ 3: Initialize policy networks ${\pi }_{{\omega }_p}$, ${\pi }_{{\omega }_e}$ and value networks $V_{{\omega }_p}$, $V_{{\omega }_e}$ 4: for episode = 1, 2, … do 5:      Update curriculum parameters ($L\left(ep\right)$, $\theta \left(ep\right)$, $t_p\left(ep\right)$) 6:      Initialize a data buffer $\mathcal{D}$ for each agent (pursuers and evader) 7:      Collect a set of trajectories for all agents by running policies in the environment. Store transitions $(s_t,a_t,r_t,s_{t+1})$ in $\mathcal{D}$. 8:      {— Compute advantages and returns —} 9:      for each agent $j\in \left\{\mathrm{pursuers},\mathrm{evader}\right\}$ do 10:         Compute advantage estimates ${\widehat{A}}_t$ for all time steps in ${\mathcal{D}}_j$ using GAE. 11:         Compute returns $R_t$ for all time steps in ${\mathcal{D}}_j$. 12:     end for 13:     {— Update networks —} 14:     for K optimization epochs do 15:          for each agent $j\in \left\{\mathrm{pursuers},\mathrm{evader}\right\}$ do 16:               Compute the total loss $L^{\mathrm{Total}}$ using the current batch of data from ${\mathcal{D}}_j$. 17:               Update the parameters of ${\pi }_{{\omega }_j}$ and $V_{{\omega }_j}$ by performing a gradient descent step on $L^{\mathrm{Total}}$. 18:           end for 19:     end for 20: end for

3.4. Reward Function Design

The design of the reward function is paramount for guiding agents toward complex mission objectives, especially those with sparse terminal conditions. A key innovation of this framework is a prediction-based reward component, $R_{\mathrm{prediction}}$, engineered to provide dense, forward-looking guidance. This component is crucial for enabling agents to learn effective strategies for satisfying state-dependent terminal constraints and is designed to be generalizable across different system dynamics.

The total reward for the pursuers, $R_p$, is constructed as a weighted sum of three components: a prediction reward ($R_{\mathrm{prediction}}$), a terminal reward ($R_{\mathrm{terminal}}$), and an efficiency penalty ($R_{\mathrm{efficiency}}$). The overall structure is

$$R_p={\lambda }_{\mathrm{pred}}{R}_{\mathrm{prediction}}+{\lambda }_{\mathrm{term}}{R}_{\mathrm{terminal}}+{\lambda }_{\mathrm{eff}}{R}_{\mathrm{efficiency}}$$

(16)

where ${\lambda }_{\mathrm{pred}}$, ${\lambda }_{\mathrm{term}}$, and ${\lambda }_{\mathrm{eff}}$ are positive weighting hyperparameters that balance the influence of predictive guidance, terminal objective satisfaction, and control effort minimization. Their specific values are determined through empirical tuning and are reported in the simulation section.

Reflecting the adversarial nature of the game, the evader’s reward function, $R_e$, is designed with opposing signs:

$$R_e=-{\mu }_{\mathrm{pred}}{R}_{\mathrm{prediction}}-{\mu }_{\mathrm{term}}{R}_{\mathrm{terminal}}-{\mu }_{\mathrm{eff}}{R}_{\mathrm{efficiency}}$$

(17)

where ${\mu }_i$ are also positive weighting hyperparameters.

To provide a more intelligent, forward-looking signal than simple distance-based rewards, the prediction reward, $R_{\mathrm{prediction}}$, evaluates the capturability of the current state. It achieves this by projecting the system’s state forward in time over a short, curriculum-defined horizon, $t_p\left(episode\right)$, assuming zero control input during this interval. This projection uses the state transition matrix (STM), $\mathrm{\Phi }(∆t)$, which represents the analytical solution to the linearized CW equations (Equation (1)) over a time interval $∆t$. The STM is a 6 × 6 matrix that maps an initial relative state to a future state, and its form is well established in astrodynamics [27]. It can be expressed in a partitioned form as

$$\mathrm{\Phi }(∆t)=\left[\begin{array}{cc}{\mathrm{\Phi }}_{rr}(∆t)& {\mathrm{\Phi }}_{rv}(∆t)\\ {\mathrm{\Phi }}_{vr}(∆t)& {\mathrm{\Phi }}_{vv}(∆t)\end{array}\right]$$

(18)

where the 3 × 3 sub-matrices relate position to position (${\mathrm{\Phi }}_{rr}$), velocity to position (${\mathrm{\Phi }}_{rv}$), and so on. For brevity, the full analytical expressions for these sub-matrices are provided in Appendix A.

The prediction process begins with the current six-dimensional relative state vector, ${\mathbf{x}}_{tp}\left(t\right)$, which comprises the relative position and velocity. It is defined as

$${\mathbf{x}}_{tp}\left(t\right)={[{\mathbf{r}}_{tp}{\left(t\right)}^{\top },{\mathbf{v}}_{tp}{\left(t\right)}^{\top }]}^{\top }$$

(19)

where ${\mathbf{r}}_{tp}\left(t\right)$ and ${\mathbf{v}}_{tp}\left(t\right)$ are the relative position and velocity, respectively.

Using the state transition matrix, the predicted state, ${\mathbf{x}}_{tp,\mathrm{pred}}$, is then calculated as

$${\mathbf{x}}_{tp,\mathrm{pred}}=\mathrm{\Phi }\left(t_p\left(episode\right)\right)·{\mathbf{x}}_{tp}\left(t\right)$$

(20)

The predicted state vector, ${\mathbf{x}}_{tp,\mathrm{pred}}$, contains the predicted relative position, ${\mathbf{r}}_{tp,pred}$, and velocity, ${\mathbf{v}}_{tp,pred}$:

$${\mathbf{x}}_{tp,\mathrm{pred}}={[{\mathbf{r}}_{tp,\mathrm{pred}}^{\top },{\mathbf{v}}_{tp,\mathrm{pred}}^{\top }]}^{\top }$$

(21)

The reward function is then calculated based on the predicted position component, ${\mathbf{r}}_{tp,pred}$. The reward function is given by

$$\begin{array}{cc}\hfill R_{\mathrm{prediction}}=& w_d·exp\left(-{\displaystyle \frac{k_L·max(0,\parallel {\mathbf{r}}_{tp,pred}{\parallel -L\left(ep\right))}^2}{L{\left(ep\right)}^2}}\right)\hfill \\ \hfill & +w_a·exp\left(-{\displaystyle \frac{k_{\theta }·max{(0,\angle ({\mathbf{r}}_{tp,pred},\mathbf{u})-\theta \left(ep\right))}^2}{\theta {\left(ep\right)}^2}}\right)\hfill \end{array}$$

(22)

where $w_d$ and $w_a$ are weights for the distance and angle components and $k_L,k_{\theta }>0$ are shaping factors. The notations $L\left(ep\right)$ and $\theta \left(ep\right)$ are shorthand for $L\left(episode\right)$ and $\theta \left(episode\right)$, respectively, representing the curriculum-dependent parameters at the current episode.

The overall concept is illustrated in Figure 6. This structure incentivizes actions that lead to favorable future states, not just those that myopically reduce the current error.

The terminal reward, $R_{\mathrm{terminal}}$, provides a large, discrete reward or penalty based on the final state at the end of an episode, directly enforcing the mission objective. It is formulated as

$$R_{\mathrm{terminal}}=\left\{\begin{array}{c}+\varphi ,\mathrm{if}∥{\mathbf{r}}_{tp}∥\le L\left(ep\right)\mathrm{and}\angle ({\mathbf{r}}_{tp},\mathbf{u})\le \theta \left(ep\right)\hfill \\ -\psi ·\left(w_d^{\prime }{\displaystyle \frac{max(0,∥{\mathbf{r}}_{tp}∥-L\left(ep\right))}{L\left(ep\right)}}\right.\hfill \\ \left.+w_a^{\prime }{\displaystyle \frac{max(0,\angle ({\mathbf{r}}_{tp},\mathbf{u})-\theta \left(ep\right))}{\theta \left(ep\right)}}\right),\mathrm{otherwise}\hfill \end{array}\right.$$

(23)

where $\varphi$ is a substantial positive reward for success and $\psi$ is a penalty coefficient. $w_d^{\prime }\ge 0$ and $w_a^{\prime }\ge 0$ are weights for the distance and angle error terms.

The efficiency penalty, $R_{\mathrm{efficiency}}$, discourages excessive control effort. It is defined as a quadratic penalty on the velocity increment, $∆\mathbf{v}$, applied at the current decision step:

$$R_{\mathrm{efficiency}}=-\beta {\parallel ∆\mathbf{v}\parallel }^2$$

(24)

where $\beta$ is a positive weighting factor.

4. Simulation and Results

In this section, the proposed framework is validated through a two-stage simulation process. First, a detailed analysis is conducted in a multi-spacecraft orbital game to rigorously test the core algorithm. Then, the same method is applied to a multi-drone aerial scenario to demonstrate its generalizability and confirm that its performance advantages are transferable across domains.

4.1. Simulation Setup

To evaluate the performance of the proposed method, multi-agent pursuit-evasion game simulations were conducted within the challenging context of local orbital maneuvering near GEO. These simulations benchmarked our proposed PPO algorithm (with curriculum learning and prediction reward) against a traditional PPO algorithm (without these features) and the Soft Actor–Critic (SAC) algorithm, a state-of-the-art off-policy method included for a comprehensive comparison. To ensure a fair comparison, all algorithms shared identical hyperparameter settings where applicable.

The orbital motion was simulated by numerically integrating the high-fidelity nonlinear equations of relative motion derived from the two-body problem. The C-W equations, as detailed in Section 2.1, were used as a linearized approximation only within the agent’s internal model for the prediction-based reward calculation. The reference frame is centered on a point in a GEO at (45° E, 0° N). For each evaluation episode, the initial positions were set as follows to ensure varied engagement geometries: the evader started from a fixed nominal position, while the two pursuers were randomly and independently sampled from a spherical shell region defined relative to the evader. The key mission parameters are listed in

Table 2. Simulation parameters for the multi-spacecraft mission.

Parameter	Value
Reference Orbit	Geostationary (GEO) at 45° E, 0° N
Scenario	2 Pursuers vs. 1 Evader
Evader Initial Position	(80, 70, 150) km
Pursuer Initial Position Sampling	Randomly sampled from a spherical shell
- Min Relative Distance from Evader	80 km
- Max Relative Distance from Evader	120 km
Terminal Time ($t_f$)	60,000 s
Final Capture Cone Length ($L_{\mathrm{final}}$)	50 km
Final Capture Cone Angle (${\theta }_{\mathrm{final}}$)	30°

, and the DRL hyperparameters are detailed in

Table 3. DRL hyperparameter settings.

Hyperparameter	Value
RL Algorithm Parameters
Optimizer	Adam
Learning rate ($\alpha$)	$1\times {10}^{-4}$
Discount factor ($\gamma$)	0.99
GAE parameter ($\lambda$)	0.95
PPO clipping ($ϵ$)	0.2
Training epochs per update (K)	10
Minibatch size	128
Network Architecture
Hidden layers	[256, 256, 128]
Activation function	ReLU
Output activation	Tanh
Reward Function Weights
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{\lambda }_{\mathrm{pred}},{\mu }_{\mathrm{pred}}$	1.0
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{\lambda }_{\mathrm{term}},{\mu }_{\mathrm{term}}$	1.0
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{\lambda }_{\mathrm{eff}},{\mu }_{\mathrm{eff}}$	1.0
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{w}_d,w_a$ (Prediction)	0.5, 0.5
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{k}_L,k_{\theta }$ (Prediction)	5.0, 5.0
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\varphi$ (Success Reward)	200.0
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\psi$ (Failure Penalty Coefficient)	100.0
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{w}_d^{\prime },w_a^{\prime }$ (Terminal Penalty)	0.5, 0.5
$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\beta$ (Efficiency)	0.01

.

It is important to discuss the selection of the terminal capture cone parameters. The final values of $L=50$ km and $\theta ={30}^{\circ }$ are chosen to represent a long-range engagement scenario in GEO. In this context, the objective is not a precise docking but the establishment of a safe inspection or co-location corridor, which is consistent with the operational scale in this orbital regime.

The curriculum learning strategy dynamically adjusted several key parameters based on the training episode number, facilitating a gradual increase in task difficulty. The specific initial and final values for these parameters, which were linearly interpolated over a total of 60,000 training episodes, are summarized in

Table 4. Curriculum learning parameter schedule over 60,000 episodes.

Parameter	Symbol	Initial Value	Final Value
Capture Cone Generatrix Length	$L\left(ep\right)$	100 km ($L_{\mathrm{initial}}$)	50 km ($L_{\mathrm{final}}$)
Capture Cone Half-Opening Angle	$\theta \left(ep\right)$	60 degrees (${\theta }_{\mathrm{initial}}$)	30 degrees (${\theta }_{\mathrm{final}}$)
Prediction Horizon	$t_p\left(ep\right)$	5 s ($t_{p,\mathrm{initial}}$)	10 s ($t_{p,\mathrm{final}}$)

.

The simulation training was conducted on a 64-bit Windows 10 operating system with 32 GB of RAM, an Intel^® Core™ i7-11800H CPU (Intel Corporation, Santa Clara, CA, USA), and an NVIDIA T600 Laptop GPU (NVIDIA Corporation, Santa Clara, CA, USA).

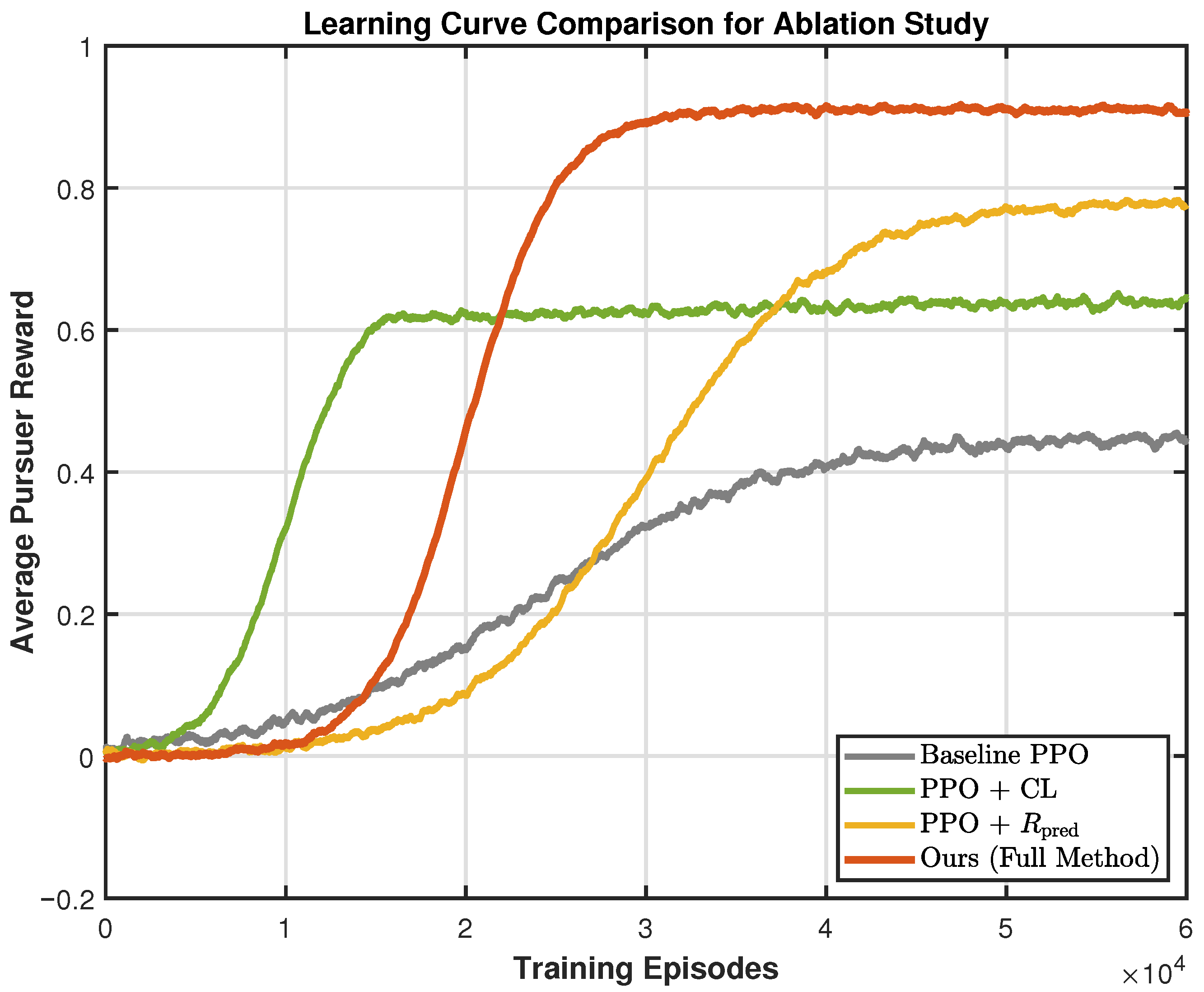
4.2. Training Process and Ablation Study

To rigorously evaluate the effectiveness of the two key innovations proposed in this framework—curriculum learning (CL) and the prediction-based reward ($R_{\mathrm{prediction}}$)—a comprehensive ablation study was conducted. The performance of our full proposed method was benchmarked against several ablated versions and a standard PPO baseline. Four distinct configurations for the pursuer agents were trained, while the evader agent consistently employed the full method to serve as a challenging and consistent opponent:

• Baseline PPO: A standard PPO implementation where the reward is based only on the current state error, without the benefits of CL or $R_{\mathrm{prediction}}$.
• PPO + CL: The baseline PPO augmented solely with the curriculum learning strategy.
• PPO + $R_{\mathrm{prediction}}$: The baseline PPO augmented solely with the prediction-based reward function.
• Ours (Full Method): The complete proposed framework that integrates both CL and $R_{\mathrm{prediction}}$.

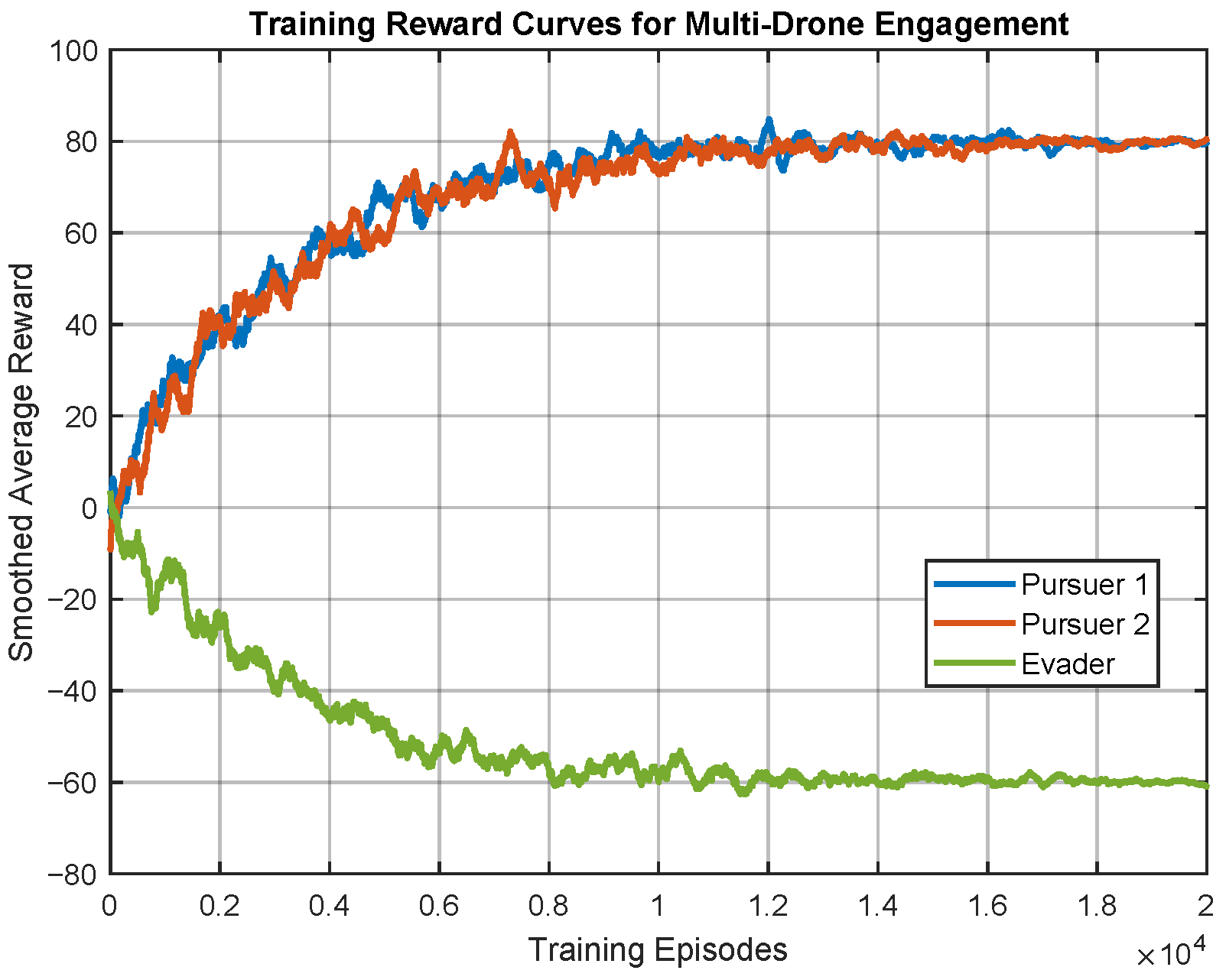
The learning dynamics of these configurations are visualized in Figure 7. This plot shows the average cumulative episodic reward for the pursuer agents, smoothed over a window of training episodes. To facilitate a clearer comparison of the learning trends on a consistent scale, the reward values for the spacecraft scenario shown in this figure have been scaled by a factor of 0.01 (i.e., divided by 100). This scaling brings the y-axis values into a range that highlights the relative differences in convergence, while the drone scenario plots (e.g., Figure 13) display the original, unscaled reward values.

The results depicted in Figure 7 clearly illustrate the contribution of each component. The Baseline PPO agent struggles significantly with the task’s complexity and the sparse nature of the terminal reward, resulting in a slow and unstable learning progress. The introduction of curriculum learning (PPO + CL) provides a notable improvement, especially in the initial training phase. By starting with an easier task, the agent quickly learns a foundational policy, leading to a much faster initial rise in rewards. Separately, augmenting the baseline with only the prediction reward (PPO + $R_{\mathrm{prediction}}$) enables the agent to eventually achieve a substantially higher reward plateau. This confirms that the dense, forward-looking signal from $R_{\mathrm{prediction}}$ provides superior guidance for finding a more optimal policy.

Crucially, the combination of both components in our full method (Ours) yields the best performance. It benefits from the rapid initial learning kickstarted by CL and the high-quality, long-term guidance of $R_{\mathrm{prediction}}$, resulting in both the fastest convergence and the highest final reward. This demonstrates a clear synergistic effect, where the two innovations complement each other to overcome the challenges of the complex pursuit-evasion task.

To provide a quantitative validation of these findings, the final pursuit success rate of each configuration was evaluated over 1000 independent test scenarios after training was complete. The results are summarized in

Table 5. Ablation study results on final pursuit success rate.

Configuration (Pursuer Agents)	Success Rate (%)
Baseline PPO	45.3%
PPO + CL	65.7%
PPO + $R_{\mathrm{prediction}}$	78.1%
Ours (Full Method)	90.7%

.

The quantitative results in Table 5 strongly corroborate the insights from the learning curves. Both CL and $R_{\mathrm{prediction}}$ individually provide significant improvements over the baseline, increasing the success rate by 20.4 and 32.8 percentage points, respectively. Their combination, however, achieves the highest performance with a 90.7% success rate, a remarkable 45.4 percentage point improvement over the baseline. This analysis validates that both proposed components are critical and effective contributors to the overall performance of our framework.

4.3. Performance Evaluation and Comparison

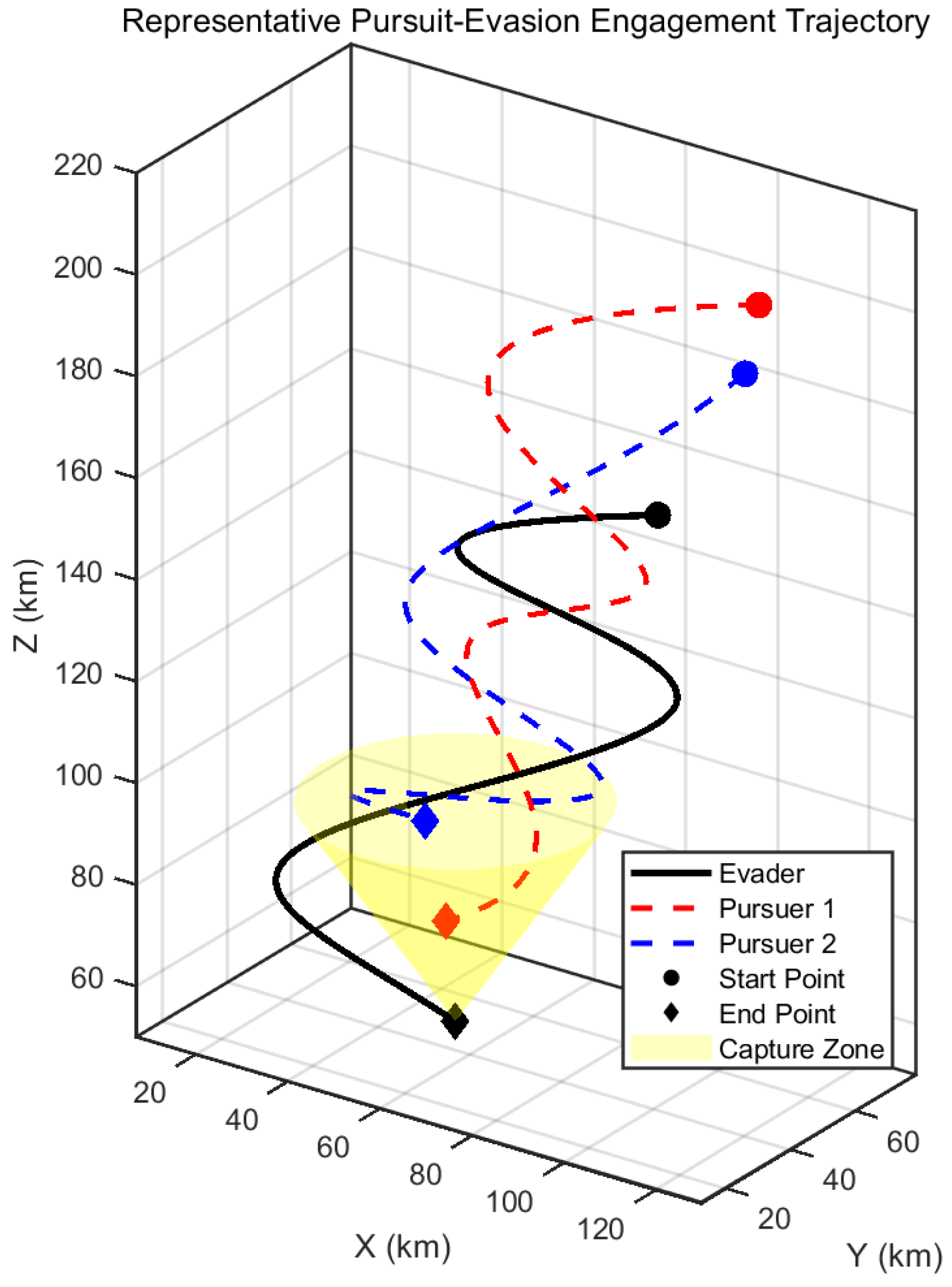
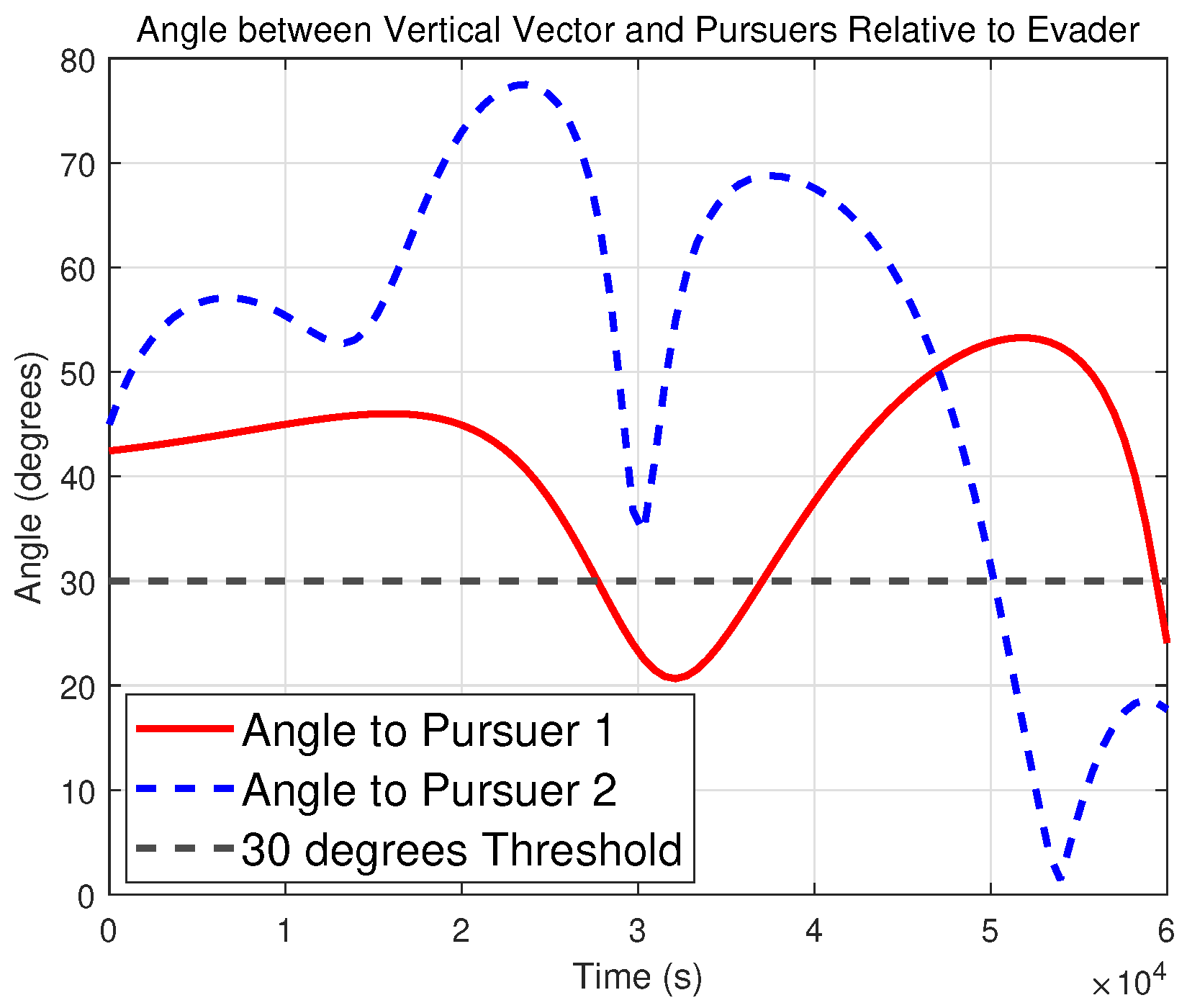
Following the training process, a comprehensive evaluation consisting of 1000 scenarios was conducted. One representative engagement is illustrated in Figure 8, demonstrating the successful approach of the pursuers into the evader’s capture zone. The relative distance and relative angle between the pursuers and the evader over time for this engagement are shown in Figure 9 and Figure 10, respectively, confirming that the terminal conditions were met.

To demonstrate the enhanced game-playing capabilities of the trained agents, 1000 scenarios were simulated with agents employing different algorithms. The SAC algorithm was included in our comparative analysis. The pursuit success rates of the pursuers are summarized in

Table 6. Pursuit success rates with different maneuvering strategies.

	Pursuer Strategy
Evader Strategy	Proposed Algorithm	Traditional PP	SAC
Proposed Algorithm	85.6%	78.4%	2.1%
Traditional PPO	90.7%	81.3%	11.9%
SAC	93.5%	87.6%	18.8%

.

The superiority of the proposed algorithm is clearly demonstrated by the results in Table 6. When the pursuers use the proposed algorithm, they achieve higher success rates against all evader strategies compared to traditional PPO or SAC. Conversely, when the evader uses the proposed algorithm, it is significantly more effective at evading (i.e., the pursuers’ success rate is lowest). For instance, a pursuer using the proposed algorithm has an 85.6% success rate against an equally intelligent evader, but this rate drops to 78.4% if the pursuer uses traditional PPO. These findings confirm that the proposed method enhances the strategic capabilities of both pursuers and evaders and is a more effective approach for this multi-agent game than both traditional PPO and SAC.

In addition to the success rate, a more comprehensive performance assessment was conducted by evaluating key efficiency metrics: the average time to capture and the average control effort ($∆$V). These metrics were averaged over all successful pursuit scenarios for each algorithm match-up where the pursuer used a given strategy against the strongest evader. For clarity, the strongest evader refers to an agent trained with our full proposed algorithm, but possessing the exact same physical constraints (e.g., maximum $∆$V) as all other agents to ensure a fair comparison. The results are presented in

Table 7. Efficiency metrics against the strongest evader.

Pursuer Algorithm	Avg. Capture Time (s)	Avg. Control Effort ($∆$V, m/s)
Traditional PPO	54,100	132.5
SAC	51,800	115.3
Proposed Algorithm	49,200	98.7

.

The data in Table 7 reveals further advantages of our method. Not only is it more successful, but it is also more efficient. Our algorithm achieves capture approximately 9.1% faster than traditional PPO and 5.0% faster than SAC. More importantly, it is significantly more fuel-efficient, requiring 25.5% less $∆$V than traditional PPO and 14.4% less than SAC. This superior efficiency can be attributed to the proactive, non-myopic policies learned via the prediction reward, which enable agents to plan smoother, more direct trajectories and avoid costly last-minute corrections. This comprehensive analysis confirms that our proposed framework yields policies that are not only more effective but also more efficient and practical for real-world applications.

To further illustrate the strategic differences between the learned policies, a qualitative comparison of their typical behaviors was performed. Figure 11 shows a representative trajectory generated by the SAC-trained pursuers under the same initial conditions as the case shown in Figure 8.

By visually comparing the trajectory from our proposed method (Figure 8) with that from SAC (Figure 11), a clear difference in strategy can be observed. The policy learned by our framework generates smoother, more proactive, and seemingly more coordinated trajectories. The pursuers appear to anticipate the evader’s future position and move towards a future intercept point. In contrast, the SAC-trained agents, while still effective, tend to exhibit more reactive or hesitant maneuvers, often involving more pronounced course corrections. This qualitative evidence corroborates the quantitative findings in Table 7, suggesting that our framework’s superior efficiency stems from its ability to learn more strategically sound and less myopic policies.

4.4. Robustness Test Under Perturbations

To evaluate the robustness of the learned policies against unmodeled dynamics and external disturbances, a further set of experiments was conducted. In these tests, a stochastic perturbation force was applied to all agents at each decision step. This perturbation was modeled as a random acceleration vector, where each component was independently sampled from a zero-mean Gaussian distribution, $\mathcal{N}(0,{\sigma }_a^2)$. The standard deviation of the perturbation, ${\sigma }_a$, was set to a small fraction of the maximum control capability. This was done to simulate a range of realistic, unmodeled effects, such as minor thruster misalignments, sensor noise leading to control execution errors, or other unpredictable external forces.

The performance of our proposed algorithm, along with the baselines, was evaluated over 1000 test scenarios in both the nominal (no perturbation) and the perturbed environments. The resulting pursuit success rates are compared in

Table 8. Pursuit success rate comparison in nominal and perturbed environments.

Algorithm	Success Rate (Nominal, %)	Success Rate (Perturbed, %)	Performance Drop (%)
Traditional PPO	81.3%	62.5%	−23.1%
SAC	85.5%	70.1%	−18.0%
Proposed Algorithm	90.7%	83.2%	−8.3%

.

The results presented in Table 8 highlight the superior robustness of our proposed framework. While all algorithms experience a performance degradation in the presence of perturbations, the policy learned by our method is significantly more resilient. The success rate of our algorithm drops by only 8.3%, whereas traditional PPO and SAC suffer much larger drops of 23.1% and 18.0%, respectively.

This enhanced robustness can be attributed to two factors. First, the prediction-based reward function implicitly encourages the agent to seek states that are not just currently good, but also inherently stable and less sensitive to small deviations. Second, the curriculum learning strategy, by exposing the agent to a wide range of scenarios (from easy to hard), may lead to a more generalized policy that is less overfitted to the ideal dynamics. These findings suggest that our framework is not only effective in nominal conditions but also possesses a high degree of robustness, making it more suitable for real-world deployment.

4.5. Scalability to Larger Team Sizes

To evaluate the scalability of the proposed framework, the experiments were extended to include a larger team size. Specifically, the DRL framework was applied to a 3-vs.-1 engagement scenario. The core algorithm, including the curriculum learning strategy and the prediction-based reward, remained unchanged. The only adaptation required was a modification of the neural network’s input layer to accommodate the state information of the additional pursuer. The model was subsequently retrained from scratch for this new scenario.

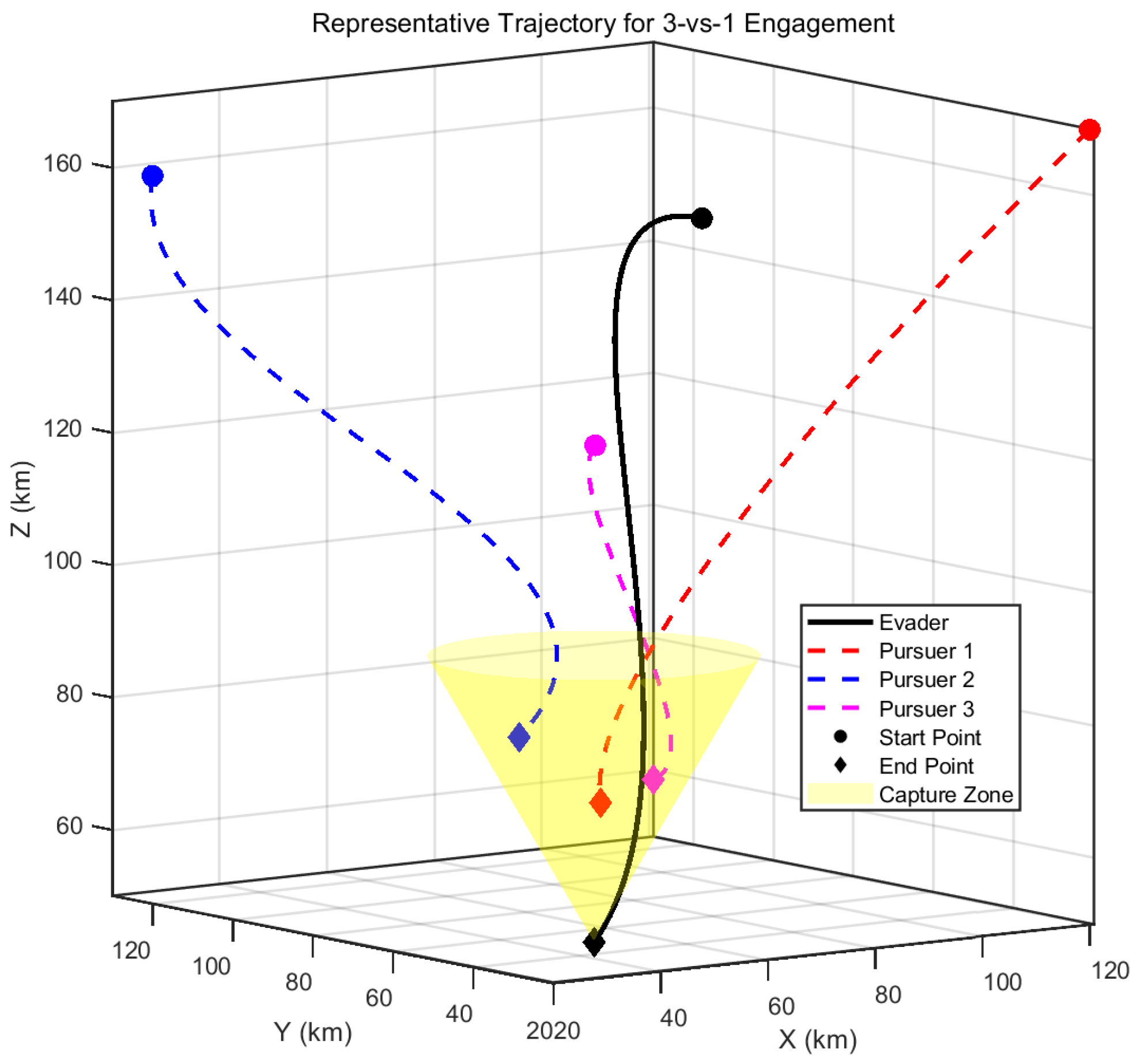
The performance of the fully trained policy was evaluated over 500 test scenarios. The key performance metrics are summarized and compared with the original 2-vs.-1 baseline in

Table 9. Performance comparison for 2-vs.-1 and 3-vs.-1 scenarios.

Scenario	Pursuit Success Rate (%)	Avg. Capture Time (s)
2 vs. 1 (Baseline)	90.7%	49,200
3 vs. 1	95.2%	45,100

. A representative successful trajectory is visualized in Figure 12, demonstrating effective multi-agent coordination.

The results demonstrate the excellent scalability of our framework. In the 3-vs.-1 scenario, the pursuers effectively leverage their numerical advantage to achieve a higher success rate (95.2%) and a faster capture time compared to the 2-vs.-1 baseline. The successful application of our framework to this more complex scenario with minimal modifications strongly supports its potential as a scalable solution for multi-agent autonomous systems.

4.6. Generalizability to Multi-Drone Airspace Pursuit-Evasion

While this study primarily validates the proposed DRL framework within a multi-spacecraft orbital game, its core methodology is designed to be generalizable. The framework’s modularity allows for its direct application to multi-drone pursuit-evasion scenarios in airspace by primarily substituting the underlying dynamics model. This section outlines how the key architectural components, such as the self-play PPO structure, curriculum learning, and the predictive reward function, are translated to a drone-based application.

4.6.1. Dynamics Model and State-Action Spaces

The primary adaptation for the multi-drone scenario involves substituting the orbital dynamics with an appropriate model for UAV flight. A full 6-DOF (six-degree-of-freedom) dynamic model for a quadrotor is complex, involving aerodynamic effects and rotor dynamics [37]. While such high-fidelity models are essential for low-level controller design, they introduce significant complexity that can be prohibitive for learning high-level, multi-agent strategic policies.

Therefore, for the purpose of this study, which focuses on the strategic decision-making aspect of the pursuit-evasion game, a simplified point-mass kinematic model is employed. This is a common and effective abstraction in multi-UAV planning and game theory research [38]. In this model, the state of a drone i is represented by its position ${\mathbf{p}}_i={[p_x,p_y,p_z]}^{\top }$ and velocity ${\mathbf{v}}_i={[v_x,v_y,v_z]}^{\top }$. The agent’s action ${\mathbf{a}}_i={[a_x,a_y,a_z]}^{\top }$ corresponds to a desired acceleration command, which is assumed to be tracked perfectly by a low-level controller. The state propagation over a time step $∆t$ is then given by

$$\begin{array}{cc}\hfill {\mathbf{p}}_i(k+1)& ={\mathbf{p}}_i\left(k\right)+{\mathbf{v}}_i\left(k\right)∆t+{\displaystyle \frac{1}{2}}{\mathbf{a}}_i\left(k\right)∆t^2\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\mathbf{v}}_i(k+1)& ={\mathbf{v}}_i\left(k\right)+{\mathbf{a}}_i\left(k\right)∆t\hfill \end{array}$$

(26)

This abstraction allows the DRL framework to focus on learning the high-level strategic interactions, which is the primary contribution of this work, rather than the intricacies of flight control. The agent’s state observation consists of the relative positions and velocities between agents, which is analogous to the spacecraft scenario.

4.6.2. Constraint and Objective Adaptation

The game’s objectives and constraints translate directly. The pursuer’s goal is to maneuver into a capture cone—a virtual conical region centered on the evader. This cone is defined by a length L and a half-opening angle $\theta$, and its central axis is typically oriented relative to the evader’s state (e.g., opposing its velocity vector), representing a common engagement criterion in aerial adversarial scenarios [23]. Collision avoidance constraints between drones (Equation (7)) and actuator saturation limits (e.g., maximum acceleration) are also directly applicable.

4.6.3. Prediction Reward Function Transferability

The key innovation of the prediction reward function ($R_{\mathrm{prediction}}$) is highly transferable. The prediction of the future relative state, originally performed using the CW state transition matrix, instead uses a simple linear kinematic projection based on the current relative velocity ${\mathbf{v}}_{tp}$ [39]:

$${\mathbf{r}}_{tp,pred}={\mathbf{r}}_{tp}\left(t\right)+{\mathbf{v}}_{tp}\left(t\right)·t_p$$

(27)

The reward is then calculated using the same shaped exponential function based on this predicted state ${\mathbf{r}}_{tp,pred}$ and the current capture cone parameters ($L\left(ep\right)$, $\theta \left(ep\right)$). This demonstrates that the predictive guidance principle is independent of the specific system dynamics.

4.6.4. Curriculum Learning Application

The curriculum learning strategy is entirely dynamics-agnostic. The process of starting with a large, easy-to-achieve capture zone (large $L_{\mathrm{initial}}$, ${\theta }_{\mathrm{initial}}$) and gradually tightening these parameters to their final, more challenging values (Equations (8) and (9)). This is a general principle for accelerating training in goal-oriented tasks. It would be applied identically in a multi-drone simulation to guide the agents from simple to complex maneuvering strategies.

4.6.5. Illustrative Simulation for Multi-Drone Engagement

To empirically validate the framework’s generalizability, a concise simulation of a 2-vs.-1 multi-drone pursuit-evasion scenario was conducted with randomized initial conditions to ensure diverse engagement geometries. The simulation uses the point-mass kinematic model described above, with parameters scaled appropriately for an aerial engagement, as detailed in

Table 10. Simulation parameters for multi-drone pursuit-evasion task.

Parameter	Value
Scenario	2 Pursuers, 1 Evader
Nominal Initial Pursuer Positions	(0, 0, 10) m; (10, 0, 10) m
Nominal Initial Evader Position	(100, 50, 10) m
Initial Position Randomization Radius	5 m
Maximum Acceleration	5 ${\mathrm{m}/\mathrm{s}}^2$
Safety Distance ($d_{\mathrm{safe}}$)	2 m
Final Capture Cone Length ($L_{\mathrm{final}}$)	5 m
Final Capture Cone Angle (${\theta }_{\mathrm{final}}$)	45°
RL Hyperparameters	Identical to Spacecraft Simulation (Table 3)

. The identical DRL architecture, including the PPO algorithm, prediction reward, and curriculum learning, was applied without modification.

The training process demonstrated stable convergence, akin to the spacecraft scenario, as shown in Figure 13. To conduct a meaningful performance evaluation, a validation test of 500 scenarios per match-up was performed. As presented in

Table 11. Pursuit success rates in multi-drone simulation (500 scenarios per match-up).

	Pursuer Strategy
Evader Strategy	Proposed Algorithm	Traditional PPO	SAC
Proposed Algorithm	88.5%	80.7%	74.1%
Traditional PPO	94.2%	85.1%	79.8%
SAC	96.8%	90.3%	65.5%

, the comparative analysis for the drone engagement yields results that are highly consistent with the spacecraft section. They confirm that the strategic advantages of the proposed algorithm are preserved in the drone domain. For instance, when both sides use the proposed algorithm, pursuers achieve an 88.5% success rate. This rate increases to 94.2% against a traditional PPO evader, while a traditional PPO pursuer’s success rate drops to 80.7% against the proposed evader. A representative trajectory of a successful capture is depicted in Figure 14.

In addition to success rates, the average capture time was also evaluated to provide a more comprehensive assessment of policy efficiency. The results, averaged over all successful scenarios for each match-up, are presented in

Table 12. Average capture time (in seconds) in the multi-drone scenario.

	Pursuer Strategy
Evader Strategy	Proposed	Trad. PPO	SAC
Proposed	12.8 s	13.5 s	14.1 s
Trad. PPO	12.1 s	13.2 s	13.8 s
SAC	11.9 s	12.7 s	15.5 s

.

The capture time results provide further insights. Our proposed algorithm, when used by the pursuers against the strongest evader (also using our proposed algorithm), achieves a fast capture time of 12.8 s. This demonstrates that the high success rate is not achieved at the cost of prolonged engagement times. The analysis of these multiple performance metrics in the drone domain further strengthens the conclusion that our framework’s advantages are robustly transferable.

4.6.6. Validation in an Obstacle-Rich Environment

To further test the adaptability of our framework in more complex and diverse aerial environments, static obstacles were introduced into the 2-vs-.1 drone scenario. The environment was populated with several large, spherical obstacles. Handling this required two minor adaptations to the DRL agent. First, the state representation was augmented to include the relative position and distance to the nearest obstacle. Second, a collision penalty term was added to the reward function to encourage obstacle avoidance. This penalty is defined as

$$R_{\mathrm{obstacle}}=-c·exp(-d_{\mathrm{obs}})$$

(28)

where $d_{\mathrm{obs}}$ is the distance to the surface of the nearest obstacle and c is a positive scaling hyperparameter. The agent’s total reward in this environment is the sum of the previously defined rewards and $R_{\mathrm{obstacle}}$.

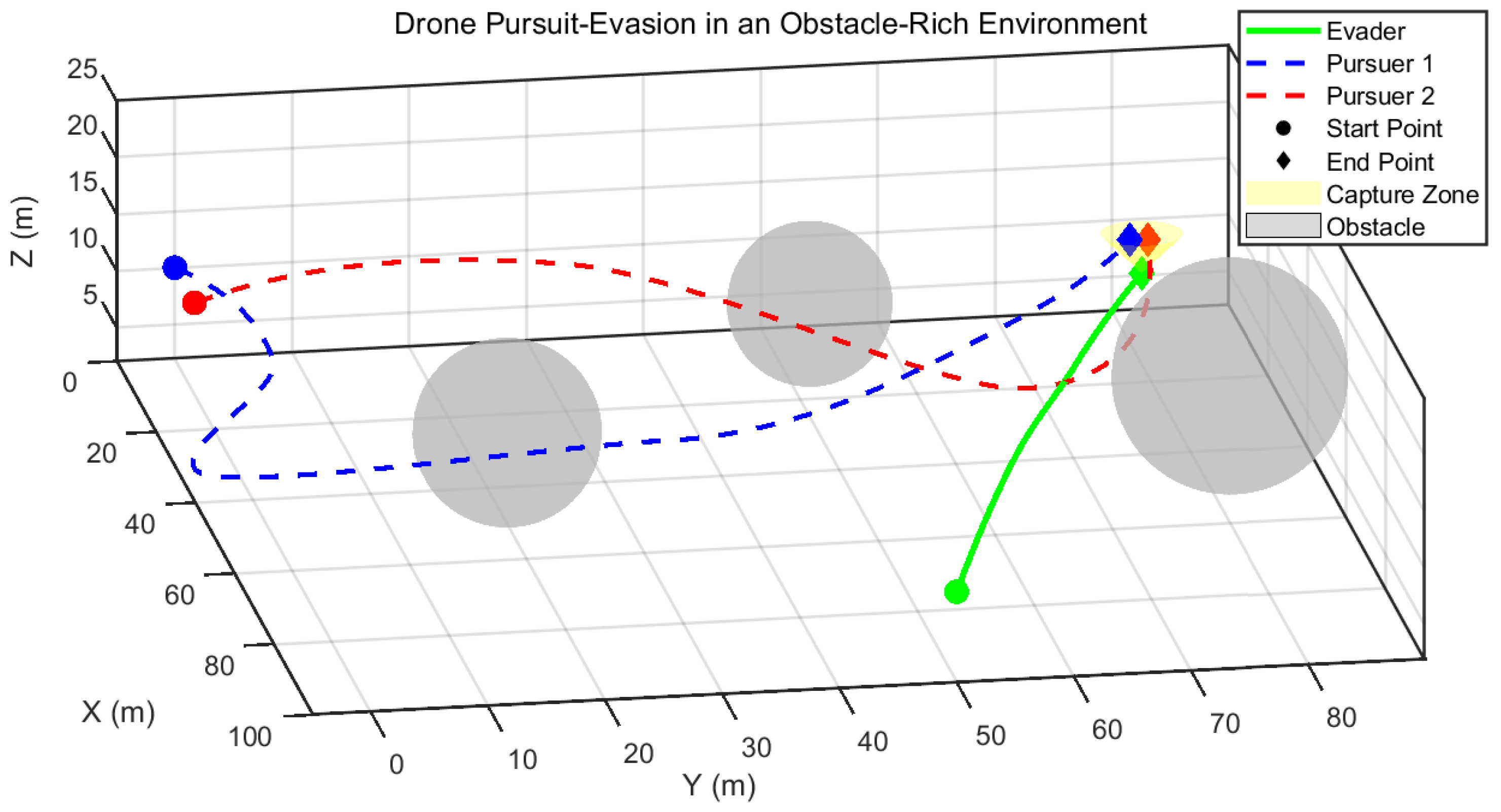
The model was then retrained in this new, more challenging environment. A representative trajectory from a successful capture in the obstacle-rich environment is shown in Figure 15. The figure clearly illustrates the policy’s ability to navigate the complex environment, guiding the pursuers to effectively avoid obstacles while coordinating their attack.

The quantitative performance in this cluttered environment was compared to the obstacle-free case, as summarized in

Table 13. Performance comparison in drone scenarios with and without obstacles.

Environment	Success Rate (%)	Avg. Capture Time (s)
Obstacle-Free	94.2%	12.8 s
Obstacle-Rich	89.6%	14.5 s

.

As expected, the presence of obstacles makes the task more challenging, resulting in a slightly lower success rate and a longer average capture time. Nevertheless, the algorithm still achieves a high success rate of 89.6%, demonstrating that the core principles of our framework—particularly the forward-looking guidance from the prediction reward—can be effectively adapted to learn complex, multi-objective behaviors such as simultaneous pursuit and collision avoidance. This result further underscores the versatility and robustness of the proposed approach.

In summary, adapting the proposed framework for multi-drone pursuit-evasion primarily involves substituting the environment’s physics engine. As demonstrated by the illustrative simulation, the core learning algorithm, predictive reward structure, and curriculum-based training strategy remain robust and highly effective in a fundamentally different physical domain. This empirical validation demonstrates that the method’s comparative advantages are preserved across different domains. Such a result strongly underscores the generalizability of our approach for developing autonomous decision-making systems for diverse adversarial games.

5. Conclusions

In this paper, a generalizable deep reinforcement learning framework was proposed for autonomous pursuit-evasion games and validated in both multi-spacecraft and multi-drone scenarios. The framework integrates a self-play PPO architecture with two key innovations: a dynamics-agnostic curriculum learning (CL) strategy and a transferable prediction-based reward function. Comprehensive simulation results confirmed that this synergistic approach yields highly effective, efficient, and robust policies. In the primary spacecraft validation, the proposed method achieved a high pursuit success rate of 90.7%. Furthermore, it demonstrated remarkable resilience, with a performance drop of only 8.3% under stochastic perturbations. These results represent a significant improvement over standard DRL baselines. The CL strategy was shown to accelerate training, while the prediction reward proved crucial for achieving these high success rates by effectively handling complex terminal constraints.

Despite the promising results, this study has several limitations that offer avenues for future research. The dynamics models, while realistic, still represent a simplification of the true physics. Specifically, for the spacecraft scenario, a key limitation is the model mismatch between the high-fidelity nonlinear environment and the agent’s internal prediction model, which relies on the linearized CW equations. A quantitative analysis of the performance degradation directly caused by this model error was not conducted in this study. Investigating the bounds of this error and developing policies that are even more robust to such model inaccuracies (e.g., by incorporating online system identification or more precise onboard models) is a critical direction for future work. Furthermore, real-world factors such as communication delays and sensor noise were not considered, and the framework’s scalability to larger and more complex team engagements requires further validation.

Building upon these findings and limitations, future research will proceed along several key directions. First, a primary thrust will be the validation of the framework in higher-fidelity simulation environments (e.g., considering orbital perturbations and complex aerodynamics) and eventually on physical hardware testbeds. Second, future work will focus on extending the framework to handle more complex scenarios, including the introduction of environmental factors like communication delays and the deployment of heterogeneous agent teams. Finally, investigating the strategic robustness of the trained policies against a wider range of sophisticated, unforeseen adversarial tactics remains a crucial area for ensuring real-world viability.