Resilient Task Allocation for UAV Swarms: A Bilevel PSO-ILP Optimization Approach

Abstract

To address the severe challenges of task allocation for UAV swarms in uncertain complex environments, this paper introduces the concept of equivalent load, constructs the load capability matrix of a single UAV and the task required load matrix of the task area, and designs a new task resilience capability indicator accordingly to conduct research on a resilience-based optimization framework. Aiming at this multi-objective optimization problem, the “Problem Decomposability Theorem” is proposed, which theoretically proves the feasibility of decomposing the UAV swarm problem into “lower-level Integer Linear Programming (ILP) cost optimization” and “upper-level Particle Swarm Optimization (PSO) resilience optimization”. Based on this, a Particle Swarm Optimization–Integer Linear Programming (PSO-ILP) two-layer nested optimization algorithm is designed. Simulation experiments covering three task areas, five payload types and multiple UAV types are carried out, and the results show that the proposed method has outstanding performance in multi-objective optimization, especially in terms of algorithm convergence and the comprehensive efficiency of swarm load cost and task resilience. In particular, when the interruption probability is in the range of 0.2 to 0.6, it can not only maintain high task resilience but also achieve cost minimization, with a significant improvement in resilience performance. These results not only enrich the theoretical research on UAV swarm resilience but also provide a universal solution for UAV swarm task optimization in multiple fields.

1. Introduction

UAV swarms are widely used in fields such as delivery relief [1,2], agricultural irrigation [3], cooperative hunting [4] and others. In these complex task scenarios [5,6,7,8,9], various factors affect the task performance of UAV swarms. Environmental factors such as adverse weather and complex terrain can affect the flight stability and sensor performance of UAVs to a certain extent. Sudden interruptions such as physical collisions and signal interference can cause varying degrees of damage to the UAV’s body and modules, thereby affecting the UAV’s task performance. As these systems increasingly operate in dynamic, uncertain environments, resilience has become a critical design consideration for maintaining operational effectiveness during disturbances [10,11,12,13].

The theoretical foundations of system resilience were established by Vugrin et al. as early as 2010 [14]. Over subsequent decades, resilience research has expanded from natural world to diverse domains including economics, sociology and industrial studies. Following the development of resilience frameworks for critical infrastructure and economic systems, the concept has been widely applied to various complex networks. A significant advancement in the field of engineering applications emerged in 2016, when Tran et al. [15,16] developed a general resilience-assessment framework, taking into account the typical cases of System-of-Systems (SOS) networks. Their approach quantifies system performance changes during disruptions as a core resilience metric, offering valuable methodological support for assessing the resilience of the rapidly developing UAV swarm systems.

UAV swarm resilience evaluation [17] quantifies a system’s capacity to maintain operational performance during external disruptions. As highlighted by Ordoukhanian et al. [18], resilient multi-UAV operations face three fundamental challenges: real-time disruption identification, dynamic resource allocation and performance-recovery latency. Based on Tran’s resilience-assessment framework, recent studies have introduced methodological refinements: Bai et al. [19] established a standardized performance metric, Li et al. [20] developed assessment criteria for heterogeneous networks, Zhou et al. [13] addressed the handling of partial failure scenarios and Guo et al. [21] proposed a resilience-enhancement approach-based cooperative task. These contributions are primarily focused on resilience research related to system performance in the field of UAV communication, with the research focus having gradually shifted from assessment to improvement strategies. Notable approaches include Kong et al.’s [22] resource-supplementation method for adversarial environments, Sun et al.’s [23] multi-swarm reconfiguration model, Wubben et al.’s [24] leader-loss-mitigation technique and Li et al.’s [25] continuous-attack adaptation through soft resource optimization and task reallocation method under continuous attack conditions to enhance the resilience of UAV swarms. Although these methods have shown effectiveness in post-disruption recovery, their implementation requires non-negligible time intervals. In addition, there are many other types of research related to UAV swarm resilience-improvement methods, mainly focusing on designing recovery strategies after interruptions occur. Although these methods effectively address post-disruption recovery, they mainly focus on reactive strategies rather than proactive resilience design during the task-allocation phase.

As illustrated in Figure 1, sudden disruptions can trigger a rapid decline in system performance, with the solid and dashed lines depicting the performance trajectories under different scenarios. The system operates at a “normal level” in its normal state until the initial disruption occurs at time $t_1$. After that, the performance enters an “absorption” phase, continuing to decline and reaching a nadir at $t_2$; it then enters a “maintenance” phase until recovery actions are initiated at $t_3$. Different final states (A, B, C) correspond to varying degrees of recovery, such as full recovery or partial recovery, which constitute a typical resilience trajectory (as shown by the solid line). In severe cases (dashed line D), performance may drop below the “break level” before recovery strategies can be deployed. The system may even collapse directly, especially when encountering consecutive disruptions. This temporal constraint underscores two core points: first, the critical significance of adopting proactive resilience measures during the task-allocation phase; second, considering redundant UAVs at this stage is a necessary prerequisite for UAV swarms to implement scheduling strategies and ensure the recoverability of task performance. However, the fundamental challenge of UAV swarm task allocation lies in optimizing task performance under strict resource constraints. Phadke et al. [11] critically identified that current allocation methodologies frequently neglect essential swarm system attributes that directly influence operational resilience. Traditional task-allocation problems, categorized by distinct constraints, include the vehicle routing problem (VRP), multiple traveling salesman problem (MTSP) and multiple processor resource-allocation problem (MPRAP). In UAV swarm operations, however, the swarm must simultaneously address two competing objectives: maximizing task effectiveness and minimizing operational expenditures.

The essence of the aforementioned problem is a combinatorial optimization problem between an integer number of UAVs and an integer number of tasks. Traditionally, Integer Linear Programming (ILP) has often been employed for its solution. For instance, Mirza et al. successfully implemented multi-objective optimization for drone coordination and resource allocation using ILP techniques [26]. In logistics applications, Nishira et al. minimized optimal delivery time through ILP-based drone route planning [27], while Gao et al. effectively solved task-allocation problems in medium-scale multi-robot systems via similar methodologies [28]. However, as the scale of UAV swarms and task complexity continue to expand, conventional ILP approaches are increasingly plagued by combinatorial explosion. Recent studies have focused on hybrid techniques integrating Branch and Bound with Cutting Plane methods [29,30,31,32], which exhibit superior performance in reducing solution spaces and identifying optimal solutions. The development of open-source tools—such as COIN-OR’s PuLP modeling framework and the CBC (COIN-OR Branch and Cut) solver—has substantially lowered the barrier to research in linear and integer programming [33].

Despite these advancements, ILP-based methods show limited scalability in dynamic task-allocation scenarios for drone swarms. In contrast, swarm intelligence algorithms have emerged as particularly effective alternatives in practical applications. Guo et al. [34] proposed an optimized discrete particle swarm optimization algorithm to address the requirement of multi-UAV cooperative task execution. Xiong et al. [35] put forward an improved multi-objective grey wolf optimization algorithm, which is applied to task allocation in heterogeneous target reconnaissance by multiple UAVs. Qin et al. [36] presented a seagull optimization algorithm driven by deep reinforcement learning to solve the problem of multi-UAV task allocation in plateau ecological restoration. Other approaches focus on fully decentralized optimization frameworks, such as those based on the Alternating Direction Method of Multipliers (ADMM), which enhance system scalability and resilience against single points of failure by removing the need for a central controller [37,38,39]. While these methods demonstrate strong performance in deterministic environments, they suffer from notable limitations when addressing stochastic interruption scenarios.

A critical limitation emerges from the inherent uncertainty in payload loss during disruptive events. Existing allocation strategies that account for maximum expected loss often lead to substantially increased operational costs and excessive resource redundancy, as documented in prior studies [7,40,41,42]. This necessitates proactive resilience-integrated allocation frameworks that intrinsically embed robustness at the planning stage without compromising operational efficiency.

In view of the limitations in existing UAV swarm task-allocation methods, this paper presents a comprehensive study based on task resilience. By leveraging a bilevel nested structure, we design an innovative task-allocation-optimization algorithm. This algorithm is specifically tailored to address the multi-objective optimization challenges in UAV swarms, with a particular emphasis on task resilience. This study presents three key innovations:

(1)

By introducing the concept of equivalent load, this paper deeply integrates UAV capabilities (types, payloads) with task requirements, constructs a multi-dimensional quantitative indicator system related to UAV swarm tasks and further establishes a quantitative assessment model for task resilience. This research effectively addresses the deficiency of insufficient attention to task resilience in the existing field of task allocation.

(2)

The “problem decomposability theorem” is proposed, and a two-layer PSO-ILP optimization algorithm is designed to jointly optimize swarm load costs and task resilience. Specifically, the lower layer focuses on minimizing load costs, while the upper layer optimizes the weighted fitness value of load costs and resilience, thereby effectively solving the complex multi-objective optimization problem in UAV swarm task allocation.

(3)

The uncertain and stochastic disturbance characteristics of task resilience during task execution under different interference probabilities (0.2–0.6) are investigated, fully verifying the effectiveness of the PSO-ILP algorithm in coping with sudden interruptions and maintaining high task capacity performance in various disturbed scenarios.

This paper is organized as follows: Section 2 explores the related Work in UAV swarm optimization, task-allocation framework and resilience model. Section 3 constructs the mathematical model of the UAV swarm task scenario. Section 4 elaborates on the theoretical basis of the two-layer nested optimization method and conducts algorithm design. Section 5 carry out simulation experiments and result analysis based on typical scenarios. Section 6 summarizes the research achievements and future research directions.

2. Preliminaries

2.1. UAV Swarm Task-Allocation Framework

The task-allocation framework for the UAV swarm is illustrated in Figure 2 [10]. In this framework, we introduce the concept of equivalent load to quantify the different types of tasks in the UAV swarm’s task list as well as the task capabilities of individual UAVs. The process begins with defining task scenarios, from which a “Task Required Load” matrix is derived. Concurrently, the available UAV fleet is defined by its “UAV Loads Configuration” and corresponding “Load Capacity Matrix” for each UAV type. The central “Task-Allocation Optimization” module processes these inputs. It performs “Task Splitting” to break the overall mission into subtasks and allocates UAVs to form “Subtask Alliances”. Crucially, the optimization provides “Extra” (redundant) loads for each alliance to enhance resilience against disruptions. A “Task completion test” provides feedback to the allocation and analysis stages. For example, during task execution, surveying UAVs carry more surveying payloads than other types of UAVs, and communication UAVs are equipped with more communication payloads. Based on the changes in parameters such as the swarm’s payload capacity, task capabilities and interruption probability, we can evaluate and optimize the task coalitions obtained from UAV swarm task allocation in multi-task scenarios.

The UAV swarm task-allocation problem studied herein is characterized by several key features:

A basic task is defined as an indivisible unit, and all such tasks executable by UAV swarms require corresponding task payloads—collectively referred to as “task load.” For instance, surveying tasks demand surveying payloads, communication tasks require communication payloads and rescue tasks necessitate transport payloads.

The load capacity matrix for different UAV types is defined according to the variety of UAV models, their task-performing abilities and the quantity of “carrying” task loads.

Furthermore, the entire task can be decomposed into a sequence of subtasks, which are assigned to individual tasks within each task zone. The load-requirement matrix for each subtask is derived from the load demand matrix of each task in the corresponding task domain.

Focusing on the types, quantities and load capacity matrices of UAVs, along with considerations of the task zones environment, task goals and various constraints, this study explores an optimal task-allocation strategy. It involves the systematic assignment of subtasks and the allocation of specific numbers of different UAV types to each subtask, forming task alliances to accomplish individual subtasks and thus enhancing the overall operational efficiency of the UAVs.

2.2. Basic Concepts and Definitions

Within the UAV swarm task-allocation framework, the concept of payload features prominently across various matrices—including the load capability matrix of different UAV types, the load required matrix for operational units in each task zone and the task load required matrix for individual subtasks. A unified quantification of these payloads is foundational to research on optimizing UAV swarm task-allocation strategies. To this end, this paper introduces the concept of “equivalent payload” to theoretically resolve the issue of load-measurement metrics in UAV swarms.

Definition 1.

Equivalent load: The equivalent load serves as the fundamental unit for various types of task payloads. By setting a unified basic measurement unit for each type of task to quantify its task capability, it can form a core quantitative indicator for measuring the installed payload capacity of UAVs, matching task payload requirements and optimizing scheduling. Specifically, its calculation logic is to divide the actual effectiveness of the UAV in a specific task by the benchmark unit effectiveness set for that task type to obtain the corresponding equivalent load value. This concept has dual functions: first, it can be used to define the installed task payload capacity of a single UAV, clarify the capability boundary of each UAV in performing specified tasks, lay the foundation for constructing the capability matrix of each component in the UAV swarm and provide a comparable standard for the task capabilities of different UAVs; second, it can quantify the payload required for each task area and task execution, which not only helps formulate the corresponding task payload-requirement matrix, but also provides data support for subsequent task scheduling and task alliance reconstruction, making task arrangement more scientific and operable.

For example, if “an effective search range of 100 square kilometers per unit time” is set as 1 basic unit of search-type payload: when the installed search payload of a UAV is 2, it means that the UAV can complete a search task of 200 square kilometers per unit time; and when a task requires 10 search-type payloads, it means that a search task of 100 square kilometers can be completed within 10 unit times, or a search task of 1000 square kilometers can be completed within 1 unit time, etc.

This framework is specifically designed to optimize the configuration of task alliances composed of diverse UAVs for individual subtasks and to assess the effectiveness of task capacity. The introduction of the concept of “task capacity” within this framework provides a quantitative measure for evaluating the extent of task fulfillment, which serves as a foundational basis for the subsequent calculation of task resilience metrics.

Definition 2.

Task capacity: Task capacity ($TC\left(t\right)$) represents the ratio of the total payload carried by the UAV swarms to the total task payload demand at time t. The calculation formula is presented in Equation (1), which ${\epsilon }_i\left(t\right)$ represents the equivalent loads carried by the UAV at time t, $N_U$ is the number of UAVs and $\mathcal{U}\left(t\right)$ represents the total number of task-required loads at time t.

$$TC\left(t\right)={\displaystyle \frac{1}{\mathcal{U}\left(t\right)}}·\sum _{i=1}^{N_U}{\epsilon }_i\left(t\right)$$

(1)

2.3. Task Resilience Model

A portion of the redundant task payload is added to the target tasks assigned to the UAV swarms during the task pre-allocation stage to counter abrupt interruption during the execution of tasks. By considering redundancy of the task payload demands, the UAV swarms can maintain its task capability above the baseline level, even experiencing payload losses caused by an abrupt interruption during the task-execution period.

Existing research on UAV swarm resilience has primarily focused on the dynamic variation of UAV swarm performance. However, as an inherent attribute of a system, resilience measurement and analysis during the task pre-allocation phase ensure that the UAV swarms can continue to carry out operational tasks and implement recovery strategies under abrupt interruption. This paper presents a task resilience model for the pre-allocation phase, introducing a probabilistic interruption factor into the UAV task capability model, thereby transforming a time-varying metric into a probability-varying metric.

Task resilience can be applied to not only early-stage static task allocation but also dynamic task allocation during task execution. It represents a metric with greater potential for engineering applications than traditional system performance indicators, such as “complex network information exchange volume.” The calculation of UAV swarm task resilience is presented in Equation (2). It is influenced by both the interruption probability and task capacity, being positively correlated with task capacity and negatively correlated with interruption probability. This calculation applies to performance measurement across various levels of tasks.

$$R=\left\{\begin{array}{cc}[a+{\displaystyle \frac{{\sum }_{t=t_0}^{t_{final}}(TC\left(t\right)-T{C}_{break})}{(T{C}_0-T{C}_{break})·(t_{final}-t_0)}}]·{\displaystyle \frac{e^{b·(P-1)}}{a+1}}\hfill & TC\left(t\right)\ge T{C}_{break}\hfill \\ 0\hfill & TC\left(t\right)<T{C}_{break}\hfill \end{array}\right.$$

(2)

where $TC\left(t\right)$ represents the task capability under the current interruption probability. $T{C}_0$ represents the required baseline task capacity. $t_0$ represents the start time of the task. $t_{final}$ represents the moment corresponding to the end of the task. $T{C}_{break}$ denotes the break level of task capability, which is the task capability required by the UAV swarms to maintain a base level during the task. P is the interruption probability of the UAV swarms during task execution. In the simulation experiments, the specific values for these variables are determined based on the required duration of the simulation.

To adjust for the impact of different UAVs or tasks on the measurement of task resilience, this paper introduces a task baseline deviation factor a and an interruption probability deviation factor b into the formula, ensuring consistent measurement of task resilience-calculation results.

The task resilience is illustrated as a surface plot and a contour plot with task capacity and interruption probability as independent variables, as shown in Figure 3a,b, respectively. These figures demonstrate the variation in task resilience for UAV swarms at different levels of task capability and interruption probability, given a task baseline of 0.7. In particular, the specific values of a and b can be adjusted according to the characteristics of different tasks to make them conform to the physical laws shown in Figure 3: Specifically, when the UAV swarm’s task capability falls below the task collapse threshold, the task resilience value will remain at 0, not changing with an increase in interruption probability. Conversely, when the UAV swarm’s task capability exceeds the task collapse threshold, the task resilience value is greater for a given interruption probability as the task capability strengthens. Similarly, as the interruption probability increases, the task resilience value that the UAV swarms maintained with the same level of task capability is also greater. Both plots illustrate that Task Resilience is positively correlated with Task Capacity; for a given threat level (P), having more capacity leads to higher resilience. The plots also reflect the model’s characteristic where, above the break level, the calculated resilience value increases with the interruption probability. The dashed line in (b) represents a sample task capacity baseline ($T{C}_0=0.7$). In summary, the task resilience capability index constructs an evaluation framework with both forward-looking and practical value by integrating the quantitative relationships between task capability, interruption probability and task completion degree. Its core value lies in transforming resilience planning during the pre-allocation phase from qualitative judgment to quantitative calculation. It not only retains the rigid constraints on the task baseline but also adapts to the resilience requirements of different operational scenarios through deviation factors. This index not only provides an optimizable quantitative target for UAV swarm task allocation but also offers a systematic measurement tool for enhancing the robustness of UAV swarm applications in complex environments.

3. Problem Modeling

3.1. Scenario Configuration Definition

The task scenario consists of separate targets of the task and single UAVs of the swarm.

Table 1. Major notations for variables and parameters.

Notation	Explanation
V	The set of UAVs in swarm
L	The set of loads in UAV
B	The set of task areas
M	The set of UAV task
P	The set of interruption probability
$LC$	The set of cost by loads
$N_U$	Number of UAV types
$N_L$	Number of load types
$N_B$	Number of operational task areas
$\mathbf{A}$	Task alliance configuration matrix
$\mathbf{E}$	Load capacity matrix
$\mathbf{Q}$	Target unit number matrix
$\mathbf{F}$	Target damage matrix
$\mathbf{U}$	Task required load matrix
$\mathbf{EX}$	Resilience enhancing (extra) load matrix

shows the notations for variables and parameters used throughout this paper.

3.1.1. UAV Configuration Parameters

UAV swarm types: The set of UAV swarm types is denoted as $V=\left\{v_i\mid i\in [0,N_U]\right\}$, where $v_i$ represents the $i^{th}$ type of UAV, and $N_U$ represents the total number of UAV types. For example, when set $V=\left\{v_1,v_2,v_3\right\}$, it represents that there are three types of UAVs ($v_1$, $v_2$ and $v_3$) in the swarms.

UAV load types: A single UAV has the capacity to carry a variety of $N_L$ loads; the set of UAV load types is denoted as $L=\left\{l_j\mid j\in [0,N_L]\right\}$, and the load cost set is denoted as $LC=\left\{l{c}_j\mid j\in [0,N_L]\right\}$, where $l_j$ represents the $j^{th}$ type of load, $N_L$ represents the number of load types and $l{c}_j$ represents the cost (USD) of $l_j$; for example, when set to $L=\left\{l_1,l_2,l_3\right\}$, it represents that there are three types of loads ($l_1$, $l_2$ and $l_3$).

Load capacity matrix: the equivalent load number matrix of various loads designed for each UAV, $\mathbf{E}$$={\left[\begin{array}{c}{e}_{ij}\end{array}\right]}_{N_u\times N_L}$, where $e_{ij}$ represents the number of $l_j$ carried by $v_i$.

3.1.2. Configuration Parameters of Target Units

Task area set: The area where target units are concentrated, which is denoted as $B=\left\{b_k\mid k\in [0,N_B]\right\}$, where $N_B$ represents the task area number, $b_k$ represents the task area.

Target unit set: The set of target units existing in task areas, denoted as $S=\left\{s_m\mid m\in [0,N_S]\right\}$, where $N_S$ represents the number of target unit types.

Interruption probability set: The set of interruption probabilities existing in task areas, denoted as $P=\left\{p_k\mid k\in [0,N_B]\right\}$, where $p_k$ represents the interruption probability in $b_k$.

Target unit number matrix: The matrix represents the number of each type of target unit that existed in task areas, which is denoted as $\mathbf{Q}={\left[q_{km}\right]}_{N_B\times N_S}$, where $q_{km}$ represents the number of targets unit $s_m$ that existed in $b_k$.

Target damage matrix: The matrix represents the required loads to complete a single target task, which is denoted as $\mathbf{F}={\left[f_{mj}\right]}_{N_S\times N_L}$, where $f_{mj}$ represents the number of required loads in a single target task.

The task required load matrix: This is the required equivalent load for a swarm to finish all tasks, which is denoted as $\mathbf{U}={\left[u_{kj}\right]}_{N_B\times N_L}$, where $u_{kj}$ represents the number of required loads. The calculation of the task required load matrix is presented in Equation (3):

$$\mathbf{U}=\mathbf{Q}\times \mathbf{F}$$

(3)

3.1.3. Configuration Parameters of Task

Task set: The whole UAV swarm’s task can be divided into $N_B$ subtasks according to the number of task areas. This set is denoted as $M=\left\{\begin{array}{c}{m}_k\mid k\in [0,N_B]\end{array}\right\}$.

Task alliance: This is a collection of individual UAVs capable of meeting the task payload requirements; the simplest task alliance refers to a collection of individual UAVs that can meet the task payload requirements with the minimum number of types, which is denoted as $\mathbf{A}={\left[\begin{array}{c}{a}_1,a_2,\dots ,a_{N_B}\end{array}\right]}^{\mathrm{T}}$, where $a_k={\left[a_{ki}\right]}_{N_B\times N_U}$, $a_{ki}$ represents the number of UAVs $v_i$ allocated by task $m_k$.

3.2. Mathematical Model

This paper raises a problem based on optimization with task-allocation background, where the objective function considers both the cost of the UAV swarms and the task resilience of the UAV swarms. By adopting a reasonable task-allocation method, under given constraints, the task alliance that minimizes the cost of the UAV swarms and maximizes the task resilience is solved.

Let $c_i$ be the total cost of UAV $v_i$, which consists of two parts: UAV cost $g^U\left(v_i\right)$ and load cost $g^L\left(v_i\right)$, where $g^U\left(v_i\right)$ is positively correlated with the total number of loads carried by UAVs, and the proportionality constant is ${\gamma }_i$. The calculation of UAV cost and load cost are presented in Equations (4) and (5) below.

$$g^U\left(v_i\right)={\gamma }_i·\sum _{j\in [0,N_L]}{e}_{ij},\forall i\in [0,N_U]$$

(4)

$$g^L\left(v_i\right)=\sum _{j\in [0,N_L]}{e}_{ij}·l{c}_j,\forall i\in [0,N_U]$$

(5)

Based on Equations (4) and (5), the total cost of UAV $v_i$ is presented in Equation (6):

$$c_i=g^L\left(v_i\right)+g^U\left(v_i\right),\forall i\in [0,N_U]$$

(6)

According to the calculation equations above, the objective function is to minimize the total cost of task alliance and maximize the task resilience as shown in Equation (7), where $R_k$ represents the task resilience of sub-task $m_k$, ${\lambda }_1$ and ${\lambda }_2$ are normalized parameters.

$$minJ={\lambda }_1·\sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{a}_{ki}·c_i-{\lambda }_2·\sum _{k=1}^{N_B}{R}_k$$

(7)

Equation (7) represents the objective function for a fundamentally multi-objective optimization problem, which aims to satisfy two conflicting goals simultaneously:

Cost Minimization: To minimize the total operational cost of the UAV swarm, represented by the term ${\sum }_{i=1}^{N_U}{\sum }_{k=1}^{N_B}{a}_{ki}·c_i$.

Resilience Maximization: To maximize the overall task resilience of the swarm across all subtasks, represented by the term ${\sum }_{k=1}^{N_B}{R}_k$.

These objectives are inherently in conflict, as achieving higher resilience typically requires the allocation of redundant resources, which in turn increases the total cost.

To solve this multi-objective problem, we employ the widely used weighted sum method. This technique converts the vector of objectives into a single scalar objective function by assigning a weight to each objective. The normalized parameters ${\lambda }_1$ and ${\lambda }_2$ serve as these weighting factors, controlling the relative importance of cost minimization versus resilience maximization in the final solution. By adjusting these weights, a decision-maker can explore the trade-off between the two competing objectives and select a solution that best fits the specific operational priorities. This formulation allows our PSO-ILP algorithm to efficiently search for a single, optimal solution that represents the desired balance between cost and resilience.

There are the following constraints that Equation (7) should obey:

$$0\le \sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{a}_{ki}·c_i\le C_0$$

(8)

$$\sum _{i=1}^{N_U}{a}_{ki}·e_{ij}\ge q_{km}·f_{mj},\forall m\in [0,N_S],k\in [0,N_B],j\in [0,N_L]$$

(9)

$$a_{ki}\in {\mathbb{Z}}^{+},R_k\ge 0,\forall k\in [0,N_B],i\in [0,N_U]$$

(10)

where Constraint (8) requires that the total cost of task alliance does not exceed the expected cost $C_0$, Constraint (9) requires that the number of each type of load carried by a swarm should exceed the task required load and Constraint (10) requires that the value of task resilience is positive and the UAV number should be a positive integer.

4. Design of Bilevel Nested Optimization

4.1. Problem Analysis

In adversarial environments, the UAV swarm task-allocation problem formulated in Section 3.2 constitutes a non-convex integer nonlinear programming problem, presenting two inherent challenges: (1) The calculation of task resilience relies on a feasible task alliance, and the task capacity needs to be obtained via simulation. This renders the direct solution of the problem intractable. (2) Integer programming encounters efficiency bottlenecks when addressing large-scale problems [43,44]. The nonlinear characteristics of the task resilience model make it difficult to apply algorithms effectively.

To overcome the aforementioned difficulties, this paper proposes a novel bilevel-optimization framework that decomposes the problem into two hierarchically organized phases. In the initial phase, a feasible task alliance configuration is generated using conventional integer linear programming (ILP), deliberately excluding resilience considerations to ensure computational tractability. The subsequent phase implements Monte Carlo simulations to evaluate the alliance’s resilience performance under various disturbance scenarios, followed by gradient-free optimization iterations to enhance robustness. Within this structure, the lower-level problem serves as an integer linear solver based on the branch-and-bound algorithm, and the selection of optimization variables, model and optimization algorithm design for the upper-level optimizer is crucial.

The upper- and lower-optimization problems are linked via the task resilience capability indicator. An analysis of this indicator reveals a straightforward method to guarantee enhanced task resilience. Specifically, this is achieved by augmenting the constraints of the original payload capability matrix to include the payload quantity for each UAV type. Consequently, it is feasible to introduce a slack variable within the inner loop to equivalently compensate for the “task resilience capability penalty term” that is removed from the objective function.

The constraint in Equation (9) ensures that the $N_L$ types of load quantities supplied by the UAV alliance for $N_B$ subtasks are sufficient to meet the task requirements. However, when the UAV swarms are subjected to external probabilistic interruptions, the load values in the load capacity matrix $\mathit{E}$ will decrease. Similarly, during the interruptions, the load of the UAVs will also be consumed, leading to a reduction in the task-requirement matrix $\mathit{U}$. During the task period, the load consumption by UAVs and target units is illustrated in Equations (11) and (12).

$$elos{s}_{ij}\left(t\right)=\sum _{t=t_D}^t{e}_{ij}·p_k·rand,\forall i\in [0,N_U],k\in [0,N_B],j\in [0,N_L]$$

(11)

$$ulos{s}_{mj}\left(t\right)=elos{s}_{mj}\left(t\right)·coeff,\forall m\in [0,N_B],j\in [0,N_L]$$

(12)

where $e_{ij}$ is the existing loads $l_j$ of UAV $v_i$, $t_D$ is the beginning time of the interruption, $t_{final}$ is the end time of the task. $p_k$ is the interruption probability of area $b_k$. $elos{s}_{ij}\left(t\right)$ represents the consumption number of loads $l_j$ of UAV $v_i$ during the interruptions at time t. $ulos{s}_{mj}\left(t\right)$ represents the consumption number of loads $l_j$ of target unit $s_m$ at time t. $rand$ is a random number following $rand\sim U(0,1)$. $coeff$ is a coefficient constant number.

We introduce a compensation load matrix to ensure the task capacity value above the baseline level during the probability interruptions, denoted in Equation (13).

$$\mathbf{EX}={\left[e{x}_{kj}\right]}_{N_B\times N_L}$$

(13)

The compensation load value is inversely proportional to task resilience. It will adjust according to the changes of task resilience to ensure that the UAV swarms maintain optimal task resilience while completing the task. The performance of the UAV swarms is defined as a weighted function of its resilience capability and compensation load. Consequently, optimizing this function to its maximum value corresponds to optimal overall swarm performance.

4.2. Bilevel-Optimization Modeling: Theoretical Decomposition and Hierarchical Implementation

4.2.1. Original Problem Abstract: Difficulty Analysis from a Solving Perspective

From the perspective of algorithm design, the task-allocation problem defined in Section 3.2 (Equations (4)–(10)) is classified as a mixed-integer nonlinear programming (MINLP) problems. To clarify the computational complexity and justify the bilevel decomposition, this paper focuses on rephrasing the problem from two aspects: computational coupling and scale complexity.

Let $\mathbf{X}=\left[\begin{array}{c}x{b}_{ki}\end{array}\right]\in {\mathbb{Z}}^{N_U\times N_B}$ denote the UAV-task-allocation matrix, where $x{b}_{ki}$ is a binary decision variable that determines whether the i-th UAV is assigned to the k-th subtask. For resilience optimization, the compensation load matrix $\mathbf{EX}=\left[e{x}_{kj}\right]\in {\mathbb{R}}^{N_B\times N_L}$ is introduce as continuous auxiliary variables. The original objective function (Equation (7)) and constraints (Equations (8)–(10)) can be rephrased as Equation (14), where $R_k$ is the resilience of subtask $m_k$.

$$\begin{array}{c}{\displaystyle \underset{\mathbf{X},\mathbf{EX}}{min}}J\left(\mathbf{X},\mathbf{EX}\right)={\lambda }_1{\displaystyle \sum _{i,k}}x{b}_{ki}·a_{ki}·c_i-{\lambda }_2{\displaystyle \sum _k}{R}_k\\ s.t.\left\{\begin{array}{cc}R\left(\mathbf{X},\mathbf{EX}\right)\ge R_0\hfill & (\mathit{Resilence}\mathit{baseline},\mathit{derived}\mathit{from}\mathit{Section}3.2)\hfill \\ {\sum }_{i,k}x{b}_{ki}·a_{ki}·c_i\le C_0\hfill & (\mathit{Cost}\mathit{contraint},\mathit{rephrased}\mathit{from}\mathit{Equation}(\mathit{8}\left)\right)\hfill \\ \sum _i{a}_{ki}·e_{ij}-e{x}_{kj}\ge q_{sm}·f_{mj}\hfill & (\mathit{Feaxibity}\mathit{with}\mathit{compensation},\mathit{extended}\mathit{from}\mathit{Equation}(\mathit{9}\left)\right)\hfill \\ a_{ki}\in {\mathbb{Z}}^{+},e{x}_{kj}\in {\mathbb{R}}^{+}\hfill & \left(\mathit{Variable}\mathit{types}\right)\hfill \end{array}\right.\end{array}$$

(14)

Through the analysis of the above problem, it has the following difficulties:

(1)

Computational Coupling: The resilience $R(\mathbf{X},\mathbf{EX})$ (corresponding to $R_k$ in Section 3.2) needs to be evaluated through Monte Carlo simulation, lacks an analytical expression and is incompatible with traditional MINLP solvers.

(2)

Scale Complexity: When the number of UAVs $N_U>20$, the combinatorial explosion of discrete variables x leads to an exponential growth in computation time [45].

4.2.2. Theoretical Basis of Bilevel Decomposition: Problem Decomposability Theorem

As previously analyzed, the original task-allocation problem constitutes an intractable mixed-integer nonlinear programming (MINLP) problem due to variable coupling and scale-related complexity, rendering direct solution infeasible. To surmount this challenge, the core approach of this research lies in achieving mathematical decomposition of the problem by introducing the compensation load as a slack variable.

The feasibility of such decomposition is predicated on a key assumption: during the optimization process, decision-making regarding the compensation load (slack variable) can be treated as independent of that concerning UAV configurations. It is crucial to clarify that this independence does not imply a physical separation; rather, leveraging the mathematical properties of slack variables, it enables the disentanglement of originally coupled decision variables into two hierarchical levels. Specifically, the upper level determines the resilience buffer by optimizing the compensation load, while the lower level solves for UAV configurations based on the fixed compensation load. This gives rise to a bilevel-optimization structure that aligns with the logical hierarchy inherent in mission planning. The rationale underlying this assumption is elaborated as follows.

Therefore, separating the optimization of the compensation load from the UAV configuration is a reasonable mathematical abstraction of a realistic planning process, enabling the transformation of a complex MINLP problem into two more tractable subproblems. This assumption may be less applicable when the task interruption probability is extremely high and the swarm configuration requires dynamic real-time adjustments, which calls for more in-depth theoretical research and exploration in the future.

By constructing a theorem, it is proven that the original problem can be decomposed into “lower-level integer linear programming (ILP) + upper-level resilience optimization”, providing a mathematical basis for the bilevel model.

Assumption 1 (Compensation-Configuration Independence).

The decision-making of the compensation load matrix $\mathbf{EX}$ has no direct real-time dependence on the UAV configuration $\mathbf{X}$, that is, the compensation strategy can be independently optimized as a “resilience safeguard” and then fed back to adjust the configuration.

Theorem 1 (Problem Decomposability).

If Assumption 1 holds, the original problem (4.1) can be equivalently decomposed into the following two levels of optimization, and the two levels form an iterative optimization relationship through variable transmission:

Lower-Level Problem (ILP): When $\mathbf{EX}$ is fixed, solve for the cost-optimal UAV configuration $\mathbf{X}$, in the form of Equation (15). At this point, $\mathbf{EX}$ serves as a known constraint parameter, determining the feasible boundary after load compensation and directly influencing the optimal solution space of $\mathbf{X}$:

$$\left\{\begin{array}{c}\underset{x}{min}C\left(\mathbf{X}\right)=\sum _{i,k}x{b}_{ki}·a_{ki}·c_i\hfill \\ s.t.\left\{\begin{array}{cc}\sum _i{a}_{ki}·e_{ij}-q_{sm}·f_{nj}-e{x}_{kj}\ge 0\hfill & \forall k,j\hfill \\ C\left(\mathbf{X}\right)\le C_0\hfill \\ a_{ki}\in {\mathbb{Z}}^{+}\hfill \end{array}\right.\hfill \end{array}\right.$$

(15)

Upper-Level Problem (Resilience Optimization): Based on the lower-level optimal solution ${\mathbf{X}}^{*}\left(\mathbf{EX}\right)$, solve for the resilience-optimal compensation load $\mathbf{EX}$, in the form of Equation (16). At this point, ${\mathbf{X}}^{*}$ becomes the benchmark configuration for resilience assessment, and adjustments to $\mathbf{EX}$ will form new parameters that are fed back to the lower level, driving the iterative optimization of the configuration scheme:

$$\left\{\begin{array}{c}\underset{\mathbf{EX}}{min}R\left({\mathbf{X}}^{*}\left(\mathbf{EX}\right),\mathbf{EX}\right)\hfill \\ s.t.\left\{\begin{array}{c}R\left({\mathbf{X}}^{*}\left(\mathbf{EX}\right),\mathbf{EX}\right)\ge 0\hfill \\ e{x}_{kj}\le {\mathbf{EX}}_{max}\hfill & \forall k,j\hfill \\ \mathbf{EX}\in {\mathbb{R}}^{+}\hfill \end{array}\right.\hfill \end{array}\right.$$

(16)

The correctness of the decomposability of the aforementioned problem can be established through the following derivation and proof of necessity and sufficiency.

(1)

Proof of Necessity

Proposition 1.

If $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ is the optimal solution to the original problem, then ${\mathbf{X}}^{★}={\mathbf{x}}^{*}\left({\mathbf{EX}}^{★}\right)$ and ${\mathbf{EX}}^{★}$ is the optimal solution to the upper-level problem.

Proof. 

Assumption for contradiction: Suppose ${\mathbf{X}}^{★}\ne {\mathbf{x}}^{*}\left({\mathbf{EX}}^{★}\right)$, i.e., there exists ${\mathbf{x}}^{\prime }$ that satisfies the constraints of the lower-level problem and $\mathcal{C}\left({\mathbf{X}}^{\prime }\right)<\mathcal{C}\left({\mathbf{X}}^{★}\right)$.

Derivation of contradiction: Since $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ satisfies the constraints of the original problem, ${\mathbf{X}}^{\prime }$ also satisfies all constraints of the original problem (as the lower-level constraints are a subset of the original problem’s constraints). In this case, $\mathcal{J}({\mathbf{X}}^{\prime },{\mathbf{EX}}^{★})={\lambda }_1\mathcal{C}\left({\mathbf{X}}^{\prime }\right)-{\lambda }_2\sum R_k<{\lambda }_1\mathcal{C}\left({\mathbf{X}}^{★}\right)-{\lambda }_2\sum R_k=\mathcal{J}({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$, which contradicts the optimality of $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ for the original problem.

Conclusion: ${\mathbf{X}}^{★}$ must be the optimal solution to the lower-level problem under ${\mathbf{EX}}^{★}$, i.e., ${\mathbf{X}}^{★}={\mathbf{X}}^{*}\left({\mathbf{EX}}^{★}\right)$.

Furthermore, if ${\mathbf{EX}}^{★}$ is not the optimal solution to the upper-level problem, there exists ${\mathbf{EX}}^{\prime }$ such that $\mathcal{R}({\mathbf{X}}^{*}\left({\mathbf{EX}}^{\prime }\right),{\mathbf{EX}}^{\prime })>\mathcal{R}({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ while satisfying the upper-level constraints. In this case, $({\mathbf{X}}^{*}\left({\mathbf{EX}}^{\prime }\right),{\mathbf{EX}}^{\prime })$ would yield a better objective function value $\mathcal{J}$ for the original problem (since ${\lambda }_2>0$), contradicting the optimality of $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$. Thus, ${\mathbf{EX}}^{★}$ must be the optimal solution to the upper-level problem.    □

(2)

Proof of Sufficiency

Proposition 2.

If ${\mathbf{EX}}^{★}$ is the optimal solution to the upper-level problem and ${\mathbf{X}}^{★}={\mathbf{X}}^{*}\left({\mathbf{EX}}^{★}\right)$, then $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ is the optimal solution to the original problem.

Proof. 

Feasibility verification:

-

The constraints of the lower-level problem are a subset of the original problem’s constraints, so ${\mathbf{X}}^{★}$ satisfies all constraints on $\mathbf{X}$ in the original problem.

-

The constraints of the upper-level problem include the core constraints on $\mathbf{EX}$ in the original problem (e.g., resilience baselines, non-negativity), so ${\mathbf{EX}}^{★}$ satisfies the constraints of the original problem.

-

Therefore, $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ is a feasible solution to the original problem.

Optimality verification:

-

Assume there exists a feasible solution $({\mathbf{X}}^{\prime },{\mathbf{EX}}^{\prime })$ to the original problem such that $\mathcal{J}({\mathbf{X}}^{\prime },{\mathbf{EX}}^{\prime })<\mathcal{J}({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$.

-

By definition of the lower-level problem, ${\mathbf{X}}^{*}\left({\mathbf{EX}}^{\prime }\right)$ is the cost-optimal solution under ${\mathbf{EX}}^{\prime }$, so $\mathcal{C}\left({\mathbf{X}}^{*}\left({\mathbf{EX}}^{\prime }\right)\right)\le \mathcal{C}\left({\mathbf{X}}^{\prime }\right)$.

-

Substituting into the objective function gives:

$$\mathcal{J}({\mathbf{X}}^{*}\left({\mathbf{EX}}^{\prime }\right),{\mathbf{EX}}^{\prime })\le \mathcal{J}({\mathbf{X}}^{\prime },{\mathbf{EX}}^{\prime })<\mathcal{J}({\mathbf{X}}^{★},{\mathbf{EX}}^{★}).$$

-

However, since ${\mathbf{EX}}^{★}$ is the optimal solution to the upper-level problem,

$$\mathcal{R}({\mathbf{X}}^{*}\left({\mathbf{EX}}^{\prime }\right),{\mathbf{EX}}^{\prime })\le \mathcal{R}({\mathbf{X}}^{★},{\mathbf{EX}}^{★}).$$

-

Combined with $\mathcal{J}$ definition(including ${\lambda }_2\sum R_k$), this contradicts the above inequality. Therefore, $({\mathbf{X}}^{★},{\mathbf{EX}}^{★})$ is the optimal solution to the original problem.

   □

(3)

Conclusion.

Through the proofs of necessity and sufficiency, we establish that the original problem is fully equivalent to the decomposed “lower-level ILP + upper-level resilience optimization” framework under Assumption 1, thereby completing the proof of Theorem 1.

4.2.3. Lower-Level-Optimization Model: Task-Feasible Configuration via ILP

Based on the lower-level problem of Theorem 1, a lower-level-optimization model is constructed, focusing on the economical allocation of UAVs under a given compensation strategy.

Optimization Variables: UAV sub-task-allocation matrix $\mathbf{X}=\left[\begin{array}{c}x{b}_{ki}\end{array}\right]$(discrete integer variables).

Objective Function: Minimize the swarm task cost, consistent with problem (4.2), as shown in Equation (17), where $N_U$ is the number of UAV types, $N_B$ is the number of task areas, $c_i$ is the cost of a single UAV $v_i$ and $a_{ki}$ is the number of UAV $v_i$ allocated by task $m_k$.

$$min{J}_{lower}=\sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{a}_{ki}·c_i$$

(17)

Constraints:

• Task Feasibility:
  Ensure task requirements are met after compensation, i.e., as Equation (18):

  $$\sum _{i=1}^{N_U}{a}_{ki}·e_{ij}-q_{km}·f_{mj}-e{x}_{kj}\ge 0,\forall m\in [0,N_S],k\in [0,N_B],j\in [0,N_L]$$

  (18)
• Cost Upper Bound:
  Consistent with the original problem, i.e., in the form of Equation (19):

  $$0\le \sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{a}_{ki}·c_i\le C_0$$

  (19)
• Integer Constraint:
  UAV configurations are discrete allocations, i.e., in the form of Equation (20):

  $$a_{ki}\in {\mathbb{Z}}^{+},\forall k\in [0,N_B],i\in [0,N_U]$$

  (20)

Solution Method: Use an integer linear programming solver (such as the branch-and-bound method) to quickly generate a “task-feasible, cost-optimal” UAV configuration, providing a basis for upper-level resilience optimization.

4.2.4. Upper-Level-Optimization Model: Resilience-Oriented Compensation Loads

Based on the upper-level problem of Theorem 1, an upper-level-optimization model is constructed, focusing on improving resilience by adjusting compensation loads under a given configuration strategy.

Optimization Variables:

Compensation load matrix $\mathbf{EX}=\left[\begin{array}{c}e{x}_{kj}\end{array}\right]$ (continuous variables).

Objective Function:

Balance cost and resilience, consistent with the original problem’s objective, adjusted by weights ${\lambda }_1$, ${\lambda }_2$, as shown in Equation (21):

$$min{J}_{\mathrm{upper}}={\lambda }_1·\sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{\alpha }_{ki}·c_i-{\lambda }_2·\sum _{k=1}^{N_B}{R}_k$$

(21)

Constraints:

• Resilience Baseline:

Ensure task resilience meets the threshold, as in Equation (22):

$$R_k\ge R_0\forall k\in [0,N_B]$$

(22)

• Cost Upper Bound:

This is consistent with the lower-level constraints to ensure total cost control, as shown in Equation (23):

$$0\le \sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{a}_{ki}·c_i\le C_0\forall k\in [0,N_B]$$

(23)

• Compensation Load Upper Bound:

Avoid excess resource use from overcompensation, per Equation (24):

$$e{x}_{kj}\le E{X}_{Max}\forall k\in [0,N_B],j\in [0,N_L]$$

(24)

Solution Method: Evaluate the resilience R under different $\mathbf{EX}$ via Monte Carlo simulation, adjust compensation loads with heuristic algorithms (e.g., PSO) to achieve the “resilience-optimal” goal, then feedback to update the lower level.

4.3. Design of Bilevel Nested Optimization Based on PSO-ILP

From the model of the layer-optimization problem, the traditional ILP algorithm can be used for the lower-layer optimization, while the upper-layer-optimization algorithm needs to use a swarm intelligence-optimization algorithm. There are many swarm intelligence-optimization algorithms, including genetic algorithm [46,47], particle swarm algorithm [48,49], grey wolf algorithm [50], tuna algorithm [51], whale algorithm [52] and ant colony algorithm [53]. The particle swarm algorithm is easy to implement and has relatively low complexity, especially suitable for the rapid solution of low-dimensional, continuous variable nonlinear processing and other optimization problems; it belongs to the basic algorithm of the population intelligence algorithm, like the genetic algorithm, and is very suitable for use in combination with other algorithms. The dimension of the compensation load matrix of the upper-layer-optimization problem is the number of load species, and the dimensionality is certainly not too high, while the nonlinear processing term in the upper-layer model is mainly the resilience index calculation, which is a typical continuous variable. Therefore, we choose the particle swarm algorithm as the upper-layer-optimization algorithm.

Figure 4 illustrates the overall framework of the optimization process of the PSO-ILP (particle swarm optimization–integer linear programming) algorithm. The workflow begins with the initial target requirements for the entire mission. This total required load is then divided into subtasks based on predefined geographical task areas, where each area contains a specific set of targets. The lower layer (ILP) then allocates a cost-optimal task alliance for each subtask. These alliances are subjected to simulated random interruptions, and their performance is evaluated. The results are passed to the upper layer (PSO), which updates the compensation load matrix (EX) to improve resilience. The optimized EX matrix is then returned to the lower layer to refine the allocation in an iterative feedback loop. Figure 5 is the flowchart of the PSO-ILP bilevel nested optimization process. The process starts with initial parameters and an initial task alliance from the ILP. The core of the algorithm is the interaction loop between the two layers. The lower layer (ILP) is responsible for finding a cost-optimal, feasible task alliance (A) for a given compensation load matrix (EX). The upper layer (PSO) evaluates the fitness of this solution (considering both cost and resilience) and updates the EX matrix to guide the search towards a more robust solution. This iterative process continues until a maximum number of iterations is reached or the solution converges. Algorithm 1 shows the pseudocode of the optimization process.

Algorithm 1 PSO-ILP Bilevel Nested Optimization

Require: Load capacities matrix $\mathbf{E}$, target units matrix $\mathbf{Q}$, target unit damage matrix $\mathbf{F}$, interruption probability P, task capacity baseline $T{C}_0$, number of UAV types $N_U$, number of load types $N_L$, number of task areas $N_B$, number of target unit types $N_S$, and max iterate number $N_{iter}$. Ensure: List of fitness values $\mathcal{F}$, task capacity $TC$, task resilience R, optimal task alliance $\mathbf{A}$, and final compensation load matrix $\mathbf{EX}$.  1: Calculate the required load for every single task according to Equation (3).  2: Initialize compensation load matrix $\mathbf{EX}$ and a solution of task alliance $\mathbf{A}$ according to Equation (15).  3: Calculate the initial fitness value ${\mathit{Fitness}}_0$ with PSO according to Equation (26).  4: $\mathit{bestFitness}\leftarrow {\mathit{Fitness}}_0$.  5: for$iter\leftarrow 1$ to $N_{iter}$ do  6:        for $i\leftarrow 1$ to $N_B$ do  7:              Simulate probabilistic interruption with probability P.  8:              Calculate task capacity $TC$ according to Equation (1).  9:              if $TC>T{C}_0$ then 10:                   Calculate the i-th fitness value ${\mathit{Fitness}}_i$ with PSO according to Equation (26). 11:                   if ${\mathit{Fitness}}_i<\mathit{bestFitness}$ then 12:                         $\mathit{bestFitness}\leftarrow {\mathit{Fitness}}_i$. 13:                         Update the best known solution for task alliance $\mathbf{A}$. 14:                   end if 15:              end if 16:        end for 17:        Update compensation load matrix $\mathbf{EX}$ according to Equation (16). 18: end for 19: Record the final results: list of fitness values $\mathcal{F}$, task capacity $TC$, task resilience R, task alliance $\mathbf{A}$ and compensation load matrix $\mathbf{EX}$.

4.3.1. Basic PSO Algorithm Principle

Particle swarm optimization (PSO), introduced in 1995 by Eberhart and Kennedy, is an algorithm inspired by bird predication behavior, which seeks the optimal solution to optimization problems by simulating cooperation and information sharing among group individuals in the process of foraging.

Within the population, every particle is regarded as an ideal moving entity and expanded to an n-dimensional space. The position of the particle in the n-dimensional space is denoted as a vector ${\mathbf{z}}_i=(z_{i1},z_{i2},\cdots ,z_{iN})$, and the flight speed is represented as a vector ${\mathcal{V}}_i=({\mathcal{V}}_{i1},{\mathcal{V}}_{i2},\cdots ,{\mathcal{V}}_{iN})$. Each particle moves at a specific speed in a given space, which defines its historical optimal position ${\mathbf{p}}_{\mathbf{i}}=(p_{i1},p_{i2}\cdots p_{iN})$ and the optimal position of the entire population ${\mathbf{p}}_g=(p_{g1},p_{g2}\cdots p_{gN})$. Particles continuously adjust their moving velocities and gradually converge toward the global optimal position by comparing discrepancies between their current positions and both their historical optimal positions and the global optimal position. The performance of each particle is evaluated based on its fitness value. In each iteration, particles update themselves by tracking their individual optimal positions and the global optimal position of the swarm. The position and velocity update mode of the particle swarm is as Equation (25):

$$\begin{array}{cc}\hfill {\mathcal{V}}_{ij}^{k+1}& =w·{\mathcal{V}}_{ij}^k+c_1·rand·(p_{ij}^k-z_{ij}^k)+c_2·rand·(p_{gj}^k-z_{ij}^k)\hfill \\ \hfill {\mathcal{V}}_{ij}^{k+1}& =\left\{\begin{array}{cc}{\mathcal{V}}_{max}\hfill & {\mathcal{V}}_{ij}^{k+1}>{\mathcal{V}}_{max}\hfill \\ -{\mathcal{V}}_{max}\hfill & {\mathcal{V}}_{ij}^{k+1}<-{\mathcal{V}}_{max}\hfill \end{array}\right.\hfill \\ & z_{ij}^{k+1}=z_{ij}^k+{\mathcal{V}}_{ij}^{k+1}\hfill \end{array}$$

(25)

where k is the number of particle iterations; w is the inertia weight; $c_1$ is the weight coefficient for the particle to track its historical optimal value; $c_2$ is the weight coefficient for the optimal value of the particle-tracking population. $rand\left(\right)$ is a random number that follows $rand\sim U(0,1)$. ${\mathcal{V}}_{ij}^k$ and $z_{ij}^k$ are the velocity and position of the $j^{th}$ dimension of particle i in the $k^{th}$ iterations. $p_{ij}^k$ and $p_{gj}^k$ are the individual best position and global best position of the $j^{th}$ dimension of a particle i in $k^{th}$ iterations, respectively.

4.3.2. Upper-Layer Optimization of PSO Algorithm Implementation

The interior optimization problem, a classic integer linear program (ILP), is tackled by adopting a standard ILP model. The “compensation load matrix” is established for the task alliance and functions as an input to the upper-optimization model. A notable difficulty is that its compensation values for current and future periods are stochastic in nature and lack an identifiable pattern. This work aims to apply the PSO algorithm to solve the upper-optimization problem since it can effectively handle local optimization and global optimization problems. The upper-layer-optimization problem model, which is described as follows, facilitates the easy development of the PSO implementation algorithm for this problem.

(1)

The compensation load matrix $\mathbf{EX}$ serves as the particle in the PSO algorithm;

(2)

Fitness function construction: The model constraints of the upper-optimization problem are integrated into the objective function of optimization in the form of penalty terms, as presented in Equation (26):

$$Fitness={\lambda }_1·\sum _{i=1}^{N_U}\sum _{k=1}^{N_B}{a}_{ki}·c_i-{\lambda }_2·\sum _{k=1}^{N_B}{R}_k+\sum _{i=1}^{N_B}{e}^{(T{C}_0-T{C}_i)·\beta }$$

(26)

where $\beta$ is the weight factor of the penalty item, which needs to be determined based on the quantity values of the other two items, and the default value of $\beta$ is 100.

(3)

Numerous studies have demonstrated that adjusting inertia weights significantly impacts the performance of PSO. Given that the primary function of the optimization variable $\mathbf{EX}$ is to compensate for resilience factors unassessed by the lower-level optimizer, the rationality of its value depends heavily on resilience indices, which directly influence the algorithm’s global convergence. To address this challenge, inertia weights are dynamically adjusted based on evaluations of the task resilience capability index. Let the integrated value W of the resilience capability for completing all current subtasks be defined as ${\sum }_{k=1}^{N_B}{R}_k$. Assuming the baseline integrated value for completing all subtasks is $W_{\mathrm{basic}}$ and the average integrated value of the particle swarm is $\overline{W}$, the following rules apply: if the integrated value exceeds $W_{\mathrm{basic}}$, their average is taken as ${\overline{W}}_{max}$; if it is less than $W_{\mathrm{basic}}$, their average is denoted as ${\overline{W}}_{min}$.

The inertia weight coefficient is computed as shown in Equation (27). When the value of W is superior to $W_{basic}$, it implies that the resilience is stronger, and $\mathbf{EX}$ is near the global optimum. At this point, the inertia weight coefficient w can be assigned a smaller value to speed up the convergence to the global optimum, with the minimum value $w_{min}$ typically being equal to 0.1. When the value of W is inferior to $W_{basic}$, it indicates that the resilience is rather weak, and $\mathbf{EX}$ has optimized the difference.

$$w=\left\{\begin{array}{cc}{w}_{min}\times {\displaystyle \frac{{\overline{W}}_{max}-W_{\mathrm{basic}}}{|W-W_{\mathrm{basic}}|}}\hfill & W\ge W_{\mathrm{basic}}\hfill \\ 1.5-{\displaystyle \frac{1}{1+e^{0.01·({\overline{W}}_{min}-W_{\mathrm{basic}})}}}\hfill & W<W_{\mathrm{basic}}\hfill \end{array}\right.$$

(27)

4.3.3. PSO-ILP Bilevel Nested Optimization Process

In the present study, the methodology for determining optimal parameters in UAV swarm task planning bears similarity to a nested optimization framework, where PSO is integrated with an integer programming approach.

Specifically, the first parameter to be optimized is the number of unmanned aerial vehicles (UAVs), that is, the appropriate deployment of UAVs with different loads such that the total number of loads in the UAV swarms is not less than the number of loads needed for the task. This optimization problem can be mathematically depicted and solved by using an integer programming algorithm. The number of UAVs is the optimal object, and the total load of UAVs is the constraint. The resilience capability, which matches the compensating load matrix, is the second parameter to be enhanced in this research.

As the resilience capability varies with the compensatory load matrix, the optimal value solution problem is comparable to an optimization problem involving a particle swarm technique. Where $e{x}_{ij}$ represents the optimal local solution and R represents the ideal global solution. Meanwhile, the value of the resilience capability is decided by the task capacity and interruption probability as estimated by an algorithm for integer programming. Therefore, the resilience capability, the number of UAVs and the compensatory load form a cascade framework for the particle swarm algorithm and integer programming method.

In conclusion, the resilience performance of the UAV swarms that needs to be optimized is the weighted value of the number of UAVs and the resilience capability. Thus, the UAV swarms will have a certain rate of resilience capability before it encounters interruptions.

4.3.4. Convergence Criteria

The termination of the PSO-ILP algorithm is determined by a hybrid stopping condition, ensuring both a finite runtime and termination upon solution convergence.

For the simulation experiments presented in this paper, the primary stopping criterion was a fixed maximum number of iterations ($N_{iter}=30$). This approach ensures a consistent computational budget across all experimental runs, which is crucial for a fair comparison of the final solution quality under different scenarios.

In addition to the maximum iteration limit, the algorithm incorporates a convergence-based early stopping criterion to terminate if the search process stagnates. As depicted in the flowchart (Figure 5), the optimization process can be concluded if the absolute improvement in the global best fitness value (J) between two consecutive iterations, $k-1$ and k, falls below a predefined threshold, $\tau$. This condition is expressed as:

$$\left|J\right(k)-J(k-1\left)\right|<\tau$$

(28)

For our implementation, the convergence threshold was set to $\tau ={10}^{-4}$. This value was chosen empirically to signify that the algorithm has reached a stable solution, and further iterations are unlikely to yield significant improvements to the objective function.

5. Experimental Simulation, Results and Analysis

To verify the effectiveness of PSO-ILP bilevel nested optimization under an abrupt interruption, this study conducts two sets of simulation experiments. First, we set up the simulation scenario of the following experiments. And then in experiment 1, the process of optimization of fitness value and task resilience is analyzed to prove the effectiveness of PSO-ILP bilevel nested optimization. In experiment 2, the total number and the total cost of UAVs’ task alliances of three algorithms are selected to analyze the priority of PSO-ILP. Finally, in experiment 3, a scenario based on the Lanchester model is created, and the task complete performance of PSO-ILP with task resilience under this scenario is analyzed in comparison with two other algorithms.

5.1. Task Scenario Setting

To validate the effectiveness of the proposed PSO-ILP bilevel nested optimization algorithm and to robustly evaluate its performance under various disturbances, this section constructs a representative task scenario. The detailed configuration of this scenario and the rationale for its design are described below.

5.1.1. Basic Scenario Configuration

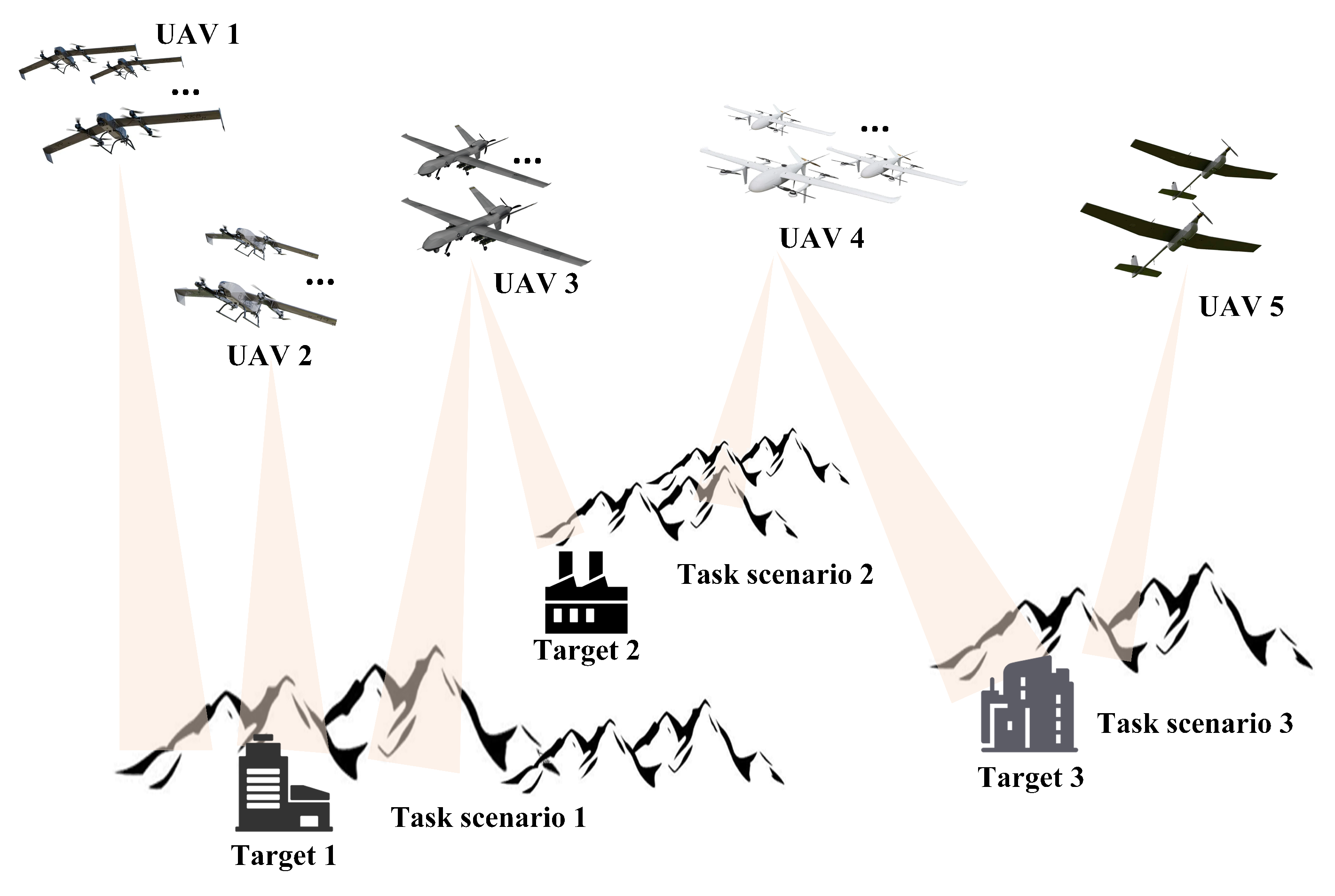
Figure 6 presents a diagram of the task zones for the UAV swarm mission. This figure illustrates a heterogeneous UAV swarm comprising multiple UAV types (e.g., UAVs $v_1$ through $v_5$), which is tasked with mitigating threats across three geographically distinct mission scenarios. Each scenario contains primary targets, serving as the objective for a dedicated task alliance. The mission scenario for the UAV swarm encompasses three task areas, within each of which there exist five distinct target types that may pose threats to the UAV swarm.

We constructed a task scenario using a network approach (as shown in Figure 7), which illustrates the target configuration in our simulation. This configuration includes the specific distribution of 33 target nodes (8 nodes for target s1, 4 nodes for target s2, 6 nodes for target s3, 7 nodes for target s4 and 8 nodes for target s5) across three task areas. This setup is designed to create heterogeneous subtasks with different load requirements, thereby providing a more challenging and realistic test case with an asymmetric node distribution for the allocation algorithm. The central purple squares (A1, A2, A3) represent the optimized task alliances, the colored circles (s1–s5) represent target types, the dashed lines indicate the allocation relationship between targets and alliances, and the solid lines represent communication links between alliances.

The specific distribution of the 33 total target nodes (e.g., 8 of s1, 4 of s2) among the three task areas was intentionally designed to be asymmetric. This was done to create heterogeneous subtasks with distinct load requirements, thereby providing a more challenging and realistic test case for the allocation algorithm. The central purple squares (A1, A2, A3) represent the optimized task alliances, colored circles (s1–s5) represent the target types, dashed lines indicate the allocation of targets to alliances and solid lines represent inter-alliance communication links.

Table 2. Some parameters of UAV configuration.

UAV	${\mathit{l}}_1$	${\mathit{l}}_2$	${\mathit{l}}_3$	${\mathit{l}}_4$	${\mathit{l}}_5$	${\mathit{\gamma }}_{\mathit{i}}$
$v_1$	12	2	1	1	0	80
$v_2$	2	10	1	0	1	70
$v_3$	2	2	11	1	1	80
$v_4$	4	3	2	3	2	100
$v_5$	0	1	1	1	6	60

presentes some parameters of UAVs according to the definitions in the problem-modeling section, including the capacity configuration of $v_1\sim v_5$. $\gamma$ is the cost coefficient of a single UAV.

Table 3. Some parameters of target unit configuration.

Target Unit	${\mathit{l}}_1$	${\mathit{l}}_2$	${\mathit{l}}_3$	${\mathit{l}}_4$	${\mathit{l}}_5$
$s_1$	200	160	120	80	80
$s_2$	210	150	100	75	80
$s_3$	190	165	105	80	85
$s_4$	205	155	110	85	75
$s_5$	195	170	130	90	90
$lc$	10	13	17	25	50

presents some parameters of target units, including the target requirement configuration of $s_1\sim s_5$. $lc$ is the cost coefficient of a single load. The algorithms are requested to give the best solution set of task alliances $\mathbf{A}$ to satisfy the fitness value given by Equation (26).

5.1.2. Rationale and Representativeness of Scenario Design

The parameter settings for this simulation (three task areas, five UAV types, five load types) are intended to establish a representative, medium-scale complex scenario rather than to simulate an extreme, large-scale problem. The rationale for this design is mainly reflected in the following aspects:

Non-trivial decision space: This scenario is designed to pose a substantial challenge to the algorithm’s solution-finding capabilities. In the upper-level optimization, the dimensions of the compensation load matrix EX are $N_B\times N_L=3\times 5=15$, which means the PSO algorithm must search within a 15-dimensional continuous space. In the lower-level optimization, the number of variables in the task-allocation matrix A is $N_B\times N_U=3\times 5=15$. For a bilevel nested optimization problem, handling 15 coupled decision variables is a computationally non-trivial task, sufficient to validate the effectiveness and convergence of the PSO-ILP algorithm when dealing with multivariable, nonlinear problems.

High heterogeneity to reflect complexity: The complexity of the scenario is manifested not only in its scale but also in its inherent heterogeneity.

UAV heterogeneity: Table 2 clearly shows that different UAVs possess distinct load specializations and costs. For instance, $v_1$ serves as an efficient platform for the $l_1$ load, whereas $v_5$ specializes in the $l_5$ load. This forces the algorithm to make trade-offs between using low-cost, specialized UAVs and employing high-cost, general-purpose UAVs to enhance resilience.

Task heterogeneity: Table 3 indicates that different targets have varying combinations of load requirements. Meanwhile, the distribution of targets across the three areas is non-uniform, as shown in Figure 7. This dual heterogeneity ensures that the three subtasks have distinct demand profiles, thereby effectively testing the algorithm’s ability to allocate resources in a customized manner for subtasks with different characteristics.

Balance between computational feasibility and statistical validity: As stated in Experiments 1 and 2, a reliable statistical evaluation of the algorithm’s performance requires hundreds of repeated simulation runs (100 and 150 times, respectively). The current medium-scale setting allows for the completion of these extensive Monte Carlo simulations within an acceptable timeframe, enabling the acquisition of statistically significant average results. If the scenario scale were excessively large, the prolonged computation time for a single run would make it difficult to conduct sufficient repeated experiments to verify the algorithm’s stability and robustness.

In summary, the design of the current experimental scenario strikes a deliberate balance among problem representativeness, decision-making complexity and computational feasibility. It is sufficient to simulate the core challenges in UAV swarm task allocation, such as resource heterogeneity, diverse demands and the trade-off between cost and resilience, thereby providing a solid and reasonable testbed for validating the effectiveness of the PSO-ILP algorithm.

5.2. Task Resilience-Simulation-Evaluation Model

During the task execution, the UAV swarms are vulnerable to sudden interferences from themselves or the environment. As a result, the task capacity will decline due to the loss of the equivalent load during the task process. To dynamically assess the task load losses caused by the interaction between the UAV swarms and the environment, the interaction between the UAV swarms and the environment can be equated to the adversarial relationship between red and blue sides. Thus, the Lanchester model [54] can be applied to conduct an equivalent analysis of its uncertain disturbances.

Based on the Lanchester model given by Equations (11) and (12), this paper examines the total load of both sides in the task process and utilizes the total load to simulate the initial scale of both sides. According to the load-consumption model, for each task area, the total effective loads $Loa{d}_U\left(t\right)$ carried by UAV swarms and the required loads $Loa{d}_S\left(t\right)$ for the targets at time t can be presented as in Equation (29):

$$\left\{\begin{array}{c}Loa{d}_U\left(t\right)=Loa{d}_U\left(0\right)-\sum _{i=1}^{N_U}\sum _{j=1}^{N_L}elos{s}_{ij}\left(t\right)\hfill \\ \\ Loa{d}_S\left(t\right)=Loa{d}_S\left(0\right)-\sum _{m=1}^{N_S}\sum _{j=1}^{N_L}elos{s}_{mj}\left(t\right)\hfill \end{array}\right.$$

(29)

5.3. Experiment and Analysis

5.3.1. Experiment 1: PSO-ILP Optimization Process and Multi-Objective Effects

Table 4. Experiment 1: PSO-ILP algorithm parameters.

Parameter Name	dim	Particle Size	Iterate Number	Particle Speed	Search Range	Cognitive Coeff	Social Coeff
Parameter value	15	20	30	40	100	2	2

shows the relevant parameters of the PSO-ILP algorithm, where dim is set to 15 to represent the number of dimensions of PSO, the particle size is set to 20 to represent the number of PSO particles and the number of iterations is set to 30; these settings were found to provide a sufficient balance between thorough exploration of the 15-dimensional search space and computational feasibility. The particle speed is 40, which prevents particles from moving too rapidly out of the effective search area. The search range is 100, ensuring they remain within a plausible range. Both the cognitive coefficient and the social coefficient are 2. This is a standard setting recommended in the canonical PSO literature, which is widely demonstrated to provide a good balance between individual particle exploration and swarm-wide information exploitation.

Under the task settings described in the simulation experiment, the PSO-ILP algorithm was used to carry out 100 task-allocation-optimization experiments, and the average value of the experimental results was taken as the final optimization result. The specific results are shown in Figure 8. The green curve shows the fitness values decline when the PSO-ILP algorithm updates its best solutions. The best solutions of this task scenario update four times when the iterate number equals 20, 25, 45 and 58. Meanwhile, the blue curve illustrates the decline in the UAV number; when the normalized coefficient ${\lambda }_1$ grows from 0.4 to 0.5, the total UAV number declines from 1376 to 1350. Finally, the value of task resilience is also affected by ${\lambda }_1$. When ${\lambda }_1=0.8$, the task resilience reaches the peak. The red curve in the main graph reflects the change of the target fitness function in the PSO-ILP algorithm with the increase in the number of iterations. In the initial stage, the model was solved by the CBC solver [55] in the PuLP module, and a set of feasible task alliances for the UAV swarm problem was obtained. Based on this alliance, the initial value of the target fitness was calculated. As an upper-level algorithm, PSO optimizes the compensation load matrix through iteration, making the target fitness value show an overall downward trend, and converging to a value close to 1.102 after 80 iterations. The inset in the upper right corner of the main graph synchronously shows the changing trends of the two optimization objectives during the convergence of the fitness value. It can be seen that with the convergence of the fitness value, the number of UAV task alliances decreases, while the resilience of the UAV swarm task shows an overall upward trend with the increase in the number of iterations. Whenever the PSO-ILP algorithm obtains a new fitness value, the optimal solutions of the two optimization objectives will be updated accordingly. The curve in the upper right subgraph clearly proves the effectiveness of the PSO-ILP algorithm in dealing with multi-objective problems during the optimization process.

5.3.2. Experiment 2: Task Capacity and Algorithm Effectiveness Under Interruptions

(1)

Task Capability and Algorithm Performance Under Different Interruption Intensities

This experiment focuses on the task capability performance of UAVs in dynamic confrontation processes, and delves into the actual effectiveness of the PSO-ILP algorithm under different interruption intensities. The simulation time is measured by program-execution intervals, with a total of 150 experiments conducted. It focuses on analyzing the variation patterns of task capabilities of the three subtasks within the swarm when the interruption intensities are 0.2, 0.4 and 0.6.

Focusing on the scenario with interruption level 1 as the specific analytical target, Figure 9a–c depict the capability curves of the UAV swarm in executing three subtasks under interruption probabilities of 0.2, 0.4 and 0.6, respectively. This 3 × 3 matrix of plots illustrates the algorithm’s performance across diverse conditions, where each row corresponds to a distinct interruption level (with Level 1 being the lowest and Level 3 the highest) and each column represents a specific interruption probability (P = 0.2, 0.4, 0.6). The red dashed line in each plot denotes the task baseline ($T{C}_0=0.9$), below which task performance is deemed degraded. Owing to the compensation loads allocated to each task by the PSO-ILP algorithm during the task-allocation phase, the execution capabilities of the three subtasks all exceed 1 at the initial stage of task execution. As the confrontation proceeds, task capabilities gradually degrade over time due to load losses; however, the optimization mechanism inherent in the PSO-ILP algorithm remains effective.

When the interruption probability is 0.2, the capabilities of the three subtasks oscillate around their respective equilibrium points (close to 0.9) (occurring at t = 30, t = 60 and t = 100, respectively), reflecting the algorithm’s initial effect in maintaining task stability. When the simulation reaches t = 120, although the performance of subtask 1 has experienced three significant declines, it reaches a new balance around 0.4 under the regulation of the algorithm. This is because the remaining effective loads and the dynamic adjustment of the algorithm work together to prevent the task from completely collapsing. When the interruption probability rises to 0.4, the performance of subtask 1 declines four times at t = 65, t = 85, t = 117 and t = 142, the performance of subtask 2 only declines for the first time at t = 140, while the performance of subtask 3 remains above the task baseline throughout the process—demonstrating the PSO-ILP algorithm’s ability to provide differentiated protection for different subtasks. When the interruption probability reaches 0.6, although subtasks 1 and 2 both experience more than two declines (the performance of subtask 1 drops to zero when the simulation is close to 100), subtask 3 still remains stable above the baseline. This fully proves that the PSO-ILP algorithm can ensure the continuous execution of core tasks in a high-interruption environment and maintain the relative stability of task performance in a short period.

(2)

Task Resilience Comparison and PSO-ILP Effectiveness Validation

To further verify the effectiveness of the PSO-ILP algorithm under different interruption probabilities, we solved the problem using the PSO-ILP algorithm and the CBC solver provided by the PuLP module, respectively, in the same experimental scenario described above, and conducted a comparative analysis of the task resilience values of the UAV task alliances obtained by the two algorithms. Figure 10 compares the task resilience values of UAV task alliances solved by the CBC-ILP algorithm and the PSO-ILP algorithm for different interruption probabilities while also illustrating the task resilience values for both task alliances when the interruption probabilities are 0.2, 0.3, 0.4, 0.5 and 0.6. The bar chart compares the task resilience of the three subtasks (T1, T2, T3) for the baseline CBC-ILP algorithm (Algo 1) and the proposed PSO-ILP algorithm (Algo 2). The comparison is performed across five different interruption probabilities. The results show that the resilience values achieved by PSO-ILP are consistently higher than those of the baseline method, with the performance gap widening as the interruption probability increases. When the interruption probability is 0.2, the task capabilities of both task alliances remain at a level close to task requirements due to the lower UAV payload loss caused by interruptions. At this point, the task resilience of both task alliances for all three subtasks exceeds 0.95. Meanwhile, the resilience values of subtask 2 and subtask 3 exceed 0.98, slightly higher than subtask 1’s value. This is because subtask 2 and subtask 3 have higher task objectives and require more payloads than subtask 1. To ensure the UAV swarm’s task capability after an interruption, subtasks 2 and 3 are allocated a larger number of redundant UAVs and redundant payloads than subtask 1. When the interruption probability is 0.3, the average task resilience of each subtask under the CBC-ILP algorithm falls below 0.9, while the average task resilience of the PSO-ILP algorithm can still exceed 0.9. This is because the compensation payloads calculated by the CBC-ILP algorithm are a fixed value. When the interruption probability increases, the quantity of redundant payloads in subtasks with fewer task objectives is significantly lower than the amount of payload lost. In contrast, the compensation payloads calculated by the PSO-ILP algorithm are an adaptive value that adjusts itself according to the actual payload loss, allowing the task alliance to maintain higher task capabilities. From an interruption probability of 0.4 to 0.6, both algorithms show a sharp decline in task resilience values. This is due to the constraint on the quantity of compensation payloads limiting the UAVs’ ability to maintain their task payloads. When payload losses caused by interruptions exceed the maximum value of compensation payload, the UAVs’ task resilience drops sharply. In these three interruption probability scenarios, the task resilience values for all three subtasks of PSO-ILP consistently outperform those of CBC-ILP, demonstrating the superiority of the PSO-ILP algorithm in extreme interference scenarios.

In the context of actual task operations, the parameters such as the task baseline and the task collapse threshold for different tasks involving UAV swarms are adjusted according to the specific circumstances. Additionally, the interruption probability of the UAV swarms may be influenced by other uncertain factors during the task. To mitigate the impact of these uncertainties on the measurement of the UAV swarm’s task resilience, this paper introduces the task baseline offset factor a and the interruption probability offset factor b to ensure the non-negativity of the task resilience-calculation results. Figure 11. illustrates the trend in task resilience as the task baseline offset factor a and the interruption probability offset factor b take on different values. The plot shows the change in the calculated task resilience value as the interruption probability offset factor (b, on the x-axis) varies. The parameter b is a unitless adjustment factor used to scale the impact of the raw interruption probability in the resilience formula (Equation (2)). The range of [1.0, 5.0] was selected for this sensitivity analysis to demonstrate the full dynamic effect of this parameter on the resilience score. Each of the three curves corresponds to a different value of the task baseline offset factor ($a=0.5,1.5,4.5$). The graph illustrates that resilience decreases exponentially with an increasing b, while a higher value of a consistently yields a higher resilience score. It can be observed that as the task baseline offset factor increases, the task resilience values show an overall upward trend. This is because an increase in the offset factor a counteracts the impact of the decrease in task capability on the task resilience values. Simultaneously, when the interruption probability offset factor b increases, the task resilience exhibits an exponential decline. Moreover, as the value of b increases, the influence of the task baseline offset factor a on the task resilience values gradually diminishes. When the value of b rises to 5, the impact of the task baseline offset factor a on task resilience becomes negligible. In summary, by introducing the offset factors, a more realistic measurement of task resilience can be achieved to accommodate different operational requirements.

It is evident that the UAV swarm task-allocation scheme based on the PSO-ILP bilevel nested optimization algorithm that takes task resilience into account possesses a superior ability to sustain task capacity performance when faced with sudden interruptions from operational areas.

5.3.3. Experiment 3: Task-Allocation-Optimization Results by Different Algorithms

Based on the cost parameters of UAVs, game units and task scenarios in

Table 5. The optimal task alliances of three subtasks with three algorithms.

Algorithms	Field No.	${\mathit{v}}_1$	${\mathit{v}}_2$	${\mathit{v}}_3$	${\mathit{v}}_4$	${\mathit{v}}_5$	Total Cost (Dollars)
ILP (without resilience)	$b_1$	66	58	44	210	40	2,299,481
	$b_2$	90	80	60	269	58
	$b_3$	86	80	58	277	55
CBC-ILP (with resilience)	$b_1$	77	69	51	247	46	2,891,355
	$b_2$	104	94	70	317	67
	$b_3$	101	94	68	324	65
PSO-ILP (with resilience)	$b_1$	87	56	43	193	41	2,669,066
	$b_2$	89	80	59	261	56
	$b_3$	86	81	57	268	53

, we applied these parameters to three different algorithms, respectively, to obtain optimized solutions.

Considering the existence of interruption probability, we conducted the experiment under the same scenario 100 times and took the average values as the final results; Table 5 presents a comparison of three different task alliances among three different methods along with the results of these optimizations in detail, with the average optimal task alliances obtained from 100 simulation runs for each algorithm. The table itemizes the number of UAVs of each type ($v_1\sim v_5$) allocated to the three task areas ($b_1,b_2,b_3$) and lists the resulting total cost for each configuration. These detailed allocation results in Table 5 provide the underlying data for the aggregated comparison of total UAV numbers and costs presented subsequently, quantitatively demonstrating the superiority of the proposed PSO-ILP method in balancing cost and resilience.

Figure 12 presents a comparison of the ILP algorithm without considering task resilience (method 1), the CBC-ILP algorithm with task resilience consideration (method 2) and the PSO-ILP algorithm with task resilience consideration (method 3) in terms of the number of drones, the cost of drones and the resilience of the UAV swarms for the optimal task-allocation scheme. The ILP algorithm without considering task resilience (method 1) requires a total of 1531 UAVs with a total cost of USD 2,299,481. The ILP algorithm with task resilience consideration, specifically the CBC-ILP(method 2), requires a total of 1794 UAVs with a total cost of USD 2,891,355. The PSO-ILP algorithm with task resilience consideration (method 3) requires a total of 1360 UAVs with a total cost of USD 2,669,066. The results show that the task-allocation scheme using the PSO-ILP algorithm needs fewer drones than the other two systems. When compared to the CBC-ILP algorithm, the overall cost of the PSO-ILP-based scheme is lower. It is feasible to achieve the lowest overall cost while maintaining task resilience.

To sum up, the optimized task alliances simulated with the PSO-ILP algorithm have the lowest total UAV numbers among the three algorithms. Also, when considering task resilience, the total cost of the PSO-ILP algorithm is much better than the ILP algorithm. Compared with the other two algorithms, the results of the PSO-ILP algorithm are superior.

5.4. Discussions

Experimental results demonstrate that the proposed PSO-ILP bilevel nested optimization algorithm exhibits superior performance in multi-objective optimization of cost-effectiveness and task resilience, particularly in interference scenarios involving sudden interruptions. On the basis of appropriately increasing task costs, it achieves a significant improvement in task resilience capacity. Results from Experiment 1 reveal that the PSO-ILP algorithm possesses effective multi-objective optimization capabilities: as iterations proceed, the target fitness function converges stably, accompanied by a reduction in the number of task alliances and an enhancement in task resilience, reflecting its ability to balance multiple optimization objectives. Experiment 2 highlights the advantages of incorporating task resilience capacity into multi-objective optimization. Under varying interruption intensities, UAV swarms employing the PSO-ILP algorithm can maintain stable task-execution capabilities. Notably, when the interruption probability reaches 0.5 or higher, their task resilience is significantly superior to that of the CBC-ILP algorithm, demonstrating strong adaptability to sudden interruptions. Experiment 3 further validates the practical application advantages of the algorithm. Compared with the ILP and CBC-ILP algorithms, while maintaining task resilience, it requires fewer UAVs and achieves lower total costs, underscoring its cost-effectiveness edge. In contrast to previous studies that mostly focused on single objectives or static scenarios, this research comprehensively considers multiple factors such as cost, resilience and dynamic interruptions, thereby addressing the limitation of incomplete considerations in existing studies.

6. Conclusions

The proposed PSO-ILP bilevel-optimization framework provides an innovative solution for resilient task allocation in UAV swarms operating in disturbed environments. Unlike traditional passive recovery strategies, this framework directly embeds resilience considerations into the task-allocation phase through a functionally layered architecture. It adopts a bilevel nested design where the lower ILP layer generates feasible task alliances and the upper PSO layer optimizes the compensation load matrix, achieving a collaborative optimization of cost and task resilience. Simulation results demonstrate that the framework exhibits excellent performance in multiple dimensions. Compared with the other algorithms, it has advantages in terms of convergence, the number of drones required to complete the same tasks and total cost. In particular, it consistently maintains higher task resilience in scenarios with interruption probabilities ranging from 0.2 to 0.6, with the advantages becoming more prominent in high-interruption environments. This study breaks through the limitations of single-objective optimization and provides a technical path that balances robustness and economy for task allocation in UAV swarms under complex environments. Future research will first advance the scalability of the PSO-ILP algorithm through theoretical analysis and experimental verification regarding its performance in handling large-scale tasks and UAVs. It will then extend to dynamic scenarios, exploring task reconfiguration under real-time disturbances like sudden target changes or UAV damage, and integrate intelligent algorithms to boost instant environmental adaptability—thus further enhancing practical value.