Secure Communication and Resource Allocation in Double-RIS Cooperative-Aided UAV-MEC Networks

Highlights

What are the main findings?

• Proposes double-RIS cooperative UAV-MEC system: multi-dimensional paths via collaboration enhance legitimate links, suppress eavesdropping.
• Integrates Lyapunov optimization and PPO, outperforming benchmarks in secure energy efficiency and queue stability.

What is the implication of the main finding?

• Double-RIS collaboration resolves urban UAV-MEC link blockage and security issues, boosting robustness.
• Lyapunov–DRL integration enables real-time resource allocation in high-dimensional stochastic systems, aiding UAV-MEC deployment.

Abstract

In complex urban wireless environments, unmanned aerial vehicle–mobile edge computing (UAV-MEC) systems face challenges like link blockage and single-antenna eavesdropping threats. The traditional single reconfigurable intelligent surface (RIS), limited in collaboration, struggles to address these issues. This paper proposes a double-RIS cooperative UAV-MEC optimization scheme, leveraging their joint reflection to build multi-dimensional signal paths, boosting legitimate link gains while suppressing eavesdropping channels. It considers double-RIS phase shifts, ground user (GU) transmission power, UAV trajectories, resource allocation, and receiving beamforming, aiming to maximize secure energy efficiency (EE) while ensuring long-term stability of GU and UAV task queues. Given random task arrivals and high-dimensional variable coupling, a dynamic model integrating queue stability and secure transmission constraints is built using Lyapunov optimization, transforming long-term stochastic optimization into slot-by-slot deterministic decisions via the drift-plus-penalty method. To handle high-dimensional continuous spaces, an end-to-end proximal policy optimization (PPO) framework is designed for online learning of multi-dimensional resource allocation and direct acquisition of joint optimization strategies. Simulation results show that compared with benchmark schemes (e.g., single RIS, non-cooperative double RIS) and reinforcement learning algorithms (e.g., advantage actor–critic (A2C), deep deterministic policy gradient (DDPG), deep Q-network (DQN)), the proposed scheme achieves significant improvements in secure EE and queue stability, with faster convergence and better optimization effects, fully verifying its superiority and robustness in complex scenarios.

1. Introduction

In the transition toward sixth-generation (6G) wireless networks, the rapid expansion of smart devices and large-scale Internet of Things (IoT) applications (e.g., smart cities, industrial monitoring, and real-time video analytics) has led to a massive surge in data traffic, along with growing demands for low-latency computation and reliable communication in complex environments [1,2]. To address these challenges, unmanned aerial vehicle–mobile edge computing (UAV-MEC) systems have emerged as a promising technology, drawing significant attention for their ability to leverage UAVs’ mobility and flexible deployment to extend edge computing capabilities into scenarios where ground infrastructure is sparse or overloaded [3,4]. As aerial edge nodes, UAVs can dynamically establish communication links to handle the computation offloading needs of ground users (GUs), providing a viable solution to reduce delays caused by long-distance data transmission to central clouds [5]. However, in dense urban environments, obstacles such as buildings and signal attenuation often destabilize direct communication links between UAVs and GUs—increasing transmission energy consumption—while the broadcast nature of wireless signals makes task data vulnerable to interception by eavesdroppers, posing threats to physical layer security [6,7]. These combined challenges underscore the critical need for innovative technological solutions to enhance the communication reliability and security of UAV-MEC systems.

Against this backdrop, reconfigurable intelligent surfaces (RISs), as an emerging technology capable of dynamically reconstructing wireless propagation environments, offer a promising solution to enhance the secure transmission performance of MEC systems [8,9]. Composed of numerous low-cost passive reflective elements, RISs can flexibly shape signal propagation paths by dynamically adjusting in real time the phase shifts and amplitude attenuations of each element, thereby improving the quality of legitimate links while suppressing eavesdropping channels. This renders it a key enabling technology for physical layer security and energy-efficiency (EE) optimization [10]. Current research on secure transmission in RIS-aided MEC systems has achieved significant progress. For instance, [11,12] investigate resource allocation strategies for RIS-aided secure MEC networks, enhancing security through joint resource allocation and phase shift regulation. Ref. [13] proposes a physical layer security scheme for hybrid RIS-aided multiple-input multiple-output (MIMO) communications, maximizing secrecy capacity by optimizing reflection coefficients and verifying the inhibitory effect of RISs on multi-antenna eavesdropping scenarios. Ref. [14] optimizes secure computation efficiency for space–air–ground eavesdroppers in UAV-RIS-aided MEC networks, introducing multi-RIS deployment but without exploring their collaboration mechanisms. Ref. [15] designs a UAV-RIS-aided multi-layer MEC security scheme for full-duplex eavesdroppers, suppressing eavesdropping signals through RIS beamforming. While these studies have validated the effectiveness of RISs in enhancing secure transmission in MEC systems, they predominantly focus on single RISs or multiple distributed RISs, where each RIS operates independently without inter-RIS collaboration. Such a model exhibits notable limitations: constrained by practical conditions, a single RIS can only provide limited passive beamforming gain for GUs; a single reflection path struggles to bypass obstacles in complex environments; furthermore, the power scaling order of a single RIS or non-collaborative distributed RISs is merely proportional to the square of the number of reflective elements, failing to meet high-performance requirements in complex scenarios. These limitations have thus spurred the academic community to focus on research into multi-RIS collaboration mechanisms.

Multi-RIS collaboration offers significant advantages over single RISs, providing a new pathway to overcome the performance bottlenecks of traditional single RISs. Ref. [16] revealed that in double passive RIS collaborative communication, the beamforming gain scales with the fourth power of the total number of reflective elements—markedly outperforming the quadratic growth characteristic of single RISs. This property establishes a theoretical foundation for constructing high-gain secure transmission links. Further research [17] extended double-RIS collaboration to multi-user scenarios, demonstrating that cooperative beamforming can effectively mitigate the Doppler effect in high-speed railway communications, thus validating the robustness of collaborative RISs in dynamic environments. Another study [18] generalized the double-RIS model to more universal multi-RIS collaborative systems, proving that distributed collaborative RISs can achieve higher link gain and spectral efficiency than single RISs with the same total number of elements through joint phase shift optimization. However, critical gaps remain in translating these double-RIS collaboration frameworks to practical UAV-MEC scenarios. Specifically, existing research fails to account for the dynamic channel variations induced by UAV mobility—a key feature of UAV-MEC systems—which directly impacts the phase synchronization between two RISs and degrades collaborative beamforming performance. Additionally, these studies overlook security vulnerabilities in complex communication environments, as they lack coordinated mechanisms to actively suppress eavesdroppers, such as by jointly forming signal nulls toward eavesdropper directions. Moreover, they often treat UAV trajectory planning and RIS reflection design as separate processes, ignoring the intrinsic relationship between UAV positions and the quality of RIS-GU-UAV propagation paths—an oversight that is particularly detrimental in obstacle-rich urban environments. In summary, while prior work confirms the theoretical merits of multi-RIS collaboration, their simplified treatment of UAV-induced channel dynamics and security threats hinders practical implementation in complex UAV-MEC systems.

In the research on multi-RIS-aided UAV-MEC systems, addressing dynamic environments emerges as a critical challenge. System dynamism, primarily induced by stochastic task arrival rates and time-varying wireless channel conditions, continuously disrupts system stability. Traditional studies—including those on double-RIS collaboration—often overlook this issue by assuming static channels and fixed task volumes, which fails to account for potential queue backlogs that may compromise long-term system performance. To tackle this challenge, Lyapunov optimization theory offers a robust solution. By formulating a drift-plus-penalty model, this approach transforms long-term stochastic optimization problems into deterministic online optimization tasks, effectively balancing immediate performance and queue length control [19,20]. Simultaneously, the high-dimensional nature of optimization problems presents another significant hurdle, especially for double-RIS systems: the intertwined optimization of phase shift synchronization between two RISs, UAV trajectory adjustments, and resource allocation across computation and communication domains creates complex variable correlations that render traditional optimization methods ineffective. Deep reinforcement learning (DRL) has shown promise in addressing this challenge. As an advanced machine learning paradigm, DRL excels in navigating high-dimensional action spaces and adapting to dynamic changes through sequential decision-making, approximating optimal policies via neural networks to generate real-time multi-dimensional resource allocation strategies [21,22]. The integration of Lyapunov optimization and DRL thus provides a targeted solution: Lyapunov optimization ensures long-term stability amid dynamic tasks and channels (a gap in existing double-RIS models), while DRL handles the high-dimensional complexity of synchronized phase shift and trajectory optimization (overcoming oversimplified decoupling in prior work). Together, they address key limitations in practical double-RIS-aided UAV-MEC systems, advancing secure and efficient task offloading.

To address the aforementioned challenges, this paper constructs a double-RIS-aided UAV-MEC system model that accounts for the impact of eavesdroppers on secure transmission. With dual optimization objectives of queue stability and secure EE, this paper proposes an efficient resource allocation scheme based on Lyapunov theory and the proximal policy optimization (PPO) algorithm. The primary contributions of this work are as follows:

• A double-RIS cooperative UAV-MEC network architecture is proposed, leveraging spatial diversity and signal coupling effects of two RISs to construct phase-aligned superimposed beams at legitimate users for maximum signal enhancement while creating phase cancellation patterns towards potential eavesdroppers to suppress information leakage. This framework explicitly addresses phase synchronization and hardware imperfections overlooked in prior studies, jointly optimizing RIS phase-shift matrices, user transmit powers, UAV trajectories, computational resource allocation, UAV receive beamforming vectors under stochastic task arrivals, time-varying channel dynamics, and long-term queue stability constraints—bridging the gap between theoretical gain and practical deployment.
• Using Lyapunov optimization theory, the original problem is reformulated into a deterministic online optimization problem with queue stability guarantees by constructing a drift-plus-penalty function. This addresses the critical oversight of dynamic task/channel handling in existing double-RIS research, decomposing per-slot subproblems to balance immediate secure EE and queue backlog penalties and effectively decoupling interdependent variables (e.g., RIS phase shifts and UAV trajectories) to reduce computational complexity.
• A deep reinforcement learning-based dynamic resource allocation strategy is developed, modeling the system as a Markov decision process and employing the PPO algorithm to approximate optimal policies. This approach overcomes the high-dimensional optimization barrier in synchronized double-RIS and UAV trajectory design—unresolved in traditional methods—enabling end-to-end adaptive resource scheduling by mapping high-dimensional system states to continuous control actions, outperforming baseline schemes such as single-RIS and non-cooperative double-RIS configurations.

The rest of this paper is organized as follows. Section 2 presents our double-RIS cooperative-aided UAV-MEC network model and the associated optimization problems. In Section 3, we introduce the process of transforming the problem using Lyapunov optimization theory and detail the proposed algorithm framework based on the PPO algorithm. Section 4 analyzes the effectiveness of the algorithm through extensive simulation experiments, presenting and discussing the key results. Finally, Section 5 provides a summary of this paper and outlines future research directions.

2. System Model and Problem Formulation

In this section, we construct a double-RIS cooperative-aided UAV-MEC network model and formulate the communication, task queue, and energy consumption models, as well as the core optimization problem for secure energy efficiency maximization.

2.1. Overview

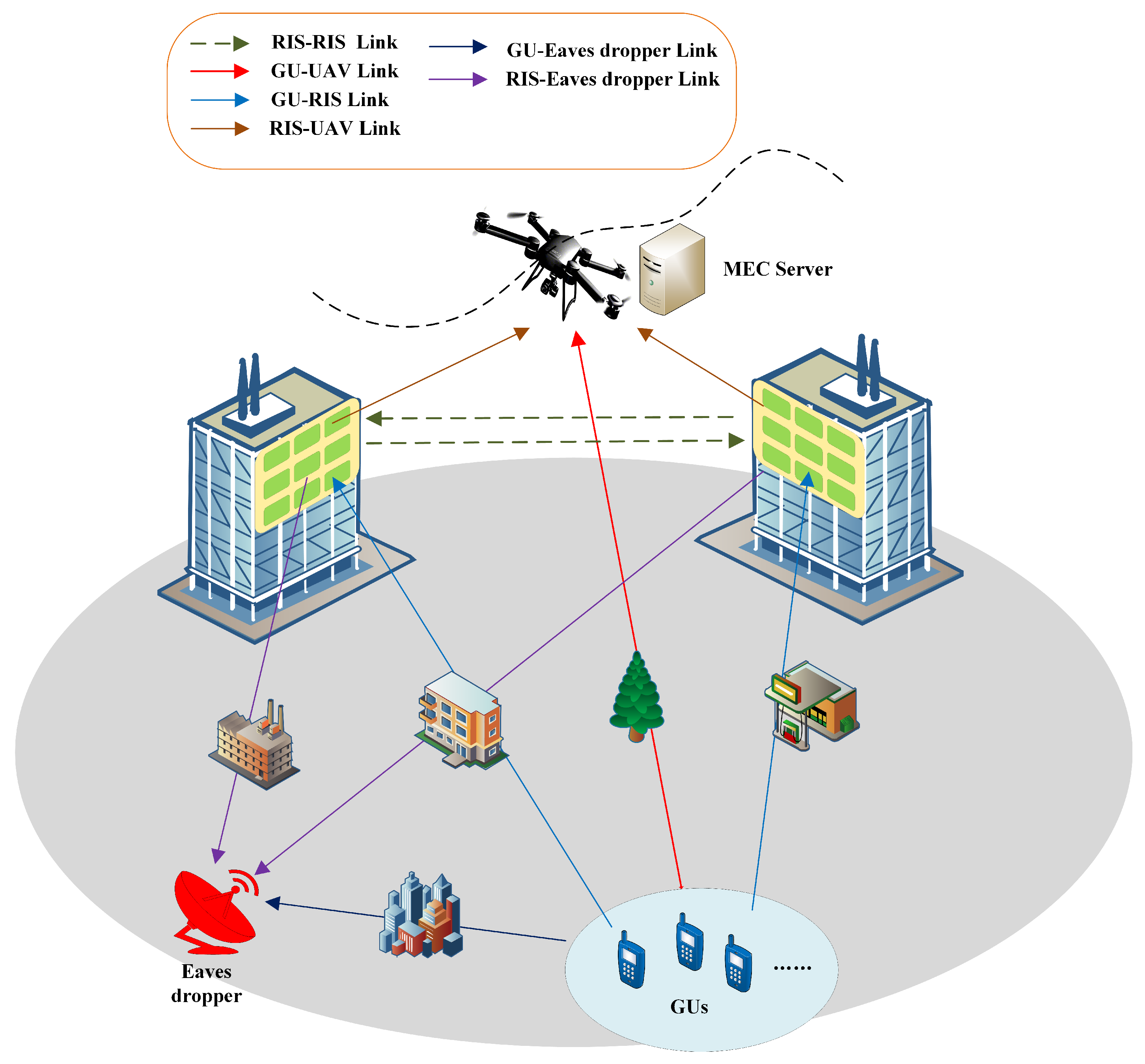
As depicted in Figure 1, we consider a double-RIS cooperative-aided UAV-MEC network architecture comprising a multi-antenna UAV equipped with an MEC server, two geographically distributed RISs, and K single-antenna GUs. A single-antenna eavesdropper is present in the network, attempting to intercept the transmission channels. We assume RIS1 and RIS2 consist of $M_1=M_{1x}\times M_{1y}$ and $M_2=M_{2x}\times M_{2y}$ passive reflecting elements, respectively, while the UAV is equipped with a uniform rectangular array antenna featuring $M_T=M_{Tx}\times M_{Ty}$ elements, where $M_{1x}$, $M_{1y}$ and $M_{2x}$, $M_{2y}$ denote the horizontal and vertical element counts of RIS1 and RIS2, respectively, and $M_{Tx}$, $M_{Ty}$ represent the number of horizontal and vertical antennas in the UAV’s array. The set of all GUs is denoted as $\mathcal{K}=\{1,2,\dots ,K\}$. The entire mission duration T is discretized into N equal time slots, denoted by $\mathcal{N}=\{1,2,\dots ,N\}$, each with a duration $\tau =T/N$. Within each time slot, the UAV’s position ${\mathbf{S}}_u\left(n\right)=[x_u\left(n\right),y_u\left(n\right),H_u]$ remains fixed at a height $H_u$ to minimize energy consumption, while the positions of GUs and RISs are static. Specifically, GU k is located at ${\mathbf{S}}_k=[x_k,y_k,0]$, RIS1 at ${\mathbf{S}}_{R1}=[x_{R1},y_{R1},H_{R1}]$, RIS2 at ${\mathbf{S}}_{R2}=[x_{R2},y_{R2},H_{R2}]$, and the eavesdropper at ${\mathbf{S}}_e=[x_e,y_e,0]$. GUs offload tasks to the UAV via composite links: direct path, RIS1-reflected path, RIS2-reflected path, and RIS1-RIS2 cascaded reflected path.

2.2. Communication Model

In realistic urban scenarios, communication links can be categorized into two types based on their propagation characteristics: ground links (between ground nodes such as GUs, eavesdroppers, and RISs) and aerial links (between aerial nodes such as the UAV and RISs). Ground links are inherently subject to significant obstructions from buildings, foliage, and other urban structures, thus being modeled using the Rician fading model to account for both line-of-sight (LoS) and non-line-of-sight (NLoS) components. In contrast, aerial links (between the UAV and RISs) are LoS-dominated due to their elevated deployment heights, with negligible multipath effects, thus being modeled as pure LoS links.

We first define the channel gain matrices involved in the system: ${\mathbf{h}}_{k,\mathrm{R}1}\left(n\right)\in {\mathbb{C}}^{M_1\times 1}$, ${\mathbf{h}}_{k,\mathrm{R}2}\left(n\right)\in {\mathbb{C}}^{M_2\times 1}$, ${\mathbf{h}}_{k,\mathrm{E}}\left(n\right)\in {\mathbb{C}}^{1\times 1}$, ${\mathbf{h}}_{k,\mathrm{U}}\left(n\right)\in {\mathbb{C}}^{M_T\times 1}$, ${\mathbf{h}}_{\mathrm{R}1,\mathrm{E}}\left(n\right)\in {\mathbb{C}}^{1\times 1}$, and ${\mathbf{h}}_{\mathrm{R}2,\mathrm{E}}\left(n\right)\in {\mathbb{C}}^{1\times 1}$ explicitly denote the complex-valued channel gains from GU k to RIS1, from GU k to RIS2, from GU k to the eavesdropper, from GU k to the UAV (direct link), from RIS1 to the eavesdropper, and from RIS2 to the eavesdropper, respectively. Specifically, ${\mathbf{h}}_{k,\mathrm{R}1}\left(n\right)$ and ${\mathbf{h}}_{k,\mathrm{R}2}\left(n\right)$ comprehensively characterize the cascaded channels incorporating the phase shifts of each passive reflecting element in RIS1 and RIS2, whereas ${\mathbf{h}}_{k,\mathrm{U}}\left(n\right)$ precisely models the direct propagation link between the GU and the UAV’s antenna array. Ground links primarily include links between GUs and RISs, GUs and eavesdroppers, and RISs and eavesdroppers. Taking the link between GU k and RIS1 as an illustrative example, its channel is modeled using the Rician fading model as [23]

$${\mathbf{h}}_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)=\sqrt{{\displaystyle \frac{{\beta }_0}{{\left(d_k^{\mathrm{R}1-\mathrm{G}}\right)}^{a^{\mathrm{R}1-\mathrm{G}}}}}}\left[\sqrt{{\displaystyle \frac{k^{\mathrm{R}1-\mathrm{G}}}{1+k^{\mathrm{R}1-\mathrm{G}}}}}{h}_k^{\mathrm{R}1-\mathrm{G},\mathrm{LoS}}+\sqrt{{\displaystyle \frac{1}{1+k^{\mathrm{R}1-\mathrm{G}}}}}{\tilde{h}}_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)\right],$$

(1)

where

$$\begin{array}{cc}\hfill {\mathbf{h}}_k^{\mathrm{R}1-\mathrm{G},\mathrm{LoS}}& =e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}{d}_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)}\hfill \\ \hfill & \times {\left[e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{x}sin{\theta }_k^{\mathrm{R}1-\mathrm{G}}cos{\delta }_k^{\mathrm{R}1-\mathrm{G}}},\dots ,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_x(M_{Rx}-1)sin{\theta }_k^{\mathrm{R}1-\mathrm{G}}cos{\delta }_k^{\mathrm{R}1-\mathrm{G}}}\right]}^H\hfill \\ \hfill & \otimes {\left[1,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{y}sin{\theta }_k^{\mathrm{R}1-\mathrm{G}}sin{\delta }_k^{\mathrm{R}1-\mathrm{G}}},\dots ,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_y(M_{Ry}-1)sin{\theta }_k^{\mathrm{R}1-\mathrm{G}}sin{\delta }_k^{\mathrm{R}1-\mathrm{G}}}\right]}^H\hfill \end{array}$$

(2)

is the LoS component. ${\beta }_0$ is the unit path gain, ${\lambda }_c=c/f_r$ represents the carrier wavelength. ${\tilde{h}}_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)\sim \mathcal{CN}(0,1)$ (circularly symmetric complex Gaussian) denotes the NLoS random component, $a^{\mathrm{R}1-\mathrm{G}}\ge 0$ is the path loss exponent, and $k^{\mathrm{R}1-\mathrm{G}}\ge 0$ is the Rician factor (characterizing the ratio of LoS to NLoS power). $sin{\theta }_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)={\displaystyle \frac{H_u\left(n\right)}{d_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)}}$, $cos{\delta }_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)={\displaystyle \frac{|y_{\mathrm{R}1}-y_k\left(n\right)|}{\sqrt{{(x_{\mathrm{R}1}-x_k\left(n\right))}^2+{(y_{\mathrm{R}1}-y_k\left(n\right))}^2}}}$ and $sin{\delta }_k^{\mathrm{R}1-\mathrm{G}}\left(n\right)={\displaystyle \frac{|x_{\mathrm{R}1}-x_k\left(n\right)|}{\sqrt{{(x_{\mathrm{R}1}-x_k\left(n\right))}^2+{(y_{\mathrm{R}1}-y_k\left(n\right))}^2}}}$ describe the angle of arrival; $d_k^{\mathrm{R}1-\mathrm{G}}$ is the three-dimensional distance from GU k to RIS1; $\Delta R_x$ and $\Delta R_y$ are the vertical and horizontal distances between RIS elements, respectively.

Aerial links primarily include links between RISs and the UAV, and between the RISs themselves. Given their elevated deployment, these links are dominated by LoS propagation with negligible multipath effects. Taking the link between RIS1 and the UAV as an example, its channel gain is modeled as [23]

$${\mathbf{h}}_{\mathrm{R}1,\mathrm{U}}\left(n\right)=\sqrt{{\displaystyle \frac{{\beta }_0}{{\left(d^{\mathrm{U}-\mathrm{R}1}\left(n\right)\right)}^{a^{\mathrm{U}-\mathrm{R}1}}}}}·e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}{d}^{\mathrm{U}-\mathrm{R}1}\left(n\right)}{\mathbf{a}}_{\mathrm{U}-\mathrm{R}1}{\mathbf{a}}_{\mathrm{R}1-\mathrm{U}},$$

(3)

where

$$\begin{array}{cc}\hfill & {\mathbf{a}}_{\mathrm{U}-\mathrm{R}1}\hfill \\ \hfill & ={\left[1,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{Tx}sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)·cos{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)},\dots ,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{Tx}(M_{Tx}-1)·sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)·cos{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)}\right]}^H\hfill \\ \hfill & \otimes {\left[1,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{Ty}sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)sin{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)},\dots ,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{Ty}(M_{Ty}-1)sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)sin{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)}\right]}^H,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\mathbf{a}}_{\mathrm{R}1-\mathrm{U}}\hfill \\ \hfill & ={\left[1,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{x}sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)·cos{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)},\dots ,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_x(M_{Rx}-1)·sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)·cos{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)}\right]}^H\hfill \\ \hfill & \otimes {\left[1,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_{y}sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)sin{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)},\dots ,e^{-j{\displaystyle \frac{2\pi }{{\lambda }_c}}\Delta R_y(M_{Ry}-1)sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)sin{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)}\right]}^H,\hfill \end{array}$$

(5)

where ${\mathbf{a}}_{\mathrm{U}-\mathrm{R}1}$ and ${\mathbf{a}}_{\mathrm{R}1-\mathrm{U}}$ are the array response vectors of the UAV and RIS1, respectively. $a^{\mathrm{U}-\mathrm{R}1}$ is the path loss exponent of the aerial link; $d^{\mathrm{U}-\mathrm{R}1}\left(n\right)$ is the three-dimensional distance between the UAV and RIS1; $sin{\theta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)={\displaystyle \frac{|H_u\left(n\right)-H_R|}{d^{\mathrm{U}-\mathrm{R}1}\left(n\right)}}$, $cos{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)={\displaystyle \frac{|y_R-y_u\left(n\right)|}{\sqrt{{(x_R-x_u\left(n\right))}^2+{(y_R-y_u\left(n\right))}^2}}}$ and $sin{\delta }^{\mathrm{U}-\mathrm{R}1}\left(n\right)={\displaystyle \frac{|x_R-x_u\left(n\right)|}{\sqrt{{(x_R-x_u\left(n\right))}^2+{(y_R-y_u\left(n\right))}^2}}}$ describe the angle of arrival; $R_{Tx}$ and $R_{Ty}$ are the vertical and horizontal distances between adjacent elements of the UAV’s antenna array, respectively. Following a similar derivation, the channel gains of other aerial links (e.g., RIS2 to UAV, RIS1 to RIS2) can be obtained.

In practical dynamic urban environments, acquiring perfect channel state information (CSI) is challenging due to the passive nature of RIS elements, time-varying propagation channels, and the covertness of eavesdroppers [24]. To balance realism and tractability, we adopt a differentiated CSI acquisition strategy based on the above link models: for legitimate links (including both ground and aerial legitimate links, e.g., GU to RIS1/RIS2, RIS1/RIS2 to UAV, direct GU to UAV), the UAV obtains imperfect CSI with bounded estimation errors via periodic pilot feedback and Bayesian estimation algorithms. Specifically, the estimated CSI $\widehat{\mathbf{h}}$ is modeled as $\widehat{\mathbf{h}}=\mathbf{h}+\Delta \mathbf{h}$, where $\mathbf{h}$ is the true channel gain, and $\Delta \mathbf{h}$ is the estimation error with $\parallel \Delta \mathbf{h}\parallel \le ϵ$ ($ϵ$ is a small positive constant denoting the error bound); for eavesdropping links (e.g., GU to eavesdropper, RIS1/RIS2 to eavesdropper), due to the unpredictable mobility and silent behavior of the eavesdropper, only statistical information (e.g., average path loss and Rician fading distribution) is available instead of instantaneous CSI. Based on the above channel models and CSI acquisition strategies, the estimated total channel gain between user k and the UAV (integrating all legitimate paths) in the n-th time slot is

$$\begin{array}{cc}\hfill {\widehat{\mathbf{g}}}_k^{\mathrm{UAV}}\left(n\right)& =\left|{\widehat{\mathbf{h}}}_{k,\mathrm{U}}\left(n\right)+{\left({\widehat{\mathbf{h}}}_{k,\mathrm{R}1}\left(n\right)\right)}^H{\mathsf{\Psi }}^1\left(n\right){\widehat{\mathbf{h}}}_{\mathrm{R}1,\mathrm{R}2}\left(n\right){\mathsf{\Psi }}^2\left(n\right){\widehat{\mathbf{h}}}_{\mathrm{R}1,\mathrm{U}}\left(n\right)\right.\hfill \\ \hfill & +{\left({\widehat{\mathbf{h}}}_{k,\mathrm{R}2}\left(n\right)\right)}^H{\mathsf{\Psi }}^2\left(n\right){\widehat{\mathbf{h}}}_{\mathrm{R}2,\mathrm{R}1}\left(n\right){\mathsf{\Psi }}^1\left(n\right){\widehat{\mathbf{h}}}_{\mathrm{R}2,\mathrm{U}}\left(n\right)+{\left({\widehat{\mathbf{h}}}_{k,\mathrm{R}1}\left(n\right)\right)}^H{\mathsf{\Psi }}^1\left(n\right){\widehat{\mathbf{h}}}_{\mathrm{R}1,\mathrm{U}}\left(n\right)\hfill \\ \hfill & \left.+{\left({\widehat{\mathbf{h}}}_{k,\mathrm{R}2}\left(n\right)\right)}^H{\mathsf{\Psi }}^2\left(n\right){\widehat{\mathbf{h}}}_{\mathrm{R}2,\mathrm{U}}\left(n\right)\right|,\hfill \end{array}$$

(6)

where ${\widehat{\mathbf{h}}}_{·}$ denotes estimated channel gains with bounded errors.

For the eavesdropping link, the statistical average total channel gain (integrating all eavesdropping paths) is

$$\begin{array}{cc}\hfill {\overline{\mathbf{g}}}_k^{\mathrm{E}}\left(n\right)& =\mathbb{E}\left\{\left|{\mathbf{h}}_{k,\mathrm{E}}\left(n\right)+{\left({\mathbf{h}}_{k,\mathrm{R}1}\left(n\right)\right)}^H{\mathsf{\Psi }}^1\left(n\right){\mathbf{h}}_{\mathrm{R}1,\mathrm{R}2}\left(n\right){\mathsf{\Psi }}^2\left(n\right){\mathbf{h}}_{\mathrm{R}1,\mathrm{E}}\left(n\right)\right.\right.\hfill \\ \hfill & +{\left({\mathbf{h}}_{k,\mathrm{R}2}\left(n\right)\right)}^H{\mathsf{\Psi }}^2\left(n\right){\mathbf{h}}_{\mathrm{R}2,\mathrm{R}1}\left(n\right){\mathsf{\Psi }}^1\left(n\right){\mathbf{h}}_{\mathrm{R}2,\mathrm{E}}\left(n\right)+{\left({\mathbf{h}}_{k,\mathrm{R}1}\left(n\right)\right)}^H{\mathsf{\Psi }}^1\left(n\right){\mathbf{h}}_{\mathrm{R}1,\mathrm{E}}\left(n\right)\hfill \\ \hfill & \left.\left.+{\left({\mathbf{h}}_{k,\mathrm{R}2}\left(n\right)\right)}^H{\mathsf{\Psi }}^2\left(n\right){\mathbf{h}}_{\mathrm{R}2,\mathrm{E}}\left(n\right)\right|\right\},\hfill \end{array}$$

(7)

where $\mathbb{E}\{·\}$ denotes the expectation over the statistical distribution of eavesdropping channels.

Here, ${(•)}^H$ denotes the Hermitian transpose, and ${\mathsf{\Psi }}^1\left(n\right)$ and ${\mathsf{\Psi }}^2\left(n\right)$ are the reflection coefficient matrices of RIS1 and RIS2, respectively, given by

$${\mathsf{\Psi }}^1\left(n\right)=\mathrm{diag}\left(e^{j{\psi }_{1,1}^1\left(n\right)},\dots ,e^{j{\psi }_{m_{\mathrm{Rx}},m_{\mathrm{Ry}}}^1\left(n\right)},\dots ,e^{j{\psi }_{M_{\mathrm{Rx}},M_{\mathrm{Ry}}}^1\left(n\right)}\right),$$

(8)

$${\mathsf{\Psi }}^2\left(n\right)=\mathrm{diag}\left(e^{j{\psi }_{1,1}^2\left(n\right)},\dots ,e^{j{\psi }_{m_{\mathrm{Rx}},m_{\mathrm{Ry}}}^2\left(n\right)},\dots ,e^{j{\psi }_{M_{\mathrm{Rx}},M_{\mathrm{Ry}}}^2\left(n\right)}\right).$$

(9)

Each GU transmits data to the UAV over its own channel. According to Shannon’s formula, the transmission rate from GU k to the UAV (using estimated CSI) in the n-th time slot is

$$R_k^{\mathrm{UAV}}\left(n\right)=W{log}_2\left(1+{\displaystyle \frac{P_k\left(n\right){\left|{\mathbf{w}}_k^H{\widehat{\mathbf{g}}}_k^{\mathrm{UAV}}\left(n\right)\right|}^2}{N_0·{\mathbf{w}}_k^H{\mathbf{w}}_k}}\right),$$

(10)

where W is the channel bandwidth, ${\mathbf{w}}_k$ is the UAV’s receive beamforming vector, $P_k\left(n\right)$ is GU k’s transmit power, and $N_0$ is the noise power spectral density.

The average transmission rate from GU k to the eavesdropper in the n-th time slot is

$$R_k^{\mathrm{E}}\left(n\right)=W{log}_2\left(1+{\displaystyle \frac{P_k\left(n\right)·{\overline{\mathbf{g}}}_k^{\mathrm{E}}\left(n\right)}{N_0}}\right),$$

(11)

Due to the presence of the eavesdropper, the secure offloading rate from GU k to the UAV is defined as

$$R_k^{\sec }\left(n\right)=max\left\{R_k^{\mathrm{UAV}}\left(n\right)-R_k^{\mathrm{E}}\left(n\right),0\right\},$$

(12)

and the secure transmission task amount of GU k is

$$D_k^{\sec }\left(n\right)=R_k^{\sec }\left(n\right)\tau .$$

(13)

2.3. Task Queue Model

In the proposed system architecture, ground users generate massive volumes of task data that exceed the real-time processing capabilities of individual computing units. To address this challenge, we implement a distributed buffering mechanism where each user device and the UAV-mounted edge server maintain dedicated task queues. During each time slot, newly generated tasks are first stored in local queues, after which a dynamic task partitioning strategy is applied: a portion of tasks is processed locally on the user device, while the remaining portion is offloaded to the UAV’s queue for remote processing. We assume that user k generates a task in each time slot with data size $A_k\left(n\right)$, following a stochastic process with mean arrival rate $\mathbb{E}\left\{A_k\left(n\right)\right\}={\lambda }_k$, where ${\lambda }_k$ represents the average number of tasks generated per slot. The computational complexity of processing 1-bit data is characterized by $\phi$, defined as the number of CPU cycles required. Let $f_k^l\left(n\right)$ denote the CPU frequency allocated to local processing on user k’s device, and $f_k^u\left(n\right)$ represent the CPU frequency assigned by the UAV to process tasks offloaded from user k. These frequencies are subject to the following operational constraints:

$$\mathrm{C}1:f_k^l\left(n\right)\le F^l,k\in \mathcal{K},n\in \mathcal{N},$$

(14)

$$\mathrm{C}2:\sum _{k\in \mathcal{K}}{f}_k^u\left(n\right)\le F^u,k\in \mathcal{K},n\in \mathcal{N},$$

(15)

where $F^l$ is the maximum CPU frequency of user devices, and $F^u$ denotes the UAV’s maximum processing frequency. Based on these frequencies, the amount of data processed locally by user k and remotely by the UAV for user k within a time slot $\tau$ are, respectively,

$$D_k^l\left(n\right)={\displaystyle \frac{f_k^l\left(n\right)·\tau }{\phi }},$$

(16)

$$D_k^u\left(n\right)={\displaystyle \frac{f_k^u\left(n\right)·\tau }{\phi }}.$$

(17)

Let ${\mathcal{Q}}_k\left(n\right)$ represent the task backlog in user k’s local queue at time slot n and $\mathcal{L}\left(n\right)$ denote the total task backlog in the UAV’s queue. Both queues operate on a first-come, first-served (FCFS) basis, with tasks arriving in slot n scheduled for processing starting from slot $n+1$. The evolution of these queues can be described by

$$Q_k(n+1)={\left[Q_k\left(n\right)-D_k^l\left(n\right)-D_k^{sec}\left(n\right)\right]}^{+}+A_k\left(n\right),$$

(18)

$$L(n+1)={\left[L\left(n\right)-\sum _{k\in \mathcal{K}}{D}_k^u\left(n\right)\right]}^{+}+\sum _{k\in \mathcal{K}}{D}_k\left(n\right),$$

(19)

where ${\mathsf{\Omega }}_k\left(n\right)$ is the amount of data offloaded from user k to the UAV in slot n, and the max function ensures non-negative queue lengths. For the system to operate stably, the time-averaged expected queue lengths must satisfy

$$\mathrm{C}3:\underset{N\to \infty }{lim}{\displaystyle \frac{1}{N}}\sum _{n=0}^{N-1}\mathbb{E}\left\{Q_k\left(n\right)\right\}<\infty ,$$

(20)

$$\mathrm{C}4:\underset{N\to \infty }{lim}{\displaystyle \frac{1}{N}}\sum _{n=0}^{N-1}\mathbb{E}\left\{L\left(n\right)\right\}<\infty .$$

(21)

These stability constraints are crucial for maintaining system performance under stochastic conditions, including variable task arrivals, channel fluctuations, and dynamic resource allocation. By ensuring bounded time-averaged queue lengths, we prevent system congestion caused by infinite backlogs, guarantee acceptable average processing delays, and ultimately maintain reliable service quality for all users. This stability forms the foundation for efficient task execution in the edge computing framework, enabling timely processing of user tasks and enhancing overall system usability in practical deployments.

2.4. Energy Consumption Model

The total energy consumed in the designed system is composed of three main parts: computing energy, offloading energy, and UAV flight energy. As passive RISs are used here, their energy consumption is so minimal that it can be ignored in the analysis.

2.4.1. Computing Energy Consumption

Computing energy consumption includes two aspects: the energy consumed by GUs for local task processing and the energy consumed by the UAV for processing offloaded tasks. They are, respectively, expressed as

$$e_k^l\left(n\right)=\kappa ·{\left[f_k^l\left(n\right)\right]}^3·\tau ,$$

(22)

$$e_k^u\left(n\right)=\kappa ·{\left[f_k^u\left(n\right)\right]}^3·\tau ,$$

(23)

where $\kappa$ is the effective capacitance coefficient of the CPU. The cubic relationship between energy consumption and frequency is consistent with the classic energy consumption characteristics of complementary metal–oxide–semiconductor (CMOS) circuits, where power consumption increases nonlinearly with the operating frequency of the processor.

2.4.2. Offloading Energy Consumption

In the n-th time slot, GU k will offload part of its tasks. Each GU is equipped with a communication module that can adjust the transmission power, and the energy consumed for task offloading transmission is

$$e_k^{\mathrm{off}}\left(n\right)=P_k\left(n\right)·\tau ,$$

(24)

where $P_k\left(n\right)$ is the transmission power used by GU k when offloading tasks in the n-th time slot.

2.4.3. Flight Energy Consumption

The flight energy consumption of the UAV is generated when it moves from the current position to the next position, including two parts: the energy for maintaining altitude and the propulsion energy. Considering that the duration $\tau$ of each time slot is short enough, for the convenience of calculation, it is assumed that the UAV flies at a constant speed in a straight line between two consecutive positions. In addition, the UAV maintains a fixed flight altitude, so the energy consumption for maintaining altitude is a fixed value, and only the propulsion energy consumption needs to be optimized. Based on the analytical model of rotor UAVs, the propulsion energy consumption in the n-th time slot is [24]

$$e_f\left(n\right)={\displaystyle \frac{M_g·\tau ·{\left|v\left(n\right)\right|}_2^2}{2}},$$

(25)

where $M_g$ is the mass of the UAV, and ${\parallel v\left(n\right)\parallel }_2$ is the flight speed of the UAV in the n-th time slot. The total energy consumption of the system in the n-th time slot is the sum of all the above energy consumption components:

$$e_{\mathrm{tot}}\left(n\right)=\sum _{k\in \mathcal{K}}\left\{e_k^l\left(n\right)+e_k^u\left(n\right)+e_k^{\mathrm{off}}\left(n\right)\right\}+\epsilon ·e_f\left(n\right),$$

(26)

where $\epsilon$ is the energy conversion coefficient of the propulsion system.

2.5. Problem Formulation

For the system to sustain long-term operation and deliver high-quality services to users, a comprehensive optimization of the system’s secure transmission rate and energy consumption is essential. However, an exclusive focus on secure transmission rate and system energy consumption might result in excessive queue backlogs, preventing timely processing of user tasks and thus failing to meet user requirements. Therefore, taking into account the stability of task queues, we perform a joint optimization of resource allocation, UAV trajectory, and RIS phase shifts. The objective is to maximize the network’s security EE, defined as the ratio of the long-term total secure transmission rate achieved by all GUs to the total energy consumption:

$$\eta \left(n\right)={\displaystyle \frac{{lim}_{\mathrm{N}\to \infty }\frac{1}{\mathrm{N}}\mathbb{E}\left[{\sum }_{n\in \mathcal{N}}\left\{R_{\mathrm{tot}}\left(n\right)\tau \right\}\right]}{{lim}_{\mathrm{N}\to \infty }\frac{1}{\mathrm{N}}\mathbb{E}\left[{\sum }_{n\in \mathcal{N}}\left\{e_{\mathrm{tot}}\left(n\right)\right\}\right]}}={\displaystyle \frac{{\overline{R}}_{\mathrm{tot}}\left(n\right)\tau }{{\overline{e}}_{\mathrm{tot}}\left(n\right)}},$$

(27)

where $R_{\mathrm{tot}}\left(n\right)={\sum }_{k\in \mathcal{K}}{R}_k\left(n\right)$. The aim of this research is to maximize the long-term average EE of all GUs under resource constraints while ensuring the stability of average queue lengths. Thus, the problem can be formulated as

$$\begin{array}{ccc}\mathrm{P}1:\hfill & \hfill & \underset{\Xi \left(n\right)}{max}\mathsf{\eta }\left(n\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & C1,C2,C3,C4,\hfill \end{array}$$

(28a)

$$\begin{array}{ccc}\hfill & C5:\hfill & 0\le P_k\left(n\right)\le P_{max},\hfill \end{array}$$

(28b)

$$\begin{array}{ccc}\hfill & C6:\hfill & 0\le {\psi }_{m_{Rx},m_{Ry}}^1\left(n\right)\le 2\pi ,\hfill \end{array}$$

(28c)

$$\begin{array}{ccc}\hfill & C7:\hfill & 0\le {\psi }_{m_{Rx},m_{Ry}}^2\left(n\right)\le 2\pi ,\hfill \end{array}$$

(28d)

$$\begin{array}{ccc}\hfill & C8:\hfill & 0\le ∥v\left(n\right)∥\le v_{max},\hfill \end{array}$$

(28e)

$$\begin{array}{ccc}\hfill & C9:\hfill & {\mathbf{w}}_k^H\left(n\right){\mathbf{w}}_k\left(n\right)=1.\hfill \end{array}$$

(28f)

The optimization problem P1 is designed to maximize the security EE $\eta \left(n\right)$. The set of optimization variables $\mathsf{\Xi }\left(n\right)$ includes the phase shift matrices of the two RISs, the beamforming vector of user k at time slot n, the UAV’s flight speed vector, the transmit power of user k, and the local computing frequency as well as the offloading computing frequency for task k. This problem is subject to multiple constraints: $C1$ and $C2$ pertain to computing resource allocation; $C3$ and $C4$ ensure the stability of user and UAV task queues; $C5$ restricts the transmit power of user k to the range from 0 to the maximum transmit power $P_{\max }$; $C6$ and $C7$ limit the phase angles of the two RIS units to the range of 0 to $2\pi$; $C8$ constrains the norm of the UAV’s speed vector to be between 0 and the maximum speed $v_{\max }$; and $C9$ enforces the normalization of the beamforming vector of user k.

3. Problem Solution

The previous section formulated the secure EE maximization problem P1, which involves multi-dimensional variable coupling and stochastic dynamics. This section presents a solution framework: first, using Lyapunov optimization to transform it into per-slot subproblems, then modeling it as a model-free Markov decision process (MDP) solved by PPO, and finally analyzing algorithm complexity.

3.1. Lyapunov Optimization

To address the complexity of problem P1, which involves coupled variables and stochastic dynamics leading to NP-hard complexity, we employ Lyapunov optimization techniques. This approach excels at transforming long-term stochastic optimization problems into tractable per-slot decisions while maintaining queue stability. Building upon foundational methodologies in [25,26], we develop an online optimization framework that integrates queue state information with system performance objectives. We begin by defining a quadratic Lyapunov function to characterize the system’s queue backlog state:

$$U\left(n\right)=\sum _{k\in \mathcal{K}}{\displaystyle \frac{Q_k{\left(n\right)}^2}{2}}+{\displaystyle \frac{L{\left(n\right)}^2}{2}},$$

(29)

where $Q_k\left(n\right)$ represents user k’s local task queue and $L\left(n\right)$ denotes the UAV’s task queue at timeslot n. This function quantifies the “energy” of the queue system, with larger values indicating greater backlog congestion. The conditional Lyapunov drift, measuring the expected change in queue energy between consecutive timeslots, is defined as

$$\Delta U\left(n\right)=\mathbb{E}\left\{U(n+1)-U\left(n\right)\mid \mathsf{\Theta }\left(n\right)\right\},$$

(30)

where the state vector $\mathsf{\Theta }\left(n\right)$ captures all current queue backlogs:

$$\mathsf{\Theta }\left(n\right)\triangleq \left\{Q_1\left(n\right),Q_2\left(n\right),\dots ,Q_K\left(n\right),L\left(n\right)\right\}.$$

(31)

To balance queue stability with the primary objective of maximizing security EE, we introduce a drift-plus-penalty function.

$${\Delta }_{V}U\left(n\right)=\left\{\Delta U\left(n\right)-V·\mathbb{E}\left\{\eta \left(n\right)\mid \mathsf{\Theta }\left(n\right)\right\}\right\},$$

(32)

where $V\ge 0$ is a control parameter regulating the trade-off between system performance ($\eta \left(n\right)$) and queue stability. Minimizing this function ensures both bounded queues and near-optimal efficiency. To derive an upper bound for ${\Delta }_{V}U\left(n\right)$, we use queue evolution properties and apply the inequality ${\{{[a-b]}^{+}+c\}}^2\le a^2+b^2+c^2+2a(c-b)$ to the user queue update equation, yielding

$$\begin{array}{cc}\hfill Q_k{(n+1)}^2-Q_k{\left(n\right)}^2& \le {\left\{{\left[Q_k\left(n\right)-D_k^l\left(n\right)-D_k^{sec}\left(n\right)\right]}^{+}+A_k\left(n\right)\right\}}^2-Q_k{\left(n\right)}^2\hfill \\ \hfill & \le B_k^a\left(n\right)-2Q_k\left(n\right)\left(D_k^l\left(n\right)+D_k^{sec}\left(n\right)\right),\hfill \end{array}$$

(33)

where $B_k^a\left(n\right)=Q_k{\left(n\right)}^2+A_k{\left(n\right)}^2+2Q_k\left(n\right)A_k\left(n\right)$ is a constant independent of optimization variables. For the UAV queue, using the inequality ${\{{[x+\sum y_i]}^{+}+\sum z_j\}}^2-x^2\le \sum {(x+y_i)}^2+\sum {(x+z_j)}^2-(Y+Z)x^2+{[\sum y_i^{\max }+\sum z_j^{\max }]}^2$ produces

$$\begin{array}{cc}\hfill L{(n+1)}^2-L{\left(n\right)}^2& \le {\left\{{\left[L\left(n\right)-\sum _{k\in \mathcal{K}}{D}_k^u\left(n\right)\right]}^{+}+\sum _{k\in \mathcal{K}}{D}_k^{sec}\left(n\right)\right\}}^2-L{\left(n\right)}^2\hfill \\ \hfill & \le B^b\left(n\right)+\sum _{k\in \mathcal{K}}\left\{D_k^u{\left(n\right)}^2+D_k^{sec}{\left(n\right)}^2+2L\left(n\right)\left(D_k^{sec}\left(n\right)-D_k^u\left(n\right)\right)\right\},\hfill \end{array}$$

(34)

with $B^b\left(n\right)={\left[{\sum }_{k\in \mathcal{K}}{D}_k^{l-umax}\right]}^2$ as another constant term. Combining these results and dividing by 2, we obtain the drift-plus-penalty bound.

$$\begin{array}{cc}\hfill {\Delta }_{V}U\left(n\right)& \le \mathbb{E}\left\{{\displaystyle \frac{B^b\left(n\right)}{2}}+\sum _{k\in \mathcal{K}}\left({\displaystyle \frac{B_k^a\left(n\right)}{2}}+C_k\left(n\right)\right)-V\eta \left(n\right)\mid \mathsf{\Theta }\left(n\right)\right\},\hfill \end{array}$$

(35)

where $C_k\left(n\right)$ is defined as

$$C_k\left(n\right)=D_k^u{\left(n\right)}^2+D_k^{sec}{\left(n\right)}^2+2L\left(n\right)\left(D_k^{sec}\left(n\right)-D_k^u\left(n\right)\right)-2Q_k\left(n\right)\left(D_k^l\left(n\right)+D_k^{sec}\left(n\right)\right).$$

(36)

Since $B^b\left(n\right)$ and $B_k^a\left(n\right)$ are constants, minimizing ${\Delta }_{V}U\left(n\right)$ reduces to solving the following per-slot optimization problem:

$$\begin{array}{cc}\hfill \mathrm{P}2:& \underset{\mathsf{\Xi }\left(n\right)}{min}\sum _{k\in \mathcal{K}}{C}_k\left(n\right)-V\eta \left(n\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\mathrm{C}1,\mathrm{C}2,\mathrm{C}5,\mathrm{C}6,\mathrm{C}7,\mathrm{C}8,\mathrm{C}9,\hfill \end{array}$$

(37)

3.2. MDP Module

Given that the server onboard the UAV boasts stronger computing power and can run more service programs, the UAV is adopted as the agent in this scenario; since the onboard server has superior computing capabilities and can operate more service programs, the UAV is also employed as the agent in this section. The UAV only needs to acquire information from the current environmental state to make decisions, while the transition probability of such continuous states remains unknown—thus, the entire system can be modeled as a model-free MDP with unknown transition probabilities. The PPO algorithm is chosen to solve the UAV edge computing system in this paper due to its significant advantages: it excels in dynamic decision-making, can quickly determine the model’s optimization direction, and is well-suited to handle the unknown transition probability characteristics of model-free MDPs. By analyzing the MDP quadruple, the interaction process between the agent and the environment can be modeled as follows: At a certain time step t, the agent acquires the environmental state $s\left(t\right)$, executes an action $a\left(t\right)$ according to its own policy, the environment transitions to the subsequent state $s(t+1)$, and then the agent receives a reward $r\left(t\right)$. The three basic elements of MDP (state, action, and reward) are defined as follows:

3.2.1. State

The UAV can observe its own position and the positions of RISs and request users to obtain their positions and task information. Therefore, the state of the UAV at time t can be expressed as

$$s\left(t\right)=\left\{{\mathbf{h}}_k^U\left(n\right),{\mathbf{h}}_k^E\left(n\right),R_k^{l-u}\left(n\right),{\mathbf{S}}_u\left(n\right),A_k\left(n\right),Q_k\left(n\right),L\left(n\right)\right\}.$$

(38)

3.2.2. Action

The UAV needs to comprehensively consider the user situation, send offloading decision information to users, continuously adjust its position, and optimize RIS phase shifts, transmission power, and receiving beamforming. The action of the UAV can be expressed as

$$a\left(t\right)=\left\{{\mathsf{\Psi }}^1,{\mathsf{\Psi }}^2,{\mathbf{w}}_k\left(n\right),v\left(n\right),P_k\left(n\right),f_k^l\left(n\right),f_k^u\left(n\right)\right\}.$$

(39)

3.2.3. Reward

After the UAV executes an action, a reward needs to be given to the agent based on environmental feedback information. The reward function includes the objective value and various penalties, which can be expressed as

$$r\left(t\right)=\varpi \left(\sum _{k\in \mathcal{K}}{C}_k\left(n\right)-V\eta \left(n\right)\right)+{\mu }_f{P}_f+{\mu }_O{P}_O,$$

(40)

where $P_f$ denotes the penalty when the computing frequency allocated by the UAV to users exceeds the maximum frequency $f_{max}^u\left(n\right)$; $P_O$ denotes the penalty when the UAV flies out of the service area; and $\varpi$, ${\mu }_f$, and ${\mu }_O$ are weight coefficients used to balance the orders of magnitude. The penalty terms can be calculated as follows:

$$P_f=max\left(\sum _{k\in \mathcal{K}}{f}_k^u\left(n\right)-f_{max}^u\left(n\right),0\right)/f_{max}^u\left(n\right),$$

(41)

$$P_O=\left|q\left(n\right)-\mathrm{clip}({\mathbf{S}}_u\left(n\right),0,W)\right|/v_{max},$$

(42)

where $\mathrm{clip}(x,a,b)$ represents the clipping function, which restricts the value of x to the range $(a,b)$. If the penalty is excessively large, the reward clipping method can be adopted to stabilize the learning process.

3.3. PPO Algorithm Application

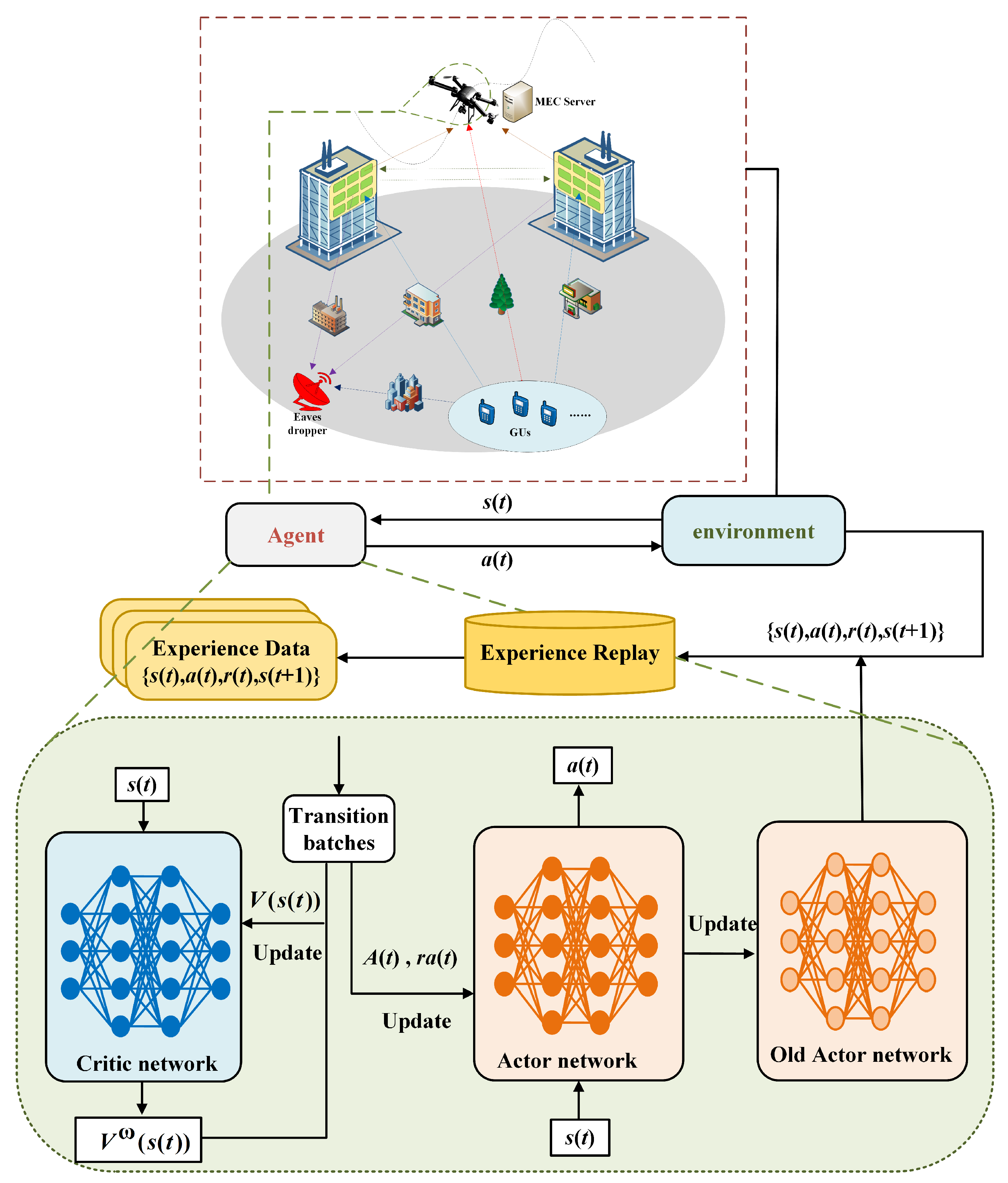
PPO is based on the trust region policy optimization algorithm, which introduces a clipping factor into the objective function to stabilize the magnitude of action updates within a proximal range; as an on-policy algorithm, it requires less cache space during training and features faster training speed, thus being more suitable for small edge nodes such as UAVs, with its training framework illustrated in Figure 2. During the training process, the agent continuously interacts with the environment to acquire experiential information; after an episode concludes, it retrieves a new batch of collected experiential information from the experience buffer to update its policy, where for each update, the Actor network and Critic network utilize the policy loss function and the state-value loss function as their respective objectives. The loss function of the Actor network is as follows:

$$L^{\mathrm{actor}}\left(\theta \right)=\mathbb{E}\pi \theta \left[min\left[\mathrm{ra}\left(t\right)\widehat{A}\left(t\right),\mathrm{clip}\left(\mathrm{ra}\left(t\right),1-ϵ,1+ϵ\right)\widehat{A}\left(t\right)\right]+\psi S\left(s\left(t\right)\right)\right],$$

(43)

where $\theta$ denotes the parameters of the Actor network; $\mathrm{ra}\left(t\right)={\displaystyle \frac{{\pi }_{\theta }\left(a\left(t\right)\left|s\right(t)\right)}{{\pi }_{\theta }^{\prime }\left(a\left(t\right)\left|s\right(t)\right)}}$ represents the update ratio of the action distribution between the new and old policies; $ϵ$ is the clipping factor that limits the update ratio; $\psi S\left(s\right(t\left)\right)$ denotes the policy entropy at state $s\left(t\right)$; and $\widehat{A}\left(t\right)$ is the advantage function estimate, which typically adopts the Generalized Advantage Estimation (GAE) method, with its calculation method given by

$$A\left(t\right)=\sum _{l=0}^{\infty }{\left(\gamma \lambda \right)}^l\left(r\left(t\right)+\gamma V\left(s\left(t+1\right)\right)-V\left(s\left(t\right)\right)\right),$$

(44)

where $V_i\left(s\left(t\right)\right)={\sum }_{l=0}^{\infty }{\gamma }^l{R}_i\left(t\right)$ represents the target state value. The loss function corresponding to the state value $V^{\omega }\left(s\left(t\right)\right)$ fitted by the Critic network $\omega$ is

$$L^{critic}\left(\omega \right)={\displaystyle \frac{1}{2}}{\left[V^{\omega }\left(s\left(t\right)\right)-V\left(s\left(t\right)\right)\right]}^2.$$

(45)

Based on the above analysis, this section proposes a weighted energy consumption optimization scheme based on PPO, whose training process is described in Algorithm 1.

Algorithm 1 Training Process of Weighted Energy Consumption Optimization Scheme Based on PPO

Require:  Maximum number of episodes $E{p}_{\max }$, episode length $epl$, number of sampling steps before update $SC$, number of PPO updates $PE$, discount factor $\gamma$, PPO clipping factor $ϵ$, GAE parameter $\lambda$ Ensure:  Trained Actor network and Critic network  1: Initialize parameters of various neural network models.  2: for Episode = 1 to $E{p}_{\max }$ do  3:     Initialize the environment and obtain the initial state.  4:     for $t=1$ to N do  5:         The UAV agent obtains the state $s\left(t\right)$ from the environment.  6:         The UAV agent executes the action $a\left(t\right)$.  7:         The UAV agent evaluates the reward $r\left(t\right)$.  8:         Store the experience $\left\{s\right(t),a(t),r(t),s(t+1\left)\right\}$ in the experience buffer.  9:     end for 10:     if Episode × $epl=SC$ then 11:         for epoch = 1 to $PE$ do 12:            Update the Actor network parameter $\theta$ according to Equation (43). 13:            Update the Critic network parameter $\omega$ according to Equation (45). 14:         end for 15:     end if 16: end for 17: Return $\theta$, $\omega$

3.4. Analysis of Algorithm Complexity

For a fully connected neural network with J layers, the basic computational complexity of a single network is $O\left({\sum }_{j=2}^{J-1}{V}_{j-1}{V}_j+V_j{V}_{j+1}\right)$ (where $V_j$ represents the number of neurons in the j-th layer). The Lyapunov method achieves a significant reduction in complexity by transforming the original high-dimensional non-convex NP-hard optimization problem into a deterministic subproblem per time slot: The original problem requires traversing a solution space that grows exponentially with the variable dimensions, with a complexity of $O\left({(M_1+M_2+4K+2)}^N\right)$. After introducing Lyapunov optimization, by constructing a drift-penalty function to decouple the temporal coupling between variables and decomposing the cross-slot global optimization into slot-wise local decisions, the problem complexity is reduced to $O(M_1+M_2+4K+2)$, achieving an optimization from exponential to linear order.

The training complexity of the PPO algorithm is $O\left({\displaystyle \frac{2{ϵ}_{max}·epl·PE}{SC·\Gamma }}{\sum }_{j=2}^{J-1}(V_{j-1}{V}_j+V_j{V}_{j+1})\right)$ (where $\mathsf{\Gamma }$ is the number of sample reuse rounds), and the single-step decision complexity is $O\left({\sum }_{j=2}^{J-1}{V}_{j-1}{V}_j+V_j{V}_{j+1}\right)$. The DDPG algorithm, which maintains four networks (Actor, Critic, and their target networks) and requires noise generation, has a complexity of $O\left(4\varpi ·\zeta ·{\sum }_{j=2}^{J-1}(V_{j-1}{V}_j+V_j{V}_{j+1})\right)$ (where $\varpi$ is the soft update coefficient and $\zeta$ is the noise calculation overhead). The DQN algorithm, constrained by the maintenance of the experience replay buffer, has a complexity of $O\left({\sum }_{j=2}^{J-1}(V_{j-1}{V}_j+V_j{V}_{j+1})+\Pi log\Pi \right)$ (where $\Pi$ is the replay buffer capacity). In comparison, PPO reduces the environmental interaction cost by a factor of $\Gamma$ through $\Gamma$-fold sample reuse and eliminates the additional overhead of target network updates ($\varpi =0$) and replay buffer sorting (the $\Pi log\Pi$ term), demonstrating significant complexity advantages in continuous action spaces.

4. Result Analysis

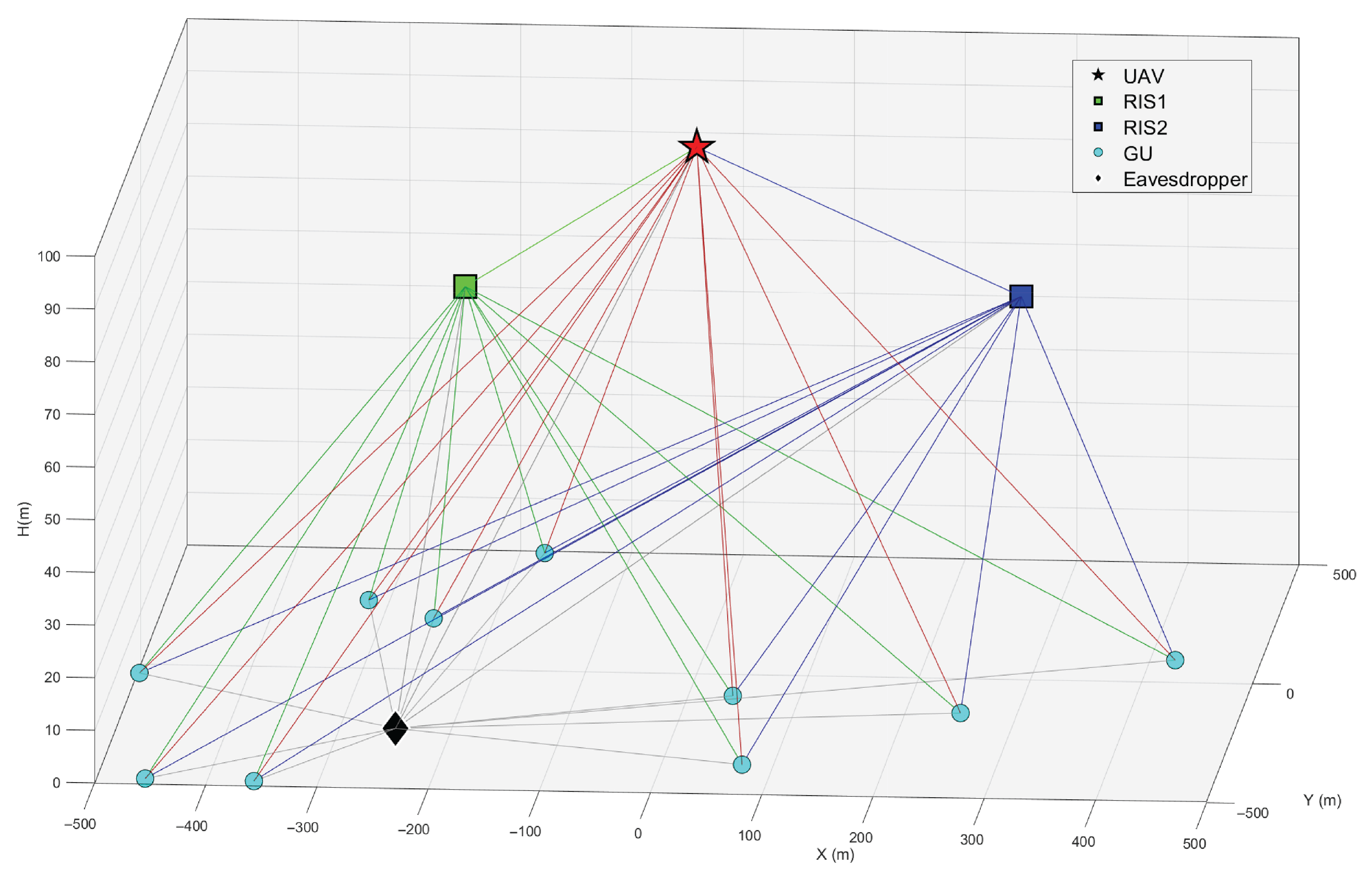
We evaluate the proposed algorithm from the perspectives of average queue backlog and average total secure energy efficiency through extensive numerical experiments. A schematic diagram of the simulated 3D scenario is illustrated in Figure 3. The scenario involves a UAV, two collaborative RISs (RIS1 and RIS2), 10 GUs randomly distributed within a 3D area of 1000 × 1000 m², and a single-antenna eavesdropper located at ${\mathbf{S}}_e=[-250,-250,0]$. The set of all GUs is denoted as $\mathcal{K}=\{1,2,\dots ,10\}$. Specifically, RIS1 is deployed at coordinates ${\mathbf{S}}_{R1}=(-250,500,50)$ and RIS2 at ${\mathbf{S}}_{R2}=(250,500,50)$, with a consistent deployment height of $H_{R1}=H_{R2}=50$ m for both RISs. The UAV is equipped with a uniform rectangular array (URA) antenna, having an initial position of ${\mathbf{S}}_u\left(1\right)=(-500,-500,100)$ and a maximum speed of $v_{max}=15$ m/s. Both RIS1 and RIS2 adopt a 20 × 20 array structure, consisting of $M_1=20\times 20$ and $M_2=20\times 20$ passive reflecting elements, respectively. The entire mission duration T is discretized into $N=300$ equal time slots, each with a duration of $\tau =1$ s. Key simulation parameters are summarized in

Table 1. Numerical simulation network parameters.

Notation	Definition	Value
W	Communication bandwidth	$2\mathrm{MHz}$
$P_{max}$	Maximum transmit power of GU	$500\mathrm{mW}$
$N_0$	Noise power density	$1\times {10}^{-9}\mathrm{dBm}/\mathrm{Hz}$
$\phi$	Process density	${10}^3\mathrm{cycles}/\mathrm{bit}$
$A_k$	Average task arrival rate	$1\mathrm{M}\mathrm{bit}/\mathrm{Hz}$
$M_g$	Weight of UAV	$9.8\mathrm{kg}$
${\beta }_0$	Unit path loss	$1\times {10}^{-7}$
$f_r$	Communication carrier frequency	$1\mathrm{GHz}$
$\kappa$	CPU capacitance coefficient	${10}^{-27}$
$F^l$	Maximum CPU frequency of user	$1\mathrm{GHz}$
$F^U$	Maximum CPU frequency of UAV	$10\mathrm{GHz}$
$\Delta Rx,\Delta Ry$	Distance between array antennas	$1\mathrm{m},1\mathrm{m}$
V	Trade-off control coefficient	$1\times {10}^7$
$\epsilon$	UAV energy attenuation factor	$3\times {10}^{-3}$
$a^{U-R1},a^{U-R2},a^{R1-G}$	Path loss exponents	$1,1,3.6$
$k^{R1-G},k^{R2-G}$	Rician factor	$2\mathrm{dB},2\mathrm{dB}$
-	Actor learning rate	0.0001
-	Critic learning rate	0.0001
$E_{p_{max}}$	Maximum number of episodes	700
SC	Sampling steps before PPO update	2000
PE	Number of PPO updates	16
$\lambda$	GAE parameter	0.95
${\gamma }_{MU}$	Discount factor	0.9

.

Figure 4 shows a comparison of convergence curves of different DRL algorithms in the scenario with 10 users (K = 10), where the vertical axis represents the average cumulative reward per episode and the horizontal axis represents the number of training steps. The experimental results indicate that as training progresses, the average cumulative reward per episode of all four algorithms shows an upward trend, demonstrating that DRL methods can optimize strategies through continuous learning, enabling the system performance to gradually improve and stabilize. Specifically, the proposed PPO algorithm exhibits the optimal performance: its convergence speed is significantly faster than that of the Advantage Actor–Critic (A2C) and Deep Deterministic Policy Gradient (DDPG) algorithms, showing a rapid upward trend in the early stage of training, entering a stable phase in advance, and ultimately achieving the highest cumulative reward value. In contrast, the DDPG algorithm has the most significant reward fluctuations and a slower convergence speed, mainly due to its deterministic action output mechanism, which leads to insufficient stability in the policy gradient update direction and limits its exploration ability in continuous action spaces. The Deep Q-Network (DQN) algorithm, which is natively suitable for discrete action spaces, performs the worst in the continuous resource allocation optimization problem involved in this experiment; it not only converges slowly but also achieves the lowest cumulative reward value after stabilization, further verifying its limitations in continuous action space scenarios. These experimental results fully prove that the PPO algorithm, relying on its clipping mechanism for policy updates and efficient sample utilization, exhibits better convergence stability and strategy optimization capabilities than the other three DRL algorithms in complex continuous action space optimization problems, providing a reliable solution for the model proposed in this paper.

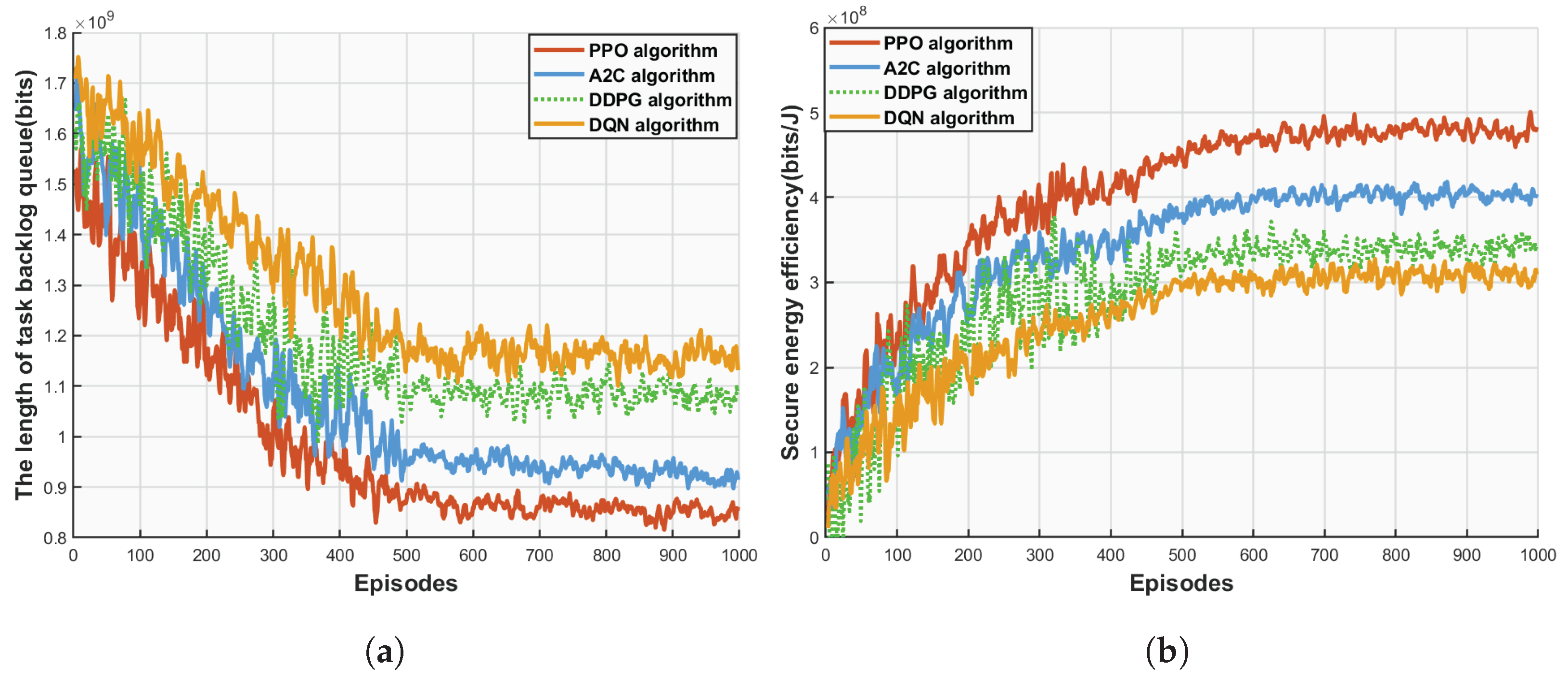
Figure 5 clearly demonstrates the significant superiority of the PPO algorithm in the double-RIS cooperative UAV-MEC system. In Figure 5a, as the number of training episodes increases from 0 to 1000, the task queue lengths of the four algorithms (PPO, A2C, DDPG, and DQN) all show a decreasing trend. Among them, the PPO algorithm exhibits the most prominent downward trend: it decreases rapidly in the initial stage, maintains the lowest queue level throughout the process, and finally stabilizes at a low level close to 8.5 × 10⁸ bits, with extremely small fluctuation amplitude. In contrast, although the A2C algorithm also shows a decreasing trend, its queue length at stabilization is significantly higher than that of PPO. The DDPG and DQN algorithms decrease more slowly, especially DQN, which not only has the highest initial queue length (close to 1.15 × 10⁹ bits) but also remains at a relatively high level when stabilized, showing a significant gap compared with PPO. In Figure 5b, the secure energy efficiency of the four algorithms all increases with the number of training episodes, and the PPO algorithm also performs the best: it rises rapidly from the initial stage, remains ahead of other algorithms, and finally stabilizes at a high level close to 4.9 × 10⁸ bits/J. Although the growth trend of the A2C algorithm is similar to that of PPO, its energy efficiency at stabilization is significantly lower than that of PPO. The growth of DDPG and DQN is relatively slow, especially DQN, which has the lowest energy efficiency throughout the process, with a huge gap compared with PPO. Overall, both in terms of the optimization effect of task queue length and the improvement amplitude of secure EE, the PPO algorithm far surpasses A2C, DDPG, and DQN, fully proving that it can more efficiently balance task processing and resource allocation in this scenario, providing an efficient and reliable solution for the model, and highlighting its unique advantages in solving complex continuous action space optimization problems.

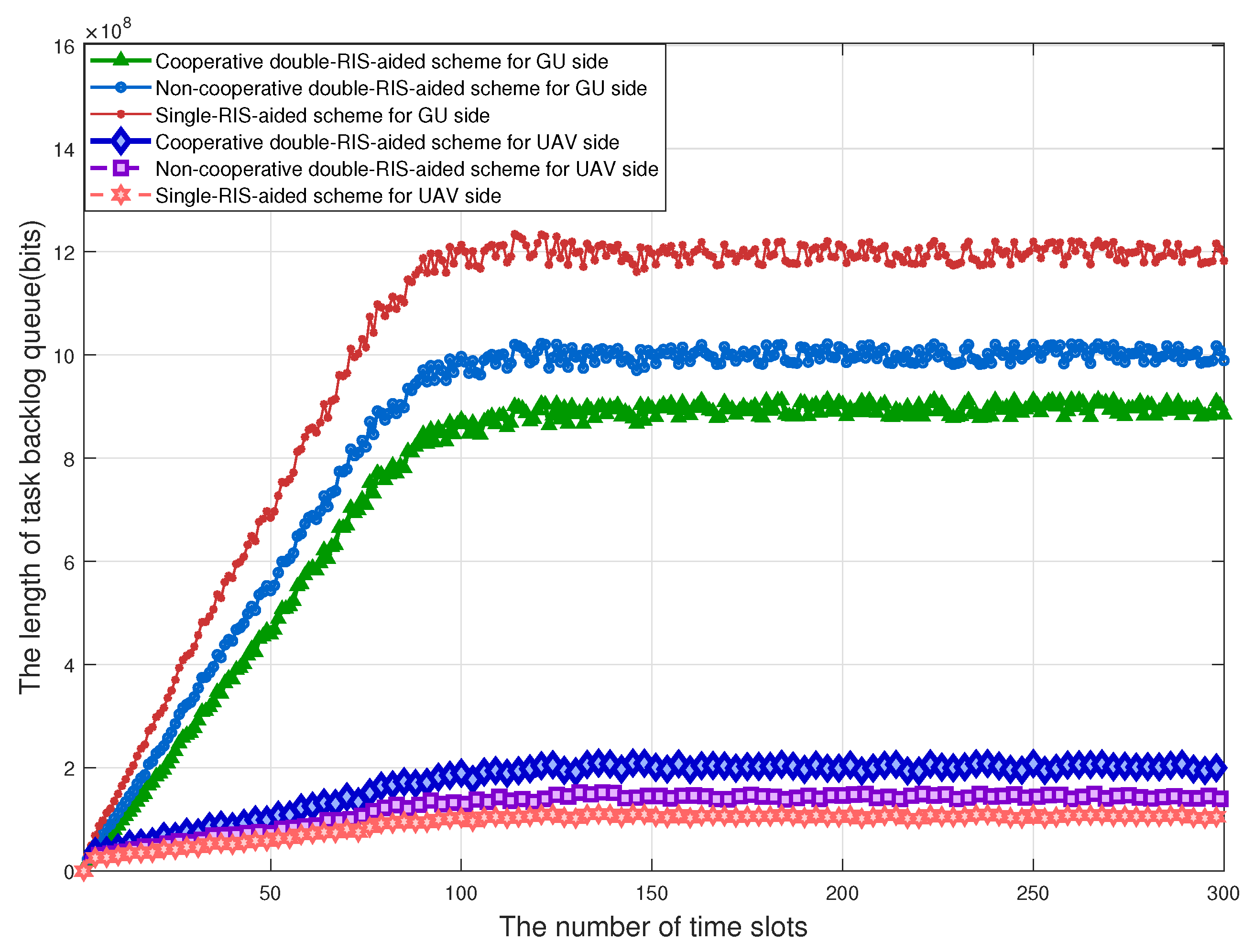
Figure 6 compares the queue stability performance of the UAV-MEC system under different RIS assistance schemes, where the vertical axis represents the queue length and the horizontal axis represents the number of time slots. The experimental results show that the user queue length is significantly longer than the UAV queue length, mainly because the UAV has stronger computing processing capabilities and higher task processing efficiency, resulting in a smaller queue backlog. In terms of the time evolution trend, as the number of time slots increases, the user queues of all schemes exhibit a characteristic of “rapid growth–slow growth–stabilization”, while the UAV queues show a trend of “gradual growth–stabilization”. In the initial stage, limited by channel conditions, the efficiency of user task offloading is low, leading to rapid accumulation of queues; as the system operation enters a stable period, the amount of task generation reaches a dynamic balance with the amount of local and edge processing, and the queue length maintains stable fluctuations. The performance differences between different RIS assistance schemes are particularly significant: the double-RIS cooperative scheme has the shortest user queue length and the longest UAV queue length, which benefits from the higher channel gain generated by the cooperative reflection of multiple RISs, enabling more user tasks to be efficiently offloaded to the UAV and significantly reducing the backlog at the user end; the double-RIS non-cooperative scheme, which does not utilize the cooperative gain between RISs, has a slightly longer user queue length than the cooperative scheme, and the UAV queue is correspondingly shorter; the single-RIS scheme, due to the lowest channel gain and limited task offloading capability, results in the longest user queue length and the shortest UAV queue length. These results indicate that the RIS cooperation mechanism directly affects the task offloading strategy by improving channel quality, thereby exerting a significant regulatory effect on queue stability, verifying the advantage of multi-RIS cooperation in balancing the loads of users and the UAV.

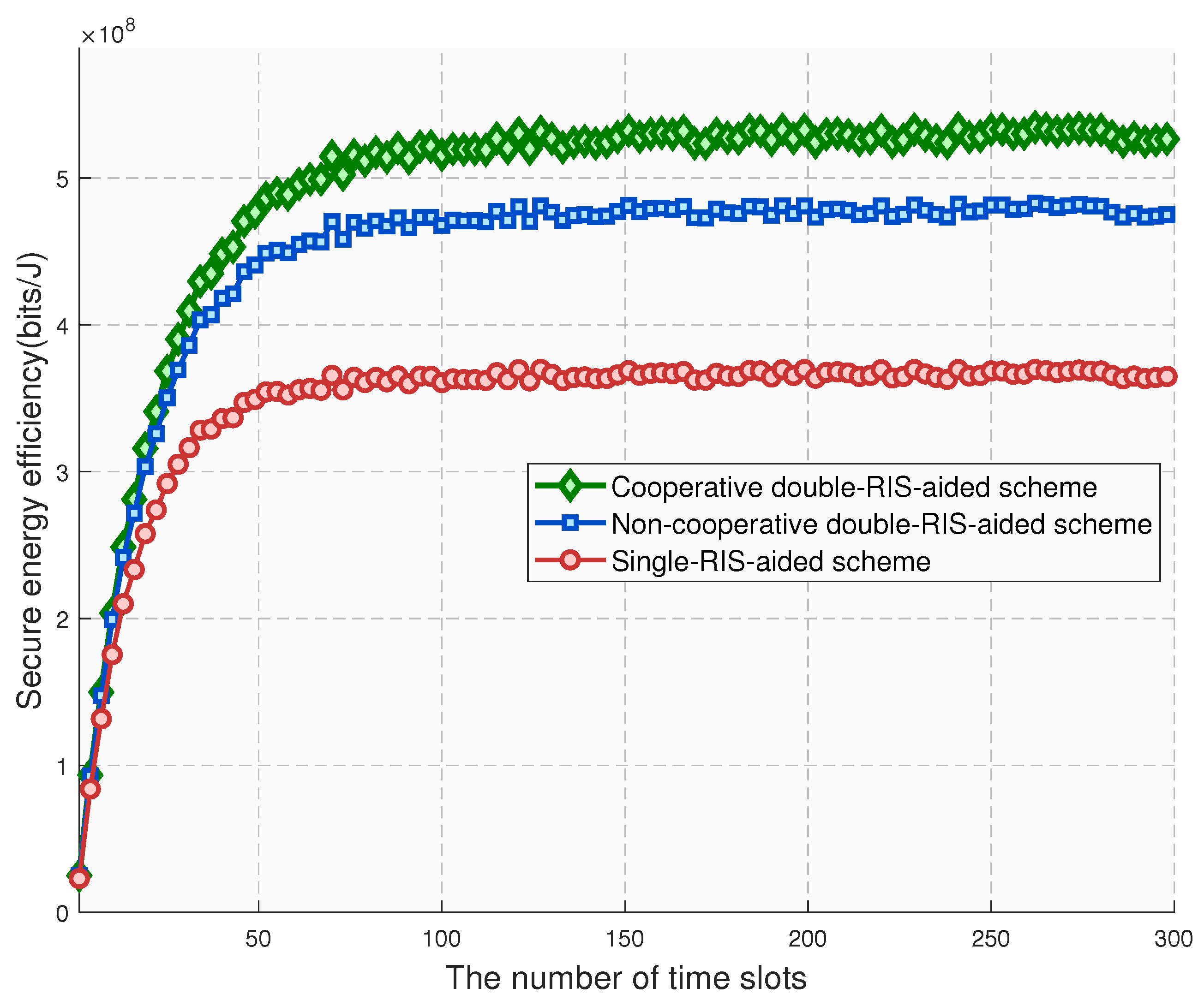
Figure 7 presents the dynamic variation trend of the system’s secure EE under different RIS assistance schemes, where the vertical axis represents the secure EE value and the horizontal axis represents the number of time slots. The experimental results show that the system’s secure EE exhibits an evolutionary characteristic of “initial fluctuation–gradual improvement–stabilization” during operation: in the initial stage, limited by channel conditions, the system’s secure EE is at a relatively high level; as the time slots progress, the secure EE gradually improves and finally remains within a stable range, which is closely related to the optimization of transmission efficiency after the channel gain stabilizes. There are significant differences in the secure EE performance among different RIS assistance schemes: the system’s secure EE increases in turn from the single-RIS scheme to the double-RIS non-cooperative scheme to the double-RIS cooperative scheme. Specifically, the double-RIS cooperative scheme, relying on the collaborative reflection effect of multiple RIS units, can maximize the channel gain, reduce transmission energy consumption while increasing the amount of secure task transmission, thus achieving the highest secure EE; the double-RIS non-cooperative scheme, which does not fully utilize the cooperative gain between RISs, has a slightly lower secure EE than the cooperative scheme; the single-RIS scheme, due to limited channel gain and low secure transmission efficiency, shows the worst performance in terms of secure EE. These results verify that the multi-RIS cooperative mechanism can improve secure EE, indicating that the collaborative optimization of the system’s security performance and EE can be effectively achieved by optimizing the RIS configuration to enhance channel gain.

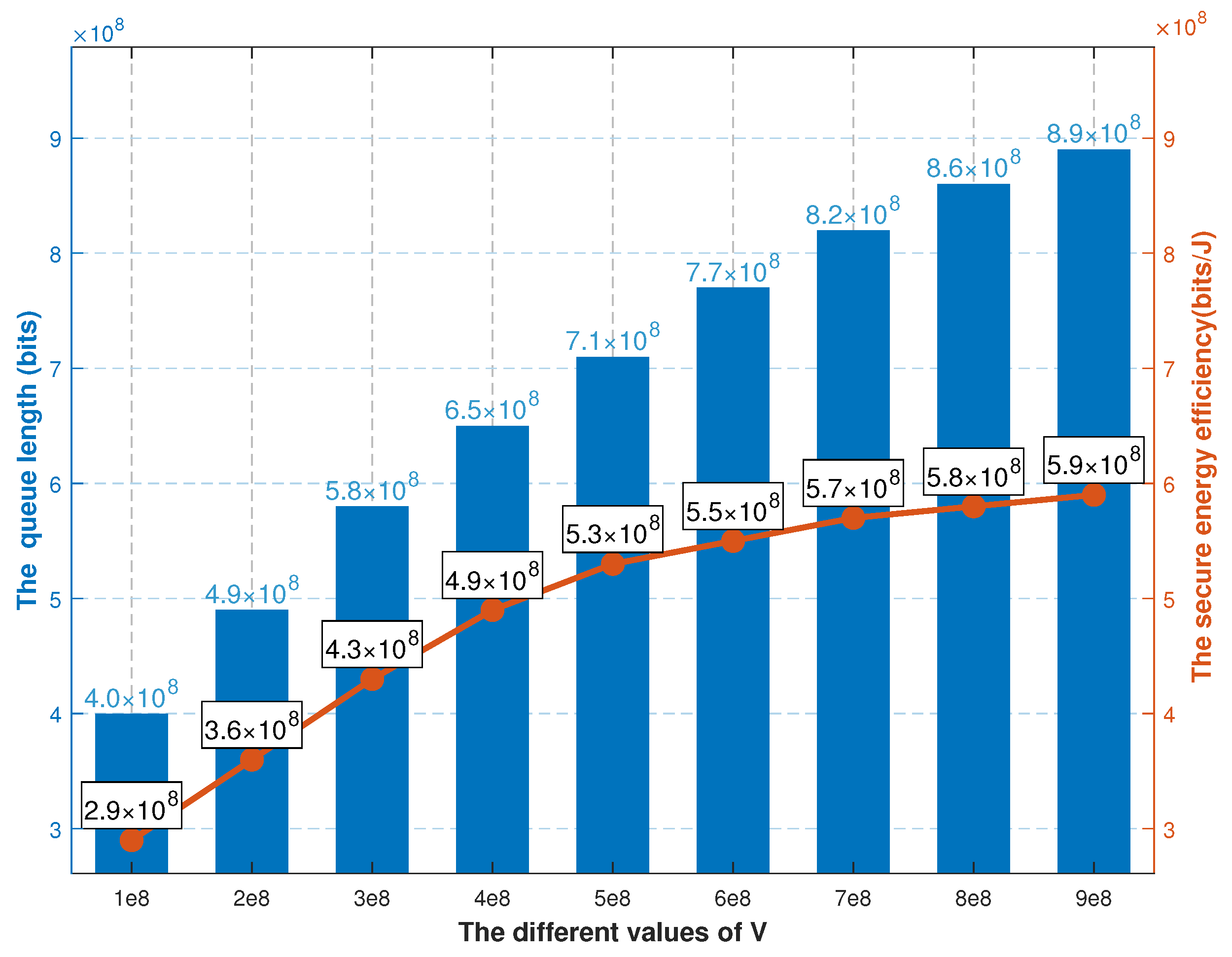
Figure 8 illustrates the relationship between the average user queue length and the system’s average secure EE under different values of the control factor V, where the horizontal axis represents the control factor V, the left vertical axis denotes the average user queue length, and the right vertical axis indicates the system’s average secure EE. The experimental results clearly demonstrate the regulatory effect of the control factor V on system performance, revealing the dynamic trade-off between queue stability and secure EE. Specifically, as the control factor V increases, the average user queue length shows a significant upward trend, while the system’s average secure EE improves simultaneously. The core mechanism behind this phenomenon lies in the fact that the control factor V, as a key parameter in the Lyapunov optimization framework for balancing queue stability and system utility, directly determines the weight allocation of these two objectives in the optimization process: when V takes a small value, the system prioritizes ensuring queue stability, suppressing task backlogs to guarantee service quality, and in this case, the queue length remains at a low level, but the secure EE is mediocre due to limited optimization efforts; when V increases, the weight of the penalty term for secure EE in the system rises significantly, and the optimization objective shifts toward enhancing secure EE— to pursue higher secure transmission efficiency and energy utilization efficiency, the system appropriately relaxes the constraints on queue backlogs, leading to an increase in task accumulation at the user end and thus a rise in the average queue length. Further analysis indicates that the regulatory effect of the control factor V verifies the flexibility of the proposed optimization framework: by adjusting the value of V, refined regulation of queue stability and secure EE can be achieved to meet performance requirements in different scenarios; for instance, in scenarios with high real-time requirements, a smaller V can be selected to prioritize queue stability, while in scenarios sensitive to security and EE, V can be increased to obtain higher secure EE at the cost of partial queue stability. This result fully demonstrates the effectiveness of the control factor V in coordinating the system’s multi-objective optimization, providing important references for parameter configuration in practical applications.

To further explore the impact of other factors on the system’s secure EE, Figure 9 provides quantitative insights through comparative experiments. Figure 9a focuses on the task generation rate (horizontal axis, in Mbits) and average secure EE (vertical axis). Experimental data show that the secure EE of all four schemes (proposed scheme, A2C algorithm scheme, double-RIS non-cooperative scheme, and single-RIS scheme) decreases as the task generation rate increases. Specifically, when the task generation rate ranges from 0.6 Mbits to 1.4 Mbits, the proposed scheme exhibits secure EE values from $4.98\times {10}^8$ bits/J to $6.22\times {10}^8$ bits/J; the A2C algorithm scheme ranges from $4.42\times {10}^8$ bits/J to $5.71\times {10}^8$ bits/J; the double-RIS non-cooperative scheme ranges from $4.12\times {10}^8$ bits/J to $5.43\times {10}^8$ bits/J; and the single-RIS scheme ranges from $3.43\times {10}^8$ bits/J to $4.71\times {10}^8$ bits/J. Figure 9b examines the effect of RIS element quantity (horizontal axis, total number of $M_1+M_2$), with results indicating that secure EE increases for all schemes as the number of RIS elements grows. For the proposed scheme, values rise from $5.19\times {10}^8$ bits/J to $6.07\times {10}^8$ bits/J as elements increase from 200 to 1800; the A2C algorithm scheme ranges from $4.71\times {10}^8$ bits/J to $5.49\times {10}^8$ bits/J; the double-RIS non-cooperative scheme ranges from $4.39\times {10}^8$ bits/J to $5.26\times {10}^8$ bits/J; and the single-RIS scheme ranges from $3.73\times {10}^8$ bits/J to $4.64\times {10}^8$ bits/J. These results highlight the superiority of the proposed scheme: in Figure 9a, it maintains the highest secure EE across all task generation rates, as the PPO algorithm dynamically optimizes resource allocation in continuous action spaces while the enhanced channel gain from double-RIS cooperation ensures stable secure transmission efficiency. In Figure 9b, the proposed scheme achieves the most significant improvement with increasing RIS elements, thanks to its collaborative phase shift optimization that fully leverages hardware potential. Compared to the other three schemes, the proposed approach consistently outperforms, underscoring its robust adaptability to varying environmental factors.

5. Conclusions

This paper investigates a double-RIS cooperative-aided UAV-MEC system and proposes a corresponding optimization scheme: leveraging Lyapunov optimization theory, the long-term stochastic optimization problem with queue stability constraints is transformed into a slot-by-slot deterministic decision problem, significantly reducing real-time optimization complexity, while the PPO algorithm, selected to solve the transformed high-dimensional continuous optimization problem, outperforms A2C, DDPG, and DQN in both policy stability and optimization effect. Simulation results demonstrate the proposed scheme’s superiority over benchmarks: in secure energy efficiency, the double-RIS cooperative scheme exceeds the non-cooperative double-RIS scheme by 17.6% and the single-RIS scheme by 33.3%; in queue stability, its user task queue length is 25.6% shorter than the non-cooperative scheme and 47.6% shorter than the single-RIS scheme, with strong robustness shown by maintaining superior performance amid varying task generation rates and RIS element counts, verifying its adaptability to environmental dynamics and hardware configurations for reliable UAV-MEC operation. While the current framework focuses on mitigating passive eavesdropping as a foundational security measure, future work will extend to multi-UAV and multi-RIS scenarios and incorporate defenses against complex threats like active jamming and spoofing, integrating anti-jamming beamforming and authentication mechanisms to enhance comprehensive security resilience for practical deployments.