Tethered Drones: A Comprehensive Review of Technologies, Challenges, and Applications

Abstract

Tethered drones—defined in this work as multirotor aerial platforms physically connected to a ground station via a cable—have emerged as a transformative subclass of Tethered Unmanned Aerial Vehicles (TUAVs), offering enhanced power autonomy, communication robustness, and safety through a physical ground connection. This review provides a comprehensive analysis of the current state of tethered drone systems technology, focusing on critical system components such as power delivery, data transmission, tether management, and modeling frameworks. Emphasis is placed on the tether multifunctional role—not only as a physical link but also as a sensor, actuator, and communication channel—impacting both hardware design and control strategies. By consolidating fragmented research across disciplines, this work offers a unified reference for the design, implementation, and advancement of TUAV systems, with tethered drones as their principal application.

1. Introduction

Unmanned Aerial Vehicles (UAVs) have already established themselves as a revolutionary tool in several application fields for some time now. As a natural consequence, UAV’s advantages and limitations have been pointed out by the scientific community, leading researchers to study progressively more efficient solutions. Among these, Tethered Unmanned Aerial Vehicles (TUAVs) have emerged as a compelling alternative to conventional untethered systems. Early investigations into tethered aerial systems date back to the 1960s and were conducted leveraging the technologies available at the time, such as helicopters [1] or rotor platforms of varying designs [2,3]. In general, the term UAV encompasses a broad variety of aerial configurations. However, for the purposes of this review, the discussion is explicitly limited to standard multirotor platforms, which will be referred to as UAVs or drones throughout the manuscript. This choice reflects the predominance of multirotor systems in current research, commercial, and industrial applications, where their mechanical simplicity, precise controllability, and ease of deployment have made them the preferred choice for tethered operations. It is nonetheless important to acknowledge other UAV configurations that have been investigated in the context of tethered flight, including balloon-based systems [4], airfoil-type UAVs [5], fixed-wing aircraft [6,7], and hybrid configurations such as tail-sitter fixed-wing VTOL systems [8,9]. Despite the growing interest and deployment of tethered drone systems across both commercial and governmental sectors, a comprehensive synthesis of current technologies, operational frameworks, and research challenges remain limited. The objective of this review is to systematically examine State-of-the-Art tethered drone technology, with a focus on key enabling components such as power delivery mechanisms, Tether Management Systems (TMS), communication architecture, and system modeling and integration. This work aims to bridge the gap between fragmented research efforts and practical applications, offering a consolidated resource for researchers and engineers. In particular, the unique contribution of this review lies in its holistic synthesis of TUAV system components, control strategies, and application scenarios, with special emphasis on the coupled dynamics of drone–tether–winch subsystems. By integrating engineering perspectives from modeling, control, sensing, and operation, this review establishes a unified framework for understanding and advancing TUAV technologies, addressing a critical gap not previously covered in the literature.

1.1. New Features

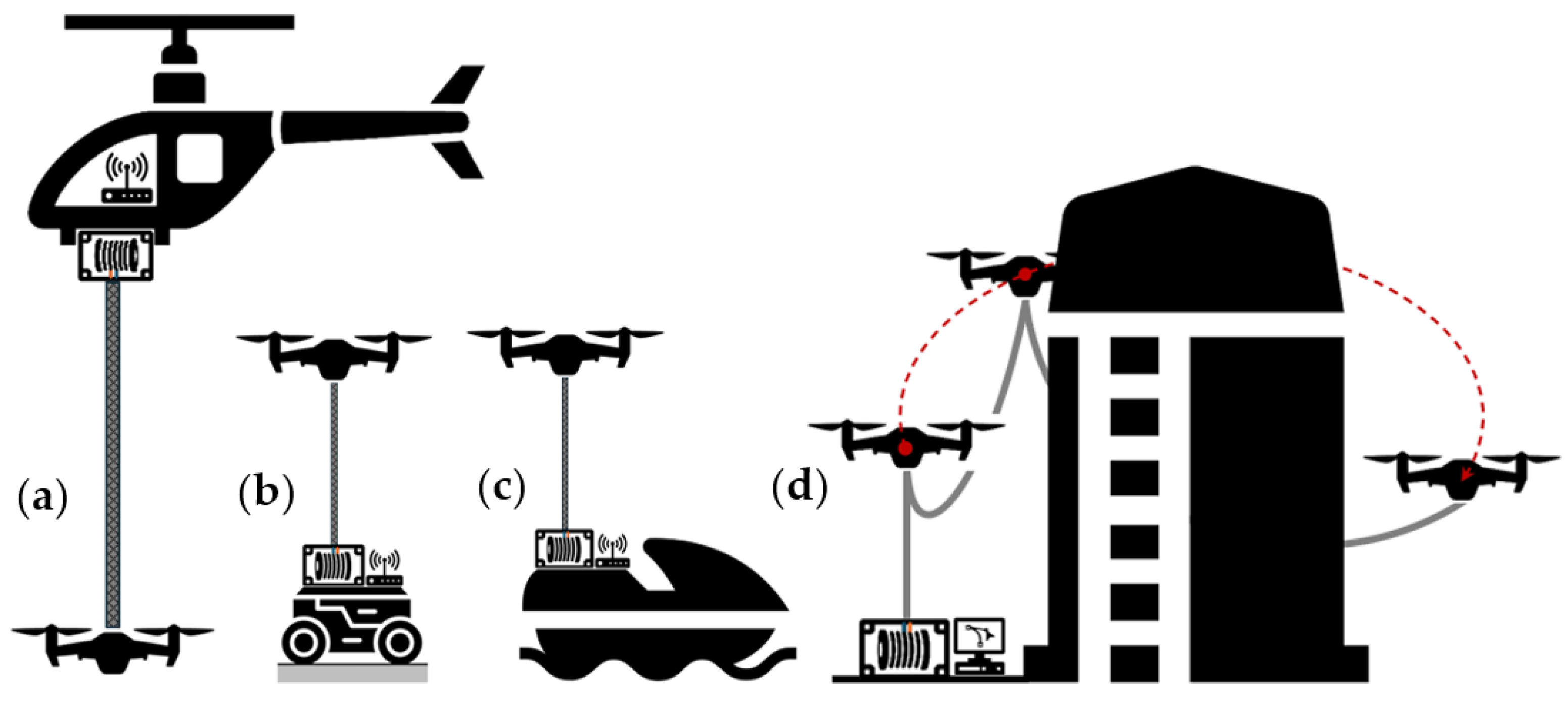
Unlike free-flying/untethered UAVs, tethered drones are physically connected to a ground station via a cable capable of transmitting power, data, or both. This configuration enables significantly extended flight durations and enhances operational stability by leveraging the tether as a physical constraint that attenuates disturbances [10,11]. Furthermore, TUAVs exhibit a tightly coupled dynamic behavior resulting from the interaction between the aerial platform and the tether cable. This coupling introduces unique challenges in modeling, control, and stability, setting TUAVs apart from their untethered counterparts. An overview of these newly introduced features is illustrated in Figure 1.

1.1.1. Power Supply

One of the primary concerns associated with multirotor UAVs is their limited flight autonomy, which typically reaches up to 40 min before requiring battery recharging or replacement. Several approaches have been proposed to overcome this limitation [12]. By drawing power from a ground-based source via a tether cable, tethered drones can operate for extended durations, potentially indefinitely, thus ensuring uninterrupted operation, consistent performance, and improved energy efficiency. Moreover, the removal of onboard batteries increases the drone’s payload capacity and eliminates issues related to battery lifespan and maintenance [13].

1.1.2. Wired Data Communication

The employment of a tether cable in UAV systems is not limited to power transmission alone; it also plays a pivotal role in enabling robust and efficient data communication between the aerial platform and the ground station. Optical fibers integrated into the tether establish a wired backhaul connection, enabling high-bandwidth data transfer, which is essential for bandwidth-intensive applications such as high-definition video streaming, real-time sensor data processing, and emerging 6G communication frameworks [14]. Compared to untethered UAVs relying on wireless links, TUAVs benefit from significantly higher data throughput and reduced transmission latency, due to the inherently greater capacity and stability of the wired connection [15]. Additionally, the physical tether minimizes path loss, ensuring stronger and more consistent signal quality [16]. As a result, the tether not only sustains the drone’s power but also establishes a secure, interference-resistant, and low-latency data communication channel.

1.1.3. Flight Safety Measure

The integration of a tether cable into UAV systems significantly enhances flight safety by introducing mechanical constraints that physically limit the aerial platform’s movement. This constraint acts as a passive safety mechanism, mitigating risks associated with power failures, operator errors, and extreme environmental conditions such as strong gusts. Additionally, the tether contributes to system safety by preventing fly-away incidents, minimizing collision risks, and aiding compliance with regulatory safety requirements. Studies analyzing the interaction between sudden UAV movements and tether dynamics help define potential danger zones, primarily influenced by tether strength and impact parameters such as velocity and angle [17]. This constraint not only defines a safe flight boundary but also facilitates regulatory compliance in restricted airspaces, where physically constrained systems are often subjected to less stringent certification requirements. These advantages make TUAVs particularly appealing for sensitive, high-risk, or long-duration missions. However, the introduction of a tether also creates new safety challenges, particularly in terms of obstacle avoidance and collision management. The cable itself becomes an additional element in the flight environment that is susceptible to entanglement or collision, especially in cluttered or confined spaces. A critical concern is the potential interference between the tether and the drone’s propellers, which must be proactively addressed. This is especially relevant in slack tether conditions or when operating in suspended TUAV configurations [18,19]. Mitigation strategies include the use of propeller guards or ducted propeller designs, possibly combined with swiveling arms that extend beyond the main airframe to keep the tether safely clear of the propulsion system [20]. In complex environments such as urban canyons or vegetated areas, the risk of tether or platform collision increases. Ensuring a collision-free flight path becomes a key safety priority and can be addressed through advanced navigation strategies. Research has emphasized safe landing phase planning [21], as well as collaborative navigation approaches, both with ground robots for mapping and obstacle detection [22,23], and with cooperative TUAV swarms for coordinated movement [24,25]. In some cases, it may be beneficial for the tether to intentionally interact with the environment: for example, by planning tether contact points on static structures, a TUAV can effectively reshape its reachable configuration space, thereby expanding its operability to levels comparable with non-tethered systems [26].

1.2. Application Fields

UAVs have been implemented in many different fields throughout recent years, paving the way for the development of tethered technologies. These enhanced systems leverage the advantages discussed above to surpass the limitations of conventional UAVs. As a result, tethered drones have become increasingly valuable in a variety of mission-critical and time-sensitive applications, which are outlined in the following sections.

1.2.1. Agriculture

In agriculture, UAVs are already used for tasks such as crop spraying, pollination, pruning, and monitoring plant health. Tethered drones further enhance these capabilities by enabling continuous operation. In greenhouse settings, a tethered drone mounted on a mobile ground station can function as a flying end-effector for precision tasks within crop rows [27]. In open fields, multiple ground-tethered UAVs operating in grid formations can serve as an effective bird deterrence system, leveraging centralized control and extended flight time to manage multiple threats simultaneously [28].

1.2.2. Marine Emergency

Thanks to their maneuverability and elevated vantage point, in marine applications, TUAVs support tasks such as oil slick thickness monitoring during spill events [29] and search and rescue operations in mass casualty incidents [30,31]. They can also act as aerial communication relays, maintaining stable links and coordination during emergency maritime missions [32].

1.2.3. Load Transportation

A notable application of tethered drone systems involves aerial load transportation via cable-suspended mechanisms. While these cables may not carry power, they share similar dynamic modeling with power-transmitting tethers. A growing interest in drone-based delivery of goods and medical supplies has driven development in this area. To overcome payload capacity and counteract load swing while improving flight stability, recent approaches have introduced cooperative multi-drone systems, offering improved scalability and fault tolerance through load-sharing redundancy [33,34,35,36]. Advancements in this field have also focused on suspended load characterization, including the deployment of mobile grippers for object grasping in dynamic outdoor environments [37].

1.2.4. Inspection and Monitoring

The enhanced endurance and stability of TUAVs can be leveraged for long-duration infrastructure inspection tasks, such as bridge inspections performed by a suspended TUAV that emulates traditional bucket truck-based inspections [19,38]. Additionally, creeping TUAVs clinging to the underside of bridges at controlled distances have demonstrated precise crack detection using high-resolution image stitching algorithms [39]. Tethered drones have also been deployed in challenging underground environments, such as coal mine sites, where GNSS signals are unavailable, radio communication is limited, and visual cues are scarce. In such scenarios, TUAVs have successfully mapped stone mine pillars and assessed structural integrity in confined and debris-filled spaces [20,40]. Beyond civil infrastructure, TUAVs are also gaining traction in high-demand inspection scenarios such as nuclear power plants, where continuous monitoring and extended endurance are critical [41]. Similarly, in aviation environments, tethered systems can support airfield inspections, weather and traffic surveillance, wildlife deterrence, and emergency response coordination [42,43].

1.2.5. Airborne Wind Energy (AWE)

Over the past decade, tethered aircraft have been explored for Airborne Wind Energy (AWE) systems, which aim to harvest high-altitude wind more efficiently and with less material than conventional turbines. Among these, tethered drones have been used to follow predefined flight paths while carrying energy-harvesting elements, such as rigid wings [44] or Magnus-based devices [45,46], exploiting the tether tension and the ground-based winch as a power generator.

1.2.6. Meteorology

The extended flight endurance of TUAVs is well-suited for environmental monitoring, particularly in atmospheric sensing applications. For instance, arrays of temperature sensors integrated along the tether can capture vertical temperature profiles with accuracy comparable to meteorological towers, supporting dynamic climate and weather studies [47,48].

1.2.7. Painting

The uninterrupted power supply provided by tethered configurations also enables unconventional applications, such as in the arts. Equipped with a stippling mechanism and benefiting from extended flight time, a drone can autonomously apply tens of thousands of ink dots to a canvas without human intervention [49].

1.2.8. Cellular Networks

UAV-assisted heterogeneous networks have gained significant attention for enhancing cellular coverage and capacity. In this context, TUAVs can serve as aerial base stations (ABSs) or relay nodes, particularly useful when terrestrial base stations (TBSs) are overloaded or unavailable [50]. Leveraging their stable positioning and continuous power supply, TUAVs have been shown to support user association, resource allocation, and 3D placement optimization to improve overall network performance [51]. By minimizing path loss and maximizing end-to-end signal-to-noise ratios, TUAV-ABSs can effectively offload traffic and support multiple ground users during peak demand [52,53]. Depending on the network topology, TUAVs can also act both as high-altitude relays [54] and as TBSs replacements [55], linking untethered UAV relays and ground users. In next-generation networks, TUAV-based drone cells can serve as mobile fronthaul links, offering robust, high-bandwidth connectivity for 6G communications [14]. To balance the trade-off between power availability and deployment flexibility, intermittently tethered UAVs (iTUAVs) have been proposed, enabling temporary anchoring at ground stations before relocating to optimize mobile user coverage [56].

1.2.9. Firefighting

While the tether cable has primarily been discussed as a means for power and data transmission, its physical presence can also enable alternative functions in critical operations such as firefighting. In these scenarios, the tether may be replaced or supplemented by a water hose, enabling the TUAV to deliver high-pressure water jets from an aerial position over hazardous fire zones, thus minimizing risk to human responders [57]. Recent implementations feature recoil-compensated designs that account for the reactive forces of both the water jet and hose dynamics, enhancing flight stability during prolonged firefighting operations [58].

1.2.10. Field of Defense

TUAVs have become increasingly valuable in defense operations, enabling extended surveillance and reconnaissance missions where continuous situational awareness is critical and risk to human life is high [59]. TUAV swarms enhance intelligence, surveillance, and reconnaissance (ISR) and defense operations by enabling rapid deployment, persistent multi-angle surveillance, and safe operation in confined or complex environments. In law enforcement or military scenarios, swarms can be used to secure perimeters, monitor vehicle checkpoints, or provide overwatch in urban terrain [25].

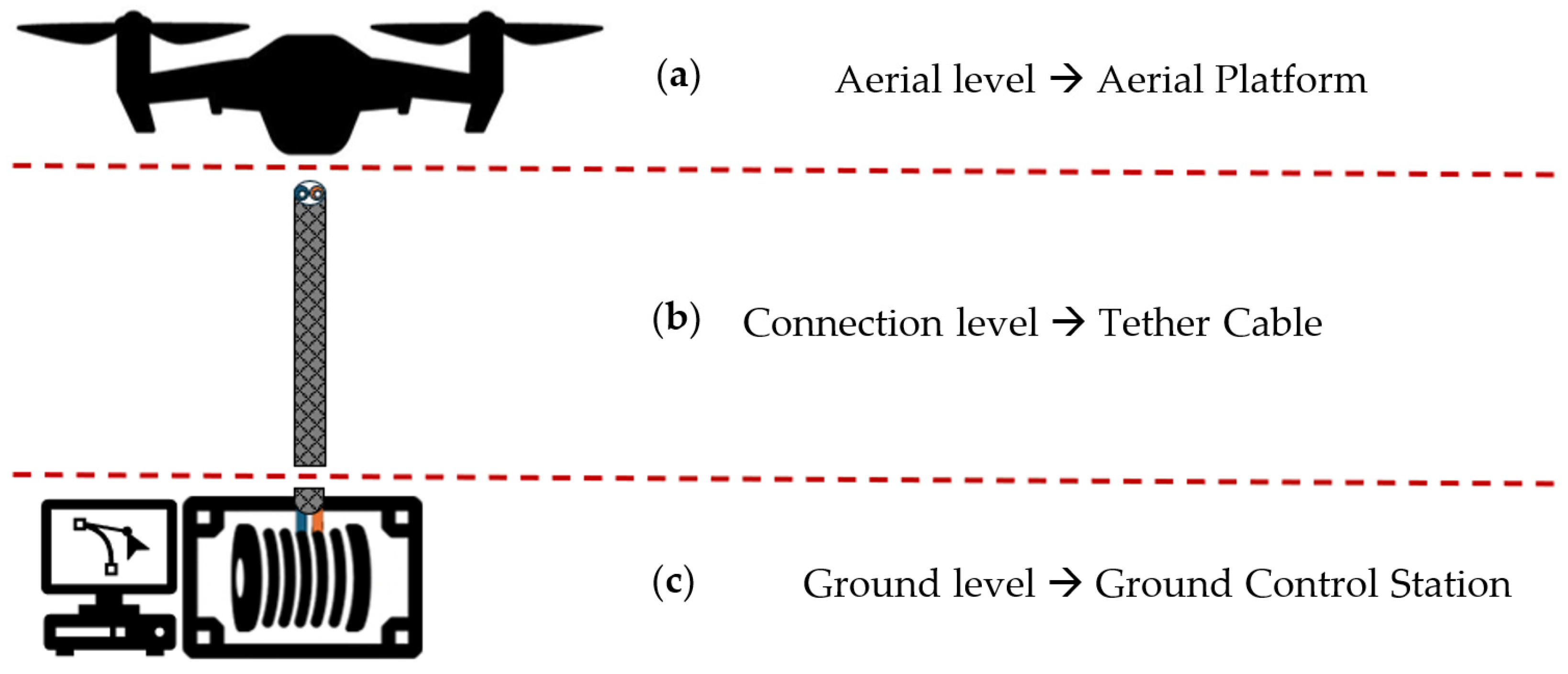
2. System Description

The following section aims to outline the components and spatial configurations of a TUAV multirotor system. For clarity, the system is divided into three levels: aerial, connection, and ground, each encompassing one or more components depending on their spatial arrangement, as illustrated in Figure 2. Although onboard hardware and sensors are integral to the system, they have been intentionally excluded here, as their complexity and relevance warrant dedicated discussion in a separate chapter.

2.1. Aerial Platform

In a broader sense, the term “Unmanned Aerial Vehicle” encompasses various aerial platforms, provided they are uncrewed. Consequently, the aerial component of a TUAV system is not necessarily a drone by default. Early research on tethered systems primarily focused on helicopters, leveraging existing technologies [1]. Subsequent studies explored alternative rotor-based platforms, such as rotorcraft with a free-flapping, single-rotor configuration lacking a tail rotor [2], and the gyromill, a rotorcraft comprising two counter-rotating single-blade rotors and a transverse fuselage with movable fin and tailplane [3]. Helicopters remained the predominant tethered aerial platform due to their VTOL capabilities [60,61], with significant advancements in tethered helicopter systems attributed to the work of Sandino and the research group led by A. Ollero [62,63,64,65], which laid foundational groundwork for the development of tethered drone literature. This review, however, focuses specifically on the current State of the Art in tethered multirotor drone systems, which offer greater flexibility in spatial and geometric configurations.

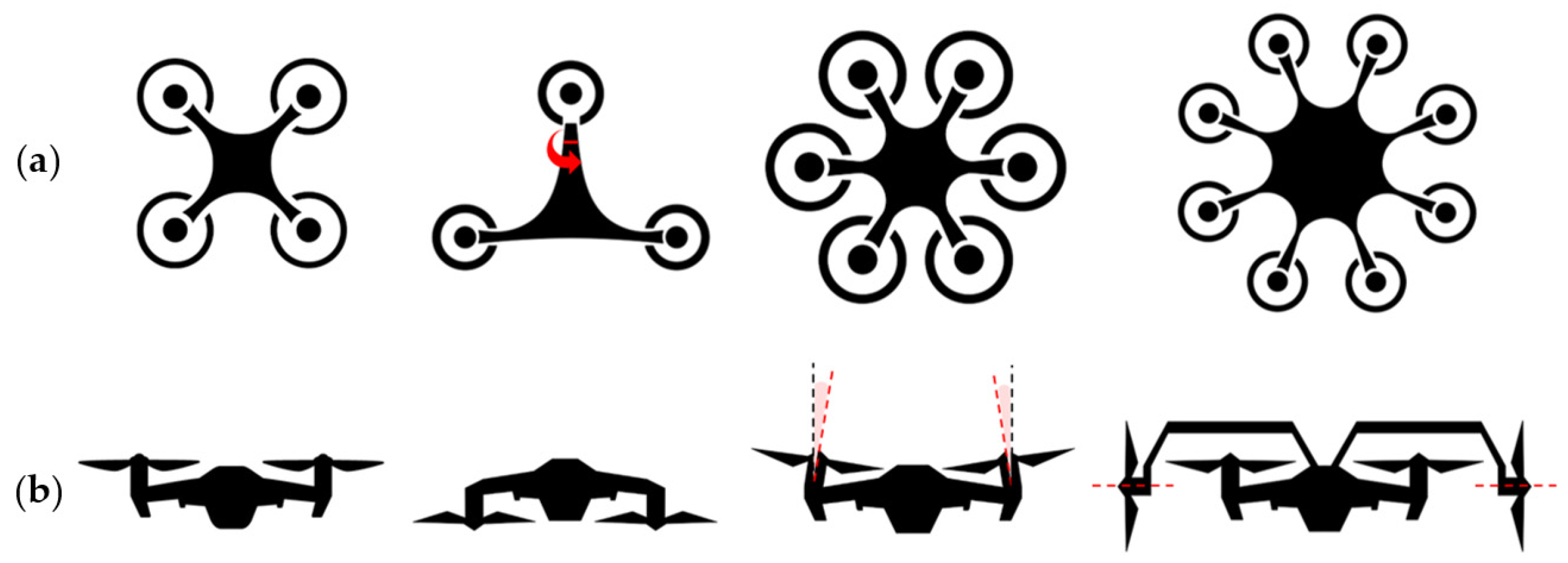
Airframe Configurations

TUAV airframes can be classified according to key physical design parameters that affect flight dynamics and operational roles. Two primary classification criteria are commonly adopted: the number of propellers and the orientation of the propulsion system. These classification schemes are illustrated in Figure 3. The first classification of TUAVs relates to the number of propellers, which inherently influences the drone’s size and lifting capability. The quadrotor is the most common configuration due to its geometric symmetry and balanced trade-off between maneuverability, payload capacity, and weight efficiency. Tethered hexarotors have been developed for extended endurance [66] and heavy-duty operations supporting payloads up to 30 kg [67]. Similarly, tethered octocopter configurations have been investigated for comparable purposes [68,69]. An alternative solution is the tilt-trirotor, an asymmetric three-rotor system capable of hybrid flight modes, functioning both as a fixed-wing aircraft and a rotorcraft [70]. A second classification criterion is given by the propeller orientation, a critical factor in the UAV’s design. The suspended TUAV configuration, with rotors facing downward, is commonly adopted in scenarios where the aerial platform operates below the control station level, such as in bridge inspections, minimizing the risk of tether entanglement [18,19,38]. Tilt-rotor multicopters offer improved wind disturbance rejection and fault tolerance, enabled by servos adjusting rotor tilt angles [71]. A distinctive layout involves a quadcopter frame augmented with two laterally placed horizontal rotors, designed to counteract aerodynamic drag [58]. For operations in confined or collision-prone environments, ducted propellers offer improved propulsion efficiency and increase–d protection, albeit with reduced flight performance [20]. An innovative design further integrates ducted propulsion with tiltable rotors, featuring two vertical ducted propellers mounted on rotating shafts [72].

2.2. Tethered Connection

The connection level represents the physical and functional link between the aerial platform and the ground station. It includes both the tether cable, which serves as a mechanical, electrical, and data conduit, and the aerial power conversion module, responsible for adapting the ground-supplied power to the UAV’s onboard requirements. This section addresses the structural and functional characterization of both those two elements.

2.2.1. Aerial Power Module

The aerial power module is responsible for converting the high-voltage power transmitted through the tether into a regulated low-voltage supply suitable for the UAV’s propulsion and onboard electronics. This unit is a critical interface between the tethered ground supply and the UAV’s power architecture, and its design is primarily constrained by efficiency, thermal management, and weight. A high-frequency AC multi-phase transmission system can be adopted to minimize cable and onboard converter size, hence enabling larger payloads and extended mission durations [41,73]. The onboard conversion module employs resonant energy transfer to improve efficiency [41,73,74] and incorporates modular converter designs—such as parallel DC-DC converters and isolated compartments—to further reduce the system’s bulk [73,74,75]. To address thermal challenges, forced-air ventilation mitigates overheating under peak loads [75], while aluminum heat sinks and dual cooling fans support effective thermal dissipation [66]. To ensure safe emergency landings during power failures, a backup battery system is typically connected in parallel to the UAV’s DC bus, automatically activating when a voltage drop is detected [66]. These systems often include pre-charged batteries, solid-state relays (SSRs), and fast-switching diodes to enable rapid activation. Integration with the low-voltage power bus and logic-controlled triggering circuits ensures reliable operation and minimal interference with the main power supply chain [76].

2.2.2. Tether Cable

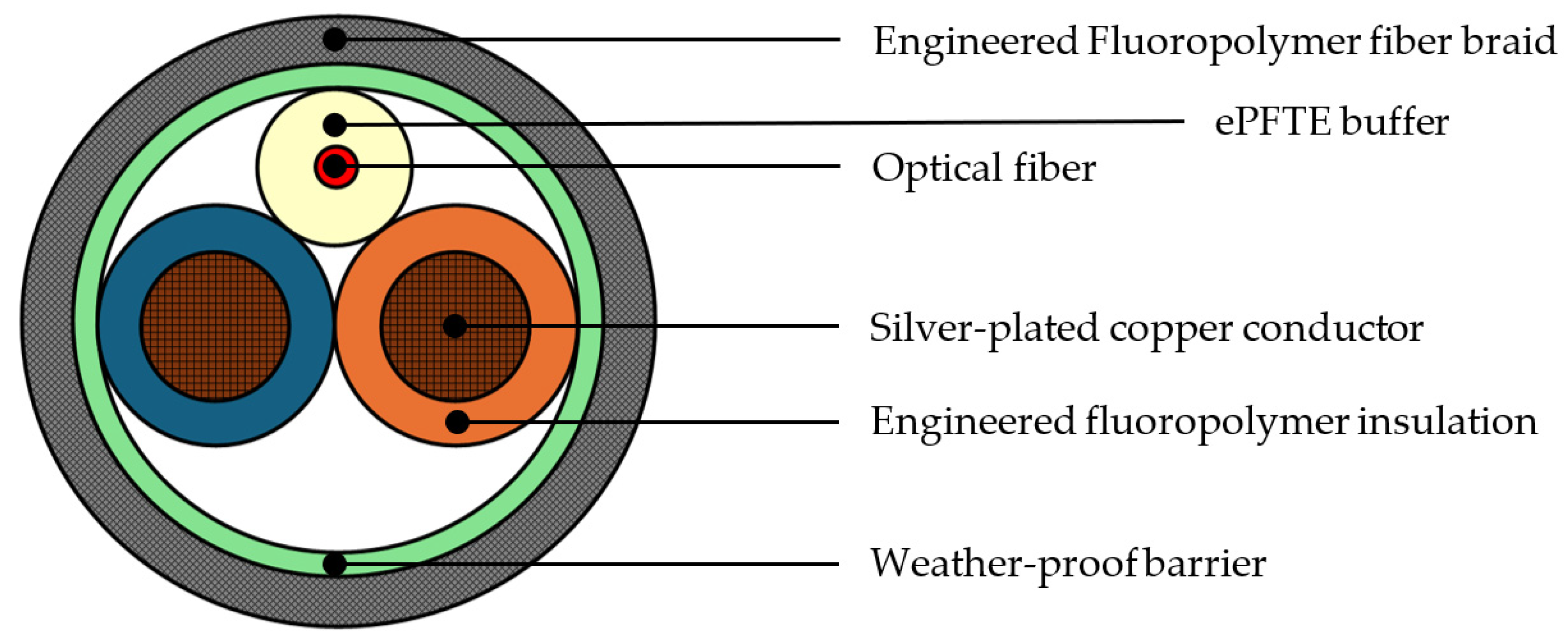
Cable selection is a key design phase in TUAV system integration, requiring careful consideration of multiple performance parameters. This typically involves a trade-off between minimizing transmission power losses and reducing overall cable weight to preserve aerial payload capacity [77,78]. A standard tether cable, illustrated in Figure 4, is composed of several concentric layers, each serving a distinct function [79,80]:

• An outer fluoroplastic insulation sheath for environmental protection;
• High-voltage copper conductors, each with individual insulation jackets for safe power transmission;
• An integrated optical fiber module containing one or multiple fiber-optic lines for high-speed data communication;
• An inner Kevlar harness, providing tensile strength and durability under mechanical stress.

Figure 4. Standard drone tether cable section and structural composition [79].

Figure 4. Standard drone tether cable section and structural composition [79].

While fiber-optic communication is widely regarded as the optimal solution for data transmission in TUAV systems, several alternative technologies allow wired data transmission via electrical conductors embedded in the tether [81]. Among these, Power Line Communication (PLC) has gained interest in its ability to transmit both power and data over the same wire pair, thereby reducing cable complexity. Another common alternative is the use of twisted-pair Ethernet cables, which can offer a compatible solution with typical UAV onboard hardware. Despite the feasibility of these electrical methods, optical fiber remains the preferred choice for high-performance TUAV applications due to its complete immunity to electromagnetic interference (EMI), low latency, and exceptionally high data throughput, which support real-time video streaming, sensor feedback, and control commands.

2.3. Ground Control Station

The Ground Control Station (GCS) in a tethered UAV system serves as the central hub for power delivery, flight monitoring, and UAV control, enabling safe and stable operation throughout extended missions. Unlike conventional UAVs, tethered platforms require specialized ground infrastructure to manage continuous power transmission, communication links, and tether handling mechanisms. The primary components of a typical GCS include [82]:

• Power Supply Unit: Converts and regulates AC or DC inputs (typically from grid, generator, or battery pack) to DC outputs suitable for transmission through the tether.
• TMS: Includes an automated winch for tether deployment/retrieval and a slip ring for uninterrupted electrical connection during rotation.
• Communication Interfaces: Facilitates real-time control and telemetry via ground-to-air communication modules.
• Monitoring and Control Interface: A user-accessible interface (e.g., a laptop or control console) running mission planning and UAV management software (e.g., QGroundControl), providing operators with live data and system status.

The GCS is designed to ensure reliable power and data links, precise tether tension control, and robust mission coordination, which are essential for safe TUAV operations.

2.3.1. Tether Management System

The TMS is a compact, ruggedized ground unit that integrates key components of a TUAV’s ground level. Its primary roles include storing excess tether, sensing and controlling tether parameters, and in some cases, housing the power supply, such as a battery pack. Typical TMS components include

• Tether cable and spool/reel;
• DC motor actuator;
• Tether sensors (length, tension, elevation, and azimuth angles);
• Control unit;
• Landing platform;
• Power source.

This section presents an overview of experimental TMS configurations, while detailed sensing and control strategies are addressed in later chapters. A critical requirement of any TMS is rapid spool response, ensuring the system reacts promptly to UAV movement. Uniform cable distribution and accurate tension sensing are achieved through various winding mechanisms, including pulley systems [67,83], plane-fixed tether outlets [61,84], passive sensorized followers [83,85,86], and rotary rods [41]. To prevent cable twisting during spool rotation, slip rings are commonly employed [18,86]. Tether angles can be sensed via a universal joint, while tension can be measured using spring-loaded lever arms [40,87] or indirectly estimated using a powder clutch applying a constant torque, assuming a known spool diameter [83]. Notably, one configuration uses a vertically rotating spool to optimize spatial layout [41]. Some advanced TMS setups also integrate the landing platform into the system structure, which can be fixed [84,87], elevated [61], or self-leveling [40], increasing system stability and adaptability.

2.3.2. Commercial Off-the-Shelf Systems

Several commercial TMS solutions are available on the market, typically emphasizing mechanical robustness and power transmission efficiency, aspects often peripheral to current academic research. These systems are generally compact, rugged, and box-shaped, designed to operate with external power units. Tether tension control varies by manufacturer, ranging from constant-tension mechanisms [88,89], to set-velocity winding [90], and multi-mode tension settings with retract functions [91,92]. Only a few commercial models support battery operation [93], and just one is reported to provide real-time cable departure angles [94]. Some all-in-one COTS solutions integrate the drone, tether cable, and aerial power module into a single package. For example, Fotokite offers a tethered hexacopter with a rectangular frame and rooftop deployment cases tailored for firefighting and first-response applications [95]. Hoverfly provides modular, network-capable systems designed for ISR missions and variable-height communications, supporting a range of payloads in an open architecture design [96].

2.4. Multi-Robot Systems

An overview of tethered multi-robot systems is presented in this section to complete the analysis of TUAV configurations. Previous examples have already highlighted the versatility and potential of tethered platforms. As illustrated in Figure 5, the specific characteristics of the operational environment dictate the overall system architecture, particularly when coordinating heterogeneous robotic units, such as aerial and ground-based elements.

2.4.1. TUAV/UGV Team

In inspection and exploration tasks, integrating a TUAV with an Unmanned Ground Vehicle (UGV) unlocks new operational capabilities. One key advantage is the creation of a mobile tether anchor point, with the UGV serving as a moving power and tether management unit. This enhances the UAV’s maneuverability in cluttered or confined environments while reducing the risk of tether entanglement [40]. In such configurations, the UGV may carry the battery pack, winch, and tether sensors, acting as a full ground segment for the airborne platform, even when using a tracked or wheeled base [97]. This setup supports collaborative navigation, with TUAV and UGV sharing data for joint environment mapping and enhanced situational awareness [26,70]. A marsupial robot configuration, where the TUAV assists the UGV’s motion planning, has been shown to enable safe traversal through unknown terrain using tether-based path planning derived from tether dynamics [23]. Beyond sensing, the TUAV has also been employed for tether attachment to elevated structures, facilitating UGV ascent by enabling it to lift its own weight via an integrated winch system [98]. Additionally, a multi-UGV setup can enhance TUAV pose stabilization by applying distributed tether forces to counteract environmental disturbances such as wind [88].

2.4.2. TUAV/USV Team

A distinct operational scenario is presented by the marine environment, where the multi-physics complexity demands additional modeling, particularly concerning surface water dynamics, often addressed through the floating buoy model [99]. Several studies have demonstrated that the forward-surge velocity of a buoy can be controlled by adjusting the thrust of a tethered UAV connected via a taut cable [100,101,102]. This work was later extended by the same research group to consider slack cable configurations, allowing greater freedom of movement for the UAV around the buoy [103]. In such systems, the tethered UAV operates in coordination with a floating platform, typically an Unmanned Surface Vehicle (USV) serving as the buoy component. Similar to TUAV–UGV cooperative teams, the aerial agent enhances the visual navigation capabilities of the marine vehicle, particularly in search and rescue missions, by providing an elevated field of view [30].

2.4.3. TUAV Swarm

Among multi-robot TUAV configurations, one notable concept is the UAV swarm, wherein multiple drones operate in a coordinated manner, often connected via tethers. This layout, referred to as a System of Tethered Multicopters (STeM) [104], features serially connected UAVs cooperating to transport payloads [34,35] or to support precision spraying tasks using a suspended tube with an integrated nozzle and tethered power line [105]. Cable management across swarm units remains a primary challenge, especially in complex environments with obstacle-dense zones [24]. Cable anchoring and reeling at each intermediate drone is typically managed via a gimbaled winch [104] or a pulley-based double-gimbal mechanism [106]. Depending on operational needs, the tether’s ground anchoring may be either fixed or mobile [106]. Additionally, multi-UAV cooperation can be leveraged for tethered docking and deployment scenarios, for example involving a helicopter-like UAV platform deploying a tethered quadrotor for frequent delivery missions [107].

2.4.4. TUAV + Manipulator

An emerging application of TUAVs involves their integration into multi-robot systems where the aerial vehicle is physically coupled with a robotic arm. In a particularly innovative configuration, the system is composed of two cooperative robotic entities: a UAV providing mobility and positioning, and a tether-driven continuum robot acting as a flexible manipulator. The ground station, functioning as a third key subsystem, houses actuators and control units, transmitting mechanical power through the tether to the robotic arm mounted on the UAV. This approach highlights the potential of TUAV-based multi-robot systems for enabling physical interaction with the surrounding environment [108,109].

Although each of the multi-robot TUAV configurations discussed in this section demonstrates unique operational advantages, they also pose substantial engineering challenges that limit real-world deployment. A comparative overview of these configurations is provided in

Table 1. Comparative analysis of multi-robot TUAV configurations.

Configuration	Typical Applications	Key Advantages	Operational Challenges	Unresolved Issues
TUAV + UGV	Subsurface inspection Mapping	Mobile tether anchor Improved access in cluttered spaces	Tether entanglement Coordination in uneven terrain	Robust path planning with moving tether base
TUAV + USV	Search and rescue Oil spill monitoring	Aerial perspective for maritime operations	Tether dynamics due to waves Buoy motion affecting TUAV stability	Multi-physics modeling of cable-surface interactions
TUAV Swarm	Load transport Formation flight Coverage	Redundancy Scalable payload handling	Cable collision Synchronization Spacing management	Real-time cable-aware formation and decentralized control
TUAV + Manipulator	Bridge inspection Fine manipulation	Aerial manipulation Contact tasks	Actuation delay Vibration Payload-induced instability	Integrated modeling and control of aerial base and deformable arm dynamics

, highlighting their typical applications, key strengths, operational limitations, and ongoing research gaps. TUAV–UGV teams benefit from increased maneuverability and terrain adaptability but are highly sensitive to tether routing complexity, especially in GPS-denied environments. TUAV–USV cooperation introduces new modeling complexities due to surface wave dynamics, requiring robust adaptive control to handle oscillatory tether tension. TUAV swarms offer increased task parallelism and fault tolerance yet suffer from entanglement risks and demand sophisticated cable-aware coordination algorithms. Finally, the integration of robotic arms, such as the tendon-driven continuum robot, significantly expands manipulation capabilities but complicates control due to structural flexibility and added inertial dynamics. These trade-offs emphasize the need for integrated modeling, real-time coordination algorithms, and cross-domain simulations that include tether mechanics, multi-agent behavior, and dynamic environments.

3. Mathematical Modeling

Mathematical modeling of tethered aerial systems first appeared in the literature in the early 1960s, initially focused on helicopters [1], rotorcraft platforms [2,3], and general tethered flight vehicles [110]. While early studies did not consider tethered multirotor UAVs, they provided foundational concepts for later developments. Although tethered helicopters with tail rotors fall outside the scope of this review, key contributions, such as those from Sandino’s group [62,63,64,65], remain valuable for understanding rotor-tether dynamics. This chapter provides an overview of modeling approaches for the core components of a tethered multirotor UAV system:

• The multirotor UAV platform;
• The tether cable;
• The automated winch mechanism.

3.1. Multirotor UAV Model

While various rotor configurations exist, this section focuses on the quadrotor UAV, as it is the most widely modeled platform in the literature. The mathematical formulation adopts several common assumptions to simplify the dynamics [111]:

• Rigid UAV frame;
• Symmetric configuration;
• Center of Gravity (CoG) aligned with the body-fixed frame;
• Rigid propellers;
• Thrust and drag forces proportional to the square of rotor speed.

For clarity, the shorthand notation below will be used for trigonometric functions further in the dissertation.

$$\begin{array}{c}\sin \left(\mathrm{∎}\right)=s_{\mathrm{∎}}\\ \cos \left(\mathrm{∎}\right)=c_{\mathrm{∎}}\\ \tan \left(\mathrm{∎}\right)=t_{\mathrm{∎}}\end{array}$$

(1)

3.1.1. Cartesian Reference Frame

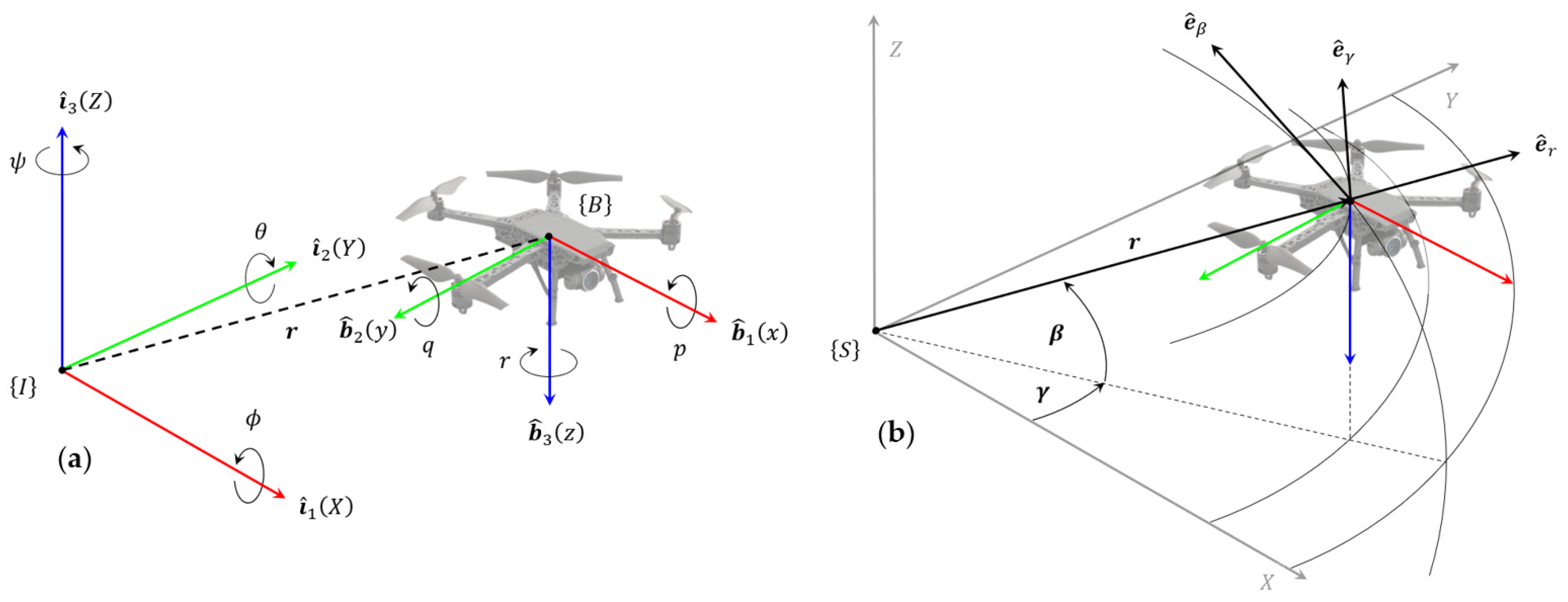
The UAV’s motion is usually described using two Cartesian reference frames, as illustrated in Figure 6a: an inertial frame $\left\{I\right\}$, fixed to the ground with unit vectors $\left\{{\widehat{\mathsf{ı}}}_1,{\widehat{\mathsf{ı}}}_2,{\widehat{\mathsf{ı}}}_3\right\}$, and a body-fixed frame $\left\{B\right\}$, located at the UAV’s CoG and typically defined with unit vectors $\left\{{\widehat{\mathit{b}}}_1,{\widehat{\mathit{b}}}_2,{\widehat{\mathit{b}}}_3\right\}$, using the right-hand rule [112] or the North-East-Down (NED) convention, where ${\widehat{\mathit{b}}}_3$ points downwards [113]. The attitude orientation of the UAV with respect to the inertial frame is defined using Euler angles, typically in the ZYX sequence, and represented by the rotation matrix ${\mathit{R}}_B^I\in {SO}^3$. The relation between the two Cartesian frames is expressed as [114]

$$\left[\begin{array}{c}{\hat{\mathsf{ı}}}_1\\ {\widehat{\mathsf{ı}}}_2\\ {\widehat{\mathsf{ı}}}_3\end{array}\right]=\left[\begin{array}{ccc}{c}_{\theta }{c}_{\psi }& s_{\varphi }{s}_{\theta }{c}_{\psi }-c_{\varphi }{s}_{\psi }& c_{\varphi }{s}_{\theta }{c}_{\psi }+s_{\varphi }{s}_{\psi }\\ c_{\theta }{s}_{\psi }& s_{\varphi }{s}_{\theta }{s}_{\psi }+c_{\varphi }{c}_{\psi }& c_{\varphi }{s}_{\theta }{s}_{\psi }-s_{\varphi }{s}_{\psi }\\ -s_{\theta }& s_{\varphi }{c}_{\theta }& c_{\varphi }{c}_{\theta }\end{array}\right]\left[\begin{array}{c}{\widehat{\mathit{b}}}_1\\ {\widehat{\mathit{b}}}_2\\ {\widehat{\mathit{b}}}_3\end{array}\right]={\mathit{R}}_B^I\left[\begin{array}{c}{\widehat{\mathit{b}}}_1\\ {\widehat{\mathit{b}}}_2\\ {\widehat{\mathit{b}}}_3\end{array}\right]$$

(2)

Angular rates are defined starting from the angular velocity in the body-fixed frame ${\mathit{\omega }}_B=p{\widehat{\mathit{b}}}_1+q{\widehat{\mathit{b}}}_2+r{\widehat{\mathit{b}}}_3$, which is related to the inertial frame through the following relation.

$${\mathit{\omega }}_B=\left[\begin{array}{c}p\\ q\\ r\end{array}\right]=\left[\begin{array}{ccc}1& 0& -s_{\theta }\\ 0& c_{\varphi }& s_{\varphi }{c}_{\theta }\\ 0& -s_{\varphi }& c_{\varphi }{c}_{\theta }\end{array}\right]\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]={\mathit{R}}_{\omega }\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]$$

(3)

The time rate of change in Euler angles is calculated by inverting the previous expression.

$$\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]={\mathit{R}}_{\omega }^{-1}\left[\begin{array}{c}p\\ q\\ r\end{array}\right]={\mathit{T}}_{\omega }\left[\begin{array}{c}p\\ q\\ r\end{array}\right]=\left[\begin{array}{ccc}1& s_{\varphi }{t}_{\theta }& c_{\varphi }{t}_{\theta }\\ 0& c_{\varphi }& -s_{\varphi }\\ 0& s_{\varphi }/c_{\theta }& c_{\varphi }/c_{\theta }\end{array}\right]\left[\begin{array}{c}p\\ q\\ r\end{array}\right]$$

(4)

3.1.2. Spherical Reference Frame

An alternative and effective representation is the spherical reference frame [103], particularly useful when modeling tether dynamics, as later discussed in the unified model section. The UAV’s Cartesian position ${\mathit{r}}_C=\left\{x_C,y_C,z_C\right\}\in {\mathbb{R}}^3$ is expressed in the spherical frame $\left\{S\right\}$ with the coordinates $\left\{r,\beta ,\gamma \right\}$ and corresponding unit vectors $\left\{{\widehat{\mathbf{e}}}_r,{\widehat{\mathit{e}}}_{\beta },{\widehat{\mathit{e}}}_{\gamma }\right\}$. Here, $r$ is the radial distance from the origin, $\beta \in \left(\left.-\pi /2,\pi /2\right]\right.$ is the elevation angle from the horizontal plane, and $\gamma \in \left(\left.-\mathsf{\pi },\mathsf{\pi }\right]\right.$ is the azimuth angle between the positive $x_C$ axis and the projection of $r$ on the $\left\{x_C,y_C\right\}$ plane, as illustrated in Figure 6b. The transformation from spherical to Cartesian coordinates is achieved through two sequential rotations:

$${\mathit{R}}_S^C={\mathit{R}}_{\gamma }{\mathit{R}}_{\beta }=\left[\begin{array}{ccc}{c}_{\beta }{c}_{\gamma }& -s_{\beta }{c}_{\gamma }& -s_{\gamma }\\ c_{\beta }{s}_{\gamma }& -s_{\beta }{s}_{\gamma }& c_{\gamma }\\ s_{\beta }& c_{\beta }& 0\end{array}\right]$$

(5)

Afterwards, relations between Cartesian and spherical frames are established.

$${\mathit{r}}^C={\mathit{R}}_S^C\cdot {\mathit{r}}^S⟹{\mathit{r}}^S={\mathit{R}}_C^S\cdot {\mathit{r}}^C,$$

(6)

where ${\mathit{R}}_C^S={\left({\mathit{R}}_S^C\right)}^T$.

3.1.3. Equations of Motion

The Equations of Motion (EoM) for a TUAV system can be derived using either the Euler–Newton or Euler–Lagrange formalisms [111]. In the body-fixed frame, the UAV’s translational and rotational dynamics are governed by Newton’s second law, which relates external forces and moments ${\left[\begin{array}{cc}{\mathit{F}}_B& {\mathit{\tau }}_B\end{array}\right]}^T$ to the time derivatives of the linear and angular momenta $\mathit{P}$ and $\mathit{L}$ [114].

$$\begin{array}{l}{\mathit{F}}_B={\left({\displaystyle \frac{d\mathit{P}}{dt}}\right)}_B+{\mathit{\omega }}_B\times {\mathit{P}}_B\\ {\mathit{\tau }}_B={\left({\displaystyle \frac{d\mathit{L}}{dt}}\right)}_B+{\mathit{\omega }}_B\times {\mathit{L}}_B\end{array}\Rightarrow \left[\begin{array}{c}{\mathit{F}}_B\\ {\mathit{\tau }}_B\end{array}\right]=\left[\begin{array}{cc}m\mathit{I}& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_B\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{V}}}_B\\ {\dot{\mathit{\omega }}}_B\end{array}\right]+\left[\begin{array}{c}{\mathit{\omega }}_B\times m{\mathit{V}}_B\\ {\mathit{\omega }}_B\times {\mathit{I}}_B{\mathit{\omega }}_B\end{array}\right],$$

(7)

where $\mathit{I}$ is the 3 $\times$ 3 identity matrix, $m$ is the UAV mass, ${\mathit{I}}_B$ is the constant inertia tensor, and ${\mathit{V}}_B={\left[\begin{array}{ccc}u& v& w\end{array}\right]}^T$ is the vector of linear velocities in the body frame. Due to symmetry assumptions previously made, the inertia tensor has the form of a diagonal matrix.

$${\mathit{I}}_B=\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ 0& I_{yy}& 0\\ 0& 0& I_{zz}\end{array}\right]$$

(8)

Using the Euler-Lagrange approach [115], the UAV’s dynamics are expressed in terms of a set of generalized coordinates ${\mathit{q}}_L={\left[\begin{array}{ccc}x& y& \begin{array}{ccc}z& \varphi & \begin{array}{cc}\theta & \psi \end{array}\end{array}\end{array}\right]}^T$, representing its translational and rotational degrees of freedom. The Lagrangian $L$ is defined as the difference between kinetic and potential energy:

$$L=K\left({\mathit{q}}_L,{\dot{\mathit{q}}}_L\right)-U\left({\mathit{q}}_L\right)$$

(9)

The EoM are derived from

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial {\dot{\mathit{q}}}_L}}\right)-{\displaystyle \frac{\partial L}{\partial {\mathit{q}}_L}}={\mathit{Q}}_B,$$

(10)

where ${\mathit{Q}}_B$ is the vector of external forces and moments, expressed in the body-fixed frame. The matrix-condensed form of EoM becomes

$$\left[\begin{array}{cc}m\mathit{I}& \mathbf{0}\\ \mathbf{0}& {{\mathit{R}}_B^I\cdot \mathit{I}}_B\end{array}\right]{\ddot{\mathit{q}}}_L+\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{T}}_{\omega }\left({\mathit{\omega }}_B\times {\mathit{I}}_B{\mathit{\omega }}_B\right)\end{array}\right]{\dot{\mathit{q}}}_L+\left[\begin{array}{c}m\mathit{g}\\ \mathbf{0}\end{array}\right]={\mathit{R}}_B^I\cdot {\mathit{Q}}_B$$

(11)

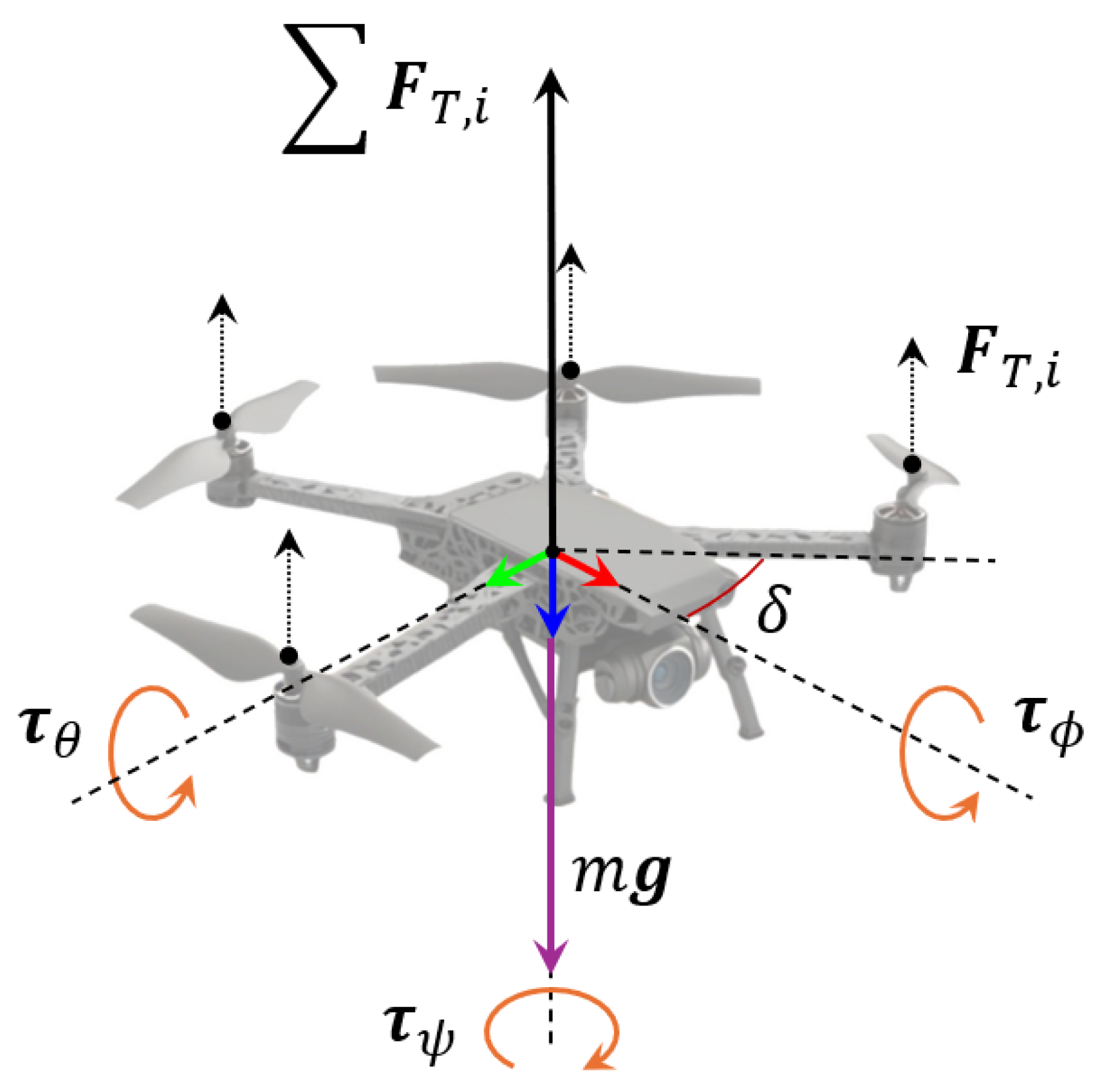
The final form of the UAV’s EoM depends on the external forces and moments considered, as illustrated in Figure 7. The main active force is the collective thrust $F_T$ generated by the rotors, each one spinning at angular velocity ${\omega }_i$:

$$F_T={\sum }_{i=1}^4{C}_T{\omega }_i^2,$$

(12)

where $C_T>0$ is the thrust coefficient, typically obtained from static tests. Rotor drag, resulting from blade aerodynamics, induces a net yaw torque based on the rotational direction of each rotor:

$${\tau }_{\psi }={\sum }_{i=1}^4{\left(-1\right)}^n{C}_Q{\omega }_i^2,$$

(13)

with $C_Q>0$ as the drag coefficient. Assuming an X-configuration quadrotor, the angle $\delta$ between each arm and the body axis must be considered when computing rolling and pitching moments:

$$\begin{array}{c}{\tau }_{\varphi }=l\cdot s_{\delta }\left({\omega }_2^2+{\omega }_3^2-{\omega }_1^2-{\omega }_4^2\right)\\ {\tau }_{\theta }=l\cdot c_{\delta }\left({\omega }_3^2+{\omega }_4^2-{\omega }_1^2-{\omega }_2^2\right)\end{array}$$

(14)

To improve physical realism, more advanced models may also incorporate effects such as hub forces, gyroscopic moments, and ground effects [113]. The extended EoM for the quadrotor are

$$\left\{\begin{array}{ccc}m\ddot{x}& =& \left(c_{\varphi }{s}_{\theta }{c}_{\psi }+s_{\varphi }{s}_{\psi }\right)F_T\\ m\ddot{y}& =& \left(c_{\varphi }{s}_{\theta }{s}_{\psi }-s_{\varphi }{c}_{\psi }\right)F_T\\ m\ddot{z}& =& \left(c_{\varphi }{c}_{\psi }\right)F_T-mg \\ I_{xx}\ddot{\varphi }& =& \dot{\theta }\dot{\psi }\left(I_{yy}-I_{zz}\right)+{\tau }_{\varphi }\\ I_{yy}\ddot{\theta }& =& \dot{\varphi }\dot{\psi }\left(I_{zz}-I_{xx}\right)+{\tau }_{\theta }\\ I_{zz}\ddot{\varphi }& =& \dot{\varphi }\dot{\theta }\left(I_{xx}-I_{yy}\right)+{\tau }_{\psi }\end{array}\right.$$

(15)

EoM are commonly formulated using the traditional Euler angle parametrization. However, it is well known that Euler angle parametrizations suffer from singularities, particularly when the pitch angle $\theta$ approaches ±90°, leading to a phenomenon known as gimbal lock. In such configurations, two of the three rotation axes become aligned, resulting in a loss of one degree of freedom and introducing numerical instability and ambiguity in the attitude representation. This issue poses significant challenges for UAV control and estimation algorithms, especially during aggressive maneuvers or when operating in near-singular configurations. To overcome these limitations, quaternion-based representations are often adopted. Quaternions provide a globally non-singular, compact, and computationally efficient means of representing orientation, making them well-suited for real-time UAV attitude dynamics and control. The UAV’s attitude dynamics can therefore also be described using quaternion notation [68,69,116]:

$$\dot{\mathit{q}}=\left[\begin{array}{c}{\dot{q}}_0\\ {\dot{q}}_1\\ {\dot{q}}_2\\ {\dot{q}}_3\end{array}\right]={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}0& -p& -q& -r\\ p& 0& r& -q\\ q& -r& 0& p\\ r& q& -p& 0\end{array}\right]\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right],$$

(16)

where $\mathit{q}={\left[\begin{array}{cccc}{q}_0& q_1& q_2& q_3\end{array}\right]}^T$ is the unit quaternion representing the UAV orientation. The quaternion formulation ensures a smooth and continuous description of the UAV’s attitude over the entire 3D rotation space, avoiding the singularities inherent to Euler angles and thereby improving robustness in both estimation and control applications.

3.2. Tether Cable Model

The tether cable plays a critical role in the dynamic behavior of a TUAV system, mainly because of physical constraints. Its mechanical response depends heavily on configuration and tension conditions. When connected between a ground anchor and a flying drone, the cable can primarily exhibit two geometric configurations: a taut cable, modeled as a straight line under high tension, and a slack cable, where gravitational effects dominate, causing the cable to deflect into the characteristic catenary curve [117]. This section introduces the fundamental modeling approaches for both regimes, outlining their assumptions, applicability, and relevance to tethered flight dynamics.

3.2.1. Tether Statics

In static conditions, the tether can assume two primary configurations: taut and slack. In the taut cable case, the tether acts as a position and force constraint, enhancing UAV stability and defining a safe operating boundary via the winch control system [10]. When the tether is short, lightweight, and inextensible, it can be approximated as a massless, rigid link, exerting a single tensile force aligned with the cable [118]. In contrast, a slack tether is influenced by gravity and aerodynamic forces. This configuration, together with a fast-responding TMS, allows the system to absorb wind disturbances, heave disturbances, and cable stiffness, assuming quasi-static behavior, valid when aerodynamic forces are negligible relative to cable tension [114,119]. The tether shape is modeled using the catenary equations, derived from the static equilibrium of an infinitesimal cable segment [120,121]:

$$\left\{\begin{array}{l} z\left(r\right)=\lambda \cosh \left({\displaystyle \frac{r}{\lambda }}+c_1\right)+c_2\\ \lambda ={\displaystyle \frac{T_0}{{\rho }_{l}g}}\end{array},\right.$$

(17)

where $z$ is the vertical coordinate, $r=x^2+y^2$ is the radial coordinate, and $\lambda$ is the catenary scale factor, further defined by the horizontal tension at the anchor point $T_0$, the linear mass density of the cable ${\rho }_l$, and the gravity acceleration $g$; $c_1,c_2$ are integration constants defined by boundary conditions. In symmetric setups, as the one illustrated in Figure 8, simplified forms are used to calculate tether parameters such as elevation angle $\beta$ and curved cable length $L$ [122]:

$$\left\{\begin{array}{c}z=\lambda \left[\cosh \left({\displaystyle \frac{r}{\lambda }}\right)-1\right] \\ {\displaystyle \frac{dz}{dr}}=t_{\beta }=\sinh \left({\displaystyle \frac{r}{\lambda }}\right) \\ L=\lambda \sinh \left({\displaystyle \frac{r}{\lambda }}\right) \end{array}\right.$$

(18)

While most models assume a fixed anchor point, adaptations exist for mobile bases such as UGVs [97] or USVs [119]. Similar principles have also been applied to hose-based tether systems [58]. Overall, static models are most appropriate for low-speed or hovering applications, where inertial effects are minimal.

3.2.2. Tether Dynamics

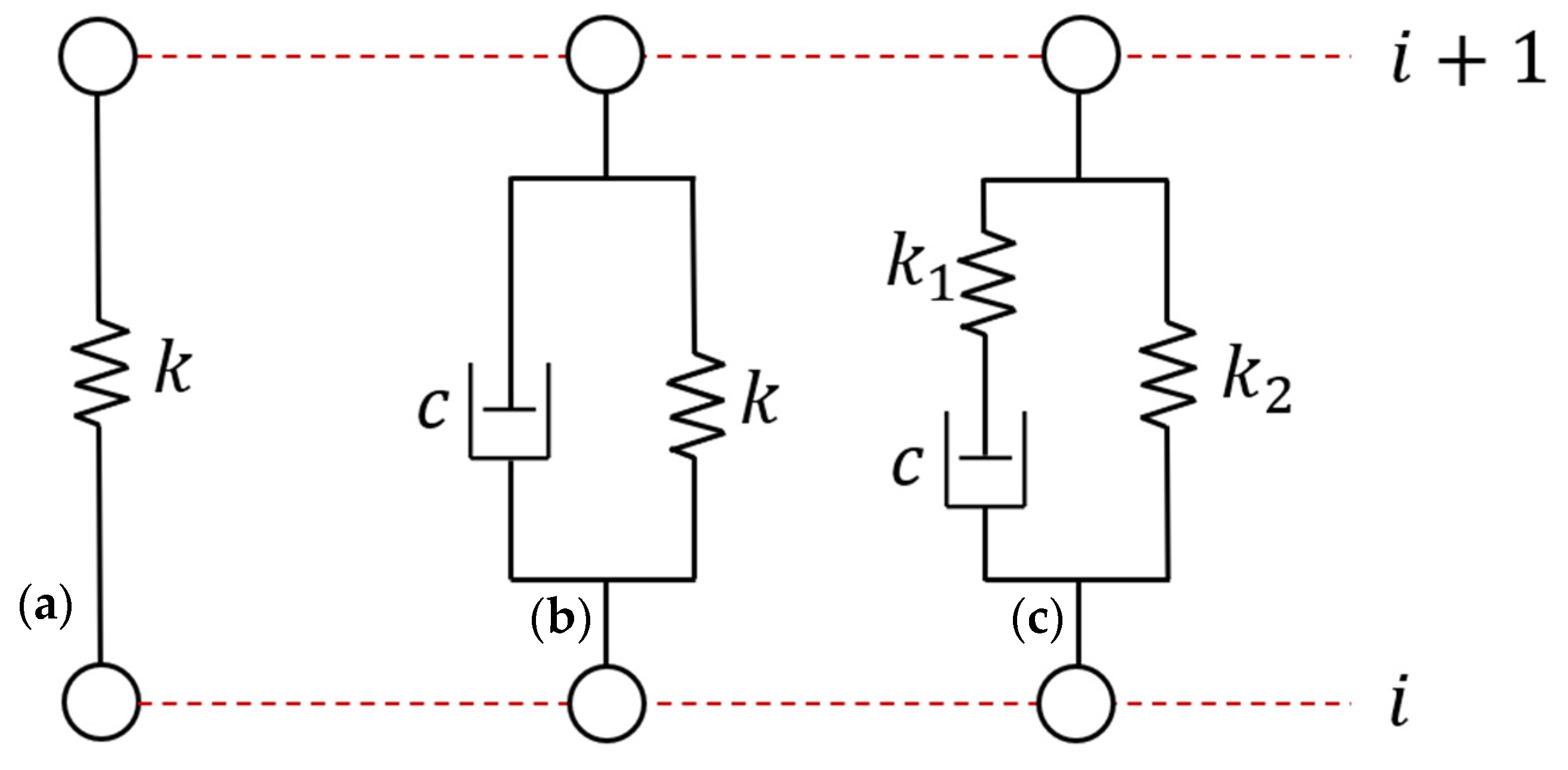
Tether dynamics modeling captures time-dependent behaviors such as inertia, tension propagation, and vibrational effects, which become critical during high-speed maneuvers, wind disturbances, or any condition where oscillations may destabilize the UAV. These dynamics can be addressed using two main approaches:

• A discrete model, where the tether is divided into lumped segments;
• A continuous model, where the tether is treated as a deformable elastic body.

In discrete formulations, the tether is modeled as a series of rigid or viscoelastic elements, as illustrated in Figure 9. Common choices include the Kelvin–Voigt and Standard Linear Solid (SLS) models [123]. For slack cables, segment masses are typically placed at the upper joints, with forces transmitted via springs [124] or spring-damper pairs [2]. The same principle can be adapted to taut cables using a single linear-elastic [125] or viscoelastic element [63,68,69].

When cables are long, thin, and under constant tension, they can be modeled as 2D elastic strings using wave-based partial differential equations (PDEs) of an elastic string, under some basic assumptions [126]:

• Bending, shear and torsional deformations are negligible;
• Cable density $\rho$, section $A$, Young’s modulus $E$ are constant;
• Cable tension is dominant along the longitudinal direction;
• Small angles approximation.

Longitudinal and transverse dynamics are governed, respectively, by

$$\begin{array}{c}{\displaystyle \frac{{\partial }^2{u}_1}{\partial t^2}}={\displaystyle \frac{E}{\rho }}{\displaystyle \frac{{\partial }^2{u}_1}{\partial x^2}}\\ {\displaystyle \frac{{\partial }^2{u}_2}{\partial t^2}}={\displaystyle \frac{T_0}{\rho A}}{\displaystyle \frac{{\partial }^2{u}_2}{\partial x^2}}\end{array},$$

(19)

with wave speeds $\left(c_l,c_t\right)$ and natural frequencies $\left(f_{n,l},f_{n,t}\right)$ given by [17,127]:

$$\begin{array}{cc}{c}_l=\sqrt{{\displaystyle \frac{E}{\rho }}} & f_{n,l}={\displaystyle \frac{n}{2L_0}}{c}_l\\ c_t=\sqrt{{\displaystyle \frac{T_0}{\rho A}}}& f_{n,t}={\displaystyle \frac{n}{2L_0}}{c}_t\end{array}$$

(20)

Here, $u_1$ and $u_2$ are the longitudinal and transverse displacements, $L_0$ is the undeformed string length, and $n$ is the vibration mode. Lagrangian dynamic strain and the related strain energy in the cable are calculated using [29,127]:

$$\epsilon \left(s,t\right)={\displaystyle \frac{\partial u_1}{\partial s}}-\kappa u_2+{\displaystyle \frac{1}{2}}\left[{\left({\displaystyle \frac{\partial u_1}{\partial s}}-\kappa u_2\right)}^2+{\left({\displaystyle \frac{\partial u_2}{\partial s}}+\kappa u_1\right)}^2\right],$$

(21)

$$e\left(s,t\right)={\displaystyle \frac{EA}{2}}{\int }_0^{L_0}{\epsilon }^{2}ds,$$

(22)

where $s$ is the arc length and $\kappa$ is the equilibrium curvature. For stiff or short tethers, bending effects are non-negligible and the Euler–Bernoulli beam model is used [128]. Continuous models support modal analysis [129], impact stress analysis [17], finite element implementations [29], and vibration response prediction [127]. UAV motion or wind can excite tether vibrations. When those external disturbance frequencies align with the cable natural frequencies, resonance may occur, generating large-amplitude oscillations. 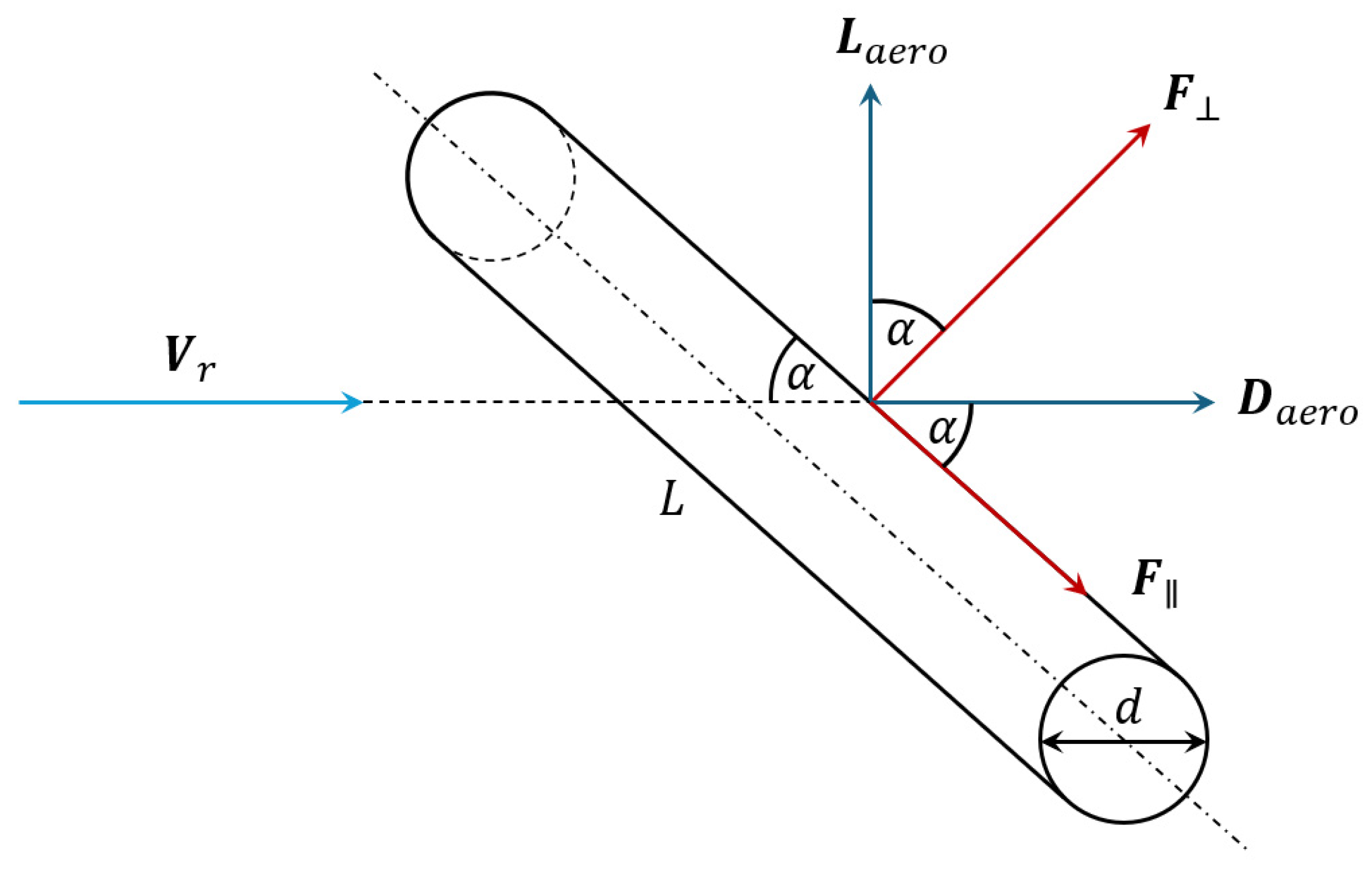Aerodynamic forces $\left(L_{aero},D_{aero}\right)$ acting on cable segments of length $l$ and diameter $d$ are modeled using the cross-flow principle [116,130]:

$$\left\{\begin{array}{c}{L}_{aero}={\displaystyle \frac{1}{2}}{\rho }_{a}d{\left|V_r^B\right|}^2{C}_l\\ D_{aero}={\displaystyle \frac{1}{2}}{\rho }_{a}d{\left|V_r^B\right|}^2{C}_d\end{array},\right.$$

(23)

where ${\rho }_a$ is the air density at a given altitude, $V_r^B$ is the relative velocity between the wind flow and the cable segment, and $\left(C_l,C_d\right)$ are the lift and drag coefficients. Considering the incidence angle $\alpha$ of the wind flow, the projected aerodynamic forces, as illustrated in Figure 10, are

$$\left\{\begin{array}{c}{F}_{\parallel }=-L_{aero}{\mathrm{s}}_{\alpha }+D_{aero}{\mathrm{c}}_{\alpha }\\ { F}_{\perp }= L_{aero}{\mathrm{c}}_{\alpha }+D_{aero}{\mathrm{s}}_{\alpha } \end{array}\right.$$

(24)

3.2.3. Tether Electrical Model

As the primary role of the tether is power transmission, basic electrical modeling is essential. The internal resistance of the cable $R$, which causes voltage and power losses, is defined by

$$R=\rho {\displaystyle \frac{L}{A}} ,$$

(25)

where $\rho$ is the conductor’s resistivity, $L$ is the cable length, and $A$ the cross-sectional area. The corresponding voltage drop and power loss are [84]:

$$V_{drop}=R\cdot i ,$$

(26)

$$P_{loss}=V_{drop}\cdot i=R\cdot i^2,$$

(27)

where $i$ is the operating current. Minimizing $P_{loss}$ while keeping the cable lightweight introduces a design trade-off between cable diameter and length, key factors in TUAV endurance and lift capacity. For AC power transmission, cable inductance also becomes relevant, contributing to additional losses at higher frequencies [41].

3.3. Automated Winch Model

The ground-controlled winch consists of a hollow spool mounted to a permanent magnet DC motor, used to control tether length and tension [125]. This section addresses the mechanical and electrical modeling of the winch; sensor-related aspects are discussed in a later chapter.

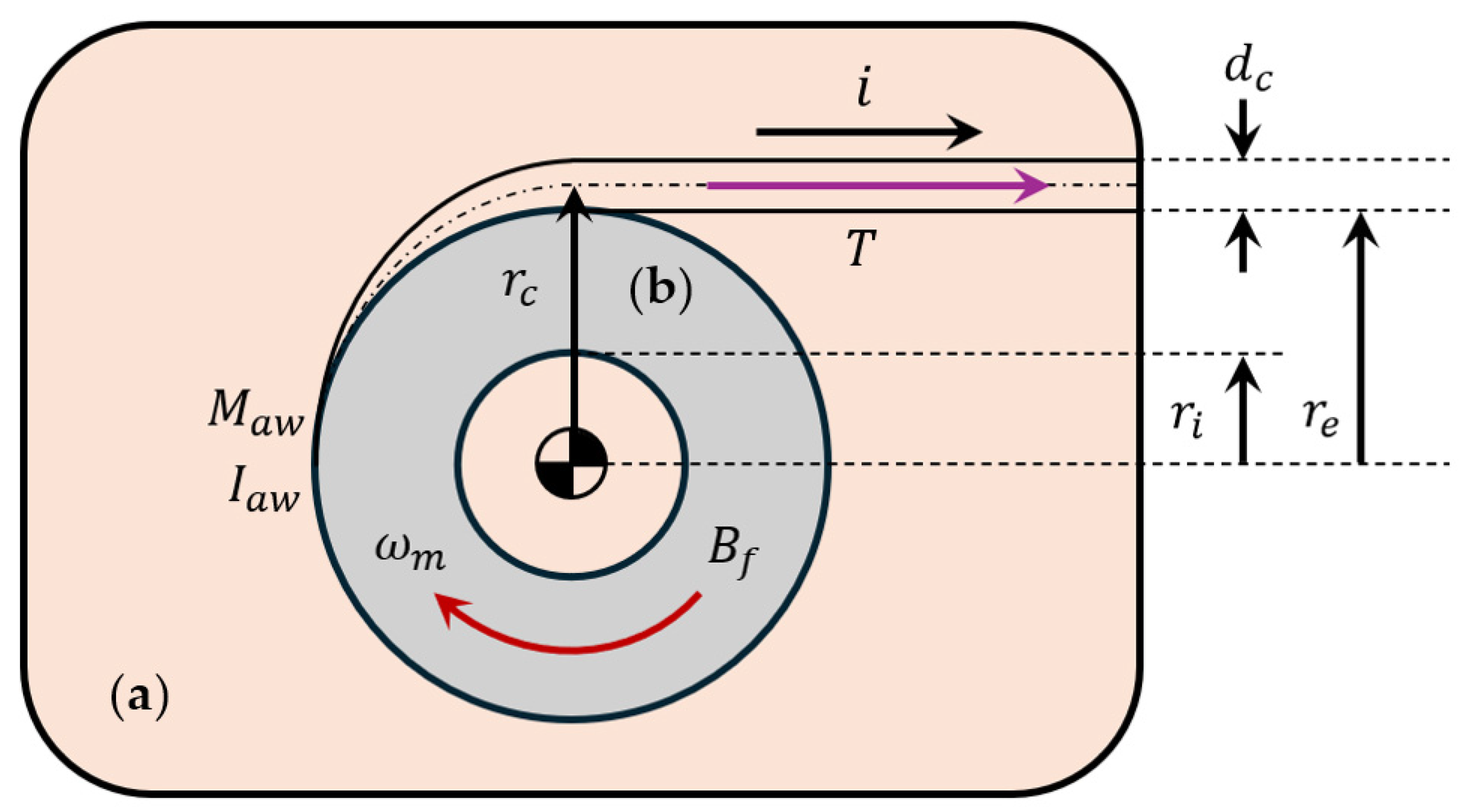
3.3.1. Mechanical Model

To model the system, the total mass $M_{aw}$ and moment of inertia $I_{aw}$ of the winch assembly are given by [104]

$$M_{aw}=M_m+M_s+M_c=M_m+M_s+\left[L_0-r_c\vartheta \right]{\rho }_l,$$

(28)

$$I_{aw}=I_m+I_s+I_c=I_m+{\displaystyle \frac{1}{2}}{M}_s\left(r_e^2+r_i^2\right)+M_c{\left({\displaystyle \frac{r_c}{2}}\right)}^2 ,$$

(29)

where the subscripts $m$, $s$ and $c$ indicate, respectively, the DC motor, the spool and a cable of diameter $d_c$; furthermore, $r_e$ and $r_i$ are the external and internal radii of the spool, $\vartheta =\vartheta \left(t\right)$ is the motor angular progress, and $r_c$ is the effective winding radius, calculated as

$$r_c=r_e+{\displaystyle \frac{L_0-r_e\vartheta }{2\pi r_e}}{\displaystyle \frac{d_c}{2}}$$

(30)

Both geometric and dynamic parameters of the winch model are illustrated in Figure 11.

Cable length $L$ can be estimated from a motor angle encoder using a second-order polynomial fit [85]:

$$L\cong L_{poly}=a_L{\vartheta }^2+b_L\vartheta +c_L ,$$

(31)

where $a_L$, $b_{L,}$ and $c_L$ are polynomial coefficients to be experimentally determined. Assuming a single cable layer, the unwinding rate $\dot{L}$ is calculated as [63]

$$\dot{L}=r_c{\omega }_m,$$

(32)

where ${\omega }_m$ is the motor shaft speed. If the cable is treated as a linear spring, tension $T$ is expressed as [106,125]

$$\begin{array}{cc}T& =K_c\left(L-r_c\vartheta \right) \\ K_c& \left\{\begin{array}{ccc}=0& for& r_c\vartheta \le 0\\ >0& for& r_c\vartheta >0\end{array}\right.\end{array},$$

(33)

where $K_c$ is the cable elasticity coefficient and $\left(L-r_c\vartheta \right)$ represent its longitudinal deformation.

3.3.2. Electrical Model

The motor’s electrical dynamics are modeled by [106,125]:

$$V_m=L_m{\displaystyle \frac{di}{dt}}+R_{m}i+k_e{\omega }_m,$$

(34)

where $V_m$ and $i$ are motor’s voltage and current, and $\left(L_m,R_m,k_e\right)$ are the motor’s inductance, resistance, and back-emf constant, respectively. The electromechanical model becomes [106,125,131]:

$$I_{aw}{\displaystyle \frac{d{\omega }_m}{dt}}=k_{t}i-B_f{\omega }_m-r_{c}T,$$

(35)

where $k_t$ is the torque constant and $B_f$ is the viscous friction coefficient of the motor.

3.4. TUAV Unified Model

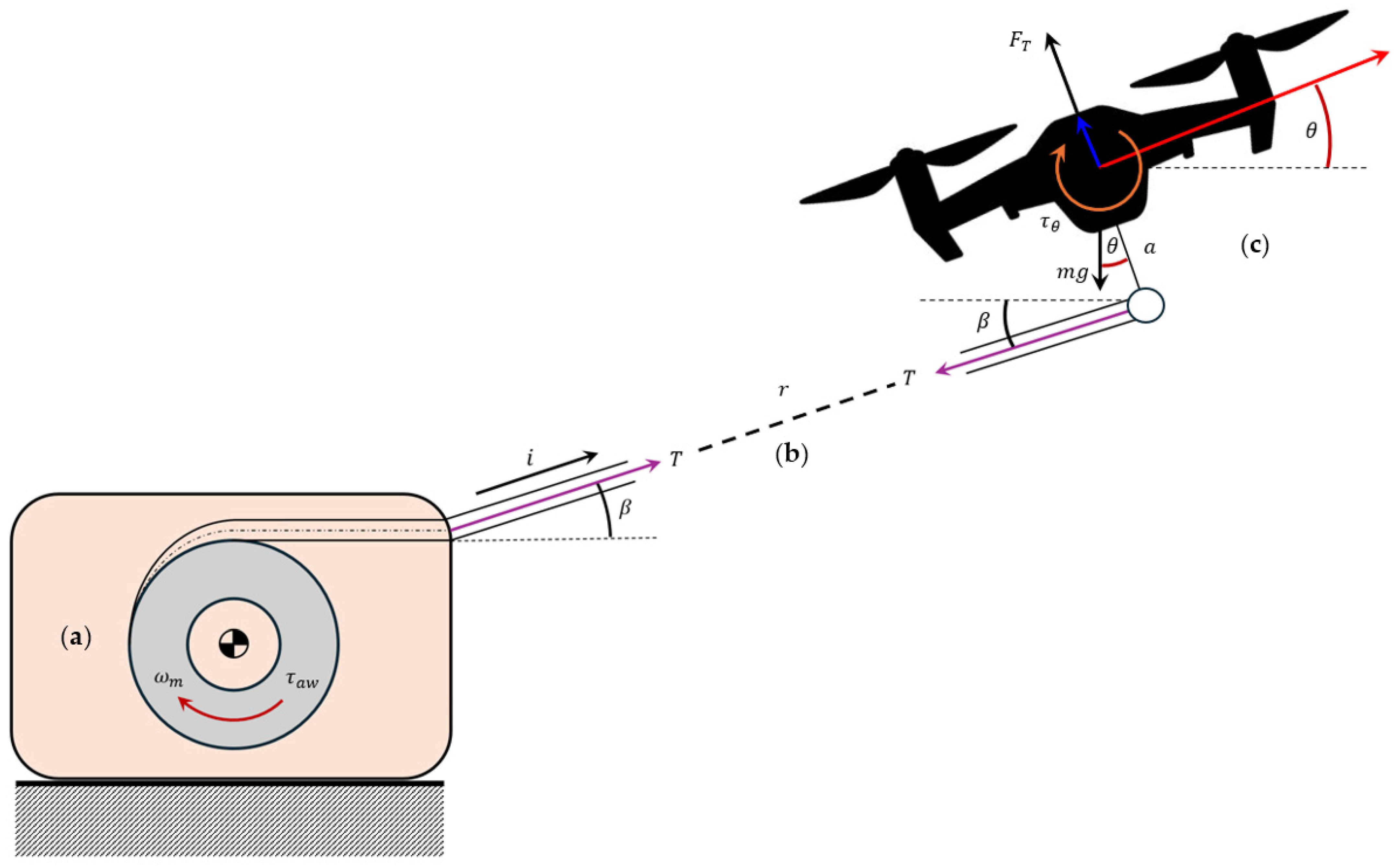
The complete dynamics of a TUAV system are fully characterized only when the tether cable and automated winch dynamics are integrated into the drone’s core EoM motion. Depending on the level of fidelity and assumptions made different unified models can be formulated. This section outlines the main modeling strategies used in the literature to describe the coupled drone–tether–winch dynamics.

3.4.1. Tethered Drone Dynamic Model

In a taut tether configuration, the UAV and winch dynamics are coupled through the tension force acting along the cable. Unified models often neglect cable mass and elasticity, assuming a massless, inextensible link to simplify the analysis. A basic 2D Cartesian model introduces the effect of cable tension $T$ on UAV translational dynamics [132]:

$$\left\{\begin{array}{l}m\ddot{x}=mg{s}_{\theta }-T{s}_{\theta +\beta }\\ m\ddot{z}=F_T-mg{c}_{\theta }-F_T{c}_{\theta +\beta }\end{array}\right.,$$

(36)

where $\theta$ is the drone pitch angle and $\beta$ the elevation angle. The taut cable condition is enforced by the constraint $T\left(t\right)>0$ at each time instant. The tension is derived from force equilibrium along the cable direction as

$$T=F_T{c}_{\theta +\beta }-mg{c}_{\beta }+mL{\dot{\beta }}^2$$

(37)

By representing the tension vector in spherical coordinates as ${\mathit{T}}^S={\left[\begin{array}{ccc}-T& 0& 0\end{array}\right]}^T$, and considering an off-center tether attachment defined by a lever arm $\mathit{a}={\left[\begin{array}{ccc}{a}_x& a_y& a_z\end{array}\right]}^T$, the set of EoM (14) is updated to reflect the influence of these external forces and moments, expressed in the inertial frame as follows [103,133]:

$$\mathit{F}=\left[\begin{array}{c}{F}_{Tx}\\ F_{Ty}\\ F_{Tz}\end{array}\right]={\mathit{R}}_B^I\cdot {\mathit{F}}_T^B+{{\mathit{R}}_B^I{\mathit{R}}_S^B\cdot \mathit{T}}^S ,$$

(38)

$$\mathit{\tau }=\left[\begin{array}{c}{\tau }_{\varphi }\\ {\tau }_{\theta }\\ {\tau }_{\psi }\end{array}\right]+\mathit{a}\times \left({{\mathit{R}}_B^I{\mathit{R}}_S^B\cdot \mathit{T}}^S\right),$$

(39)

where ${\mathit{R}}_S^B$ and ${\mathit{R}}_B^I$ are the rotation matrices mapping from spherical to body-fixed, and from body-fixed to inertial frames, respectively. For full coupling with the winch dynamics, an initial passive model assumes a constant torque ${\tau }_{aw}$, with cable length governed by drone thrust alone. The resulting system is [134,135,136]

$$\left\{\begin{array}{l} m\ddot{\mathit{r}}=-{{\mathit{R}}_B^I{\mathit{R}}_S^B\cdot \mathit{T}}^S+{\mathit{R}}_B^I\cdot {\mathit{F}}_T^B-mg{\mathit{e}}_3\\ I_{aw}{\displaystyle \frac{\ddot{L}}{r_c}}={\tau }_{aw}+r_{c}T\end{array}\right. ,$$

(40)

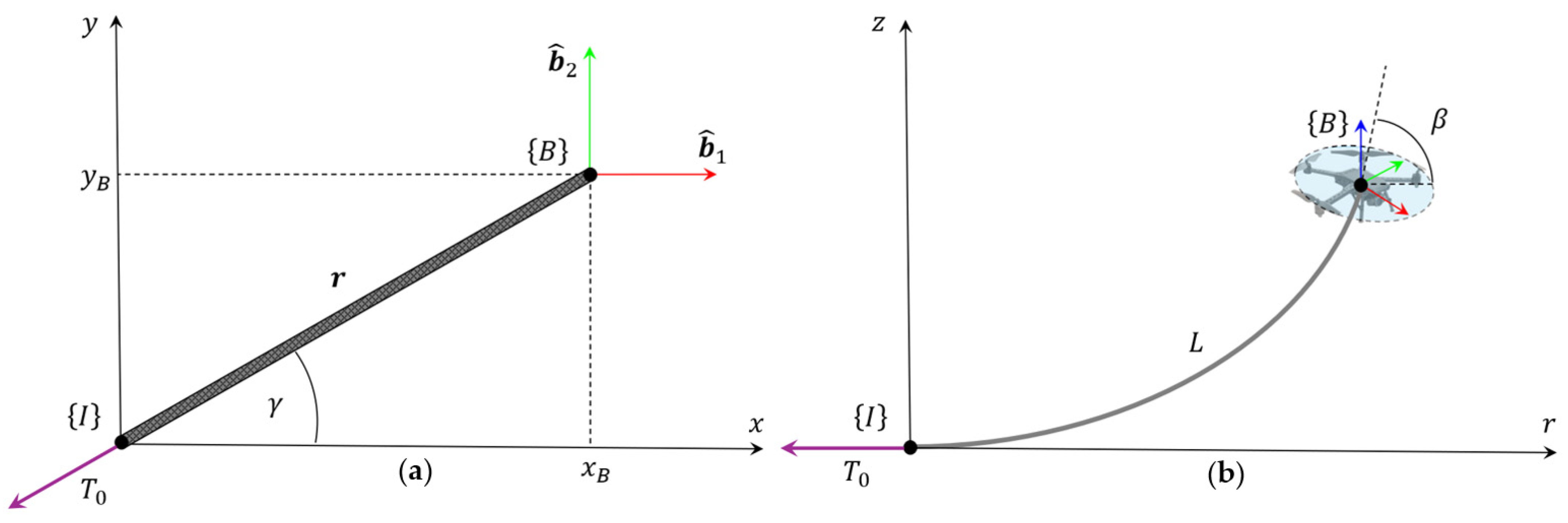
where the term $\ddot{L}$ represents the cable length variation acceleration. Using a spherical-coordinate-based inertial frame, UAV dynamics can be expressed in terms of radial position, elevation, and azimuth angles. Since tension acts solely along the radial direction, the 3D model can be reasonably reduced to a 2D planar case by neglecting azimuthal effects [125], as illustrated in Figure 12. Defining the drone’s CoG in polar coordinates ${\mathit{q}}_p=\left\{r\in \mathbb{R}>0,\beta \in \left[0,\pi \right]\right\}$, the EoM are given as [99,100,101,125]

$$\left\{\begin{array}{ccc}\hfill m\ddot{r}& =& mr{\dot{\beta }}^2-mg{s}_{\beta }+F_T{s}_{\beta +\theta }-T\hfill \\ \hfill m{r}^2\ddot{\beta }& =& -2mr\dot{r}\dot{\beta }-mgr{c}_{\beta }+F_{T}r{c}_{\beta +\theta }\hfill \\ \hfill I\ddot{\theta }& =& {\tau }_{\theta }\hfill \end{array}\right.$$

(41)

Adding a controllable winch, where cable length is regulated via the motor torque ${\tau }_{aw}$ and angular speed ${\omega }_m$, leads to a fully coupled model [10,11]:

$$\left\{\begin{array}{ccc}\hfill I_{aw}{\displaystyle \frac{{\dot{\omega }}_m}{r_c}}& =& {\tau }_{aw}-B_f{\omega }_m-r_{c}T\hfill \\ \hfill m{r}^2\ddot{\beta }& =& -2mr\dot{r}\dot{\beta }-mgr{c}_{\beta }+F_{T}r{c}_{\beta +\theta }\hfill \\ \hfill I\ddot{\theta }& =& {\tau }_{\theta }\hfill \end{array} ,\right.$$

(42)

subject to the taut cable constraint

$$\begin{array}{cc}T\left(t\right)=T\left(r\left(t\right),\beta \left(t\right),\theta \left(t\right)\right)=mr{\dot{\beta }}^2-mg{s}_{\beta }+F_T{s}_{\beta +\theta }-m\ddot{r}>0& \forall t\ge 0\end{array}$$

(43)

The term $B_f{\omega }_m$ accounts for losses due to viscous friction [45,46], while tether length and UAV motion are related via $\ddot{L}=\ddot{r}={\dot{\omega }}_m/r_c$. This model captures the key mechanical interactions in TUAV systems involving a taut cable and active winch.

3.4.2. Tethered Drone Power Draw Model

The nominal power required from the ground power supply is defined as

$$P_{nom}={\displaystyle \frac{P_T}{{\eta }_{el}}} ,$$

(44)

where $P_T$ is the total power drawn by the drone due to thrust generation and ${\eta }_{el}$ accounts for losses in the tether voltage conversion system. Following the helicopter theory approach, drone power consumption can be analyzed in three stages: ideal, mechanical, and electrical power. The ideal thrust power is estimated as [25]

$$P_{T,id}={\displaystyle \frac{{\left(W_d+W_t\right)}^{\frac{3}{2}}}{\sqrt{2{\rho }_a{A}_r}}},$$

(45)

where $W_d$ and $W_t$ are the weights of the drone and deployed tether, ${\rho }_a$ is the air density, and $A_r$ is the rotor disk area. The mechanical power accounts for aerodynamic inefficiencies via the figure of merit (FOM):

$$P_{T,m}={\displaystyle \frac{P_{T,id}}{S_{FOM}}}$$

(46)

Finally, incorporating motor efficiency ${\eta }_m$, the total electrical power required by the drone becomes

$$P_T={\displaystyle \frac{{\left(W_d+W_t\right)}^{\frac{3}{2}}}{{\eta }_m{S}_{FOM}\sqrt{2{\rho }_a{A}_r}}}$$

(47)

Substituting into Equation (42) yields the drone’s effective power demand. To obtain the overall TUAV power model, tether transmission losses (25) are added:

$$P_{tot}=P_{nom}+P_{loss}$$

(48)

3.5. Comparative Analysis and Modeling Trade-Offs

The mathematical modeling of TUAV systems spans multiple interconnected domains, namely, the aerial platform, the tether cable, and the winch mechanism. However, synthesizing these distinct models into a unified and computationally efficient framework remains an open challenge, particularly when seeking a balance between physical accuracy and real-time implementability. Each modeling domain is introduced below, and a comparative overview of their advantages, limitations, and best-use scenarios is summarized in

Table 2. Comparative analysis of TUAV subsystem modeling approaches.

Subsystem	Model Type	Advantages	Limitations	Best Use Cases
UAV	Euler-Lagrange	Systematic Good for symbolic manipulation	Complex to apply for multi-body extensions or contact dynamics	General modeling Analytical studies
	Newton-Euler	Intuitive formulation Efficient numerically	Less modular for symbolic derivation or constraint analysis	Real-time control Simulation
	Geometric/ Quaternion-based	Avoids singularities Full 3D attitude	Requires specialized tools Harder to interpret physically	Aggressive flight Full 3D attitude tracking
Tether	Lumped-mass (Discrete)	Low computation Supports real-time control	Limited spatial resolution Not ideal for slack conditions	Taut tethers Fast embedded Simulation
	PDE-based (Continuous)	High fidelity Captures vibrations and curvature	Computationally expensive Sensitive to parameter tuning	Offline simulation Shape dynamics Modal analysis
	Taut Cable Assumption	Simplifies coupling with UAV Constraint-based	Ignores bending, sag, and wave effects	Hovering Low-speed flight
	Slack Cable/ Catenary Model	Realistic in low-tension or long tether conditions	Requires nonlinear solvers Hard to integrate into control loops	TUAV–UGV/USV Variable tension or suspended setups
Winch	Passive (Predefined Torque)	Easy to implement in decoupled models	Ignores UAV-winch coupling Limited accuracy	Preliminary control design Constant-tension scenarios
	Active (Controlled Actuation)	Real-time tether length/tension control High precision	Requires detailed modeling and sensor feedback Numerical stiffness	Coordinated control Landing protocols Dynamic reeling

.

3.5.1. UAV Platform Dynamics Modeling

The UAV platform is commonly modeled as a rigid body using either the Euler–Lagrange or Newton–Euler approach. The former provides a structured, energy-based formulation well-suited for generalized coordinates and symbolic derivation, while the latter offers a more intuitive force–moment representation in Cartesian space, making it popular in control applications due to its simplicity and numerical efficiency. These models typically assume a symmetric, rigid multirotor and neglect effects such as propeller gyroscopic forces, frame flexibility, or aerodynamic drag unless higher-fidelity models are employed. While adequate for trajectory tracking and basic control, such simplifications limit accuracy during aggressive maneuvers, physical interaction, or in the presence of external loads. Quaternion-based or geometric methods are sometimes used to avoid singularities in full 3D attitude representation.

3.5.2. Tether Cable Dynamics

The tether, being a slender, flexible element, introduces complex dynamics that are highly sensitive to its tension state, mass distribution, and environmental interactions. Discrete models segment the tether into a series of viscoelastic links or rigid rods connected by joints with spring-damper properties. These models are computationally lightweight and can be efficiently integrated into real-time simulation or control loops. They are particularly suitable for taut tether conditions, where the tether behaves nearly as a straight constraint with minimal curvature, such as in hovering or slow, controlled maneuvers. However, these models often fail to capture the rich vibrational behavior and shape deformations present in slack or partially tensioned regimes, where gravitational and aerodynamic effects dominate. Continuous models, on the other hand, treat the tether as a deformable elastic body governed by wave-based PDEs. These allow for the simulation of longitudinal and transverse vibrations, mode shapes, and strain energy distributions, making them ideal for high-fidelity offline simulations and modal analysis. Incorporating catenary geometry, aerodynamic forces, and nonlinear tension propagation, these models offer a much closer approximation to physical behavior, especially in long or low-tension cables. However, their computational cost, sensitivity to parameter uncertainties, and complexity in boundary conditions make them impractical for embedded control applications. The choice between taut vs. slack tether modeling further influences both the form of equations and their solvability. Taut cable models often treat the tether as a massless inextensible link, simplifying integration with the UAV dynamics but neglecting internal cable dynamics. Slack models, by contrast, necessitate catenary equations and more elaborate curvature analysis, making them better suited for applications like TUAV/UGV or TUAV/USV systems operating with varying cable geometries or contact points.

3.5.3. Integrated UAV-Tether-Winch Dynamics

More advanced models fully couple the UAV, tether, and winch dynamics. The winch subsystem, typically represented by electromechanical models with motor inertia, spool radius, and tension feedback, introduces actuation dynamics that affect both cable length and force regulation. These integrated models are essential when using active TMS for coordinated drone-winch control. At a basic level, the winch can be modeled as a passive element applying a constant or predefined torque. This simplification eases integration with UAV dynamics and suffices when tether length is not actively regulated. However, it neglects the dynamic interaction between spool inertia and UAV motion, which can degrade performance during fast reeling or slack transitions. More sophisticated models treat the winch as an active actuator with closed-loop torque or speed control. These require detailed representations of motor dynamics, gear systems, and real-time tension feedback. The core trade-off lies in model coupling: loosely coupled models support modular development and faster computation, while fully coupled models offer higher fidelity at the cost of calibration effort and sensor integration (e.g., tension, length, and angle sensors). Real-time estimation remains challenging due to noise measurement, encoder quantization, and tension variability.

In conclusion, selecting an appropriate modeling strategy for TUAV systems depends strongly on the application domain High-fidelity models are indispensable for simulation, planning, and offline optimization, while reduced-order or simplified models are better suited for embedded control and real-time operation. Bridging these regimes remains a key open challenge, particularly in the context of multi-agent coordination, aerial manipulation, and tether-aware autonomous navigation.

4. Control

Controlling TUAVs presents unique challenges compared to conventional free-flying multicopters, primarily due to the dynamic coupling between the aerial platform and the TMS. In addition to the standard objectives of attitude stabilization, trajectory tracking, and disturbance rejection, TUAV control must also handle tether-specific issues such as tension regulation, cable length management, and interactions with environmental forces transmitted through the tether (e.g., wind disturbances and tether-induced constraints). The effective design of TUAV controllers relies heavily on a comprehensive understanding of the system’s dynamics. As outlined in Section 3, the TUAV, tether cable, and automated winch form an interconnected mechanical and electromechanical system whose behavior is governed by coupled nonlinear dynamics. These models establish the physical constraints and interaction mechanisms that any control strategy must respect, such as tether tension transmission, actuator limitations, and dynamic coupling. Therefore, the modeling frameworks presented in the previous chapter provide the foundation upon which the control architectures in this chapter are developed.

4.1. State-Space Model

Modeling the dynamics of a tethered drone system requires an effective state-space formulation that accounts for interactions between the system’s components, along with actuator dynamics and external disturbances. This model provides the foundation for developing control strategies that ensure the stable, responsive, and energy-efficient operation of the TUAV system.

4.1.1. Linearized Dynamics

To design effective control strategies for a TUAV system, a suitable representation is provided by a Linear Time-Invariant (LTI) state-space model that captures the key dynamics of the coupled UAV-tether-winch system while ensuring tractability for control design. Given the nonlinear nature of both UAV and tether dynamics (described in Section 3.1, Section 3.2 and Section 3.3) a linearization process is necessary around a nominal operating point, typically corresponding to a steady hover. This linearization is derived from the full dynamic models presented in Equations (40)–(42) and is based on several standard assumptions, namely:

• Small-angle approximation, simplifying rotational dynamics and decoupling vertical and lateral motion $\Rightarrow s_{\theta }\approx \theta , c_{\theta }\approx 1$;
• Tether mass, deformation, and damping effects are negligible;
• Negligible aerodynamic effects.

A proper LTI system-space model is formulated as

$$\begin{array}{l}\dot{\mathit{x}}=\mathit{A}\mathit{x}+\mathit{B}\mathit{u}\\ \mathit{y}=\mathit{C}\mathit{x}\end{array} ,$$

(49)

where [125,132]:

• $\mathit{x}\in {\mathbb{R}}^n$ is the state vector, accounting for both mechanical and electrical variables of the TUAV system;
• $\mathit{u}\in {\mathbb{R}}^m$ is the control inputs vector;
• $\mathit{y}\in {\mathbb{R}}^p$ is the objective output vector to be controlled, such as the UAV position, orientation, and tether length;
• $\mathit{A}, \mathit{B},$ and $\mathit{C}$ are the system matrices derived from the linearized EoM.

In early formulations, the control input vector $\mathit{u}$ for a tethered UAV system often mirrors that of a conventional multicopter in a 3D Cartesian space, defined as [137]

$$\mathit{u}=\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right]=\left[\begin{array}{c}{F}_T\\ {\tau }_{\varphi }\\ {\tau }_{\theta }\\ {\tau }_{\psi }\end{array}\right]$$

(50)

A more complete representation, however, incorporates the actuated winch dynamics, particularly in the 2D planar case defined by the polar coordinates $\left\{r,\beta \right\}$ for a fixed azimuth $\gamma$, as previously described in Equation (42). In this context, the control input vector simplifies to

$$\mathit{u}=\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right]=\left[\begin{array}{c}{F}_T\\ {\tau }_{\theta }\\ u_3\end{array}\right]$$

(51)

Here, the third input $u_3$ refers either to the winch’s control torque ${\tau }_{aw}$ [11] or the angular acceleration of the winch motor ${\dot{\omega }}_m$ [10]. In the polar frame, the thrust input $u_1$ can be further decomposed into its radial and elevation components, ${\left[\begin{array}{cc}{u}_T& u_{\beta }\end{array}\right]}^T$, and combined with $u_3$ for coordinated control of UAV positioning and tether length [10].

4.1.2. Nonlinear Dynamics

To capture the full dynamics of a tethered drone system, a nonlinear state-space model must be employed. Unlike linear time-invariant (LTI) models, this formulation retains the system’s inherent nonlinearities, making it suitable for advanced nonlinear control strategies. The nonlinear state-space formulation corresponds directly to the full-state UAV–tether–winch model of Equation (42) and can be written as [45,46,103]

$$\begin{array}{l}{\dot{\mathit{x}}}_1={\mathit{x}}_2\\ {\dot{\mathit{x}}}_2=\mathit{A}\left(\mathit{x}\right)+\mathit{B}\left(\mathit{x}\right)\mathit{u}+\mathit{d}\left(\mathit{x}\right)\end{array},$$

(52)

where:

• $\mathit{x}={\left[\begin{array}{cc}{\mathit{x}}_1& {\mathit{x}}_2\end{array}\right]}^T$ is the system state vector, with ${\mathit{x}}_1$ representing position-related states and ${\mathit{x}}_2$ velocity-related states, structured as a first-order system well-suited for hierarchical (outer/inner loop) control;
• $\mathit{A}\left(\mathit{x}\right)$ captures nonlinear effects from rigid-body dynamics, including Euler forces, Coriolis, centrifugal, and gravitational terms;
• $\mathit{B}\left(\mathit{x}\right)$ is the input matrix, derived from the nonlinear EoM;
• $\mathit{d}\left(\mathit{x}\right)$ models external disturbances such as wind or friction, and includes residual modeling uncertainties.

4.2. Control Techniques

Standard UAV control methods, such as Proportional-Integral-Derivative (PID) stabilization, Model Predictive Control (MPC), and adaptive schemes, are well-established in the literature. However, they need a proper reformulation to correctly address the TUAV control problem. The following subsections review control strategies tailored to tethered drone systems, focusing on tether tension and length regulation, coordinated drone-winch control, and hybrid methods that integrate flight dynamics with tether constraints. These approaches are analyzed to highlight their modeling assumptions and control implementation requirements.

4.2.1. Proportional-Integral-Derivative Control

PID control remains one of the most prevalent strategies adopted for linearized TUAV models due to its simplicity and ease of implementation. Within aerial platforms, PID or simpler Proportional-Derivative (PD) controllers are typically employed to stabilize attitude and regulate position by applying proportional, integral, and derivative gains to the tracking errors [138], which are retrieved from the linearized UAV dynamics expressed in Equation (15). This linear control law can also incorporate tether dynamics through tension feedback and lever arm considerations. More advanced implementations adopt a hierarchical cascade structure of nested control loops [114]. In spherical coordinates, the position tracking error is expressed in terms of the tether variables, which are subsequently used in the control computation [139]. On the ground side, PID control is commonly employed to regulate the winch dynamics, as described in Equations (32) and (35). The winch controller can be designed to regulate either the motor torque or the tether length, typically based on feedback from the tether length error [18,86], and in some cases for adjustable landing platform orientation control [40]. Gain tuning methods include the Ziegler–Nichols heuristic and gain scheduling across different operational ranges. Even in nonlinear control frameworks, PID-like strategies are adapted. Referring to the unified model in Equation (42), PD control laws are employed alongside nested saturation functions to constrain winch actuation input $u_3$. Similarly, tangential and attitude dynamics, represented by $u_{\beta }$ and $u_2$, can be regulated using PD controllers following appropriate trigonometric reformulations [10,11].

4.2.2. Pole Placement

A fundamental control strategy for linearized TUAV systems is pole placement, which enables precise shaping of the system’s closed-loop dynamics. This technique is especially effective when a desired trajectory [134,136]. This method has been effectively used in TUAV systems to compute both the winch torque required for tension or cable length regulation and to control the UAV’s position, velocity, and attitude tracking [104].

4.2.3. Linear Quadratic Regulator

The Linear Quadratic Regulator (LQR) is an optimal control technique well-suited for LTI or linear time-varying (LTV) approximations of TUAV systems. Unlike classic PID controllers that rely on heuristic tuning, LQR minimizes a quadratic cost function to achieve a trade-off between state tracking performance and control effort, later computing the control gains by solving the derived algebraic Riccati’s equation. By expressing the unified dynamic model of Equation (42) in a linear time-invariant (LTI) state-space form, as shown in Equation (49), the LQR method is effectively applied to both position control [118] and attitude stabilization [125] in TUAV systems. For the automated winch, LQR can be extended with integral action, yielding a Linear Quadratic Integral (LQI) controller, to regulate tether length and tension while minimizing steady-state errors [106]. Additionally, LQR performance can be further enhanced through gain scheduling techniques [118].

4.2.4. Model Predictive Control

MPC has proven to be an effective technique for controlling tethered drone systems. MPC addresses an optimal control problem at each time step by computing control actions that optimize a predefined performance criterion while satisfying system constraints. This is achieved through tailored cost functions that incorporate constraints such as tether tension, as formulated in Equations (37) and (43). Additional constraints include the actuation limits of the UAV and the winch actuator of the TMS, the latter being modeled electrically as described in Equation (34). In a linear MPC framework, the system dynamics are modeled in discrete time and linearized around a nominal operating point. An MPC formulation enables the coordinated control of both the UAV and the winch through a unified state-space representation. This approach maintains tether tautness while ensuring smooth and feasible trajectory tracking by minimizing a standard quadratic cost function, subject to state and input constraints. Linear MPC has demonstrated its effectiveness in stabilizing the UAV’s position and preserving tether tension under varying operational conditions. Its implementation within a Quadratic Programming (QP) framework highlights its suitability for real-time control applications [125]. In the context of formation control for tethered drones, a supervisory linear MPC strategy can be employed, wherein a finite horizon optimal control problem (FHOCP) is solved at each control step to generate reference positions and yaw angles for all UAVs within the system. The tailored cost function incorporates penalties on these reference variables, as well as on their rate of change, to promote smooth trajectory tracking. Furthermore, state and input constraints are explicitly formulated to account for limitations on tether length, UAV altitude, and the spatial configuration imposed by the formation and tether geometry [104]. A Nonlinear Model Predictive Control (NMPC) approach is well-suited for managing the complex dynamics of a tethered UAV, particularly during landing on inclined surfaces. This method effectively captures nonlinear UAV-tether interactions. The cost function is designed to penalize deviations from the target landing position and orientation, as well as slack variables related to soft landing constraints, thereby promoting a smooth and controlled descent. System constraints are embedded within the nonlinear optimization problem, which is solved in real time using a Sequential Quadratic Programming scheme (RTI-SQP) [140].

4.2.5. Feedback Linearization

Given the highly nonlinear nature of tethered UAV (TUAV) systems, particularly when incorporating automated winch dynamics, feedback linearization presents a valuable control design strategy. This technique employs static and dynamic feedback transformations to convert the original nonlinear system into an equivalent, fully linear, and decoupled system across all state configurations [134,135,136]. The tracking of any given desired trajectories can be achieved by applying any linear control technique to the equivalent linear system, such as pole placement [134,136], a PID control law [44,45], or a LQR-linear MPC combined problem [125].

4.2.6. Active Disturbance Rejection Control

Active Disturbance Rejection Control (ADRC) can be employed within the attitude control loop of a TUAV operating in coordination with a ground-based unmanned vehicle [141], or for the outer position control loop [107]. The principal control objective is to counteract the destabilizing influence of cable-induced disturbances on the UAV, enhancing overall flight stability. The ADRC framework comprises three fundamental components:

• Tracking Differentiator (TD): Used for smoothing reference signals and extracting tracking errors, providing clean input for the control loop;
• State Observer: Extended State Observer (ESO) for estimating internal system states and external disturbances [141] or Switching Extended State Observer (SESO), improving robustness under varying dynamic conditions [107];
• Nonlinear State Error Feedback (NLSEF): Generates control actions based on observed states and errors, actively compensating for estimated disturbances.

Due to the inherent complexity and parameter sensitivity of the ADRC scheme, a Particle Swarm Optimization (PSO) algorithm is utilized to optimize key observer parameters. This optimization is performed by minimizing the Integral of the Time-weighted Absolute Error (ITAE) criterion, thereby ensuring a fast and accurate system response [141].

4.2.7. Backstepping Control

Backstepping control techniques have proven to be highly effective in addressing the typical TUAV systems’ challenges such as external disturbances and tether dynamics. Classic backstepping control can stabilize both position and attitude by first addressing position regulation through a Lyapunov-based virtual control law, followed by a PID-like law for attitude stabilization. This approach has been effectively implemented by integrating the fully coupled system dynamics described in Equation (42) into the nonlinear state-space formulation presented in Equation (52). It enables the maintenance of relative positioning between the UAV and an oscillating tethered base, such as a buoy, under the influence of environmental disturbances including wind gusts, water currents, and buoy-induced motion [101]. Backstepping is also applied in both loops to ensure stability and compensate for varying external forces, such as the recoil from a water jet in firefighting operations [58]. Integral backstepping employs an iterative backstepping process to stabilize the roll, pitch, and yaw angles, ensuring finite-time convergence to the desired reference values. By introducing integral terms, the method eliminates steady-state tracking errors and achieves rapid attitude stabilization [107]. Lastly, adaptive control can be integrated with backstepping to manage wind disturbances in tethered drone systems. An adaptive estimator predicts wind forces, modeled according to Equations (23) and (24), while the backstepping control law ensures coordination between the UAV and a mobile ground base, such as a UGV, using feedback mechanisms to minimize tracking errors over time [142].

4.2.8. Geometric Control

The geometric control method for tethered quadrotor systems effectively addresses the between the drone’s motion and the tether’s tension, avoiding singularities and simplifying the control design process by using a global coordinate system. The formulation aligns with the dynamics captured in the unified model under the taut tether assumption, as described in Equations (40)–(42). The control law is divided into two components: the perpendicular component ensures the tether follows the desired trajectory by controlling the link dynamics, while the parallel component manages the tether’s tension, maintaining it taut and stable. The method aims for asymptotic stabilization of both the tether’s direction and tension independently, driving them both to their desired values. Additionally, the method accounts for flexible tether dynamics, adjusting the tension as needed to prevent undesirable vibrations [143]. Building on this foundation, advanced geometric control also applies to multiple UAVs (swarms). The control law stabilizes both the tether’s orientation and the quadrotor’s attitude, ensuring that the thrust produced by each drone’s propeller matches the required thrust vector [106].

4.2.9. Sliding Mode Control

In the control strategy for tethered drones, a Sliding Mode Control (SMC) approach is adopted to maintain the drone’s trajectory within a safe flight region, despite external disturbances and modeling inaccuracies. The dynamic formulation underlying this control technique is derived from the unified model described by Equation (42), which is later incorporated into the nonlinear state-space representation given in Equation (52). SMC design involves defining a sliding surface incorporating proportional, derivative, and integral error terms to guide the system toward desired reference trajectories. The control law is structured in two parts: a feedback term derived from feedback linearization and SMC, and a feedforward term compensating for estimated disturbances such as aerodynamic forces, described by Equations (23) and (24). Stability is analytically proven through Lyapunov theory, ensuring convergence of tracking errors. To mitigate the well-known chattering issue in SMC, a smooth hyperbolic tangent function replaces the discontinuous sign function. Control parameters are tuned using pole placement to balance speed and damping across control loops, prioritizing fast tether reeling dynamics [46].

4.2.10. Impedance Control

The impedance control technique is designed to enable tethered drones to interact compliantly and stably with external environments, such as physical surfaces or dynamic contact forces transmitted through the tether. The impedance controller is built around a compliant model defined by inertia, damping, and stiffness matrices, essentially replicating the behavior of a mass-spring-damper system. The control law incorporates the desired trajectory and compensates for external forces, including the interaction force from the environment and an observer-based estimated disturbance, and inertial, rotational, and gravitational dynamics, including a feedforward term. The method ensures that the drone can maintain stability and adapt its motion naturally in response to external forces, while still adhering to a desired motion profile [144]. Impedance control can also be used for the ground winch control problem. As an outer loop controller, it computes the desired position offset based on measured or estimated tether tension, while the inner loop, based on position control (PID), adjusts the motor voltage to achieve the necessary tether length to maintain the desired tension. This architecture supports stable real-time adaptation to disturbances while ensuring accurate tether tracking [107].

4.2.11. Admittance Control

The admittance control technique for tethered drone systems offers a dynamic framework that interprets external forces and torques to modulate the drone’s motion in a compliant and responsive manner. The control strategy hinges on estimating external interactions, such as those from a human operator or the tether, at the drone’s CoG and torque about the yaw axis, using pose measurements and rotor speeds. By shaping the drone’s behavior as a mass-damper system and setting virtual parameters for inertia and damping, the drone can be tuned to respond smoothly to estimated external inputs. These inputs, once estimated, are used to generate reference trajectories for the drone’s position and yaw angle. The reference motion, treated as a system output under virtual mechanical properties, reacts proportionally to the force and torque signals, enabling intuitive and stable interaction dynamics. Finally, using the principle of differential flatness, the full set of required inputs, including thrust and torques, can be derived to drive the drone along the desired trajectory [145].

4.2.12. Fuzzy Logic Control

The fuzzy logic control method for a tethered drone system offers a robust and interpretable approach to managing the drone’s pitch and yaw in coordination with a mobile ground base, e.g., a UGV/rover. The core of this method lies in a force feedback control strategy, where the drone adjusts its orientation based on the tether forces and their rates, caused by the rover’s motion. The fuzzy controller interprets two main variables: the difference between measured and equilibrium tether force, and the rate of change of that force. These inputs influence the drone’s pitch and yaw through linguistic rules defined over Gaussian membership functions, which ensure smooth control transitions. The rule base, constructed through intuitive reasoning, ensures that conflicting inputs can result in neutral outputs, minimizing unnecessary drone adjustments. The outputs from the fuzzy logic controllers are interpreted as desired pitch and yaw angles, which are then fed into a lower-level PD-based attitude controller. This controller computes the necessary adjustments in rotor speeds to achieve the desired drone orientation [142].

4.3. Comparative Evaluation of TUAV Control Techniques

The previous section presented a range of control strategies adapted for TUAVs, spanning classical, nonlinear, robust, and emerging data-driven methods. While these techniques are often developed in response to the unique dynamics introduced by the tether (e.g., underactuation, cable tension feedback, and coupled ground–aerial dynamics), their practical deployment is influenced by trade-offs between computational complexity, control accuracy, real-time feasibility, and sensitivity to modeling errors. These trade-offs are comparatively summarized in

Table 3. Comparative summary of TUAV control techniques across application scenarios.

Control Technique	Complexity	Real-Time Feasibility	Robustness	Application Domains	Limitations
Linear Control	Low– Medium	High	Low– Medium	Hovering Station-keeping Trajectory tracking (linearized)	Linear regimes Sensitive to modeling errors
Backstepping	Medium	Medium	Medium– High	Underactuated TUAVs Cable force incorporation	Complex to design Requires accurate system structure
Geometric Control	Medium–High	High	Medium– High	Full pose control on SE(3) Agile maneuvers	Complex tuning Assumes known dynamics
SMC	Medium	Medium- High	High	Disturbance rejection Tension control	Chattering Noisy in measurement-driven implementation
Adaptive Control	High	Medium	High	Systems with uncertain parameters (mass, stiffness)	Slower convergence Stability proofs required
MPC	Very High	Low- Medium	High	Obstacle avoidance Constrained multi-robot planning	Optimization overhead Less suited for onboard execution
Tether Force-Based Control	Medium	Medium- High	Medium	Tension regulation Tether-aware-reeling	Relies on accurate force sensing Underperforms in delay
Event- Triggered Control	Medium	High	Medium	Energy-efficient control Sparse updates	Trigger logic tuning Can miss rapid disturbances
ADRC	Medium–High	Medium	High	Environments with high uncertainty or external forces	Observer design and tuning complexity

, which outlines the strengths, limitations, and typical application domains of each control strategy.

Linear controllers such as PID, LQR, and pole placement remain foundational for TUAV control due to their simplicity and high real-time reliability. However, their effectiveness is limited to linearized regimes and they often underperform under nonlinearity, actuator constraints, or modeling uncertainty. Backstepping and geometric control, including feedback linearization, address these limitations by explicitly handling underactuated dynamics and full pose control, but they require precise system models and careful gain design. Robust strategies like SMC and Adaptive Control improve disturbance rejection and adaptivity in the presence of model uncertainties. Yet, they often suffer from chattering or slow adaptation, respectively. MPC provides constraint-aware trajectory generation but incurs high computational costs, limiting its real-time usability on embedded platforms. More recent methods such as ADRC aim to blend disturbance rejection with observer-based design but remain underexplored in aerial applications. Meanwhile, Event-triggered control offers significant energy savings and reduced computation in sparse-update settings, though tuning the triggering logic is nontrivial. These observations highlight that no single control strategy universally dominates. The choice must be driven by mission constraints (e.g., maneuver aggressiveness, hardware limits, operating environment) and platform resources (e.g., onboard computation, sensor suite, communication delays). Future work may focus on hybrid architectures, combining learning with physics-based control to balance robustness, efficiency, and generalizability.

5. Hardware and Sensors

The operation of TUAVs requires a well-integrated combination of onboard avionics, ground-based systems, and an array of sensors to ensure full controllability of all system parameters. The tether cable introduces new hardware requirements, demanding specialized onboard and ground-based components. Additionally, sensor integration plays a crucial role in state estimation, environmental awareness, and monitoring under varying flight conditions. This chapter delves into the essential components of tethered drone systems, distinguishing between aerial and ground-based hardware and sensors.

5.1. Hardware

5.1.1. Avionics/Onboard Hardware

The avionics suite is the central nervous system of a TUAV, encompassing all onboard electronic systems that manage flight dynamics, navigation, and communication. The key hardware components typically found in TUAV systems are listed below, and a more detailed overview of their functions, roles, and representative variants is provided in Table 4.

• GPS/RTK Module;
• UWB Modules/Tags;
• Flight Controller;
• Companion Computer;
• Microcontroller;
• Wireless Communication Module;
• RC Receiver.

Table 4. Overview of onboard hardware components in tethered drone systems.

Hardware Component	Description	Variants/Brands
GPS/RTK	Module providing up to centimeter-level positioning accuracy, essential for precise navigation and hovering capabilities in tethered UAV operations.	RTK u-blox ZED-F9P [34,48]  RTK Here2 [57]  Other RTKs [85,97]  Double GPS [146]
UWB	Transceiver modules/tags providing precise positioning data of the UAV/payload within a smaller range, crucial for operations in GPS-denied environments.	DWM1001C UWB [40]  LinkTrack UWB [34]  UWB tag [147]
Flight Controller	Autopilot device, like the Pixhawk series, serves as primary control unit, processing redundant integrated sensor inputs to stabilize and control the UAV’s flight.	ArduPilot [48,97]  PX4 [40,44,57,118,146,148]
Companion Computer	Small computer unit working alongside flight controllers to handle complex computations, enabling advanced functionalities like image processing and autonomous navigation, via serial MAVLink protocol communication with the flight controller.	NVIDIA Jetson [34,148]  UDOO X86 II ULTRA [40,87]  Intel NUC 11 [40]  Raspberry Pi 3+ [97]  Odroid Xu [85,147]
Microcontroller	Small low-power control unit used to manage onboard auxiliary devices such as servos, payload mechanisms, or sensors, offloading flight controllers, or companion computer computational effort.	Arduino [87,105,146]  GR-SAKURA [137]
Communication Module	Onboard wireless communication module to establish connection with ground station computer.	ROHM BP3591 [137]

Table 4. Overview of onboard hardware components in tethered drone systems.

Hardware Component	Description	Variants/Brands
GPS/RTK	Module providing up to centimeter-level positioning accuracy, essential for precise navigation and hovering capabilities in tethered UAV operations.	RTK u-blox ZED-F9P [34,48]  RTK Here2 [57]  Other RTKs [85,97]  Double GPS [146]
UWB	Transceiver modules/tags providing precise positioning data of the UAV/payload within a smaller range, crucial for operations in GPS-denied environments.	DWM1001C UWB [40]  LinkTrack UWB [34]  UWB tag [147]
Flight Controller	Autopilot device, like the Pixhawk series, serves as primary control unit, processing redundant integrated sensor inputs to stabilize and control the UAV’s flight.	ArduPilot [48,97]  PX4 [40,44,57,118,146,148]
Companion Computer	Small computer unit working alongside flight controllers to handle complex computations, enabling advanced functionalities like image processing and autonomous navigation, via serial MAVLink protocol communication with the flight controller.	NVIDIA Jetson [34,148]  UDOO X86 II ULTRA [40,87]  Intel NUC 11 [40]  Raspberry Pi 3+ [97]  Odroid Xu [85,147]
Microcontroller	Small low-power control unit used to manage onboard auxiliary devices such as servos, payload mechanisms, or sensors, offloading flight controllers, or companion computer computational effort.	Arduino [87,105,146]  GR-SAKURA [137]
Communication Module	Onboard wireless communication module to establish connection with ground station computer.	ROHM BP3591 [137]

5.1.2. Ground-Level Hardware

The ground station serves as the command center for TUAV operations, housing equipment necessary for control, communication, and data processing. In indoor experimental setups, it is often surrounded by a testbed infrastructure to evaluate and validate simulation results. The typical components found at the ground level are listed below, while Table 5 provides a detailed overview of their functions and commonly used variants in TUAV systems.

• Ground Station Computer;
• Ground Single board Computer (SBC);
• Microcontroller;
• Wireless Communication Module;
• RTK Base Antennas/UWB Anchors;
• Motion Capture System;
• Meteorological Stations;
• RC Transmitters.

Table 5. Overview of ground control station hardware components in tethered drone systems.

Hardware Component	Description	Variants/Brands
Main Computer	Main system coordinates all other microcomputers/controllers’ activities and provides interfaces to the human operators, integrating the Robot Operating System (ROS) framework to communicate with other TUAV devices.	Linux Operative System  ROS framework integration [40,44,87,147,148]
SBC	Compact, energy-efficient Single Board Computers for the handling of autonomous operations with the possibility to be even placed on mobile unmanned robots.	Advantech MIO5393 [148]
Microcontroller	Ground-level small low-power control unit role in managing subsystems, such as the TMS.	Arduino UNO R3 [40]  ESP32 [44]  DF-Robot Mega2560 [85]
Communication Module	Module enabling data transmission between the drone and ground station via Wi-Fi network or IEEE 802.15.4 protocol, ensuring seamless data communication.	ESP32 Wi-Fi [44]  Digi XBee 3 Zigbee 3 [48,105]
RTK Antennas/  UWB Anchors	Stationary systems enable precise localization accuracy (RTK antennas) or allow it where GPS signals are weak or obstructed (UWB anchors), working together with their aerial counterparts;	UWB anchors [147,149]
Motion Capture System	Multi-camera system for tracking the UAV’s position and movement, determining the aerial platform “ground truth” and aiding in precise navigation and control;	Vicon [44,83,86,87]  OptiTrack [30,120]  Kinect [105]
Meteorological Station	Instruments to monitor environmental conditions, offering critical data for flight planning and safety.	Anemometer [44]  DAVIS Vantage Vue [57]

Table 5. Overview of ground control station hardware components in tethered drone systems.

Hardware Component	Description	Variants/Brands
Main Computer	Main system coordinates all other microcomputers/controllers’ activities and provides interfaces to the human operators, integrating the Robot Operating System (ROS) framework to communicate with other TUAV devices.	Linux Operative System  ROS framework integration [40,44,87,147,148]
SBC	Compact, energy-efficient Single Board Computers for the handling of autonomous operations with the possibility to be even placed on mobile unmanned robots.	Advantech MIO5393 [148]
Microcontroller	Ground-level small low-power control unit role in managing subsystems, such as the TMS.	Arduino UNO R3 [40]  ESP32 [44]  DF-Robot Mega2560 [85]
Communication Module	Module enabling data transmission between the drone and ground station via Wi-Fi network or IEEE 802.15.4 protocol, ensuring seamless data communication.	ESP32 Wi-Fi [44]  Digi XBee 3 Zigbee 3 [48,105]
RTK Antennas/  UWB Anchors	Stationary systems enable precise localization accuracy (RTK antennas) or allow it where GPS signals are weak or obstructed (UWB anchors), working together with their aerial counterparts;	UWB anchors [147,149]
Motion Capture System	Multi-camera system for tracking the UAV’s position and movement, determining the aerial platform “ground truth” and aiding in precise navigation and control;	Vicon [44,83,86,87]  OptiTrack [30,120]  Kinect [105]
Meteorological Station	Instruments to monitor environmental conditions, offering critical data for flight planning and safety.	Anemometer [44]  DAVIS Vantage Vue [57]

5.2. Sensors

While the hardware components of a TUAV system define its computational backbone, sensors serve as its perceptual core, enabling real-time awareness, stability, and control. With the integration of a tether cable, however, additional sensing elements become necessary to monitor cable dynamics and ground-based interactions. This section explores the diverse range of sensors used in tethered drone systems, again distinguishing between aerial and ground levels. Together, these sensing systems provide the data needed for navigation, state estimation, disturbance rejection, and safe interaction with the environment.

5.2.1. Tethered Drone Sensors

A range of onboard sensors are integrated into TUAV systems to support perception, navigation, and tether-aware control. The key sensor types commonly used are listed below, and their functions along with representative variants are further detailed in Table 6.

• Onboard Camera;
• Range Sensor;
• Mapping Sensor;
• Additional IMU;
• Tension Sensor;
• Angle Sensor;
• Contact Force Sensor.

Table 6. Overview of onboard drone sensors in tethered drone systems.

Sensor	Description	Variants/Brands
Onboard Camera	Camera device used for visual-inertial odometry (VIO) and SLAM, localization relative to ArUco boards, aerial photogrammetry, and proximity viewing.	Intel RealSense T265 [40]  RGB global shutter + 2D gimbal [97]  CMOS + global shutter [146]  Sony HDR-AZ1 + 3D gimbal [137,150]
Range Sensor	Device measuring distances for obstacle avoidance, indoor ceiling detection, and drone altitude awareness.	Garmin Lidar Lite [40]  Ouster OS1 [20,23]
Mapping Sensor	Usually a LiDAR depth camera for SLAM applications.	Intel RealSense L515 [40]  Kinect [85]
Additional IMU	External IMUs can be used to detect tether angles and to improve flight controller internal IMU accuracy.	Xsens MTi [144]
Tension Sensor	Load cell-based sensors that detect tension force in the cable.	Fulcrum + load cell [86,119]  Tensile load cell [105]
Angle Sensor	Detects tether departure angles from UAV body or gimbal joints.	Potentiometers [86,119]  Cardan joint + potentiometers [137,151]  TOF-based [38]  2d-axis joystick [87,105]  Custom gimbal [97]
Contact Force Sensor	Detects physical forces and torques at the drone interface with external environment.	On End-effector [144]

Table 6. Overview of onboard drone sensors in tethered drone systems.

Sensor	Description	Variants/Brands
Onboard Camera	Camera device used for visual-inertial odometry (VIO) and SLAM, localization relative to ArUco boards, aerial photogrammetry, and proximity viewing.	Intel RealSense T265 [40]  RGB global shutter + 2D gimbal [97]  CMOS + global shutter [146]  Sony HDR-AZ1 + 3D gimbal [137,150]
Range Sensor	Device measuring distances for obstacle avoidance, indoor ceiling detection, and drone altitude awareness.	Garmin Lidar Lite [40]  Ouster OS1 [20,23]
Mapping Sensor	Usually a LiDAR depth camera for SLAM applications.	Intel RealSense L515 [40]  Kinect [85]
Additional IMU	External IMUs can be used to detect tether angles and to improve flight controller internal IMU accuracy.	Xsens MTi [144]
Tension Sensor	Load cell-based sensors that detect tension force in the cable.	Fulcrum + load cell [86,119]  Tensile load cell [105]
Angle Sensor	Detects tether departure angles from UAV body or gimbal joints.	Potentiometers [86,119]  Cardan joint + potentiometers [137,151]  TOF-based [38]  2d-axis joystick [87,105]  Custom gimbal [97]
Contact Force Sensor	Detects physical forces and torques at the drone interface with external environment.	On End-effector [144]

5.2.2. TMS Sensors

The TMS incorporates a dedicated set of sensors designed to monitor cable-related states and environmental conditions. The main sensor types used in such setups are listed below, while Table 7 provides a detailed overview of their measurement functions and representative hardware implementations.

• Tension Sensor;
• Angle Sensor;
• Length Sensor;
• Temperature Sensor.

Table 7. Overview of TMS sensor suite in tethered drone systems.

Sensor	Description	Variants/Brands
Tension Sensor	Device designed to measure tether tension through various mechanisms, including spring-loaded lever arms, powder clutches, torque sensors, or roller-based tension meters.	Spring + potentiometer [40,85,87]  Kistler 4502a torque sensor [44]  Powder clutch setup [83]  Tension meter [152]
Angle Sensor	Measures tether departure angles at the TMS using a geometry similar to the aerial counterpart, with slight structural variations.	Cardan joint + potentiometers [40,87]  Turntable + vertical moving arm [83,85,97]
Length Sensor	Deployed tether length is measured via DC motor encoder by counting shaft rotations.	Digital rotary encoder [19,38,40,83,87,152]  Hall-effect sensor [85]
Temperature Sensor	Array of digital thermometers spaced along the tether, calibrated against a bead thermistor for accurate temperature sensing.	DS18B20 [47,48]

Table 7. Overview of TMS sensor suite in tethered drone systems.

Sensor	Description	Variants/Brands
Tension Sensor	Device designed to measure tether tension through various mechanisms, including spring-loaded lever arms, powder clutches, torque sensors, or roller-based tension meters.	Spring + potentiometer [40,85,87]  Kistler 4502a torque sensor [44]  Powder clutch setup [83]  Tension meter [152]
Angle Sensor	Measures tether departure angles at the TMS using a geometry similar to the aerial counterpart, with slight structural variations.	Cardan joint + potentiometers [40,87]  Turntable + vertical moving arm [83,85,97]
Length Sensor	Deployed tether length is measured via DC motor encoder by counting shaft rotations.	Digital rotary encoder [19,38,40,83,87,152]  Hall-effect sensor [85]
Temperature Sensor	Array of digital thermometers spaced along the tether, calibrated against a bead thermistor for accurate temperature sensing.	DS18B20 [47,48]

6. Localization and Navigation

The ability to accurately localize and autonomously navigate is fundamental to the effective operation of TUAVs, particularly in environments that are GPS-denied, visually degraded, or highly constrained. As with all other aspects discussed in this review, the tether introduces both challenges and unique opportunities for enhancing perception and control. Consequently, localization and navigation strategies for tethered drone systems can adopt tailored approaches that go beyond conventional aerial robotics paradigms. This chapter provides a comprehensive overview of state estimation techniques, localization methods, and navigation strategies that can be applied to tethered drones. Collectively, these approaches illustrate the evolving role of the tether as a valuable sensing and actuation element, fostering intelligent and autonomous operation in complex and constrained environments.

6.1. State and Disturbance Observers

In tethered drone systems, accurate state and disturbance estimation are crucial for localization, autonomous navigation, and control, particularly in GPS-denied environments where external sensors may be limited or uncertain. To mitigate these challenges, various observer-based techniques are employed to estimate the system’s internal states and external disturbances, ensuring precise control and improved system performance. Several observer-based estimation techniques are commonly used in tethered drone systems, leveraging sensor fusion strategies, disturbance compensation, and state reconstruction approaches to enhance localization accuracy and enable autonomous flight:

• Extended Kalman Filter (EKF) is a widely used state observer in TUAV systems, integrating IMU data, tether-derived variables, and sometimes motor inputs to estimate position, velocity, and attitude [122,153,154]. It enables 3D drone state and cable tension estimation, particularly in GPS-denied or vibration-prone environments where it helps mitigate sensor noise [151];
• Unscented Kalman Filter (UKF) offers improved estimation in nonlinear systems by avoiding explicit linearization and has been applied to estimate angular states like pitch and roll from accelerometer and gyroscope data [132,155]. Its variant, the Square Root UKF (SR-UKF), enhances computational efficiency and supports real-time estimation of external disturbances, such as forces and torques acting on the UAV [145];
• High-Gain Observers (HGO) operates on a nonlinear dynamic system after it has been transformed into a triangular canonical form. The observer applies a dynamic update including a gain-scaled correction term to ensure fast convergence of the estimate to the true state. To recover the full original system state, the observer leverages additional information from the accelerometer to reconstruct the full state. HGO, therefore, not only can estimate the transformed state accurately but also to serve as a foundation for reconstructing the full physical state of the, even in the presence of model uncertainties or measurement noise [134,135];
• Hybrid Disturbance Observer (HDO) combines momentum- and acceleration-based approaches to estimate disturbances like tether tension, improving control performance and system stability [144];
• Fixed-time Extended State Observer (ESO) provides robust state and disturbance estimation with guaranteed convergence in a fixed time, enabling precise trajectory tracking and fast response under dynamic conditions [34];
• Neuro-estimator is constructed as a feedforward multilayer perceptron (MLP) neural network. It has been used to estimate the equivalent mass of a quadrotor system in real time, adapting to disturbances such as suspended loads. When the accompanying analytic mass model fails, due to singularities, the neural network maintains estimation accuracy, effectively enhancing system robustness [156]. In a TUAV context, where tether forces vary with slack or tension states, such an adaptive estimator could serve to approximate and compensate for these dynamic effects.

6.2. Localization Methods

Accurate localization remains a fundamental requirement for the safe and effective operation of tethered drones, particularly in environments where GPS signals are unavailable or unreliable, as well as in confined or constrained operational spaces. Various methods have been developed to address this challenge, ranging from conventional techniques originally designed for free-flying UAVs to more specialized approaches that exploit the presence of the tether.

6.2.1. Traditional Methods

Localization of TUAVs can still rely on traditional methods that have been extensively adopted for free-flying UAVs:

• Inertial feedback: Classic inertial localization methods use sensors like accelerometers, gyroscopes, and barometers to estimate UAV position based on its motion and orientation. However, these systems typically drift over time and are particularly challenged by conditions such as slack or wind-induced displacement, requiring external correction methods;
• Radio-based: In GPS-denied environments, tethered UAVs often use radio-based techniques such as triangulation, trilateration, and RSSI-based systems. These methods estimate position through geometric relationships between the UAV and ground anchors equipped with radio modules. While effective, these approaches require clear lines of sight and are susceptible to environmental factors like signal reflection, interference, and spoofing [157];
• External positioning systems: Localization systems relying on GNSS, UWB, or LIDAR offer external positioning solutions. UWB and LiDAR systems use distance measurements to determine relative positions between the UAV and ground stations or environment features, while GNSS can provide absolute positioning data. Although these systems improve accuracy, they remain highly dependent on environmental conditions and can suffer from signal loss or obstruction [147].

6.2.2. Tether-Enhanced Methods

These classic approaches are effective in many scenarios but face challenges when GPS is unavailable or when the UAV operates in environments where precise control is crucial. The introduction of tether cables, along with their unique parameters, provides a novel enhancement to localization techniques, expanding the capabilities of tethered drone systems by integrating their dynamic behavior into the position estimation process. Tether-based localization methods are

• Sensor fusion with tether parameters: The combination of tether mechanical parameters (length, angles, tension) and inertial sensor data enables advanced techniques like the EKF to estimate the UAV’s position and velocity, allowing for indoor operations in constrained spaces. In situations where the tether is slack, more sophisticated models, such as catenary curves, are employed to account for the flexible nature of the cable [87,120,122];
• Neural network-based: Such localization methods offer a data-driven approach to estimating UAV position through supervised regression techniques. A multilayer perceptron (MLP) can be used to predict the drone’s position based on tether variables, including four angular measurements, tether length, and horizontal tension producing output estimates for the drone’s spatial coordinates and relative yaw angle [87]. Data acquisition is conducted in controlled indoor environments by placing the drone at known 3D coordinates and recording tether parameters. The training process involved Bayesian regularization to enhance generalization, and subsets are tested to evaluate performance through regression accuracy and error metrics [19];
• Vision-based: In a complementary approach, a downward-facing camera on the drone captures images of a ground robot and an EfficientPose deep neural network (DNN) estimates the drone’s relative 6D pose with respect to the robot. This relative pose was then fused with SLAM data from the ground robot to localize the UAV within the global reference frame [148].

Incorporating tether mechanical feedback lets tethered drone systems gain a new layer of precision, allowing for real-time position adjustments, robust tracking even in dynamic or adverse conditions, and more accurate localization when traditional systems usually fall short. These enhancements overcome the limitations of GPS-denied environments and scarce visibility, opening up new possibilities for tethered UAV operations in both outdoor and indoor scenarios.

6.3. Navigation Strategies

Tethered drone systems require navigation strategies that accommodate deployments in environments where GPS is unavailable, visual references are unreliable, or precise coordination with ground assets is essential. As a result, these strategies must address not only spatial planning and localization but also the dynamics of the tether and its potential contact with surrounding obstacles. Navigation methods in literature span a broad spectrum of algorithmic categories, with several approaches specifically tailored to distinct multi-robot system configurations. In this section, navigation strategies are grouped by the primary algorithmic paradigm, followed by a brief discussion of system setup, tether role, and key navigation features.

6.3.1. Sampling-Based Global Planning

Sampling-based algorithms efficiently explore high-dimensional configuration spaces and are well-suited for tether-aware path planning due to their flexibility and scalability.

• Rapidly exploring Random Trees (RRT and RRT*): RRT has been extended for tether-aware planning in UAV-UGV collaborative systems. The tether is modeled as a catenary curve and integrated into the path evaluation via a “checkCatenary” function. A subsequent nonlinear optimization stage smooths the path while accounting for tether-induced constraints. This enables beyond-line-of-sight operations, with tether dynamics incorporated as real-time navigation constraints [23]. The UAV, powered via a tether to a mobile UGV, benefits from a dual-layer map-incremental planner that supports real-time replanning in unknown environments [70];
• Lazy Theta*: Operating over a 3D voxel grid, Lazy Theta* generates an initial path which is refined using catenary-based tether modeling. A sparse factor graph ensures path smoothness, energy efficiency, and tether safety, demonstrating a seamless integration from sampling-based planning to optimization-based refinement [22];
• PRM, RRT-Connect, and BIT*: These planners facilitate multi-UAV coordination under a shared tether, leveraging global planning with a complementary force-aware local planner. This hybrid setup ensures tether feasibility, minimizes drag, and mitigates inter-UAV collision risks while navigating high-dimensional constraint spaces [25].

6.3.2. Optimization-Based Planning

These approaches formulate navigation as a continuous optimization problem, enabling smooth trajectories with real-time constraints such as tether dynamics and sensor feedback.

• Convex Quadratic Programming (QP) with LiDAR Constraints: A real-time convex QP formulation guides the formation flight of tethered UAVs in unknown environments without relying on prior maps. A supervisory controller synthesizes feasible trajectories using LiDAR and tether data, offering adaptive, reactive control albeit without global foresight [24];
• Receding Horizon Control with CVT Optimization: This grid-based planning approach uses a receding horizon strategy and Lloyd’s algorithm to dynamically optimize UAV formations. Cost functions evaluate each grid cell based on energy expenditure, proximity to targets, tether constraints, and inter-agent spacing [28].

6.3.3. Reactive and Vector Field-Based Navigation

Reactive methods directly translate sensor input or geometric models into control signals, bypassing full map-based planning.

• Velocity Vector Field: A tether-parameterized vector field guides UAVs without GPS, leveraging geometric tether models. The horizontal component aligns the drone with a vertical descent axis, while vertical descent only initiates near the landing site. A feedforward term enables alignment with moving platforms [21];
• Reactive Wall-Following via LiDAR: LiDAR-based wall-following replaces visual odometry, employing edge detection and a switched vector field to guide landings. Tether feedback allows return navigation without external localization [40].

6.3.4. Visual Servoing and Visual-Inertial Guidance

Vision-based methods enable relative navigation and cooperative operation in GPS-denied environments.

• AprilTag-Based Visual Servoing: A tethered UAV uses AprilTags and PID control to maintain relative position to a UGV, enabling GPS-free operation [158];
• Visual Servoing for Surface Vessels: Blob tracking allows the UAV to guide USVs via line-of-sight. Switching between heading-based turning and PID control supports agile, cooperative missions [30];
• Visual-Inertial Odometry (VIO): VIO fused with range and inertial sensors via an Extended Kalman Filter enables robust localization in GPS-denied, sloped terrains. The drone plans motion primitives while implicitly accounting for tether geometry, assisting UGV path correction [98];
• ArUco Marker Guidance: Downward-facing cameras enable the UAV to track ArUco markers on a UGV, forming a visual-inertial feedback loop for GPS-independent navigation in tethered systems [159].

6.3.5. Contact-Aware and Constraint-Driven Planning

These strategies explicitly consider tether contact with the environment and cable dynamics.

• Ray-Casting vs. Contact-Based Planning: Two alternative strategies address tether-obstacle interactions, ray-casting enforces unobstructed tether lines, while contact-based planning allows for tether wrapping around obstacles. Both utilize occupancy maps and tether localization to generate feasible 3D paths [26];
• Cooperative Tension Optimization: In multi-UAV transport missions, dynamic formation optimization minimizes asymmetric tension while avoiding collisions. Although path planning occurs in 2D, 3D tension vectors and tether geometry are incorporated into the optimization framework [35].

6.3.6. Terrain-Aware and Nature-Inspired Planning

These planners are designed to handle rough terrain and unstructured environments through bio-inspired heuristics.

• Ant Colony Optimization for 3D Terrain: An enhanced ACO algorithm evaluates terrain complexity, obstacle risks, and tether feasibility to optimize 3D paths for UAV/UGV teams. This method promotes adaptive routing and efficient navigation across uneven landscapes [149].

6.3.7. Differential GNSS-Based Navigation

Highly accurate landing systems leverage GNSS-based methods for constrained environments such as maritime platforms.

• Double-Difference GNSS for Precision Landing: This approach reduces vertical errors and baseline noise, enabling high-precision UAV landings on moving ship decks. Tethered UAVs benefit from improved alignment and safety in complex maritime scenarios [160].

The range of navigation strategies developed for tethered drone systems underscores the importance of selecting approaches that align with specific platform configurations, operational environments, and task requirements. The tether itself emerges not only as a limiting factor but as a multifunctional asset, serving roles in sensing, localization, and even actuation. Advancing the field may involve hybrid frameworks that integrate global planning with local adaptability, leverage tether properties for energy-efficient routing, and incorporate onboard perception for resilient, autonomous operation.

7. Conclusions

This review has provided a comprehensive synthesis of the current landscape of TUAV systems, with a focus on tethered multirotor platforms, constituting the most prevalent and versatile subclass of these aerial platforms. From their foundational architecture and dynamic modeling to their diverse and expanding range of applications, tethered drones have emerged as a robust solution for scenarios requiring extended endurance and continuous communication.

Through a detailed analysis of system components, this survey underscores the multifaceted role of the tether. No longer a mere constraint, the tether has evolved into a multifunctional asset serving as a structural, sensory, and computational element. Its integration into navigation, localization, and control systems introduces a paradigm shift, enabling novel functionalities in both structured and unstructured environments.

To quantify the scope and impact of this review, 160 peer-reviewed publications, primarily from the past two decades, were analyzed. These works span control theory, mechatronic design, modeling, and real-world deployment. The original contribution of this survey lies in its systematic integration of dynamic modeling and control strategies, linking physical tether dynamics, winch actuation, and control design in a unified and structured way. This level of synthesis, absent in prior works, offers a bridge between theoretical research and practical application.

Despite the presented advancements, several open challenges remain. Accurate modeling of tether dynamics in turbulent or cluttered environments, real-time estimation and control of tether tension, and seamless coordination across multi-agent systems with shared tethers represent critical areas for future research.

To support practical deployment and strengthen collaboration between academia and industry, we propose the following actionable steps:

• Standardize modular TMS hardware and software interfaces to promote interoperability and rapid integration;
• Publicly release simulation environments and datasets for benchmarking control strategies and validating dynamic models;
• Establish joint validation protocols to reconcile simulation models with field performance across varying operational conditions;
• Foster co-design partnerships between researchers and industry stakeholders to align technical development with application-specific requirements in fields such as infrastructure monitoring, public safety, and maritime operations.

Future directions should explore the synergy between AI-based planning, adaptive control, and onboard sensor fusion, ultimately pushing toward fully autonomous, resilient, and energy-aware tethered aerial systems. As TUAV technology continues to mature, it is poised to play a pivotal role in persistent aerial operations across domains ranging from infrastructure monitoring and environmental sensing to emergency response and collaborative robotics.