A Visual Guidance and Control Method for Autonomous Landing of a Quadrotor UAV on a Small USV
Abstract
1. Introduction
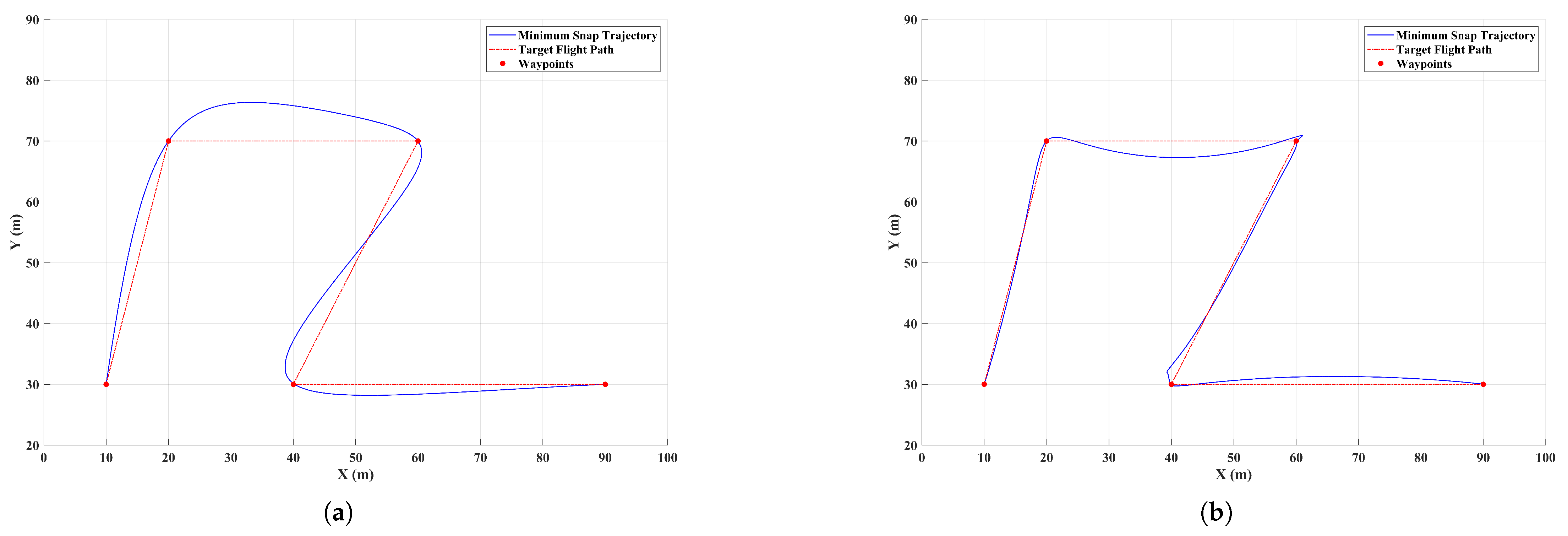
- An improved minimum snap trajectory planning algorithm is proposed to refine the flight trajectory based on given waypoints, ensuring trajectory smoothness while keeping the deviation between the generated trajectory and the target flight path within an acceptable range. This guides the UAV in approaching the USV in narrow river environments while improving flight stability during trajectory tracking and reducing energy consumption caused by frequent velocity changes.
- Based on a small USV adapted for operating in narrow rivers, a landing platform with a vertically placed fiducial marker is designed to separate the UAV landing area from the fiducial marker detection region in order to mitigate the interference from lighting and shadows on the fiducial marker. Additionally, an event-triggered visual guidance and control method is introduced to enhance UAV stability by optimizing heading and position control during the autonomous landing process.
- An autonomous landing system is developed comprising a USV, quadrotor UAV, and wireless ground station. The system design involves both hardware setup and software development. Outdoor experimental results show that the proposed method enables stable and autonomous landing of a UAV on a small USV, demonstrating the feasibility of the PX4 and ROS2 systems.
2. System Modeling
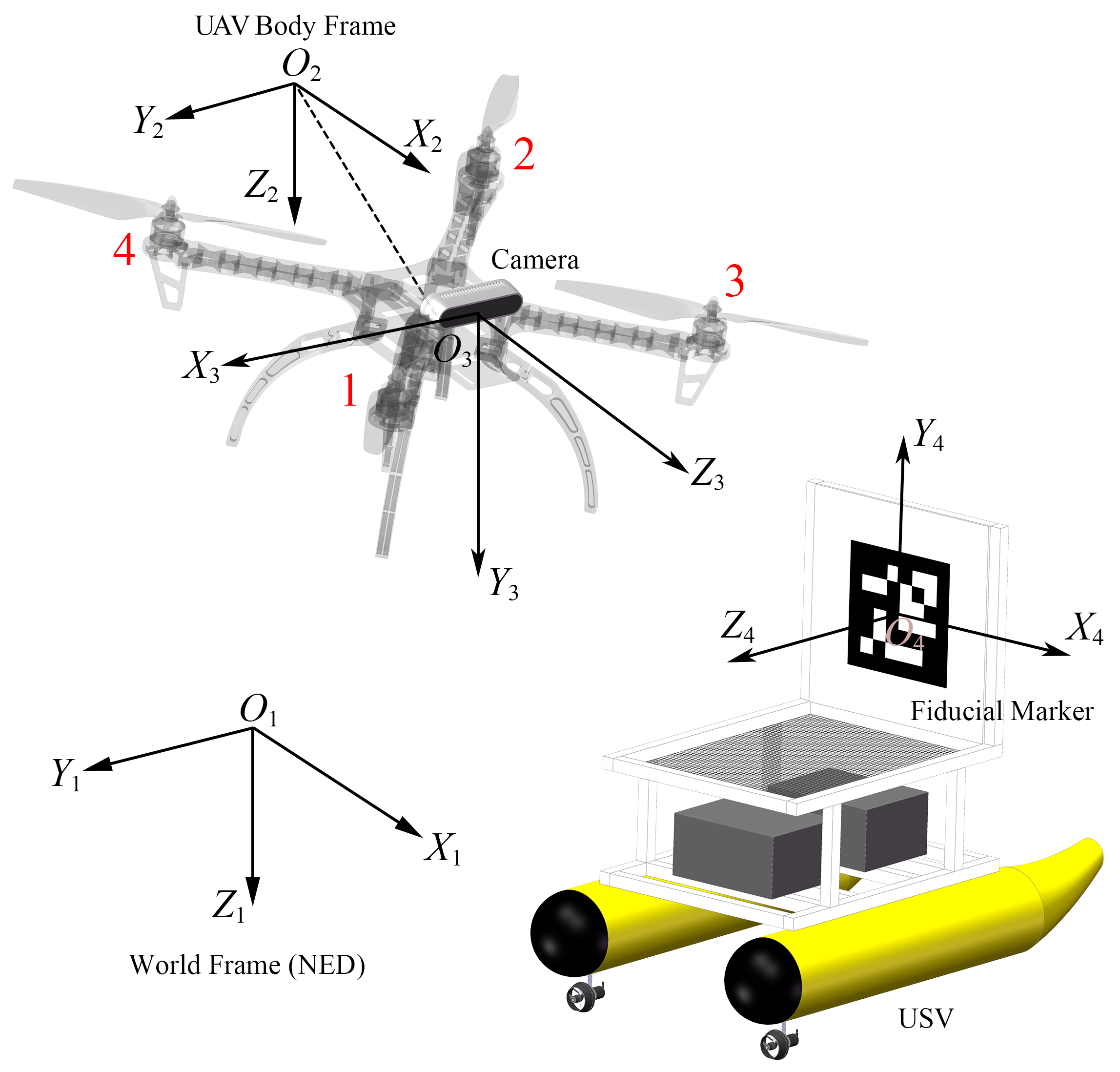
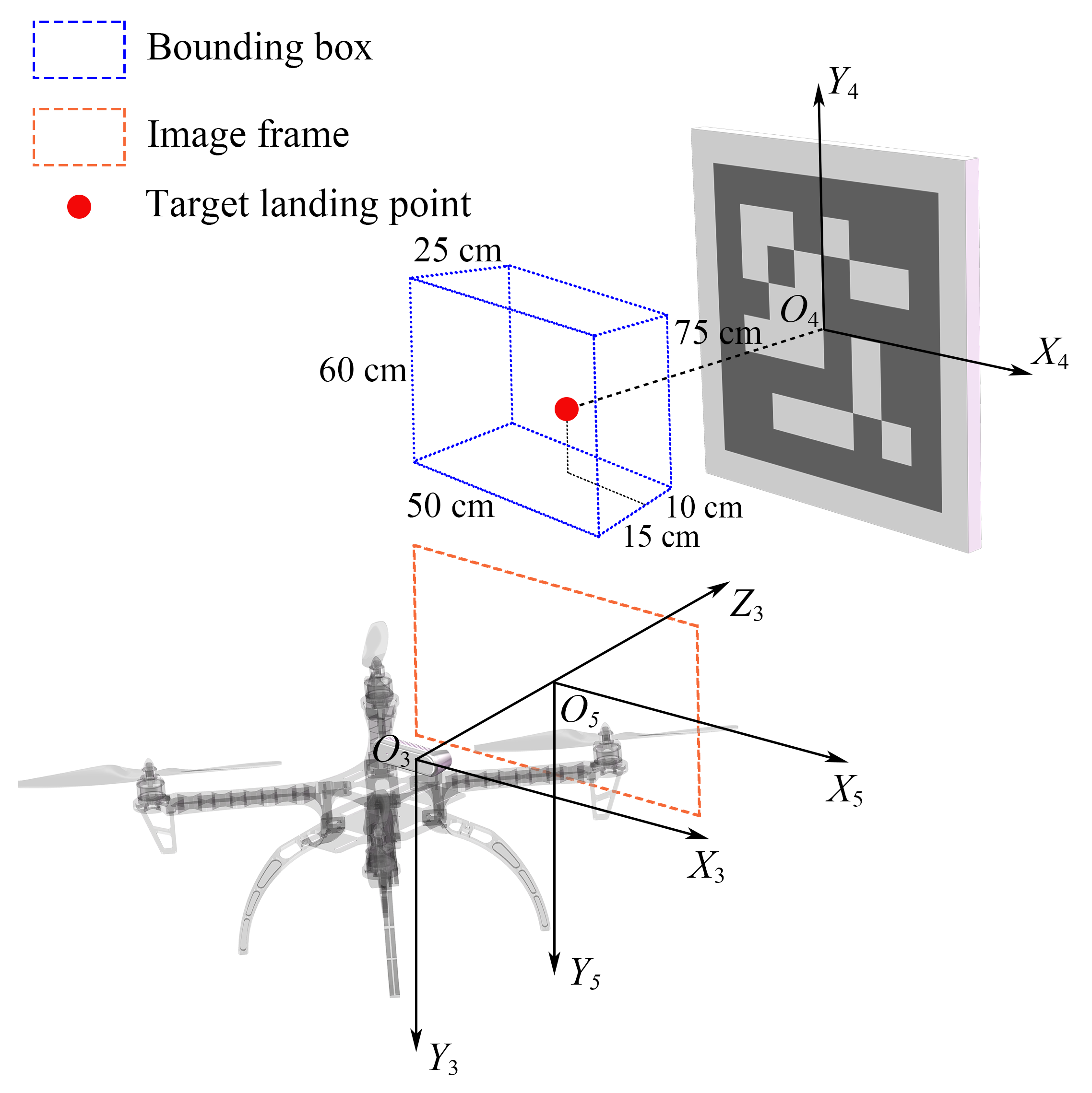
2.1. Coordinate System Definition
2.2. UAV Dynamics Model
2.3. Finite State Machine
- Idle: This is the initial stage of the system. The UAV hovers in the air, waiting for further commands. After receiving the landing command from the ground station, the system transitions to the Approaching stage.
- Approaching: At the beginning of the Approaching stage, the UAV automatically computes an optimized trajectory based on desired waypoints, then initiates trajectory tracking. When the UAV’s front-facing camera detects the fiducial marker on the landing platform, the state automatically switches to the Landing stage.
- Landing: In this stage, the UAV approaches the landing platform based on visual guidance. When the relative pose error between the UAV and the ArUco fiducial marker falls below the threshold value, the motors are shut down and the UAV falls onto the landing platform, completing the landing.
3. Trajectory Generation
3.1. Cost Function and Constraints
3.2. Improved Minimum Snap Algorithm
| Algorithm 1: Improved Minimum Snap Algorithm |
| 1. Initialize: P = {, , , |
| 2. While |
| 3. |
| 4. For to |
| 5. |
| 6. |
| 7. |
| 8. End For |
| 9. Get by solving Equation (8) |
| 10. |
| 11. For to |
| 12. |
| 13. |
| 14. End For |
| 15. |
| 16. |
| 17. Else |
| 18. . |
| 19. |
| 20. End If |
| 21. End While |
4. Visual Guidance and Control
4.1. Camera Calibration
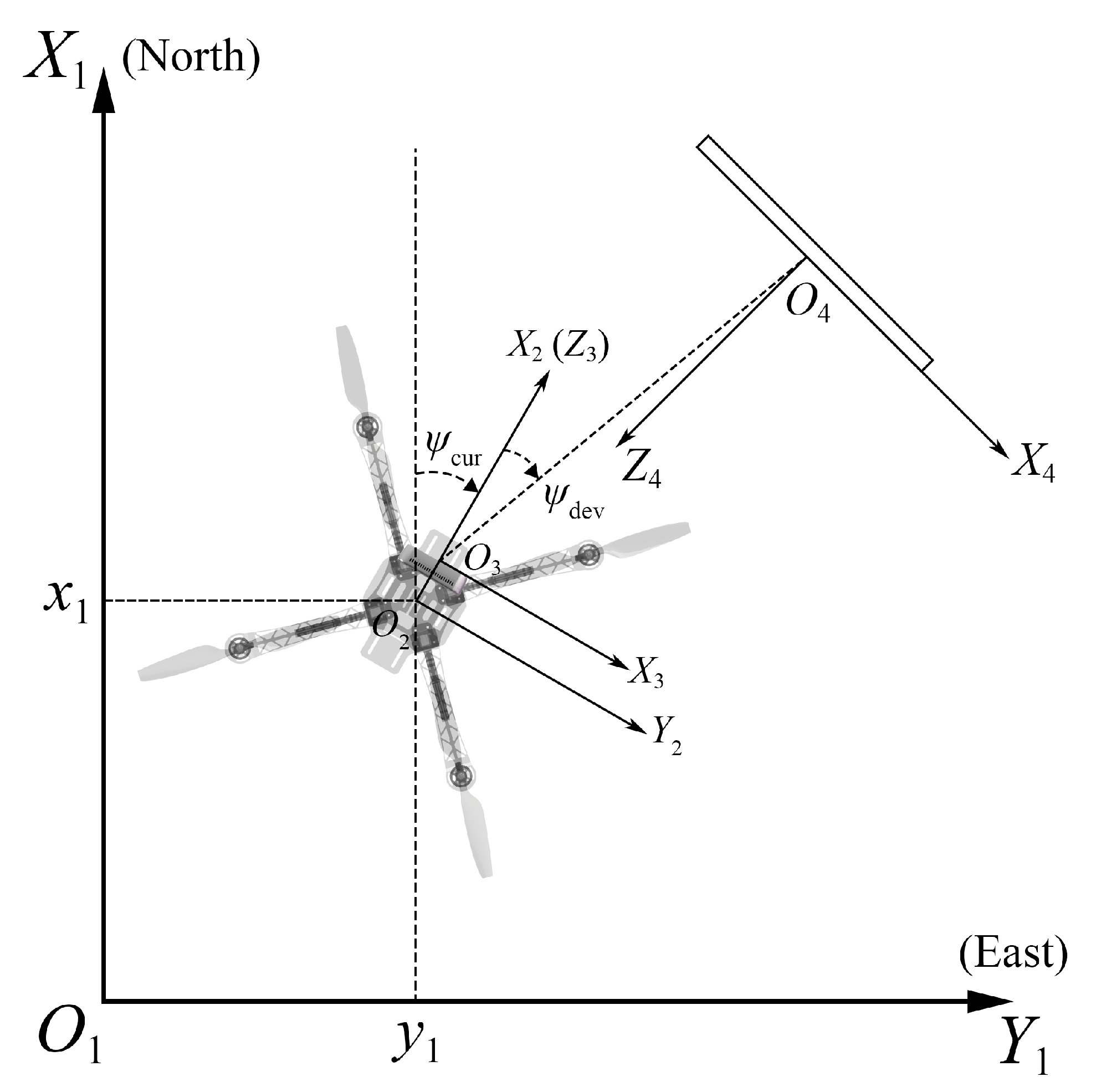
4.2. Heading Control
4.3. Position Control
4.4. Failsafe Mechanism
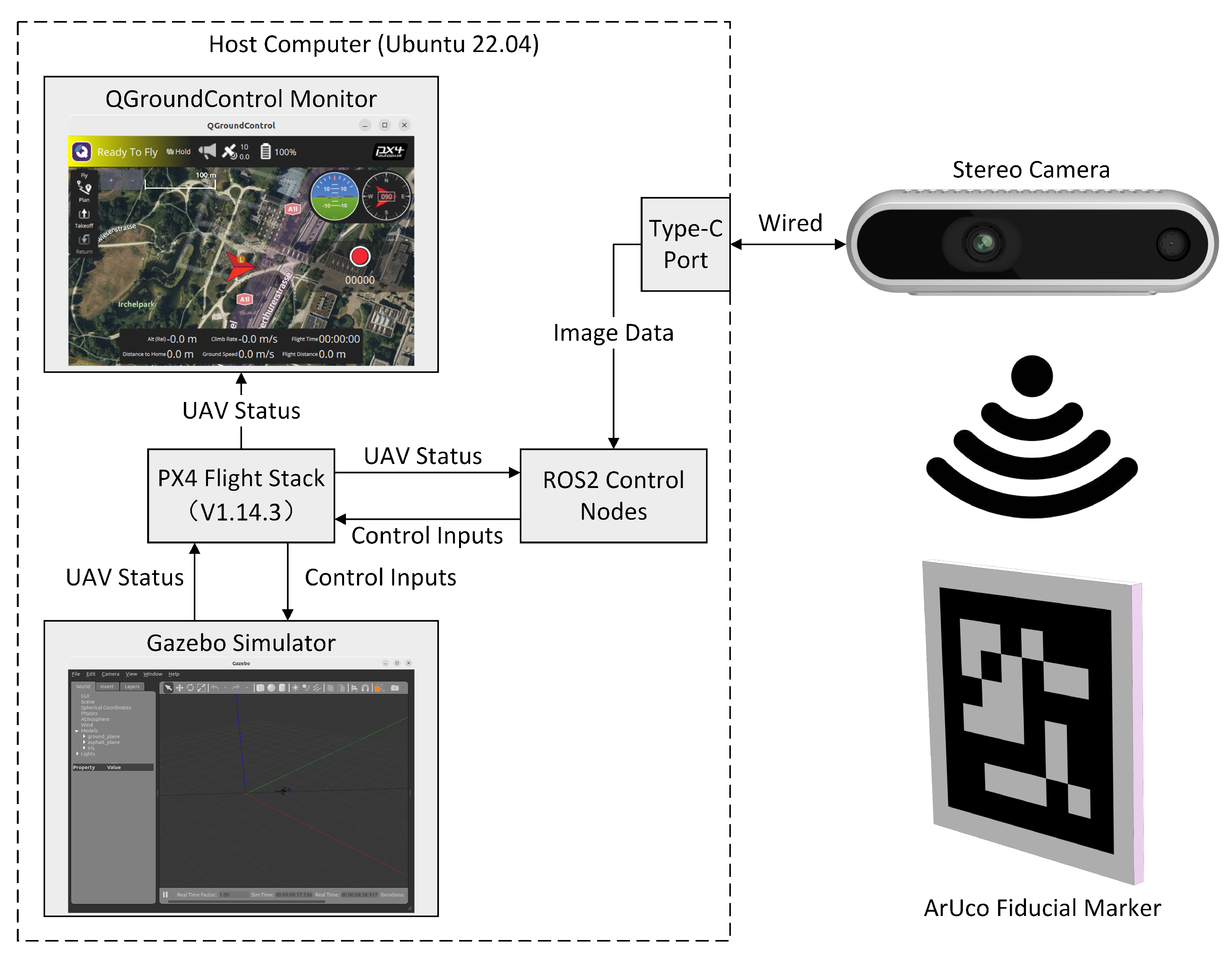
5. System Architecture
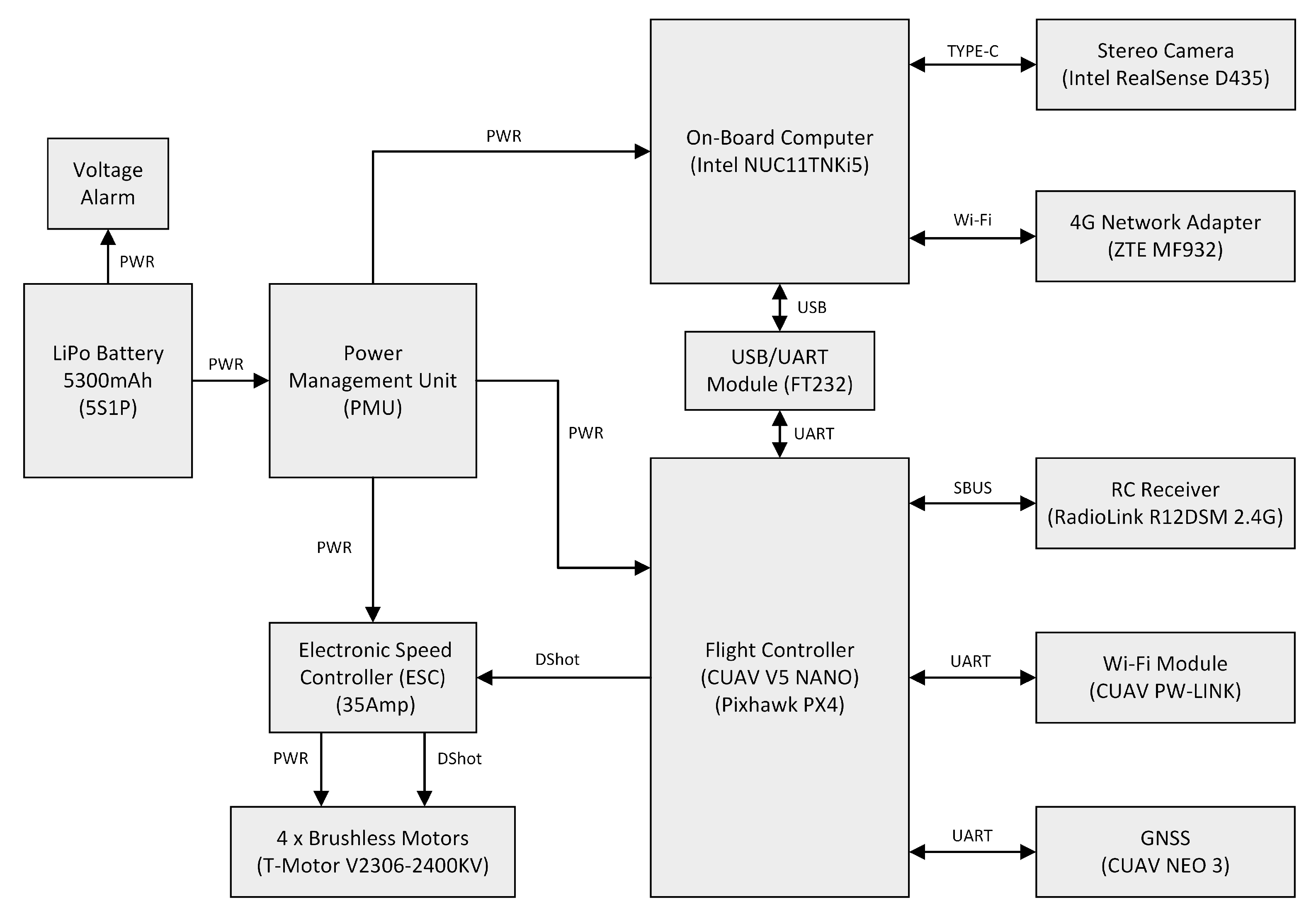
5.1. Hardware Setup
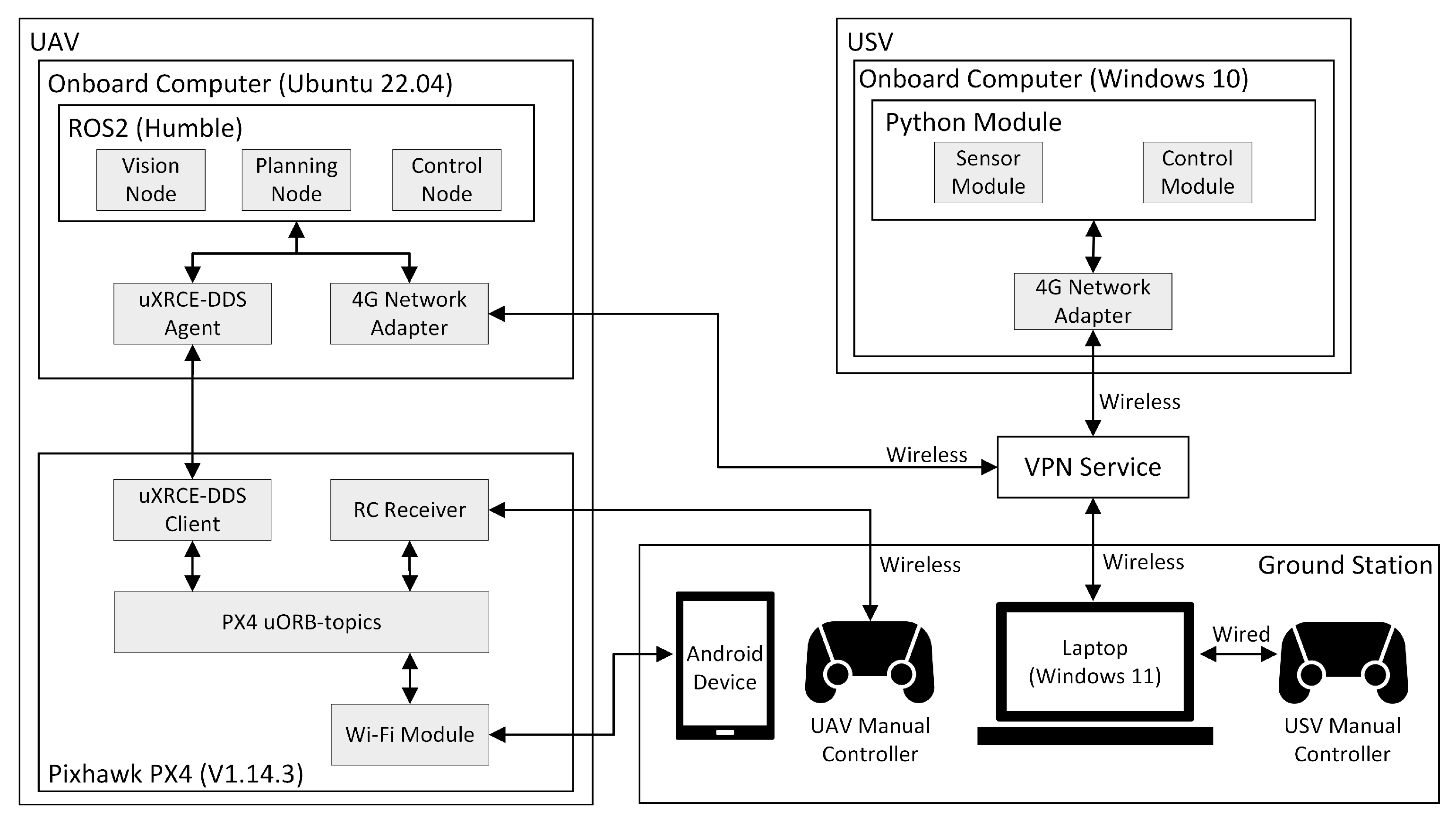
5.2. System Communication
6. Experiments
6.1. Stationary Platform
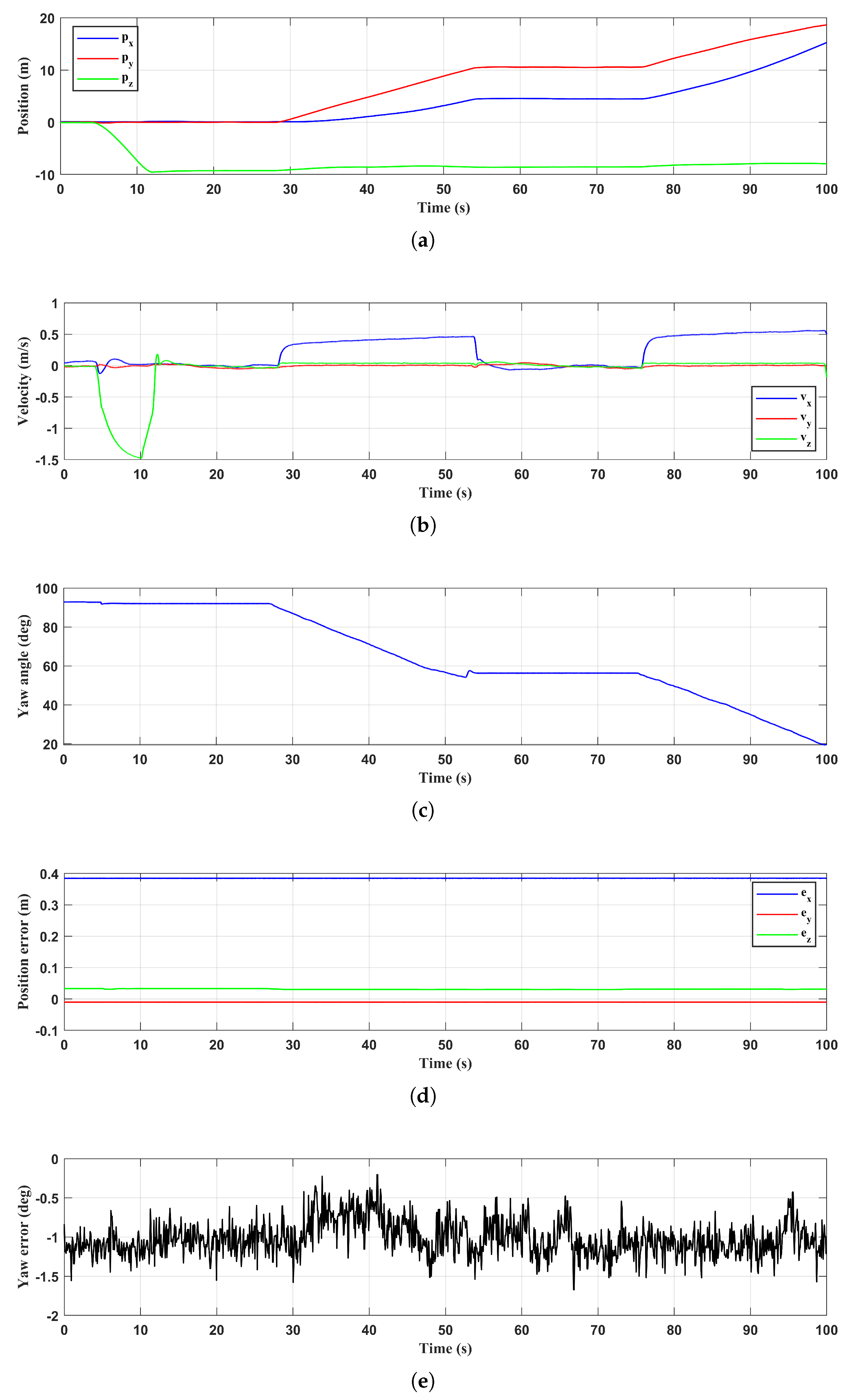
6.1.1. Event-Triggered Mechanism Validation
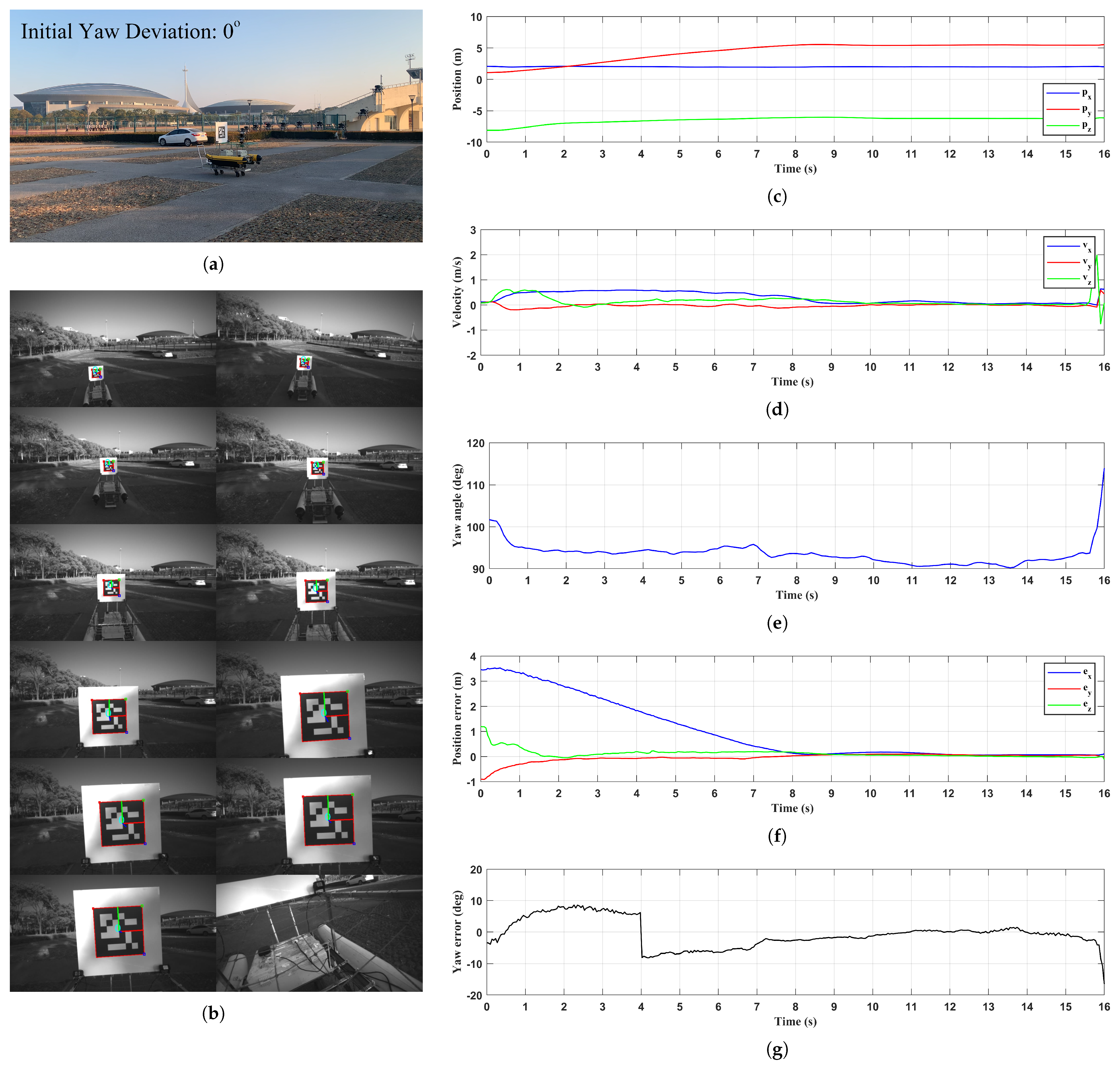
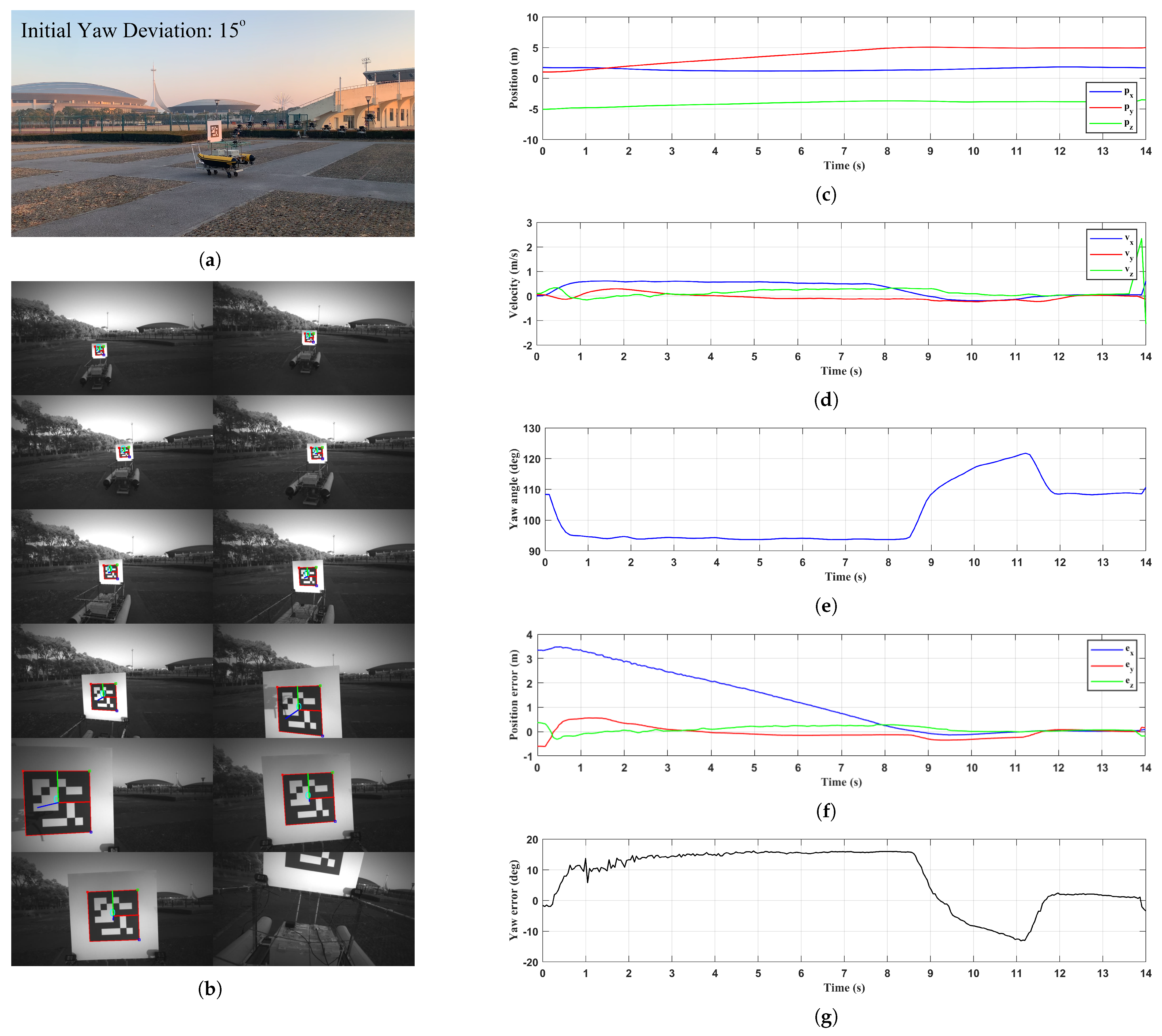
6.1.2. Yaw Deviation Adjustment
6.1.3. Approaching and Landing
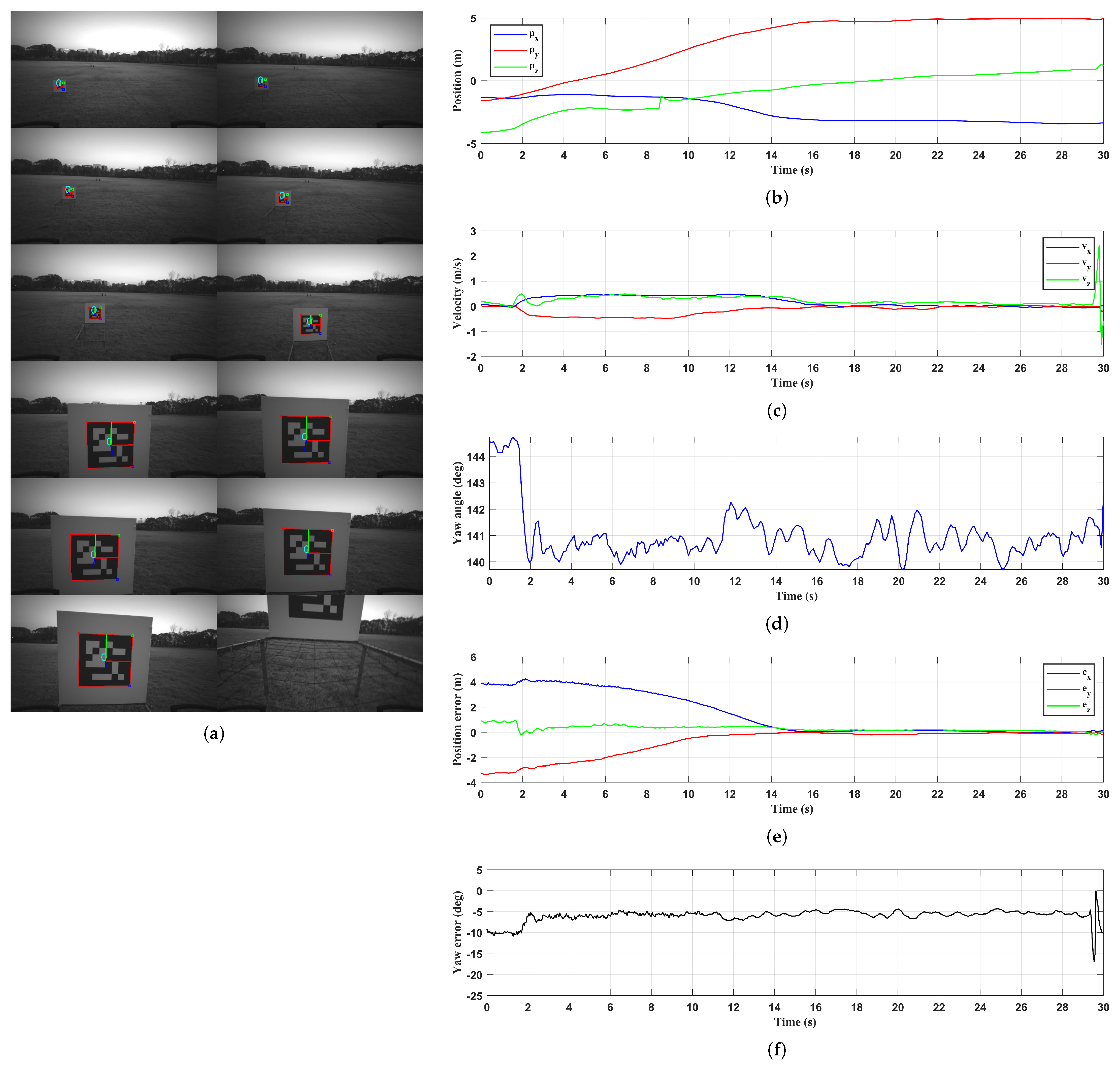
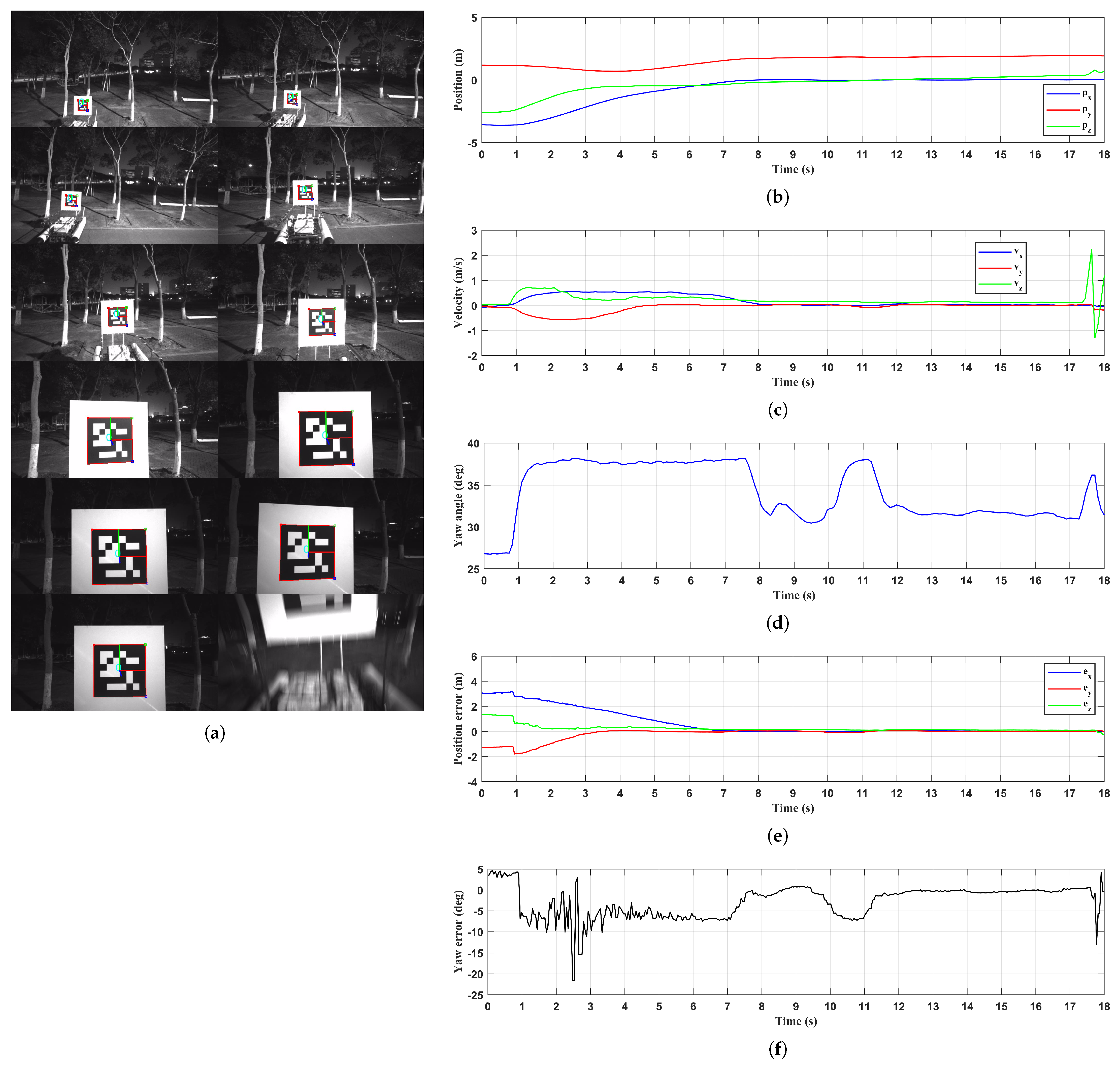
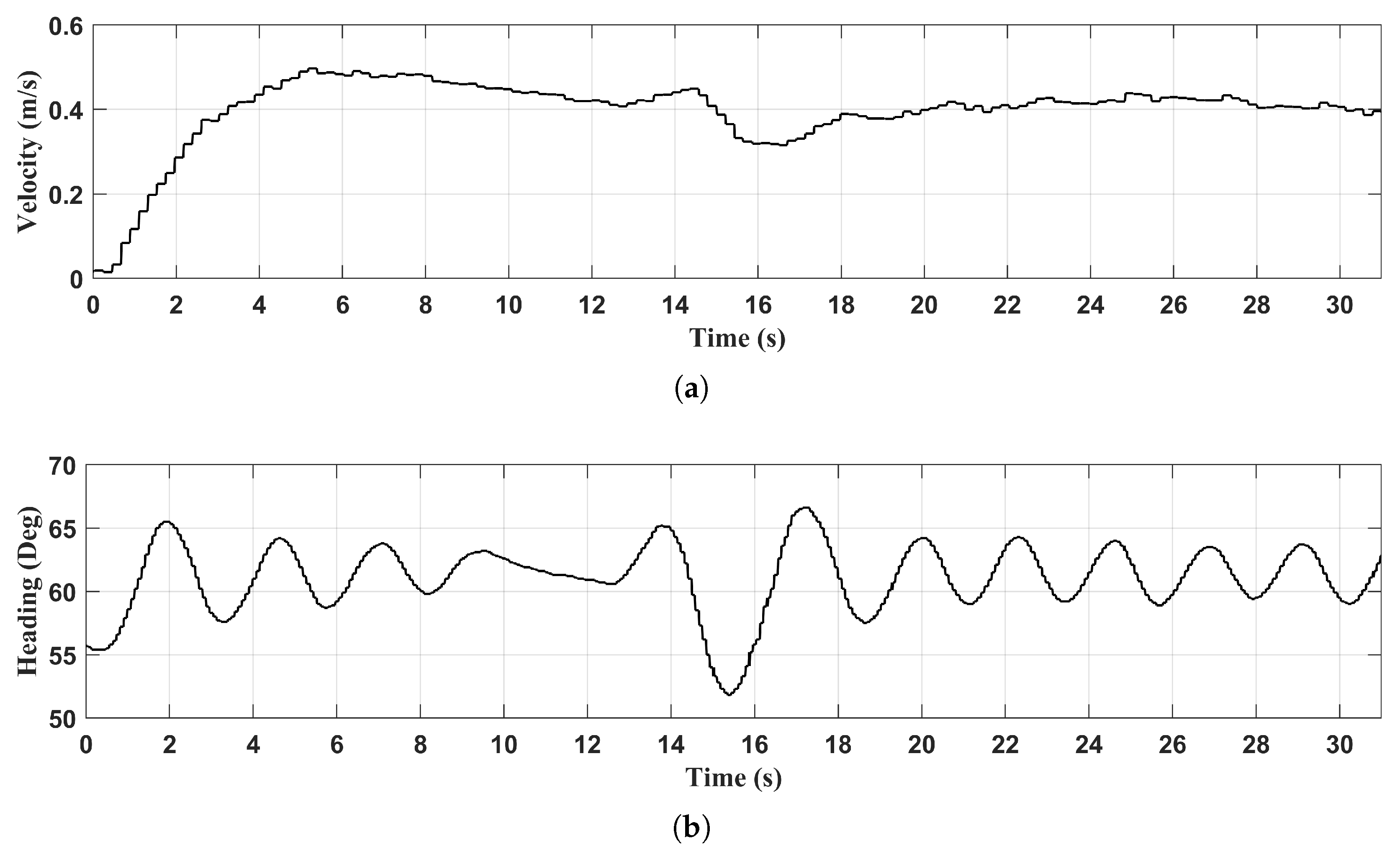
6.2. Moving Platform
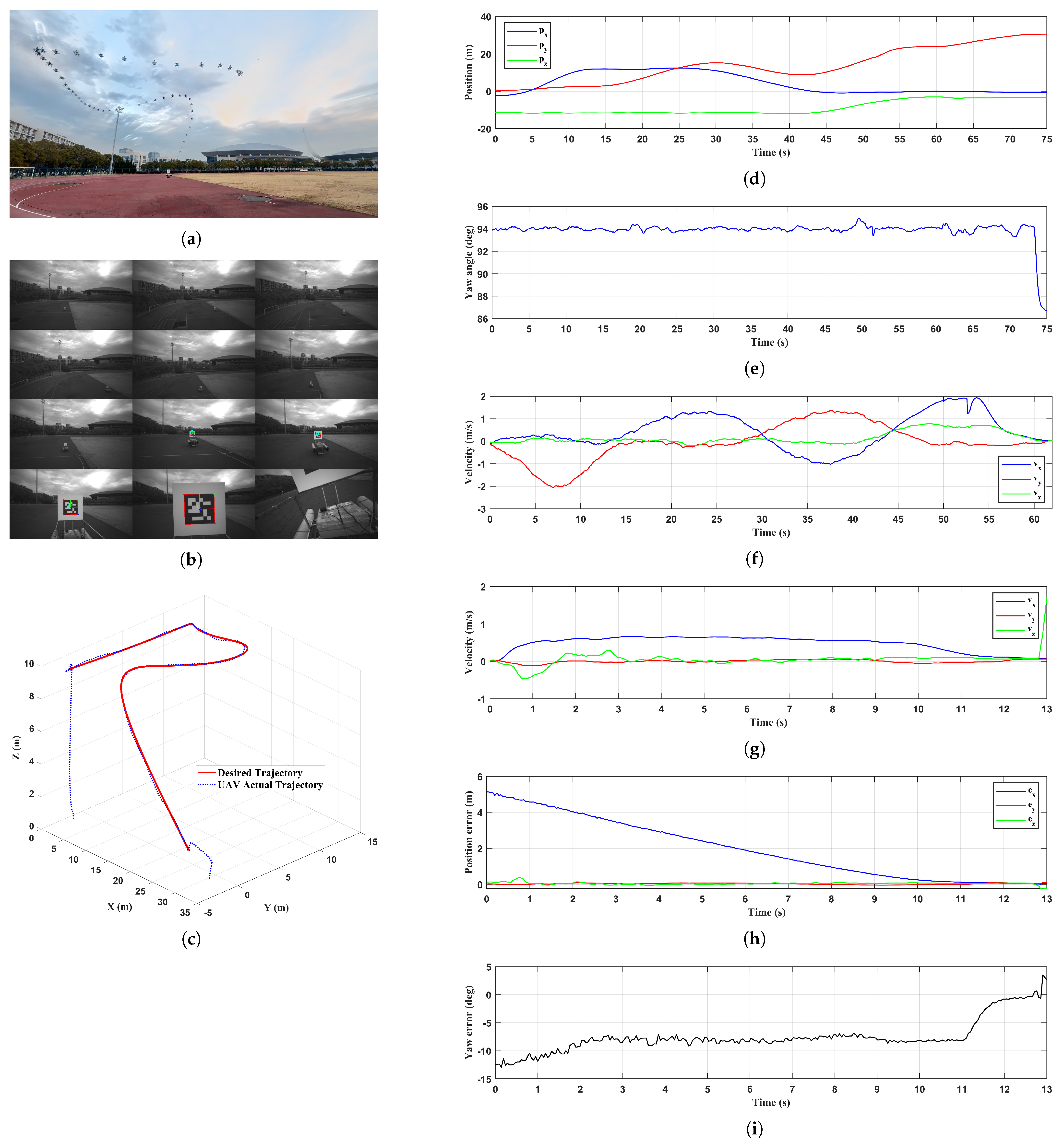
6.2.1. Terrestrial Environment
6.2.2. River Environment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yang, X.; Zhao, J.; Zhao, L.; Zhang, H.; Li, L.; Ji, Z.; Ganchev, I. Detection of River Floating Garbage Based on Improved YOLOv5. Mathematics 2022, 10, 4366. [Google Scholar] [CrossRef]
- Liao, Y.-H.; Juang, J.-G. Real-Time UAV Trash Monitoring System. Appl. Sci. 2022, 12, 1838. [Google Scholar] [CrossRef]
- Duan, H.; Liu, S. Unmanned Air/Ground Vehicles Heterogeneous Cooperative Techniques: Current Status and Prospects. Sci. China Technol. Sci. 2010, 53, 1349–1355. [Google Scholar] [CrossRef]
- Grlj, C.G.; Krznar, N.; Pranjić, M. A Decade of UAV Docking Stations: A Brief Overview of Mobile and Fixed Landing Platforms. Drones 2022, 6, 17. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Jiang, C.; Zhang, W. A Survey of Maritime Unmanned Search System: Theory, Applications and Future Directions. Ocean. Eng. 2023, 285, 115359. [Google Scholar] [CrossRef]
- Specht, M. Methodology for Performing Bathymetric and Photogrammetric Measurements Using UAV and USV Vehicles in the Coastal Zone. Remote Sens. 2024, 16, 3328. [Google Scholar] [CrossRef]
- Usama, A.; Dora, M.; Elhadidy, M.; Khater, H.; Alkelany, O. First Person View Drone-FPV. In The International Undergraduate Research Conference; The Military Technical College: Cairo, Egypt, 2021; Volume 5, pp. 437–440. [Google Scholar]
- Wilson, A.; Kumar, A.; Jha, A.; Cenkeramaddi, L.R. Embedded Sensors, Communication Technologies, Computing Platforms and Machine Learning for UAVs: A Review. IEEE Sens. J. 2021, 22, 1807–1826. [Google Scholar] [CrossRef]
- Zeng, Q.; Jin, Y.; Yu, H.; You, X. A UAV Localization System Based on Double UWB Tags and IMU for Landing Platform. IEEE Sens. J. 2023, 23, 10100–10108. [Google Scholar] [CrossRef]
- Ochoa-de Eribe-Landaberea, A.; Zamora-Cadenas, L.; Peñagaricano-Muñoa, O.; Velez, I. UWB and IMU-Based UAV’s Assistance System for Autonomous Landing on a Platform. Sensors 2022, 22, 2347. [Google Scholar] [CrossRef]
- Gyagenda, N.; Hatilima, J.V.; Roth, H.; Zhmud, V. A Review of GNSS-Independent UAV Navigation Techniques. Robot. Auton. Syst. 2022, 152, 104069. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Yan, Y. UAV Formation Trajectory Planning Algorithms: A Review. Drones 2023, 7, 62. [Google Scholar] [CrossRef]
- Demiane, F.; Sharafeddine, S.; Farhat, O. An Optimized UAV Trajectory Planning for Localization in Disaster Scenarios. Comput. Netw. 2020, 179, 107378. [Google Scholar] [CrossRef]
- Shao, G.; Ma, Y.; Malekian, R.; Yan, X.; Li, Z. A Novel Cooperative Platform Design for Coupled USV–UAV Systems. IEEE Trans. Ind. Inform. 2019, 15, 4913–4922. [Google Scholar] [CrossRef]
- Ji, J.; Yang, T.; Xu, C.; Gao, F. Real-Time Trajectory Planning for Aerial Perching. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 10516–10522. [Google Scholar]
- Gao, Y.; Ji, J.; Wang, Q.; Jin, R.; Lin, Y.; Shang, Z.; Cao, Y.; Shen, S.; Xu, C.; Gao, F. Adaptive Tracking and Perching for Quadrotor in Dynamic Scenarios. IEEE Trans. Robot. 2023, 40, 499–519. [Google Scholar] [CrossRef]
- Xin, L.; Tang, Z.; Gai, W.; Liu, H. Vision-Based Autonomous Landing for the UAV: A Review. Aerospace 2022, 9, 634. [Google Scholar] [CrossRef]
- Polvara, R.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R. Vision-Based Autonomous Landing of a Quadrotor on the Perturbed Deck of an Unmanned Surface Vehicle. Drones 2018, 2, 15. [Google Scholar] [CrossRef]
- Park, Y.; Park, C.; Song, W.; Lee, C.; Kwon, J.; Park, J.; Noh, G.; Lee, D. Fiducial Marker-Based Autonomous Landing Using Image Filter and Kalman Filter. Int. J. Aeronaut. Space Sci. 2024, 25, 190–199. [Google Scholar] [CrossRef]
- Krogius, M.; Haggenmiller, A.; Olson, E. Flexible Layouts for Fiducial Tags. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1898–1903. [Google Scholar]
- Xu, Z.-C.; Hu, B.-B.; Liu, B.; Wang, X.; Zhang, H.-T. Vision-Based Autonomous Landing of Unmanned Aerial Vehicle on a Motional Unmanned Surface Vessel. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6845–6850. [Google Scholar]
- Nguyen, T.-M.; Nguyen, T.H.; Cao, M.; Qiu, Z.; Xie, L. Integrated Uwb-Vision Approach for Autonomous Docking of Uavs in Gps-Denied Environments. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9603–9609. [Google Scholar]
- Procházka, O.; Novák, F.; Báča, T.; Gupta, P.M.; Pěnička, R.; Saska, M. Model Predictive Control-Based Trajectory Generation for Agile Landing of Unmanned Aerial Vehicle on a Moving Boat. Ocean. Eng. 2024, 313, 119164. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum Snap Trajectory Generation and Control for Quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric Tracking Control of a Quadrotor UAV on SE (3). In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5420–5425. [Google Scholar]
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An Operator Splitting Solver for Quadratic Programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef]
- Lian, L.; Zong, X.; He, K.; Yang, Z. Trajectory Optimization of Unmanned Surface Vehicle Based on Improved Minimum Snap. Ocean. Eng. 2024, 302, 117719. [Google Scholar] [CrossRef]
- Tayebi Arasteh, S.; Kalisz, A. Conversion between Cubic Bezier Curves and Catmull–Rom Splines. SN Comput. Sci. 2021, 2, 398. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Energy Consumption in Unmanned Aerial Vehicles: A Review of Energy Consumption Models and Their Relation to the UAV Routing. In Information Systems Architecture and Technology: Proceedings of 39th International Conference on Information Systems Architecture and Technology–ISAT 2018: Part II; Springer: Berlin/Heidelberg, Germany, 2019; pp. 173–184. [Google Scholar]
- Abeywickrama, H.V.; Jayawickrama, B.A.; He, Y.; Dutkiewicz, E. Comprehensive Energy Consumption Model for Unmanned Aerial Vehicles, Based on Empirical Studies of Battery Performance. IEEE Access 2018, 6, 58383–58394. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Munoz-Salinas, R.; Madrid-Cuevas, F.J.; Marin-Jimenez, M.J. Automatic Generation and Detection of Highly Reliable Fiducial Markers under Occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Munoz-Salinas, R.; Madrid-Cuevas, F.J.; Medina-Carnicer, R. Generation of Fiducial Marker Dictionaries Using Mixed Integer Linear Programming. Pattern Recognit. 2016, 51, 481–491. [Google Scholar] [CrossRef]
- Romero-Ramirez, F.J.; Munoz-Salinas, R.; Medina-Carnicer, R. Speeded up Detection of Squared Fiducial Markers. Image Vis. Comput. 2018, 76, 38–47. [Google Scholar] [CrossRef]
- Aruco Nano 4 Release. Available online: https://www.youtube.com/watch?v=U3sfuy88phA (accessed on 22 December 2022).
- Marchand, E.; Uchiyama, H.; Spindler, F. Pose Estimation for Augmented Reality: A Hands-on Survey. IEEE Trans. Vis. Comput. Graph. 2015, 22, 2633–2651. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.S. Euler–Rodrigues Formula Variations, Quaternion Conjugation and Intrinsic Connections. Mech. Mach. Theory 2015, 92, 144–152. [Google Scholar] [CrossRef]
- O’Riordan, A.; Newe, T.; Dooly, G.; Toal, D. Stereo Vision Sensing: Review of Existing Systems. In Proceedings of the 2018 12th International Conference on Sensing Technology (ICST), Limerick, Ireland, 4–6 December 2018; pp. 178–184. [Google Scholar]
- Macenski, S.; Foote, T.; Gerkey, B.; Lalancette, C.; Woodall, W. Robot Operating System 2: Design, Architecture, and Uses in the Wild. Sci. Robot. 2022, 7, eabm6074. [Google Scholar] [CrossRef]
- Macenski, S.; Soragna, A.; Carroll, M.; Ge, Z. Impact of ROS 2 Node Composition in Robotic Systems. IEEE Robot. Auton. Lett. (RA-L) 2023, 8, 3996–4003. [Google Scholar] [CrossRef]


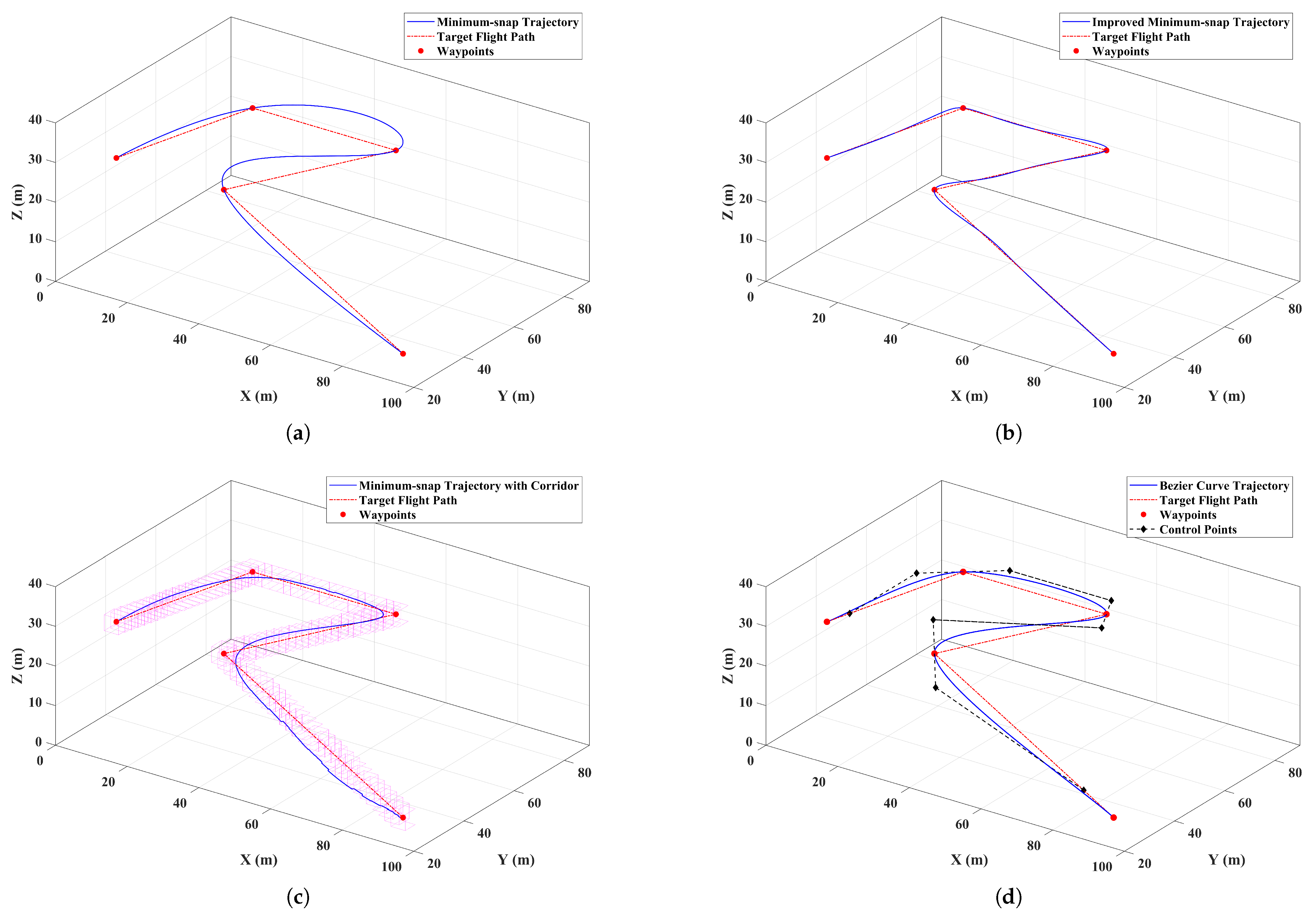





| Algorithm | Mean (m) | Standard Deviation (m) |
|---|---|---|
| Improved minimum snap | 0.4092 | 0.4760 |
| Minimum snap with corridor constraint | 1.6840 | 0.9855 |
| Minimum snap | 3.3090 | 3.6241 |
| Bézier curve | 2.1055 | 1.3185 |
| Algorithm | Trajectory Generation Time (s) | Flight Distance (m) | Flight Duration (s) | Energy Consumption (J) |
|---|---|---|---|---|
| Improved minimum snap | 0.1257 | 185.68 | 87.93 | 27,506.52 |
| Minimum snap with corridor constraint | 9.6933 | 173.35 | 101.19 | 31,581.67 |
| Minimum snap | 0.0153 | 199.45 | 110.11 | 34,418.62 |
| Bézier curve | 0.0095 | 188.72 | 99.15 | 31,009.10 |
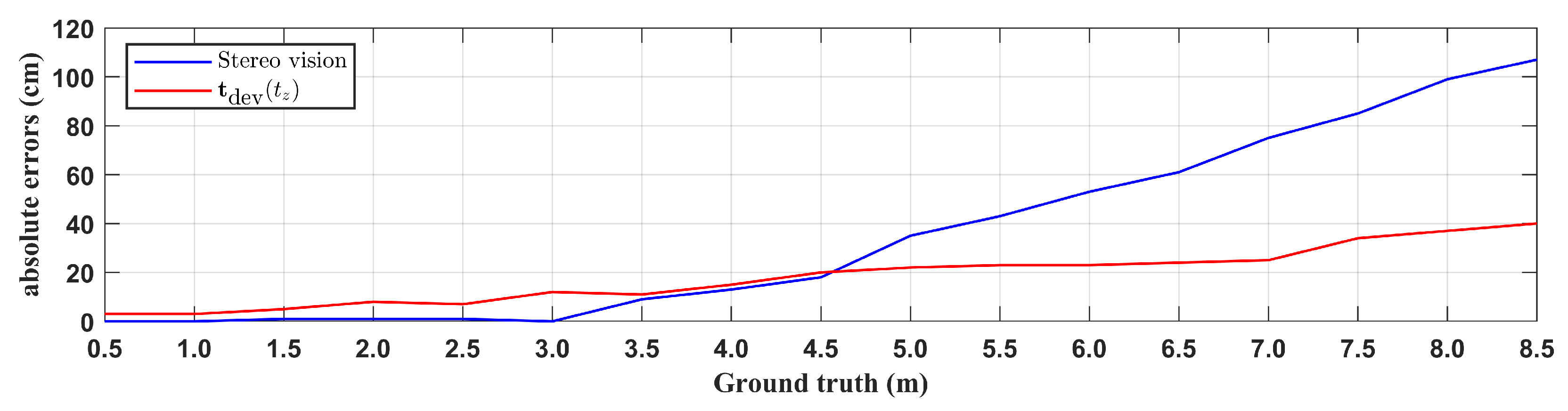
| Ground Truth (cm) | Stereo Vision (cm) | (cm) |
|---|---|---|
| 50 | 50 | 53 |
| 100 | 100 | 103 |
| 150 | 149 | 155 |
| 200 | 201 | 208 |
| 250 | 249 | 257 |
| 300 | 300 | 312 |
| 350 | 341 | 361 |
| 400 | 387 | 415 |
| 450 | 432 | 470 |
| 500 | 465 | 522 |
| 550 | 507 | 573 |
| 600 | 547 | 623 |
| 650 | 589 | 674 |
| 700 | 625 | 725 |
| 750 | 665 | 784 |
| 800 | 701 | 837 |
| 850 | 743 | 890 |
| Metric | Stereo Vision | |
|---|---|---|
| Mean Absolute Error | 35.23 cm | 18.35 cm |
| Root Mean Square Error | 51.04 cm | 21.58 cm |
| Mean Relative Error | 5.38% | 4.00% |
| Metric | Stereo Vision | |
|---|---|---|
| Mean Absolute Error | 4.56 cm | 9.33 cm |
| Root Mean Square Error | 8.01 cm | 10.78 cm |
| Mean Relative Error | 1.27% | 3.83% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Wang, J.; Zheng, X.; Zhou, Y.; Zhang, J. A Visual Guidance and Control Method for Autonomous Landing of a Quadrotor UAV on a Small USV. Drones 2025, 9, 364. https://doi.org/10.3390/drones9050364
Guo Z, Wang J, Zheng X, Zhou Y, Zhang J. A Visual Guidance and Control Method for Autonomous Landing of a Quadrotor UAV on a Small USV. Drones. 2025; 9(5):364. https://doi.org/10.3390/drones9050364
Chicago/Turabian StyleGuo, Ziqing, Jianhua Wang, Xiang Zheng, Yuhang Zhou, and Jiaqing Zhang. 2025. "A Visual Guidance and Control Method for Autonomous Landing of a Quadrotor UAV on a Small USV" Drones 9, no. 5: 364. https://doi.org/10.3390/drones9050364
APA StyleGuo, Z., Wang, J., Zheng, X., Zhou, Y., & Zhang, J. (2025). A Visual Guidance and Control Method for Autonomous Landing of a Quadrotor UAV on a Small USV. Drones, 9(5), 364. https://doi.org/10.3390/drones9050364





