Energy-Efficient UAV Trajectory Design and Velocity Control for Visual Coverage of Terrestrial Regions
Abstract
1. Introduction
1.1. Background
1.2. Motivation
1.3. Contribution
- To the best of our knowledge, this study is the first attempt to jointly optimize the UAV’s trajectory design and velocity control, for achieving visual coverage of multiple terrestrial regions with the minimized flight energy consumption of the UAV. We generalize the previous work on the UAV-enabled visual coverage by allowing the UAV to flexibly adjust both velocity and flight altitude during its entire task tour, which complicates the problem-solving due to the complex decision space.
- To minimize the UAV’s flight energy consumption, we develop a simulated annealing (SA)-based searching algorithm to identify the UAV’s photographing altitude for each region by minimizing their average altitude difference. Then, the visiting order of each region is determined based on the identified photographing altitudes by minimizing the UAV’s general tour length.
- After obtaining all candidate visual coverage paths within each region, we employ DP and geometry to jointly determine the UAV’s velocity control and trajectory within each region, as well as between any two neighboring regions.
- Extensive simulation results validate the effectiveness and superiority of the proposed approach, compared with several existing methods, in terms of the UAV’s flight energy consumption.
2. Related Work
2.1. Two-Dimensional UAV Trajectory Design
2.2. Three-Dimensional UAV Trajectory Design
2.3. UAV Visual Coverage
3. System Model and Problem Formulation
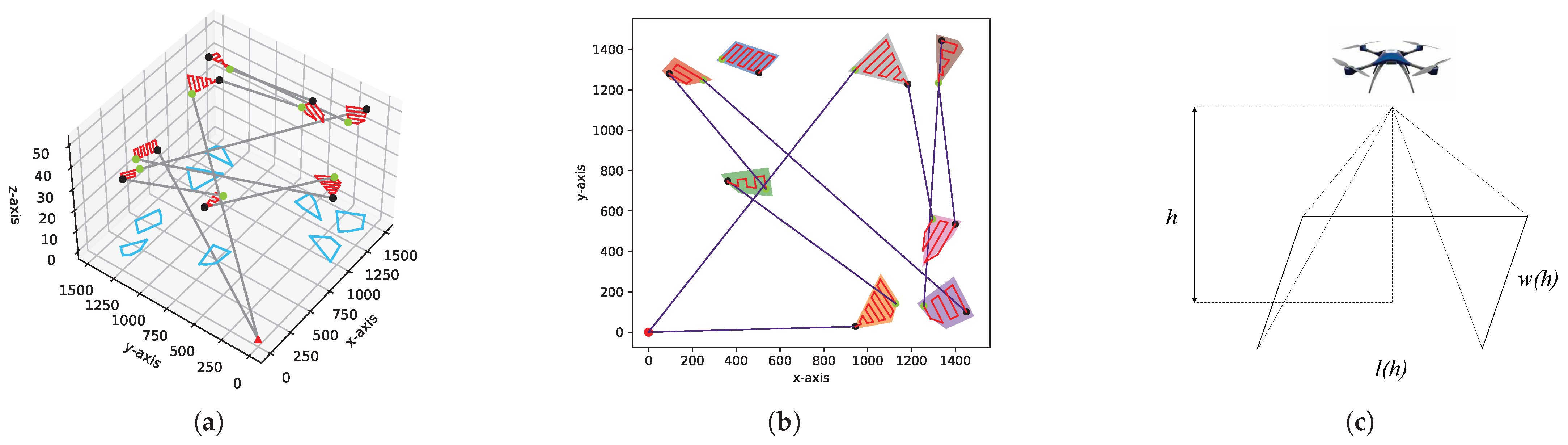
3.1. UAV Visual Coverage Model
3.2. UAV Mobility Model
3.3. UAV Flight Energy Consumption Model
3.4. Problem Formulation
4. The Proposed Method
4.1. Identifying the Photographing Altitude of Each Region
| Algorithm 1 Identifying the photographing altitude of each region |
|
4.2. Deciding the Visiting Order of Each Region
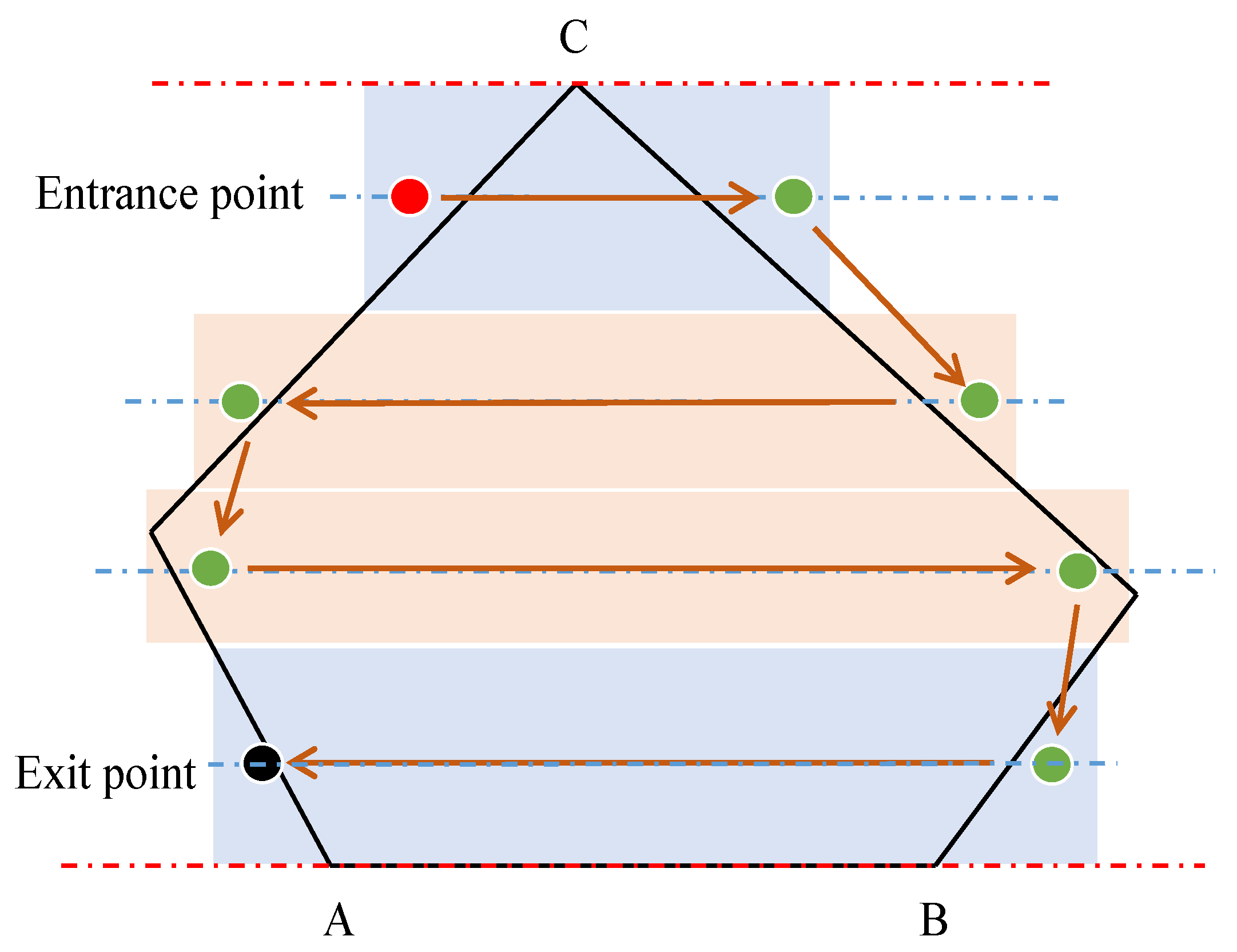
4.3. Generating Candidate Intra-Region Trajectories for Visual Coverage
| Algorithm 2 Intra-region path planning for visual coverage |
|
4.4. Joint Velocity Control and Trajectory Design
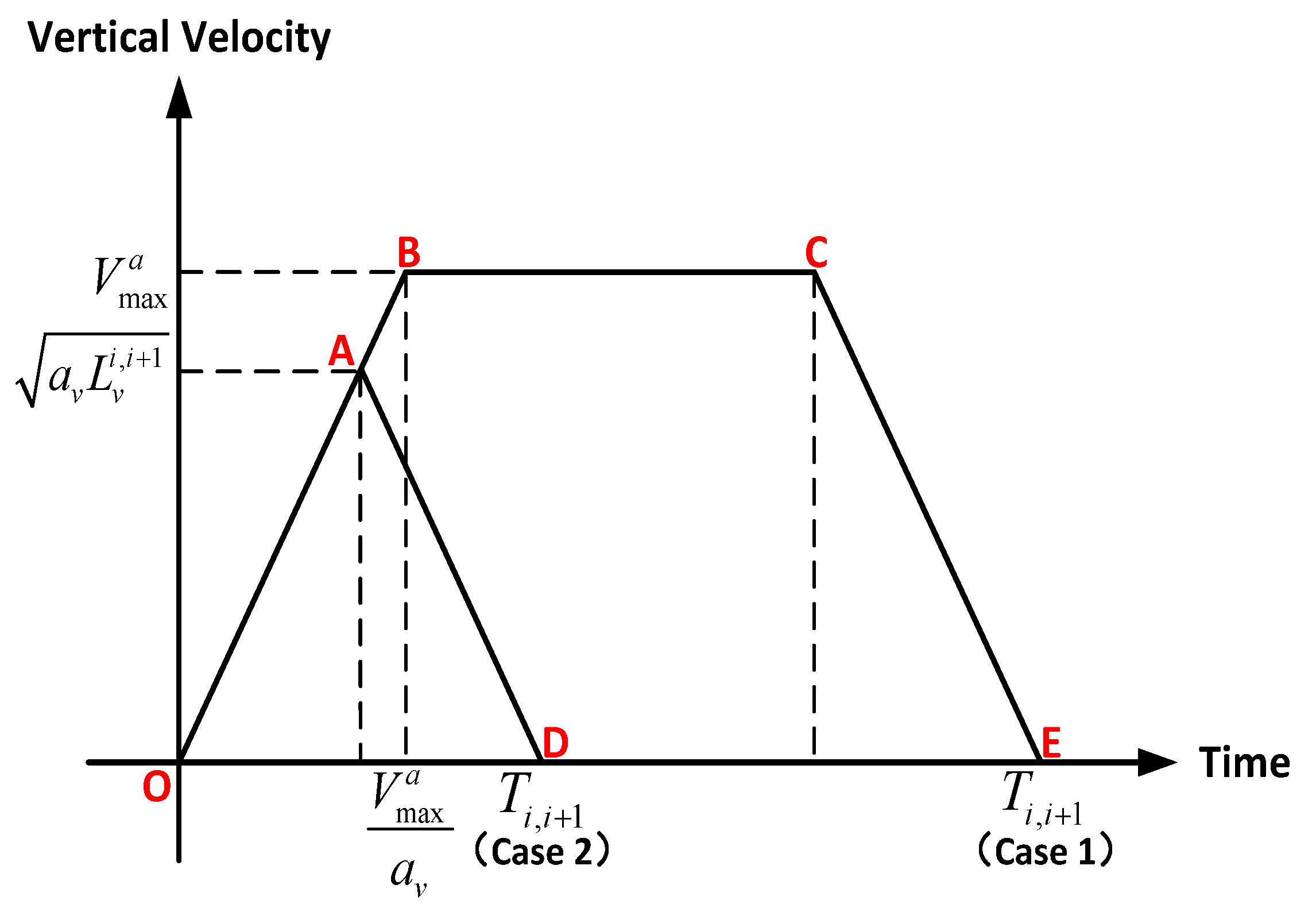
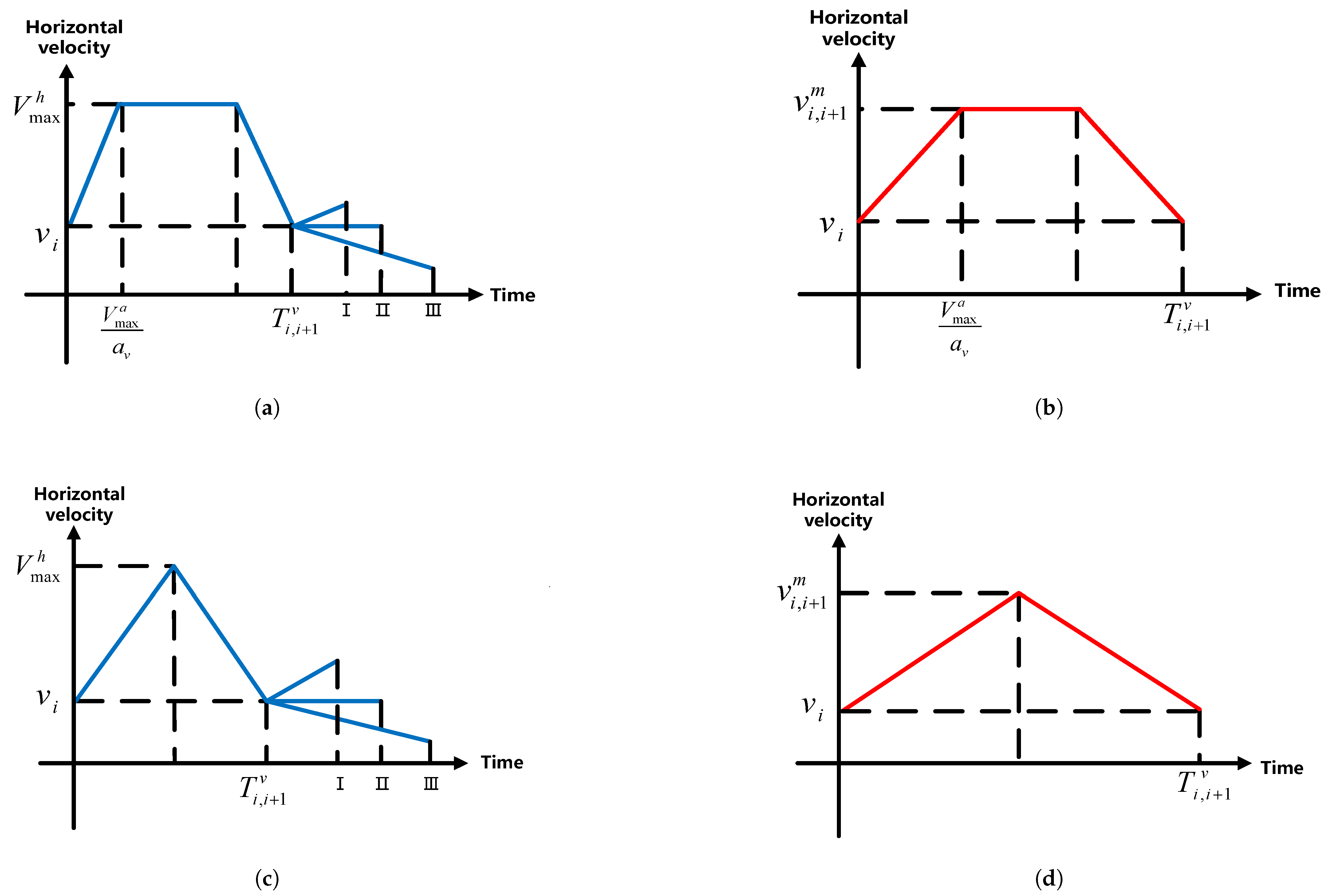
4.4.1. Analysis of UAV Velocity in the Vertical Direction
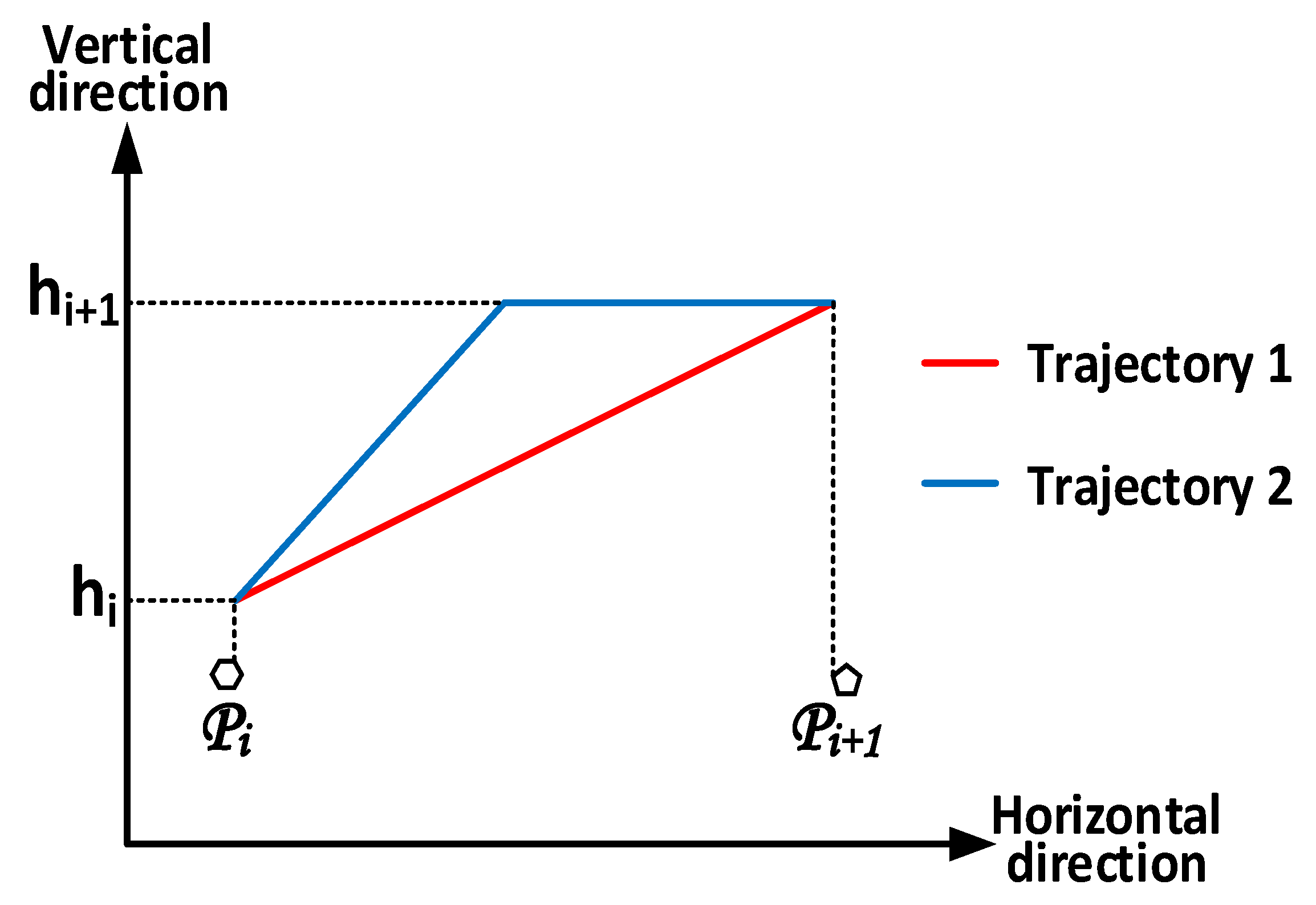
4.4.2. Analysis of UAV Velocity in the Horizontal Direction
4.4.3. Joint Optimization of Velocity and Trajectory
| Algorithm 3 Joint velocity control and trajectory design for visual coverage of terrestrial regions |
|
4.5. Computational Complexity Analysis of Algorithm 3
4.6. Limitations and Approximate Optimality
5. Evaluation
5.1. Experiment Setting
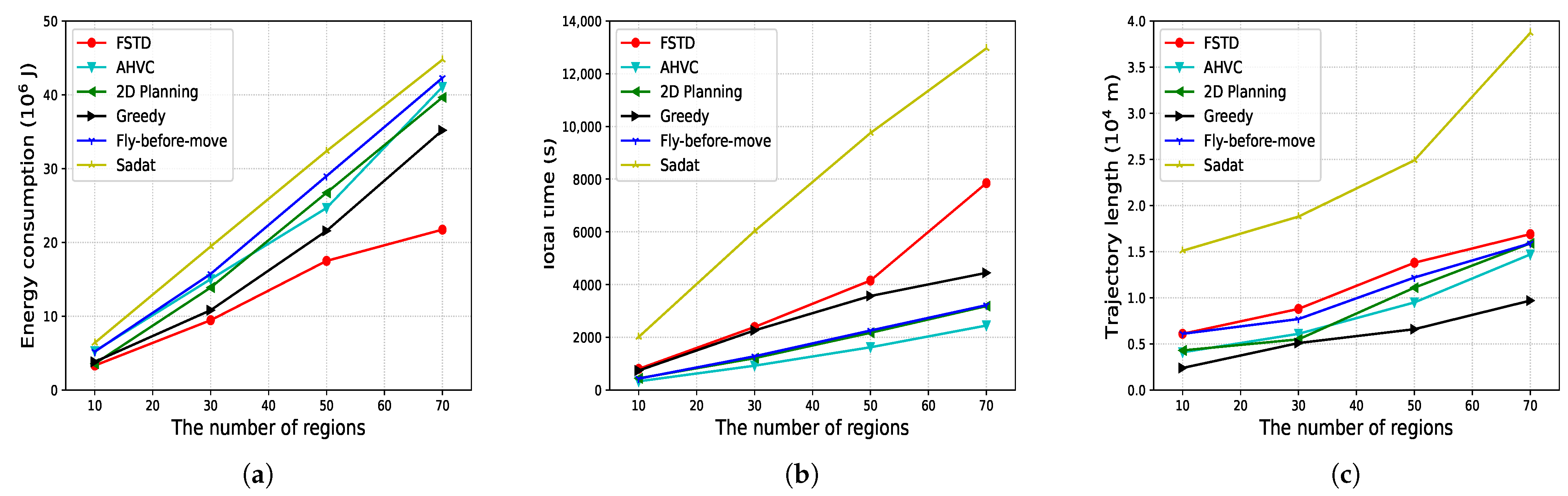
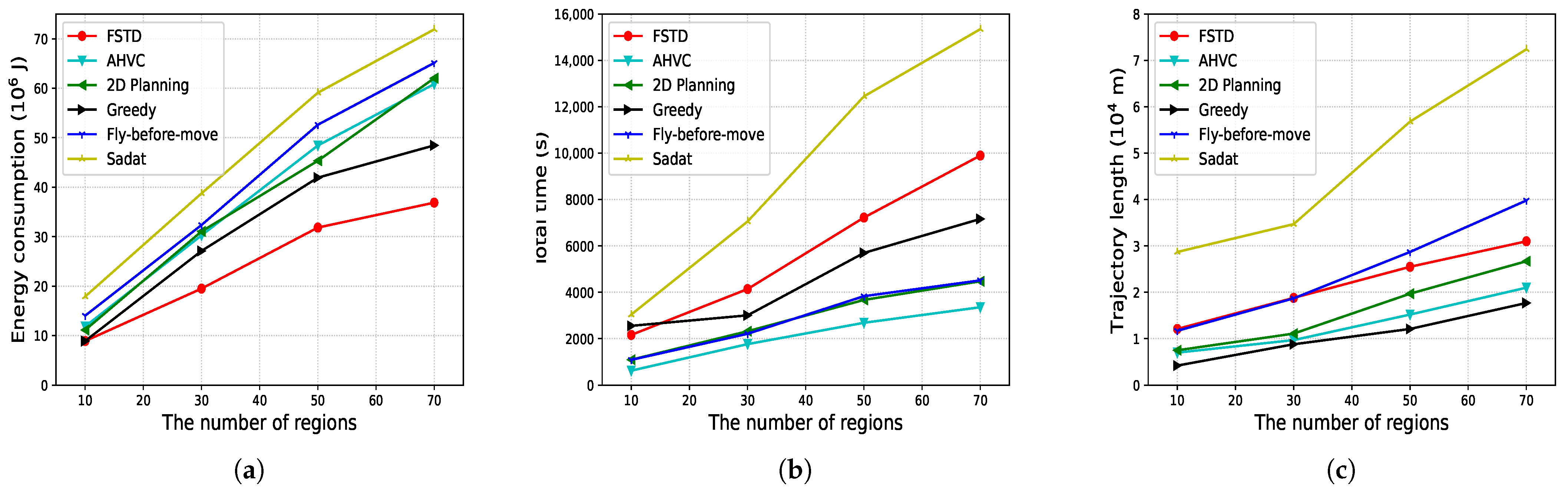
- Attaining heterogeneous visual coverage (AHVC): Based on [22], this method requires the UAV to fly at the maximum allowable velocity and the highest permissible altitude for each region. Its primary objective is to minimize the total mission time, rather than energy consumption.
- Two-dimensional planning: This baseline assumes a constant flight altitude (set to the minimum allowable altitude) and fixed velocity throughout the entire mission. The UAV plans a 2D TSP-style tour, ignoring altitude or speed variations, which simplifies trajectory planning but sacrifices adaptability [29].
- Greedy: A heuristic algorithm where, after completing the coverage of a region, the UAV selects the next unvisited region that results in the minimum incremental energy cost. This myopic strategy is simple but may lead to suboptimal global solutions.
- Fly-before-move: In this strategy, the UAV decouples vertical and horizontal movement. It first ascends or descends to the required altitude, then proceeds with horizontal flight to the next region. This sequential treatment of vertical and planar motion may cause inefficient transitions and higher energy usage.
- Sadat: Inspired by the fractal coverage approach in [51], this method uses breadth-first or depth-first search (BFS/DFS) to cover each region, which is divided into multiple sub-regions. After covering each subregion, the UAV must return to the maximum altitude before proceeding to the next one, leading to frequent altitude changes and potentially increased energy consumption.
5.2. Performance Comparison
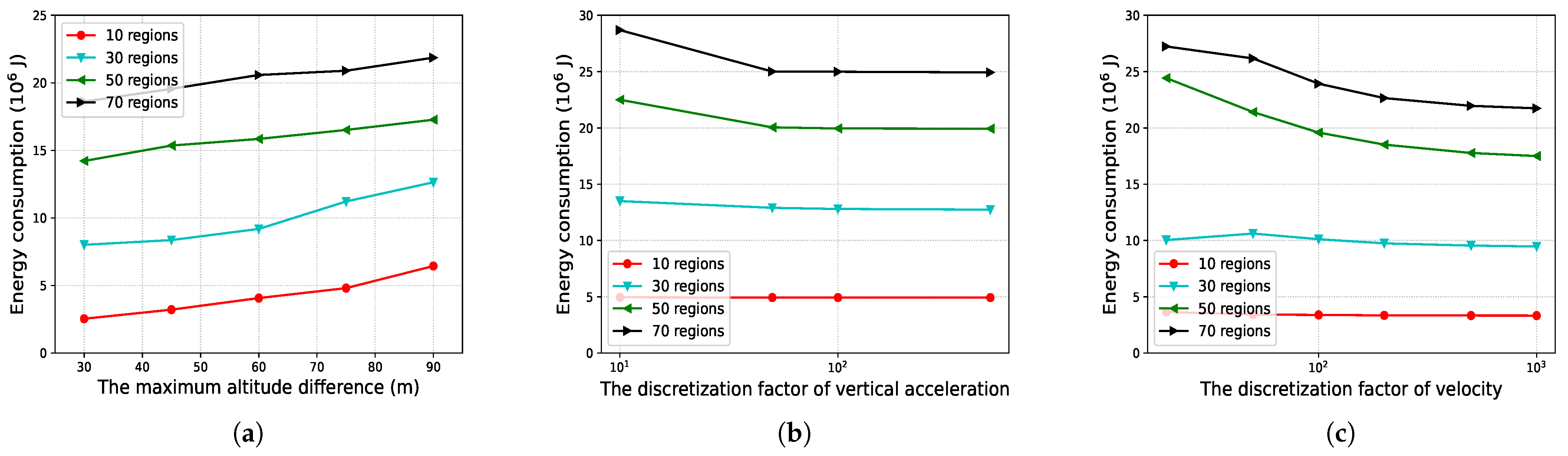
5.3. Impacts of System Parameters on Our Algorithm
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Niu, G.; Cao, Q.; Chen, C.S. Vision-based target localization with cooperative UAVs towards indoor surveillance. In Proceedings of the 2023 IEEE 98th Vehicular Technology Conference (VTC2023-Fall), Hong Kong, 10–13 October 2023; pp. 1–6. [Google Scholar]
- Liu, X.; Chen, M.; Zhangchen, X.; Tang, Y.; Fang, Y.; Shi, X.; Xu, Z. Intelligent UAV platform: Assist construction of agricultural production automation. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 1009–1012. [Google Scholar]
- Sotheara, S.; Aso, K.; Aomi, N.; Shimamoto, S. Effective data gathering and energy-efficient communication protocol in wireless sensor networks employing UAV. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2342–2347. [Google Scholar]
- Kucherov, D.; Shmelova, T.; Poshyvailo, O.; Tkachenko, V.; Miroshnichenko, I.; Ogirko, I. Mathematical model of damping of UAV oscillations in the cargo delivery problem. In Proceedings of the 2023 IEEE 4th KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 2–6 October 2023; pp. 1–6. [Google Scholar]
- Petrlík, M.; Báča, T.; Heřt, D.; Vrba, M.; Krajník, T.; Saska, M. A robust UAV system for operations in a constrained environment. IEEE Robot. Autom. Lett. 2020, 5, 2169–2176. [Google Scholar] [CrossRef]
- Saha, S.; Aich, S.; Saha, N.; Saha, S.; Chakraborty, R.; Bishnu, S.K. Deploying UAVs equipped with LIDAR for the quantification of tree biomass and the systematic classification of arboreal species. In Proceedings of the 2025 8th International Conference on Electronics, Materials Engineering and Nano-Technology (IEMENTech), Kolkata, India, 31 January–2 February 2025; pp. 1–7. [Google Scholar]
- Dong, F.; Li, L.; Lu, Z.; Pan, Q.; Zheng, W. Energy-efficiency for fixed-wing UAV-enabled data collection and forwarding. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Paredes, J.A.; Saito, C.; Abarca, M.; Cuellar, F. Study of effects of high-altitude environments on multicopter and fixed-wing UAVs’ energy consumption and flight time. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an China, 20–23 August 2017; pp. 1645–1650. [Google Scholar]
- Zhan, C.; Lai, H. Energy minimization in Internet-of-Things system based on rotary-wing UAV. IEEE Wirel. Commun. Lett. 2019, 8, 1341–1344. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Y.; Yang, S.-H. New energy consumption model for rotary-wing UAV propulsion. IEEE Wirel. Commun. Lett. 2021, 10, 2009–2012. [Google Scholar] [CrossRef]
- Zhan, C.; Huang, R. Energy efficient adaptive video streaming with rotary-wing UAV. IEEE Trans. Veh. Technol. 2020, 69, 8040–8044. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Ren, B. Energy saving quadrotor control for field inspections. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 52, 1768–1777. [Google Scholar] [CrossRef]
- Ribeiro, P.; Coelho, A.; Campos, R. On the energy consumption of rotary-wing and fixed-wing UAVs in flying networks. In Proceedings of the 2025 20th Wireless On-Demand Network Systems and Services Conference (WONS), Tyrol, Austria, 27–29 January 2025; pp. 1–4. [Google Scholar]
- Bianchi, D.; Borri, A.; Di Gennaro, S.; Preziuso, M. UAV trajectory control with rule-based minimum-energy reference generation. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 12–15 July 2022; pp. 1497–1502. [Google Scholar]
- Mathur, A.; Atkins, E. Multi-mode flight simulation and energy-aware coverage path planning for a lift+cruise QuadPlane. Drones 2025, 9, 287. [Google Scholar] [CrossRef]
- Xiong, Y.; Lu, M.; Chen, W. Modeling and maximizing angle coverage in visual sensor networks. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 2406–2409. [Google Scholar]
- Zheng, C.; Yin, H.; Li, J.; Lu, M. A multi-objective evolutionary algorithm for shortest path with maximal visual coverage. In Proceedings of the 2011 International Conference on Intelligent Computation and Bio-Medical Instrumentation, Wuhan, China, 14–17 December 2011; pp. 232–235. [Google Scholar]
- Yen, H.-H. Efficient visual sensor coverage algorithm in Wireless Visual Sensor Networks. In Proceedings of the 2013 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 1–5 July 2013; pp. 1516–1521. [Google Scholar]
- Kumar, N.; Ghosh, M.; Singhal, C. UAV network for surveillance of inaccessible regions with zero blind spots. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; pp. 1213–1218. [Google Scholar]
- Xu, C.; Liao, X.; Tan, J.; Ye, H.; Lu, H. Recent research progress of unmanned aerial vehicle regulation policies and technologies in urban low altitude. IEEE Access 2020, 8, 74175–74194. [Google Scholar] [CrossRef]
- Ko, Y.-C.; Gau, R.-H. UAV velocity function design and trajectory planning for heterogeneous visual coverage of terrestrial regions. IEEE Trans. Mob. Comput. 2023, 22, 6205–6222. [Google Scholar] [CrossRef]
- Tnunay, H.; Moussa, K.; Hably, A.; Marchand, N. Virtual leader based trajectory generation of UAV formation for visual area coverage. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Wang, H.; Zhang, S.; Zhang, X.; Zhang, X.; Liu, J. Near-optimal 3-D visual coverage for quadrotor unmanned aerial vehicles under photogrammetric constraints. IEEE Trans. Ind. Electron. 2022, 69, 1694–1704. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, M. Maximal weighted coverage deployment of UAV-enabled rechargeable visual sensor networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11293–11307. [Google Scholar] [CrossRef]
- Liao, J.; Zhang, J.; Zhang, H.; Zhou, L.; Xu, C. DRED: A DRL-based energy-efficient data collection scheme for UAV-assisted WSNs. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 846–851. [Google Scholar]
- Wu, S.; Dai, H.; Liu, L.; Xu, L.; Xiao, F.; Xu, J. Cooperative scheduling for directional wireless charging with spatial occupation. IEEE Trans. Mob. Comput. 2024, 23, 286–301. [Google Scholar] [CrossRef]
- Lin, C.; Guo, C.; Dai, H.; Wang, L.; Wu, G. Near optimal charging scheduling for 3-D wireless rechargeable sensor networks with energy constraints. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–9 July 2019; pp. 624–633. [Google Scholar]
- Xie, J.; Garcia Carrillo, L.R.; Jin, L. Path planning for UAV to cover multiple separated convex polygonal regions. IEEE Access 2020, 8, 51770–51785. [Google Scholar] [CrossRef]
- Wang, H.; Song, S.; Guo, Q.; Xu, D.; Zhang, X.; Wang, P. Cooperative motion planning for persistent 3D visual coverage with multiple quadrotor UAVs. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3374–3383. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, S. Joint visual coverage and energy consumption optimization for UAV-aided 5G-and-beyond communications. IEEE Trans. Veh. Technol. 2024, 73, 19417–19431. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, Y.; Zhang, K.; Bian, K.; Song, L. Optimal trajectory planning for UAV-relayed dynamic spectrum access. In Proceedings of the 2018 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Seoul, Republic of Korea, 22–25 October 2018; pp. 1–5. [Google Scholar]
- Wen, W.; Luo, K.; Liu, L.; Zhang, Y.; Jia, Y. Joint trajectory and pick-up design for UAV-assisted item delivery under no-fly zone constraints. IEEE Trans. Veh. Technol. 2023, 72, 2587–2592. [Google Scholar] [CrossRef]
- Lumbantoruan, H.; Adachi, K. Trajectory and communication protocol for efficient data collecting in UAV-enabled WSN. In Proceedings of the 2020 International Conference on Information Networking (ICOIN), Barcelona, Spain, 7–10 January 2020; pp. 348–353. [Google Scholar]
- Gong, J.; Chang, T.-H.; Shen, C.; Chen, X. Flight time minimization of UAV for data collection over wireless sensor networks. IEEE J. Sel. Areas Commun. 2018, 36, 1942–1954. [Google Scholar] [CrossRef]
- Dandapat, J.; Gupta, N.; Agarwal, S.; Kumbhani, B. Service time maximization for data collection in multi-UAV-aided networks. IEEE Trans. Intell. Veh. 2024, 9, 328–337. [Google Scholar] [CrossRef]
- Dai, X.; Duo, B.; Yuan, X.; Renzo, M.D. Energy-efficient UAV communications in the presence of wind: 3D modeling and trajectory design. IEEE Trans. Wirel. Commun. 2024, 23, 1840–1854. [Google Scholar] [CrossRef]
- Silvirianti; Shin, S.Y. Energy-efficient multidimensional trajectory of UAV-aided IoT networks with reinforcement learning. IEEE Internet Things J. 2022, 9, 19214–19226. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, G. Trajectory planning and energy optimization for UAV-assisted vehicular networks in urban scenarios. In Proceedings of the 2022 IEEE 8th International Conference on Computer and Communications (ICCC), Chengdu, China, 9–12 December 2022; pp. 758–764. [Google Scholar]
- PhotographyLife. Prime vs Zoom Lenses. PhotographyLife 2025. Available online: https://photographylife.com/prime-vs-zoom-lenses (accessed on 11 November 2023).
- Li, B.; Na, Z.; Liu, R.; Lin, B. Energy consumption minimization of rotary-wing UAVs for data distribution. IEEE Commun. Lett. 2023, 27, 1819–1823. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing from the sky: A tutorial on UAV communications for 5G and beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Wu, L.; Sun, Q.; Xu, H.; Song, X.; Zhang, Y. Design of hybrid simulated annealing algorithm for UAV scheduling based on coordinated task scheduling. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 1669–1674. [Google Scholar]
- Zhang, Q.; Xu, W.; Liang, W.; Peng, J.; Liu, T.; Wang, T. An improved algorithm for dispatching the minimum number of electric charging vehicles for wireless sensor networks. Wirel. Netw. 2019, 25, 1371–1384. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Gajjar, S.; Bhadani, J.; Dutta, P.; Rastogi, N. Complete coverage path planning algorithm for known 2D environment. In Proceedings of the 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 19–20 May 2017; pp. 963–967. [Google Scholar]
- Zhou, Y.; Sun, R.; Yu, S.; Sun, Y.; Sun, L. A complete coverage path planning algorithm for cleaning robots based on the distance transform algorithm and the rolling window approach in dynamic environments. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 1335–1340. [Google Scholar]
- Zheng, Y.; Tu, X.; Yang, Q. Optimal multi-agent map coverage path planning algorithm. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 6055–6060. [Google Scholar]
- Vasquez-Gomez, J.I.; Marciano-Melchor, M.; Valentin, L.; Herrera-Lozada, J.C. Coverage path planning for 2D convex regions. J. Intell. Robot. Syst. 2020, 97, 81–94. [Google Scholar] [CrossRef]
- Sadat, S.A.; Wawerla, J.; Vaughan, R. Fractal trajectories for online non-uniform aerial coverage. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]

| Notation | Definition |
|---|---|
| N | The number of regions |
| The i-th region | |
| The UAV’s photographing altitude of | |
| The altitude constraints related to | |
| The altitude constraints related to the UAV | |
| The length and width for the field of view of the camera when the flight altitude is h | |
| Maximum ascending and descending velocities of the UAV | |
| Minimum and maximum horizontal velocities of the UAV | |
| The maximum vertical acceleration of the UAV | |
| The maximum horizontal acceleration of the UAV | |
| T | Task completion time |
| Time constraint of the task | |
| The energy consumption of the UAV to visually cover | |
| The energy consumption of the UAV to transition from to | |
| The real-time position of the UAV at time t |
| Notation | Definition |
|---|---|
| The discretization factors of DP | |
| The UAV’s complete flight trajectory | |
| H | The set of photographing altitudes of all regions |
| The set of Euclidean distance between each pair of geometric center points of neighboring regions | |
| The visiting order of each region | |
| The i-th region visited by the UAV | |
| The set of velocities used to cover each region | |
| The cooling rate of SA | |
| The total number of edges of region | |
| The edge formed by connecting the
j-th vertex and the (j + 1)-th vertex of region | |
| The j-th candidate path within region | |
| The total number of candidate paths within region | |
| The final and initial temperature of SA | |
| The number of internal and external loops of SA |
| Notation | Definition | Value |
|---|---|---|
| M | The mass of the UAV | 10 |
| g | The gravity acceleration | 9.8 |
| A | Rotor disc area | 0.79 |
| s | Rotor solidity | 0.05 |
| Fuselage drag ratio | 0.3 | |
| Mean rotor induced velocity in hover | 7.2 | |
| Tip speed of the rotor blade | 200 | |
| Coefficient in the propulsion power formula | 580 | |
| Coefficient in the propulsion power formula | 1438 |
| Algorithm | Key Features | Objective |
|---|---|---|
| AHVC | Max velocity and max altitude per region | Minimize total mission time |
| 2D Planning | Fixed altitude (minimum allowed), constant velocity | Simplified planning ignoring altitude and speed variability |
| Greedy | Chooses next region with minimum incremental energy | Myopic local energy optimization |
| Fly-before-move | Performs vertical then horizontal flight sequentially | Decouples movement phases, simplified control |
| Sadat | DFS/BFS-based region subdivision with frequent altitude reset | Fractal-style coverage, high altitude variation |
| FSTD | AHVC | 2D Planning | Greedy | Fly-Berore-Move | Sadat | |
|---|---|---|---|---|---|---|
| Scenario 1 | 17.50 | 24.67 | 26.73 | 21.57 | 29.00 | 32.37 |
| Scenario 2 | 31.84 | 48.43 | 45.34 | 41.93 | 52.62 | 59.10 |
| FSTD | AHVC | 2D Planning | Greedy | Fly-Berore-Move | Sadat | |
|---|---|---|---|---|---|---|
| Scenario 1 | 21.73 | 41.06 | 39.65 | 35.19 | 42.29 | 44.75 |
| Scenario 2 | 36.87 | 60.85 | 62.03 | 48.45 | 65.12 | 71.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jia, R.; Zheng, Z.; Li, M. Energy-Efficient UAV Trajectory Design and Velocity Control for Visual Coverage of Terrestrial Regions. Drones 2025, 9, 339. https://doi.org/10.3390/drones9050339
Li H, Jia R, Zheng Z, Li M. Energy-Efficient UAV Trajectory Design and Velocity Control for Visual Coverage of Terrestrial Regions. Drones. 2025; 9(5):339. https://doi.org/10.3390/drones9050339
Chicago/Turabian StyleLi, Hengchao, Riheng Jia, Zhonglong Zheng, and Minglu Li. 2025. "Energy-Efficient UAV Trajectory Design and Velocity Control for Visual Coverage of Terrestrial Regions" Drones 9, no. 5: 339. https://doi.org/10.3390/drones9050339
APA StyleLi, H., Jia, R., Zheng, Z., & Li, M. (2025). Energy-Efficient UAV Trajectory Design and Velocity Control for Visual Coverage of Terrestrial Regions. Drones, 9(5), 339. https://doi.org/10.3390/drones9050339





