Event-Triggered-Based Neuroadaptive Bipartite Containment Tracking for Networked Unmanned Aerial Vehicles
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Motivations
1.4. Contributions
1.5. Organization
2. Preliminaries
2.1. Communication Network
2.2. Neural Network
2.3. Some Useful Lemmas
3. Problem Description
3.1. Model of UAVs
3.2. Description of Containment Control Problem
4. Main Results
4.1. Event-Triggered Bipartite Containment Control Scheme Design
4.2. Stability Analysis
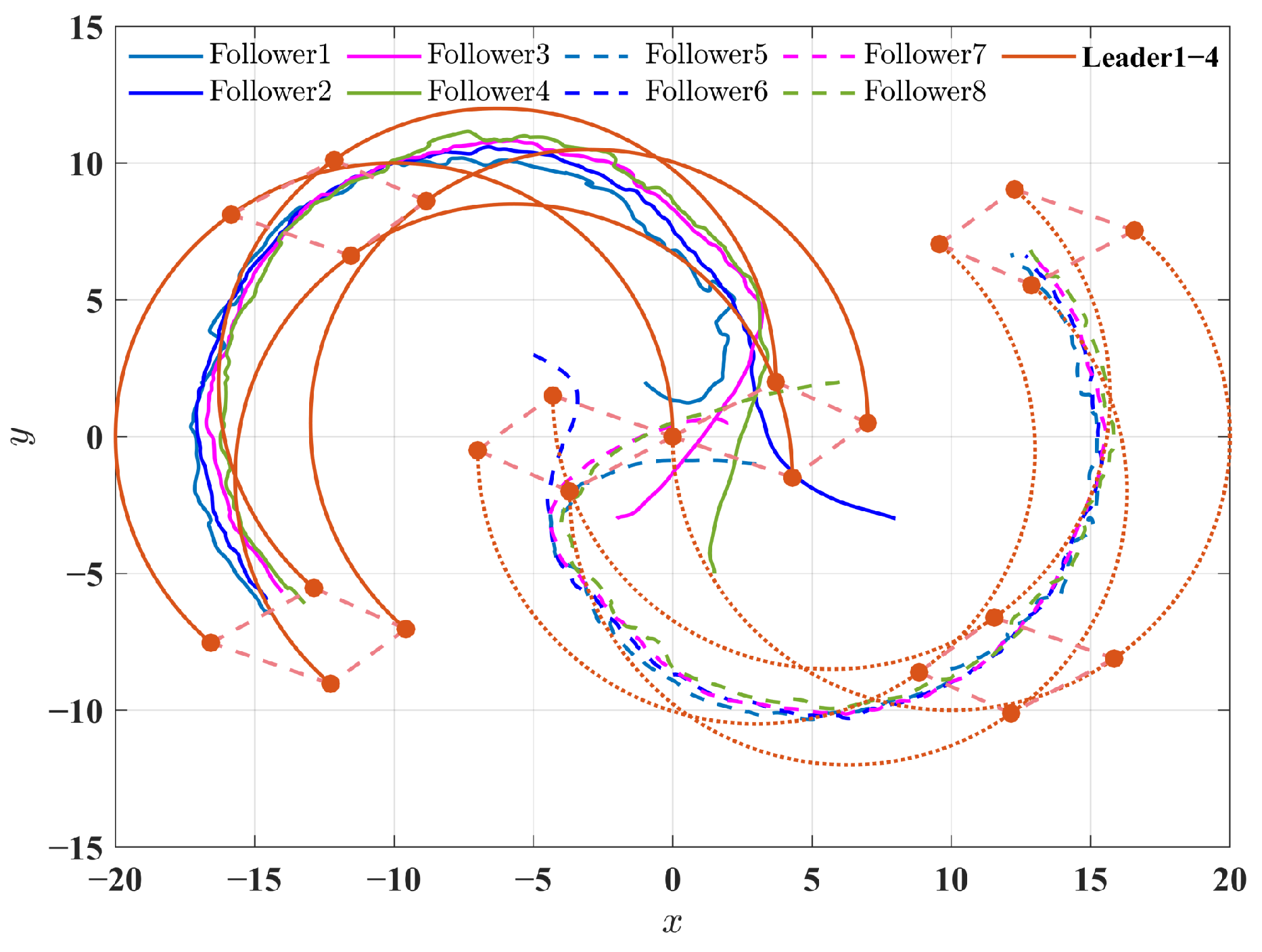
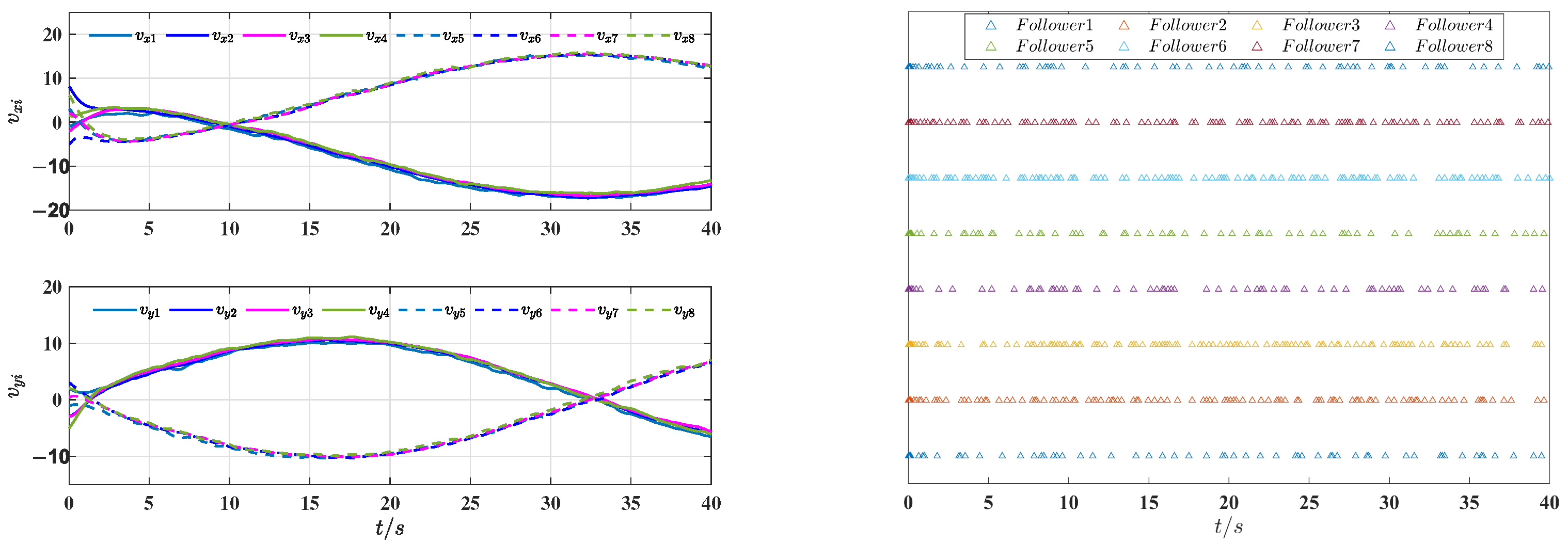
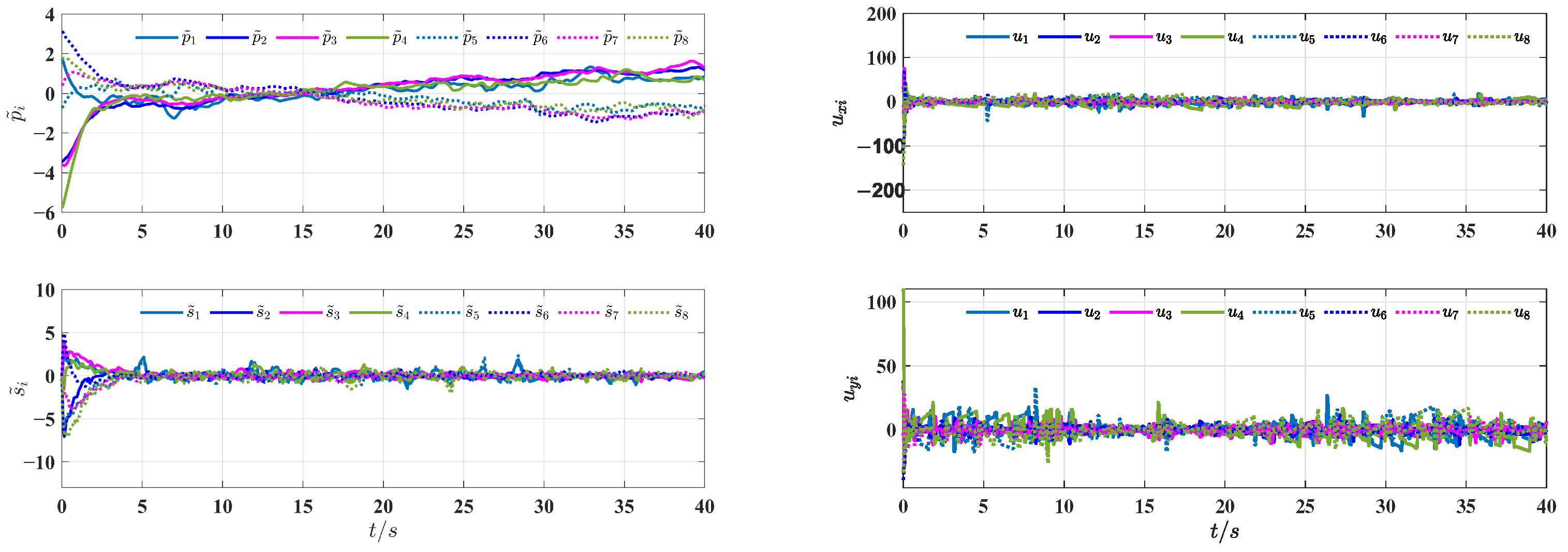
5. Numerical Simulation
5.1. The Effectiveness of the Proposed Control Scheme
5.2. Comparisons with Existing Time-Triggered and Static Event-Triggered Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
References
- Xiong, S.X.; Xie, X.P.; Jiang, G.P. A distributed containment tracking control of the UAV formation with prescribed performance subject to collision avoidance. Int. J. Robust Nonlinear Control 2024, 34, 5813–5832. [Google Scholar] [CrossRef]
- Yan, S.; Feng, J.; Pan, F. A distributed task allocation method for multi-UAV systems in communication-constrained environments. Drones 2024, 8, 342. [Google Scholar] [CrossRef]
- Li, W.; Qin, K.; Li, G.; Shi, M.; Zhang, X. Robust bipartite tracking consensus of multi-agent systems via neural network combined with extended high-gain observer. ISA Trans. 2023, 136, 31–45. [Google Scholar] [CrossRef]
- Wang, J.; Fang, W.; Qiu, H.; Wang, Y. The Impact of Automation Failure on Unmanned Aircraft System Operators’ Performance, Workload, and Trust in Automation. Drones 2025, 9, 165. [Google Scholar] [CrossRef]
- Alharasees, O.; Adali, O.H.; Kale, U. Human factors in the age of autonomous UAVs: Impact of artificial intelligence on operator performance and safety. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; pp. 798–805. [Google Scholar]
- Alharasees, O.; Kale, U. Human Factors and AI in UAV Systems: Enhancing Operational Efficiency Through AHP and Real-Time Physiological Monitoring. J. Intell. Robot. Syst. 2025, 111, 5. [Google Scholar] [CrossRef]
- Xiao, W.; Zhou, Q.; Liu, Y.; Li, H.; Lu, R. Distributed reinforcement learning containment control for multiple nonholonomic mobile robots. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 896–907. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: London, UK, 2008; Volume 27. [Google Scholar]
- Liang, H.; Chen, L.; Pan, Y.; Lam, H.K. Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative–antagonistic interactions. IEEE Trans. Fuzzy Syst. 2022, 31, 1362–1376. [Google Scholar] [CrossRef]
- Li, W.; Ren, R.; Shi, M.; Lin, B.; Qin, K. Seeking Secure Adaptive Distributed Discrete-Time Observer for Networked Agent Systems Under External Cyber Attacks. IEEE Trans. Consum. Electron. 2025. [Google Scholar] [CrossRef]
- Li, W.; Shi, M.; Shi, L.; Lin, B.; Qin, K. Containment tracking for networked agents subject to nonuniform communication delays. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3658–3669. [Google Scholar] [CrossRef]
- Li, P.; Jabbari, F.; Sun, X.M. Containment control of multi-agent systems with input saturation and unknown leader inputs. Automatica 2021, 130, 109677. [Google Scholar] [CrossRef]
- Santilli, M.; Franceschelli, M.; Gasparri, A. Secure rendezvous and static containment in multi-agent systems with adversarial intruders. Automatica 2022, 143, 110456. [Google Scholar] [CrossRef]
- Sang, J.; Ma, D.; Zhou, Y. Group-consensus of hierarchical containment control for linear multi-agent systems. IEEE/CAA J. Autom. Sin. 2023, 10, 1462–1474. [Google Scholar] [CrossRef]
- Fan, S.; Peng, F.; Liu, X.; Wang, T.; Qiu, J. Bipartite containment control of multi-agent systems subject to adversarial inputs based on zero-sum game. Inf. Sci. 2024, 681, 121234. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, X.; Han, T.; Yan, H. Distributed adaptive finite-time bipartite containment control of linear multi-agent systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4354–4358. [Google Scholar] [CrossRef]
- Li, W.; Qin, K.; Shi, M.; Shao, J.; Lin, B. Dynamic target enclosing control scheme for multi-agent systems via a signed graph-based approach. IEEE/CAA J. Autom. Sin. 2023, 10, 560–562. [Google Scholar] [CrossRef]
- Chen, L.; Shi, L.; Cheng, Y.; Shao, J. Bipartite containment control for general linear multiagent systems under denial-of-service attacks. In Proceedings of the 2021 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Chengdu, China, 18–20 June 2021; pp. 495–500. [Google Scholar]
- He, S.; Dai, S.L.; Zhao, Z.; Zou, T.; Ma, Y. UDE-based distributed formation control for MSVs with collision avoidance and connectivity preservation. IEEE Trans. Ind. Inform. 2023, 20, 1476–1487. [Google Scholar] [CrossRef]
- Xu, J.; Cui, Y.; Xing, W.; Huang, F.; Du, X.; Yan, Z.; Wu, D. Distributed active disturbance rejection formation containment control for multiple autonomous underwater vehicles with prescribed performance. Ocean Eng. 2022, 259, 112057. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Nazari, M. Disturbance observer-based nonlinear feedback control for position tracking of electro-hydraulic systems in a finite time. Eur. J. Control 2022, 67, 100659. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Fan, D.; Zhang, X.; Wen, C. Exponential Regulation of Uncertain Nonlinear Triangular Impulsive Systems: A Logic-Based Switching Gain Approach. IEEE Trans. Autom. Control 2025. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Shi, Z.; Gao, Z. Neural-network-based finite-time bipartite containment control for fractional-order multi-agent systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7418–7429. [Google Scholar] [CrossRef]
- Li, W.; Yue, J.; Shi, M.; Lin, B.; Qin, K. Neural network-based dynamic target enclosing control for uncertain nonlinear multi-agent systems over signed networks. Neural Netw. 2025, 184, 107057. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Liang, H.; Ahn, C.K. Neural-network-based predefined-time adaptive consensus in nonlinear multi-agent systems with switching topologies. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 9995–10005. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Han, Y.; Zhu, S.; Zeng, Z. Neural network-based fixed-time tracking and containment control of second-order heterogeneous nonlinear multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 11565–11579. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.M.; Han, Q.L.; Zhang, B.L. An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems. IEEE Trans. Ind. Inform. 2016, 13, 4–16. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Duan, J.; Zhang, J. Distributed bipartite consensus of linear multiagent systems based on event-triggered output feedback control scheme. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6743–6756. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Li, H.; He, W. Event-triggered adaptive bipartite containment control for stochastic multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 5843–5852. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Li, W.; Wang, Y. Adaptive event-triggered bipartite containment control of linear multiagent systems under directed topologies. IEEE Trans. Control Netw. Syst. 2022, 10, 516–525. [Google Scholar] [CrossRef]
- Jiang, D.; Wen, G.; Peng, Z.; Huang, T.; Rahmani, A. Fully distributed dual-terminal event-triggered bipartite output containment control of heterogeneous systems under actuator faults. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 5518–5531. [Google Scholar] [CrossRef]
- Lin, G.; Ren, H.; Zhou, Q.; Wang, X. Fuzzy dynamic event-triggered containment control for human-in-the-loop MASs with error constraints. IEEE Trans. Fuzzy Syst. 2024, 32, 2496–2508. [Google Scholar] [CrossRef]
- Wang, X.; Pang, N.; Xu, Y.; Huang, T.; Kurths, J. On state-constrained containment control for nonlinear multiagent systems using event-triggered input. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2530–2538. [Google Scholar] [CrossRef]
- Xiao, Y.; Che, W.W. Event-triggered fully distributed H∞ containment control for MASs. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2676–2684. [Google Scholar] [CrossRef]
- Wu, X.; Ding, S.; Xu, N.; Niu, B.; Zhao, X. Periodic event-triggered bipartite containment control for nonlinear multi-agent systems with input delay. Int. J. Syst. Sci. 2024, 55, 2008–2022. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Li, X.; Xiao, J. Bipartite containment control of fractional multi-agent systems with input delay on switching signed directed networks. ISA Trans. 2023, 135, 130–137. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, Q.; Chen, Z. Distributed containment control for bounded unknown second-order nonlinear multi-agent systems with dynamic leaders. Neurocomputing 2015, 168, 1138–1143. [Google Scholar] [CrossRef]
- Cao, Y.; Stuart, D.; Ren, W.; Meng, Z. Distributed containment control for multiple autonomous vehicles with double-integrator dynamics: Algorithms and experiments. IEEE Trans. Control Syst. Technol. 2010, 19, 929–938. [Google Scholar] [CrossRef]
- Guo, J.; Qi, J.; Wang, M.; Wu, C.; Yang, G. Collision-Free Distributed Control for Multiple Quadrotors in Cluttered Environments With Static and Dynamic Obstacles. IEEE Robot. Autom. Lett. 2023, 8, 1501–1508. [Google Scholar] [CrossRef]
- Fei, Y.; Sun, Y.; Shi, P. Robust hierarchical formation control of unmanned aerial vehicles via neural-based observers. Drones 2022, 6, 40. [Google Scholar] [CrossRef]
- Hu, J.; Yu, J.; Cao, J. Distributed containment control for nonlinear multi-agent systems with time-delayed protocol. Asian J. Control 2016, 18, 747–756. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, J.; Zhan, X.; Han, T.; Yan, H. Observer-Based Adaptive Time-Varying Formation-Containment Tracking for Multiagent System With Bounded Unknown Input. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1479–1491. [Google Scholar] [CrossRef]
- Zhou, H.; Tong, S. Adaptive Neural Network Event-Triggered Output-Feedback Containment Control for Nonlinear MASs With Input Quantization. IEEE Trans. Cybern. 2023, 53, 7406–7416. [Google Scholar] [CrossRef] [PubMed]

| Variables | Definition |
|---|---|
| , | The position/velocity of ith UAV |
| , | The position/velocity of ith UAV at triggered instant |
| , | The auxiliary variables |
| , | The auxiliary variables at triggered instant |
| , | Local measurement errors |
| Triggered function | |
| The nonlinear term | |
| Approximation of neural network weight matrices | |
| Radial basis function | |
| The control input of ith follower UAV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Lin, B.; Li, M.; Li, Z.; Zhang, X.; Shi, M.; Qin, K. Event-Triggered-Based Neuroadaptive Bipartite Containment Tracking for Networked Unmanned Aerial Vehicles. Drones 2025, 9, 317. https://doi.org/10.3390/drones9040317
Chen B, Lin B, Li M, Li Z, Zhang X, Shi M, Qin K. Event-Triggered-Based Neuroadaptive Bipartite Containment Tracking for Networked Unmanned Aerial Vehicles. Drones. 2025; 9(4):317. https://doi.org/10.3390/drones9040317
Chicago/Turabian StyleChen, Bowen, Boxian Lin, Meng Li, Zhiqiang Li, Xinyu Zhang, Mengji Shi, and Kaiyu Qin. 2025. "Event-Triggered-Based Neuroadaptive Bipartite Containment Tracking for Networked Unmanned Aerial Vehicles" Drones 9, no. 4: 317. https://doi.org/10.3390/drones9040317
APA StyleChen, B., Lin, B., Li, M., Li, Z., Zhang, X., Shi, M., & Qin, K. (2025). Event-Triggered-Based Neuroadaptive Bipartite Containment Tracking for Networked Unmanned Aerial Vehicles. Drones, 9(4), 317. https://doi.org/10.3390/drones9040317






