Prescribed Performance Sliding Mode Fault-Tolerant Tracking Control for Unmanned Morphing Flight Vehicles with Actuator Faults
Abstract
1. Introduction
- (1)
- By decomposing the integrated dynamics into attitude and velocity subsystems, the developed framework simplifies controller architecture and improves fault tolerance characteristics. This decomposition effectively mitigates control complexity arising from high-dimensional coupling effects;
- (2)
- (3)
- Compared to methods in the Refs. [10,30,31,32], the proposed modular scheme demonstrates a lower computational burden. By integrating SMC with PPC, the scheme achieves rapid response to reduce conservatism and enhances fault tolerance through switching control laws, thereby improving stability. These synergistic merits enhance its practical value in engineering applications.
2. Problem Formulation
2.1. The Longitudinal Nonlinear Dynamics Model of the Unmanned MFV
2.2. Actuator Fault Model and Control Objective
3. Controllers Design
3.1. Prescribed Performance Sliding Mode Controller Design for Attitude Subsystem
3.2. Prescribed Performance Sliding Mode Controller Design for Velocity Subsystem
4. Simulation and Analysis
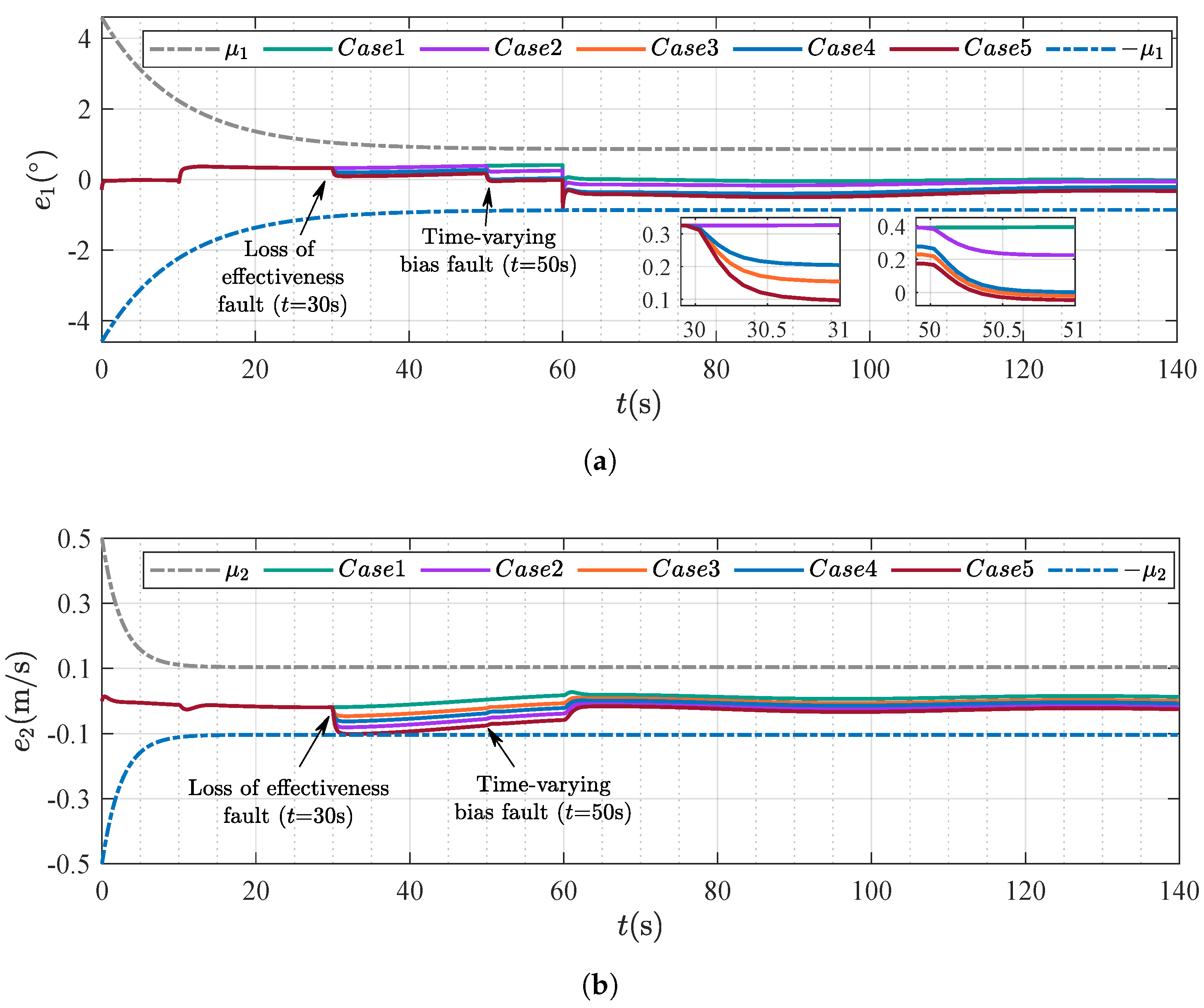
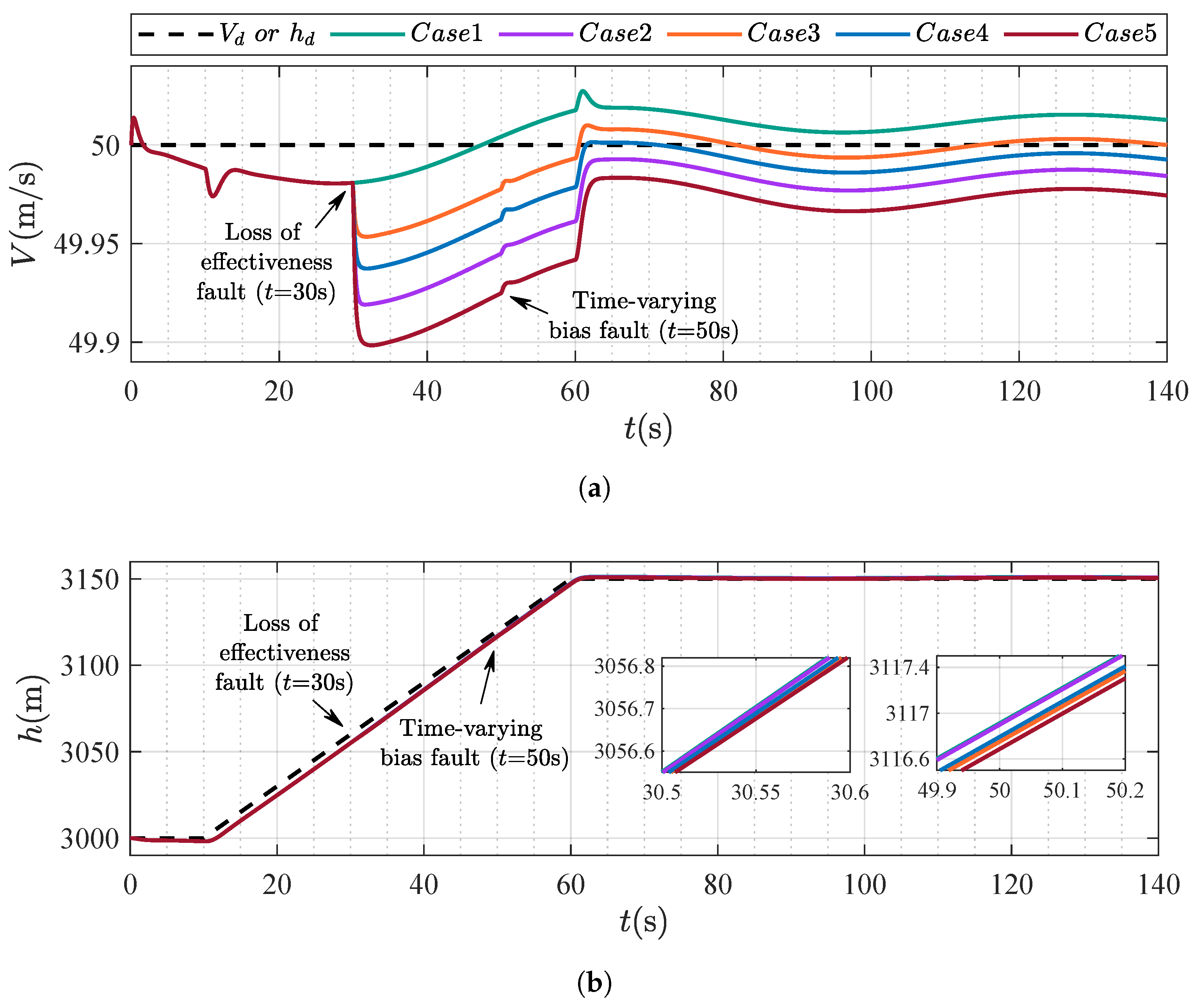
4.1. Scenario 1: Robustness Validation Under Diverse Actuator Fault Conditions
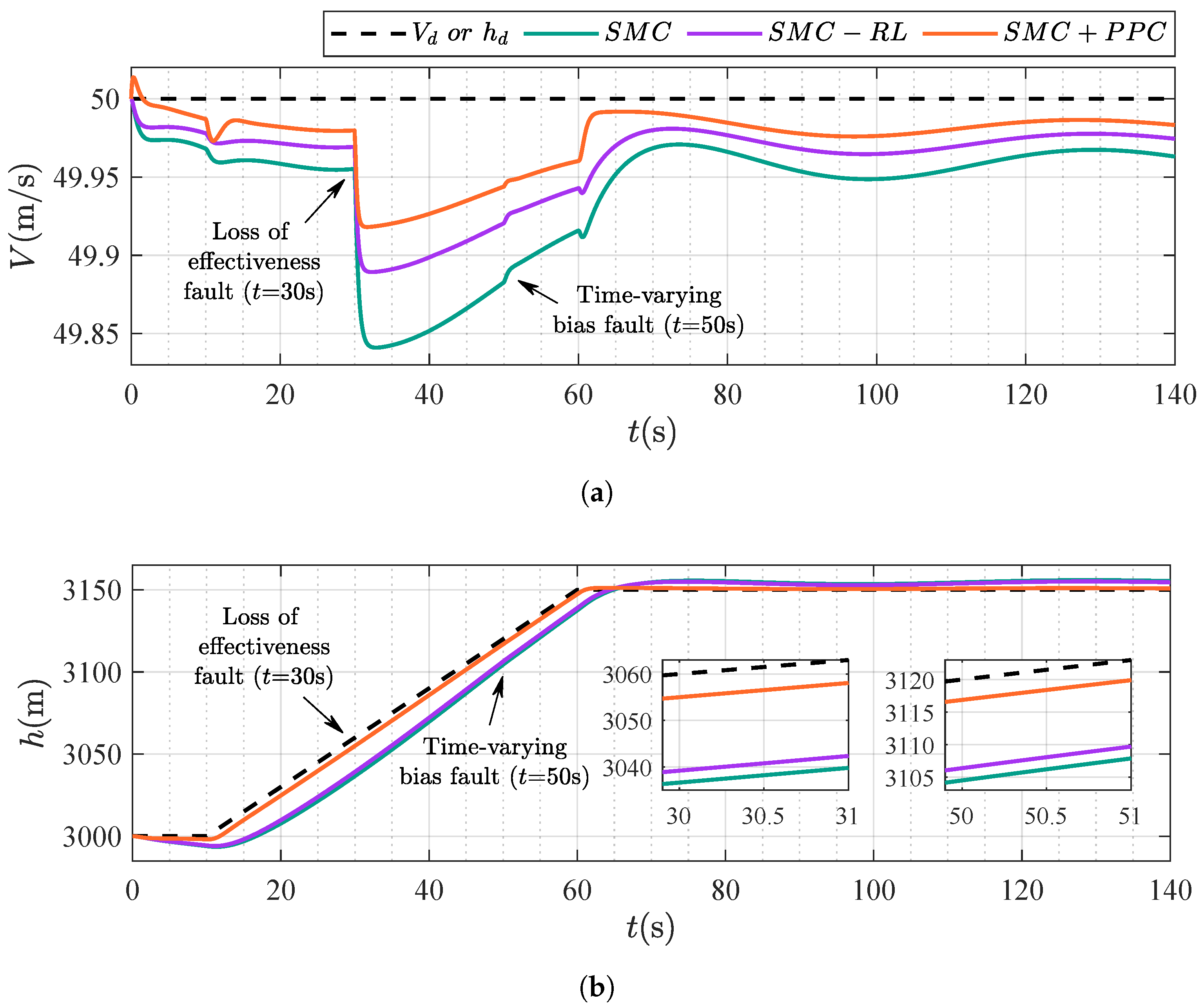
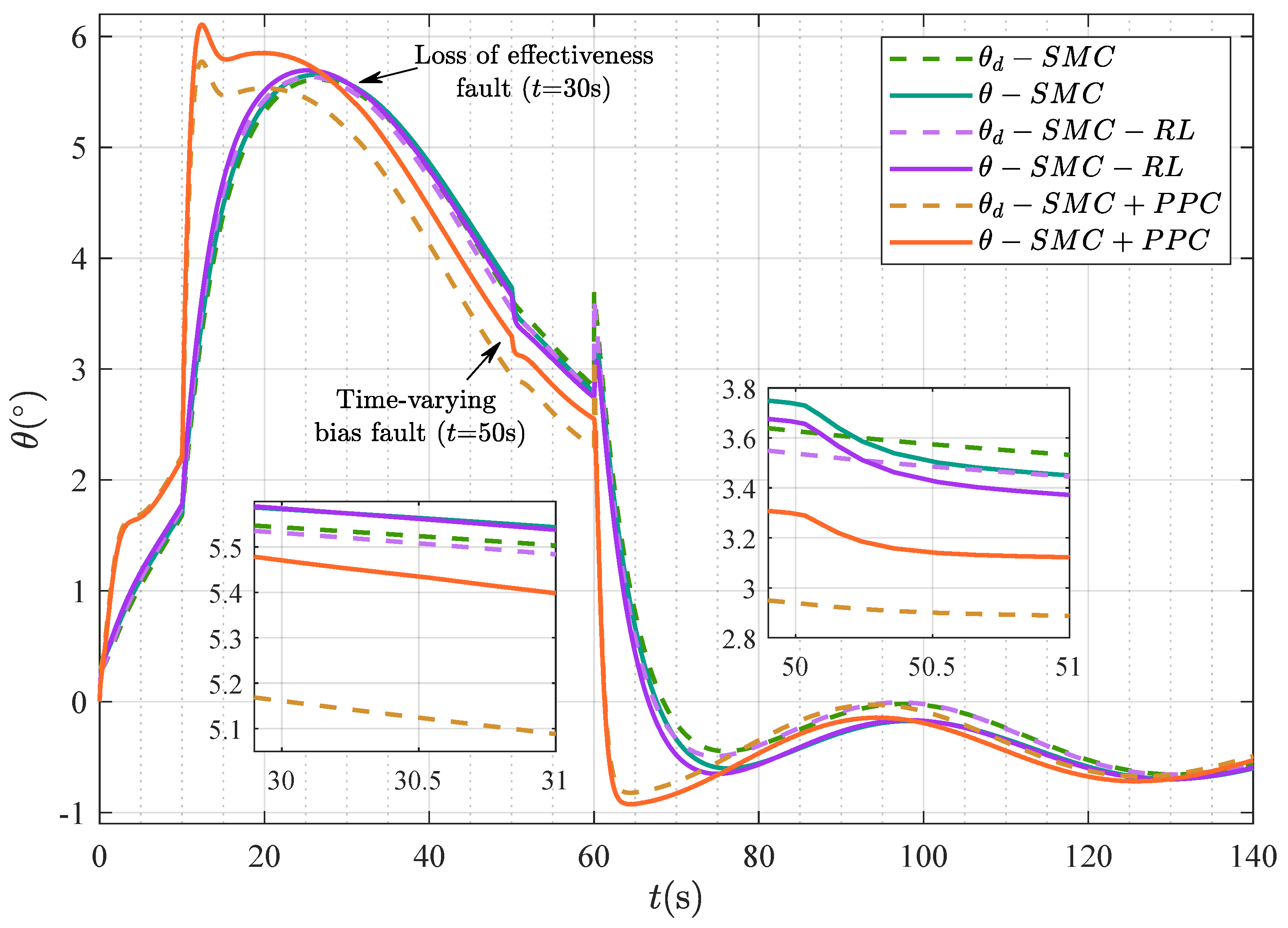
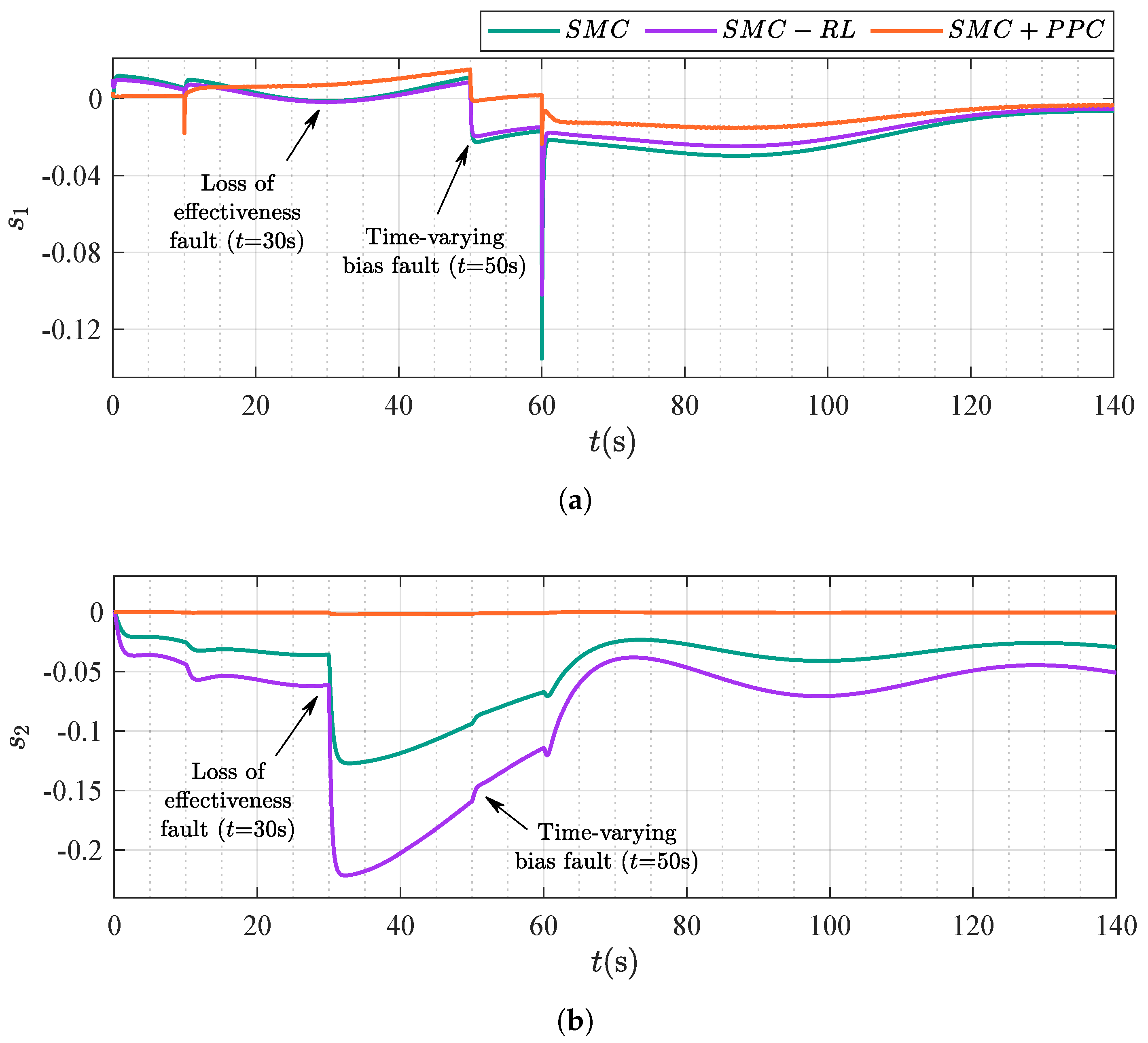
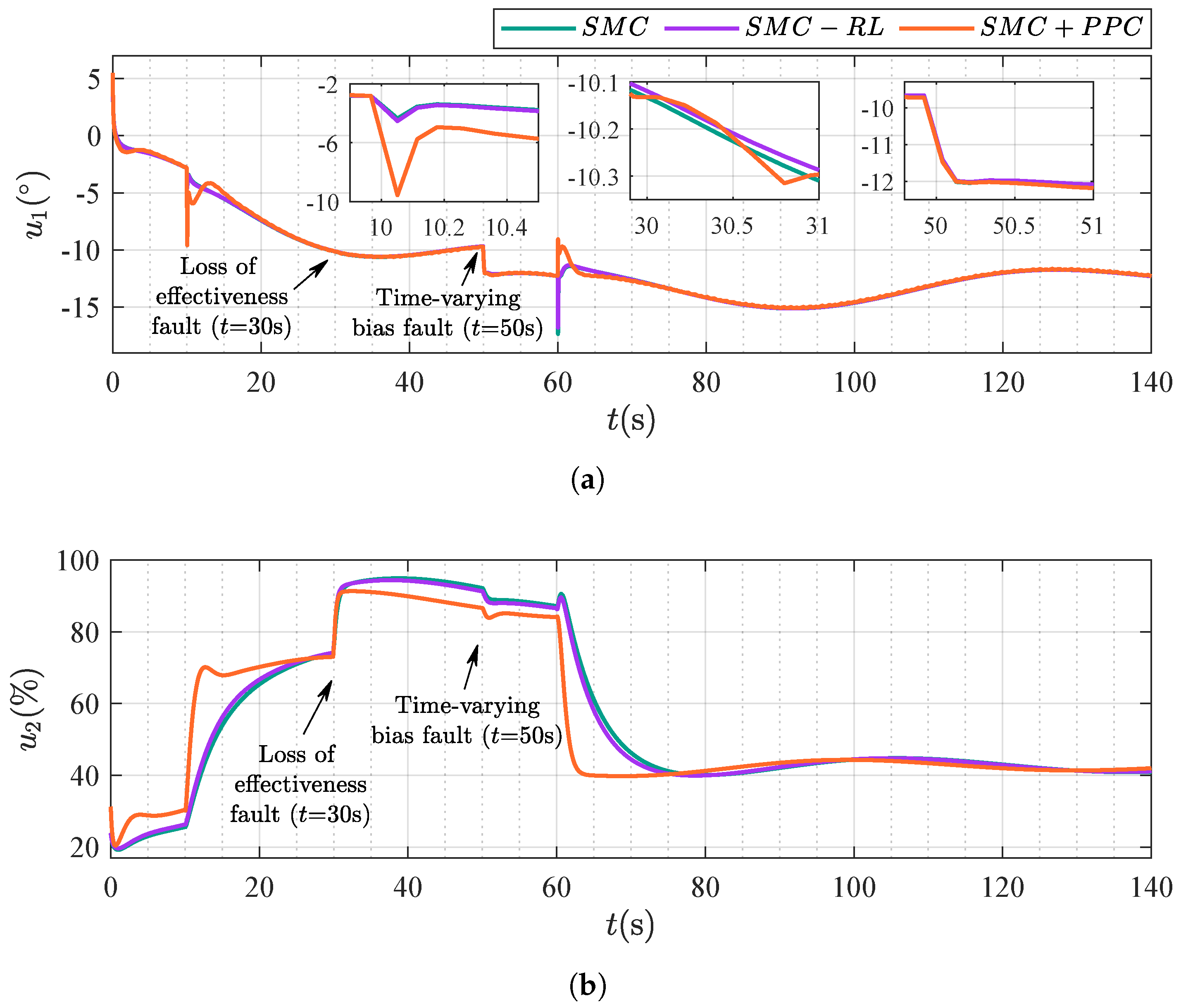
4.2. Scenario 2: Comparison Between Different Control Strategies
- when s
- with and when s
5. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
References
- Ajaj, R.M.; Jankee, G.K. The transformer aircraft: A multi-mission unmanned aerial vehicle capable of symmetric and asymmetric span morphing. Aerosp. Sci. Technol. 2018, 76, 512–522. [Google Scholar] [CrossRef]
- Ran, M.; Wang, C.; Liu, H.; Wang, W.; Lyu, J. Research status and future development of morphing aircraft control technology. Acta Aeronaut. Astronaut. Sin. 2022, 43, 424–441. (In Chinese) [Google Scholar] [CrossRef]
- Parancheerivilakkathil, M.S.; Pilakkadan, J.S.; Ajaj, R.M.; Amoozgar, M.; Asadi, D.; Zweiri, Y.; Friswell, M.I. A review of control strategies used for morphing aircraft applications. Chin. J. Aeronaut. 2024, 37, 436–463. [Google Scholar] [CrossRef]
- Yan, B.; Li, Y.; Dai, P.; Liu, S. Aerodynamic analysis, dynamic modeling, and control of a morphing aircraft. J. Aerosp. Eng. 2019, 32, 04019058. [Google Scholar] [CrossRef]
- Bai, B.; Dong, C. Modeling and LQR switch control of morphing aircraft. In Proceedings of the 2013 6th International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–29 October 2013; pp. 148–151. [Google Scholar] [CrossRef]
- Fan, W.; Liu, H.H.T.; Kwong, R.H.S. Gain-scheduling control of flexible aircraft with actuator saturation and stuck faults. J. Guid. Control Dyn. 2017, 17, 497–502. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Liu, L. Longitudinal adaptive control of morphing aircraft based on guardian maps theory. Int. J. Aeronaut. Space Sci. 2025. [Google Scholar] [CrossRef]
- Cai, G.; Yang, Q.; Mu, C.; Li, X. Design of linear parameter-varying controller for morphing aircraft using inexact scheduling parameters. IET Control Theory Appl. 2022, 17, 493–503. [Google Scholar] [CrossRef]
- Cai, G.; Wu, T.; Hao, M.; Liu, H.; Zhou, B. Dynamic event-triggered gain-scheduled H∞ control for a polytopic LPV model of morphing aircraft. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 93–106. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, L.; Xu, J. Adaptive fault-tolerant controller for morphing aircraft based on the L2 gain and a neural network. Aerosp. Sci. Technol. 2022, 132, 107985. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, P.; Wu, H. A new control design for a morphing UAV based on disturbance observer and command filtered backstepping techniques. Sci. China Technol. Sci. 2019, 62, 1845–1853. [Google Scholar] [CrossRef]
- Gong, L.; Wang, Q.; Dong, C. Disturbance rejection control of morphing aircraft based on switched nonlinear systems. Nonlinear Dyn. 2019, 96, 975–995. [Google Scholar] [CrossRef]
- Meng, F.; Wang, T.; Chen, G. Prescribed performance-based active anti-disturbance backstepping control for morphing aircraft. Aerosp. Sci. Technol. 2024, 152, 109386. [Google Scholar] [CrossRef]
- Shi, R.; Song, J. Dynamics and control for an in-plane morphing wing. Aircr. Eng. Aerosp. Technol. 2013, 85, 24–31. [Google Scholar] [CrossRef]
- Huang, R.; Hu, H.; Zhao, Y. Single-input/single-output adaptive flutter suppression of a three-dimensional aeroelastic system. J. Guid. Control Dyn. 2012, 35, 659–665. [Google Scholar] [CrossRef]
- Xu, S.; Guan, Y.; Wei, C.; Xu, H. Broad learning system-based model-free adaptive robust control for hypersonic morphing aircraft with appointed-time prescribed performance. Eng. Appl. Artif. Intell. 2025, 143, 109962. [Google Scholar] [CrossRef]
- Luo, M.; Gao, M.; Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J. Fluids Struct. 2016, 61, 262–273. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Suzuki, S.; Namiki, A.; Liu, H.; Li, Z. Design and implementation of UAV velocity controller based on reference model sliding mode control. Drones 2023, 7, 130. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Luo, J. An asymmetrically variable wingtip anhedral angles morphing aircraft based on incremental sliding mode control: Improving lateral maneuver capability. Chin. J. Aeronaut. 2024, 38, 103166. [Google Scholar] [CrossRef]
- Wei, C.; Luo, J.; Yin, Z. A review of prescribed performance control for spacecraft attitude. J. Astronaut. 2019, 40, 1167–1176. (In Chinese) [Google Scholar] [CrossRef]
- Ghanooni, P.; Habibi, H.; Yazdani, A.; Wang, H.; MahmoudZadeh, S.; Ferrara, A. Prescribed performance control of a robotic manipulator with unknown control gain and assigned settling time. ISA Trans. 2023, 145, 330–354. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J. Fixed-time RBFNN-based prescribed performance control for robot manipulators: Achieving global convergence and control performance improvement. Mathematics 2023, 11, 2307. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Q. Prescribed performance fault-tolerant attitude tracking control for UAV with actuator faults. Drones 2024, 8, 204. [Google Scholar] [CrossRef]
- Yuan, L.; Zheng, J.; Wang, X.; Ma, L. Attitude control of a mass-actuated fixed-wing UAV based on adaptive global fast terminal sliding mode control. Drones 2024, 8, 305. [Google Scholar] [CrossRef]
- Zhao, S.; Li, X.; Bu, X.; Zhang, D. Prescribed performance tracking control for hypersonic flight vehicles with model uncertainties. Int. J. Aerosp. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Hu, Q.; Shao, X.; Guo, L. Adaptive fault-tolerant attitude tracking control of spacecraft with prescribed performance. IEEE/ASME Trans. Mechatronics 2018, 23, 331–341. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, B.; Xiong, R.; Xiang, Z.; Liu, L.; Fan, H.; Xue, C. Attitude tracking control of hypersonic vehicle based on an improved prescribed performance dynamic surface control. Aeronaut. J. 2023, 128, 875–895. [Google Scholar] [CrossRef]
- Ding, Y.; Yue, X.; Chen, G.; Si, J. Review of control and guidance technology on hypersonic vehicle. Chin. J. Aeronaut. 2021, 35, 1–18. [Google Scholar] [CrossRef]
- Wen, L.; Tao, G.; Jiang, B.; Chen, W. Adaptive compensation of persistent actuator failures using control-separation-based LQ design. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5030–5045. [Google Scholar] [CrossRef]
- Chao, D.; Qi, R.; Jiang, B. Adaptive fault-tolerant attitude control for hypersonic reentry vehicle subject to complex uncertainties. J. Frankl. Inst. 2022, 359, 5458–5487. [Google Scholar] [CrossRef]
- Liu, S.; Whidborne, J.F. Observer-based incremental backstepping sliding-mode fault-tolerant control for blended-wing-body aircrafts. Neurocomputing 2021, 464, 546–561. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Q.; Hu, C.; Dong, C. Fixed-time observer based fault tolerant attitude control for reusable launch vehicle with actuator faults. Aerosp. Sci. Technol. 2020, 107, 106314. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, B.; Song, X.; Zhang, S. Fault-tolerant control allocation for over-actuated discrete-time systems. J. Frankl. Inst. 2015, 352, 2297–2313. [Google Scholar] [CrossRef]
- Khan, S.; Grigorie, T.; Botez, R.; Mamou, M.; Mébarki, Y. Fuzzy logic-based control for a morphing wing tip actuation system: Design, numerical simulation, and wind tunnel experimental testing. Biomimetics 2019, 4, 65. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, J.; Huang, S.; Lin, Y.; Jiang, J. Computational study of axisymmetric divergent bypass dual throat nozzle. Aerosp. Sci. Technol. 2019, 86, 177–190. [Google Scholar] [CrossRef]
- Yan, B.; Dai, P.; Liu, R.; Xing, M.; Liu, S. Adaptive super-twisting sliding mode control of variable sweep morphing aircraft. Aerosp. Sci. Technol. 2019, 92, 198–210. [Google Scholar] [CrossRef]
- Yin, M. Coordinated Control of Deformation and Flight for Morphing Aircraft. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
- Zheng, W. Research on Nonlinear Control Method of Morphing Aircraft. Master’s Thesis, Harbin Institude of Technology, Harbin, China, 2022. [Google Scholar]

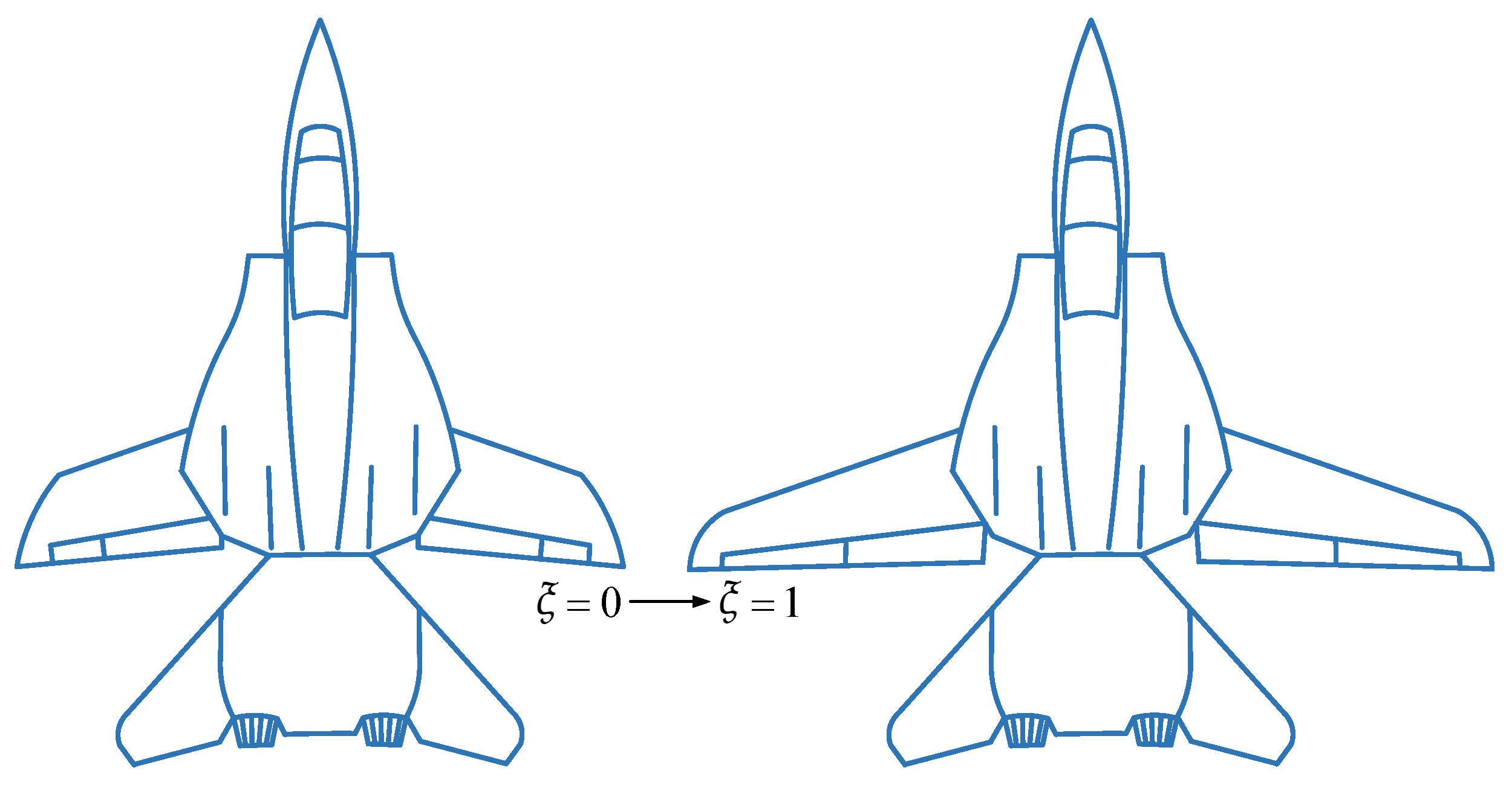
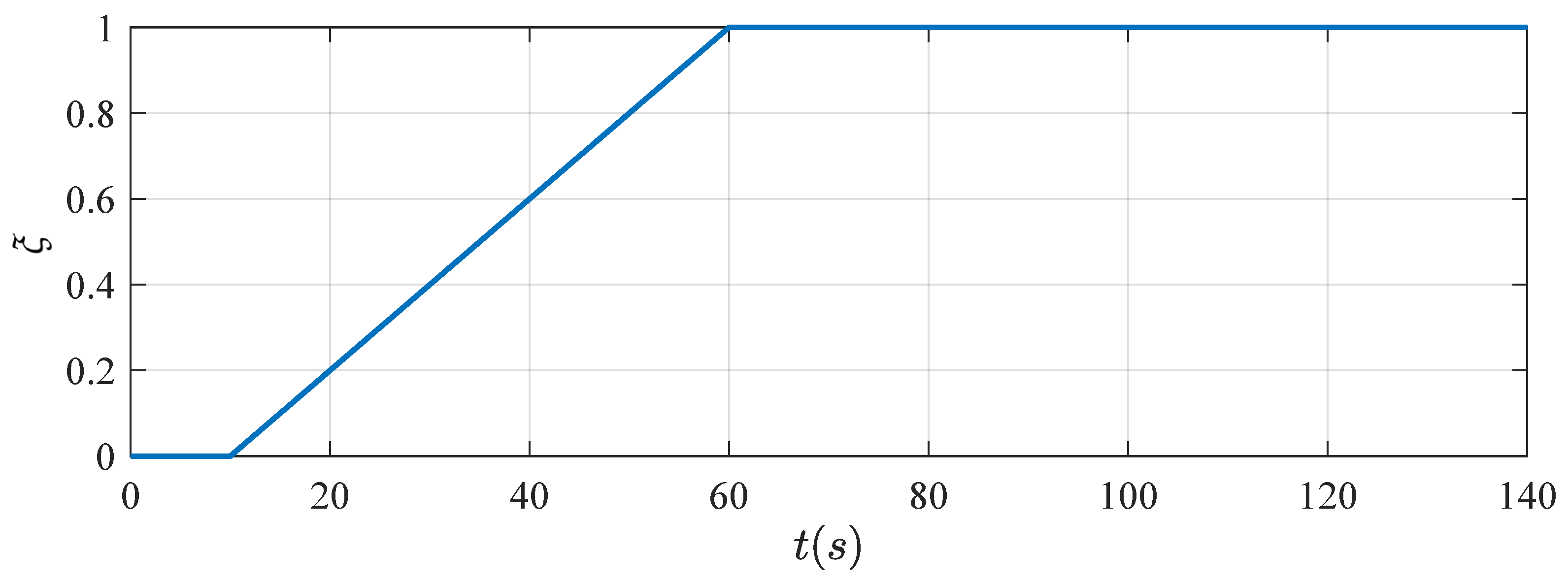
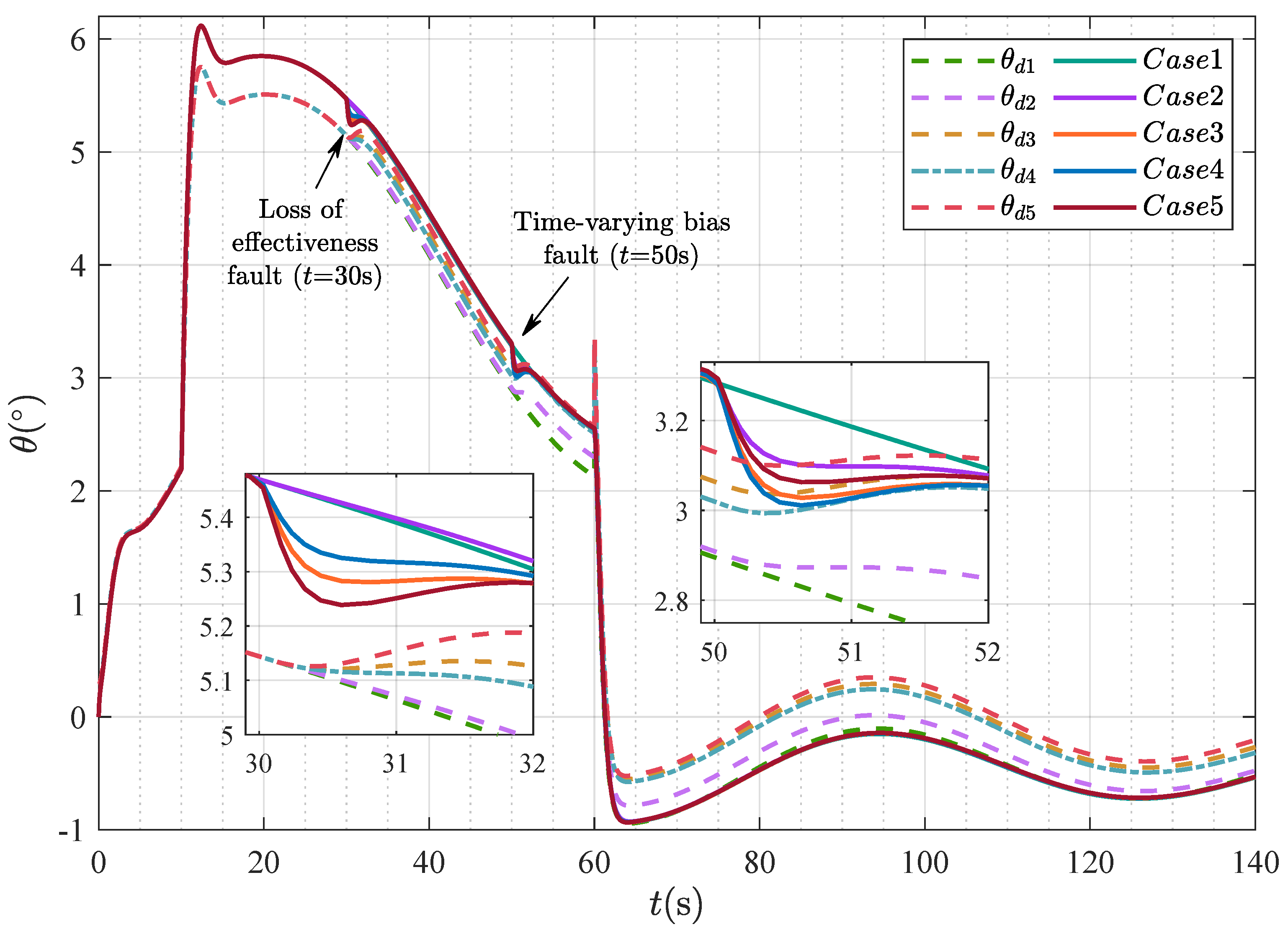
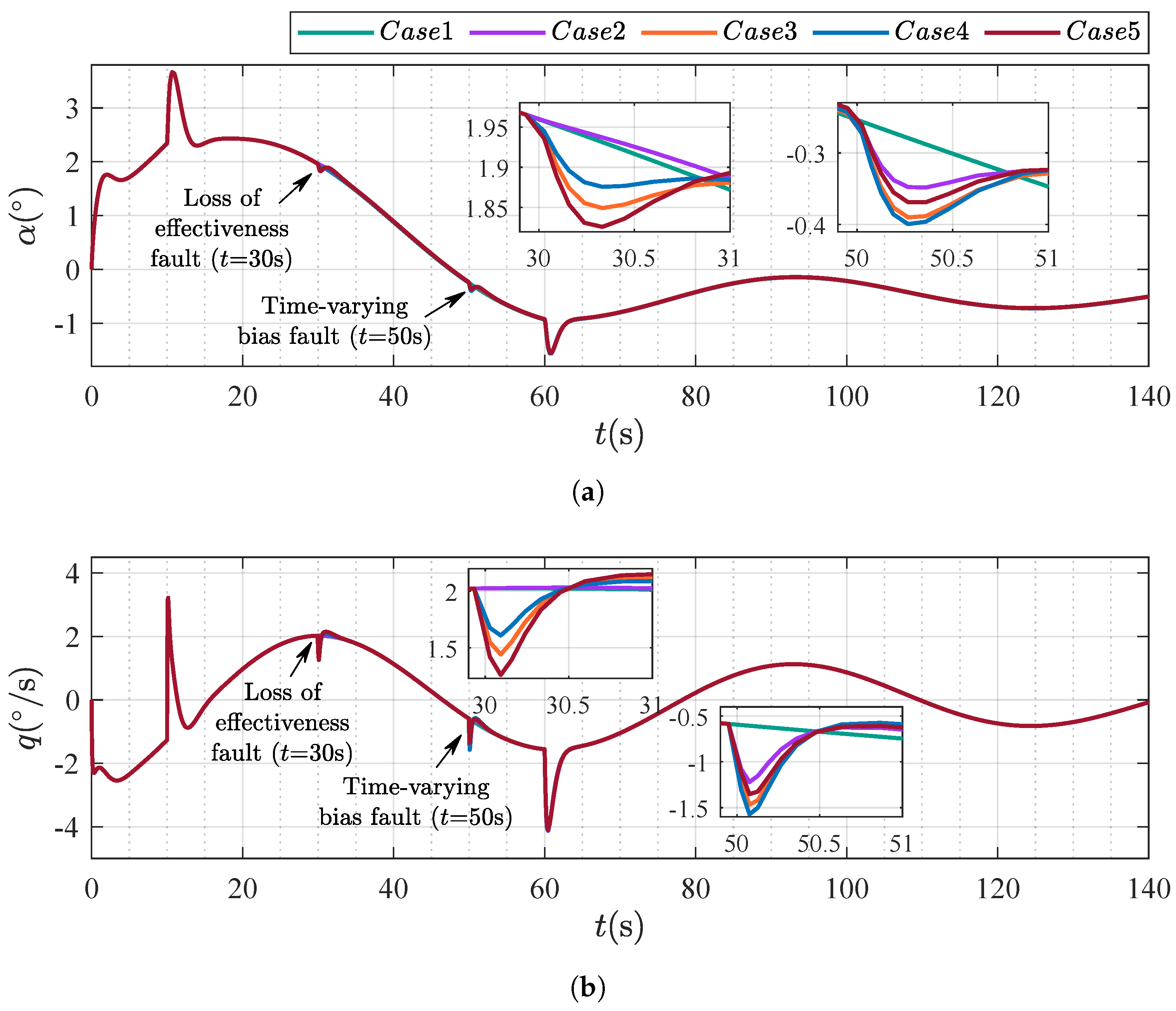

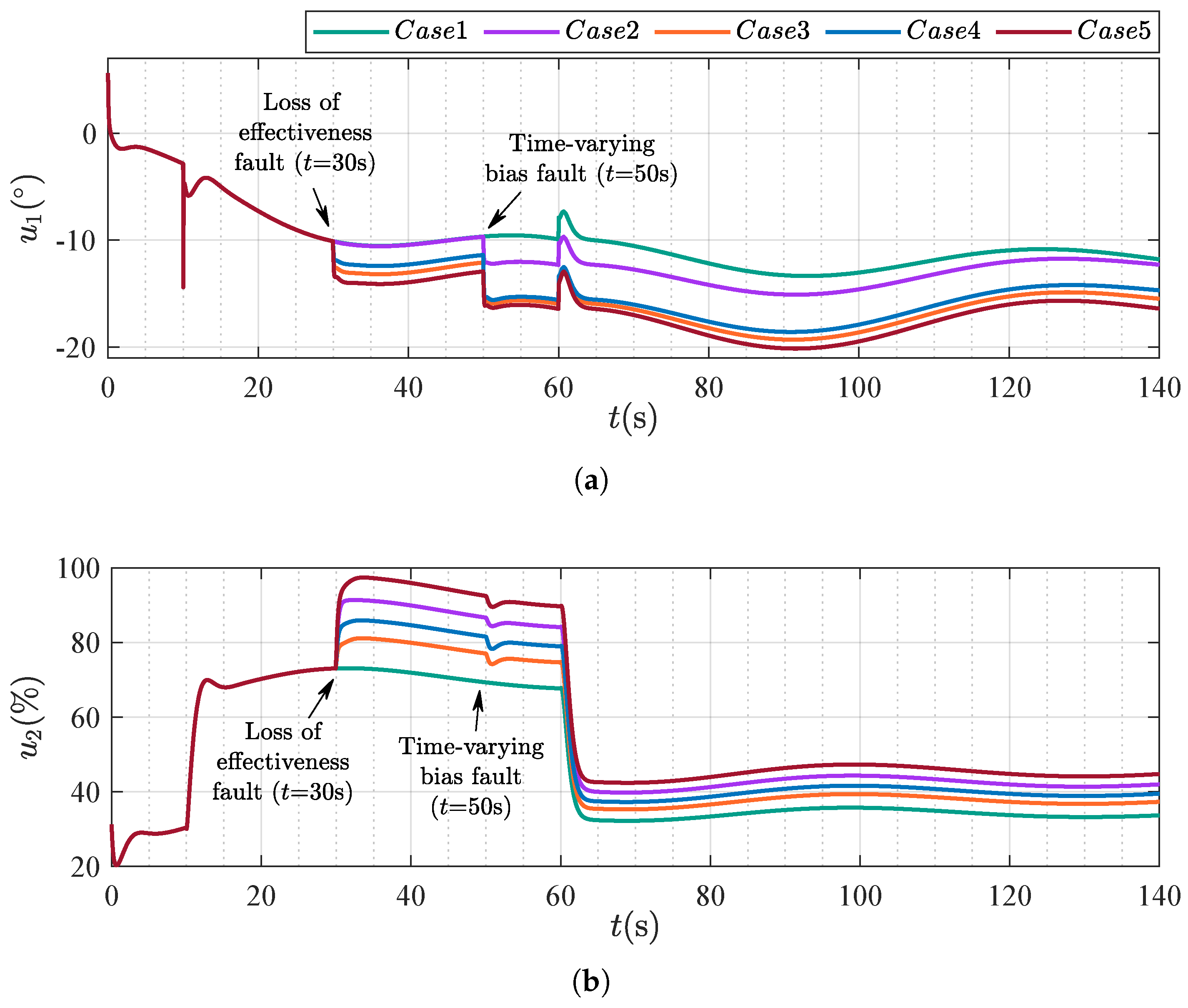
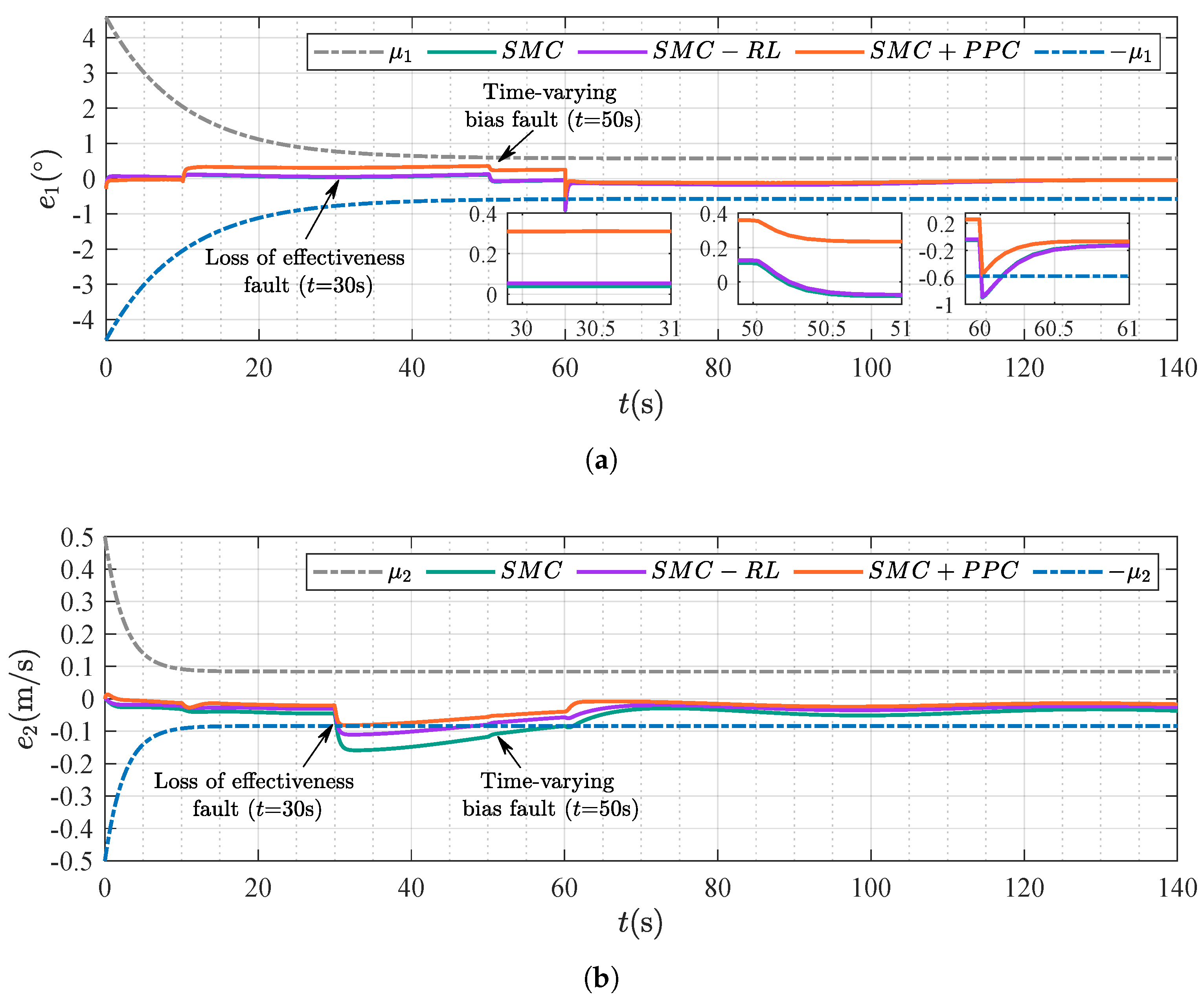

| The Fault Indicator | Actuator Working State |
|---|---|
| Without fault | |
| Loss of effectiveness fault | |
| Time-varying bias fault | |
| Both loss of effectiveness and time-varying bias fault |
| Variable | Value |
|---|---|
| 50 m/s | |
| 0° | |
| 0° | |
| 3000 m |
| Meaning | Symbol | Value |
|---|---|---|
| Mass | m | 1247 kg |
| Wing reference area | 17.09 m2 | |
| Mean geometric chord | 1.74 m | |
| Pitch moment of inertia | 4067.5 kg·m2 | |
| Gravitational acceleration | g | 9.8 m/s2 |
| Case | Loss of Effectiveness | Time-Varying Bias |
|---|---|---|
| Case1 | ||
| Case2 | ||
| Case3 | ||
| Case4 | ||
| Case5 |
| Methods | Parameters |
|---|---|
| SMC | |
| SMC-RL | |
| SMC+PPC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Cai, G.; Xu, H.; Shang, Y.; Hu, C. Prescribed Performance Sliding Mode Fault-Tolerant Tracking Control for Unmanned Morphing Flight Vehicles with Actuator Faults. Drones 2025, 9, 292. https://doi.org/10.3390/drones9040292
Ye Z, Cai G, Xu H, Shang Y, Hu C. Prescribed Performance Sliding Mode Fault-Tolerant Tracking Control for Unmanned Morphing Flight Vehicles with Actuator Faults. Drones. 2025; 9(4):292. https://doi.org/10.3390/drones9040292
Chicago/Turabian StyleYe, Ziqi, Guangbin Cai, Hui Xu, Yiming Shang, and Changhua Hu. 2025. "Prescribed Performance Sliding Mode Fault-Tolerant Tracking Control for Unmanned Morphing Flight Vehicles with Actuator Faults" Drones 9, no. 4: 292. https://doi.org/10.3390/drones9040292
APA StyleYe, Z., Cai, G., Xu, H., Shang, Y., & Hu, C. (2025). Prescribed Performance Sliding Mode Fault-Tolerant Tracking Control for Unmanned Morphing Flight Vehicles with Actuator Faults. Drones, 9(4), 292. https://doi.org/10.3390/drones9040292





