A Review of Path Following, Trajectory Tracking, and Formation Control for Autonomous Underwater Vehicles
Abstract
1. Introduction
- (1)
- A comprehensive review of AUV motion control technology is conducted, covering the three core directions of path following, trajectory tracking, and formation control. The characteristics, applicable scenarios, advantages, and limitations of various motion control methods are summarized in detail. In addition, a systematic classification of different control methods is conducted and we summarize the control strategies proposed to address these problems.
- (2)
- The main problems and challenges in the field of AUV motion control are identified and summarized. These include environmental adaptation problems and system characterization problems. The impact of key factors in the marine environment on AUV motion control is discussed in depth. Additionally, the constraints imposed by AUV system characteristics, such as nonlinear dynamics, dynamic coupling, and model uncertainty, are analyzed in the context of motion control.
- (3)
- The shortcomings of current research are summarized, and future development trends are anticipated. These trends include the further development of intelligent control methods, the optimization of multi-AUV cooperative operations, and the enhancement of adaptability to complex environments.
2. AUV Motion Control Methods
2.1. Path-Following Control
2.1.1. Classical PID Control and Its Extensions
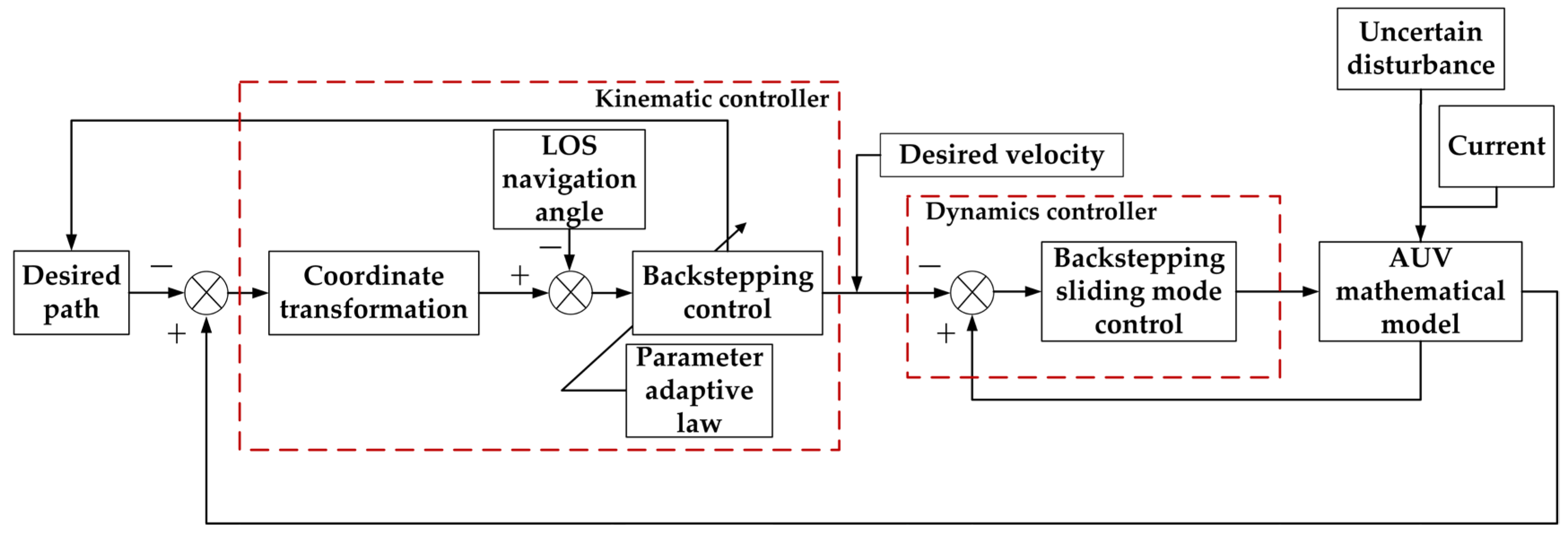
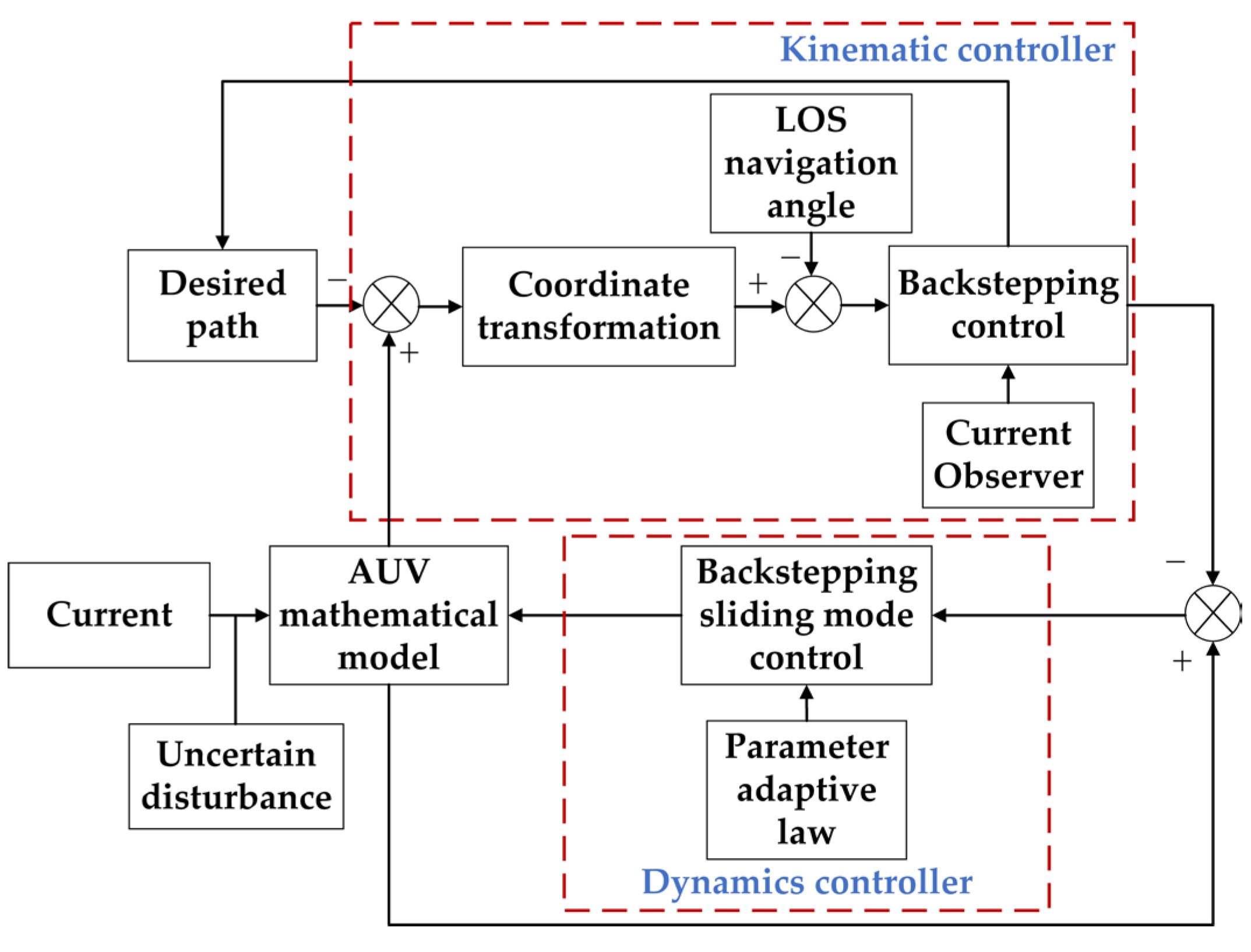
2.1.2. Sliding-Mode Control and Its Improvement
2.1.3. Model Predictive Control
2.1.4. Intelligent Controls
2.2. Trajectory Tracking Control
2.2.1. Sliding-Mode Control
2.2.2. Feedback Linearization and MPC
2.2.3. Intelligent Controls
2.2.4. Adaptive Control
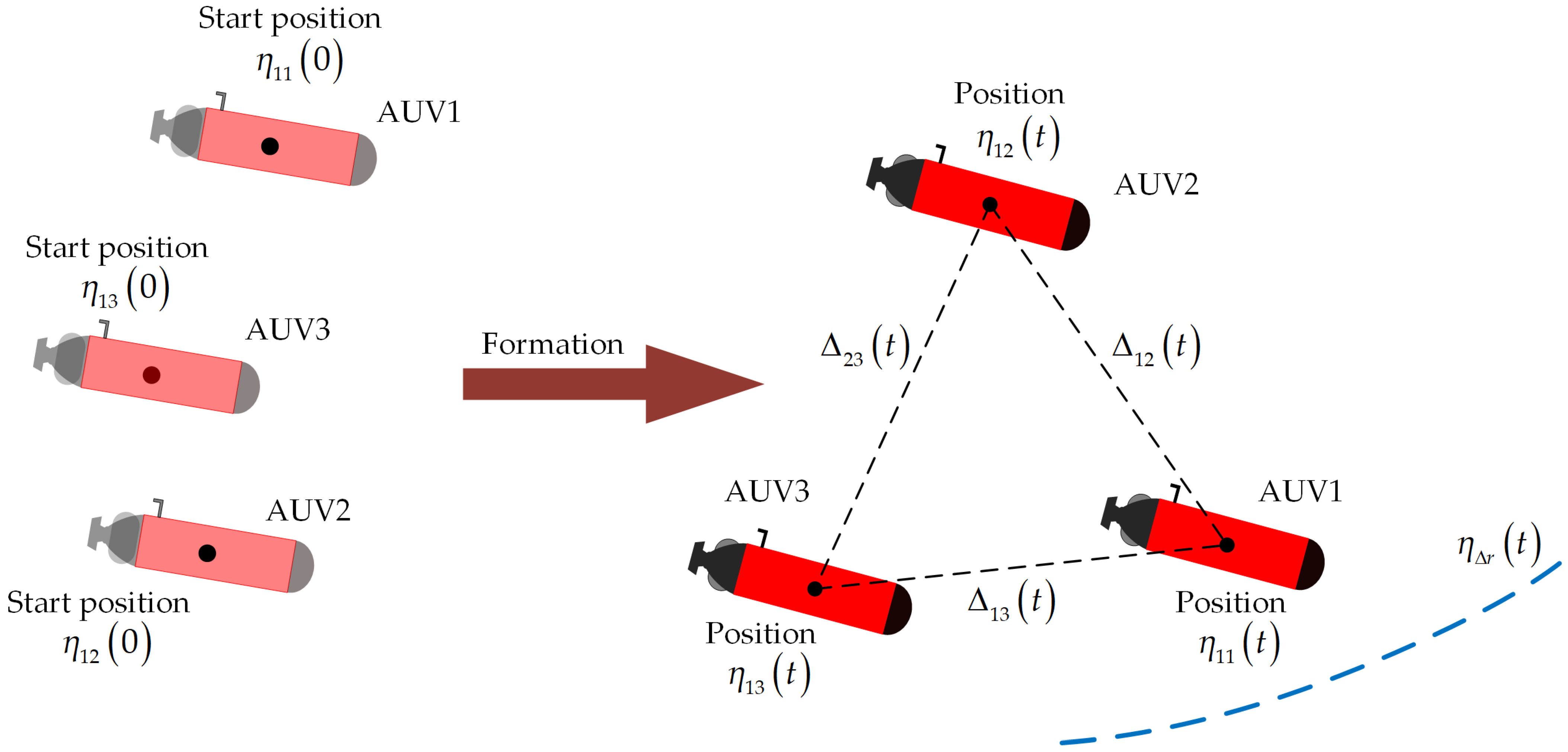
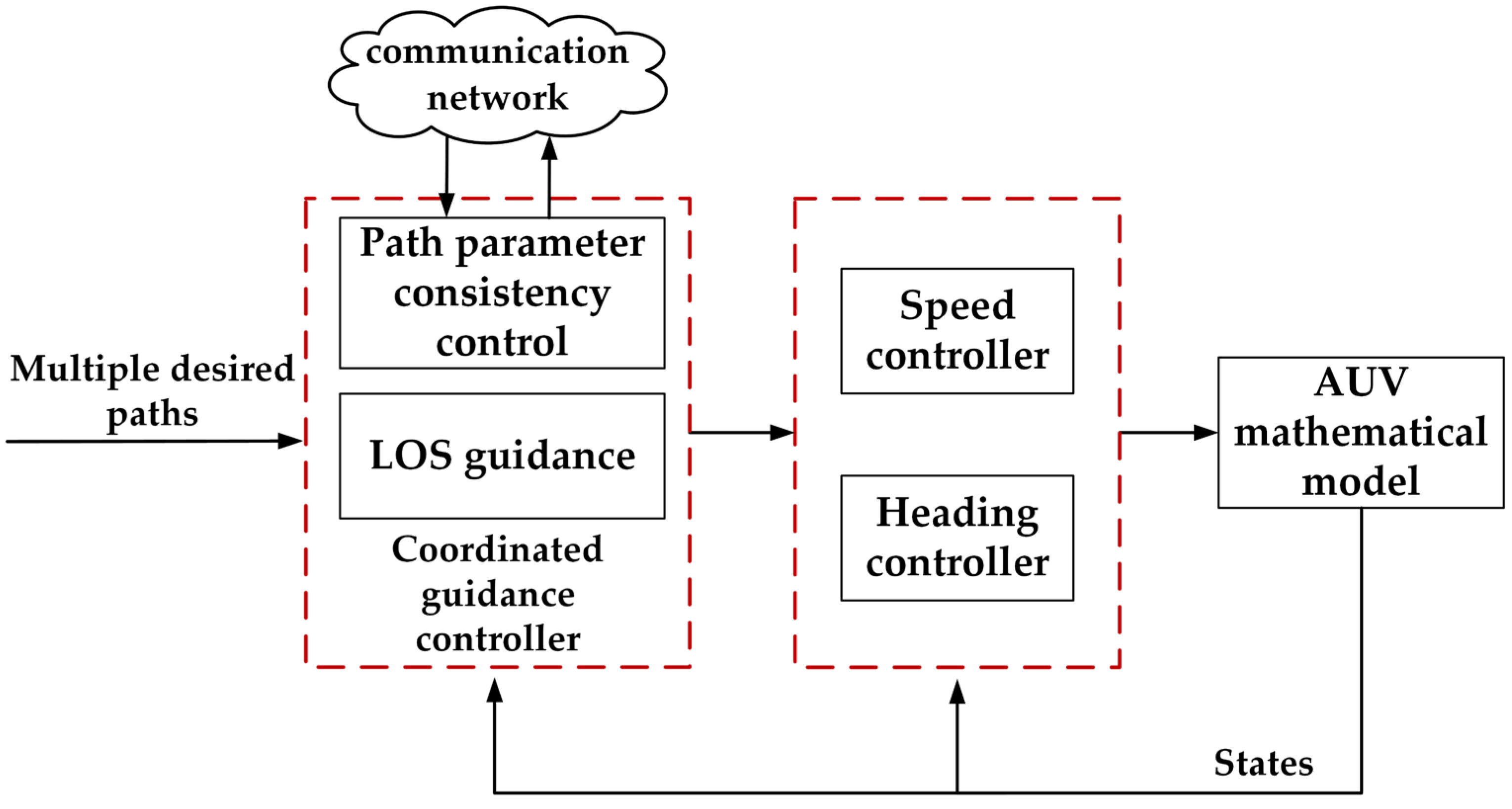
2.3. Formation Control
2.3.1. Leader–Follower Method
2.3.2. Consistency Control Method
2.3.3. Virtual Structure Method
2.3.4. Behavior-Based Method
3. Analysis and Discussion
3.1. Impact of the Complex Environment on AUV Control
3.1.1. Effects of Currents
3.1.2. Effects of Ocean Waves
3.1.3. Effects of Water Density Stratification
3.1.4. Effects of Sea Ice
3.1.5. Other Factors
3.2. Impact of System Characteristics on AUV Control
3.2.1. Model Uncertainty and External Disturbances
3.2.2. Coupling and Nonlinear Characteristics
3.2.3. Constraint Properties
3.3. Future Research Directions
- Enhancing Intelligent Control and Autonomous Decision-Making
- 2.
- High-Precision Navigation and Multi-Sensor Fusion
- 3.
- Multi-AUV Cooperative Operations and Distributed Control Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- AUV (autonomous underwater vehicle): A self-guided unmanned vehicle that operates underwater without real-time human control.
- Path following: Control strategy guiding the AUV along a predefined geometric path without explicit timing constraints.
- Trajectory tracking: Control strategy ensuring the AUV follows a time-dependent spatial trajectory.
- Formation control: Techniques to coordinate multiple AUVs to maintain relative positioning during cooperative missions.
- PID (proportional–integral–derivative) control: A classical feedback controller widely used for its simplicity and reliability.
- Sliding-mode control (SMC): A nonlinear robust control strategy known for its strong disturbance rejection.
- Model predictive control (MPC): An optimization-based control strategy that uses a model to predict and optimize future system behavior.
- Reinforcement learning (RL): A type of machine learning where agents learn optimal policies through interactions with the environment.
- Fuzzy logic control: A rule-based control method that handles uncertainty and imprecision using fuzzy set theory.
- Adaptive control: A control method that adjusts controller parameters in real time to cope with system uncertainties.
- Consistency control: A distributed control method that ensures multiple agents agree on certain variables through local interactions.
- Virtual structure: A formation control method treating all vehicles as rigidly connected parts of a single virtual object.
- Underactuated system: A system with fewer control inputs than degrees of freedom, common in AUV design.
- Observer: A computational tool to estimate unmeasurable internal states or disturbances in a control system.
References
- Panda, J.P.; Mitra, A.; Warrior, H.V. A Review on the Hydrodynamic Characteristics of Autonomous Underwater Vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021, 235, 15–29. [Google Scholar] [CrossRef]
- Ma, W.; Hu, Z. Current Researches and Development Trend on AUV. Fire Control Command Control 2008, 6, 10–13. [Google Scholar]
- Wynn, R.B.; Huvenne, V.A.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous Underwater Vehicles (AUVs): Their Past, Present and Future Contributions to the Advancement of Marine Geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Pallayil, V.; Lin, Y.-T.; Fischell, E.; Kukulya, A.L.; Knobles, D.P.; Wilson, P.S. Integration and Testing of a Low-Profile Hydrophone Array with REMUS 100 AUV for Seabed Characterization and Marine Mammal Detection Application. In Proceedings of the 2019 IEEE Underwater Technology (UT), Kaohsiung, Taiwan, 16–19 April 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Blomberg, A.E.A.; Sæbø, T.O.; Hansen, R.E.; Pedersen, R.B.; Austeng, A. Automatic Detection of Marine Gas Seeps Using an Interferometric Sidescan Sonar. IEEE J. Ocean. Eng. 2017, 42, 590–602. [Google Scholar] [CrossRef]
- Vasilijevic, A.; Nad, D.; Mandic, F.; Miskovic, N.; Vukic, Z. Coordinated Navigation of Surface and Underwater Marine Robotic Vehicles for Ocean Sampling and Environmental Monitoring. IEEE-ASME Trans. Mechatron. 2017, 22, 1174–1184. [Google Scholar] [CrossRef]
- Roman, C.; Mather, R. Autonomous Underwater Vehicles as Tools for Deep-Submergence Archaeology. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2010, 224, 327–340. [Google Scholar] [CrossRef]
- Bogue, R. Underwater Robots: A Review of Technologies and Applications. Ind. Robot Int. J. 2015, 42, 186–191. [Google Scholar] [CrossRef]
- Bovio, E.; Cecchi, D.; Baralli, F. Autonomous Underwater Vehicles for Scientific and Naval Operations. Annu. Rev. Control 2006, 30, 117–130. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.K.; Robi, P.S. Advancements in the Field of Autonomous Underwater Vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Li, Y. Research on Motion Control Technology for Mini Underwater Vehicle. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2007. [Google Scholar]
- Do, K.D. Control of Ships and Underwater Vehicles: Design for Underactuated and Nonlinear Marine Systems; Springer: London, UK, 2009; ISBN 978-1-84882-730-1. [Google Scholar]
- Li, Y. Research of Multifunctional Autonomous Underwater Vehicle on Motion Control. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2013. [Google Scholar]
- Wei, Y.; Peng, F.; Sheng, C.; Zhou, W. Control Method of the stability of AUV. J. Huazhong Univ. Sci. Technol. Nat. Sci. 2014, 42, 127–132. [Google Scholar]
- Xiang, X.; Yu, C.; Lapierre, L.; Zhang, J.; Zhang, Q. Survey on Fuzzy-Logic-Based Guidance and Control of Marine Surface Vehicles and Underwater Vehicles. Int. J. Fuzzy Syst. 2018, 20, 572–586. [Google Scholar] [CrossRef]
- Xiang, X. Research on Path Following and Coordinated Control for Second-Order Nonholonomic AUVs. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2010. [Google Scholar]
- Liang, X.; Wan, L.; Blake, J.I.R.; Shenoi, R.A.; Townsend, N. Path Following of an Underactuated AUV Based on Fuzzy Backstepping Sliding Mode Control. Int. J. Adv. Robot. Syst. 2016, 13, 122. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wan, L.; Ma, Q. Three-Dimensional Path Following of an Underactuated AUV Based on Fuzzy Backstepping Sliding Mode Control. Int. J. Fuzzy Syst. 2018, 20, 640–649. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, X.; Lapierre, L.; Zhang, Q.; Li, W. Approach-Angle-Based Three-Dimensional Indirect Adaptive Fuzzy Path Following of under-Actuated AUV with Input Saturation. Appl. Ocean Res. 2021, 107, 102486. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Xue, Z. Fuzzy Sliding Mode Control Based on RBF Neural Network for AUV Path Tracking. In Proceedings of the Intelligent Robotics and Applications (ICIRA 2019), Part II; Yu, H., Liu, J., Liu, L., Ju, Z., Liu, Y., Zhou, D., Eds.; Springer International Publishing AG: Cham, Switzerland, 2019; Volume 11741, pp. 637–648. [Google Scholar]
- Ma, D.; Chen, X.; Ma, W.; Zheng, H.; Qu, F. Neural Network Model-Based Reinforcement Learning Control for AUV 3-D Path Following. IEEE Trans. Intell. Veh. 2024, 9, 893–904. [Google Scholar] [CrossRef]
- Wang, D.; He, B.; Shen, Y.; Li, G.; Chen, G. A Modified ALOS Method of Path Tracking for AUVs with Reinforcement Learning Accelerated by Dynamic Data-Driven AUV Model. J. Intell. Robot. Syst. 2022, 104, 49. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, J.; Sha, Q.; He, B.; Li, G. Deep Interactive Reinforcement Learning for Path Following of Autonomous Underwater Vehicle. IEEE Access 2020, 8, 24258–24268. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, H.; Qin, H.; Wan, L.; Li, Y.; Cao, J.; Su, Y. A Novel Adaptive Second Order Sliding Mode Path Following Control for a Portable AUV. Ocean Eng. 2018, 151, 82–92. [Google Scholar] [CrossRef]
- He, L.; Zhang, Y.; Li, S.; Li, B.; Yuan, Z. Three-Dimensional Path Following Control for Underactuated AUV Based on Ocean Current Observer. Drones 2024, 8, 672. [Google Scholar] [CrossRef]
- Yu, C.; Xiang, X.; Zhang, Q.; Xu, G. Adaptive Fuzzy Trajectory Tracking Control of an Under-Actuated Autonomous Underwater Vehicle Subject to Actuator Saturation. Int. J. Fuzzy Syst. 2018, 20, 269–279. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wang, N.; Zhang, R.; Li, Y. Three-Dimensional Trajectory Tracking of an Underactuated AUV Based on Fuzzy Dynamic Surface Control. IET Intell. Transp. Syst. 2020, 14, 364–370. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, Z.; Zhang, J.; Zhou, J.; Jiang, A.; Du, X. Trajectory Tracking Control of UUV Based on Backstepping Sliding Mode with Fuzzy Switching Gain in Diving Plane. IEEE Access 2019, 7, 166788–166795. [Google Scholar] [CrossRef]
- Kang, S.; Rong, Y.; Chou, W. Antidisturbance Control for AUV Trajectory Tracking Based on Fuzzy Adaptive Extended State Observer. Sensors 2020, 20, 7084. [Google Scholar] [CrossRef] [PubMed]
- Gan, W.-Y.; Zhu, D.-Q.; Xu, W.-L.; Sun, B. Survey of Trajectory Tracking Control of Autonomous Underwater Vehicles. J. Mar. Sci. Technol. 2017, 25, 13. [Google Scholar] [CrossRef]
- Wang, X. Dynamic Behavior and Control Strategy of the Hybrid Autonomous Underwater Vehicle. Ph.D. Thesis, Tianjin University, Tianjin, China, 2009. [Google Scholar]
- Wang, Y.; Hou, Y.; Ye, M.; Lai, Z.; Cao, L.; Wu, D. Adaptive Hierarchical Interval Type-2 Fuzzy Control for Trajectory Tracking of an Underactuated AUV with Uncertain Dynamics. Trans. Inst. Meas. Control 2024, in press. [CrossRef]
- Liu, X.; Sun, B.; Su, Z. Adaptive Sliding Mode Control for AUV Based on Backstepping and Neural Networks. Meas. Sci. Technol. 2025, 36, 016215. [Google Scholar] [CrossRef]
- Yu, G.; He, F.; Liu, H. Fuzzy Neural Network Adaptive AUV Control Based on FTHGO. Ships Offshore Struct. 2025, 20, 13–25. [Google Scholar] [CrossRef]
- Fang, Y.; Huang, Z.; Pu, J.; Zhang, J. AUV Position Tracking and Trajectory Control Based on Fast-Deployed Deep Reinforcement Learning Method. Ocean Eng. 2022, 245, 110452. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Chen, C.L.P. Reinforcement Learning Based Model-Free Optimized Trajectory Tracking Strategy Design for an AUV. Neurocomputing 2022, 469, 289–297. [Google Scholar] [CrossRef]
- Li, Z.; Wang, M.; Ma, G. Adaptive Optimal Trajectory Tracking Control of AUVs Based on Reinforcement Learning. ISA Trans. 2023, 137, 122–132. [Google Scholar] [CrossRef]
- Guo, Q.; Li, Y.; Liu, H.; Xiang, J. An Underactuated AUV Tracking Algorithm Based on Backstepping Adaptive Sliding Mode Control. In Proceedings of the 2020 Chinese Automation Congress (CAC 2020), Shanghai, China, 6–8 November 2020; IEEE: New York, NY, USA, 2020; pp. 3765–3770. [Google Scholar]
- Yan, T.; Xu, Z.; Yang, S.X.; Gadsden, S.A. Formation Control of Multiple Autonomous Underwater Vehicles: A Review. Intell. Robot. 2023, 3, 1–22. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Ma, X.-W.; Bai, G.-Q.; Sha, Y.; Liu, J. Multi-Autonomous Underwater Vehicle Formation Control and Cluster Search Using a Fusion Control Strategy at Complex Underwater Environment. Ocean Eng. 2020, 216, 108048. [Google Scholar] [CrossRef]
- Das, B.; Subudhi, B.; Pati, B.B. Cooperative Formation Control of Autonomous Underwater Vehicles: An Overview. Int. J. Autom. Comput. 2016, 13, 199–225. [Google Scholar] [CrossRef]
- Gao, W.; Yang, J.; Liu, J.; Xu, B.; Shi, H. Cooperative Location of multiple UUVs based on hydro-acoustic communication delay. Syst. Eng. Electron. 2014, 36, 539–545. [Google Scholar]
- Huang, H.; Zhang, G.; Li, Y.; Li, J. Fuzzy Sliding-Mode Formation Control for Multiple Underactuated Autonomous Underwater Vehicles. In Proceedings of the Advances in Swarm Intelligence; Tan, Y., Shi, Y., Li, L., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 503–510. [Google Scholar]
- Van, M.; Sun, Y.; Mcllvanna, S.; Nguyen, M.-N.; Zocco, F.; Liu, Z. Control of Multiple AUV Systems With Input Saturations Using Distributed Fixed-Time Consensus Fuzzy Control. IEEE Trans. Fuzzy Syst. 2024, 32, 3142–3153. [Google Scholar] [CrossRef]
- Li, X.; Qin, H.; Li, L.; Xue, Y. Adaptive Fixed-Time Fuzzy Formation Control for Multiple AUV Systems Considering Time-Varying Tracking Error Constraints and Asymmetric Actuator Saturation. Ocean Eng. 2024, 297, 116936. [Google Scholar] [CrossRef]
- Li, X.; Zhu, D. An Adaptive SOM Neural Network Method for Distributed Formation Control of a Group of AUVs. IEEE Trans. Ind. Electron. 2018, 65, 8260–8270. [Google Scholar] [CrossRef]
- Meng, C.; Mo, T.; Zhang, X. Distributed Fixed-Time Dynamic Event-Triggered Leaderless Formation Control for Multiple AUVs Based on FRBFDO. Ocean Eng. 2024, 307, 118241. [Google Scholar] [CrossRef]
- Cao, W.; Yan, J.; Yang, X.; Luo, X. Reinforcement Learning-Based Formation Control of Autonomous Underwater Vehicles with Model Interferences. In Proceedings of the 2021 Proceedings of the 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; Peng, C., Sun, J., Eds.; IEEE: New York, NY, USA, 2021; pp. 4020–4025. [Google Scholar]
- Das, B.; Subudhi, B.; Pati, B.B. Adaptive Sliding Mode Formation Control of Multiple Underwater Robots. Arch. Control Sci. 2014, 24, 515–543. [Google Scholar] [CrossRef]
- Liu, M.; Xu, B.; Peng, X. Cooperative Path Planning for Multi-AUV in Time-Varying Ocean Flows. J. Syst. Eng. Electron. 2016, 27, 612–618. [Google Scholar] [CrossRef]
- Li, D.; Du, L. AUV Trajectory Tracking Models and Control Strategies: A Review. J. Mar. Sci. Eng. 2021, 9, 1020. [Google Scholar] [CrossRef]
- McCue, L. Handbook of Marine Craft Hydrodynamics and Motion Control [Bookshelf]. IEEE Control Syst. Mag. 2016, 36, 78–79. [Google Scholar] [CrossRef]
- Li, N.; Curuklu, B.; Bastos, J.; Sucasas, V.; Sanchez Fernandez, J.A.; Rodriguez, J. A Probabilistic and Highly Efficient Topology Control Algorithm for Underwater Cooperating AUV Networks. Sensors 2017, 17, 1022. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, D.; Pang, W. Formation Transformation Control Based on Leader-Follower Strategy for Multi-AUV System. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; IEEE: New York, NY, USA, 2023; pp. 2881–2886. [Google Scholar]
- Yang, Y.; Xiao, Y.; Li, T. A Survey of Autonomous Underwater Vehicle Formation: Performance, Formation Control, and Communication Capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Wang, F.; Wan, L.; Li, Z.; Su, Y.; Xu, Y. A Survey on Development of Motion Control for Underactuate AUV. China Shipbldg. 2010, 51, 227–241. [Google Scholar]
- Zhou, J.; Zhao, X.; Chen, T.; Yan, Z.; Yang, Z. Trajectory Tracking Control of an Underactuated AUV Based on Backstepping Sliding Mode With State Prediction. IEEE Access 2019, 7, 181983–181993. [Google Scholar] [CrossRef]
- Hou, Y.; Wei, Y. Trajectory Tracking of Intervention-Autonomous Underwater Vehicle via a Robust Adaptive Finite-Time Control. Int. J. Control 2022, in press. [CrossRef]
- Mao, J.; Lv, H.; Yang, J.; Liu, L. Path following control of deep sea mining vehicle based on fuzzy PID. Ocean Eng. 2021, 39, 151–161. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, X.; Bai, B.; Song, Q. Path following control of PID controller parameters optimized by genetic algorithm. Manuf. Autom. 2022, 44, 78–81. [Google Scholar]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Control for Dynamic Positioning and Way-Point Tracking of Underactuated Autonomous Underwater Vehicles Using Sliding Mode Control. J. Intell. Robot. Syst. 2019, 95, 1113–1132. [Google Scholar] [CrossRef]
- Rodriguez, J.; Castaneda, H.; Gordillo, J.L. Design of an Adaptive Sliding Mode Control for a Micro-AUV Subject to Water Currents and Parametric Uncertainties. J. Mar. Sci. Eng. 2019, 7, 445. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, C.; Xu, H.; Zhang, G.; Wang, Y. Three-Dimensional Path Tracking Control of the Underactuated AUV Based on Backstepping Sliding Mode. In Proceedings of the 2019 4th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS 2019), Nagoya, Japan, 13–15 July 2019; IEEE: New York, NY, USA, 2019; pp. 95–103. [Google Scholar]
- Jiang, Y.; Guo, C.; Yu, H.; Han, Y.; Zhang, C. Three-Dimensional Path Following for an Underactuated AUV Adopted Adaptive Sliding Mode Control. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; IEEE: New York, NY, USA, 2019; pp. 447–452. [Google Scholar]
- He, L.; Zhang, Y.; Fan, G.; Liu, Y.; Wang, X.; Yuan, Z. Three-Dimensional Path Following Control of Underactuated AUV Based on Nonlinear Disturbance Observer and Adaptive Line-of-Sight Guidance. IEEE Access 2024, 12, 83911–83924. [Google Scholar] [CrossRef]
- Taniguchi, T.; Umeda, J.; Fujiwara, T.; Kim, K.; Sato, T.; Inaba, S. Path Following Control of Autonomous Underwater Vehicle Using Nonlinear Model Predictive Control. In Proceedings of the ASME 39th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2020), Volume 6B; The American Society of Mechanical Engineers: New York, NY, USA, 2020; p. V06BT06A046. [Google Scholar]
- Shen, C.; Shi, Y.; Buckham, B. Path-Following Control of an AUV: A Multiobjective Model Predictive Control Approach. IEEE Trans. Control Syst. Technol. 2019, 27, 1334–1342. [Google Scholar] [CrossRef]
- Wang, X.; Yao, X.; Zhang, L. Path Planning under Constraints and Path Following Control of Autonomous Underwater Vehicle with Dynamical Uncertainties and Wave Disturbances. J. Intell. Robot. Syst. 2020, 99, 891–908. [Google Scholar] [CrossRef]
- Yao, X.; Wang, X.; Wang, F.; Zhang, L. Path Following Based on Waypoints and Real-Time Obstacle Avoidance Control of an Autonomous Underwater Vehicle. Sensors 2020, 20, 795. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Ma, C.; Yan, X.; Jiang, D. Path-Following Optimal Control of Autonomous Underwater Vehicle Based on Deep Reinforcement Learning. Ocean Eng. 2023, 268, 113407. [Google Scholar] [CrossRef]
- Jiang, D.; Huang, J.; Fang, Z.; Cheng, C.; Sha, Q.; He, B.; Li, G. Generative Adversarial Interactive Imitation Learning for Path Following of Autonomous Underwater Vehicle. Ocean Eng. 2022, 260, 111971. [Google Scholar] [CrossRef]
- Zhao, H. Method for Robot Path Tracking Based on Fuzzy Adaptive Tuning PID Control. Comput. Meas. Control 2024, 32, 146–152. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory Tracking Sliding Mode Control of Underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef]
- Jalalnezhad, M.; Fazeli, S. Sliding Mode Control of AUV Trajectory Tracking in the Presence of Disturbance. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 239, 950–965. [Google Scholar] [CrossRef]
- Yon, Z.; Gong, P.; Zhang, W.; Wu, W. AUV Trajectory Tracking Based on Nonlinear Model Predictive Control. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC 2021), Kunming, China, 22–24 May 2021; IEEE: New York, NY, USA, 2021; pp. 6055–6059. [Google Scholar]
- Yan, Z.; Zhang, C.; Tian, W.; Cai, S.; Zhao, L. Distributed Observer-Based Formation Trajectory Tracking Method of Leader-Following Multi-AUV System. Ocean Eng. 2022, 260, 112019. [Google Scholar] [CrossRef]
- Yue, L.; Yan, Z.; Zhou, J.; Zhang, M. Formation Trajectory Tracking of Discrete-Time Distributed Multi-AUVs with Nonconvex Control Inputs and Weak Communication. J. Mar. Sci. Eng. 2023, 11, 1362. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, Z.; Qu, X.; Li, Y.; Zhang, R. 3D Trajectory Tracking Control of an Underactuated AUV Based on Adaptive Neural Network Dynamic Surface. Int. J. Veh. Des. 2020, 84, 203–218. [Google Scholar] [CrossRef]
- Panda, J.P. Machine Learning for Naval Architecture, Ocean and Marine Engineering. J. Mar. Sci. Technol. 2023, 28, 1–26. [Google Scholar] [CrossRef]
- Bao, H.; Zhu, H.; Liu, D. Improved SSA-RBF Neural Network-Based Dynamic 3-D Trajectory Tracking Model Predictive Control of Autonomous Underwater Vehicles with External Disturbances. Optim. Control Appl. Methods 2024, 45, 138–162. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, X.; Zhang, Q.; Li, W. Neural Network-Based Adaptive Trajectory Tracking Control of Underactuated AUVs with Unknown Asymmetrical Actuator Saturation and Unknown Dynamics. Ocean Eng. 2020, 218, 108193. [Google Scholar] [CrossRef]
- Ma, T.; Chen, Z. Trajectory Tracking Controller Design for Underactuated AUVs Based on Adaptive Robust Control. In Proceedings of the 2024 9th International Conference on Automation, Control and Robotics Engineering (CACRE 2024), Jeju Island, Republic of Korea, 18–20 July 2024; Zhang, F., Zhang, L., Eds.; IEEE: New York, NY, USA, 2024; pp. 305–309. [Google Scholar]
- Er, M.J.; Gong, H.; Liu, Y.; Liu, T. Intelligent Trajectory Tracking and Formation Control of Underactuated Autonomous Underwater Vehicles: A Critical Review. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 543–555. [Google Scholar] [CrossRef]
- Cui, H.; Shi, X.; Cui, R. Leader-follower formation control of autonomous underwater vehicles. J. Unmanned Undersea Syst. 2007, 15, 42–44. [Google Scholar] [CrossRef]
- Cui, R.; Xu, D.; Yan, W. Leader-follower formation control method of autonomous underwater vehicles using position information only. Acta Armamentarii 2008, 29, 980–984. [Google Scholar]
- Gao, Z.; Guo, G. Adaptive Formation Control of Autonomous Underwater Vehicles with Model Uncertainties. Int. J. Adapt. Control Signal Process. 2018, 32, 1067–1080. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, L.; Xing, W.; Yao, S. Formation consensus control of multi–AUV system withswitching topology. J. Harbin Eng. Univ. 2023, 44, 587–593. [Google Scholar]
- Yu, X. Research on Consensus Based Underwater Multi-Agent Formation Control. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2024. [Google Scholar]
- Zhen, Q.; Wan, L.; Zhang, Y.; Jiang, D. Consensus-Based Formation Control and Gyroscopic Obstacle Avoidance for Multiple Autonomous Underwater Vehicles on SE(3). J. Mar. Sci. Eng. 2024, 12, 2350. [Google Scholar] [CrossRef]
- Yan, T.; Xu, Z.; Yang, S.X. Consensus Formation Tracking for Multiple AUV Systems Using Distributed Bioinspired Sliding Mode Control. IEEE Trans. Intell. Veh. 2023, 8, 1081–1092. [Google Scholar] [CrossRef]
- Lewis, M.A.; Tan, K.-H. High Precision Formation Control of Mobile Robots Using Virtual Structures. Auton. Robots 1997, 4, 387–403. [Google Scholar] [CrossRef]
- Zhen, Q.; Wan, L.; Li, Y.; Jiang, D. Formation Control of a Multi-AUVs System Based on Virtual Structure and Artificial Potential Field on SE(3). Ocean Eng. 2022, 253, 111148. [Google Scholar] [CrossRef]
- Tan, K.-H.; Lewis, M.A. Virtual Structures for High-Precision Cooperative Mobile Robotic Control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS ’96), Osaka, Japan, 8 November 1996; Volume 1, pp. 132–139. [Google Scholar]
- Atta, D.; Subudhi, B. Decentralized Formation Control of Multiple Autonomous Underwater Vehicles. Int. J. Robot. Autom. 2013, 28, 303–310. [Google Scholar] [CrossRef]
- Li, W.; Farrell, J.A.; Pang, S.; Arrieta, R.M. Moth-Inspired Chemical Plume Tracing on an Autonomous Underwater Vehicle. IEEE Trans. Robot. 2006, 22, 292–307. [Google Scholar] [CrossRef]
- Wang, Q.; He, B.; Zhang, Y.; Yu, F.; Huang, X.; Yang, R. An Autonomous Cooperative System of Multi-AUV for Underwater Targets Detection and Localization. Eng. Appl. Artif. Intell. 2023, 121, 105707. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, X.; Zhu, Z.; Chen, C.; Yang, P. Behavior-Based Formation Control of Swarm Robots. Math. Probl. Eng. 2014, 2014, 205759. [Google Scholar] [CrossRef]
- Gan, W.; Zhu, D. Complete Coverage Belief Function Path Planning Algorithm of Autonomous Underwater Vehicle Based on Behavior Strategy. J. Syst. Simul. 2018, 30, 1857–1868. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-Based Formation Control for Multirobot Teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Burlutskiy, N.; Touahmi, Y.; Lee, B.H. Power Efficient Formation Configuration for Centralized Leader-Follower AUVs Control. J. Mar. Sci. Technol. 2012, 17, 315–329. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, X.; Luo, G.; Liu, G. A Formation Control Method for AUV Group Under Communication Delay. Front. Bioeng. Biotechnol. 2022, 10, 848641. [Google Scholar] [CrossRef]
- Xu, P. Behavior-Based Formation Control of Multi-AUV. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2013. [Google Scholar]
- Chen, X.; Bose, N.; Brito, M.; Khan, F.; Thanyamanta, B.; Zou, T. A Review of Risk Analysis Research for the Operations of Autonomous Underwater Vehicles. Reliab. Eng. Syst. Saf. 2021, 216, 108011. [Google Scholar] [CrossRef]
- Li, X.; Zhu, D.; Qian, Y. A Survey on Formation Control Algorithms for Multi-AUV System. Unmanned Syst. 2014, 2, 351–359. [Google Scholar] [CrossRef]
- Brito, M.P.; Griffiths, G.; Trembranis, A. Eliciting expert judgment on the probability of Loss of an AUV operating in four environments. In National Oceanography Centre Southampton Research and Consultancy Report; Report No. 48; National Oceanography Centre: Southampton, UK, 2008; p. 198. [Google Scholar]
- Brito, M.P.; Griffiths, G.; Challenor, P. Risk Analysis for Autonomous Underwater Vehicle Operations in Extreme Environments: Risk Analysis for Autonomous Underwater Vehicle Operations in Extreme Environments. Risk Anal. 2010, 30, 1771–1788. [Google Scholar] [CrossRef] [PubMed]
- Borhaug, E.; Pavlov, A.; Pettersen, K.Y. Integral LOS Control for Path Following of Underactuated Marine Surface Vessels in the Presence of Constant Ocean Currents. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4984–4991. [Google Scholar]
- Caharija, W.; Candeloro, M.; Pettersen, K.Y.; Sørensen, A.J. Relative Velocity Control and Integral LOS for Path Following of Underactuated Surface Vessels. IFAC Proc. Vol. 2012, 45, 380–385. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Integral LOS Path Following for Curved Paths Based on a Monotone Cubic Hermite Spline Parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Fossen, T.I.; Aguiar, A.P. A Uniform Semiglobal Exponential Stable Adaptive Line-of-Sight (ALOS) Guidance Law for 3-D Path Following. Automatica 2024, 163, 111556. [Google Scholar] [CrossRef]
- Fossen, T.I. An Adaptive Line-of-Sight (ALOS) Guidance Law for Path Following of Aircraft and Marine Craft. IEEE Trans. Control Syst. Technol. 2023, 31, 2887–2894. [Google Scholar] [CrossRef]
- Wei, H.; Guo, C.; Han, Y.; Wu, Y.; Zheng, X.; Wang, C. Influence of the Stratification Parameters on the Wake Field of an Underwater Vehicle in a Two-Layer Stratified Flow. Ocean Eng. 2024, 312, 119000. [Google Scholar] [CrossRef]
- Cao, L.; Huang, F.; Liu, C.; Wan, D. Vortical Structures and Wakes of a Sphere in Homogeneous and Density Stratified Fluid. J. Hydrodyn. 2021, 33, 207–215. [Google Scholar] [CrossRef]
- Cao, L.; Gao, G.; Guo, E.; Wan, D. Hydrodynamic Performances and Wakes Induced by a Generic Submarine Operating near the Free Surface in Continuously Stratified Fluid. J. Hydrodyn. 2023, 35, 396–406. [Google Scholar] [CrossRef]
- Li, S.; Zeng, J.; Wang, Y. Navigation Under the Arctic Ice by Autonomous & Remotely Operated Underwater Vehicle: Navigation Under the Arctic Ice by Autonomous & Remotely Operated Underwater Vehicle. Robot 2011, 33, 509–512. [Google Scholar] [CrossRef]
- Zeng, J. Research on Navigation and Trajectory Tracking of Autonomous/Remotely Operated Underwater Vehicles in Arctic Ice Conditions. Master’s Thesis, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang, China, 2009. [Google Scholar]
- Cao, X.; Ren, L.; Sun, C. Research on Obstacle Detection and Avoidance of Autonomous Underwater Vehicle Based on Forward-Looking Sonar. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 9198–9208. [Google Scholar] [CrossRef]
- Murrant, K.; Gash, R.; Mills, J. Dynamic Path Following in Ice-Covered Waters with an Autonomous Surface Ship Model. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–4. [Google Scholar]
- Su, Y. Research on Roll and Yaw Integrated Stabilization Control Strategy of AUV Low-Speed During Diving Near Sea Surface. Master’s Thesis, Harbin Engineering University, Harbin, China, 2022. [Google Scholar]
- Zhao, W. The Control Method for the Roll Motion of the AUV During the Diving Process. Master’s Thesis, Harbin Engineering University, Harbin, China, 2019. [Google Scholar]
- Pan, J. Research on Pitch and Depth Control of AUV Diving Under Wave Disturbance. Master’s Thesis, Harbin Engineering University, Harbin, China, 2022. [Google Scholar]
- Prateek; Arya, R. An Underwater Localization Scheme for Sparse Sensing Acoustic Positioning in Stratified and Perturbed UASNs. Wirel. Netw. 2022, 28, 241–256. [Google Scholar] [CrossRef]
- Bai, G.; Chen, Y.; Hu, X.; Shi, Y.; Jiang, W.; Zhang, X. Multi-AUV Dynamic Trajectory Optimization and Collaborative Search Combined with Task Urgency and Energy Consumption Scheduling in 3-D Underwater Environment with Random Ocean Currents and Uncertain Obstacles. Ocean Eng. 2023, 275, 113841. [Google Scholar] [CrossRef]
- Bai, G.; Chen, Y.; Hu, X.; Cui, J. Correction Redistribution Mechanism Based on Forward-Reverse Solutions and Real-Time Path Dynamic Adaptive Re-Planning for Multi-AUVs Collaborative Search. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7583–7601. [Google Scholar] [CrossRef]
- Zhong, N.; Potenza, A.; Smith, S.L. Autonomous Navigation in Ice-Covered Waters with Learned Predictions on Ship-Ice Interactions. arXiv 2024, arXiv:2409.11326. [Google Scholar]
- Shu, Y.; Zhu, Y.; Xu, F.; Gan, L.; Lee, P.T.-W.; Yin, J.; Chen, J. Path Planning for Ships Assisted by the Icebreaker in Ice-Covered Waters in the Northern Sea Route Based on Optimal Control. Ocean Eng. 2023, 267, 113182. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Shen, Y.; Dai, N.; He, B. Multi-AUV Cooperative Control and Autonomous Obstacle Avoidance Study. Ocean Eng. 2024, 304, 117634. [Google Scholar] [CrossRef]
- Yao, X.; Wang, X.; Jiang, X.; Wang, F. Control for 3D Path-Following of Underactuated Autonomous Underwater Vehicle under Current Disturbance. Harbin Gongye Daxue Xuebao/J. Harbin Inst. Technol. 2019, 51, 37–45. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-Sight Path Following for Dubins Paths With Adaptive Sideslip Compensation of Drift Forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z.; Wang, H. Predictor-Based LOS Guidance Law for Path Following of Underactuated Marine Surface Vehicles with Sideslip Compensation. Ocean Eng. 2016, 124, 340–348. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, Z.; Wang, D.; Chen, C.L.P. Line-of-Sight Target Enclosing of an Underactuated Autonomous Surface Vehicle with Experiment Results. IEEE Trans. Ind. Inform. 2020, 16, 832–841. [Google Scholar] [CrossRef]
- Yu, C.; Liu, C.; Lian, L.; Xiang, X.; Zeng, Z. ELOS-Based Path Following Control for Underactuated Surface Vehicles with Actuator Dynamics. Ocean Eng. 2019, 187, 106139. [Google Scholar] [CrossRef]
- He, L.; Zhang, Y.; Liu, Y.; Bai, C.; Li, L. Backstepping Sliding Mode Control for Path Following of Underactuated AUV Affected by Ocean Currents. In Proceedings of the 2024 IEEE International Conference on Unmanned Systems (ICUS), Nanjing, China, 18–20 October 2024; pp. 858–864. [Google Scholar]
- Moe, S.; Caharija, W.; Pettersen, K.Y.; Schjølberg, I. Path Following of Underactuated Marine Surface Vessels in the Presence of Unknown Ocean Currents. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3856–3861. [Google Scholar]
- Belleter, D.; Maghenem, M.A.; Paliotta, C.; Pettersen, K.Y. Observer Based Path Following for Underactuated Marine Vessels in the Presence of Ocean Currents: A Global Approach. Automatica 2019, 100, 123–134. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. ESO-Based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles With Exact Sideslip Compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Command-filtered Fixed-time Trajectory Tracking Control of Surface Vehicles Based on a Disturbance Observer. Int. J. Robust Nonlinear Control 2019, 29, 4348–4365. [Google Scholar] [CrossRef]
- Rong, S.; Wang, H.; Li, H.; Sun, W.; Gu, Q.; Lei, J. Performance-Guaranteed Fractional-Order Sliding Mode Control for Underactuated Autonomous Underwater Vehicle Trajectory Tracking with a Disturbance Observer. Ocean Eng. 2022, 263, 112330. [Google Scholar] [CrossRef]
- Wen, J.; Dai, H.; He, J.; Sun, L.; Gao, L. Intelligent Decision-Making Method for AUV Path Planning Against Ocean Current Disturbance via Reinforcement Learning. IEEE Internet Things J. 2024, 11, 38965–38975. [Google Scholar] [CrossRef]
- Yoo, B.; Kim, J. Path Optimization for Marine Vehicles in Ocean Currents Using Reinforcement Learning. J. Mar. Sci. Technol. 2016, 21, 334–343. [Google Scholar] [CrossRef]
- Yao, X.; Wang, F.; Yuan, C.; Wang, J.; Wang, X. Path Planning for Autonomous Underwater Vehicles Based on Interval Optimization in Uncertain Flow Fields. Ocean Eng. 2021, 234, 108675. [Google Scholar] [CrossRef]
- Qu, N.; Chen, G.; Shen, Y. A Three-Dimensional Path Planning System for AUV Diving Process Considering Ocean Current and Energy Consumption. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021; IEEE: New York, NY, USA, 2021. [Google Scholar]
- Wu, J.; Liu, J.; Chen, K. Backstepping sliding mode control of auv three-dimensional trajectories tracking under time-varying interference. Ship Sci. Technol. 2022, 44, 82–87. [Google Scholar]
- Muñoz, F.; Cervantes-Rojas, J.S.; Valdovinos, J.M.; Sandre-Hernández, O.; Salazar, S.; Romero, H. Dynamic Neural Network-Based Adaptive Tracking Control for an Autonomous Underwater Vehicle Subject to Modeling and Parametric Uncertainties. Appl. Sci. 2021, 11, 2797. [Google Scholar] [CrossRef]
- Liu, H.; Lyu, Y.; Lewis, F.L.; Wan, Y. Robust Time-Varying Formation Control for Multiple Underwater Vehicles Subject to Nonlinearities and Uncertainties. Int. J. Robust Nonlinear Control 2019, 29, 2712–2724. [Google Scholar] [CrossRef]
- Wang, Z.; Xiang, X.; Guan, X.; Pan, H.; Yang, S.; Chen, H. Deep Learning-Based Robust Positioning Scheme for Imaging Sonar Guided Dynamic Docking of Autonomous Underwater Vehicle. Ocean Eng. 2024, 293, 116704. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, H.; Hong, L.; Yu, X.; Chen, J.; Chen, B. Anti-Disturbance Control Strategy in Capture Stage for AUV Dynamic Base Docking with Optical Guided Constraints. Ocean Eng. 2024, 311, 118946. [Google Scholar] [CrossRef]
- Gu, N.; Wang, D.; Peng, Z.; Wang, J.; Han, Q.-L. Advances in Line-of-Sight Guidance for Path Following of Autonomous Marine Vehicles: An Overview. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 12–28. [Google Scholar] [CrossRef]
- Hu, S.; Xiao, S.; Yang, J.; Zhang, Z.; Zhang, K.; Zhu, Y.; Zhang, Y. AUV Path Planning Considering Ocean Current Disturbance Based on Cloud Desktop Technology. Sensors 2023, 23, 7510. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, J.; Huang, R.; Gao, Y.; Peng, X.; Yuan, W. Path Planning for Autonomous Underwater Vehicles (AUVs) Considering the Influences and Constraints of Ocean Currents. Drones 2024, 8, 348. [Google Scholar] [CrossRef]
- Peng, S. Research on Containment Control Algorithms of Underwater Vehicle Under Stochastic Environmental Disturbances. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2023. [Google Scholar]
- Qiao, L.; Zhang, W. Double-Loop Integral Terminal Sliding Mode Tracking Control for UUVs With Adaptive Dynamic Compensation of Uncertainties and Disturbances. IEEE J. Ocean. Eng. 2019, 44, 29–53. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.; Wilson, P.A.; Liu, X. Adaptive Neural Network-Based Backstepping Fault Tolerant Control for Underwater Vehicles with Thruster Fault. Ocean Eng. 2015, 110, 15–24. [Google Scholar] [CrossRef]
- Yan, J.; Li, X.; Yang, X.; Luo, X.; Hua, C.; Guan, X. Integrated Localization and Tracking for AUV With Model Uncertainties via Scalable Sampling-Based Reinforcement Learning Approach. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6952–6967. [Google Scholar] [CrossRef]
- Patre, B.M.; Londhe, P.S.; Waghmare, L.M.; Mohan, S. Disturbance Estimator Based Non-Singular Fast Fuzzy Terminal Sliding Mode Control of an Autonomous Underwater Vehicle. Ocean Eng. 2018, 159, 372–387. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, M.; Li, D.; Lin, R. Gaze-Assisted Prescribed Performance Controller for AUV Trajectory Tracking in Time-Varying Currents. J. Mar. Sci. Eng. 2024, 12, 1643. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, Y.; Zhang, W.; Chen, X.; Yang, H. Multi-Time-Scale 3-D Coordinated Formation Control for Multi-Underactuated AUV with Uncertainties: Design and Stability Analysis Using Singular Perturbation Methods. Ocean Eng. 2021, 230, 109053. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoo, S.J. Distributed Event-Driven Adaptive Three-Dimensional Formation Tracking of Networked Autonomous Underwater Vehicles with Unknown Nonlinearities. Ocean Eng. 2021, 233, 109069. [Google Scholar] [CrossRef]
- Xu, J.; Cui, Y.; Xing, W.; Huang, F.; Yan, Z.; Wu, D.; Chen, T. Anti-Disturbance Fault-Tolerant Formation Containment Control for Multiple Autonomous Underwater Vehicles with Actuator Faults. Ocean Eng. 2022, 266, 112924. [Google Scholar] [CrossRef]
- Cui, Y.; Xu, J.; Xing, W.; Huang, F.; Yan, Z.; Wu, D.; Chen, T. Anti-Disturbance Cooperative Formation Containment Control for Multiple Autonomous Underwater Vehicles with Actuator Saturation. Ocean Eng. 2022, 266, 113026. [Google Scholar] [CrossRef]
- Shojaei, K. Three-Dimensional Tracking Control of Autonomous Underwater Vehicles with Limited Torque and without Velocity Sensors. Robotica 2018, 36, 374–394. [Google Scholar] [CrossRef]
- Lapierre, L.; Soetanto, D. Nonlinear Path-Following Control of an AUV. Ocean Eng. 2007, 34, 1734–1744. [Google Scholar] [CrossRef]
- Jia, H. Study of Spatial Target Tracking Nonlinear Controlof Underactuated UUV Based on Backstepping. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2012. [Google Scholar]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory Tracking Control of an Autonomous Underwater Vehicle Using Lyapunov-Based Model Predictive Control. IEEE Trans. Ind. Electron. 2018, 65, 5796–5805. [Google Scholar] [CrossRef]
- Sharma, M.; Verma, A. Wavelet Reduced Order Observer Based Adaptive Tracking Control for a Class of Uncertain Nonlinear Systems Using Reinforcement Learning. Int. J. Control Autom. Syst. 2013, 11, 496–502. [Google Scholar] [CrossRef]
- Cui, R.; Zhang, X.; Cui, D. Adaptive Sliding-Mode Attitude Control for Autonomous Underwater Vehicles with Input Nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Dunbar, W.B. Distributed Receding Horizon Control of Dynamically Coupled Nonlinear Systems. IEEE Trans. Autom. Control 2007, 52, 1249–1263. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Zhu, G.; Lewis, F.L. Simple Adaptive Trajectory Tracking Control of Underactuated Autonomous Underwater Vehicles under LOS Range and Angle Constraints. IET Control Theory Appl. 2020, 14, 283–290. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Luo, M.; Yang, C. MPC-Based 3-D Trajectory Tracking for an Autonomous Underwater Vehicle with Constraints in Complex Ocean Environments. Ocean Eng. 2019, 189, 106309. [Google Scholar] [CrossRef]
- Sarhadi, P.; Noei, A.R.; Khosravi, A. Model Reference Adaptive PID Control with Anti-Windup Compensator for an Autonomous Underwater Vehicle. Robot. Auton. Syst. 2016, 83, 87–93. [Google Scholar] [CrossRef]
- Wei, H.; Shen, C.; Shi, Y. Distributed Lyapunov-Based Model Predictive Formation Tracking Control for Autonomous Underwater Vehicles Subject to Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5198–5208. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, M.; Zhang, C.; Zeng, J. Decentralized Formation Trajectory Tracking Control of Multi-AUV System with Actuator Saturation. Ocean Eng. 2022, 255, 111423. [Google Scholar] [CrossRef]
- Du, J.; Li, J.; Lewis, F.L. Distributed 3-D Time-Varying Formation Control of Underactuated AUVs With Communication Delays Based on Data-Driven State Predictor. IEEE Trans. Ind. Inform. 2023, 19, 6963–6971. [Google Scholar] [CrossRef]

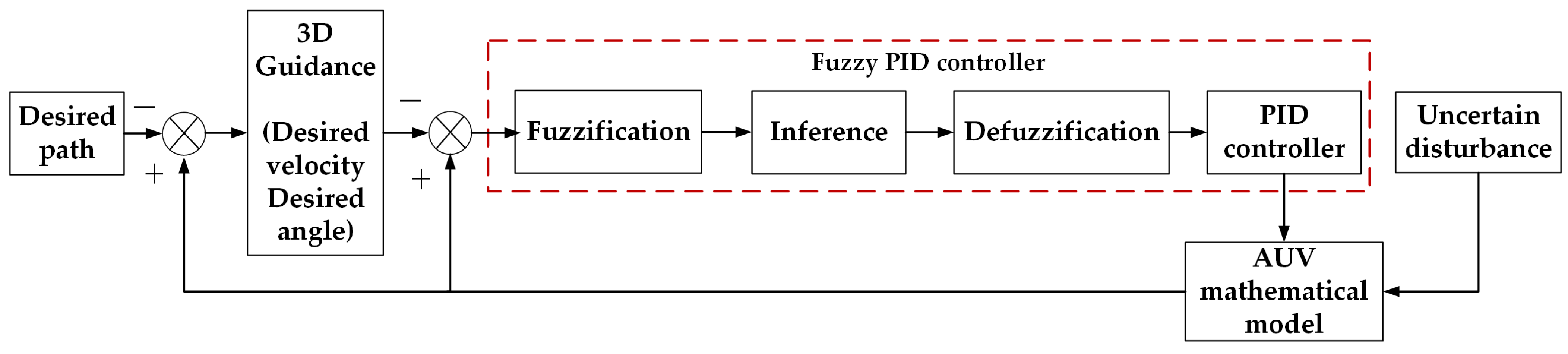
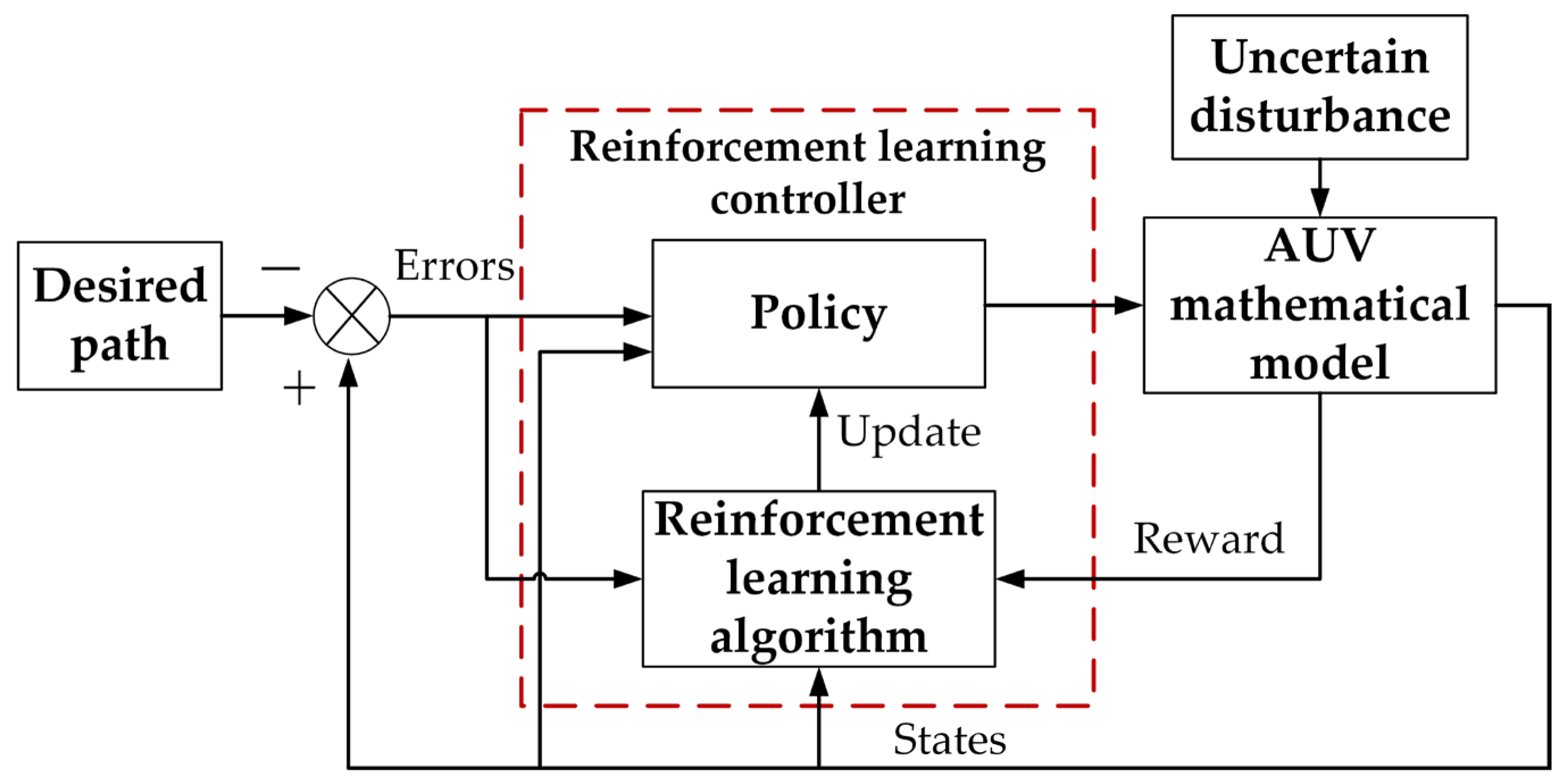
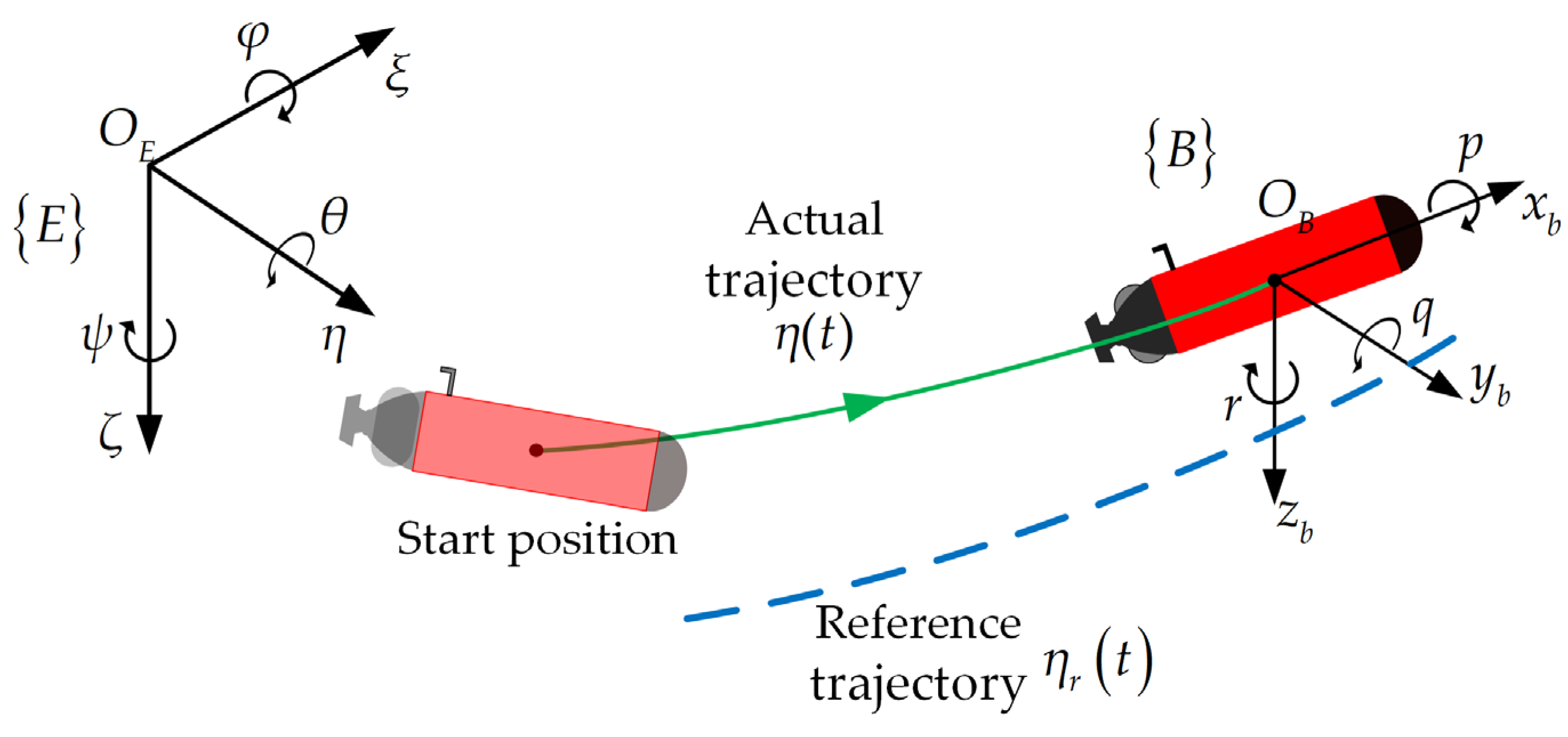
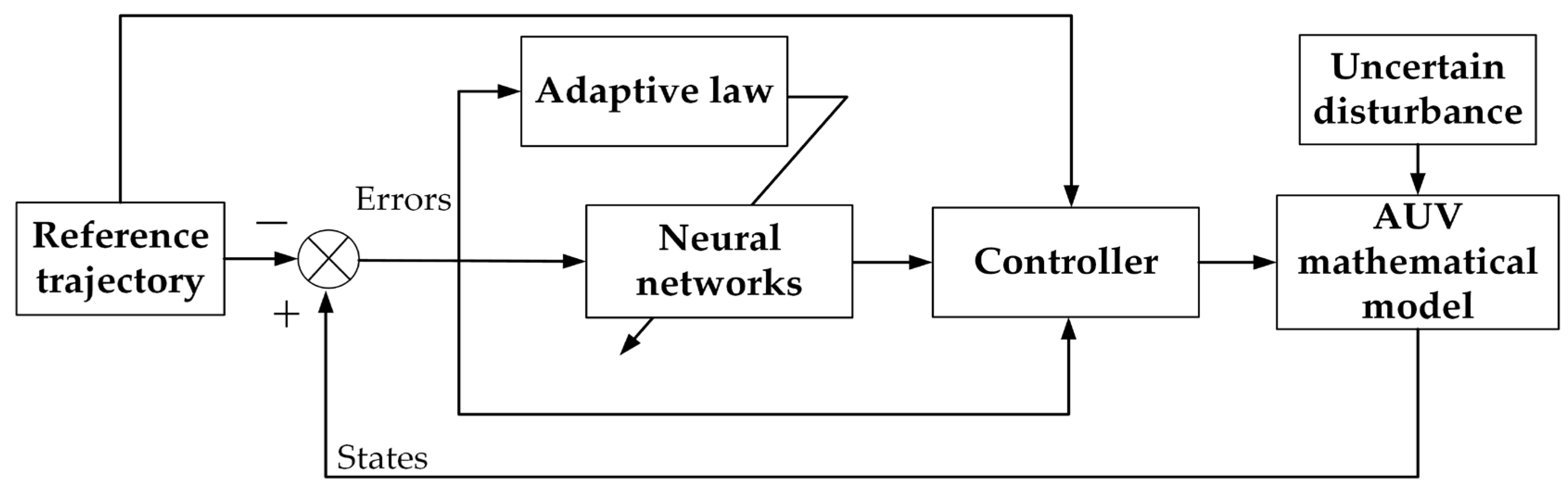
| Paper | Publication Year | Main Contents |
|---|---|---|
| [49] | 2014 | adaptive sliding-mode control for formation control |
| [17] | 2016 | path-following control via fuzzy backstepping sliding-mode control |
| [24] | 2018 | path-following control using adaptive second-order sliding-mode control |
| [46] | 2018 | formation control using adaptive self-organizing map neural network |
| [20] | 2019 | path-following control based on fuzzy sliding-mode control with radial basis function neural networks |
| [38] | 2020 | trajectory tracking control based on backstepping and adaptive sliding-mode control |
| [48] | 2021 | formation control based on reinforcement learning |
| [22] | 2022 | path-following control integrating reinforcement learning and dynamic data-driven models |
| [35] | 2022 | trajectory control using rapidly deployed deep reinforcement learning |
| [54] | 2023 | formation transformation control algorithm based on leader–follower strategy |
| [25] | 2024 | 3d path-following control method based on backstepping sliding-mode control |
| [33] | 2025 | trajectory tracking control method based on adaptive sliding-mode control using backstepping and neural networks |
| Control Methods | Path-Following Control | Trajectory Tracking Control | Formation Control |
|---|---|---|---|
| fuzzy logic control | [17,18,19] | [25,26,27,28,29,30,31] | [43,44,45] |
| neural network control | [20,21] | [33,34] | [46,47] |
| reinforcement learning control | [22,23] | [35,36,37] | [48] |
| adaptive dynamic programming control | [24] | [38] | [48] |
| Intelligent Control Method | Advantages | Disadvantages |
|---|---|---|
| fuzzy logic control | handle uncertainties [18,24,28], no precise model needed [18,26], strong robustness [24,29] | complex rule design [18,28], high computational cost [24,28], no guarantee of global optimum [18,26] |
| neural network control | adaptability [20,33,34], strong nonlinear mapping ability [20,33], data-driven [20,34] | large training data requirement [20,34], risk of overfitting [20,33], poor interpretability |
| reinforcement learning control | self-learning [21,23,36], ability to adapt to complex environments [21,35,37], long- term optimization [21,36] | slow convergence [20,34], difficulty in balancing exploration and exploitation [20,23], sensitivity to initial conditions [21,36] |
| adaptive dynamic programming control | online parameter tuning [24,32,38], strong robustness [24,29], suitability for unknown systems [24,32] | complex design [24,32], stability issues [24,29], high computational cost [24,32] |
| Control Methods | Application Scenarios | Strengths | Limitations |
|---|---|---|---|
| PID control | path tracking and positioning [59] and simple dynamic systems [72] | wide applicability [59], strong robustness [60], simple to implement [72] | poor adaptability to nonlinear systems [59], limited dynamic performance [60], complex parameter tuning [58] |
| sliding-model control | nonlinear and uncertain systems [61], path tracking and dynamic positioning [62] | strong robustness [61], fast dynamic response [62], adaptation to complex dynamics [63] | high-frequency vibration problems [61], sensitivity to noise [62], high implementation complexity [63] |
| model predictive control | path planning and tracking [66], complex dynamic systems [67] | optimization ability [66], adaptation to complex dynamics [67], predictive ability [68] | difficulty in implementation [66], high computational complexity [68], reliance on precise models [69] |
| intelligent controls | complex tasks and dynamic environments [21], autonomous decision-making and optimization [70] | autonomous learning ability [21], adaptation to complex dynamics [70], high flexibility [71] | lack of real-time performance [23], high dependence on environment [21], long training time [70] |
| Control Methods | Robustness | Adaptability | Computational Cost | Implementation Simplicity | Practical Applicability |
|---|---|---|---|---|---|
| PID control | medium | low | low | high | good |
| sliding-model control | high | medium | medium | medium | good |
| model predictive control | high | high | high | low | medium |
| neural network control | medium | high | high | low | medium |
| reinforcement learning | medium | high | very high | low | emerging |
| Control Methods | Applicable Conditions | Advantages | Disadvantages |
|---|---|---|---|
| leader–follower method | cooperative operations of multiple AUVs, with a leader guiding the formation’s movement | computational complexity [54], high control accuracy [84], reduced enhanced system robustness [85] | high communication demand [84], dependent on leader [86] |
| consistency control method | local interaction enables variable consistency | reduced dependence on global information [87,88], strong distributed autonomy [89], high robustness [90] | inadequate adaptation to dynamic environmental factors [89], face vibration issues [90] |
| virtual structure method | high-precision formations with high fault tolerance requirements | strong fault tolerance [91], high flexibility [40,92] | dependent on global information [40,91,92,93,94], high communication requirements [92] |
| behavior-based method | unstructured tasks with self-organized formations | high flexibility, adaptable to dynamic environments [95,96] | lack of global coordination [97], weak precise control ability [98,99] |
| Focus Problem | Path-Following Control | Trajectory Tracking Control | Formation Control | Main Methods and Techniques |
|---|---|---|---|---|
| environmental adaptability issues | current disturbances [65,107,108,109,110,111], water density stratification [112,113,114], sea ice (navigation failure) [115,116,117,118], waves (pose disturbance) [119,120,121] | current/wave disturbances [74,81], water density stratification [122] | current disturbances, sea ice [123,124,125,126], communication delays [127] | guidance law improvement [107,108,109,110,111,128,129,130], observer techniques [131,132,133,134,135,136,137,138], intelligent algorithms [117,118,139,140,141,142], sliding-mode control [25,65,119,120,121,133,143] |
| limitations of traditional methods | dependent on parameter assumptions [128,129], unmodeled dynamics leading to instability [144] | observation error hypothesis [25,138] | complex communication needs are hard to meet [145] | insufficient adaptability to environmental and system dynamics, relies on idealized assumptions |
| underwater communication problems | communication delays affect coordination [146,147] | acoustic noise interference [146] | low transmission rate and packet loss affect formations [127], sonar has a limited field of view [146] | disturbance rejection control [147], deep learning [127,146,147] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Xie, M.; Zhang, Y. A Review of Path Following, Trajectory Tracking, and Formation Control for Autonomous Underwater Vehicles. Drones 2025, 9, 286. https://doi.org/10.3390/drones9040286
He L, Xie M, Zhang Y. A Review of Path Following, Trajectory Tracking, and Formation Control for Autonomous Underwater Vehicles. Drones. 2025; 9(4):286. https://doi.org/10.3390/drones9040286
Chicago/Turabian StyleHe, Long, Mengting Xie, and Ya Zhang. 2025. "A Review of Path Following, Trajectory Tracking, and Formation Control for Autonomous Underwater Vehicles" Drones 9, no. 4: 286. https://doi.org/10.3390/drones9040286
APA StyleHe, L., Xie, M., & Zhang, Y. (2025). A Review of Path Following, Trajectory Tracking, and Formation Control for Autonomous Underwater Vehicles. Drones, 9(4), 286. https://doi.org/10.3390/drones9040286







