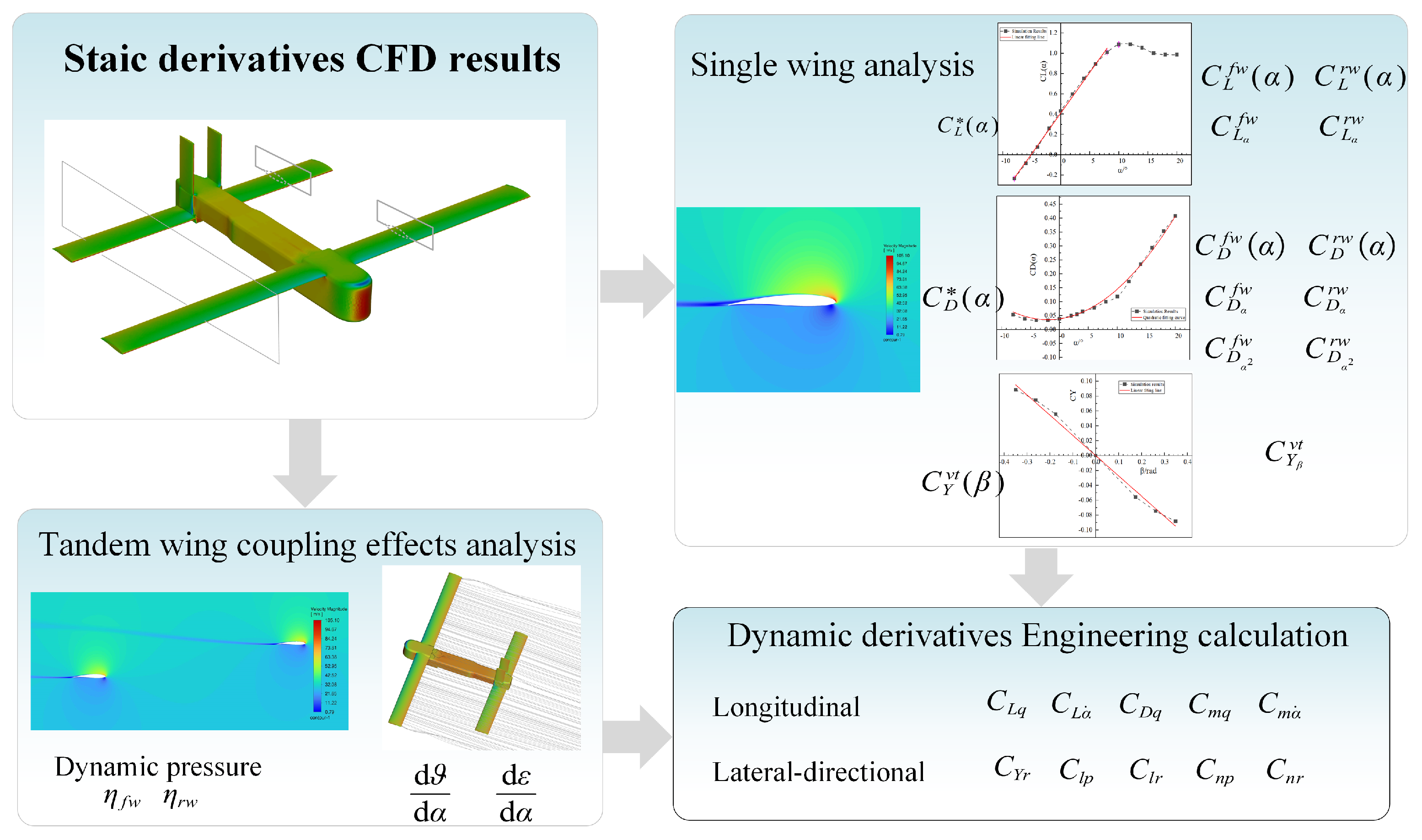
4.2. Reference Values Obtained by Dynamic Derivative CFD Simulations
To verify the effectiveness of the proposed method, this paper uses the dynamic derivative CFD simulations as reference values. We calculate the dynamic derivatives in both the longitudinal and lateral directions. A forced oscillation analysis method with a simple harmonic oscillation (SHO) mode is adopted to obtain longitudinal coupled dynamic derivatives
[
45,
60], and the quasi-steady method is used for solving the longitudinal angular rate derivative
[
43], where the subscript * is
L,
D and
m. Researchers have applied the aforementioned method for dynamic derivative CFD simulations across different flight platforms and have validated its effectiveness using wind tunnel data [
46,
61]. According to Equation (
6), we only need to consider the angular rate derivatives for the roll and yaw directions. Therefore, steady roll and yaw movements are simulated to obtain the
and
, where the subscript * can be
Y,
l, and
n. As the UAV primarily operates in cruise flight, the CFD simulation uses a cruise flight speed of 30 m/s and an altitude of 300 m above sea level. All numerical simulations were conducted in ANSYS FLUENT 2023R1 with tailored methodologies for distinct aerodynamic derivatives. For the longitudinally coupled dynamic derivatives, a transient solver is employed, a transient pressure-based solver incorporating the Sliding Mesh Method (SMM) [
62] was used to simulate UAV oscillatory motions, utilizing the realizable
turbulence model with standard wall functions. The first-order implicit transient formulation is utilized, with the Roe-FDS flux scheme and cell-based gradient reconstruction for the least squares applied for numerical accuracy. The second-order upwind scheme is used for spatial discretization. The Courant number is set to 20, and default under-relaxation factor values are employed. A fixed-time-step-size marching scheme with the user-specified method is implemented to ensure stability and precision. In parallel, the angle rate derivatives simulations implemented a steady-state framework through the Multiple Reference Frame (MRF) [
63] approach, retaining an identical turbulence model while adopting a coupled pressure–velocity solver for enhanced convergence. Spatial discretization preserved second-order upwind accuracy with identical Courant number conditioning, complemented by standardized relaxation factors.
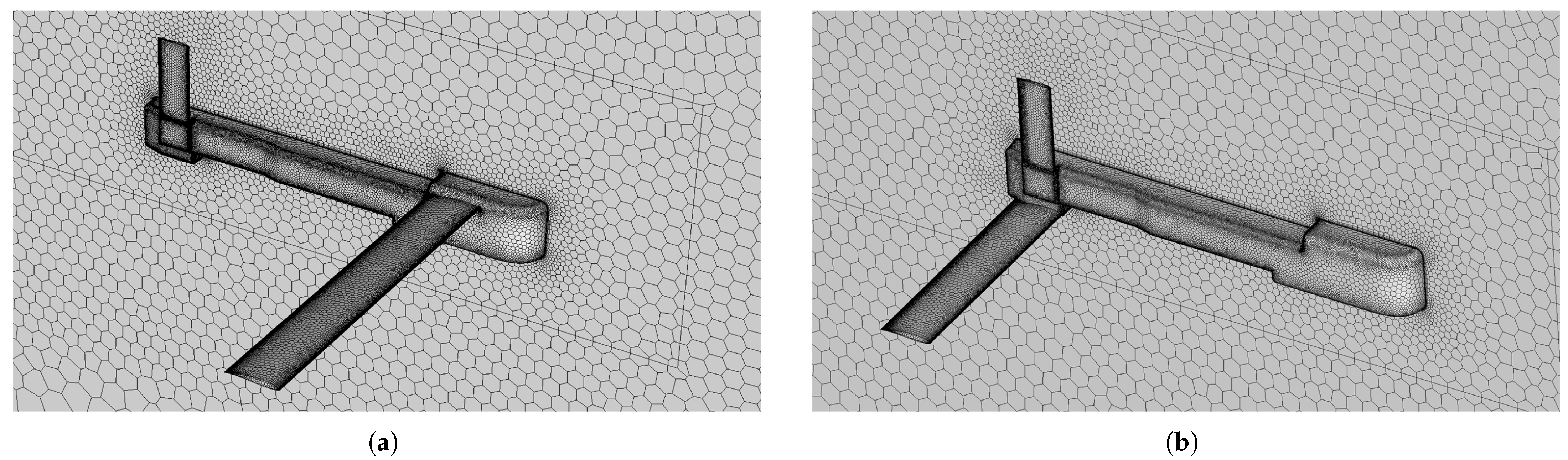
The entire computational fluid domain is a spherical region with a diameter of 20 m. Using ANSYS Fluent Meshing 2023R1, an unstructured computational grid was generated. The process began with the creation of a triangular surface mesh, followed by the configuration of boundary layer parameters, and concluded with the generation of a poly-hexcore volume mesh. In this context, the first layer’s height and the number of boundary layers are directly linked to the
value, which is determined by the turbulence model employed in the simulation. For RANS-based CFD simulations of external aerodynamic flows, three turbulence models are typically used: Spalart–Allmaras (SA),
, and
. The SA model is a single-equation approach and performs well for simple geometries but shows limitations in predicting shear and separated flows. The
model is a two-equation approach; while offering high accuracy for boundary layer resolution, it imposes stringent grid requirements (
and at least 15 boundary layers). For example, achieving
on the SULA90 would require a first-layer thickness of
mm, significantly increasing mesh density and compromising grid quality at wing–body junctions due to extreme aspect ratios. To balance accuracy and computational efficiency, the realizable
model was selected. This model permits a relaxed
threshold of 30 and a reduced boundary layer count of 10 while still capturing essential boundary layer physics. The first layer’s height was set to
mm using the last ratio offset method with a transition ratio of
. The UAV surface mesh and boundary layers on the UAV wall are depicted in
Figure 5a. The far field was assigned a pressure–far-field boundary condition, while the UAV wall was defined as the no-slip wall.
The Sliding Mesh Method (SMM) is a dynamic mesh technique for or longitudinal coupled dynamic derivative simulations. The fluid domain is partitioned into static and dynamic zones, as shown in
Figure 5b. The dynamic zone encompasses the mesh within a 5 m diameter inner sphere and the UAV wall, actuated by longitudinal oscillatory motions governed by a User-Defined Function (UDF) file, while the static zone extends to the far-field boundary. In contrast, angular rate derivatives simulations are steady-state simulations, only requiring a single fluid domain, though configured with corresponding rotational velocities to replicate the UAV’s uniform rotation. The longitudinal coupled dynamic derivative case utilized a volumetric mesh comprising
million elements, whereas the angular rate derivatives case employed
million elements. The above simulations were run on a workstation AMD EPYC 9554 series 128-core CPU, finishing in 64 h and 20 min. The detailed procedure is as follows.
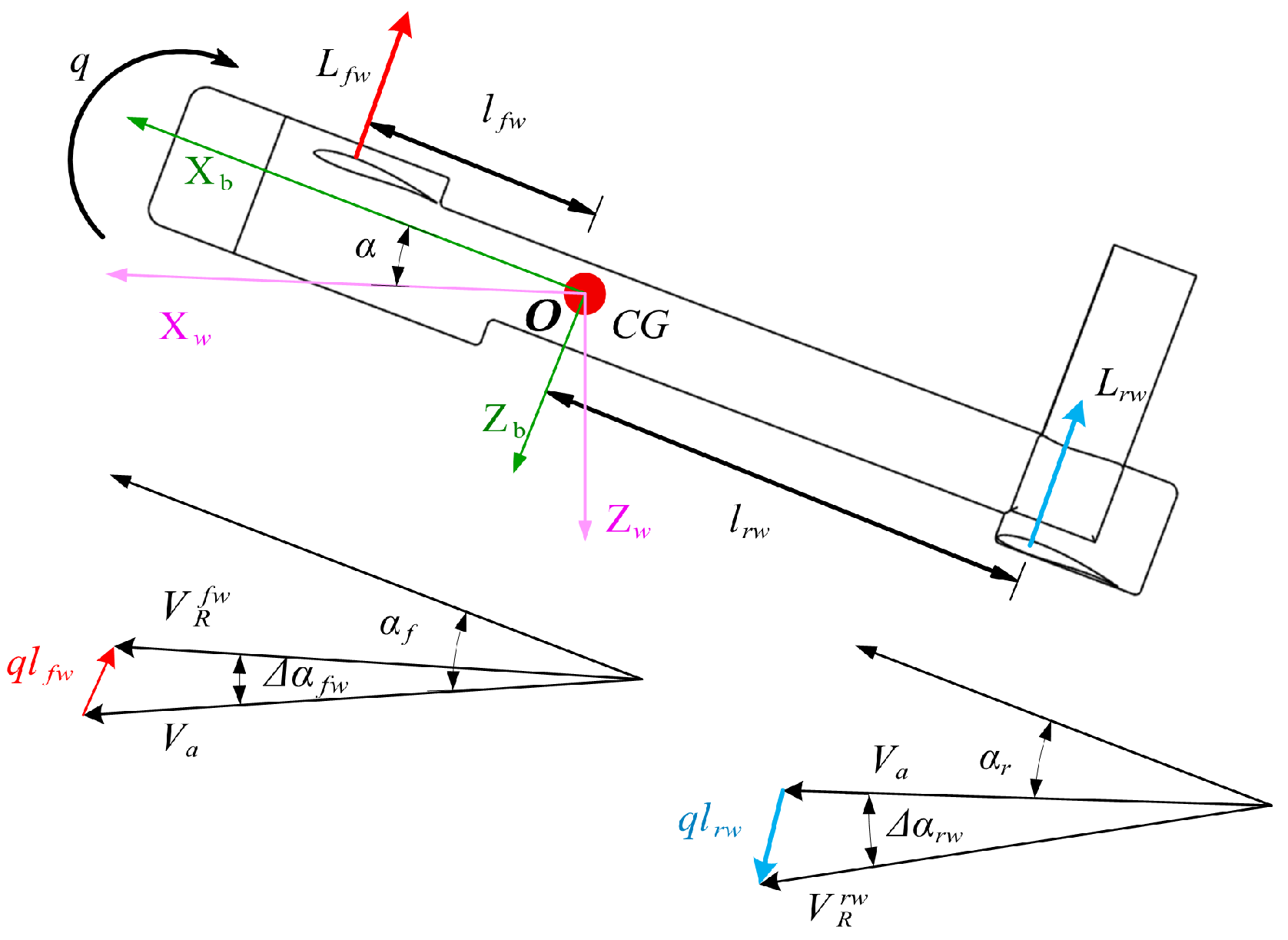
(1) Longitudinal coupled dynamic derivative analysis: The AOA vibration equation is given by
where
is the initial flight AOA and is set as zero, and the oscillation amplitude
is set as 2 deg. The equation of the oscillation angular rate is
. In the equation, the reduced frequency
,
, so
. The numerical simulations adopt a fixed time step (
s) with a convergence threshold limiting iterations to 50 per step. A total of 144 time steps are calculated, thereby yielding a complete harmonic oscillation period of
s. The results from
to
s were fitted using the Least Squares Method (LSM). The
and
fitting formula is shown in Equation (
30), and the
fitting formula is shown in Equation (
31).
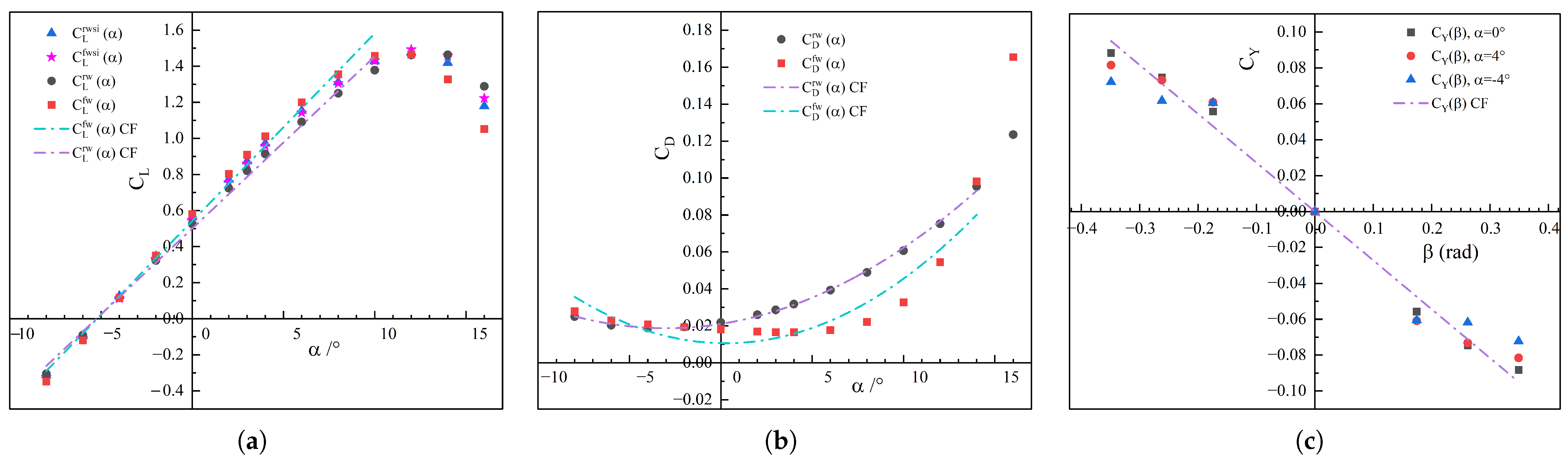
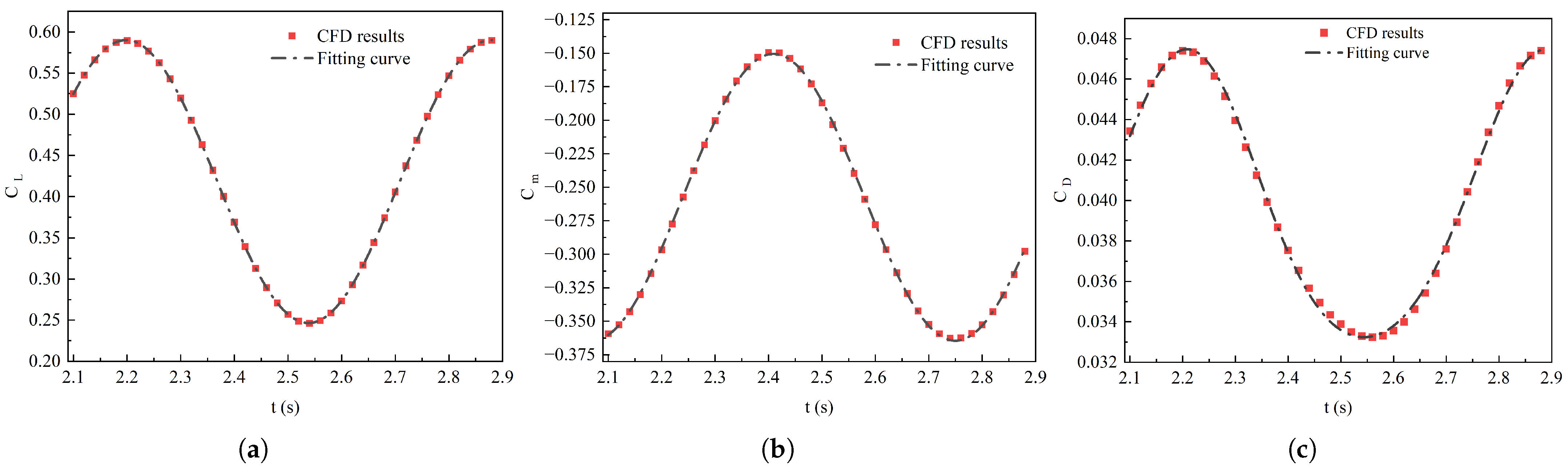
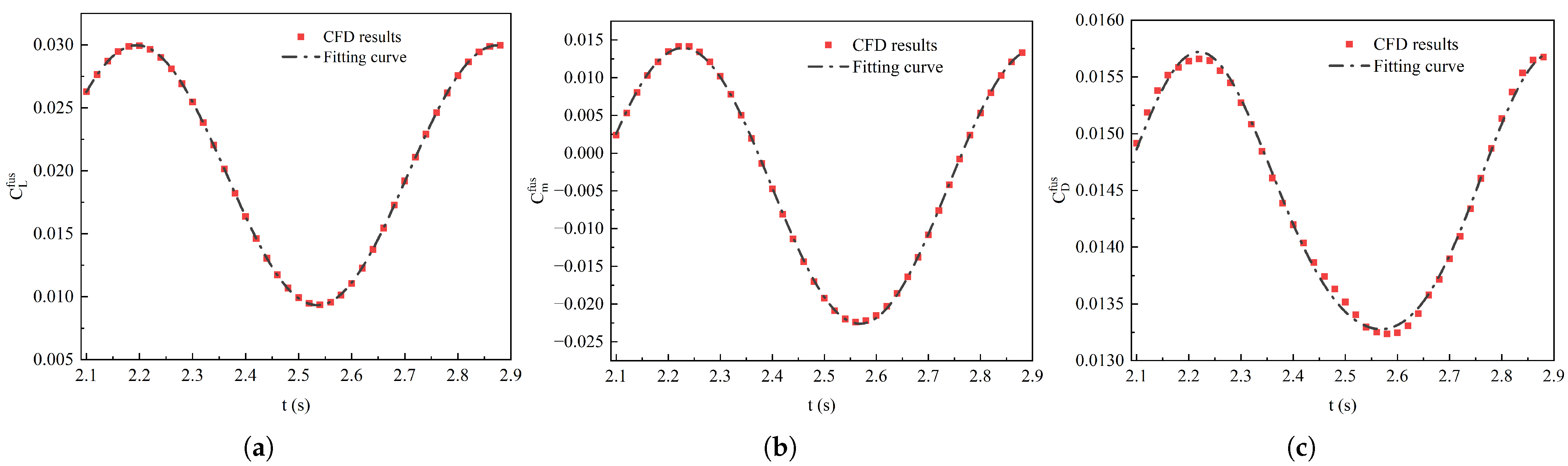
The fitting curves of
,
and
for the whole SULA90 are shown in
Figure 6a–c. The fitting curves of
,
and
for the fuselage are shown in
Figure 7a–c. The detailed computational method for longitudinal coupling derivatives is presented in
Appendix A.2.
(2) Longitudinal pitch angular rate derivative analysis: The AOA is also set to zero, and the pitch rate
q is taken as
,
,
, and
. A linear fit is used to analyze how
,
and
change with respect to
(
), as shown in
Figure 8a. The slope of the fitting line represents the pitch angular rate derivative
, where the subscript * can be
L,
D and
m.
Table 2 shows the detailed longitudinal dynamic derivative results for the whole UAV and the fuselage. It can be observed that the fuselage primarily affects the drag dynamic derivatives (e.g.,
and
) while having minimal impact on the lift dynamic derivatives (e.g.,
and
) and pitching moment dynamic derivatives (e.g.,
and
).
(3) Lateral-directional angular rate derivative analysis: The AOA is also set to zero, and the roll rate
p is taken as
,
,
, and
for a total of four simulations. A linear fit is used to analyze how
and
change with respect to
(
), as shown in
Figure 8b. The slope of the fitting line represents the roll angular rate derivatives, so we obtain
and
. The AOA and yaw rate
r are the same as roll angular rate derivative analysis. A linear fit is used to analyze how
,
and
change with respect to
(
), as shown in
Figure 8c. The slope of the fitting line represents the yaw angular rate derivatives, so we obtain
and
and
.
4.3. Comparison Results
Research indicates that the accuracy of dynamic derivatives depends on the chosen control method. The aircraft primarily employs two control methods: open-loop and closed-loop control. Compared to closed-loop control, open-loop control demands higher precision [
22,
64]. W. B. Blake [
30] summarized the accuracy criteria for both methods in
Table 3. Since the modern UAV primarily utilizes closed-loop control, the proposed method meets the precision requirements for closed-loop control, which means it is suitable for engineering applications. So, the relative difference of the longitudinal dynamic derivative should not exceed
, and the absolute difference of the lateral-directional derivative should not exceed
/rad.
The dynamic derivative calculations in the CEHM method require three types of aerodynamic parameters, which are derived from static derivatives CFD simulation results. The CFD simulations used in the CEHM are presented in
Appendix A.3, while the calculation process and results of the three types of parameters are provided in
Appendix A.4 and the detailed results of the static derivatives CFD simulations are provided in
Appendix A.5. To validate the effectiveness of the CEHM method, two widely used aerodynamic estimation software tools were employed for comparison: XFLR5 (version 6.61) and OpenVSP (version 3.41.2). Since the CEHM method omits the influence of the fuselage when estimating dynamic derivatives, XFLR5 and OpenVSP also neglect fuselage effects to ensure consistency in the calculations. The simulation models for these tools are shown in
Figure 9. The computation times for CEHM and XFLR5 are on the order of seconds, while OpenVSP requires minutes. The CFD simulations employed as input for CEHM required 24 h and 46 min, equating to a quarter of the computational duration entailed by traditional full-CFD methods. The dynamic derivative results calculated at zero AOA are summarized in
Table 4. Using the CFD simulation results as the reference values, we evaluate the effectiveness of the CEHM method by calculating the relative differences for longitudinal dynamic derivatives and the absolute difference for lateral-directional dynamic derivatives.
The relative differences (RDs) for the dynamic derivatives are summarized in
Table 4. To facilitate a more meaningful comparison, the dynamic derivatives in the CFD calculation results provided in the table are adjusted by subtracting the fuselage effects according to
Table 2. Given the relatively minor influence of the fuselage on lateral-directional dynamic derivatives, the CFD-derived lateral-directional dynamic derivatives presented in the table are based on full-aircraft computational results. For
, the relative differences for the CEHM method remain below
, satisfying the stringent criteria for open-loop control. The relative differences for XFLR5 and OpenVSP closely approach
. Regarding
, all three methods exhibit relative differences within
, with the CEHM method achieving the highest precision at a relative difference of
. While XFLR5 is incapable of computing
, OpenVSP demonstrates a substantial relative discrepancy of
, which aligns with closed-loop control prerequisites. In contrast, the CEHM method yields a relative difference of
for
, which meets the open-loop control requirement. Furthermore, XFLR5 and OpenVSP lack the capability to compute acceleration derivatives such as
and
, which are critical for simulating high-maneuverability flight dynamics. The CEHM method, conversely, not only calculates these acceleration derivatives but also attains an acceptable accuracy. For
, both XFLR5 and OpenVSP exhibit relative errors exceeding
, whereas the CEHM method demonstrates the smallest relative difference at
, accompanied by an absolute difference of
/rad, as illustrated in
Table 4; this value approaches the permissible tolerance range. For
and
, only the CEHM method produces results within the required accuracy. For
and
, although all three methods meet the requirements, the CEHM method achieves the highest accuracy, with an absolute difference of about half of the results from XFLR5 and OpenVSP.