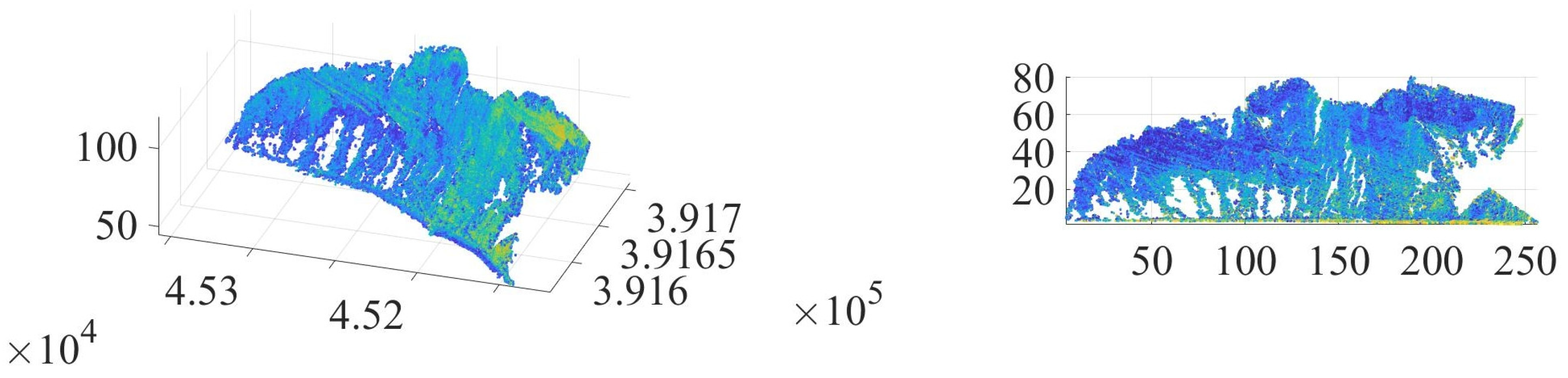Combining UAV Photogrammetry and TLS for Change Detection on Slovenian Coastal Cliffs

Abstract

This article examines the combined use of UAV (Unmanned Aerial Vehicle) photogrammetry and TLS (Terrestrial Laser Scanning) to detect changes in coastal cliffs in the Strunjan Nature Reserve. Coastal cliffs present unique surveying challenges, including limited access, unstable reference points due to erosion, GNSS (Global Navigation Satellite System) signal obstruction, dense vegetation, private property restrictions and weak mobile data. To overcome these limitations, UAV and TLS techniques are used with the help of GNSS and TPS (Total Positioning Station) surveying to establish a network of GCPs (Ground Control Points) for georeferencing. The methodology includes several epochs of data collection between 2019 and 2024, using a DJI Phantom 4 RTK for UAV surveys and a Riegl VZ-400 scanner for TLS. The data processing includes point cloud filtering, mesh comparison and a DoD (DEM of difference) analysis to quantify cliff surface changes. This study addresses the effects of vegetation by focusing on vegetation-free regions of interest distributed across the cliff face. The results aim to demonstrate the effectiveness and limitations of both methods for detecting and monitoring cliff erosion and provide valuable insights for coastal management and risk assessment.

1. Introduction

Coastal cliffs are highly susceptible to different natural phenomena: rain, wind, frost, and sea influences. It is of vital importance to monitor the cliff surface to provide safety for people and property.

Cliffs are very specific surveying-wise. Most of them are accessible only through a narrow passage by sea. This presents a significant challenge for terrestrial surveying methods. Due to constant geological and natural processes and influences, it is very hard to identify stable reference points.

Our case study presents additional challenges. Most of the surveyed area is orientated to the north, weakening the reception of GNSS (Global Navigation Satellite System) signals. The mobile data signal is weak or non-existent; therefore an RTK (Real-Time Kinematic) GNSS survey is not possible. Dense vegetation and private properties on the top edge of the cliffs prevent setting the GCPs (Ground Control Points) above the cliff walls. Additionally, the vegetation growing from the walls also affects the comparison of survey time series.

The aim of this article is to combine, compare and analyze UAV (Unmanned Aerial Vehicle) photogrammetry and TLS (Terrestrial Laser Scanning) surveying for purposes of detecting and monitoring the changes in cliff surfaces on a selected part of coastal cliffs in the Strunjan Nature Reserve by Moon Bay, also known as St. Cross Bay. The location of the cliffs is shown in Figure 1.

TLS is now a well-established method for monitoring coastal cliff surfaces. Rosser et al. [3] presented a novel approach to monitoring cliff processes using TLS, focusing on hard rock cliffs. Their study emphasizes the limitations of traditional aerial methods and demonstrates how TLS can provide detailed, on-site data about cliff erosion, including small-scale failures that are often overlooked by conventional techniques. Their research showcases 16 months of monitoring data from a near-vertical cliff in North Yorkshire, UK, revealing significant insights into the spatial and temporal patterns of cliff collapse. More recently, Tyszkowski, et al. [4] provided seasonal observations of coastal changes using TLS over a one-year period on Fårö Island, Sweden. Their findings illustrate how TLS can effectively capture dynamic changes along coastal cliffs and contribute to understanding erosion processes in various environments. Between these two studies, many others [5,6,7,8] have been published that have successfully utilized TLS for detecting and analyzing changes in coastal cliff surfaces.

The UAV is also increasingly appearing in the literature in relation to the detection of coastal cliff changes, either in combination with TLS or as a standalone method. Doran et al. [9] utilize UAVs to create a high-resolution time series of point clouds for monitoring cliff dynamics over four years at Demons Bluff, Victoria, Australia. The methodology allows for the identification of potential future collapses, aiding in risk management for coastal areas. Son et al. [10] discuss a case study integrating UAV and TLS technologies for environmental monitoring, demonstrating the efficiency of UAVs compared to TLS in terms of time and accuracy for volumetric calculations in a waste stockpile area. Minervino Amodio et al. [11] highlight the use of UAV-derived Digital Elevation Models (DEMs) for assessing coastal vulnerability, showcasing significant variations in vulnerability indexes over time along the Molise coast. Jaud et al. [12] explore various imaging angles for UAV surveys of coastal cliffs, emphasizing the importance of optimal angles for effective monitoring and data collection. Konsolaki et al. [13] combine close-range remote sensing techniques, including UAVs, to monitor cliff stability and assess failure potential at Navagio Beach, providing insights into effective monitoring strategies.

2. Materials and Methods

For any change detection task, a stable reference frame with very accurate positions of the reference points must be provided. Absolute position measurements, e.g., with RTK GNSS, can be precise but are not accurate enough, especially under unfavorable conditions. Therefore, a relative measurement in relation to a stable reference is the best option.

2.1. Control Points Network

In our study, both the UAV and TLS methods rely on GCPs for georeferencing. In the UAV-based approach, the GCPs are established using anchor bolts that allow the central attachment of 40 × 40 cm plastic plates featuring a black-and-white target design. The same anchor bolts are utilized for TLS, where the GCP targets consist of round tiles with a diameter of 5 cm and a retroreflective surface.

A total of 22 GCPs were placed along the coastline for the UAV surveys, as illustrated in Figure 2 (right). Four of these were located within the study area and were surveyed by both UAV and TLS. Furthermore, seven GCPs were positioned within the study area specifically for TLS acquisition, as shown in Figure 2 (left).

The coordinates of the reference points were determined within the national coordinate system by surveying the geodetic network. In this method, horizontal angles, vertical angles and slope distances between the stations are measured using a conventional geodetic instrument, the tacheometer (also called a TPS—Total Positioning Station), and GCPs, which are connected to form a geometric network. The positions of the network points, which are located at optimal locations, are also determined using GNSS measurements. Finally, the exact positions of all points within the network are calculated using geodetic network adjustment. TPS Leica TS30 and GNSS Leica GS 18 (Leica, Heerbrugg, Switzerland) were used to survey the network.

During the four years of measurements, some points were destroyed, some were displaced and some remained stable. For the TLS GCPs, it soon became clear that the stability of points is not obvious. Along each TLS scan, we remeasured the GCPs with TPSs. This ensures highly accurate relative positioning between the GCPs, which nevertheless remain in the local coordinate system. These coordinates are transformed using six-parameter similarity transformation to align with the GCP positions from the previous survey. The transformed coordinates are then compared with those of the previous survey. Significant deviations indicate that a point has shifted. In this case, the transformed coordinates are used for the current survey.

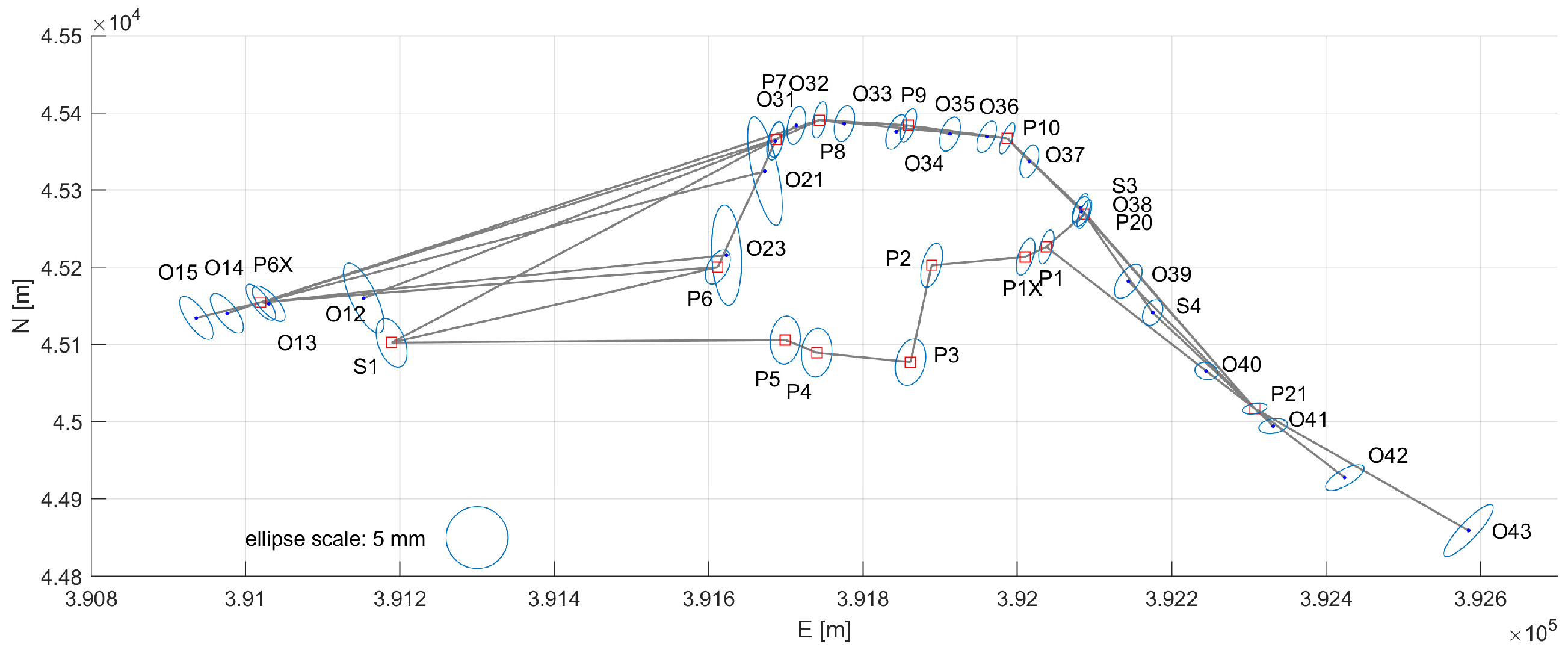
Before the last scanning in 2024, the geodetic network of GCPs was remeasured. The network with standard error ellipses of the points is displayed in Figure 3. The network was improved by closing the traverse and adding a GNSS static point with more favorable conditions, ensuring the higher reliability of the GCP coordinates.

A quick deformation analysis revealed that (a) destroyed or significantly displaced points have to be stabilized anew and (b) the measurement campaign in 2024 is of significantly better quality. The most realistic changes can be obtained by adapting coordinates from 2020 for the geodetic datum, and the coordinate changes are between −3 and +3 cm. Standard deviations are within 15 mm in all three coordinate components.

2.2. TLS Measurements

Ten consecutive measurements were conducted during the autumn and spring seasons from 2020 to 2024. Utilizing a Riegl VZ-400 scanner with a specified spatial accuracy of 3 mm and a maximum range of 600 m [14], we scanned the cliff area from the selected position (Figure 4) ranging between 300 and 550 m, achieving a resolution of 1.6 cm at a distance of 400 m in the “long-range” mode. GCPs were scanned using the fine target-scanning feature within the RiSCAN PRO 2.0 software (http://www.riegl.com/products/software-packages/riscan-pro/, accessed on 19 April 2019), which automatically configures the resolution and scanning mode.

At each scanning epoch, we performed verification and correction of the TLS GCP coordinates through precise polar measurements. Additionally, we replaced and remeasured the points that were gone or had moved due to the natural forces of waves or erosion.

The resulting dataset from each survey comprises a georeferenced point cloud containing approximately 30 million points. Prior to further processing, the point cloud undergoes rough clipping and filtering algorithms to minimize interference from vegetation. Geometric feature filtering is employed, removing points with fewer than 2000 neighbors within a 1 m radius and those with a planarity factor of less than 0.3 within a 0.2 m radius. Due to the challenging terrain configuration, some points on the cliff are filtered out, while some vegetation points may still be present. Manual clipping of such a large area across multiple measurements would be excessively time-consuming.

2.3. UAV Measurements

UAV surveys were performed with the DJI Phantom 4 RTK. The goal was to fly as close as possible, but at a safe distance, to the cliff walls to capture morphologic details at high resolution. All UAV flights were automated with pre-planned missions. As the cliffs are steep and most of them are inclined around 45°, a regular topographic survey with nadir images taken from a constant height from the take-off points was not an option. The height differences exceed 50 m in some parts. Even capturing nadir images at a selected height above ground applying the so-called terrain-following mode is not optimal, because some specific features could remain undetected. The optimal solutions would be taking images with their optical axis perpendicular to the cliff walls. The Phantom 4 RTK features a flight mode called “Angled Flight Route” that is well suited for such tasks. An example of creating an Angled Flight Route mission is shown in Figure 5 (left).

The selected distance from the surface was 25 m for most areas and 15 m for 2 specific regions (07 and 11). The Ground Sampling Distance (GSD) at those distances is 0.68 and 0.41 cm, respectively. The distances chosen represent a compromise between resolution and flight safety.

The surveyed area was split into 11 sectors; each of them was captured by a predefined Angled Flight Route mission. Sectors 7 and 11 were observed at 15 m, as they were the most interesting for the project geologists and posed no safety risk, and all other sectors at a distance of 25 m from the imaginary plane. Figure 6 shows the sectors with their respective labels. Sector 5 is the one that was also observed with TLS.

The UAV flights were performed in the RTK GNSS. Because of the weak or non-existent data mobile network in some parts, it was impossible to use the Slovenian CORS (Continuously Operating Reference Station) network in real time. Therefore, four base station points were stabilized and measured in the geodetic traverse along with the GCPs. Three of them, labeled S2, S3 and S4 (see Figure 6), lying between the sea and the cliff walls, were used as RTK base stations utilizing DJI D-RTK 2. An example of the base station set on a point is shown in Figure 5 (right). Besides the direct georeferencing of aerial images, the GCPs were also used in the processing.

2.4. TLS and UAV Surveys

Ten TLS and eight UAV surveys were carried out between April 2019 and April 2024. They are listed in

Table 1. TLS and UAV survey epochs.

	TLS Epochs	UAV Epochs	TPS CP Campaign
1	17 April 2019
2	28 January 2020
3	9 November 2020	9 November 2020	28 October 2020
4	14 April 2021	26 March 2021
5	13 October 2021	15 October 2021
6	28 March 2022	22 March 2022
7	29 October 2022	7 December 2022
8	10 April 2023	7 April 2023
9	16 January 2024	12 September 2023
10	5 April 2024	21 March 2024	5 April 2024

. Seven consecutive and six cumulative pairs can be created for comparison.

It was not always possible to execute both UAV and TLS surveys simultaneously. Some of the epochs are 2 weeks within each other (labeled in green); some are further apart (red and yellow labels).

Table 2. Consecutive and cumulative pairs.

Epoch Pair			Consecutive	Epoch Pair			Cumulative
I	3	4	November 2020 and April 2021
II	4	5	April 2021 and October 2021	VIII	3	5	November 2020 and October 2021
III	5	6	October 2021 and March 2022	IX	3	6	November 2020 and March 2022
IV	6	7	March 2022 and November 2022	X	3	7	November 2020 and November 2022
V	7	8	November 2022 and April 2023	XI	3	8	November 2020 and April 2023
VI	8	9	April 2023 and January 2024	XII	3	9	November 2020 and January 2024
VII	9	10	January 2024 and April 2024	XIII	3	10	November 2020 and April 2024

lists consecutive and cumulative pairs, created from TLS and UAV epochs.

Since more than half of the consecutive pairs are red, which means a poor temporal match, we have selected two additional epoch pairs with green values from Table 1. They are listed in

Table 3. Additional pairs.

Epoch Pair			Selected
XV	6	8	March 22—April 23
XVI	8	10	April 23—April 24

.

2.5. Methods of Comparison

2.5.1. Mesh Comparison (M3C2)

Surface changes can be represented graphically as (1) distances between point clouds or (2) distances between surface models such as M3C2 [15,16]. The latter method is far better, as the former does not provide signed values. The standard linear color scale for visualizing changes uses red to indicate negative changes (erosion), blue for positive changes and white for changes smaller than the accuracy threshold. In Figure 7, negative changes are clearly visible in the steep sections—rockfall events—while material accumulation can be observed on the scree slopes below the cliff.

2.5.2. DEM of Difference of DEM (DoD)

Since we want to evaluate the differences between the methods quantitatively and not just visually, we consider a DoD grid [17] to be the most appropriate way to represent these differences. Due to the presence of harder flysch layers—ledges that protrude from the cliff face—we need to choose a projection plane for the DEM that is roughly parallel to the cliff surface to avoid shadows in the surface model. This ensures that the height component is perpendicular to the average plane of the cliff wall, while the x-axis remains horizontal (Figure 8).

The next challenge is vegetation. Due to the fundamentally different data acquisition methods, interfering vegetation affects the data collected with each method differently. In order to properly evaluate the differences between the methods, errors caused by unremoved vegetation cannot be ignored. The most effective way to mitigate these issues appears to be to analyze smaller vegetation-free patches that are distributed as evenly as possible over the entire cliff surface (Figure 9).

The regions of interest (ROIs) are rectangular, which allows for easier resampling in the DEM. Their sizes and positions re manually selected to ensure that there is no obstructive vegetation in any of the measurement epochs for the UAV and TLS, while maximizing the ROI areas. Ten clearly defined ROIs of different sizes are defined in a uniform coordinate system that is identical for all data collected with both methods.

For each ROI, the captured point cloud is resampled into a raster with a density of 2 cm (which corresponds approximately to the point density in the field). This results in matrices with 2500 cells per square meter, where the cell values represent the terrain elevation (in metric units) in a direction perpendicular to the average plane of the cliff face (Figure 9,

Table 4. Dimensions and areas of ROIs.

ROI	Dim [m]	Area [m2]
ROI1	45 × 15	675
ROI2	10 × 10	100
ROI3	10 × 10	100
ROI4	10 × 10	100
ROI5	5 × 5	25
ROI6	10 × 10	100
ROI7	5 × 6	30
ROI8	6 × 12	72
ROI9	9 × 9	81
ROI10	10 × 10	100
ROI1	45 × 15	675

).

The DoD for each pair of epochs and both data acquisition methods is simply calculated as the difference between the matrices representing the DEM of each ROI in each epoch. The DoD is easily represented graphically (see Figure 10), using the same standard color scale as M3C2: a linear gradient from red (a decrease in terrain level) to white (no change) and to blue (an increase in terrain level).

3. Results

3.1. UAV Results

The UAV survey data were processed in Agisoft Metashape software (https://www.agisoft.com/, accessed on 12 November 2020). The results of the SfM/MVS processing were dense point clouds, 3D models, DSMs (Digital Surface Models), DTMs (Digital Terrain Models) and orthophotos. Point clouds, 3D models or DTMs were used to compare UAV surveys across epochs or to combine UAV and TLS data. As sectors 1 and 2 (see Figure 5) are separate, they were processed individually. Sectors 3 to 10 were processed together to improve the results and achieve a better fit. During the observation period, some GCP anchor bolts shifted due to rockfalls or were covered by scree. The absence of GCPs in certain areas can lead to weaker solutions for individual sectors. All adjacent sectors were processed together to remedy the lack of GCPs in certain locations.

For the last UAV survey, on 21 March 2024, 2102 images of sectors 3–10 resulted in over 513 million points in the point cloud. The mesh of the 3D model has over 204 million faces. Both include only the cliffs; the forested areas above the cliffs have been removed. A 3D model of the area is displayed in Figure 11.

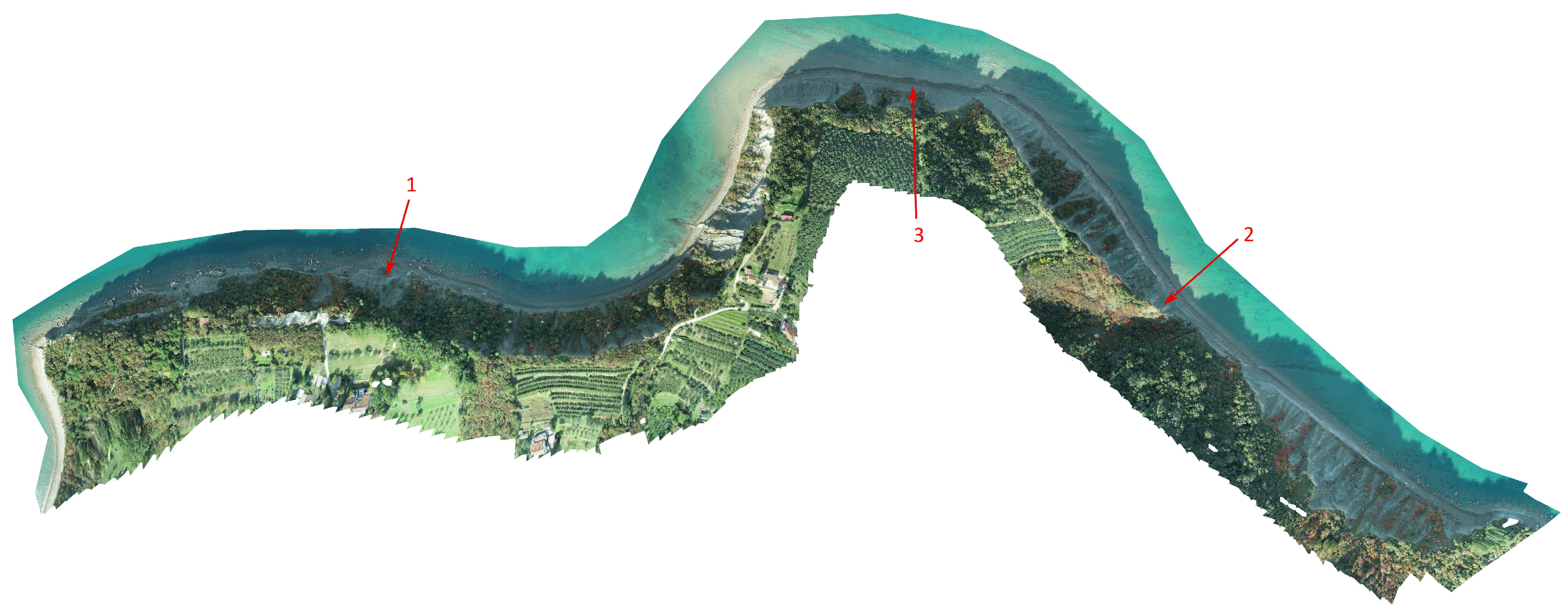
During the time of observation, some minor rockfalls occurred. By comparing terrain layers of different epochs, such cases are easily detected. Some of the bigger detected rockfalls are shown in Figure 12 and Figure 13.

3.2. UAV Surveys with Different Positioning Modes

The UAV survey on 15 October 2021 was performed in two ways. One was RTK using a DJI D-RTK 2 (DJI, Shenzhen, China) base station, so-called direct georeferencing [18]. The other method was without external corrections (RTK or PPK), using autonomous GNSS positioning, which means that the solution is based solely on the received GNSS satellite data. One of the GCPs, O22, was found to be destroyed. To perform a quality control of the different positioning modes, the remaining three GCPs and two points (T1, T2) near the top of the cliff were used. The locations of the points can be seen in Figure 14. The distance between O21 and O24 is 172 m, and the height difference between the GCPs and test points T1 and T2 is 70 m. Points T1 and T2 are distinctive features on the cliff, and the coordinates of T1 and T2 are measured on point clouds. The coordinates of the GCPs are determined in the georeferencing part of the processing.

According to our tests, the differences between the RTK and PPK (Post-Processing Kinematic) coordinates are within 6 cm in each component. Similar values were determined by [19]. It has also been shown that the PPK method achieves an accuracy of less than 5 cm with only a few GCPs [20]. This indicates that such results can also be achieved without GCPs, as the PPK method is both reliable and very accurate.

The RTK and PPK solutions are treated as of the same quality, so only RTK and autonomous solutions are compared. Coordinate discrepancies between different solutions and given coordinates are stated in

Table 5. Coordinate discrepancies of RTK solutions.

Solution	Point	ΔE (m)	ΔN (m)	Δh (m)
RTK—no GCP	O21	0.08	−0.04	0.01
	O23	0.05	0.00	0.00
	O24	0.03	−0.01	0.02
	T1	−0.04	0.05	−0.03
	T2	0.01	−0.02	0.01
RTK + GCP: O23	O21	0.07	−0.04	0.01
	O23	0.04	0.00	0.00
	O24	0.03	−0.01	0.02
	T1	0.02	0.03	0.04
	T2	−0.01	−0.05	0.00
RTK + GCP: O21, O24	O21	0.06	−0.04	0.01
	O23	0.04	0.00	0.00
	O24	0.02	−0.01	0.02
	T1	0.02	0.04	0.03
	T2	0.01	−0.04	−0.03
RTK + GCP: O21, O23, O24	O21	0.06	−0.04	0.01
	O23	0.04	0.00	0.00
	O24	0.02	−0.01	0.02
	T1	0.02	0.05	0.07
	T2	0.00	−0.01	0.01

and

Table 6. Coordinate discrepancies of autonomous solutions.

Solution	Point	ΔE (m)	ΔN (m)	Δh (m)
auton.—no GCP	O21	−1.74	0.76	0.99
	O23	−1.72	1.30	1.61
	O24	−1.48	1.8	1.72
	T1	−0.96	0.48	0.03
	T2	−1.01	0.39	0.00
auton. + GCP: O23	O21	−0.10	1.12	0.18
	O23	0.00	0.00	0.01
	O24	0.14	−0.21	−0.35
	T1	−0.07	−0.14	0.91
	T2	0.01	−0.17	0.89
auton. + GCP: O21, O24	O21	0.00	0.01	0.01
	O23	−0.10	−0.20	0.24
	O24	0.00	0.00	0.01
	T1	−0.78	−0.22	1.04
	T2	−0.74	−0.32	1.07
auton. + GCP: O21, O23, O24	O21	0.01	0.05	−0.02
	O23	−0.07	−0.13	0.10
	O24	0.05	0.09	−0.06
	T1	0.17	−0.71	−0.15
	T2	0.18	−0.77	−0.15

.

The RTK results indicate that the use of GCPs offers only a minimal improvement, as the accuracy at T1 and T2 is within the accuracy of the coordinate reading, which is about 5 cm.

The situation differs significantly for autonomous solutions, where GCPs play a crucial role. However, since GCPs can only be placed in the lower part of the cliff, the accuracy improvement is limited to that region. As a result, coordinate errors at T1 and T2 may still exceed 1 m, rendering the solution unreliable for practical applications.

3.3. Comparison Between UAV and TLS Results

The sum of all positive cell values can be calculated for each DoD. Multiplied by the cell area, this gives the total volume increase corresponding to sedimentation—an unexpected phenomenon on a vertical cliff. Similarly, the addition of all negative cell values gives the total volume of erosion. An important statistical parameter for each DoD is the mean change value, which is calculated as the average of all cell values. Since the distribution of cell values is not standardized, histograms of cell value distributions provide valuable insights into the similarity of the changes between the two DoDs.

The differences in DoDs between the acquisition methods for a given ROI and epoch pair are simply calculated as the difference between the respective DoDs. These differences can be visualized using the same graphical approach. However, since they represent discrepancies between the change detection of the two methods, a different color scale is used. The mean value of the DoD differences corresponds to the difference between the mean cell values. The degree of similarity between the changes detected by TLS and UAV can also be quantified using the correlation coefficient between the vectorized DoD representations.

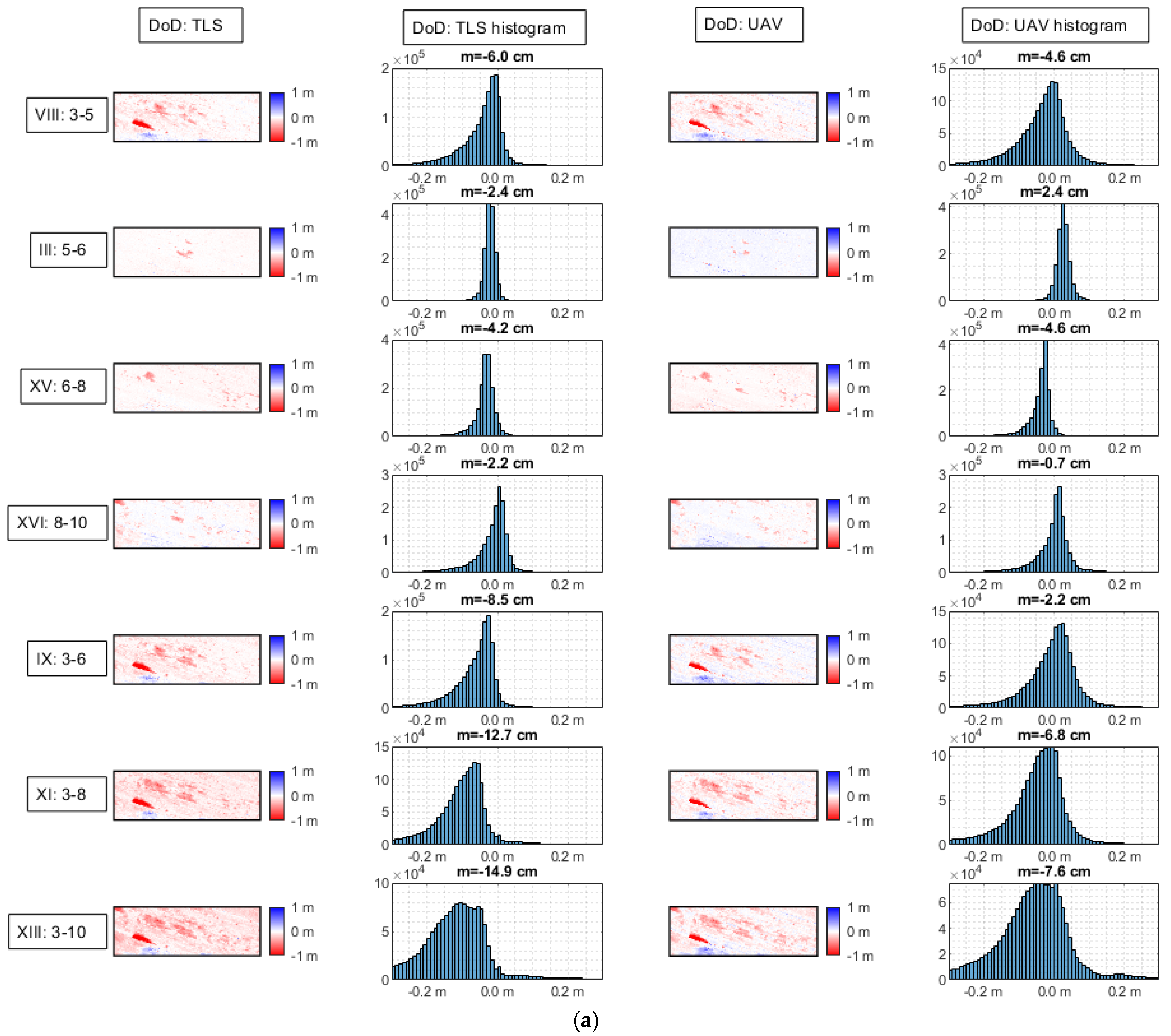
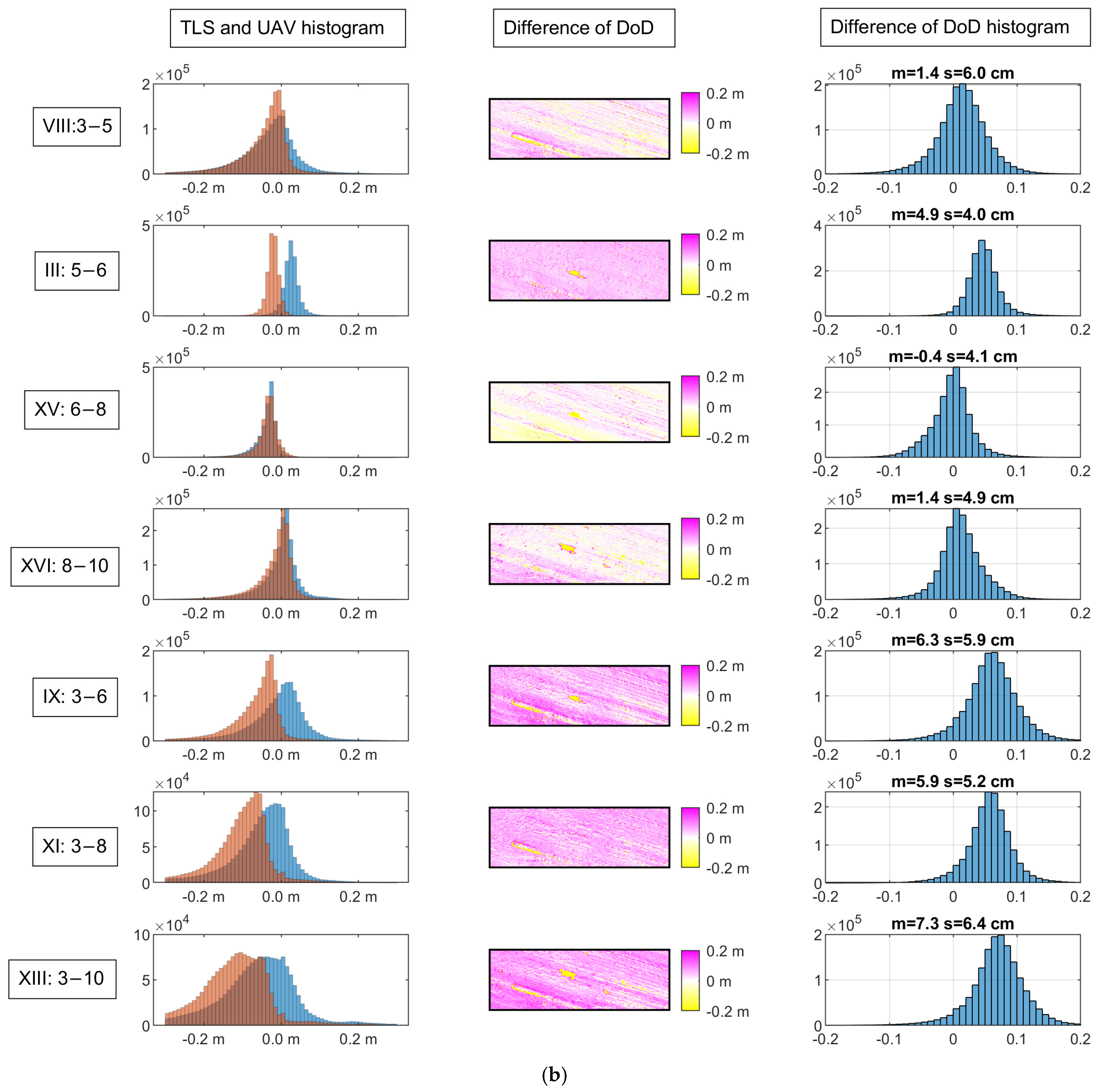
The results can be plotted for all or selected epoch pairs for each ROI. For ROI1—the largest and potentially most representative—the results for selected epoch pairs are shown in Figure 15a,b.

If the changes derived from the UAV were identical to those obtained from the TLS, the histograms (columns 2 and 4 in Figure 15a and column 1 in Figure 15b) would consistently show similar shapes. A shift in the GCPs would likely cause a shift in the surface—at least within a small ROI. Similar histogram shapes indicate that comparable changes were detected, while a shift between the histograms indicates that the detected magnitudes are either over- or underestimated.

The “Difference of DoD” (column 2 in Figure 15b) should ideally appear white, and its histogram on the right should follow a standard normal distribution representing the sum of the random errors of both methods. A uniform color in the “Diff of DoD” visualization indicates a consistent offset across the entire ROI, likely due to georeferencing discrepancies. Conversely, localized patches in the “Diff of DoD” visualization indicate details that were only captured by one of the two compared methods.

Table 7. Numerical values of comparison of DoDs from UAV and TLS capture of cliff surface of ROI1. Epoch pair stands for epoch pair from Table 2 and Table 3, V+ and V− are positive and negative volume difference, mean is average change over whole region of interest. Corr. coef. is for correlation coefficient between TLS and UAV DoDs and Mean diff. is average difference between UAV and TLS DoDs.

	TLS			UAV
Epoch pair	V+ [m3]	V− [m3]	mean [cm]	V+ [m3]	V− [m3]	mean [cm]	Corr. coef.	Mean diff. [cm]
VIII: 3–5	4.73	−45.5	−6.03	10.81	−42.01	−4.61	0.911	1.4
III: 5–6	0.97	−17.5	−2.44	18.86	−2.56	2.41	0.431	4.9
XV:6–8	0.82	−29.28	−4.21	0.65	−31.88	−4.62	0.711	−0.4
XVI: 8–10	6.52	−21.31	−2.19	11.33	−16.37	−0.74	0.761	1.4
IX: 3–6	2.98	−60.28	−8.47	17.35	−32.25	−2.2	0.914	6.3
XI: 3–8	2.63	−88.39	−12.68	7	−53.13	−6.82	0.938	5.9
XIII: 3–10	3.75	−104.29	−14.87	11.62	−62.79	−7.57	0.921	7.3

shows numerical values for the data from Figure 15a,b. V+ stands for a positive change in volume (sedimentation), V- for a negative change in volume (erosion) and mean value for the average change in height over the entire area of ROI1. The correlation coefficient between the two DoDs and the average difference between them are also calculated.

4. Discussion

4.1. RTK and Autonomous Positioning of UAV Surveys

According to the results listed in Table 5 and Table 6 and due to the severe limitations in setting GCPs, direct georeferencing, whether RTK or PPK, is the only option. With autonomous solutions, the position error can easily exceed 1 m at a distance of more than 50 m from the GCPs.

In the case of direct georeferencing, the results (Table 5 upper part) show that no GCPs are required. However, some of our other cases prove the opposite. The height component is especially vulnerable. The use of GCPs is highly advisable, as also mentioned in Liu et al. [18]. The geometric distribution should be similar over the whole observed area. As already mentioned, this task is impossible to fulfill on steep cliff walls. Therefore, the GCPs should be placed at least on the accessible lower parts of the cliffs.

4.2. UAV Surveys

UAV surveys can be carried out in the nadir or oblique manner. Nadir imagery may miss some topographic features in steep terrain. In addition, there are large differences in the scales of the captured images. Therefore, oblique imaging is preferred for steep rock faces. To capture the terrain at a similar GSD, the drone should fly at a similar distance from the wall. The drone used was able to fly and capture images perpendicular to the target surface.

After SfM/MVS processing, UAV photogrammetry delivers various products that are suitable for comparisons, analyzes and visualizations. Point clouds, meshes or DTMs can be used for terrain comparisons, whether at different epochs using the same technique or in conjunction with TLS. With the results of periodic UAV surveys, rockfalls can be easily identified.

4.3. Comparison Between UAV and TLS Results

The results only for the largest and most representative area, ROI1, are presented in Figure 15a,b and Table 7. Epoch pairs were selected where the TLS and UAV measurements were close in time. The pair of epochs to be compared is indicated on the left-hand side of Figure 15a,b.

The first column in Figure 15a shows the detected changes (DoD) for TLS technology; the third column shows the same for the UAV. The second and fourth columns contain the histograms of the DoD changes. In the TLS histograms, we find that most of the changes are negative, which is to be expected for a steep cliff where large amounts of material cannot accumulate. However, in ROI1 there is a section of scree below the cliff where material can accumulate. The average values of the histograms increase with the increasing time interval between the epochs (see also Table 7, column “TLS mean”).

The fourth column in Figure 15a shows the DoD histograms for the UAV method. The first row (3–5) is very similar to the TLS data. In the second row (5–6), however, there is a clear discrepancy, with UAV showing a change of 4.3 cm (see Table 7, column “Mean diff.”), which is quite surprising and probably due to a shift in the GCPs. For epoch pairs 6–8 and 8–10, the changes are again almost identical to TLS (see Table 7). In the last three rows (3–6, 3–8 and 3–0), a consistent offset of 6–7 cm is observed. These three discrepancies are probably due to a shift in GCPs between epochs 5 and 6, which is reflected in all epoch pairs where the first epoch is smaller than 5 and the second epoch is larger than 6.

The standard deviations of the differences between the UAV and TLS DoDs (columns 2 and 3 in Figure 15b) are consistently around 5 cm, which indicates the sum of the accuracies of both measurement methods. So, even if there is an absolute difference (probably due to georeferencing), the dispersion of the differences remains constant, which means that both methods captured the same surface shape. This suggests that there are no internal distortions or errors, which is promising for the use of UAVs. However, greater caution is required with GCPs.

Looking specifically at the three consistent epoch pairs (3–5, 6–8, 8–10), the average differences are only 14, −4 and 14 mm, respectively, with dispersions of 60, 41 and 49 mm. For the pairs with offsets (5–6, 3–6, 3–8, 3–10), the average differences are 49, 63, 59 and 73 mm, respectively, indicating that a shift has probably occurred between epochs 3 and 5 (14 mm). Otherwise, the offset is consistent. There is no clear trend in the dispersion of differences. The most plausible explanation is that the dispersion is simply the sum of the random errors of both acquisition methods.

5. Conclusions

Detecting changes in steep terrain, such as cliffs, is a challenging endeavor. First of all, ground targets must be set. We have established a closed geodetic traverse with a combination of GNSS and TPS surveying to ensure the highest possible accuracy and quality control. The UAV flight must be carried out in direct georeferencing mode (RTK or PPK). For steep rock faces, the use of a special flight mode that follows the terrain and captures oblique images is very advantageous compared to normal flight at a constant altitude and nadir imaging.

The TLS survey of cliffs is even more demanding. The flat area at the foot of the cliffs is usually too narrow to obtain a proper viewpoint for the TLS. Bays and straits have better potential for cliff TLS surveys. But in such cases, the range of the TLS is a limiting factor. Also, accuracy and resolution decrease with distance. We surveyed part of the cliffs with UAV and TLS. To mitigate other interfering factors, such as vegetation, the area was divided into different ROIs. To keep the article within a manageable scope, only one ROI is presented with results. The comparison (see Section 4.3) shows some small discrepancies between the two surveying methods but generally leads to similar trends. Considering the limitations of setting up TLS and a UAV open space with the option to fly close to the cliff faces, it can be concluded that UAV is more suitable for cliff surveying.

In any case, several restrictions must be considered when surveying. Accessibility is usually the most limiting factor. When surveying by UAV, rain, wind and tides must be taken into account. Some parts of our case study can only be reached at low tide. Vegetation is another issue. For this reason, we conducted the surveys in early spring and late fall or early winter when the foliage is at its lowest. Not to forget, the cliffs, unlike most other rocks, are active. There is constant erosion caused by rain, seawater and wind. The erosion sometimes leads to a rockfall. Even if a GCP is set to the highest accuracy, the actual location can shift due to erosion or be destroyed by a rockfall.

Traditional surveying methods, such as GNSS and TPS, face even more limitations when surveying steep and rugged terrain. The inaccessibility of most of the surveyed area is the biggest setback. The other significant downside is the speed of point capture. TLS and especially UAV overcome both shortcomings with ease.

In the future, we will continue the surveys to determine the average rate of erosion-induced changes. During the upcoming surveys, we will try different capturing methods, different instruments and additional processing of the acquired data. Laser scanning with a UAV is also on the list of future options. As soon as that is available, we will look into the integration of photogrammetric and laser scanning data.