Exploring the Feasibility of Airfoil Integration on a Multirotor Frame for Enhanced Aerodynamic Performance
Abstract
1. Introduction
1.1. Motivation
- Fixed-wing UAVs have a design similar to traditional airplanes featuring a rigid wing structure. Lift is generated by horizontal airflow flowing over the main wing, while horizontal thrust is provided by motors. The aircraft is navigated using control surfaces such as ailerons, elevators, and rudders;
- Rotary-wing UAVs can be categorized as either multirotor or single-rotor. These rely on rotors for both lift and control, which enables them to hover in one place and perform vertical takeoff and landing (VTOL) unlike the fixed-wing UAVs. However, this advantage comes with a trade-off: rotary-wing UAVs typically have shorter flight times. Among these, multirotors are the most common type;
- Hybrids, as the name suggests, combine features of fixed-wing and rotary-wing UAVs, commonly using the fixed-wing configuration for cruise flight and rotary-wing configuration for takeoff, hover, and landing.
1.2. Objective
1.3. Research Contributions
- A novel investigation into the integration of airfoil-shaped arms in a multirotor UAV to enhance aerodynamic efficiency;
- CFD analysis comparing a standard quadrotor frame with an airfoil-integrated design, assessing aerodynamic benefits;
- A detailed evaluation of the impact of airfoil integration on downforce, drag, and flight time across different flight conditions;
- A methodology for designing and implementing airfoil structures in multirotor UAV frames without increasing structural complexity;
- Insights into the potential applications of airfoil-integrated UAVs in military, agricultural, and industrial settings, emphasizing efficiency improvements.
2. Multirotor UAV Development Considerations
2.1. UAV Component Selection
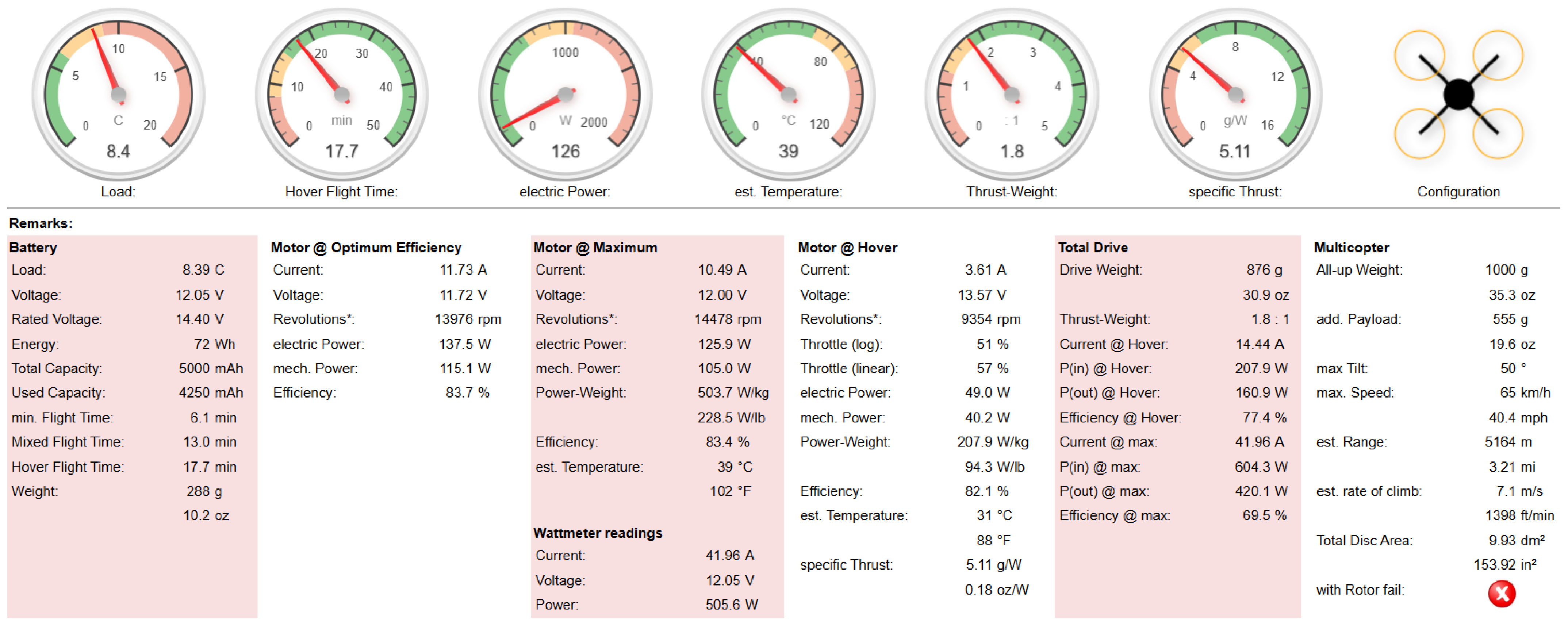
2.2. eCalc Simulator
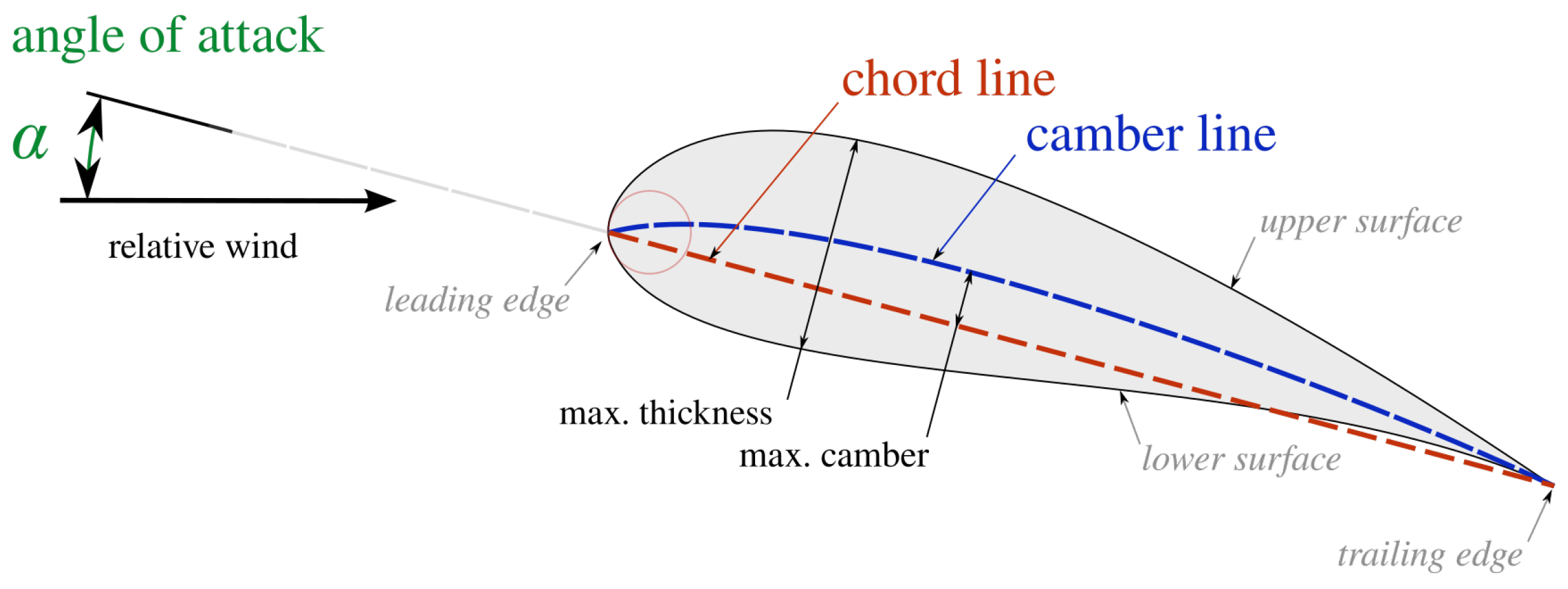
2.3. Airfoil Design and Selection
- Leading edge—at the front of the airfoil;
- Trailing edge—at the rear of the airfoil;
- Chord line—defined by drawing a straight line from the leading edge to the trailing edge;
- Camber line—represents the center line between the upper and lower surfaces;
- Angle of attack (AoA)—the angle between the chord line and the relative wind direction.
- = drag force [N];
- = lift force [N];
- = density of the fluid [kg/m3];
- v = fluid velocity relative to the body [m/s];
- A = reference cross-sectional area [m2].

2.3.1. Flow Visualization and Separation

2.3.2. NACA Airfoils
2.4. Computational Fluid Dynamics
Process Description
- Define the physics of the simulation, including compressibility, hydrostatic pressure, heat transfer, gravity, turbulence, humidity, cavitation, solar heating, and free surfaces.
- Define the analysis parameters, including steady-state or transient conditions, set the number of iterations, specify the size of time steps, and determine save intervals.
- Utilize optional “adaptation functions” to progressively enhance the mesh by conducting the simulation multiple times. After each run, the adaptation process modifies the mesh based on the results, and the updated mesh is used for the next cycle. This approach results in a mesh that is optimized for the specific simulation, featuring finer resolution in high-gradient areas and coarser resolution in other regions.
3. UAV Development—Standard Frame
3.1. UAV Propulsion Components
3.2. eCal Performance Estimates
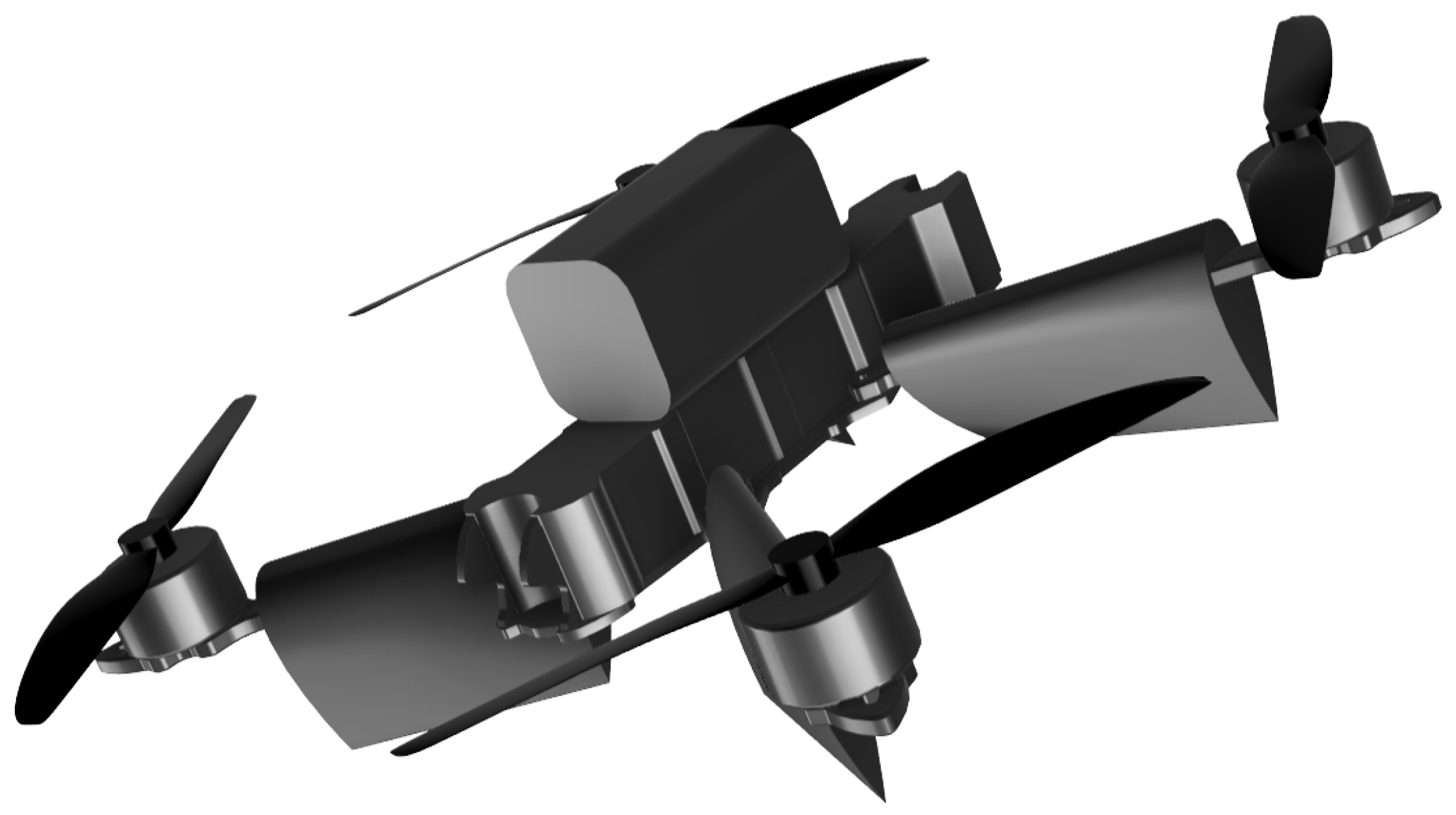
4. UAV Improvement—Airfoil Frame
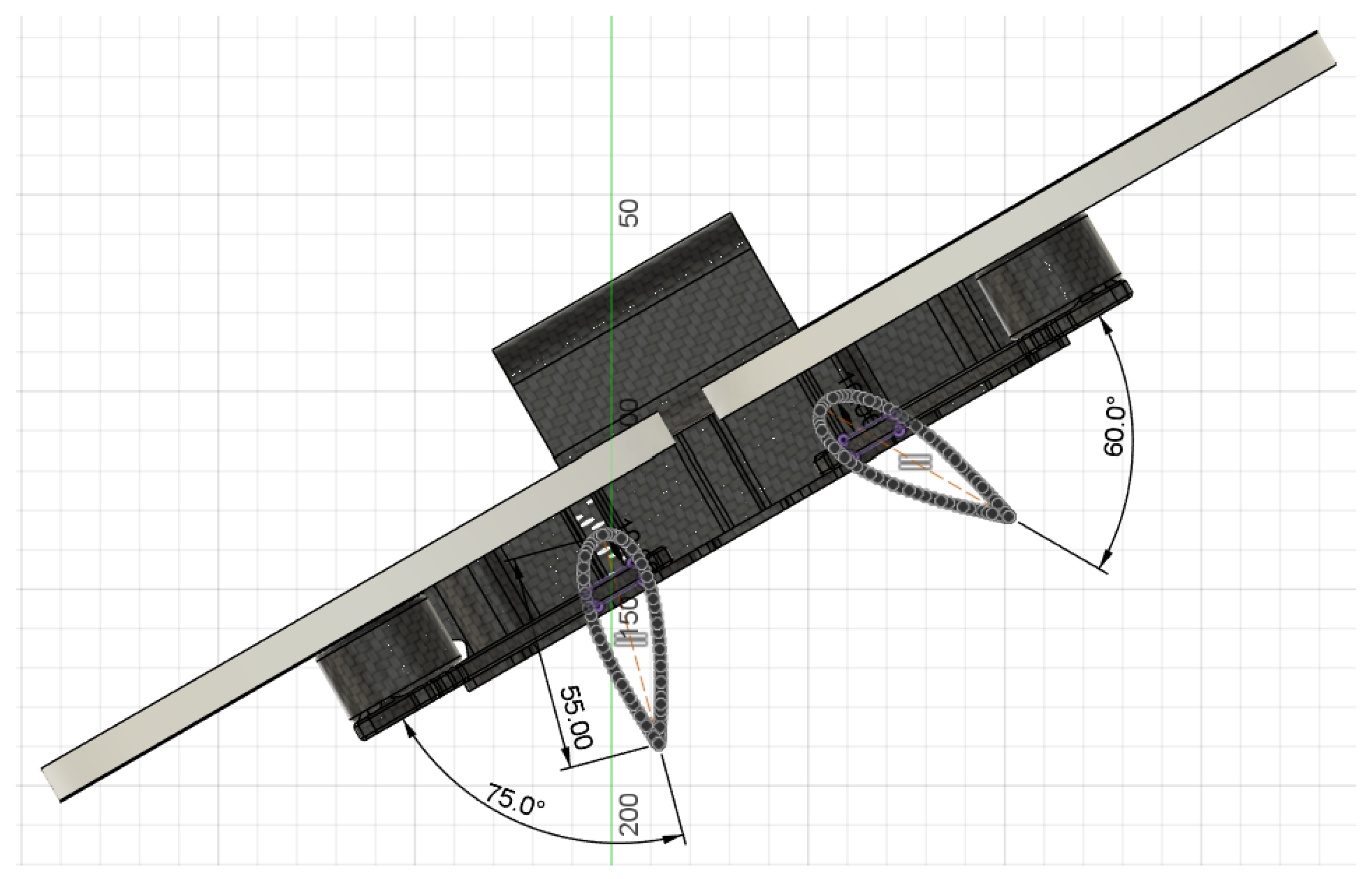
4.1. Simulated Flight Conditions
4.2. Airfoil Selection and Implementation
- Simple geometry, which allows for easy manufacturing and modification;
- Robust performance across various conditions;
- Less sensitivity to surface imperfections compared to more advanced airfoils, making them suitable for 3D printing, which will be the method used for future real-world tests;
- Predictable and gentle stall characteristics, resulting in a gradual loss of lift rather than a sudden drop, thus ensuring stability when the flow around the arms changes.
- Thick airfoil design, more specifically 30% thickness, which not only covers the entire frame arm but also enhances structural strength;
- Higher AoA before stalling compared to thinner airfoils, which is beneficial for this scenario because it helps to avoid flow separation and consequent extra drag;
- A symmetrical shape, which is well suited for high Reynolds numbers, where turbulent flow is predominant, such as below UAV’s propellers. Additionally, the airfoil produces no pitching moment when the AoA is zero, ensuring consistent behavior, and it performs similarly whether the airflow is in a positive or negative AoA.
4.3. Airframe CFD Study Process Description
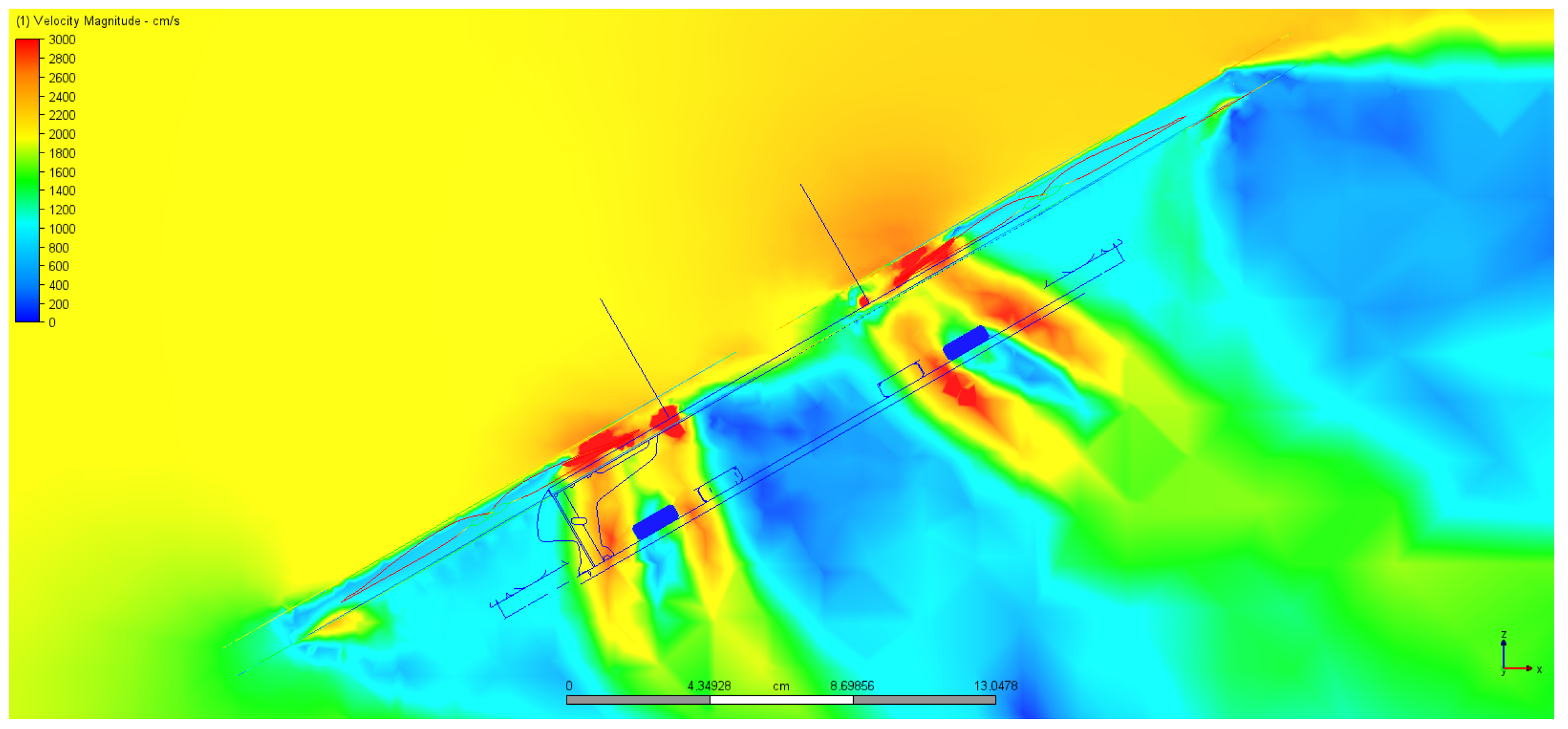
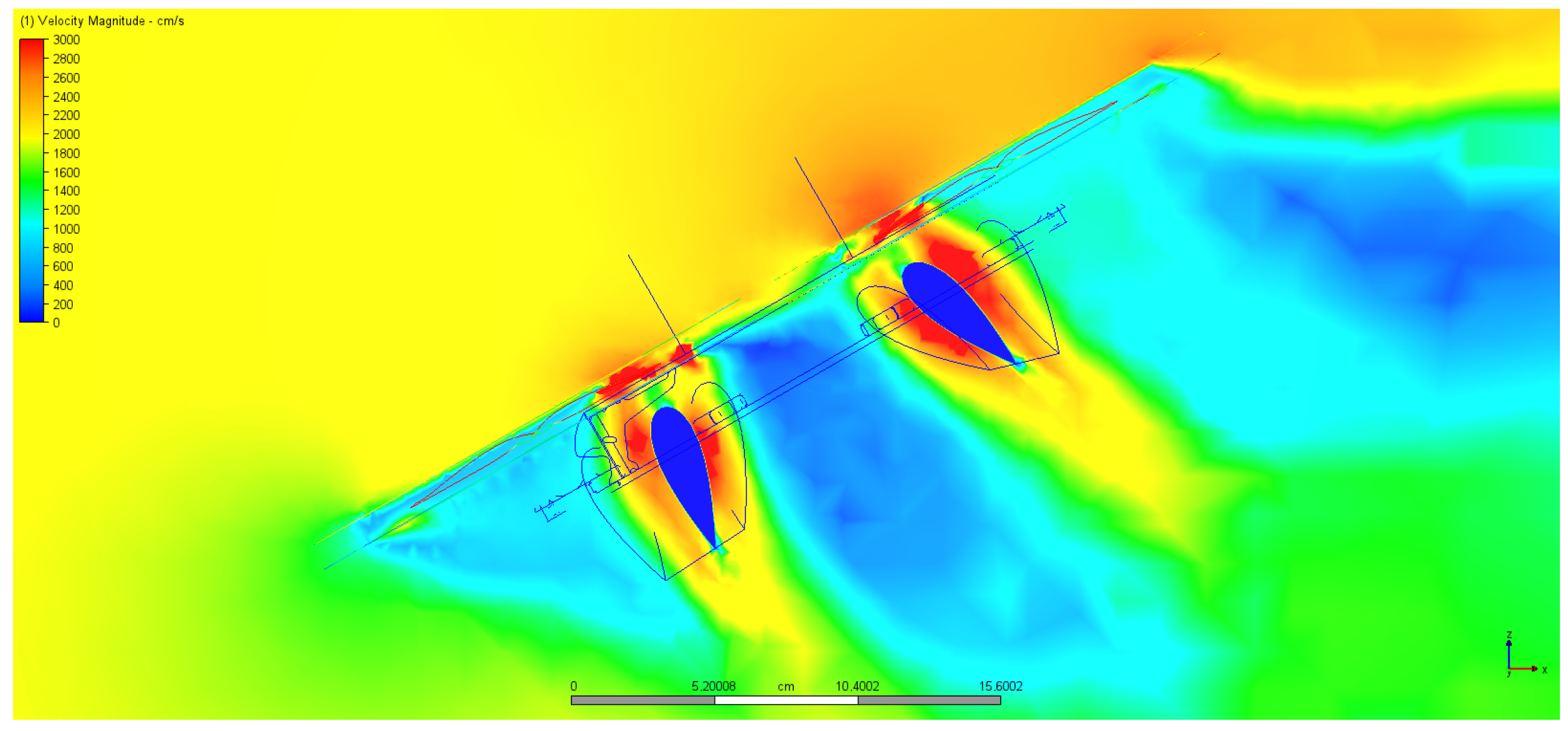
5. Results
5.1. Processing of CFD Simulations Results
5.1.1. Frameless UAV
- = −5.779 N (negative, meaning forward thrust);
- = 0.003 N (approximately zero as expected due to the symmetry of the simulation);
- = 10.420 N (positive, meaning upward thrust).
5.1.2. Standard Frame UAV
- = −4.223 N (negative, meaning forward thrust);
- = −0.084 N (approximately zero as expected due to the symmetry of the simulation);
- = 9.389 N (positive, meaning upward thrust).
5.1.3. Airfoil Frame UAV
- = −3.818 N (negative, meaning forward thrust);
- = −0.092 N (approximately zero as expected due to the symmetry of the simulation);
- = 10.523 N (positive, meaning upward thrust).
5.2. CFD Simulations and Processed Results
5.2.1. Horizontal Flight—Varying External Airflow Speed with Fixed Propeller Rotation
5.2.2. Horizontal Flight—Varying Propeller Rotation with Fixed External Airflow
5.2.3. Leveled Flight—Varying External Airflow Speed with Fixed Propeller Rotation
5.2.4. Leveled Flight—Varying Propeller Rotation with Fixed External Airflow
6. Simulation Result Analysis
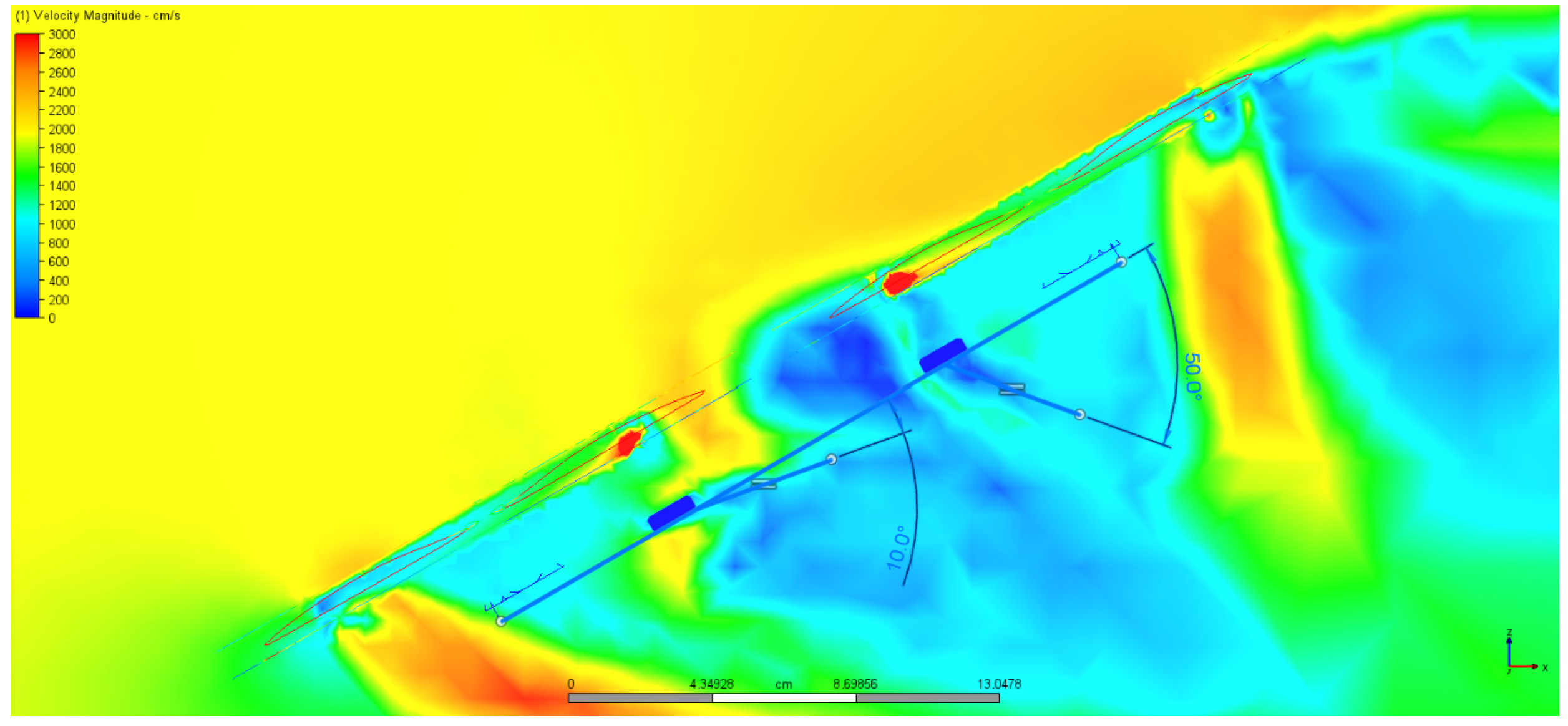
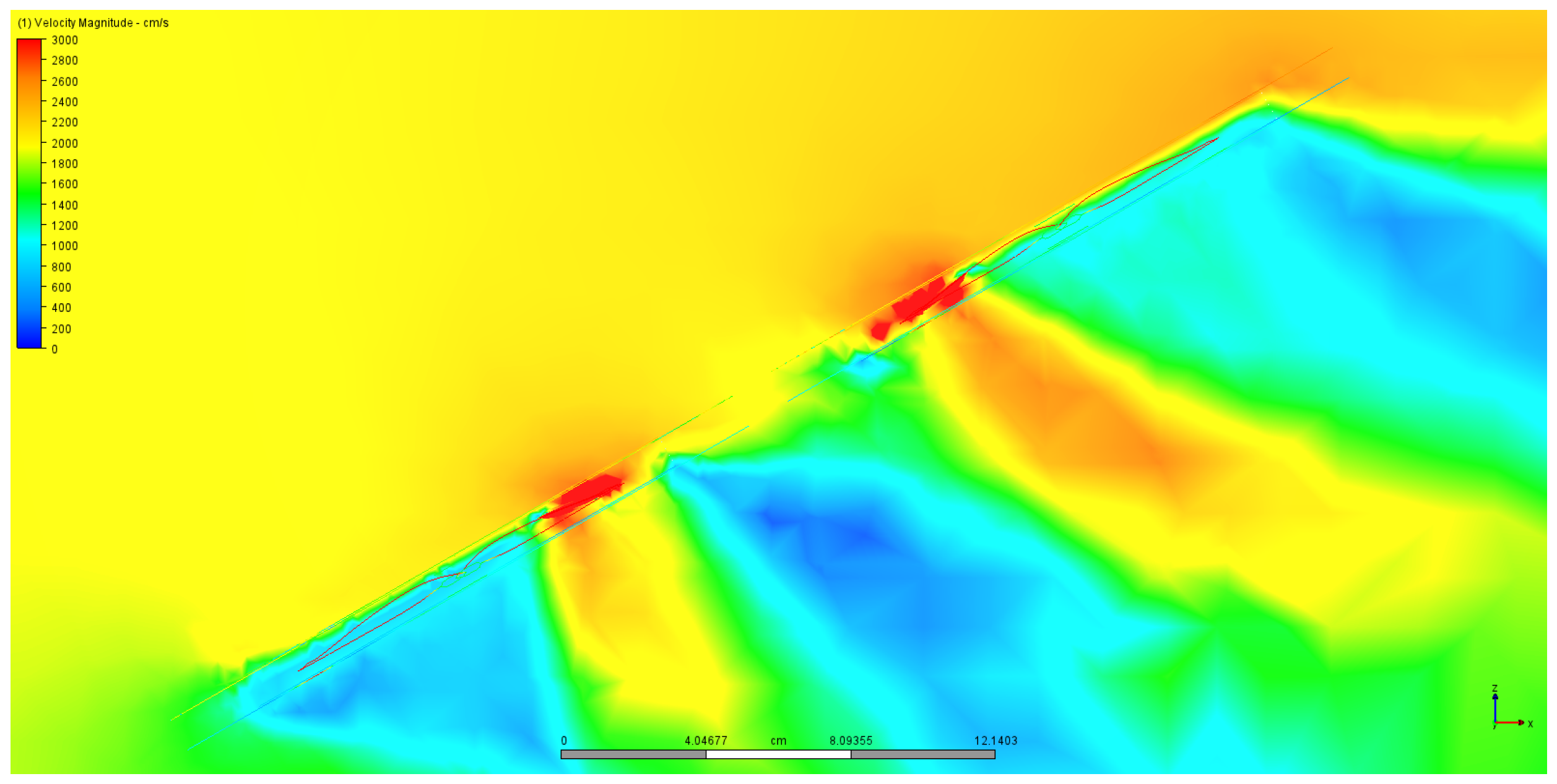
6.1. Horizontal Flight—Lift/Downforce Analysis
6.2. Horizontal Flight—Drag Analysis
- —horizontal component of the maximum UAV propellers’ thrust;
- D—drag of the UAV;
- m—mass of the UAV;
- a—acceleration of the UAV.
6.3. Leveled Flight—Lift/Downforce Analysis
6.4. Leveled Flight—Horizontal Forces Analysis
7. Conclusions
- Demonstrated that modifying UAV arms with airfoil shapes can enhance aerodynamic efficiency without major structural changes;
- Provided a comparative evaluation of a standard quadrotor frame and an airfoil-integrated design through CFD-based aerodynamic analysis, highlighting differences in drag and downforce;
- Showed that airfoil arms significantly reduce downforce, leading to lower effective weight on the motors and reducing overall power consumption;
- Proposed a systematic approach to incorporating airfoil structures into UAV frames while maintaining structural simplicity and manufacturability.
- Highlighted how airfoil-integrated UAVs could benefit fields such as military reconnaissance, agriculture, and industrial inspections, where extended flight duration is critical.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
DURC Statement
Conflicts of Interest
Appendix A. UAV Propulsion-Related Components
Appendix A.1. Frame
Appendix A.2. Propellers
Appendix A.3. Motors
Appendix A.4. Electronic Speed Controller
Appendix A.5. Battery
Appendix B. NACA Airfoil Families

- x = coordinate along the length of the airfoil, from 0 to c (which stands for chord length);
- = camber coordinates.
| Family | Advantages | Disadvantages | Applications |
|---|---|---|---|
| 4-Digit | 1. Good stall characteristics 2. Small center of pressure movement across large speed range 3. Roughness has little effect | 1. Low maximum lift coefficient 2. Relatively high drag 3. High pitching moment | 1. General aviation 2. Horizontal tails Symmetrical: 3. Supersonic jets 4. Helicopter blades 5. Shrouds 6. Missile/rocket fins |
| 5-Digit | 1. Higher maximum lift coefficient 2. Low pitching moment 3. Roughness has little effect | 1. Poor stall behavior 2. Relatively high drag | 1. General aviation 2. Piston-powered bombers, transports 3. Commuters 4. Business jets |
| 16-Series | 1. Avoids low-pressure peaks 2. Low drag at high speed | 1. Relatively low lift | 1. Aircraft propellers 2. Ship propellers |
| 6-Series | 1. High maximum lift coefficient 2. Very low drag over a small range of operating conditions 3. Optimized for high speed | 1. High drag outside of the optimum range of operating conditions 2. High pitching moment 3. Poor stall behavior 4. Very susceptible to roughness | 1. Piston-powered fighters 2. Business jets 3. Jet trainers 4. Supersonic jets |
| 7-Series | 1. Very low drag over a small range of operating conditions 2. Low pitching moment | 1. Reduced maximum lift coefficient 2. High drag outside of the optimum range of operating conditions 3. Poor stall behavior 4. Very susceptible to roughness | Seldom used |
| 8-Series | Unknown | Unknown | Very seldom used |
Appendix C. Manufacturing Process
Appendix D. Mesh Sensitivity Study
| Element Count (Horizontal Flight) | |||
|---|---|---|---|
| Frame | Mesh Refinement Factor | ||
| 1 | 0.7 | Difference [%] | |
| Frameless | 439,447 | 971,060 | 121.0 |
| Standard Frame | 3,098,588 | 5,294,369 | 70.9 |
| Airfoil Frame | 2,988,214 | 4,919,442 | 64.6 |
| Element Count (Leveled Flight) | |||
|---|---|---|---|
| Frame | Mesh Refinement Factor | ||
| 1 | 0.7 | Difference [%] | |
| Frameless | 430,154 | 948,855 | 120.6 |
| Standard Frame | 2,809,963 | 5,067,615 | 80.3 |
| Airfoil Frame | 2,622,667 | 4,339,435 | 65.5 |
| Horizontal Flight | ||||
|---|---|---|---|---|
| Force | Frame | Mesh Refinement Factor | Difference [%] | |
| 1 | 0.7 | |||
| Fx [N] | Frameless | −5.779 | −5.650 | 2.2 |
| Standard Frame | −4.223 | −4.282 | 1.4 | |
| Airfoil Frame | −3.818 | −3.945 | 3.3 | |
| Fy [N] | Frameless | 0.003 | −0.008 | - |
| Standard Frame | −0.084 | −0.009 | - | |
| Airfoil Frame | −0.092 | −0.003 | - | |
| Fz [N] | Frameless | 10.420 | 10.231 | 1.8 |
| Standard Frame | 9.389 | 9.515 | 1.3 | |
| Airfoil Frame | 10.523 | 10.845 | 3.1 | |
| Average | 2.2 | |||
| Leveled Flight | ||||
|---|---|---|---|---|
| Force | Frame | Mesh Refinement Factor | Difference [%] | |
| 1 | 0.7 | |||
| Fx [N] | Frameless | 0.027 | 0.031 | - |
| Standard Frame | −0.003 | −0.091 | - | |
| Airfoil Frame | −0.371 | −0.290 | - | |
| Fy [N] | Frameless | 0.023 | −0.032 | - |
| Standard Frame | 0.052 | 0.012 | - | |
| Airfoil Frame | 0.153 | −0.042 | - | |
| Fz [N] | Frameless | 14.377 | 14.245 | 0.9 |
| Standard Frame | 12.551 | 12.483 | 0.5 | |
| Airfoil Frame | 13.247 | 13.841 | 4.5 | |
| Average | 2.0 | |||
Appendix E. Turbulence Model Verification
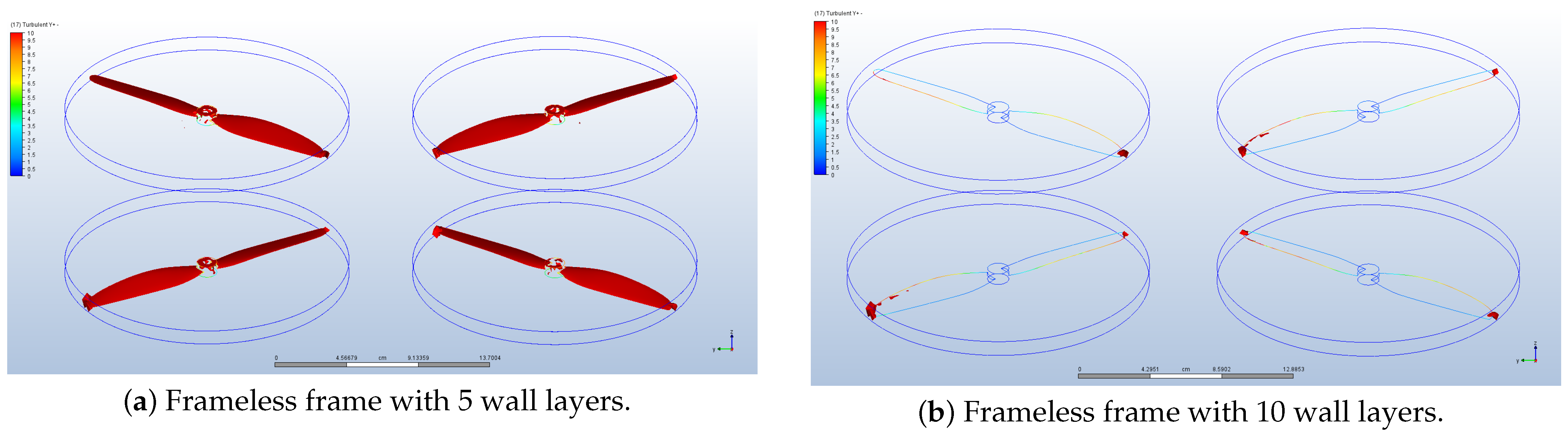

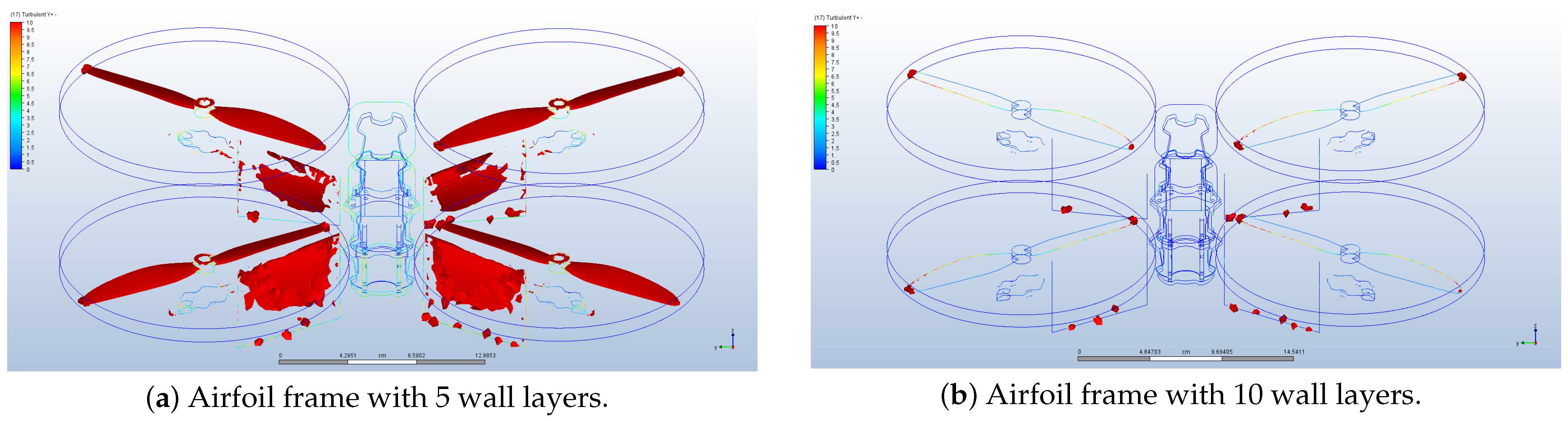
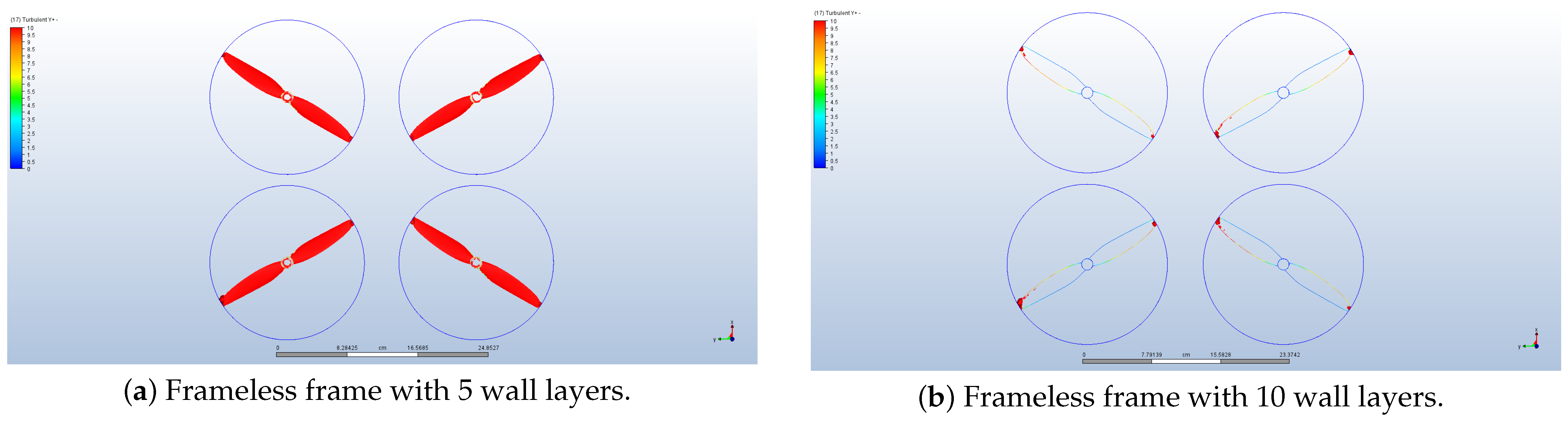
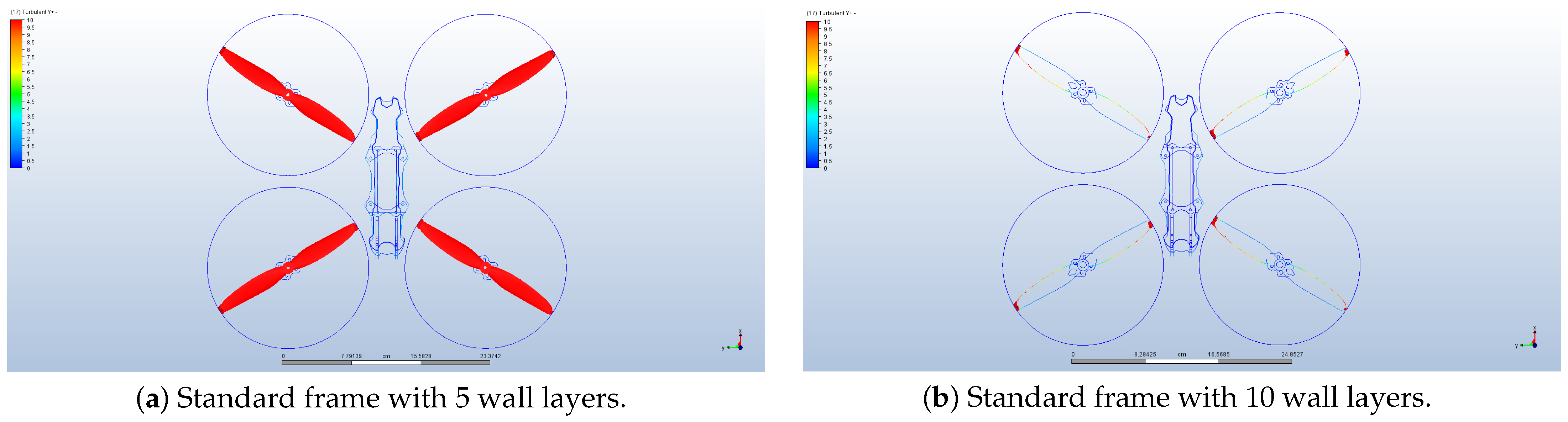

| Horizontal Flight | ||||||
|---|---|---|---|---|---|---|
| Force | Frame | Wall Layers | Difference [%] | Average per Axis [%] | Total Average [%] | |
| 5 | 10 | |||||
| Fx [N] | Frameless | −5.779 | −6.203 | 7.3 | 8.4 | 6.4 |
| Standard Frame | −4.223 | −4.576 | 8.4 | |||
| Airfoil Frame | −3.818 | −4.177 | 9.4 | |||
| Fy [N] | Frameless | 0.003 | 0.036 | - | - | |
| Standard Frame | −0.084 | −0.033 | - | |||
| Airfoil Frame | −0.092 | −0.049 | - | |||
| Fz [N] | Frameless | 10.420 | 10.883 | 4.4 | 4.4 | |
| Standard Frame | 9.389 | 9.926 | 5.7 | |||
| Airfoil Frame | 10.523 | 10.838 | 3.0 | |||
| Leveled Flight | ||||||
|---|---|---|---|---|---|---|
| Force | Frame | Wall Layers | Difference [%] | Average per Axis [%] | Total Average [%] | |
| 5 | 10 | |||||
| Fx [N] | Frameless | 0.027 | 0.013 | - | - | 7.1 |
| Standard Frame | −0.003 | 0.199 | - | |||
| Airfoil Frame | −0.371 | −0.246 | - | |||
| Fy [N] | Frameless | 0.023 | 0.015 | - | - | |
| Standard Frame | 0.052 | 0.031 | - | |||
| Airfoil Frame | 0.153 | 0.065 | - | |||
| Fz [N] | Frameless | 14.377 | 15.580 | 8.4 | 7.1 | |
| Standard Frame | 12.551 | 13.398 | 6.7 | |||
| Airfoil Frame | 13.247 | 14.054 | 6.1 | |||
| Element Count (Horizontal Flight) | ||||
|---|---|---|---|---|
| Frame | Wall Layers | Difference [%] | Average [%] | |
| 5 | 10 | |||
| Frameless | 439,447 | 496,226 | 12.9 | 11.2 |
| Standard Frame | 3,098,588 | 3,434,247 | 10.8 | |
| Airfoil Frame | 2,988,214 | 3,282,803 | 9.9 | |
| Element Count (Leveled Flight) | ||||
|---|---|---|---|---|
| Frame | Wall Layers | Difference [%] | Average [%] | |
| 5 | 10 | |||
| Frameless | 430,154 | 492,193 | 14.4 | 12.5 |
| Standard Frame | 2,809,963 | 3,144,662 | 11.9 | |
| Airfoil Frame | 2,622,667 | 2,915,429 | 11.2 | |
References
- Hardin, P.J.; Hardin, T.J. Small-scale remotely piloted vehicles in environmental research. Geogr. Compass 2010, 4, 1297–1311. [Google Scholar] [CrossRef]
- Young, L.; Yetter, J.; Guynn, M. System analysis applied to autonomy: Application to high-altitude long-endurance remotely operated aircraft. In Proceedings of the Infotech@ Aerospace, Arlington, VA, USA, 26–29 September 2005; p. 7103. [Google Scholar]
- Chabot, D. Trends in drone research and applications as the Journal of Unmanned Vehicle Systems turns five. J. Unmanned Veh. Syst. 2018, 6, vi–xv. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Nahiyoon, S.A.; Ren, Z.; Wei, P.; Li, X.; Li, X.; Xu, J.; Yan, X.; Yuan, H. Recent Development Trends in Plant Protection UAVs: A Journey from Conventional Practices to Cutting-Edge Technologies—A Comprehensive Review. Drones 2024, 8, 457. [Google Scholar] [CrossRef]
- Frachtenberg, E. Practical drone delivery. Computer 2019, 52, 53–57. [Google Scholar] [CrossRef]
- Viana, J.; Cercas, F.; Correia, A.; Dinis, R.; Sebastião, P. MIMO Relaying UAVs Operating in Public Safety Scenarios. Drones 2021, 5, 32. [Google Scholar] [CrossRef]
- Álvarez González, M.; Suarez-Bregua, P.; Pierce, G.J.; Saavedra, C. Unmanned Aerial Vehicles (UAVs) in Marine Mammal Research: A Review of Current Applications and Challenges. Drones 2023, 7, 667. [Google Scholar] [CrossRef]
- Munawar, H.S.; Ullah, F.; Heravi, A.; Thaheem, M.J.; Maqsoom, A. Inspecting Buildings Using Drones and Computer Vision: A Machine Learning Approach to Detect Cracks and Damages. Drones 2022, 6, 5. [Google Scholar] [CrossRef]
- Pan, L.; Song, C.; Gan, X.; Xu, K.; Xie, Y. Military Image Captioning for Low-Altitude UAV or UGV Perspectives. Drones 2024, 8, 421. [Google Scholar] [CrossRef]
- Rennie, J. Drone Types: Multi-Rotor vs. Fixed-Wing vs. Single Rotor vs. Hybrid Vtol. AUAV Com 2016, 19, 2024. [Google Scholar]
- Ducard, G.J.; Allenspach, M. Review of designs and flight control techniques of hybrid and convertible VTOL UAVs. Aerosp. Sci. Technol. 2021, 118, 107035. [Google Scholar] [CrossRef]
- Kunertova, D. The war in Ukraine shows the game-changing effect of drones depends on the game. Bull. At. Sci. 2023, 79, 95–102. [Google Scholar] [CrossRef]
- Seo, K.I.; Cho, S.K.; Park, S.H. A Case Study on FPV Drone Combats of the Ukrainian Forces. J. Converg. Cult. Technol. 2023, 9, 263–270. [Google Scholar]
- Stewart, M.; Martin, S.; Barrera, N. Unmanned aerial vehicles: Fundamentals, components, mechanics, and regulations. Unmanned Aer. Veh. 2021, 3, 1–70. [Google Scholar]
- Liu, R.l.; Zhang, Z.j.; Jiao, Y.f.; Yang, C.h.; Zhang, W.j. Study on Flight Performance of Propeller-Driven UAV. Int. J. Aerosp. Eng. 2019, 2019, 6282451. [Google Scholar] [CrossRef]
- Biczyski, M.; Sehab, R.; Whidborne, J.F.; Krebs, G.; Luk, P. Multirotor sizing methodology with flight time estimation. J. Adv. Transp. 2020, 2020, 9689604. [Google Scholar] [CrossRef]
- Nagel, L. How Does Drone Payload Affect Flight Time. 2024. Available online: https://www.tytorobotics.com/blogs/articles/how-does-drone-payload-affect-flight-time (accessed on 12 September 2024).
- Kumar, V.A.; Sivaguru, M.; Janaki, B.R.; Eswar, K.S.; Kiran, P.; Vijayanandh, R. Structural optimization of frame of the multi-rotor unmanned aerial vehicle through computational structural analysis. In Proceedings of the Journal of Physics: Conference Series, Volume 1849, 2nd National Conference on Recent Advancement in Physical Sciences, (NCRAPS) 2020, Uttarakhand, India, 19–20 December 2020; Volume 1849, p. 012004. [Google Scholar]
- Müller, M. eCalc: The Most Reliable RC Calculator on the Web. Online Resource. 2014. Available online: https://www.ecalc.ch (accessed on 12 February 2025).
- Eppler, R. Airfoil Design and Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jha, D.; Singh, M.; Thakur, A. A novel computational approach for design and performance investigation of small wind turbine blade with extended BEM theory. Int. J. Energy Environ. Eng. 2021, 12, 563–575. [Google Scholar] [CrossRef]
- AirShaper. Fundamentals of Airfoil Design and Selection. Available online: https://airshaper.com/videos/airfoil-design-for-a-drone/kAXN3MlQxxc (accessed on 11 September 2024).
- Anderson, J. A History of Aerodynamics: And Its Impact on Flying Machines; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- LaNasa, P.J.; Upp, E.L. 2—Basic Flow Measurement Laws. In Fluid Flow Measurement, 3rd ed.; LaNasa, P.J., Upp, E.L., Eds.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 19–29. [Google Scholar] [CrossRef]
- Haryanto, I.; Utomo, T.S.; Sinaga, N.; Rosalia, C.A.; Putra, A.P. Optimization of maximum lift to drag ratio on airfoil design based on artificial neural network utilizing genetic algorithm. Appl. Mech. Mater. 2014, 493, 123–128. [Google Scholar] [CrossRef]
- HopsonRoad. Coefficient of Lift (CL) and Coefficient of Drag (CD) and Their Ratio as a Function of Angle of Attack for a Hypothetical Sail. The Status of Flow Between Attached to Separated is Shown in Relation to the Curve. Available online: https://commons.wikimedia.org/wiki/File:Coefficients_of_Lift_and_Drag_for_a_Hypothetical_Sail.png#file (accessed on 12 February 2025).
- Kay, N.J.; Richards, P.J.; Sharma, R.N. Influence of turbulence on cambered and symmetrical airfoils at low Reynolds numbers. AIAA J. 2020, 58, 1913–1925. [Google Scholar] [CrossRef]
- Merzkirch, W. Flow Visualization; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Chang, P.K. Separation of Flow; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Prandtl, L.; Oswatitsch, K.; Wieghardt, K. Flugkörper, Antriebe und Strömungsmaschinen. In Führer Durch die Strömungslehre; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1990; pp. 430–524. [Google Scholar] [CrossRef]
- Abbott, I.H.; Von Doenhoff, A.E.; Stivers, L., Jr. Summary of Airfoil Data. Technical Report, National Advisory Committee for Aeronautics (NACA), 1945. Report No.: NACA Report No. 824. Available online: https://ntrs.nasa.gov/citations/19930090976 (accessed on 12 February 2025).
- Anderson, J.D.; Wendt, J. Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1995; Volume 206. [Google Scholar]
- Kopal, Z. Tables of Supersonic Flow Around Cones; Number 1; Massachusetts Institute of Technology: Cambridge, MA, USA, 1947. [Google Scholar]
- Moretti, G.; Abbett, M. A time-dependent computational method for blunt body flows. AIAA J. 1966, 4, 2136–2141. [Google Scholar] [CrossRef]
- Team, A. Autodesk CFD: Simulation Software for Engineering Complex Liquid, Gas, and Air Systems. Version 2024. Available online: https://www.autodesk.com/eu/products/cfd/overview (accessed on 13 November 2024).
- Zhai, Z.J.; Zhang, Z.; Zhang, W.; Chen, Q.Y. Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: Part 1—Summary of prevalent turbulence models. Hvac&R Res. 2007, 13, 853–870. [Google Scholar]
- GEPRC. GEP-Mark4-7 Frame. Available online: https://geprc.com/product/gep-mark4-7-frame/ (accessed on 20 December 2024).
- Gemfan. Gemfan LR 7035-2 for Long Range. Available online: https://www.gfprops.com/product/index/details/id/10785.html (accessed on 20 December 2024).
- T-Motor. F90 2806.5 Long Range Motor 5-6S KV1300. Available online: https://shop.tmotor.com/products/brushless-motor-x8-fpv-drones-f90-2806-5?srsltid=AfmBOoox2djP41i6SgBQwhez03oQTZr8chCSSo_n31AIIdTqwLZFLMUg (accessed on 10 March 2025).
- Holybro. Tekko32 F4 Metal 4in1 65A ESC. Available online: https://holybro.com/products/tekko32-f4-metal-4in1-65a-esc-65a (accessed on 20 December 2024).
- Samsung. Samsung INR21700-50S 5000mAh—35A. Available online: https://www.nkon.nl/pt/rechargeable/li-ion/21700-20700-size/samsung-inr21700-50s-5000mah-35a.html (accessed on 20 December 2024).
- Team, A. Autodesk Fusion: More Than CAD, It’s the Future of Design and Manufacturing. Version 2024. Available online: https://www.autodesk.com/eu/products/fusion-360/overview?term=1-YEAR&tab=subscription (accessed on 13 November 2024).
- Hwang, M.h.; Cha, H.R.; Jung, S.Y. Practical Endurance Estimation for Minimizing Energy Consumption of Multirotor Unmanned Aerial Vehicles. Energies 2018, 11, 2221. [Google Scholar] [CrossRef]
- Tools, A. Airfoil Tools. Available online: http://airfoiltools.com/ (accessed on 12 November 2024).
- Community, A. Connect ESCs and Motors. Available online: https://ardupilot.org/copter/docs/connect-escs-and-motors.html (accessed on 13 September 2024).
- Prusa, J. Prusa Slicer. Available online: https://www.prusa3d.com/page/prusaslicer_424/ (accessed on 19 November 2024).
- Bulota, M.; Budtova, T. Highly porous and light-weight flax/PLA composites. Ind. Crop. Prod. 2015, 74, 132–138. [Google Scholar] [CrossRef]
- Standau, T.; Zhao, C.; Murillo Castellón, S.; Bonten, C.; Altstädt, V. Chemical modification and foam processing of polylactide (PLA). Polymers 2019, 11, 306. [Google Scholar] [CrossRef]
- Xiao, K.; Meng, Y.; Dai, X.; Zhang, H.; Quan, Q. A lifting wing fixed on multirotor UAVs for long flight ranges. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 1605–1610. [Google Scholar]
- Autodesk CFD 2024. Centrifugal Pumps and Axial Fans. Available online: https://help.autodesk.com/view/SCDSE/2024/ENU/?guid=GUID-013A783C-807F-4340-BB8B-16A3AF52EECA (accessed on 13 November 2024).
- Autodesk CFD 2024. Turbulence. Available online: https://help.autodesk.com/view/SCDSE/2024/ENU/?guid=GUID-E9E8ACA1-8D49-4A49-8A35-52DB1A2C3E5F (accessed on 13 November 2024).
- Help, A. Compressible Flow. Available online: https://help.autodesk.com/view/SCDSE/2024/ENU/?guid=GUID-620F44CE-9506-4C48-9E9C-6C689345B008 (accessed on 13 September 2024).
- Help, A. Advection Schemes. Available online: https://help.autodesk.com/view/SCDSE/2024/ENU/?guid=GUID-F691B334-CCE2-47E9-B6C4-21666712C163 (accessed on 13 September 2024).
- Liang, O. Types of Multirotor. 2016. Available online: https://oscarliang.com/types-of-multicopter/ (accessed on 11 September 2024).
- Achtelik, M.; Doth, K.M.; Gurdan, D.; Stumpf, J. Design of a multi rotor MAV with regard to efficiency, dynamics and redundancy. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4779. [Google Scholar]
- Toglefritz, L. Types of Multirotor. Available online: https://toglefritz.com/types-of-multirotor/ (accessed on 18 November 2024).
- Bondyra, A.; Gardecki, S.; Gasior, P.; Giernacki, W. Performance of coaxial propulsion in design of multi-rotor UAVs. In Proceedings of the Challenges in Automation, Robotics and Measurement Techniques: Proceedings of AUTOMATION-2016, Warsaw, Poland, 2–4 March 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 523–531. [Google Scholar]
- Theys, B.; Dimitriadis, G.; Hendrick, P.; De Schutter, J. Influence of propeller configuration on propulsion system efficiency of multi-rotor Unmanned Aerial Vehicles. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 195–201. [Google Scholar]
- Liang, O. The Ultimate Guide to FPV Drone Propellers: How to Choose the Best Props for Your Quadcopter. 2024. Available online: https://oscarliang.com/propellers/ (accessed on 11 September 2024).
- Kovtun, A. Influence of the shape and number of blades on the efficiency of the UAV propeller. Aerosp. Tech. Technol. 2024, 31–37. [Google Scholar] [CrossRef]
- Podsędkowski, M.; Konopiński, R.; Obidowski, D.; Koter, K. Variable Pitch Propeller for UAV-Experimental Tests. Energies 2020, 13, 5264. [Google Scholar] [CrossRef]
- Ramesh, M.; Vijayanandh, R.; Kumar, G.R.; Mathaiyan, V.; Jagadeeshwaran, P.; Kumar, M.S. Comparative structural analysis of various composite materials based unmanned aerial vehicle’s propeller by using advanced methodologies. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Jaipur, India, 5–6 November 2020; IOP Publishing: Bristol, UK, 2021; Volume 1017, p. 012032. [Google Scholar]
- Putra, H.; Fikri, M.; Riananda, D.; Nugraha, G.; Baidhowi, M.; Syah, R. Propulsion selection method using motor thrust table for optimum flight in multirotor aircraft. AIP Conf. Proc. 2020, 2226, 060008. [Google Scholar]
- Uçar, U.U.; Adem, A.; Tanyeri, B. A Multi-Criteria Solution Approach for UAV Engine Selection in Terms of Technical Specification. Bitlis Eren Üniversitesi Fen Bilim. Derg. 2022, 11, 1000–1013. [Google Scholar] [CrossRef]
- Bershadsky, D.; Haviland, S.; Johnson, E.N. Electric multirotor UAV propulsion system sizing for performance prediction and design optimization. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; p. 0581. [Google Scholar]
- Liang, O. Understanding ESCs for FPV Drones: How to Choose the Best Electronic Speed Controller. 2024. Available online: https://oscarliang.com/esc/ (accessed on 11 September 2024).
- Delbecq, S.; Budinger, M.; Ochotorena, A.; Reysset, A.; Defaÿ, F. Efficient sizing and optimization of multirotor drones based on scaling laws and similarity models. Aerosp. Sci. Technol. 2020, 102, 105873. [Google Scholar] [CrossRef]
- Liang, O. Using LiPo Batteries for FPV Drones: Beginner’s Guide with Top Product Recommendations. 2024. Available online: https://oscarliang.com/lipo-battery-guide/ (accessed on 20 December 2024).
- Leishman, J.G. Introduction to Aerospace Flight Vehicles; Embry-Riddle Aeronautical University: Daytona Beach, FL, USA, 2023. [Google Scholar]
- Scott, J. NACA Airfoil Series. Available online: https://aerospaceweb.org/question/airfoils/q0041.shtml (accessed on 19 November 2024).
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Chennakesava, P.; Narayan, Y.S. Fused deposition modeling-insights. In Proceedings of the International Conference on Advances in Design and Manufacturing ICAD&M, Tiruchirappalli, Tamil Nadu, India, 5–7 December 2014; Volume 14, p. 1345. [Google Scholar]
- Rajan, K.; Samykano, M.; Kadirgama, K.; Harun, W.S.W.; Rahman, M.M. Fused deposition modeling: Process, materials, parameters, properties, and applications. Int. J. Adv. Manuf. Technol. 2022, 120, 1531–1570. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, X.; Zhao, W.; Wang, G.; Liu, B. An overview of research on FDM 3D printing process of continuous fiber reinforced composites. J. Phys. Conf. Ser. 2019, 1213, 052037. [Google Scholar] [CrossRef]
- Oktay, T.; Eraslan, Y. Mesh Independence Study on Computational Fluid Dynamics (CFD) Analysis of a Quad-rotor UAV Propeller. In Proceedings of the 3rd International European Conference on Interdisciplinary Scientific Researches, Comrat, Moldova, 15–16 January 2021. [Google Scholar]
- Support, A. How to Manually Perform a Mesh Sensitivity Study in Simulation CFD. Available online: https://www.autodesk.com/support/technical/article/caas/sfdcarticles/sfdcarticles/How-to-manually-perform-a-mesh-sensitivity-study-in-Simulation-CFD.html (accessed on 11 February 2025).
- Davidson, A.A.; Salim, S.M. Wall y+ strategy for modelling rotating annular flow using CFD. In Proceedings of the 2018 International MultiConference of Engineers and Computer Scientists, IMECS 2018, Hong Kong, China, 14–16 March 2018; Newswood Limited: Hong Kong, China, 2018. [Google Scholar]
- Ariff, M.; Salim, S.M.; Cheah, S.C. Wall y+ approach for dealing with turbulent flow over a surface mounted cube: Part 1—low Reynolds number. In Proceedings of the Seventh International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 9–11 December 2009; CSIRO Publishing Melbourne: Melbourne, Australia, 2009; pp. 1–6. [Google Scholar]
- Autodesk CFD 2024. Additional Mesh Adaptation Parameters. Available online: https://help.autodesk.com/view/SCDSE/2024/ENU/?guid=GUID-D074870E-E00C-460C-B611-42B3FABCE418 (accessed on 17 February 2025).
- Support, A. Best Practices for Running a Rotating Region Analysis in Autodesk CFD. Available online: https://www.autodesk.com/support/technical/article/caas/sfdcarticles/sfdcarticles/What-are-the-best-practices-for-running-a-rotating-region-analysis-in-Simulation-CFD.html (accessed on 14 February 2025).
- Autodesk CFD 2024. Wall Layers. Available online: https://help.autodesk.com/view/SCDSE/2024/ENU/?guid=GUID-F9C4DDB4-8111-4F25-8EDE-D7C38B3BAD99 (accessed on 17 February 2025).







| Component | Reasons for Selection | |
|---|---|---|
| Frame | GEPRC MK4 7 inch [38] | Common quadrotor configuration; |
| Simplicity; | ||
| Lightness; | ||
| Carbon fiber (impact-resistant); | ||
| Affordable; | ||
| Largest size acceptable for this mission; | ||
| Propeller | Gemfan LR 7035 2-Blades [39] | Maximum diameter for the selected frame; |
| Low pitch; | ||
| High efficiency; | ||
| Two blades; | ||
| Motor | T-Motor F90 1300 KV [40] | Adequate size for required torque; |
| Low KV for higher efficiency; | ||
| ESC | Holybro Tekko32 F4 Metal 4in1 65A ESC [41] | Metal-cased mosfets for improved heat dissipation; |
| Large maximum current rating; | ||
| Four-in-one configuration (less complexity and lighter); | ||
| Battery | Samsung INR21700-50S 5000 mAh—35A (4S Pack) [42] | Li-ion chemistry (high energy density); |
| Highest capacity and continuous discharge current Li-ion cell available at this time. |
| [N] | [N] | [N] | [N] | [N] | AAW [g] | ||
|---|---|---|---|---|---|---|---|
| 15 m/s External Flow Speed at 20,000 rpm | |||||||
| Frameless | −6.263 | −0.026 | 11.081 | - | - | - | - |
| Standard Frame | −5.126 | −0.036 | 10.36 | 1.137 | 0.676 | −0.721 | 73.5 |
| Airfoil Frame | −5.147 | −0.091 | 11.361 | 1.116 | 0.387 | 0.280 | −28.6 |
| 20 m/s External Flow Speed at 20,000 rpm | |||||||
| Frameless | −5.779 | 0.003 | 10.420 | - | - | - | - |
| Standard Frame | −4.223 | −0.084 | 9.389 | 1.556 | 0.520 | −1.031 | 105.1 |
| Airfoil Frame | −3.818 | −0.092 | 10.523 | 1.961 | 0.383 | 0.103 | −10.5 |
| 25 m/s External Flow Speed at 20,000 rpm | |||||||
| Frameless | −5.080 | 0.002 | 9.231 | - | - | - | - |
| Standard Frame | −2.925 | 0.019 | 8.064 | 2.155 | 0.461 | −1.167 | 119.0 |
| Airfoil Frame | −2.044 | −0.031 | 9.400 | 3.036 | 0.379 | 0.169 | −17.2 |
| [N] | [N] | [N] | [N] | [N] | AAW [g] | ||
|---|---|---|---|---|---|---|---|
| 20 m/s External Flow Speed at 15,000 rpm | |||||||
| Frameless | −2.715 | −0.001 | 4.939 | - | - | - | - |
| Standard Frame | −1.366 | 0.034 | 4.247 | 1.349 | 0.451 | −0.692 | 70.6 |
| Airfoil Frame | −0.779 | −0.034 | 5.066 | 1.936 | 0.378 | 0.127 | −12.9 |
| 20 m/s External Flow Speed at 20,000 rpm | |||||||
| Frameless | −5.779 | 0.003 | 10.420 | - | - | - | - |
| Standard Frame | −4.223 | −0.084 | 9.389 | 1.556 | 0.520 | −1.031 | 105.1 |
| Airfoil Frame | −3.818 | −0.092 | 10.523 | 1.961 | 0.383 | 0.103 | −10.5 |
| 20 m/s External Flow Speed at 25,000 rpm | |||||||
| Frameless | −9.688 | 0.008 | 17.411 | - | - | - | - |
| Standard Frame | −7.780 | −0.024 | 15.906 | 1.908 | 0.638 | −1.505 | 153.5 |
| Airfoil Frame | −7.670 | −0.152 | 17.539 | 2.018 | 0.394 | 0.128 | -13.1 |
| [N] | [N] | [N] | [N] | [N] | AAW [g] | ||
|---|---|---|---|---|---|---|---|
| 5 m/s Descending Flow at 20,000 rpm | |||||||
| Frameless | 0.010 | −0.009 | 14.181 | - | - | - | - |
| Standard Frame | 0.000 | 0.011 | 12.080 | - | - | −2.101 | 214.2 |
| Airfoil Frame | −0.363 | 0.086 | 12.852 | - | - | −1.329 | 135.5 |
| Steady External Flow at 20,000 rpm | |||||||
| Frameless | 0.027 | 0.023 | 14.377 | - | - | - | - |
| Standard Frame | −0.003 | 0.052 | 12.551 | - | - | −1.826 | 186.2 |
| Airfoil Frame | −0.371 | 0.153 | 13.247 | - | - | −1.130 | 115.2 |
| 5 m/s Ascending Flow at 20,000 rpm | |||||||
| Frameless | 0.016 | 0.009 | 14.183 | - | - | - | - |
| Standard Frame | −0.026 | −0.113 | 12.941 | - | - | −1.242 | 126.6 |
| Airfoil Frame | −0.279 | 0.133 | 13.898 | - | - | −0.285 | 29.1 |
| [N] | [N] | [N] | [N] | [N] | AAW [g] | ||
|---|---|---|---|---|---|---|---|
| Steady External Flow at 15,000 rpm | |||||||
| Frameless | 0.005 | −0.010 | 8.308 | - | - | - | - |
| Standard Frame | −0.002 | 0.032 | 7.085 | - | - | −1.223 | 124.7 |
| Airfoil Frame | −0.165 | 0.042 | 7.473 | - | - | −0.835 | 85.1 |
| Steady External Flow at 20,000 rpm | |||||||
| Frameless | 0.027 | 0.023 | 14.377 | - | - | - | - |
| Standard Frame | −0.003 | 0.052 | 12.551 | - | - | −1.826 | 186.2 |
| Airfoil Frame | −0.371 | 0.153 | 13.247 | - | - | −1.130 | 115.2 |
| Steady External Flow at 25,000 rpm | |||||||
| Frameless | 0.014 | −0.013 | 23.054 | - | - | - | - |
| Standard Frame | −0.003 | 0.120 | 19.657 | - | - | −3.397 | 346.4 |
| Airfoil Frame | −0.346 | 0.284 | 20.776 | - | - | −2.278 | 232.3 |
| Lift | |||
|---|---|---|---|
| Flight Condition | Standard Frame [N] | Airfoil Frame [N] | Comparison [%] |
| 15 m/s at 20,000 rpm | −0.721 | 0.280 | 138.8 |
| 20 m/s at 20,000 rpm | −1.031 | 0.103 | 110.0 |
| 25 m/s at 20,000 rpm | −1.167 | 0.169 | 114.5 |
| 20 m/s at 15,000 rpm | −0.692 | 0.127 | 118.4 |
| 20 m/s at 25,000 rpm | −1.505 | 0.128 | 108.5 |
| Average | −1.023 | 0.161 | 118.0 |
| Aerodynamic Added Weight (AAW) | |||
|---|---|---|---|
| Flight Condition | Standard Frame [g] | Airfoil Frame [g] | Comparison [%] |
| 15 m/s at 20,000 rpm | 73.5 | −28.6 | −138.8 |
| 20 m/s at 20,000 rpm | 105.1 | −10.5 | −110.0 |
| 25 m/s at 20,000 rpm | 119.0 | −17.2 | −114.5 |
| 20 m/s at 15,000 rpm | 70.6 | −12.9 | −118.4 |
| 20 m/s at 25,000 rpm | 153.5 | −13.1 | −108.5 |
| Average | 104.3 | −16.5 | −118.0 |
| Momentary Weight | |||
|---|---|---|---|
| Flight Condition | Standard Frame (Frame + AAW) [g] | Airfoil Frame (Frame + Airfoils + AAW) [g] | Comparison [%] |
| 15 m/s at 20,000 rpm | 1074 | 1019 | −5.0 |
| 20 m/s at 20,000 rpm | 1105 | 1037 | −6.1 |
| 25 m/s at 20,000 rpm | 1119 | 1031 | −7.9 |
| 20 m/s at 15,000 rpm | 1071 | 1035 | −3.3 |
| 20 m/s at 25,000 rpm | 1153 | 1035 | −10.3 |
| Average | 1104 | 1032 | −6.5 |
| Flight Time Estimate from eCalc (Mixed Flight Time) | |||
|---|---|---|---|
| Flight Condition | Standard Frame [min] | Airfoil Frame [min] | Comparison [%] |
| 15 m/s at 20,000 rpm | 12.0 | 12.7 | 5.8 |
| 20 m/s at 20,000 rpm | 11.7 | 12.5 | 6.8 |
| 25 m/s at 20,000 rpm | 11.5 | 12.6 | 9.6 |
| 20 m/s at 15,000 rpm | 12.1 | 12.5 | 3.3 |
| 20 m/s at 25,000 rpm | 11.1 | 12.5 | 12.6 |
| Average | 11.7 | 12.6 | 7.6 |
| Drag | |||
|---|---|---|---|
| Flight Condition | Standard Frame [N] | Airfoil Frame [N] | Comparison [%] |
| 15 m/s at 20,000 rpm | 1.137 | 1.116 | −1.8 |
| 20 m/s at 20 000 rpm | 1.556 | 1.961 | 26.0 |
| 25 m/s at 20,000 rpm | 2.155 | 3.036 | 40.9 |
| 20 m/s at 15,000 rpm | 1.349 | 1.936 | 43.5 |
| 20 m/s at 25,000 rpm | 1.908 | 2.018 | 5.8 |
| Average | 1.621 | 2.013 | 22.9 |
| Drag Coefficient () | |||
|---|---|---|---|
| Flight Condition | Standard Frame | Airfoil Frame | Comparison [%] |
| 15 m/s at 20,000 rpm | 0.676 | 0.387 | −42.7 |
| 20 m/s at 20,000 rpm | 0.520 | 0.383 | −26.4 |
| 25 m/s at 20,000 rpm | 0.461 | 0.379 | −17.8 |
| 20 m/s at 15,000 rpm | 0.451 | 0.378 | −16.2 |
| 20 m/s at 25,000 rpm | 0.638 | 0.394 | −38.3 |
| Average | 0.549 | 0.384 | −28.3 |
| Lift | |||
|---|---|---|---|
| Flight Condition | Standard Frame [N] | Airfoil Frame [N] | Comparison [%] |
| 15,000 rpm | −1.223 | −0.835 | 31.7 |
| 20,000 rpm | −1.826 | −1.130 | 38.1 |
| 25,000 rpm | −3.397 | −2.278 | 32.9 |
| −5 m/s at 20,000 rpm | −2.101 | −1.329 | 36.7 |
| +5 m/s at 20,000 rpm | −1.242 | −0.285 | 77.1 |
| Average | −1.958 | −1.171 | 43.3 |
| Aerodynamic Added Weight (AAW) | |||
|---|---|---|---|
| Flight Condition | Standard Frame [g] | Airfoil Frame [g] | Comparison [%] |
| 15,000 rpm | 124.7 | 85.1 | −31.7 |
| 20,000 rpm | 186.2 | 115.2 | −38.1 |
| 25,000 rpm | 346.4 | 232.3 | −32.9 |
| −5 m/s at 20,000 rpm | 214.2 | 135.5 | −36.7 |
| +5 m/s at 20,000 rpm | 126.6 | 29.1 | −77.1 |
| Average | 199.6 | 119.4 | −43.3 |
| Momentary Weight | |||
|---|---|---|---|
| Flight Condition | Standard Frame (Frame + AAW) [g] | Airfoil Frame (Frame + Airfoils + AAW) [g] | Comparison [%] |
| 15,000 rpm | 1125 | 1133 | 0.8 |
| 20,000 rpm | 1186 | 1163 | −1.9 |
| 25,000 rpm | 1346 | 1280 | −4.9 |
| −5 m/s at 20,000 rpm | 1214 | 1184 | −2.5 |
| +5 m/s at 20,000 rpm | 1127 | 1077 | −4.4 |
| Average | 1200 | 1167 | −2.6 |
| Flight Time Estimate from eCalc (Hovering Flight Time) | |||
|---|---|---|---|
| Flight Condition | Standard Frame [min] | Airfoil Frame [min] | Comparison [%] |
| 15,000 rpm | 14.7 | 14.5 | −1.4 |
| 20,000 rpm | 13.5 | 14.0 | 3.7 |
| 25,000 rpm | 11.0 | 12.0 | 9.1 |
| −5 m/s at 20,000 rpm | 13.0 | 13.6 | 4.6 |
| +5 m/s at 20,000 rpm | 14.7 | 15.7 | 6.8 |
| Average | 13.4 | 14.0 | 4.6 |
| Longitudinal Force | ||
|---|---|---|
| Flight Condition | Standard Frame [N] | Airfoil Frame [N] |
| 15,000 rpm | −0.007 | −0.170 |
| 20,000 rpm | −0.030 | −0.398 |
| 25,000 rpm | −0.017 | −0.360 |
| −5 m/s at 20,000 rpm | −0.010 | −0.373 |
| +5 m/s at 20,000 rpm | −0.042 | −0.295 |
| Average | −0.021 | −0.319 |
| Transversal Force | ||
|---|---|---|
| Flight Condition | Standard Frame [N] | Airfoil Frame [N] |
| 15,000 rpm | 0.042 | 0.052 |
| 20,000 rpm | 0.029 | 0.130 |
| 25,000 rpm | 0.133 | 0.297 |
| −5 m/s at 20,000 rpm | 0.020 | 0.095 |
| +5 m/s at 20,000 rpm | −0.122 | 0.124 |
| Average | 0.020 | 0.140 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freitas, A.A.C.; Azevedo, V.W.G.; Aguiar, V.H.A.; Lopes, J.M.A.; Caldeira, R.M.A. Exploring the Feasibility of Airfoil Integration on a Multirotor Frame for Enhanced Aerodynamic Performance. Drones 2025, 9, 202. https://doi.org/10.3390/drones9030202
Freitas AAC, Azevedo VWG, Aguiar VHA, Lopes JMA, Caldeira RMA. Exploring the Feasibility of Airfoil Integration on a Multirotor Frame for Enhanced Aerodynamic Performance. Drones. 2025; 9(3):202. https://doi.org/10.3390/drones9030202
Chicago/Turabian StyleFreitas, António André C., Victor Wilson G. Azevedo, Vitor Hugo A. Aguiar, Jorge Miguel A. Lopes, and Rui Miguel A. Caldeira. 2025. "Exploring the Feasibility of Airfoil Integration on a Multirotor Frame for Enhanced Aerodynamic Performance" Drones 9, no. 3: 202. https://doi.org/10.3390/drones9030202
APA StyleFreitas, A. A. C., Azevedo, V. W. G., Aguiar, V. H. A., Lopes, J. M. A., & Caldeira, R. M. A. (2025). Exploring the Feasibility of Airfoil Integration on a Multirotor Frame for Enhanced Aerodynamic Performance. Drones, 9(3), 202. https://doi.org/10.3390/drones9030202







