E²VRP-CPP: An Energy-Efficient Approach for Multi-UAV Multi-Region Coverage Path Planning Optimization in the Enhanced Vehicle Routing Problem

Abstract

Unmanned Aerial Vehicles (UAVs) are widely used in applications such as land assessment, surveillance, and rescue operations, where they are often required to cover multiple disjoint regions. Coverage Path Planning (CPP) aims to determine optimal paths for UAVs to cover these areas. While CPP for single regions has been extensively studied, multi-region CPP with multiple UAVs remains underexplored. Existing methods typically focus on minimizing path length, but often neglect the nonlinear variations in energy consumption during flight, limiting their practical applicability. This paper addresses the multi-UAV, multi-region CPP as a variant of the Vehicle Routing Problem (VRP) with energy estimation. We propose an approach that optimizes UAV flight speeds to minimize energy consumption, supported by an accurate energy estimation algorithm. In addition, a heuristic algorithm is developed to balance the distribution of tasks among UAVs, considering both the scanning and transit times. Experiments using real-world data from the Changsha urban area demonstrate that our approach outperforms state-of-the-art methods in computational efficiency and energy savings, highlighting its potential for practical UAV deployment.

1. Introduction

Unmanned aerial vehicles (UAVs) have become indispensable tools in various fields, including disaster assessment [1], search and rescue operations [2], logistics delivery [3], agriculture [4], mapping [5], and even military applications [6]. Their ability to rapidly deploy and operate autonomously makes them ideal for tasks requiring data collection over large and often inaccessible areas. However, as UAV technology continues to evolve, efficiently managing energy consumption while ensuring complete coverage remains a critical challenge, particularly in complex and resource-constrained environments. Coverage Path Planning (CPP) [7] is a fundamental problem in UAV operations aimed at determining an optimal path for a UAV to ensure complete coverage of a specified Area of Interest (AOI) using the onboard sensor’s footprint. The primary goal of CPP is to achieve exhaustive coverage of the AOI, whether by leveraging the field of view of a camera sensor or acquiring sufficiently dense measurements through LiDAR technology. This comprehensive coverage is essential for applications such as mapping, environmental monitoring, and search and rescue operations, where precise data acquisition over the entire area is crucial. Traditionally, CPP research has concentrated on single-region coverage, with a focus on minimizing path length and operational time to enhance efficiency while guaranteeing full area coverage.

Despite advances in single-region CPP [1], scenarios that require the coverage of multiple disjointed regions have received comparatively less attention. These multi-region scenarios are increasingly relevant in practical applications such as disaster response, where rapid information collection from several key areas is needed, or in surveillance operations that involve monitoring distinct regions. The complexity of covering multiple regions lies in the need for efficient coordination and task allocation among UAVs to ensure comprehensive coverage without excessive energy consumption.

Traditionally, CPP for UAVs has focused on minimizing flight path length to achieve comprehensive area coverage. These methods often assume that UAVs fly at a constant speed [8,9,10] and overlook the fact that energy consumption rates vary significantly with different maneuvers, such as hovering, accelerating, and climbing [11]. This simplification can lead to suboptimal energy usage and limit the effectiveness of UAV operations, especially in scenarios where precise energy management is crucial.

The multi-regional coverage path planning problem can be viewed as an integration of the Vehicle Routing Problem (VRP) and Coverage Path Planning (CPP), with the addition of energy constraints. In this framework, VRP determines the optimal visiting order of discrete Areas of Interest (AOIs) for each UAV, while CPP guides the strategy for efficiently covering each AOI. The challenge lies in not only optimizing the sequence of AOI visits and detailed coverage paths but also managing energy consumption to ensure that UAVs operate within battery limits during complex maneuvers such as hovering, accelerating, and climbing. Related work, termed Energy Constrained Multiple TSP-CPP (EMTSP-CPP) [8], addresses the same problem of covering multiple disjointed areas but employs different methodologies, utilizing maximum range constraints to manage UAV energy consumption. Another study assumes constant UAV speeds to streamline calculations, ensuring that coverage paths keep UAVs within their endurance limits [9].

To address these limitations, we propose the E²VRP-CPP method, an innovative solution to the multi-UAV, multi-region CPP problem. The E²VRP-CPP, which stands for Energy-Efficient Vehicle Routing Problem for Coverage Path Planning, prioritizes energy efficiency as its primary objective. This approach models the problem as a variant of the Vehicle Routing Problem (VRP), incorporating rigorous energy constraints within the planning process. We leverage established models for optimal flight speed and precise energy consumption estimation [11] to construct a robust framework that coordinates UAV operations for maximal efficiency and coverage. The methodology includes calculating optimal UAV speeds to minimize energy consumption and employing a systematic back-and-forth coverage strategy [12] for each Area of Interest (AOI) to ensure comprehensive coverage. Furthermore, we develop a heuristic algorithm that not only optimizes the sequence of region visits and coverage path but also balances the workload among UAVs to enhance operational efficiency while maintaining computational feasibility.

The main contributions of this paper include:

• Developed the E²VRP-CPP model that integrates an advanced energy consumption model considering UAV dynamics, acceleration, deceleration, and motor efficiency—into multi-UAV coverage path planning, prioritizing energy efficiency.
• Designed a heuristic algorithm that jointly optimizes task allocation and path planning under energy constraints, ensuring real-time computational efficiency.
• Conducted extensive experiments with real-world Changsha urban data, demonstrating that our approach reduced total energy consumption by up to 36.6% and maximum energy consumption by up to 50.4% across 36 scenarios, highlighting the practical benefits of our energy-efficient framework.

The remainder of the paper is organized as follows: Section 2 reviews related work, highlighting the limitations of current approaches. Section 3 details the problem formulation and proposed methodology. Section 4 presents experimental results, and Section 5 concludes with a discussion of future research directions.

2. Related Work

2.1. Multi-UAV CPP Problem

In the domain of CPP for unmanned aerial vehicles (UAVs), scholarly efforts have prominently focused on optimizing the coverage of an expansive single region. This optimization is facilitated through the systematic decomposition of a large Area of Interest (AOI) into smaller, more manageable sub-regions. This decomposition employs precise methodologies such as Trapezoidal [13], Boustrophedon [14], and Morse [15] techniques for exact decomposition, as well as Rectangular and Hexagonal grid methods for approximate approaches. Once decomposition is achieved, these sub-regions are assigned to UAVs, which then execute tailored coverage strategies designed to maximize operational efficiency. Chief among these strategies are the back-and-forth [16] and spiral [17] coverage patterns, meticulously chosen based on the geometric characteristics of each sub-region to ensure exhaustive coverage with minimal overlap and redundancy.

2.2. Multi-Region CPP Problem

Recent advancements in multi-region CPP have predominantly focused on optimizing inter-regional visiting sequences and intra-regional coverage methodologies for effectively managing disjointed Areas of Interest (AOIs). The problem was first modeled in 2020 as a TSP-CPP [18], emphasizing optimal region visiting sequences and minimizing travel distance. In 2022, researchers extended this model by incorporating UAV energy constraints, framing it as an Energy Constrained Multiple Traveling Salesman Problem with Coverage Path Planning (EMTSP-CPP) [8]. This study employed a Branch-and-Bound method for near-optimal solutions and leveraged Genetic Algorithms for larger-scale applications, demonstrating notable improvements in both efficiency and solution quality. Additionally, recent work [9] proposes using a mixed integer linear programming (MILP) approach to derive optimal coverage paths for autonomous, heterogeneous UAVs across multiple regions. To enhance computational efficiency, a clustering-based algorithm inspired by density-based methods was introduced, classifying regions into clusters to facilitate approximately optimal path planning. This dual methodology ensures comprehensive coverage while maintaining practical feasibility for efficient task execution. In [19], a novel approach optimizes UAV trajectory design by dynamically adjusting speed and altitude for location-dependent visual coverage. This method employs a three-component algorithm to improve task completion time, utilizing strategies for selecting photographing altitudes, determining visit order through an auxiliary traveling salesman problem, and choosing optimal coverage paths, demonstrating superiority over traditional methods in simulation studies. Overall, advancements in multi-region UAV coverage have optimized visiting sequences and energy use, enhancing efficiency and adaptability in complex environments.

2.3. Energy Efficient CPP Problem

A significant challenge for quadrotor UAVs is their limited battery life, which restricts the duration of missions. Consequently, energy consumption is a crucial factor in UAV path planning. Existing methods [8,9,10] often incorporate energy constraints by assuming constant velocity coverage, with limitations expressed as restricted path lengths or flight endurance. However, this assumption fails to account for the energy-intensive maneuvers required in CPP tasks, such as frequent turns, accelerations, decelerations, ascents, and descents, which can quickly deplete energy reserves and lead to mission failure. To address these challenges, ref. [20] employs a route-based optimization model with column generation to precisely estimate energy needs across various mission phases. Additionally, ref. [21] introduces an energy-aware grid-based approach that achieves up to 17% energy savings during mapping missions over irregular-shaped areas by utilizing an accurate energy model and applying pruning techniques to optimize path computation. Despite their advantages, these methods are typically applicable only to straightforward scenarios and lack the adaptability needed for complex environmental changes. Thus, more precise energy consumption estimation models [11] can be used to assess the robustness and flexibility of UAVs in executing CPP tasks.

3. Problem Statement and Adopted Framework

3.1. Problem Definition and Assumptions

In this study, we address the challenge of deploying M identical quadrotor UAVs, denoted as $\{U_1,U_2,\dots ,U_M\}$, to cover N discrete, non-overlapping regions, represented by $\{R_1,R_2,\dots ,R_N\}$. Each UAV is tasked with departing from a common depot, returning to this point after completing its mission. The depot’s location is fixed and known as ${\mathbf{P}}_0$. Each region is defined as a convex polygon, characterized by a set of vertices $\{V_{i1},V_{i2},\dots ,V_{i{m}_i}\}$, where $m_i$ denotes the number of vertices in region $R_i$.

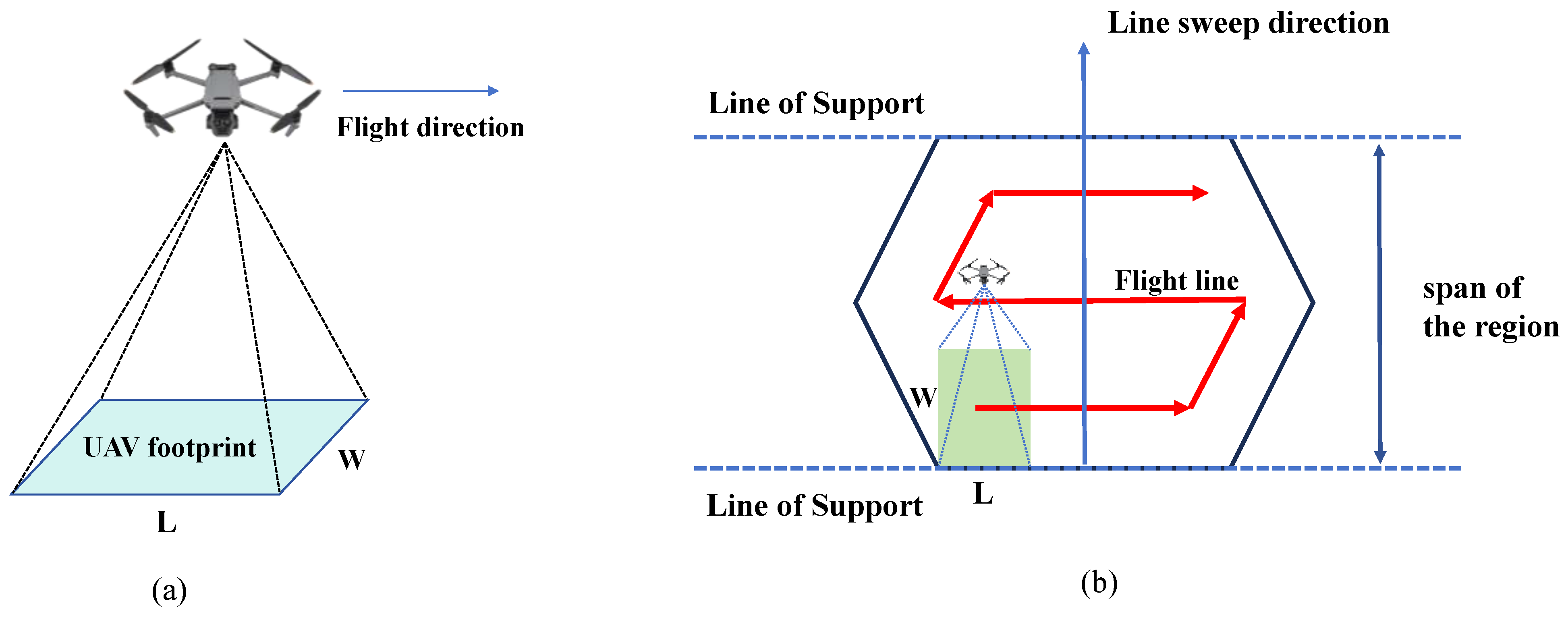
Each UAV is equipped with identical sensors with a scanning width W, determining the area covered during flight. Figure 1a illustrates the UAV footprint, where L represents its scanning length and w represents its scanning width. The UAVs must operate within a maximum energy capacity $E_{\mathrm{bound}}$, imposing a constraint on mission duration and necessitating efficient path planning to minimize energy consumption. Additionally, the UAVs are subject to dynamic constraints, including maximum speed $V_{\max }$ and maximum acceleration $a_{\max }$, requiring precise control during maneuvers such as turning and altitude adjustments, which impact energy usage.

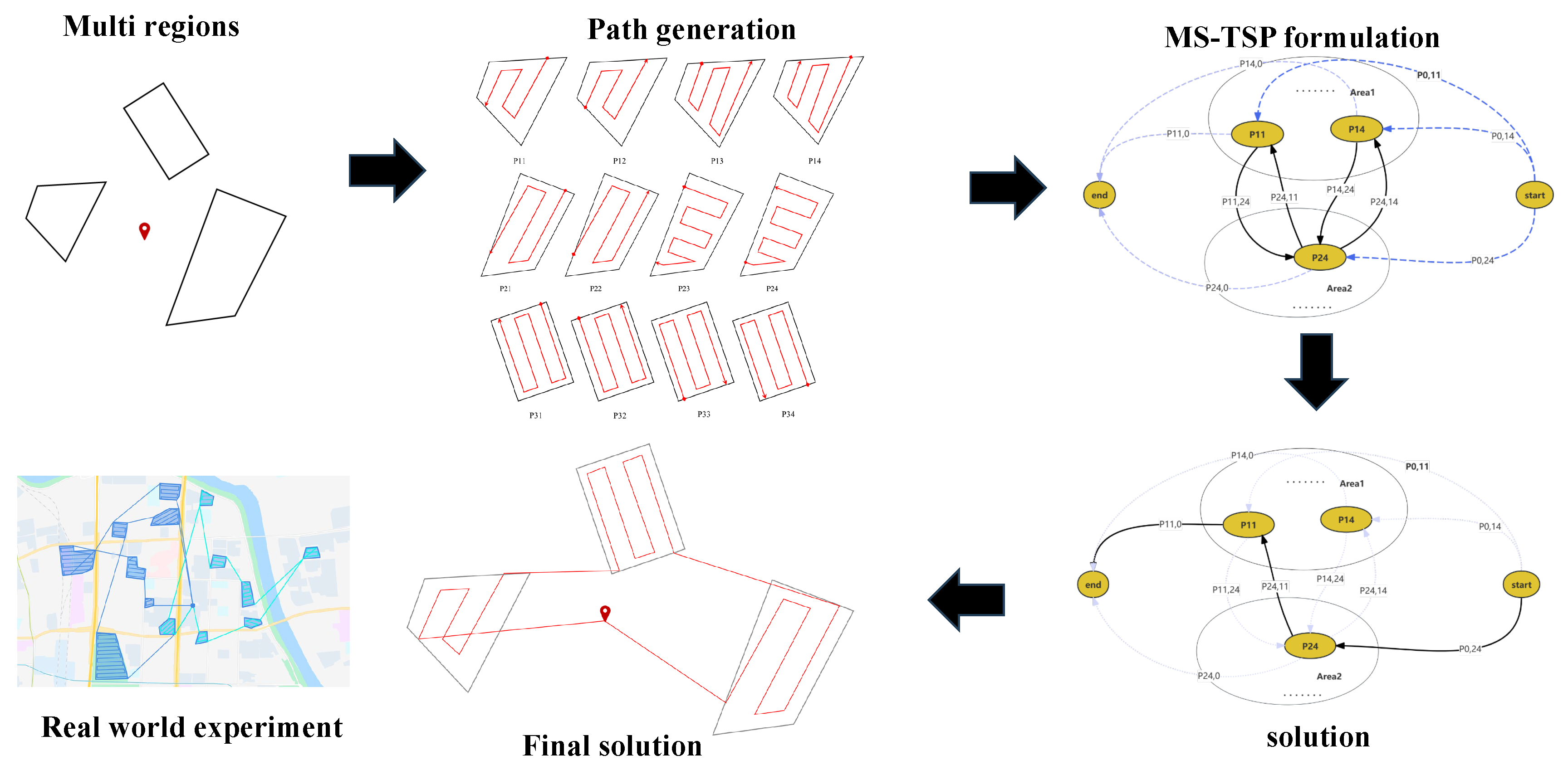
The path planning problem is simplified to two dimensions as the UAVs fly at a constant altitude. The objective is to devise flight paths that maximize coverage efficiency while ensuring each UAV operates within its energy constraints. This problem extends traditional coverage path planning by integrating real-world constraints, necessitating a careful balance between coverage efficiency and energy management to achieve optimal performance. To address this challenge, we propose a novel framework that combines energy-efficient path planning with coverage optimization, ensuring both objectives are simultaneously achieved through an integrated approach, as shown in the Figure 2.

Specifically, the figure illustrates our workflow for solving the multi-UAV, multi-region coverage problem. Data Input: The process begins with the input of task region vertex data and relevant UAV parameters. Candidate Path Generation: For each sub-region, candidate paths are generated based on a BF (back-and-forth) pattern, and an energy evaluation model is used to calculate the energy consumption of each candidate path. Problem Formulation: The problem is then modeled as a classical Multiple Set Traveling Salesman Problem (MS-TSP). Heuristic Algorithm Design: A heuristic algorithm is designed to efficiently solve the formulated problem. Solution Generation: The final solution is derived, representing the optimal or near-optimal flight paths. Experimental Validation: Finally, real-world experiments using actual map data and UAVs are conducted to validate the performance and practicality of the proposed approach.

3.2. Estimation of Path Energy Consumption

In this section, we address the estimation of energy consumption for unmanned aerial vehicles (UAVs) engaged in CPP tasks. By leveraging UAV physical parameters, we compute the optimal speed and endurance, drawing on methodologies detailed in existing literature [11]. Our approach integrates comprehensive models to predict power consumption and battery dynamics accurately.

The core of our method is the power consumption model. The hover power demand can be determined using momentum theory. The induced velocity at hover, $v_{i,h}$, is calculated as:

$$v_{i,h}=\sqrt{{\displaystyle \frac{T_h}{2\rho A_{\mathrm{prop}}}}}=\sqrt{{\displaystyle \frac{mg}{2\rho \pi r_{\mathrm{prop}}^2{N}_r}}}$$

(1)

where $T_h$ is the thrust per propeller required to hover, m is the UAV mass, $\rho$ is the air density, $A_{\mathrm{prop}}$ is the propeller disk area, $r_{\mathrm{prop}}$ is the propeller radius, and $N_r$ is the number of rotors. The mechanical hover power, $P_h$, is expressed as:

$$P_h={\displaystyle \frac{T_h{v}_{i,h}}{{\eta }_P}}={\displaystyle \frac{{\left(mg\right)}^{3/2}}{{\eta }_P\sqrt{2\rho \pi N_r}{r}_{\mathrm{prop}}}}$$

(2)

where ${\eta }_P$ denotes propeller efficiency.

For evaluating the optimal speed for maximum endurance or range, we rely on empirical relationships derived from simulation data. The normalized speeds, ${\widehat{v}}_e=v_e/v_{i,h}$ and ${\widehat{v}}_r=v_r/v_{i,h}$, are determined as follows:

$${\widehat{v}}_{\left[e\right|r]}^{-1}=c_{0,\left[r\right|e]}+c_{1,\left[r\right|e]}{v}_{i,h}+c_{2,\left[r\right|e]}A$$

(3)

where $c_{0,\left[r\right|e]},c_{1,\left[r\right|e]},c_{2,\left[r\right|e]}$ are regression coefficients obtained from simulations. According to [11], the values are: $c_0=0.041546$, $c_1=0.041122$, and $c_2=0.00053292$.

Battery modeling is also pivotal in our framework. The effective battery capacity, influenced by power consumption, is modeled by a third-order polynomial:

$$\kappa ={\displaystyle \frac{C_{\mathrm{eff}}}{C}}=d_0+d_1{P}_{\mathrm{cell}}+d_2{P}_{\mathrm{cell}}^2+d_3{P}_{\mathrm{cell}}^3$$

(4)

where $P_{\mathrm{cell}}$ is the normalized power consumption per cell, with coefficients specified in the reference data. According to [11], the values are: $d_0=0.9876$, $d_1=-0.0020$, $d_2=-5.2484\times {10}^{-5}$, and $d_3=1.2230\times {10}^{-7}$.

By incorporating these models, our framework facilitates accurate energy consumption estimation, addressing the complexities of UAV dynamics and battery performance. This approach enhances the reliability and efficiency of UAV mission planning in diverse operational scenarios. In summary, given the waypoints of a path, our energy estimation model can calculate the energy consumption for that path.

3.3. Back-and-Forth Algorithm

In this study, we adopt a back-and-forth pattern to generate candidate coverage paths for each region. In this method, a set of parallel lines of support (LOS) is employed to define the back-and-forth path (BFP) for a convex polygonal region, ensuring complete coverage of the area, as illustrated in Figure 1b. The span of the region is defined as the distance between the LOS, which intersects the polygon at a single vertex or edge. The path segments aligned with the LOS direction are referred to as flight lines. The line sweep direction, which is perpendicular to the flight lines, represents the UAV’s movement direction.

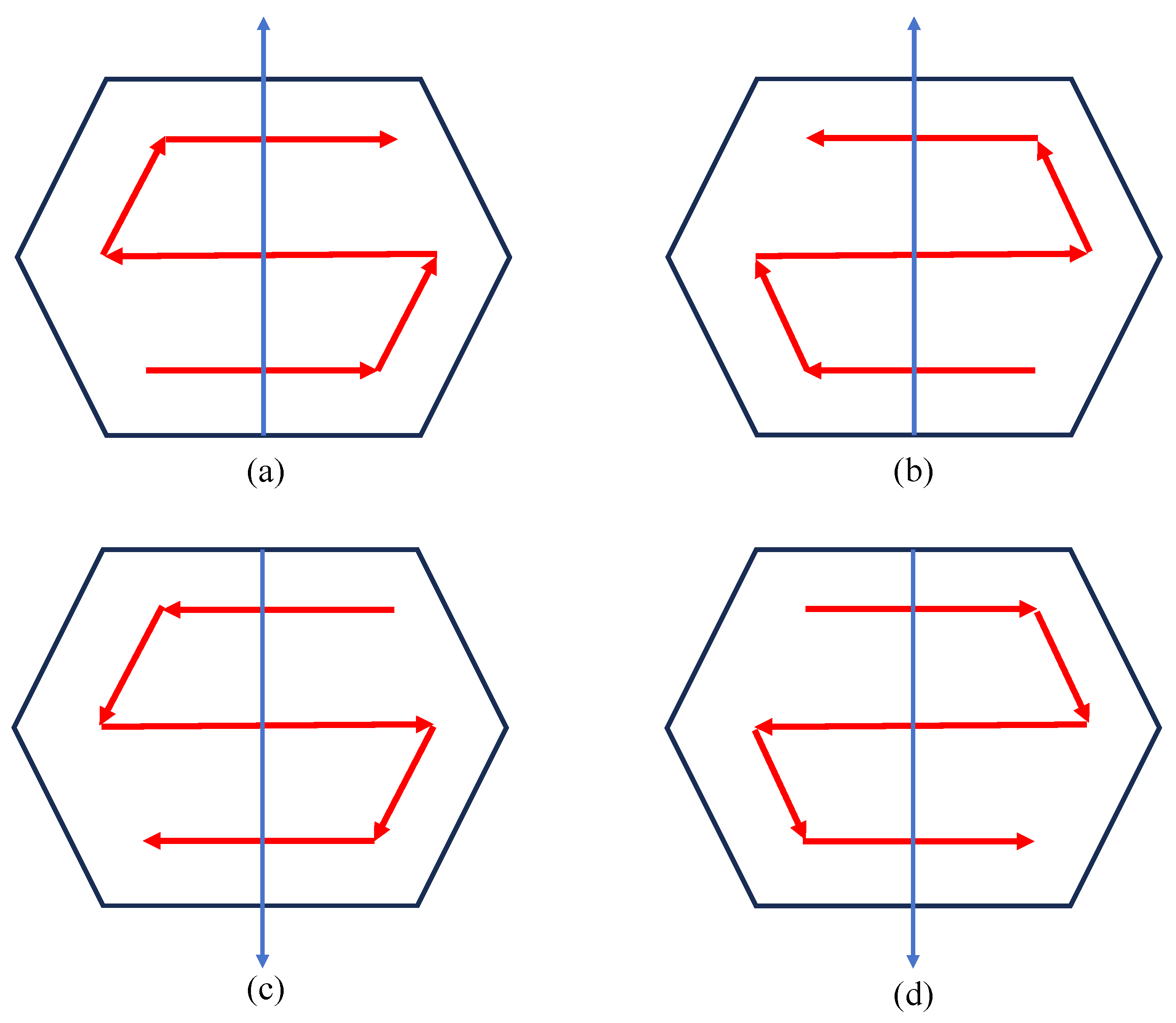
Drawing upon the back-and-forth coverage path planning (BFP) algorithm [22], which guarantees full coverage of the polygon, our approach modifies the original BFP pattern to generate candidate paths that ensure comprehensive coverage of the entire region. Specifically, For any given edge of the polygon, two possible starting points are defined at each end of the edge at a specified distance from it. In other cases, as shown in Figure 3, By changing the sweeping direction, we obtain two additional start points, leading to four candidate sweeping paths for the same edge. In principle, each edge can generate four candidate paths; however, constructing candidate paths for all edges is not required. Statistical analysis suggests that the most energy-efficient paths tend to align with the sweeping direction along the polygon’s longest edge. Consequently, in our study, we prioritize selecting the longest edge of the polygon as the sweeping direction for path generation.

Combining the results from Section 3.2 and Section 3.3, for a given region, we can generate candidate paths and compute the energy consumption for each one. This output serves as the input for the next Section 3.4, where the energy-optimal path is determined through further optimization.

3.4. E²VRP-CPP Solver

Previous studies on this problem have generally focused on generating candidate coverage paths, followed by the development of Mixed Integer Linear Programming (MILP) models to address the problem, incorporating various constraints and objective functions. However, solving MILP problems of this nature is inherently NP-hard, resulting in significant computational complexity that limits the scalability of exact solutions for large-scale instances. The high dimensionality and combinatorial nature of the problem demand extensive computational resources and time, which can be prohibitive in practical applications where timely solutions are critical.

To overcome these challenges, we propose a heuristic algorithm tailored specifically to the Energy-Efficient Vehicle Routing Problem for Coverage Path Planning (E²VRP-CPP). See Algorithm 1 for the pseudocode. This approach is designed to efficiently approximate solutions by leveraging problem-specific insights and heuristics that guide the search process. By focusing on energy efficiency and coverage optimization, our heuristic method aims to provide high-quality solutions that are computationally feasible, even for large problem instances.

The heuristic algorithm begins with the construction of an initial solution using a Greedy Random Search Procedure (GRP), as shown in Algorithm 2. This initial solution serves as the foundation upon which further improvements are made. The algorithm then employs a Tabu Search strategy to iteratively refine the solution, ensuring that energy consumption constraints derived from the optimal endurance estimates are respected throughout the search process.

Algorithm 1 E²VRP-CPP

Input: Areas of Interest AOIs, Number of UAVs $N_{\mathrm{UAV}}$, UAV_parameters, Energy Constraint $E_{\mathrm{bound}}$

Output: Optimal Path $P_{\mathrm{opt}}$

1: $P_{\mathrm{opt}}$$\leftarrow \left\{\right\}$

2: $E_{\max }\leftarrow \infty$ {maximum path energy from best_paths}

3: $N_{\mathrm{paths}}\leftarrow N_{\mathrm{UAV}}$ {number of paths to generate}

4: while $E_{\max }>E_{\mathrm{bound}}$ do

5:    $E_{\mathrm{tot}}\leftarrow \infty$

6:    MSTSP_nodes $\leftarrow \left\{\right\}$

7:    for all $AOI\in \mathrm{AOIs}$ do

8:     candidate_paths_$AOI\leftarrow$ get_candidate_coverage_paths(AOI, $N_{\mathrm{paths}}$)

9:     nodes_set $\leftarrow \left\{\right\}$

10:   for all $p\in \mathrm{paths}\_AOI$ do

11:    add p to nodes_set

12:   end for

13:   add nodes_set to MSTSP_nodes

14:  end for

15:  construct MSTSP_instance from MSTSP_nodes

16:  paths ← solve(MS-TSP_instance, UAV_parameters)

17:  $E\leftarrow {max}_{p\in \mathrm{paths}}$ path_cost (p)

18:  if $E<E_{\max }$ then

19:   $E_{\max }\leftarrow E$

20:   $E_{\mathrm{tot}}\leftarrow {\sum }_{p\in \mathrm{paths}}$ path_cost (p) {sum of path energies over generated paths}

21:   $P_{\mathrm{opt}}$← paths

22:  end if

23: end while

24: return Optimal Path $P_{\mathrm{opt}}$

Algorithm 2 MS-TSP Solver

Input: MS-TSP_instance

Output: best_Solution

1: initial_solution ← GRP(MS-TSP_instance)

2: best_Solution ← initial_solution {Initialize best solution as the initial solution}

3: iteration ← 0

4: tabuList ← {initial_solution}

5: while iteration < maxIterations do

6:    GENERATE new_solution using one of the strategies:

7:    G1: Random Shift

8:    G2: Best Shift

9:    G3: Best Swap

10:     G4: Direction Change

11:  current_Solution ← arg minS∈new_solution\tabuList cost(new_solution)

12:  if cost(current_Solution) < cost(best_Solution) then

13:   best_Solution ← current_Solution

14:   iteration ← 0

15:  else

16:   iteration ← iteration + 1

17:  end if

18:  tabuList ← tabuList ∪ {current_Solution}

19: end while

20: Return: best_Solution

The heuristic algorithm comprises several key moves designed to explore the solution space effectively:

• Random-shift: Selects and relocates a random segment within or between routes to introduce variability and prevent local optima, with increasing emphasis over iterations.
• Best-shift: Removes a random segment and reinserts it at the optimal position across routes, found through an exhaustive search for cost-effectiveness.
• Best-swap: Exchanges a random segment with the best segment in another route, using exhaustive search to improve solution quality.
• Best-direction-switch: Alters the traversal direction of the best segment to enhance path efficiency through strategic orientation adjustments.

Each move is systematically applied to the initial solution, guided by the energy constraints and the search for optimal coverage. The Tabu Search mechanism incorporates memory structures to prevent cycling back to previously visited solutions, thereby enhancing the efficiency and effectiveness of the search process. This iterative refinement approach ensures that the solutions generated are not only feasible within the energy constraints but also optimized for minimal energy consumption and maximal coverage efficiency.

4. Experimental Setup and Evaluation

In this section, we conduct several experiments to validate the effectiveness and efficiency of the proposed algorithm. The simulations were performed on a machine equipped with an Intel Core i9-14900KF CPU (32 CPUs, 24 physical cores, 1 thread per core), 16 GB of RAM, and running Ubuntu 20.04 OS. The UAV used in the experiments was DJI Mavic 3, with task regions randomly selected from a map of Changsha City to simulate realistic scenarios. The experimental code was implemented using C++(compiled with g++ version 9.4.0) and Python(version 3.8.10). These configurations aim to replicate real-world scenarios and ensure that the proposed algorithm performs robustly and efficiently under various operational conditions.

4.1. Simulation Setup

To address the multi-region CPP problem, we evaluate both multi-UAV and single-UAV configurations by comparing the performance of the Greedy algorithm [23] and our proposed E²VRP-CPP.

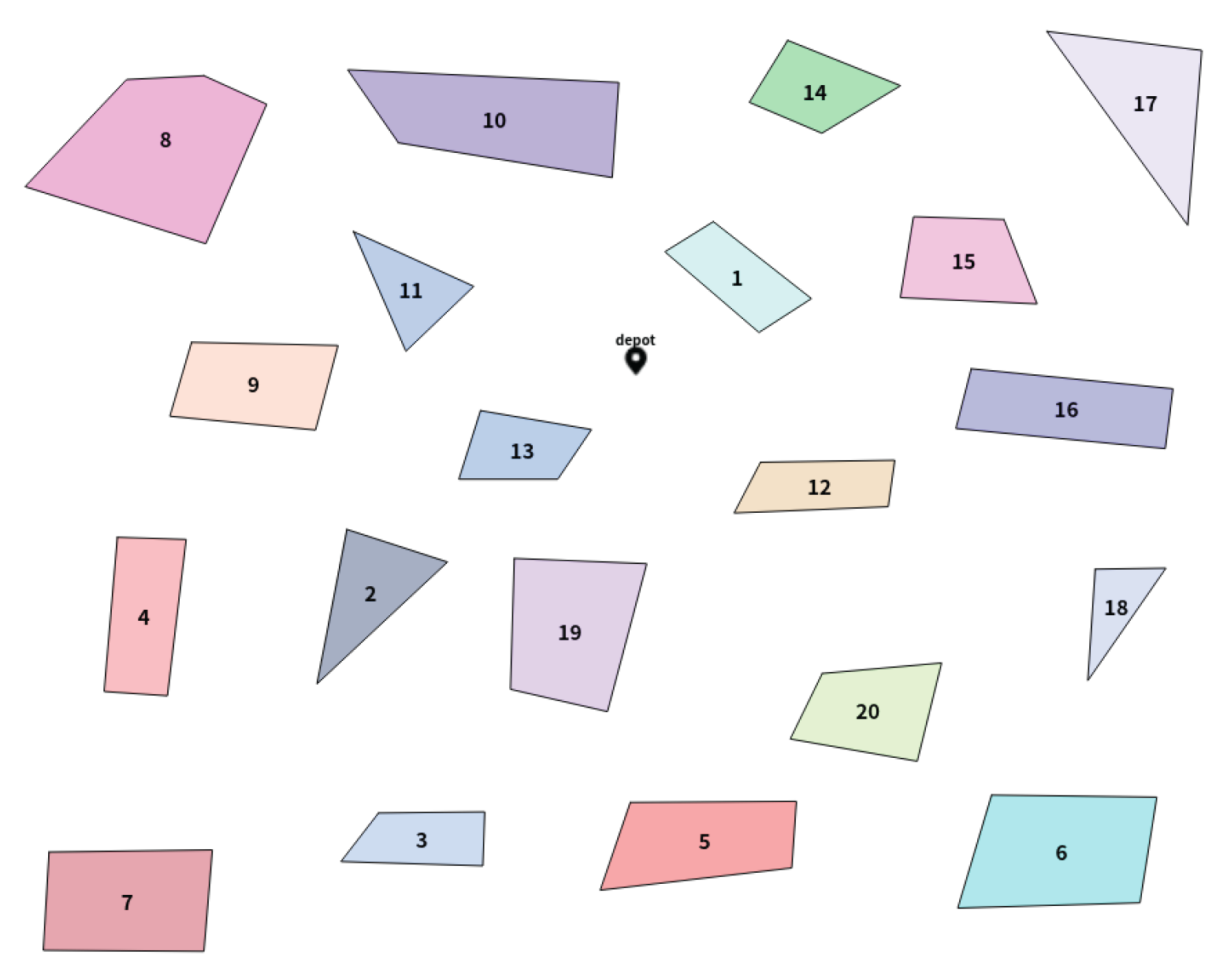
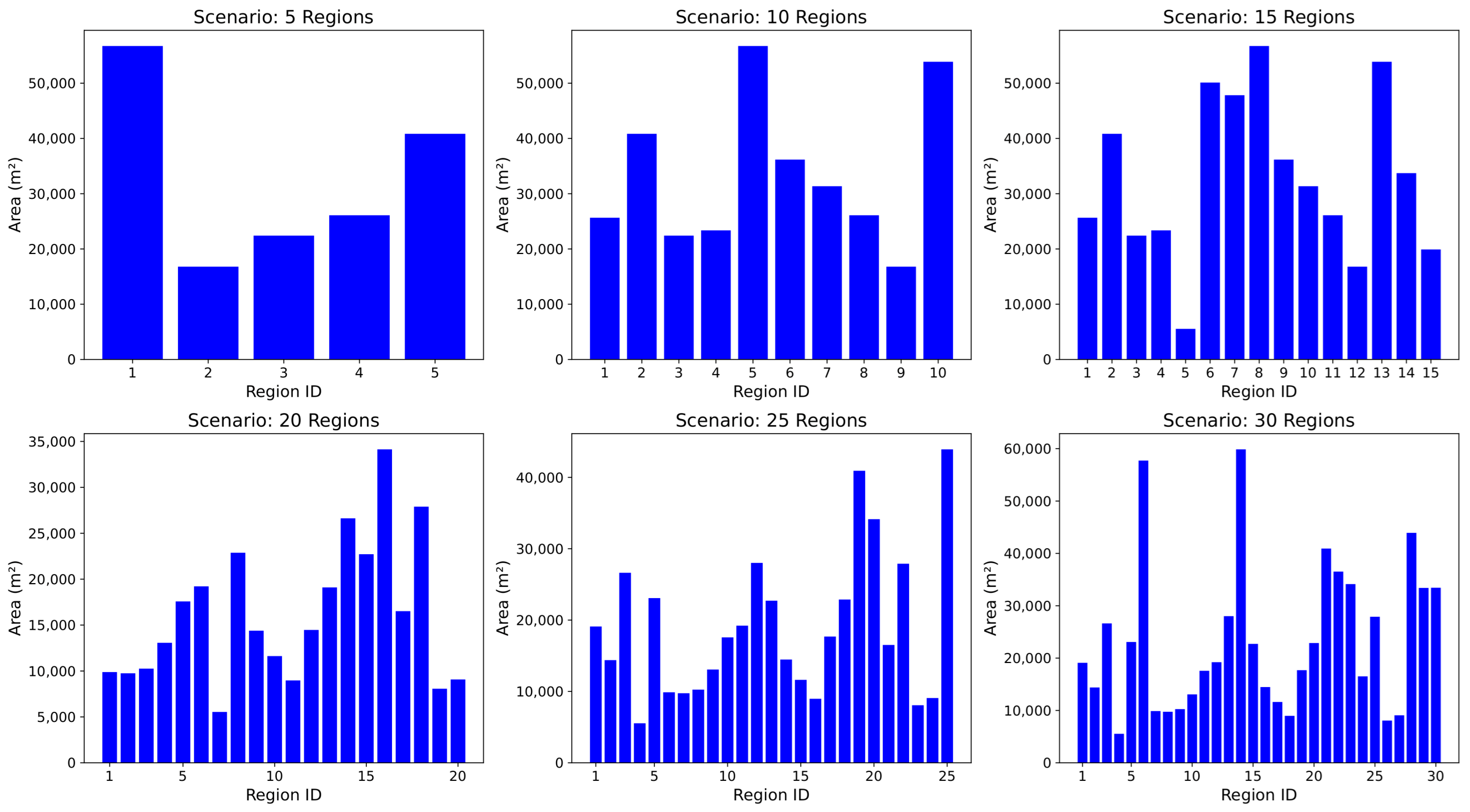
The task region data are derived from a map of Changsha. In our experimental setup, regions were randomly delineated using a dedicated mapping tool, and the resulting boundaries were exported as GeoJSON data. After appropriate preprocessing, these data serve as input to our algorithm. To simulate environments of increasing complexity and scale, the number of regions is systematically varied across scenarios with 5, 10, 15, 20, 25, and 30 regions. For each scenario, we compute detailed area statistics—including total area, average area, and area standard deviation—to provide a comprehensive view of the experimental setup. For example, Figure 4 illustrates a scenario with 20 regions, and

Table 1. Summary of Region Areas.

Number of Regions	Total Area (m2)	Average Area (m2)	Area Std Dev (m2)
5	162,894.7909	32,578.95817	16,173.00105
10	333,331.6348	33,333.16348	13,506.27036
15	490,461.6523	32,697.44349	14,833.40330
20	321,800.5842	16,090.02921	7644.252379
25	475,435.0319	19,017.40128	10,167.46822
30	696,409.2117	23,213.64039	14,193.43035

below summarizes the key statistical metrics for all scenarios. Additionally, Figure 5 shows bar charts of the area of each sub-region for the six scenarios, indicating that the randomly annotated task regions do not follow any specific distribution pattern. This also demonstrates the general applicability and robustness of our algorithm across different data distributions.

The UAV used in the experiments was the DJI Mavic 3, as shown in the

Table 2. UAV Parameters.

Metric	Value
Drone weight	0.90 kg
Number of propellers	4
Battery cell capacity	5-Ah (4 cells)
UAV unfolded area	0.0215 m²
Maximum energy of UAV	77 Wh
Propeller radius	0.119 m
Acceleration rate	2 m/s²
Allowed path deviation	2 m
Scanning width	20 m

below. The number of UAVs in the experiments varied, with values set to 1, 2, 3, 4, 5, and 6. In each case, the UAVs took off from the same location and returned to the starting point upon completing the task. Based on the optimal speed and maximum endurance calculation methods discussed in Section 3.2, the optimal flight speed was determined to be 13.17 m per second, with a maximum endurance of 2344 s.

4.2. Verification of Method Effectiveness and Efficiency

To rigorously validate our algorithm, we perform a structured three-fold evaluation. First, we benchmark against leading state-of-the-art algorithms to validate comparative effectiveness. Second, we assess scalability by examining performance across various operational scopes. Finally, we analyze computational efficiency, focusing on response times under different swarm sizes and environmental conditions.

4.2.1. Comparative Analysis

To evaluate the effectiveness of our algorithm, we compare its performance with the Greedy algorithm in various coverage scenarios. Figure 6 presents the flight distances for each UAV in a 4-UAV setup in different coverage areas (5, 10, 15, 20, 25, and 30). The results demonstrate that our approach consistently outperforms the Greedy algorithm, achieving shorter flight distances for all UAVs. In addition, our method ensures a more balanced distribution of the flight distances between UAVs, minimizing the variance between the travel distances of individual UAVs.

We simultaneously compared the total energy consumption and the maximum energy of a single path across 36 scenarios of different scales, as shown in

Table 3. Total energy consumption and maximum energy of a single path across 36 scenarios.

Instance			Energy Cost						Time
Num	N	M	Total			Max			Ours	Greedy
			Ours	Greedy	%	Ours	Greedy	%
1	1	5	68,065	80,471	15.4%	68,065	80,471	15.4%	0.022761	0.001004
2	2	5	69,608	83,671	16.8%	36,225	45,842	21.0%	0.030138	0.001013
3	3	5	75,484	89,930	16.1%	28,074	45,289	38.0%	0.038185	0.000579
4	4	5	76,163	86,394	11.8%	28,074	29,676	5.4%	0.044387	0.000639
5	5	5	75,484	83,856	10.0%	28,074	48,627	42.3%	0.0027	0.000556
6	6	5	79,128	84,940	6.8%	28,218	31,259	9.7%	0.001949	0.000547
7	1	10	124,316	159,251	21.9%	124,316	159,251	21.9%	0.191857	0.001341
8	2	10	126,854	166,717	23.9%	64,375	85,156	24.4%	0.232867	0.001512
9	3	10	135,439	169,099	19.9%	46,898	79,567	41.1%	0.252022	0.000871
10	4	10	144,468	179,319	19.4%	37,408	54,893	31.9%	0.230722	0.001061
11	5	10	151,908	181,167	16.2%	31,503	50,121	37.1%	0.250626	0.00128
12	6	10	155,639	172,954	10.0%	28,318	45,034	37.1%	0.19171	0.001652
13	1	15	173,729	245,007	29.1%	173,729	245,007	29.1%	1.006399	0.001863
14	2	15	178,436	232,377	23.2%	89,468	122,276	26.8%	0.583359	0.002495
15	3	15	186,298	254,402	26.8%	62,655	91,663	31.6%	1.142829	0.001646
16	4	15	196,510	249,512	21.2%	49,511	72,063	31.3%	2.037928	0.002184
17	5	15	201,551	260,390	22.6%	41,397	79,776	48.1%	0.850912	0.001992
18	6	15	207,750	277,100	25.0%	36,172	72,895	50.4%	0.71487	0.003384
19	1	20	201,083	271,737	26.0%	201,083	271,737	26.0%	1.758195	0.003232
20	2	20	276,986	345,472	19.8%	138,570	173,368	20.1%	1.285618	0.002526
21	3	20	354,733	415,926	14.7%	118,556	143,636	17.5%	2.285061	0.005166
22	4	20	434,398	488,211	11.0%	108,775	136,296	20.2%	1.694054	0.004872
23	5	20	509,311	557,802	8.7%	103,362	127,037	18.6%	2.1924	0.00259
24	6	20	587,852	566,255	−3.8%	98,962	123,650	20.2%	4.475977	0.009634
25	1	25	254,732	351,132	27.5%	254,732	351,132	27.5%	1.863377	0.00653
26	2	25	329,171	436,356	24.6%	164,924	218,709	24.6%	2.368285	0.006187
27	3	25	406,989	538,992	24.5%	135,948	186,733	27.2%	3.986639	0.005017
28	4	25	483,718	583,844	17.1%	121,383	149,633	18.9%	4.17127	0.005671
29	5	25	562,078	642,443	12.5%	112,981	149,981	24.7%	2.664901	0.00514
30	6	25	635,748	739,657	14.0%	107,581	142,927	24.7%	2.865114	0.007637
31	1	30	268,640	424,007	36.6%	268,640	424,007	36.6%	7.983452	0.01237
32	2	30	284,061	426,898	33.5%	142,414	228,214	37.6%	5.515077	0.009247
33	3	30	284,653	448,656	36.6%	95,683	152,381	37.2%	3.968321	0.008271
34	4	30	291,380	415,063	29.8%	73,671	141,797	48.0%	4.066404	0.009648
35	5	30	300,812	429,322	29.9%	60,809	107,265	43.3%	9.609281	0.008921
36	6	30	313,603	483,552	35.1%	52,750	106,320	50.4%	7.025549	0.008595

. The results indicate that both total and maximum energy consumption were reduced by more than 20% using our algorithm. Specifically, the total energy savings reached a maximum of 36.6%, while the maximum energy savings peaked at 50.4%. However, in the 24th scenario, our algorithm resulted in a 3.8% increase in total energy compared to the Greedy approach. We attribute this to the more balanced distribution of tasks in our algorithm, which leads to more UAVs participating in the task, thereby increasing the overall energy consumption.

4.2.2. Scalability Analysis

In this section, we assess the scalability of our algorithm by examining its performance in solving coverage path planning for varying numbers of UAVs (from 1 to 6) in a fixed environment with 30 regions. The convergence behavior of the algorithm across these different UAV configurations is shown in Figure 7. The six subplots display the iterative convergence of the algorithm in terms of total energy consumption for each UAV configuration. As illustrated, our algorithm consistently reaches convergence within a limited number of iterations, regardless of the number of UAVs involved.

The results demonstrate that the algorithm’s performance remains stable even as the scale of the problem increases, validating its scalability. This scalability ensures that the proposed algorithm can efficiently handle coverage path planning tasks with varying numbers of UAVs in larger and more complex environments without significant degradation in convergence speed. The rapid convergence observed across all UAV configurations further highlights the robustness and efficiency of our approach in solving real-world, large-scale path planning problems.

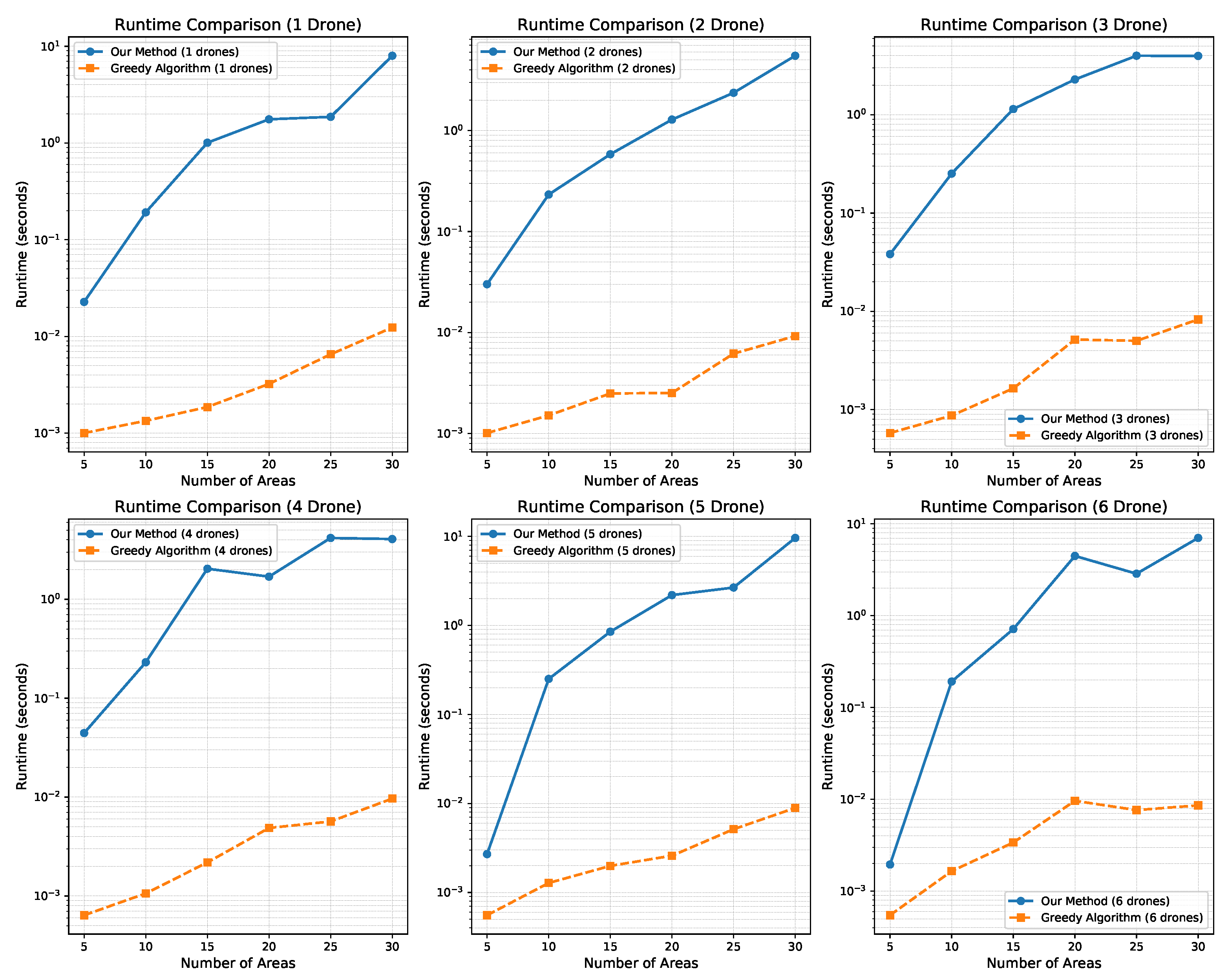
4.2.3. Computing Time Analysis

In this section, we analyze the computational efficiency of our algorithm by comparing its solution time with that of the Greedy approach. Figure 8 presents the computation times of both algorithms for different task areas, ranging from 5 to 30 regions, with varying numbers of UAVs (from 1 to 6). Each subplot shows the time required to obtain a solution for both algorithms across these different scenarios.

As shown in Figure 8, the Greedy algorithm consistently outperforms our algorithm in terms of computation time. However, our algorithm demonstrates competitive performance, with solution times consistently below 2 s for smaller task areas (less than 20 regions). Even when the task area increases in size, our algorithm continues to deliver solutions within reasonable time limits, providing satisfactory results for larger-scale problems.

Furthermore, while the Greedy algorithm achieves faster solution times, our approach strikes a balance between computational efficiency and solution quality. In many cases, our algorithm achieves significantly better solution quality, as evidenced by the comparative results in the previous section, while still maintaining a reasonable computation time. This makes our algorithm particularly suitable for real-time or near-real-time applications, where both speed and solution quality are crucial.

5. Conclusions

In this paper, we introduced the E²VRP-CPP algorithm, a novel approach to multi-UAV coverage path planning designed to minimize energy consumption while ensuring efficient coverage of multiple disjointed regions. Through rigorous experimental validation, including comparative, scalability, and computational efficiency analyses, we demonstrated the algorithm’s effectiveness in outperforming state-of-the-art methods. The results show that E²VRP-CPP not only achieves superior energy efficiency but also maintains high coverage completeness and solution quality on varying scales of operations.

The scalability analysis demonstrated that our approach remains robust and efficient even as task complexity increases, making it well-suited for realistic, moderately scaled, and dynamic operational environments. Additionally, the computing time analysis highlighted the algorithm’s ability to balance speed with accuracy, ensuring its applicability in real-time scenarios where rapid decision-making is crucial.

Future work will focus on further optimizing the algorithm to handle more complex and dynamic operational environments. In particular, we plan to develop a hybrid framework that combines offline global optimization with online local optimization. In the offline phase, a near-global optimal plan for task allocation and route planning will be computed using comprehensive global information. During the online phase, real-time adaptive strategies will be employed to perform lightweight local adjustments in response to unexpected changes, such as UAV failures, inaccessible regions, or areas requiring re-scanning. Considering that UAVs often operate in outdoor environments with limited computational resources, it is essential to design algorithms with a lower computational complexity. This approach will ensure a better balance between solution time and solution quality, making the algorithm practical for real-time applications without compromising performance. In addition, our goal is to integrate advanced energy management techniques to further extend the operational range of UAVs. Furthermore, future work will also consider more complex polygon shapes and the presence of no-fly zones and obstacles within them, thereby enhancing the robustness and applicability of our approach in realistic operational scenarios. Moreover, while our current experimental scenario of 6 UAVs covering 30 regions is moderate in scale, real-world dense environments often require handling many more discrete regions, which motivates our ongoing research into multi-UAV, multi-depot, and multi-region coverage. In general, the E²VRP-CPP algorithm represents a significant advancement in UAV path planning, offering a robust, energy-efficient, and comprehensive solution for coverage in diverse applications.