Physical-Layer Security Enhancement for UAV Downlink Communication Using Joint Precoding and Artificial Noise Design in Generalized Spatial Directional Modulation

Abstract

This paper proposes a novel joint precoding and artificial noise design framework for generalized spatial directional modulation (AN-GSDM) in unmanned aerial vehicle (UAV) communications, aimed at enhancing the physical-layer security of downlink UAV communication systems. The key innovation lies in the dynamic co-optimization of multi-beam control and artificial noise (AN) power allocation under mobility constraints, enabling real-time adaptation to varying channel conditions. This approach jointly optimizes the precoding matrix and power-control factor, facilitating the effective management of multi-beams and AN to maximize the secrecy rate. The secrecy rate expression is derived, and the corresponding joint optimization problem is formulated. Due to the non-convex nature of the problem and the lack of a closed-form solution, an alternating iterative algorithm is proposed. This algorithm alternates between optimizing the precoding matrix using gradient descent and deriving a suboptimal closed-form solution for the power-control factor. Simulation results confirm that the proposed algorithm significantly enhances security by maximizing the secrecy rate, reducing eavesdroppers’ achievable rate to near zero, while simultaneously maintaining legitimate user’s rate. The approach not only strengthens security but also preserves system effectiveness, demonstrating robust convergence properties. This makes it a practical and promising solution for secure UAV communication.

1. Introduction

Anticipating future advancements in mobile communications, unmanned aerial vehicle (UAV) communication systems are expected to play a pivotal role in the development of space–air–ground integrated networks (SAGINs) for sixth-generation (6G) communications [1,2,3]. As emphasized in [1], UAVs have become indispensable for the realization of SAGINs due to their remarkable versatility and adaptability. In particular, references [4,5] highlight their extensive applications across various domains, such as surveillance and disaster management. In the context of secure communication, UAVs offer significant potential as nodes for enhancing data confidentiality, providing innovative solutions to safeguard sensitive information during transmission.

Nevertheless, the openness inherent in wireless communication environments—especially in air-to-ground channels—introduces significant vulnerabilities. In particular, waveform leakage increases the risk of signal interception, making secure and reliable communication within UAV networks an urgent research priority. To mitigate interception risks, significant advancements have been made in the realm of physical layer security (PLS) technologies [6]. Unlike conventional encryption techniques, these approaches leverage the unique characteristics of wireless channels to enhance data security [7]. Specifically, the use of artificial noise (AN) and directional modulation (DM) has garnered considerable attention as effective strategies for enhancing the security of wireless communication systems. For instance, AN, as proposed in [8], manipulates the null space of the legitimate receiver’s channel to effectively jam the eavesdropper’s reception without imposing an additional burden on the legitimate receiver. Additionally, the integration of UAV trajectory design and AN to thwart eavesdropping from multiple colluding curious users was introduced in [9]. Another significant contribution was presented in [10], where an optimal power allocation strategy was investigated to maximize secrecy rates in the presence of AN, ensuring that the legitimate receiver’s signal strength remains adequately protected. Despite these advancements, several challenges persist in the effective application of AN, particularly regarding the efficiency of AN in dynamic, multi-user environments. The fundamental trade-off between interference power and effective signal energy remains a critical area of exploration, underscoring the need for further optimization to improve the practical implementation of AN in secure communication systems.

On the other hand, DM has attracted considerable attention for its potential to enhance communication security [11]. In particular, the study in [12] introduced a novel approach by combining DM with beamforming to focus the transmitted signal toward a specific receiver, thus reducing the likelihood of interception by unauthorized users. Additionally, the integration of DM with multiple antennas was explored in [13] to improve the robustness of secure communications in multipath environments. This strategy enhanced the transmission’s security by mitigating the effects of eavesdroppers situated in diverse spatial regions. Furthermore, the work presented in [14] proposed a dynamic directional modulation (DDM) technique to enhance the privacy of wireless transmissions, which was evaluated using information leakage measures. Despite the effectiveness of these techniques, the security performance of DM approaches is significantly compromised when eavesdroppers are in close proximity to legitimate users. This limitation underscores the ongoing challenges in optimizing DM strategies to ensure robust security in dynamic and adversarial environments.

While both AN and DM techniques have shown promise in enhancing communication security, their combined application has also been investigated. As highlighted in [15,16,17], integrating AN with DM has the potential to improve the secrecy rate and overall security of the system by exploiting spatial diversity and effective interference management, thus offering stronger protection against eavesdropping. However, these approaches still face significant challenges in optimizing key system parameters, such as power control and beamforming design, to achieve an optimal balance between security enhancement and system efficiency. Moreover, transmission rates are often constrained, further complicating the implementation of these techniques in practical scenarios.

To address these limitations, several advanced solutions have been proposed, with a particular focus on the utilization of cooperative receivers. Specifically, DM with cooperative receivers (DM-CR), introduced in [18], secures transmissions by utilizing cooperative receivers and incorporating a predefined distortion factor to ensure robust performance regardless of the eavesdropper’s location. Building on this, spatial DM (SDM), as presented in [19], combined DM with spatial modulation (SM) to bolster resilience against distributed eavesdroppers and enhance transmission rates. To further improve transmission rates, generalized SDM (GSDM) [20] employed distributed receivers to encode information through signal indices, thereby reinforcing security. Additionally, the work in [21] proposed a DM with distributed receiver selection (DM-DRS) technique, which activated a specific subset of receivers to modulate information using receiver indices, complemented by a scrambling matrix to obstruct interception attempts. Furthermore, SDM integrated with AN [22] combined the strengths of SM, DM, and AN to achieve concurrent improvements in both security and transmission rates. Collectively, these advancements exploit the unique properties of wireless channels, significantly enhancing information security in UAV communication systems.

Despite these achievements, existing research on DM and AN technologies predominantly focuses on static channel conditions, precoding schemes, or power allocation, often neglecting the benefits of joint optimization across multiple parameters, such as precoding matrices and power-control factors, in dynamic UAV scenarios. This oversimplification poses challenges, as it prevents the full utilization of potential security enhancements. Additionally, the non-convex nature of the associated optimization problems complicates the design of efficient algorithms. Therefore, overcoming these limitations is crucial for achieving optimal performance in UAV communications under practical deployment conditions.

In this paper, we propose an AN-GSDM framework to enhance the security of downlink UAV communication systems. Specifically, we derive the secrecy rate expression for the AN-GSDM system and formulate a joint optimization problem. To address the non-convex nature of this problem, we develop an alternating iterative algorithm. The key contributions of this work are as follows: (1) We introduce artificial noise (AN) into the generalized spatial directional modulation (GSDM) system to further enhance its security. We analyze the impact of multiple parameters, including the precoding matrix and power-control factors, on the secrecy rate of the AN-GSDM system. (2) The proposed method jointly optimizes the precoding matrix and power-control factors to efficiently manage multi-beam transmissions and artificial noise. By leveraging approximation techniques and alternating optimization, we solve the non-convex joint optimization problem, making the approach more applicable to real-world systems. (3) Simulation results validate the superior security performance and robust convergence properties of the proposed approach. Moreover, the method demonstrates strong performance even under high dynamic conditions and with localization errors, highlighting its practical viability in real-world UAV communication scenarios.

Compared to traditional systems, the AN-GSDM framework, combined with the proposed joint optimization algorithm, maximizes security and offers numerous practical applications, including UAV military confidential communications, UAV private information image transmission, and UAVs serving as relay stations for private information transmission. For instance, in widely used 5G and upcoming 6G systems, UAVs acting as relay stations can transmit private information. Some distributed receiving stations may be compromised by external intrusions, turning them into eavesdroppers. In such cases, UAVs can obtain the location and channel information of legitimate receivers and, to some extent, the information of eavesdroppers. By introducing the AN-GSDM system and jointly optimizing the precoding matrix and power allocation factor, this approach enhances the spatial distribution of resources—such as the precoding matrix controlling the power and beam distribution of the useful signal, and the power allocation factor controlling the distribution of noise power. This ensures that sensitive information is protected from interception by eavesdroppers, thereby safeguarding the security of private information transmission. This approach aligns with the advancements in integrating UAVs into 5G and beyond networks, as discussed in the recent literature [23]. By incorporating the AN-GSDM framework, UAVs can efficiently manage multi-beam transmissions and artificial noise, optimizing power resources to ensure secure communication channels even in the presence of potential eavesdroppers.

The remainder of this paper is organized as follows: Section 2 introduces the system model for AN-GSDM. Section 3 presents the proposed iterative algorithm for jointly optimizing the precoding matrix and power-control factor to maximize the secrecy rate. Section 4 provides simulation results to validate the analytical findings and illustrate the effectiveness of the proposed scheme. Finally, Section 5 concludes this paper, summarizing its key contributions and potential implications.

2. System Model

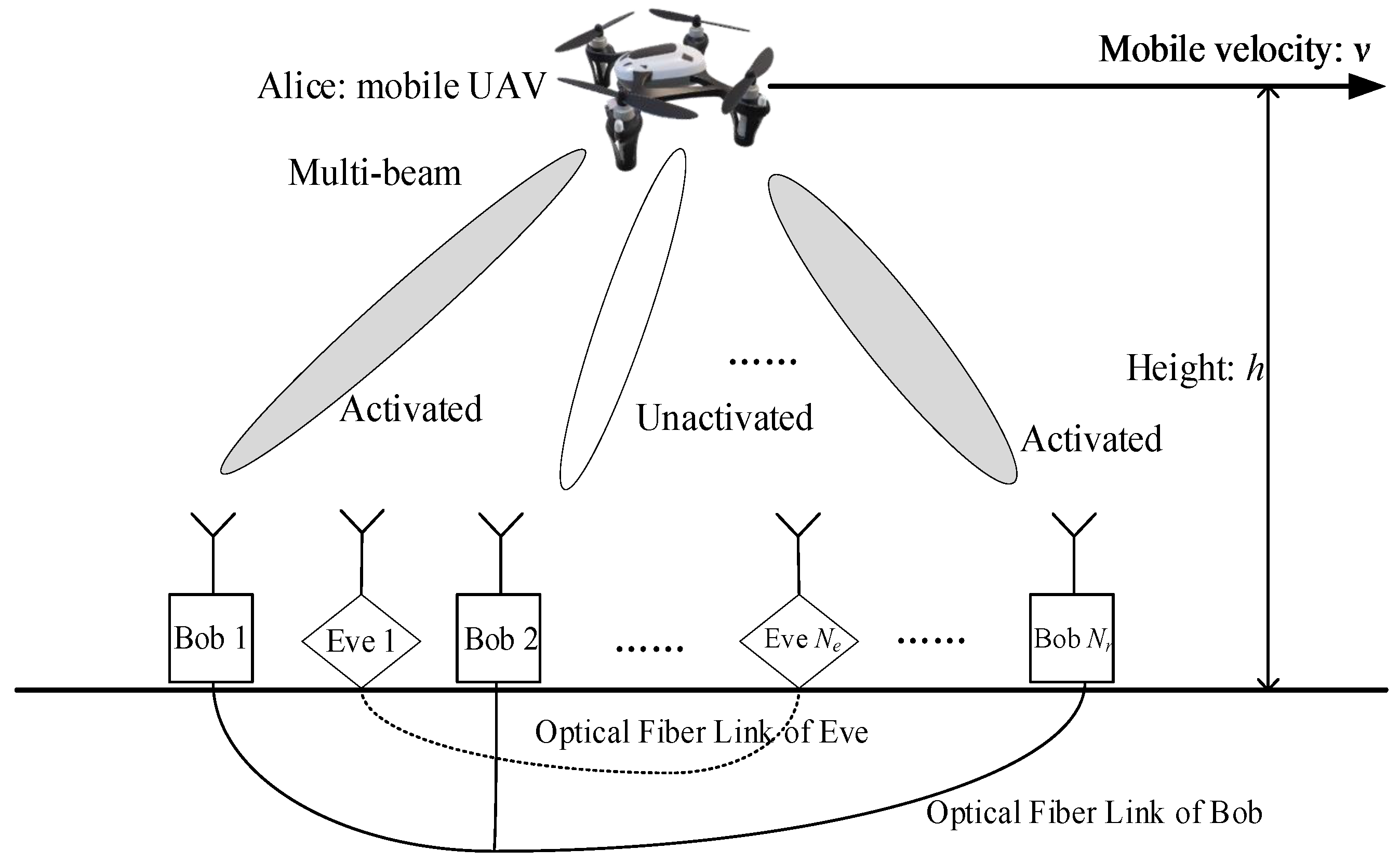
As shown in Figure 1, consider a downlink UAV communication system employing AN-GSDM, where the mobile UAV transmitter, Alice, is equipped with $N_t$ antennas, and the legitimate user, Bob, is equipped with $N_r$ ($N_r<N_t$) cooperative single-antenna receivers, which are located in different spatial directions and interconnected via optical fiber links. Additionally, Bob activates $N_u$ receivers for communication in a single time slot, where $N_u<N_r$, meaning that only a subset of Bob’s receivers participate in the transmission. Meanwhile, the eavesdropper, Eve, is equipped with $N_e$ ($N_e<N_t$) cooperative single-antenna receivers, which are also interconnected via optical fiber links.

Unlike the single-beam transmission in SDM, GSDM introduces receiver subset selection (RSS), which allows information to be transmitted through $N_u$ activated beams selected from $N_r$ available beams. This enables the transmission of $k_1={\log }_2{C}_{N_r}^{N_u}$ bits of information. Note that $k_1$ might be a fractional value. In practical system design, it is typically rounded down to meet encoding requirements. However, for performance analysis, such as the security rate, the exact value of $k_1$ can be used. The $N_u$ activated antennas use traditional M-dimensional amplitude and phase modulation (APM), allowing for the transmission of $k_2=N_u{\log }_{2}M$ bits of information. Furthermore, the total number of transmitted bits is $k=k_1+k_2$. The multiple beams are used to transmit information in GSDM to Bob’s multiple distributed receivers, which serve to enhance both the secrecy rate and transmission performance.

The transmitted symbol vector ${\mathbf{s}}_l^m$ is ${\mathbf{s}}_l^m={\mathbf{I}}_l{\mathbf{b}}_m$, where ${\mathbf{I}}_l\left(l=1,2,\cdots ,2^{k_1}\right)$, is a matrix consisting of $N_u$ column vectors selected from the identity matrix ${\mathbf{I}}_{N_r}$, corresponding to the $N_u$ activated receivers. ${\mathbf{b}}_m\left(m=1,2,\cdots ,2^{k_2}\right)$ denotes a column vector constructed from $N_u$ symbols selected from conventional APM symbols.

Without loss of generality, assume that Alice is equipped with a uniform linear array (ULA), where the phase center is the geometric center of the array. The channel vector between Alice and the receiver located in the direction of angle $\theta$ is then expressed as

$$\mathbf{h}(\theta )={\displaystyle \frac{1}{\sqrt{N_t}}}{\left[e^{-j\left({\displaystyle \frac{N_t-1}{2}}\right){\displaystyle \frac{2\pi }{\lambda }}dcos\theta },e^{-j\left({\displaystyle \frac{N_t-1}{2}}-1\right){\displaystyle \frac{2\pi }{\lambda }}dcos\theta },\dots ,e^{j\left({\displaystyle \frac{N_t-1}{2}}\right){\displaystyle \frac{2\pi }{\lambda }}dcos\theta }\right]}^H,$$

(1)

where $\lambda$ is wavelength and d is is the antenna spacing of ULA. Let ${\mathsf{\Theta }}_b=\left({\theta }_b^1,\cdots ,{\theta }_b^{N_r}\right)$ be the set of arrival angles for Bob’s receivers, and let ${\mathsf{\Theta }}_e=\left({\theta }_e^1,\cdots ,{\theta }_e^{N_e}\right)$ be the set of arrival angles for Eve’s receivers. The legitimate downlink channel between Alice and Bob, as well as the eavesdropping downlink channel between Alice and Eve, can be represented, respectively, as follows:

$$\mathbf{H}\left({\mathsf{\Theta }}_b\right)={\left[\mathbf{h}\left({\theta }_b^1\right),\cdots ,\mathbf{h}\left({\theta }_b^{N_r}\right)\right]}^H,\mathbf{H}\left({\mathsf{\Theta }}_e\right)={\left[\mathbf{h}\left({\theta }_e^1\right),\cdots ,\mathbf{h}\left({\theta }_e^{N_e}\right)\right]}^H.$$

(2)

To enhance the security, multi-beam precoding and AN are introduced to obscure the eavesdropper’s ability. The transmitted symbol with precoding and AN is

$${\mathbf{x}}_l^m=\zeta \mathbf{P}{\mathbf{s}}_l^m+{\mathbf{V}}^0{\mathbf{n}}_a,$$

(3)

where $\mathbf{P}$ is a precoding matrix with power constrain $\mathrm{tr}\left(\mathbf{P}{\mathbf{P}}^H\right)=P_t$, $\zeta$ is the power-control factor, and ${\mathbf{V}}^0{\mathbf{n}}_a$ is random AN. Consider designing the AN in the null space of Bob’s channel, ensuring that it does not affect the signal received by Bob but interferes with the signal received by Eve. Thus, ${\mathbf{V}}^0$ can be obtained by performing singular value decomposition on $\mathbf{H}\left({\mathsf{\Theta }}_b\right)$, such that it satisfies $\mathbf{H}=\mathbf{U}\left[\mathbf{D},\mathbf{0}\right]{\left[{\mathbf{V}}^{\mathbf{1}},{\mathbf{V}}^{\mathbf{0}}\right]}^H$. ${\mathbf{n}}_a$ is complex Gaussian white noise with a mean of 0 and element-wise variance ${\sigma }_a^2={\displaystyle \frac{\left(1-{\zeta }^2\right)P_t}{N_t-N_r}}$.

The received signals for Bob and Eve are, respectively,

$${\mathbf{y}}_b=\zeta \mathbf{H}\left({\mathsf{\Theta }}_b\right)\mathbf{P}{\mathbf{s}}_l^m+\underset{\triangleq \mathbf{0}}{\underbrace{\mathbf{H}\left({\mathsf{\Theta }}_b\right){\mathbf{V}}^0{\mathbf{n}}_a}}+{\mathbf{n}}_b=\zeta \mathbf{H}\left({\mathsf{\Theta }}_b\right)\mathbf{P}{\mathbf{s}}_l^m+{\mathbf{n}}_b,$$

(4)

$${\mathbf{y}}_e=\zeta \mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{s}}_l^m+\underset{\triangleq \mathbf{n}}{\underbrace{\mathbf{H}\left({\mathsf{\Theta }}_e\right){\mathbf{V}}^0{\mathbf{n}}_a+{\mathbf{n}}_e}},$$

(5)

where ${\mathbf{n}}_r$ and ${\mathbf{n}}_e$ are zero-mean complex Gaussian white noise with element-wise variances of ${\sigma }_b^2$ and ${\sigma }_e^2$, respectively. $\mathbf{n}$ consists of AN-caused interference and thermal noise with variance $\mathsf{\Sigma }={\sigma }_a^2\mathbf{H}\left({\mathsf{\Theta }}_e\right){\mathbf{V}}^0{\left({\mathbf{V}}^0\right)}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)+{\sigma }_e^2{\mathbf{I}}_{N_e}$. It is noted that $0\le \zeta \le 1$, when $\zeta =1$, with the above two models representing the case without AN.

Due to the inherent mobility of the UAV, the relative positions between Alice, Bob, and Eve are continuously changing. This dynamic movement leads to variations in the angles of arrival (AoAs) of the transmitted signals at both the legitimate receiver and the eavesdropper. Consequently, the fluctuations in these AoAs introduce challenges in maintaining a secure communication link, as the UAV must adapt its transmission strategy in real time to mitigate eavesdropping risks. To address this, it becomes essential to optimize the precoding matrix and power-control factor based on the constantly changing arrival angles. By doing so, the system can effectively manage the interference on Eve introduced by the AN while simultaneously ensuring the reliable reception of data by the legitimate receiver, thus enhancing the overall transmission security.

3. Enhancing Security Through Joint Precoding and Artificial Noise Design

The precoding matrix $\mathbf{P}$ is responsible for controlling multiple beams, while the power-control factor $\zeta$ governs both the AN power and beam gain. These two parameters are tightly coupled and jointly contribute to secure transmission. Optimizing only one of them in isolation would be insufficient to enhance security. Specifically, through joint optimization of these parameters, the multi-beam parameters and artificial noise power (i.e., the interference caused to Eve) can be controlled under different positions and signal-to-noise ratios (SNRs), thereby maximizing the enhancement of transmission security. In this section, we take the secrecy rate as the objective for security enhancement and conduct a thorough analysis and optimization.

3.1. Problem Formulation

Suppose that the joint maximum likelihood detector is employed for both Bob and Eve; the achievable rates between Alice and both Bob and Eve can be computed separately. Define $\mathcal{S}$ as the set of all transmitted symbols and $∥·∥$ as the Frobenius norm, with Bob’s rate $R_b$ being [22,24]

$$R_b=k-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\mathbb{E}}_{{\mathbf{n}}_r}\left[{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_b\right)\right)\right],$$

(6)

where ${\mathsf{\Omega }}_b={\displaystyle \frac{-{∥\zeta \mathbf{H}\left({\mathsf{\Theta }}_b\right)\mathbf{P}\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right)+{\mathbf{n}}_b∥}^2+{∥{\mathbf{n}}_b∥}^2}{{\sigma }_b^2}}$.

The AN makes the rate calculation for Eve slightly more complex. In order to derive Eve’s rate, we multiple ${\mathsf{\Sigma }}^{-1/2}$ on both sides of Equation (5), and then we can similarly obtain the expression of Eve’s rate as

$$R_e=k-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\mathbb{E}}_{\mathbf{n}}\left[{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_e\right)\right)\right],$$

(7)

where ${\mathsf{\Omega }}_e=-{∥\zeta {\mathsf{\Sigma }}^{-1/2}\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right)+{\mathsf{\Sigma }}^{-1/2}\mathbf{n}∥}^2+{∥{\mathsf{\Sigma }}^{-1/2}\mathbf{n}∥}^2$.

The secrecy rate R is defined as the difference between the achievable rates of Bob and Eve, and it can be written as

$$R={\left[{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\mathbb{E}}_{{\mathbf{n}}_b,\mathbf{n}}\left[{\log }_2\left({\displaystyle \frac{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_e\right)}{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_b\right)}}\right)\right]\right]}^{+},$$

(8)

where ${\left[·\right]}^{+}=max\left\{·,0\right\}$.

As a result, the secrecy rate optimization problem through joint precoding and power-control factor design is formulated as

$$\begin{array}{cc}\hfill & \underset{\mathbf{P},\zeta }{max}R\left(\mathbf{P},\zeta \right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}\mathrm{tr}\left(\mathbf{P}{\mathbf{P}}^H\right)\le P_t\hfill \\ \hfill & 0\le \zeta \le 1,\hfill \end{array}$$

(9)

Note that the optimization problem is non-convex and contains highly complex terms, making it intractable to derive a globally optimal closed-form solution. Furthermore, the expectation operator requires averaging over multiple noise realizations, which adds significant computational complexity. For this optimization problem, a more efficient approach is necessary to avoid the difficulties associated with solving explicit expressions.

In this scenario, both Eve and Bob are assumed to have identical reception capabilities, representing the “worst-case” scenario in practical systems. Under these conditions, Eve’s achievable rate serves as an “upper bound”, while the system’s secrecy rate represents the “lower bound” of secure communication. The optimization design aims to maximize the “lower bound” of the secrecy rate while minimizing (approaching zero) the “upper bound” of Eve’s achievable rate. By developing an optimization algorithm in this context, even if Eve has weaker reception capabilities than Bob (e.g., if Eve does not fully understand the GSDM symbol mapping rules), the actual achievable secrecy rate will exceed the optimized value, thus enhancing the system’s security. This approach ensures that the system’s security rate exceeds the optimized security rate derived in this paper under practical scenarios where Eve possesses limited or incomplete information.

3.2. Secrecy Rate Optimization Through Joint Precoding and Artificial Noise Design

In this subsection, we propose a low-complexity approach to solve the optimization problem in (9). We consider an alternating optimization method. When $\zeta$ is fixed, we derive a lower bound for the secrecy rate and optimize this bound to enhance the secrecy rate. When $\mathbf{P}$ is fixed, we use a method based on maximizing the product of the SNR at Bob and the interference-to-signal-plus-noise ratio (ISNR) at Eve to obtain a suboptimal solution for $\zeta$. This alternating optimization approach is commonly used in many classical algorithms, such as variational Bayesian methods. Since each alternating optimization step guarantees an increase in the secrecy rate, the convergence of the algorithm is naturally ensured.

In the following, we are committed to solving the optimization problems for the two parameters separately.

(1) Optimizing $\mathbf{P}$ with fixed $\zeta$: For fixed $\zeta$, combining [25] with Jensen’s inequality, and through a tedious yet straightforward derivation, we obtain the lower bound of Bob’s rate $R_b$ and Eve’s rate $R_e$ as

$$\begin{array}{cc}\hfill R_b\ge & k-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}{\mathbb{E}}_{{\mathbf{n}}_r}\left[exp\left({\mathsf{\Omega }}_b\right)\right]\right)\hfill \\ \hfill =& k-N_b\left({\log }_{2}e-1\right)-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_b^{\prime }\right)\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill R_e\ge & k-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}{\mathbb{E}}_{\mathbf{n}}\left[exp\left({\mathsf{\Omega }}_e\right)\right]\right)\hfill \\ \hfill =& k-N_b\left({\log }_{2}e-1\right)-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_e^{\prime }\right)\right)\hfill \end{array}$$

(11)

with ${\mathsf{\Omega }}_b^{\prime }={\displaystyle \frac{-{∥\zeta \mathbf{H}\left({\mathsf{\Theta }}_b\right)\mathbf{P}\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right)∥}^2}{2{\sigma }_b^2}}$ and ${\mathsf{\Omega }}_e^{\prime }=-{\displaystyle \frac{1}{2}}{∥\zeta {\mathsf{\Sigma }}^{-1/2}\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right)∥}^2$. According to [25], the lower bound of those two secrecy rate expressions, when increased by a constant $N_b\left({\log }_{2}e-1\right)$ and $N_e\left({\log }_{2}e-1\right)$, respectively, provide a tighter lower bound that can be approximated as the secrecy rate. Therefore, we have the following:

$$R_{b,L}=k-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_b^{\prime }\right)\right),$$

(12)

$$R_{e,L}=k-{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left(\sum _{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_e^{\prime }\right)\right).$$

(13)

Thus, we can obtain the lower bound $R_L(\mathbf{P})$ for the secrecy rate $R(\mathbf{P})$ as

$$R_L\left(\mathbf{P}\right)={\left[R_{b,L}-R_{e,L}\right]}^{+}={\left[{\displaystyle \frac{1}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\log }_2\left({\displaystyle \frac{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_e^{\prime }\right)}{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_b^{\prime }\right)}}\right)\right]}^{+}$$

(14)

The subproblem centers around finding the optimal $\mathbf{P}$ that maximizes the lower bound of the secrecy rate $R_L\left(\mathbf{P}\right)$, which is formulated as

$$\begin{array}{cc}\hfill & \underset{\mathbf{P}}{max}{R}_L\left(\mathbf{P}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}\mathrm{tr}\left(\mathbf{P}{\mathbf{P}}^H\right)\le P_t.\hfill \end{array}$$

(15)

We resort to a gradient descent to solve the above problem, and we further need to compute the gradient of the objective function with respect to $\mathbf{P}$, which is given by

$$\begin{array}{cc}\hfill {▽}_{\mathbf{P}}{R}_L\left(\mathbf{P}\right)& ={\displaystyle \frac{{\log }_{2}e}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\displaystyle \frac{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}{\mathsf{\Xi }}_b\mathbf{P}\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right){\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right)}^{H}exp\left({\mathsf{\Omega }}_b^{\prime }\right)}{{\sigma }_b^2{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_b^{\prime }\right)}}-\hfill \\ & {\displaystyle \frac{{\log }_{2}e}{2^k}}\sum _{{\mathbf{s}}_l^m\in \mathcal{S}}{\displaystyle \frac{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}{\mathsf{\Xi }}_e\mathbf{P}\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right){\left({\mathbf{s}}_l^m-{\mathbf{s}}_i^m\right)}^{H}exp\left({\mathsf{\Omega }}_e^{\prime }\right)}{{\sum }_{{\mathbf{s}}_i^m\in \mathcal{S}}exp\left({\mathsf{\Omega }}_e^{\prime }\right)}}\hfill \end{array}$$

(16)

with ${\mathsf{\Xi }}_b={\zeta }^2{\mathbf{H}}^H\left({\mathsf{\Theta }}_b\right)\mathbf{H}\left({\mathsf{\Theta }}_b\right)$ and ${\mathsf{\Xi }}_e={\zeta }^2{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right){\left({\mathsf{\Sigma }}^{-1/2}\right)}^H{\mathsf{\Sigma }}^{-1/2}\mathbf{H}\left({\mathsf{\Theta }}_e\right)$.

The proposed algorithm-based gradient descent to solve (15) is summarized in Algorithm 1.

Algorithm 1 An iterative algorithm based on gradient descent to solve $\mathbf{P}$ for maximizing the secrecy rate with fixed $\zeta$

initialization: Set the initial step size $\delta$, the minimum step size ${\delta }_{\min }$, the iteration index $t=0$, and the maximum iteration number $t_{\max }$. Set the fixed power-control factor $\zeta$. Set the initial precoding matrix ${\mathbf{P}}_0$ with constrain $\mathrm{tr}\left({\mathbf{P}}_0{\mathbf{P}}_0^H\right)\le P_t$. while $t<t_{\max }$ do Set $t=t+1$. Compute $R_{L,t-1}=R_L({\mathbf{P}}_{t-1})$ based on (14). If $\delta \ge {\delta }_{\min }$, go to the next step. Otherwise, output ${\mathbf{P}}_{t-1}$ and stop. Compute the gradient ${▽}_{\mathbf{P}}{R}_L\left({\mathbf{P}}_{t-1}\right)$ based on (16). Set ${\mathbf{P}}_t^{\prime }={\mathbf{P}}_{t-1}+\delta {▽}_{\mathbf{P}}{R}_L\left({\mathbf{P}}_{t-1}^{\prime }\right)$. ${\mathbf{P}}_t^{\prime }={\displaystyle \frac{\sqrt{P_t}{\mathbf{P}}_t^{\prime }}{\sqrt{\mathrm{tr}({\mathbf{P}}_t^{\prime }{({\mathbf{P}}_t^{\prime })}^H)}}}$. Compute $R_{L,t}^{\prime }=R_L({\mathbf{P}}_t)$ based on (14). If $R_{L,t}^{\prime }>R_{L,t-1}$, set $R_{L,t}=R_{L,t}^{\prime }$, ${\mathbf{P}}_t={\mathbf{P}}_t^{\prime }$. Otherwise, set $\delta =\delta /2$ and return to Step 3. end Output: $\mathbf{P}={\mathbf{P}}_t$.

(2) Optimizing $\zeta$ with fixed $\mathbf{P}$: For a fixed precoding matrix $\mathbf{P}$, the optimization problem in (9) centers around finding a $\zeta$ that maximizes the secrecy rate. Based on the approach proposed in [26], we maximize the product of the SNR at Bob and the ISNR at Eve to obtain a suboptimal closed-form solution for $\zeta$. Intuitively, the physical meaning of this approach is to adjust the value of $\zeta$ in order to maximize the SNR at Bob while increasing the interference at Eve and reducing the signal strength at Eve, thereby enhancing the secrecy rate. Specifically, the product of the SNR at Bob and the ISNR at Eve is

$$F\left(\zeta \right)=\underset{\mathrm{SNR}\mathrm{at}\mathrm{Bob}}{\underbrace{{\displaystyle \frac{{\zeta }^2\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_b\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_b\right)\right)}{{\sigma }_b^2}}}}\times \underset{\mathrm{ISNR}\mathrm{at}\mathrm{Eve}}{\underbrace{{\displaystyle \frac{\left(1-{\zeta }^2\right)P_t\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right){\mathbf{V}}^0{\left({\mathbf{V}}^0\right)}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)}{\left(N_t-N_r\right)\left({\sigma }_e^2+{\zeta }^2\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)\right)}}}}$$

(17)

Let ${\zeta }^2=\kappa$, and then the first derivative of the function $F\left(\kappa \right)$ with respect to $\kappa$ is

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial F\left(\kappa \right)}{\partial \kappa }}=& {\displaystyle \frac{P_t\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_b\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_b\right)\right)\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right){\mathbf{V}}^0{\left({\mathbf{V}}^0\right)}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)}{{\sigma }_b^2}}\hfill \\ & \times {\displaystyle \frac{-\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right){\kappa }^2-2{\sigma }_e^2\kappa +{\sigma }_e^2}{\left(N_t-N_r\right)\left({\sigma }_e^2+{\zeta }^2\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)\right)}}\hfill \end{array}$$

(18)

Solving the equation ${\displaystyle \frac{\partial F\left(\kappa \right)}{\partial \kappa }}=0$ under the condition $0\le \kappa \le 1$, we obtain the closed-form solution for $\kappa$, which is

$${\kappa }_{opt}={\displaystyle \frac{-{\sigma }_e^2+\sqrt{{\sigma }_e^4+{\sigma }_e^2\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)}}{\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)}}$$

(19)

It can be noticed that when $\kappa <{\kappa }_{opt}$, we have ${\displaystyle \frac{\partial F\left(\kappa \right)}{\partial \kappa }}>0$, and when $\kappa >{\kappa }_{opt}$, we have ${\displaystyle \frac{\partial F\left(\kappa \right)}{\partial \kappa }}<0$. Thus, ${\kappa }_{opt}$ is the largest value in $0\le \kappa \le 1$, and the closed-form solution for $\zeta$ is

$$\zeta =\sqrt{{\displaystyle \frac{-{\sigma }_e^2+\sqrt{{\sigma }_e^4+{\sigma }_e^2\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)}}{\mathrm{tr}\left(\mathbf{H}\left({\mathsf{\Theta }}_e\right)\mathbf{P}{\mathbf{P}}^H{\mathbf{H}}^H\left({\mathsf{\Theta }}_e\right)\right)}}}$$

(20)

Finally, we obtain the algorithm for joint optimization of $\mathbf{P}$ and $\zeta$, as shown in Algorithm 2. When the UAV is moving, there may be inaccuracies in the acquisition of Bob’s and Eve’s channel state information. During secrecy rate optimization, the actual channel matrices used for Bob and Eve are $\mathbf{H}\left({\mathsf{\Theta }}_b^{\prime }\right)$ and $\mathbf{H}\left({\mathsf{\Theta }}_e^{\prime }\right)$, respectively, where ${\mathsf{\Theta }}_b^{\prime }$ and ${\mathsf{\Theta }}_e^{\prime }$ represent the estimated arrival angle information of Bob and Eve by the UAV.

Note that in the previous section, we only presented the system model for a ULA configuration with a Line-of-Sight (LOS) channel. This model is applicable to scenarios with high flight altitudes and open ground areas, covering many practical applications. Although we have provided only this specific channel model, the AN-GSDM framework is actually applicable to any channel model, as long as the channel matrix for both the legitimate receiver and the eavesdropper can be accurately (or approximately) obtained. The system optimization design can then proceed based on this information.

In the following simulations, we will introduce various types of channel models, including Rician [27], Kronecker [28], Saleh–Valenzuela (SV) [29], and CDL channels [30]. The Rician channel model represents rich scattering channels, considering multipath interference (both LOS and Non-Line-of-Sight (NLOS) paths), as well as the Kronecker channel correlation. The SV and CDL channels provide a detailed description of multipath structures.

The physical meaning of the precoding matrix varies across different channel models. For example, in rich scattering models, traditional beamforming becomes ineffective (due to the lack of directionality), and the precoding matrix controls the spatial power distribution rather than the physical beam directions. In the SV model, precoding may optimize several angle clusters, forming multiple beams that cover the main directions of these clusters, or it may focus on interference suppression. In the LOS model, Eve’s location and angle are directly related, and precoding controls the beams to degrade the signal quality in Eve’s direction. In the multipath model, Eve might receive signals through multiple paths, and the precoding needs to consider all possible paths to design more complex interference strategies. Although the implementation of these objectives changes with different channel characteristics, the essence of precoding remains the same: it is a spatial resource optimization strategy aimed at enhancing physical-layer security.

Algorithm 2 An iterative algorithm for the joint optimization of $\mathbf{P}$ and $\zeta$ for maximizing the secrecy rate.

initialization: Set the iteration index $d=0$, and the maximum iteration number $d_{\max }$. Set the initial power-control factor ${\zeta }_0$, and the error tolerance $\epsilon$. while $d<d_{\max }$ and ${∥R_{L,d}-R_{L,d-1}∥}^2>\epsilon$ do Set $d=d+1$. Compute ${\mathbf{P}}_t$ by substituting ${\zeta }_{d-1}$ into Algorithm 1, and set ${\mathbf{P}}_d={\mathbf{P}}_t$. Compute ${\zeta }_d$ by substituting ${\mathbf{P}}_d$ into (20). Compute $R_{L,d}=R_L({\mathbf{P}}_d,{\zeta }_d)$ based on (14). end Output: $\mathbf{P}={\mathbf{P}}_d$, $\zeta ={\zeta }_d$.

4. Simulation and Discussion

Simulations are conducted to evaluate the effectiveness of the proposed security optimization (denoted as ‘Proposed’) algorithm for the GDSM system. During the simulations, we set $N_t=4$, $N_r=3$, $N_u=2$, $N_e=2$ and $P_t=N_r$. The angles of Bob’s distributed receivers are ${\mathsf{\Theta }}_b=\left({30}^{\circ },{50}^{\circ },{70}^{\circ }\right)$, and the angles of Eve’s distributed receivers are ${\mathsf{\Theta }}_e=\left({20}^{\circ },{45}^{\circ }\right)$. Quadrature Phase Shift Keying (QPSK) is employed for APM realization, and each simulated secrecy rate is obtained through ${10}^4$ Monte Carlo realizations. When executing the proposed algorithm, we set $d_{max}=20$, ${\zeta }_0=0.8$, $\epsilon ={10}^{-4}$, $\delta =0.5$, ${\delta }_{min}={10}^{-4}$, and $t_{max}=50$. We assume identical noise power at both Bob and Eve, and the SNR is defined as $1/{\sigma }_b^2$. The channel data are generated based on the models provided in Equation (2), which defines the channel matrices for Bob and Eve, respectively.

Both mobile and stationary UAV scenarios are considered, corresponding to cases with and without processing delay. When there is no processing delay, the angles of Bob and Eve used for the joint design of precoding and power-control factors at the UAV are accurate. Conversely, in the presence of processing delay, the angles of Bob and Eve at the UAV are obtained from the previous time step, leading to deviations from the current angle values. In addition, conventional zero-forcing (ZF) precoding [22] ($\mathbf{P}=\mathbf{H}\left({\mathsf{\Theta }}_b\right){(\mathbf{H}\left({\mathsf{\Theta }}_b\right){\mathbf{H}}^H\left({\mathsf{\Theta }}_b\right))}^{-1}$, denoted as ‘ZF’) and the precoding method ($\mathbf{P}=\mathbf{H}\left({\mathsf{\Theta }}_b\right)/N_t$, denoted as ‘Maxbeam’) that maximize the power in Bob’s direction [20], combined with different power control factors $\zeta$, are used as benchmarks.

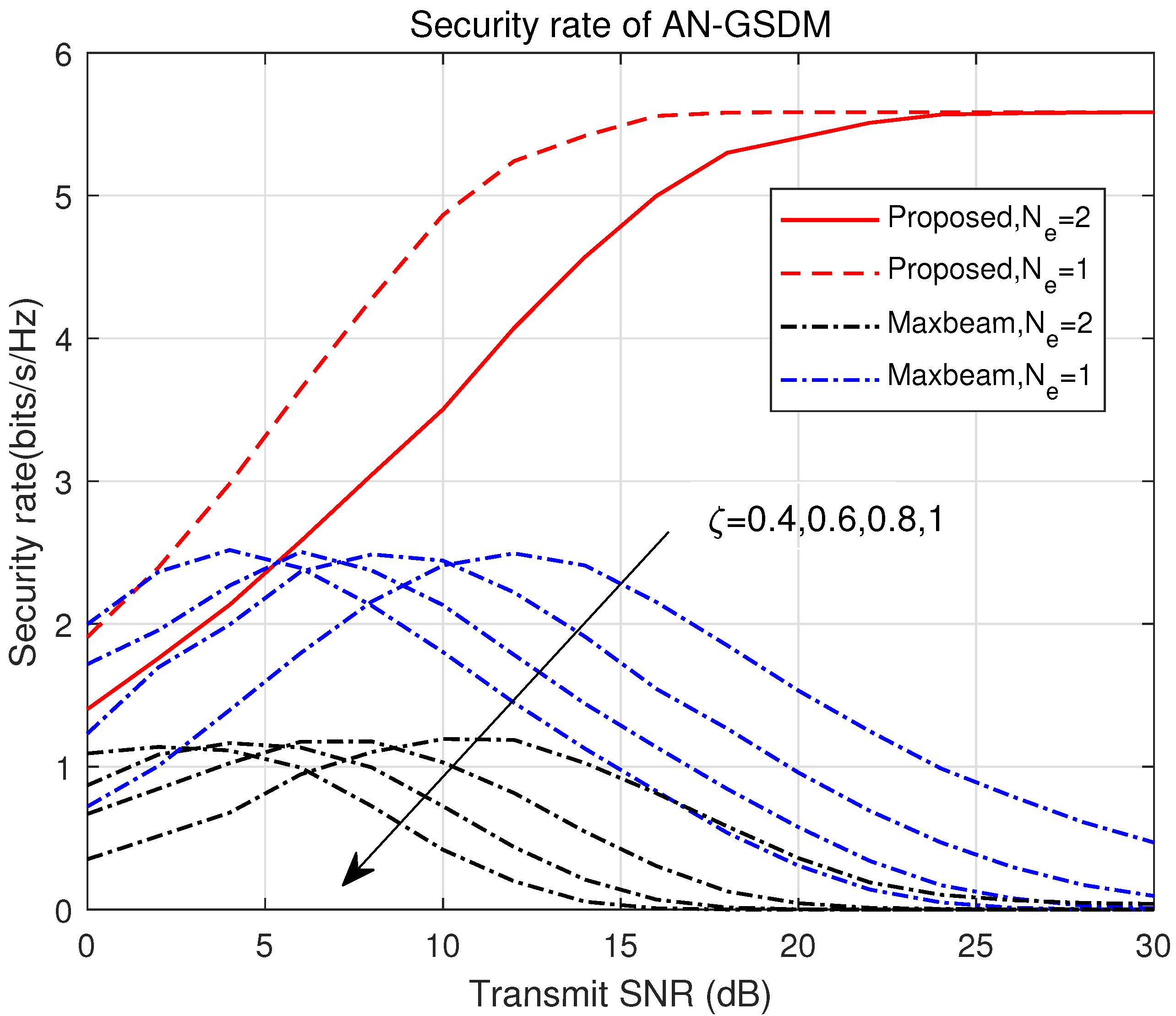
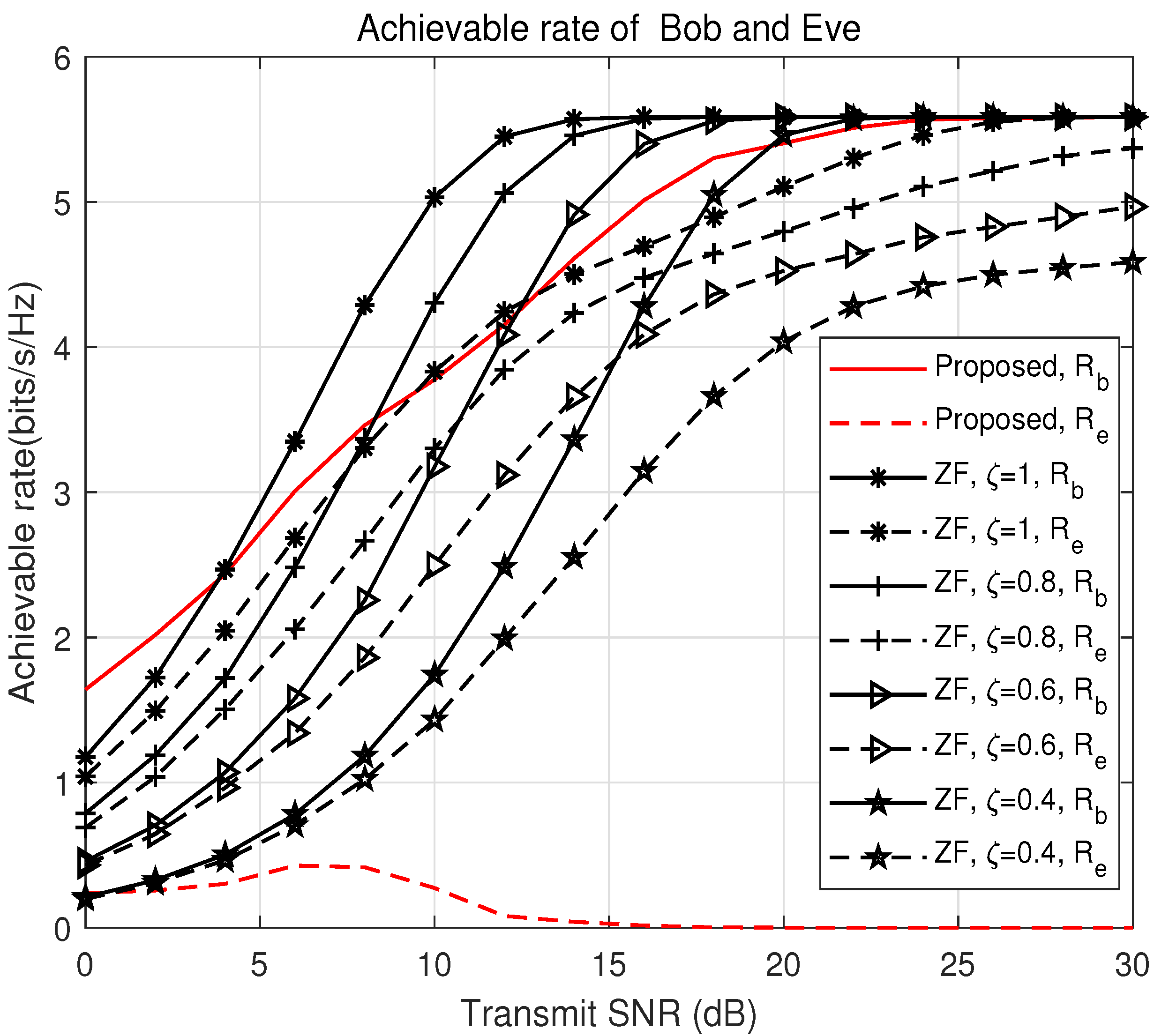
Figure 2 and Figure 3 present the system’s secrecy rate, and Figure 4 and Figure 5 present the achievable rates at Bob and Eve, under various precoding and power-control factors. The secrecy rate is defined as the difference between Bob’s and Eve’s achievable rates. Although maximizing this relative difference is critical, minimizing Eve’s absolute achievable rate is equally important. By reducing Eve’s achievable rate to the greatest extent possible, we can fundamentally restrict its ability to intercept information, even when Bob’s rate remains constant or decreases slightly. In addition, we show the secrecy rate when $N_e=1$ and ${\mathsf{\Theta }}_e={25}^{\circ }$ in Figure 2 and Figure 3.

The results in Figure 2, Figure 3, Figure 4 and Figure 5 demonstrate that the proposed optimization algorithm significantly outperforms the benchmarks in terms of the secrecy rate. Unlike the benchmarks, which fail to consider Eve’s location when controlling multiple beams and do not jointly optimize the precoding matrix and power-control factor, the proposed algorithm successfully mitigates information leakage. By employing a joint design approach, the algorithm balances the trade-off between maintaining Bob’s achievable rate and suppressing Eve’s interception capabilities. As the number of eavesdroppers increases, the secrecy rate decreases under low SNR conditions due to enhanced interference from multiple eavesdroppers. However, this decline is more pronounced in the low-SNR regime, where the number of eavesdroppers has a larger relative impact due to weaker signal strength. At this stage, the system faces higher interference from Eve, and further optimizations may be needed to counteract the increased noise levels. However, at a high SNR, the optimized secrecy rate eventually saturates, indicating the effectiveness of the proposed scheme in mitigating information leakage even in the presence of multiple eavesdroppers. Interestingly, this saturation suggests that the algorithm is nearing the optimal operating point, where increasing the SNR no longer provides substantial benefits in terms of secrecy rate improvement. Thus, while a high SNR is crucial for system performance, it does not lead to unlimited improvement in secrecy, implying that a careful balance of parameters is required.

Figure 6 and Figure 7 demonstrate the performance of the proposed algorithm under the Rician, Kronecker, SV, and CDL channel models. Similar to the results under the LOS channel, the optimization performance of the proposed algorithm significantly outperforms the baseline algorithms. Whether in the rich scattering Rician channel or the Kronecker channel with channel correlation, the proposed algorithm consistently delivers a substantial improvement in the system’s secrecy rate. This indicates that the proposed multi-beam optimization and power allocation strategy effectively suppresses the eavesdropper’s reception capability while ensuring the communication quality for the legitimate receiver across different channel environments. From the simulation results, although the secrecy rate in complex channel models (such as the Rician and Kronecker channels) is impacted by multipath interference, the proposed algorithm still maintains its advantage over traditional methods. In the SV and CDL channels, despite the additional challenges introduced by multipath propagation, the proposed precoding optimization strategy effectively handles interference suppression and maintains high security performance. In conclusion, regardless of the channel model, the proposed algorithm demonstrates strong advantages in enhancing physical-layer security and can adapt to dynamic variations in different propagation environments.

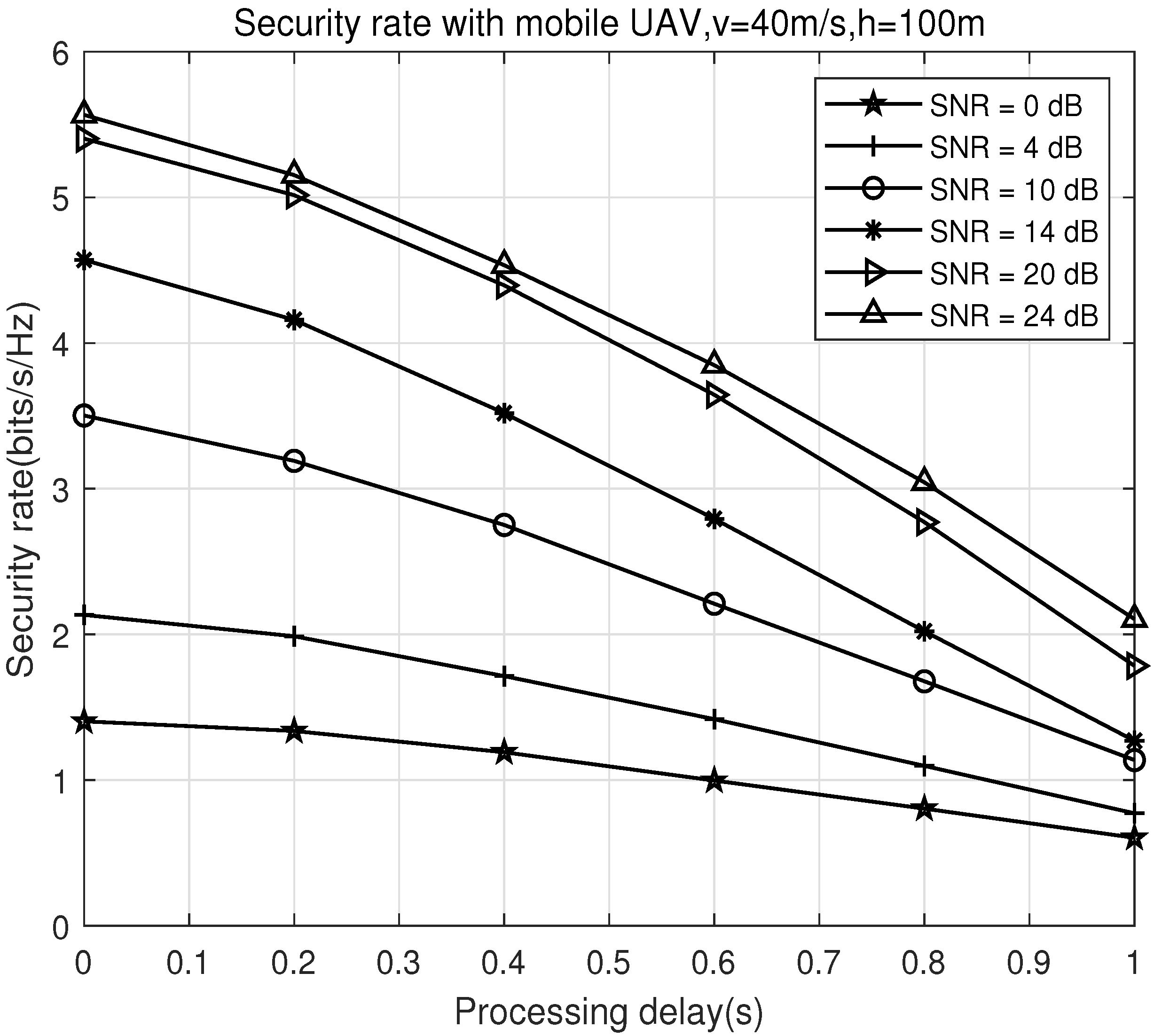
In Figure 8 and Figure 9, we analyze the performance of the proposed algorithm under the scenario of a moving UAV, considering processing delay and angular estimation errors. In Figure 8, the UAV height is set to $h=100\mathrm{m}$ and the speed is $v=40\mathrm{m}/\mathrm{s}$. The curves show the secrecy rate performance under different SNRs with a processing delay. As the SNR increases, the impact of processing delay on secrecy rate becomes more significant. At higher SNRs, the impact of processing delay is amplified because the UAV’s position and angle estimates are increasingly sensitive to delay, leading to greater angular inaccuracies for both Bob and Eve. This results in a decline in the secrecy rate. The increase in processing delay results in increasingly inaccurate angular information for Bob and Eve, leading to a decline in the secrecy rate. Therefore, the processing delay should be minimized to improve security. 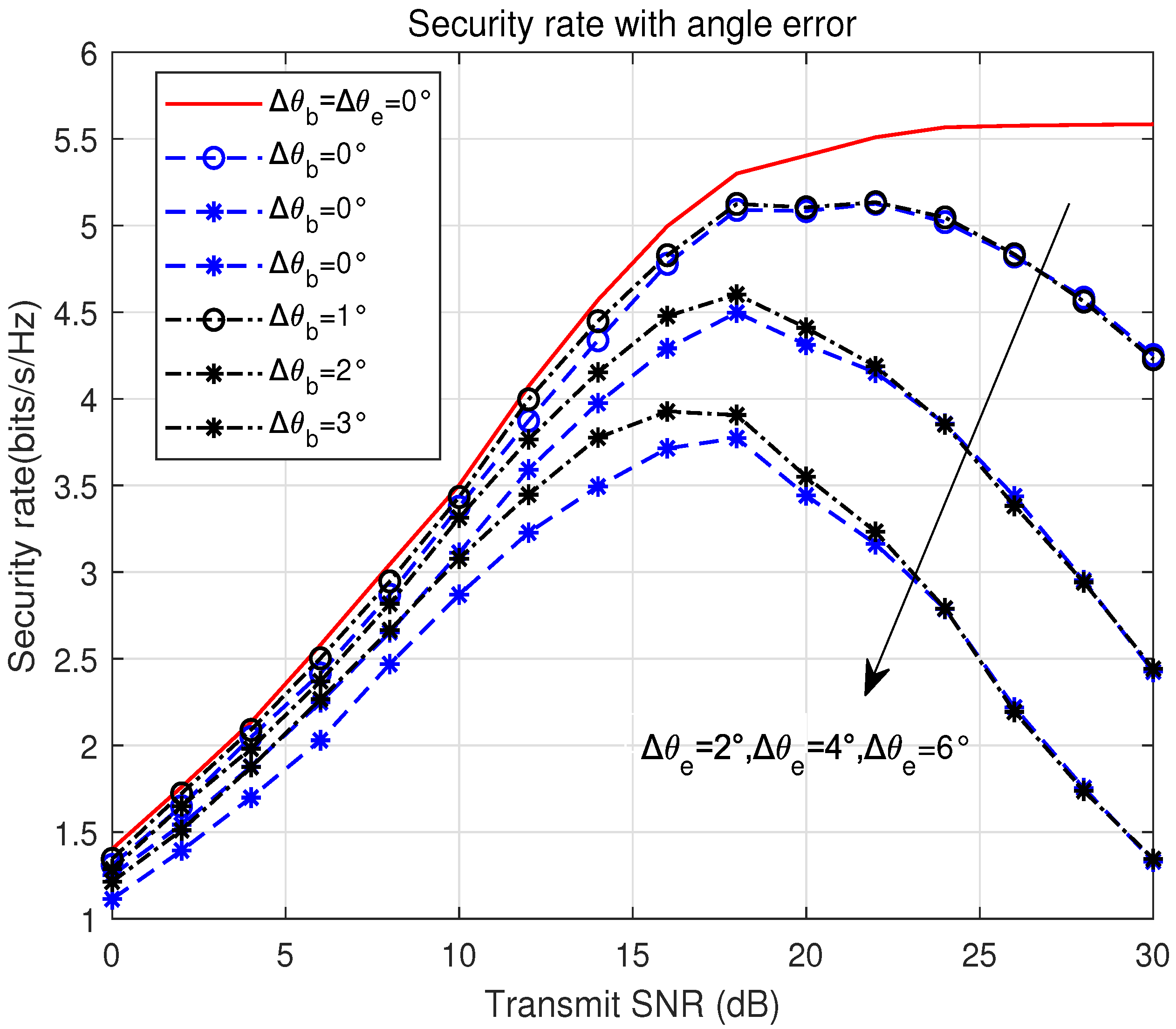In Figure 9, we present the secrecy rate when there are estimation biases in the arrival angles of Bob and Eve, assuming positive biases for both. Again, the secrecy rate is more sensitive to errors under high SNRs. Under higher SNR conditions, even small biases in the angle estimates lead to significant performance degradation, as the accuracy of angle information directly influences the alignment of the beams and the power distribution across the system. Additionally, the results indicate that the relative bias in Bob and Eve’s angle information significantly impacts the secrecy rate. This further suggests that the accuracy of the relative positions of Bob and Eve, as obtained by UAV Alice, has a greater effect on the secrecy rate than the absolute angular information. Therefore, ensuring that Alice accurately measures the relative angles between Bob and Eve becomes critical. This information should be continuously updated to mitigate the effects of angular errors.

Figure 10 shows the convergence behavior of the proposed algorithm under different SNRs. Over a wide range of SNRs, the proposed algorithm exhibits good convergence, with convergence achieved within two to six iterations. However, as the SNR increases, the number of iterations required for convergence also increases, suggesting that higher SNR scenarios are more computationally demanding. This may result in longer processing times; thus, real-time applications may require adjustments to optimize for convergence time. As the SNR increases, the number of iterations required for convergence increases, due to the fixed choice of the initial iteration value. Therefore, in practical applications, the initial iteration value can be flexibly chosen based on the SNR to accelerate convergence.

The proposed algorithm, while effective in improving the secrecy rate and enhancing the physical layer security, does have certain limitations. Firstly, the algorithm requires iterative optimization, as there is no closed-form analytical expression available for the problem. This iterative process increases the computational complexity, especially when the number of iterations or system parameters is large. Additionally, the algorithm necessitates the availability of partial channel state information (CSI) of both the legitimate user (Bob) and the eavesdropper (Eve), which may not always be feasible in practical systems due to limited feedback or imperfect channel estimation. Furthermore, the algorithm’s performance might degrade under extreme conditions, such as a very low SNR, high mobility scenarios, or when the system operates with inaccurate angle of arrival (AoA) estimations.

Future research will focus on addressing these limitations. One direction is to develop more efficient optimization techniques, potentially by leveraging machine learning approaches or adopting adaptive methods that reduce the dependency on iterative processes. Additionally, efforts will be made to enhance the algorithm’s robustness against incomplete or imperfect CSI, including the development of robust estimation and feedback protocols. Another avenue for improvement is extending the algorithm to handle dynamic environments, such as fast-moving UAVs or networks with fluctuating channel conditions, to ensure reliable security performance across diverse real-world applications.

5. Conclusions

This paper proposed a joint optimization framework designed to enhance the security of downlink UAV communication systems by integrating AN-GSDM. The proposed algorithm alternates between optimizing the precoding matrix and the power-control factor, effectively managing multi-beam transmissions and artificial noise (AN) to maximize the secrecy rate. Simulation results demonstrate the algorithm’s superior performance in improving transmission security by both maximizing the secrecy rate and ensuring robust protection against eavesdropping. Specifically, the algorithm minimizes Eve’s achievable rate to near zero, effectively rendering eavesdropping infeasible, while maintaining the achievable rate for Bob. Additionally, the proposed method successfully tackles the challenges posed by non-convex optimization and dynamic UAV communication environments, exhibiting strong convergence properties and offering a practical, efficient solution. The findings underscore the potential of this optimization framework to significantly enhance security in UAV communication systems, particularly in scenarios with increasing numbers of eavesdroppers or dynamic channel conditions. Future work will focus on refining the algorithm to improve scalability and performance in more complex multi-user environments, as well as exploring the integration of additional channel models and further optimization techniques.