Consensus-Based Formation Control for Heterogeneous Multi-Agent Systems in Complex Environments

Abstract

The purpose of this paper is to develop formation control strategies for heterogeneous multi-intelligent-agent systems in complex environments, with the goal of enhancing their performance, reliability, and stability. Complex flight conditions, such as navigating narrow gaps in urban high-rise buildings, pose considerable challenges for agent control. To address these challenges, this paper proposes a consensus-based formation strategy that integrates graph theory and multi-consensus algorithms. This approach incorporates time-varying group consistency to strengthen fault tolerance and reduce interference while ensuring obstacle avoidance and formation maintenance in dynamic environments. Through a Lyapunov stability analysis, combined with minimum dwell time constraints and the LaSalle invariance principle, this work proves the convergence of the proposed control scheme under changing network topologies. Simulation results confirm that the proposed strategy significantly improves system performance, mission execution capability, autonomy, synergy, and robustness, thereby enabling agents to successfully maintain formation and avoid obstacles in both homogeneous and heterogeneous clusters in complex environments.

1. Introduction

A heterogeneous multi-intelligent-agent system (MAS) comprises multiple types of agents with diverse functionalities to collaboratively accomplish complex tasks. Compared with homogeneous intelligent agent systems, heterogeneous systems have significant advantages in task allocation, resource utilization, flexibility, and robustness. By employing rational task division, efficient information sharing, and strategic path planning, heterogeneous multi-intelligent-agent systems are able to perform tasks safely and efficiently in complex terrains and multi-obstacle environments.

While the potential of these systems is vast, they are particularly challenged in dynamic, real-world environments, especially when it comes to maintaining stable formations under rapidly changing conditions. The effectiveness of traditional formation control strategies is limited in such contexts, especially for homogeneous systems. For instance, in scenarios like navigating narrow gaps between high-rise buildings or conducting search and rescue missions in mountainous, unpredictable environments, single-agent systems fail to meet the required precision and coordination. In contrast, multi-agent formation control strategies introduce more promising solutions. However, even these strategies face significant hurdles. Complex terrain, dynamic environmental factors, and coordination difficulties inherent in heterogeneous agents complicate the task further. Though traditional centralized control methods excel in accuracy, they lack scalability and fault tolerance, making them unsuitable for larger or more complex agent systems. Distributed control strategies, on the other hand, offer a more scalable and fault-tolerant solution, but they are not without their own challenges, including maintaining global coordination in dynamic environments. In recent years, many studies have focused on developing distributed control algorithms, including consistency algorithms, leader–follower methods, and graph-theory-based techniques. These approaches have made significant progress in multi-agent formation control, but they are still limited by the inherent complexity of dynamic environments. The fundamental challenge remains how to effectively coordinate heterogeneous agents across complex, real-time environments. Additionally, while many solutions aim to enhance system robustness and efficiency, they often overlook real-time adaptability and precise coordination among agents.

Table 1. Limitations of existing methods.

Method	Centralized Control	Distributed Control	Proposed Method
Scalability	not suitable for large-scale systems	better than centralized but still limited	scalable to large multi-agent systems
Fault Tolerance	single point of failure	resilient to some faults	robust against faults and jamming
Flexibility	requires centralized coordination)	agents work independently but with fixed rules	dynamic subgrouping and real-time adaptability
System Stability	precise control	difficult to guarantee under changing conditions	ensures stability with time-varying topologies
Complexity of Environment	struggles with dynamic and complex environments	can handle complex environments but with limited real-time response	effective in complex and dynamic environments (urban flight, mountainous terrain)

presents an overview of the limitations found in existing methods when applied to complex environments.

The core idea of distributed formation control strategy is to achieve global coordinated control through localized information interactions. Classical distributed control algorithms include consistency algorithms, leader–follower method and graph theory based methods. Coherence algorithms achieve state consistency among agents through the design of tailored protocols. Thiago et al. [1] presented a nonlinear robust formation flight controller for a swarm of unmanned aerial vehicles. It is based on the virtual leader approach and is capable of establishing and maintaining formations with time-varying configurations. Cappello et al. [2] designed a distributed control law based on linear quadratic differential countermeasures for a linear heterogeneous multi-agent system. Tan et al. [3], under a fixed communication topology, adopted a prediction-based control protocol to enable multi-agent systems with saturation constraints and communication delays to achieve global consensus. Wang et al. [4] combined algebraic graph theory with a distributed backstepping approach to propose a powerful distributed adaptive tracking control method to address inherent nonlinearities and uncertainties in system parameters. Chen et al. [5] designed formation containment control algorithms for second-order nonlinear multiagent systems with communication delays, and used variable gain techniques to eliminate the effect of communication delays on leader formation control. Zhang et al. [6] studied the distributed $H\infty$ consensus problem for heterogeneous multi-agent systems with non-convex constraints. Li et al. [7] studied the problem of cooperative output regulation for linear multi-agent systems, designed a distributed adaptive observer-based controller, and further proposed a distributed output feedback control method for the special case of undirected graphs.

Although homogeneous intelligent agent formation control has achieved remarkable results in practical applications, it still faces certain limitations in complex environments. To address the challenges of formation control in complex environments, heterogeneous multi-agent formation control strategies have been developed. Heterogeneous formation control faces challenges in modeling, control and communication, and requires more flexible and adaptive control methods. In recent years, control strategies for heterogeneous multi-intelligent-agent systems, such as smooth-mode control and neural network-based control methods, have received extensive attention. Lu et al. [8] investigated the consensus problem in heterogeneous multi-agent systems comprising second-order linear and nonlinear agents. Input saturation algorithms and input unsaturation algorithms were proposed to ensure consensus among agents within the heterogeneous systems. Park et al. [9] distributed connectivity protection and collision avoidance formation tracking for networked uncertain underactuated surface systems with heterogeneous limited communication ranges. Xiong et al. [10] investigated the discrete-time-formation containment-tracking control problem for linear heterogeneous multi-unmanned aircraft systems under leader–follower formation with switching directional topology and unknown external perturbations, and proposed a distributed containment control strategy. Hua et al. [11] designed a distributed sliding mode observer to implement formation tracking control with unknown leader inputs. Combining finite-time stability theory and event-triggered mechanism, Duan et al. [12] proposes a control protocol based on leader state observer to realize consistency.

The development of consistency theory provides theoretical support for distributed formation control methods. Group consistency has gradually gained attention as an effective formation control method. Grouping consistency refers to dividing agents into groups, achieving intra-group consistency while maintaining appropriate inter-group positions. The grouping-consistency algorithm based on group behavior, groups agents using clustering methods, where each group independently achieves consistency, thus simplifying the complexity of formation control. The group consistency strategy of time-varying formation can dynamically adjust the formation structure according to the environmental changes and mission requirements, thus enabling flexible formation control. The application of group consistency in heterogeneous multi-intelligent-agent systems shows its significant advantages in improving system autonomy, synergy, and robustness. Duan et al. [13] explored fixed-time time-varying output formation-holding control for a heterogeneous general-purpose multi-agent system consisting of a virtual leader, multiple leaders, and followers. Hua et al. [14] investigated the problem of fault-tolerant time-varying formation control for high-order linear multi-agent systems in the presence of actuator failures. A fully distributed formation control protocol was proposed, utilizing an adaptive online update strategy. Lan et al. [15] explored a distributed time-varying optimal formation protocol for a class of second-order uncertain nonlinear dynamic multi-agent systems based on an adaptive neural network state observer with backstepping and simplified reinforcement learning. Mo et al. [16] investigated mean-square $H\infty$ antagonistic formation control for second-order multi-agent systems with multiplicative noise and external interference in a directed symbol topology. Zhao et al. [17] studied the group consensus problem for discrete-time multi-agent systems with fixed and randomly switching topologies.

In summary, multi-intelligent-agent formation control strategies have made significant progress in distributed control, homogeneous and heterogeneous intelligent agent control, and group consistency strategies. However, formation control in complex flight environments continues to encounter significant challenges that necessitate further research and exploration. Future research directions include optimizing existing control algorithms, developing more adaptive and intelligent control strategies, and verifying the effectiveness of new approaches through simulation and field experiments. These studies will provide important support for the performance enhancement of multi-intelligence systems and the enhancement of mission execution capabilities in practical applications.

In this article, a consensus-based formation approach is proposed for heterogeneous multi-intelligent-agent systems, leveraging time-varying group consistency to reinforce fault tolerance and anti-jamming capacity. Specifically, the following three contributions are emphasized:

First, building on distributed-consensus theory, we derive the conditions for stable and flexible formation control in complex environments. By incorporating time-varying formation, we transform the problem of maintaining group consistency under changing topologies into a more tractable framework, simplifying the analysis of system stability. Second, we introduce a parametric mechanism that enables dynamic subgrouping and diverse convergence objectives. This mechanism defines analytical bounds on formation parameters to rapidly generate feasible configurations, ensuring real-time responsiveness to varying mission demands. Third, we propose a combined strategy that merges the theoretical rigor of our group consistency approach with robust Lyapunov-based stability proofs including minimum dwell time constraints and the LaSalle invariance principle to guarantee the system remains stable when formation configurations change over time.

Although existing approaches address some components of multi-agent formation control, our proposed methodology distinguishes itself by combining nonlinear dynamics, optimal subgroup coordination, and real-time adjustments to formation structures. This comprehensive approach significantly enhances the system’s self-sufficiency, collaborative performance, and overall resilience, thereby presenting strong potential for future applications in heterogeneous multi-intelligent-agent systems.

2. Methods

2.1. Graph Theory

Graph theory is a mathematical framework that studies graphs composed of nodes (points) and edges (lines) that connect these nodes. Multi-intelligent-agent systems use graph theory to study and characterize their network topology. In multi-intelligent-agent systems, the graph theory is employed to analyze and characterize network topology, where individual agents are represented as nodes, and their communication links are modeled as edges. This representation enables a comprehensive algebraic characterization of the system’s structure, which is further analyzed using stability theory.

In this paper, weighted undirected graphs are adopted to model communication relationships to describe the communication relations in a multi-intelligent-agent system. The definition of undirected graph in this paper is first given $G$.

Definition 1

([18]). For a multi-intelligent-agent system with a single leader $G=(V,E,A)$ where $V=\{v_0,v_1,\dots ,v_N\}$ is the set of nodes, the $v_0$ represents the leader in the multi-intelligent-agent system, and matrix ${B=diag\{a}_{i0},a_{20},\dots a_{N0}\}$ is the adjacency matrix of the leader; if there is a communication transmission between nodes $v_i$ and $v_0$, then $a_{i0}> 0$. $A=\left[a_{ij}\right]\in R^{N\times N}$ is the graph $G$ the weighted adjacency matrix of the leader; if $\left(v_i,v_j\right)\in E$, then $a_{ij}>0$; otherwise, $a_{ij}=0$. $D=\left[d_{ij}\right]\in R^{N\times N}$ is the in-degree matrix, $d_{ii}={\sum }_{j=1}^N \left|a_{ij}\right|,d_{ij}=0,i\ne j$. The Laplace matrix is defined as $L=D-A$; then, there are $L=\left[l_{ij}\right]\in R^{N\times N}$ that $H=L+B$. In the subsequent research of this paper, if there is communication between the leader and the follower, take $a_{i0}=1$; otherwise, it is $a_{i0}=0$.

Definition 2

([18]). For multi-leader multi-intelligent-agent systems $G=(V,E,A)$, where $V=\left\{v_1,v_2,\cdots ,v_N,v_{N+1},\cdots ,v_{N+M}\right\}$, $N$ and $M$ represent followers and leaders. Respectively, where followers form a subgraph $G_F=\left(v_f,e_f,a_f\right)$, nodes $v_f=\left\{v_1,v_2,\cdots v_N\right\}$, and the set of edges $e_f\subseteq v_f\times v_f$. The graph $G$ of the Laplace matrix is defined as $L=D-A$, where $A=\left[a_{ij}\right]\in R^{(N+M)\times (N+M)}$ is the adjacency matrix, and $D=diag\left\{D_1,D_2,\cdots ,D_N,D_{N+1},\cdots ,D_{N+M}\right\}\in R^{(N+M)\times (N+M)}$is the incidence matrix, where $D_i={\sum }_{j=1}^{N+M} a_{ij}$ is the degree of the node $i$. The Laplace matrix is of the following form:

$$L=\left[\begin{array}{cc}{L}_F& L_L\\ 0_{M\times N}& 0_{M\times M}\end{array}\right]$$

(1)

where $L_F\in R^{N\times N},L_L\in R^{N\times N}$, the matrix $L_F$’s non-diagonal elements reflect the $N$relationships between the individual followers, while the matrix $L_L$reflects the neighborhood relationship between the followers and the leader. Since the leader can only send messages to subordinate followers, in the Laplace matrix $L$, the leader does not have any incoming edges, i.e., no incoming degree nodes. Therefore, the Laplace matrix $L$ has all 0 rows, indicating that the leader has no incoming nodes. $M$ rows are all 0, indicating that there is no direct relationship between the leader and other members.

Lemma 1

([18]). For an undirected graph $G$, its Laplace matrix $L$ has the following characteristics:

• $L$ has a zero eigenvalue, whose corresponding eigenvector is $1_N=(\mathrm{1,1},\cdots ,1{)}^T$, and all its nonzero eigenvalues are positive real numbers.
• $L$ is a semipositive definite symmetric matrix and satisfies $1^{T}L=0$.
• The eigenvalues of $0,{\lambda }_1,{\lambda }_2,\cdots {\lambda }_N$, and $0\le {\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_N$. It is common to define the second smallest eigenvalue of the matrix $L$ as ${\lambda }_1$, to be the algebraic connectivity of the graph $G$ of the algebraic connectivity while having the following:

  $${\lambda }_1(L)=\underset{x^T{1}_{1,x}=0,x\ne 0}{min} {\displaystyle \frac{x^{T}Lx}{x^{T}x}}$$

  (2)
• For any vector $x={\left(x_1,x_2,x_3,\cdots ,x_N\right)}^T\in R^N$, satisfy the following:

$$x^{T}Lx={\displaystyle \frac{1}{2}}\sum _{i=1}^N \sum _{j=1}^N a_{ij}{\left(x_j-x_i\right)}^2$$

(3)

Multi-intelligent-agent systems must consider communication constraints during the design of formation-grouping strategies, where the communication strength between the $i\text{-}$th and $j\text{-}$th agents is affected by the relative distance. To account for communication constraints, the element $a_{ij}$ in the adjacency matrix $A$ is adjusted accordingly. The modified matrix elements represent values in continuous space, and ${\bar{a}}_{ij}$ can be expressed as follows:

$${\bar{a}}_{ij}\left(∥x_{ij}\left(t\right)∥\right)=\left\{\begin{array}{c}1\\ {\displaystyle \frac{1}{2}}\left[1+\mathit{cos}(\pi {\displaystyle \frac{\frac{‖x_{ij}\left(t\right)‖}{R}-\tau }{1-\tau }})\right]\\ 0\end{array}\right. \begin{array}{c} ‖x_{ij}\left(t\right)‖\in \left.[0,\tau R\right)\\ ‖x_{ij}\left(t\right)‖\in \left.[\tau R,R\right)\\ ‖x_{ij}\left(t\right)‖\in \left.[R,inf\right)\end{array}$$

(4)

where $x_{ij}$ is the relative position vector between the $i$ th agent and the $j$ th agent, $\tau$ is defined in this paper as the communication-limited decay rate, $R$ is the farthest communication boundary, and $\parallel \cdot \parallel$ is a 2-norm indicating the distance between the two. The modified adjacency matrix is defined as $\overline{A}$, and the elements of the matrix are ${\bar{a}}_{ij}$. The Laplace matrix is $\overline{L}$, where its elements are continuous functions of time and correspond to a undirected graph. In graph theory, a path is a finite-length sequence of vertices starting from any vertex and consisting of neighbors of edges. If a path exists between the $i\text{-}$th agent and the $j\text{-}$th agent, it implies connectivity between the agents.

2.2. Multi-Consensus Theory

In a heterogeneous multi-agent system with $n$ agents, multiple agents are considered to have reached consensus if the states of the agents reach smooth agreement with each other, and the consensus agreement between the $i\text{-}$th and $j\text{-}$th agents is defined as follows:

$$\left\{\begin{array}{l}\underset{\mathit{t}\to \infty }{\lim } ∥{\mathit{x}}_{\mathit{i}}(\mathit{t})-{\mathit{x}}_{\mathit{j}}(\mathit{t})∥=0\\ \underset{t\to \infty }{\lim } {\mathit{v}}_{\mathit{i}}(\mathit{t})=\underset{\mathit{t}\to \infty }{\lim } {\mathit{v}}_{\mathit{j}}(\mathit{t})=0\end{array}\right.$$

(5)

This formula implies that when the position deviations and velocities among the agents in the formation align, the system achieves consensus, enabling coordinated formation behavior. When a group of intelligences achieves distinct consensus states, the multi-intelligent-agent system completes the grouping and can realize a multi-objective task. If there is a need to generalize the methods of this section and states, such as position velocity, to multiple dimensions, the Crowe inner product can be used.

The Laplace matrix $\widehat{L}$ under multiple consensus is given below:

$$\widehat{L}=\left[\begin{array}{cccc}{L}_{11}& {\displaystyle \frac{{\omega }_1}{{\omega }_2}}{L}_{12}& \cdots & {\displaystyle \frac{{\omega }_1}{{\omega }_n}}{L}_{1n}\\ {\displaystyle \frac{{\omega }_2}{{\omega }_1}}{L}_{21}& L_{22}& \cdots & {\displaystyle \frac{{\omega }_2}{{\omega }_n}}{L}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{{\omega }_n}{{\omega }_1}}{L}_{n1}& {\displaystyle \frac{{\omega }_n}{{\omega }_2}}{L}_{n2}& \cdots & L_{nn}\end{array}\right]$$

(6)

where ${\omega }_i$ denotes the intelligence degree of the multi-intelligence agent, and $L_{ij}$ denotes the element of the Laplace matrix for $(i,j)$. In a multi-intelligent-agent system, if two agents share the same intelligence degree, they can achieve consensus, satisfying the above equation when ${\omega }_i={\omega }_j$, the intelligent agent $i$ and the intelligent agent $j$ satisfy the above equation. In other words, under different degrees of intelligence, agents with varying intelligence degrees can achieve multiple consensus states and form distinct groups. Therefore, multi-intelligent-agents can be grouped into clusters of varying sizes and configurations by assigning appropriate degrees of intelligence to different goals when performing multi-objective tasks. Multiple consensus can be achieved more conveniently through intelligence degree assignments compared to traditional protocols that align all agents to the same state.

2.3. Stability Theory

The Lyapunov stability theory is an important control theory which analyzes system stability through state equations and energy consumption processes. Among them, the indirect method determines the stability of the system by analyzing the equilibrium points of the system equations and the distribution of the eigenvalues of the linear equation of state in the complex plane. The direct method, on the other hand, evaluates stability by defining an energy function and demonstrating its negative definiteness with the choice of method depending on specific application requirement.

The obstacle avoidance potential function is designed as follows:

$$\begin{array}{c}{G}_1\left(x_{ij}\right)=\left\{\begin{array}{cc}{k}_1{\int }_{x_{ij}}^{r_{out}} g_1\left(s\right)ds,& x_{ij}\in \left[r_{in },r_{out}\right]\\ 0,& \mathit{otherwise} \end{array}\right.\end{array}$$

(7)

where:

$$\begin{array}{c}{g}_1\left(x_{ij}\right)={\displaystyle \frac{1}{2}}\left[1+\cos \left(\pi {\displaystyle \frac{x_{ij}-r_{in}}{r_{\mathit{out} }-r_{in}}}\right)\right]\end{array}$$

(8)

Then, the collision avoidance control for agent $i$ at $x_i$ is defined as follows:

$$\begin{array}{c}{u}_i^q={\displaystyle \sum _{j\in N_i^q}} {\nabla }_{x_i}{G}_1\left(x_{ij}\right)\end{array}$$

(9)

where ${\nabla }_{x_i}$ is the gradient along $x_i$.

In the collision avoidance area, the relative distance between the two agents is less than $r_{\mathrm{out}}$. The smaller the relative distance, the greater the input of the control law. The MAS can comply collision avoidance.

• The connectivity preserving potential function is designed as follows:

$$\begin{array}{c}{G}_2\left(x_{ij}\right)=\left\{\begin{array}{cc}{k}_2{\int }_x^{{\rho }_{ij}} g_2\left(s\right)ds,& x_{ij}\in \left(r_{out},R\right]\\ 0,& \mathit{otherwise}\end{array}\right.\end{array}$$

(10)

where:

$$\begin{array}{c}{g}_2\left(x_{ij}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\left[1+\cos \left(\pi {\displaystyle \frac{x_{ij}-r_{out}}{d_{ij}-r_{out}}}\right)\right],& x_{ij}\in \left(r_{out},{\rho }_{ij}\right]\\ 1+\cos \left(\pi {\displaystyle \frac{x_{ij}-R}{R-{\rho }_{ij}}}\right),& x_{ij}\in \left({\rho }_{ij},R\right]\end{array}\right.\end{array}$$

(11)

where ${\rho }_{ij}={\rho }_i-{\rho }_j$ refers to the required relative position. ${\rho }_i$ refers to the target state of the agent $i$ when forming a formation shape.

Then, the connectivity preservation control input of agent $i$ can be designed as follows:

$$\begin{array}{c}{u}_i^l={\displaystyle \sum _{j\in N_i^l}} {\nabla }_{x_i}{G}_2\left(x_{ij}\right)\end{array}$$

(12)

When $x_{ij}>R$. This design allows the connection to be broken between agents if necessary. Therefore, the network can be flexibly changed to achieve the desired formation.

• Another point to note, the agent spacing of the expected formation should be set between $\left[r_{out},R\right]$. In other words, the states of agent $i$ and agent $j$ need to satisfy the following equation: $0<r_{out}\le ∥{\rho }_{ij}∥\le R,\forall i,j\in V,{\omega }_i={\omega }_j,i\ne j$.

In this paper, we propose decentralized multi-consensus control methods with collision avoidance and connectivity preservation:

$$\begin{array}{c}{u}_i=-{\omega }_i^2{\displaystyle \sum _{j\in N_i^t}} {\nabla }_{x_i}{G}_1\left(x_{ij}\right)-{\omega }_i^2{\displaystyle \sum _{j\in N_i^l}} {\nabla }_{x_i}{G}_2\left(x_{ij}\right)-\alpha {\displaystyle \sum _{j\in N_i}} S\left({\epsilon }_i^{\rho },{\epsilon }_j^{\rho },v_m\right)-\beta v_i\end{array}$$

(13)

where:

$$\begin{array}{c}S\left({\epsilon }_i^{\rho },{\epsilon }_j^{\rho },v_m\right)\triangleq \left\{\begin{array}{c}{\displaystyle \frac{v_m}{\left|{\epsilon }_i^{\rho }-\frac{{\omega }_i}{{\omega }_j}{\epsilon }_j^{\rho }\right|}}\left({\epsilon }_i^{\rho }-{\displaystyle \frac{{\omega }_i}{{\omega }_j}}{\epsilon }_j^{\rho }\right)\\ {\epsilon }_i^{\rho }-{\displaystyle \frac{{\omega }_i}{{\omega }_j}}{\epsilon }_j^{\rho }\end{array}\right.\begin{array}{c} \left|{\epsilon }_i^{\rho }-{\displaystyle \frac{{\omega }_i}{{\omega }_j}}{\epsilon }_j^{\rho }\right|>v_m\\ \left|{\epsilon }_i^{\rho }-{\displaystyle \frac{{\omega }_i}{{\omega }_j}}{\epsilon }_j^{\rho }\right|>v_m\end{array}\end{array}$$

(14)

where $v_m$ is the maximum safe speed ${\epsilon }_k^p=x_k-{\rho }_k,k=\mathrm{1,2},\dots ,n$, and $\alpha ,\beta >0$. When the subgroup reaches the target, $v_i=0$.

For the multi-consensus formation-grouping control law proposed in the previous section, the Lyapunov function is defined as follows:

$$\begin{array}{rr}V=& {\sum }_{i=1}^N \left\{{\sum }_{j\in N_i^q} G_1\left(x_{ij}\right)+{\sum }_{j\in N_i^l} G_2\left(x_{ij}\right)+\right.\\ & \left.{\left({\displaystyle \frac{1}{{\omega }_i}}\right)}^2\alpha {\int }_0^t S{\left({\epsilon }_i^{\rho },{\epsilon }_j^{\rho },v_m\right)}^{T}d{\epsilon }_i^{\rho }+{\sum }_{i=1}^n {{\displaystyle \frac{v_i}{{\omega }_i}}}^2\right\}\end{array}$$

(15)

Proving stability in the formation-group control of multi-intelligent-agent systems requires consideration of two cases. The first case involves a static network of connections, while the second addresses dynamic networks. When communication is restricted, the topology of the undirected graph changes over time. In the case of target formation change, changes in network topology are segmented and continuous. To address the above situation, this paper analyzes the Lyapunov function of the dynamic topology graph $G$ and establishes stability proofs.

When the control input of the system is a multi-consensus control law, the following three conditions need to be satisfied to achieve formation targets for arbitrary numbers of agents in both dynamically and statically connected networks during the formation process:

Intelligence level needs to meet the following: ${\omega }_i\ne 0,\forall i\in V$;

• The initial value of the Lyapunov $V\left(0\right)$ is a constant;
• The relationship between neighboring agents needs to satisfy $0<r_{\mathrm{out}}\le ∥{\rho }_{ij}∥\le R,\forall i,j\in V,{\omega }_i={\omega }_j,i\ne j$.

The process of proving stability begins with calculating the connectivity components of the Lyapunov function.

$${\sum }_{\mathit{j}\in {\mathit{N}}_{\mathit{i}}^{\mathit{q}}} {\dot{\mathit{G}}}_1\left({\mathit{x}}_{\mathit{i}\mathit{j}}\right)={\left({\dot{\mathit{x}}}_{\mathit{i}}\right)}^{\mathit{T}}{\sum }_{\mathit{j}\in {\mathit{N}}_{\mathit{i}}^{\mathit{q}}} {\nabla }_{{\mathit{x}}_{\mathit{i}}}{\mathit{G}}_1\left({\mathit{x}}_{\mathit{i}\mathit{j}}\right)$$

(16)

where ${\left({\dot{x}}_i\right)}^T={\left(v_i\right)}^T$ and there are as follows:

$${\int }_0^{\mathit{t}} \mathit{S}{\left({\mathit{\epsilon }}_{\mathit{i}}^{\mathit{\rho }},{\mathit{\epsilon }}_{\mathit{j}}^{\mathit{\rho }},{\mathit{v}}_{\mathit{m}}\right)}^{\mathit{T}}\mathit{d}{\mathit{\epsilon }}_{\mathit{i}}^{\mathit{\rho }}={\int }_0^{\mathit{t}} \mathit{S}{\left({\mathit{\epsilon }}_{\mathit{i}}^{\mathit{\rho }},{\mathit{\epsilon }}_{\mathit{j}}^{\mathit{\rho }},{\mathit{v}}_{\mathit{m}}\right)}^{\mathit{T}}{\mathit{v}}_{\mathit{i}}d\mathit{\tau }$$

(17)

Based on the above Equation (8), and the Lyapunov function (Equation (9)) can be transformed into the following:

$$\dot{V}=\sum _{i=1}^N \left\{{\left({\dot{x}}_i\right)}^T\sum _{j\in N_i^q} {\nabla }_{x_i}{G}_1\left(x_{ij}\right)+{\left({\dot{x}}_i\right)}^T\sum _{j\in N_i^q} {\nabla }_{x_i}{G}_2\left(x_{ij}\right)+\alpha {\left({\displaystyle \frac{1}{{\omega }_i}}\right)}^{2}S{\left({\epsilon }_i^{\rho },{\epsilon }_j^{\rho },v_m\right)}^T{v}_i+{\hat{v}}_i\dot{{\hat{v}}_i}\right\}$$

(18)

In Equation (10), the following equation exists:

$${\sum }_{\mathit{i}=1}^{\mathit{n}} {\stackrel{\mathit{ˆ}}{\mathit{v}}}_{\mathit{i}}\dot{{\stackrel{\mathit{ˆ}}{\mathit{v}}}_{\mathit{i}}}={\sum }_{\mathit{i}=1}^{\mathit{n}} {\displaystyle \frac{{\stackrel{\mathit{ˆ}}{\mathit{v}}}_{\mathit{i}}{\mathit{u}}_{\mathit{i}}}{{\mathit{\omega }}_{\mathit{i}}}}$$

(19)

where $\hat{u}={\left[{\displaystyle \frac{u_1}{{\omega }_1}},{\displaystyle \frac{u_2}{{\omega }_2}},\dots ,{\displaystyle \frac{u_n}{{\omega }_n}}\right]}^T$, then $\dot{V}$ can be written as follows:

$$\dot{V}=\sum _{i=1}^N \left\{{\left(v_i\right)}^T\sum _{j\in N_i^q} {\nabla }_{x_i}{G}_1\left(x_{ij}\right)+{\left(v_i\right)}^T\sum _{j\in N_i^l} {\nabla }_{x_i}{G}_2\left(x_{ij}\right)+\alpha {\left({\displaystyle \frac{1}{{\omega }_i}}\right)}^{2}S{\left({\epsilon }_i^{\rho },{\epsilon }_j^{\rho },v_m\right)}^T{v}_i+{\displaystyle \frac{{\hat{v}}_i{u}_i}{{\omega }_i}}\right\}$$

(20)

In the above equation, $v={\left[v_1,v_2,\dots ,v_n\right]}^T$, define $\Lambda \triangleq diag\left[{\omega }_1,{\omega }_2,\dots ,{\omega }_n\right]$ and there are the following:

$$G_1^{\ast }=\left[{\sum }_{j\in N_i^q} {\nabla }_{x_1}{G}_1\left(x_{1j}\right),{\sum }_{j\in N_i^q} {\nabla }_{x_2}{G}_1\left(x_{2j}\right),\cdots \right.,{\left.{\sum }_{j\in N_i^q} {\nabla }_{x_n}{G}_1\left(x_{nj}\right)\right]}^T$$

(21)

then:

$$S^{\ast }=\left[s\left(x_1^{\rho },x_j^{\rho },v_m\right),s\left(x_2^{\rho },u_j^{\rho },v_m\right),\cdots ,s\left(u_m^{\rho },{\epsilon }_j^p,v_m\right)\right]$$

(22)

According to the multi-consensus control law given in the previous section, we derive the following:

$$\dot{V}=v^T{G}_1^{\ast }+v^T{G}_2^{\ast }+\alpha {\mathsf{\Lambda }}^{-2}{v}^T{S}^{\ast }+{\hat{v}}^T\widehat{u}$$

(23)

One can easily obtain the equation $\widehat{u}={\mathsf{\Lambda }}^{-1}u,\widehat{v}={\mathsf{\Lambda }}^{-1}v$, the multi-consensus control law $u$ can be alternatively written as follows:

$$u=-{\mathsf{\Lambda }}^2{G}_1^{\ast }-{\mathsf{\Lambda }}^2{G}_2^{\ast }-\alpha S^{\ast }-\beta v$$

(24)

Bringing Equation (16) in the multi-consensus control law into the derivative of the Lyapunov function, one obtains the following:

$$\begin{gathered} \dot{V}=v^T{G}_1^{\ast }+{\nu }^T{G}_2^{\ast }+\alpha {\Lambda }^{-2}{v}^T{S}^{\ast }+{\hat{\nu }}^T{\Lambda }^{-1}\left(-{\Lambda }^2{G}_1^{\ast }-{\Lambda }^2{G}_2^{\ast }-\alpha S^{\ast }-\beta v\right) \\ =\alpha {\Lambda }^{-2}{v}^T{S}^{\ast }-\alpha {\hat{v}}^T{\Lambda }^{-1}{S}^{\ast }-\beta {\hat{v}}^T\hat{v} \\ =-\beta {\hat{v}}^T\hat{v}\le 0 \end{gathered}$$

(25)

To prove the determination of the Lyapunov stability of a control law requires demonstrating two aspects: first, that the Lyapunov function VV is semi-positive definite. The second point is that the derivative of the Lyapunov function $\dot{V}$ is negative semi-definite, as demonstrated by Equation (17). In this paper, the initial value of the Lyapunov function $V_0$ is constant, and $V$ remains a positive constant throughout.

$$V\left(t\right)\le V\left(0\right)=\Theta \ll \infty , \forall t\ge 0$$

(26)

The Lyapunov function needs to satisfy two threshold constraints for connectivity preservation:

$$\left\{\begin{array}{l}V\left(t\right)\le G_1\left(r_{in}\right)\\ V\left(t\right)\le G_2\left(R\right)\end{array}\right.$$

(27)

Let $V_0=V\left(0\right)$, then:

$$\left\{\begin{array}{l}{\bar{G}}_1={\int }_{r_{in}}^{r_{out}} g_1\left(s\right)ds\\ {\bar{G}}_2={\int }_{r_{in}}^R g_2\left(s\right)ds\end{array}\right.$$

(28)

The maximum value of the connectivity function is $G_1^{\mathrm{m}\mathrm{a}\mathrm{x}}=k{\bar{G}}_1$, $G_2^{\mathrm{m}\mathrm{a}\mathrm{x}}=k{\bar{G}}_2$, then:

$$\left\{\begin{array}{l}{V}_0\le k{\bar{G}}_1\\ V_0\le k{\bar{G}}_2\end{array}\right.$$

(29)

In order to ensure the connectivity during the formation grouping process, it is necessary to set $k$ to a suitable value that satisfies the above inequality, and let $\Gamma =\left\{\right(\bar{x}\left(t\right),v\left(t\right))\mid V(t)\le V(0), \forall t\ge 0\}$, according to the Lasalle invariance principle, when $t\to \infty$, each solution from $\Gamma$ is close to the maximal invariant set $\mathcal{W}=\left\{\right(\bar{x}\left(t\right),v\left(t\right))\in \Gamma \mid \dot{V}(t)=0\}$. In Equation (20), $\dot{V}=0$ is satisfied when and only when ${\hat{v}}_i=0,\forall i\in V$. When $\dot{V}=0$, $v_1=v_2=\cdots =v_n=0.$ This indicates that all intelligences reach the same velocity, and it is the velocity of intelligences that reaches a stable consensus.

When $t\to \infty ,u_i$ can be simplified as:

$$\begin{array}{ll}{u}_i={\dot{v}}_i=& -{\omega }_i^2{\sum }_{j\in N_i^q} {\nabla }_{x_i}{G}_1\left(x_{ij}\right)-{\omega }_i^2{\sum }_{j\in N_i^l} {\nabla }_{x_i}{G}_2\left(x_{ij}\right)\\ & -\alpha {\sum }_{j\in N_i} S\left({\epsilon }_i^{\rho },{\epsilon }_j^{\rho },v_m\right)=0\end{array}$$

(30)

thus:

$$u=-\alpha \widehat{L}\bar{x}=-\alpha \Lambda \mathcal{L}\hat{x}=0_n$$

(31)

We expect the control input $u_i=0$ only when a single agent in a multi-agent system achieves multi-consensus. The above procedure is a stability proof in static networks, and we need to extend Lyapunov’s stability proof to the case where the network topology is dynamic. In this paper, we define the network topology graph as $G\left(t\right)$, where moment $t$ is the Laplace matrix. ${\mathcal{L}}_{G\left(t\right)}. {\omega }_i$ varies with the dynamics of the subgroups assigned by the intelligences. Therefore, the multi-consensus control law is a segmented continuous function. The control input function jumps when the network topology graph of the target formation changes.

Next, this paper analyzes the stability of the dynamic network in this context for the above system. In this paper, the concept of dwell time is utilized to analyze the dynamic network. In switched systems, the concept of minimum dwell time (MDT) is employed in this paper. In the MDT concept, if the subsystems before and after switching are a progressively stable system, then the switching system is also a progressively stable system. We assume that the network changes at moment $t_k$ and the next moment of change is moment $t_{k+1}$. But the network topology is fixed from $t_k$ to $t_{k+1},$ and this time interval is large enough. In this paper, the residence time is defined as $\tau \left(t\right)$, which refers to the time interval between the network change moments, and is specified as follows:

$$\tau \left(t_k\right)=t_{k+1}-t_k,\forall k\in N$$

(32)

In this paper, the minimum residence time is defined as ${\tau }_d$, and the minimum dwell time ${\tau }_d$ is sufficiently large to guarantee the stability of the dynamic system. All time intervals of network topology switching are larger than the minimum dwell time, $\tau \left(t_k\right)\ge {\tau }_d>0$. Thereafter, the set of all possible network topology maps in the multi-intelligent-agent system is $G_c$. If the initial topology map of the multi-intelligent-agent system is an element in $G_c$, the transformed topology map is still in $G_c$ under the action of the control law, thus $G_0\in G_c$ and then $G_t\in G_c,\forall t\ge 0$.

Since ${\tau }_d\le \tau \left(t_k\right)$ and ${\tau }_d$ are large enough, the network topology of the multi-intelligent-agent system achieves asymptotic stability starting from $G_0$. If the network topology $G_t$ at a given moment achieves asymptotic stability, the intermediate switching system also maintains stability, ensuring the overall multi-agent system remains stable in dynamic networks. It is worth noting that the multi-consensus grouping control law proposed in this paper relies on a topological network constraint, ensuring that the initial network of the multi-agent system is fully connected. In addition, the grouping control algorithm in this paper allows for network disconnections between the subgroups. Although agents within a subgroup may not directly communicate with one another, each subgroup can reach formation grouping based on intelligence $\omega$.

3. Modeling and Analysis

3.1. Problem Analysis in Complex Environments

Obstacle avoidance and formation control are crucial and challenging tasks in complex environments. Such environments typically encompass densely structured areas such as urban high-rise buildings, narrow alleyways, and other densely structured areas. The characteristics of these environments make it necessary for agents to possess advanced capabilities in autonomous perception, decision-making, and control.

Maintaining a stable formation structure in complex environments is a challenge. Agents in a formation must constantly adjust their positions to adapt to environmental dynamics while preserving relative positions within the formation. Agents within the formation must collaborate and effectively distribute tasks to enhance efficiency. This requires the multi-intelligent system to exhibit autonomy, synergy, and robustness, thereby improving overall performance and mission execution of the system through advanced control strategies and algorithms.

3.2. Formation Control Modeling

$M$ agents are assigned leadership roles in each formation. The leader is responsible for planning and dynamically updating the formation’s trajectory to ensure obstacle avoidance. The leader usually needs to be equipped with more powerful sensors and processors to better sense the environment and perform path planning. The remaining agents follow the leader. They can be divided into different formations, with the intelligences within each formation maintaining safe spacing and relative positions under the leader’s guidance. The followers can adjust their speed and direction according to the leader’s instructions.

This paper examines a heterogeneous multi-agent system comprising $N$ followers and $M$ leaders, $i=\mathrm{1,2},\cdots ,N,N+1,\cdots ,N+M$, respectively. The relationship between leaders and followers is represented by an undirected topological graph $G=\{V,E,A\}$, where the dynamical equations of the leaders satisfy the following form:

$$\left\{\begin{array}{l}{\dot{x}}_i\left(t\right)=v_i\left(t\right)\\ {\dot{v}}_i\left(t\right)=u_{i0}\left(t\right)\end{array},i\in M.\right.$$

(33)

where $x_i\left(t\right)\in R^M$ and $v_i\left(t\right)\in R^M$ represent the position and velocity states of the leader. $u_{i0}\left(t\right)\in R$ denotes the leader’s control input.

For the second-order heterogeneous multi-intelligence system, assume that the system consists of $N_1$ first-order agents and $N_2$ second-order agents, satisfying $N_1+N_2=N$, and $N_1$ and $N_2$ are positive constants, where the kinetic equations of the first-order and second-order followers satisfy the following form:

$$\begin{array}{rrrr}{\dot{x}}_i\left(t\right)=u_i\left(t\right)+f_i\left(x_i\right)+d_i\left(t\right),& & & i\in N_1\\ & & & \end{array}$$

(34)

$$\left\{\begin{array}{cc}{\dot{x}}_i\left(t\right)=v_i\left(t\right),& \\ {\dot{v}}_i\left(t\right)=u_i\left(t\right)+d_i\left(t\right),& \end{array} \right.i\in N_2$$

(35)

where $x_i\left(t\right)\in R^{N_1}$ is the position information of the first-order agent, $x_i\left(t\right)\in R^{N_2}$, $v_i\left(t\right)\in R^{N_2}$ represent the position and velocity states of second-order agent, $u_i\left(t\right)\in R$ is the control input of the first-order and second-order intelligences, and $d_i\left(t\right)$ is the external perturbation.

Definition 3

([19]). A heterogeneous multi-agent system defined by Equations (25)–(27) achieves preset time-inclusive control consistency if it satisfies Equation (28):

$$\begin{array}{l}\left\{\begin{array}{cc}\underset{t\to t_f}{lim} ∥x_i\left(t\right)-{\sum }_{j=N+1}^{N+M} h_{ij}{x}_j∥=0,& \forall i\in N+M,\hfill \\ ∥x_i\left(t\right)-{\sum }_{j=N+1}^{N+M} h_{ij}{x}_j∥=0,& \forall t>t_f,\hfill \end{array}\right.\\ \left\{\begin{array}{cc}\underset{t\to f_f}{lim} ∥v_i\left(t\right)-{\sum }_{j=N+1}^{N+M} h_{ij}{v}_j∥=0,& \forall i\in N+M,\hfill \\ ∥v_i\left(t\right)-{\sum }_{j=N+1}^{N+M} h_{ij}{v}_j∥=0,& \forall t>t_f.\hfill \end{array}\right.\end{array}$$

(36)

where $t_f$ is the preset time for the multi-intelligent-agent system to reach containment consistency, the convergence time $t_f$ can be given arbitrarily and is not affected by the initial value of the system and the control parameters, when $t>t_f$, each follower can converge at the preset time.

3.3. Heterogeneous Multi-Intelligent-Agent Formation Collaborative Obstacle Avoidance Controller

3.3.1. Controller Design

In the controller design of this paper, the control input $u_i$ consists of the base control input $u_{ij}$, the obstacle avoidance control input $u_{iv}$, and the velocity inhibition term $V_C$. The base control input $u_{ij}$ is used to adjust the position of the intelligent agent, bringing it closer to the target position. Setting the target position as $x_i^d$, we can define the control input as follows:

$$u_{ij}=-K_p\left(x_i\left(t\right)-x_i^d\left(t\right)\right)-K_v{v}_i\left(t\right)$$

(37)

where $K_p$ and $K_v$ are the gain matrices for position and velocity, respectively. According to the synergistic goal requirement, it can be rewritten as follows:

$$u_{ij}=\alpha \left(X_C(:,i)-{\displaystyle \frac{W\left(i\right)}{W\left(j\right)}}{X}_C(:,j)\right)$$

(38)

where $X_C$ is the difference between the current position and the target position.

The obstacle avoidance control input $u_{iv}$ is used to prevent collisions between agents. Letting the distance between the agents be $d_{ij}=∥x_i-x_j∥$, we can design the obstacle avoidance control input as follows:

$$u_{iv}=\left\{\begin{array}{cc}{k}_{iv}\left(1-{\displaystyle \frac{d_{ij}}{d_{min}}}\right){\displaystyle \frac{x_i-x_j}{d_{ij}}}& d_{ij}<d_{min}\\ 0& d_{ij}\ge d_{min}\end{array}\right.$$

(39)

where $d_{min}$ is the minimum distance for obstacle avoidance, and $k_{iv}$ is the obstacle avoidance gain. According to the obstacle avoidance system, the objective can be rewritten as follows:

$$\begin{array}{cc}{u}_{iv}=\left(0.5\left(1+\mathit{cos}\left(\pi {\displaystyle \frac{d_{ij}-s}{s-s_i}}\right)\right)+1\right)\cdot {\displaystyle \frac{X_C\left(:,i\right)-X_C\left(:,j\right)}{‖X_C\left(:,i\right)-X_C\left(:,j\right)‖}}& d_{ij}\in \left(s_i,s\right)\\ u_{iv}=\left(0.5\left(1+\mathit{cos}\left(\pi {\displaystyle \frac{R-d_{ij}}{R-R_p}}\right)\right)+1\right)\cdot {\displaystyle \frac{X_C\left(:,i\right)-X_C\left(:,j\right)}{‖X_C\left(:,i\right)-X_C\left(:,j\right)‖}}& d_{ij}\in \left(R_p,R\right)\end{array}$$

(40)

where $s$ and $s_i$ are thresholds for obstacle avoidance distances, and $R_p$ and $R$ are other distance thresholds.

In order to limit the speed of the agents, it is necessary to introduce a speed inhibition term $V_C$:

$$V_C=-K_v{v}_i$$

(41)

where $K_v$ is the speed inhibition gain.

This results in the following control input expression:

$$u_i=-u_{ij}-u_{i_v}-\beta V_C\left(:,i\right)$$

(42)

where $u_i$ is the control input, $u_{ij}$ is the base control input, $u_{iv}$ is the obstacle avoidance control input, and $V_C(:,i)$ is the velocity inhibition term. The parameter β is a constant used to control the magnitude of the velocity term’s influence in the control law. Substitution yields the following:

$$\begin{array}{cc}{u}_i=-\alpha \left(X_C\left(:,i\right)-{\displaystyle \frac{W\left(i\right)}{W\left(j\right)}}{X}_C\left(:,i\right)\right)-\left(0.5\left(1+\mathit{cos}\left(\pi {\displaystyle \frac{d_{ij}-s}{s-s_i}}\right)\right)+1\right)\cdot {\displaystyle \frac{X_C\left(:,i\right)-X_C\left(:,j\right)}{‖X_C\left(:,i\right)-X_C\left(:,j\right)‖}}-K_v{v}_i& d_{ij}\in \left(s_i,s\right)\\ u_i=-\alpha \left(X_C\left(:,i\right)-{\displaystyle \frac{W\left(i\right)}{W\left(j\right)}}{X}_C\left(:,i\right)\right)-\left(0.5\left(1+\mathit{cos}\left(\pi {\displaystyle \frac{R-d_{ij}}{R-R_p}}\right)\right)+1\right)\cdot {\displaystyle \frac{X_C\left(:,i\right)-X_C\left(:,j\right)}{‖X_C\left(:,i\right)-X_C\left(:,j\right)‖}}-K_v{v}_i& d_{ij}\in \left(R_p,R\right)\end{array}$$

(43)

Next, a time-varying queueing-based packet consistency protocol is proposed:

$$u_i=\left\{\begin{array}{cc}{K}_1\left({\theta }_i-h_i\right)+K_2\left\{{\displaystyle \sum _{v_i\in N_{1i}}}{a}_{ij}\left[{\theta }_j-h_j\right]-\left[{\theta }_i-h_i\right]+{\displaystyle \sum _{v_j\in N_{2i}}}{a}_{ij}\left({\theta }_j-h_j\right)\right\}+{\dot{h}}_{iv}& i\le N\\ K_1\left({\theta }_i-h_i\right)+K_2\left\{{\displaystyle \sum _{v_i\in N_{1i}}}{a}_{ij}\left({\theta }_j-h_j\right)+{\displaystyle \sum _{v_j\in N_{2i}}}{a}_{ij}\left[{\theta }_j-h_j\right]-\left[{\theta }_i-h_i\right]\right\}+{\dot{h}}_{iv}& i\ge N+1\end{array}\right.$$

(44)

The relationship between $K_1$ and $K_2$ satisfies $K=-K_1=K_2=\left[k_1,k_2\right]$, which are the controller parameters to be designed. Assume that the system consists of $N+M$ agents, where the state of each agent is denoted by ${\theta }_i\left(t\right)$, with $i=1, 2, ..., N+M$.

• Let $\theta \left(t\right)={\left[\begin{array}{ccccccc}{\theta }_1^T\left(t\right)& {\theta }_2^T\left(t\right)& \cdots & {\theta }_N^T\left(t\right)& {\theta }_{N+1}^T\left(t\right)& \cdots & {\theta }_{N+M}^T\left(t\right)\end{array}\right]}^T$ be the set of state geometries of the smart agent, then $h\left(t\right)={\left[\begin{array}{ccccccc}{h}_1^T\left(t\right)& h_2^T\left(t\right)& \cdots & h_N^T\left(t\right)& h_{N+1}^T\left(t\right)& \cdots & h_{N+M}^T\left(t\right)\end{array}\right]}^T$ is the set of formation queueing functions, where $h_{\sigma i}\left(t\right)=h_i\left(t\right)={\left[h_{ix}\left(t\right) h_{iv}\left(t\right)\right]}^T$. The position component of $h\left(t\right)$ is ${ h}_x\left(t\right)={\left[\begin{array}{ccccccc}{h}_x\left(t\right)& h_{2x}\left(t\right)& \cdots & h_{nx}\left(t\right)& h_{\left(n+1\right)x}\left(t\right)& \cdots & h_{\left(n+m\right)x}\left(t\right)\end{array}\right]}^T$, and the velocity component is $h_v\left(t\right)={\left[\begin{array}{ccccccc}{h}_v\left(t\right)& h_{2v}\left(t\right)& \cdots & h_{nv}\left(t\right)& h_{\left(n+1\right)v}\left(t\right)& \cdots & h_{\left(n+m\right)v}\left(t\right)\end{array}\right]}^T$. The goal of the system is to make all agents’ states θ_i(t) converge to a common trajectory h_i(t), i.e., $\underset{t\to \infty }{lim}\left({\theta }_i\left(t\right)-h_i\left(t\right)\right)=0$.

The system is then rewritten according to the protocol as follows:

$$\begin{array}{ll}\dot{\theta }\left(t\right)=& \left(I_{N+M}\otimes \left(-B_{2}K+B_1{B}_2^T\right)-L\otimes \left(B_{2}K\right)\right)\theta \left(t\right)\\ & -\left(I_{N+M}\otimes \left(-B_{2}K\right)-L\otimes \left(B_{2}K\right)\right)h\left(t\right)+\left(I_{N+M}\otimes B_2\right){\dot{h}}_v\left(t\right)\end{array}$$

(45)

where $B_1$ and $B_2$ are system matrices, $L$ is the Laplacian matrix, and $K$ is the control gain matrix.

3.3.2. Proof of Stability

The adjacency matrix $A$ describes the connectivity between agents, determined by the Euclidean distance between agents:

$$A(i,j)=\left\{\begin{array}{c}1 d_{ij}<t_R\\ 0.5\left(1+cos\left(\pi \left({\displaystyle \frac{d_{ij}-t_R}{R-t_R}}\right)\right)\right)\\ 0 d_{ij}>t_R\end{array}\right. t_R<d_{ij}<R$$

(46)

where $d_{ij}$ represents the distance agents $i$ and $j$, and $t_R$ and $R$ are distance thresholds.

• Definition of degree matrix $D$:

$$D(i,i)={\sum }_{j=1}^k A(i,j)$$

(47)

Definition of Laplace matrix $L_c$:

$$L_c=D-A$$

(48)

Normalize the Laplace matrix $L_c$:

$$L(i,j)={\displaystyle \frac{W\left(i\right)}{W\left(j\right)}}{L}_c(i,j)$$

(49)

where $W\left(i\right)$ is the weight associated with the $i$th intelligence.

• The Lyapunov function is chosen as a quadratic function of the agent states:

$$V\left(x\right)={\displaystyle \frac{1}{2}}{\sum }_{i=1}^{M+N} \left[{∥x_i-x_i^d∥}^2+{∥v_i∥}^2\right]$$

(50)

Calculate the time derivative of the Lyapunov function $V\left(x\right)$:

$$\dot{V}(x)={\sum }_{i=1}^{M+N} \left[{\left(x_i-x_i^d\right)}^{\mathrm{\top }}{\dot{x}}_i+v_i^{\mathrm{\top }}{\dot{v}}_i\right]$$

(51)

Since ${\dot{x}}_i=v_i$ and ${\dot{v}}_i=u_i$, therefore the following:

$$\dot{V}(x)={\sum }_{i=1}^{M+N} \left[{\left(x_i-x_i^d\right)}^{\mathrm{\top }}{v}_i+v_i^{\mathrm{\top }}{u}_i\right]$$

(52)

Substituting into the control input yields:

$$\begin{array}{c}\begin{array}{cc}\dot{V}\left(x\right)={\displaystyle \sum _{i=1}^{M+N}}\left[{\left(x_i-x_i^d\right)}^T{v}_i+v_i^T\left(-\alpha \left(X_C\left(:,i\right)-{\displaystyle \frac{W\left(i\right)}{W\left(j\right)}}{X}_C\left(:,i\right)\right)-\left(0.5\left(1+\mathit{cos}\left(\pi {\displaystyle \frac{d_{ij}-s}{s-s_i}}\right)\right)+1\right)\cdot {\displaystyle \frac{X_C\left(:,i\right)-X_C\left(:,j\right)}{‖X_C\left(:,i\right)-X_C\left(:,j\right)‖}}-K_v{v}_i\right)\right]& d_{ij}\in \left(s_i,s\right)\\ \dot{V}\left(x\right)={\displaystyle \sum _{i=1}^{M+N}}\left[{\left(x_i-x_i^d\right)}^T{v}_i+v_i^T\left(-\alpha \left(X_C\left(:,i\right)-{\displaystyle \frac{W\left(i\right)}{W\left(j\right)}}{X}_C\left(:,i\right)\right)-\left(0.5\left(1+\mathit{cos}\left(\pi {\displaystyle \frac{R-d_{ij}}{R-R_p}}\right)\right)+1\right)\cdot {\displaystyle \frac{X_C\left(:,i\right)-X_C\left(:,j\right)}{‖X_C\left(:,i\right)-X_C\left(:,j\right)‖}}-K_v{v}_i\right)\right]& d_{ij}\in \left(R_p,R\right)\end{array}\end{array}$$

(53)

Simplify to obtain the following:

$$\begin{gathered} \dot{V}\left(x\right)=\sum _{i=1}^{M+N}\left[{\left(x_i-x_i^d\right)}^T{v}_i-K_p{\left(x_i-x_i^d\right)}^T{v}_i-K_v{‖v_i‖}^2\right] \\ ={\sum }_{i=1}^{M+N}\left[-K_p{\left(x_i-x_i^d\right)}^T{v}_i-K_v{‖v_i‖}^2\right] \end{gathered}$$

(54)

Since $K_p$ and $K_v$ are positive, each term of $\dot{V}\left(x\right)$ is nonpositive:

$$\dot{V}\left(x\right)=-K_v{\sum }_{i=1}^{M+N}{‖v_i‖}^2$$

(55)

$-K_v{\sum }_{i=1}^{M+N}{‖v_i‖}^2$ shows that the sum of the squared velocities remains non-negative. The system is asymptotically stable since $\dot{V}\left(x\right)<0$ and the velocity term in $\dot{V}\left(x\right)$ contributes to the reduction in the system’s kinetic energy.

4. Experiment and Simulation

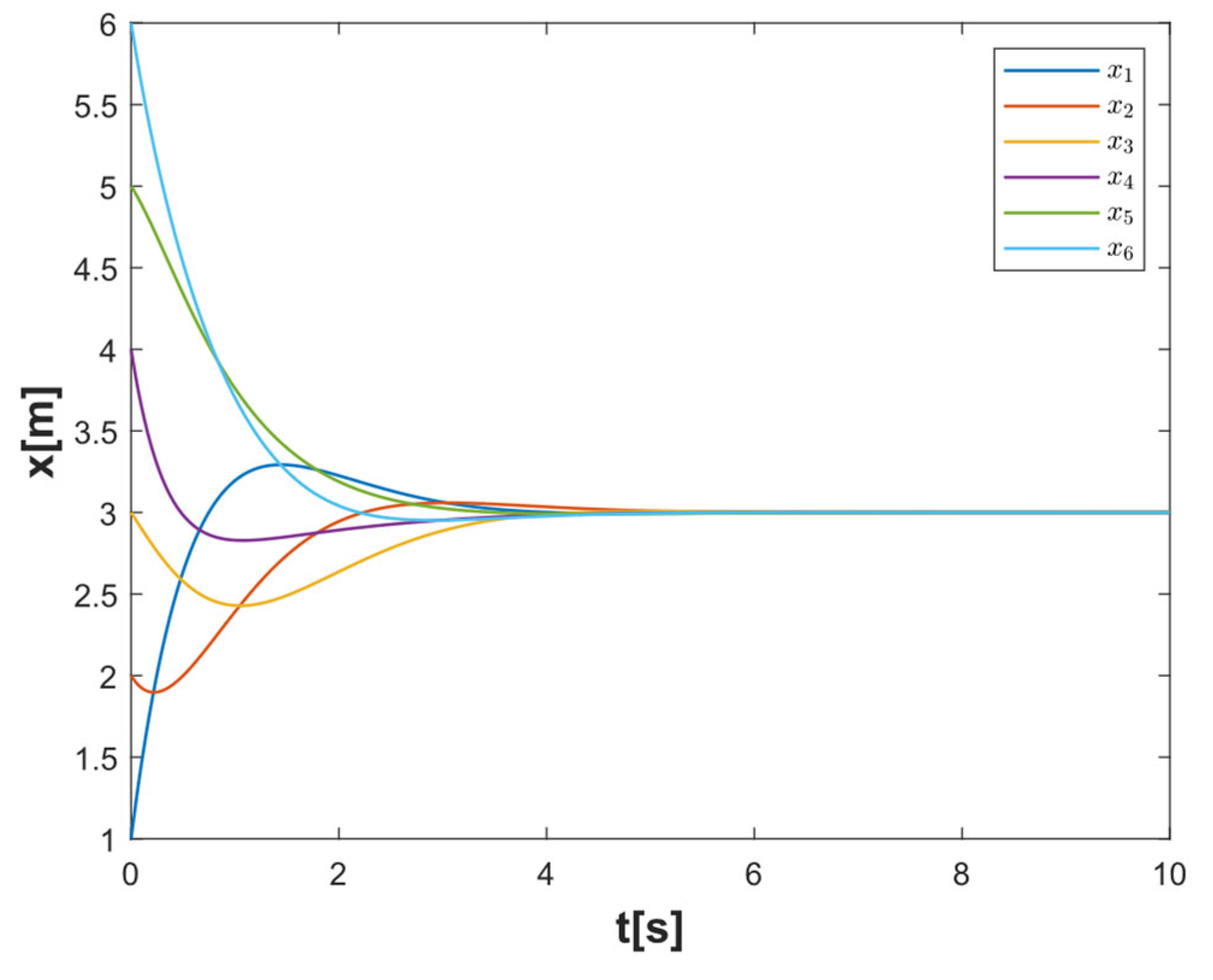
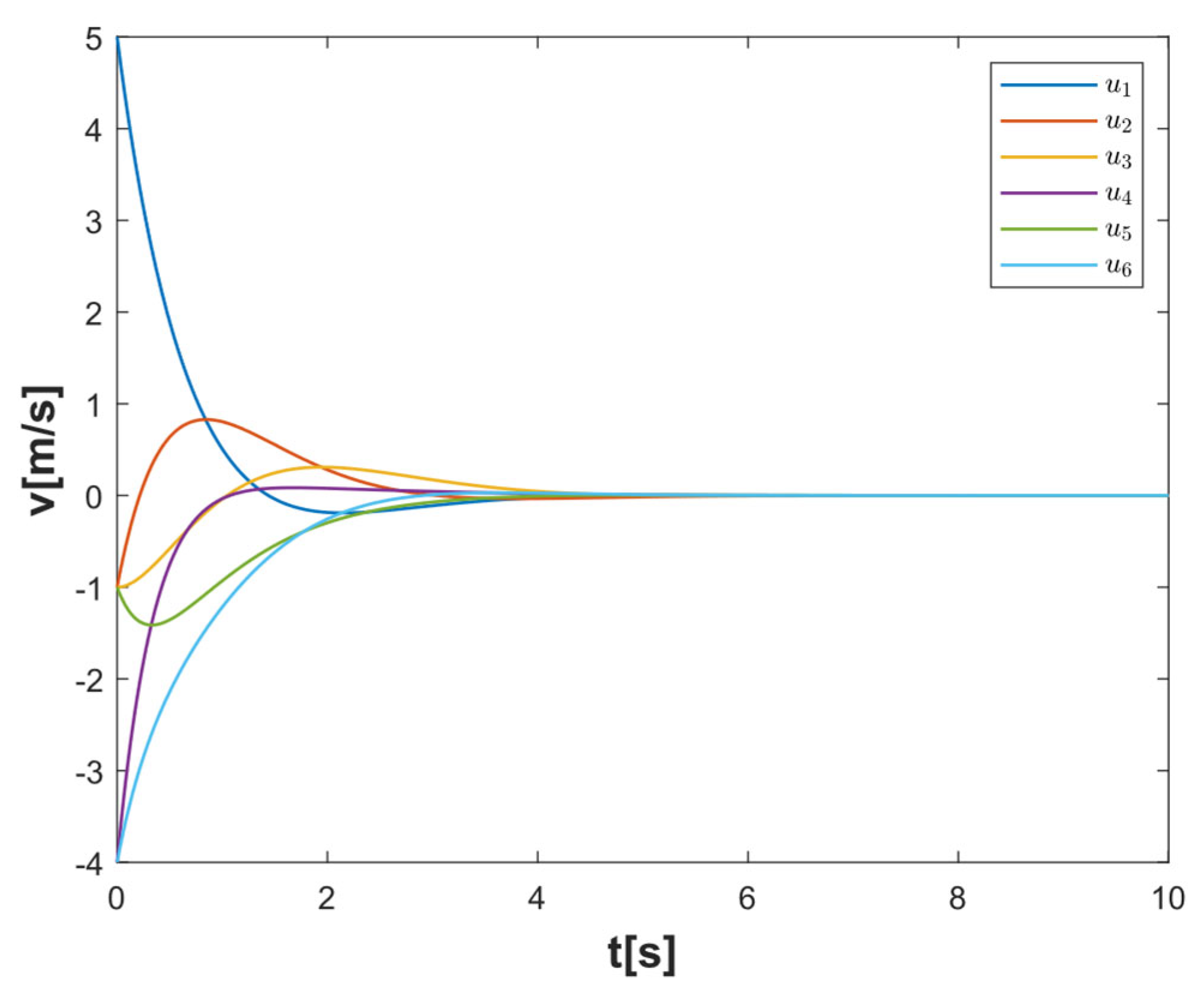
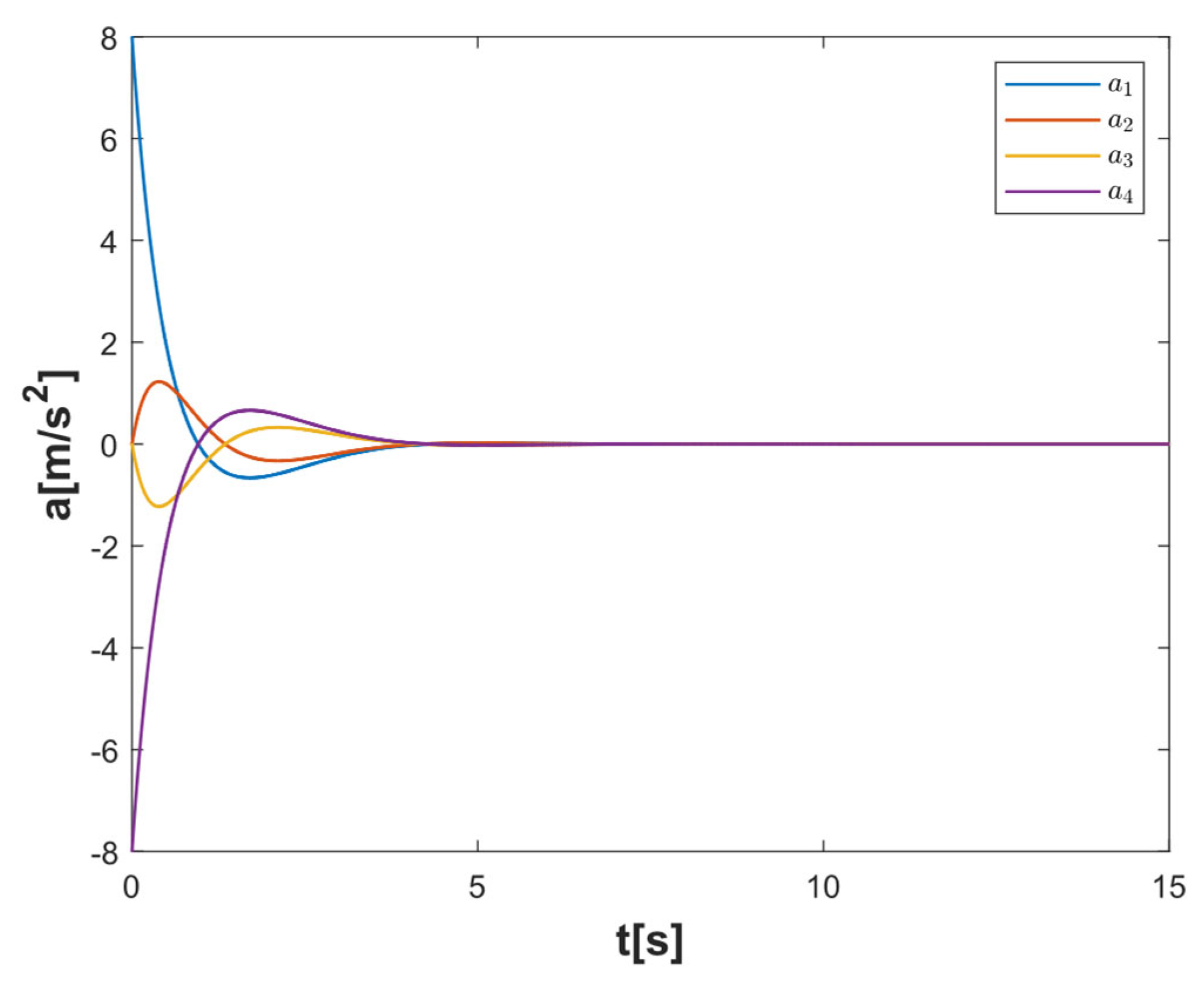
4.1. Simulation Verification of System Consistency

The consistency of the constructed multi-intelligent-agent system is simulated and verified as a first step. Among them, agents 1–6 are modeled as first-order systems, while agents 7–10 are second-order systems. This structure is designed to simulate the interaction and coordination between multiple agents operating in complex environments.

For the model construction, the kinematic and dynamic models are defined of each agent and its interconnection mechanism. The state of each first-order intelligence is represented by its position and velocity, while the second-order intelligence introduces acceleration as its state variable on the basis of the first-order intelligence. The leader agent sets the target position and transmits positional information to the followers, who adjust their own motion state by receiving and processing this information to achieve consensus.

In the experimental process, MATLAB2022b is used to construct the simulation environment for the proposed multi-agent system. In order to verify the behavior of the system in a dynamic environment, a series of experimental scenarios are designed, encompassing both fixed-target and dynamic-target cases. In each experiment, the system records position, velocity, acceleration, and other state parameters of each intelligent agent and observes system convergence iteratively.

From Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, the heterogeneous multi-agent system achieves a steady state at the predefined time point $t=5 s$, and each agent accurately follows the leader’s state information. The experimental results show that the follower agents progressively converge toward the leader’s target position, and the system demonstrates effective collaboration and consistency.

Through the above simulation verification, it can be concluded that the constructed multi-agent system achieves consistency under the specified conditions, providing a robust theoretical and experimental foundation for subsequent research.

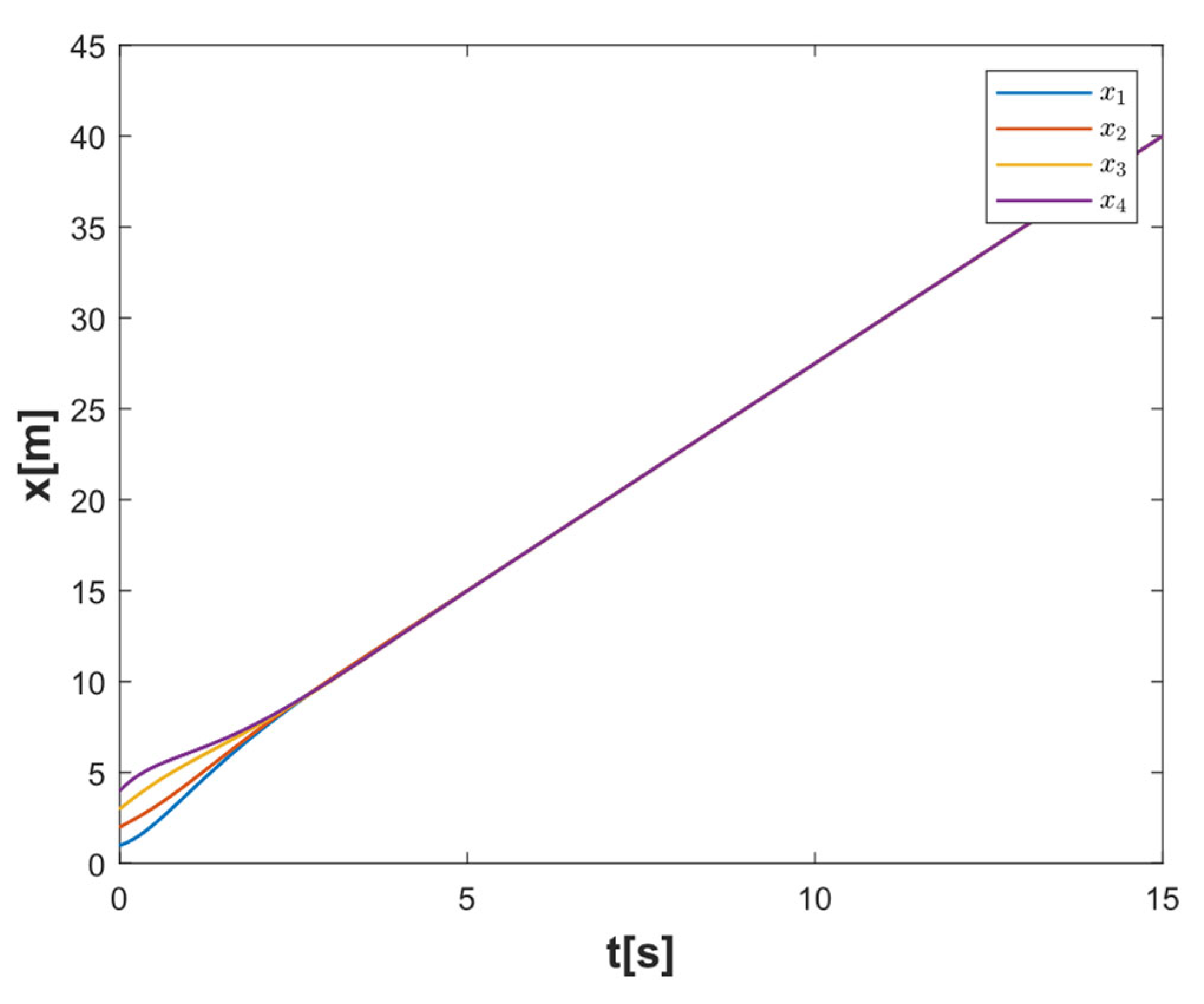
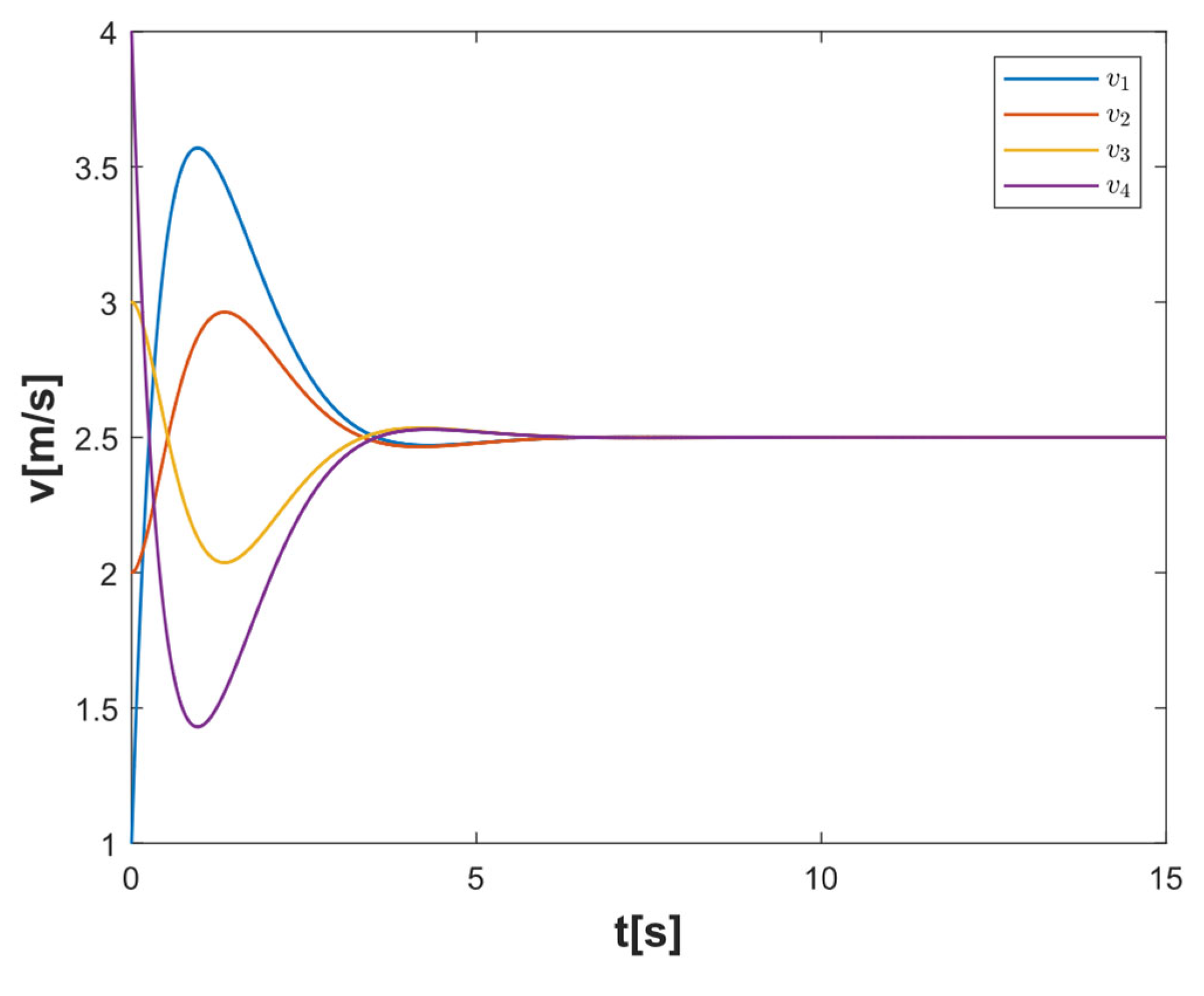
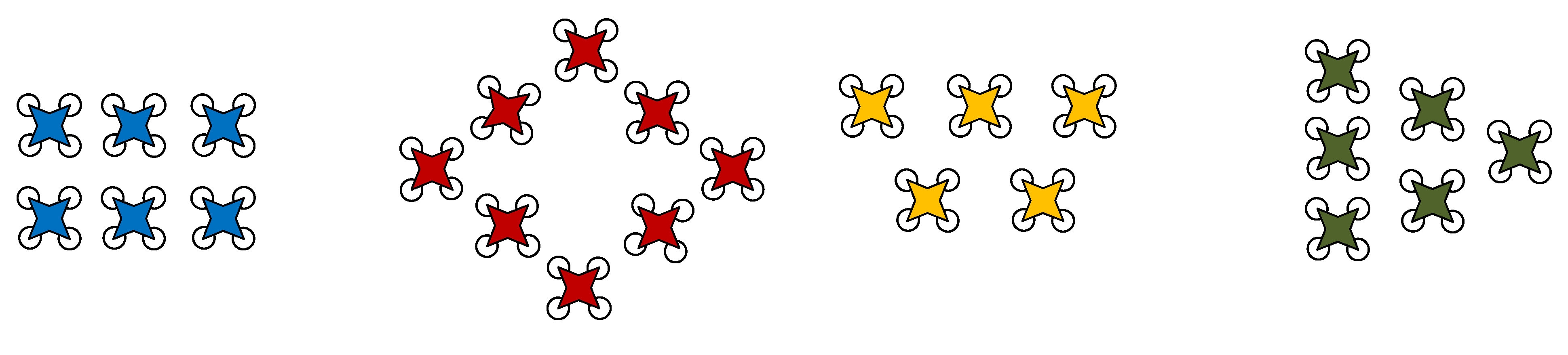
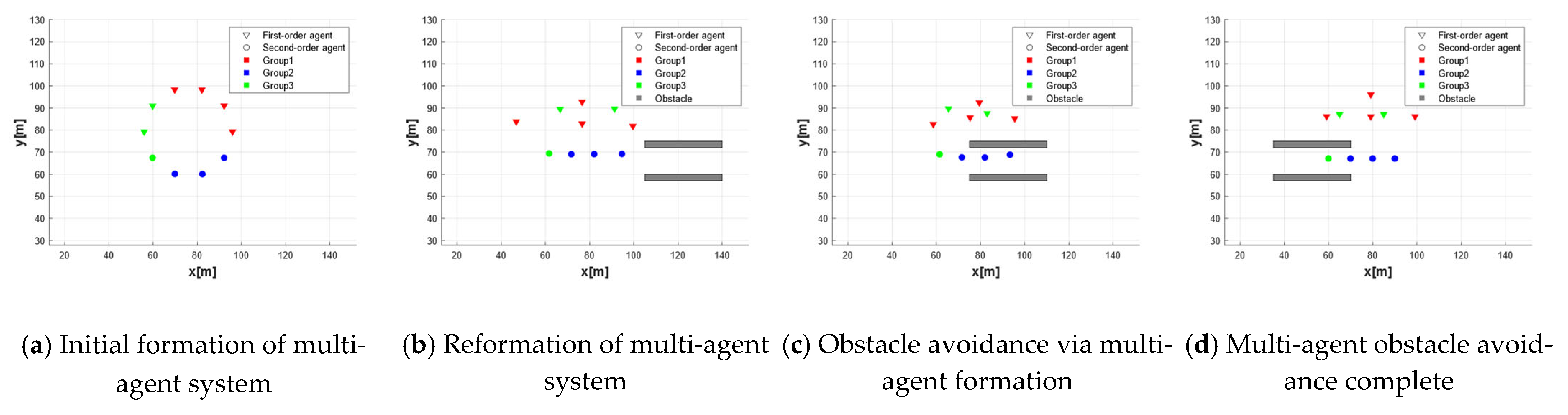
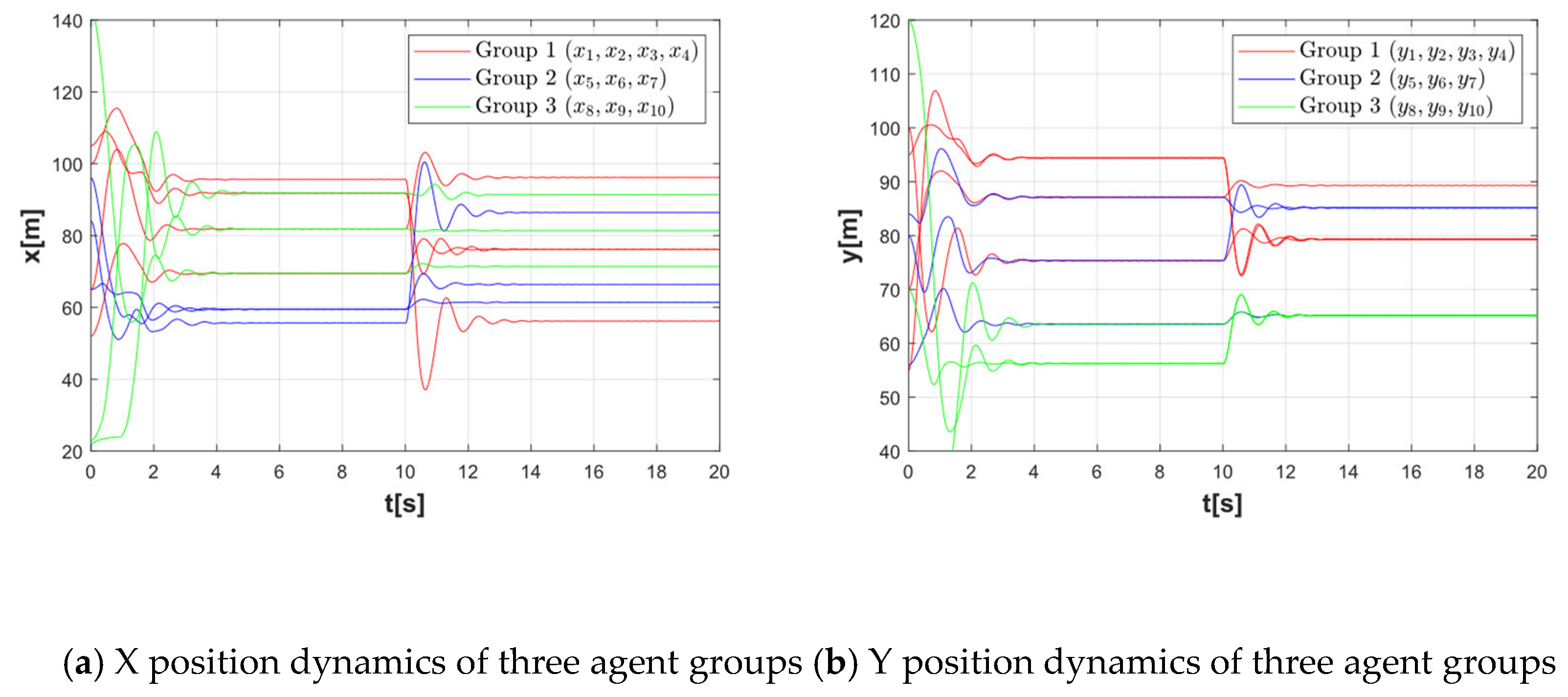
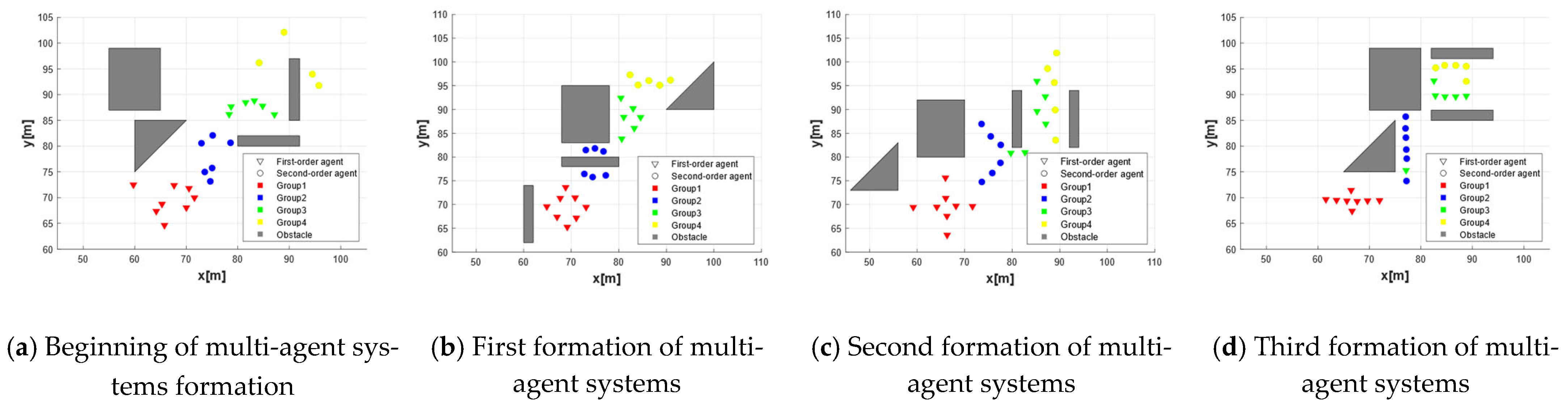
4.2. Formation and Obstacle Avoidance Performance Simulation Verification

The design and validation of formation control algorithms usually rely on simulations to evaluate algorithm performance across varying conditions, ensuring that agents can achieve the desired formation shapes as expected. Different formation shapes offer different advantages in performing specific tasks. For example, a grid or line formation covers larger areas, making it ideal for search-and-rescue operations, whereas a ring or wedge formation is well suited for surveillance and reconnaissance, offering enhanced situational awareness and protection. Figure 6 illustrates the formation shapes of the multi-agent system in the simulation. The experiment validates the formation control algorithm by simulating dynamic formation process. In our simulations, we assume ideal conditions where the reference trajectories are smooth, and the disturbances acting on the system are bounded. To simulate the effect of external disturbances, we introduce small random position perturbations at the initial setup, representing factors like wind. However, the range of these disturbances is limited, and we assume that the disturbances are small enough for the system to adapt and ultimately form the desired formation. These assumptions provide a clear understanding of how the system behaves under ideal conditions.

Table 2. Parameters for numerical simulations.

Parameter	Value
$\mathrm{Communication} \mathrm{boundary}, R$	50 [m]
$\mathrm{Formation}-\mathrm{limit} \mathrm{boundary}, R^{\prime }$	40 [m]
$\mathrm{Exclusion} \mathrm{outer} \mathrm{boundary}, r_{out}$	5 [m]
$\mathrm{Exclusion} \mathrm{inner} \mathrm{boundary}, r_{in}$	0.5 [m]
$\mathrm{Potential} \mathrm{function} \mathrm{gain}, (k_{1 },k_{2 }$)	(8, 2)
$\mathrm{Control} \mathrm{parameters}, (\alpha ,\beta$)	(1.5, 1.5)
$\mathrm{Intelligence} \mathrm{degree}, \omega$	(1, 1.1, 1.2)
$\mathrm{Communication} \mathrm{attenuation} \mathrm{rate}, \tau$	0.6
$\mathrm{Connectivity} \mathrm{lower} \mathrm{bound}, ϵ$	0.4

provides the relevant parameters used in the simulation experiments.

To validate the formation control and obstacle avoidance performance of a heterogeneous multi-agent system in complex environments, the simulation involves ten agents, comprising six first-order and four second-order agents. Obstacles are set up in the simulation environment to replicate challenges found in complex urban environments and evaluate the agents’ path-planning and formation-keeping capabilities.

The simulation results in Figure 7 illustrate the evolution of the formation shape over time. From the figure, it can be observed that the agents initially form a circular formation and subsequently adjust to a straight-line and triangular formation based on the operational requirements for navigating gaps and avoiding obstacles. In this study, first-order agents use a simplified dynamics model, which is able to form a stable triangular formation and move along the edges of obstacles when it encounters them, thus keeping the formation stable. The second-order intelligent agent has a more complex dynamics model, allowing for finer motion control. When encountering narrow gaps in tall buildings, second-order agents can precisely navigate straight paths through narrow gaps between obstacles, thereby preserving formation stability. Figure 8 demonstrates the real-time consensus dynamics of first-order and second-order agents. These change processes show that the formation shape adjustments and control strategies are effectively implemented in a dynamic environment.

To further validate the effectiveness of the proposed formation control and obstacle avoidance strategies, this simulation introduces dynamically changing obstacle scenarios and expands the number of agents to 25. These agents are divided into four groups (Group 1 to Group 4), where each group maintains formation stability while avoiding obstacles. The simulation results in Figure 9 demonstrate that the multi-agent system can effectively avoid obstacles and maintain formation stability in dynamic environments. The system exhibits excellent path-planning capabilities and coordination in dynamic conditions. Each group collaborates to construct the initial formation and successfully avoids obstacles in dynamic environments while maintaining intra-group consistency. The dynamic obstacles in the simulation include moving geometries such as triangular, rectangular, and elongated shapes, which represent different types of obstacles commonly encountered in complex environments. Specifically, moving triangular obstacles simulate sharp-edged objects such as traffic signs, building roof peaks, or rocky outcrops in mountainous regions. Rectangular obstacles represent objects like building facades, billboards, or large transport vehicles that are commonly found in urban settings. Lastly, elongated obstacles are used to model long structures such as bridges, power lines, or cargo transportation vehicles that may be encountered during flight in urban or mountainous areas. The simulation results show that the heterogeneous multi-agent system can effectively achieve formation control in complex environments, and first-order agents and second-order agents each show their advantages in different tasks. Specifically, first-order agents excel at maintaining formation stability and avoiding obstacles, while the second-order agents excel in path traversal and precise control. These results indicate that the formation control strategy proposed in this study can not only effectively address challenges in complex environments but also contribute significantly to practical applications, providing substantial support for deploying multi-agent systems in real-world complex environments.

5. Conclusions

The research presented in this paper demonstrates significant advancements in formation control and obstacle avoidance for UAV-based multi-agent systems. These results enhance the agility and adaptability of multi-agent systems in highly dynamic and complex environments while improving the system’s robustness and reliability. These findings are of great significance in promoting the application of UAVs in fields such as rescue, inspection, logistics, and more. Particularly in urban environments, the complex terrain and high building density demand greater collaboration capabilities and autonomous decision-making from multi-agent systems. This research addresses obstacle avoidance challenges while ensuring formation stability, offering a robust solution for UAVs operating in urban environments.

In addition, this research introduces novel concepts and methods for designing control strategies for heterogeneous multi-agent systems. The constituent agents of a heterogeneous multi-agent system exhibit diverse capabilities and performance, making their effective coordination critical for achieving optimal system performance. The formation control strategy proposed in this study optimizes system performance by analyzing the characteristics and capabilities of different agents and assigning tasks accordingly. This strategy can be applied to a broader spectrum of heterogeneous multi-agent systems, offering novel insights and methodologies for advancing research and development in related domains.