An Anti-Disturbance Attitude Control Method for Fixed-Wing Unmanned Aerial Vehicles Based on an Integral Sliding Mode Under Complex Disturbances During Sea Flight
Abstract
1. Introduction
- A double-loop integral sliding mode control (ISMC) system is developed to accommodate attitude control amidst parameter uncertainties, such as fuel consumption during flight. An additional DO is integrated into the inner loop to estimate unpredictable external factors like sea-level wave disturbances. This composite integral sliding mode control based on disturbance observer (ISMC-DO) system not only achieves precise attitude control, but also fortifies the resistance of the UAV to external disturbances. The two-degrees-of-freedom controller predicated on ISMC-DO can effectively observe low-altitude wave disturbances, refine attitude tracking accuracy, and simultaneously ensure optimal tracking and anti-disturbance performance.
- While most studies traditionally rely on constant or square-wave instructions for attitude tracking, this paper diverges by employing ISMC-DO combined with the quaternion theory to track complex combat maneuver commands. To circumvent the singularity issues encountered during large-angle maneuvers, an outer loop for quaternion attitude control is formulated to acquire the desired angular velocity. Through extensive attitude tracking and aerobatic maneuver experiments, this paper validates the feasibility of executing complex combat maneuvers, such as looping, the split-S, and the Immelmann turn, thereby providing a theoretical and practical underpinning for high-precision combat maneuver tracking.
2. Model Description
2.1. Modeling of Fixed-Wing UAV
2.2. Control Goal
- Initially, we introduce a double-closed-loop ISMC system designed to mitigate model uncertainties and decouple the relationships among the triad of attitude angles. Namely, the control goals are , , so as to achieve and , where is the desired attitude angle vector, is the desired angular velocity vector, is the sliding surface of the attitude angle control loop, and is the sliding surface of the angular velocity control loop.
- In consideration of the impact that sea-level wave disturbances have on low-altitude attitude tracking, a DO is incorporated to estimate these unknown disturbances. Let the disturbance estimated by DO be . The goal of the DO is to minimize the estimation error .
- Finally, to ensure accurate tracking of specialized combat maneuvers, the challenges of singularity in large-angle maneuvers are addressed through the adoption of the quaternion theory for the outer loop of the attitude control system. Let the quaternion describe the attitude, and the desired quaternion be . The quaternion tracking error is . The control goal is that within the completion time of the large-angle maneuver, , where is a given small positive number.
3. An Anti-Disturbance Attitude Control Method Based on ISMC-DO and Quaternions for Large-Angle Maneuvering Problems
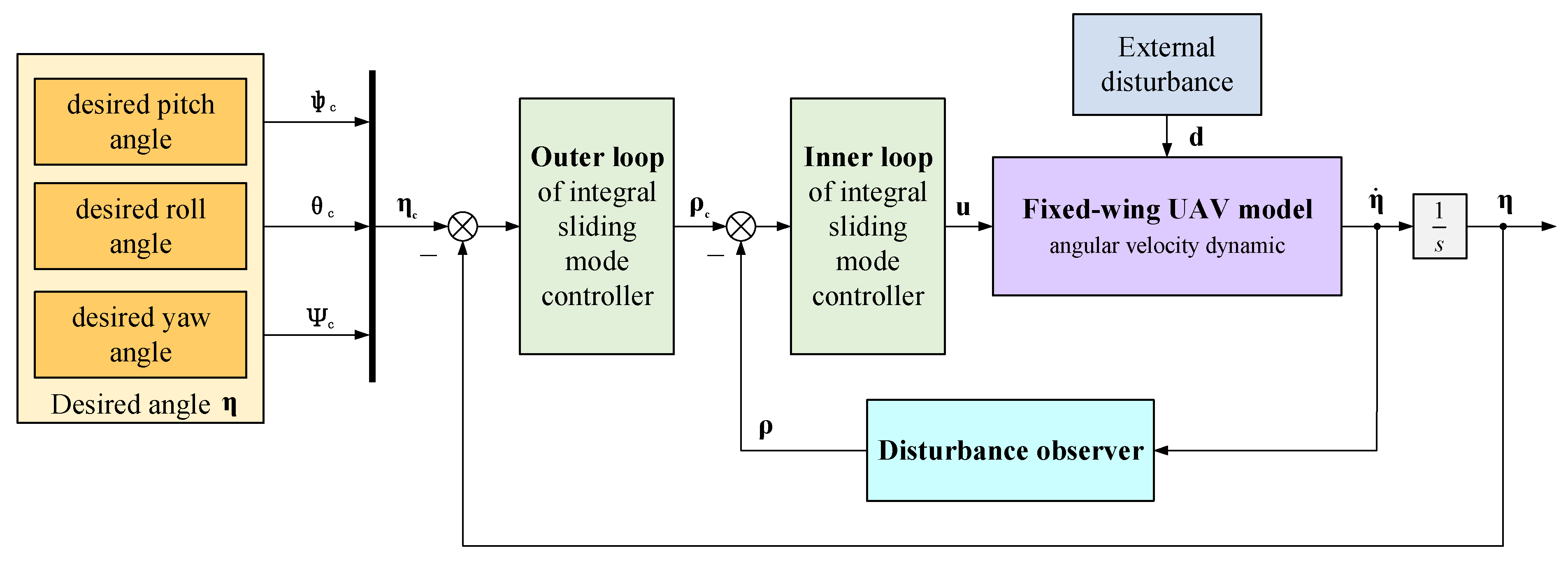
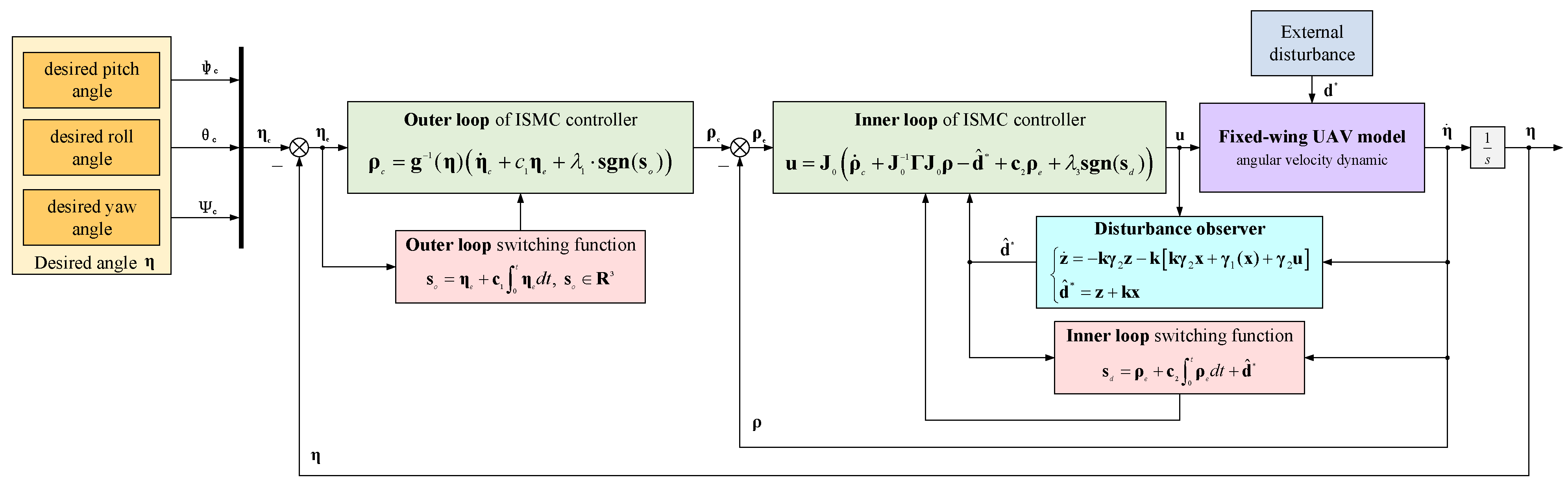
3.1. Design of Integral Sliding Mode Controller Based on Disturbance Observer
3.2. Attitude Controller Based on Quaternions for Combat Maneuvers
3.3. Stability Analysis
4. Simulation
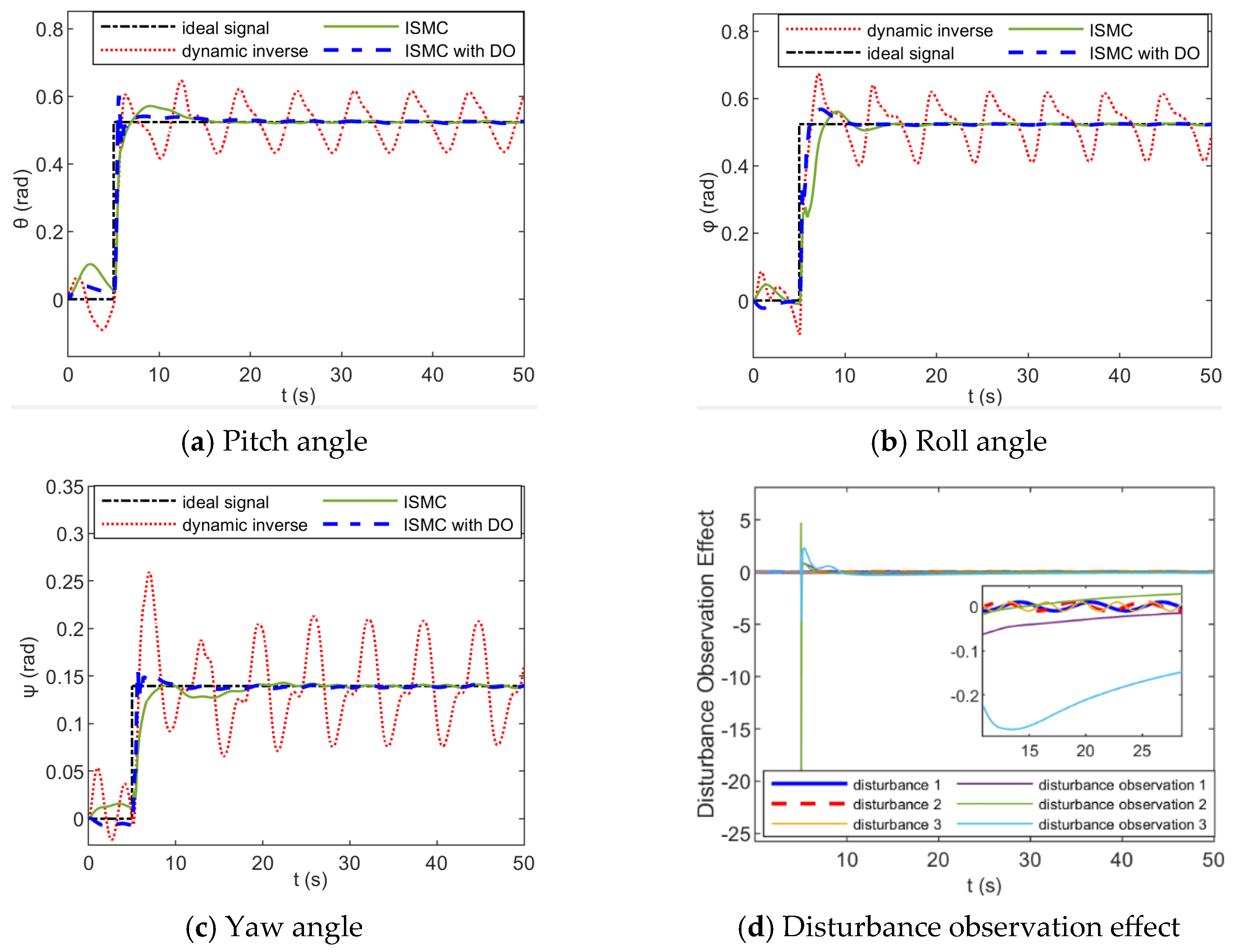
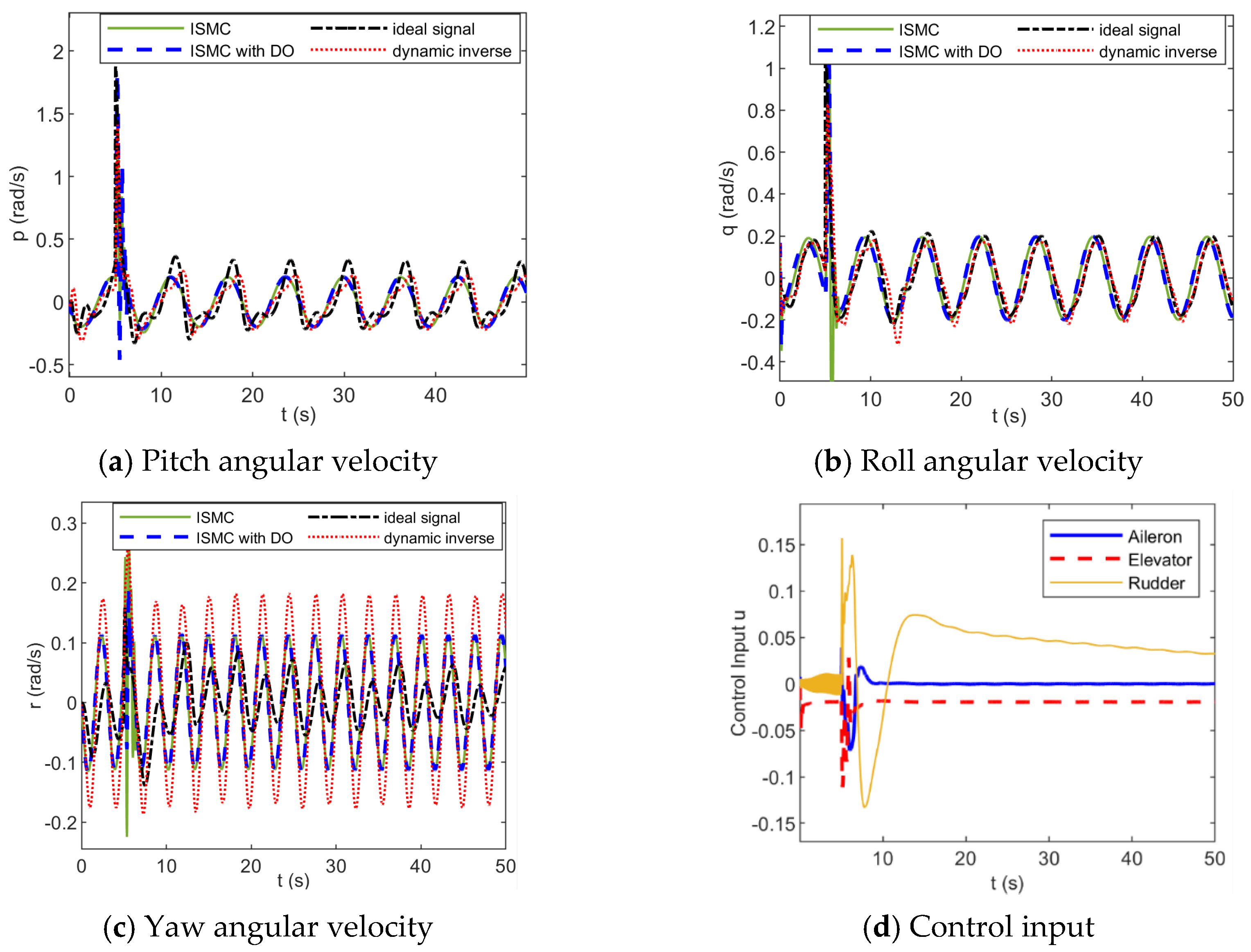
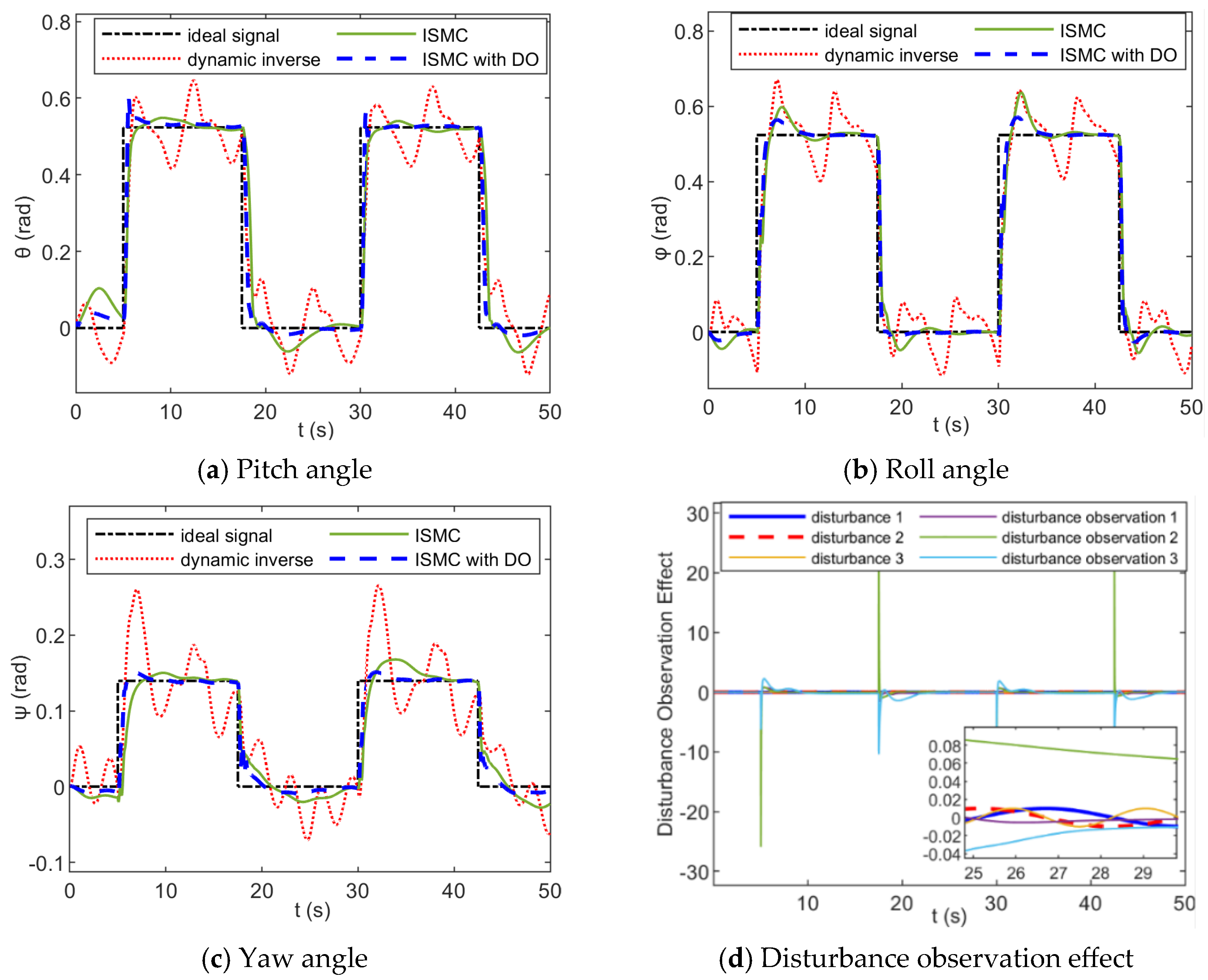
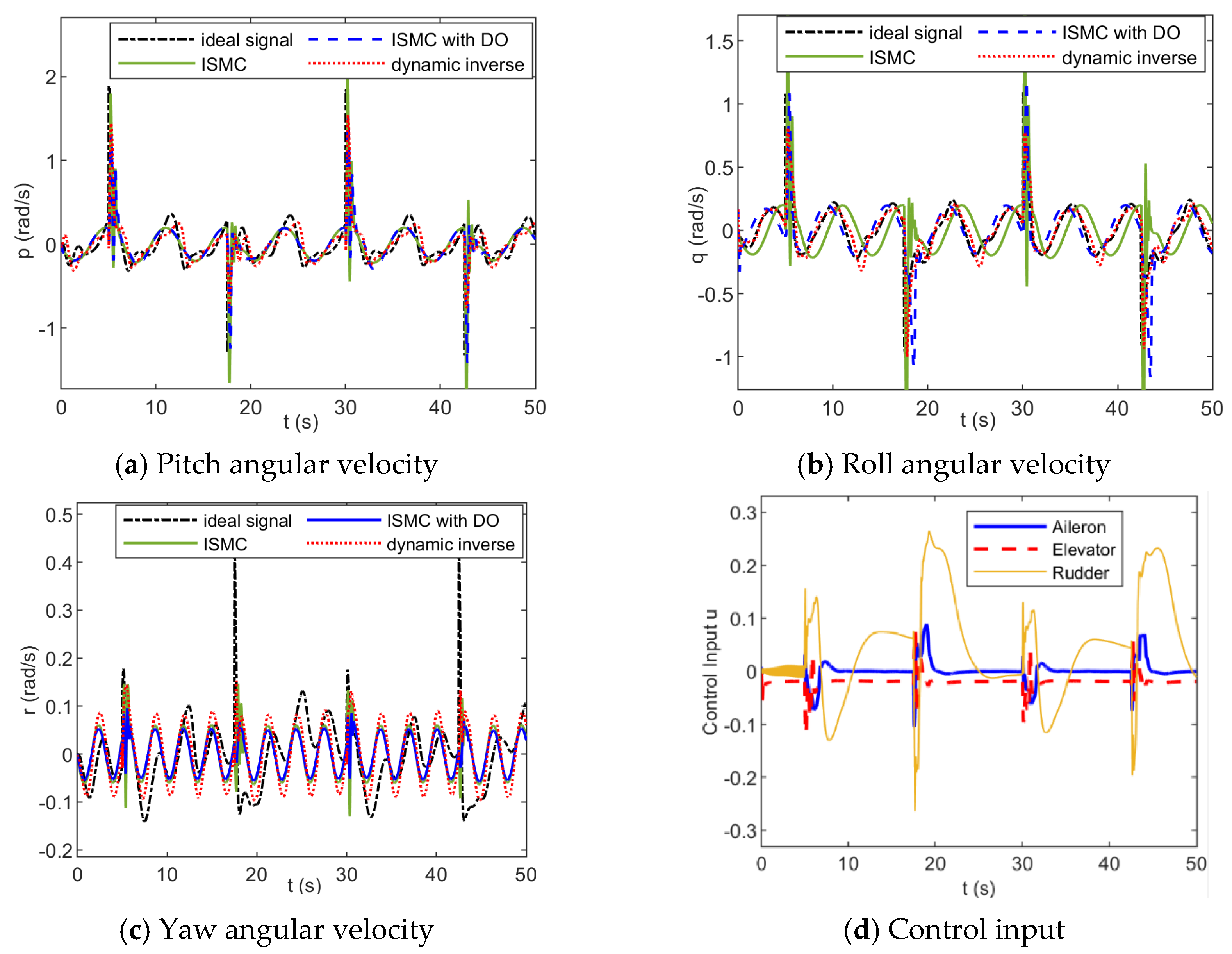
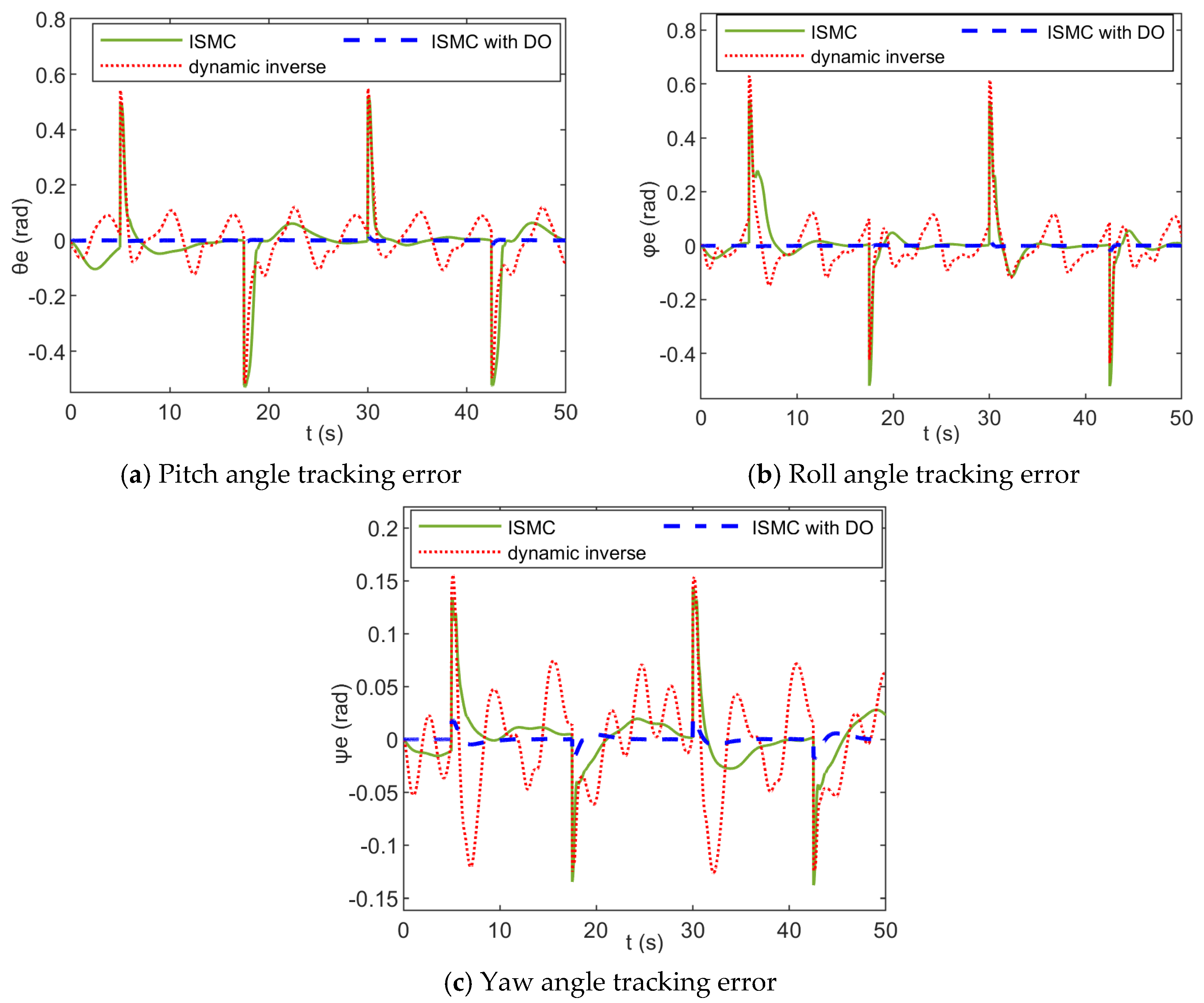
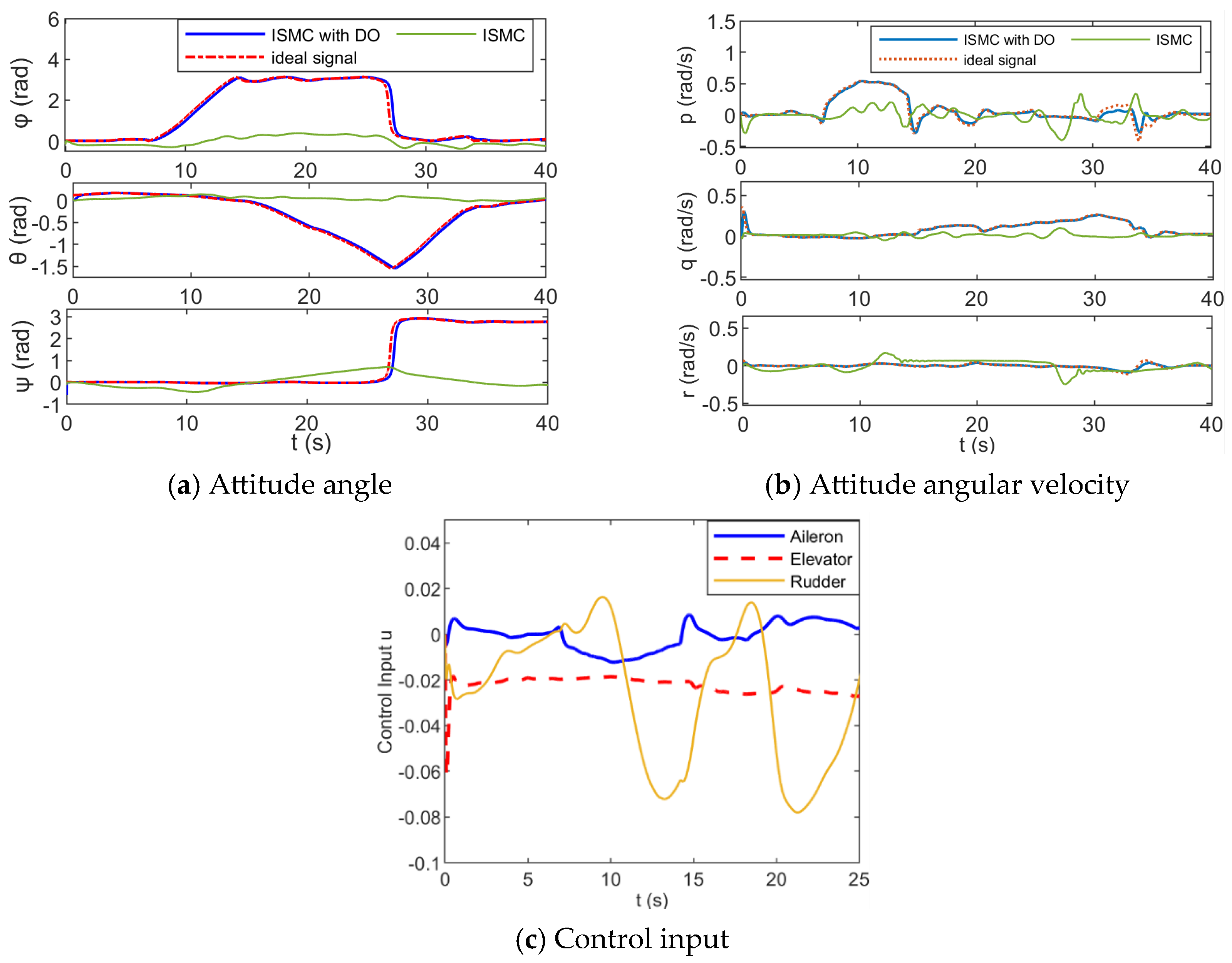
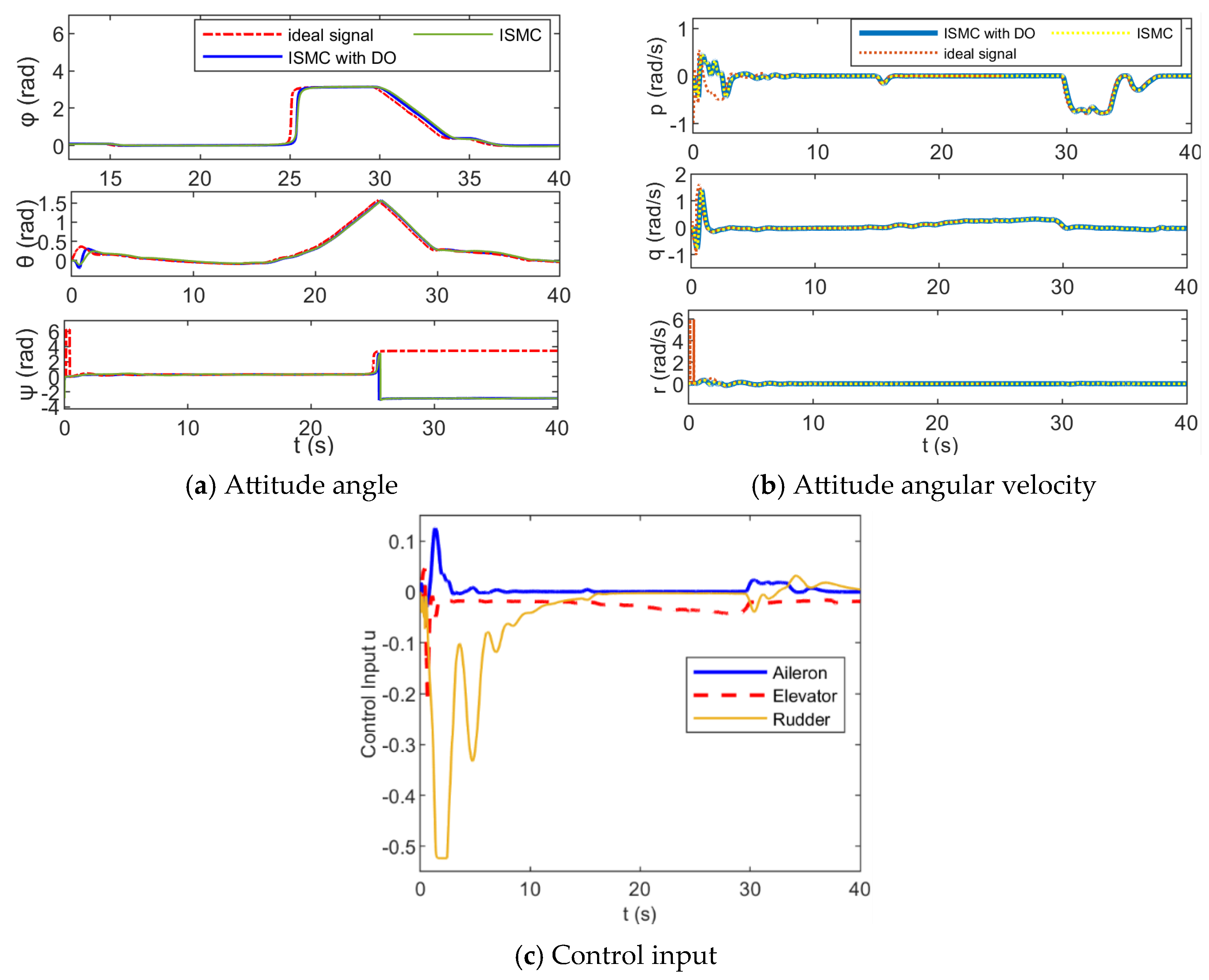
4.1. Anti-Disturbance Attitude Control of Fixed-Wing UAVs Under Sea-Level Low-Altitude Flight
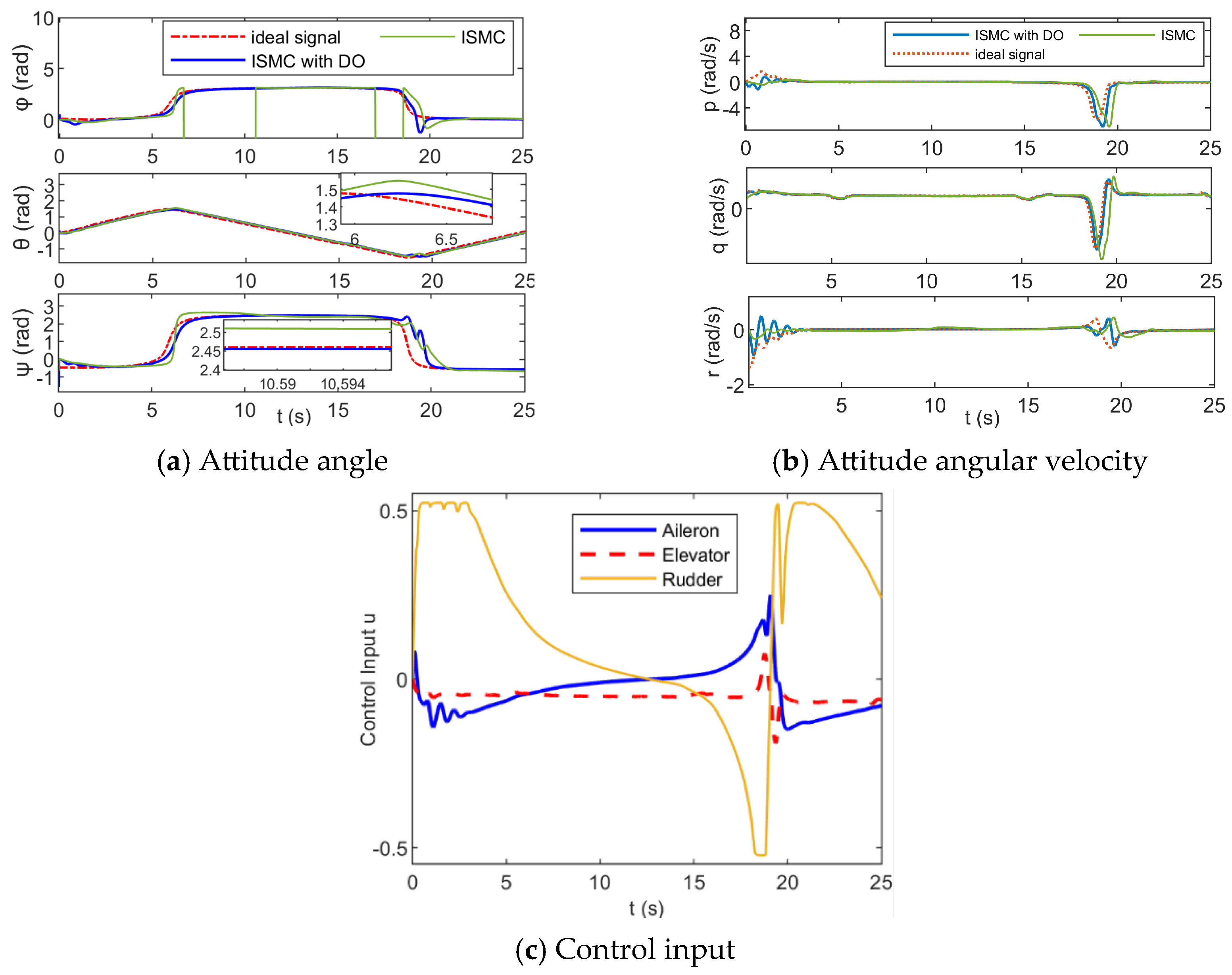
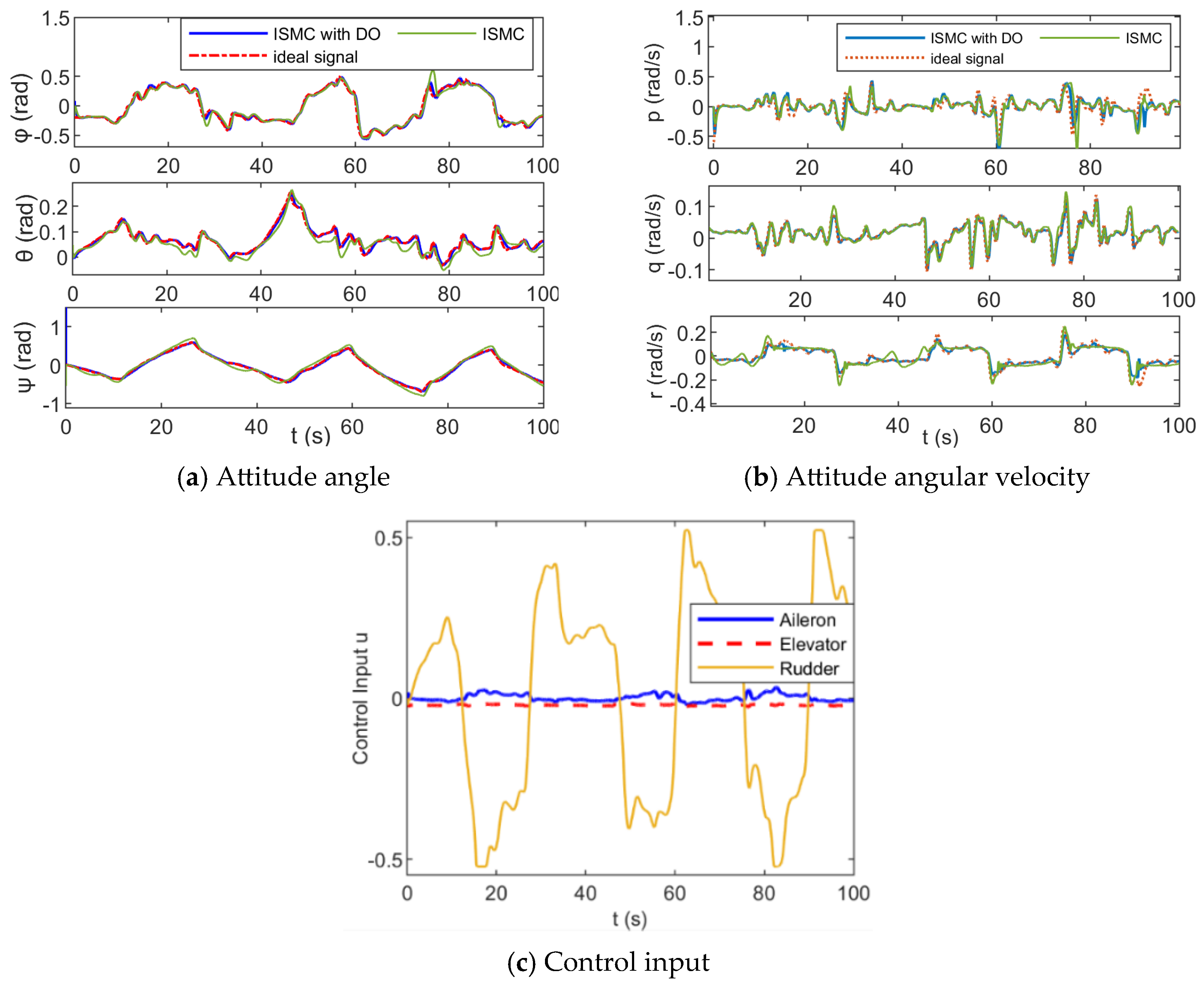
4.2. Anti-Disturbance Attitude Control of Fixed-Wing UAVs Under Large-Angle Maneuvering
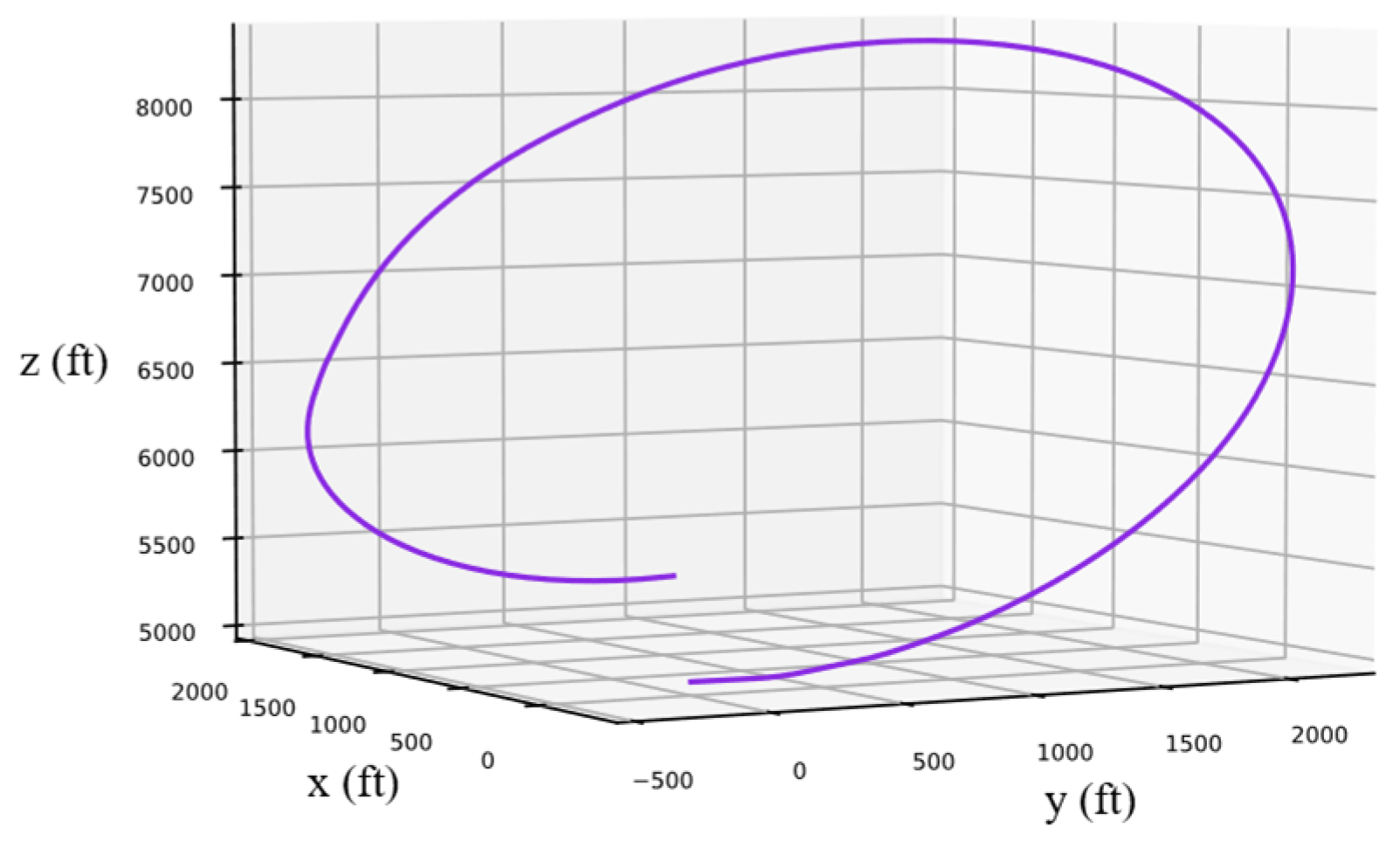
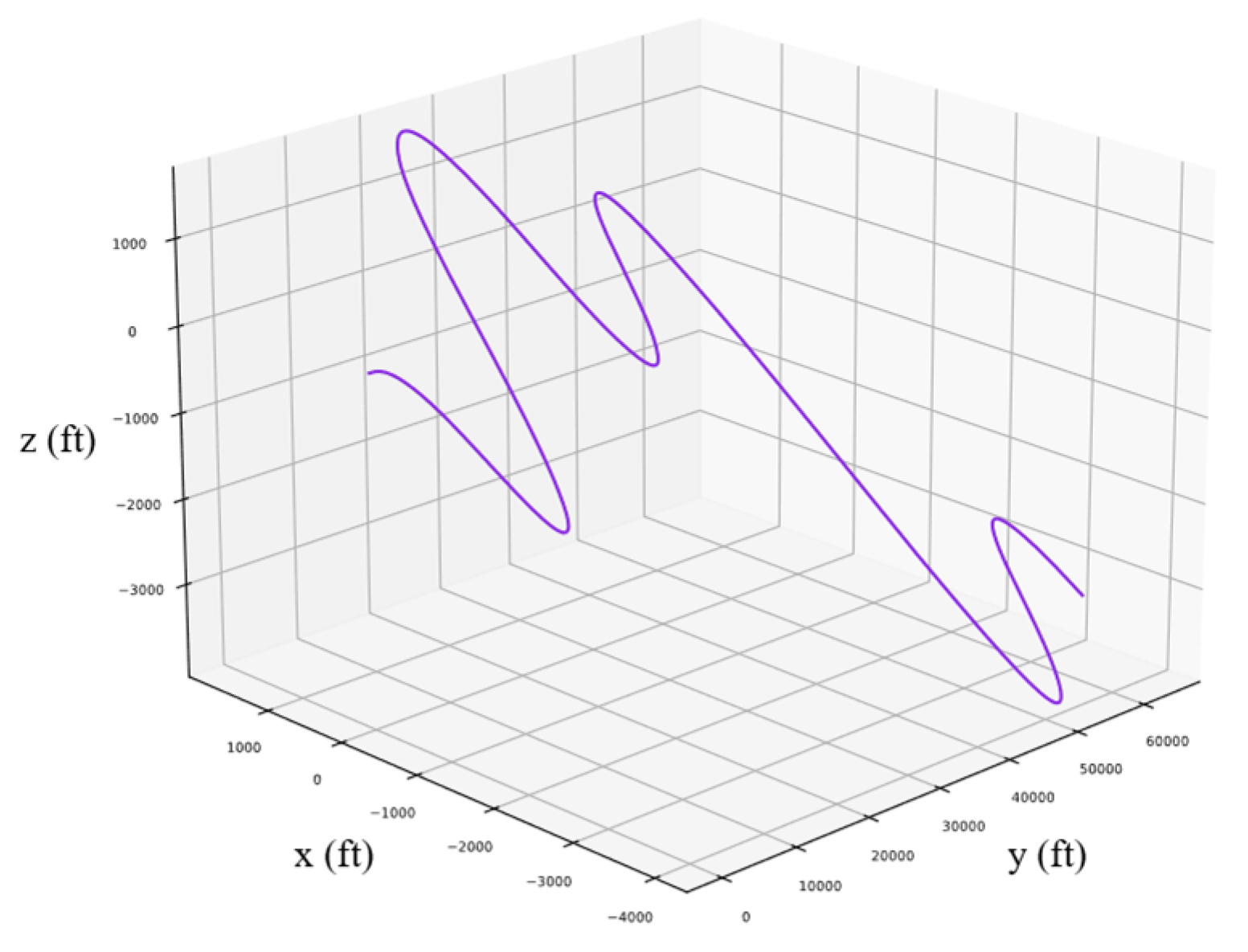
4.2.1. Simulation of Attitude Control of “Looping”
4.2.2. Simulation of Attitude Control of “Split-S”
4.2.3. Simulation of Attitude Control of “Pougatcheff Cobra Maneuver”
4.2.4. Simulation of Attitude Control of “Immelmann Turn”
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Liu, Z.; Cong, Y.; Li, J.; Chen, H. Miniature fixed-wing UAV swarms: Review and outlook. Acta Aeronaut. Astronaut. Sin. 2020, 41, 23732. [Google Scholar] [CrossRef]
- Wu, Z.; Ni, J.; Qian, W.; Bu, X.; Liu, B. Composite prescribed performance control of small unmanned aerial vehicles using modified nonlinear disturbance observer. ISA Trans. 2021, 116, 30–45. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Shi, Z.; Zhong, Y. Robust adaptive three-dimensional trajectory tracking control scheme design for small fixed-wing UAVs. ISA Trans. 2023, 141, 377–391. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Zhang, W.; Chen, H.; Shi, J. Robust control strategy for multi-UAVs system using MPC combined with Kalman-consensus filter and disturbance observer. ISA Trans. 2023, 135, 35–51. [Google Scholar] [CrossRef]
- De Marco, A.; D’Onza, P.M.; Manfredi, S. A deep reinforcement learning control approach for high-performance aircraft. Nonlinear Dyn. 2023, 111, 17037–17077. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, D.; Tang, S.; Xiong, W.; Yang, S.-H. Cooperative maneuver decision making for multi-UAV air combat based on incomplete information dynamic game. Def. Technol. 2023, 27, 308–317. [Google Scholar] [CrossRef]
- Nian, X.-H.; Zhou, W.-X.; Li, S.-L.; Wu, H.-Y. 2-D path following for fixed wing UAV using global fast terminal sliding mode control. ISA Trans. 2022, 136, 162–172. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, Z.; Zhu, X. Flight quality characteristics and observer-based anti-windup finite-time terminal sliding mode attitude control of aileron-free full-wing configuration UAV. Aerosp. Sci. Technol. 2021, 112, 106638. [Google Scholar] [CrossRef]
- SaiCharanSagar, A.; Vaitheeswaran, S.M.; Shendge, P.D. Uncertainity Estimation Based Approach To Attitude Control of Fixed Wing UAV. IFAC-Pap. 2016, 49, 278–283. [Google Scholar] [CrossRef]
- Olavo, J.L.G.; Thums, G.D.; Jesus, T.A.; Pimenta, L.C.d.A.; Torres, L.A.B.; Palhares, R.M. Robust Guidance Strategy for Target Circulation by Controlled UAV. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1415–1431. [Google Scholar] [CrossRef]
- Baldi, S.; Sun, D.; Xia, X.; Zhou, G.; Liu, D. ArduPilot-Based Adaptive Autopilot: Architecture and Software-in-the-Loop Experiments. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4473–4485. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y.; Wu, X.; Dong, H.; Wang, C.; Tang, J.; Shen, C.; Liu, J. Attitude-Induced error modeling and compensation with GRU networks for the polarization compass during UAV orientation. Measurement 2022, 190, 110734. [Google Scholar] [CrossRef]
- Mullen, J.; Bailey, S.C.C.; Hoagg, J.B. Filtered dynamic inversion for altitude control of fixed-wing unmanned air vehicles. Aerosp. Sci. Technol. 2016, 54, 241–252. [Google Scholar] [CrossRef]
- Yu, X.; Yang, J.; Li, S. Finite-time path following control for small-scale fixed-wing UAVs under wind disturbances. J. Frankl. Inst. 2020, 357, 7879–7903. [Google Scholar] [CrossRef]
- Sufendi; Trilaksono, B.R.; Nasution, S.H.; Purwanto, E.B. Design and implementation of hardware-in-the-loop-simulation for uav using pid control method. In Proceedings of the 2013 3rd International Conference on Instrumentation, Communications, Information Technology and Biomedical Engineering (ICICI-BME), Bandung, Indonesia, 7–8 November 2013; pp. 124–130. [Google Scholar]
- Azar, A.T.; Serrano, F.E.; Koubaa, A.; Taha, M.A.; Kamal, N.A. Chapter 9-Fast terminal sliding mode controller for high speed and complex maneuvering of unmanned aerial vehicles. In Unmanned Aerial Systems; Koubaa, A., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 203–230. [Google Scholar]
- Groves, K.; Sigthorsson, D.; Serrani, A.; Yurkovich, S.; Bolender, M.; Doman, D. Reference command tracking for a linearized model of an air-breathing hypersonic vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; p. 6144. [Google Scholar]
- Bauersfeld, L.; Spannagl, L.; Ducard, G.J.J.; Onder, C.H. MPC Flight Control for a Tilt-Rotor VTOL Aircraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2395–2409. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernández-González, O.; Valencia-Palomo, G.; López-Estrada, F.R.; Rodríguez-Mata, A.E.; Garrido, J. Filtered Observer-Based IDA-PBC Control for Trajectory Tracking of a Quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Durán-Delfín, J.E.; García-Beltrán, C.D.; Guerrero-Sánchez, M.E.; Valencia-Palomo, G.; Hernández-González, O. Modeling and Passivity-Based Control for a convertible fixed-wing VTOL. Appl. Math. Comput. 2024, 461, 128298. [Google Scholar] [CrossRef]
- Sartori, D.; Quagliotti, F.; Rutherford, M.J.; Valavanis, K.P. Design and development of a backstepping controller autopilot for fixed-wing UAVs. Aeronaut. J. 2021, 125, 2087–2113. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, J.; Yu, H. Review of modeling and control in UAV autonomous maneuvering flight. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1920–1925. [Google Scholar]
- Lungu, M. Backstepping and dynamic inversion combined controller for auto-landing of fixed wing UAVs. Aerosp. Sci. Technol. 2020, 96, 105526. [Google Scholar] [CrossRef]
- Wang, X.; Tan, C.P.; Wu, F.; Wang, J. Fault-Tolerant Attitude Control for Rigid Spacecraft Without Angular Velocity Measurements. IEEE Trans. Cybern. 2021, 51, 1216–1229. [Google Scholar] [CrossRef]
- Reinhardt, D.; Johansen, T.A. Control of Fixed-Wing UAV Attitude and Speed based on Embedded Nonlinear Model Predictive Control. IFAC-Pap. 2021, 54, 91–98. [Google Scholar] [CrossRef]
- Wang, X.; Tan, C.P. Output Feedback Active Fault Tolerant Control for a 3-DOF Laboratory Helicopter With Sensor Fault. IEEE Trans. Autom. Sci. Eng. 2024, 21, 2689–2700. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, G.; Dong, Q. Adaptive dynamic programming-based adaptive-gain sliding mode tracking control for fixed-wing unmanned aerial vehicle with disturbances. Int. J. Robust Nonlinear Control 2023, 33, 1065–1097. [Google Scholar] [CrossRef]
- He, H.; Duan, H. A multi-strategy pigeon-inspired optimization approach to active disturbance rejection control parameters tuning for vertical take-off and landing fixed-wing UAV. Chin. J. Aeronaut. 2022, 35, 19–30. [Google Scholar] [CrossRef]
- Castañeda, H.; Salas-Peña, O.S.; León-Morales, J.d. Extended observer based on adaptive second order sliding mode control for a fixed wing UAV. ISA Trans. 2017, 66, 226–232. [Google Scholar] [CrossRef]
- Hou, Y.; Lv, M.; Liang, X.; Yang, A. Fuzzy adaptive fixed-time fault-tolerant attitude tracking control for tailless flying wing aircrafts. Aerosp. Sci. Technol. 2022, 130, 107950. [Google Scholar] [CrossRef]
- Wang, X.; Sun, S.; Tao, C.; Xu, B. Neural sliding mode control of low-altitude flying UAV considering wave effect. Comput. Electr. Eng. 2021, 96, 107505. [Google Scholar] [CrossRef]
- Mahgoub, Y.; El-Badawy, A. Nonlinear disturbance observer-based control of a structural dynamic model of a twin-tailed fighter aircraft. Nonlinear Dyn. 2022, 108, 315–328. [Google Scholar] [CrossRef]
- Petrlík, M.; Báča, T.; Heřt, D.; Vrba, M.; Krajník, T.; Saska, M. A Robust UAV System for Operations in a Constrained Environment. IEEE Robot. Autom. Lett. 2020, 5, 2169–2176. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Ren, B. Energy Saving Quadrotor Control for Field Inspections. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1768–1777. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Z.; Gao, Z.; Zhang, W. Reinforcement Learning-Based Fault-Tolerant Control for Quadrotor UAVs Under Actuator Fault. IEEE Trans. Ind. Inform. 2024, 20, 13926–13935. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, M.; Shi, P. Disturbance Utilization-Based Tracking Control for the Fixed-Wing UAV With Disturbance Estimation. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 1337–1349. [Google Scholar] [CrossRef]
- Xu, L.; Qi, G. Function observer based on model compensation control for a fixed-wing UAV. Aerosp. Sci. Technol. 2024, 152, 109325. [Google Scholar] [CrossRef]
- Chan, P.T.; Rad, A.B.; Wang, J. Indirect adaptive fuzzy sliding mode control: Part II: Parameter projection and supervisory control. Fuzzy Sets Syst. 2001, 122, 31–43. [Google Scholar] [CrossRef]
- Chen, W.H. Nonlinear Disturbance Observer Based Dynamic Inversion Control of Missiles. IFAC Proc. Vol. 2001, 34, 463–468. [Google Scholar] [CrossRef]
- Ariyibi, S.O.; Tekinalp, O. Quaternion-based nonlinear attitude control of quadrotor formations carrying a slung load. Aerosp. Sci. Technol. 2020, 105, 105995. [Google Scholar] [CrossRef]
- Yao, X.; Lian, Y.; Ju, H.P. Disturbance-observer-based event-triggered control for semi-Markovian jump nonlinear systems. Appl. Math. Comput. 2019, 363, 124597. [Google Scholar] [CrossRef]
- Cao, S.; Wang, X.; Zhang, R.; Yu, H.; Shen, L. From Demonstration to Flight: Realization of Autonomous Aerobatic Maneuvers for Fast, Miniature Fixed-Wing UAVs. IEEE Robot. Autom. Lett. 2022, 7, 5771–5778. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Quality | 9296.13 | ||
| Pneumatic reference area | 27.64 | ||
| Average aerodynamic chord length | 3.37 | ||
| Reference wingspan | 9.232 | ||
| Moment of inertia of pitch axis | 12,875.2 | ||
| Moment of inertia of roll axis | 75,674.1 | ||
| Moment of inertia of yaw axis | 85,552.7 | ||
| Pitch axis inertia matrix change | 800 | ||
| Roll axis inertia matrix change | 900 | ||
| Yaw axis inertia matrix change | 1000 |
| Parameter | Location Limit | Unit | Rate limit | Unit |
|---|---|---|---|---|
| Elevator | ||||
| Aileron | ||||
| Rudder | ||||
| Leading edge flap |
| Parameter | Symbol | Value |
|---|---|---|
| Parameters of ISMC inner loop | ||
| 6.5 | ||
| Parameters of ISMC outer loop | ||
| 2 | ||
| Parameters of DO | 3 | |
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, S.; Yao, Y.; Zhu, F. An Anti-Disturbance Attitude Control Method for Fixed-Wing Unmanned Aerial Vehicles Based on an Integral Sliding Mode Under Complex Disturbances During Sea Flight. Drones 2025, 9, 164. https://doi.org/10.3390/drones9030164
Sui S, Yao Y, Zhu F. An Anti-Disturbance Attitude Control Method for Fixed-Wing Unmanned Aerial Vehicles Based on an Integral Sliding Mode Under Complex Disturbances During Sea Flight. Drones. 2025; 9(3):164. https://doi.org/10.3390/drones9030164
Chicago/Turabian StyleSui, Shuaishuai, Yiping Yao, and Feng Zhu. 2025. "An Anti-Disturbance Attitude Control Method for Fixed-Wing Unmanned Aerial Vehicles Based on an Integral Sliding Mode Under Complex Disturbances During Sea Flight" Drones 9, no. 3: 164. https://doi.org/10.3390/drones9030164
APA StyleSui, S., Yao, Y., & Zhu, F. (2025). An Anti-Disturbance Attitude Control Method for Fixed-Wing Unmanned Aerial Vehicles Based on an Integral Sliding Mode Under Complex Disturbances During Sea Flight. Drones, 9(3), 164. https://doi.org/10.3390/drones9030164






