Dynamic Event-Triggered-Based Finite-Time Distributed Tracking Control of Networked Multi-UAV Systems

Abstract

The distributed tracking of multiple unmanned aerial vehicles (UAVs) is a hotspot due to its broad applications in various fields, while continuous communication among UAVs is often impractical, especially in time-sensitive tasks or environments with limited bandwidth. With this in mind, this paper presents a finite-time leader-following distributed tracking control scheme for general multi-agent systems, with a particular emphasis on its application for networked UAVs. Theoretically, a dynamic event-triggered mechanism is proposed, which features a novel finite-time stable dynamic variable within its triggering rule, ensuring that neither controller updates nor trigger detection requires continuous communication. This event-triggered finite-time controller facilitates efficient network resource management and timely mission response in UAV cooperation, enhancing adaptability to onboard wireless communication networks and time-sensitive tasks. The method allows for the customization of parameters in the internal dynamic variables to adjust the convergence rate and event-triggering frequency of the system, while also preventing Zeno behavior. Moreover, a Lyapunov-based analysis is conducted to theoretically verify the finite-time stability of the closed-loop system and its applicability in directed communication networks. Finally, some numerical simulations are performed to validate the effectiveness of the proposed distributed control scheme for networked multi-UAV systems.

1. Introduction

In recent years, with the advancement of intelligent technologies, the research and application of unmanned aerial vehicle (UAV) systems have increased significantly. In particular, networked multi-UAV systems capable of coordinated formation, such as for target tracking, have found widespread applications in both military and civilian domains, including reconnaissance [1,2], escorting [3,4], and traffic monitoring [5,6]. Consequently, there has been a growing interest in the distributed coordination control of multi-UAV systems in industry and academia [7,8,9]. It is worth noting that, as a fundamental technology for achieving UAVs coordination, the distributed consensus tracking control of multi-agent systems (MASs) has garnered considerable attention [10,11,12]. However, regular consensus protocols of MASs focus on asymptotic convergence driven by continuous communication or continuous control among agents. These methods face challenges in environments where UAVs need to react quickly to dynamic changes while dealing with the constraints imposed by wireless communication. Therefore, investigating distributed consensus tracking control protocols, which do not rely on continuous communication but can ensure the timely achievement of cooperative behaviors, is a significant research direction for advancing the capabilities of multi-UAV systems in real-world applications.

This paper addresses the aforementioned challenges by exploring the implementation of an event-triggered (ET) mechanism in distributed finite-time consensus tracking control. Each UAV updates its control input and broadcasts state information whenever a specified event occurs. The control input is designed to ensure the finite-time stability of the networked UAV system, facilitating the timely achievement of control objectives. Additionally, the lower event frequency reduces the utilization of the wireless communication network. The ET finite-time controller enables efficient network resource management and quick mission response in UAV cooperation, enhancing adaptability to onboard wireless communication networks and time-sensitive practical tasks. However, the implementation of such a complex distributed controller presents significant design challenges.

An increasing number of studies have demonstrated that ET control effectively reduces unnecessary communication overhead and enhances system efficiency, while ensuring the maintenance of desired control performance [13,14,15,16,17]. Thanks to this advantage, ET control has received extensive attention, and some variant methodologies have been developed. In [18,19], the ET control method is applied to address the leader-following consensus problems of linear MASs under undirected networks. Since networks with directed topologies are more common, the results on leader-following consensus control of linear multi-agent systems based on ET under directed networks have been found in [20,21,22]. Manuel Mazo and Paulo Tabuada proposed three implementations of decentralized event-triggered, distributed event-triggered, and distributed self-triggered policies over sensor/actuator networks in [23,24]. It is important to note that the exclusion of Zeno behavior is a crucial aspect of ET control, as it ensures the practicality of the approach and avoids the occurrence of infinite events within a finite time span. The majority of current event-triggering mechanisms depend on system state and/or time information, which can result in an increase in the frequency of triggers as thresholds diminish over time, potentially leading to unnecessary instant triggering.

As research into ET mechanisms advances, there is an acute need to develop more adaptable ET conditions that can extend the interval between events, thereby reducing communication costs. To meet this demand, dynamic event-triggered (DET) strategies have been introduced. In 2004, Girard first proposed a DET mechanism to deal with scheduling stabilizing control tasks for linear systems [25]. Unlike the traditional static ET mechanism, the DET mechanism allows for a longer average event interval by introducing an additional non-negative dynamic variable that depends on its own dynamics. Therefore, DET control strategies have been widely applied to the consensus problem of MASs as evidenced in [26,27,28,29,30]. The authors in [26,27,28] investigate the DET consensus problem for single-integrator or double-integrator systems. The consensus of general linear MASs is studied in [29,30] with DET conditions. However, these studies often necessitate continuous access to the neighboring agents’ state information for event-triggering functions, which contradicts the original intent of introducing event-triggering strategies to save communication energy. To resolve this issue, the authors in [31,32,33,34] propose model-based DET consensus control protocols for linear MASs. By employing a model-based event-triggering scheme, the system state at update intervals is estimated. Subsequently, event-triggering functions are designed based on the estimation error to determine when to transmit the actual system state, thereby eliminating the need for continuous communication. However, it is worth noting that most of the above ET schemes guarantee the asymptotic consensus of MASs, with little consideration of the timeliness of MASs under the ET mechanism.

Recently, designing finite-time ET consensus protocols for MASs has been suggested by some researchers as an important yet challenging area worthy of further investigations [35,36]. Since ET mechanisms inherently aim to decrease the frequency of sampled actions and/or control updates, which poses a challenge in maintaining fast convergence rates, it is thus challenging and meaningful to investigate a finite-time ET approach suitable for MASs, with the aim of achieving rapid convergence while reducing communication overheads. The research results on finite-time ET consensus control strategies for single-order or second-order MASs can be found in [37,38,39,40]. To increase the applicability of these models, researchers have generalized their results to encompass general linear MASs. For example, Cao et al. [41] proposed an event-based strategy that ensures finite-time consensus for general linear MASs over undirected graphs. To tackle the challenge of requiring continuous access to neighboring states during the triggering detection, Du et al. [42] proposed a novel model-based ET controller to achieve finite-time consensus for general linear MASs under directed graphs. However, research on finite-time dynamic event-triggered (FTDET) mechanisms, particularly for general linear MASs, remains limited. Liu et al. [43] proposed a DET mechanism for first-order MASs and developed a finite-time control protocol based on triggered states, eliminating the need for continuous communication. Wen et al. [44] introduced a finite-time consensus control algorithm for first-order MASs with disturbances, combining a dynamic event-trigger mechanism with a sliding mode control protocol. Luo et al. [45] extended this work by proposing a finite-time leader-following consensus control algorithm for second-order MASs with mismatched disturbances. Furthermore, Luo et al. [46] developed a finite-time observer-based distributed DET strategy for general linear leader–follower MASs with unmeasurable states. Despite these advancements, achieving an optimal balance between reducing communication overhead and accelerating cooperative behavior remains a significant challenge for general linear MASs.

Motivated by the above discussion, this paper focuses on the finite-time leader-following control issue for general linear MASs under directed interaction to achieve a faster convergence rate while reducing communication overhead. A FTDET approach is proposed with a designable dynamic internal variable. The main contributions are summarized as follows.

(1)

A novel leader-following consensus control scheme for multi-UAV systems under communication constraints is introduced, which ensures accurate trajectory tracking. The scheme eliminates the need for continuous neighboring state access during controller updates and trigger detections, effectively reducing communication resource consumption. The proposed control scheme guarantees control performance within a finite time, providing a solution for UAVs to swiftly respond to complex situational changes in various collaborative tasks under inevitable directed wireless communication constraints.

(2)

A novel DET mechanism is designed by introducing a power term that not only reduces communication overheads but also enhances the convergence rate while avoiding Zeno behavior. Unlike the finite-time consensus under DET mechanisms as presented in [44,45], the designable exponential term introduced in the internal dynamic variable enhances the design flexibility and enables parameter tuning based on performance requirements. In particular, the convergence rate and the triggering frequency can be modified by adjusting the parameters of the triggering function.

(3)

The proposed control scheme has been proven to be applicable to general linear MASs under directed network topologies. By using the Lyapunov and finite-time theories, a positive diagonal matrix is introduced to demonstrate the finite-time stability of the closed-loop system, addressing the finite-time leader-following consensus problem based on DET in directed graphs. Compared to the studies referenced in [33,34], this study exhibits strong generality in terms of system models, convergence rate, and topological structure, offering significant theoretical and practical values.

The subsequent sections of this work are structured as follows: Section 2 presents relevant mathematical theories and formulates the problem at hand. Section 3 gives the main results of this study. Section 4 demonstrates the effectiveness of the proposed control scheme through numerical simulation examples. Finally, Section 5 summarizes all works and discusses potential directions for future research.

2. Preliminaries

This section will commence with an introduction to the fundamental principles of graph theory and an overview of the preliminary findings. Subsequently, the research problem addressed in this paper will be formulated, thereby establishing a foundation for the further derivation and analysis of this topic.

2.1. Graph Theory

We consider a leader–follower MAS comprising a leader, labeled as node 0, and N followers represented by a weighted directed graph $\mathcal{G}$. The graph is characterized by $\mathcal{G}=\left\{\mathcal{V},\mathcal{E},\mathcal{A}\right\}$, where $\mathcal{V}=\left\{1,2,\cdots ,N\right\}$ is the nodes set, $\mathcal{E}=\mathcal{V}\times \mathcal{V}$ is the edges set, and $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ is the adjacency matrix, respectively. If agent i is able to receive the information from agent j, then $a_{ij}>0$, $\left(j,i\right)\in \mathcal{E}$, and $a_{ij}=0$ otherwise. The neighbor index set of node i is represented by ${\mathcal{N}}_i=\left\{j|\left(j,i\right)\subseteq \mathcal{E}\right\}$, and the in-degree of node i is the number of its neighbor nodes, expressed as $\left|{\mathcal{N}}_i\right|$. The diagonal element $a_{ii}=0$ for $i=1,2,\cdots ,N$. $\mathcal{D}=diag\left\{d_1,\cdots ,d_N\right\}$ is a diagonal matrix, which represents the connection matrix between the follower and the leader. If the follower i can receive the information from the leader directly, then $d_i>0$; otherwise, $d_i=0$. Let $\mathcal{H}=\mathcal{L}+\mathcal{D}$ represent the topology information of the leader–follower MASs. The Laplacian matrix of $\mathcal{G}$ is defined as $\mathcal{L}=\left[l_{ij}\right]\in {\mathbb{R}}^{N\times N}$, where for $i=j$, $l_{ii}={\sum }_{i=1}^N{a}_{ij}$; for $i\ne j$, $l_{ij}=-a_{ij}$. The diagonal elements $l_{ii}$ sum the weights of all outgoing edges from node i, representing the out-degree of node i in the graph $\mathcal{G}$. A directed path from node i to j is a sequence of edges $(i,i_1),(i_1,i_2),\dots ,(i_k,j)$ in a directed graph with distinct nodes. If there exists a path between any two agents, then the graph is said to be connected.

2.2. Useful Lemmas

To move on, some lemmas will be presented for the purpose of facilitating the subsequent finite-time convergence analysis.

Lemma 1

(see Wang [47]). Consider an autonomous system $\dot{\mathit{x}}=f\left(\mathit{x}\left(t\right)\right)$, with $\mathit{x}\left(0\right)={\mathit{x}}_0$, where $\mathit{x}\left(t\right)={\left[x_1,x_2,\cdots ,x_n\right]}^T\in {\mathbb{R}}^n$ represents the system state. If there exists a positive definite continuous radially unbounded function $V\left(\mathit{x}\right):{\mathbb{R}}^n\to {\mathbb{R}}_{\ge 0}$ such that $\dot{V}\left(\mathit{x}\right)\le -{\iota }_{1}V\left(\mathit{x}\right)-{\iota }_2{V}^p\left(\mathit{x}\right)$, where $p\in \left(0,1\right)$, ${\iota }_1,{\iota }_2>0$, then it is said that the origin of (1) is finite time stable, and the settling time T can be given by

$$T\le {\displaystyle \frac{1}{{\iota }_1(1-p)}}ln\left({\displaystyle \frac{{\iota }_1{V}^{1-p}\left(0\right)+{\iota }_2}{{\iota }_2}}\right).$$

(1)

Lemma 2

(see Hardy [48]). Let $y_1,y_2,\cdots ,y_n\ge 0$ and $0<q<1$. Then, one has ${\left({\sum }_{i=1}^n{y}_i\right)}^q\le {\sum }_{i=1}^n{y}_i^q\le n^{1-q}{\left({\sum }_{i=1}^n{y}_i\right)}^q$.

Lemma 3.

Given $x,y\in \mathbb{R}$ and $ϵ>0$, Young’s inequality holds that $xy<{\displaystyle \frac{x^2}{2ϵ}}+{\displaystyle \frac{ϵy^2}{2}}$.

2.3. Problem Formulation

Currently, most autonomous multi-UAV systems employ a hierarchical framework for trajectory tracking, consisting of a trajectory generator and a flight control system. The trajectory generator module integrates various algorithms that supply the lower-level flight control system with crucial reference information for navigation, including position, velocity, and acceleration. The lower-level flight control system is typically composed of two layers: the inner-loop and the outer-loop controllers. In this configuration, the outer-loop is utilized to propel the UAV to the desired position at the specified velocity, while the inner-loop is tasked with maintaining the desired attitude. Consequently, at the flight control level, UAVs can be treated as point mass models, and the dynamics of each UAV can be broadly described by the following second-order system:

$$\left\{\begin{array}{c}\dot{p_i}=v_i,\hfill \\ \dot{v_i}={\displaystyle \frac{f_i}{m_i}},\hfill \end{array}\right.$$

(2)

where $p_i,v_i,{\displaystyle \frac{f_i}{m_i}}$ denote the position, velocity, and acceleration of each UAV, respectively.

In this paper, we present a methodology for abstracting multi-UAVs cooperative formation tracking as a consensus tracking control problem of MASs, which enables each UAV to track a generated reference trajectory. We consider a networked system comprising N followers and a leader. To enhance the generalizability of the research presented in this paper, it is obvious that the UAV can be represented as a general linear system. This approach is reasonable, given that the second-order systems constitute a specific instance of general linear systems, thereby facilitating the broader applicability of the findings.

The dynamics of the ith follower can be described by

$${\dot{x}}_i\left(t\right)=A{x}_i\left(t\right)+B{u}_i\left(t\right),i=1,2,\cdots ,N.$$

(3)

Additionally, the dynamics of the leader agent is defined as

$${\dot{x}}_0\left(t\right)=A{x}_0\left(t\right),$$

(4)

where $x_i\left(t\right)\in {\mathbb{R}}^n$ and $x_0\left(t\right)\in {\mathbb{R}}^n$ are the states of follower i and the leader, respectively, and $u_i\left(t\right)\in {\mathbb{R}}^m$ is the control input of follower i. $A\in {\mathbb{R}}^{n\times n}$ and $B\in {\mathbb{R}}^{n\times m}$ are the state constant matrix and the input constant matrix, respectively. To facilitate the reduction of a general linear system to a second-order system, thereby providing position and velocity information in the context of multi-UAV flight control, matrices A and B as defined in the system of Equations (3) and (4) of each UAV are given by

$$A=\left[\begin{array}{cc}{0}_{3\times 3}& I_3\\ 0_{3\times 3}& 0_{3\times 3}\end{array}\right];B=\left[\begin{array}{c}{0}_{3\times 3}\\ I_3\end{array}\right].$$

Assumption 1.

The matrix pair $\left(A,B\right)$ is stabilizable.

Lemma 4

(see Xu [49]). Under the premise of Assumption 1, for any given positive real number $ϵ>0$ and any positive definite matrix $Q>0$, there exists a positive definite solution $P>0$ that satisfies the following Riccati equality:

$$A^{T}P+PA-ϵPB{B}^{T}P+Q=0.$$

(5)

Assumption 2.

The topology of MASs is directed and has a directed spanning tree, with the leader being the root node.

Lemma 5

(see Li [50]). Under Assumption 2, there exists a positive diagonal matrix $\Xi =\mathrm{diag}\left(\mathit{\xi }\right)$ generated from $\mathit{\xi }={\left[{\xi }_1,{\xi }_2,\cdots ,{\xi }_N\right]}^{\mathrm{T}}$, where ${\xi }_i$ is equal to the reciprocal of the $i^{th}$ component of ${\left({\mathcal{H}}^T\right)}^{-1}\mathbf{1}$ such that $\Lambda =1/2\left(\Xi \mathcal{H}+{\mathcal{H}}^{\mathrm{T}}\Xi \right)$ is symmetric and positive definite.

Remark 1.

The undirected graph, as a special case of directed graph, can be converted to a directed graph by considering each undirected edge as two directed edges. Therefore, the results in this paper are certainly applicable to undirected graphs. It is worth noting that Assumption 2 needs to be satisfied.

3. Main Results

The objective of this paper is to design a distributed DETC strategy such that the leader-following consensus can be achieved. In this section, we will construct an estimator and propose a novel model-based distributed control protocol at first. Subsequently, a new DET mechanism will be introduced. Ultimately, it will be proved that this scheme ensures a finite-time leader-following consensus and reduces the frequency of controller updates. Furthermore, a comprehensive analysis of Zeno behavior will be conducted, showing that appropriate parameter selection can prevent such behavior.

Definition 1.

If for any given initial state, there exists a finite time T such that

$$\underset{t\to T}{lim}∥x_i\left(t\right)-x_0\left(t\right)∥=0,$$

then the finite-time leader-following consensus is said to be achieved.

The principal challenges associated with the design of the finite-time DET control protocol for MASs can be attributed to three key factors.

(1)

Complexity of stability analysis: compared to static event triggering mechanisms, the dynamic event-triggered mechanism relies on an internal dynamic variable, so the strong coupling of information within the distributed control protocol and the DET mechanism increases the difficulty of the stability analysis and proof.

(2)

Balance between system performance and communication frequency: since event-triggered strategies inherently aim to reduce the frequency of sampled actions and/or control updates, it is a challenge to improve the convergence rate while reducing the communication frequency.

(3)

Avoiding Zeno behavior: the event triggering strategy requires rigorous mathematical analysis to exclude Zeno behavior, while the introduction of dynamic variables increases the complexity of excluding Zeno behavior.

3.1. Consensus Tracking Controller Design

Unlike some other studies where controllers employ state values of the triggering instants, the controller presented in this paper is updated on a continuously basis, using estimated values during the event intervals. The design of the estimator is as follows:

$${\widehat{x}}_j\left(t\right)=e^{A\left(t-t_k^j\right)}{x}_j\left(t_k^j\right),t\in \left[t_k^j,t_{k+1}^j\right)$$

(6)

where $t_k^j$ is the last triggering instant of agent j. Due to the fact that the differential equations ${\dot{x}}_0\left(t\right)=A{x}_0\left(t\right)$ and ${\dot{\widehat{x}}}_0\left(t\right)=A{x}_0\left(t\right)$ have the identical solution under the same initial conditions, for the sake of simplicity, the following analysis will replace ${\widehat{x}}_0\left(t\right)$ with $x_0\left(t\right)$. In this paper, the leader’s role is confined to the revelation of its initial states, thereby eliminating the necessity for the continuous transmission of its state information to the connected follower agents. This approach significantly reduces the communication burden within the network, aligning with the objectives of ET control systems that aim to optimize the use of resources.

The measurement error $e_i\left(t\right)$ and the tracking error ${\delta }_i\left(t\right)$ are given by

$$e_i\left(t\right)={\widehat{x}}_i\left(t\right)-x_i\left(t\right),$$

(7)

$${\delta }_i\left(t\right)=x_i\left(t\right)-x_0\left(t\right).$$

(8)

Then, a distributed model-based DET leader-following consensus protocol is presented by

$$\left\{\begin{array}{c}{u}_i=-{\mu }_{1}K{q}_i\left(t\right)-{\mu }_{2}K\mathrm{sig}{\left(q_i\left(t\right)\right)}^{\gamma },\hfill \\ q_i\left(t\right)=\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left({\widehat{x}}_i\left(t\right)-{\widehat{x}}_j\left(t\right)\right)+d_i\left({\widehat{x}}_i\left(t\right)-x_0\left(t\right)\right),\hfill \end{array}\right.$$

(9)

where $\mathrm{sig}{(·)}^{\gamma }=\mathrm{sign}(·){\left|·\right|}^{\gamma }$, $0<\gamma \le 0.5$, ${\mu }_1,{\mu }_2>0$ is the coupled control gain, $K=B^{T}P$ is the feedback gain matrix, and P is a positive define matrix to be designed later.

Remark 2.

Equation (6) demonstrates that agent i can obtain the estimated state of its neighbors over the update interval due to that all agents possess an identical system matrix A. It can be further seen from Equation (9) that the control input of agent i is constantly updated using the estimated values derived from Equation (6). This indicates that communication among agents occurs exclusively at designed event times, thereby eliminating the need for continuous communication.

3.2. Event-Triggering Function Design

In order to save communication resources, a novel DET function is designed, which makes each agent broadcast its own state information to its neighbors only at its own triggering time. The DET function is defined by

$$f_i\left(t,e_i\left(t\right),{\delta }_i\left(t\right),{\eta }_i\left(t\right)\right)={\omega }_1{∥e_i\left(t\right)∥}^2+{\omega }_2{∥{\delta }_i\left(t\right)∥}^{2\gamma }+{\omega }_3{∥e_i\left(t\right)∥}^{2\gamma }-{\pi }_i{\eta }_i\left(t\right),$$

(10)

where ${\pi }_i>0$, ${\omega }_1,{\omega }_2,{\omega }_3$ will design later. Let ${\vartheta }_i\left(t\right)={\omega }_1{∥e_i\left(t\right)∥}^2+{\omega }_2{∥{\delta }_i\left(t\right)∥}^{2\gamma }+{\omega }_3{∥e_i\left(t\right)∥}^{2\gamma }$, and then the internal dynamic variable ${\eta }_i\left(t\right)$ can be governed by following dynamic system

$${\dot{\eta }}_i\left(t\right)=-{\beta }_i\left({\eta }_i\left(t\right)+{\eta }_i^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)\right)-{\sigma }_i{\vartheta }_i\left(t\right),$$

(11)

where the initial value ${\eta }_i\left(0\right)>0$, $0<{\sigma }_i<1$, ${\beta }_i>{\pi }_i-{\sigma }_i{\pi }_i>0$, $0<{\displaystyle \frac{m_1}{m_2}}\le 0.5$ with both $m_1$ and $m_2$ being integers.

The triggering time sequence $t_k^i$ for the agent i is determined as follows:

$$\begin{array}{cc}\hfill t_0^i& =0,\hfill \\ \hfill t_{k+1}^i& =inf\left\{t>t_k^i|f_i\left(t,e_i\left(t\right),{\delta }_i\left(t\right),{\eta }_i\left(t\right)\right)\ge 0\right\}.\hfill \end{array}$$

(12)

Remark 3.

In this paper, a novel model-based ET scheme is proposed to estimate the state during the update intervals, which means that each agent does not need to maintain continuous communication with its neighbors. It can be seen from the DET function (10) that ${\omega }_1{∥e_i\left(t\right)∥}^2+{\omega }_2{∥{\delta }_i\left(t\right)∥}^{2\gamma }+{\omega }_3{∥e_i\left(t\right)∥}^{2\gamma }$ is the triggering error and ${\pi }_i{\eta }_i\left(t\right)$ is the dynamic threshold. Note that each agent i relies on only two estimators for its ET conditions, which represents a significant departure from the method described in [51], which utilizes ${\mathcal{N}}_i$ estimators to ascertain neighbor information. This not only simplifies the computational task for each agent but also lightens the overall load on the system, allowing for more agile and responsive control mechanisms. Specifically, the term $e_i$ denotes the measurement error between the estimated state based on linear dynamic evolution and the actual state, whereas ${\delta }_i$ represents the tracking error between the current state and the leader’s estimated state. When the triggering error is substantial enough to violate agent i’s triggering condition in Equation (12), the state of agent i is transmitted to its neighbors for controller updates. Furthermore, in order to achieve finite-time leader-following consensus, the terms ${∥{\delta }_i\left(t\right)∥}^{2\gamma }$ and ${∥e_i\left(t\right)∥}^{2\gamma }$ are integrated into the triggering error, with an additional ${\eta }_i^{{\displaystyle \frac{m_1}{m_2}}}$ incorporated into the dynamic threshold.

The dynamic variable $\eta \left(t\right)$, serving as a crucial component of the DET mechanism, necessitates proof of its non-negativity. Combined with (11) and (12), when the system is not triggered, the internal dynamic variable ${\eta }_i\left(t\right)$ satisfies the inequality ${\vartheta }_i\left(t\right)<{\pi }_i{\eta }_i\left(t\right)$, so it can be obtained that

$${\dot{\eta }}_i\left(t\right)\ge -{\beta }_i\left({\eta }_i\left(t\right)+{\eta }_i^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)\right)-{\sigma }_i{\pi }_i{\eta }_i\left(t\right).$$

(13)

Due to $0<{\displaystyle \frac{m_1}{m_2}}⩽0.5$, it follows that ${\displaystyle \frac{m_2}{m_2-m_1}}>1$. According to the comparison principle, we can obtain

$${\eta }_i\left(t\right)\ge {\eta }_i\left(0\right)\left(e^{-\left({\beta }_i+{\sigma }_i{\pi }_i\right)\left({\displaystyle \frac{m_2}{m_2-m_1}}\right)t}\right)>0.$$

(14)

Remark 4.

It is worth noting that the dynamic variable ${\eta }_i$ is time-varying, which monotonically converges to zero within a finite time. This characteristic plays a crucial role in the proof of the FTDET control algorithm proposed in this paper. The thresholds proposed in the literature [33] cannot be used to achieve finite-time ET control because they asymptotically converge to zero. While certain studies, such as [44,45], have successfully achieved FTDET control by incorporating a term such as ${\eta }_i^{{\displaystyle \frac{1}{2}}}$, this paper broadens the scope of potential values for the ratio ${\displaystyle \frac{m_1}{m_2}}$. This extension permits a more comprehensive investigation of the influence of this parameter on the finite-time convergence properties and the event-triggering frequency of the system.

Remark 5.

The selection of parameters in Equation (11) indeed plays a crucial role in determining the behavior of the control system, particularly with regard to its event-triggering frequency. The parameters ${\beta }_i,{\displaystyle \frac{m_1}{m_2}}$ and ${\sigma }_i$ exert a direct influence on the rate of convergence of the dynamic variable ${\eta }_i\left(t\right)$ to zero. To elaborate, an increase in the values of ${\beta }_i,{\displaystyle \frac{m_1}{m_2}}$ and ${\sigma }_i$ results in a faster convergence of ${\eta }_i\left(t\right)$, thereby increasing the event-triggering frequency. Conversely, a reduction in these parameter values will result in a slower convergence rate and a corresponding decrease in the event-triggering frequency. An increased event-triggering frequency thus implies a higher rate of state broadcasting among agents, which in turn accelerates the convergence of the tracking error. However, it is also important to consider that if ${\eta }_i\left(t\right)$ converges too rapidly, particularly at a rate exceeding that of the tracking error, the potential for the Zeno behavior arises. In summary, by correctly adjusting these parameters, it is possible to achieve a balance between the event-triggering frequency and the convergence rate of the system.

3.3. Stability Analysis

The closed-loop tracking error system using (9) can be rewritten as

$$\begin{array}{cc}\hfill {\dot{\delta }}_i\left(t\right)=& {\dot{x}}_i\left(t\right)-{\dot{x}}_0\left(t\right)\hfill \\ \hfill =& A{\delta }_i\left(t\right)-{\mu }_{1}BK\left(q_i\left(t\right)\right)-{\mu }_{2}BKsig{\left(q_i\left(t\right)\right)}^{\gamma }\hfill \\ \hfill =& A{\delta }_i\left(t\right)-{\mu }_{1}BK\left(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left({\delta }_i\left(t\right)-{\delta }_j\left(t\right)+\left(e_i\left(t\right)-e_j\left(t\right)\right)\right)+d_i\left({\delta }_i\left(t\right)+e_i\left(t\right)\right)\right)\hfill \\ \hfill & -{\mu }_{2}BKsig{\left(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}\left({\delta }_i\left(t\right)-{\delta }_j\left(t\right)+\left(e_i\left(t\right)-e_j\left(t\right)\right)\right)+d_i\left({\delta }_i\left(t\right)+e_i\left(t\right)\right)\right)}^{\gamma }.\hfill \end{array}$$

(15)

Denote $\mathit{\delta }\left(t\right)={\left[{\delta }_1^T\left(t\right),{\delta }_2^T\left(t\right),\cdots ,{\delta }_N^T\left(t\right)\right]}^T$, $\mathit{e}\left(t\right)={\left[e_1^T\left(t\right),e_2^T\left(t\right),\cdots ,e_N^T\left(t\right)\right]}^T$, then its compact set form can be written as

$$\begin{array}{cc}\hfill \dot{\mathit{\delta }}\left(t\right)=& \left(I_N\otimes A-{\mu }_1\mathcal{H}\otimes B{B}^{T}P\right)\delta \left(t\right)-\left({\mu }_1\mathcal{H}\otimes B{B}^{T}P\right)\mathit{e}\left(t\right)\hfill \\ \hfill & -\left({\mu }_2{I}_N\otimes B{B}^{T}P\right)sig{\left(\left(\mathcal{H}\otimes I_N\right)\left(\delta \left(t\right)+\mathit{e}\left(t\right)\right)\right)}^{\gamma }.\hfill \end{array}$$

(16)

Then, the finite-time leader-following consensus problem for general MASs (3) and (4) is transformed into the stability problem of $\mathit{\delta }\left(t\right)$.

Theorem 1.

Suppose that Assumptions 1 and 2 holds. For given scalars $0<\gamma \le 0.5$, ${\mu }_1,{\mu }_2>0$, $0<{\sigma }_i<1$, ${\pi }_i>0$, ${\beta }_i>{\pi }_i-{\sigma }_i{\pi }_i>0$, $0<{\displaystyle \frac{m_1}{m_2}}\le 0.5$, the linear MASs (3) and (4) under the control protocol (9) and DET function (12) can achieve finite-time leader-following consensus if there exist $P>0$, $ϵ>0$, $Q>0$ satisfying (4). Furthermore, the settling time can be

$$T\le {\displaystyle \frac{1}{{\iota }_1(1-\alpha )}}ln\left({\displaystyle \frac{{\iota }_1{V}^{1-\alpha }\left(0\right)+{\iota }_2}{{\iota }_2}}\right),$$

(17)

where ${\iota }_1=min\left\{{\displaystyle \frac{{\lambda }_{min}\left(\Xi \otimes Q\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}},{\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right\}$, ${\iota }_2=min\left\{{\displaystyle \frac{{\lambda }_{min}\left(H^{T}H\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}},{\beta }_i\right\}$, $\alpha =max\left\{\gamma ,{\displaystyle \frac{m_1}{m_2}}\right\}$.

Proof. 

Take into account the following Lyapunov function as

$$\begin{array}{cc}\hfill V\left(t\right)& =V_1\left(t\right)+V_2\left(t\right)\hfill \\ \hfill & ={\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes P\right)\mathit{\delta }\left(t\right)+\sum _{i=1}^N{\eta }_i\left(t\right),\hfill \end{array}$$

(18)

where P is a positive definite matrix, and $\Xi$ is a positive diagonal matrix introduced in Lemma 5. Based on the above analysis, $V\left(t\right)$ is positive definite.

Calculating the time derivative of $V_1\left(t\right)$ along with (16) yields

$$\begin{array}{cc}\hfill V_1=& 2{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes P\right)\dot{\mathit{\delta }}\left(t\right)\hfill \\ \hfill =& 2{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes P\right)\left[\left(I_N\otimes A-{\mu }_1\mathcal{H}\otimes B{B}^{T}P\right)\mathit{\delta }\left(t\right)-\left({\mu }_1\mathcal{H}\otimes B{B}^{T}P\right)\mathit{e}\left(t\right)\right.\hfill \\ \hfill & \left.-\left({\mu }_2{I}_N\otimes B{B}^{T}P\right)sig{\left(\left(H\otimes I_N\right)\left(\mathit{\delta }\left(t\right)+\mathit{e}\left(t\right)\right)\right)}^{\gamma }\right]\hfill \\ \hfill =& {\mathit{\delta }}^T\left(t\right)\left[\left(\Xi \otimes \left(A^{T}P+PA\right)\right)-\left({\mu }_1\left({\mathcal{H}}^T\Xi +\Xi \mathcal{H}\right)\otimes PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)\hfill \\ \hfill & -2{\mathit{\delta }}^T\left(t\right)\left({\mu }_1\Xi \mathcal{H}\otimes PB{B}^{T}P\right)\mathit{e}\left(t\right)\hfill \\ \hfill & -2{\mathit{\delta }}^T\left(t\right)\left({\mu }_2\Xi \otimes PB{B}^{T}P\right)sig{\left(\left(\mathcal{H}\otimes I_N\right)\left(\mathit{\delta }\left(t\right)+\mathit{e}\left(t\right)\right)\right)}^{\gamma }.\hfill \end{array}$$

(19)

Using Lemma 5, analyzing the first term in Equation (19) yields

$$\begin{array}{cc}\hfill & {\mathit{\delta }}^T\left(t\right)\left[\left(\Xi \otimes \left(A^{T}P+PA\right)\right)-\left({\mu }_1\left({\mathcal{H}}^T\Xi +\Xi \mathcal{H}\right)\otimes PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)\hfill \\ \hfill & ⩽{\mathit{\delta }}^T\left(t\right)\left[\left(\Xi \otimes \left(A^{T}P+PA\right)\right)-2{\mu }_1{\lambda }_{min}\left(\Lambda \right)\left(I_N\otimes PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right),\hfill \end{array}$$

(20)

where $\Lambda =1/2\left(H^T\Xi +\Xi H\right)$ is symmetric and positive definite.

Based on Young’s inequality, the second term in Equation (19) can be obtained as

$$\begin{array}{cc}\hfill & -2{\mathit{\delta }}^T\left(t\right)\left({\mu }_1\Xi H\otimes PB{B}^{T}P\right)\mathit{e}\left(t\right)\hfill \\ \hfill ⩽& {\mu }_1{a}_1{\mathit{\delta }}^T\left(t\right)\left(\Xi \Xi \otimes PB{B}^{T}P\right)\mathit{\delta }\left(t\right)+{\mu }_1{\displaystyle \frac{1}{a_1}}{\mathit{e}}^T\left(t\right)\left(\mathcal{H}{\mathcal{H}}^T\otimes PB{B}^{T}P\right)\mathit{e}\left(t\right)\hfill \\ \hfill ⩽& {\mu }_1{a}_1{\mathit{\delta }}^T\left(t\right)\left(\Xi \Xi \otimes PB{B}^{T}P\right)\mathit{\delta }\left(t\right)+{\mu }_1{\displaystyle \frac{{\lambda }_{max}\left(\mathcal{H}{\mathcal{H}}^T\right)}{a_1}}{\mathit{e}}^T\left(t\right)\left(I_N\otimes PB{B}^{T}P\right)\mathit{e}\left(t\right),\hfill \end{array}$$

(21)

where $a_1>0$.

The last term in Equation (19) can be bounded by

$$\begin{array}{cc}\hfill & -2{\mathit{\delta }}^T\left(t\right)\left({\mu }_2\Xi \otimes PB{B}^{T}P\right)sig{\left(\left(H\otimes I_N\right)\left(\mathit{\delta }\left(t\right)+\mathit{e}\left(t\right)\right)\right)}^{\gamma }\hfill \\ \hfill =& -2{\mathit{\delta }}^T\left(t\right)\left({\mu }_2\Xi \otimes PB{B}^{T}P\right)sig{\left(\mathit{q}\left(t\right)\right)}^{\gamma }\hfill \\ \hfill ⩽& {\mu }_2{a}_2{\mathit{\delta }}^T\left(t\right)\left(\Xi \Xi \otimes PB{B}^{T}P\right)\mathit{\delta }\left(t\right)+{\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{∥\mathit{q}\left(t\right)∥}_{2\gamma }^{2\gamma }\hfill \\ \hfill ⩽& {\mu }_2{a}_2{\mathit{\delta }}^T\left(t\right)\left(\Xi \Xi \otimes PB{B}^{T}P\right)\mathit{\delta }\left(t\right)+{\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{∥\mathit{q}\left(t\right)∥}^{2\gamma },\hfill \end{array}$$

(22)

where $a_2>0$.

Further, according to Lemma 2, we cope with the second term of (22) as follows:

$$\begin{array}{cc}\hfill & {\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{∥\mathit{q}\left(t\right)∥}^{2\gamma }\hfill \\ \hfill =& {\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{∥\left(\mathcal{H}\otimes I_N\right)\mathit{\delta }\left(t\right)+\left(\mathcal{H}\otimes I_N\right)\mathit{e}\left(t\right)∥}^{2\gamma }\hfill \\ \hfill ⩽& {\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{\left(2{∥\left(\mathcal{H}\otimes I_N\right)\mathit{\delta }\left(t\right)∥}^2+2{∥\left(\mathcal{H}\otimes I_N\right)\mathit{e}\left(t\right)∥}^2\right)}^{\gamma }\hfill \\ \hfill ⩽& {\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }\left({∥\left(\mathcal{H}\otimes I_N\right)\mathit{\delta }\left(t\right)∥}^{2\gamma }+{∥\left(\mathcal{H}\otimes I_N\right)\mathit{e}\left(t\right)∥}^{2\gamma }\right)\hfill \\ \hfill ⩽& \left({\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }+1\right){∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }-{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & +{\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{e}\left(t\right)∥}^{2\gamma }.\hfill \end{array}$$

(23)

Note that, according to (11), the derivative of $V_2$ has

$${\dot{V}}_2=-{\beta }_i{\eta }_i\left(t\right)-{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)-{\sigma }_i{\vartheta }_i\left(t\right).$$

(24)

Therefore, using (20)–(24) yields

$$\begin{array}{cc}\hfill \dot{V}=& {\dot{V}}_1+{\dot{V}}_2\hfill \\ \hfill ⩽& {\mathit{\delta }}^T\left(t\right)\left[\left(\Xi \otimes \left(A^{T}P+PA\right)\right)-{\mu }_1{\lambda }_{min}\left(\Lambda \right)\left(I_N\otimes PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)\hfill \\ \hfill & -{\mathit{\delta }}^T\left(t\right)\left[{\mu }_1{\lambda }_{min}\left(\Lambda \right)\left(I_N\otimes PB{B}^{T}P\right)-\left({\mu }_1{a}_1+{\mu }_2{a}_2\right)\left(\Xi \Xi \otimes PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)\hfill \\ \hfill & -{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & +{\mu }_1{\displaystyle \frac{{\lambda }_{max}\left(\mathcal{H}{\mathcal{H}}^T\right){\lambda }_{max}\left(PB{B}^{T}P\right)}{a_1}}{∥\mathit{e}\left(t\right)∥}^2\hfill \\ \hfill & +\left({\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }+1\right){∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & +{\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{e}\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & -\sum _{i=1}^N\left({\beta }_i{\eta }_i\left(t\right)+{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)+{\sigma }_i{\vartheta }_i\left(t\right)\right),\hfill \end{array}$$

(25)

where ${\mu }_1{\lambda }_{min}\left(\Lambda \right)-\left({\mu }_1{a}_1+{\mu }_2{a}_2\right){\xi }_i^2>0$.

Let

$$\begin{array}{cc}\hfill {\omega }_1& ={\mu }_1{\displaystyle \frac{{\lambda }_{max}\left(\mathcal{H}{\mathcal{H}}^T\right){\lambda }_{max}\left(PB{B}^{T}P\right)}{a_1}},\hfill \\ \hfill {\omega }_2& =\left({\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }+1\right){∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma },\hfill \\ \hfill {\omega }_3& ={\mu }_2{\displaystyle \frac{{\lambda }_{max}\left(PB{B}^{T}P\right)}{a_2}}{\left(Nn\right)}^{1-\gamma }{2}^{\gamma }{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }.\hfill \end{array}$$

According to the triggering law, one has

$$\begin{array}{cc}\hfill \dot{V}⩽& {\mathit{\delta }}^T\left(t\right)\left[\Xi \otimes \left(A^{T}P+PA-{\mu }_1{\lambda }_{min}\left(\Lambda \right){\lambda }_{min}\left({\Xi }^{-1}\right)PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)-{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & -\sum _{i=1}^N\left({\beta }_i{\eta }_i\left(t\right)+{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)\right)+\sum _{i=1}^N\left(1-{\sigma }_i\right){\vartheta }_i\left(t\right)\hfill \\ \hfill ⩽& {\mathit{\delta }}^T\left(t\right)\left[\Xi \otimes \left(A^{T}P+PA-{\mu }_1{\lambda }_{min}\left(\Lambda \right){\lambda }_{min}\left({\Xi }^{-1}\right)PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)-{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & -\sum _{i=1}^N\left({\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right){\eta }_i\left(t\right)-\sum _{i=1}^N{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right).\hfill \end{array}$$

(26)

Noting that $A^{T}P+PA-ϵPB{B}^{T}P+Q=0$ with $ϵ={\mu }_1{\lambda }_{min}\left(\Lambda \right){\lambda }_{min}\left({\Xi }^{-1}\right)$, we can obtain

$$\begin{array}{cc}\hfill \dot{V}⩽& {\mathit{\delta }}^T\left(t\right)\left[\Xi \otimes \left(A^{T}P+PA-{\mu }_1{\lambda }_{min}\left(\Lambda \right){\lambda }_{min}\left({\Xi }^{-1}\right)PB{B}^{T}P\right)\right]\mathit{\delta }\left(t\right)-{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }\hfill \\ \hfill & -\sum _{i=1}^N\left({\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right){\eta }_i\left(t\right)-\sum _{i=1}^N{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)\hfill \\ \hfill ⩽& -{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes Q\right)\mathit{\delta }\left(t\right)-\sum _{i=1}^N\left({\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right){\eta }_i\left(t\right)\hfill \\ \hfill & -{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }{∥\mathit{\delta }\left(t\right)∥}^{2\gamma }-\sum _{i=1}^N{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right),\hfill \end{array}$$

(27)

where ${\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i>0$.

After analysis, the first two terms of (27) can be obtained as

$$\begin{array}{cc}\hfill & -{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes Q\right)\mathit{\delta }\left(t\right)-\sum _{i=1}^N\left({\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right){\eta }_i\left(t\right)\hfill \\ \hfill & =-\left({\displaystyle \frac{{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes Q\right)\mathit{\delta }\left(t\right)}{{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes P\right)\mathit{\delta }\left(t\right)}}\right)V_1-\sum _{i=1}^N\left({\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right){\eta }_i\left(t\right)\hfill \\ \hfill & \le -{\iota }_{1}V,\hfill \end{array}$$

(28)

where ${\iota }_1=min\left\{{\displaystyle \frac{{\lambda }_{min}\left(\Xi \otimes Q\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}},{\beta }_i-{\pi }_i+{\sigma }_i{\pi }_i\right\}$.

Similarly, the last two terms of (27) can be obtained as

$$\begin{array}{cc}\hfill -{∥\left(\mathcal{H}\otimes I_N\right)∥}^{2\gamma }& {∥\mathit{\delta }\left(t\right)∥}^{2\gamma }-\sum _{i=1}^N{\beta }_i{{\eta }_i}^{\gamma }\left(t\right)\hfill \\ \hfill & =-{∥{\displaystyle \frac{{\mathit{\delta }}^T\left(t\right)\left({\mathcal{H}}^T\mathcal{H}\otimes I_N\right)\mathit{\delta }\left(t\right)}{{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes P\right)\mathit{\delta }\left(t\right)}}{\mathit{\delta }}^T\left(t\right)\left(\Xi \otimes P\right)\mathit{\delta }\left(t\right)∥}^{\gamma }-\sum _{i=1}^N{\beta }_i{{\eta }_i}^{{\displaystyle \frac{m_1}{m_2}}}\left(t\right)\hfill \\ \hfill & \le -\left({\displaystyle \frac{{\lambda }_{min}\left({\mathcal{H}}^T\mathcal{H}\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}}\right)V_1^{\gamma }-{\beta }_{min}{V}_2^{{\displaystyle \frac{m_1}{m_2}}}.\hfill \end{array}$$

(29)

According to (28) and (29), (27) can further obtain

$$\begin{array}{c}\hfill \dot{V}\le -{\iota }_{1}V-\left({\displaystyle \frac{{\lambda }_{min}\left({\mathcal{H}}^T\mathcal{H}\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}}\right)V_1^{\gamma }-{\beta }_{min}{V}_2^{{\displaystyle \frac{m_1}{m_2}}}.\end{array}$$

(30)

According to $\dot{V}\le 0$, V will converge to $V\le 1$ within a finite time. Consequently, $0<V_1\left(t\right)<1$, $0<V_2\left(t\right)<1$. Furthermore, letting $\alpha =max\left\{\gamma ,{\displaystyle \frac{m_1}{m_2}}\right\}$, one has $V_2^{{\displaystyle \frac{m_1}{m_2}}}\ge V_2^{\alpha }$, $V_1^{\gamma }\ge V_1^{\alpha }$. In summary of the aforementioned analysis, we have

$$\begin{array}{cc}\hfill \dot{V}& \le -{\iota }_{1}V-\left({\displaystyle \frac{{\lambda }_{min}\left({\mathcal{H}}^T\mathcal{H}\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}}\right)V_1^{\alpha }-{\beta }_{min}{V}_2^{\alpha }\hfill \\ \hfill & \le -{\iota }_{1}V-{\iota }_2{V}_1^{\alpha }-{\iota }_2{V}_2^{\alpha }\hfill \\ \hfill & \le -{\iota }_{1}V-{\iota }_2{(V_1+V_2)}^{\alpha }\hfill \\ \hfill & =-{\iota }_{1}V-{\iota }_2{V}^{\alpha },\hfill \end{array}$$

(31)

where ${\iota }_2=min\left\{{\displaystyle \frac{{\lambda }_{min}\left({\mathcal{H}}^T\mathcal{H}\right)}{{\lambda }_{max}\left(\Xi \otimes P\right)}},{\beta }_i\right\}$.

Therefore, according to Lemma 2, the leader-following consensus can be achieved within a settling time, which is bounded by $T\le {\displaystyle \frac{1}{{\iota }_1(1-\alpha )}}ln\left({\displaystyle \frac{{\iota }_1{V}^{1-\alpha }\left(0\right)+{\iota }_2}{{\iota }_2}}\right)$. □

Remark 6.

The selection of parameters in Equation (9) does indeed affect the overall performance of the control system. Specifically, the parameter γ plays a crucial role. An increase in γ results in a slower convergence of the tracking error and a reduction in the event-triggering frequency. Moreover, according to Equation (17), the settling time T reveals that the value of α is determined by the larger of γ or ${\displaystyle \frac{m_1}{m_2}}$, rather than being solely dictated by the power terms of the controller as suggested in [42]. Consequently, an increase in the value of α results in a corresponding increase in the upper bound T for the finite-time convergence.

Remark 7.

It can be observed that the connections among the leader and the followers will directly affect the leader–follower matrix $\mathcal{H}$, while they will indirectly affect the selection of the controller parameter K, thus affecting the finite-time convergence and the event triggering frequency of the system. As the number of followers capable of receiving information directly from the leader increases, there is a corresponding rise in the number of triggering events and an acceleration in the convergence rate. Although a greater number of agents with direct access to the leader’s information can achieve faster convergence, this comes at the cost of increased network or communication burden and a higher frequency of triggering events.

The exclusion of Zeno behavior is a crucial aspect of the effectiveness of the ET mechanism. Next, the Zeno behavior will be discussed in detail.

Theorem 2.

Under the controller (9) and the DETC (12), Zeno behavior can be excluded during the time interval $t\in \left[0,min\left\{T_f,T_{\eta }-\chi \right\}\right]\cup \left[T_f,\infty \right]$, where $\chi >0$. This guarantees the existence of a positive upper bound on the time interval between two consecutive triggered events of agent i, which is represented by the variable τ and is given by $\tau =t_{k+1}^i-t_k^i>0$.

Proof. 

For agent i, its state can be given by $x_i=e^{A(t-t_{k_i}^i)}x\left(t_{k_i}^i\right)+{\int }_{t_{k_i}^i}^t{e}^{A(t-s)}B{u}_i\left(s\right)\mathrm{d}s$, where $t_{k_i}^i\le s<t_{k_i+1}^i$. It follows that from (9), we can obtain

$$\begin{array}{cc}\hfill e_i=& {\int }_{t_{k_i}^i}^t{e}^{A\left(t-s\right)}B{u}_i\left(s\right)\mathrm{d}s\hfill \\ \hfill =& {\int }_{t_{k_i}^i}^t(e^{A(t-s)}{\mu }_{1}BK\sum _{j\in {\mathcal{N}}_i}{a}_{ij}{\phi }_{ij}+d_i{\phi }_{i0}+e^{A(t-s)}{\mu }_{2}BKsig{\left(\sum _{j\in {\mathcal{N}}_i}{a}_{ij}{\phi }_{ij}+d_i{\phi }_{i0}\right)}^{\gamma }\mathrm{d}s,\hfill \end{array}$$

(32)

where ${\phi }_{ij}=\left(e^{A(s-t_{k_i}^i)}x\left(t_{k_i}^i\right)-e^{A(s-t_{k_j}^j)}x\left(t_{k_j}^j\right)\right)$ and ${\phi }_{i0}=\left(e^{A(s-t_{k_i}^i)}x\left(t_{k_i}^i\right)-x_0\left(t\right)\right)$.

So, it follows that

$$\begin{array}{cc}\hfill ∥e_i∥⩽& \left({\mu }_1∥BK∥M_1+{\mu }_2∥BK∥M_2\right)\left(t-t_{k_i}^i\right),\hfill \end{array}$$

(33)

where $M_1$ and $M_2$ are the upper bound of $e^{A(t-s)}{q}_i\left(s\right)$ and $e^{A(t-s)}sig{\left(q_i\left(s\right)\right)}^{\gamma }$, respectively. From (17) and (31), we can obtain that leader-following consensus is achieved, and the errors $q_i\left(t\right)$ and ${\delta }_i\left(t\right)$ are convergent and bounded.

According to Equations (10) and (33), when an event is triggered, the inter-event time interval $\tau$ must be greater than or equal to ${\tau }^{\prime }$, which is the solution of

$${\omega }_1{\varsigma }^2{\left({\tau }^{\prime }\right)}^2+{\omega }_2{\varsigma }^{2\gamma }{\left({\tau }^{\prime }\right)}^{2\gamma }+\kappa ={\pi }_i{\eta }_i\left(t\right),$$

(34)

where $\varsigma ={\mu }_1∥BK∥M_1+{\mu }_2∥BK∥M_2$, ${\kappa }^{\prime }={\omega }_2{\kappa }^{2\gamma }$, with $\kappa$ denoting the upper bound of $∥{\delta }_i\left(t\right)∥$.

It can be observed that if ${\eta }_i\ne 0$, then the event interval $\tau$ is guaranteed to be greater than some positive value ${\tau }^{\prime }$, and hence $\tau \ge {\tau }^{\prime }>0$. However, it is challenging to guarantee that the lower bound of the event interval is strictly positive, given that the value of ${\eta }_i\left(t\right)$ will eventually approach zero within a finite time. As the threshold approaches zero, the lower bound of the event interval goes to zero as well. Consequently, if ${\eta }_i\left(t\right)$ converges to zero at a rapid rate, agents may be compelled to communicate more frequently, which could result in an increase in the triggering frequency.

To gain further insight into Zeno behavior, we compare the time required for the system to achieve consensus with the time required for the internal dynamic variables to converge to zero. Let $T_f$ denote the finite time when leader-following consensus is achieved. Let $T_{\eta }$ denote the time when ${\eta }_i\left(t\right)$ converges to zero. Motivated by [42], we discuss two different scenarios regarding the finite-time convergence and dynamic variable convergence:

(1)

If $T_f<T_{\eta }$, the finite-time consensus is achieved prior to the convergence of each agent’s dynamic threshold to zero. Under this condition, the Zeno behavior is excluded for $t\in \left[0,T_f\right]$ because ${\eta }_i\ne 0$ during this interval. Zeno behavior is naturally non-existent, ensuring that it is excluded at all times.

(2)

If $T_f\ge T_{\eta }$, the dynamic thresholds of all agents have already reached zero by the time consensus is established. In this case, Zeno behavior is avoided both prior to $T_{\eta }$ and subsequent to $T_f$.

Based on the analysis of these two scenarios, it is evident that the Zeno behavior can be excluded by carefully selecting parameters so that the system reaches the finite-time consensus prior to the convergence of the dynamic threshold of each agent to zero. □

Although the proposed strategy does not entirely eliminate the possibility of Zeno behavior over the entire time span, it significantly reduces communication resource consumption. Unlike conventional FTDET strategies, this approach allows for adjusting the system’s convergence rate and triggering frequency through parameter tuning. Moreover, it eliminates the requirement for continuous communication with neighbors during both controller updates and triggering function evaluations. This leads to a substantial reduction in communication overhead and improved design flexibility.

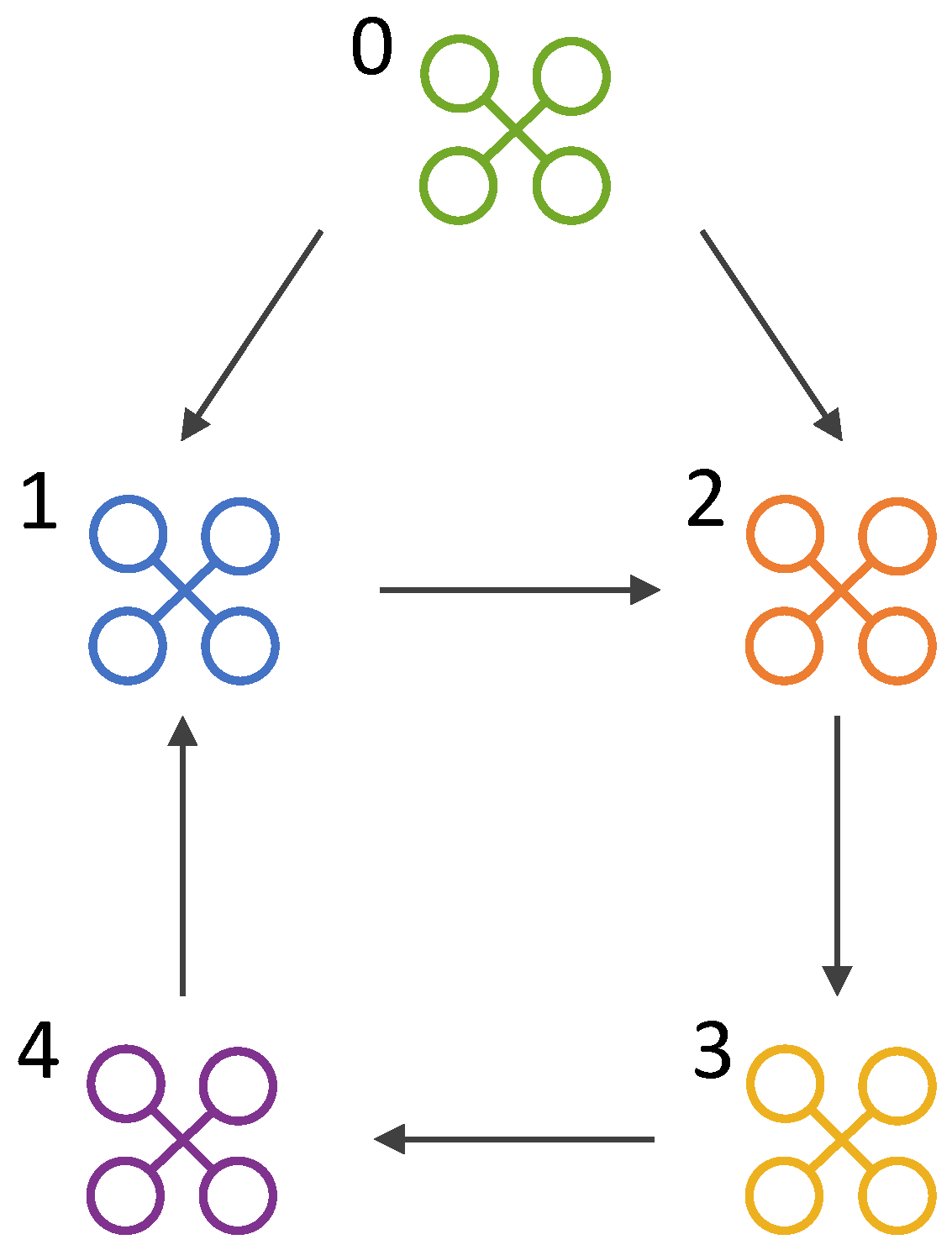
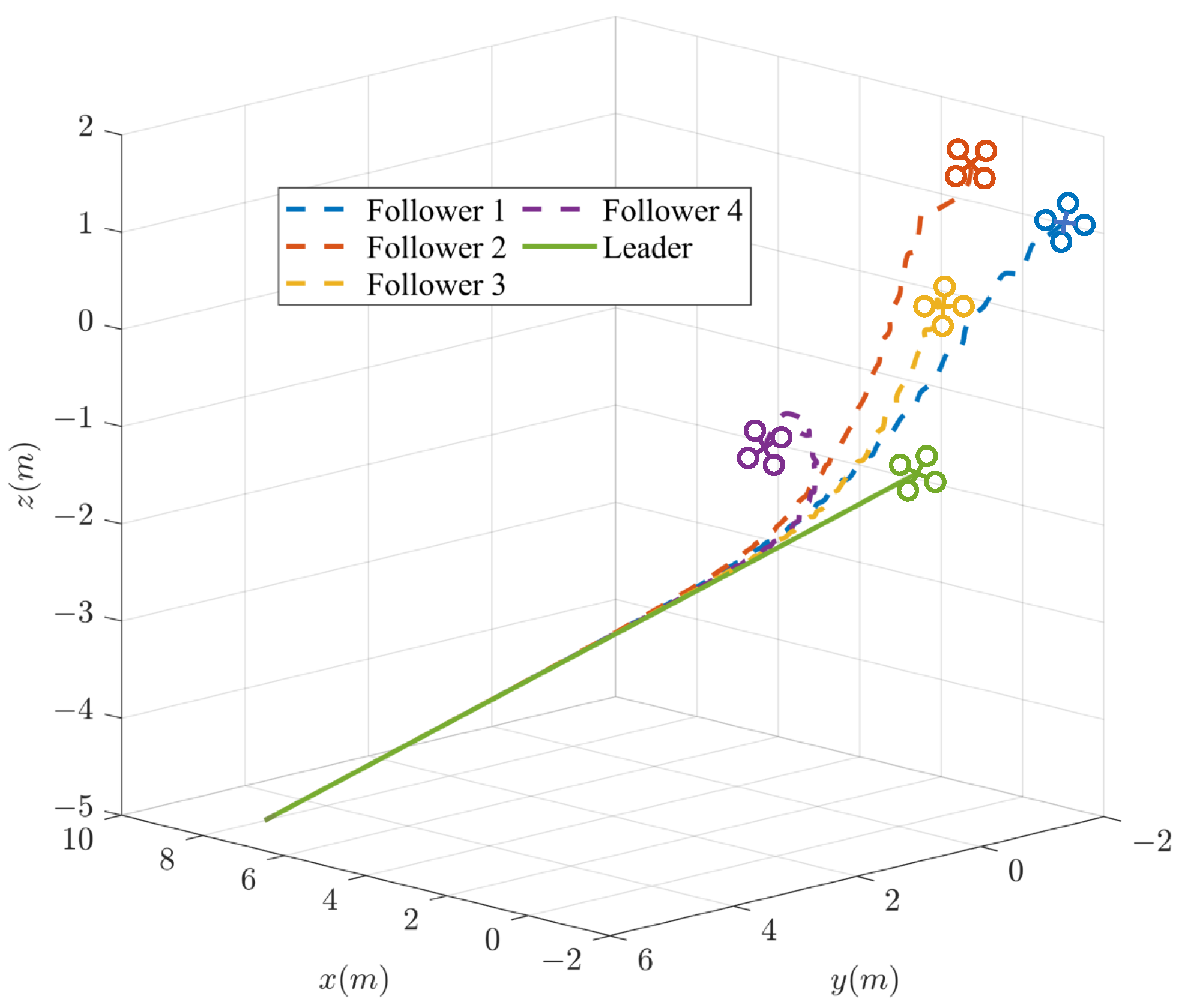
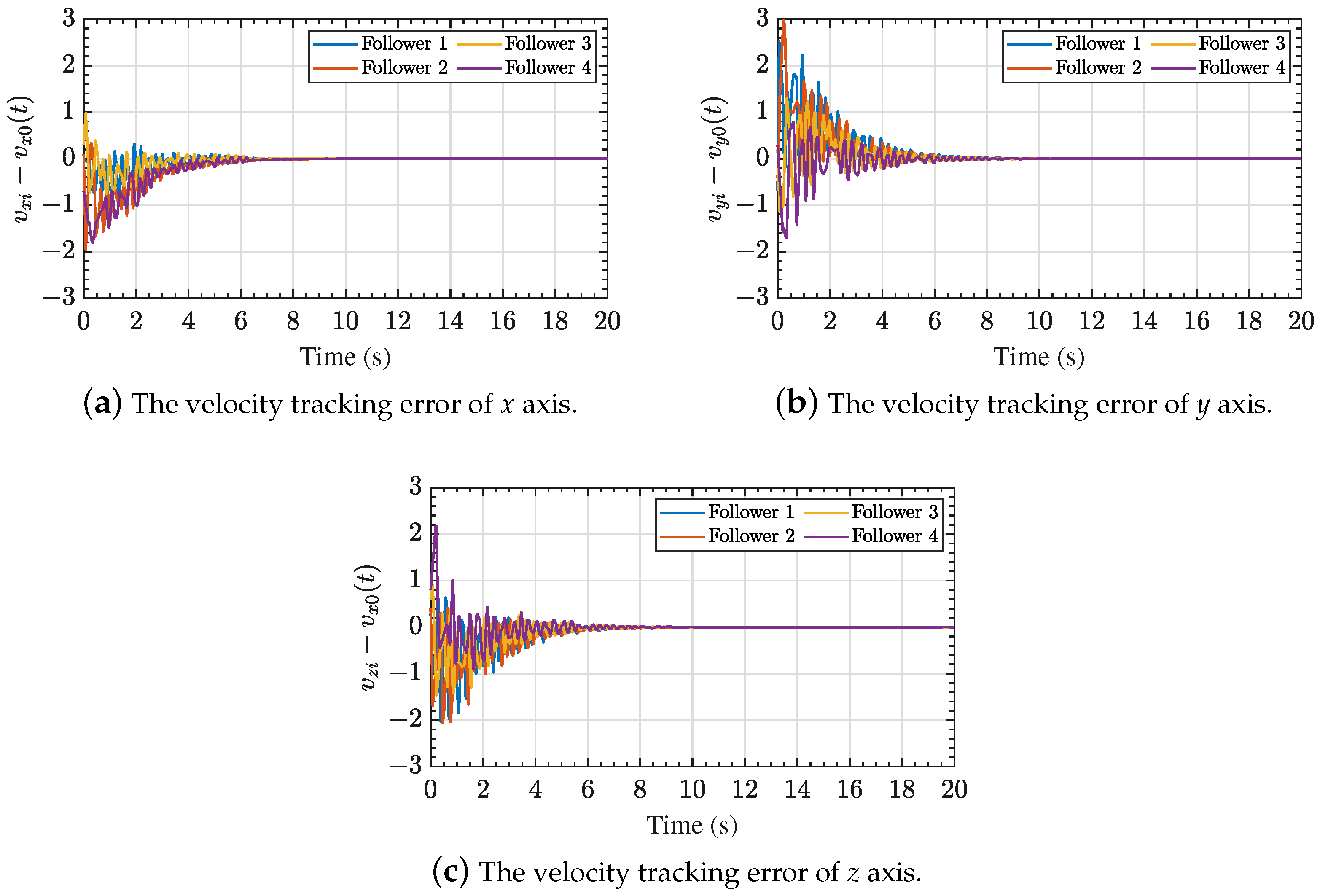
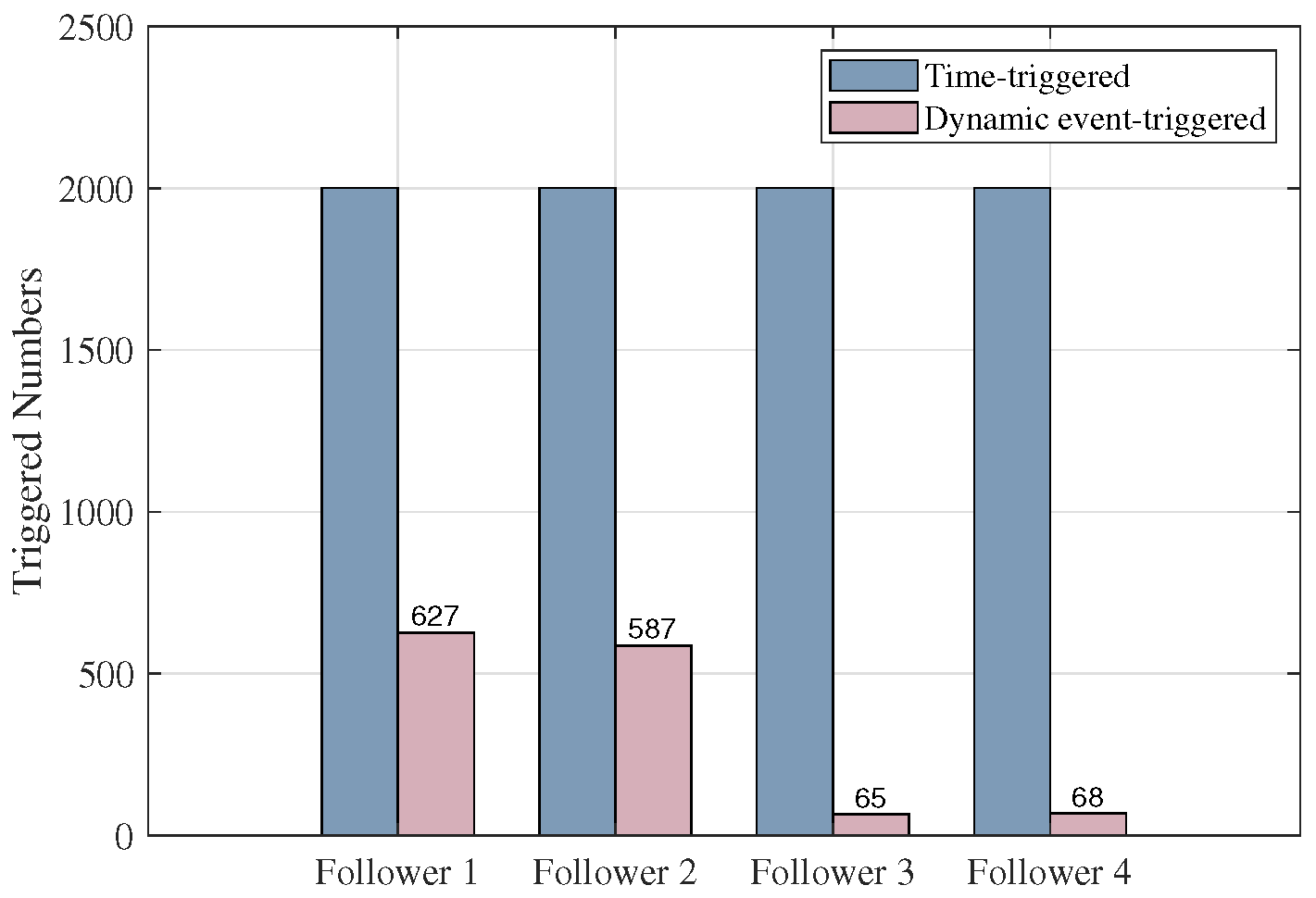
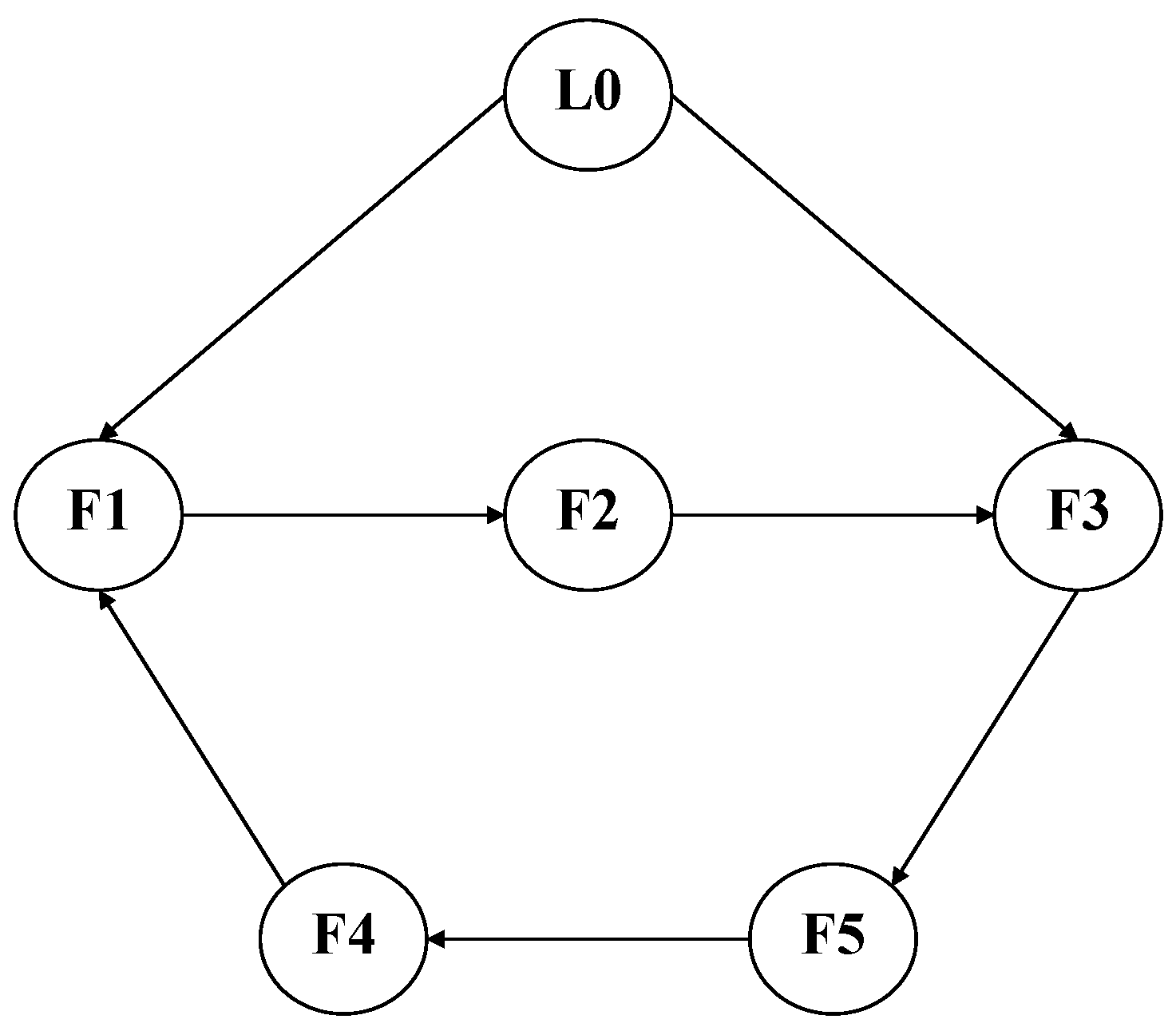
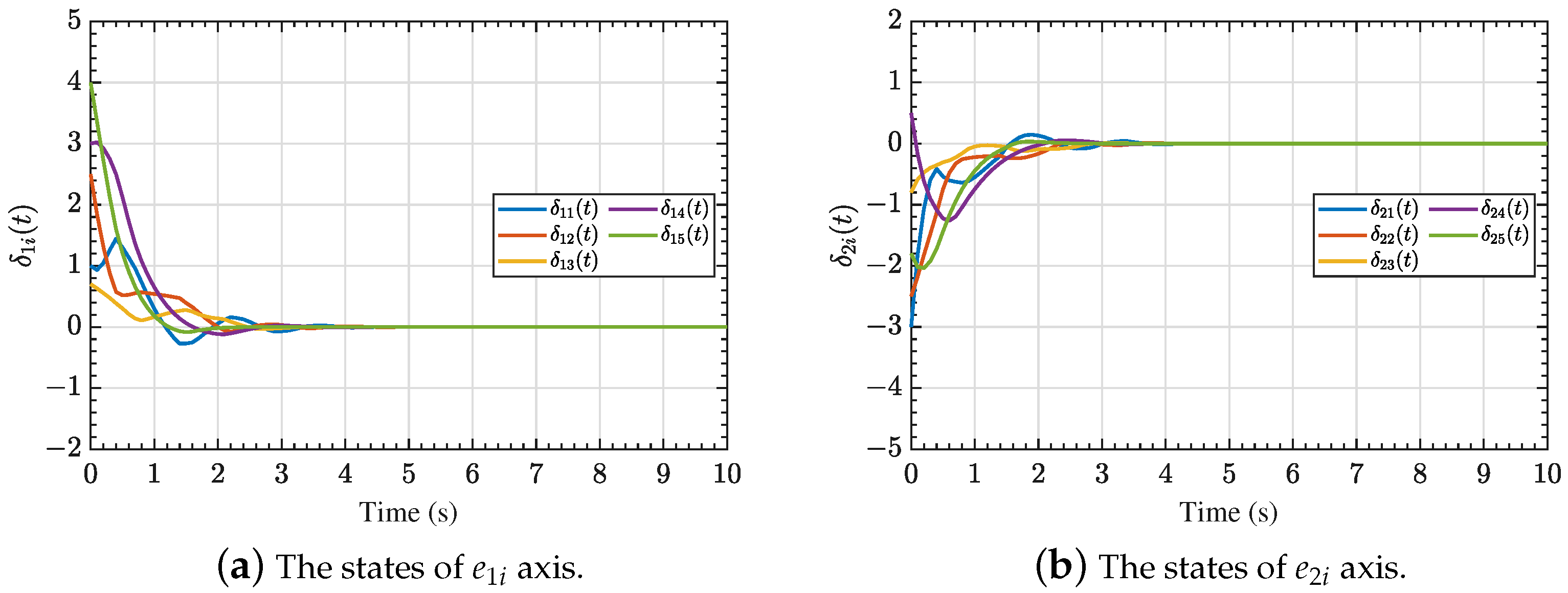
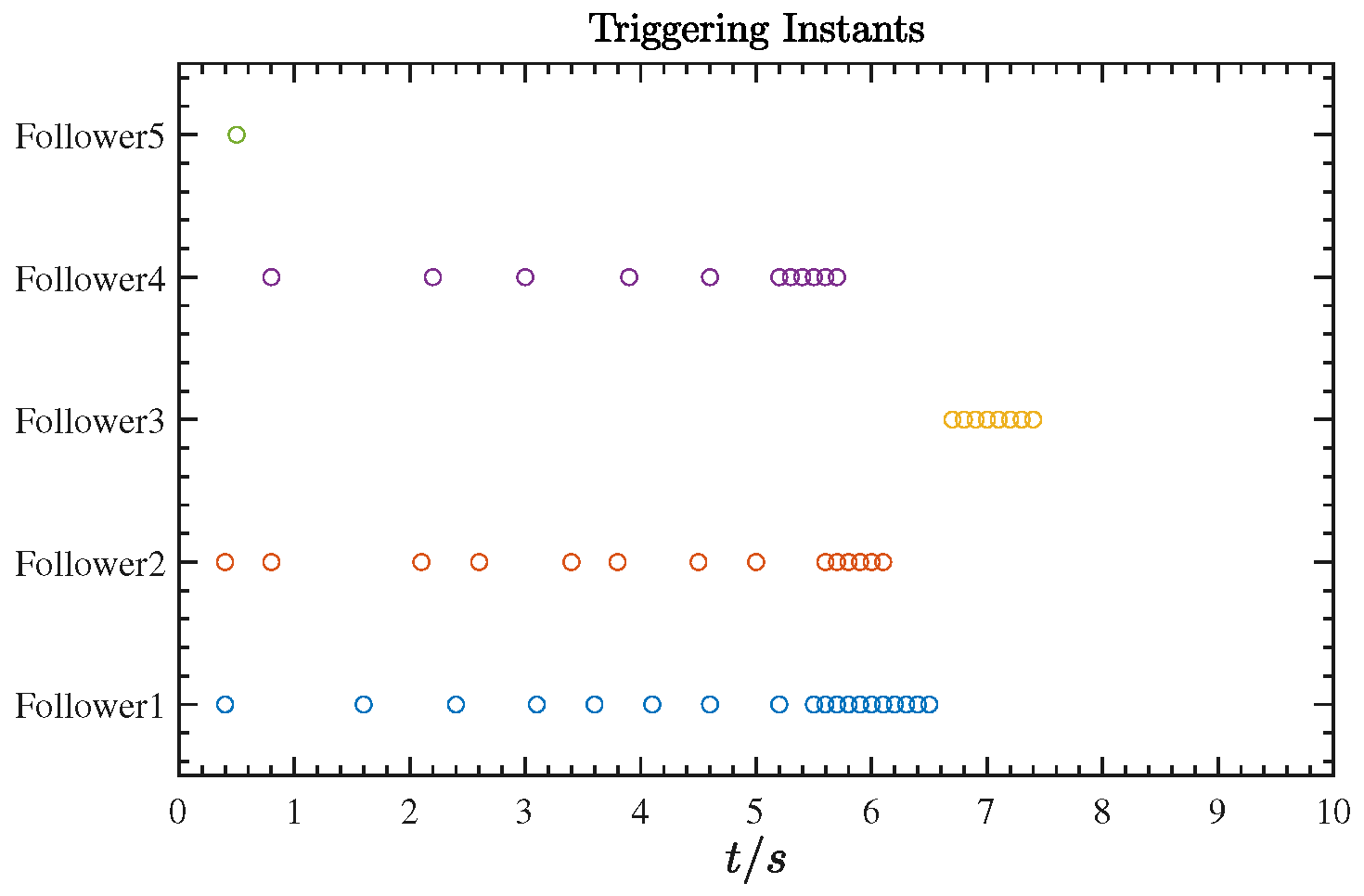
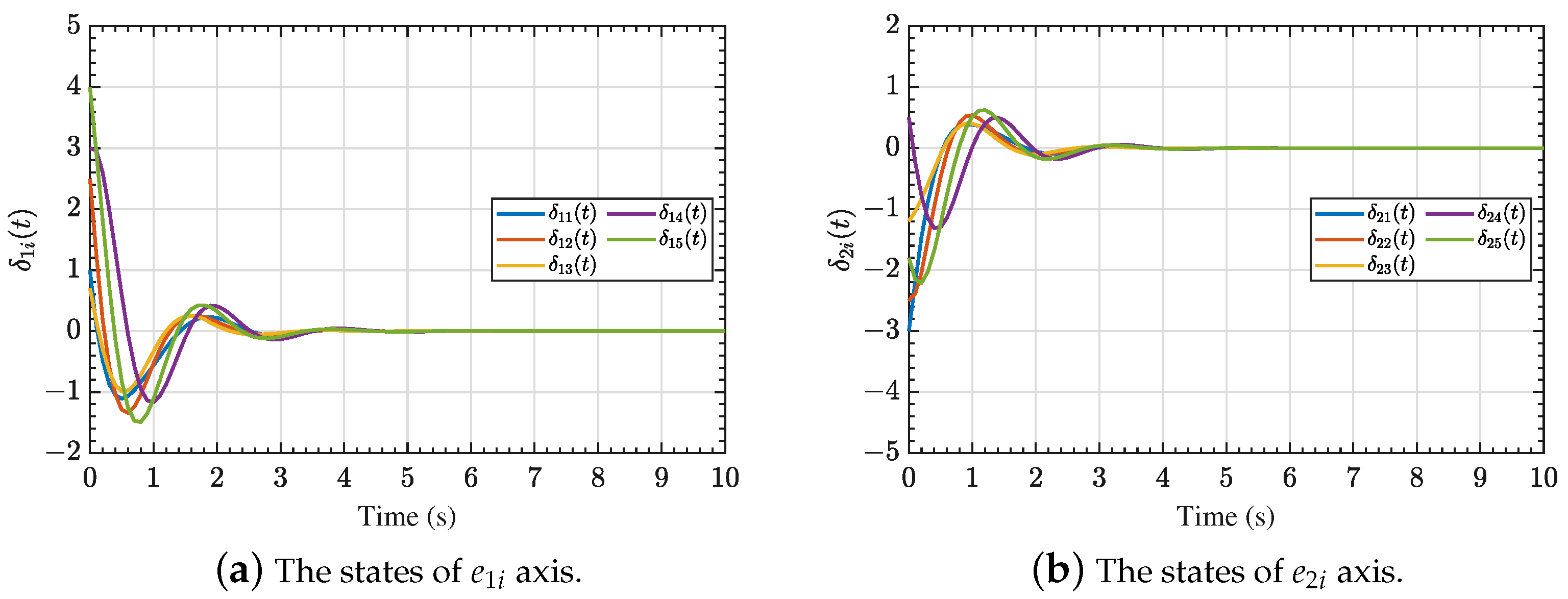
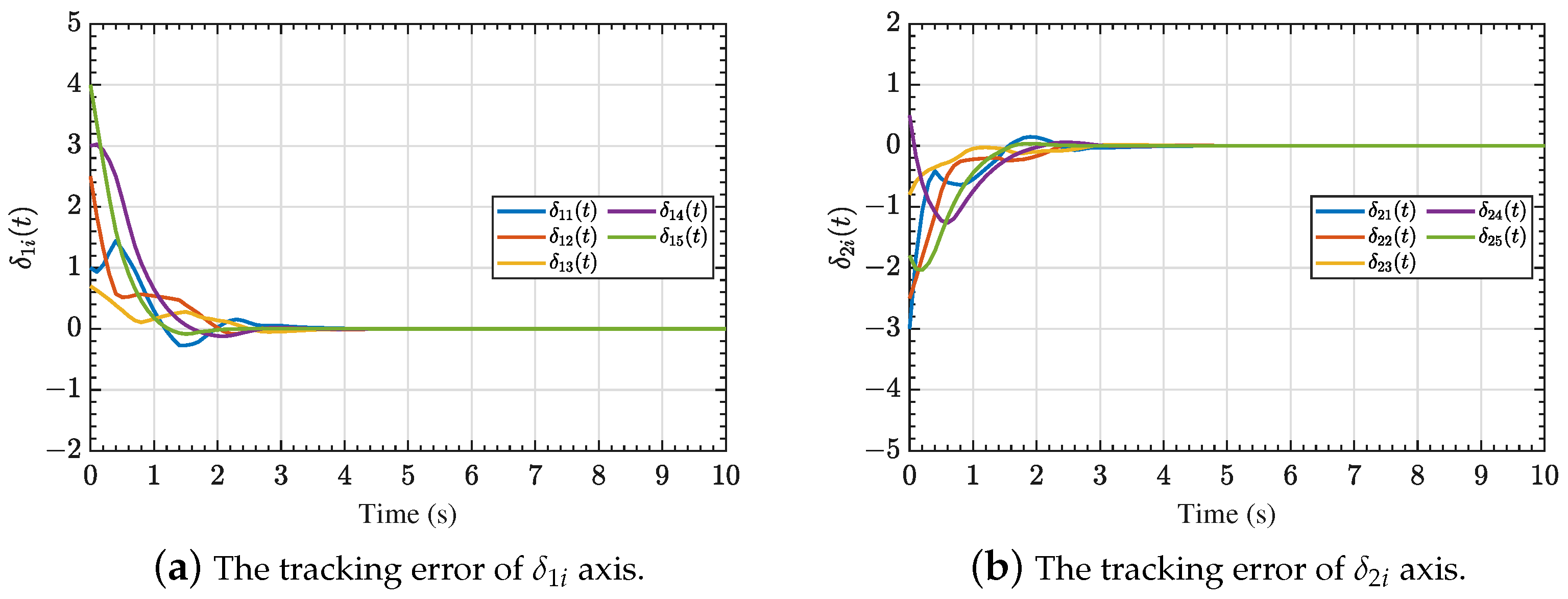
4. Simulation Results

This section presents a series of numerical results that substantiate the theoretical findings outlined in Section 3. The first example concerns a second-order multi-UAV system, and it serves to validate the rapid coordination capabilities of multi-UAV system under the aforementioned dynamic event-triggering mechanism. The second Example 2 further validates the effectiveness of the distributed control protocol (9) and the dynamic event-triggering mechanism (12) in addressing the leader–follower problem of general linear MASs. These examples collectively illustrate the broad applicability and efficacy of our proposed methodology.

Example 1.

Suppose that each UAV is modeled as a second-order system in the 3-D plane, and the matrix A and B of the system in Equations (3) and (4) of each UAV is represented as

$$A=\left[\begin{array}{cc}{0}_{3\times 3}& I_3\\ 0_{3\times 3}& 0_{3\times 3}\end{array}\right];B=\left[\begin{array}{c}{0}_{3\times 3}\\ I_3\end{array}\right].$$

The directed graph of multi-UAV system is shown in Figure 1, which contains one leader and four followers. It is evident that the directed graph meets the Assumption 2. The initial states of the leader and the followers are given as

$$\left[\begin{array}{ccccc}{\mathit{x}}_0\left(0\right)& {\mathit{x}}_1\left(0\right)& {\mathit{x}}_2\left(0\right)& {\mathit{x}}_3\left(0\right)& {\mathit{x}}_4\left(0\right)\end{array}\right]=\left[\begin{array}{ccccc}-2& -1& 0.5& -1.3& 1\\ 1& -2& -1.5& 0.2& 1.5\\ -1& 1& 1.5& 0.5& -1\\ 0.5& 0.5& 0.6& 0.8& -0.2\\ 0.2& -0.5& -0.2& 0.4& 0.5\\ -0.2& 0.1& 0.2& 0.4& 0.6\end{array}\right].$$

The controller parameters are selected as ${\mu }_1=4.0$, ${\mu }_2=0.5$, $\gamma =1/2$. The trigger parameters are selected as $\beta =\left[0.6,0.6,0.6,0.6\right]$, $\sigma =\left[0.5,0.5,0.4,0.4\right]$, $\pi =\left[0.6,0.6,0.5,0.5\right]$, ${\displaystyle \frac{m_1}{m_2}}={\displaystyle \frac{1}{2}}$.

The trajectories of the multi-UAV system are shown in Figure 2. Within the 3-D plane, the leader is indicated in green, while the four followers are marked blue, orange, yellow and purple, respectively. It is observable that, at the initial moment, the positions of the UAVs are dispersed. However, under the distributed controller (9) and DET mechanism (12), all followers achieve consensus with the leader’s position within a finite time. Figure 3 illustrates the velocity tracking error among the UAVs, demonstrating that the velocity tracking error converges to zero within a finite-time. Figure 4 contrasts the scenario without ET, revealing that the DET approach reduces the triggering frequency of the followers by $68.65\%$, $70.65\%$, $96.75\%$, and $96.6\%$, respectively. This indicates that the DET approach markedly decreases the frequency of information transmission and control updates.

Example 2.

A group of networked MASs consisting of a leader and five followers is considered, where

$$A=\left[\begin{array}{cc}0& 2\\ -2& -4\end{array}\right];B=\left[\begin{array}{cc}1& 1\end{array}\right].$$

It is evident that the system characterized by matrices A and B is stabilizable. Figure 5 depicts the communication network that interconnects the followers and the leader. It can be observed that a directed spanning tree is present within the communication topology that encompasses the leader and the followers.

Accordingly, the Laplacian matrix $\mathcal{L}$ and the leader–follower interaction matrix $\mathcal{H}$ are formulated as follows:

$$\mathcal{L}=\left[\begin{array}{ccccc}1& 0& 0& -1& 0\\ -1& 1& 0& 0& 0\\ 0& -1& 1& 0& 0\\ 0& 0& 0& 1& -1\\ 0& 0& -1& 0& 1\end{array}\right];\mathcal{H}=\left[\begin{array}{ccccc}2& 0& 0& -1& 0\\ -1& 1& 0& 0& 0\\ 0& -1& 2& 0& 0\\ 0& 0& 0& 1& -1\\ 0& 0& -1& 0& 1\end{array}\right].$$

According to the Riccati ARE, we can obtain that

$$P=\left[\begin{array}{cc}0.2944& 0.0910\\ 0.0910& 0.0970\end{array}\right];K=\left[\begin{array}{cc}0.3853& 0.1879\end{array}\right].$$

To demonstrate the effectiveness of the DET mechanism on control performance, some comparative test are carried out. Different from the static ET mechanism proposed by Xu et al. [22], we propose a novel finite-time DET mechanism for the leader-following consensus problem of general linear MASs. Unlike the traditional static ET mechanism, the DET mechanism allows for a longer average event interval by introducing an additional non-negative dynamic variable that depends on its own dynamics. To compare the convergence rate and the triggering numbers, we perform simulations at the same initial conditions of agents. The initial states of the followers are given as ${\left[-1,-2\right]}^{\mathrm{T}}$, ${\left[0.5,1.5\right]}^{\mathrm{T}}$, ${\left[-1.3,0.2\right]}^{\mathrm{T}}$, ${\left[1,1.5\right]}^{\mathrm{T}}$, ${\left[2,-0.8\right]}^{\mathrm{T}}$, and the initial states of the leader are given as ${\left[-2,1\right]}^{\mathrm{T}}$. The controller parameters of our method are selected as ${\mu }_1=2.0$, ${\mu }_2=1.0$, $\gamma =0.5$. The DET parameters of our method are selected as $\beta =\left[1.0,0.8,0.8,1.0,1.0\right]$, ${\displaystyle \frac{m_1}{m_2}}={\displaystyle \frac{1}{5}}$, $\sigma =\left[0.6,0.5,0.6,0.6,0.5\right]$, $\pi =\left[1.0,1.0,0.8,1.0,1.0\right]$. The parameters of the ET mechanism are adopted from Example 1 in [22].

As illustrated in Figure 6 and Figure 7, under our distributed controller (9) and the DET mechanism (12), all followers can achieve leader-following consensus within 4 s, facilitated by a longer average event interval. In contrast, under the ET mechanism described in Equation (7) of [22] proposed by Xu et al., although each follower has a smaller average event interval, the convergence time is 5 s, as shown in Figure 8 and Figure 9.

Table 1. Triggering numbers under different ET mechanisms.

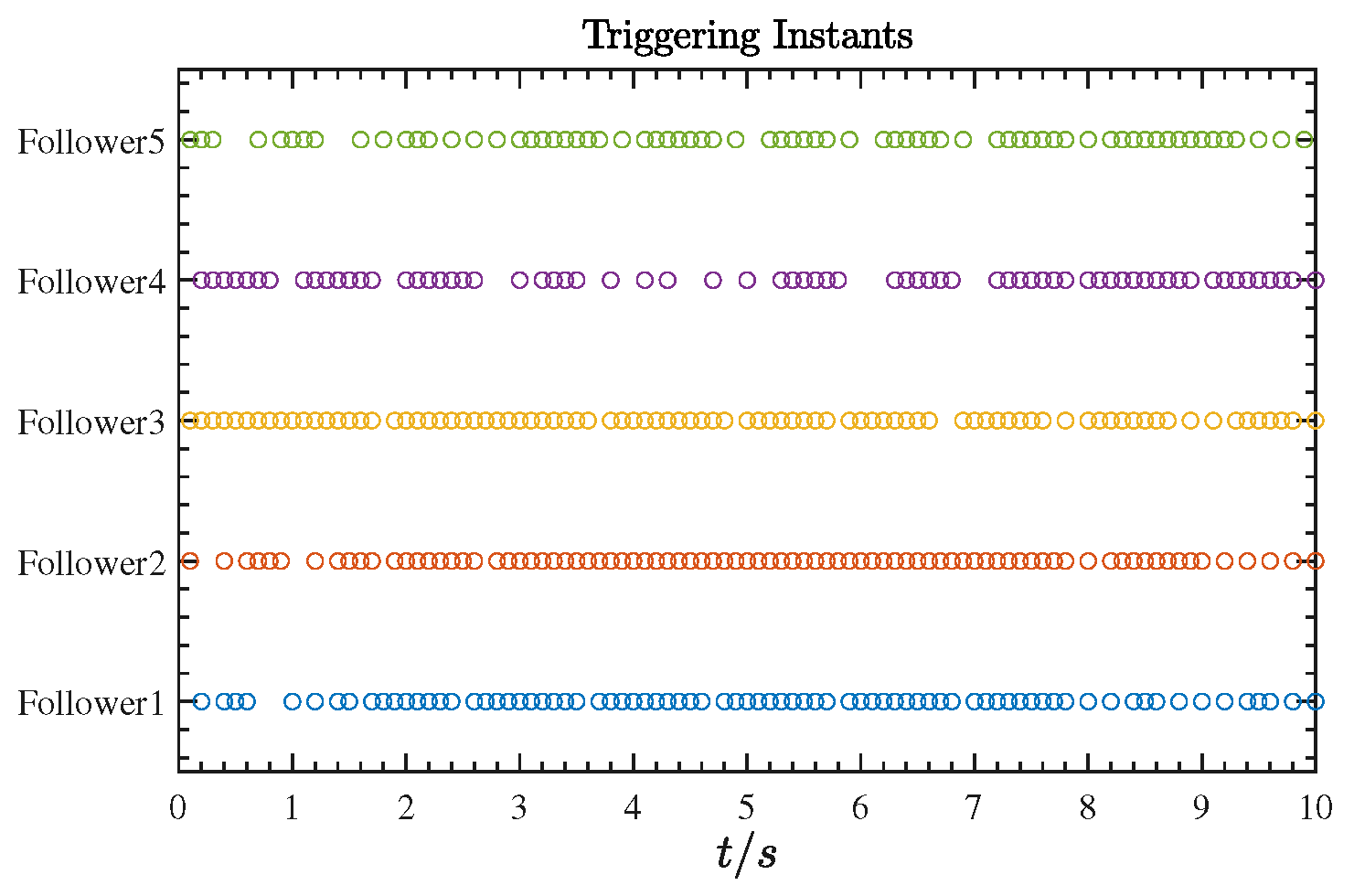
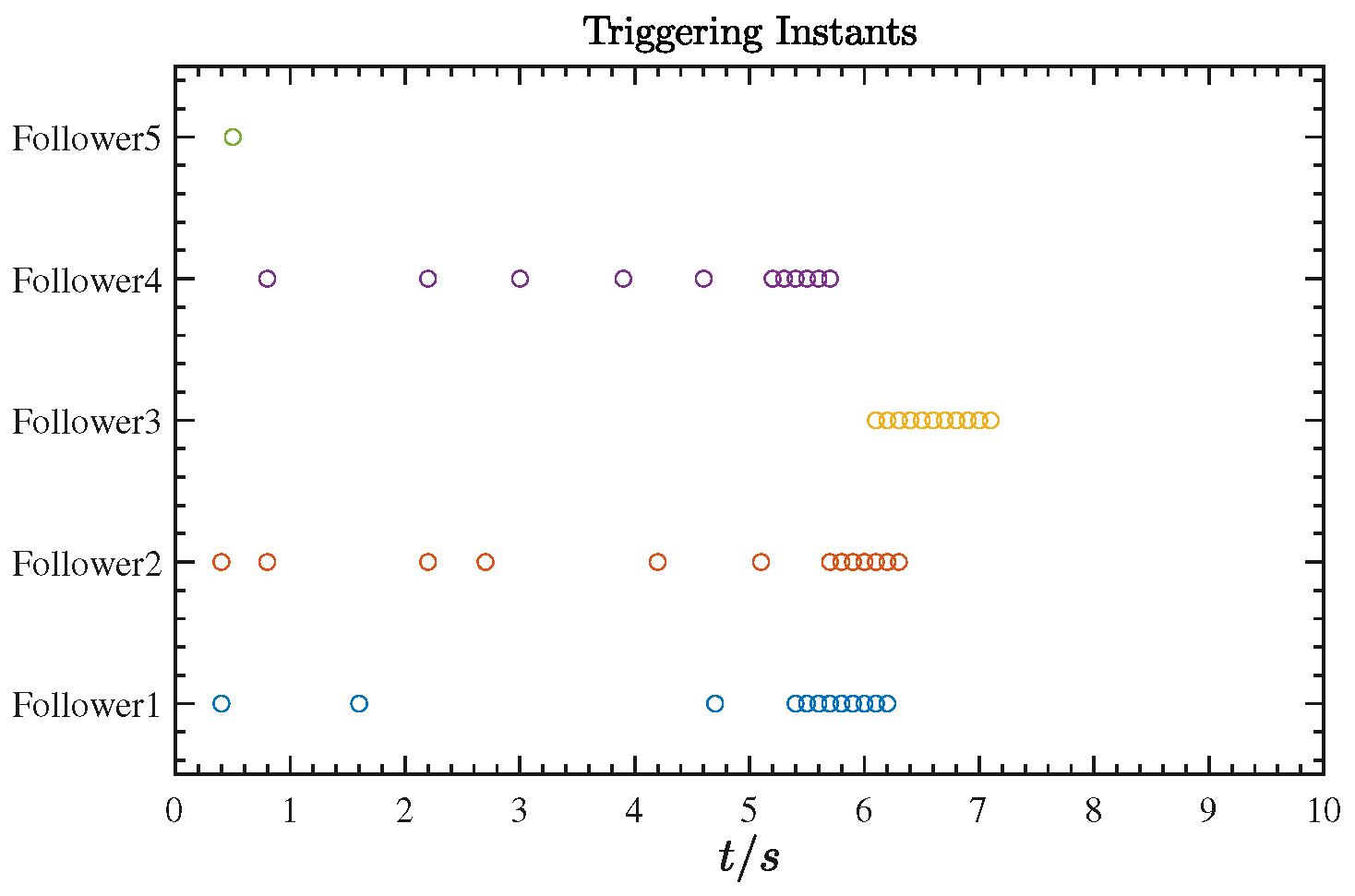
Follower	Follower 1	Follower 2	Follower 3	Follower 4	Follower 5
DET with ${\displaystyle \frac{m_1}{m_2}}={\displaystyle \frac{1}{5}}$	19	14	8	11	1
DET with ${\displaystyle \frac{m_1}{m_2}}={\displaystyle \frac{1}{6}}$	12	13	11	11	1
ET	78	85	88	69	70

compares the number of triggering events under the two mechanisms. The results indicate that the DET mechanism effectively extends the inter-event intervals, thereby reducing the frequency of information transmission and control updates. Additionally, the finite-time control approach achieves faster system convergence.

In order to further demonstrate the design flexibility of the DET mechanism proposed in this paper, i.e., the convergence speed and triggering frequency can be modified by adjusting the parameters of the triggering function, we select ${\displaystyle \frac{m_1}{m_2}}={\displaystyle \frac{1}{6}}$ and keep other parameters the same to conduct the simulation test. Figure 10 and Figure 11 present the simulation results. Similar to the results of ${\displaystyle \frac{m_1}{m_2}}={\displaystyle \frac{1}{5}}$, all followers achieve consensus with the leader within a finite time, and tracking errors converge to zero. Furthermore, as the ${\displaystyle \frac{m_1}{m_2}}$ increases, there is a rise in the number of event triggers and a faster convergence of the tracking error. This approach contrasts with traditional asymptotic consensus strategies, which rely on continuous or event-based communication and may lack efficiency. The consensus strategy proposed in this work is specifically designed to achieve leader-following consensus within a finite time, while simultaneously reducing energy consumption and communication overhead. Compared to existing FTDET strategies, the proposed method significantly reduces communication overhead and enhances design flexibility, enabling the adjustment of both the system’s convergence speed and triggering frequency through parameter tuning.

5. Conclusions

In this paper, a novel FTDET leader-following consensus control scheme is proposed for general linear MASs systems under direct networks, addressing the challenge of communication constraints. First, model-based estimation information is continuously updated over the triggering intervals, which eliminates the need for continuous communication with neighboring agents. Then, by introducing a designable power term in the dynamic internal variable, the need for communication frequency and convergence rate can be balanced. In addition, the analysis of the Zeno behavior also guarantees the feasibility of the proposed method. In future work, we will focus on more complex and dynamic networked environments, further optimize the convergence rate and triggering frequency, and explore its application in real-world UAV missions to enhance adaptability and efficiency.