Connectivity Preservation and Obstacle Avoidance Control for Multiple Quadrotor UAVs with Limited Communication Distance
Abstract
1. Introduction
- (1)
- (2)
- While previous studies like [37] have focused solely on collision avoidance and connectivity preservation among UAVs, this controller also tackles obstacle avoidance between UAVs and external obstacles.
- (3)
- In contrast to the existing static obstacle avoidance schemes reviewed in [44,45,46], the proposed control law addresses dynamic obstacle avoidance by utilizing dynamic surface control and a repulsive potential function. This work represents one of the first approaches to simultaneously handling the distributed control of quadrotor UAVs, connectivity preservation, and dynamic obstacle avoidance.
2. Preliminaries and the Problem Statement
2.1. The Dynamics of Quadrotor UAVs
2.2. Dynamic Communication Network Modeling
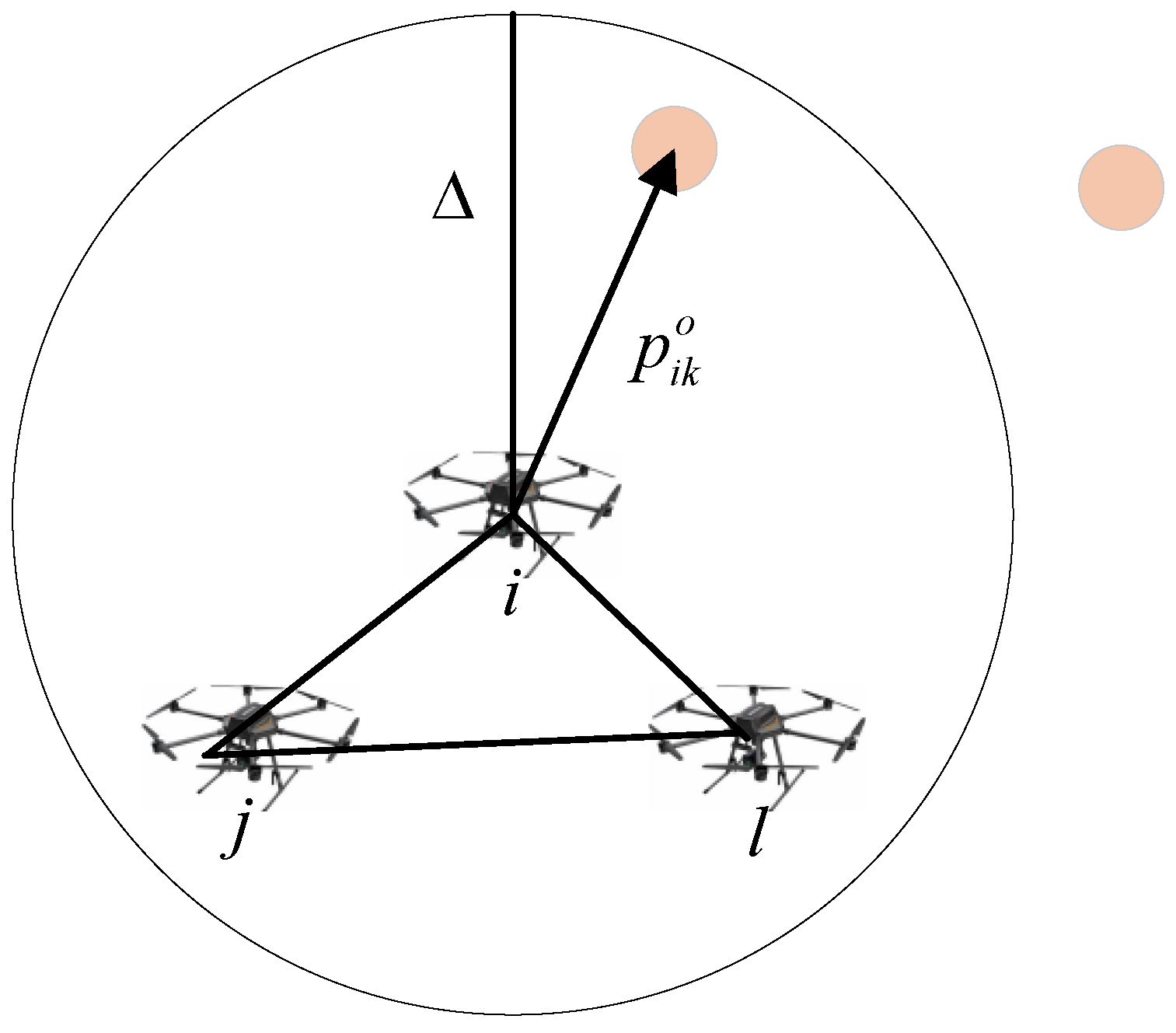
2.3. The Control Objective
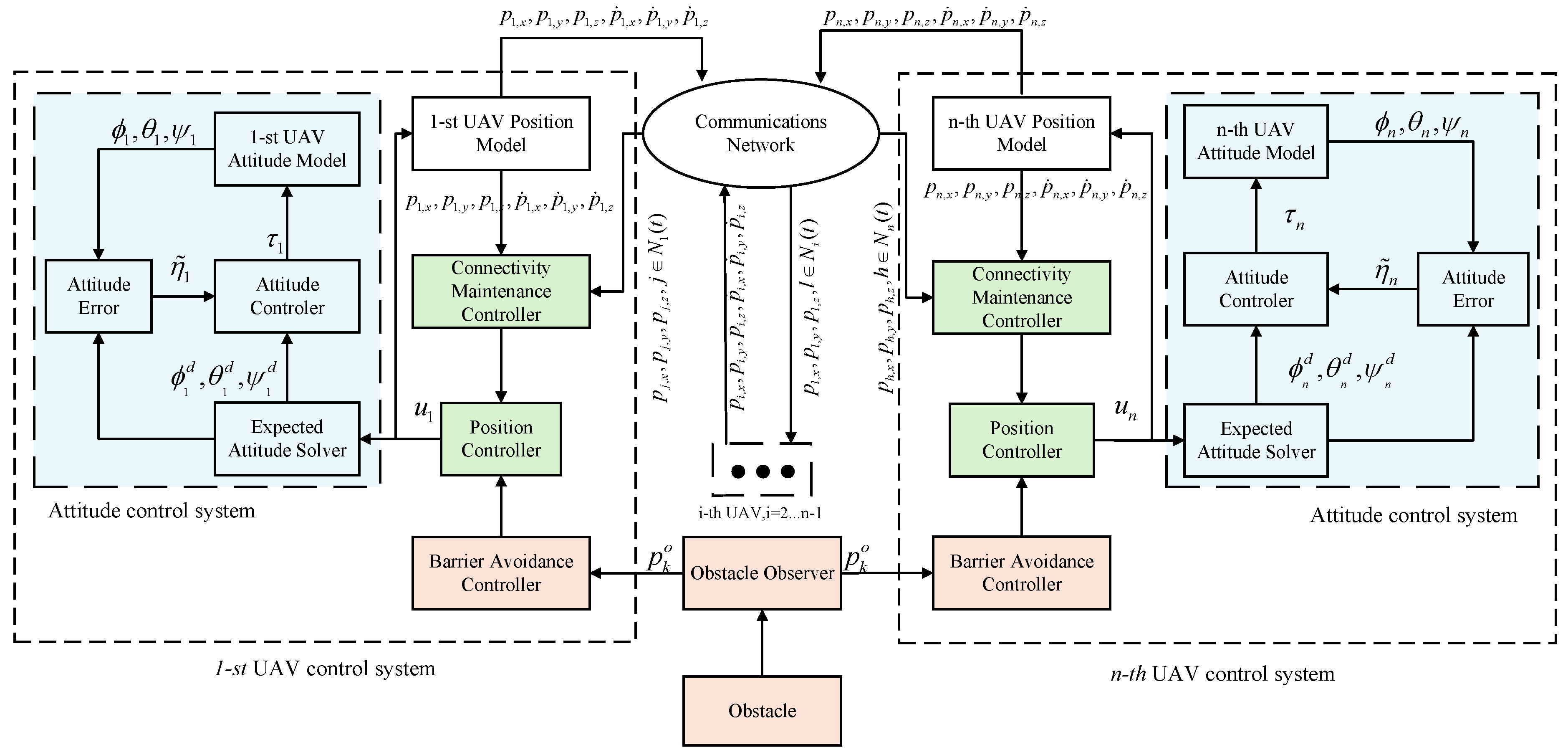
3. Distributed Controller Design
3.1. Artificial Potential Functions
- (1)
- If , is defined as follows [56,57]:where denotes the repulsive potential function, and represents the attractive potential function, with both mediating the interactions between UAVs based on their distances. The three potential functions satisfy the following conditions:
- (a)
- is a continuous and differentiable nonnegative function of ;
- (b)
- is symmetric and achieves its unique minimum while ;
- (c)
- monotonically decreases with respect to , and as ;
- (d)
- monotonically decreases with respect to , and as .
- (2)
- (1)
- being a continuous and differentiable nonnegative function of ;
- (2)
- monotonically decreasing with respect to , while ;
- (3)
- as , and as .
3.2. Position Controller Design and Analysis
- (1)
- If the initial distance between any two connected UAVs is less than Δ, i.e., , then for all ;
- (2)
- The distance between any two UAVs remains greater than at all times, i.e., for all ;
- (3)
- The distance between any UAV and any obstacle remains greater than at all times, i.e., for all ;
- (4)
- As time progresses towards infinity, the distance between each pair of connected UAVs converges to , and the velocity of each UAV approaches zero, i.e., and as .
3.3. Attitude Tracking Controller Design
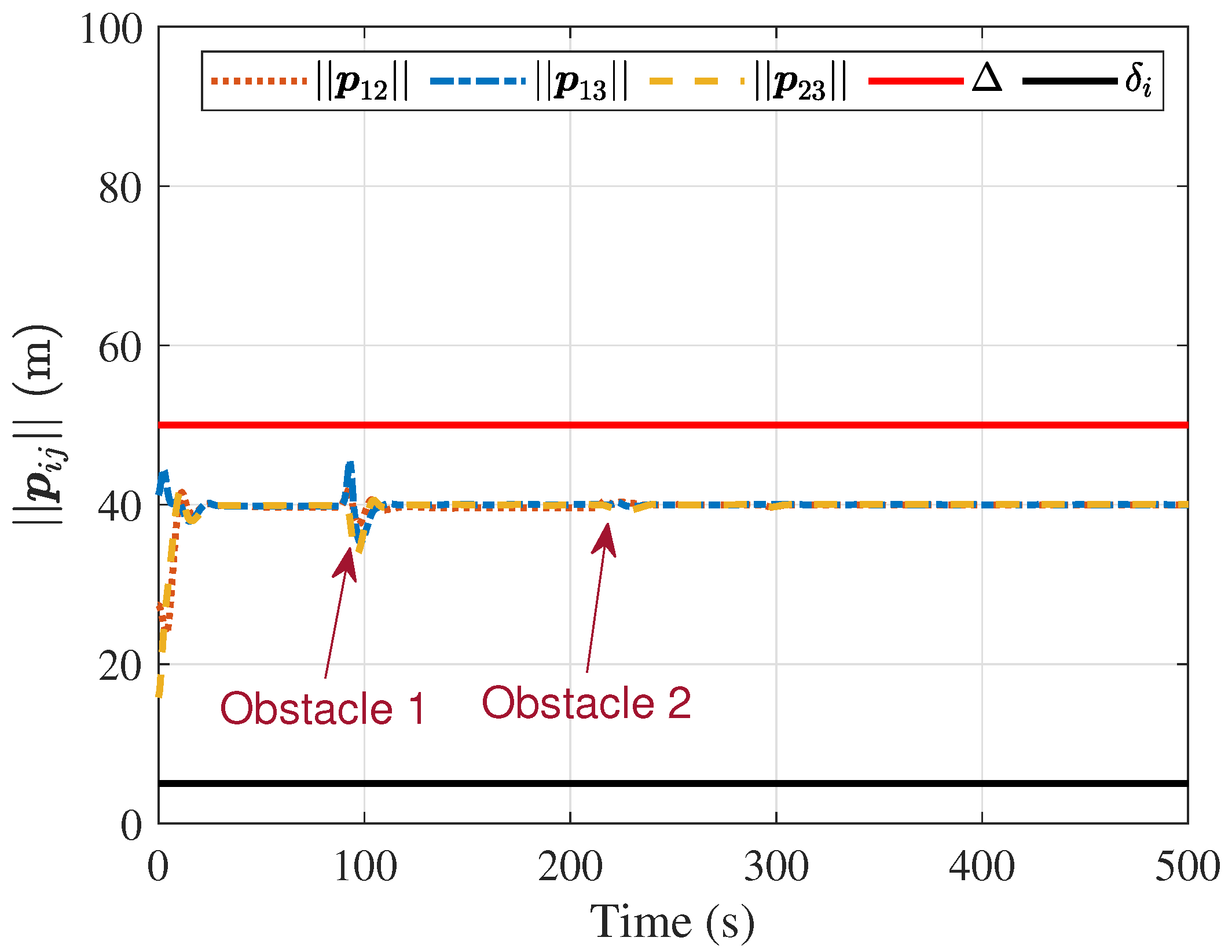
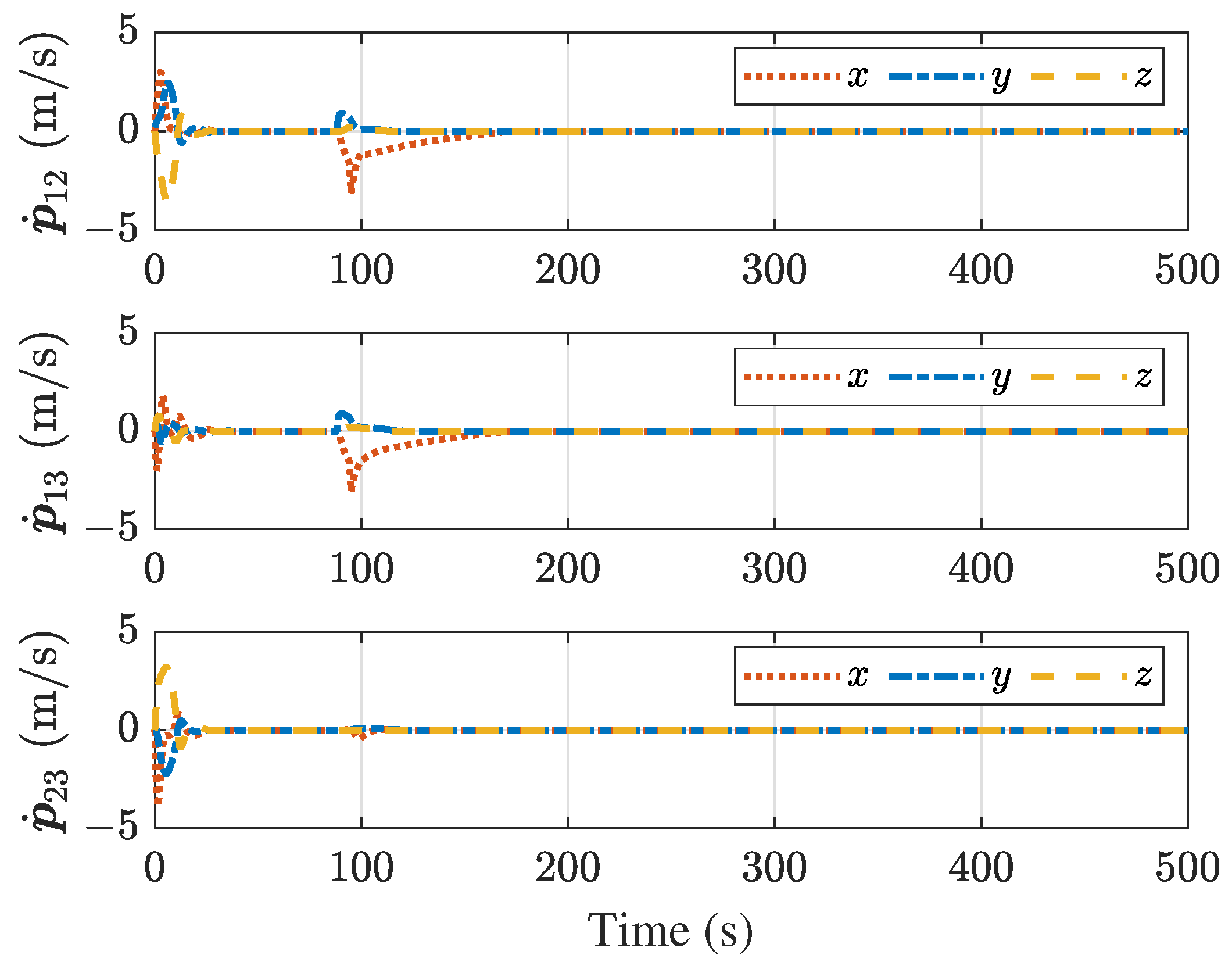
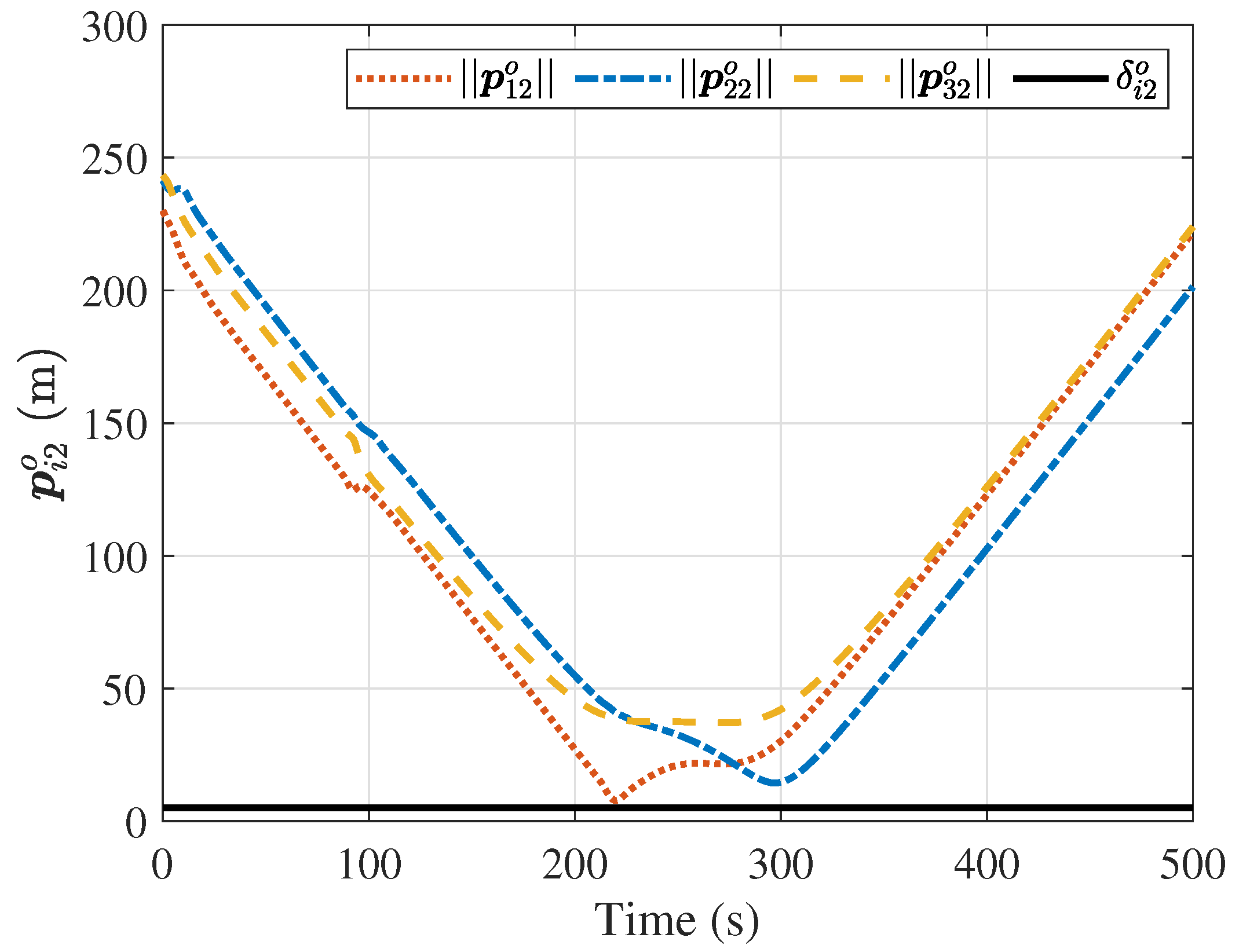
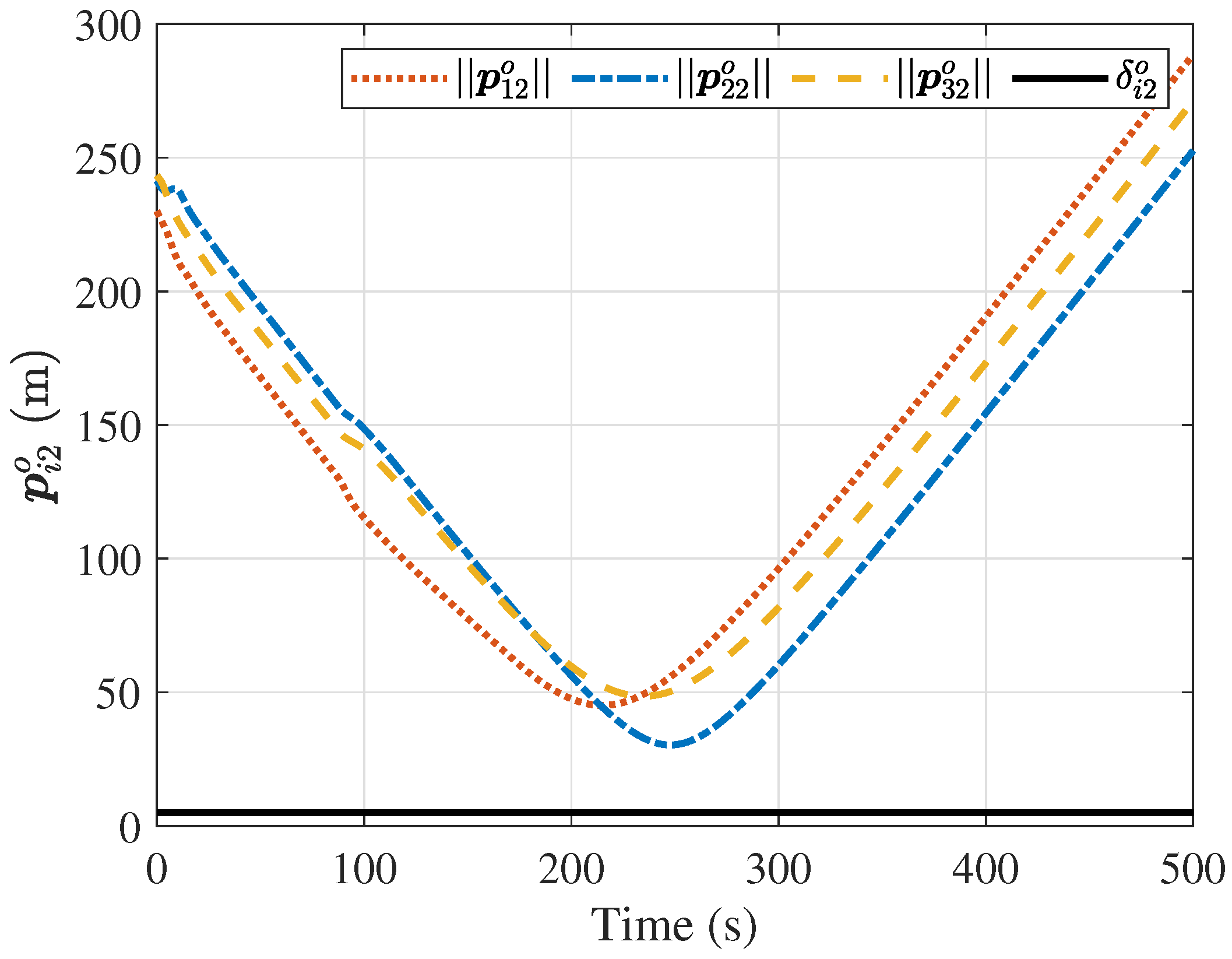
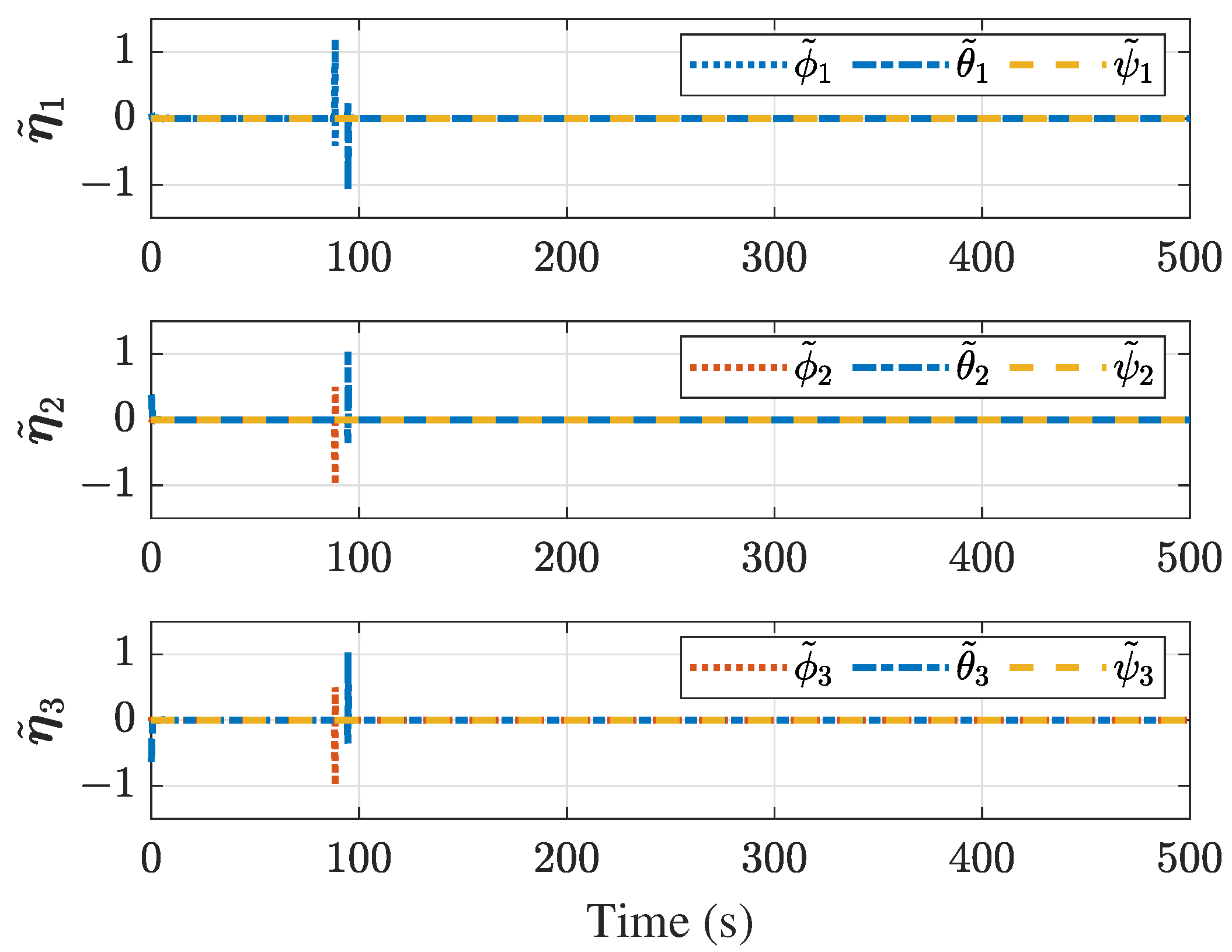
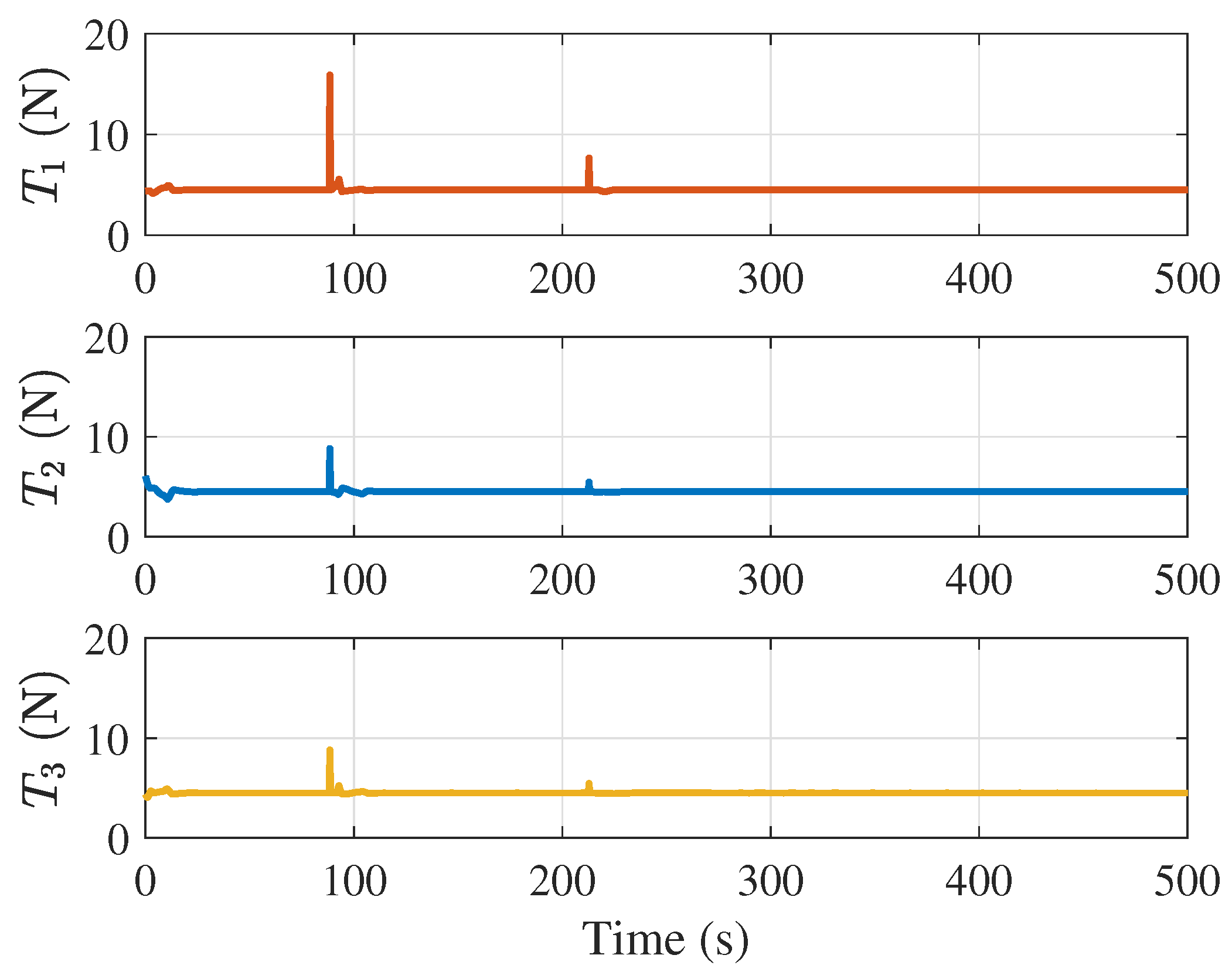
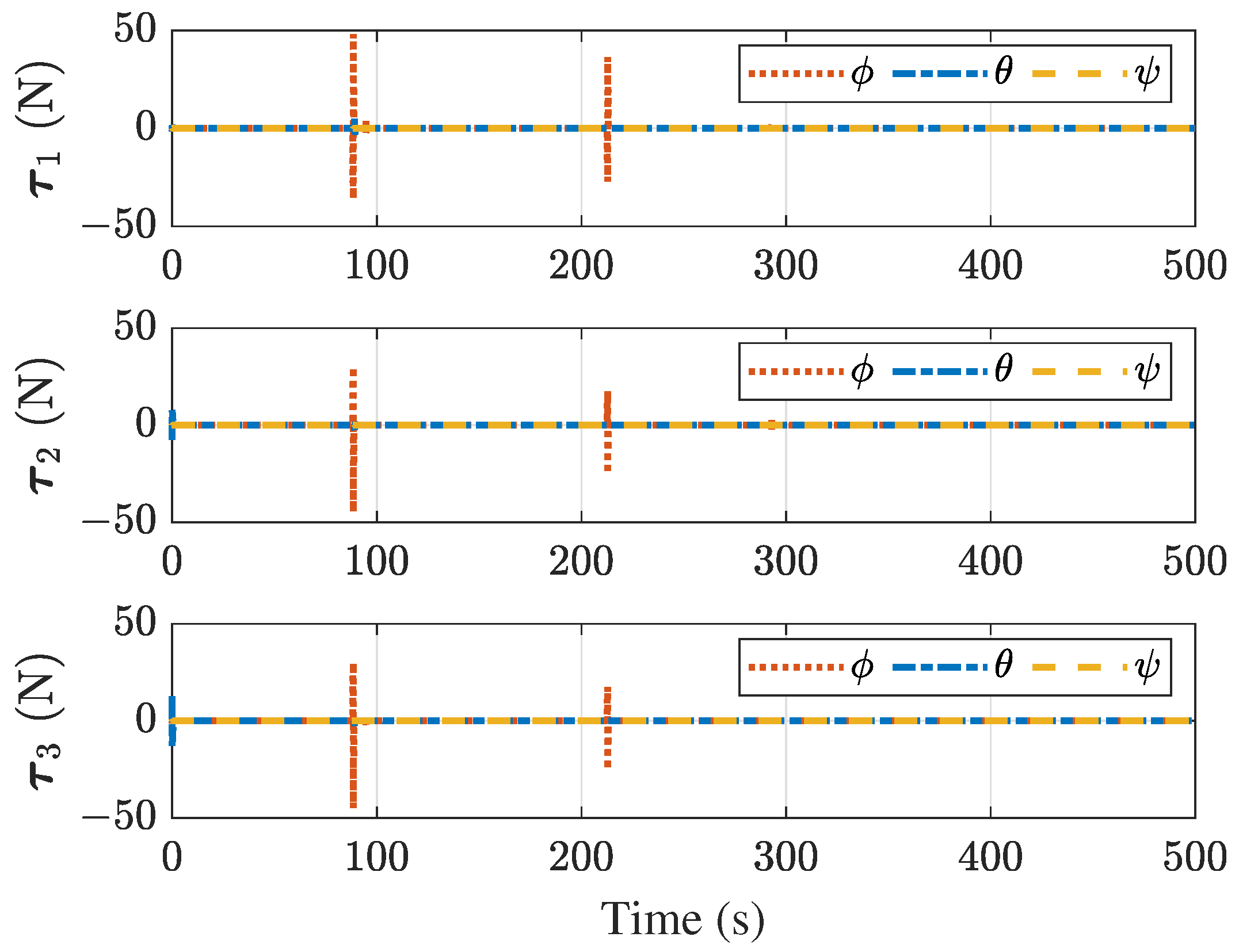
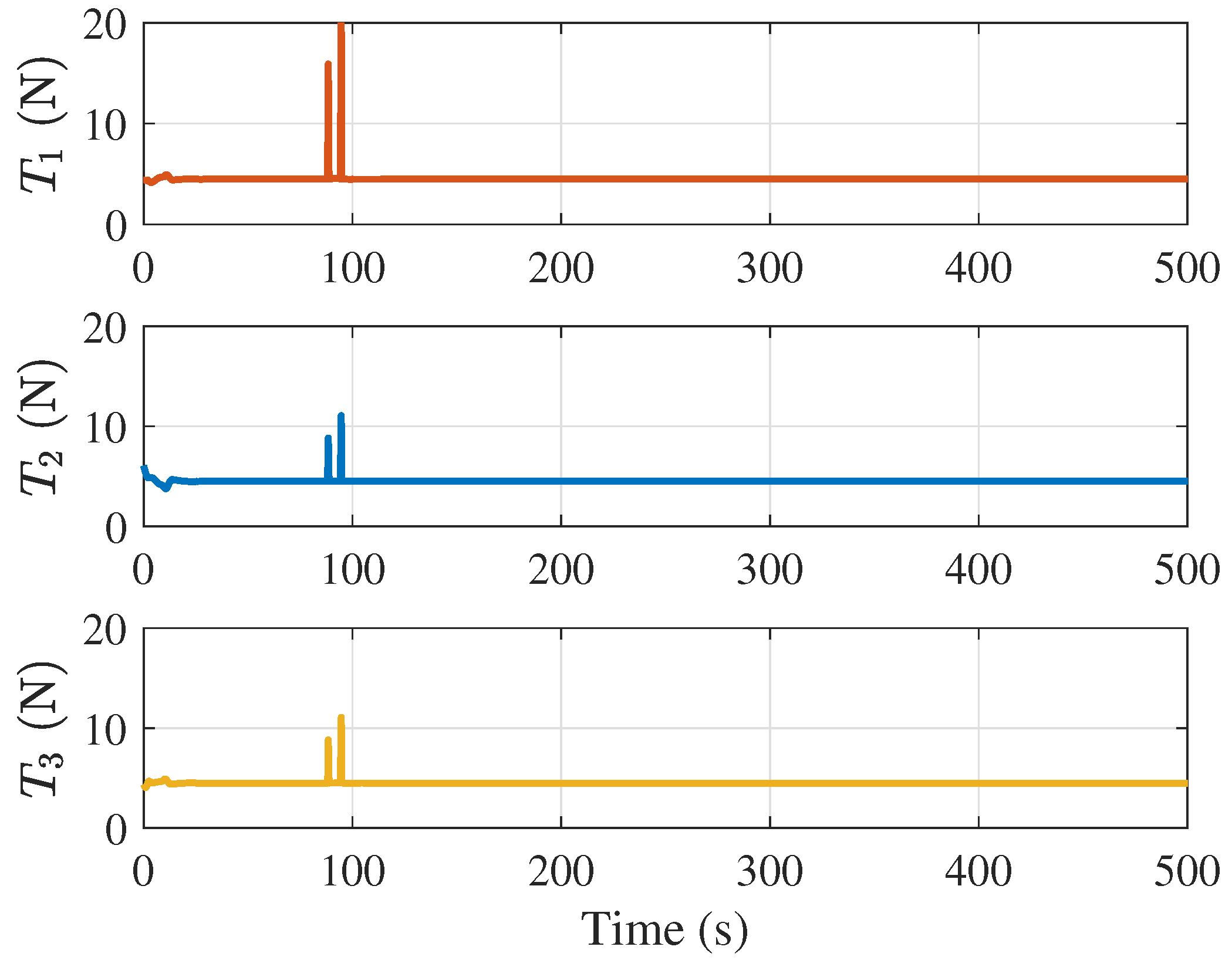
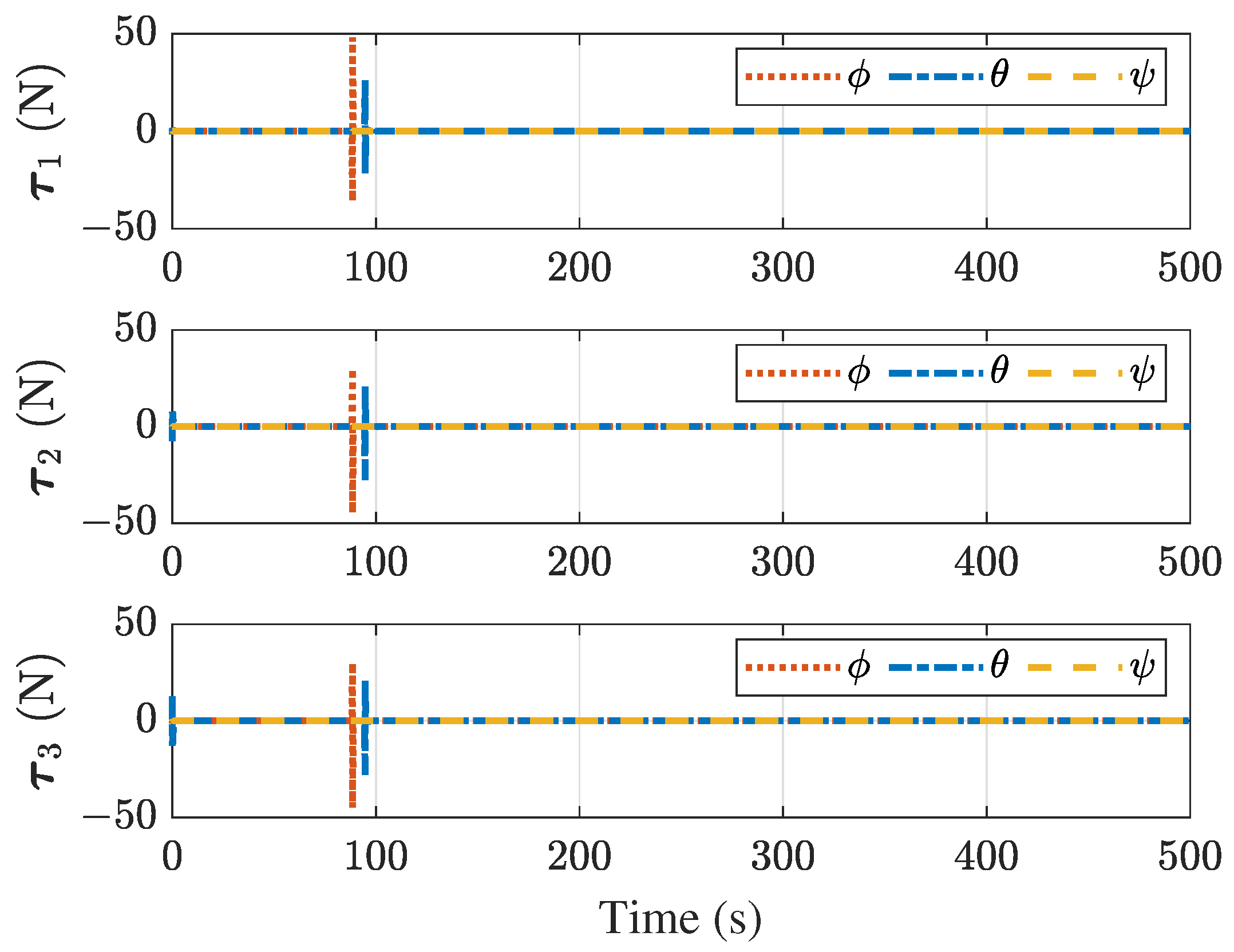
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, C.; Zhang, Y.; Liu, Z. A survey on technologies for automatic forest fire monitoring, detection, and fighting using unmanned aerial vehicles and remote sensing techniques. Can. J. For. Res. 2015, 45, 783–792. [Google Scholar] [CrossRef]
- Ariyibi, S.O.; Tekinalp, O. Quaternion-based nonlinear attitude control of quadrotor formations carrying a slung load. Aerosp. Sci. Technol. 2020, 105, 105995. [Google Scholar] [CrossRef]
- Yun, W.J.; Park, S.; Kim, J.; Shin, M.; Jung, S.; Mohaisen, D.A.; Kim, J.H. Cooperative multiagent deep reinforcement learning for reliable surveillance via autonomous multi-UAV control. IEEE Trans. Ind. Inform. 2022, 18, 7086–7096. [Google Scholar] [CrossRef]
- Huang, J.; Luo, Y.; Quan, Q.; Wang, B.; Xue, X.; Zhang, Y. An autonomous task assignment and decision-making method for coverage path planning of multiple pesticide spraying UAVs. Comput. Electron. Agric. 2023, 212, 108128. [Google Scholar] [CrossRef]
- Askarzadeh, T.; Bridgelall, R.; Tolliver, D. Monitoring nodal transportation assets with uncrewed aerial vehicles: A comprehensive review. Drones 2024, 8, 233. [Google Scholar] [CrossRef]
- Earthperson, A.; Diaconeasa, M.A. Integrating commercial-off-the-shelf components into radiation-hardened drone designs for nuclear-contaminated search and rescue missions. Drones 2023, 7, 528. [Google Scholar] [CrossRef]
- Kong, X.; Ni, C.; Duan, G.; Shen, G.; Yang, Y.; Das, S.K. Energy consumption optimization of UAV-assisted traffic monitoring scheme with tiny reinforcement learning. IEEE Internet Things J. 2024, 11, 21135–21145. [Google Scholar] [CrossRef]
- McGuire, K.N.; De Wagter, C.; Tuyls, K.; Kappen, H.J.; de Croon, G.C.H.E. Minimal navigation solution for a swarm of tiny flying robots to explore an unknown environment. Sci. Robot. 2019, 4, eaaw9710. [Google Scholar] [CrossRef]
- Dorigo, M.; Theraulaz, G.; Trianni, V. Swarm robotics: Past, present, and future. Proc. IEEE 2021, 109, 1152–1165. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; He, Z.; Li, Z.; Zhang, Q.; Ding, Z. A survey of multi-agent systems on distributed formation control. Unmanned Syst. 2024, 12, 913–926. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, C.; Guo, J.; Chadli, M.; Xiang, Z. Adaptive formation control for unmanned aerial vehicles with collision avoidance and switching communication network. IEEE Trans. Fuzzy Syst. 2023, 32, 1435–1445. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Jiang, B.; Su, C.Y.; Fu, J.; Jin, Y.; Chai, T. Distributed adaptive fault-tolerant time-varying formation control of unmanned airships with limited communication ranges against input saturation for smart city observation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 1891–1904. [Google Scholar] [CrossRef]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A survey on aerial swarm robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Jiang, B.; Fu, J.; Jin, Y. A review on fault-tolerant cooperative control of multiple unmanned aerial vehicles. Chin. J. Aeronaut. 2022, 35, 1–18. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Jiang, B.; Su, C.Y.; Fu, J.; Jin, Y.; Chai, T. Decentralized fractional-order backstepping fault-tolerant control of multi-UAVs against actuator faults and wind effects. Aerosp. Sci. Technol. 2020, 104, 105939. [Google Scholar] [CrossRef]
- Liu, H.; Ma, T.; Lewis, F.L.; Wan, Y. Robust formation trajectory tracking control for multiple quadrotors with communication delays. IEEE Trans. Control Syst. Technol. 2020, 28, 2633–2640. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, Y.; Liu, Y.; Meng, Z. Distributed control algorithm for leader-follower formation tracking of multiple quadrotors: Theory and experiment. IEEE/ASME Trans. Mechatronics 2020, 26, 1095–1105. [Google Scholar] [CrossRef]
- Wang, H.; Shan, J. Fully distributed event-triggered formation control for multiple quadrotors. IEEE Trans. Ind. Electron. 2023, 70, 12566–12575. [Google Scholar] [CrossRef]
- Yan, Z.; Han, L.; Li, X.; Dong, X.; Li, Q.; Ren, Z. Event-Triggered formation control for time-delayed discrete-Time multi-Agent system applied to multi-UAV formation flying. J. Frankl. Inst. 2023, 360, 3677–3699. [Google Scholar] [CrossRef]
- Fan, D.; Guo, K.; Lyu, S.; Yu, X.; Xie, L.; Guo, L. Quadrotor UAV: Collision resilience behaviors. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2092–2104. [Google Scholar] [CrossRef]
- Yang, Z.; Li, M.; Yu, Z.; Cheng, Y.; Xu, G.; Zhang, Y. Fault detection and fault-tolerant cooperative control of multi-uavs under actuator faults, sensor faults, and wind disturbances. Drones 2023, 7, 503. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying. IEEE Trans. Ind. Electron. 2016, 64, 5014–5024. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, G.; Xie, W.; Zhang, W.; Silvestre, C. Robust saturated formation tracking control of multiple quadrotors with switching communication topologies. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3744–3753. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, H.; Lü, J.; Gao, Q.; Feng, G. Data-driven optimal formation control for multiple nonlinear quadrotors with switching topologies. IEEE Trans. Veh. Technol. 2023, 1–11. [Google Scholar] [CrossRef]
- Li, Q.; Hua, Y.; Dong, X.; Yu, J.; Ren, Z. Time-varying formation tracking control for unmanned aerial vehicles with the leader’s unknown input and obstacle avoidance: Theories and applications. Electronics 2022, 11, 2334. [Google Scholar] [CrossRef]
- Guo, J.; Qi, J.; Wang, M.; Wu, C.; Ping, Y.; Li, S.; Jin, J. Distributed cooperative obstacle avoidance and formation reconfiguration for multiple quadrotors: Theory and experiment. Aerosp. Sci. Technol. 2023, 136, 108218. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Sun, S.; Cai, Y. Adaptive time-varying formation tracking control for multiagent systems with nonzero leader input by intermittent communications. IEEE Trans. Cybern. 2023, 53, 5706–5715. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.; Wang, S.; Ai, X. Observer-based consensus control for heterogeneous multi-agent systems with intermittent communications. Int. J. Robust Nonlinear Control 2021, 31, 6492–6506. [Google Scholar] [CrossRef]
- Zavlanos, M.M.; Pappas, G.J. Potential fields for maintaining connectivity of mobile networks. IEEE Trans. Robot. 2007, 23, 812–816. [Google Scholar] [CrossRef]
- Aragues, R.; Dimarogonas, D.V.; Guallar, P.; Sagues, C. Intermittent connectivity maintenance with heterogeneous robots. IEEE Trans. Robot. 2021, 37, 225–245. [Google Scholar] [CrossRef]
- Kan, Z.; Doucette, E.A.; Dixon, W.E. Distributed connectivity preserving target tracking with random sensing. IEEE Trans. Autom. Control 2018, 119, 8–15. [Google Scholar] [CrossRef]
- Sun, C.; Hu, G.; Xie, L.; Egerstedt, M. Robust finite-time connectivity preserving coordination of second-order multi-agent systems. Automatica 2018, 89, 21–27. [Google Scholar] [CrossRef]
- Hong, H.; Yu, W.; Fu, J.; Yu, X. Finite-time connectivity-preserving consensus for second-order nonlinear multi-agent systems. IEEE Trans. Control Netw. Syst. 2018, 6, 236–248. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, C.; Li, J.; Lu, Y.; Yang, Q. Connectivity-maintenance UAV formation control in complex environment. Drones 2023, 7, 229. [Google Scholar] [CrossRef]
- Xue, X.; Yue, X.; Yuan, J. Distributed Connectivity Maintenance and Collision Avoidance Control of Spacecraft Formation Flying. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8265–8270. [Google Scholar] [CrossRef]
- Xue, X.; Yuan, B.; Yi, Y.; Zhang, Y.; Yue, X.; Mu, L. Connectivity preservation control for multiple unmanned aerial vehicles in the presence of bounded actuation. ISA Trans. 2024, 152, 28–37. [Google Scholar] [CrossRef]
- Cong, Y.; Du, H.; Jin, Q.; Zhu, W.; Lin, X. Formation control for multiquadrotor aircraft: Connectivity preserving and collision avoidance. Int. J. Robust Nonlinear Control 2020, 30, 2352–2366. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, W.; Sun, C.; Chu, D.; Huang, T.; Li, W.; Yu, C.; Pirani, M.; Cao, D.; Khajepour, A. Eliminating uncertainty of driver’s social preferences for lane change decision-making in realistic simulation environment. IEEE Trans. Intell. Transp. Syst. 2024, 26, 1583–1597. [Google Scholar] [CrossRef]
- Hang, P.; Huang, C.; Hu, Z.; Lv, C. Decision making for connected automated vehicles at urban intersections considering social and individual benefits. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22549–22562. [Google Scholar] [CrossRef]
- Hang, P.; Zhang, Y.; Lv, C. Brain-inspired modeling and decision-making for human-like autonomous driving in mixed traffic environment. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10420–10432. [Google Scholar] [CrossRef]
- Wang, X.; Shen, L.; Liu, Z.; Zhao, S.; Cong, Y.; Li, Z.; Jia, S.; Chen, H.; Yu, Y.; Chang, Y.; et al. Coordinated flight control of miniature fixed-wing UAV swarms: Methods and experiments. Sci. China Inf. Sci. 2019, 62, 212204. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Hu, X.; Huang, Y. A new consensus theory-based method for formation control and obstacle avoidance of UAVs. Aerosp. Sci. Technol. 2020, 107, 106332. [Google Scholar] [CrossRef]
- Qian, M.; Wu, Z.; Jiang, B. Cerebellar model articulation neural network-based distributed fault tolerant tracking control with obstacle avoidance for fixed-wing UAVs. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6841–6852. [Google Scholar] [CrossRef]
- Li, X.; Sun, D.; Yang, J. A bounded controller for multirobot navigation while maintaining network connectivity in the presence of obstacles. Automatica 2013, 49, 285–292. [Google Scholar] [CrossRef]
- Chen, Z.; Emami, M.R.; Chen, W. Connectivity preservation and obstacle avoidance in small multi-spacecraft formation with distributed adaptive tracking control. J. Intell. Robot. Syst. 2021, 101, 16. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Ren, Z. Practical time-varying output formation tracking for high-order multi-agent systems with collision avoidance, obstacle dodging and connectivity maintenance. J. Frankl. Inst. 2019, 356, 5898–5926. [Google Scholar] [CrossRef]
- Yu, Z.; Qu, Y.; Zhang, Y. Distributed fault-tolerant cooperative control for multi-uavs under actuator fault and input saturation. IEEE Trans. Control Syst. Technol. 2019, 27, 2417–2429. [Google Scholar] [CrossRef]
- Liu, H.; Ma, T.; Lewis, F.L.; Wan, Y. Robust formation control for multiple quadrotors with nonlinearities and disturbances. IEEE Trans. Cybern. 2020, 50, 1362–1371. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wen, G.; Wu, D. Finite-time formation control for a group of quadrotor aircraft. Aerosp. Sci. Technol. 2017, 69, 609–616. [Google Scholar] [CrossRef]
- Zou, Y.; Meng, Z. Immersion and invariance-based adaptive controller for quadrotor systems. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 49, 2288–2297. [Google Scholar] [CrossRef]
- Kendoul, F.; Yu, Z.; Nonami, K. Guidance and nonlinear control system for autonomous flight of minirotorcraft unmanned aerial vehicles. J. Field Robot. 2010, 27, 311–334. [Google Scholar] [CrossRef]
- Moreno-Valenzuela, J.; Pérez-Alcocer, R.; Guerrero-Medina, M.; Dzul, A. Nonlinear PID-type controller for quadrotor trajectory tracking. IEEE/ASME Trans. Mechatronics 2018, 23, 2436–2447. [Google Scholar] [CrossRef]
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010; Volume 33. [Google Scholar]
- Liao, F.; Teo, R.; Wang, J.L.; Dong, X.; Lin, F.; Peng, K. Distributed formation and reconfiguration control of VTOL UAVs. IEEE Trans. Control Syst. Technol. 2017, 25, 270–277. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wen, G.; Duan, Z.; Lü, J. Distributed formation control of multiple quadrotor aircraft based on nonsmooth consensus algorithms. IEEE Trans. Cybern. 2017, 49, 342–353. [Google Scholar] [CrossRef]
- Cao, Y.; Ren, W. Distributed coordinated tracking with reduced interaction via a variable structure approach. IEEE Trans. Autom. Control 2012, 57, 33–48. [Google Scholar] [CrossRef]
- Xue, X.; Yue, X.; Yuan, J. Connectivity preservation and collision avoidance control for spacecraft formation flying in the presence of multiple obstacles. Adv. Space Res. 2021, 67, 3504–3514. [Google Scholar] [CrossRef]
- Hu, Q.; Dong, H.; Zhang, Y.; Ma, G. Tracking control of spacecraft formation flying with collision avoidance. Aerosp. Sci. Technol. 2015, 42, 353–364. [Google Scholar] [CrossRef]
- Gazi, V. Swarm aggregations using artificial potentials and sliding-mode control. IEEE Trans. Robot. 2005, 21, 1208–1214. [Google Scholar] [CrossRef]
- Haskara, I. On sliding mode observers via equivalent control approach. Int. J. Control 1998, 71, 1051–1067. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, X.; Yuan, B.; Yi, Y.; Mu, L.; Zhang, Y. Connectivity Preservation and Obstacle Avoidance Control for Multiple Quadrotor UAVs with Limited Communication Distance. Drones 2025, 9, 136. https://doi.org/10.3390/drones9020136
Xue X, Yuan B, Yi Y, Mu L, Zhang Y. Connectivity Preservation and Obstacle Avoidance Control for Multiple Quadrotor UAVs with Limited Communication Distance. Drones. 2025; 9(2):136. https://doi.org/10.3390/drones9020136
Chicago/Turabian StyleXue, Xianghong, Bin Yuan, Yingmin Yi, Lingxia Mu, and Youmin Zhang. 2025. "Connectivity Preservation and Obstacle Avoidance Control for Multiple Quadrotor UAVs with Limited Communication Distance" Drones 9, no. 2: 136. https://doi.org/10.3390/drones9020136
APA StyleXue, X., Yuan, B., Yi, Y., Mu, L., & Zhang, Y. (2025). Connectivity Preservation and Obstacle Avoidance Control for Multiple Quadrotor UAVs with Limited Communication Distance. Drones, 9(2), 136. https://doi.org/10.3390/drones9020136






