Assignment Technology Based on Improved Great Wall Construction Algorithm

Abstract

The problem of allocating multiple UAV tasks is a complex combinatorial optimization challenge, involving various constraints. This paper presents an autonomous multi-UAV cooperative task allocation method based on an improved Great Wall Construction Algorithm. A model integrating battlefield environmental factors, 3D terrain data, and threat assessments is developed for optimized task allocation and trajectory planning. The algorithm is enhanced using a good point set initialization strategy, Gaussian distribution estimation, and a Cauchy reorganization variant. The simulation results show that replacing straight-line distances with actual flight distances leads to more rational mission sequences, improving combat effectiveness under realistic terrain and threat conditions. The enhanced algorithm demonstrates superior accuracy and faster convergence.

1. Introduction

With advancements in information technology and artificial intelligence, UAVs have rapidly evolved in response to both domestic and international military demands. Initially limited to reconnaissance, assessment, early warning, and target guidance, UAVs are now integrated into multi-functional and multi-purpose intelligent combat platforms, capable of suppressing local air defense systems, executing precision ground/sea strikes, and conducting airborne electronic countermeasures [1]. As UAVs continue to demonstrate their effectiveness on modern battlefields, the environments they encounter have become increasingly complex, and the missions they are tasked with more diverse. Consequently, the demands placed on unmanned combat aircraft have escalated. However, the operational capacity of a single UAV is constrained by limitations such as reduced payload, weak computational power, and limited flight endurance, making multi-UAV collaborative operations a critical area of development [2,3].

Multi-UAV autonomous cooperative task allocation, a critical technology in multi-UAV mission planning [4], involves developing a rational task execution strategy for UAVs in dynamic and complex combat environments. This process considers UAV combat capabilities, mission requirements, and other relevant factors to optimize overall combat effectiveness [5]. A prominent example of an NP-hard problem is the multi-UAV cooperative task allocation problem, which is fundamentally a multi-constraint combinatorial optimization challenge from a computational standpoint. Research on the multi-UAV cooperative task allocation problem primarily focuses on two key aspects: task allocation modeling and algorithmic solutions for the model.

In terms of task allocation model equations, several commonly adopted models, both domestically and internationally, include the vehicle routing problem (VRP) model [6], the multi-agent traveling salesman problem (m-TSP) model [7], the contract net auction model [8], and the mixed integer linear programming (MILP) model [9]. One study [10] introduced a multi-UAV collaborative task allocation method featuring robust search capabilities and rapid convergence, leveraging a mixed integer linear programming model combined with an improved bacterial foraging optimization algorithm. Another study [11] presented a contract net auction model that accounts for the constraints between targets and UAVs. The authors of another study [12] developed a UCAV task allocation model based on constraints derived from UCAV flight characteristics and battlefield environmental factors.

In the study of algorithms designed to solve task allocation models, these approaches are generally classified into two categories: the initial category includes conventional optimization techniques, including dynamic programming [13] and linear programming using mixed integers [14]. The second group comprises intelligent optimization methods, including the whale optimization algorithm [15], pigeon-inspired optimization [16], and the algorithm based on the lion optimizer [17]. Traditional optimization techniques find it more difficult to produce excellent results in acceptable amounts of time as problem complexity rises. In contrast, swarm intelligence algorithms, which are model-agnostic and do not require gradient information, offer robust search capabilities and broad applicability, making them widely adopted for UAV mission planning problems.

The Great Wall Construction Algorithm (GWCA) [18] is a novel heuristic optimization algorithm inspired by human activities, particularly the competitive and eliminative dynamics observed among workers during the construction of the ancient Great Wall. Findings from the literature [18] indicate that the GWCA outperforms many prominent intelligent optimization algorithms and has consequently been widely applied to address a range of practical engineering challenges. However, the GWCA has certain limitations, primarily in the following areas [18]: (1) limited solution diversity; (2) susceptibility to local optima; and (3) a predominant focus on continuous optimization, making it less effective for discrete problems.

While existing task assignment models have produced significant outcomes, they still present several limitations [19]: (1) These models primarily consider straight-line distance, providing only the target strike sequence without accounting for specific flight path planning, thereby neglecting the real trajectory factor and failing to achieve optimal performance gains. (2) No single algorithm can comprehensively solve all optimization problems, which underscores the need for the continual development of new algorithms or the refinement of existing ones to more effectively address specific optimization challenges.

To address the aforementioned challenges, this paper presents a novel multi-UAV autonomous collaborative task allocation method that incorporates actual flight trajectories and integrates an enhanced version of the Great Wall Construction Algorithm (GWCA). The key contributions of this paper are as follows: (1) it introduces the concept of actual flight distance, enables tight coupling between task assignment and trajectory planning, and proposes a multi-UAV task assignment model that explicitly considers the flight trajectory; (2) to overcome the limitations of the GWCA, this work introduces an initialization strategy based on a set of good points, an estimation strategy utilizing Gaussian distribution, and a Cauchy reorganization variant strategy, ultimately proposing a GWCA that balances both exploitation and exploration capabilities; (3) the feasibility and efficiency of the proposed algorithm are validated through simulations conducted at various scales. The results demonstrate that the proposed algorithm effectively addresses the task allocation problem while considering actual flight trajectories and exhibits superior convergence speed and performance gain compared to existing algorithms.

Initially, the primary challenges encountered by UAVs in contemporary battlefield environments are outlined. As UAVs are increasingly deployed across multifunctional combat platforms, the battlefield environment and mission demands are becoming progressively more complex. Consequently, the operational capability of individual UAVs is constrained by factors such as payload limitations, computational resources, and energy consumption. Thus, multi-UAV cooperative operations have emerged as a crucial strategy to enhance combat effectiveness. The core challenge of the multi-UAV cooperative tasking problem is presented, regarding how to execute efficient tasking in complex battlefield environments, fully accounting for mission types, flight trajectories, three-dimensional terrain, and dynamic threat factors. This issue is fundamentally a multi-constrained combinatorial optimization problem, which is recognized as a classic NP-hard problem. In response to these challenges, we propose a multi-UAV autonomous cooperative task allocation method based on an enhanced GWCA. In the introduction, it is demonstrated how the method addresses several key problems in prior research: First, a multi-UAV task assignment model that comprehensively considers actual flight paths is proposed, overcoming the limitations of existing methods that only account for straight-line distances and fail to plan flight paths efficiently. Second, strategies such as optimal point set initialization, Gaussian distribution estimation, and Cauchy recombination variants are designed to address the limitations of the GWCA in multi-UAV task allocation, enhancing the development and exploration capabilities of the algorithm and resolving the issue of the algorithm’s tendency to converge to local optima.

This paper is organized to address the key challenges of multi-UAV collaborative task allocation, focusing on the innovative aspects and practical applications of the proposed algorithm. The introduction begins by providing an overview of the research background, highlighting the increasing demands and constraints of UAV systems operating in complex environments. These challenges, particularly those related to multi-constraint optimization, underscore the necessity of developing efficient and scalable solutions. To tackle these challenges, the paper introduces a novel task allocation model that integrates actual flight trajectories with mission requirements. This model accounts for various constraints, such as target assignment, communication range, and operational limits, ensuring seamless coupling between mission planning and trajectory optimization. By addressing these constraints, the model aims to enhance the overall efficiency of multi-UAV operations. This paper then builds upon the limitations of the original Great Wall Construction Algorithm (GWCA) and proposes an enhanced version. Key improvements, including optimal point set initialization, Gaussian distribution estimation, and Cauchy mutation strategies, are introduced to increase solution diversity and reduce the likelihood of the algorithm converging to local optima. A detailed description of the workflow of the improved algorithm is provided, demonstrating how it strikes a balance between exploration and exploitation. To validate the effectiveness of the proposed algorithm, extensive simulations are conducted across a range of mission scenarios. These simulations compare the performance of the improved algorithm against traditional task allocation methods, showing substantial improvements in task allocation efficiency, convergence speed, and overall performance. In conclusion, this paper summarizes its contributions and outlines future research directions. These include the integration of communication constraints and the exploration of distributed collaboration approaches to further enhance the scalability and real-world applicability of multi-UAV systems.

Section 1 examines the multifunctional roles of UAVs in military operations, with a particular focus on their coordination and tasking. The limitations of the current combat capabilities of individual UAVs necessitate the adoption of multi-UAV cooperative operations. Section 2 presents the benefit function and associated constraints for UAV mission execution and develops a mathematical framework for mission allocation through modeling. Task allocation must account for factors such as the threat level of the target, flight paths, mission duration, and other relevant parameters. Section 3 introduces an enhancement to the classical Great Wall Construction Algorithm (GWCA), incorporating strategies such as good point set initialization, Gaussian distribution estimation, and Cauchy variation to improve algorithm performance and search diversity. The fundamental concept behind the GWCA is inspired by the ancient labor division model used in the construction of the Great Wall and is iteratively updated through a dynamic optimization strategy. An enhanced version of the GWCA, named the GGC-GWCA, is proposed to address the multi-UAV collaborative task allocation problem. The task allocation scheme is further optimized through detailed strategic design, including population initialization and laborer position updates. Optimization is performed based on actual flight paths and task constraints, with the fitness function designed and solved using the GGC-GWCA to identify the optimal multi-UAV task allocation scheme. Section 4 compares various algorithms (e.g., ISA, MVO, HHO, etc.) through the simulation environment to verify the superiority of the GGC-GWCA in solving the task allocation problem.

2. Multi-UAV Autonomous Cooperative Tasking Model

We assume that a known airspace is the location of an attack mission by multiple unmanned aerial vehicles (UAVs) that are required to strike targets within the mission area. The set of UAVs is $\mathrm{U}=\{{\mathrm{U}}_1,{\mathrm{U}}_2,\dots ,{\mathrm{U}}_{\mathrm{NU}}\}$ is the number of drones, the set of mission targets is $\mathrm{T}=\{{\mathrm{T}}_1,{\mathrm{T}}_2,\dots ,{\mathrm{T}}_{\mathrm{NT}}\}$, and $NT$ is the number of targets. Because UAVs are designed to quickly destroy high-danger targets, the two most important criteria to take into account while analyzing job allocation are the target’s threat level and the assault range. Consequently, the subsequent work allocation model is created.

2.1. Benefit Function

Benefit $J_i$ derived from the $\mathrm{i}$-th rone’s attack on the $j$-th target is influenced by threat value $T_j$ associated with the target and the corresponding trajectory cost incurred during the mission. The overall benefit function governing the attacking drones’ strike capabilities can be expressed as follows:

$$\mathrm{R}={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{U}}}\left(\begin{array}{c}\mathsf{\eta }\left({\mathrm{I}}_{\mathrm{i}}\left(1\right)\right)/{\overline{\mathrm{D}}}_{\mathrm{UT}}\left(\mathrm{i},{\mathrm{I}}_{\mathrm{i}}\left(1\right)\right)+\\ {\sum }_{\mathrm{k}=2}^{\left|{\mathrm{I}}_{\mathrm{i}}\right|}\mathsf{\eta }\left({\mathrm{I}}_{\mathrm{i}}\left(\mathrm{k}\right)\right)/{\overline{\mathrm{D}}}_{\mathrm{TT}}\left({\mathrm{I}}_{\mathrm{i}}\left(\mathrm{k}-1\right),{\mathrm{I}}_{\mathrm{i}}\left(\mathrm{k}\right)\right)\end{array}\right)$$

(1)

let $I_i$ represent the sequence of attack targets assigned to the $i$-th UAV, while $\mathsf{\eta }\left({\mathrm{I}}_{\mathrm{i}}\left(k\right)\right)$ signifies the threat value of the $I_i\left(k\right)$-th target. Additionally, $D_{UT}\left(\mathrm{i},{\mathrm{I}}_{\mathrm{i}}\left(1\right)\right)$ indicates the actual flight distance from the current UAV to the first attack target, and $D_{TT}\left(I_i(k-1),I_i\left(k\right)\right)$ denotes the flight distance from the $k-1$-th target to the $k$-th target. Lastly, $\overline{D}$ represents the normalized distance. This equation illustrates that assigning varying timings to attack targets results in distinct required attack distances, which ultimately influences the overall attack effectiveness.

This work utilizes a UAV three-dimensional trajectory planning model to thoroughly account for three-dimensional terrain information and related danger considerations as input for flying lengths. To reduce duplicate computations during optimization, a distance matrix is created to represent the flight distances between the UAVs and targets, as well as among the attack targets themselves.

$$\mathrm{Distance}=\left[\begin{array}{ccc}{\mathrm{D}}_{\mathrm{UT}}\left(1,1\right)& \cdots & {\mathrm{D}}_{\mathrm{UT}}\left(1,\mathrm{NT}\right)\\ ⋮& \ddots & ⋮\\ {\mathrm{D}}_{\mathrm{UT}}\left(\mathrm{NU},1\right)& \cdots & {\mathrm{D}}_{\mathrm{UT}}\left(\mathrm{NU},\mathrm{NT}\right)\\ {\mathrm{D}}_{\mathrm{TT}}\left(1,1\right)& \cdots & {\mathrm{D}}_{\mathrm{TT}}\left(1,\mathrm{NT}\right)\\ ⋮& \ddots & ⋮\\ {\mathrm{D}}_{\mathrm{TT}}\left(\mathrm{NT},1\right)& \cdots & {\mathrm{D}}_{\mathrm{TT}}\left(\mathrm{NT},\mathrm{NT}\right)\end{array}\right]$$

(2)

$$\overline{\mathrm{D}}=\mathrm{Distance}/{\mathrm{Distance}}_{\max }$$

(3)

where $D_{UT}\left(NU,NT\right)$ denotes the actual flight distance between the current UAV $NU$ and the attack target $NT$, $D_{TT}\left(NT,NT\right)$ denotes the actual flight distance between the UAV flight and the target, and $Dstanc{e}_{max}$ denotes the maximum flight distance.

2.2. Constraints

• Target Allocation Constraint:
  The target assignment must ensure that each target is matched with a corresponding laser-equipped UAV for engagement. Furthermore, the maximum offensive capacity of each UAV must comply with the restrictions established by the weapon load limitation. The formal constraint can be expressed as

  $$\begin{gathered} {\mathrm{g}}_{\mathrm{A}}=\max \left(\begin{array}{c}‖\mathrm{s}\mathrm{i}\mathrm{gn}\left({\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{U}}}{\mathrm{x}}_{\mathrm{ij}}-1\right)‖,\\ \max \left(\left|{\mathrm{I}}_{\mathrm{i}}\right|-\left|{\mathrm{I}}_{\max }\right|\right)\end{array}\right) \\ \forall \mathrm{i}\in \left\{1,2,\dots ,{\mathrm{N}}_{\mathrm{U}}\right\}, \mathrm{j}\in \left\{1,2,\dots ,{\mathrm{N}}_{\mathrm{T}}\right\} \end{gathered}$$

  (4)

  where $x_{ij}$ denotes the assignment outcome of the $j$-th target to the $i$-th UAV, with a value of 1 indicating an assignment and a value of 0 indicating no assignment, $\left|{\mathrm{I}}_{\max }\right|$ is the maximum value of the number of targets that the UAV performs strikes against, $N_U$ denotes the number of UAVs, $N_T$ denotes the number of targets, and $‖\cdot ‖$ denotes the number of fetching paradigms. The equation mandates that each target can be given to only one UAV, guaranteeing the allocation of all targets. Moreover, given the constraints of onboard armaments, the target allocation for each UAV must not go beyond its maximum operating capacity.

2.

Constraint on Communication Range.

To guarantee the capture of accurate target position and orientation data, the laser UAV must conduct the mission within the communication range established by the ground control system. Thus, the limitation on the communication range is delineated as follows:

$${\mathrm{g}}_{\mathrm{C}}=\max ({\mathrm{D}}_{\mathrm{i}}^{\mathrm{UC}}-{\mathrm{D}}_{\mathrm{Cmax}})<0, \mathrm{i}\in \{1,2,\dots ,{\mathrm{N}}_{\mathrm{U}}\}$$

(5)

here, ${\mathrm{D}}_{\mathrm{i}}^{\mathrm{UC}}$ represents the distance between the $i$-th UAV and the ground-based charging system, while ${\mathrm{D}}_{\mathrm{Cmax}}$ signifies the maximum communication range of the ground control system.

3.

Operational Range Limitation for Individual UAVs.

Total operational range ${\mathrm{D}}_{\mathrm{i}}$ of the i-th UAV, when carrying out all its designated strike missions, is defined as follows:

$${\mathrm{D}}_{\mathrm{i}}={\mathrm{D}}_{\mathrm{UT}}\left(\mathrm{i},{\mathrm{I}}_{\mathrm{i}}\left(1\right)\right)+{\sum }_{\mathrm{k}=2}^{\left|{\mathrm{I}}_{\mathrm{i}}\right|}{\mathrm{D}}_{\mathrm{T}\mathrm{T}}\left({\mathrm{I}}_{\mathrm{i}}(\mathrm{k}-1),{\mathrm{I}}_{\mathrm{i}}\left(\mathrm{k}\right)\right)$$

(6)

where $I_i$ is the strike target sequence of the $i$-th UAV, $\left|{\mathrm{I}}_{\mathrm{i}}\right|$ is the total number of attack targets assigned to the i-th UAV, ${\mathrm{D}}_{\mathrm{UT}}\left(i,I_i\left(1\right)\right)$ is the range of the i-th UAV from the first target, and ${\mathrm{D}}_{\mathrm{TT}}\left(I_i\left(k\right),I_i\left(k+1\right)\right)$ is the distance between the $k$-th target position and the $k+1$-th target position of sequence $I_i$.

The total range constraint mandates that the cumulative range required for each UAV to execute an attack adheres to the specified design parameters, i.e.,

$$g_{\mathrm{D}}=max\left(D_i-D_{max}\right)<0,\forall i\in \{\mathrm{1,2},\dots ,N_{\mathrm{U}}\}$$

(7)

where $D_{max}$ denotes the maximum operational range of the UAV.

4.

Objective Function

The penalty function approach is used to transform the multi-constrained optimization problem into an unconstrained one, taking into consideration the aforementioned revenue function and constraints. This results in the formulation of the objective function as follows:

$$J=R-\lambda \cdot \left(g_{\mathrm{A}}+g_{\mathrm{C}}+g_{\mathrm{D}}\right)$$

(8)

here, $\lambda$ represents the penalization factor, assigned a value of 105. A higher value of $J$ signifies an improved outcome in task assignment, reflecting better overall gains.

2.3. Summary

To address the challenge of coordinating multiple UAVs in executing target strike missions within a known airspace, the proposed model prioritizes high-threat targets through an optimized task allocation strategy. Critical factors influencing task allocation are the threat levels of targets and the operational flight costs incurred by UAVs. Accordingly, the model establishes a benefit function, incorporates constraints, and defines a clear objective function. The model integrates a gain function with multiple task allocation constraints and introduces an efficient UAV task allocation methodology that holistically accounts for 3D trajectory optimization and communication demands. This approach is well suited for multi-target strike missions, effectively balancing mission gains with resource constraints and offers robust theoretical support for future optimizations and practical applications.

3. Improving the Great Wall Construction Algorithm

The improved GGC-GWCA improves population diversity, mitigates the risk of local optima, and enhances the overall algorithmic performance by incorporating a refined point set initialization strategy, Gaussian distribution estimation, and a Cauchy recombination mutation approach, building upon the traditional GWCA framework. The GWCA emulates the competitive and eliminatory processes observed in the construction of the ancient Great Wall, classifying workers into three categories, engineers, soldiers, and laborers, each employing distinct work strategies. Each worker category adopts a unique operational strategy. Engineers focus on optimizing work efficiency, soldiers engage in exploration, while laborers are tasked with carrying duties. The traditional GWCA employs a random position updating and optimization strategy; however, its reliance on globally optimal individuals often results in a decline in population diversity, which leads to the algorithm converging prematurely to a local optimum. To address this issue, the improved strategy enhances the uniformity of the search space distribution through an optimized point set initialization, thereby accelerating convergence. It further refines laborer positions via Gaussian distribution estimation to strike a balance between global search and local exploitation while introducing Cauchy variation to augment population diversity and improve convergence accuracy. The enhanced algorithm significantly improves overall performance by employing a more effective worker position updating strategy and a refined population replacement mechanism.

3.1. Basic Great Wall Construction Algorithm

The Great Wall Construction Algorithm (GWCA) [19] represents a robust, efficient, and competitive approach for addressing both constrained and unconstrained optimization problems. The GWCA is inspired by the competitive and elimination mechanisms observed among workers during the construction of the ancient Great Wall. A mathematical model simulating the labor movement is introduced to replicate the dynamic behavior of the algorithm. Unlike traditional approaches that rely on multiple models to generate new solutions, the GWCA uniquely assigns a predefined motion model to each worker at every iteration. This novel strategy highlights the GWCA’s dynamic adaptability, simplified structure, rapid convergence performance, and superior solution quality, enabling it to surpass traditional optimization methods in overall efficiency.

In the GWCA, experienced workers derive optimal benefits during the construction phase, and the hirer selects the most proficient individuals as project managers. As illustrated in Figure 1, the GWCA categorizes workers into three distinct roles: engineers, soldiers, and laborers. Engineers utilize tools to enhance efficiency, soldiers oversee the workforce, and laborers perform the physically demanding tasks. The project manager is responsible for eliminating underperforming workers. Based on the principles governing worker activity, the specific optimization strategy employed by the GWCA is as follows:

• Initialization Strategy
  Worker positions are considered as candidate solutions, and the initialization strategy leverages the logistic chaotic mapping approach [20], calculated as follows:

  $$\mathrm{P}{\mathrm{o}}_{\mathrm{i}+1}^{\mathrm{j}}\left(0\right)=\left(\mathrm{U}{\mathrm{B}}_{\mathrm{j}}-\mathrm{L}{\mathrm{B}}_{\mathrm{j}}\right)\mathrm{cx}{\mathrm{l}}_{\mathrm{j}}+\mathrm{L}{\mathrm{B}}_{\mathrm{j}}$$

  $$\mathrm{i}=1,2,\cdots ,\mathrm{n}; \mathrm{j}=1,2,\cdots ,\mathrm{d}$$

  (9)

  $$\mathrm{cx}{\mathrm{l}}_{\mathrm{j}+1}=4*\mathrm{cx}{\mathrm{l}}_{\mathrm{j}}*\left(1-\mathrm{cx}{\mathrm{l}}_{\mathrm{j}}\right)$$

  (10)

  here, $P{o}_{i+1}^j\left(0\right)$ represents the initial position value of the worker, $\mathrm{cxl}$ refers to the logistic chaotic sequence value, and $\mathrm{U}{\mathrm{B}}_{\mathrm{j}}$ and $\mathrm{L}{\mathrm{B}}_{\mathrm{j}}$ define the upper and lower bounds of the jth dimension, respectively.

2.

Engineer Strategy for Exploitation

Employers designate select workers as engineers, who are equipped with tools to enhance efficiency by moving stones. These engineers are compared with the general workers and the most efficient ones, and the specific mathematical model is expressed as follows:

$${\mathrm{E}}_{\mathrm{i}}\left(\mathrm{t}+1\right)={\mathrm{E}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}\left(\mathrm{t}\right)+\mathrm{R}+{\mathrm{E}}_{\mathrm{i}}\left(\mathrm{t}\right){\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right)\ast {\mathrm{R}}_2$$

(11)

$$\mathrm{R}={\left(-1\right)}^{\mathrm{k}}\left({\mathrm{X}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}\left(\mathrm{t}\right)-{\mathrm{E}}_{\mathrm{i}}\left(\mathrm{t}\right)\right){\mathrm{R}}_1$$

(12)

here, k represents a binary selection (0 or 1); $v_i\left(t\right)$ is the velocity update for the $i$-th engineer after t iterations; $E_{best}\left(t\right)$ refers to the most efficient worker; $E_i\left(t+1\right)$ indicates the updated position of the $\mathrm{i}$-th engineer; ${\mathrm{R}}_1$ and ${\mathrm{R}}_2$ are random numbers between 0 and 1 that introduce stochastic weights; and $R$ signifies the engineer’s lifting radius. The engineer’s position update process is illustrated in Figure 2.

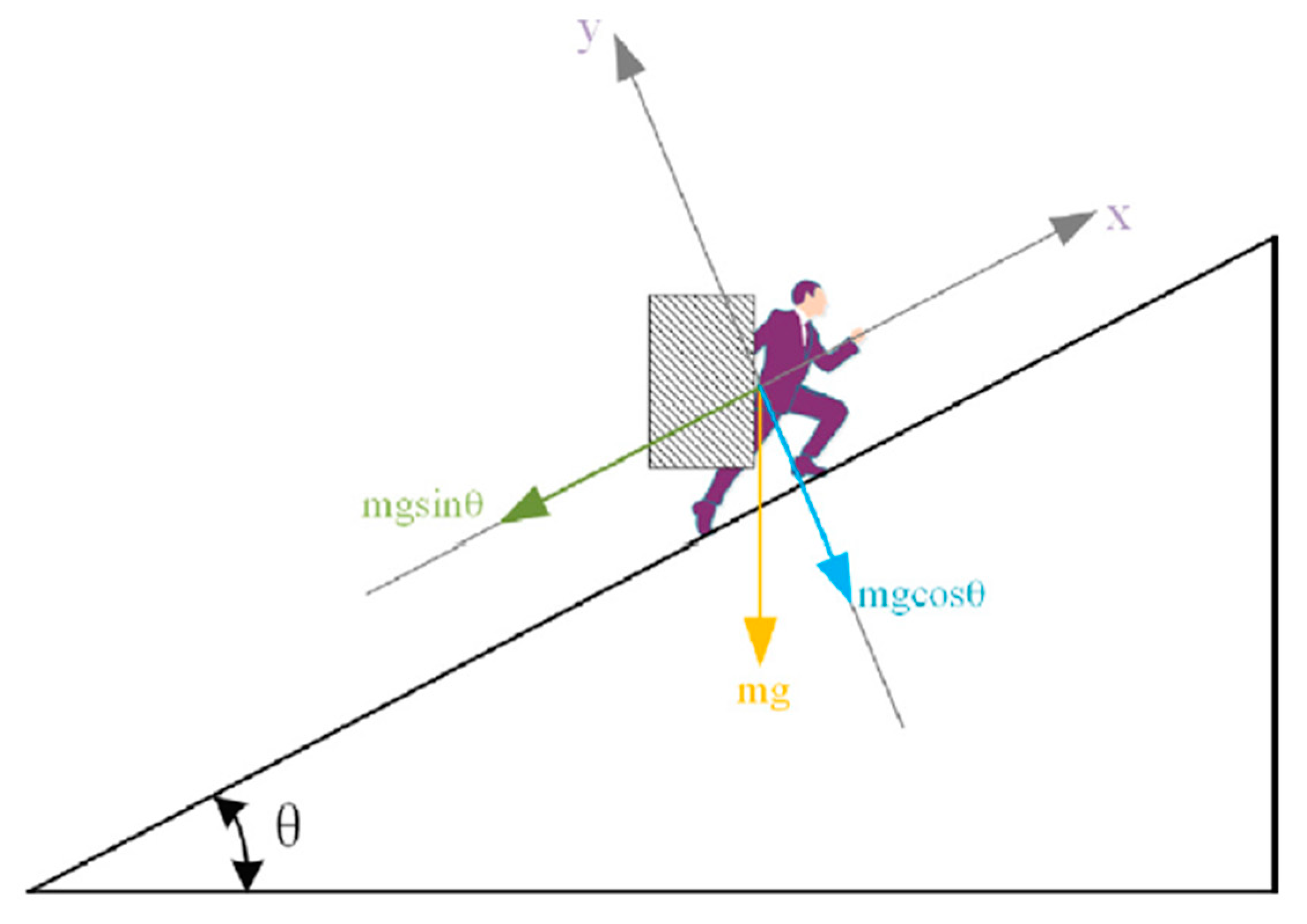
To avoid the GWCA converging to a local optimum, and in accordance with the principle illustrated in Figure 3, the speed update of the $\mathrm{i}$-th engineer for iteration t is computed as follows:

$${\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right)=\left({\displaystyle \frac{\mathrm{T}\times \mathrm{TL}}{\mathrm{m}}}-\mathrm{g}{\displaystyle \frac{\mathrm{H}\left(\mathrm{t}\right)}{\sin {\mathsf{\theta }}_{\mathrm{i}}}}\right)\mathrm{C}\left(\mathrm{t}\right)\ast \mathrm{gampdf}\left(\mathrm{t}|\mathrm{P},\mathrm{Q}\right)$$

(13)

where $m$ represents the rock mass, $g$ is the gravitational acceleration, and ${\theta }_i$ is the slope angle, varying between 0 and 80 degrees. $T$ corresponds to the tool’s thrust. The function gampdf refers to the gamma-distributed probability density function, with $P$ and $Q$ as its respective parameters. $TL$ defines the linear wear and tear of the engineer’s tool, ranging from 1 to 0. $C\left(t\right)$ refers to the fractal dimension, while $H\left(t\right)$ indicates the worker’s height. The values of $H\left(t\right)$ and $C\left(t\right)$ are computed as follows:

$$\mathrm{H}\left(\mathrm{t}\right)=1-{\displaystyle \frac{\mathrm{t}}{\mathrm{MaxIter}}}$$

(14)

$$\mathrm{C}\left(\mathrm{t}\right)=\log \left.\left((\mathrm{C}\max -\mathrm{Cmin}){\displaystyle \frac{\mathrm{MaxIter}-\mathrm{t}}{\mathrm{MaxIter}}}\min \right.\right)$$

(15)

where $t$ represents the current iteration number, $MaxIter$ defines the upper limit of iterations, and $Cmax$ and $Cmin$ represent the maximum and minimum values of C, respectively, both typically set as constant values.

$$\mathrm{gampdf}\left(\mathrm{t}|\mathrm{P},\mathrm{Q}\right)={\displaystyle \frac{{\mathrm{Q}}^{-\mathrm{P}}\ast {\mathrm{t}}^{\mathrm{P}-1}\times \exp \left(\frac{-\mathrm{t}}{\mathrm{Q}}\right)}{\Gamma \left(\mathrm{P}\right)}}$$

(16)

3.

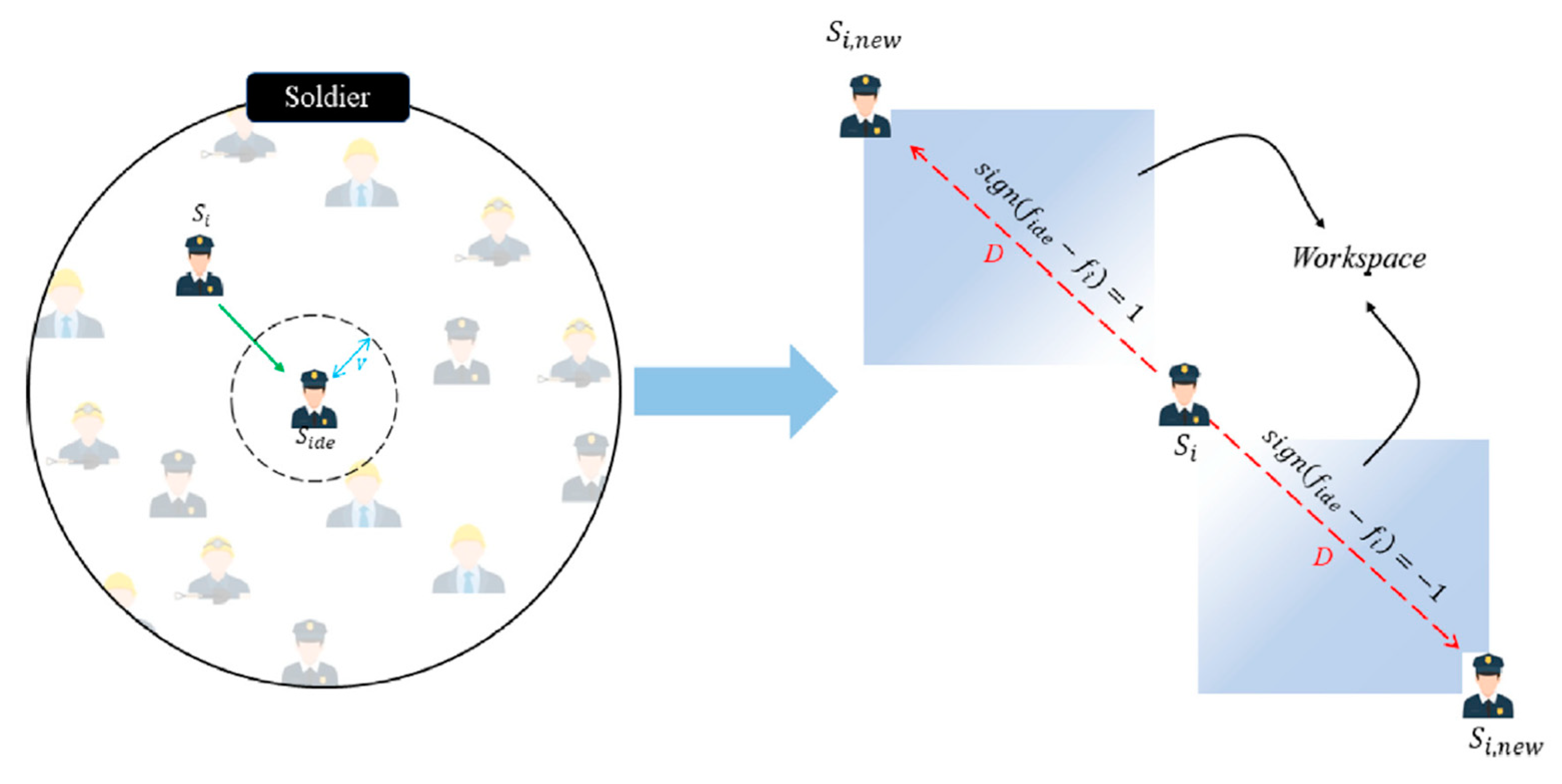
Soldier Strategy for Exploration

The soldier position is updated using the sign function, with a detailed schematic provided in Figure 4. The corresponding update equation is as follows:

$${\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right)=\mathrm{mg}{\displaystyle \frac{\mathrm{H}\left(\mathrm{t}\right)}{\sin {\mathsf{\theta }}_{\mathrm{i}}}}\mathrm{C}\left(\mathrm{t}\right)\ast \mathrm{gampdf}\left(\mathrm{t}/\mathrm{MaxIter}|\mathrm{P},\mathrm{Q}\right)$$

(17)

$${\mathrm{S}}_{\mathrm{i}}\left(\mathrm{t}+1\right)={\mathrm{S}}_{\mathrm{i}}\left(\mathrm{t}\right)+\left({\mathrm{S}}_{\mathrm{hert}}\left(\mathrm{t}\right)-{\mathrm{S}}_{\mathrm{i}}\left(\mathrm{t}\right)\right)\ast {\mathrm{R}}_3+\mathrm{sign}\left(\mathrm{f}\left(\mathrm{ide}\right)-\mathrm{f}\left(\mathrm{i}\right)\right)\ast \left(\mathrm{P}{\mathrm{o}}_{\mathrm{ide}}-{\mathrm{S}}_{\mathrm{i}}\left(\mathrm{t}\right)\right){\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right)\ast {\mathrm{R}}_4$$

(18)

here, $ide$ represents a soldier located near the $i$-th worker, while ${\mathrm{S}}_{\mathrm{best}}\left(\mathrm{t}\right)$ denotes the top-performing soldier. $S_i\left(t\right)$ specifies the position of the $i$-th laborer, and $R_3$ and $R_4$ are uniformly distributed random numbers. If the worker is positioned near the leader, $ign\left(f\left(ide\right)-f\left(i\right)\right)=1$; otherwise, $ign\left(f\left(ide\right)-f\left(i\right)\right)=-1$.

4.

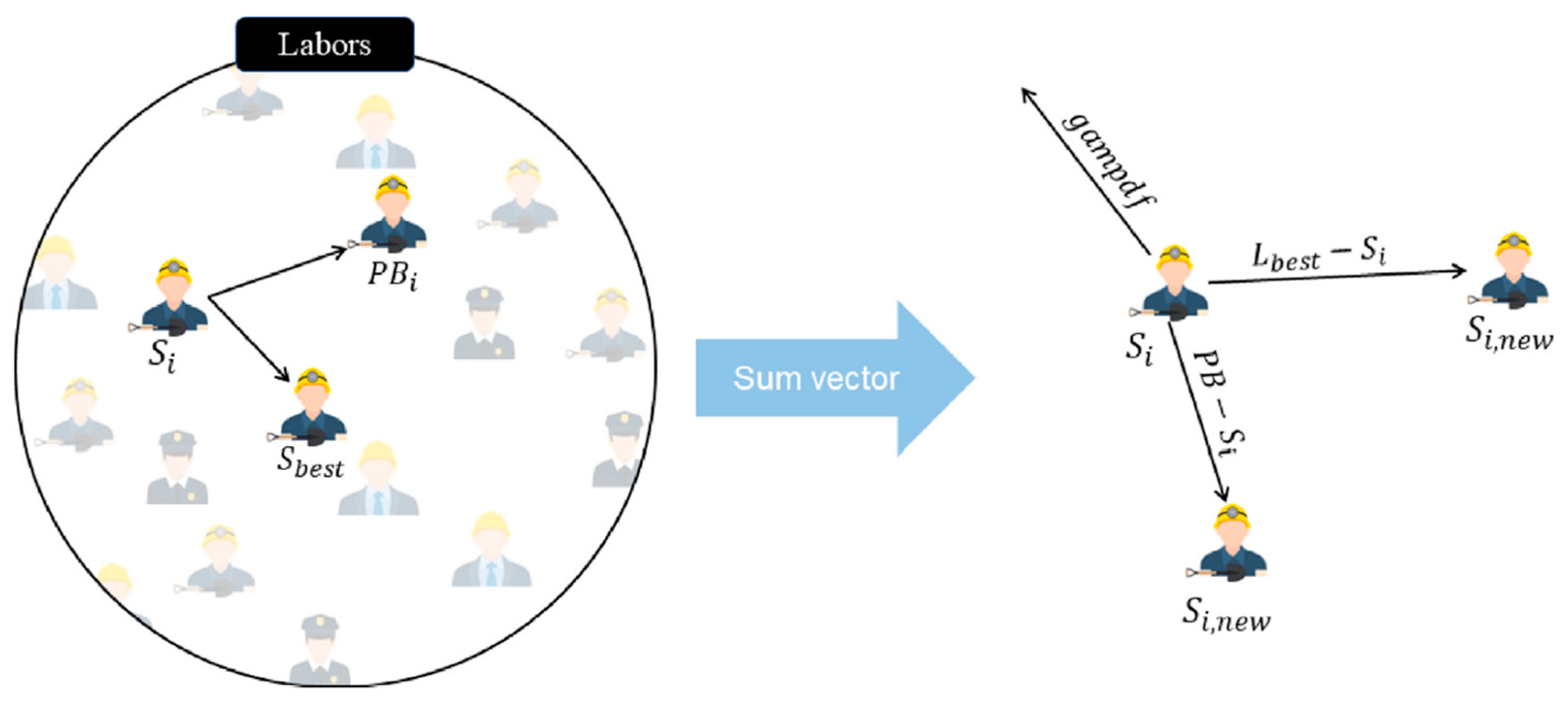
Labor Strategy

Laborers, distinct from engineers and soldiers, possess relatively frail physiques, rendering them incapable of independently handling transportation tasks. As a result, they are required to collaborate in relays to transport the rammed earth. The laborer position update equation (Figure 5) is determined as follows:

$${\mathrm{L}}_{\mathrm{i}}\left(\mathrm{t}+1\right)={\mathrm{L}}_{\mathrm{i}}\left(\mathrm{t}\right)+2\left({\mathrm{L}}_{\mathrm{best}}\left(\mathrm{t}\right)-{\mathrm{S}}_{\mathrm{i}}\left(\mathrm{t}\right)\right)\times {\mathrm{R}}_5+\left(\mathrm{P}{\mathrm{B}}_{\mathrm{i}}\left(\mathrm{t}\right)-{\mathrm{S}}_{\mathrm{i}}\right)\ast \mathrm{gampdf}\left(\mathrm{t}/\mathrm{MaxIter}\mid \mathrm{P},\mathrm{Q}\right)$$

(19)

here, $L_i\left(t+1\right)$ represents the updated position of the $i$-th laborer after iteration t + 1; $P{B}_i\left(t\right)$ signifies the personal best position achieved by the i-th laborer at iteration t; and $L_{best}\left(t\right)$ refers to the highest-performing laborer among all.

5.

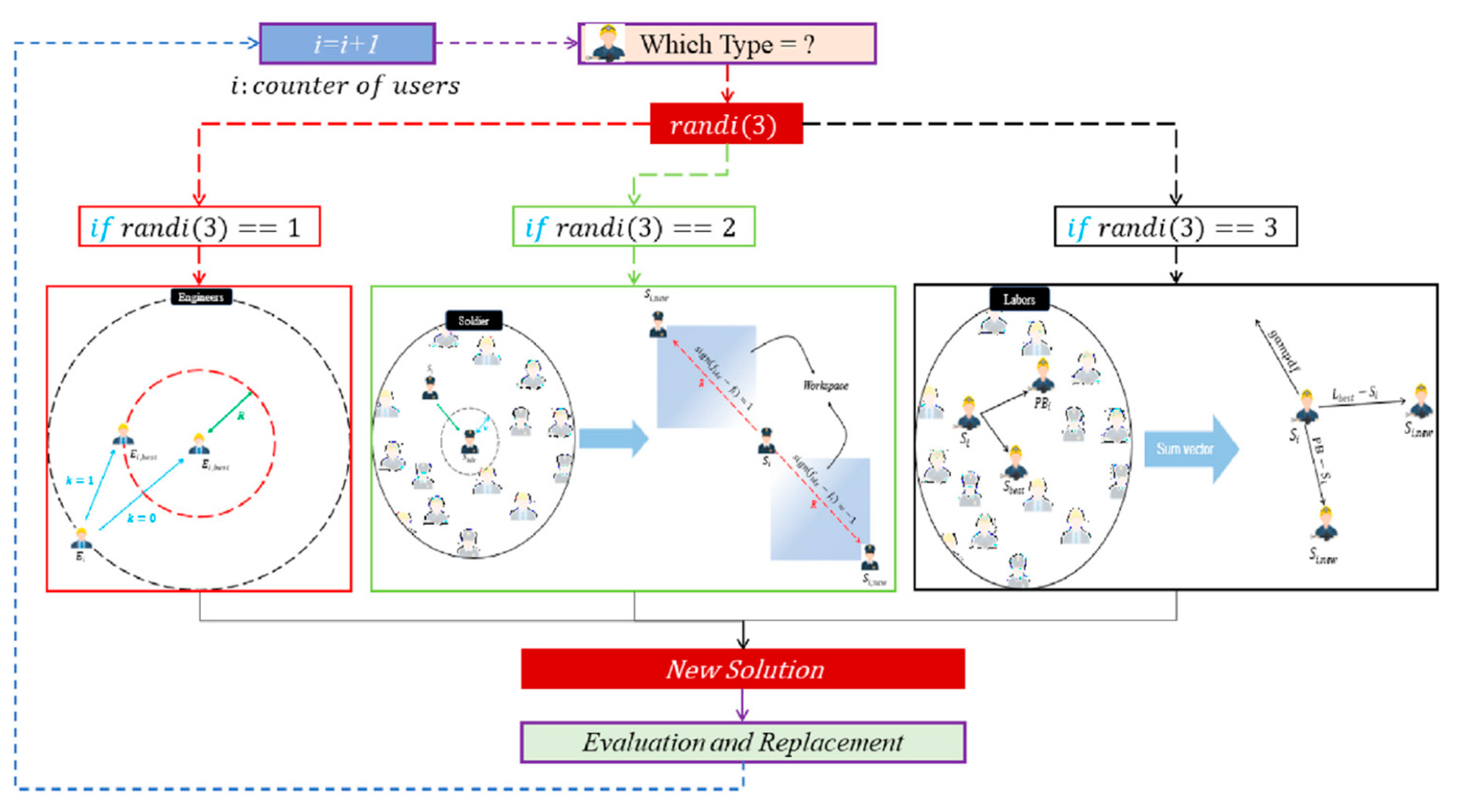
Worker Selection Strategy

In the GWCA, three distinct worker position update models are randomly chosen, and the detailed selection process is illustrated in Figure 6.

6.

Strategy for Replacement and Reorganization

During the construction of the Great Wall, a proportion, denoted as p, of workers is eliminated to ensure adherence to the construction schedule:

$$\mathrm{EL}=\mathrm{ceil}\left(\mathrm{N} \times \mathrm{p}\right)$$

(20)

$$\mathrm{P}{\mathrm{o}}_{\mathrm{i},\mathrm{new}}^{\mathrm{j}}=\left(\mathrm{U}{\mathrm{B}}_{\mathrm{j}}-\mathrm{L}{\mathrm{B}}_{\mathrm{j}}\right){\mathrm{R}}_6+\mathrm{L}{\mathrm{B}}_{\mathrm{j}}$$

$$\mathrm{i}=1,2,\cdots ,\mathrm{El};\mathrm{j}=1,2,\cdots ,\mathrm{d}$$

(21)

$$\mathrm{PN}=\left[\mathrm{PR},\mathrm{PE}\right]$$

(22)

where $ceil$ represents the downward rounding function; ${\mathrm{R}}_6$ is a uniformly distributed random number within the range of 0 to 1; $\mathrm{PR}$ denotes the position of the worker following retention; $PE$ indicates the updated position of the worker; $PN$ signifies the position of the worker in the subsequent round; and $El$ refers to the eliminated worker.

The pseudo-code of the GWCA, reflecting the optimization strategies discussed above, is provided in Algorithm 1.

Algorithm 1: Pseudo-code of the Great Wall Construction Algorithm (GWCA)

Initialize the workers’ positions as Po and generate a corresponding task report f(Po)

Based on the generated task report, allocate workers to corresponding tasks

Identify the optimal worker, denoted as Pobest, from the current pool

While 1 to MaxIter do

For 1 to N do

Update the position of the engineers based on the exploitation strategy

Update the position of the soldiers according to the exploration strategy

Update the laborers’ positions through the cooperation strateg

Generate new positions for all workers by synthesizing the updated strategies

End for

Rank the updated positions of workers and select candidate solutions based on performance

End while

Output the best-performing individual solution as determined by the GWCA algorithm

3.2. Improvement Strategy

Analyzing the GWCA, it can be seen that the GWCA mainly relies on the global optimal individuals or the optimal individuals of engineers, soldiers and laborers to develop and explore and does not fully capitalize on the effective information of the other individuals, which leads to the reduction in population diversity and thus falls into the local optimum. To enhance population diversity and improve algorithmic performance, this paper introduces an enhanced version of the Great Wall Construction Algorithm (GGC-GWCA). This improved version incorporates the good point set initialization strategy, Gaussian distribution estimation strategy, and a Cauchy reorganization variant. The detailed strategy of this approach is outlined as follows:

• Optimal Point Set Initialization Strategy
  The population initialization strategy plays a critical role in influencing the optimization speed of the algorithm. A well-designed initialization strategy ensures a more effective distribution of individuals across the search space, thereby enhancing population diversity and accelerating algorithmic convergence. To enhance the diversity of the population search and ensure an even distribution of individuals across the search space, this paper introduces an optimal point set initialization strategy [21] to refine the initial population method of the GWCA. Suppose $G_s$ represents a unit cube within an s-dimensional Euclidean space, where $r\in G_s$, the following applies:

  $${\mathrm{P}}_{\mathrm{n}}\left(\mathrm{k}\right)=\left[\left({\mathrm{r}}_1^{\left(\mathrm{n}\right)}\cdot \mathrm{k}\right),\left({\mathrm{r}}_2^{\left(\mathrm{n}\right)}\cdot \mathrm{k}\right),\cdots ,\left({\mathrm{r}}_{\mathrm{s}}^{\left(\mathrm{n}\right)}\cdot \mathrm{k}\right)\right],1\le \mathrm{k}\le \mathrm{n}$$

  (23)
  The deviation satisfies the following condition:

  $$\varphi \left(\mathrm{n}\right)=\mathrm{C}\left(\mathrm{r},\mathsf{\epsilon }\right){\mathrm{n}}^{\mathsf{\epsilon }-1}$$

  (24)
  Consequently, $P_n\left(k\right)$ is defined as the set of optimal points, where $r$ represents a specific optimal point. Here, $\left({\mathrm{r}}_1^{\left(\mathrm{n}\right)}\cdot \mathrm{k}\right)$ denotes the fractional part, $\epsilon$ is any positive constant, $C\left(r,\epsilon \right)$ is a constant dependent solely on $r,\epsilon$, and $n$ represents the total number of points. The value of $r$ is defined as follows:

  $$\mathrm{r}=\left\{2\cos \left({\displaystyle \frac{2\mathsf{\pi }\mathrm{k}}{\mathrm{p}}}\right),1\le \mathrm{k}\le \mathrm{s}\right\}$$

  (25)

  here, $p$ represents the smallest prime number that fulfills the condition ${\displaystyle \frac{\left(p-3\right)}{2}}\ge s$. The graphical representation of the initialized population distribution based on the set of optimal points is illustrated in Figure 7.

2.

Labor Update Strategy Utilizing Gaussian Distribution Estimation.

The current labor position updating strategy is based on leveraging both the global optimum of the labor population and the individual best values, combined with the $gampdf$ function. However, this method tends to converge at local optima. To address this issue, a Gaussian distribution estimation method [22] is applied for updating the positional strategy of the labor population, as defined by the following specific equation:

$$L_i\left(t+1\right)=L_i\left(t\right)+\left(L{g}_i\left(t\right)-S_i\right)\times gampdf\left(t/MaxIter|P,Q\right)$$

(26)

The term $mean\left(t\right)$ represents the weighted average position of the dominant population during the t-th iteration. This value is derived through the optimal individual group using the Gaussian distribution estimation method to determine the appropriate positional information, and it is calculated as follows:

$$\mathrm{P}{\mathrm{o}}_{\mathrm{mean}}={\sum }_{\mathrm{i}=1}^{\mathrm{N}/2}{\mathsf{\omega }}_{\mathrm{i}}\ast \mathrm{P}{\mathrm{o}}_{\mathrm{i}}$$

(27)

$${\mathsf{\omega }}_{\mathrm{i}}={\displaystyle \frac{\ln (\mathrm{N}/2+0.5)-\ln (\mathrm{i})}{{\sum }_{\mathrm{i}=1}^{\mathrm{NP}/2}(\ln (\mathrm{N}/2+0.5)-\ln (\mathrm{i}\left)\right)}}$$

(28)

$$\mathrm{Cov}(\mathrm{i})={\displaystyle \frac{1}{\mathrm{N}/2}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}/2}(\mathrm{P}{\mathrm{o}}_{\mathrm{i}}-\mathrm{P}{\mathrm{o}}_{\mathrm{mean}})\ast (\mathrm{P}{\mathrm{o}}_{\mathrm{i}}-\mathrm{P}{\mathrm{o}}_{\mathrm{mean}}{)}^{\mathrm{T}}$$

(29)

$$\mathrm{L}{\mathrm{g}}_{\mathrm{i}}=\mathrm{mean}+\mathrm{y},\mathrm{y}~\mathrm{N}\left(0,\mathrm{Cov}\right)$$

(30)

$$\mathrm{mean}=0.7({\mathrm{w}}_1\cdot \mathrm{P}{\mathrm{o}}_{\mathrm{mean}}+{\mathrm{w}}_2\cdot {\mathrm{E}}_{\mathrm{best}})+0.3\mathrm{P}{\mathrm{o}}_{\mathrm{i}}$$

(31)

$${\mathrm{w}}_1=(1-\mathrm{t}/\mathrm{MaxIter}{)}^{(1-\tan (\mathsf{\pi }\cdot (\mathrm{rand}-0.5)/\mathrm{MaxIter}\left)\right)}$$

(32)

$${\mathrm{w}}_2=1-{\mathrm{w}}_1$$

(33)

In this context, the Gaussian distribution estimation probability model leverages the existing probability distribution of the dominant population to generate a new offspring species, denoted as $L{g}_i\left(t\right)$. The term $P{o}_{mean}$ signifies the weighted value of the dominant population, while ${\omega }_i$ represents the weight coefficients arranged in descending order according to their fitness values. Additionally, $Cov$ denotes the weighted covariance matrix associated with the dominant population. The variables $w_1$ and $w_2$ denote the corresponding effect weights of the weighted mean and the globally ideal person. During the pre-optimization phase, it is crucial to explore a broad range, thereby assigning a larger influence weight to the weighted mean. Conversely, in the post-optimization phase, emphasis shifts towards local exploitation, resulting in a greater influence weight for the optimal individual. In addition to incorporating social information, this model also integrates individual information to prevent the loss of valuable individual data. Consequently, under the influence of the weighted mean, optimal individual, and self, individuals can prioritize the evolutionary trends in the population and their personal data in the early stages. In the later stages, they focus more on the optimal individual and their own information, thereby achieving a balance between exploration and exploitation, which is pivotal for enhancing the performance of intelligent optimization algorithms.

3.

Cauchy Reorganization Mutation Strategy

In the replacement and recombination strategy, the Cauchy mutation strategy is utilized to generate a new worker population, which is then merged with the updated worker population for combination. The Cauchy variation strategy [23] has the potential to enhance the diversity of the worker population while simultaneously improving the convergence accuracy of the GWCA. The specific equation of the Cauchy variation is delineated as follows:

$$\mathrm{P}{\mathrm{o}}_{\mathrm{i}}\left(\mathrm{t}+1\right)=\mathrm{P}{\mathrm{o}}_{\mathrm{i}}\left(\mathrm{t}\right)+\mathrm{P}{\mathrm{o}}_{\mathrm{i}}\left(\mathrm{t}\right)\cdot \mathrm{Caucy}\left(0,1\right)$$

(34)

where $Caucy\left(\mathrm{0,1}\right)$ represents a random number following a Cauchy distribution, as illustrated in Figure 8.

3.3. Algorithm Flow

By integrating the good point set initialization strategy, the Gaussian distribution estimation strategy, and the Cauchy variation strategy, the specific pseudo-code for the improved Great Wall Construction Algorithm (GGC-GWCA) is presented in Algorithm 2, while the overall flow is illustrated in Figure 9, accompanied by the following steps:

Algorithm 2: Enhanced Great Wall Construction Algorithm (GGC-GWCA)

Initialize the worker positions Po using the good point set initialization strategy, and generate the task report f(Po)

Arrange the workers according to the generated task report

Identify the optimal worker Pobest

While 1 to MaxIter do

For 1 to N do

Compute the updated engineer positions

Compute the updated soldier positions

Update laborer positions using the Gaussian distribution estimation strategy

Generate new worker positions

End for

Arrange the candidate solutions of the workers

Combine and refine the population using the Caucy variation strategy

End while

Output the optimal individual for the enhanced GGC-GWCA algorithm

Step 1: Initialize the parameters of the GGC-GWCA, including population positions, maximum iteration count, and other associated parameters.

Step 2: Compute the work task report value and document the optimal worker Pobest.

Step 3: Compute and update population positions based on distinct population strategies, with the labor population updated through the Gaussian distribution estimation strategy.

Step 4: Generate replacement populations and update the merged populations using the Cauchy distribution variation strategy.

Step 5: Compute the work task report value and update the optimal individual.

Step 6: Determine if the number of iterations has reached the predefined maximum. If so, output the optimal worker individuals; otherwise, return to Step 3.

4. The Application of the Enhanced Great Wall Construction Algorithm to the Multi-UAV Autonomous Cooperative Task Allocation Problem

The improved Great Wall Construction Algorithm (GGC-GWCA) is employed to address the multi-UAV autonomous collaborative task allocation problem, optimizing task distribution by mapping the algorithm’s population individuals to task nodes and the task execution sequence. The algorithm employs real-number encoding to map task allocation and UAV execution sequences to individual positions, assesses the fitness of each individual through a fitness function, and solves the optimization problem by considering multiple constraints and objectives. In the specific implementation, the constraints and reward functions are initialized first, followed by the generation of the initial population through the good point set initialization strategy. After evaluating the fitness values, the population is updated using the GGC-GWCA’s optimization strategy, ultimately yielding the optimal task allocation solution. Through this approach, the GGC-GWCA effectively addresses the optimization problem in multi-UAV collaborative task allocation, enhancing task execution efficiency and collaborative operational capabilities.

4.1. Optimizing the Solution

In the GGC-GWCA developed to address the multi-UAV autonomous cooperative task allocation problem, each population individual represents a feasible solution to the problem at hand. Consequently, the optimal solution for the multi-UAV cooperative task allocation problem corresponds to the optimal position determined by the GGC-GWCA [24]. Figure 10 illustrates the intricate relationship between the GGC-GWCA and the multi-UAV autonomous cooperative task allocation problem. As depicted in Figure 10, each population individual’s position corresponds to the traversal of task nodes and the execution sequence in the multi-UAV cooperative task allocation problem. Changes in population individual positions align with alterations in task nodes, execution sequences, or the planning and optimization process. Additionally, the fitness value directly reflects the objective function value.

4.2. Encoding Method

Through the analysis of the solution correspondence between the GGC-GWCA and the multi-UAV autonomous collaborative task allocation problem, this paper establishes that the individual position of the population aligns with the task nodes executed by the UAVs and their task execution sequence. Furthermore, this study employs the real number encoding method [25] to structure the population individuals of the GWCA. By employing the real number vector encoding method, the mapping relationship between the task assignment results and the individual positions is defined as follows:

(1) The problem’s dimension corresponds to the number of targets, and the dimensionality of each individual reflects the number of goals.

(2) The solution’s search space ranges from $\left(1,{\mathrm{N}}_{\mathrm{U}}+1\right)$.

(3) The integer portion of the individual’s position designates the UAV number, while the fractional part indicates the sequence in which the UAV performs its tasks in ascending order.

To provide a clearer illustration of the mapping relationship, an example is considered where four UAVs are deployed to strike nine targets. In this scenario, the problem dimension is set to 9, and the search range for the population individual optimization space is defined as $\left(1,5\right)$. The corresponding mapping relationship is presented in

Table 1. The mapping relationship between the population individuals and their respective encodings.

Properties of the individuals	xi1	xi2	xi3	xi4	xi5	xi6	xi7	xi8	xi9
Position of the individual	2.34	4.26	3.81	1.19	2.15	4.72	1.94	3.68	3.35
Results of the distribution process	UAV identification number			Information about the individual			Sequence of task execution
	U1			1.19	xi4		T4→T7
				1.94	xi7
	U2			2.15	xi5		T5→T1
				2.34	xi1
	U3			3.35	xi9		T9→T8→T3
				3.68	xi8
				3.81	xi3
	U4			4.26	xi2		T2→T6
				4.72	xi6

.

4.3. Design of the Fitness Function

The individual fitness function is employed to calculate the adaptability value, which evaluates the relative strengths and weaknesses of the mission plan by incorporating constraints from the multi-UAV autonomous cooperative task allocation problem, while also considering the global strike benefit function for the attacking UAVs. In this study, the individual fitness function is defined as follows:

$$\mathrm{f}\left(\mathrm{X}\right)=\mathrm{R}={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{U}}}\left(\begin{array}{c}\mathsf{\eta }\left({\mathrm{I}}_{\mathrm{i}}\left(1\right)\right)/{\overline{\mathrm{D}}}_{\mathrm{UT}}\left(\mathrm{i},{\mathrm{I}}_{\mathrm{i}}\left(1\right)\right)+\\ {\sum }_{\mathrm{k}=2}^{\left|{\mathrm{I}}_{\mathrm{i}}\right|}\mathsf{\eta }\left({\mathrm{I}}_{\mathrm{i}}\left(\mathrm{k}\right)\right)/{\overline{\mathrm{D}}}_{\mathrm{TT}}\left({\mathrm{I}}_{\mathrm{i}}(\mathrm{k}-1),{\mathrm{I}}_{\mathrm{i}}\left(\mathrm{k}\right)\right)\end{array}\right)$$

(35)

where, $X$ respectively, denote task execution programs.

4.4. Workflow of the Methodology

The core of the multi-UAV autonomous cooperative task allocation problem lies in solving an optimization problem that involves multiple constraints and objectives. Specifically, this concerns the optimization of task allocation, including task execution nodes and their execution sequence. The procedural flow of the GGC-GWCA, as applied to the optimization of multi-UAV autonomous cooperative task allocation, is depicted in Figure 11. The specific steps are outlined as follows:

Step 1: Define the multi-UAV autonomous cooperative task allocation optimization problem, specifying the objective function (revenue function) and corresponding constraints.

Step 2: Initialize the search population and configure the parameters of the GGC-GWCA. Set up the initial task allocation scheme for encoding the multi-UAV autonomous cooperative task allocation, employing the good point set initialization strategy.

Step 3: Evaluate the individual fitness value, which primarily assesses the quality and performance of each solution relative to the overall population.

Step 4: Perform the GGC-GWCA optimization strategy to update the population. Optimize the task allocation scheme by applying the engineer, soldier, and laborer position updating strategies within the GGC-GWCA.

Step 5: Check if the algorithm’s termination conditions are met. If the number of search iterations exceeds the maximum allowable iterations, stop the search and output the optimal multi-UAV autonomous cooperative task allocation scheme. If not, return to Step 4.

5. Simulation Testing and Results Analysis

The efficacy of the multi-UAV autonomous collaborative task allocation optimization method based on the GGC-GWCA is validated through simulation experiments and compared with four other benchmark algorithms. The simulation environment incorporates various task allocation parameters, including UAV and target information, as well as different distance models. Initially, the efficacy of task assignment across three distance models is examined, with the results indicating that the model accounting for terrain and flight distance outperforms the model considering only straight-line distance. Subsequently, task assignment models including the ISA, MVO, HHO, GWCA, and GGC-GWCA are evaluated, with the results demonstrating that the GGC-GWCA outperforms the other algorithms in terms of gain value and standard deviation.

The mission scale was further expanded from three UAVs striking nine targets to four UAVs targeting sixteen objectives, enabling a comparison of the performance between the GWCA and GGC-GWCA. The results indicate that the GGC-GWCA exhibits greater stability in high-dimensional task allocation and delivers superior task allocation solutions. Analysis using convergence curves and box plots reveals that the GGC-GWCA demonstrates faster convergence and superior solution quality.

Overall, the GGC-GWCA demonstrates strong performance in multi-UAV task allocation, consistently provides efficient task allocation solutions, and maintains superior performance when scaled.

5.1. Environment Configuration

To assess the effectiveness and efficiency of the multi-UAV autonomous cooperative task allocation optimization approach using the GGC-GWCA, four analytical algorithms were selected for comparative analysis in this study. The program was developed using MATLAB 2021a, and simulations were conducted in a test environment running Windows 10, with an AMD Ryzen 9 5900HX processor and Radeon Graphics and 16.0 GB of RAM.

Several studies have examined efficient task allocation and routing in delivery systems. Notably, study [26] investigates truck and high-capacity UAV parcel delivery, while another study by the authors of [27] explores priority-constrained routing for parcel delivery. Additionally, study [28] applies multi-agent deep reinforcement learning to task scheduling and resource sharing in UAV-assisted wireless sensor networks. The parameters for the intelligent optimization algorithm applied to the task allocation problem are presented in

Table 2. Parameter settings for the task allocation optimization algorithm.

Algorithm	Parameter Settings
ISA [29]	α = 0.2
MVO [29]	WEPmax = 1, WEPmin = 0.2
HHO [30]	E0 is set within the range (−1, 1)
GWCA [19]	P = 9, Q = 6, T = 8.3, m = 3, Cmax = exp(3), Cmin = exp(2)
GGC-GWCA	The parameter settings for GGC-GWCA are identical to those of GWCA

. The maximum number of iterations was set to 300, with a population size of 50 for each algorithm.

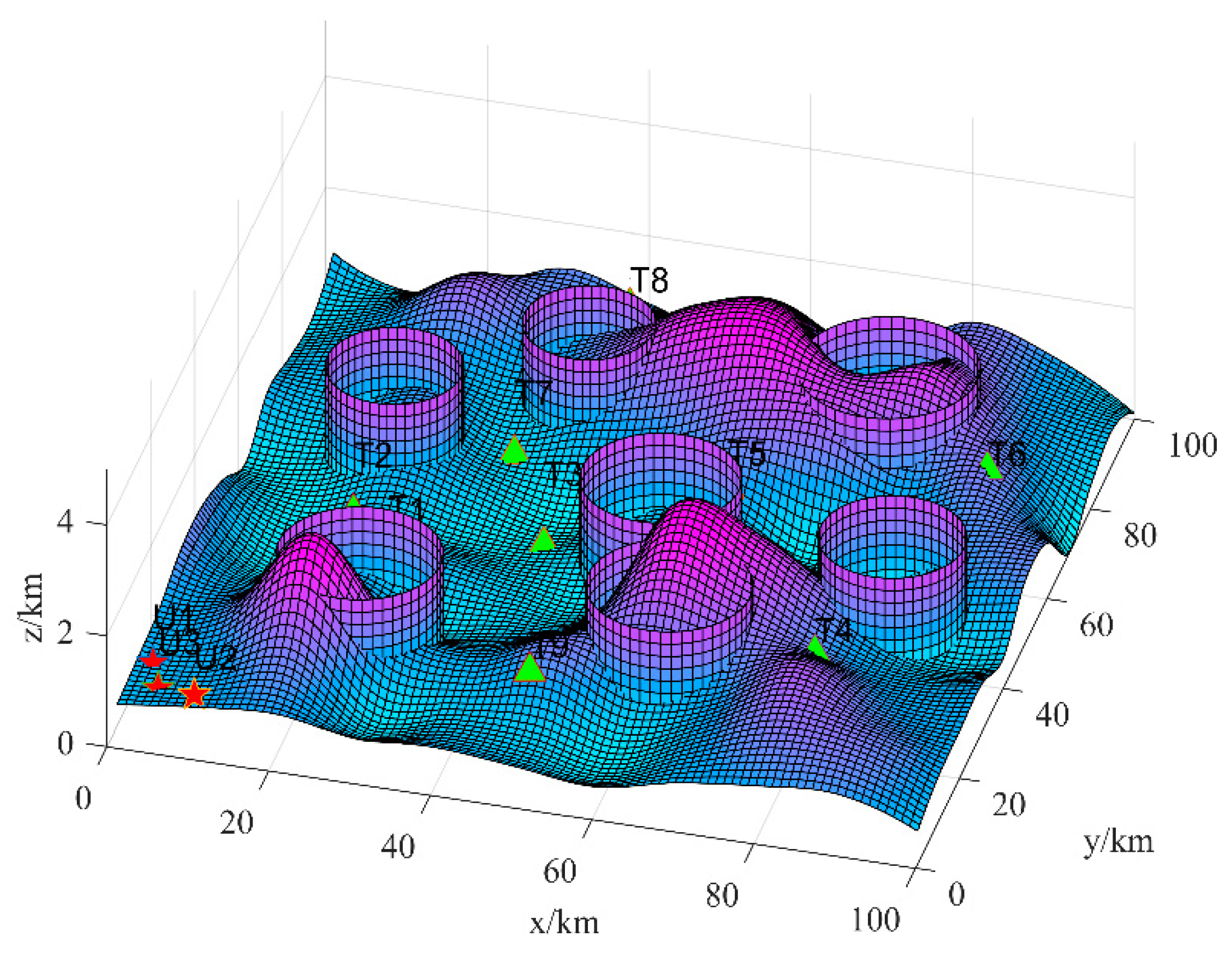
The mission entails three unmanned aerial vehicles (UAVs) engaging nine hostile targets within a 100 km × 100 km space known as the battlefield. The initial conditions for both parties are delineated in

Table 3. UAV and target information parameter settings.

Coordinates	UAV U1	UAV U2	UAV U3
X(km)	3	10	5
Y(km)	10	3	5
Coordinates	Objective T1	Objective T2	Objective T3
X(km)	24	17	40
Y(km)	40	50	52
η	0.54	0.61	0.45
Coordinates	Objective T4	Objective T5	Objective T6
X(km)	80	60	90
Y(km)	28	62	70
η	0.81	0.55	0.42
Coordinates	Objective T7	Objective T8	Objective T9
X(km)	32	39	48
Y(km)	68	95	16
η	0.66	0.49	0.5

, and each UAV is responsible for attacking up to four targets. Figure 12 illustrates the simulation configuration in its entirety. The operation of the GWCA in three-dimensional (3D) space is examined, where the UAV task assignment problem is extended to incorporate the optimization of the x, y, and z coordinates. To coordinate the task assignment of UAVs in 3D space, the GWCA efficiently allocates tasks among UAVs, ensuring that each UAV can perform its assigned task along the optimal flight path within the complex battlefield environment. The system model design is discussed, including the construction of the environment and obstacle models. The environment model incorporates various factors, such as 3D terrain, flight obstacles and meteorological conditions, which are integrated into the task assignment constraints, as well as the UAV’s obstacle avoidance capabilities. Accurate 3D modeling enables the UAV to dynamically adjust to complex environments, avoid collisions, and optimize flight paths.

5.2. Algorithm Feasibility Test

(1) Comparative Simulation of Various Distance Models

To validate the effectiveness and superiority of the proposed distance model, a comparison is conducted among three distinct models: straight-line distance (Method 1), flight distance considering only distance cost (Method 2), and flight distance accounting for both distance and altitude costs (Method 3). The optimal task allocation results for these models are presented in

Table 4. Results of task allocation for various distance models.

Method	UAV Identification Number	Attack Sequence	Gain Value
Method 1	U1	T9→T4→T6→T5	16.95
	U2	T2→T1→T3→T7
	U3	T8
Method 2	U1	T9→T4→T6→T5	16.95
	U2	T2→T4→T3→T7
	U3	T8
Method 3	U1	T2→T1→T9	17.67
	U2	T5→T3→T7→T8
	U3	T4→T6

.

From the analysis of Table 4, it is clear that the optimal allocation strategies for Method 1 and Method 2 are identical, while Method 3 offers a distinct approach due to the consideration of real-world terrain factors. UAVs, in practice, cannot always maintain a straight-line trajectory. This leads to situations where the actual flight distance far exceeds the straight-line distance in certain tasks, rendering the task allocation suboptimal and necessitating a reassessment and replanning. Furthermore, the final column of Table 4 reveals that the task allocation strategies derived from Method 1 and Method 2 do not yield the highest combat gain value. Therefore, it is essential to incorporate the actual flight distance adjusted for terrain as input. Similarly, threat factors must also be accounted for as UAVs must maneuver to avoid threats; this inevitably increases the total flight distance. In conclusion, incorporating the actual flight distance into the UAV task allocation model is crucial for optimizing combat assignment outcomes.

(2) Feasibility Analysis of the Task Allocation Model

The ISA, MVO, HHO, GWCA, and GGC-GWCA are employed in this section.

Table 5. Statistical results of task allocation.

Statistical Parameters	ISA	MVO	HHO	GWCA	GGC-GWCA
Mean Value	18.99363	18.12786	18.88795	18.04822	19.19291
Standard Deviation	0.454364	0.632836	0.626657	0.377567	0.297971
Maximum Value	19.47106	18.92365	19.47106	19.47106	19.47106

and

Table 6. Results of optimal task execution order.

Method	UAV Identification Number	Attack Sequence	Gain Value
ISA, MVO, HHO, GWCA	U1	T9→T4→T6→T5	16.95
	U2	T2→T1→T3→T7
	U3	T8
GGC-GWCA	U1	T2→T1→T9	17.67
	U2	T5→T3→T7→T8
	U3	T4→T6

contain the specific statistical findings. Table 5 demonstrates that the MPA, GEDGWO, and LGMPA achieve the optimal allocation, whereas the WOA fails to produce optimal results. The LGMPA outperforms all of the contrasted algorithms in terms of both mean value and standard deviation, underscoring its exceptional performance.

Table 6 presents the optimal task execution order for each algorithm, with the ISA, MVO, HHO, and GWCA yielding an identical gain value of 16.95, while the GGC-GWCA achieves a higher task assignment gain of 17.67, surpassing the performance of the other algorithms.

The problem size was increased to four UAVs targeting 16 adversary units from the original case of three UAVs striking 9 targets. The details of the expanded UAV and target configurations are presented in

Table 7. Parameter settings for UAV and additional target information.

Coordinates	UAV U1	UAV U2
X(km)	3	15
Y(km)	15	3
Coordinates	UAV U3	UAV U1
X(km)	6	9
Y(km)	12	8
Coordinates	Objective T10	Objective T11	Objective T12
X(km)	28	95	75
Y(km)	80	90	55
η	0.44	0.53	0.33
Coordinates	Objective T13	Objective T14	Objective T15
X(km)	36	68	93
Y(km)	32	7	22
η	0.29	0.39	0.40
Coordinates	Objective T16
X(km)	7
Y(km)	75
η	0.77

. The GWCA and GGC-GWCA, both of which yield higher average gain values, were selected for comparative analysis. Each algorithm is executed ten times, and the corresponding statistical results are provided in

Table 8. Statistical results of task allocation after expanding task size.

Statistical Parameters	GWCA	GGC-GWCA
Mean Value	76.88479	74.24741
Standard Deviation	3.3615	3.5769
Maximum Value	80.72204	80.34582

.

According to Table 8, the GGC-GWCA outperforms the GWCA in terms of mean, standard deviation, and maximal value. This indicates that the GGC-GWCA consistently offers more effective task allocation schemes and displays superior performance in high-dimensional task allocation problems.

Table 9. Results of the optimal task execution order after task size expansion.

Method	UAV Identification Number	Attack Sequence	Gain Value
GWCA	U1	T11→T6→T12→T5→T4→T15(The rose-red curve)	79.56
	U2	T13→T9→T14
	U3	T8(The brown curve)
	U4	T16→T10→T7→T3→T1→T2(The orange curve)
GGC-GWCA	U1	T13→T9→T14(The rose-red curve)	80.59
	U2	T15→T4→T5→T12→T6→T11
	U3	T8
	U4	T1→T2→T3→T7→T10→T16(The orange curve)

presents the detailed assignment scheme corresponding to the optimal gain values for the two algorithms. Figure 13 illustrates the task execution trajectory for each algorithm, considering the optimal gain values across a range of dynamic and static obstacles. The trajectory paths of different drones are given by different colored curves.

Figure 14 shows the convergence curves of the average gain values for the GWCA and GGC-GWCA over 10 runs. The results indicate that the GGC-GWCA converges faster and with greater accuracy, beginning at 390 iterations, where its gain value stabilizes at approximately 77.

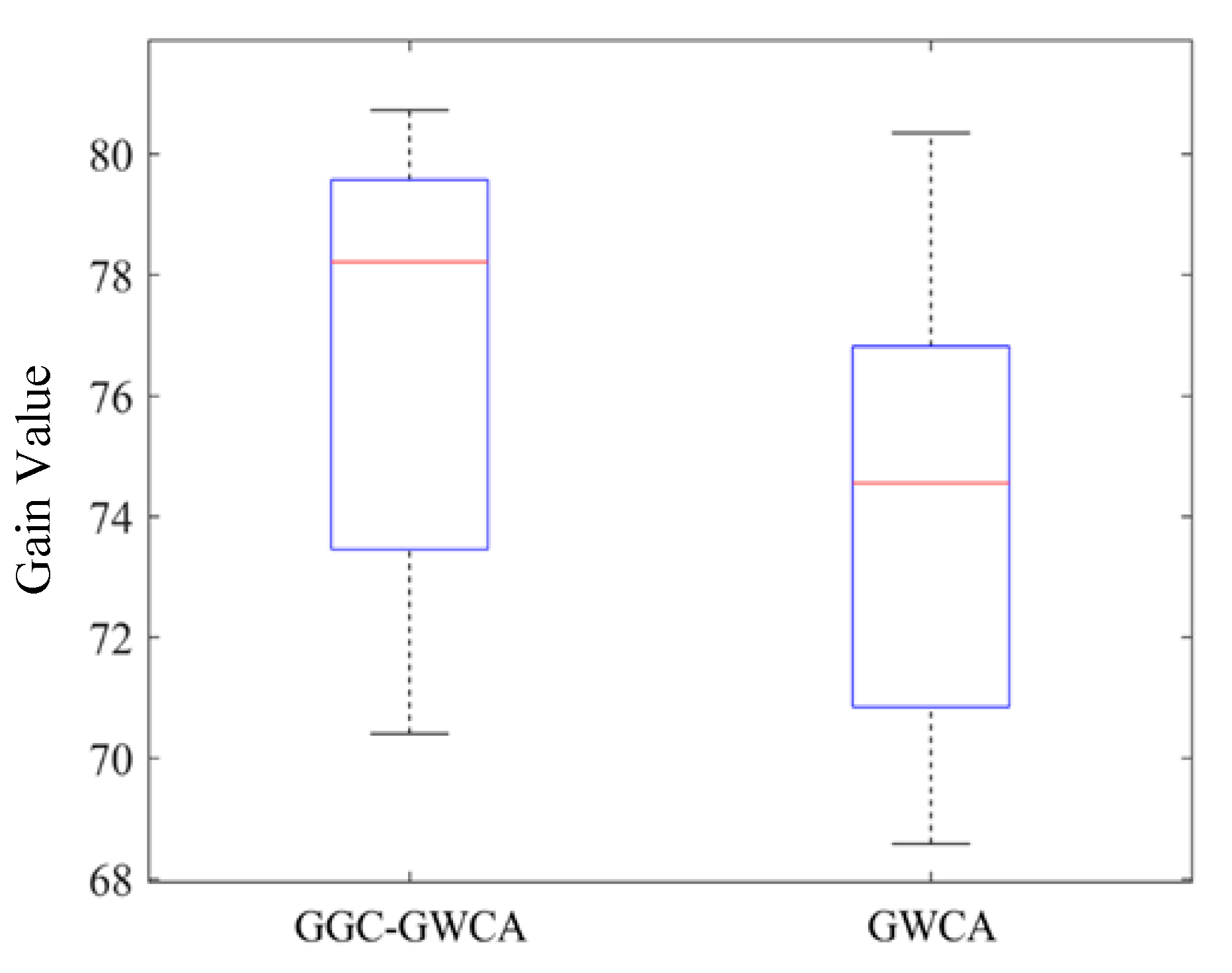
To analyze the distribution properties of the results generated by the two algorithms, a box plot is presented in Figure 15. It shows that the GGC-GWCA yields a denser distribution and produces higher-quality solutions. Figure 15 presents the box plots of the two algorithms, demonstrating that the GGC-GWCA achieves a more concentrated distribution of results, exhibiting superior solution quality and enhanced robustness.

6. Conclusions

To enhance the accuracy of solving the multi-UAV cooperative task allocation problem, this paper introduces an improved multi-UAV autonomous task allocation method, integrating the Great Wall Construction Algorithm (GWCA) and its enhanced version. Task allocation and trajectory planning are tightly coupled, with real route distance being used in place of straight-line distance to increase task allocation yield. The improved GWCA, incorporating good point set initialization, Gaussian distribution estimation, and Cauchy mutation strategies, enhances population diversity, improves exploration and exploitation capabilities, and avoids local optima. This advanced technique proficiently addresses the multi-UAV cooperative job allocation challenge. The simulation findings indicate that substituting straight-line distance with actual flight trajectory is essential for optimizing job allocation, as elaborated in this study. The improved algorithm consistently outperforms the original, providing more stable and effective allocation outcomes.

• A comparison of the simulation results for three distance models—straight-line distance (Method 1), flight distance accounting for distance cost alone (Method 2), and flight distance considering both distance and altitude costs (Method 3)—reveals that adopting the actual flight trajectory distance rather than straight-line distance better aligns with operational requirements, thereby facilitating the generation of superior task assignment plans.
• The enhanced algorithm consistently achieves superior task assignment results compared to the original algorithm.

Additionally, while the model effectively focuses on task assignment and trajectory optimization, it lacks considerations for communication constraints that can affect UAV performance in real-world scenarios, where uninterrupted connectivity is essential. Without accounting for such communication limitations, UAVs may encounter issues with data transmission and control, which are critical for operational reliability. Lastly, although the GWCA shows improved performance in simulation, its robustness has not been extensively validated across varied operational scenarios, making its reliability under different mission scales and unpredictable conditions uncertain.

Future work could explore distributed task allocation methods to alleviate computational loads, allowing each UAV to participate in local decision making and adapt to changes in real time. Additionally, integrating communication constraints into the model would improve the algorithm’s practicality, ensuring that task allocation aligns with actual communication capabilities. Finally, broader testing across diverse environments and mission conditions will help validate the algorithm’s robustness, ensuring it performs consistently across varying scales and complexities. Addressing these areas will enhance the model’s scalability, reliability, and effectiveness in multi-UAV task allocation.