Quadcopter Trajectory Tracking Based on Model Predictive Path Integral Control and Neural Network
Abstract
:1. Introduction
2. Material
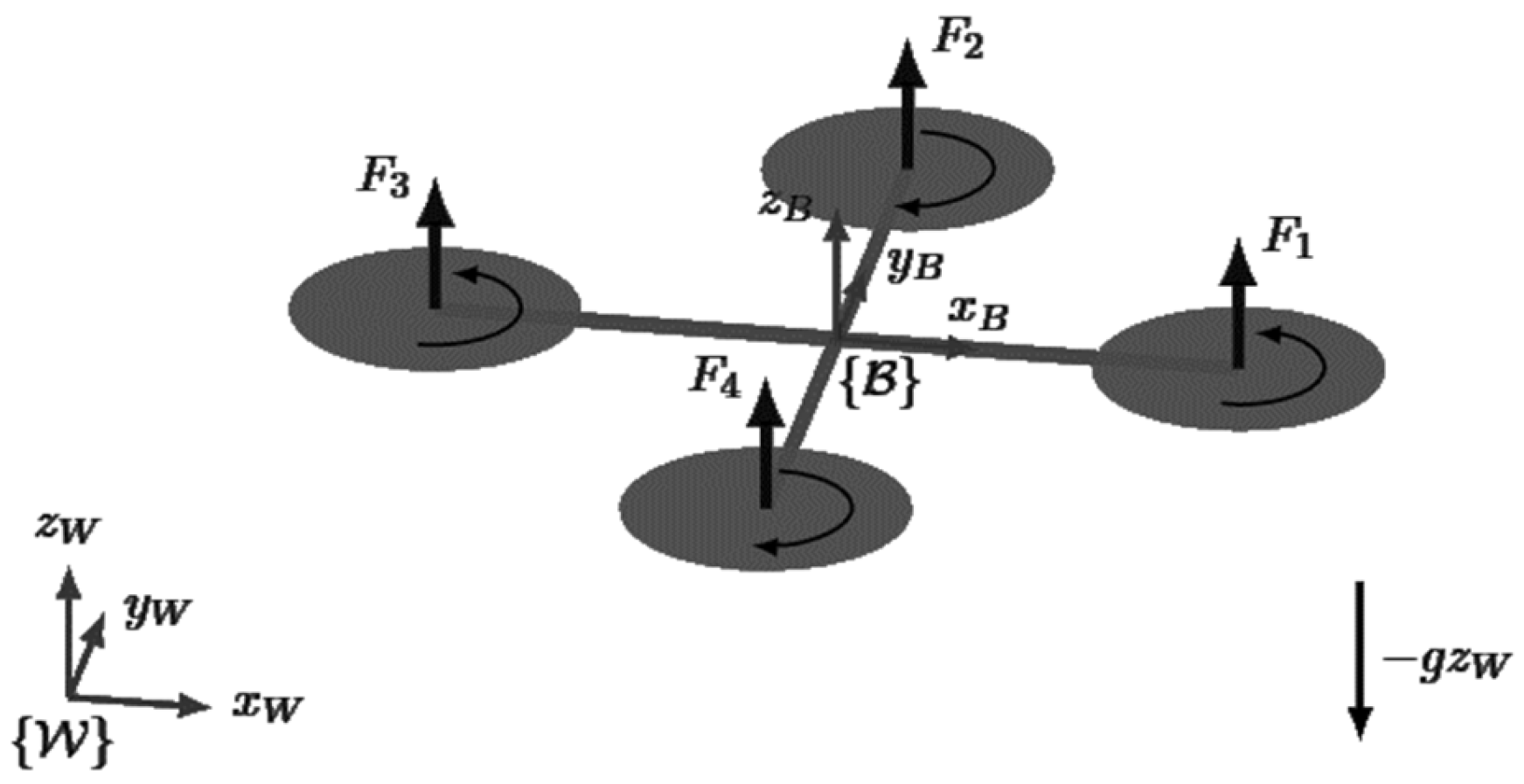
Quadcopter Model
3. Methods
3.1. Neural Network
3.1.1. Data Generation
3.1.2. NN Model and Training
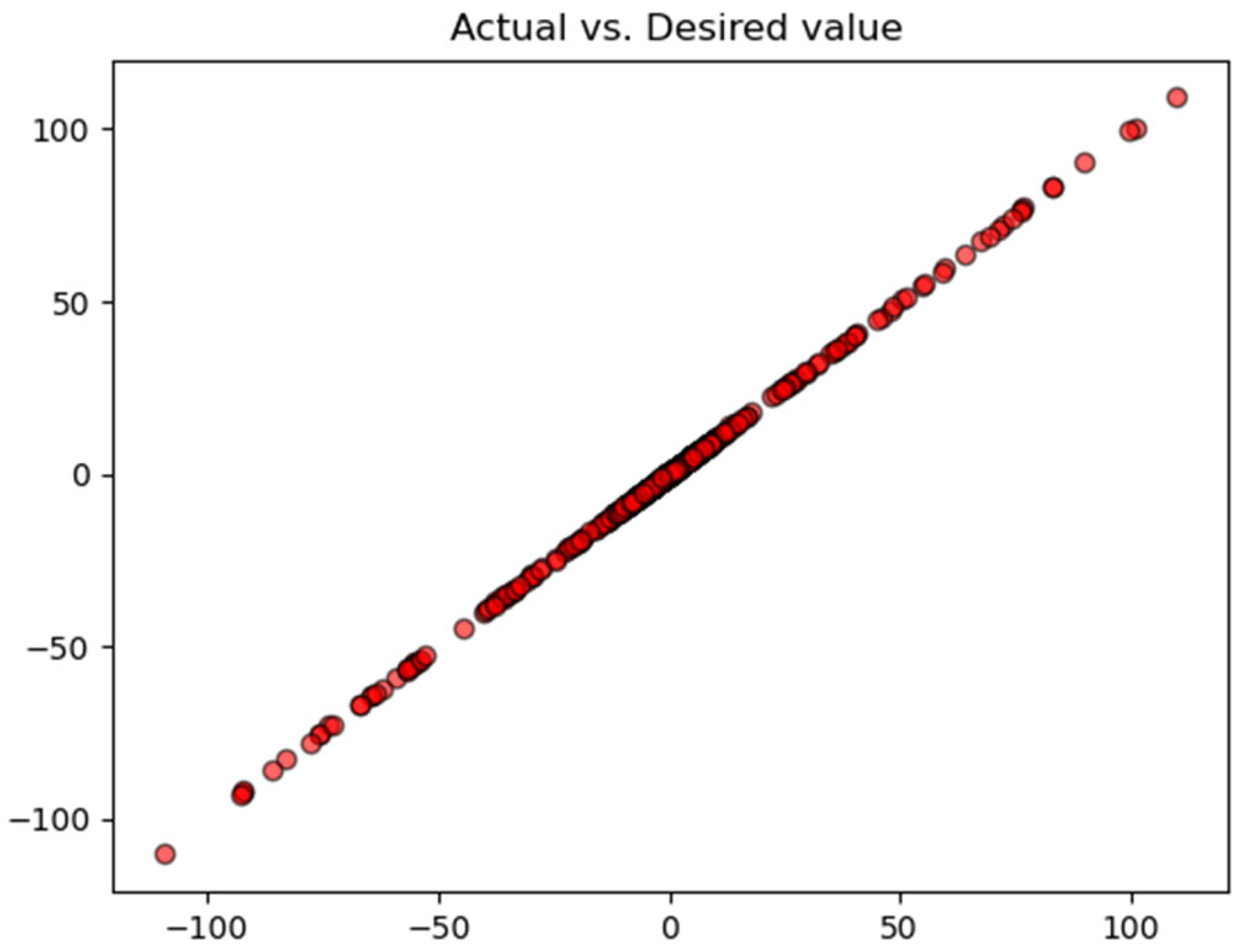
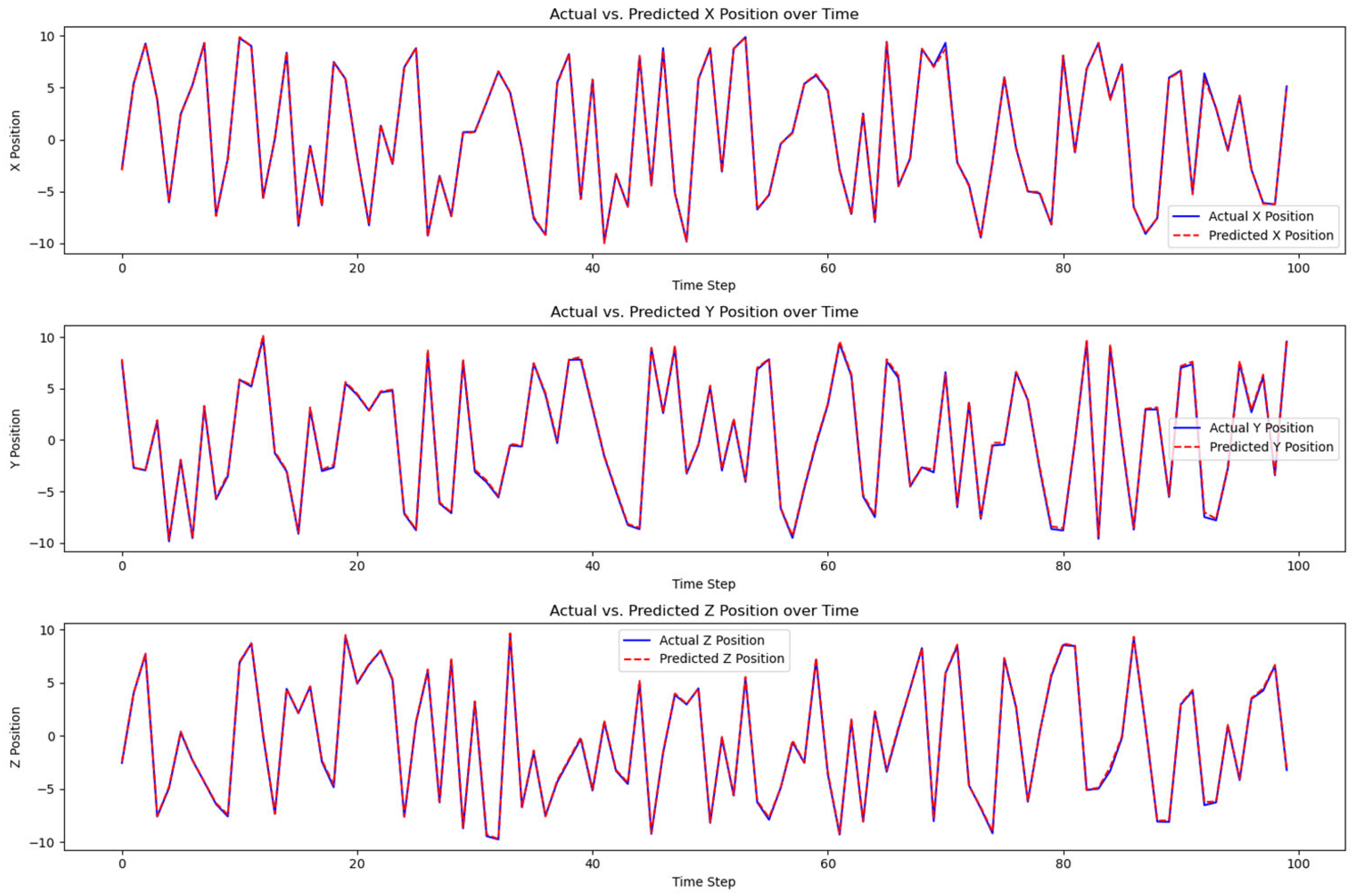
3.1.3. Validation
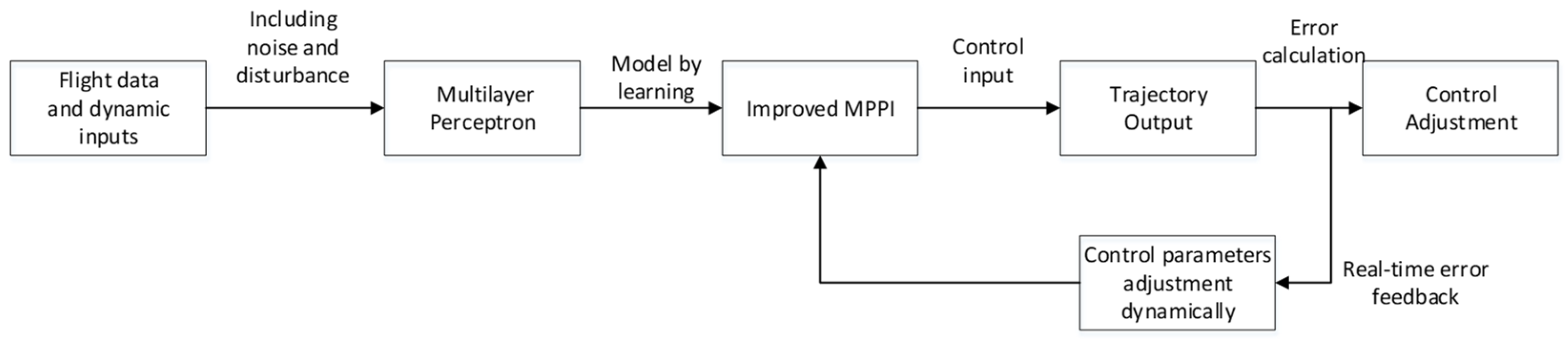
3.2. Improved Model Predictive Path Integral
3.3. Stability Analysis
3.3.1. Neural Network Convergence Analysis
3.3.2. Stability Analysis of the Closed-Loop System
4. Results
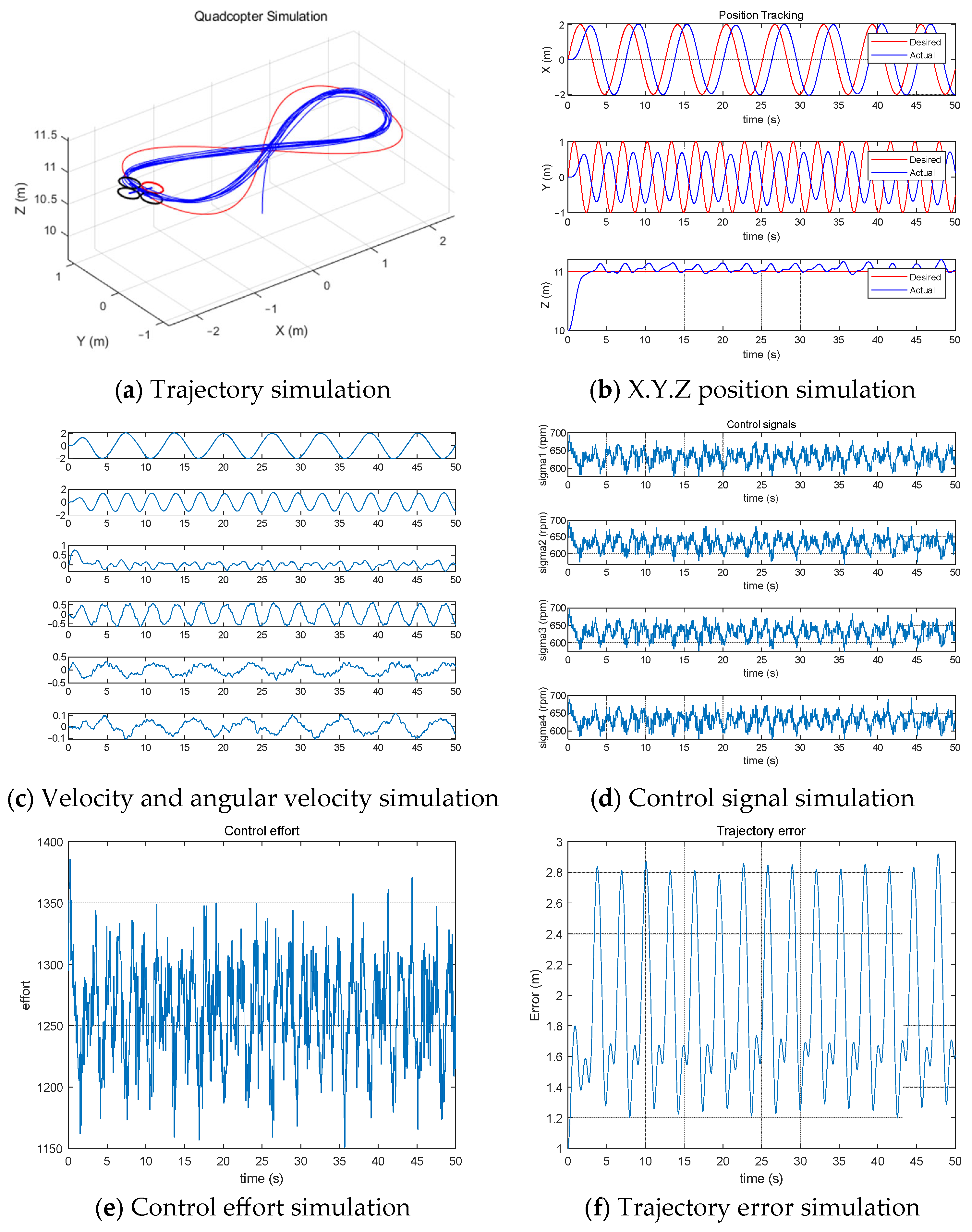
4.1. MPPI Control Without Learning Dynamics
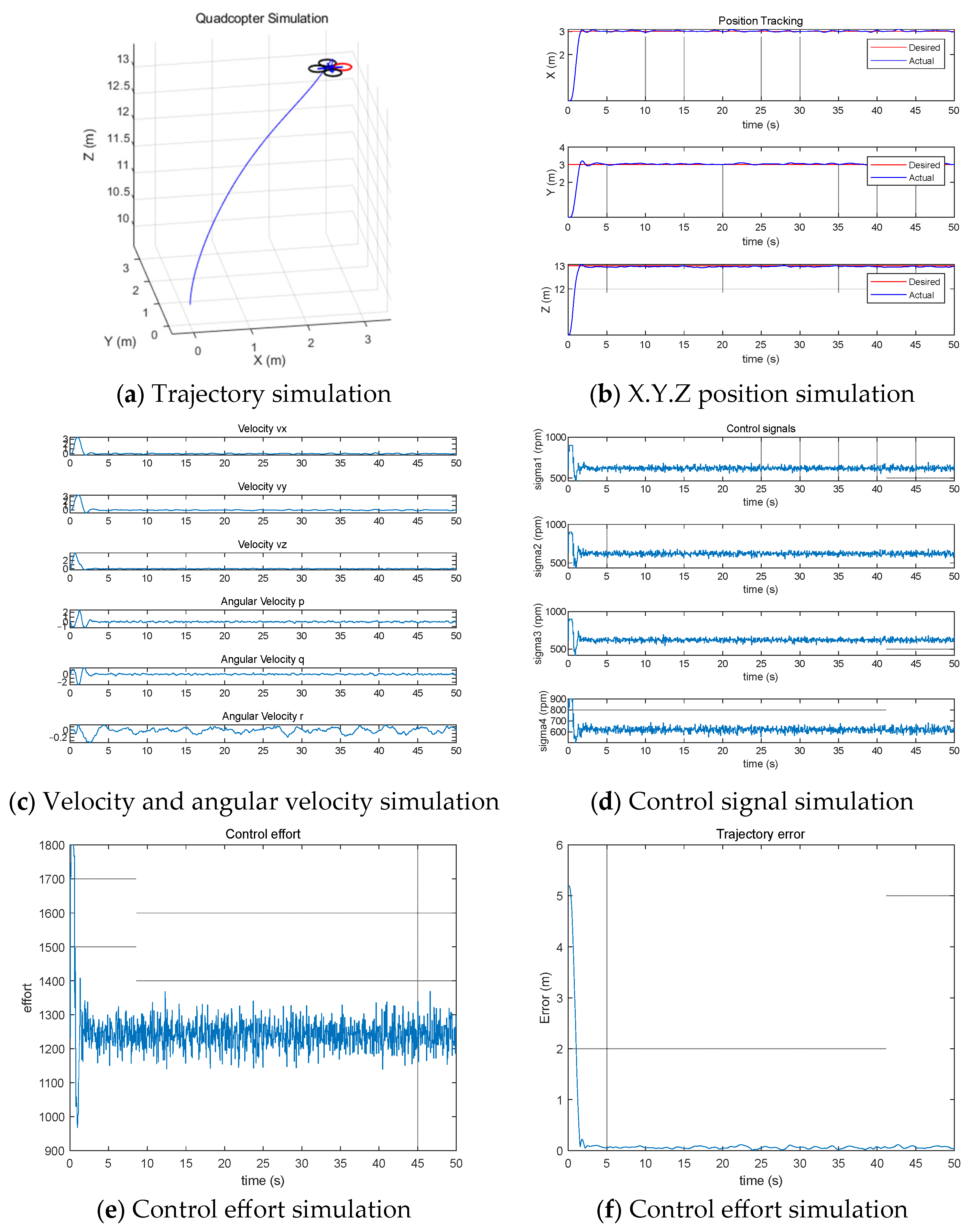
4.2. MPPI Control with Learning Dynamics with Two Hidden Layers Connected to Neural Network
4.3. MPC Control with Learning Dynamics by Multilayer Perceptron
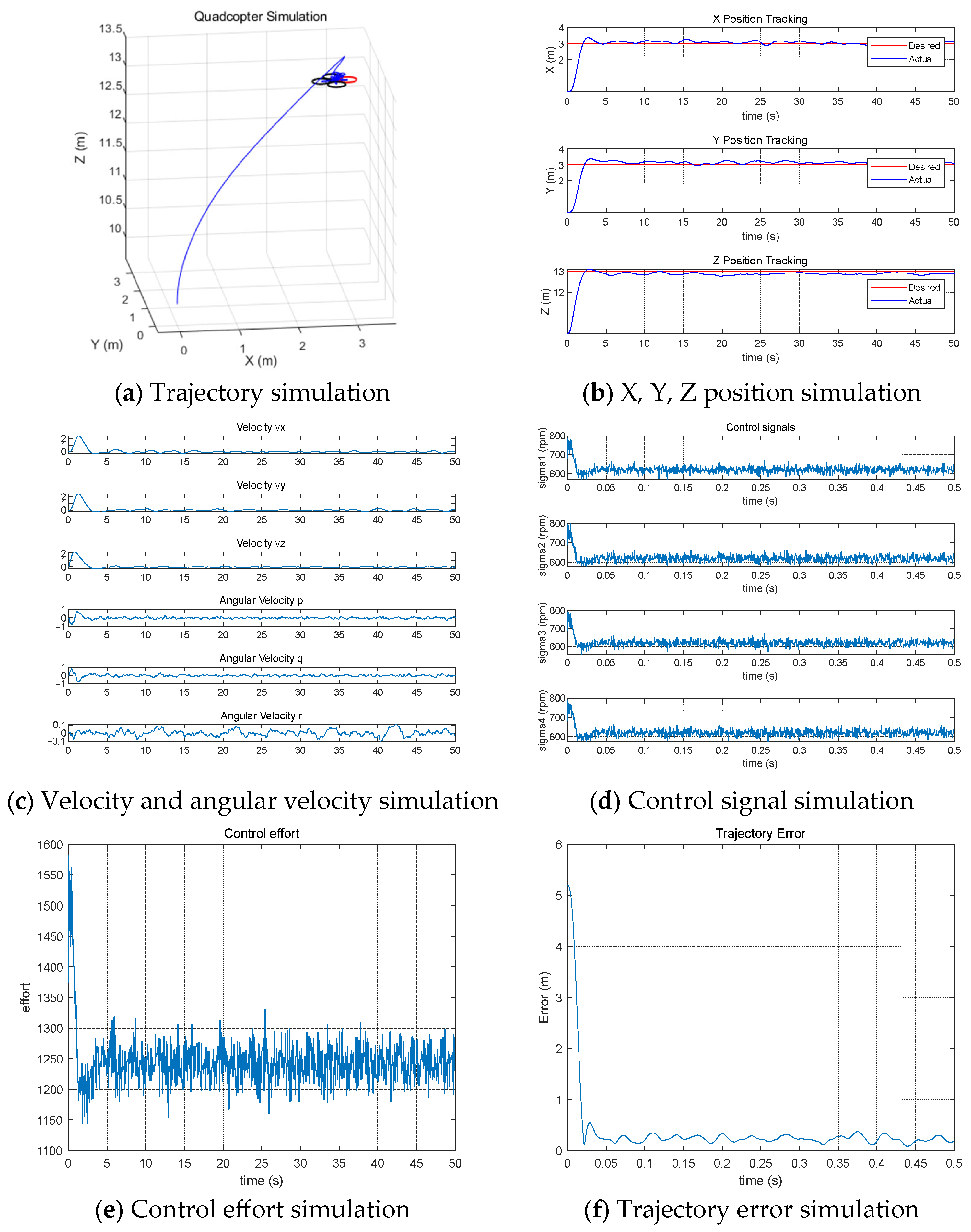
4.4. MPPI Control with Learning Dynamics by Multilayer Perceptron
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoffmann, G.; Huang, H.; Waslander, S.; Tomlin, C. Quadrotor Helicopter Flight Dynamics and Control: Theory and experiment. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Hilton Head, SC, USA, 20–23 August 2007; Volume 2. [Google Scholar]
- Brookner, E. Tracking and Kalman Filtering Made Easy; John Wiley and Sons, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Wan, E.A.; Van Der Merwe, R. The Unscented Kalman Filter for Nonlinear Estimation. In Proceedings of the IEEE Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000, Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Mellinger, D.; Michael, N.; Kumar, V. Trajectory generation and control for precise aggressive maneuvers with quadrotors. Int. J. Robot. Res. 2012, 31, 664–674. [Google Scholar] [CrossRef]
- Gonzalez, D.; Perez, J.; Milanes, V.; Nashashibi, F. A review of motion planning techniques for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1135–1145. [Google Scholar] [CrossRef]
- Mohta, K.; Watterson, M.; Mulgaonkar, Y.; Liu, S.; Qu, C.; Makineni, A.; Saulnier, K.; Sun, K.; Zhu, A.; Delmerico, J.; et al. Fast, autonomous flight in GPS-denied and cluttered environments. J. Field Robot. 2018, 35, 101–120. [Google Scholar] [CrossRef]
- Baca, T.; Hert, D.; Loianno, G.; Saska, M.; Kumar, V. Model Predictive Trajectory Tracking and Collision Avoidance for Reliable outdoor Deployment of Unmanned Aerial Vehicles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 6753–6760. [Google Scholar]
- Ryll, M.; Ware, J.; Carter, J.; Roy, N. Efficient Trajectory Planning for High Speed Flight in Unknown Environments. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 732–738. [Google Scholar]
- Theodorou, E.; Buchli, J.; Schaal, S. A Generalized Path Integral Approach to Reinforcement Learning. J. Mach. Learn. Res. 2010, 11, 3137–3181. [Google Scholar]
- Kappen, H.J. Linear Theory for Control of Nonlinear Stochastic Systems. Phys. Rev. Lett. 2005, 95, 200201. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, E.A. Nonlinear stochastic control and information theoretic dualities: Connections interdependencies and thermodynamic interpretations. Entropy 2015, 17, 3352–3375. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S. Brownian Motion and Stochastic Calculus, 2nd ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1991. [Google Scholar]
- Friedman, A. Stochastic Differential Equations and Applications; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Williams, G.; Drews, P.; Goldfain, B.; Rehg, J.M.; Theodorou, E.A. Aggressive Driving with Model Predictive Path Integral Control. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Romero, A.; Sun, S.; Foehn, P.; Scaramuzza, D. Model predictive contouring control for time-optimal quadrotor flight. IEEE Trans. Robot. 2022, 38, 3340–3356. [Google Scholar] [CrossRef]
- Ruchika, N.R. Model predictive control: History and development. Int. J. Eng. Trends Technol. IJETT 2013, 4, 2600–2602. [Google Scholar]
- Gómez, V.; Thijssen, S.; Symington, A.; Hailes, S.; Kappen, H.J. Real-Time Stochastic Optimal Control for Multi-Agent Quadrotor Systems. In Proceedings of the International Conference on Automated Planning and Scheduling (ICAPS), London, UK, 12–17 June 2016; pp. 468–476. [Google Scholar]
- Mohamed, I.S.; Allibert, G.; Martinet, P. Model Predictive Path Integral Control Framework for Partially Observable navigation: A Quadrotor Case Study. In Proceedings of the 2020 16th International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Williams, G.; Drews, P.; Goldfain, B.; Rehg, J.M.; Theodorou, E.A. Information-Theoretic Model Predictive Control: Theory and Applications to Autonomous Driving. IEEE Trans. Robot. 2018, 34, 1603–1622. [Google Scholar] [CrossRef]
- Kusumoto, R.; Palmieri, L.; Spies, M.; Csiszar, A.; Arras, K.O. Informed Information Theoretic Model Predictive Control. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 2047–2053. [Google Scholar]
- Nicol, C.; Macnab, C.; Ramirez-Serrano, A. Robust adaptive control of a quadrotor helicopter. Mechatronics 2011, 216, 927–938. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. Sliding Mode Control of a Quadrotor Helicopter. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4957–4962. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Voos, I. Nonlinear Control of a Quadrotor Micro-UAV Using Feedback-Linearization. In Proceedings of the 2009 IEEE International Conference on Mechatronics, Malaga, Spain, 14–17 April 2009; pp. 1–6. [Google Scholar]
- Zhaowei, M.; Tianjiang, H.; Lincheng, S.; Weiwei, K.; Boxin, Z.; Kaidi, Y. An Iterative Learning Controller for Quadrotor UAV Path Following at a Constant Altitude. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 4406–4411. [Google Scholar]
- Hehn, M.; D’Andrea, R. An Iterative Learning Scheme for High Performance, Periodic Quadrocopter Trajectories. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1799–1804. [Google Scholar]
- Bansal, S.; Akametalu, A.K.; Jiang, F.J.; Laine, F.; Tomlin, C.J. Learning Quadrotor Dynamics Using Neural Network for Flight Control. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Kappen, H.J. Path integrals and symmetry breaking for optimal control theory. J. Stat. Mech. Theory Exp. 2005, 2005, P11011. [Google Scholar] [CrossRef]
- Williams, G.; Aldrich, A.; Theodorou, E.A. Model predictive path integral control: From theory to parallel computation. J. Guid. Control Dyn. 2017, 40, 344–357. [Google Scholar] [CrossRef]
- Ruggiero, F.; Cacace, J.; Sadeghian, H.; Lippiello, V. Passivity-based control of VToL UAVs with a momentum-based estimator of external wrench and unmodeled dynamics. Robot. Auton. Syst. 2015, 72, 139–151. [Google Scholar] [CrossRef]







| Input | Range | Description |
|---|---|---|
| [−10, 10] | X-axis position, Y-axis position, simulates variations in horizontal position | |
| [−10, 10] | Z-axis position, considers flight requirements below the reference plane | |
| [0, 10] | Velocity | |
| [−] | Roll and pitch, prevent drone instability | |
| [−pi, pi] | Yaw, covers all possible directions | |
| [−2, 2] | Angular velocity | |
| [0, 900] | Rotor speed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhu, Q.; Elahi, A. Quadcopter Trajectory Tracking Based on Model Predictive Path Integral Control and Neural Network. Drones 2025, 9, 9. https://doi.org/10.3390/drones9010009
Li Y, Zhu Q, Elahi A. Quadcopter Trajectory Tracking Based on Model Predictive Path Integral Control and Neural Network. Drones. 2025; 9(1):9. https://doi.org/10.3390/drones9010009
Chicago/Turabian StyleLi, Yong, Qidan Zhu, and Ahsan Elahi. 2025. "Quadcopter Trajectory Tracking Based on Model Predictive Path Integral Control and Neural Network" Drones 9, no. 1: 9. https://doi.org/10.3390/drones9010009
APA StyleLi, Y., Zhu, Q., & Elahi, A. (2025). Quadcopter Trajectory Tracking Based on Model Predictive Path Integral Control and Neural Network. Drones, 9(1), 9. https://doi.org/10.3390/drones9010009





