An Intelligent 5G Unmanned Aerial Vehicle Path Optimization Algorithm for Offshore Wind Farm Inspection
Abstract
1. Introduction
2. Related Work
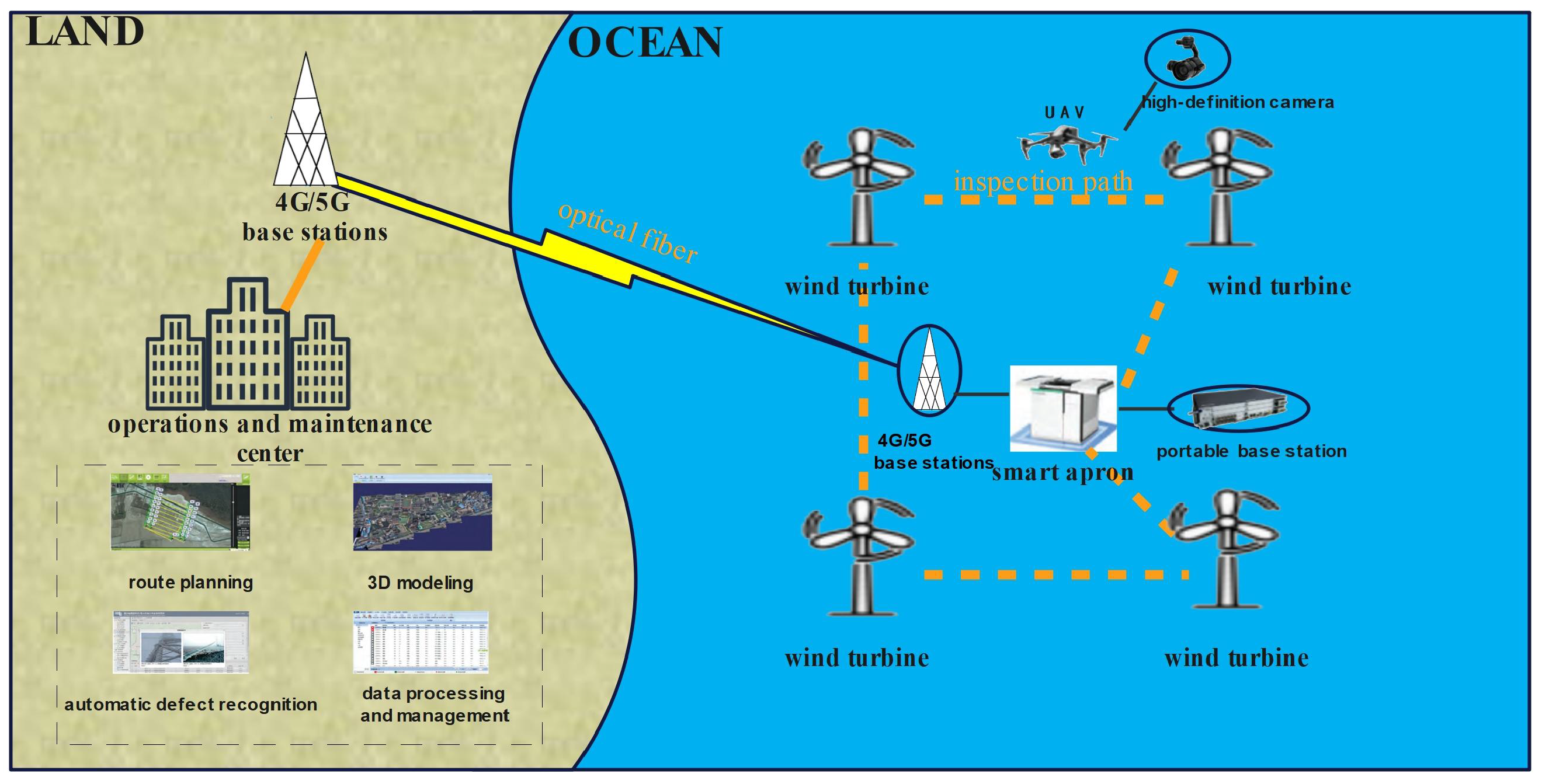
2.1. Fifth Generation Offshore Wind Farm
2.2. Related Research Overview
3. Problem Modeling
3.1. Constraints
3.1.1. Fifth Generation UAV
- 1.
- Maximum deflection angle
- 2.
- Maximum flight speed
- 3.
- Maximum flight time
- 4.
- Maximum number of inspected turbines
- 5.
- Safe flight wind conditions
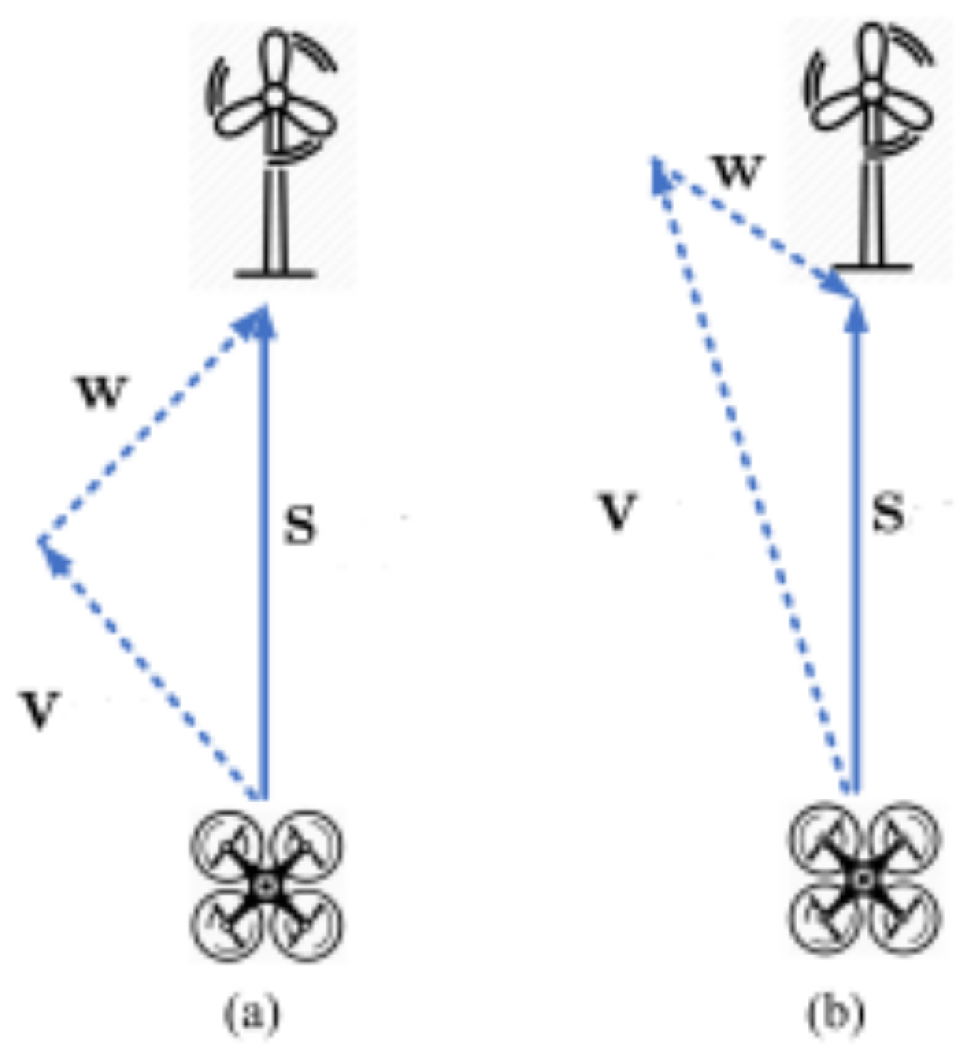
3.1.2. Sea Area Condition Information
3.2. Problem Modeling
- 1.
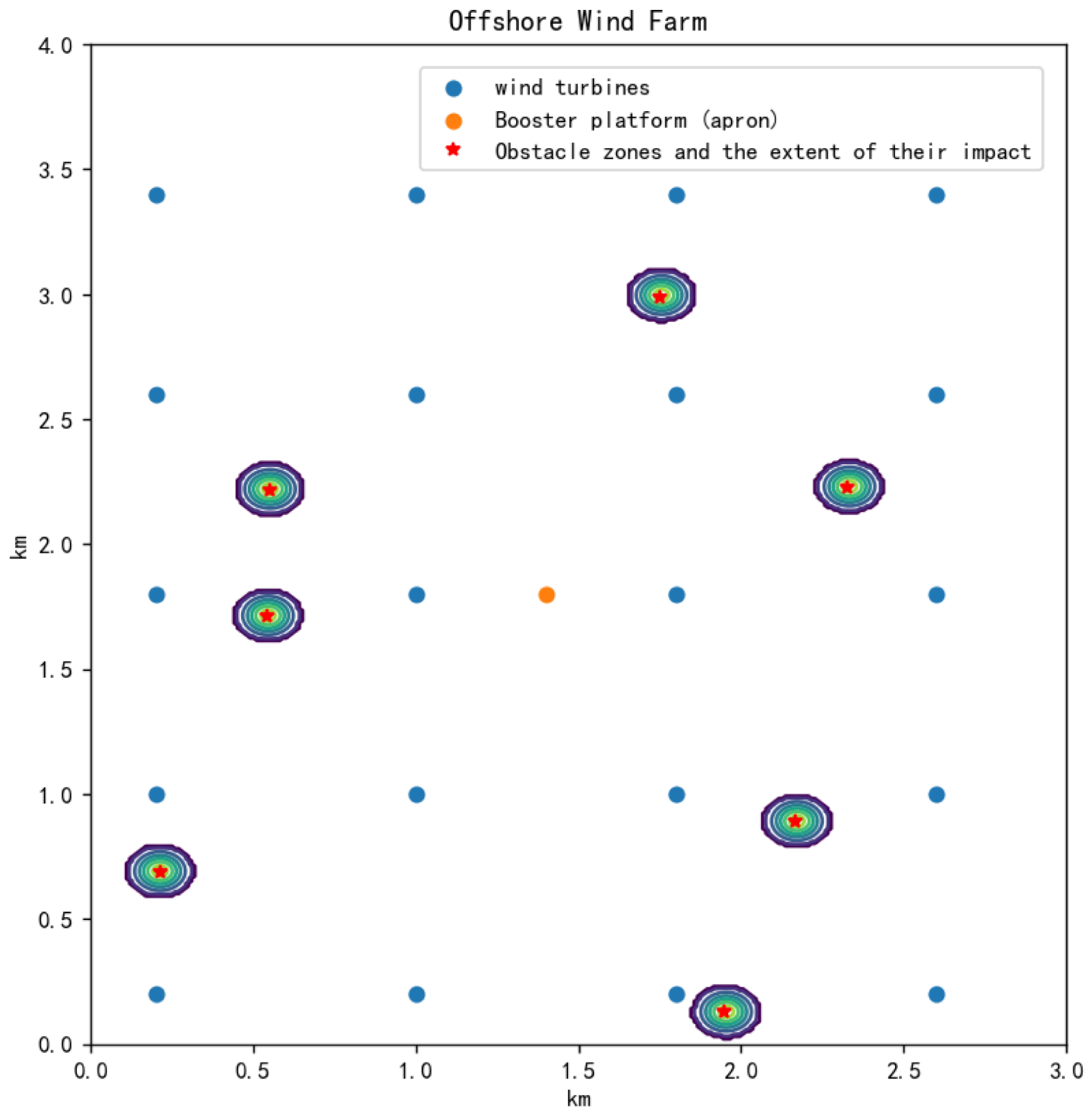
- Offshore wind farm environment modeling
- 2.
- Fifith generation UAV group task allocation
- (a)
- Coverage constraint: each wind turbine is visited exactly once:
- (b)
- Continuity constraint: the path of each UAV must be continuous:
- (c)
- Capacity constraint: the total number of wind turbines assigned to each UAV must not exceed p.
- (d)
- Flight capability constraint: the flight time of each UAV cannot exceed its maximum battery capacity :
- 3.
- Modeling of 5G UAV line patrol path optimization problem after task assignment
4. SWA-IAGA: Sea Wind-Aware Improved A*-Guided Genetic Algorithm
4.1. An Improved A* Algorithm
4.1.1. Principle of the Algorithm
- 1.
- Circular node expansion method
- 2.
- Evaluation function
- 3.
- Improved evaluation function
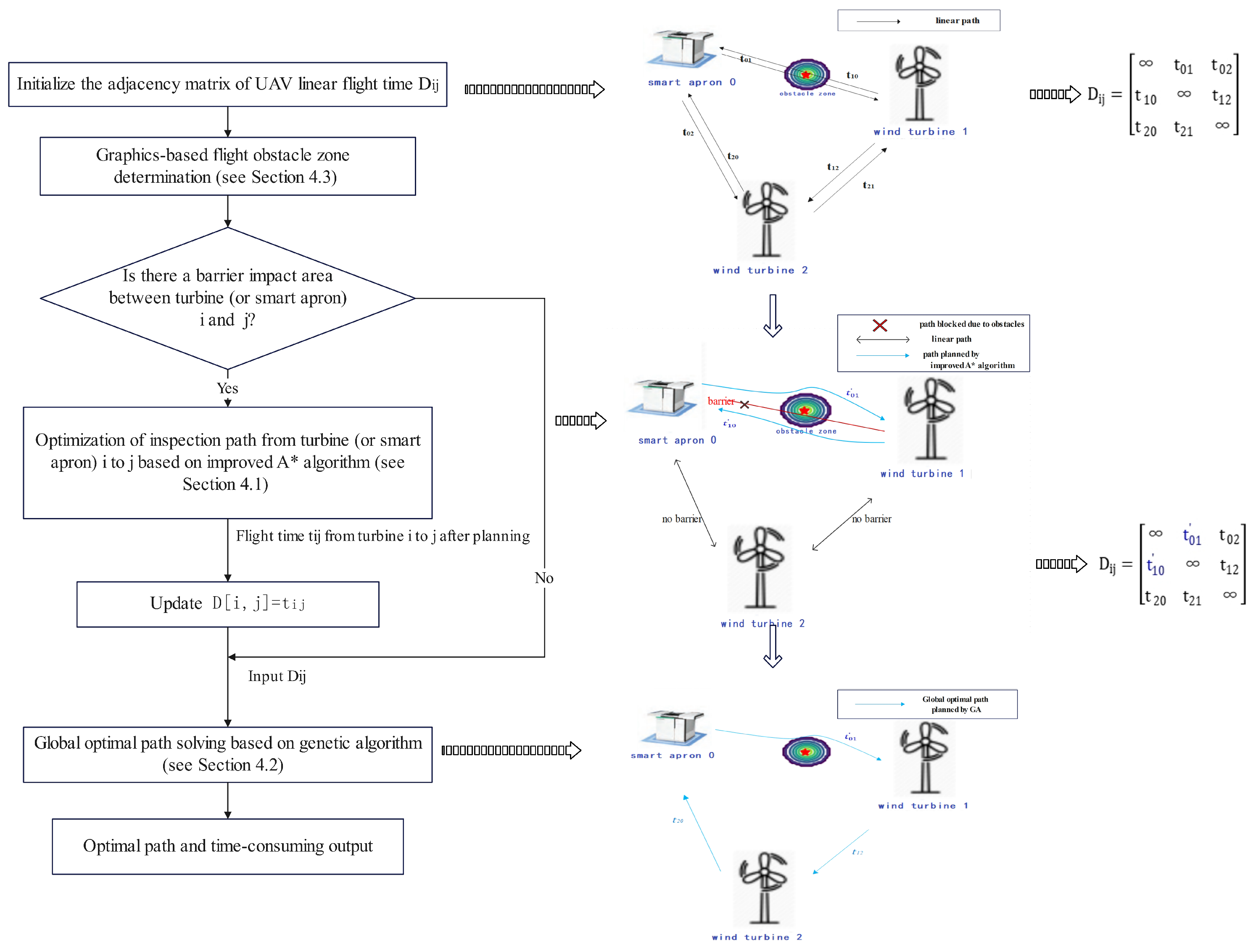
4.1.2. A* Algorithm Search Path Process
- Initialization: create an open list (OL) with the starting point A and a close list (CL) for explored nodes.
- Expansion and evaluation: remove the node N with the smallest evaluation function value from the open list and add it to the close list. Explore the neighbors of N by using circular node expansion method. For each neighbor M, if M is not in the CL, calculate g(M) (actual cost from start to M) and h(M) (estimated cost from M to end), and combine this with the hazard factor w to calculate (evaluation function). If M is not in the open list, add it to the open list and set N as its parent node.
- Update path: if M is already in the OL, compare the path through N with the existing path. If the new path is better (lower g(M)), update M’s parent and re-evaluate f(M).
- Cyclic exploration: repeat steps (b) and (c), selecting the node with the lowest evaluation function value from the OL until the end point is found or the open list is empty (indicating no reachable path).
- Construct path: once the end point is in the CL, backtrack from the end point to the start point via parent nodes to construct the shortest path.
4.2. Genetic Algorithm
4.3. Knowledge of Graphics
- Find all rasters touched by line segment AB.
- (a)
- Transformation: Translate and flip (if necessary) the line segment AB to obtain a line segment in the first quadrant, starting at the origin, and use for subsequent raster determination.
- (b)
- Traverse the line segment AB and determine the contact grid:Traverse the points on the transformed line segment AB in the x-direction in increments of 0.5 ( is the edge length of the raster metaparticle), where the coordinate of the n-th point is . For each point, perform the following judgment. If n is even: if the point is located on the boundary of the raster, the left and right rasters adjacent to the point are judged as being touched by the line segment AB. If n is odd: if the point is in the grid, the grid containing the point is judged as the contact grid; if the point is located on the boundary of a grid, the upper and lower grids are judged for contact with the line segment AB.
- (c)
- Inverse transformation: After completing the above judgment, we need to convert the obtained contact raster coordinates from the transformed coordinate system back to the original coordinate system. This involves inverse rotation and inverse translation operations on the coordinates to restore the position and direction of the line segment AB in the original space.
- Judge whether the values of the elements in the corresponding E of the line segment contact raster are all 0. If they are all 0, then it is judged that there is no obstacle zone between wind turbine i and wind turbine j. If they are not all 0, then it means that at least one of the rasters contains obstacles, and, therefore, it can be judged that there is an obstacle zone between wind turbine i and wind turbine j, and the UAV needs to take obstacle avoidance measures.
4.4. SWA-IAGA
- 1.
- Flight speed modeling and asymmetric adjacency matrix creation considering the effect of sea wind
- 2.
- Consideration of graphics-based flight obstacle zone determination
- 3.
- Obstacle avoidance path planning and flight time updating with improved A* algorithm
- 4.
- Global optimal flight path solving based on genetic algorithm
5. Simulation and Results Analysis
5.1. Fifth Generation UAV Group Patrol Task Assignment
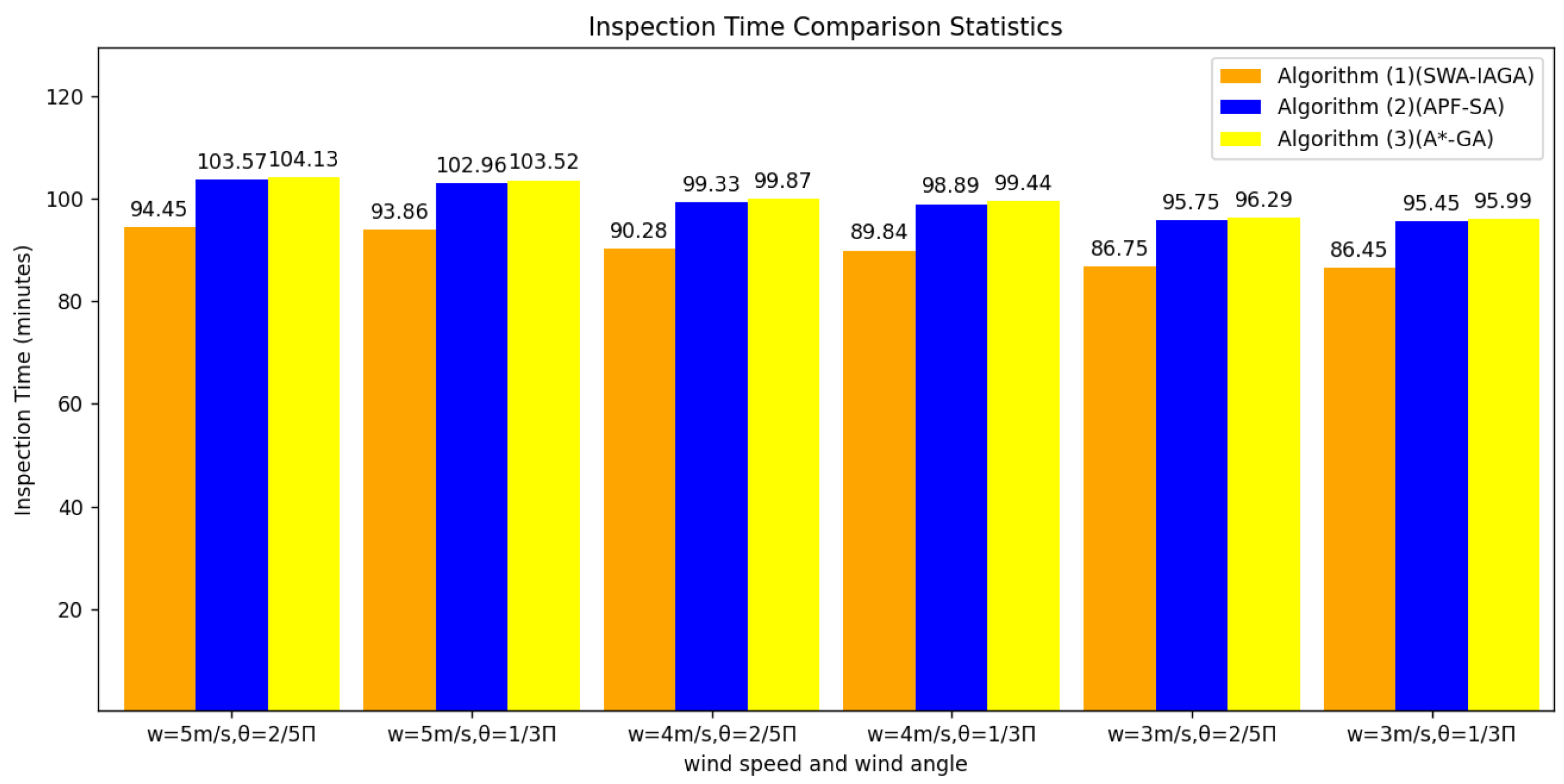
5.2. SWA-IAGA for UAV Path Planning
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TSP | traveling salesman problem |
| UAV | unmanned aerial vehicle |
| GIS | Geographic Information System |
References
- Huang, X.; Wang, G.; Lu, Y.; Jia, Z. Study on a Boat-Assisted Drone Inspection Scheme for the Modern Large-Scale Offshore Wind Farm. IEEE Syst. J. 2023, 17, 4509–4520. [Google Scholar] [CrossRef]
- Xing, X. Fully digital wind farm monitoring and inspection system based on AR augmented reality technology. IOP Conf. Ser. Earth Environ. Sci. 2020, 440, 032008. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z. Automatic detection of wind turbine blade surface cracks based on UAV-taken images. IEEE Trans. Ind. Electron. 2017, 64, 7293–7303. [Google Scholar] [CrossRef]
- Khan, S.K.; Farasat, M.; Naseem, U.; Ali, F. Performance evaluation of next-generation wireless (5G) UAV relay. Wirel. Pers. Commun. 2020, 113, 945–960. [Google Scholar] [CrossRef]
- Geraci, G.; Garcia-Rodriguez, A.; Azari, M.M.; Lozano, A.; Mezzavilla, M.; Chatzinotas, S.; Chen, Y.; Rangan, S.; Di Renzo, M. What will the future of UAV cellular communications be? A flight from 5G to 6G. IEEE Commun. Surv. Tutor. 2022, 24, 1304–1335. [Google Scholar] [CrossRef]
- Mwangi, A.; Sahay, R.; Fumagalli, E.; Gryning, M.; Gibescu, M. Towards a Software-Defined Industrial IoT-Edge Network for Next-Generation Offshore Wind Farms: State of the Art, Resilience, and Self-X Network and Service Management. Energies 2024, 17, 2897. [Google Scholar] [CrossRef]
- Nomikos, N.; Gkonis, P.K.; Bithas, P.S.; Trakadas, P. A survey on UAV-aided maritime communications: Deployment considerations, applications, and future challenges. IEEE Open J. Commun. Soc. 2022, 4, 56–78. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV Communications for 5G and Beyond: Recent Advances and Future Trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Yao, Q.; Zheng, Z.; Qi, L.; Yuan, H.; Guo, X.; Zhao, M.; Liu, Z.; Yang, T. Path planning method with improved artificial potential field—A reinforcement learning perspective. IEEE Access 2020, 8, 135513–135523. [Google Scholar] [CrossRef]
- Platanitis, K.S.; Kladis, G.P.; Petrongonas, E.; Skliros, C.; Tsourveloudis, N.C.; Zagorianos, A.D. UAV path planning for offshore swarm-based missions. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 124–133. [Google Scholar]
- Li, X.; Feng, W.; Wang, J.; Chen, Y.; Ge, N.; Wang, C.X. Enabling 5G on the ocean: A hybrid satellite-UAV-terrestrial network solution. IEEE Wirel. Commun. 2020, 27, 116–121. [Google Scholar] [CrossRef]
- Li, J.; Liu, W.; Han, Y.; Xing, H.; Yang, A.; Pan, Y. TSP Problem Based on Artificial Ant Colony Algorithm. In Lecture Notes in Real-Time Intelligent Systems; Springer: Cham, Switzerland, 2018; pp. 196–202. [Google Scholar]
- Chen, T.; Zhang, G.; Hu, X.; Xiao, J. Unmanned aerial vehicle route planning method based on a star algorithm. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1510–1514. [Google Scholar]
- Ait Saadi, A.; Soukane, A.; Meraihi, Y.; Benmessaoud Gabis, A.; Mirjalili, S.; Ramdane-Cherif, A. UAV path planning using optimization approaches: A survey. Arch. Comput. Methods Eng. 2022, 29, 4233–4284. [Google Scholar] [CrossRef]
- Cheng, C.; Sha, Q.; He, B.; Li, G. Path planning and obstacle avoidance for AUV: A review. Ocean. Eng. 2021, 235, 109355. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N.; Wu, W. A hybrid path planning algorithm considering AUV dynamic constraints based on improved A* algorithm and APF algorithm. Ocean. Eng. 2023, 285, 115333. [Google Scholar] [CrossRef]
- Chung, H.M.; Maharjan, S.; Zhang, Y.; Eliassen, F.; Strunz, K. Placement and routing optimization for automated inspection with unmanned aerial vehicles: A study in offshore wind farm. IEEE Trans. Ind. Inform. 2020, 17, 3032–3043. [Google Scholar] [CrossRef]
- Fahim, M.; Sharma, V.; Cao, T.V.; Canberk, B.; Duong, T.Q. Machine learning-based digital twin for predictive modeling in wind turbines. IEEE Access 2022, 10, 14184–14194. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Xu, R.; Cao, Z.; Jin, Z.; Guo, Z.; Wang, W.; Li, K. Three dimensional fully autonomous inspection method for wind power employing unmanned aerial vehicle based on 5G wireless communication and artificial intelligence. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; Volume 5, pp. 800–805. [Google Scholar]
- Elnabty, I.A.; Fahmy, Y.; Kafafy, M. A survey on UAV placement optimization for UAV-assisted communication in 5G and beyond networks. Phys. Commun. 2022, 51, 101564. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Lu, T.; Xu, W.; Yuen, M. Distributed and multilayer UAV networks for next-generation wireless communication and power transfer: A feasibility study. IEEE Internet Things J. 2019, 6, 7103–7115. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Y.; Wang, H. Review on monitoring and operation-maintenance technology of far-reaching sea smart wind farms. J. Mar. Sci. Eng. 2022, 10, 820. [Google Scholar] [CrossRef]
- Xie, L.; Xue, S.; Zhang, J.; Zhang, M.; Tian, W.; Haugen, S. A path planning approach based on multi-direction A* algorithm for ships navigating within wind farm waters. Ocean. Eng. 2019, 184, 311–322. [Google Scholar] [CrossRef]
- Ji, Y.; Zhao, X.; Hao, J. A Novel UAV Path Planning Algorithm Based on Double-Dynamic Biogeography-Based Learning Particle Swarm Optimization. Mob. Inf. Syst. 2022, 2022, 8519708. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zhang, P.; Li, B. UAV path planning based on improved A* algorithm. Comput. Syst. Appl. 2021, 34, 39–43. [Google Scholar]
- Yang, F.; Fang, X.; Gao, F.; Zhou, X.; Li, H.; Jin, H.; Song, Y. Obstacle Avoidance Path Planning for UAV Based on Improved RRT Algorithm. Discret. Dyn. Nat. Soc. 2022, 2022, 4544499. [Google Scholar] [CrossRef]
- Li, C.; Peng, X. Two-stage Path Optimization of UAVs Patrol on Transmission Towers Considering Obstacle Avoidance. Comput. Meas. Control 2019, 27, 159. [Google Scholar]
- Khan, A.; Zhang, J.; Ahmad, S.; Memon, S.; Qureshi, H.A.; Ishfaq, M. Dynamic positioning and energy-efficient path planning for disaster scenarios in 5G-assisted multi-UAV environments. Electronics 2022, 11, 2197. [Google Scholar] [CrossRef]
- Fan, T.; Fu, L.; Guo, C.; Zhang, Y.; Sun, L. Multi UAV Inspection Optimization for Offshore Wind Farms Considering Battery Exchange Process. IEEE Trans. Intell. Veh. 2024, 1–11. [Google Scholar] [CrossRef]
- Baker, B.M.; Ayechew, M. A genetic algorithm for the vehicle routing problem. Comput. Oper. Res. 2003, 30, 787–800. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Yang, L.; Gao, Y.; Zhao, J.; Hou, W.; Xu, F. An Intelligent 5G Unmanned Aerial Vehicle Path Optimization Algorithm for Offshore Wind Farm Inspection. Drones 2025, 9, 47. https://doi.org/10.3390/drones9010047
Jiang C, Yang L, Gao Y, Zhao J, Hou W, Xu F. An Intelligent 5G Unmanned Aerial Vehicle Path Optimization Algorithm for Offshore Wind Farm Inspection. Drones. 2025; 9(1):47. https://doi.org/10.3390/drones9010047
Chicago/Turabian StyleJiang, Congxiao, Lingang Yang, Yuqing Gao, Jie Zhao, Wenne Hou, and Fangmin Xu. 2025. "An Intelligent 5G Unmanned Aerial Vehicle Path Optimization Algorithm for Offshore Wind Farm Inspection" Drones 9, no. 1: 47. https://doi.org/10.3390/drones9010047
APA StyleJiang, C., Yang, L., Gao, Y., Zhao, J., Hou, W., & Xu, F. (2025). An Intelligent 5G Unmanned Aerial Vehicle Path Optimization Algorithm for Offshore Wind Farm Inspection. Drones, 9(1), 47. https://doi.org/10.3390/drones9010047








