Abstract
UAV-based air-ground integrated networks offer a significant benefit in terms of providing ubiquitous communications and computing services for Internet of Things (IoT) devices. With the empowerment of edge intelligence (EI) technology, they can efficiently deploy various intelligent IoT applications. However, the trajectory of UAVs can significantly affect the quality of service (QoS) and resource optimization decisions. Joint computation offloading and UAV trajectory optimization bring many challenges, including coupled decision variables, information uncertainty, and long-term queue delay constraints. Therefore, this paper introduces an air-ground integrated architecture with EI and proposes a TD3-based joint computation offloading and UAV trajectory optimization (TCOTO) algorithm. Specifically, we use the principle of the TD3 algorithm to transform the original problem into a cumulative reward maximization problem in deep reinforcement learning (DRL) to obtain the UAV trajectory and offloading strategy. Additionally, the Lyapunov framework is used to convert the original long-term optimization problem into a deterministic short-term time-slot problem to ensure the long-term stability of the UAV queue. Based on the simulation results, it can be concluded that our novel TD3-based algorithm effectively solves the joint computation offloading and UAV trajectory optimization problems. The proposed algorithm improves the performance of the system energy efficiency by 3.77%, 22.90%, and 67.62%, respectively, compared to the other three benchmark schemes.
1. Introduction
The booming deployment of new Internet of Things (IoT) applications, including virtual reality, face recognition, environmental monitoring, traffic control, and security management (as cited in [1,2,3]), has triggered an explosive growth of data traffic at the edge [4]. These computation-intensive applications impose stringent requirements on the computational and communication capabilities of IoT edge devices [5]. However, the gap between the limited computational resources of IoT devices and the escalating demands of computational tasks has resulted in a deterioration of quality of service (QoS), ultimately hindering the effective deployment and performance of IoT applications. In addition, real-time data processing tasks generated by massive machine terminals, pattern recognition, and decision recommendation require artificial intelligence (AI) technology as a powerful service paradigm to assist in solution. Therefore, a new edge intelligence (EI) [6] paradigm combining AI and mobile edge computing (MEC) technologies will be a pivotal force in promoting the evolution of 6G IoT networks. This paradigm can propel learning capabilities from remote centers to the fringes of the network.
With the support of EI technology, intelligent IoT devices can be deployed in more fields to expand vertical application scenarios, such as intelligent transportation, intelligent industry, intelligent healthcare, and intelligent agriculture [7]. These EI-powered IoT devices can realize efficient sensing, transmission, and processing of massive amounts of information, extract valuable information and features from them in order to achieve more accurate and more intelligent decision-making and control, and, thus, provide better and more efficient support for IoT applications and services [8]. However, terrestrial networks cannot achieve ultra-large-scale global connections and ubiquitous communications, primarily due to constraints posed by the radio spectrum resources, geographical coverage limitations, and operational costs [9]. Considering the demands for ultra-reliable and low-latency transmission in areas that lack terrestrial communication network coverage (such as remote mountainous and oceanic areas) and in the areas where network capacity is insufficient to support the dynamic and rapid increase of IoT services (hotspot areas or rural), airborne devices due to their inherent mobility and flexibility become a promising economic solution well suited in the above areas [10].
The airborne platforms include high-altitude platform stations (HAPs) and low-altitude unmanned aerial vehicles (UAVs), which are the key components of the air-ground integrated networks. UAVs equipped with MEC can take advantage of their high mobility and controllability, quickly flying near the target devices, thereby effectively expanding the coverage of the communication network. Despite the aforementioned advantages of UAVs, their limited computational resources and battery capacity pose significant challenges in sustaining long-term service provision to IoT devices. To meet this challenge, HAPs are introduced as a supplement for the limitations of UAVs [11]. HAPs can be deployed at high altitudes for a long time to provide stable communication services in larger areas. Consequently, the collaborative effort of UAVs and HAPs becomes imperative to deliver computing services efficiently. Based on the actual demands of computing tasks in different environments and scenarios, UAVs, HAPs, or fixed ground infrastructures flexibly support intelligent IoT applications via ground air links [12].
However, introducing UAVs/HAPs with EI technology brings new challenges in low-carbon sustainable resource optimization and device deployment optimization. In addition, the trajectory of UAVs can significantly affect the quality of service (QoS), exacerbating the difficulty of resource optimization. Hence, there is a pressing need to intensify research efforts focused on the joint computation offloading and UAVs’ trajectory optimization strategies within the context of EI-powered air-ground integrated networks. However, most of the current works [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] have some limitations, as shown in Table 1, and they can summarised as follows: (1) the proposed optimization strategies cannot solve the problems in the integrated air-ground architecture, (2) the system model does not take into account the long-term stability of the queue, and (3) convex optimization algorithms are not appropriate for rapidly changing environments.

Table 1.
Comparison of different optimization algorithms.
In order to address the above challenges, the air-ground integrated architecture with EI is introduced. It combines MEC and AI technology to provide faster and more accurate acquisition, transmission, and massive data processing. Subsequently, we propose a joint optimization problem that can maintain the long-term stability of the UAV queueing system. By applying the Lyapunov framework, we transform complex long-term optimization problems into manageable deterministic short-term time-slot models. Ultimately, we devise an algorithm that concurrently addresses computation offloading and UAV trajectory planning. To tackle the original intractable problem, we adopt the cutting-edge TD3 DRL algorithm, recasting it into a framework that maximizes cumulative rewards. Strategically designing the reward mechanism facilitates the neural network’s evolution towards superior decision-making capabilities, ultimately yielding the optimal strategies. The core contributions of this study can be concisely outlined as follows:
- We first propose an integrated network architecture incorporating UAVs, HAPs, and terrestrial communication infrastructures to support collecting, transmitting, and processing extensive IoT data. This is achieved through the strategic and flexible deployment of UAVs with EI. Based on this architecture design, UAVs can work with HAPs and remote base stations (BSs) to simultaneously process computation tasks of intelligent IoT applications.
- We define the joint computation offloading and UAVs trajectory optimization problem as a stochastic mixed-integer nonlinear programming (MINLP) problem. Considering the undeniable impact of queuing delay, we take the long-term constraints of queuing delay into problem modeling. Then, we transform the MINLP problem into a computational offloading problem and a UAV trajectory optimization problem for each time slot by using the Lyapunov optimization theory.
- We propose the TD3-based joint computation offloading and UAV trajectory optimization (TCOTO) algorithm to address the above challenge. Specifically, we consider the high coupling of task offloading and trajectory optimization strategies and transform this optimization into an MDP-based reinforcement learning problem. The UAV autonomously makes trajectory and offloading decisions based on the observed dynamic environment, such as UAV position, queue backlog, and channel state. Then, TD3 generates continuous actions to avoid overestimating the Q-value and improve training stability.
The structure of the paper is organized as follows: Section 2 reviews the related work; Section 3 outlines the system model. Section 4 gives the problem formulation and transformations. Section 5 details the approach used to address the issue. Section 6 includes simulation and performance evaluation. Moreover, Section 7 concludes the paper.
2. Related Works
2.1. The Architecture of Networks
Both references [13,14] employed UAVs, incorporating MEC servers for service delivery to ground users. Meanwhile, the author addressed the optimization of system energy efficiency through jointly optimizing UAV trajectories and user offloading decisions. Papers [15,16,17,18] added multiple UAVs to handle intensive computational tasks in order to alleviate the computational pressure of a single UAV. Differently, paper [19] introduced charging stations as its energy supplement and then proposed a priority-based DRL method for trajectory planning and charging scheduling of UAVs to maximize their energy efficiency. Furthermore, ref. [20] also factored in BSs within the network infrastructure to serve users. It arranges multiple UAVs near BSs to tackle delay-critical tasks promptly. For delay-resilient tasks, UAVs serve as intermediaries, forwarding data to BSs to conserve their limited resources. However, the previously mentioned study confined its network to one or multiple UAVs focused on data gathering and local processing, excluding BSs or HAPs. However, considering the limited computing resources of UAVs, such a network architecture cannot meet the computational demands of massive data in the IoT. Although multiple UAVs can alleviate the computational pressure, they require additional deployment costs. To solve this problem, we propose an integrated network architecture that avoids the degradation of service performance of UAVs due to insufficient computational resources through the mutual collaboration between ground and sky networks.
2.2. The Long-Term Constraints of Queue
Considering the sensitivity of future emerging services to service quality, the long-term performance of network systems will have an undeniable impact on the Smart IoT [21]. However, most of the current studies predominantly focus on short-term system performance, e.g., the paper [22] provided different service features based on different task types of users. The authors proposed an optimally embedded DRL scheme to maximize energy efficiency and service fairness. The paper [23] combined deep deterministic policy gradient (DDPG) and dueling DQN (DDQN) algorithms to deal with discrete and continuous hybrid action spaces, which were used to solve the ground equipment offloading decision and flight trajectory, respectively. Also, the algorithms proposed in the paper optimize the time allocated to the ground equipment to enhance UAV energy efficiency. The paper [24] tackled service distribution, trajectory refinement, and obstacle circumvention in a multi-UAV supported offloading framework. The authors were able to minimize user offloading delays and improve UAV energy efficiency by combining DDPG with a potential game to enable UAVs to avoid obstacles. Since the arrival of computing tasks is uncertain, it is impractical for the above literature to consider only short-term performance optimization. Recently, some studies have considered long-term performance optimization. For example, the paper [25] used the DDPG algorithm to jointly optimize UAV trajectories and task offloading strategy, thereby minimizing edge computing network latency. The paper [26] introduced a triple-learner DRL algorithm to enhance energy efficiency by simultaneously optimizing UAV trajectory planning and energy scheduling. However, these studies did not consider the impact of long-term queues on the system, so this paper introduces queuing theory and models to model and analyze the long-term queues of the system. By analyzing the system’s queuing characteristics and performance indicators, intelligent agents can better understand the impact of queues on system performance, thereby obtaining better trajectory planning and unloading task decisions.
2.3. Optimization Technique
Unlike traditional optimization methods, DRL can handle decision-making problems in dynamic scenarios without prior information, significantly simplifying problem-solving. The paper [27] introduced a Q-learning approach to concurrently optimize UAV trajectories and offloading ratios, minimizing MEC system delays for IoT devices servicing. The paper [28] embedded cognitive radios into UAVs to form a cognitive UAV-assisted network and then established backhaul links by collecting idle spectrum. The authors proposed a DDQN-based solution for the trajectory optimization, time allocation, and frequency band selection problems. This enables cognitive UAVs to make the best decisions autonomously and improve traffic offloading efficiency. The Q-learning and DDQN algorithms in the above papers performed well in relatively simple environments, but are unsuitable for problems with large action spaces. The DDPG approach in [29] efficiently tackled high-dimensional action spaces in intricate environments, yet encountered an issue with Q-value overestimation. TD3, an advanced DDPG refinement, effectively addresses this challenge, demonstrating superior performance compared to DDPG, and has garnered widespread application across various research domains. For example, the paper [30] constructed a cloud-side cooperative MEC system aimed at delivering premium user services. Then, the authors proposed a TD3 optimization algorithm to minimize the objective. The paper [31] proposed a video secure offloading scheme based on TD3, which saves system energy while ensuring system latency and video frame analysis precision. Then, through a large number of experiments, it was proven that the algorithm proposed is superior to comparative algorithms such as DDPG in terms of energy consumption and latency. Considering the diverse nature and long-term constraints of the network architecture presented in this study, relying on algorithms like DDPG could result in suboptimal performance and slow convergence. Therefore, the TD3 algorithm is needed to solve such high-dimensional optimization problems.
3. System Model
As shown in Figure 1, we propose an integrated system consisting of massive IoT devices, a UAV, an HAP, and a BS. The IoT devices generate a large amount of data for environment sensing, traffic control, or safety management tasks. We denote IoT devices set as , where k is the k-th IoT device. The UAVs fly over IoT devices to collect and process data further with the MEC services equipped on them. Given the limitations in power and computing resources of UAVs, computation tasks involving collected sensing data can be offloaded to remote BSs and HAPs to achieve improved delay and power performance. The UAV’s mission duration T is evenly divided into N time slots, represented by the set . is the t-th time slot, and its duration length is . We assume that the UAV maintains a static position throughout each time slot of duration .
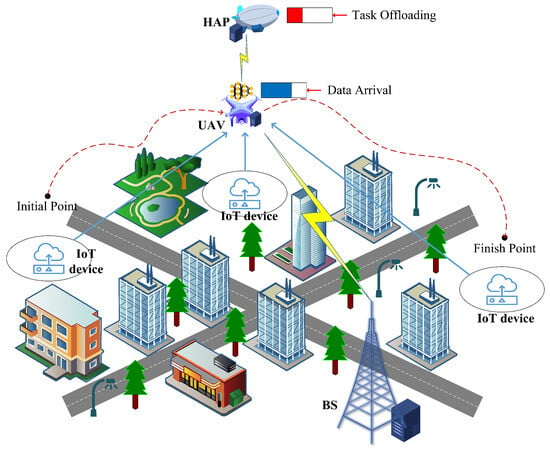
Figure 1.
System model.
The location of the k-th IoT device is , and the vertical axis coordinates are all zero. The UAV operates at a constant altitude and maximum speed to collect data generated at the IoT devices. The initial point of the UAV’s mission is and the destination of the mission is . During time slot t, the horizontal coordinates are given by , and the flight direction satisfies . Similar to [32], the system environment (, , and channel state information (CSI)) remain stable in a time slot. The positions and flight directions of the UAV in different time slots are related as follows:
where denotes the the UAV’s speed.
3.1. Communications Model
3.1.1. Data Collection
During data collection from IoT devices by the UAV, communication involves both line-of-sight (LoS) and non-line-of-sight paths (NLoS). The horizontal distance between the device k and the UAV is calculated as
Then, the path-loss can be calculated by the following equation:
where c denotes the speed of light, is the Euclidean paradigm of vector , and represents the communication carrier frequency. and indicate the extra losses for LoS and NLoS links due to free-space propagation, respectively. represents the probability of the LoS connection, which is given by
where are selected according to the environment [33].
Data collection rate from the k-th Iot device to the UAV is calculated as
We presume that the UAV employs the frequency division multiple access (FDMA) technique; denotes the fraction of channel bandwidth assigned by the UAV to IoT device k, is the total bandwidth available to be allocated by the UAV, is the power of the noise, and is the transmitting power of the edge device.
3.1.2. Computation Offloading to HAP
Due to the advantage of airborne platforms in high altitudes, the link between the UAV and the HAP is considered as LoS propagation, and its channel gain can be expressed as
where represents the channel gain of LoS propagation at a reference distance of , and is the horizontal position of the HAP, which is considered to be fixed in the air at a height of .
Then, the data rate of the communication link between the UAV and the HAP is formulated as
where and denote the bandwidth and power used in computational offloading to the HAP, respectively. The amount of computational offloading from the UAV to the HAP can be calculated by .
3.1.3. Computation Offloading to BS
Similarly, the channel gain to the BS can be expressed as
where is the coordinates of the BS on the ground and is the height of the BS.
Therefore, the communication rate between ground BS is given by
where and denote the bandwidth and power used in computational offloading to the BS, respectively. The computational offloading to the BS can be calculated as .
According to the above model, the amount of computational offloading by the UAV can be determined. can be calculated as
where is the offloading decision of the UAV, and when , it means that the UAV is offloading the computational tasks to the HAP, and vice versa, to the BS.
3.2. Queue Model
The UAV has a large buffer queue for storing collected data. The queue backlog is calculated by
where denotes the data collected by the UAV and can be processed from the next time slot. Itsignifies the overall volume of data exiting the UAV’s buffer queue. is the amount of data processed by the UAV, and it is calculated by . represents the frequency of the CPU used by the UAV for local computation, and is the computational density of the UAV, which is the number of CPU cycles needed to process a single bit.
The computation resource capacities and abilities of the BS and HAP are much more larger than that of UAVs; thereby, the data can be processed in time without causing data backlogs. The CPU frequency of the HAP is calculated by , where denotes the computational density of HAP. Similarly, the CPU frequency of the BS is calculated by , where denotes the computational density of the BS.
3.3. Energy Consumption Model
The total energy consumption accounts for the energy costs of the UAV, HAP, and BS. Consequently, can be expressed as
3.3.1. UAV Energy Consumption
The total UAV energy consumption is calculated as
where the energy of processing data on the UAV is . According to the circuit theory, , is the size of the effective switching capacitance of the CPU.
The energy consumption of the data is offloaded to the HAP or BS and can be obtained by , where the transmission energy required for offloading computational tasks to the HAP is , and to the BS is .
The flight energy of UAV movement is calculated according to the equation . Similarly to [34,35,36], is the propulsion power and its calculation formula is
where is the UAV’s velocity, denotes the tip velocity of the rotor blade, and , , , and are constants depending on the weight of the UAV and its aerodynamic parameters.
3.3.2. HAP Energy Consumption
The HAP only considers the energy consumption for computing data, and it is calculated by . The computational power of HAP is given as
where is the capacitance at the HAP, and denotes the CPU frequency of the HAP used in processing the offloaded tasks, respectively.
3.3.3. BS Energy Consumption
Similar to the HAP, the energy consumption of the BS is calculated by . The computational power of BS is given as
where is the capacitance at the BS, and denotes the CPU frequency of the BS used in processing the offloaded tasks, respectively.
4. Problem Formulation and Transformation
4.1. Problem Formulation
Considering the demands for ultra-reliable communication and seamless coverage for IoT applications in the areas of lack of terrestrial communication network coverage or network capacity is insufficient, the integrated network is proposed in this paper to meet the above challenge. However, the limited computation resources and battery capacity of airborne devices pose a significant challenge in providing services to IoT devices for extended periods. Therefore, the objective is to optimize the system’s long-term average energy efficiency by comprehensively considering bandwidth allocation for UAV data collection, UAV trajectory planning, offloading decisions, and computational resource allocation in constraints of queue stability, communication, and computation resources. The data processed consist of both the data handled locally by the UAV and the data offloaded to the HAP or BS, i.e., .
The optimization issue is defined as follows:
where denotes the optimization variables. and are constraints on the bandwidth allocation ratio, ensuring that the total bandwidth used for data collection does not exceed the total bandwidth . and give the initial point and final point of the task. and give the boundaries and maximum speed of the UAV trajectory, where and are the upper and lower boundaries, respectively. and denote the UAV’s computation frequency and transmit power constraints. means that the UAV keeps the task queue steady by ensuring that all arriving computation tasks are completed in a finite time. and are the processing weight and energy consumption weight, respectively, indicating whether the UAV favors processing more data or saving more energy in completing the task.
4.2. Problem Transformation by Lyapunov Optimization
Lyapunov optimization involves modeling a queue to address constraints within stochastic optimization problems. This approach decouples the problem from the time dimension by breaking down the operations necessary to satisfy long-term constraints into individual time slices. Furthermore, the queue’s size is factored into the algorithm. By doing so, the system can achieve a stable state, facilitating the optimization objective [37]. Consequently, Lyapunov optimization theory can be used to convert problem . Firstly, the Lyapunov function is defined as
Then, the Lyapunov drift is characterized by the expected change in the value of :
To optimize energy efficiency while maintaining queue stability, the Lyapunov drift with penalty is given by the sum of the expected Lyapunov drift and the average energy efficiency weighted by the parameter V. Thus, the Lyapunov drift plus penalty function is
where is the weight coefficient for balancing the stability of the mission queue and the optimization objective. Similar to [38], with the rise of V, the system’s constraint on the queue length becomes less, and, hence, the queue backlog will increase.
The UAV queue can be obtained by
which is transformed to give
Based on the above equation, we can obtain
where C is a positive constant.
The deterministic problem formulation for each time slot is expressed as
where the constraints – are the same as in . The objective function is expressed as
To solve , the approach relies solely on the current queue status, without requiring any knowledge of future task arrivals or wireless channel conditions. This characteristic qualifies it as an online optimization method. The following section will present a TD3-based online optimization algorithm designed to efficiently address .
5. TD3-Based Joint Computation Offloading and UAV Trajectory Optimization Algorithm
The problem , derived from Lyapunov optimization, is inherently NP-hard, featuring high dimensionality, nonlinearity, and mixed integers, which poses challenges for traditional optimization methods to solve. Additionally, the fluctuating wireless communication environment and resources contribute to its dynamic nature, which renders it particularly suitable for resolution using DRL methods [31]. To solve this NP-hard problem, we propose an algorithm based on TD3. TD3 is an enhanced version of the DDPG algorithm that alleviates the issue of overestimating the Q-function of DDPG on the Q-value, thereby achieving improved performance [39]. To tackle the issue of bias overestimation, TD3 incorporates three essential techniques: (1) clipped double Q-learning, (2) target policy smoothing regularization, and (3) delayed policy updates [40]. The following section offers a brief overview of the TD3 algorithm framework in relation to these techniques.
5.1. TD3 Framework
The TD3 algorithm comprises six DNNs: an Actor policy network with parameter , two Critic value networks with parameters and , along with their corresponding Target Actor target policy network with parameter , and Target Critic target value networks with parameters and [41]. Refer to Figure 2 for an illustration.
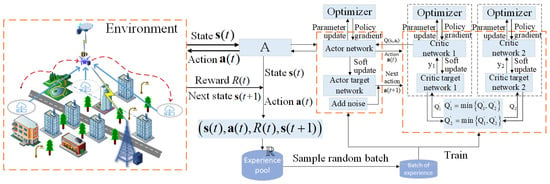
Figure 2.
TD3 network architecture and algorithm flow.
5.1.1. Experience Generation
Based on the current state , the agent derives actions through the policy network . These actions can be expressed as
where denotes a random Gaussian noise with a mean of zero and variance . denotes the boundary trimming function, which limits the noise value to a specific range. The added noise helps to avoid falling into local optima and improves exploration efficiency [42]. Initially, a higher variance is employed to capture a broader array of experience samples. Over time, this variance is systematically decreased to facilitate stable convergence of the algorithm [43]. The agent engages with the environment by executing the noisy action and subsequently receives the reward and observes the next state . This interaction forms an an experience tuple , serving as the training dataset for the online networks. The experience replay mechanism is a vital component of reinforcement learning, as it aids in breaking the correlation between experience data and enhances the algorithm’s convergence performance [44].
5.1.2. Training and Updating of Critic Network
When the replay buffer exceeds its capacity, a small random batch of tuples is sampled for training the online network. The two critic networks are updated by minimizing the temporal difference (TD) error [45]. For each tuple in the sampled batch, the Q-values are approximated by the critic networks as and , respectively. The target Q-value is
where is the discount factor. To address the Q-value overestimation issue, the smallest Q-value from the two “twin” Critic networks is selected and used to update the target Q-value. This approach helps mitigate the problem of Q-value overestimation [46].
Based on the estimated and target Q-values, the loss functions of the two evaluated Critic networks are expressed as
Then, the policy gradient of the loss function is expressed as
Lastly, we can update the parameter as follows:
where is the learning rate.
5.1.3. Training and Updating of Actor Network
The agent’s goal is to optimize the total rewards, while the Q-value measures the expected long-term rewards for taking specific actions in the current state. Throughout the entire training process, the Actor network aims to generate actions that maximize these Q-values, ultimately maximizing the cumulative reward. Consequently, the loss functions are expressed as
The parameter is updated via a deterministic policy gradient, which is denoted by the following formula:
TD3 uses the strategy of delayed Actor network update, which updates after a fixed step size. Therefore, the equation for the parameter update is as follows:
where is the learning rate.
5.1.4. Updating of Target Network
Finally, the target Actor and Critic networks are updated utilizing the soft update method, and are expressed as follows:
where and are the soft update rates.
5.2. TD3-Based Joint Computation Offloading and UAV Trajectory Optimization Algorithm Design
In order to efficiently address the problem , we introduce the TCOTO algorithm, which leverages the advanced DRL model TD3 for problem-solving. During the training process, the UAV functions as an agent, with the TCOTO network and experience buffer implemented on the UAV’s edge server. The buffer gathers and stores information about the agent’s interactions with the environment. Using this historical data, the TCOTO network refines its strategies to guide the UAV in making optimal decisions. Once the Actor network has been thoroughly trained, it can directly provide strategies for computation offloading and UAV trajectory optimization based on the current environmental conditions, continuing until the task is finished. Consequently, the basic elements of TD3 will be discussed in detail in the following sections.
5.2.1. State Space
The state space encompasses all potential states. In our proposed architecture, the state space can be represented as
where denotes the 2D coordinates of the UAV in a given area, denotes the 2D coordinates of the IoT devices, and is the length of the UAV buffer queue, respectively.
5.2.2. Action
In order to solve the computational offloading and UAV trajectory optimization problems, the agent’s actions are defined as follows:
where represents the portion of bandwidth assigned to the UAV for gathering sensor data; is the UAV’s speed and is the angle of flight, which determine the UAV’s position at the next time ; is the offloading decision of the UAV; is the amount of data the UAV offloads to the HAP or BS; is the CPU frequency used by the UAV to process data. Since the values in the action space are continuous variables, the joint problem is a continuous control problem.
5.2.3. Action
At each time slot, upon executing actions , the agent receives an instantaneous reward from the environment. Since the goal of this paper is to optimize long-term energy efficiency, the reward function can be expressed as
In addition to satisfying the objective function, the reward needs to satisfy some additional reward and penalty mechanisms to meet the constraints:
- Penalty for UAV flight trajectory outside of boundaries: UAVs may fly out of the set boundary ranges while performing computation and communication tasks. Since the IoT devices are within the boundary range, UAVs out of boundaries will waste resources. To alleviate this problem, we have designed a penalty mechanism that defines a penalty function based on the distance the UAV exceeds the boundary, which can be expressed aswhere denotes the penalty coefficient for UAV outside of boundaries. and denote the distances at which the UAV exceeds the x-axial and y-axial boundaries in the time slot , respectively.
- Reward for the UAV to reach the final position: the reward represents the “attractiveness” of the final point to the UAV, encouraging it to reach the final point within the allowed time. The additional reward is defined aswhere is the remaining available time of the mission period, and is the minimum time taken required for the UAV to reach the final point in time slot . can be expressed asThis indicates that the earlier the UAV approaches the final position, the more rewards it will receive. is the priority weight for the UAV to reach the final position before the end of the mission.
The detailed flow of the TCOTO algorithm is shown in Algorithm 1.
| Algorithm 1 TCOTO |
|
6. Simulation and Performance Evaluation
This section starts by outlining the simulation environment and the parameter settings. We then evaluate the performance of the proposed TCOTO algorithm against several benchmark algorithms and conduct a detailed analysis of the optimal strategies. Finally, we examine in detail the impact of different system parameters on performance metrics.
6.1. Parameter Setting
We analyze a network setup featuring a UAV and eight IoT devices, which are randomly placed within a remote square area measuring 1000 ∗ 1000 . The UAV operates at an altitude of . The total mission duration is set to 100 , with . The other parameters are shown in Table 2.

Table 2.
Simulation parameters.
The simulation experiments are run on the Python 3.6 development environment and TensorFlow deep learning framework. The TCOTO algorithm deploys an Actor network with four fully connected hidden layers. The actions are output through the hyperbolic tangent function and the output dimensions of 600, 300, 200, and 10. The Critic network features three dense hidden layers. The initial layer processes the input states and actions, producing a 600-dimensional output after applying the weight matrix. The other hidden layers output dimensions of 300 and 10, respectively, and the fully connected layer outputs a Q-value.
We adopt the following four benchmark algorithms with the proposed algorithm together to evaluate the joint optimization schemes.
- DQN-based Joint Computation Offloading and UAV Trajectory Optimization (DQN-COTO) Algorithm: DQN is a widely recognized DRL algorithm noted for its effectiveness in problems involving finite action and state spaces. For addressing continuous space challenges, the action space is divided into multiple distinct levels, allowing the agent to choose from these predefined options.
- AC-based Joint Computation Offloading and UAV Trajectory Optimization (AC-COTO) Algorithm: The AC algorithm is an algorithm based on value functions and random strategies. When choosing an action, it is not entirely certain, but rather based on a certain probability distribution.
- DDPG-based Joint Computation Offloading and UAV Trajectory Optimization (DDPG-COTO) Algorithm: DDPG is a well-established DRL technique designed for continuous spaces, built on the Actor-Critic (AC) framework. It differs from the AC method by using a deterministic policy, where the Actor network produces specific action values directly. Furthermore, DDPG introduces two target networks and employs soft parameter updates to boost the stability and convergence of the learning process.
- TCOTO algorithm (without HAP): To demonstrate the superiority of AGIN scenarios, we also set up the TCOTO algorithm in scenarios where HAP is not involved in data computation. This algorithm follows the same implementation as the proposed one, but the UAV has only two options: process data locally or offload them to a distant BS.
6.2. Performance Analysis
Figure 3 shows the average reward regarding four joint optimization algorithms in each iteration based on the Lyapunov drift weight coefficient . The average reward after convergence of the proposed method is improved by 4.54%, 79.66%, and 249.13% compared to the DDPG-CTO, AC-CTO, and DQN-COTO algorithms, respectively. It can be observed that, at the start of the training phase, the average reward increases as the number of episodes grows. This is because the agent has learned to choose appropriate strategies to adapt to dynamic environments, such as computation offloading and UAV trajectories. After the intelligent agent further learns reward and punishment constraints in exploration, the proposed algorithm will gradually converge, and the final average reward will fluctuate around its convergence value. The proposed TCOTO algorithm ultimately achieves a higher average reward, which means it has an advantage over the other three algorithms. During the training process, the DDPG-COTO algorithm can obtain higher rewards compared to the TCOTO algorithm because TD3 introduces delayed policy updates during updates, which can avoid premature convergence of the policy to local optima. Moreover, our TCOTO algorithm demonstrates greater stability after convergence. This is because TD3 employs two Critic networks to address the overestimation issues seen in DDPG, thereby reducing Q-value estimation errors. Due to the limited number of discrete values in the action space of DQN, there are few strategies available for the agent to choose from. Moreover, DQN does not incorporate action exploration during training, which can easily lead to convergence.
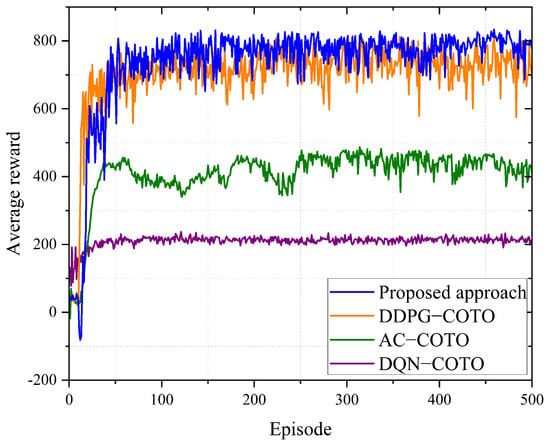
Figure 3.
Reward performance per episode.
Figure 4 shows the average energy efficiency over time slots. The average energy efficiency is obtained by dividing the amount of data processed and the energy consumption of the whole system (including UAV, HAP, and BS) at each time slot. It is evident that both the proposed algorithm and the four benchmark algorithms can achieve stable energy efficiency benefits. However, the energy efficiency of the proposed approach is increased by 3.77%, 22.90%, and 67.62% compared to the DDPG-COTO, AC-COTO, and DQN-COTO algorithms, respectively. This is because the proposed algorithm improves stability and efficiency by the three techniques introduced in Section 5, thus avoiding local optimums. Hence, the TCOTO algorithm achieves higher rewards in the training and convergence phases. UAV plans reasonable trajectories while ensuring queue stability, and making energy-saving offloading decisions for collected data, enabling the system to process more data with minimal energy consumption and avoiding resource waste. Furthermore, the energy efficiency of the TCOTO algorithm within the proposed architecture surpasses that of the system architecture without HAP. This superiority arises because the UAV can make suitable offloading decisions tailored to different environmental conditions in each time slot, thereby reducing energy consumption. This further highlights the advantages of the integrated architecture, showing that the TCOTO algorithm delivers the highest performance.
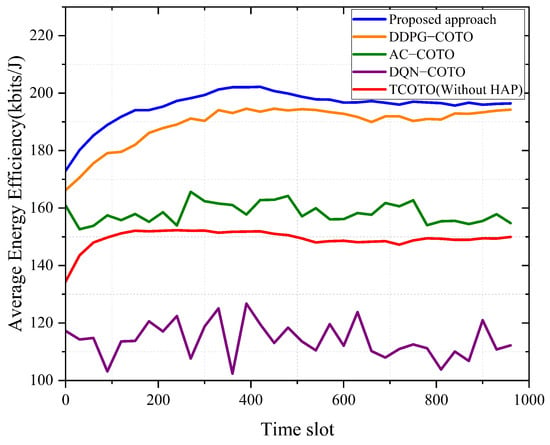
Figure 4.
Average energy efficiency of the system over time slots.
Figure 5 investigates the impact of parameter V on the average energy efficiency of the system. From the figure, it can be seen that when V is small (i.e., ), energy efficiency increases rapidly as V increases. When , energy efficiency remains relatively stable. When V is large (i.e., ), energy efficiency decreases sharply as V increases. After determining the iteration count and other parameters, the selection of parameter V will significantly affect the performance of our proposed algorithm in terms of system energy efficiency. According to Equation (20) in Section 4, we can know that as V increases, the system’s constraints on the queue will decrease, leading to an increase in queue backlog. Therefore, when , as V increases, the system’s constraint on the queue will become smaller, and at this point, the UAV will tend to collect more data. When the amount of data collected does not exceed its processing limit, the UAV can process more data at the same flight cost, thereby increasing the energy efficiency of the system. When the collected data approach the limit that the UAV can withstand (i.e., ), the growth rate of system energy efficiency tends to stabilize. But when the collected data exceed the limit that the UAV can withstand (i.e., ), the UAV requires additional energy cost to calculate or offload tasks, leading to reduced energy efficiency. With the ongoing increase in data volume, the UAV’s energy efficiency experiences a sharp decline. Therefore, we need to find a suitable value for parameter V to maintain the UAV queue at a reasonable length, thereby maximizing the system’s energy efficiency.
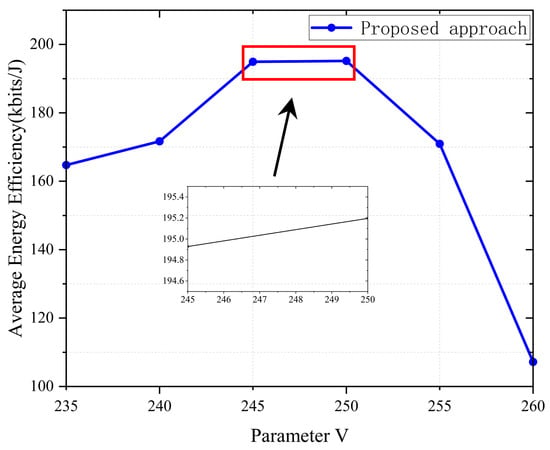
Figure 5.
Effect of parameter V on the average energy efficiency of the system.
Figure 6 shows the trajectories of UAV and randomly distributed location IoT devices. Figure 6a represents the 3D trajectories of the UAV, and Figure 6b shows the corresponding 2D trajectories. It can be seen that the UAV can correctly reach the destination to complete the data collection task of IoT devices based on all joint optimization algorithms except for the DQN-COTO, because the limited discrete actions of the DQN-COTO algorithm are not sufficient to support the UAV in making reasonable trajectory planning. In addition, the flight path determined by the proposed algorithm aligns with expectations, as the UAV naturally moves nearer to IoT devices. This approach effectively fulfills the data collection needs from these devices while also minimizing the energy consumption associated with offloading computing tasks. This is because the proposed algorithm understands the reward and penalty constraints well enough to plan better trajectories.
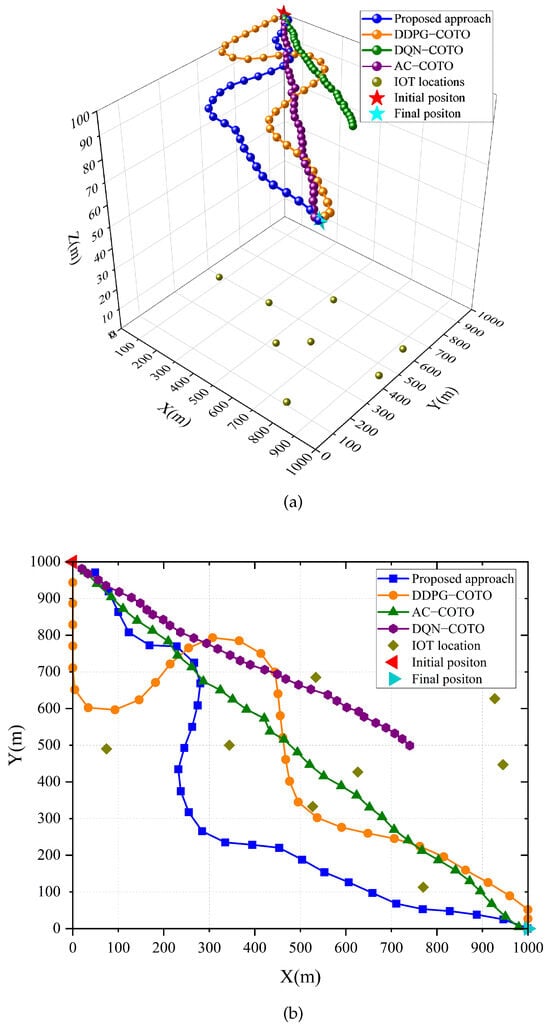
Figure 6.
(a) 3D trajectory map. (b) 2D trajectory map.
Figure 7 shows the variation of average queue backlog with time slots after the algorithm’s reward convergence. After the queue stabilizes, it is clear that the task backlog under the proposed algorithm is significantly less than that observed with the DDPG-COTO, AC-COTO, and DQN-COTO algorithms. This reduction in task backlog occurs because the TCOTO algorithm allows the UAV to adaptively modify its task offloading strategies and flight paths in response to real-time task queue conditions, enabling it to make more efficient decisions and minimize task accumulation. Since the DQN-COTO algorithm is prone to falling into local optimums, it is significantly worse than the other three algorithms at maintaining queue stability. In addition, the queue of the proposed algorithm can remain stable, while the queue of the benchmark algorithm fluctuates greatly. This is because the TCOTO algorithm has good performance in computation offloading and UAV trajectory strategy, and the data collected by the UAV can be processed quickly without causing a serious queue backlog.
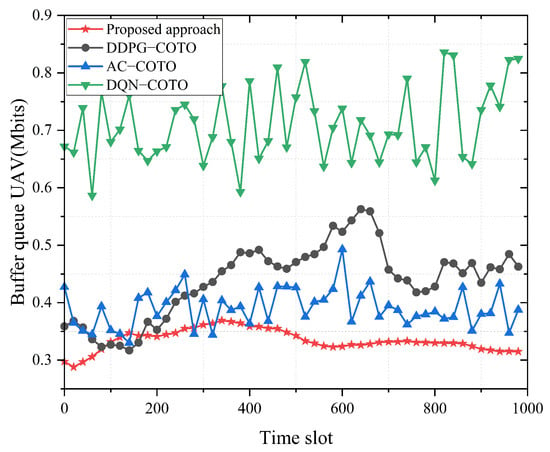
Figure 7.
Average queue length of UAV over time slots.
7. Conclusions
This paper investigated the optimization problem of joint computation offloading and UAV trajectory planning in EI-powered air-ground integrated networks. This study focus was on enhancing the long-term average energy efficiency while maintaining the stability of the UAV’s long-term queue. The proposed online algorithm integrates Lyapunov optimization and DRL methods, converting the initial long-term optimization challenge into a manageable short-term problem within each time slot. It then dynamically refines the computation offloading and UAV trajectory strategies using an effective DRL approach. Simulation results show that our proposed algorithm performs well in making decisions based on the current environment, thus significantly improving the energy efficiency of the system. The proposed algorithm improved the performance of the system energy efficiency by 3.77%, 22.90%, and 67.62%, respectively, compared to the other three benchmark schemes. In our future work, we plan to explore the maximization of energy efficiency in multi-UAV scenarios by leveraging a multi-agent DRL algorithm.
Author Contributions
Conceptualization, Q.L. (Qian Liu), Z.Q., S.W. and Q.L. (Qilie Liu); methodology, Q.L. (Qian Liu) and Z.Q.; software, Z.Q.; investigation, Q.L. (Qian Liu) and Z.Q.; writing—original draft preparation, Q.L. (Qian Liu) and Z.Q.; writing—review and editing, Q.L. (Qian Liu) and Z.Q.; visualization, Z.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the 2023 Chongqing Postdoctoral Special Funding Project (No. 2312013543381155), in part by the Youth Project of Chongqing Municipal Education Commission Science and Technology Research Program under Grant KJQN202200645, and in part by the Doctoral Initial Funding of Chongqing University of Posts and Telecommunications under Grant A2021-195(E012A2021195).
Data Availability Statement
The data are not publicly available due to ownership reasons.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Qian, L.P.; Wu, Y.; Yu, N.; Wang, D.; Jiang, F.; Jia, W. Energy-Efficient Multi-Access Mobile Edge Computing with Secrecy Provisioning. IEEE Trans. Mob. Comput. 2023, 22, 237–252. [Google Scholar] [CrossRef]
- Narayan, M.S.; Trivedi, M.C.; Dubey, A. Securing Data in the Internet of Things (IoT) using Metamorphic Cryptography—A Survey. In Proceedings of the 2023 International Conference on Computational Intelligence, Communication Technology and Networking (CICTN), Ghaziabad, India, 20–21 April 2023; pp. 401–406. [Google Scholar]
- Li, X.; He, J.; Vijayakumar, P.; Zhang, X.; Chang, V. A Verifiable Privacy-Preserving Machine Learning Prediction Scheme for Edge-Enhanced HCPSs. IEEE Trans. Ind. Inform. 2022, 18, 5494–5503. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV Communications for 5G and Beyond: Recent Advances and Future Trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Qin, P.; Fu, Y.; Xie, Y.; Wu, K.; Zhang, X.; Zhao, X. Multi-agent learning-based optimal task offloading and UAV trajectory planning for AGIN-power IoT. IEEE Trans. Commun. 2023, 71, 4005–4017. [Google Scholar] [CrossRef]
- Deng, S.; Zhao, H.; Fang, W.; Yin, J.; Dustdar, S.; Zomaya, A.Y. Edge Intelligence: The Confluence of Edge Computing and Artificial Intelligence. IEEE Internet Things J. 2020, 7, 7457–7469. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, D.; Zhou, L.; Qian, Y. Radio Resource Allocation for Integrated Sensing, Communication, and Computation Networks. IEEE Trans. Wirel. Commun. 2022, 21, 8675–8687. [Google Scholar] [CrossRef]
- Liu, W.; Jin, Z.; Zhang, X.; Zang, W.; Wang, S.; Shen, Y. AoI-Aware UAV-Enabled Marine MEC Networks with Integrated Sensing, Computation, and Communication. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Dalian, China, 10–12 August 2023; pp. 1–6. [Google Scholar]
- Alsabah, M.; Naser, M.A.; Mahmmod, B.M.; Abdulhussain, S.H.; Eissa, M.R.; Al-Baidhani, A.; Noordin, N.K.; Sait, S.M.; Al-Utaibi, K.A.; Hashim, F. 6G Wireless Communications Networks: A Comprehensive Survey. IEEE Access 2021, 9, 148191–148243. [Google Scholar] [CrossRef]
- Banafaa, M.K.; Pepeoğlu, Ö.; Shayea, I.; Alhammadi, A.; Shamsan, Z.Ö.A.; Razaz, M.A.; Alsagabi, M.; Al-Sowayan, S. A Comprehensive Survey on 5G-and-Beyond Networks with UAVs: Applications, Emerging Technologies, Regulatory Aspects, Research Trends and Challenges. IEEE Access 2024, 12, 7786–7826. [Google Scholar] [CrossRef]
- Jia, Z.; Wu, Q.; Dong, C.; Yuen, C.; Han, Z. Hierarchical Aerial Computing for Internet of Things via Cooperation of HAPs and UAVs. IEEE Internet Things J. 2023, 10, 5676–5688. [Google Scholar] [CrossRef]
- Truong, T.P.; Tran, A.T.; Nguyen, T.M.T.; Nguyen, T.V.; Masood, A.; Cho, S. MEC-Enhanced Aerial Serving Networks via HAP: A Deep Reinforcement Learning Approach. In Proceedings of the 2022 International Conference on Information Networking (ICOIN), Jeju-si, Republic of Korea, 12–15 January 2022; pp. 319–323. [Google Scholar]
- Gan, Y.; He, Y. Trajectory Optimization and Computing Offloading Strategy in UAV-Assisted MEC System. In Proceedings of the 2021 Computing, Communications and IoT Applications (ComComAp), Shenzhen, China, 26–28 November 2021; pp. 132–137. [Google Scholar]
- Lai, X.; Guo, Y.; Li, N.; Yuan, H.; Li, W. Resource Allocation and Trajectory Optimization of the U-MEC System Based on Contractual Relationship Under the Incentive of Revenue. In Proceedings of the 2023 IEEE International Conference on Unmanned Systems (ICUS), Hefei, China, 13–15 October 2023; pp. 69–74. [Google Scholar]
- Luo, Y.; Wang, Y.; Lei, Y.; Wang, C.; Zhang, D.; Ding, W. Decentralized User Allocation and Dynamic Service for Multi-UAV-Enabled MEC System. IEEE Trans. Veh. Technol. 2024, 73, 1306–1321. [Google Scholar] [CrossRef]
- Wang, L.; Wang, K.; Pan, C.; Xu, W.; Aslam, N.; Hanzo, L. Multi-Agent Deep Reinforcement Learning-Based Trajectory Planning for Multi-UAV Assisted Mobile Edge Computing. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 73–84. [Google Scholar] [CrossRef]
- Du, X.; Li, X.; Zhao, N.; Wang, X. A Joint Trajectory and Computation Offloading Scheme for UAV-MEC Networks via Multi-Agent Deep Reinforcement Learning. In Proceedings of the ICC 2023 - IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 5438–5443. [Google Scholar]
- He, Y.; Gan, Y.; Cui, H.; Guizani, M. Fairness-Based 3-D Multi-UAV Trajectory Optimization in Multi-UAV-Assisted MEC System. IEEE Internet Things J. 2023, 10, 11383–11395. [Google Scholar] [CrossRef]
- Wei, Q.; Zhou, Z.; Chen, X. DRL-Based Energy-Efficient Trajectory Planning, Computation Offloading, and Charging Scheduling in UAV-MEC Network. In Proceedings of the 2022 IEEE/CIC International Conference on Communications in China (ICCC), Foshan, China, 11–13 August 2022; pp. 1056–1061. [Google Scholar]
- Yuan, T.; Rothenberg, C.E.; Obraczka, K.; Barakat, C.; Turletti, T. Harnessing UAVs for Fair 5G Bandwidth Allocation in Vehicular Communication via Deep Reinforcement Learning. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4063–4074. [Google Scholar] [CrossRef]
- Liao, H.; Zhou, Z.; Zhao, X.; Wang, Y. Learning-Based Queue-Aware Task Offloading and Resource Allocation for Space-Air-Ground-Integrated Power IoT. IEEE Internet Things J. 2021, 8, 5250–5263. [Google Scholar] [CrossRef]
- Li, X.; Du, X.; Zhao, N.; Wang, X. Computing Over the Sky: Joint UAV Trajectory and Task Offloading Scheme Based on Optimization-Embedding Multi-Agent Deep Reinforcement Learning. IEEE Trans. Commun. 2024, 72, 1355–1369. [Google Scholar] [CrossRef]
- Lin, N.; Tang, H.; Zhao, L.; Wan, S.; Hawbani, A.; Guizani, M. A PDDQNLP Algorithm for Energy Efficient Computation Offloading in UAV-Assisted MEC. IEEE Trans. Wirel. Commun. 2023, 22, 8876–8890. [Google Scholar] [CrossRef]
- Gao, A.; Wang, Q.; Liang, W.; Ding, Z. Game Combined Multi-Agent Reinforcement Learning Approach for UAV Assisted Offloading. IEEE Trans. Veh. Technol. 2021, 70, 12888–12901. [Google Scholar] [CrossRef]
- Yan, M.; Xiong, R.; Wang, Y.; Li, C. Edge Computing Task Offloading Optimization for a UAV-Assisted Internet of Vehicles via Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 5647–5658. [Google Scholar] [CrossRef]
- Chen, J.; Yi, C.; Li, J.; Zhu, K.; Cai, J. A Triple Learner Based Energy Efficient Scheduling for Multi-UAV Assisted Mobile Edge Computing. In Proceedings of the ICC 2023–IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 3240–3245. [Google Scholar]
- Ma, X.; Yin, C.; Liu, X. Machine Learning Based Joint Offloading and Trajectory Design in UAV Based MEC System for IoT Devices. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; pp. 902–909. [Google Scholar]
- Li, X.; Cheng, S.; Ding, H.; Pan, M.; Zhao, N. When UAVs Meet Cognitive Radio: Offloading Traffic Under Uncertain Spectrum Environment via Deep Reinforcement Learning. IEEE Trans. Wirel. Commun. 2023, 22, 824–838. [Google Scholar] [CrossRef]
- Lei, H.; Ran, H.; Ansari, I.S.; Park, K.H.; Pan, G.; Alouini, M.S. DDPG-based Aerial Secure Data Collection. IEEE Trans. Commun. 2024, 72, 5179–5193. [Google Scholar] [CrossRef]
- Gong, H.; Ge, H.; Ma, S.; Sun, A.; Chen, X.; Liu, L. Task Offloading Strategy Based on TD3 Algorithm in Cloud-Edge Collaborative MEC. In Proceedings of the 2022 4th International Conference on Natural Language Processing (ICNLP), Xi’an, China, 25–27 March 2022; pp. 452–459. [Google Scholar]
- Zhao, T.; Li, F.; He, L. Secure Video Offloading in Multi-UAV-Enabled MEC Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2024, 11, 2950–2963. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, F.R.; Fu, F.; Yan, Q.; Wang, Z. Joint Offloading and Resource Allocation in Mobile Edge Computing Systems: An Actor-Critic Approach. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Peng, H.; Shen, X. Multi-Agent Reinforcement Learning Based Resource Management in MEC- and UAV-Assisted Vehicular Networks. IEEE J. Sel. Areas Commun. 2021, 39, 131–141. [Google Scholar] [CrossRef]
- Mei, H.; Yang, K.; Shen, J.; Liu, Q. Joint Trajectory-Task-Cache Optimization With Phase-Shift Design of RIS-Assisted UAV for MEC. IEEE Wirel. Commun. Lett. 2021, 10, 1586–1590. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, X.; Xia, S.; Ai, Q.; Liu, Q. Energy Minimization for UAV Swarm-Enabled Wireless Inland Ship MEC Network With Time Windows. IEEE Trans. Green Commun. Netw. 2023, 7, 594–608. [Google Scholar] [CrossRef]
- Gao, Z.; Fu, J.; Jing, Z.; Dai, Y.; Yang, L. MOIPC-MAAC: Communication-Assisted Multiobjective MARL for Trajectory Planning and Task Offloading in Multi-UAV-Assisted MEC. IEEE Internet Things J. 2024, 11, 18483–18502. [Google Scholar] [CrossRef]
- Tong, Z.; Cai, J.; Mei, J.; Li, K.; Li, K. Dynamic Energy-Saving Offloading Strategy Guided by Lyapunov Optimization for IoT Devices. IEEE Internet Things J. 2022, 9, 19903–19915. [Google Scholar] [CrossRef]
- Wu, H.; Chen, J.; Nguyen, T.N.; Tang, H. Lyapunov-Guided Delay-Aware Energy Efficient Offloading in IIoT-MEC Systems. IEEE Trans. Ind. Inform. 2023, 19, 2117–2128. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Zhou, X.; Bilal, M.; Dou, R.; Rodrigues, J.J.P.C.; Zhao, Q.; Dai, J.; Xu, X. Edge Computation Offloading With Content Caching in 6G-Enabled IoV. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2733–2747. [Google Scholar] [CrossRef]
- Zheng, C.; Pan, K.; Dong, J.; Chen, L.; Guo, Q.; Wu, S.; Luo, H.; Zhang, X. Multi-Agent Collaborative Optimization of UAV Trajectory and Latency-Aware DAG Task Offloading in UAV-Assisted MEC. IEEE Access 2024, 12, 42521–42534. [Google Scholar] [CrossRef]
- Wang, X.; Shi, H.; Li, Y.; Qian, Z.; Han, Z. Energy Efficiency Resource Management for D2D-NOMA Enabled Network: A Dinkelbach Combined Twin Delayed Deterministic Policy Gradient Approach. IEEE Trans. Veh. Technol. 2023, 72, 11756–11771. [Google Scholar] [CrossRef]
- Fan, W.; Yang, F.; Wang, P.; Miao, M.; Zhao, P.; Huang, T. DRL-Based Service Function Chain Edge-to-Edge and Edge-to-Cloud Joint Offloading in Edge-Cloud Network. IEEE Trans. Netw. Serv. Manag. 2023, 20, 4478–4493. [Google Scholar] [CrossRef]
- Xie, J.; Jia, Q.; Chen, Y.; Wang, W. Computation Offloading and Resource Allocation in Satellite-Terrestrial Integrated Networks: A Deep Reinforcement Learning Approach. IEEE Access 2024, 12, 97184–97195. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Z.; Zhang, J.; Cao, X.; Zheng, D.; Gao, Y.; Ng, D.W.K.; Renzo, M.D. Trajectory Design for UAV-Based Internet of Things Data Collection: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2022, 9, 3899–3912. [Google Scholar] [CrossRef]
- Bai, L.; Zheng, F.; Hou, K.; Liu, X.; Lu, L.; Liu, C. Longitudinal control of automated vehicles: A novel approach by integrating deep reinforcement learning with intelligent driver model. IEEE Trans. Veh. Technol. 2024, 73, 11014–11028. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).