Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning
Abstract
1. Introduction
2. Related Work
3. Methods
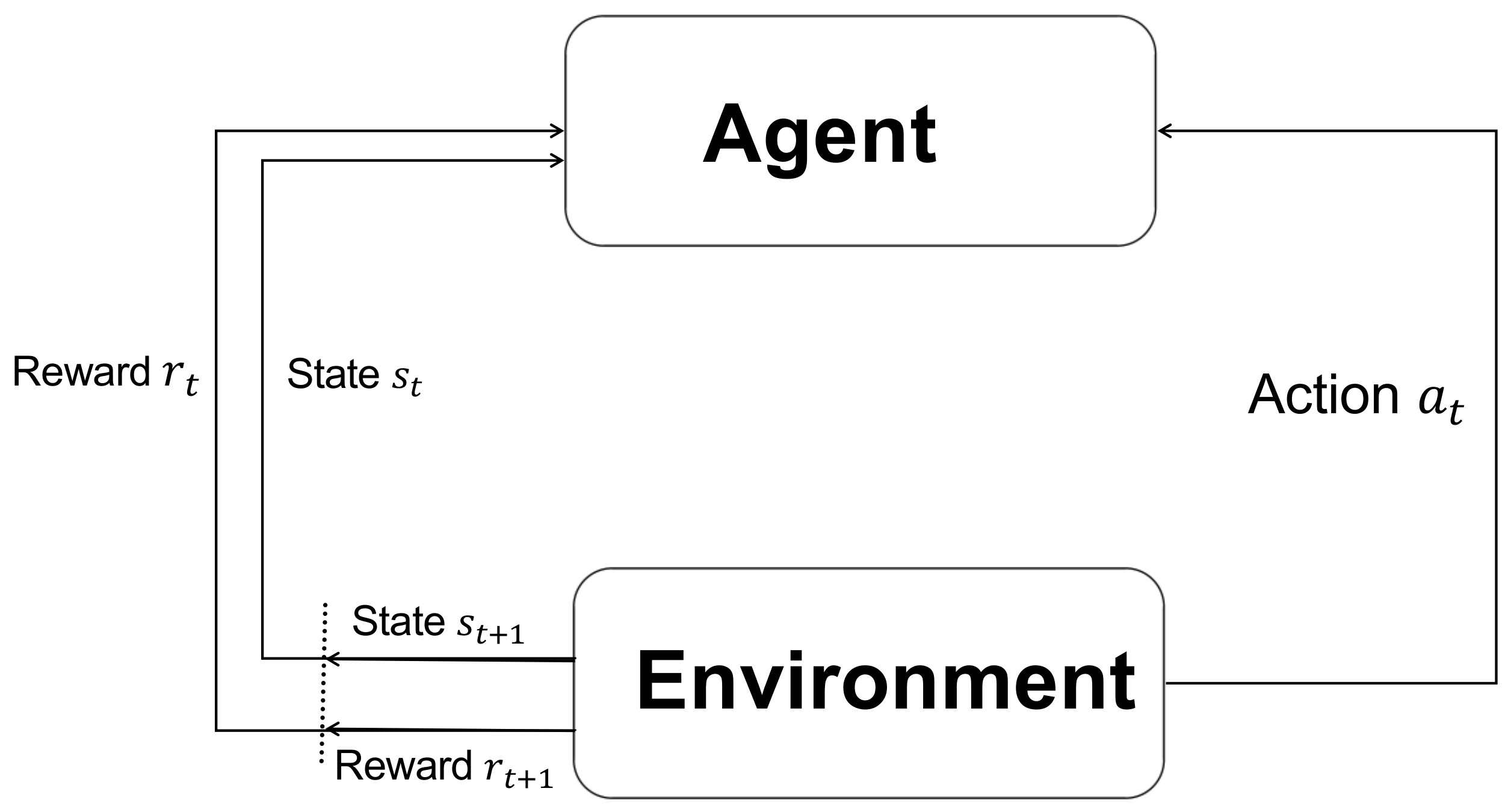
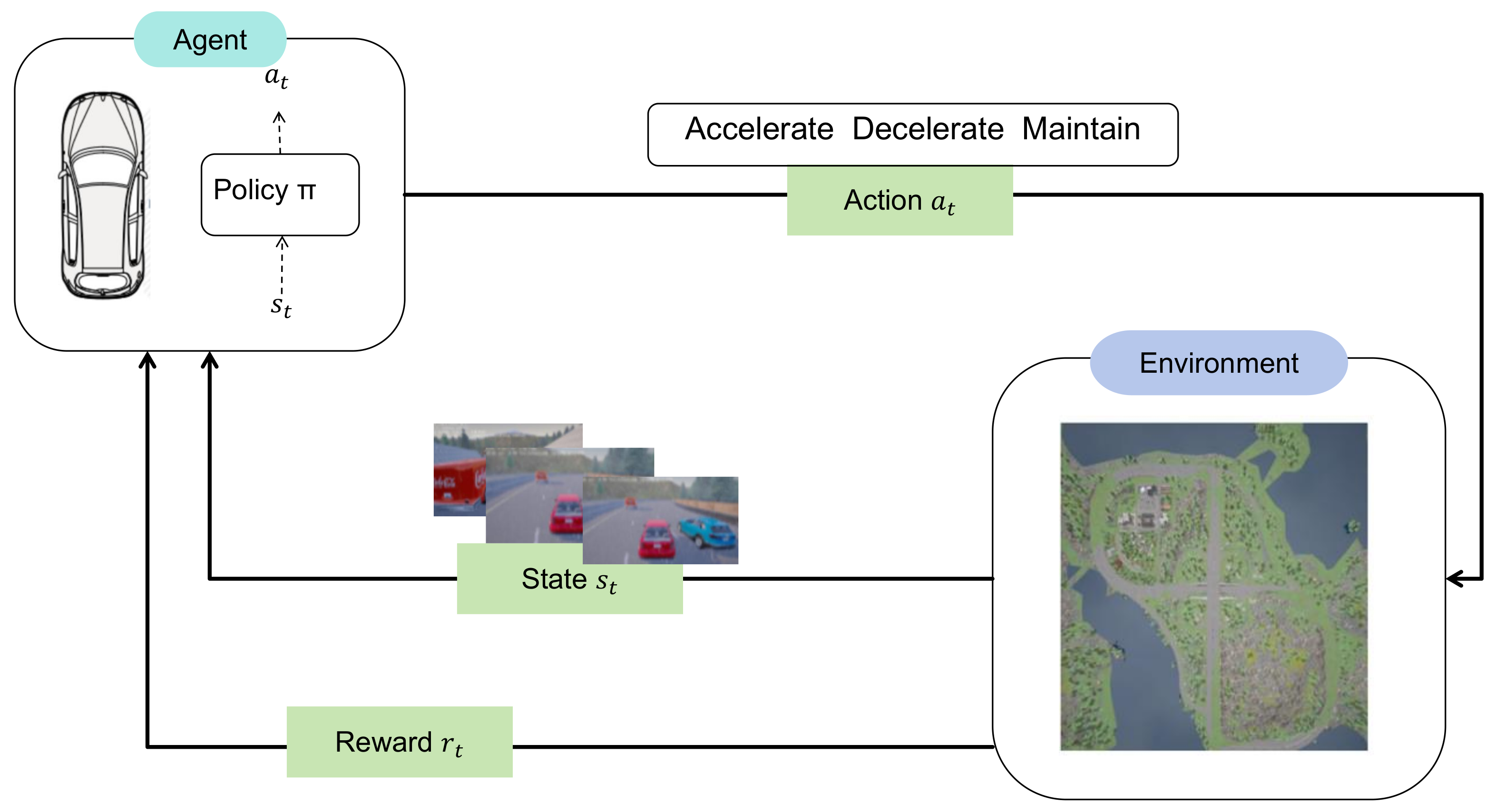
3.1. Markov Decision Process Modeling
3.1.1. State Space
State Space in DQN Variants
State Space in SAC
3.1.2. Action Space
Actions in DQN Variants
- Decelerate (target velocity: 0 units);
- Maintain speed (target velocity: 4.5 units);
- Accelerate (target velocity: 9 units).
Actions in SAC
3.1.3. Reward Function
Reward in DQN Variants
Reward in SAC
3.1.4. Discount Factor:
3.2. The Proposed Framework
3.2.1. Overview
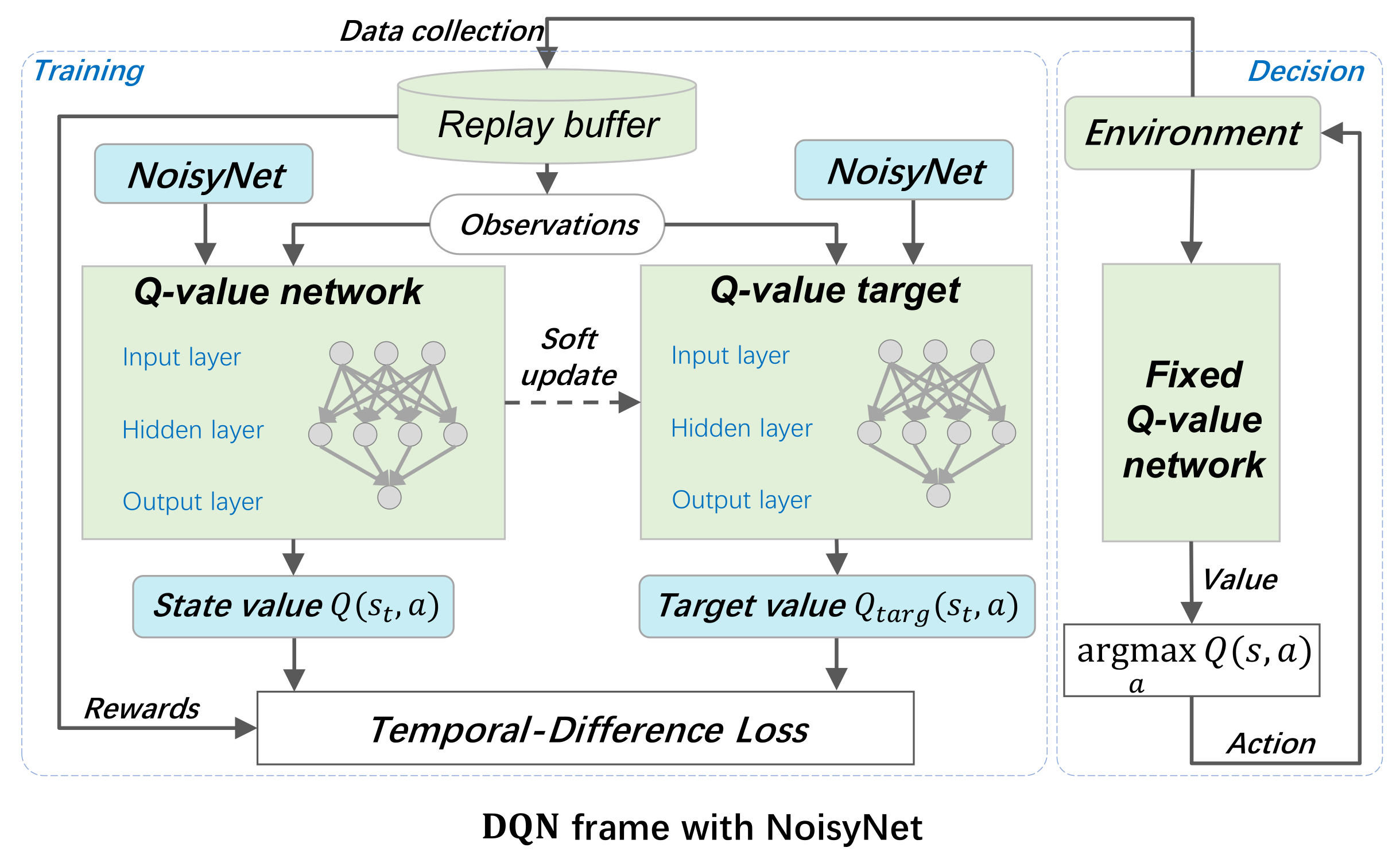
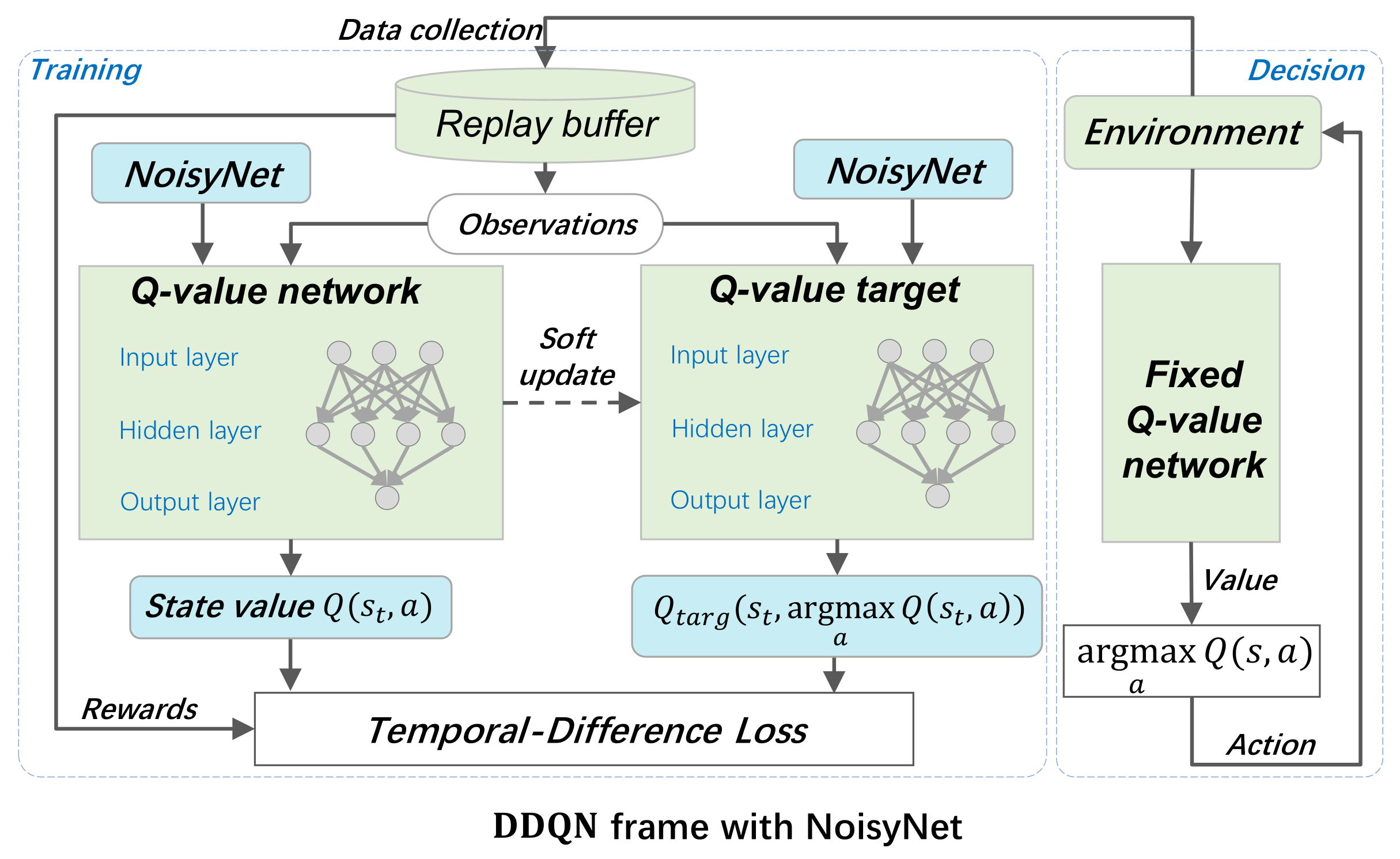
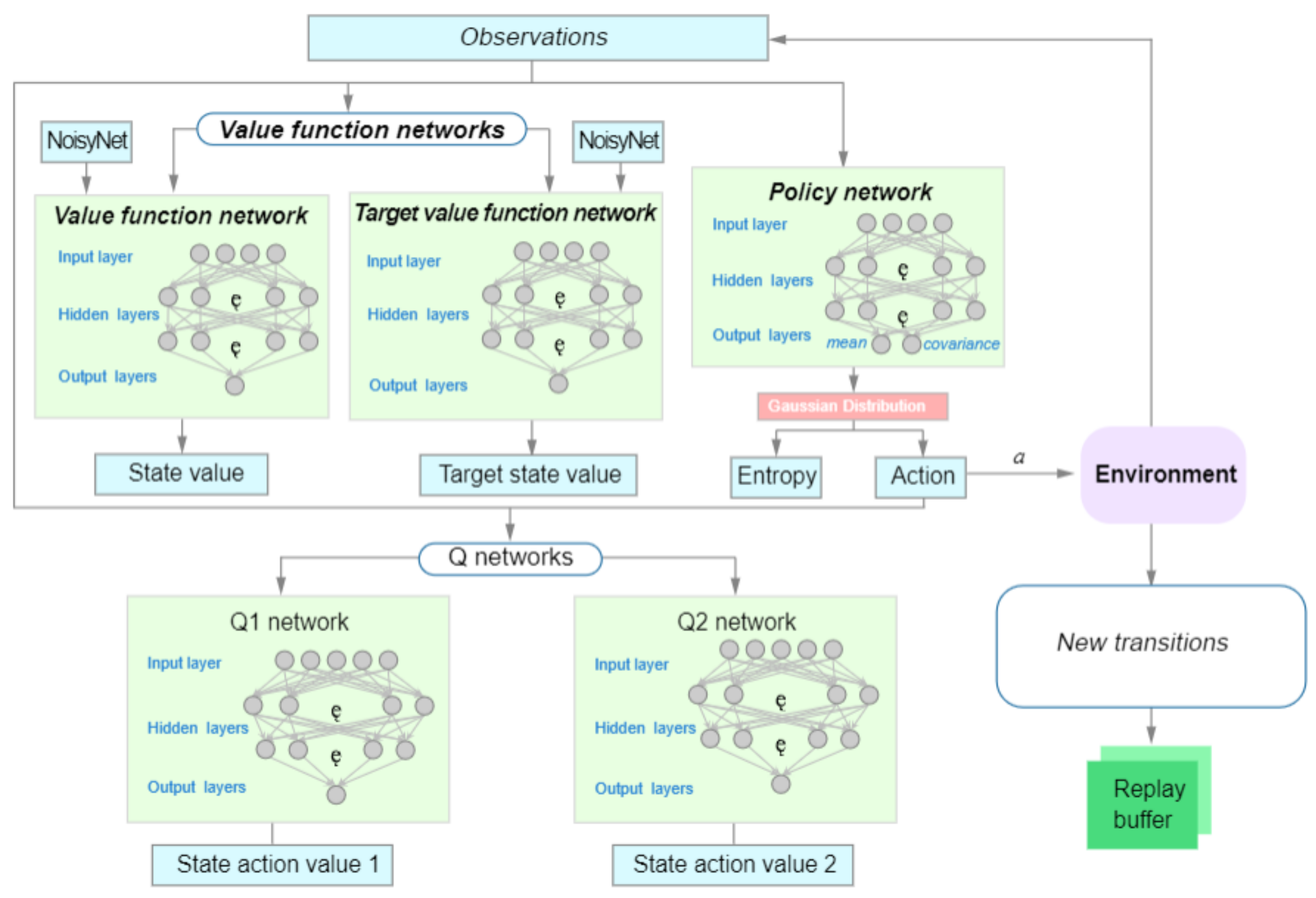
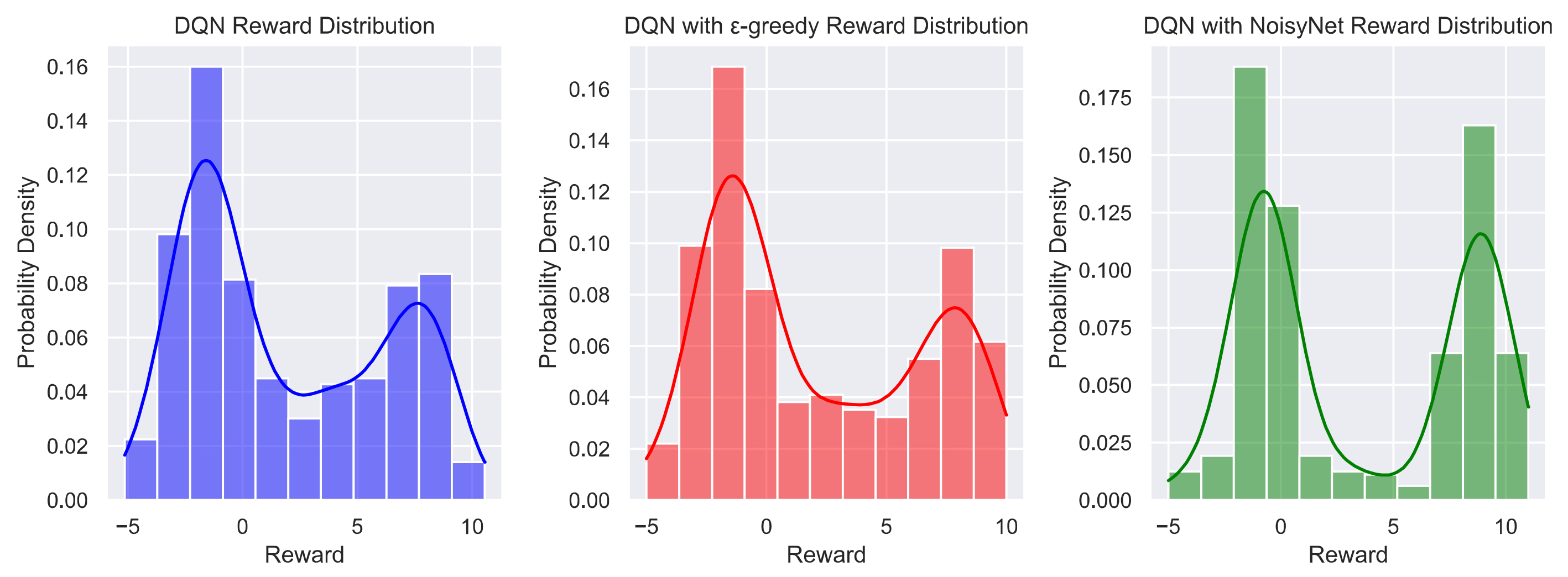
3.2.2. DQN with NoisyNet
3.2.3. DDQN with NoisyNet
| Algorithm 1 DQN with NoisyNet |
| Input: Env: Environment, : a set of random variables for the network, B: initialized as an empty replay buffer, : initial parameters of the network, : initial parameters of the target network, : capacity of the replay buffer, : batch size for training, and : interval for updating the target network Output:
|
| Algorithm 2 DDQN with NoisyNet |
| Input: Env: Environment, : a set of random variables for the network, B: initialized as an empty replay buffer, : initial parameters of the network, : initial parameters of the target network, : capacity of the replay buffer, : batch size for training, and : interval for updating the target network Output:
|
3.3. Soft Actor–Critic with Noisy Critic
| Algorithm 3 Soft Actor–Critic with Noisy Critic |
Input: Initial policy parameters ; Q-function parameters ; and empty replay buffer
|
4. Experiment
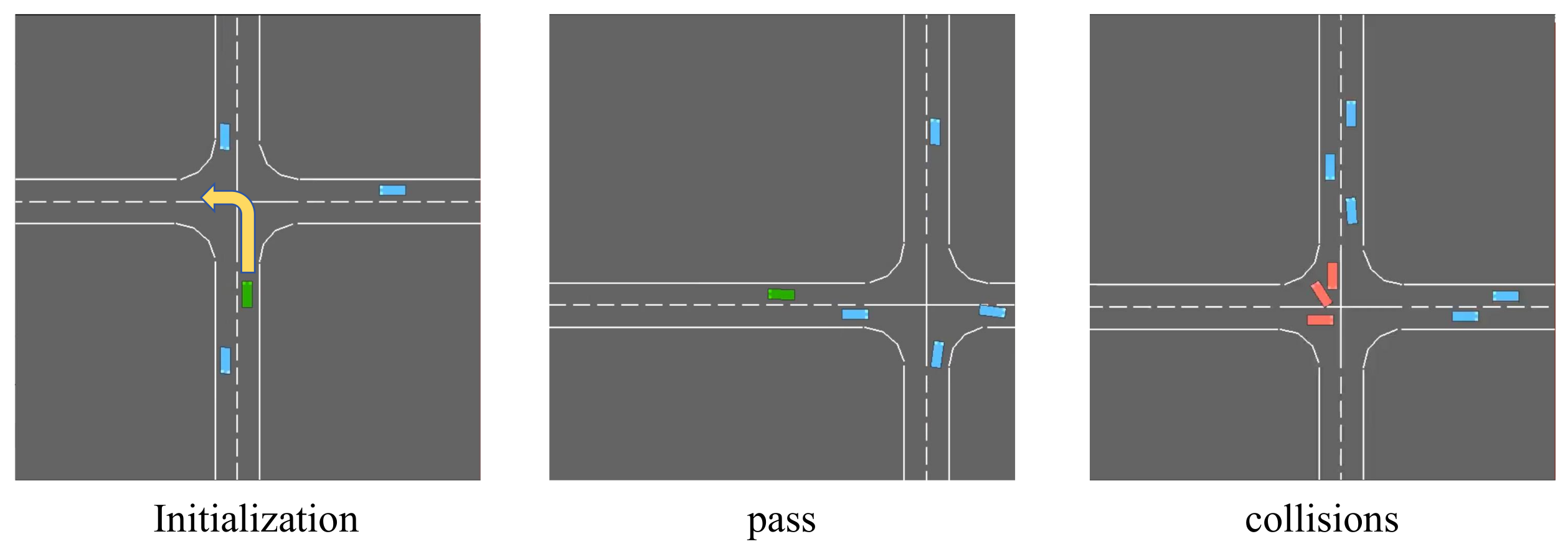
4.1. Experiment in Highway_Env
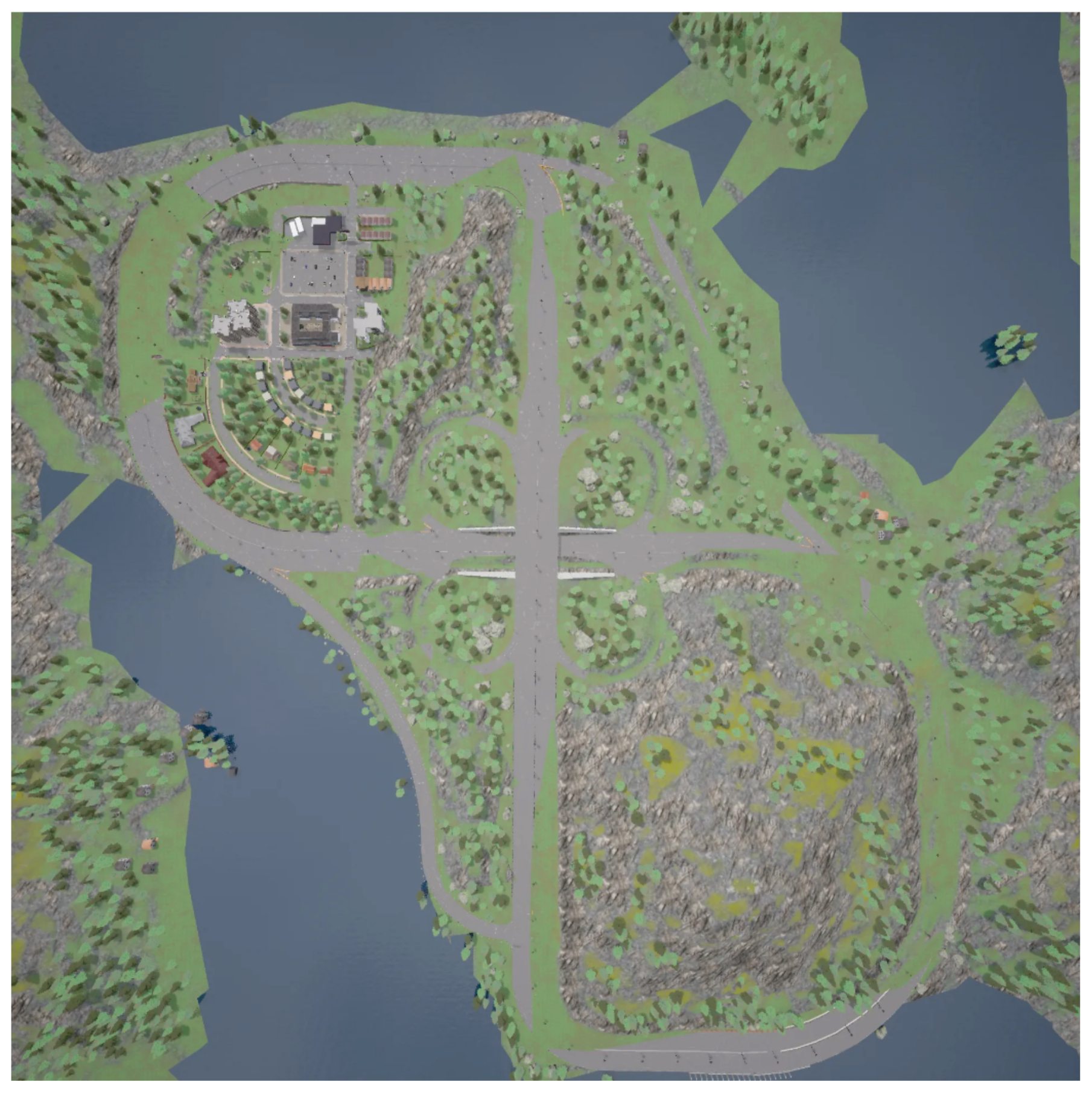
4.2. Experiment in CARLA
5. Results
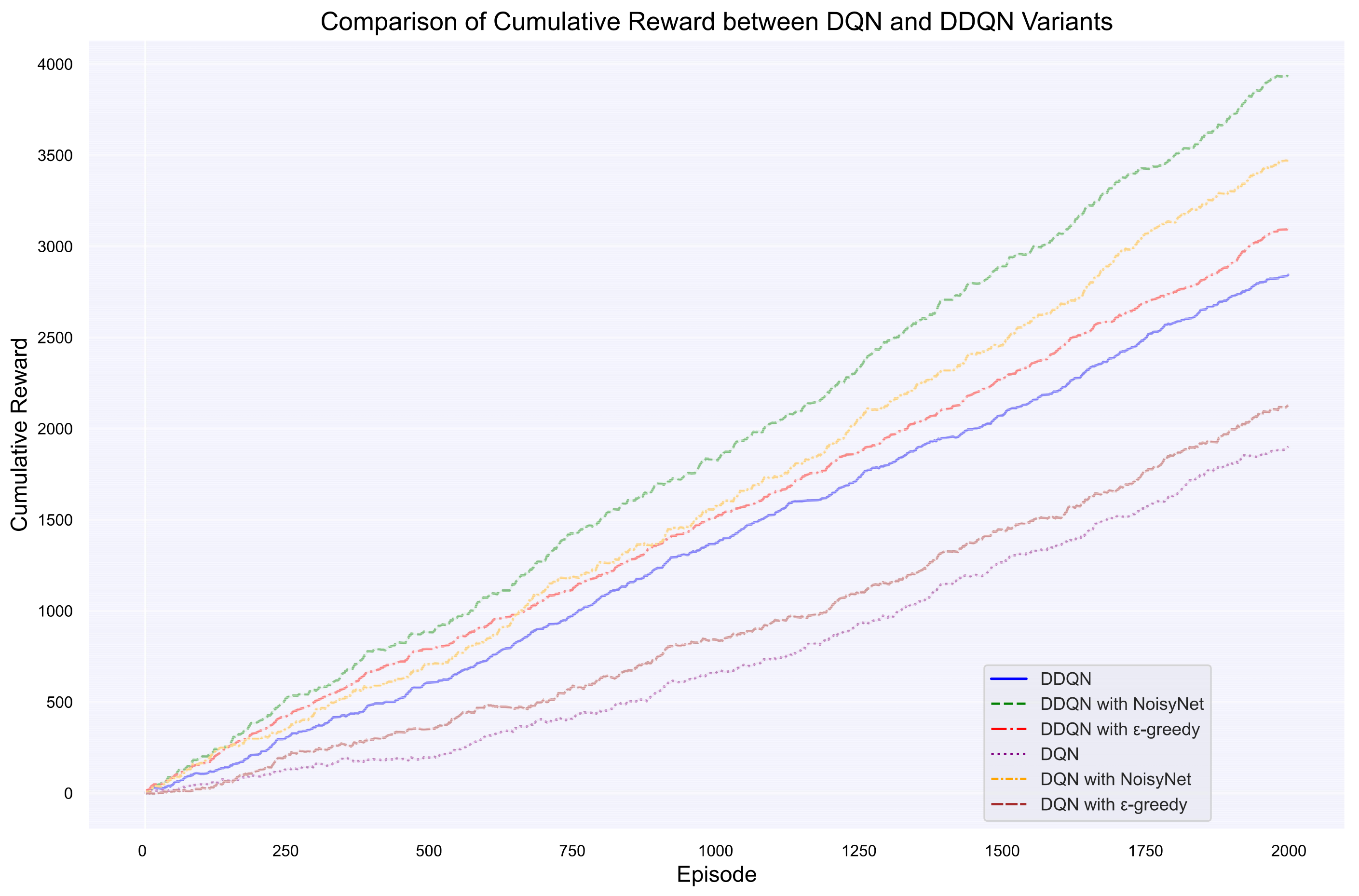
5.1. Results for Highway_Env
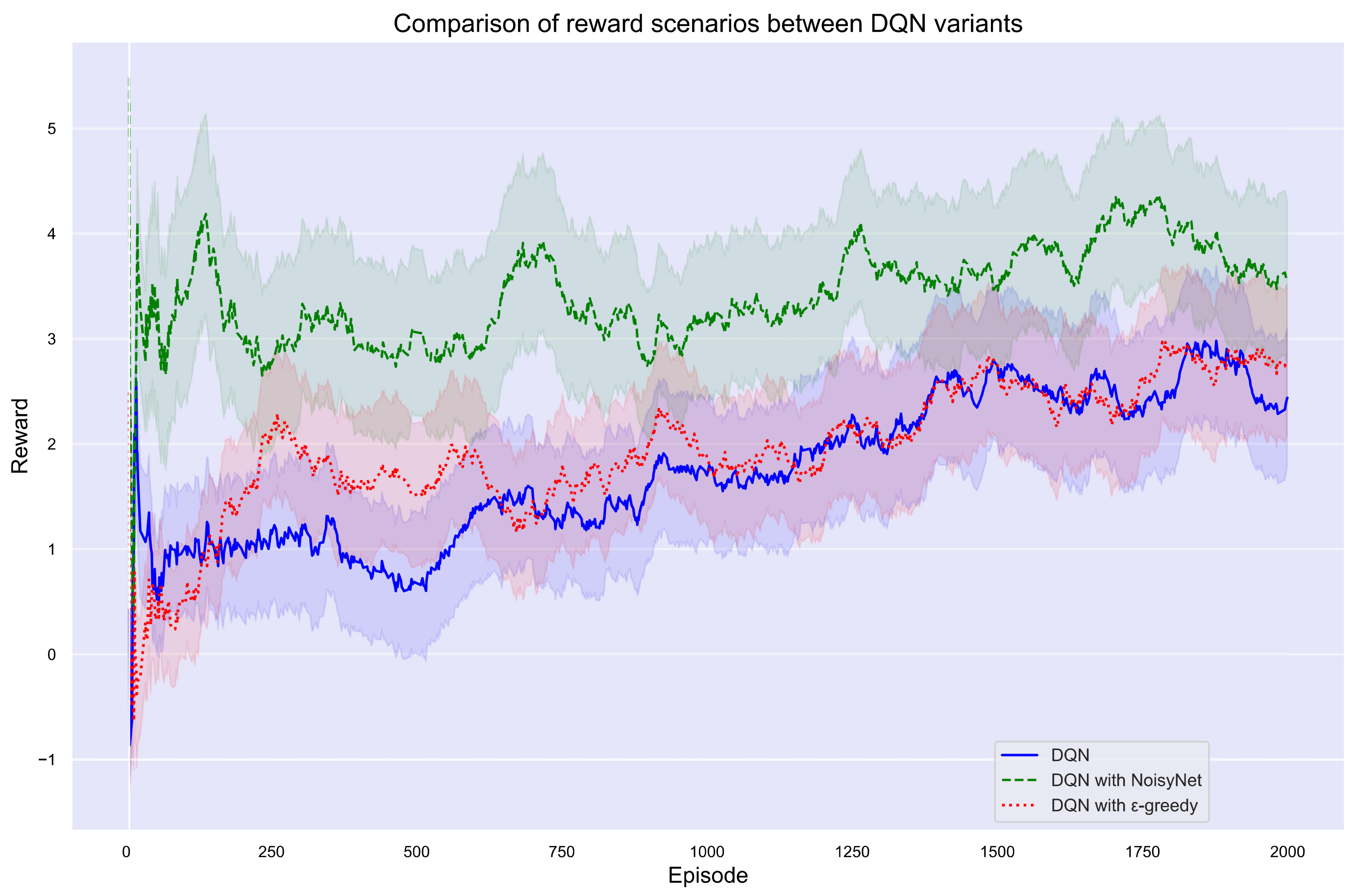
5.1.1. Rewards
5.1.2. Success Rate
5.1.3. Number of Iterations at Convergence
5.1.4. Time for Completion of Tasks
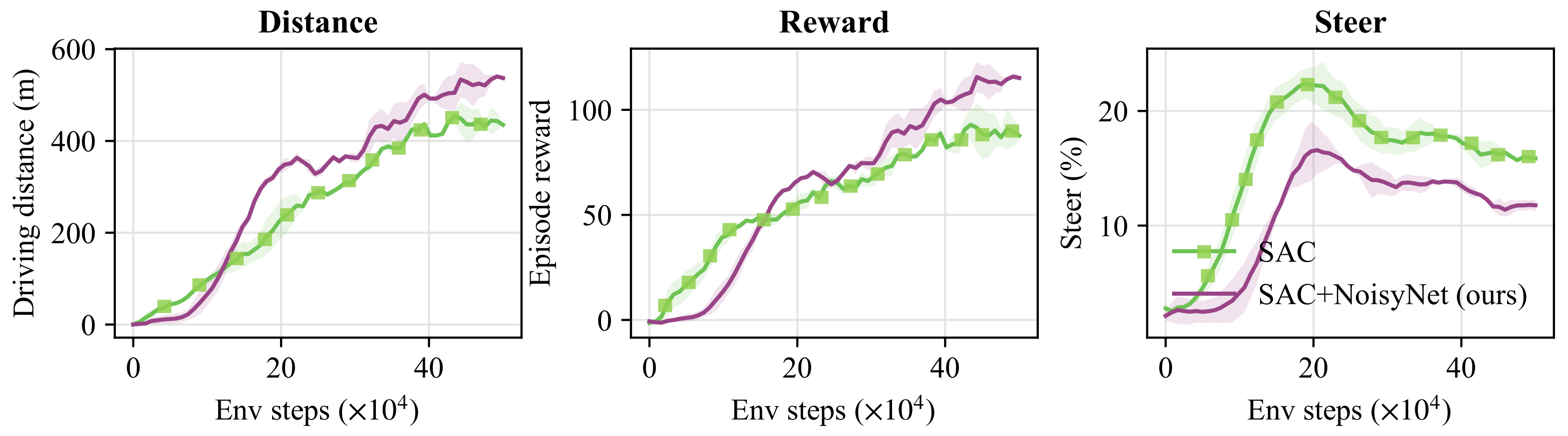
5.2. Result in CARLA
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RL | Reinforcement learning |
| SAC | Soft actor–critic |
| KDE | Kernel density estimate |
| DQN | Deep Q-network |
| DDQN | Double DQN |
| MPC | Model predictive control |
| PID | Proportional–integral–derivative |
| MDP | Markov decision process |
| UAV | Unmanned aerial vehicle |
References
- Althoff, M.; Lutz, S. Automatic generation of safety-critical test scenarios for collision avoidance of road vehicles. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1326–1333. [Google Scholar]
- Gao, F.; Duan, J.; Han, Z.; He, Y. Automatic virtual test technology for intelligent driving systems considering both coverage and efficiency. IEEE Trans. Veh. Technol. 2020, 69, 14365–14376. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, A.; Pu, J.; Yu, J. Multi-modal neural feature fusion for automatic driving through perception-aware path planning. IEEE Access 2021, 9, 142782–142794. [Google Scholar] [CrossRef]
- James, J.; Yu, W.; Gu, J. Online vehicle routing with neural combinatorial optimization and deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3806–3817. [Google Scholar]
- Zhang, Y.; Macke, W.; Cui, J.; Hornstein, S.; Urieli, D.; Stone, P. Learning a robust multiagent driving policy for traffic congestion reduction. Neural Comput. Appl. 2023, 1–14. [Google Scholar] [CrossRef]
- Zhu, L.; Gonder, J.; Bjarkvik, E.; Pourabdollah, M.; Lindenberg, B. An automated vehicle fuel economy benefits evaluation framework using real-world travel and traffic data. IEEE Intell. Transp. Syst. Mag. 2019, 11, 29–41. [Google Scholar] [CrossRef]
- Le-Anh, T.; Koster, M.D. A review of design and control of automated guided vehicle systems. Eur. J. Oper. Res. 2006, 171, 1–23. [Google Scholar] [CrossRef]
- Cheein, F.A.A.; Cruz, C.D.L.; Bastos, T.F.; Carelli, R. Slam-based cross-a-door solution approach for a robotic wheelchair. Int. J. Adv. Robot. Syst. 2009, 6, 20. [Google Scholar] [CrossRef]
- Suh, J.; Chae, H.; Yi, K. Stochastic model-predictive control for lane change decision of automated driving vehicles. IEEE Trans. Veh. Technol. 2018, 67, 4771–4782. [Google Scholar] [CrossRef]
- Wang, P.; Chan, C.-Y.; de La Fortelle, A. A reinforcement learning based approach for automated lane change maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1379–1384. [Google Scholar]
- Aradi, S. Survey of deep reinforcement learning for motion planning of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 23, 740–759. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Li, J.; Chen, Y.; Zhao, X.; Huang, J. An improved dqn path planning algorithm. J. Supercomput. 2022, 78, 616–639. [Google Scholar] [CrossRef]
- Alizadeh, A.; Moghadam, M.; Bicer, Y.; Ure, N.K.; Yavas, U.; Kurtulus, C. Automated lane change decision-making using deep reinforcement learning in dynamic and uncertain highway environments. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1399–1404. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Liao, J.; Liu, T.; Tang, X.; Mu, X.; Huang, B.; Cao, D. Decision-making strategy on the highway for autonomous vehicles using deep reinforcement learning. IEEE Access 2020, 8, 177804–177814. [Google Scholar] [CrossRef]
- Seong, H.; Jung, C.; Lee, S.; Shim, D.H. Learning to drive at unsignalized intersections using attention-based deep reinforcement learning. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 559–566. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Chen, D.; Jiang, L.; Wang, Y.; Li, Z. Autonomous driving using safe reinforcement learning by incorporating a regret-based human lane-changing decision model. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4355–4361. [Google Scholar]
- He, X.; Yang, H.; Hu, Z.; Lv, C. Robust lane change decision making for autonomous vehicles: An observation adversarial reinforcement learning approach. IEEE Trans. Intell. Veh. 2022, 8, 184–193. [Google Scholar] [CrossRef]
- Li, G.; Yang, Y.; Li, S.; Qu, X.; Lyu, N.; Li, S.E. Decision making of autonomous vehicles in lane change scenarios: Deep reinforcement learning approaches with risk awareness. Transp. Res. Part C Emerg. Technol. 2022, 134, 103452. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, S.; Zhou, Y.; Li, Z. An integrated model for autonomous speed and lane change decision-making based on deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21848–21860. [Google Scholar] [CrossRef]
- Hoel, C.-J.; Tram, T.; Sjöberg, J. Reinforcement learning with uncertainty estimation for tactical decision-making in intersections. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
- Zhang, C.; Kacem, K.; Hinz, G.; Knoll, A. Safe and rule-aware deep reinforcement learning for autonomous driving at intersections. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2708–2715. [Google Scholar]
- Chen, L.; Hu, X.; Tang, B.; Cheng, Y. Conditional dqn-based motion planning with fuzzy logic for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2020, 23, 2966–2977. [Google Scholar] [CrossRef]
- Li, G.; Li, S.; Li, S.; Qin, Y.; Cao, D.; Qu, X.; Cheng, B. Deep reinforcement learning enabled decision-making for autonomous driving at intersections. Automot. Innov. 2020, 3, 374–385. [Google Scholar] [CrossRef]
- Wu, Y.; Tucker, G.; Nachum, O. Behavior regularized offline reinforcement learning. arXiv 2019, arXiv:1911.11361. [Google Scholar]
- Kim, H.; Wan, W.; Hovakimyan, N.; Sha, L.; Voulgaris, P. Robust vehicle lane keeping control with networked proactive adaptation. Artif. Intell. 2023, 325, 104020. [Google Scholar] [CrossRef]
- Yang, J.; Kim, H.; Wan, W.; Hovakimyan, N.; Vorobeychik, Y. Certified robust control under adversarial perturbations. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 4090–4095. [Google Scholar]
- Plappert, M.; Houthooft, R.; Dhariwal, P.; Sidor, S.; Chen, R.Y.; Chen, X.; Asfour, T.; Abbeel, P.; Andrychowicz, M. Parameter space noise for exploration. arXiv 2017, arXiv:1706.01905. [Google Scholar]
- Leurent, E. An Environment for Autonomous Driving Decision-Making. 2018. Available online: https://github.com/eleurent/highway-env (accessed on 29 March 2024).
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An open urban driving simulator. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]




| Hyperparameter | Value |
|---|---|
| Camera number | 3 |
| Full FOV angles | degrees |
| Observation downsampling | |
| Initial exploration steps | 100 |
| Training frames | 500,000 |
| Replay buffer capacity | 30,000 |
| Batch size | 64 |
| Action repeat | 4 |
| Stacked frames | 3 |
| t | 0.05 s |
| 0.0001 | |
| 1.0 | |
| Learning rate | 0.0005 |
| Optimizer | Adam |
| Reward | Success Rate | Minimum Number of Times to Complete | Time for Completion of Tasks | |
|---|---|---|---|---|
| DQN | 2.62 | 52.8% | 1220 | 6.58 s |
| DQN with -greedy | 3.05 | 62.5% | 1240 | 6.41 s |
| DQN with NoisyNet | 3.72 | 88.9% | 240 | 6.01 s |
| DDQN | 2.85 | 68.6% | 370 | 6.40 s |
| DDQN with -greedy | 3.17 | 74.5% | 290 | 6.25 s |
| DDQN with NoisyNet | 4.12 | 91.2% | 210 | 5.93 s |
| Improvement | 57.25% | 72.73% | 82.79% | 10.96% |
| Methods | Distance | Eval Reward | Steer (%) |
|---|---|---|---|
| SAC | 454.1 ± 13.6 | 92.9 ± 7.0 | 22.4 ± 1.3 |
| SAC + NoisyNet (ours) | 540.5 ± 2.7 | 115.8 ± 1.5 | 16.6 ± 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Chen, J.; Zhang, F.; Liu, M.; Zhou, M. Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning. Drones 2024, 8, 470. https://doi.org/10.3390/drones8090470
Shi H, Chen J, Zhang F, Liu M, Zhou M. Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning. Drones. 2024; 8(9):470. https://doi.org/10.3390/drones8090470
Chicago/Turabian StyleShi, Haotian, Jiale Chen, Feijun Zhang, Mingyang Liu, and Mengjie Zhou. 2024. "Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning" Drones 8, no. 9: 470. https://doi.org/10.3390/drones8090470
APA StyleShi, H., Chen, J., Zhang, F., Liu, M., & Zhou, M. (2024). Achieving Robust Learning Outcomes in Autonomous Driving with DynamicNoise Integration in Deep Reinforcement Learning. Drones, 8(9), 470. https://doi.org/10.3390/drones8090470






