Fluid Dynamics of Interacting Rotor Wake with a Water Surface
Abstract
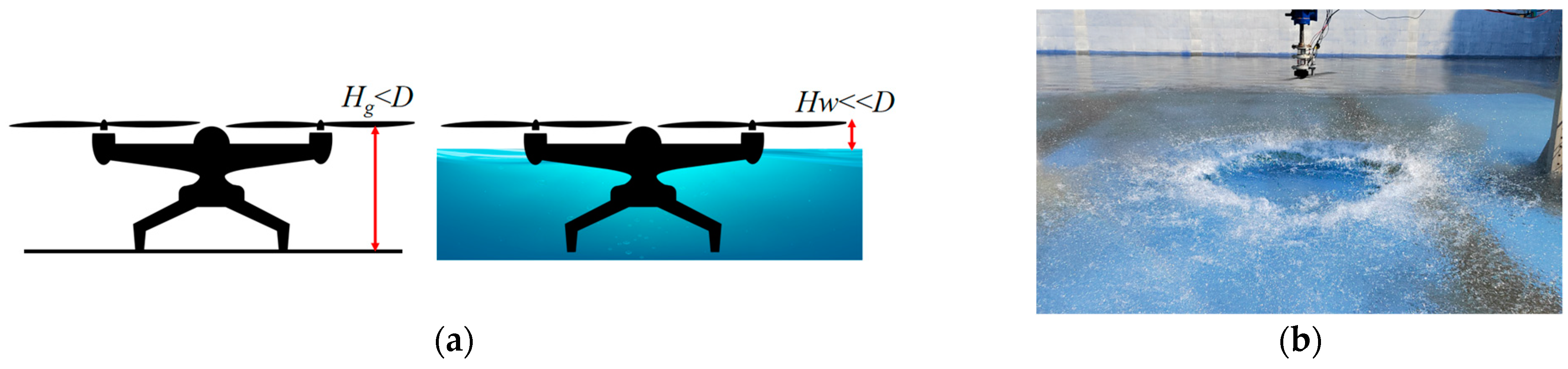
1. Introduction
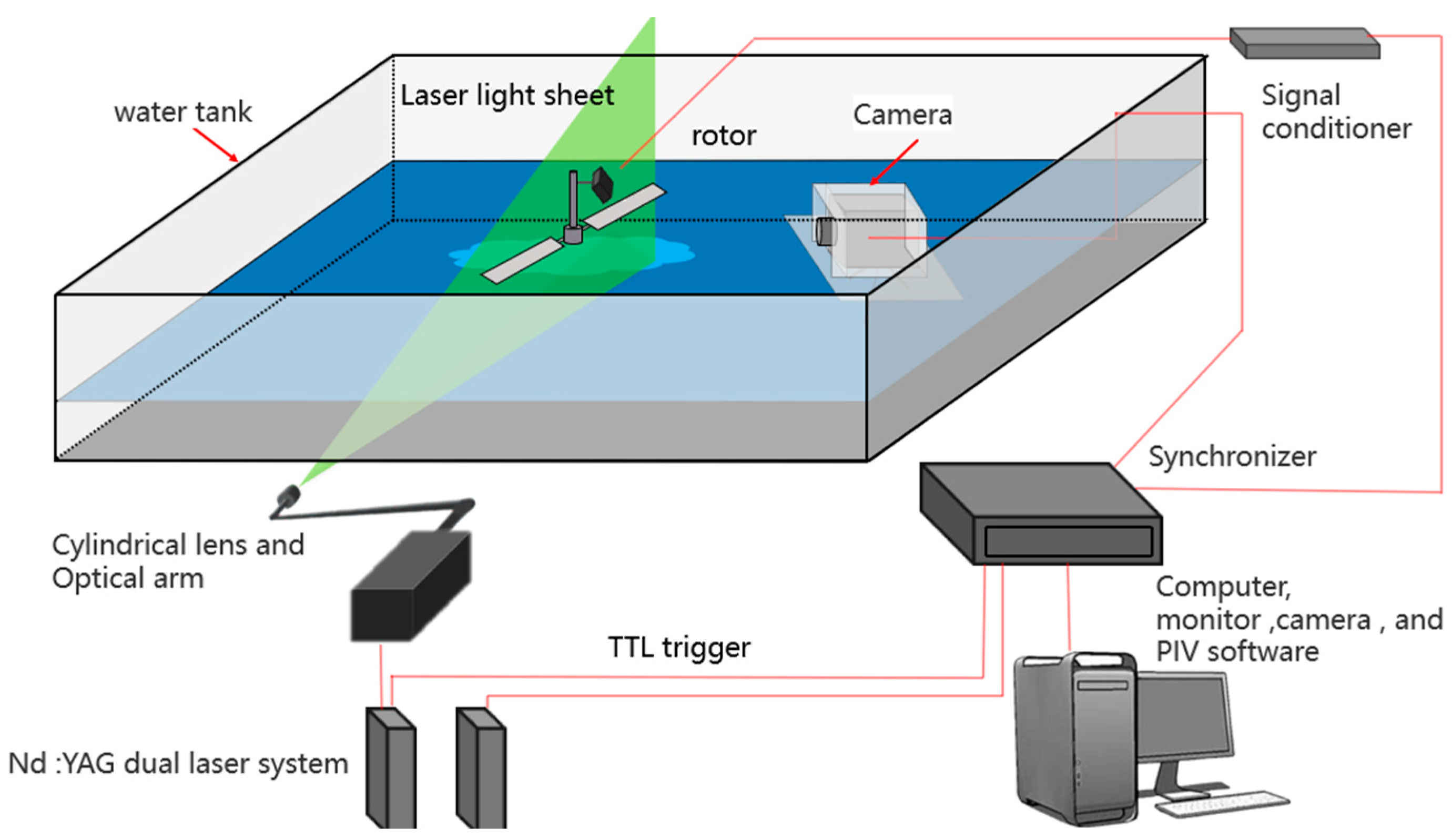
2. Experimental Setup and Measurements
2.1. Droplet Observation
2.2. Particle Image Velocimetry
3. Results and Discussions
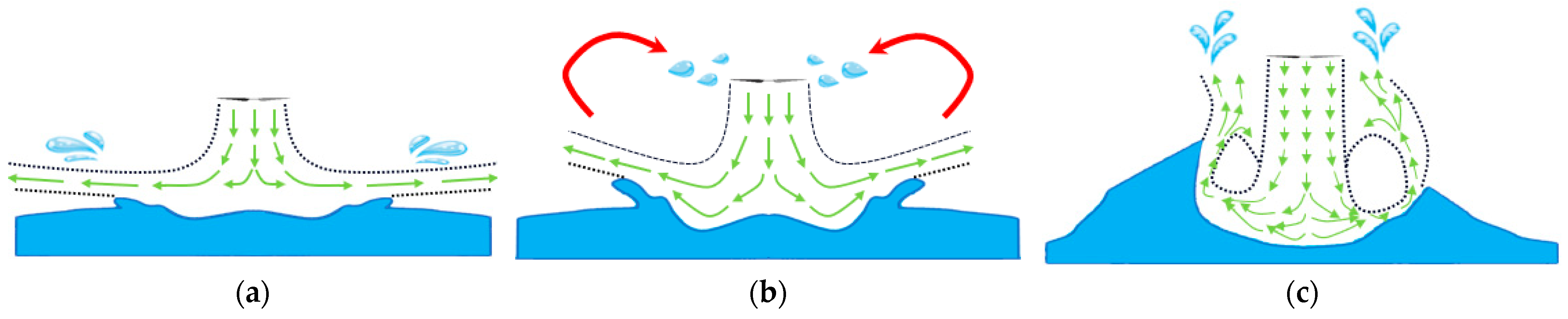
3.1. Qualitative Description of Droplet Formation and Splash
3.1.1. Dimpling Mode
3.1.2. Splashing Mode
3.1.3. Penetrating Mode
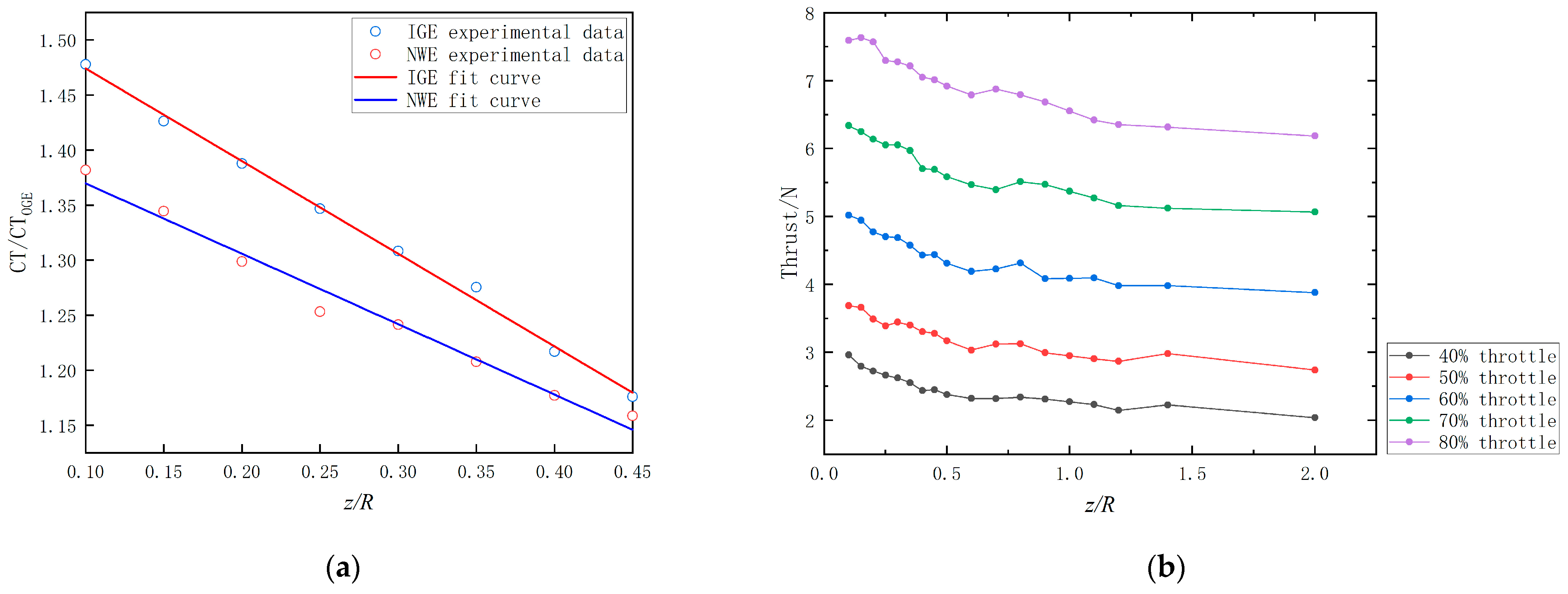
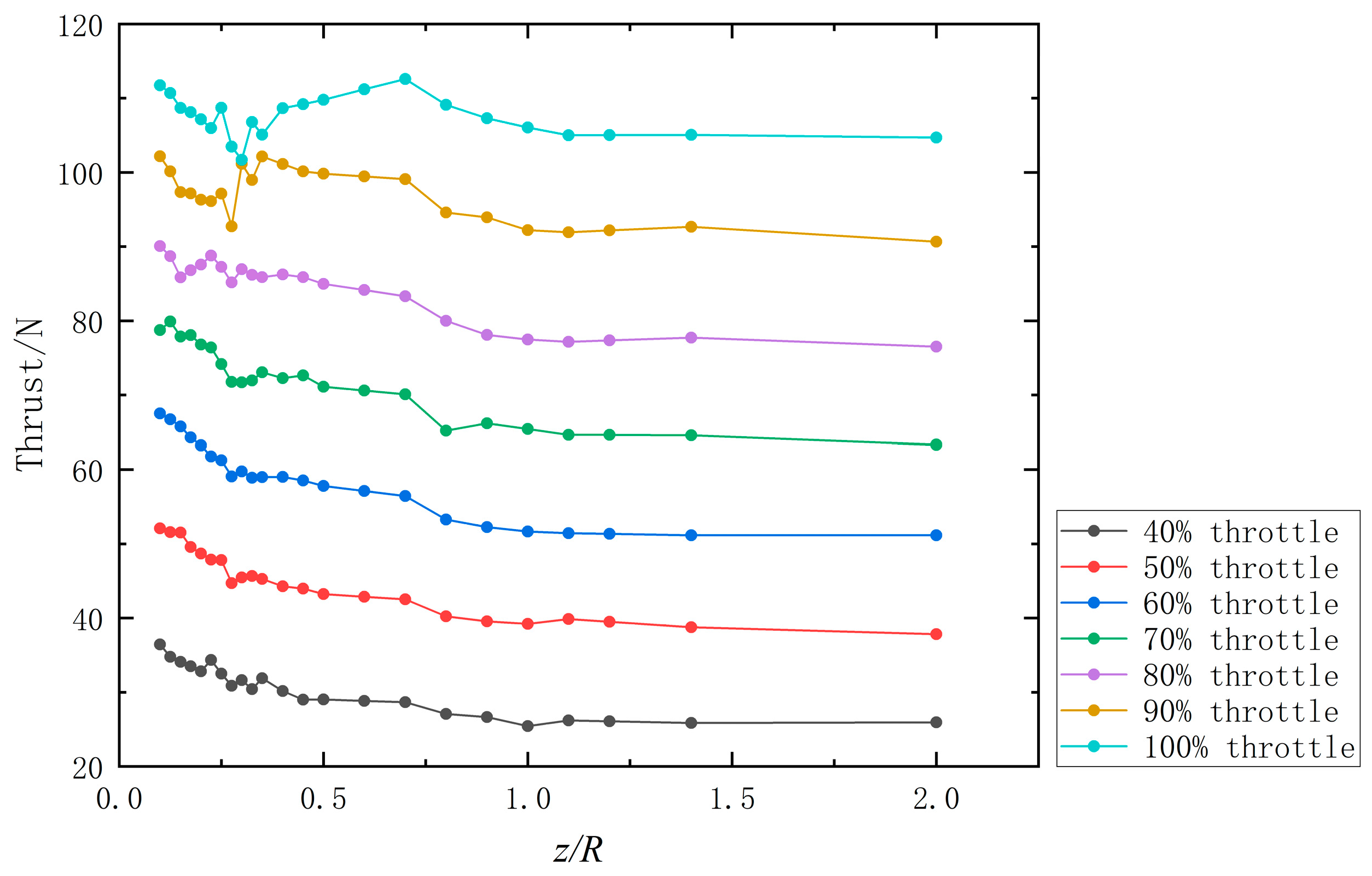
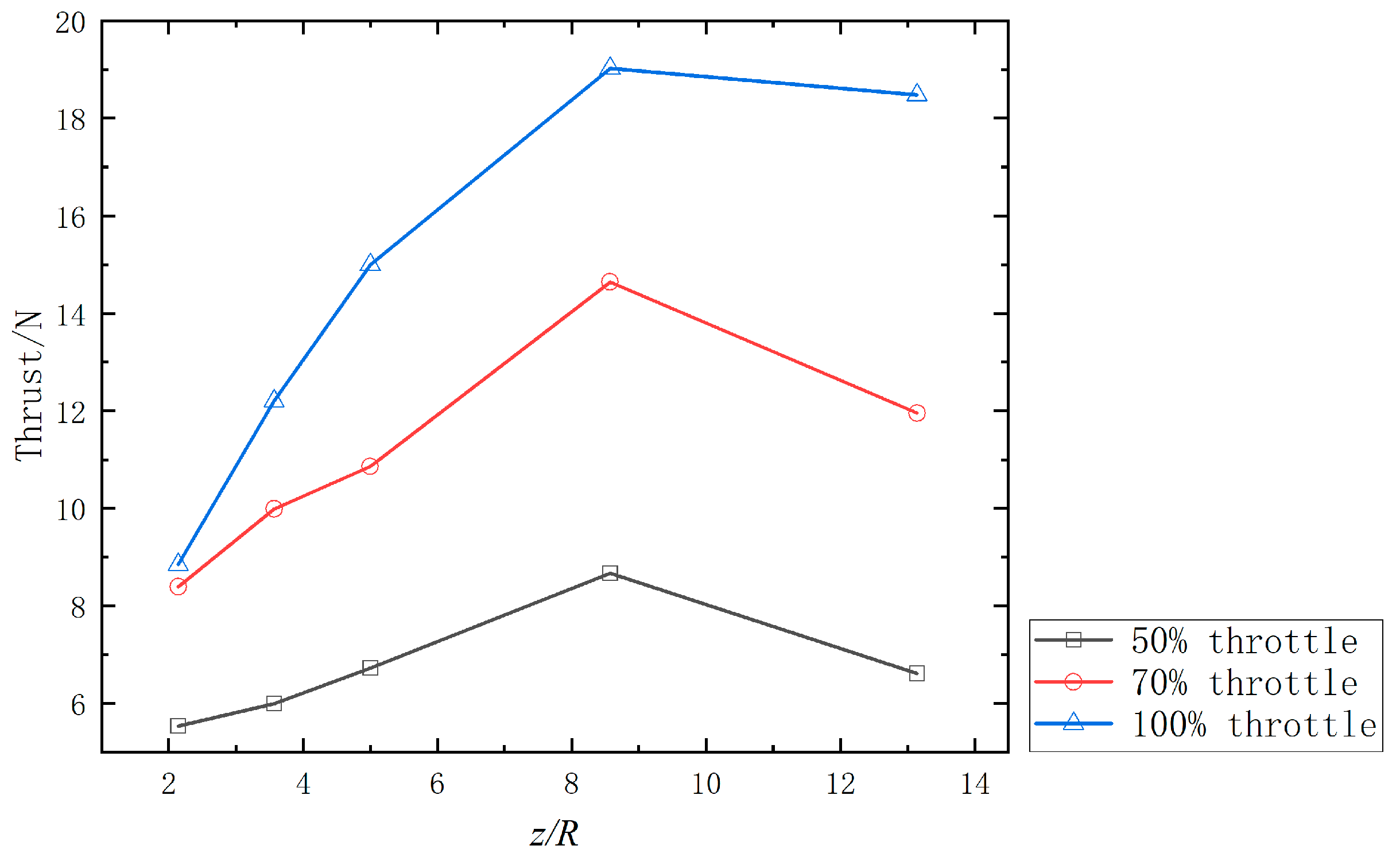
3.2. Relation between Depression Modes and Aerodynamic Characteristics of Rotor
3.2.1. Dimpling Mode
3.2.2. Splashing Mode
3.2.3. Penetrating Mode
3.3. PIV Measurements in Dimpling Mode
3.3.1. Time-Averaged Velocity Field Results
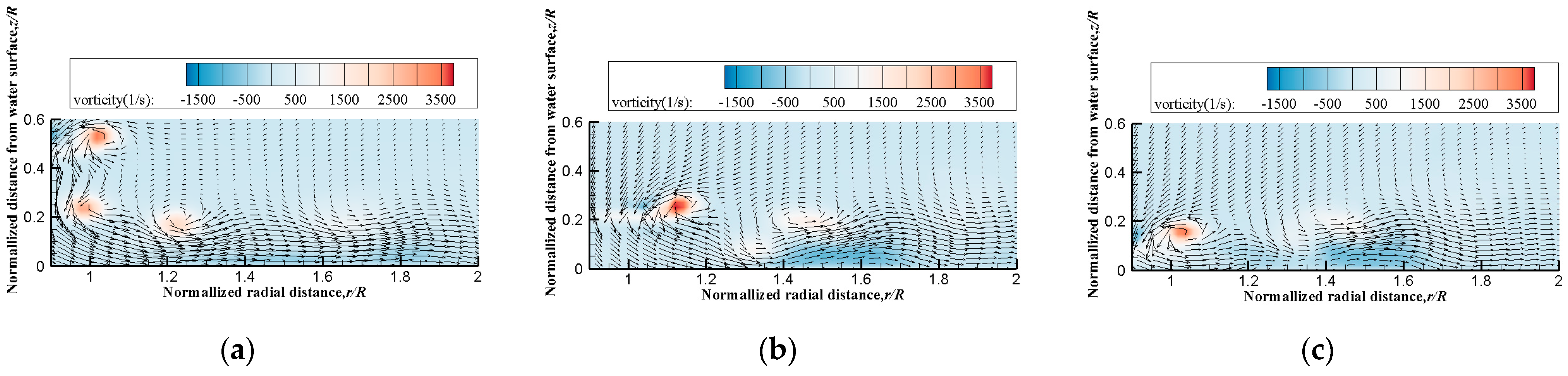
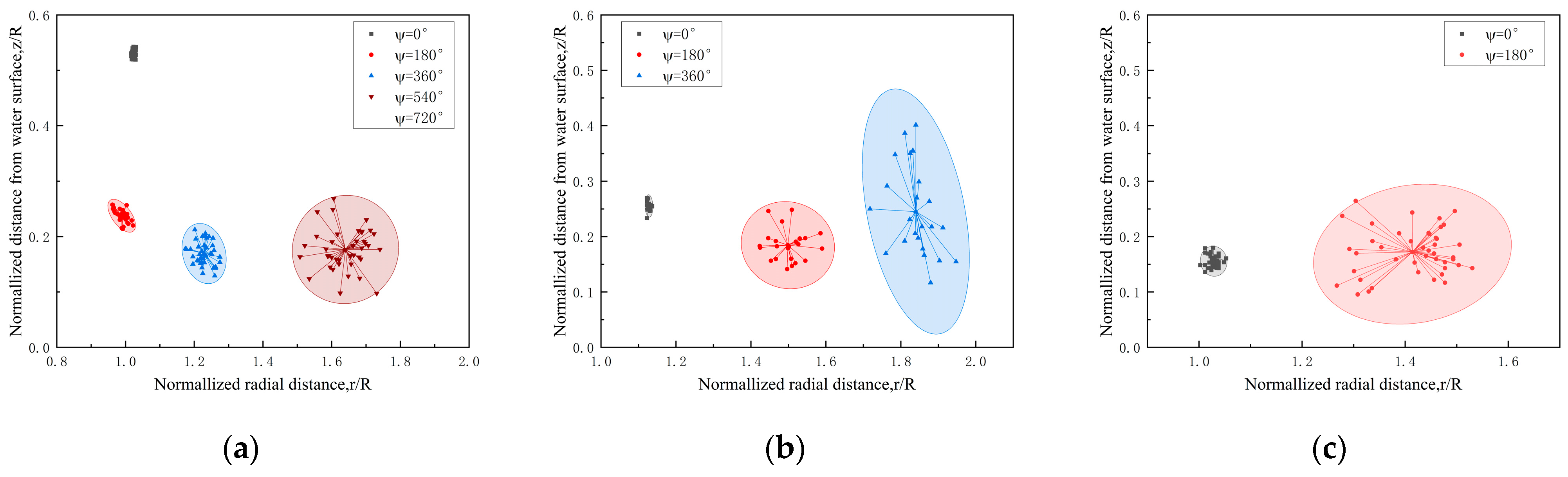
3.3.2. Phase-Averaged Vorticity Field Results
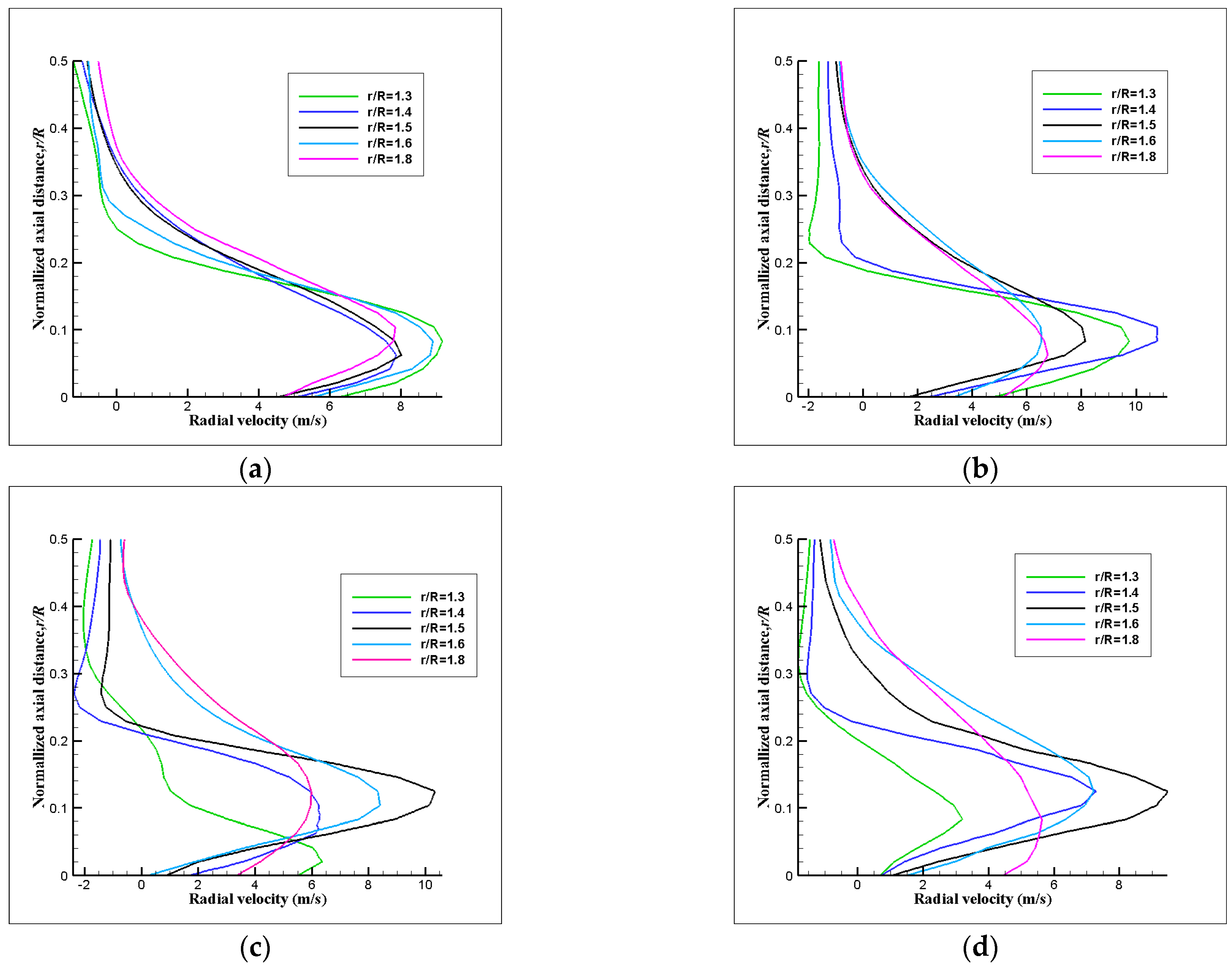
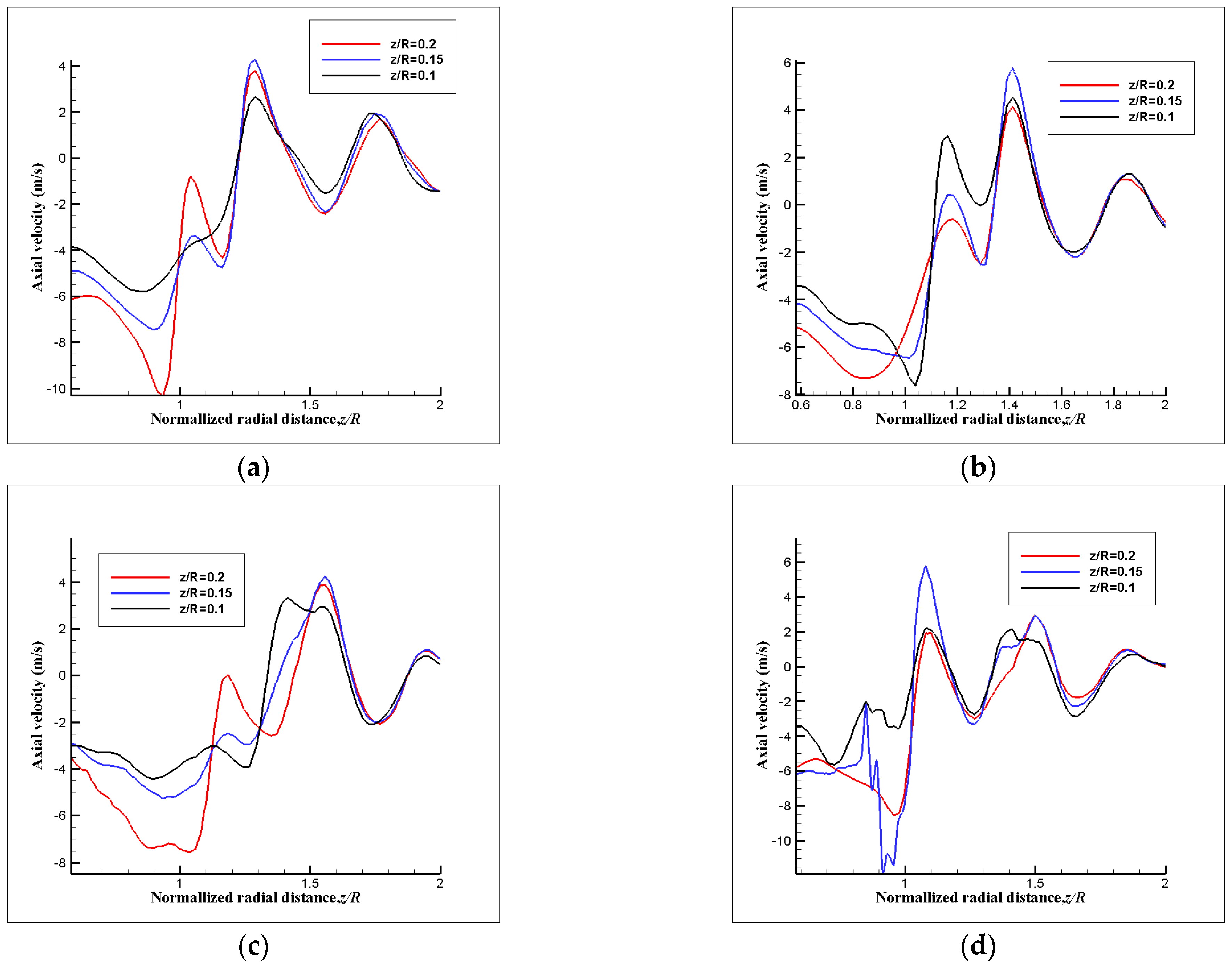
3.3.3. Phase-Averaged Velocity Profile Results
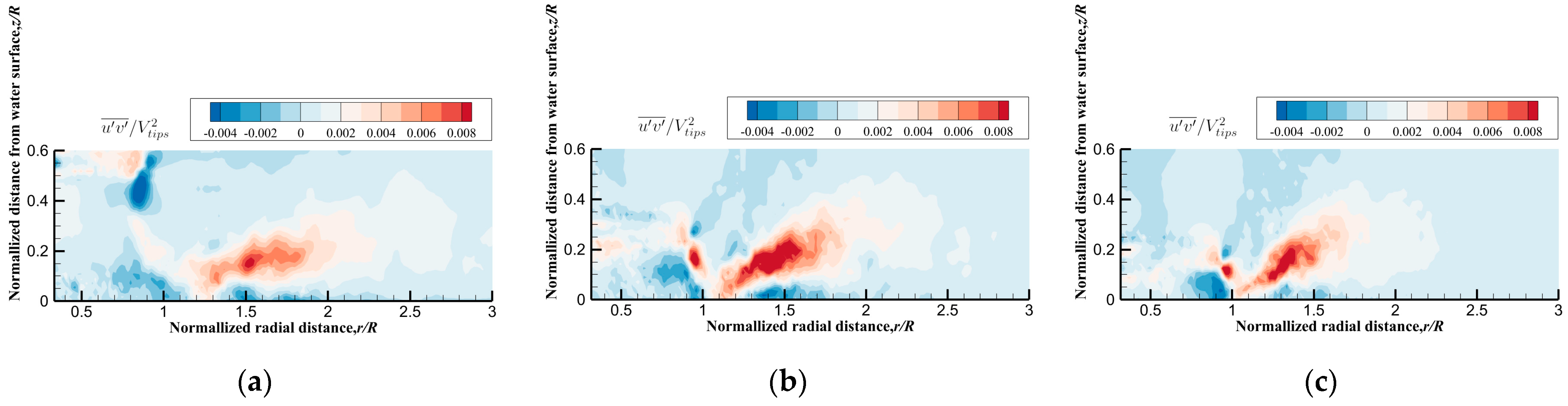
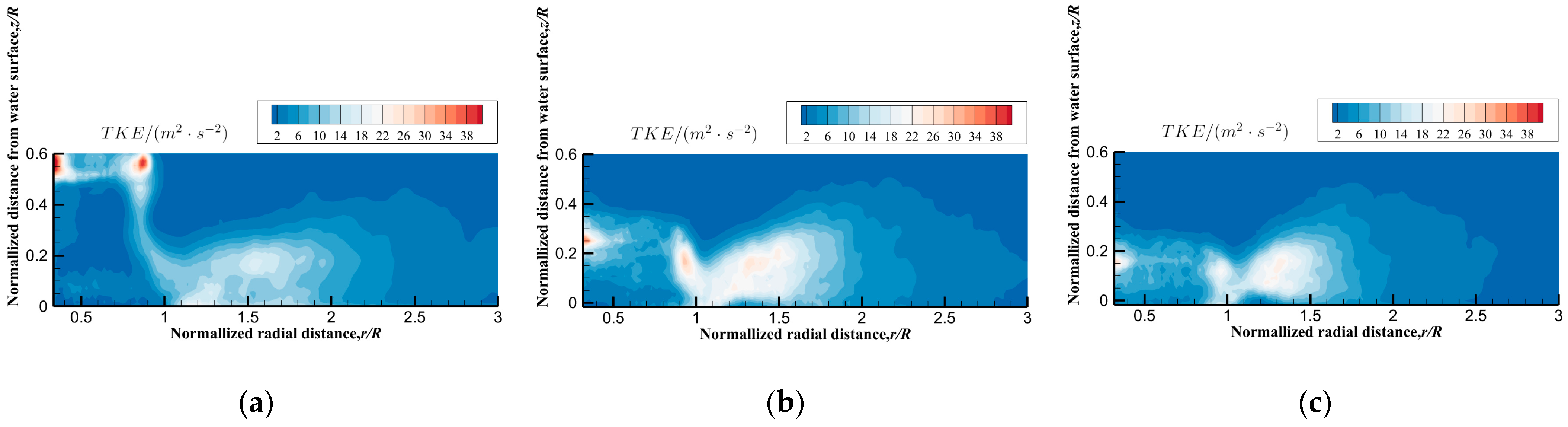
3.3.4. Fluctuating Characteristics of Rotor Wake for NWE Operation
4. Conclusions
- (1)
- Generally, considering the different mixed air–water flows patterns generated by the rotor and droplets’ splashing, NWE can be categorized into three modes: dimpling, splashing, and penetrating. This conclusion helps in the study of the relationship between models and prototypes of rotors near the water surface in the future.
- (2)
- The relationships between those three depression modes and the aerodynamic characteristics of NWE were established. The evidence obtained from this study suggests that compared with the OGE, the trend in thrust increment in NWE is the same as IGE, while this increment is smaller than that of the IGE in dimpling mode. This type of NWE can be observed on the two-bladed rotor blade with a diameter of 0.25 m. In splashing mode, a clear turning point occurs in the thrust curve, after which the thrust increment begins to decrease due to droplets. However, there is almost always a net effect of thrust increment, which means that the thrust loss due to droplets is less than the thrust increment due to the high-pressure area. This type of NWE can be observed on the two-bladed rotor blade with a diameter of 0.56 m. While in penetrating mode, the thrust loss is always present even at relatively far rotor heights off the water, the thrust loss decreases with the rotor away from the water surface. This type of NWE can be observed on the 7 cm diameter ducted fan and the 0.13 m diameter three-bladed rotor blade.
- (3)
- Important aspects of the droplet generation process were identified from high-speed imaging. The formation of finger structure was identified. Two droplet tearing-off mechanisms were revealed: water–air interface instability due to K-H instability and direct ejection due to wake impingement on the water surface. Understanding the two droplet generation mechanisms helps to study the similarities and differences between the droplet fields reduced by CMV and helicopter.
- (4)
- The PIV results show that in the dimpling mode, the rotor does not necessarily enter the vortex ring state, although the depression and the liquid crown deflect and lift the wake. Since the rotor disk is very close to the water surface, the rotor hits the water surface and develops a water surface jet along the radial direction, which quickly shears the blade tip vortex and causes it to dissipate quickly. A localized high-velocity region occurs in the surface jet caused by the stretching of the blade tip vortex, and the increased velocity gradient near the water surface may promote air–water interface instability at the water surface, tearing off more droplets.
- (5)
- The depressions and liquid crowns formed by the rotor wake are highly unsteady, which further promotes the aperiodic motion of the blade tip vortex and changes its trajectory of diffusion. Meanwhile, the turbulence fluctuation caused by the blade tip vortex above the liquid crown may promote the secondary breakup of the droplet.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, Z.; Lyu, C.; Bi, Y.; Jin, Y.; Lu, D.; Lian, L. Review of hybrid aerial underwater vehicle: Cross-domain mobility and transitions control. Ocean Eng. 2022, 248, 110840. [Google Scholar] [CrossRef]
- Tan, Y.H.; Chen, B.M. Survey on the Development of Aerial-Aquatic Hybrid Vehicles. Unmanned Syst. 2021, 9, 263–282. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, D.; Li, G.; Jing, X.; Xiao, S. Configuration Design and Trans-Media Control Status of the Hybrid Aerial Underwater Vehicles. Appl. Sci. 2022, 12, 765. [Google Scholar] [CrossRef]
- Bai, X.-Z.; Wu, W.-H.; Lin, Z.-C.; Fan, Z.-L.; Zhang, D.-X.; Gao, F.-K. The influence factors of near water effect of rotor. Acta Aerodyn. Sin. 2024, 42, 86–99. [Google Scholar] [CrossRef]
- Matus-Vargas, A.; Rodriguez-Gomez, G.; Martinez-Carranza, J. Ground effect on rotorcraft unmanned aerial vehicles: A review. Intell. Serv. Robot. 2021, 14, 99–118. [Google Scholar] [CrossRef]
- Li, D.J.; Zhou, Y.; Shi, Z.Y.; Lu, G. Autonomous Landing of Quadrotor based on Ground Effect Modelling. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 5647–5652. [Google Scholar]
- Liang, H.; Zong, Z.; Zou, L. Nonlinear lifting theory for unsteady WIG in proximity to incident water waves. Part 1: Two-dimension. Appl. Ocean Res. 2013, 43, 99–111. [Google Scholar] [CrossRef]
- Liu, X.A.; Ma, D.L.; Yang, M.Q.; Guo, Y.; Hu, H.D. Numerical Study on Airfoil Aerodynamics in Proximity to Wavy Water Surface for Various Amplitudes. Appl. Sci. 2021, 11, 4215. [Google Scholar] [CrossRef]
- Tanabe, Y.; Sugawara, H.; Sunada, S.; Yonezawa, K.; Tokutake, H. Quadrotor Drone Hovering in Ground Effect. J. Robot. Mechatron. 2021, 33, 339–347. [Google Scholar] [CrossRef]
- Fradenburgh, E.A. The Helicopter and the Ground Effect Machine. J. Am. Helicopter Soc. 1960, 5, 24–33. [Google Scholar] [CrossRef]
- Qi, D.; Feng, J.; Li, Y. Dynamic model and ADRC of a novel water-air unmanned vehicle for water entry with in-ground effect. J. Vibroeng. 2016, 18, 3743–3756. [Google Scholar] [CrossRef]
- Mi, B.G. Numerical investigation on aerodynamic performance of a ducted fan under interferences from the ground, static water and dynamic waves. Aerosp. Sci. Technol. 2020, 100, 105821. [Google Scholar] [CrossRef]
- Huo, Y.; Li, Y.; Feng, X. Water-surface take-off control of aquatic-aerial trans-domain robot with reinforcement learning. Electr. Mach. Control 2021, 25, 139–150. [Google Scholar] [CrossRef]
- Nie, X.; Hu, Z.; Sun, H.; Gen, L. Research on vertical takeoff strategy on water surface of tiltrotor cross-domain unmanned vehicle. Ship Sci. Technol. 2022, 44, 66–71. [Google Scholar]
- Yang, F.; Zhao, G.; Chen, X.; Zhao, Q.; Cao, C. Analysis of aerodynamic characteristics of rotor near water surface. Flight Dyn. 2023, 41, 1–6. [Google Scholar] [CrossRef]
- Xu, R.; Ju, S.; Zhan, Q.; Wang, X. Design of aerial-aquatic rotor test system and experimental study of rotor performance. Flight Dyn. 2024, 42, 89–94. [Google Scholar] [CrossRef]
- Wang, J.; Chen, R.; Yu, Z.; Lu, J. Ground test and numerical investigation on aerodynamic performance of a quad tilt-rotor aircraft in ground and water effects. Ocean Eng. 2023, 289, 116169. [Google Scholar] [CrossRef]
- Molloy, N.A. Impinging jet flow in a 2-phase system-basic flow pattern. J. Iron Steel Inst. 1970, 208, 943–950. [Google Scholar]
- Nguyen, A.V.; Evans, G.M. Computational fluid dynamics modelling of gas jets impinging onto liquid pools. Appl. Math. Model. 2006, 30, 1472–1484. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Buchlin, J.M.; Myrillas, K.; Berger, R. Numerical investigation of impinging gas jets onto deformable liquid layers. Appl. Math. Model. 2012, 36, 2687–2700. [Google Scholar] [CrossRef]
- Li, M.; Li, Q.; Kuang, S.; Zou, Z. Computational Investigation of the Splashing Phenomenon Induced by the Impingement of Multiple Supersonic Jets onto a Molten Slag–Metal Bath. Ind. Eng. Chem. Res. 2016, 55, 3630–3640. [Google Scholar] [CrossRef]
- Banks, R.B.; Bhavamai, A. Experimental study of the impingement of a liquid jet on the surface of a heavier liquid. J. Fluid Mech. 1965, 23, 229–240. [Google Scholar] [CrossRef]
- Lee, M.; Whitney, V.; Molloy, N. Jet-liquid interaction in a steelmaking electric arc furnace. Scand. J. Metall. 2001, 30, 330–336. [Google Scholar] [CrossRef]
- Subagyo; Brooks, G.A.; Coley, K.S.; Irons, G.A. Generation of Droplets in Slag-Metal Emulsions through Top Gas Blowing. ISIJ Int. 2003, 43, 983–989. [Google Scholar] [CrossRef]
- Lee, T.; Leishman, J.; Ramasamy, M. Fluid Dynamics of Interacting Blade Tip Vortices with a Ground Plane. J. Am. Helicopter Soc. 2010, 55, 022005. [Google Scholar] [CrossRef]
- Haehnel, R.B.; Dade, W.B. Physics of Particle Entrainment under the Influence of an Impinging Jet. In Proceedings of the 26th Army Science Conference, US Army, Orlando, FL, USA, 1–4 December 2008. [Google Scholar]
- Sydney, A.J.; Baharani, A.K.; Leishman, J.G. Understanding Brownout using Near-Wall Dual-Phase Flow Measurements. In Proceedings of the 67th Annual Forum Proceedings of the American Helicopter Society, Virginia Beach, VA, USA, 3–5 May 2011. [Google Scholar]
- Wu, Z.; Zhang, T.; Tan, H.; Zhou, H.; Chen, W.; Xie, M. Hovering rotor aerodynamics in extreme ground effect. Chin. J. Aeronaut. 2024, 37, 204–219. [Google Scholar] [CrossRef]
- Sabah, S.; Brooks, G. Splashing in Oxygen Steelmaking. ISIJ Int. 2014, 54, 836–844. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Irons, G.A. A Water Model Study of Impinging Gas Jets on Liquid Surfaces. Metall. Mater. Trans. B-Process Metall. Mater. Process Sci. 2012, 43, 302–315. [Google Scholar] [CrossRef]
- Standish, N.; He, Q.L. Drop generation due to an impinging jet and the effect of bottom blowing in the steelmaking vessel. ISIJ Int. 1989, 29, 455–461. [Google Scholar] [CrossRef]
- Cheeseman, I.C.; Bennett, N.E. The Effect of Ground on a Helicopter Rotor in Forward Flight; Aeronautical Research Council: London, UK, 1955. [Google Scholar]
- Hayden, J.S. The effect of the ground on helicopter hovering power required. In Proceedings of the AHS 32nd Annual Forum, Washington, DC, USA, 21 May 1976. [Google Scholar]
- Cao, Y.; Wu, Z.; Xu, Z. Effects of rainfall on aircraft aerodynamics. Prog. Aerosp. Sci. 2014, 71, 85–127. [Google Scholar] [CrossRef]
- Wan, T. Aerodynamic Analysis of Helicopter Rotor Blades in Heavy Rain Condition. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Dunham, J.R. Potential influences of heavy rain on general aviation airplane performance. In Proceedings of the General Aviation Technology Conference, Long Beach, CA, USA, 13–16 October 1986. [Google Scholar]
- Jasion, G.; Shrimpton, J. Prediction of Brownout Inception Beneath a Full-Scale Helicopter Downwash. Vertiflite 2012, 58, 68. [Google Scholar] [CrossRef]
- Benjamin, M.A.; Jensen, R.J.; Arienti, M. Review of Atomization: Current Knowledge and Future Requirements for Propulsion Combustors. At. Sprays 2010, 20, 485–512. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.-Z.; Zhang, Z.; Wu, W.-H.; Wang, X.; Zhan, Q.; Zhang, D.-X.; Yu, L. Fluid Dynamics of Interacting Rotor Wake with a Water Surface. Drones 2024, 8, 469. https://doi.org/10.3390/drones8090469
Bai X-Z, Zhang Z, Wu W-H, Wang X, Zhan Q, Zhang D-X, Yu L. Fluid Dynamics of Interacting Rotor Wake with a Water Surface. Drones. 2024; 8(9):469. https://doi.org/10.3390/drones8090469
Chicago/Turabian StyleBai, Xing-Zhi, Zhe Zhang, Wen-Hua Wu, Xiao Wang, Qi Zhan, Dai-Xian Zhang, and Lei Yu. 2024. "Fluid Dynamics of Interacting Rotor Wake with a Water Surface" Drones 8, no. 9: 469. https://doi.org/10.3390/drones8090469
APA StyleBai, X.-Z., Zhang, Z., Wu, W.-H., Wang, X., Zhan, Q., Zhang, D.-X., & Yu, L. (2024). Fluid Dynamics of Interacting Rotor Wake with a Water Surface. Drones, 8(9), 469. https://doi.org/10.3390/drones8090469





