Internet of Things Based Digital Twin Model Construction and Online Fault-Tolerant Control of Hypersonic Flight Vehicle
Abstract
1. Introduction
- (1)
- A novel framework for the online controller design of HFV is proposed. Based on this framework, the controller can be updated in real-time according to the exact model of HFV.
- (2)
- An IoT-based DT model is built for HFV. The measurable states of HFV are listed and the reconstruction strategy of DT is designed. Based on the measurable states and reconstruct strategy, HFVDT can approach the exact model of HFV in real time.
- (3)
- An online reconstructed MPSP controller is designed for HFV. Based on the proposed controller design method, an FTC controller can be reconstructed online according to the exact model of HFV, then the controller performance is improved.
2. Problem Formulation
2.1. Nonlinear Dynamics
2.2. Fault of HFV and Control Objective
- (1)
- Constructing a DT model for HFV in this HFVDT model, the aerodynamic coefficient can be updated in real-time according to the flight date of HFV;
- (2)
- Designing an online controller for HFVDT, and the designed controller can guarantee the controller performance by a small computing quantity.
3. IoT-Based Digital Twin Model Construction
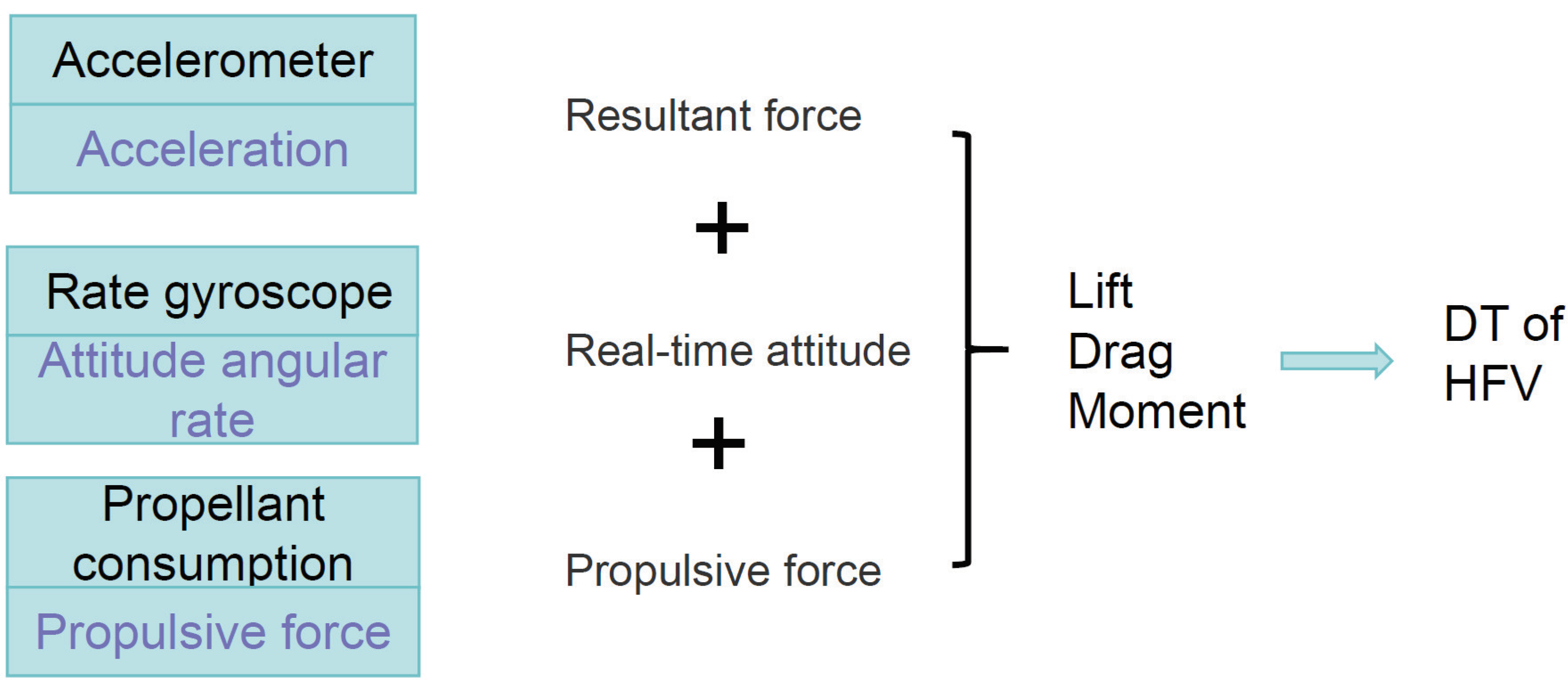
3.1. Measurable Physical States
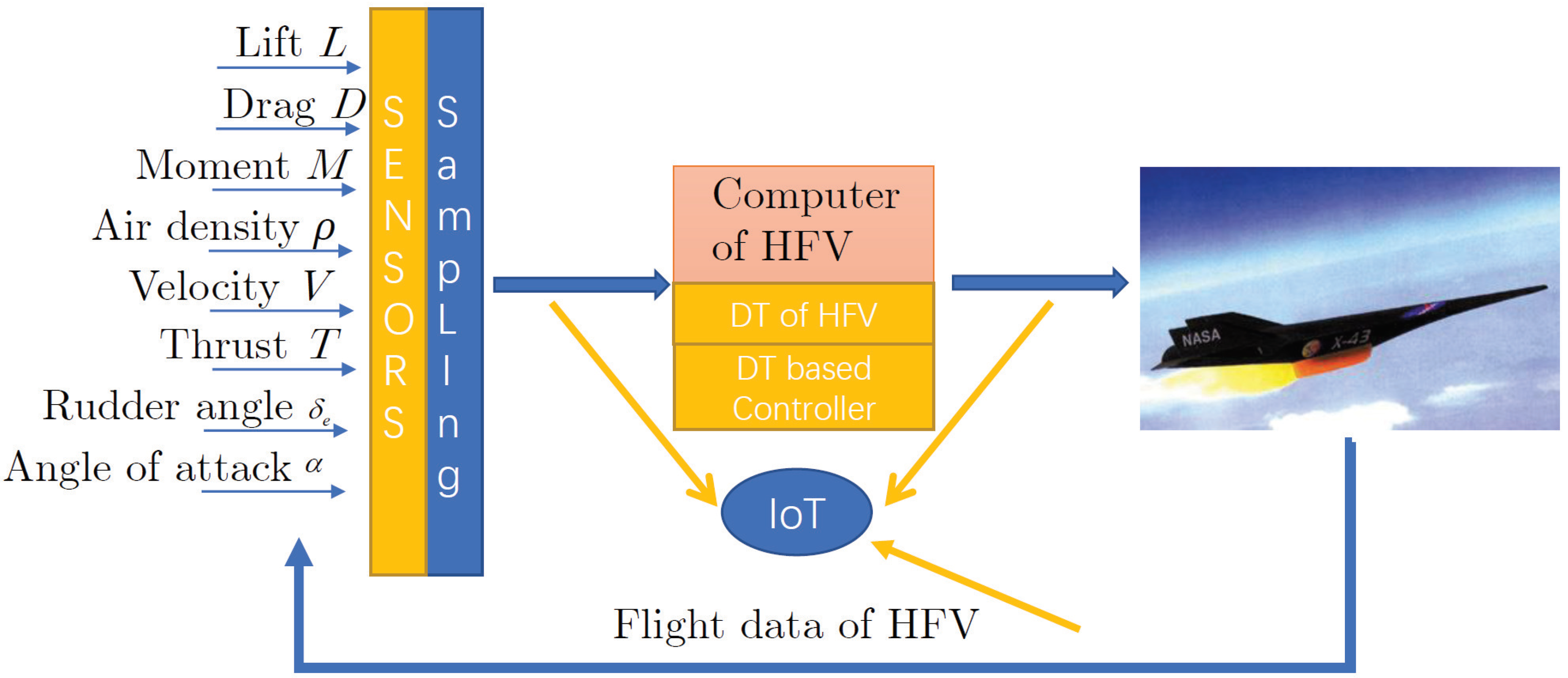
3.2. IoT-Based Flight Data Collection and Transmission
3.3. HFVDT Constructing Method
| DT Algorithm for L | |
| Step , | |
| Step 2: | |
| end |
| DT Algorithm for D | |
| Step , | |
| Step 2: | |
| end |
| DT Algorithm for M | |
| Step , | |
| Step 2: | |
| end |
4. MPSP-Based Controller Design
4.1. Constructing Method of MPSP
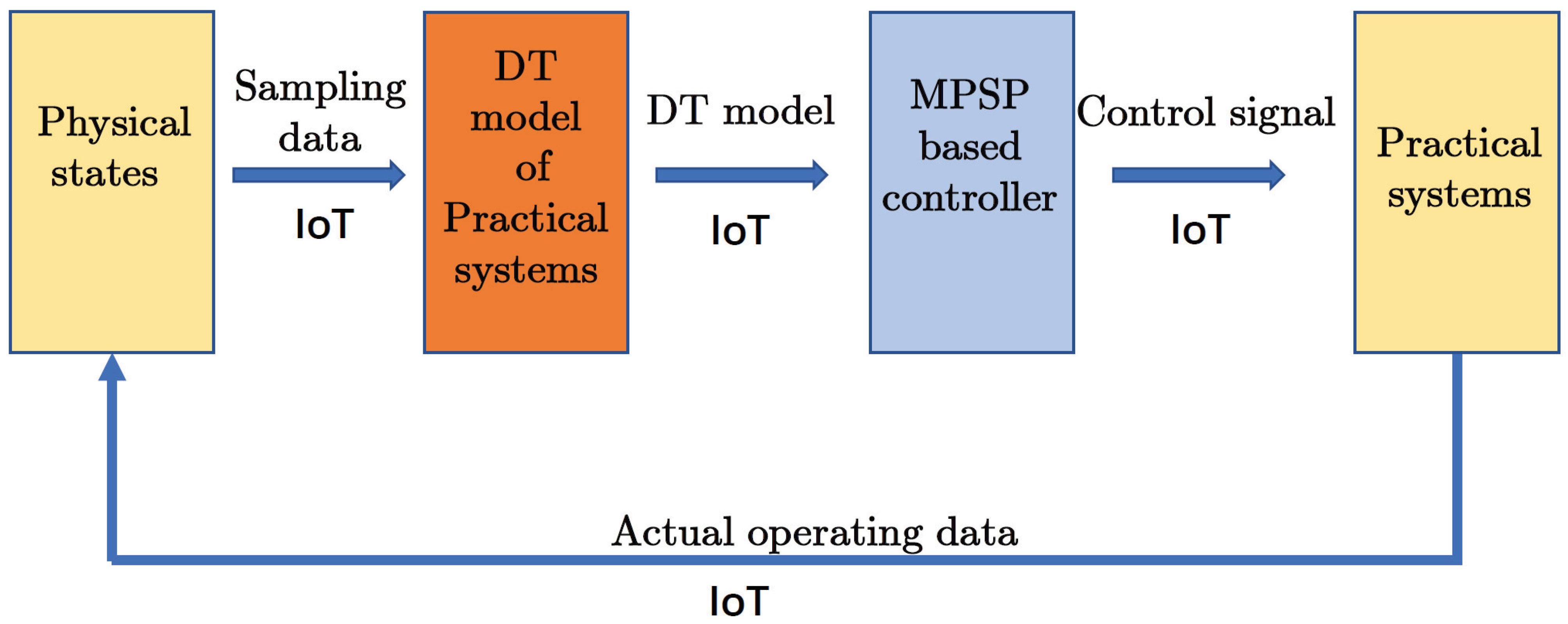
4.2. Framework of the Proposed Method
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
Correction Statement
Nomenclature
| drag coefficient | |
| ith order coefficient of contribution to | |
| ith order coefficient of contribution to | |
| constant term in | |
| lift coefficient | |
| ith order coefficient of contribution to | |
| coefficient of contribution to | |
| constant term in | |
| contribution to moment due to pitch rate | |
| contribution to moment due to angle of attack | |
| control surface contribution to moment | |
| ith order coefficient of contribution to | |
| constant term in | |
| ith order coefficient of in T | |
| mean aerodynamic chord | |
| canard coefficient in | |
| elevator coefficient in | |
| D | drag |
| g | acceleration due to gravity |
| h | altitude |
| moment of inertia | |
| L | lift |
| vehicle length | |
| M | pitching moment |
| m | vehicle mass |
| ith generalized force | |
| jth order contribution of to | |
| constant term in | |
| contribution of to | |
| Q | pitch rate |
| dynamic pressure | |
| S | reference area |
| T | trust |
| V | velocity |
| x | state of the control-oriented model |
| angle of attack | |
| ith thrust fit parameter | |
| flight path angle, | |
| canard angular deflection | |
| elevator angular deflection | |
| damping ratio for the dynamics | |
| damping ratio for elastic mode | |
| ith generalized elastic coordinate | |
| pitch angle | |
| inertial coupling term of ith elastic mode | |
| density of air | |
| stoichiometrically normalized fuel-to-air ratio | |
| constrained beam coupling constant for | |
| natural frequency for the dynamics | |
| natural frequency for elastic mode | |
| air density decay rate |
References
- Wu, X.; Xiao, B.; Wu, C.; Guo, Y. Centroidal Voronoi Tessellation and Model Predictive Control-based Macro-Micro Trajectory Optimization of Microsatellite Swarm. Space Sci. Technol. 2022, 2022, 9802195. [Google Scholar] [CrossRef]
- Bolender, M.; Doman, D. A nonlinear longitudinal dynamical model of an airbreathing hypersonic vehicle. J. Spacecr. Rocket. 2007, 44, 374–387. [Google Scholar] [CrossRef]
- Zhao, D.; Jiang, B.; Yang, H.; Tao, G. Fault-tolerant control of flexible air-breathing hypersonic vehicles in linear ODE-beam systems. Int. J. Control 2020, 93, 820–831. [Google Scholar] [CrossRef]
- Bu, X.; Wu, X.; Zhang, R.; Ma, Z.; Huang, J. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle. J. Franklin Inst. 2015, 352, 1739–1765. [Google Scholar] [CrossRef]
- Zhao, D.; Jiang, B.; Yang, H. Backstepping-based decentralized fault-tolerant control of hypersonic vehicles in PDE-ODE form. IEEE Trans. Autom. Control 2021, 67, 1210–1225. [Google Scholar] [CrossRef]
- Xia, R.; Chen, M.; Wu, Q.; Wang, Y. Neural network based integral sliding mode optimal flight control of near space hypersonic vehicle. Neurocomputing 2020, 379, 41–52. [Google Scholar] [CrossRef]
- An, H.; Fidan, B.; Wu, Q.; Wang, C.; Cao, X. Sliding mode differentiator based tracking control of uncertain nonlinear systems with application to hypersonic flight. Asian J. Control 2019, 21, 143–155. [Google Scholar] [CrossRef]
- Hu, X.; Guo, Y.; Zhang, L.; Alsaedi, A.; Hayat, T.; Ahmad, B. Fuzzy stable inversion-based output tracking for nonlinear non-minimum phase system and application to FAHVs. J. Frankl. Inst. 2015, 352, 5529–5550. [Google Scholar] [CrossRef]
- Wu, L.; Yang, X.; Li, F. Nonfragile output tracking control of hypersonic air-breathing vehicles with an LPV model. IEEE/ASME Trans. Mechatron. 2013, 18, 1280–1288. [Google Scholar] [CrossRef]
- Ye, H.; Jiang, B. Adaptive switching control for hypersonic vehicle with uncertain control direction. J. Frankl. Inst. 2020, 357, 8851–8869. [Google Scholar] [CrossRef]
- Hu, C.; Yang, X.; Wei, X.; Hu, Y. Robust model predictive control for hypersonic vehicle with state-dependent input constraints and parameter uncertainty. Int. J. Robust Nonlinear Control 2021, 31, 9676–9691. [Google Scholar] [CrossRef]
- Qi, Q.; Bu, X. Adaptive dynamic programing design for the neural control of hypersonic flight vehicles. J. Frankl. Inst. 2021, 358, 8169–8192. [Google Scholar] [CrossRef]
- Hu, X.; Xu, B.; Hu, C. Robust adaptive fuzzy control for HFV with parameter uncertainty and unmodeled dynamics. IEEE Trans. Ind. Electron. 2018, 65, 8851–8860. [Google Scholar] [CrossRef]
- Li, W.; Hou, Y.; An, F.; Xia, Q.; Li, Z.; Zhou, Q. Safety Design for the China Space Station. Space Sci. Technol. 2023, 3, 0089. [Google Scholar] [CrossRef]
- Chao, D.; Qi, R.; Jiang, B. Adaptive fault-tolerant attitude control for hypersonic reentry vehicle subject to complex uncertainties. J. Frankl. Inst. 2022, 359, 5458–5487. [Google Scholar] [CrossRef]
- Armendia, M.; Ghassempouri, M.; Ozturk, E.; Peysson, F. Twin-Control: A Digital Twin Approach to Improve Machine Tools Lifecycle; Springer Nature: Berlin/Heidelberg, Germany, 2019; p. 296. [Google Scholar]
- He, R.; Chen, G.; Dong, C.; Sun, S.; Shen, X. Data-driven digital twin technology for optimized control in process systems. ISA Trans. 2019, 95, 221–234. [Google Scholar] [CrossRef]
- Meshram, C.; Ibrahim, R.W.; Obaid, A.J.; Meshram, S.G.; Meshram, A.; Abd El-Latif, A.M. Fractional chaotic maps based short signature scheme under human-centered IoT environments. J. Adv. Res. 2021, 32, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Vo, D.T.; Nguyen, X.P.; Nguyen, T.D.; Hidayat, R.; Huynh, T.T.; Nguyen, D.T. A review on the internet of thing (IoT) technologies in controlling ocean environment. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 1–19. [Google Scholar] [CrossRef]
- Qiu, J.; Tian, Z.; Du, C.; Zuo, Q.; Su, S.; Fang, B. A survey on access control in the age of internet of things. IEEE Internet Things J. 2020, 7, 4682–4696. [Google Scholar] [CrossRef]
- Gehrmann, C.; Gunnarsson, M. A digital twin based industrial automation and control system security architecture. IEEE Trans. Ind. Inform. 2019, 16, 669–680. [Google Scholar] [CrossRef]
- Wang, J.; Ye, L.; Gao, R.X.; Li, C.; Zhang, L. Digital Twin for rotating machinery fault diagnosis in smart manufacturing. Int. J. Prod. Res. 2019, 57, 3920–3934. [Google Scholar] [CrossRef]
- Bujari, A.; Calvio, A.; Foschini, L.; Sabbioni, A.; Corradi, A. A Digital Twin Decision Support System for the Urban Facility Management Process. Sensors 2021, 21, 8460. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.; Li, Y.; Yin, Z.; Zhou, L.; Feng, J. On finite-time anti-saturated proximity control with a tumbling non-cooperative space target. Space Sci. Technol. 2023, 3, 0045. [Google Scholar] [CrossRef]
- Padhi, R.; Kothari, M. Model Predictive Static Programming: A Computationally Efficient Technique For Suboptimal Control Design. Int. J. Innov. Comput. Inf. Control 2009, 5, 399–411. [Google Scholar]
- Maity, A.; Padhi, R.; Mallaram, S.; Rao, G.M.; Manickavasagam, M. A robust and high precision optimal explicit guidance scheme for solid motor propelled launch vehicles with thrust and drag uncertainty. Int. J. Syst. Sci. 2016, 47, 3078–3097. [Google Scholar] [CrossRef]
- Kumar, P.; Anoohya, B.B.; Padhi, R. Model Predictive Static Programming for Optimal Command Tracking: A Fast MPC Paradigm. J. Dyn. Syst. Meas. Control 2019, 141, 021014. [Google Scholar] [CrossRef]
- Mathavaraj, S.; Padhi, R. Unscented MPSP for Optimal Control of a Class of Uncertain Nonlinear Dynamic Systems. J. Dyn. Syst. Meas. Control 2019, 141, 065001. [Google Scholar] [CrossRef]
- Sakode, C.M.; Padhi, R. Computationally Efficient Suboptimal Control design for Impulsive Systems based on Model Predictive Static Programming. IFAC Proc. Vol. 2014, 47, 41–46. [Google Scholar] [CrossRef]
- Dwivedi, P.N.; Bhattacharya, A.; Padhi, R. Suboptimal Midcourse Guidance of Interceptors for High-Speed Targets with Alignment Angle Constraint. J. Guid. Control Dyn. 2011, 34, 860–877. [Google Scholar] [CrossRef]
- Oza, H.B.; Padhi, R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles. J. Guid. Control Dyn. 2012, 35, 153–164. [Google Scholar] [CrossRef]
- Halbe, O.; Raja, R.G.; Padhi, R. Robust Reentry Guidance of a Reusable Launch Vehicle Using Model Predictive Static Programming. J. Guid. Control Dyn. 2014, 37, 134–148. [Google Scholar] [CrossRef]
- Sachan, K.; Padhi, R. Waypoint Constrained Multi-Phase Optimal Guidance of Spacecraft for Soft Lunar Landing. Unmanned Syst. 2019, 7, 83–104. [Google Scholar] [CrossRef]
- An, H.; Fidan, B.; Liu, J.; Wang, C.; Wu, L. Adaptive fault-tolerant control of air-breathing hypersonic vehicles robust to input nonlinearities. Int. J. Control 2019, 92, 1044–1060. [Google Scholar] [CrossRef]
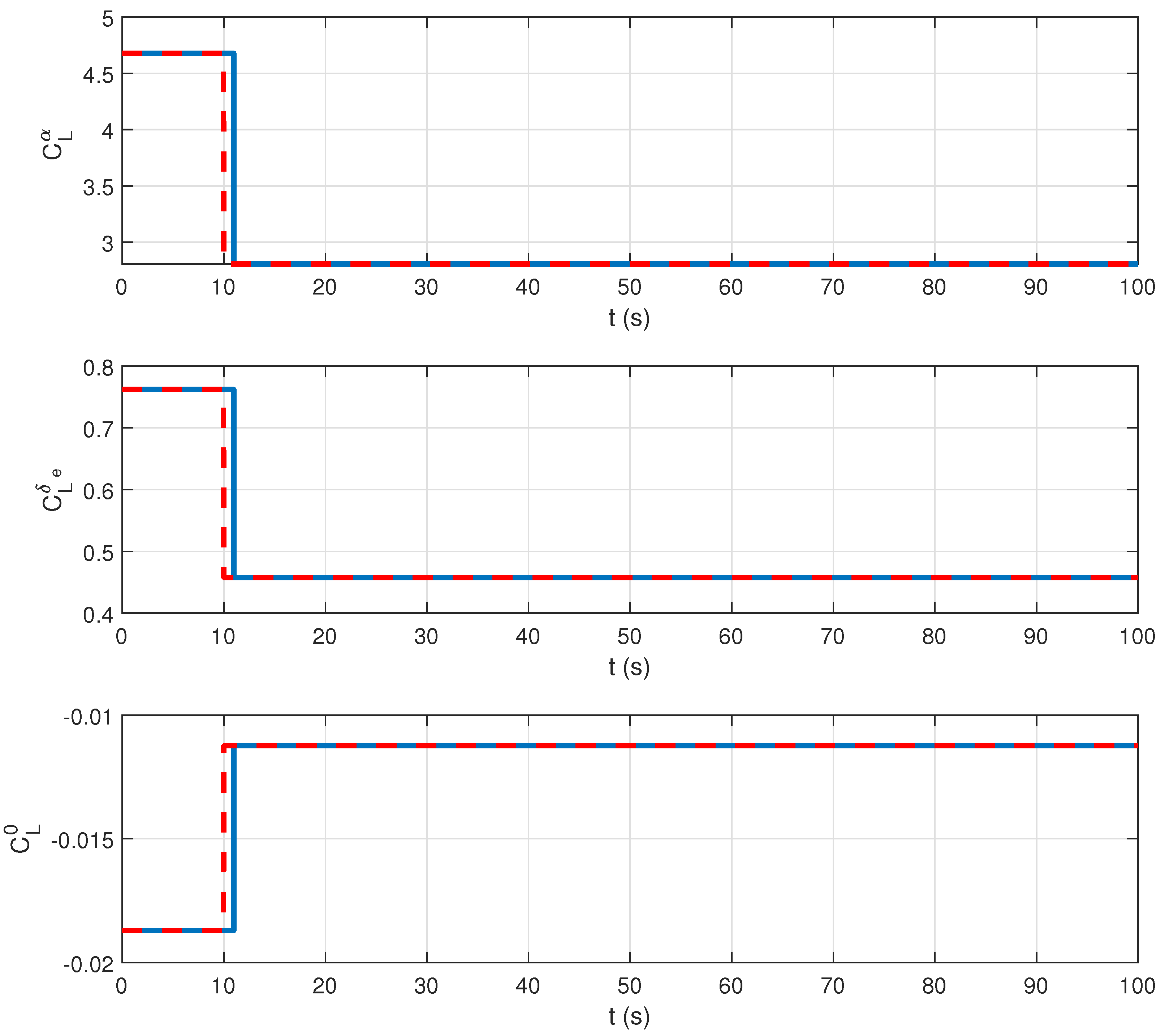
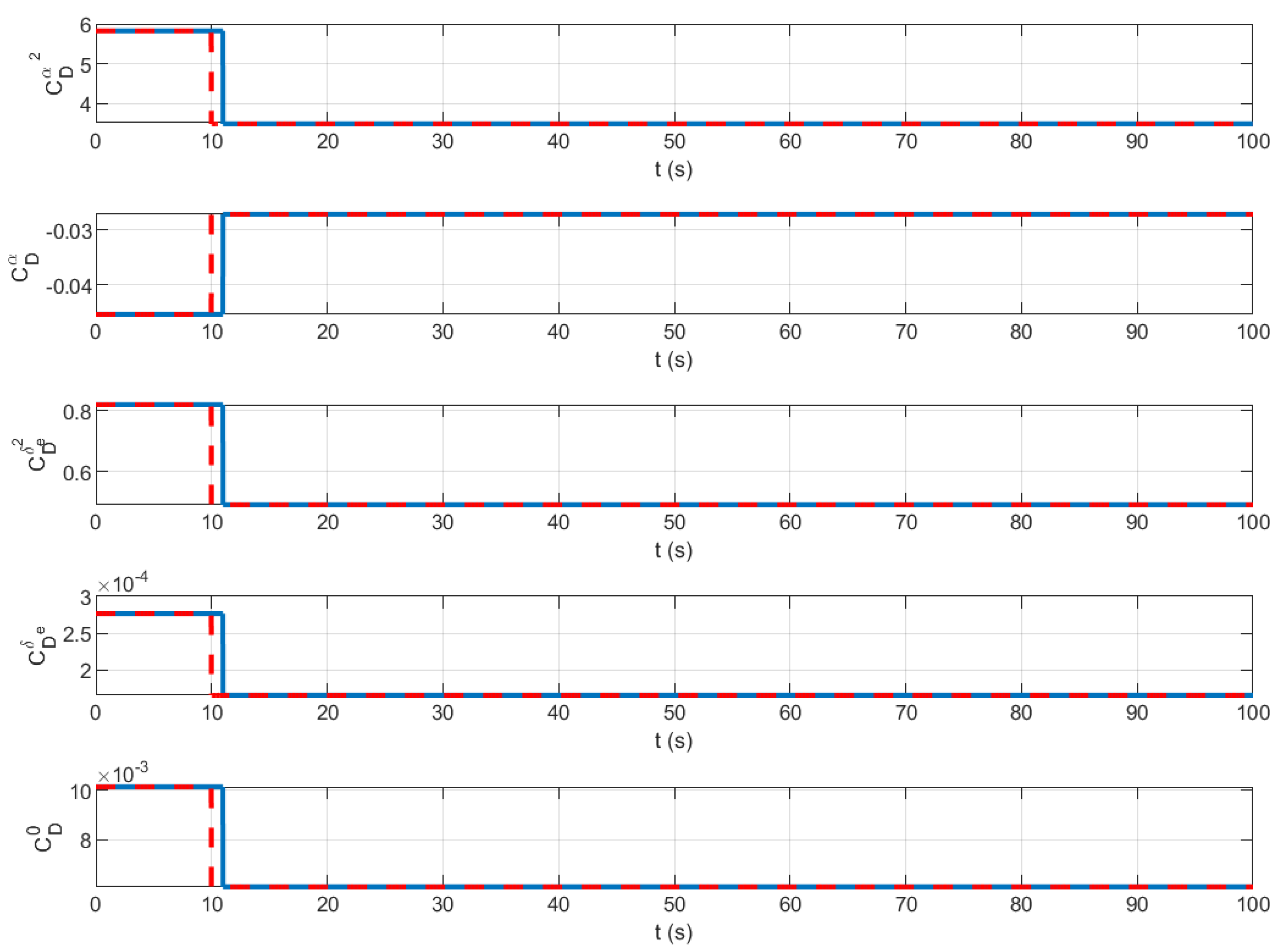
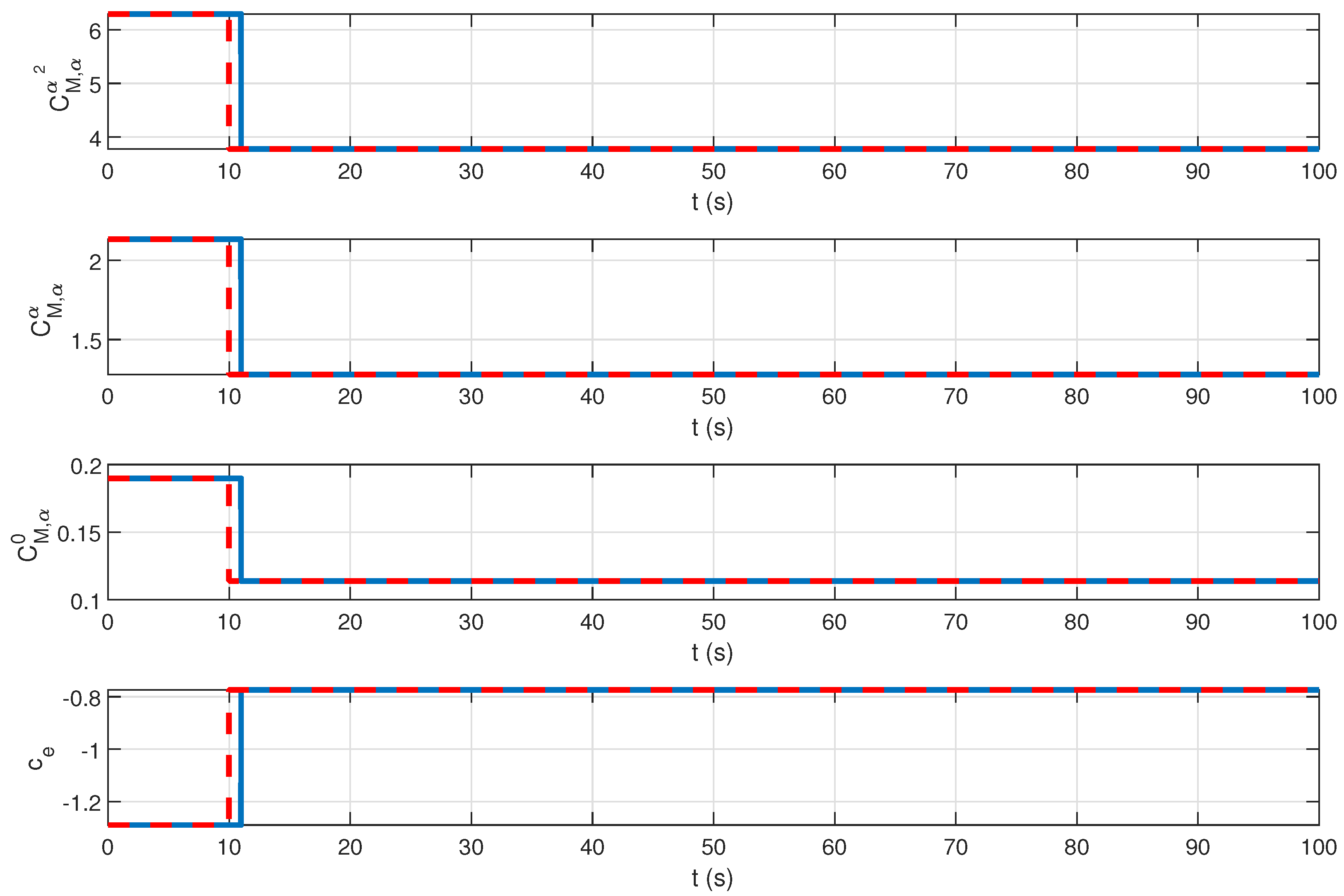
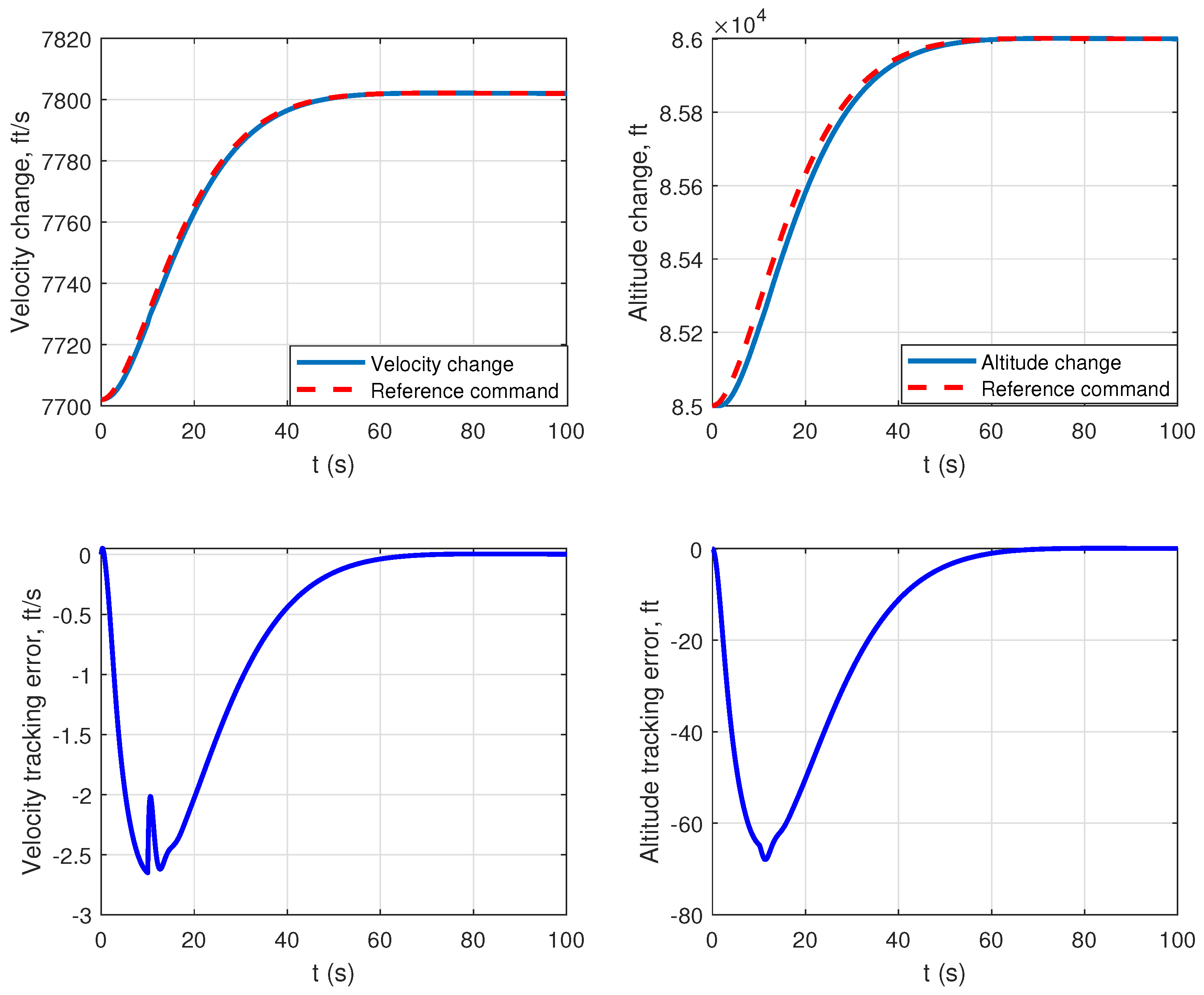
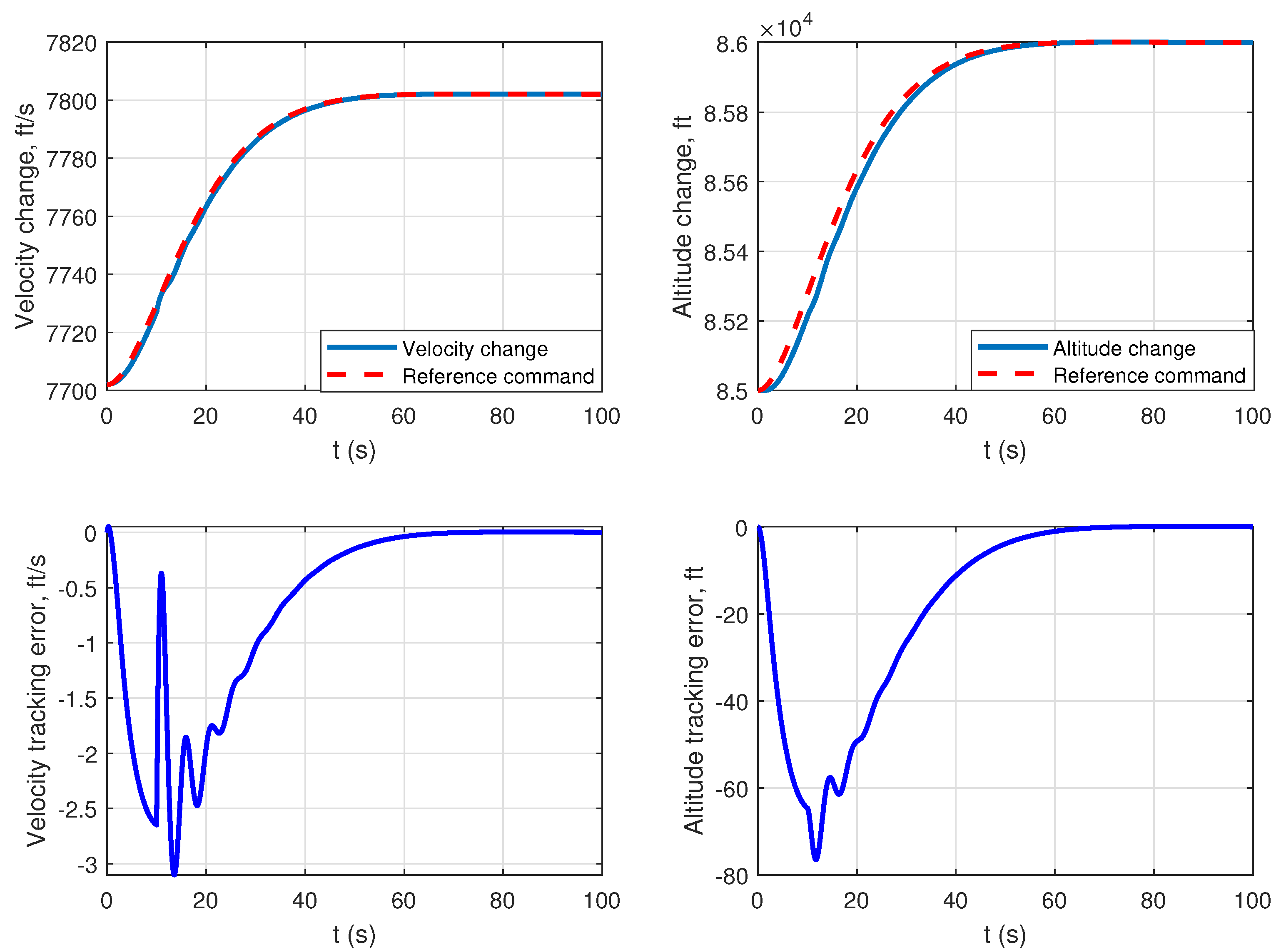
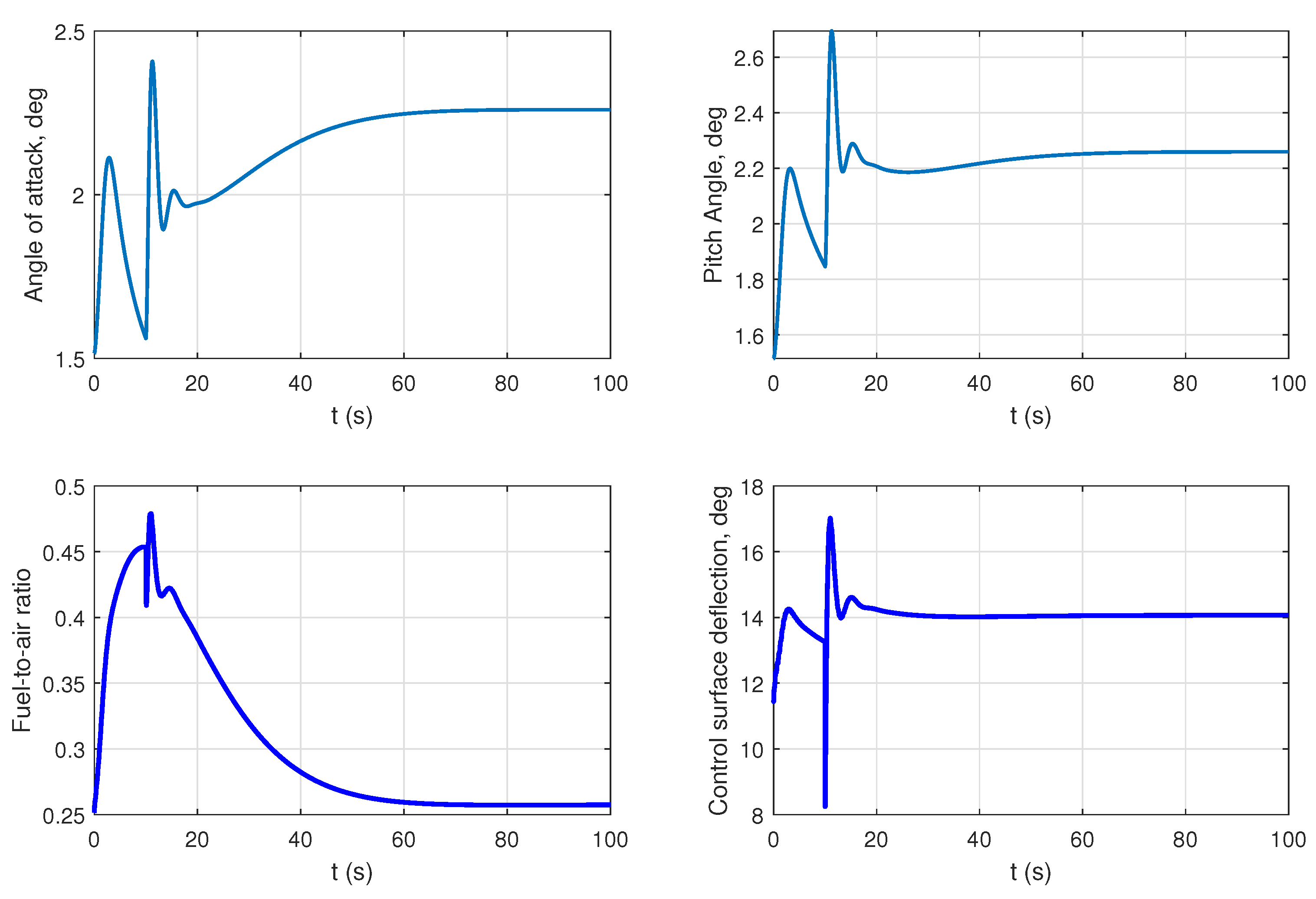
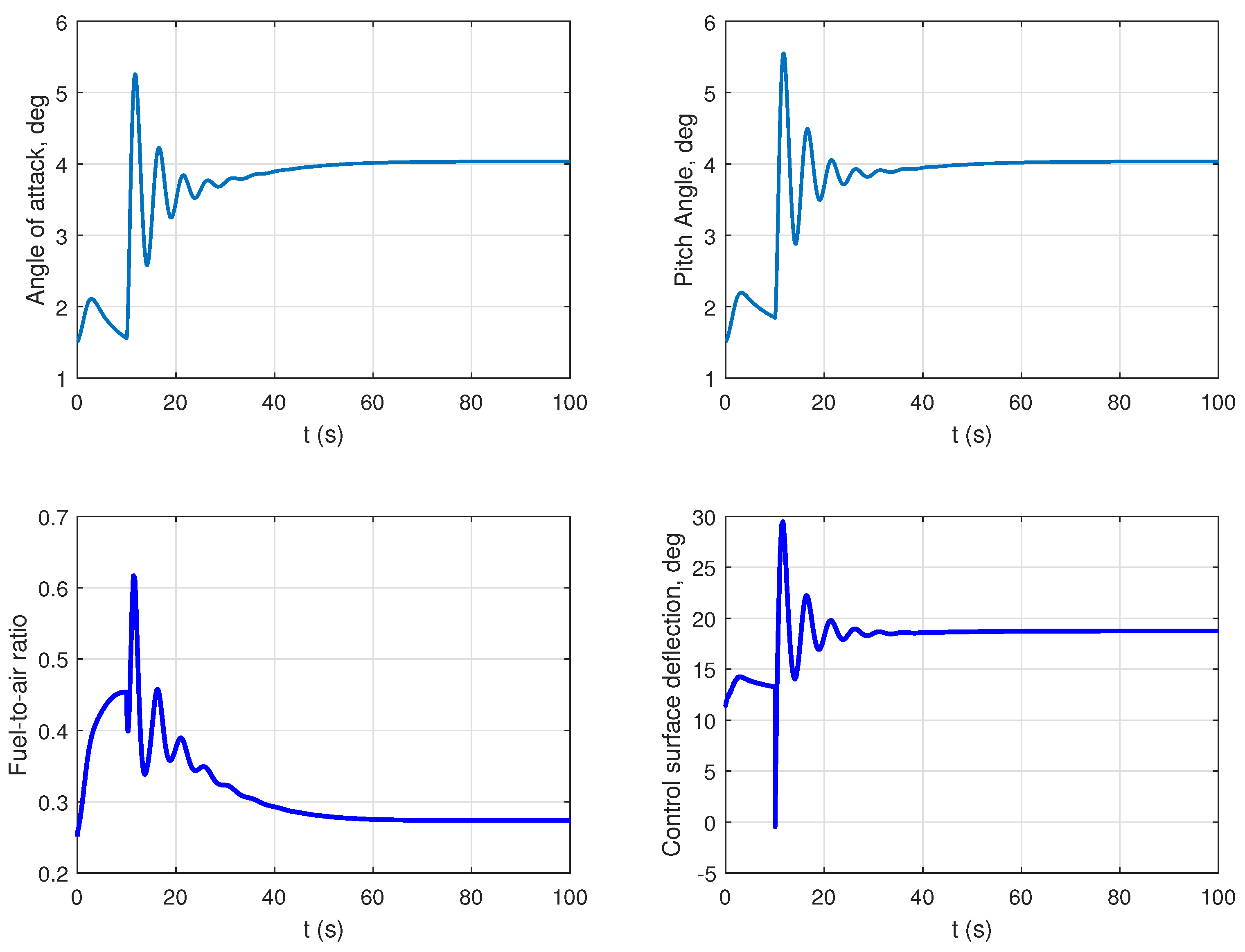
| Before Fault | After Fault |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Li, S.; Xu, J.; Hu, X. Internet of Things Based Digital Twin Model Construction and Online Fault-Tolerant Control of Hypersonic Flight Vehicle. Drones 2024, 8, 460. https://doi.org/10.3390/drones8090460
Zhang D, Li S, Xu J, Hu X. Internet of Things Based Digital Twin Model Construction and Online Fault-Tolerant Control of Hypersonic Flight Vehicle. Drones. 2024; 8(9):460. https://doi.org/10.3390/drones8090460
Chicago/Turabian StyleZhang, Daqiao, Shaopeng Li, Jian Xu, and Xiaoxiang Hu. 2024. "Internet of Things Based Digital Twin Model Construction and Online Fault-Tolerant Control of Hypersonic Flight Vehicle" Drones 8, no. 9: 460. https://doi.org/10.3390/drones8090460
APA StyleZhang, D., Li, S., Xu, J., & Hu, X. (2024). Internet of Things Based Digital Twin Model Construction and Online Fault-Tolerant Control of Hypersonic Flight Vehicle. Drones, 8(9), 460. https://doi.org/10.3390/drones8090460





