Abstract
The cooperative transportation of a cable-suspended load by two unmanned rotorcraft is analyzed. Initially, the equations describing a system composed of three point masses and two rigid cables are derived. The model is then linearized about the hovering condition, and analytical expressions are derived to describe the eigenstructure of the open-loop system. Thanks to the specific parameterization of the problem, the different dynamic modes are outlined and discussed within an analytical framework. A novel controller is designed to enable the UAVs in the formation to perform trajectory tracking, maintain formation geometry, and stabilize payload swing simultaneously. A preliminary investigation of closed-loop stability is conducted using a linear approach. Validation is performed in a realistic simulation scenario where two drones are modeled as rigid bodies under the effect of external disturbances and rotor-generated forces and moments, as obtained by Blade Element Theory. The proposed method demonstrates relative simplicity and significantly improves the flying qualities of delivery operations while minimizing hazardous payload oscillations and reducing energy demand.
1. Introduction
Two approaches are typically employed in unmanned air delivery scenarios [1]: the payload can either be rigidly attached to the drone or suspended by a cable. The rigid connection represents the most common solution, which involves the use of clamps or a sufficiently large fuselage. This configuration ensures higher stability during flight and a greater degree of controllability, as there are no additional degrees of freedom related to the payload. However, it leads to an increased takeoff mass and may be unsuitable for large payloads or on–site deliveries where landing is not possible [2,3,4]. The payload suspension technique allows for the delivery of a package without the need to land, which improves mission efficiency. Drone performance and system simplicity are preserved, with the possibility of carrying larger and heavier loads. Unfortunately, additional non–actuated degrees of freedom related to swing–induced instability are introduced [5]. For this reason, the impact of the load on the underlying system dynamics should not be neglected, as significant feedback forces may be induced on the vehicle during certain flight conditions.
Despite the relative simplicity of using a single drone to transport a single load, it is clear that the limit on payload carrying capacity poses several challenges for future air delivery scenarios and paves the way for flexible multi–agent systems. To this end, cooperative solutions have been investigated in many papers. In [6], a PID controller was developed to address the transportation of a common object with quadrotors via cables. However, the proposed control method struggled to reduce oscillations in the underdamped system. In [7], the authors developed an LQR controller combined with a Kalman filter for cooperative load transportation using two UAVs. Validation was performed experimentally using two commercial quadrotors equipped with an ultrasound altimeter, IMU, and frontal cameras. In [8], a hierarchical control scheme was designed for two quadrotors carrying a slung load. A linear controller was used for position stabilization, while a quaternion-based nonlinear controller managed the attitude loop. Finally, the authors validated the approach for both a rigid and a flexible wire through numerical simulations. In the case of an unknown payload mass, a cooperative algorithm robust to environmental disturbances was investigated in [9]. The proposed controller was designed with a decentralized architecture, where each multirotor utilizes the relative velocity and position of its neighbors to reach the desired formation shapes. A decentralized Lyapunov-based controller was also presented for aerial co–manipulation of a cable–suspended payload with two aerial robots in [10].
In the last few years, the problem of cooperative control within multi–agent scenarios has been a research focus for some of the authors, and recent papers have presented different types of control algorithms to address cooperative transportation problems. In Ref. [11], a control architecture for a two-agent formation was developed with the aim of performing trajectory tracking and maintaining formation geometry, whereas in Refs. [12,13], the formation controller was supported by an auxiliary contribution based on the proportional feedback of swing angle and rate information, obtained from an ad hoc parameterization of the payload position. In this context, it was shown that the architecture of the proposed algorithm is suitable for implementation in commercial off–the–shelf control solutions [14], with applications in search and rescue, disaster relief, environmental monitoring and surveillance, transportation, and construction.
Nonetheless, a generalized approach simultaneously allowing for (1) formation keeping, (2) trajectory tracking, and (3) payload swing damping tasks for (4) a generic rotary wing configuration is still lacking in the literature. Thus, the present research aims to fill this gap by proposing a novel control strategy that reshapes the cooperative load transportation problem into a formation stabilization task, where the dynamics of the suspended load are treated as an external disturbance to be mitigated. The controller is based on a set of simplifying assumptions that include modeling both the lifting drones and the load as point masses, according to the Lagrangian method. The highly nonlinear model is linearized about the hovering condition with the payload at rest, allowing for both stability and controllability investigations within an analytical framework. The control strategy effectively handles the nonlinear dynamic model by leveraging linearization and state feedback techniques, ensuring stability and optimal performance in cooperative UAV transportation tasks. The validity of the approach and the performance of the controller are evaluated through numerical simulations in a realistic test case, where a formation of two octarotors is detailed in terms of electric propulsion system components and blade–element characterization of propellers. Sample maneuvers are proposed in a non–dominant scenario in the presence of environmental disturbances, model uncertainties, and noisy sensor readings.
The contribution of this paper is multifold. First, a Lagrangian–based mathematical model of the loaded formation is derived and organized in a compact form. Thanks to the novel parameterization of the problem, the system representation is shown to be simple and provides the reader with a deep insight into its physical properties. After linearization, a completely analytical framework is outlined, where the natural dynamics of the coupled slung–load system are related to a reduced set of formation parameters. The simplicity of the approach is a valuable aspect when the design process or the synthesis of control laws is at a preliminary stage. In this context, the control gains of the suggested formation and payload controllers can be tuned to achieve the desired properties of dynamic modes in response to assigned flying–quality requirements. The method is of general validity and can be extended to different rotary–wing drone configurations, showing encouraging advantages in terms of maneuver times, safety of operations, and energy efficiency.
2. Mathematical Model
This section presents the mathematical description of the system. The reference frames, single–agent equation of motion, formation kinematics, and load position kinematics are presented and described according to the Lagrangian approach.
2.1. Reference Frames
An Earth–fixed North–East–Down frame, , is first considered, according to standard practice in flight mechanics. Provided is the center of gravity of the i-th agent, three sets of right–handed orthogonal reference frames are introduced:
- Two Body–fixed frames, , . The longitudinal axis is positive out of the nose of the i-th platform in its selected plane of symmetry, aims in the direction of the fuselage/frame bottom, and completes a right-handed triad.
- Two Local–Horizontal–Local–Vertical frames, , . The frame is attached to the aircraft’s center of gravity and, under the assumption of a flat and non–rotating Earth, is always parallel to .
- A vehicle structural reference frame, , used to locate the center of gravity and all platform components: the axes are parallel to the Body–fixed frame axes such that , , and . Stationlines (ST) are measured positively aft along the longitudinal axis. Buttlines (BL) are lateral distances, positive to the right, and waterlines (WL) are measured vertically, positive upward. In what follows, without loss of generality, a sample multirotor configuration is considered. In such a case, lies on the top surface of the frame and is aligned vertically with the drone’s geometric center over the plane.
A sketch of the i-th agent, including the selected reference frames, is shown in Figure 1.
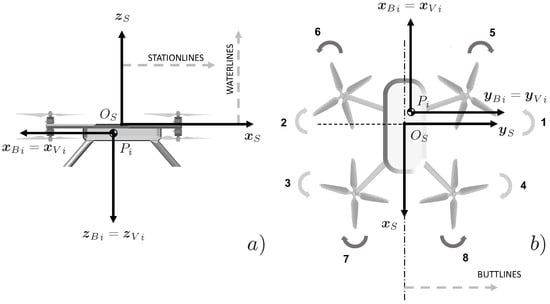
Figure 1.
Body–fixed reference frames for a sample multirotor from (a) lateral and (b) top views.
Vector transformation between and is provided by the rotation matrix [13], where defines the attitude of the i-th vehicle through the classical ‘roll’, ‘pitch’, and ‘yaw’ angles that characterize the ZYX Tait–Bryan extrinsic rotation sequence [15]. In what follows, the subscript ‘E’ is dropped for simplicity.
2.2. Equations of Motion
Let be the position of the i-th agent and its velocity with respect to the inertial frame. A suspended load with mass is connected at by a cable to the i-th agent. The drones and the suspension cables are assumed to be identical. The dynamics of each agent, as expressed in , are described by the following equations:
where m is the mass of the multirotor, is the gravitational acceleration vector, is the force exerted on the i-th agent through the cable, and is the vehicle aerodynamic disturbance. The net thrust , directed along and pointing upwards, represents the only control input to Equation (2). It is assumed that the i-th cable is directly connected to the center of gravity of the i-th agent such that has no effect on attitude motion. Each cable is modeled as massless and rigid with a constant nominal length L.
With respect to the payload position , an ad hoc parameterization is proposed which stems from the approach in [16]. Let be the midpoint between and , with the position vector obtained by the average of and , namely (see Figure 2a). Define and , where . Consider the reference frame , characterized by unit vectors , , and , with . Note that and lie on the local vertical plane that contains the vehicles, while identifies the plane’s normal direction, as shown in Figure 2b.
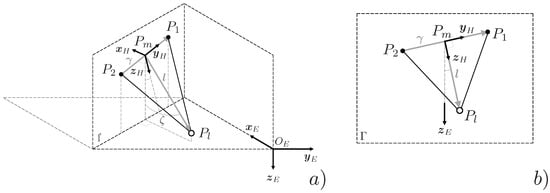
Figure 2.
Definition of oscillation angle from (a) perspective and (b) rear views.
The rotation matrix is defined by unit vector components expressed in , namely
where
Let be the unit vector directed from to , where and . The payload position is defined by the angle , which characterizes rotations about . Given , we have , and the payload position is calculated as a function of , , and . It follows that
Let be a vector of generalized coordinates. The Lagrangian equation with respect to is [16]
where is the Lagrangian function and is the vector of generalized forces. In the present framework, K is the system kinetic energy given by
where denotes the load velocity obtained from Equation (8), namely
The potential energy U is related to the vertical displacement of the agents and the suspended load and is given by
Given the energy contributions in Equations (10) and (20), and taking into account the state of the load as described by Equations (8) and (11), the Lagrangian equation is manipulated into the system:
where . For brevity, the highly nonlinear and lengthy expressions of terms , , and are not detailed in the present framework but can be provided to the reader upon request. The extended force vector consists of a control contribution, , and a disturbance term, . This last term accounts for the effects of payload drag at low oscillation speeds, where and is a drag coefficient.
3. Problem Statement and Solution
This section addresses the stability and control issues of the system described by Equations (21) and (22). The cooperative transportation problem is converted into the stabilization of a formation with the optional capability to actively damp payload oscillations. In this context, the control input to the i-th agent is expressed as , where is the contribution from a Formation Controller (FC) and is an auxiliary Payload Controller (PC).
3.1. Controller Design
Assume the i-th agent is required to keep a specified distance from a reference point , identified by vector position and moving with velocity . Let be the i-th agent’s required position, identified by . The relationships are given by and , where and indicate the current and required relative distances between the i-th agent and the reference point, respectively (see Figure 3).
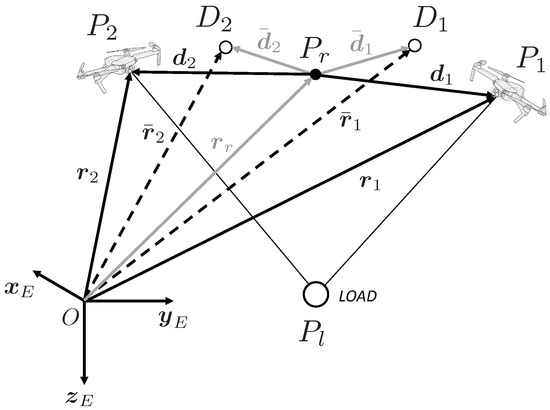
Figure 3.
Definition of current () and desired () positions of the i-th agent.
The following equation is derived:
Let , and consider Equation (1). The time derivative of Equation (23) yields
where represents the desired velocity of the i-th agent. Assuming equals , the position dynamics of the i-th vehicle with respect to the reference point become
Define and as the relative position and trajectory error variables, respectively. Considering Equation (25), we have . The following FC is proposed, based on the idea in [11] and adapted to the present application:
where , , is a trim contribution, while and are positive gain matrices. Without loss of generality, it is assumed that when the i-th agent reaches the desired position (namely , , ), the formation midpoint exactly tracks . Let be the prescribed mutual distance vector between the agents of the formation, with components expressed in and selected such that . It follows that .
The trim contribution , , allows the system described in Equations (21) and (22) to maintain the equilibrium , which represents a hovering flight where the three point masses lie on the local vertical plane (see Figure 2). In such a case, and are the desired swing-state variables, and Agent 2 is required to maintain the prescribed position . Disregarding the aerodynamic disturbances affecting the drones and the payload, the generalized equilibrium control force is calculated from Equation (22) as . Considering the first six components in , the equilibrium input is derived with components
where is the total mass.
The proposed PC is structured as
and is directed over the local horizontal plane in the direction of , where and are positive gains. The proportional contribution in Equation (29) allows the formation to track the payload position over the local horizontal plane along the preferred direction . At the same time, the derivative contribution damps the motion of the relative position vector l with respect to . This approach follows strategies used for stabilizing inverted pendulums on moving carts, where various control strategies are employed, ranging from standard PID [17] to MPC algorithms [18].
3.2. Stability and Control Analysis
In what follows, the stability of the coupled slung-load system described in Equations (21) and (22), with the control law detailed in Equations (26) and (29), is addressed within a linear framework. Let and be the state and input vectors describing the dynamics in Equations (21) and (22), respectively, linearized about the equilibrium . The standard state–space representation
is derived where is the state matrix,
and is the input matrix,
The components of the matrices in Equations (31) and (32) are detailed in Appendix A.
The stability of the linearized system with the control action in Equations (26) and (29) is first addressed in the case when such that and is a constant. Let be the error with respect to the desired state . The error dynamics are obtained from Equation (30) as
Based on a simple manipulation of Equations (26) and (29) in the linear framework, we have , where . The feedback–controlled system evolves according to , where and
To outline the dynamic modes in , the error vector is conveniently rearranged according to the order
Without loss of generality, consider the situation where and for a prescribed , which allows the dynamic analysis to be performed about the -frame axes. Based on the results in Appendix A, it is straightforward to verify that the closed-loop dynamic matrix assumes the block–diagonal form:
where
with eigenvalues , , is the subsystem matrix that describes the coupling between the vehicles’ forward motion (along ) and the payload swing state, while
with eigenvalues , , is related to the lateral and vertical behavior of the formation (along and , respectively). In the most general case, the closed–form expressions of the eigenvalues in Equations (37) and (38) cannot be determined. In this context, numerical methods can be employed for a dedicated analysis of the system’s eigenstructure [19]. Also, there exist K with the structure in Equation (34) such that both Equations (37) and (38) are Hurwitz. Consider now the general case where and . Provided the origin of the feedback dynamic system is stable and , one still obtains as as a consequence of Lemma 1 in [20].
In the case when , formation open–loop dynamics are analyzed. In particular, is characterized by null eigenvalues with multiplicity 2 and a set of purely complex poles given by
and
Similar considerations hold for , which is defined by 4 null eigenvalues and two pairs of complex poles:
Given the absence of dissipative effects related to the aerodynamic drag (which is disregarded), all dynamic modes related to Equations (39)–(42) are representative of a purely oscillating motion about the equilibrium with no damping.
4. Results
An analysis of the proposed approach is performed through numerical simulations, in which two multirotors are required to execute sample transportation tasks. Performance indicators are also defined to characterize the overall effectiveness of the proposed test cases.
4.1. Simulation Platform
Simulations are performed in Matlab® using a fourth-order Runge–Kutta solver with a frequency of 500 Hz [21]. The agents are two identical octarotors, modeled as rigid bodies following the approach and nomenclature detailed in [22]. The payload is assumed to be a point mass attached through a hook point H and is affected by aerodynamic drag, with representing the frontal area of an equivalent sphere with radius m and drag coefficient . The relevant system parameters are summarized in Table 1. Air data are calculated using the International Standard Atmosphere (ISA) model as a function of altitude [23]. Local gravitational data are provided by the World Geodetic System 1984 model as a function of vehicle latitude, longitude, and altitude [24]. Given , the force in Equation (2) is calculated as
where K is the elastic constant; and are the elastic deformation and its time derivative, respectively; and . Compared to the classical Hookes’ model in [22], cable internal damping is included with coefficient (see Table 1).

Table 1.
System parameters.
Control tasks are managed through a cascaded controller inspired by the PX4 morphology and notational framework [14]. The control algorithm stabilizes the i-th agent by tracking an Earth–fixed set–point position , velocity , or acceleration (see Figure 4, where is the acceleration set point generated by Velocity Controller). In this framework, the desired acceleration for the i-th multirotor is given by , where and are computed using Equations (26) and (29), respectively.
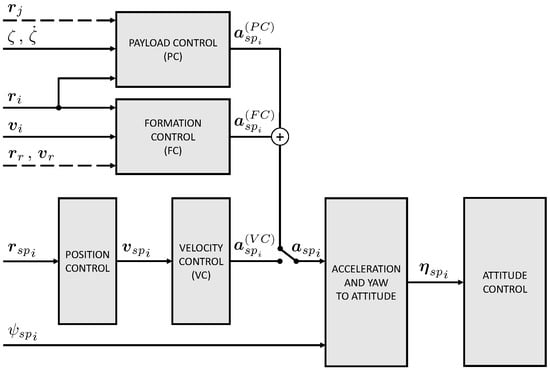
Figure 4.
The i-th agent control scheme based on the PX4 autopilot architecture [14] (, ).
Non–ideal sensor behavior is considered following the approach in [22], where noise, bias, and sensor positioning errors are introduced and described from a numerical standpoint. The onboard computer operates at a frequency of 100 Hz, and a fixed time delay, s, is implemented to account for local processing and communication issues between the agents of the formation. In this context, the dotted lines in Figure 4 depict all broadcast signals, including reference trajectory information (provided, for example, by a ground control station) and the mutual transmission of agent position data to reconstruct the term in Equation (29). The swing angle and rate are assumed to be available to each agent, as discussed in [16,22]. Zero–mean Gaussian white noise is added to each estimated value, with standard deviations of deg and deg/s, respectively.
Remark 1.
A detailed analysis of PX4 control functions and the multirotor’s capability to track a set-point acceleration is beyond the scope of the present paper. In general, different control strategies can be employed to perform attitude control and generate the required thrust, including standard PID techniques [25], linear quadratic regulators [26], active disturbance rejection controllers [27], backstepping control or feedback linearization [28], and sliding–mode methods [29,30]. Regardless of the control approach used, it is essential that attitude regulation and thrust generation have a bandwidth significantly larger than that of the closed–loop system under the control actions described in Equations (26) and (29).
4.2. Performance Indicators
The following performance indicators are defined to quantitatively characterize the performance of the closed–loop system with and without the auxiliary support of a PC:
- Maneuver time, . The simulation is assumed to be concluded at time when two conditions are simultaneously satisfied: (1) the formation control residual error falls below , where and are expressed in m and , respectively, and (2) the absolute value of remains below degrees for a predetermined time of 5 s.
- Average swing angle, . This is calculated as , where the integralis evaluated over the maneuver time domain and provides an indication of how much and for how long the payload deviates from the local vertical plane .
- Propulsive energy, . This measures the total energy delivered by the motors to the propellers and is calculated through the integralwhere is the output shaft power generated by the k-th motor, obtained from required torque and angular rate under the assumption of null friction torque. In the present case, is evaluated for Agent 1 only.
4.3. Test Cases
Consider the formation identified by m, with components expressed in . It follows that m, given m and m. In the absence of external disturbances, the nominal trim contributions in Equations (27) and (28) are N and N, respectively. The non–null eigenvalues of the open–loop forward-swing dynamics in Equations (39) and (40) are 1/s and 1/s. With respect to the lateral–vertical dynamics, Equations (41) and (42) give 1/s and 1/s. FC gains are selected as N/m and N s/m, while the PC is characterized by m/(rad s2) and m/(rad s). Table 2 lists the eigenvalues obtained for the closed-loop dynamic matrices and in Equations (37) and (38), with and without the auxiliary contribution of the PC. In both cases, the hovering equilibrium is stable, as both and are Hurwitz matrices. While the effect of the PC does not influence the linearized lateral–vertical behavior, it does affect the forward motion, particularly the complex–conjugate poles 1/s, which shift to 1/s, resulting in increased damping of the oscillatory behavior. Specifically, the damping ratio increases from to (), while the natural frequency slightly decreases from rad/s to rad/s ().

Table 2.
Eigenvalues of the feedback–controlled subsystems at hover (units: s−1).
4.3.1. Simulation Case 1
Drones are required to leave the initial state m, m, and m/s at s, with the payload at rest. The initial attitude is represented by rad. The reference point is constant at m, and the desired yaw angle is rad. A comparison is made between the sub–case with simple formation stabilization and the sub-case where active payload stabilization is added to the control action. Figure 5a shows the time history of the formation–keeping error , characterized by an asymptotic behavior that is essentially unaltered by the PC contribution. Figure 5b shows the effectiveness of the PC, where the maneuver time is reduced from s to s and the swing behavior rapidly fades. In Figure 6, the control mechanism is exemplified. To this end, the set-point acceleration components generated for Agent 1 over the local horizontal plane are reported. The provided PC is operative, and , with the two input contributions depicted separately to show partial vector opposition. For example, in the very first part of the maneuver ( s), the induction of a negative oscillation angle determines in opposition to , thus mitigating the aggressiveness of the maneuver for reduced payload swing. Table 3 lists the main performance parameters and percentage variations. The activation of the PC, which improves disturbance rejection capabilities, produces a noticeable reduction in propulsive energy to conclude the delivery task. Moreover, considering the quantity —the integral of the oscillation angle over the maneuver time —a reduction of is obtained. The same considerations apply to the average value , for which a reduction of is calculated.
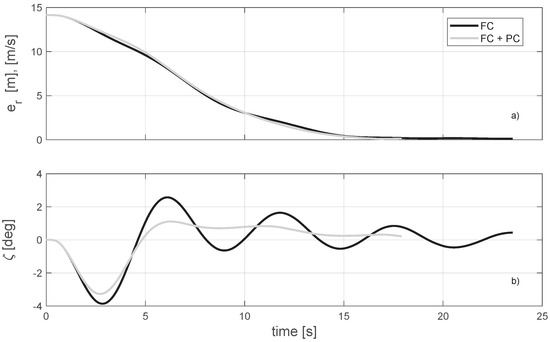
Figure 5.
Case 1: Stabilization of (a) formation–keeping residual error and (b) payload swing angle.
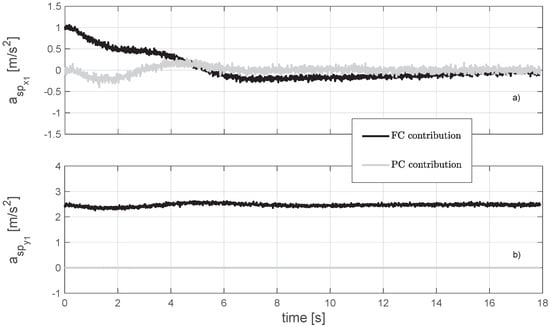
Figure 6.
(a,b) Case 1: Set–point acceleration contributions for Agent 1 with operative PC.

Table 3.
Case 1: Performance analysis.
4.3.2. Simulation Case 2
Drones start from the same initial condition as Case 1 and are required to track a rectilinear trajectory with reference point m and speed , where m/s and . The desired formation geometry is reconfigured to m such that N and N. A constant wind m/s perturbs the system during time interval s, thus simulating a discrete gust. In this case, the proportional formulation in Equation (26) for a system affected by external (drag) disturbances is expected to determine the steady-state residual errors in terms of and . Conversely, the tracking of the desired speed theoretically occurs with zero residuals, that is, m/s for . With this in mind, Condition 1 in Section 4.2, which defines the maneuver time, is adapted here to the reduced–order speed error , required to fall below m/s. Figure 7a depicts the time history of , which indicates the correct stabilization of both agents to the reference velocity. Figure 7b shows the swing angle , where the effect of wind gusts is evident in the induction of unwanted oscillations in addition to the deviation of the formation from the prescribed trajectory (see gray areas).
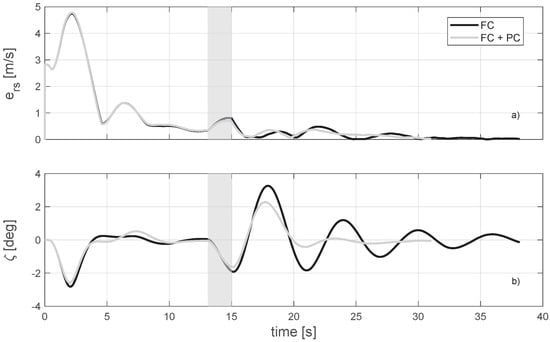
Figure 7.
Case 2: Stabilization of (a) formation–keeping residual error and (b) payload swing angle.
The time behavior of the positioning error is depicted in Figure 8, where the formation residuals remain bounded with m for . In steady–state conditions, the components of and oscillate about zero with standard deviations of m/s over the horizontal plane and m/s along the local vertical. Finally, the results of the performance analysis are reported in Table 4, highlighting the favorable effect of the PC. It should be noted that the proposed control strategy represents a starting point for implementing more complex algorithms with improved disturbance–rejection capabilities. For example, the proportional–derivative formulation in Equation (26) could benefit from an additive integral term applied to the formation error . In such a case, the accuracy of both formation–keeping and trajectory–tracking tasks would improve at the cost of extending the system state in Equation (33).
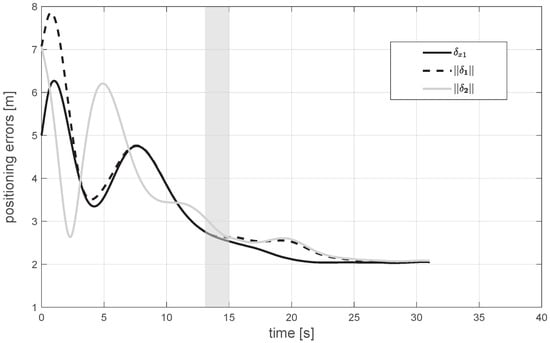
Figure 8.
Case 2: Convergence of positioning errors to a steady–state value (FC + PC).

Table 4.
Case 2: Performance analysis.
5. Conclusions
This paper presents a methodology for cooperative load transportation by two multirotors. A set of nonlinear equations describing the coupled slung-load system was derived, and a controller was proposed that allows the lifting drones to simultaneously perform formation keeping and trajectory tracking. The particular parameterization used to represent the payload swing state enabled the generation of an auxiliary control law that actively damps unwanted oscillations. Model linearization was performed about the hovering flight with the payload at rest, and descriptions of both the open-loop and closed-loop eigenvalues were provided within an analytical framework. In this context, two decoupled subsystems were shown to characterize (1) the forward and (2) the lateral and vertical formation motions, respectively.
Although the sample controller was designed for a nominal formation consisting of three point masses, its application to a realistic simulation scenario with model uncertainties, external disturbances, and measurement noise demonstrated the effectiveness of the approach. The activation of the auxiliary payload controller was shown to significantly improve the accuracy of delivery operations, with a notable reduction in both maneuver time and battery energy demand.
Numerical simulations related to different case studies showed how the proposed generalized approach guarantees overall system stability, allowing for formation keeping and trajectory tracking while providing satisfactory suspended load dynamics. This makes the proposed approach a promising solution for mission scenarios where the transportation of heavy load cannot be performed by a single drone or where the payload does not have a near–spherical shape.
Author Contributions
Conceptualization, E.C. and E.L.d.A.; methodology, E.C. and E.L.d.A.; software, E.C. and E.L.d.A.; validation, E.C., E.L.d.A. and F.G.; formal analysis, E.C., E.L.d.A. and F.G.; investigation, E.C. and E.L.d.A.; resources, E.C., E.L.d.A. and F.G.; data curation, E.C., E.L.d.A. and F.G.; writing—original draft preparation, E.L.d.A.; writing—review and editing, E.C., E.L.d.A. and F.G.; visualization, E.L.d.A. and F.G.; supervision, E.L.d.A. and F.G.; project administration, E.L.d.A. and F.G.; funding acquisition, E.L.d.A. and F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study was carried out within the MOST (Sustainable Mobility National Research Center) and received funding from the European Union’s Next-GenerationEU (PIANO NAZIONALE DI RIPRESA E RESILIENZA (PNRR)—MISSIONE 4 COMPONENTE 2, INVESTIMENTO 1.4—D.D. 1033 17/06/2022, CN00000023). This manuscript reflects only the authors’ views and opinions; neither the European Union nor the European Commission can be considered responsible for them.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| BL | Buttline |
| FC | Formation Controller |
| H | Hook point |
| IMU | Inertial Measurement Unit |
| LQR | Linear Quadratic Regulator |
| MPC | Model Predictive Control |
| PC | Payload Controller |
| PID | Proportional–Integral–Derivative |
| ST | Stationline |
| UAV | Unmanned Aerial Vehicle |
| VC | Velocity Controller |
| WL | Waterline |
References
- Estevez, J.; Garate, G.; Lopez-Guede, J.M.; Larrea, M. Review of Aerial Transportation of Suspended-Cable Payloads with Quadrotors. Drones 2024, 8, 35. [Google Scholar] [CrossRef]
- Pounds, P.E.I.; Bersak, D.R.; Dollar, A.M. Grasping From the Air: Hovering Capture and Load Stability. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2491–2498. [Google Scholar] [CrossRef]
- Chen, H.; Quan, F.; Fang, L.; Zhang, S. Aerial Grasping with a Lightweight Manipulator Based on Multi–Objective Optimization and Visual Compensation. Sensors 2019, 19, 4253. [Google Scholar] [CrossRef]
- Eskandaripour, H.; Boldsaikhan, E. Last–Mile Drone Delivery: Past, Present, and Future. Drones 2023, 7, 77. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Han, J. Trajectory planning of load transportation with multi–quadrotors based on reinforcement learning algorithm. Aerosp. Sci. Technol. 2021, 116, 106887. [Google Scholar] [CrossRef]
- Michael, N.; Fink, J.; Kumar, V. Cooperative manipulation and transportation with aerial robots. Auton. Robot. 2011, 30, 73–86. [Google Scholar] [CrossRef]
- Bacelar, T.; Madeiras, J.; Melicio, R.; Cardeira, C.; Oliveira, P. On–board implementation and experimental validation of collaborative transportation of loads with multiple UAVs. Aerosp. Sci. Technol. 2020, 107, 106284. [Google Scholar] [CrossRef]
- Ariyibi, S.O.; Tekinalp, O. Quaternion–based nonlinear attitude control of quadrotor formations carrying a slung load. Aerosp. Sci. Technol. 2020, 105, 105995. [Google Scholar] [CrossRef]
- Klausen, K.; Meissen, C.; Fossen, T.I.; Arcak, M.; Johansen, T.A. Cooperative Control for Multirotors Transporting an Unknown Suspended Load Under Environmental Disturbances. IEEE Trans. Control. Syst. Technol. 2020, 28, 653–660. [Google Scholar] [CrossRef]
- Tognon, M.; Gabellieri, C.; Pallottino, L.; Franchi, A. Aerial Co–Manipulation With Cables: The Role of Internal Force for Equilibria, Stability, and Passivity. IEEE Robot. 2018, 3, 2577–2583. [Google Scholar] [CrossRef]
- de Angelis, E.L.; Giulietti, F.; Rossetti, G. Multirotor aircraft formation flight control with collision avoidance capability. Aerosp. Sci. Technol. 2018, 77, 733–741. [Google Scholar] [CrossRef]
- de Angelis, E.L.; Giulietti, F.; Pipeleers, G. Two–time–scale control of a multirotor aircraft for suspended load transportation. Aerosp. Sci. Technol. 2019, 84, 193–203. [Google Scholar] [CrossRef]
- de Angelis, E.L.; Giulietti, F. Stability and control issues of multirotor suspended load transportation: An analytical closed–form approach. Aerosp. Sci. Technol. 2023, 135, 108201. [Google Scholar] [CrossRef]
- PX4 Development Team and Community, PX4 Autopilot User Guide (Main). Available online: https://docs.px4.io/main/en/ (accessed on 12 April 2024).
- de Ruiter, A.H.J.; Damaren, C.J.; Forbes, J.R. Spacecraft Dynamics and Control—An Introduction; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 19–24. [Google Scholar]
- de Angelis, E.L. Swing angle estimation for multicopter slung load applications. Aerosp. Sci. Technol. 2019, 89, 264–274. [Google Scholar] [CrossRef]
- Wang, J.J. Simulation studies of inverted pendulum based on PID controllers. Simul. Model. Pract. Theory 2011, 19, 440–449. [Google Scholar] [CrossRef]
- Messikh, L.; Guechi, E.H.; Blažič, S. Stabilization of the Cart–Inverted–Pendulum System Using State–Feedback Pole–Independent MPC Controllers. Sensors 2022, 22, 243. [Google Scholar] [CrossRef] [PubMed]
- Kautsky, J.; Nichols, N.K.; Van Dooren, P. Robust pole assignment in linear state feedback. Int. J. Control 1985, 41, 1129–1155. [Google Scholar] [CrossRef]
- Beard, R.W.; Lawton, J.; Hadaegh, F.Y. A Coordination Architecture for Spacecraft Formation Control. IEEE Trans. Control Syst. Technol. 2001, 9, 777–790. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical methods for ordinary differential equations in the 20th century. J. Comput. Appl. Math. 2000, 125, 1–29. [Google Scholar] [CrossRef]
- de Angelis, E.L.; Giulietti, F. An improved method for swing state estimation in multirotor slung load applications. Drones 2023, 7, 654. [Google Scholar] [CrossRef]
- NOAA-S/T 76-1562; U.S. Standard Atmosphere. U.S. Government Printing Office: Washington, DC, USA, 1976; pp. 1–241.
- Defense Mapping Agency Washington DC, Department of Defense World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems, 2nd ed.; Defense Mapping Agency, Systems Center (SG): Fairfax, VA, USA, 1991; pp. 1–170.
- Najm, A.A.; Ibraheem, I.K. Nonlinear PID controller design for a 6–DOF UAV quadrotor system. Int. J. Eng. Sci. Technol. 2019, 22, 1087–1097. [Google Scholar] [CrossRef]
- Rinaldi, F.; Chiesa, S.; Quagliotti, F. Linear quadratic control for quadrotors UAVs dynamics and formation flight. J. Intell. Robot. Syst. 2013, 70, 203–220. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Sun, M.; Zhang, X. Trajectory tracking control of a quadrotor UAV based on sliding mode active disturbance rejection control. Nonlinear Anal. Model Control 2019, 24, 545–560. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, J.; Dou, J.; Wen, B. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV. Int. J. Adapt. Control Signal Process 2018, 32, 1675–1693. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Yang, Y.; Ban, H.; Xiao, B. Fixed–time integral-type sliding mode control for the quadrotor UAV attitude stabilization under actuator failures. Aerosp. Sci. Technol. 2019, 95, 105444. [Google Scholar] [CrossRef]
- Gao, B.; Liu, Y.J.; Liu, L. Adaptive neural fault–tolerant control of a quadrotor UAV via fast terminal sliding mode. Aerosp. Sci. Technol. 2022, 129, 107818. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).