Figure 1.
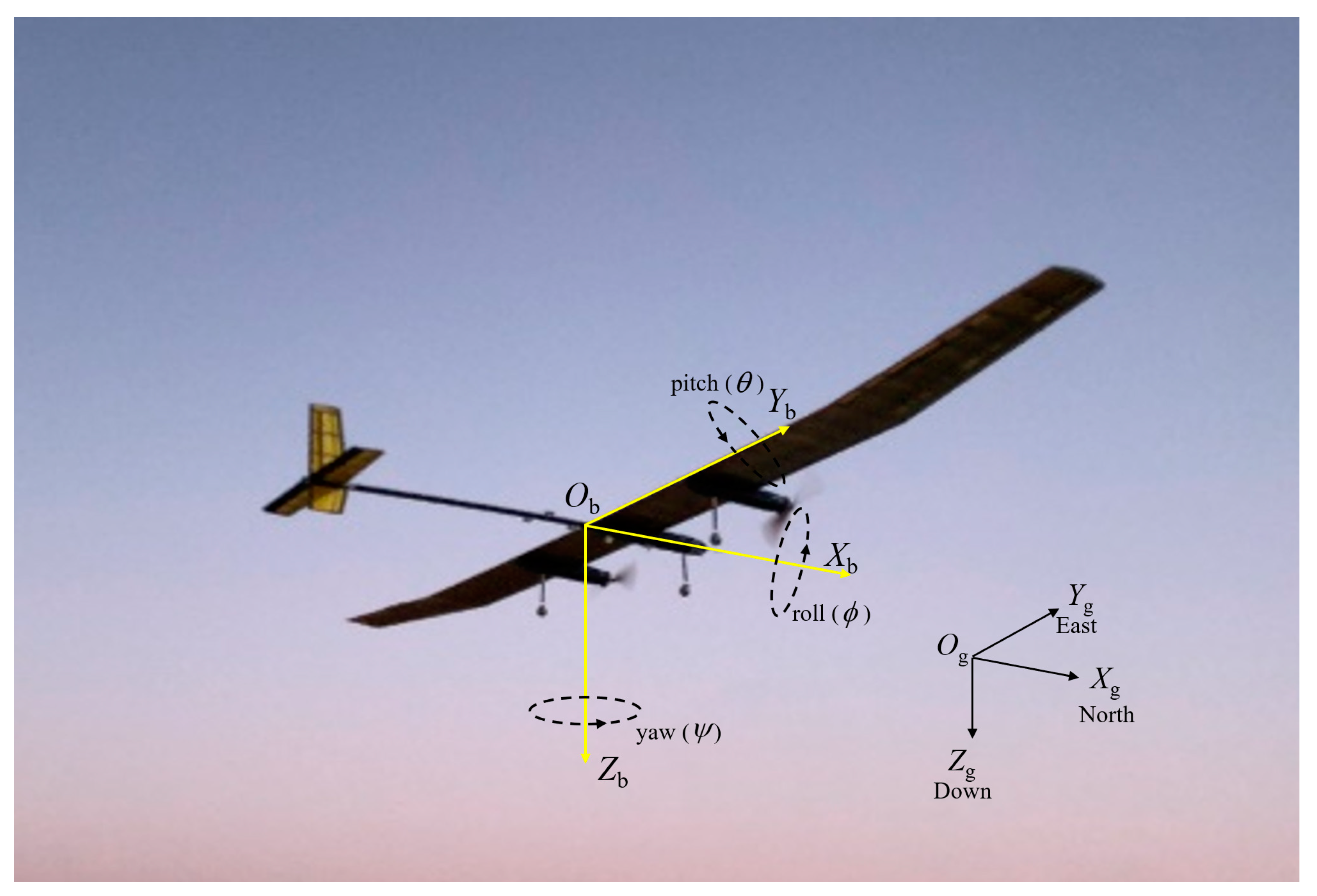
Solar-powered UAV designed by the authors’ team.
Figure 1.
Solar-powered UAV designed by the authors’ team.
Figure 2.
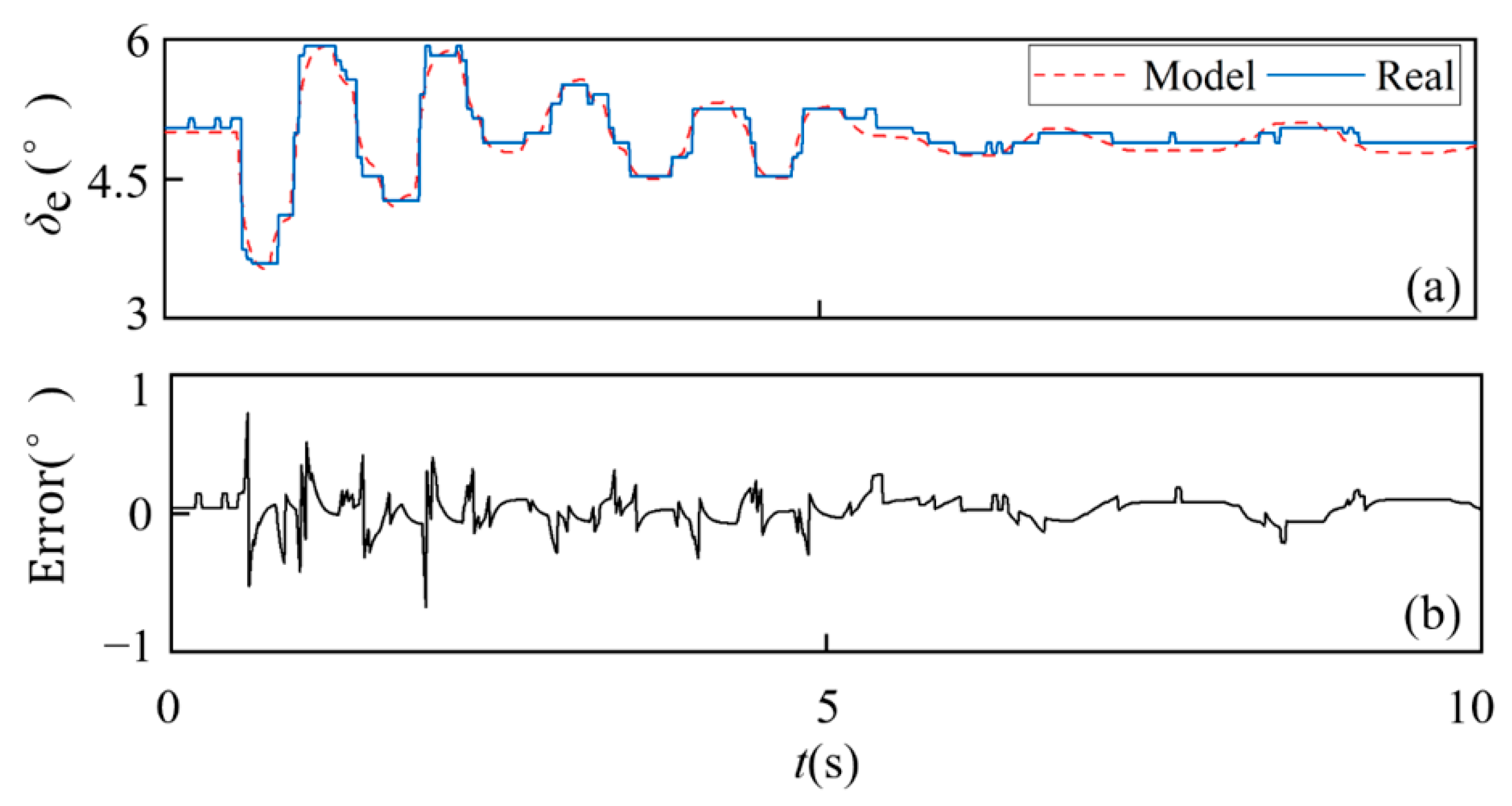
The responses obtained from mathematical servo model and real servo: (a) mathematical servo model, (b) real servo.
Figure 2.
The responses obtained from mathematical servo model and real servo: (a) mathematical servo model, (b) real servo.
Figure 3.
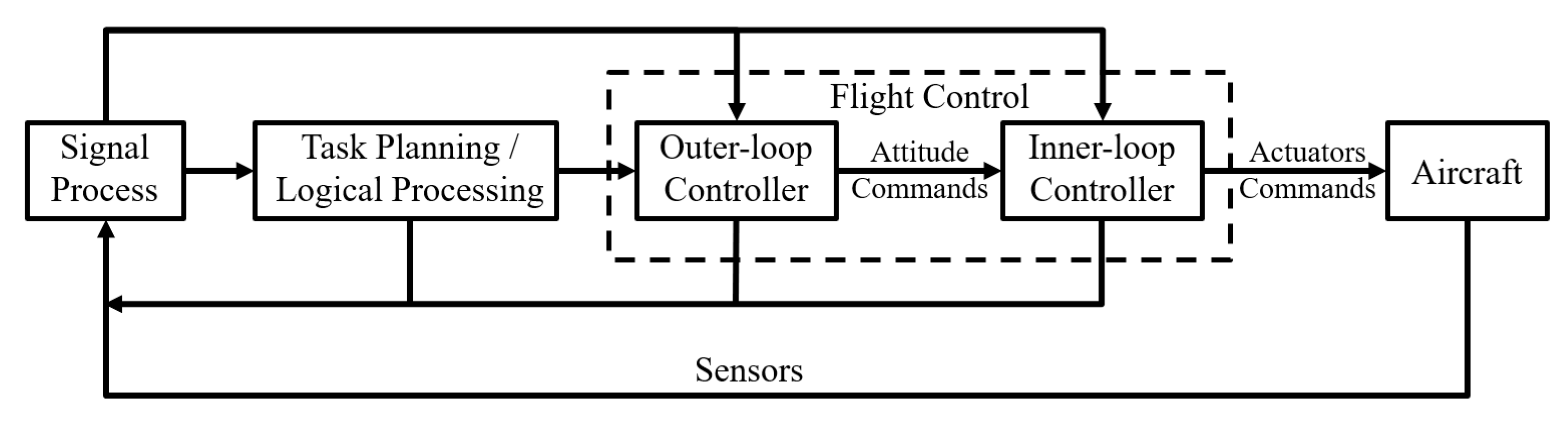
Classical flight control architecture [
26].
Figure 3.
Classical flight control architecture [
26].
Figure 4.
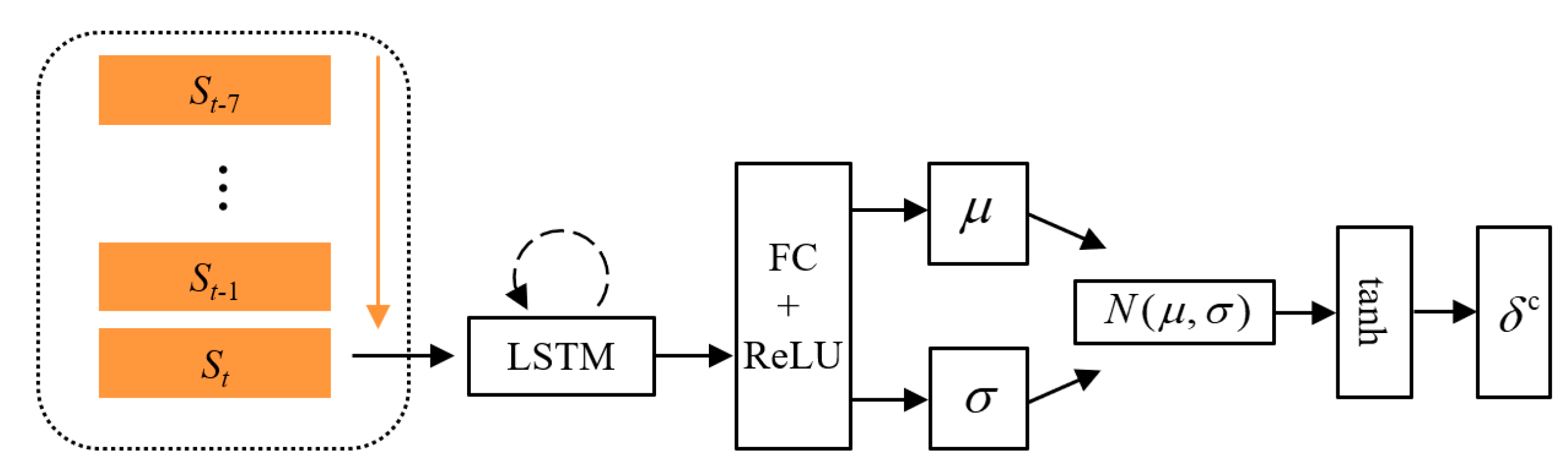
The architecture of policy neural network.
Figure 4.
The architecture of policy neural network.
Figure 5.
Schematic diagram of simulation environment composition.
Figure 5.
Schematic diagram of simulation environment composition.
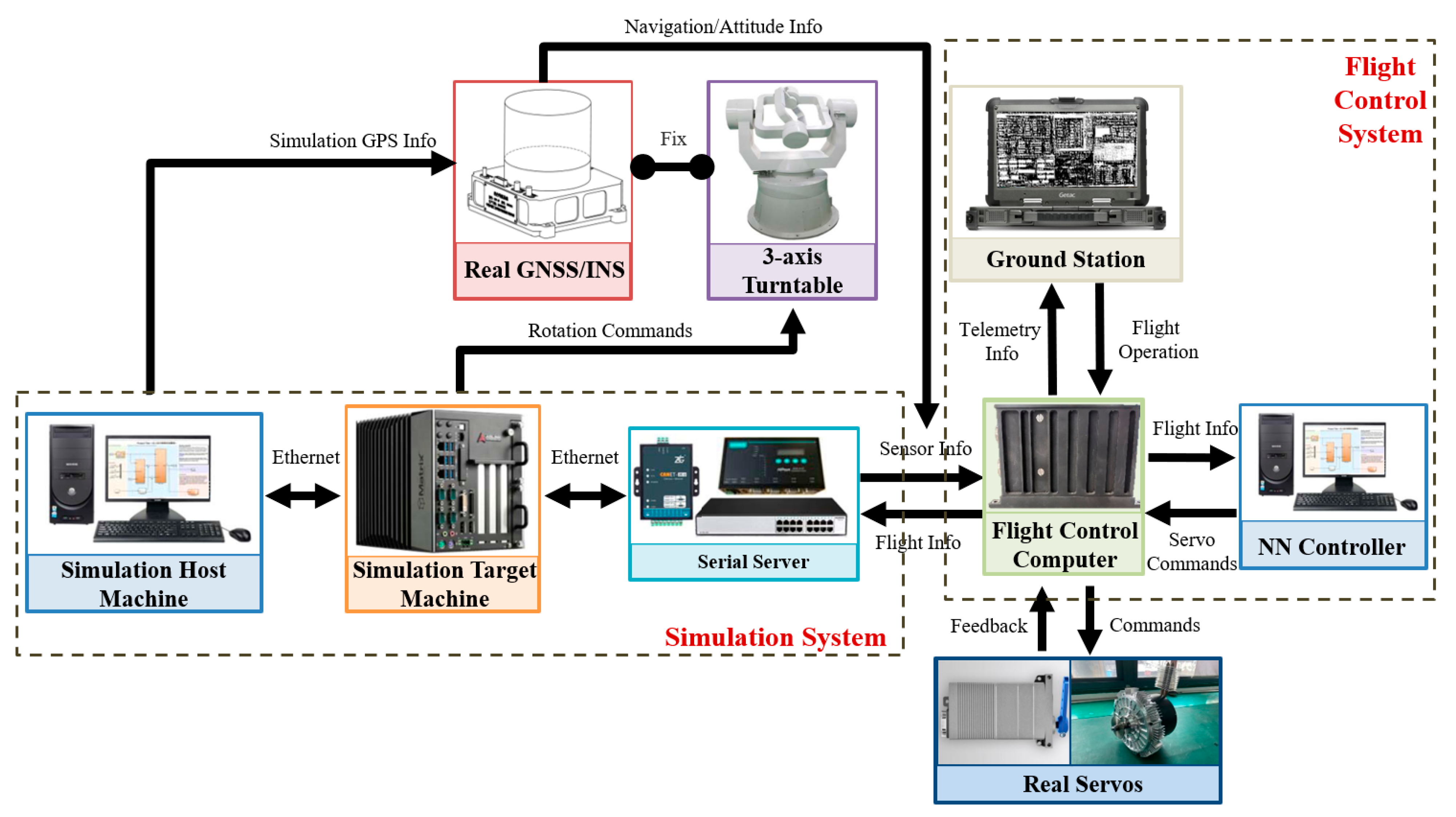
Figure 6.
Signal pathway of the hardware-in-loop simulation platform.
Figure 6.
Signal pathway of the hardware-in-loop simulation platform.
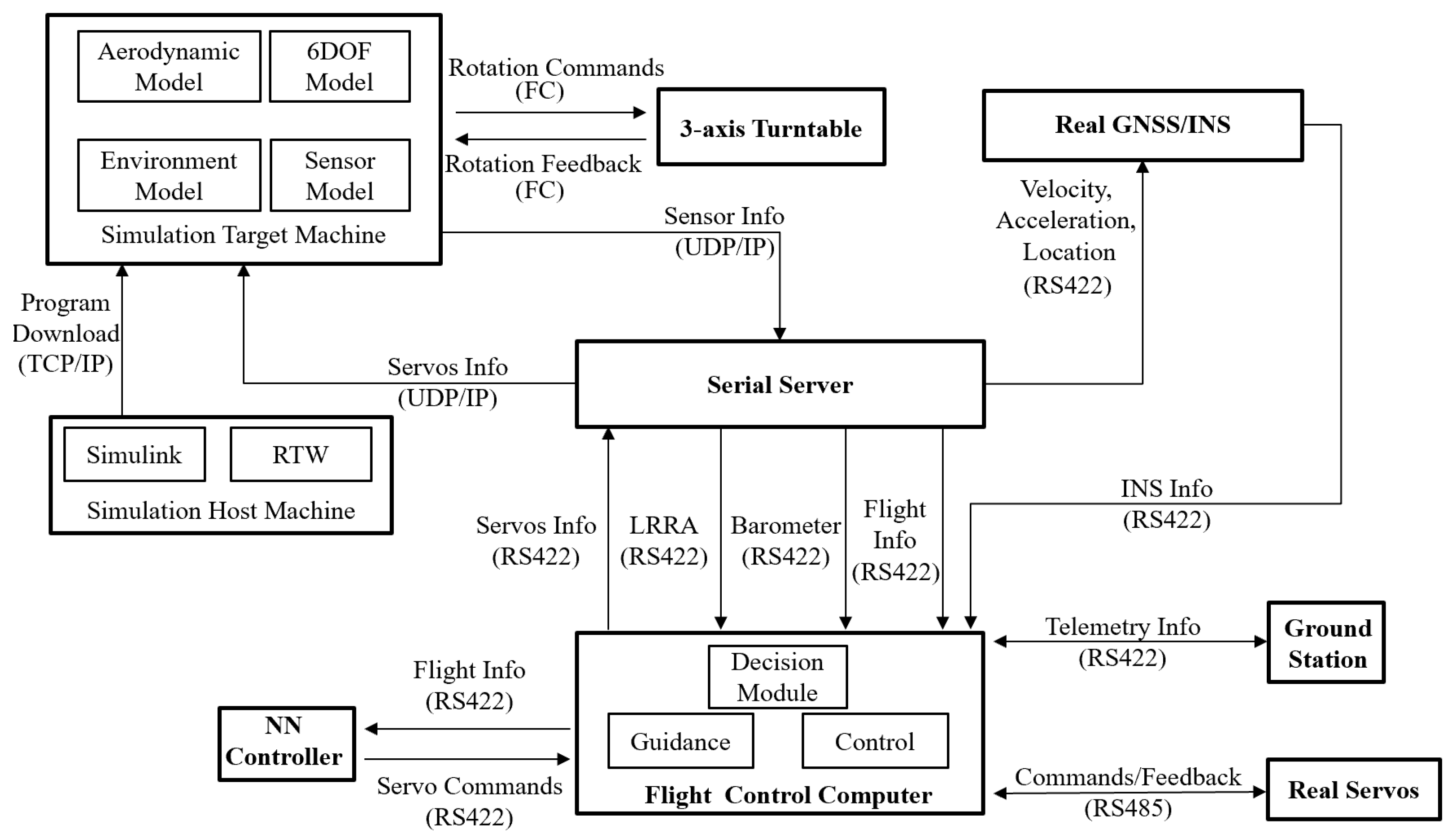
Figure 7.
Experimental setup diagram.
Figure 7.
Experimental setup diagram.
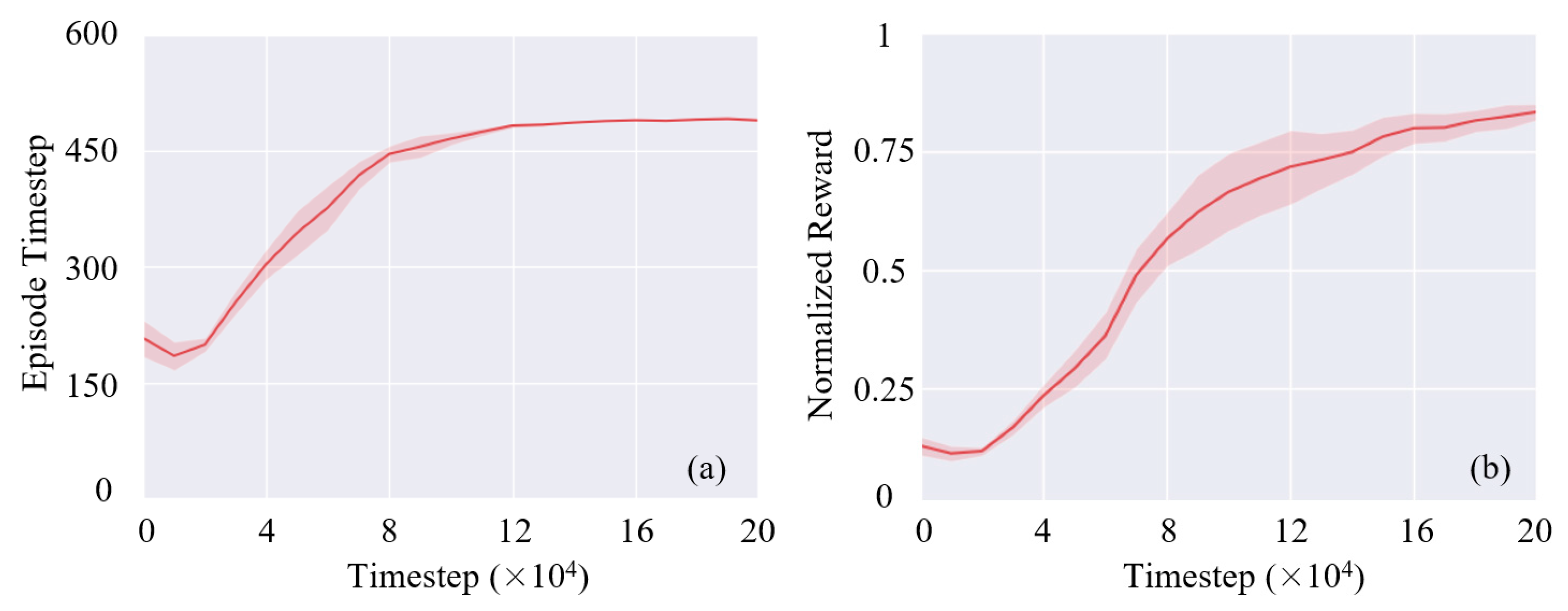
Figure 8.
The recorded curve during training, where (a) is the simulation steps of one evaluation episode, and (b) is the normalized total reward of one episode.
Figure 8.
The recorded curve during training, where (a) is the simulation steps of one evaluation episode, and (b) is the normalized total reward of one episode.
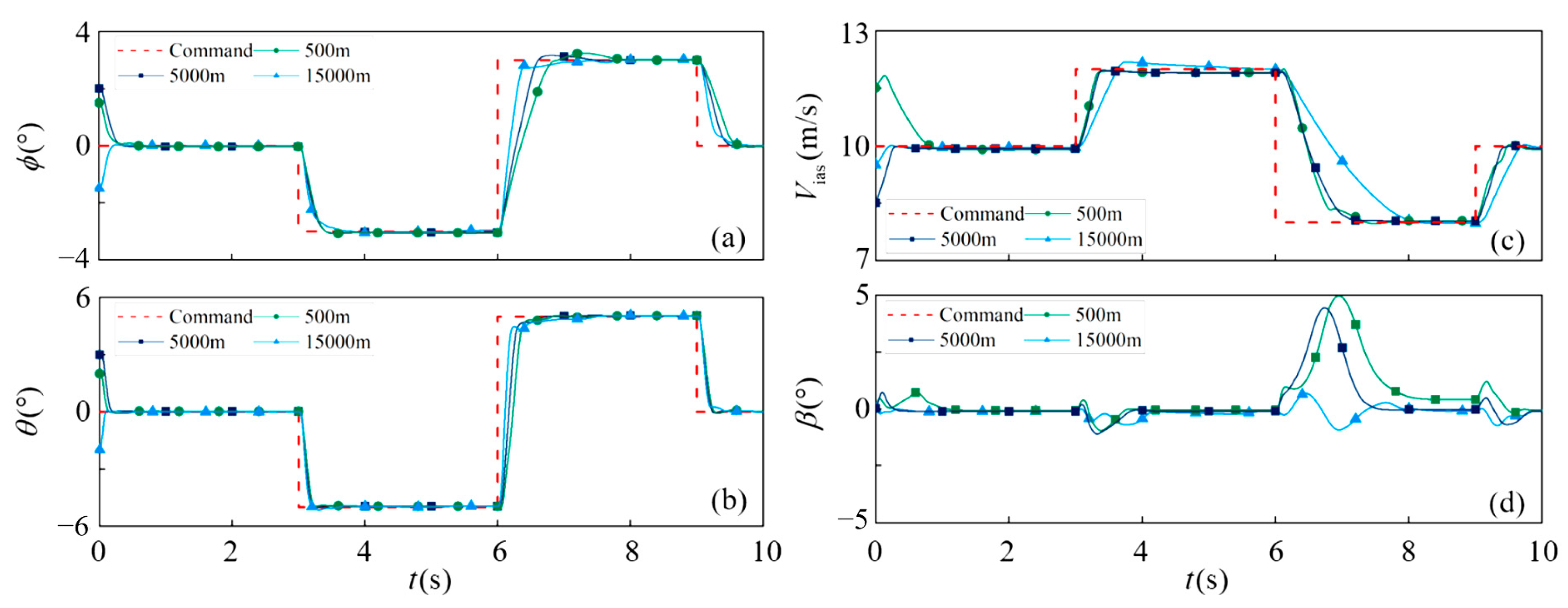
Figure 9.
The time histories of the attitude evaluated under the mathematical model: (a) ϕ, (b) Vias, (c) θ, (d) β.
Figure 9.
The time histories of the attitude evaluated under the mathematical model: (a) ϕ, (b) Vias, (c) θ, (d) β.
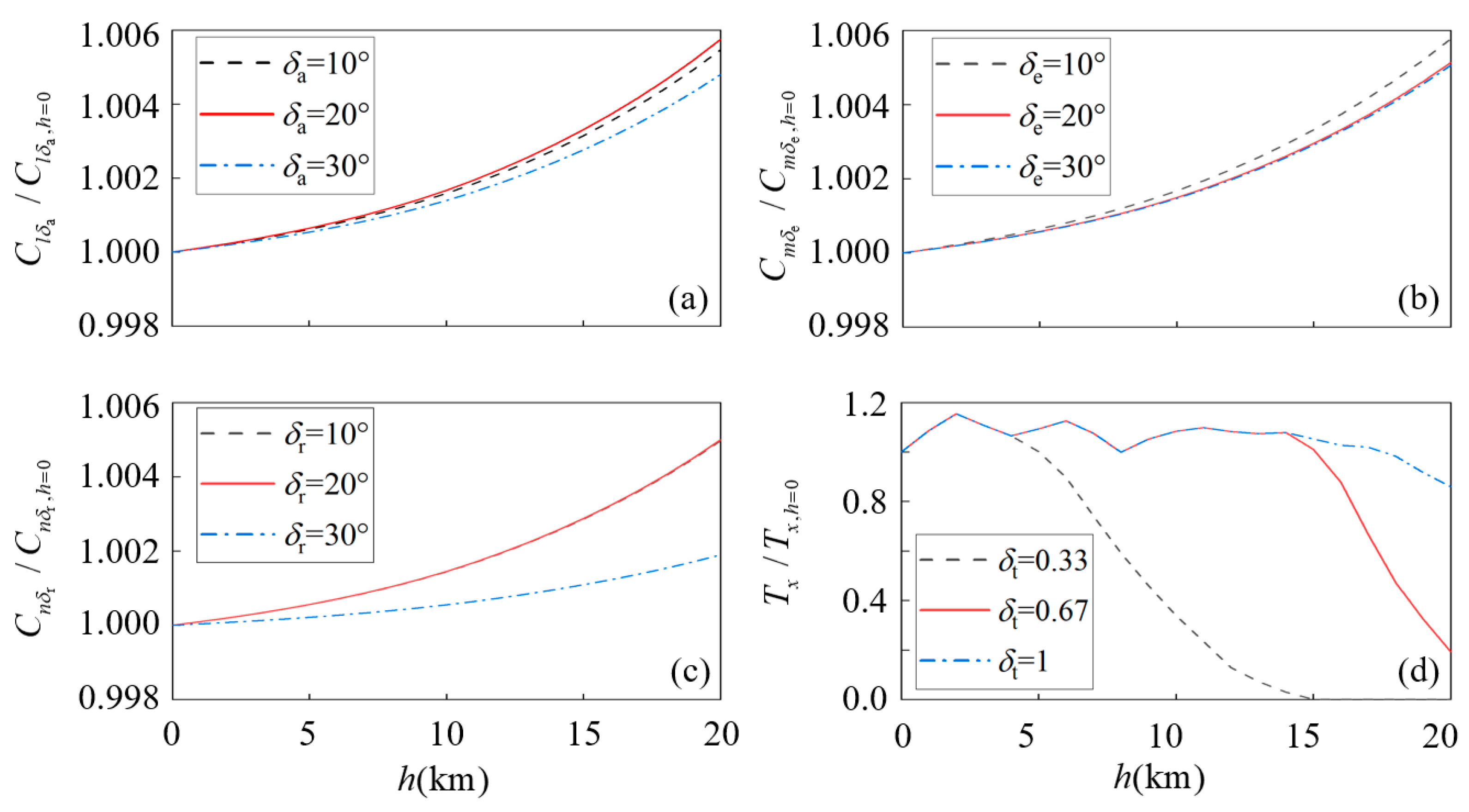
Figure 10.
The normalized actuator efficiency trends with altitude when Veas = 10 m/s.
Figure 10.
The normalized actuator efficiency trends with altitude when Veas = 10 m/s.
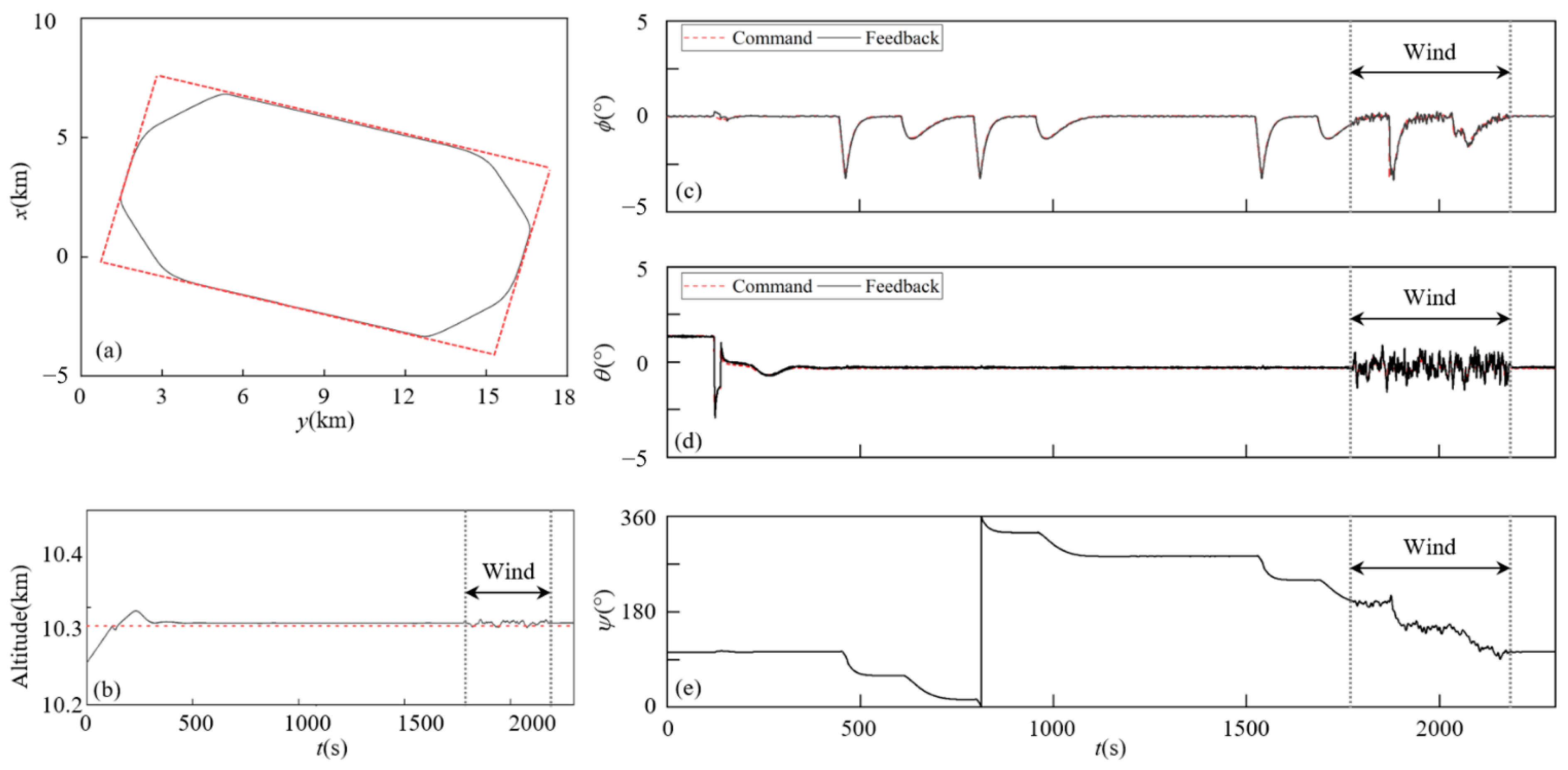
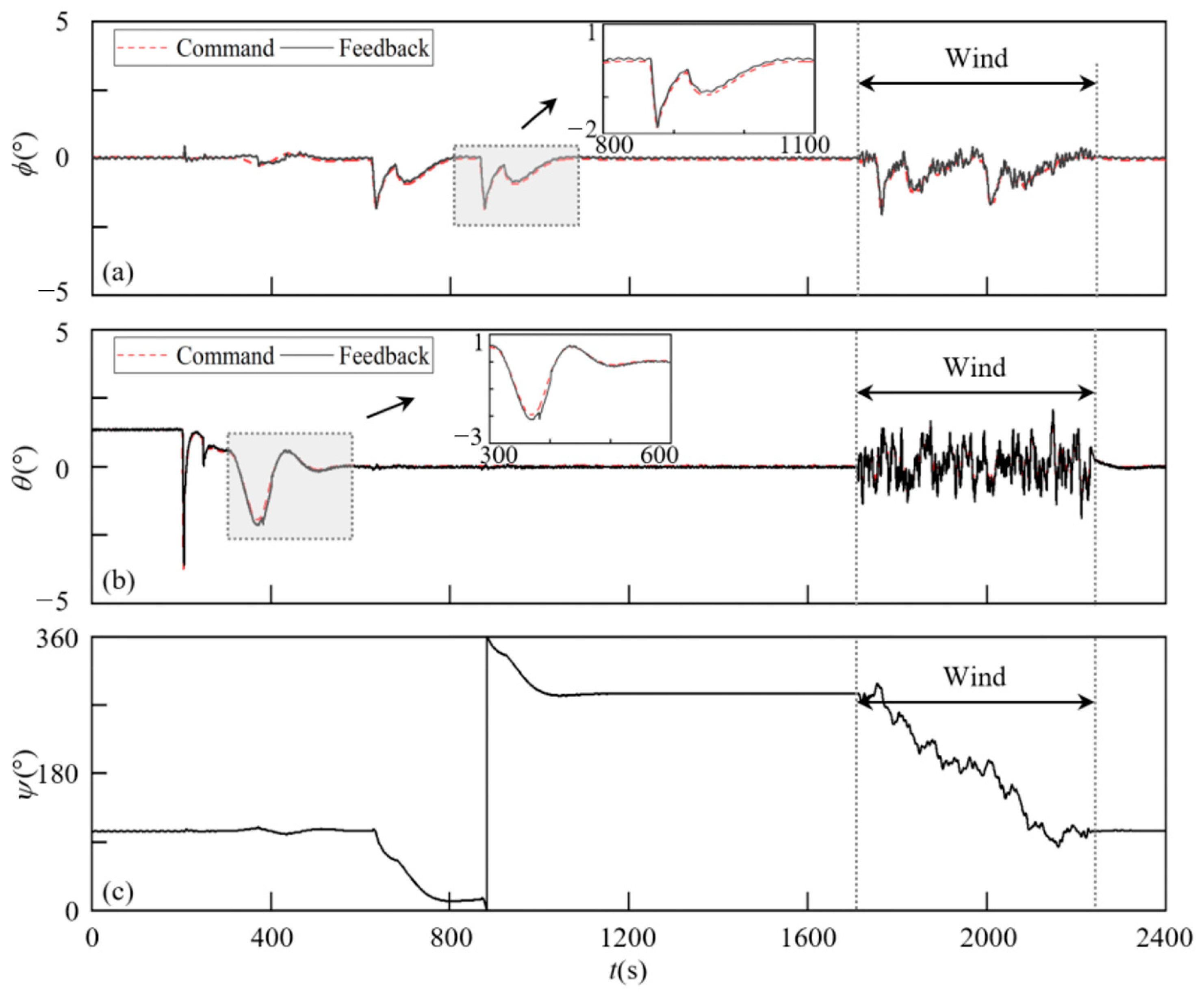
Figure 11.
The flight process at 10 km altitude: (a) x, (b) Altitude, (c) ϕ, (d) θ, (e) Ψ.
Figure 11.
The flight process at 10 km altitude: (a) x, (b) Altitude, (c) ϕ, (d) θ, (e) Ψ.
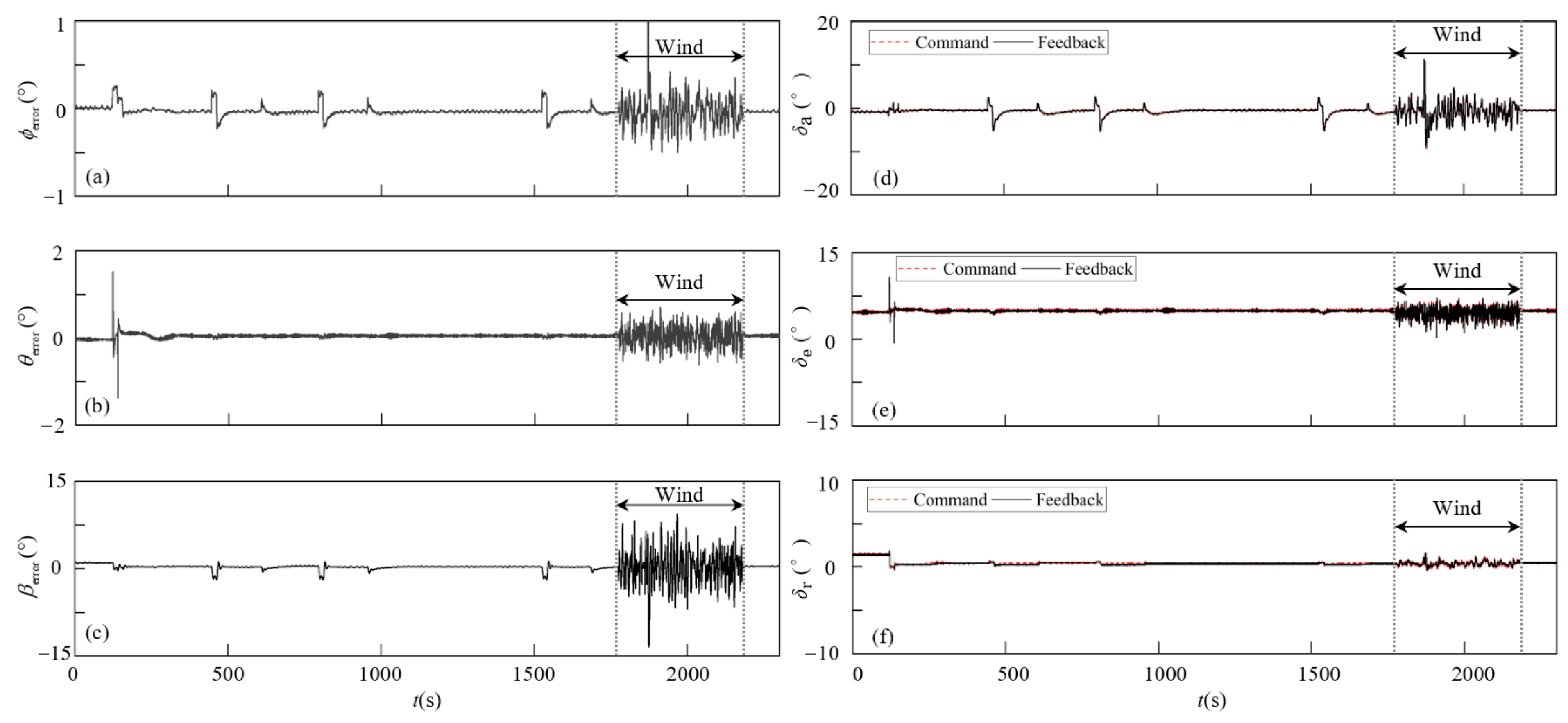
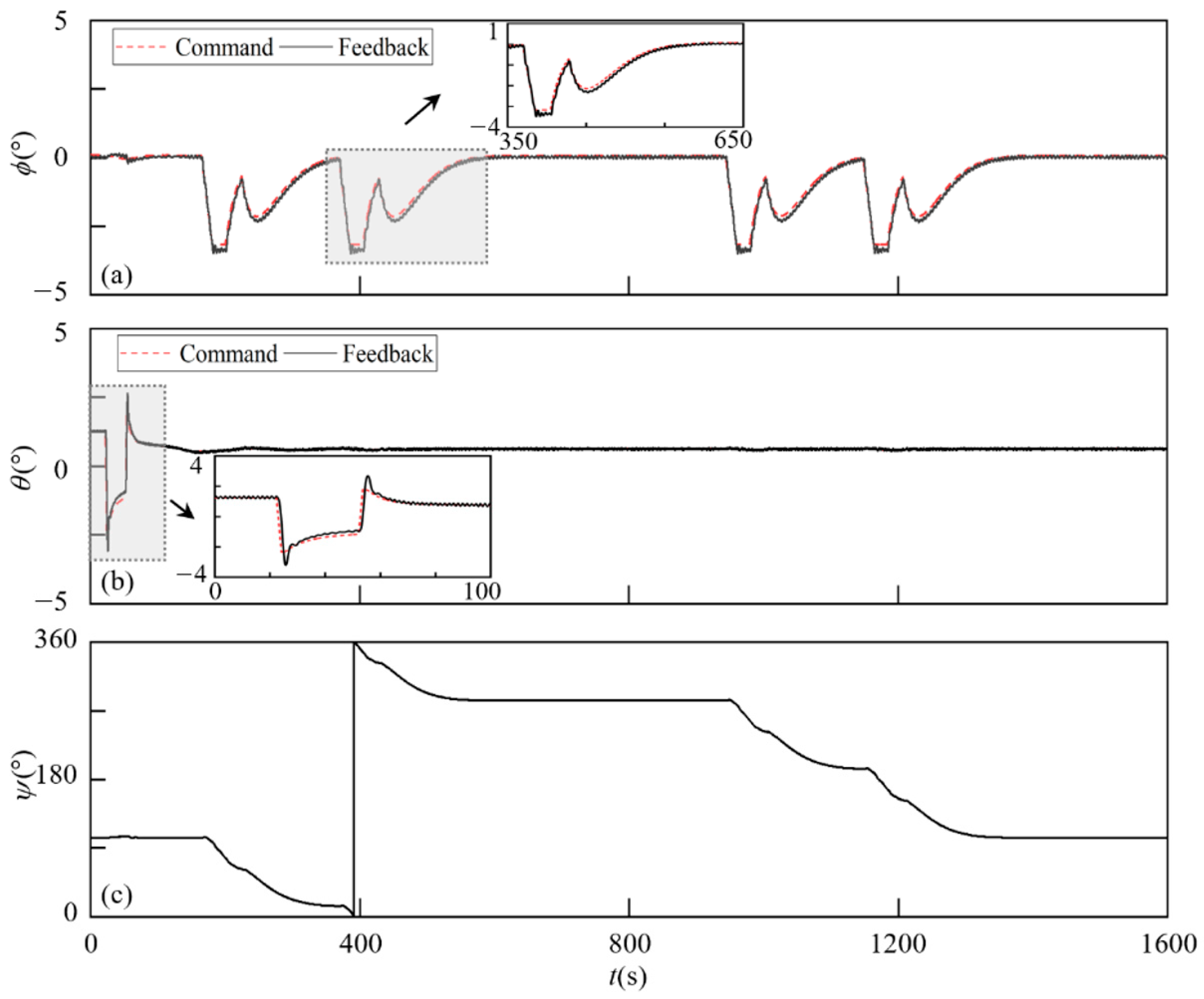
Figure 12.
The attitude tracking errors and actuator changes at 10 km altitude: (a) ϕerror, (b) θerror, (c) βerror, (d) δa, (e) δe, (f) δr.
Figure 12.
The attitude tracking errors and actuator changes at 10 km altitude: (a) ϕerror, (b) θerror, (c) βerror, (d) δa, (e) δe, (f) δr.
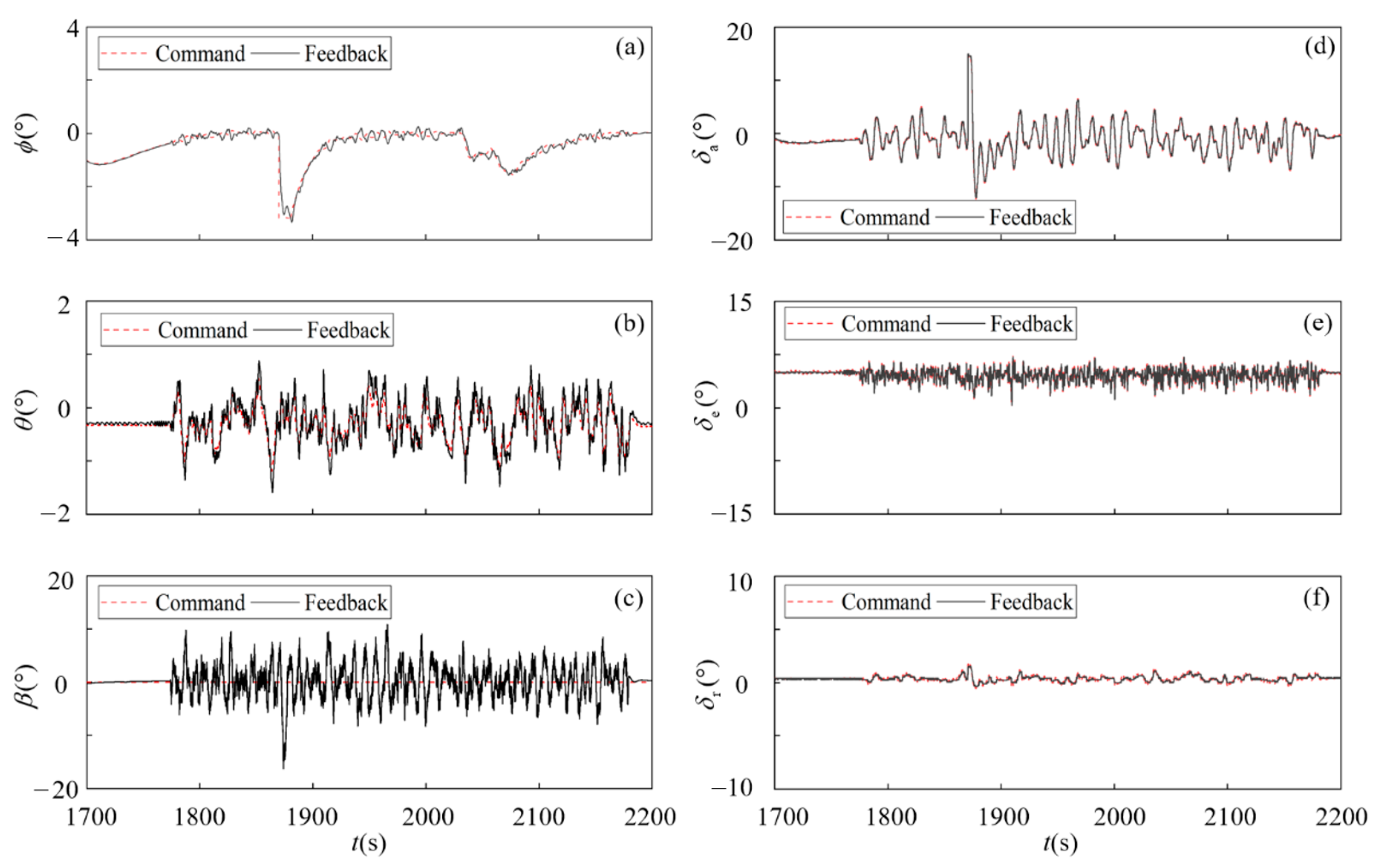
Figure 13.
Enlarged view of flight process controlled by NN in the wind at 10 km altitude: (a) ϕ, (b) θ, (c) β, (d) δa, (e) δe, (f) δr.
Figure 13.
Enlarged view of flight process controlled by NN in the wind at 10 km altitude: (a) ϕ, (b) θ, (c) β, (d) δa, (e) δe, (f) δr.
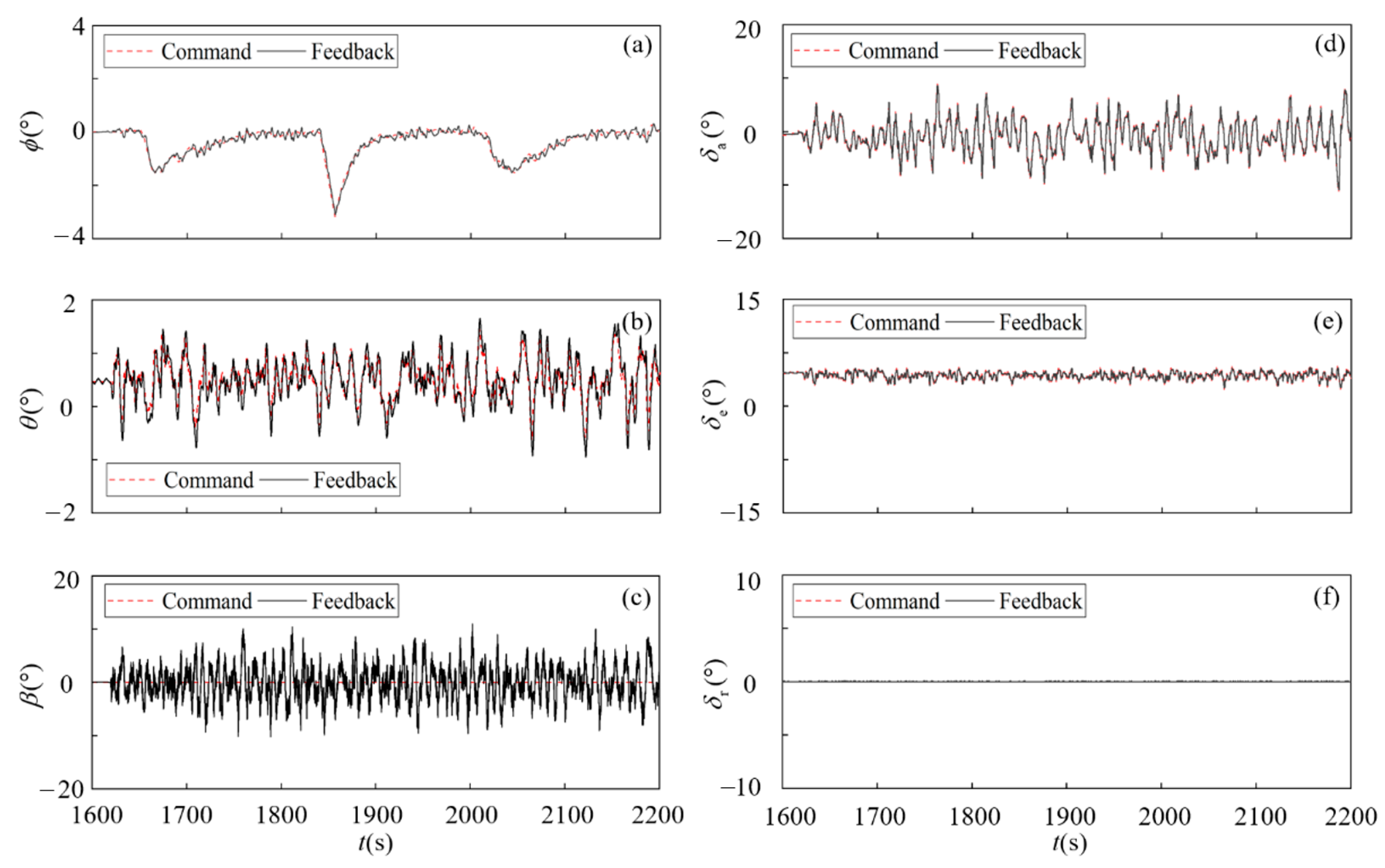
Figure 14.
Enlarged view of flight process controlled by PID in the wind at 10 km altitude: (a) ϕ, (b) θ, (c) β, (d) δa, (e) δe, (f) δr.
Figure 14.
Enlarged view of flight process controlled by PID in the wind at 10 km altitude: (a) ϕ, (b) θ, (c) β, (d) δa, (e) δe, (f) δr.
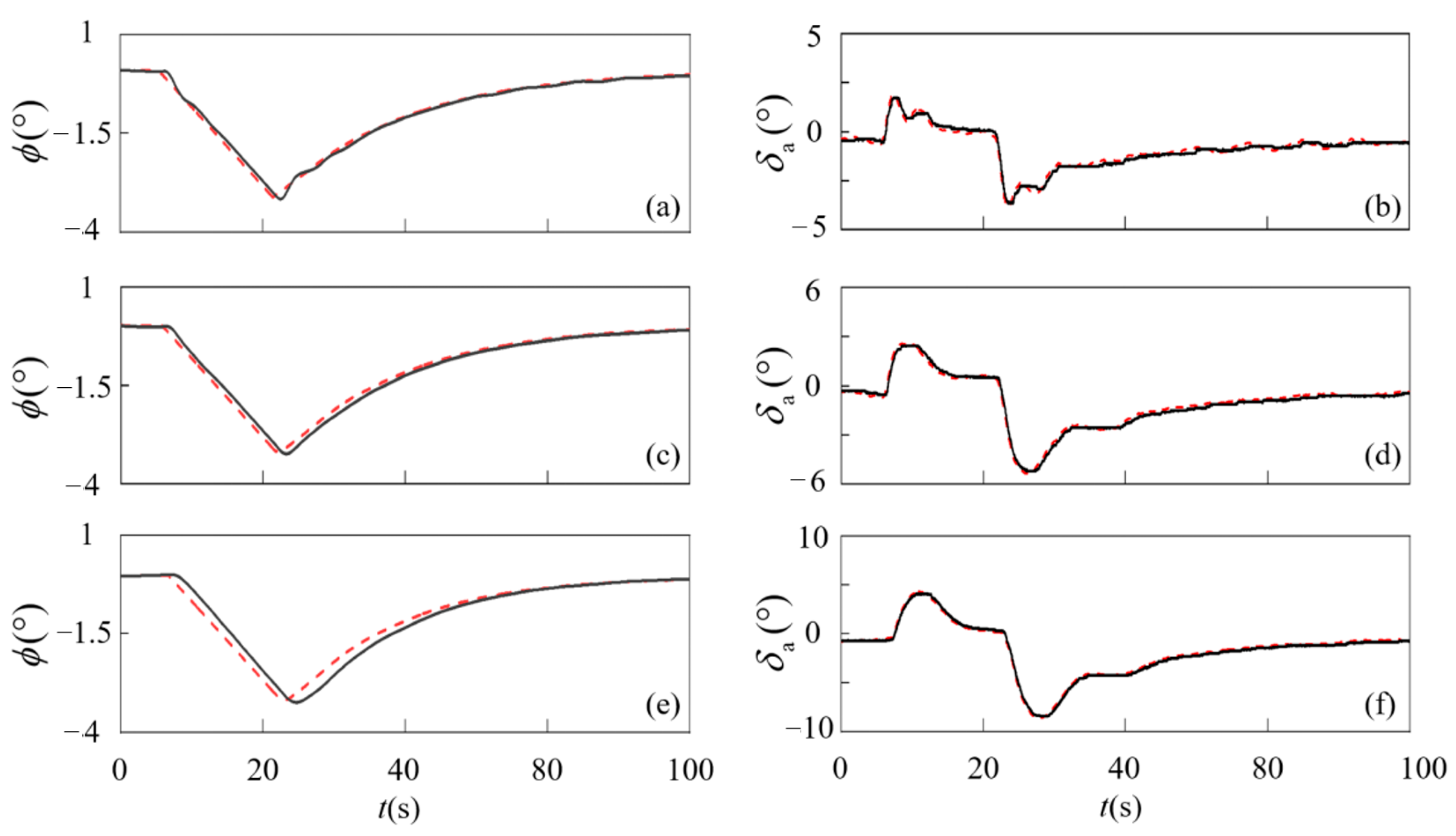
Figure 15.
Roll angle and aileron response under different parameter perturbations: (a,b) are under positive perturbation, (c,d) are under reference model, and (e,f) are under negative perturbation. The red dashed lines represent the command values, and the black solid lines represent the real response.
Figure 15.
Roll angle and aileron response under different parameter perturbations: (a,b) are under positive perturbation, (c,d) are under reference model, and (e,f) are under negative perturbation. The red dashed lines represent the command values, and the black solid lines represent the real response.
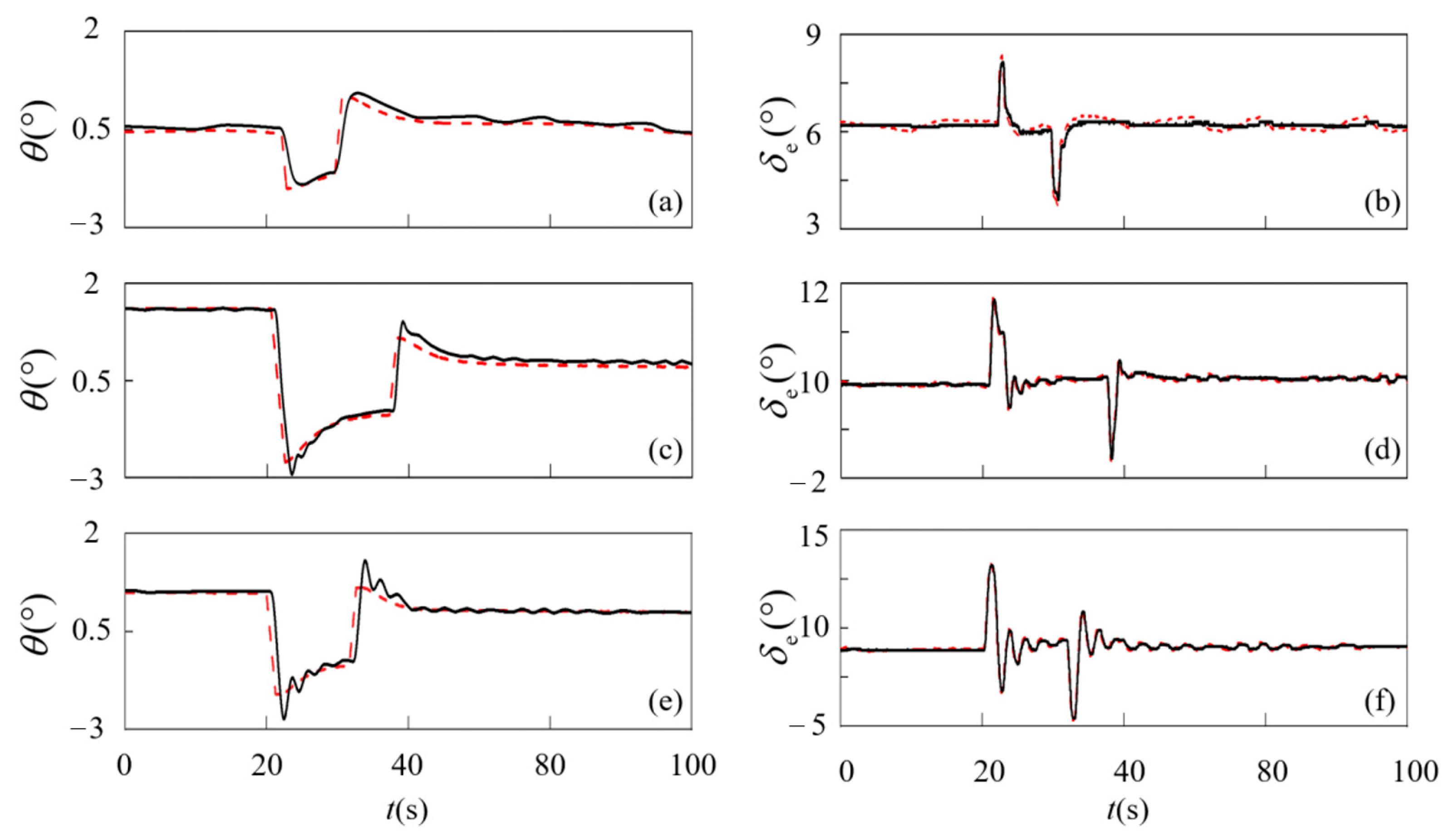
Figure 16.
Pitch angle and elevator response under different parameter perturbations: (a,b) are under positive perturbation, (c,d) are under reference model, and (e,f) are under negative perturbation. The red dashed lines represent the command values, and the black solid lines represent the real response.
Figure 16.
Pitch angle and elevator response under different parameter perturbations: (a,b) are under positive perturbation, (c,d) are under reference model, and (e,f) are under negative perturbation. The red dashed lines represent the command values, and the black solid lines represent the real response.
Figure 17.
The attitude tracking process for the route at 1 km altitude: (a) ϕ, (b) θ, (c) Ψ.
Figure 17.
The attitude tracking process for the route at 1 km altitude: (a) ϕ, (b) θ, (c) Ψ.
Figure 18.
The attitude tracking process for the route at 20 km altitude: (a) ϕ, (b) θ, (c) Ψ.
Figure 18.
The attitude tracking process for the route at 20 km altitude: (a) ϕ, (b) θ, (c) Ψ.
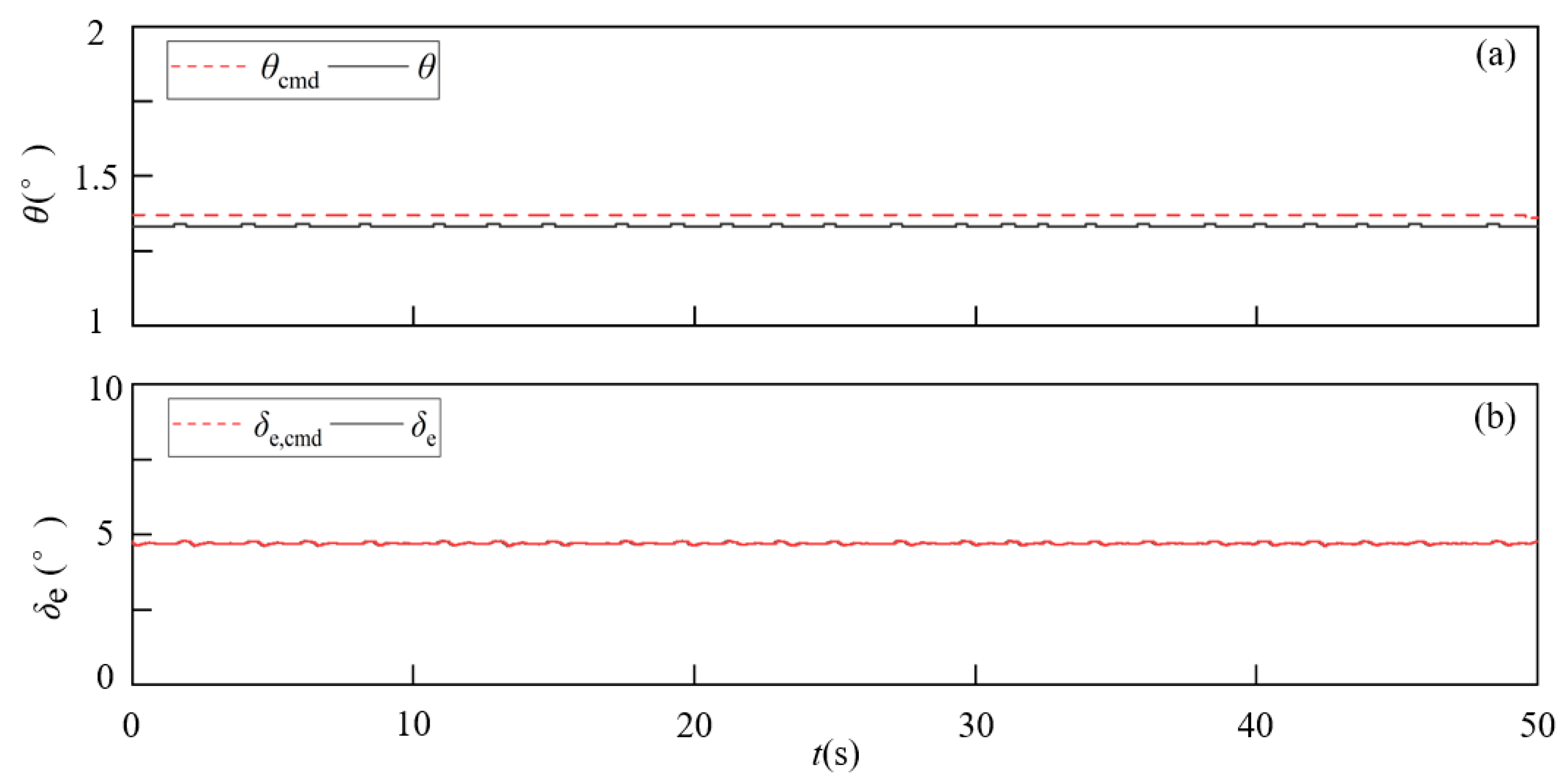
Figure 19.
Flight process under the ideal servo model: (a) θ, (b) δe.
Figure 19.
Flight process under the ideal servo model: (a) θ, (b) δe.
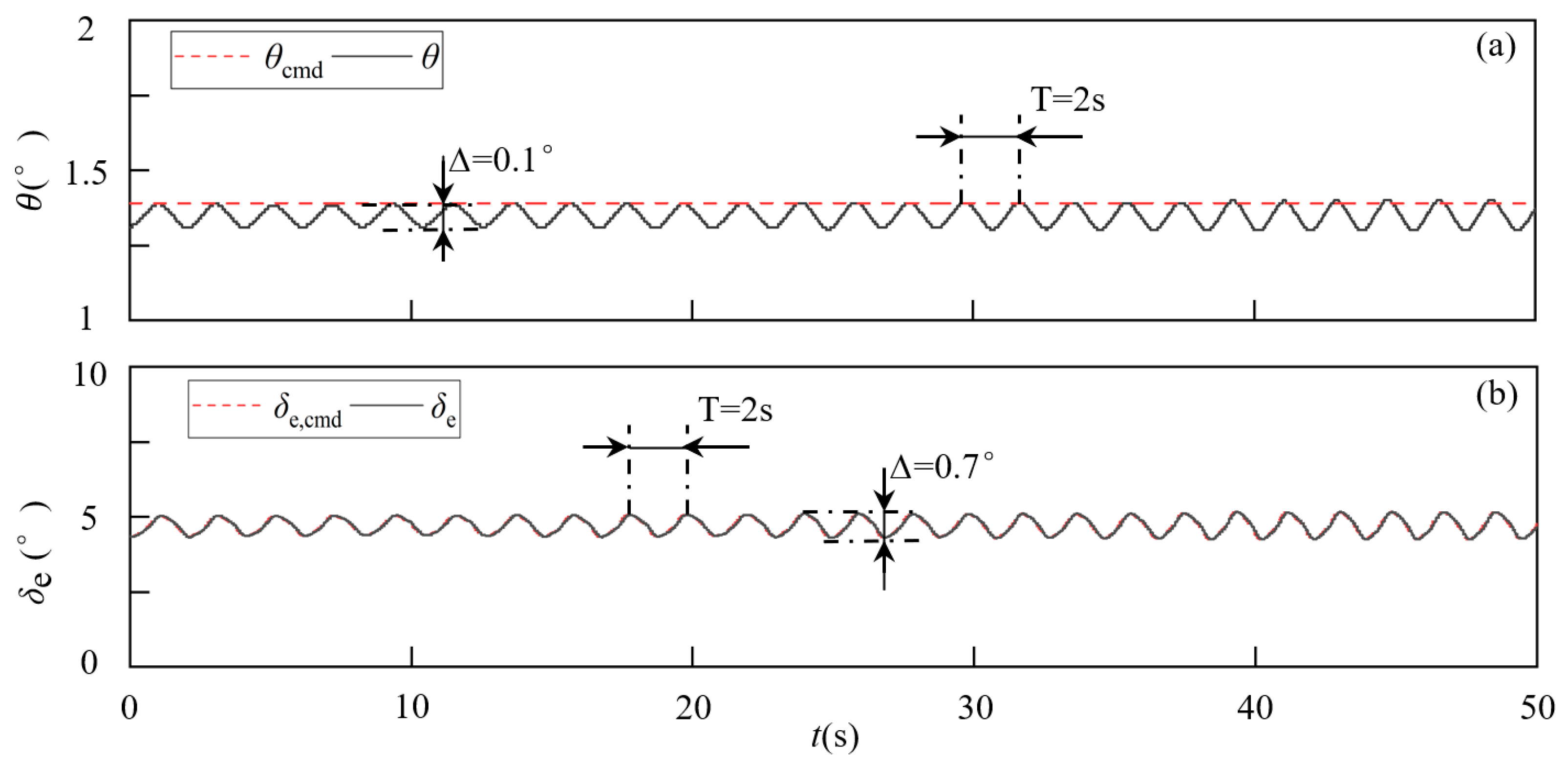
Figure 20.
Flight process under the ideal servo model with backlash: (a) θ, (b) δe.
Figure 20.
Flight process under the ideal servo model with backlash: (a) θ, (b) δe.
Table 1.
Basic parameters of the studied aircraft.
Table 1.
Basic parameters of the studied aircraft.
| Variables | Description | Value |
|---|
| Total mass | 359 |
| Wing area | 78.5 |
| Aspect ratio | 15.6 |
| Wing span | 35 |
| Wing chord | 2.27 |
| Moment of inertia matrix | |
Table 2.
Ranges of attitude and action commands.
Table 2.
Ranges of attitude and action commands.
| Parameters | Description | Range |
|---|
| Target roll angle | [−5, 5] |
| Target pitch angle | [−10, 10] |
| Target equivalent airspeed | [8, 12] |
| Aileron deflection angle command | [−30, 30] |
| Elevator deflection angle command | [−30, 30] |
| Rudder deflection angle command | [−20, 20] |
| Throttle command for propellers | [0, 1] |
Table 3.
The variance in OU noise for different state elements.
Table 3.
The variance in OU noise for different state elements.
| Parameters | Value | Unit |
|---|
| 0 | m |
| 0.001 | rad |
| 0.001 | rad/s |
| 0.01 | m/s |
| 0.001 | rad |
| 0 | rad |
Table 4.
Domain randomization parameters during training. denotes the basic reference value.
Table 4.
Domain randomization parameters during training. denotes the basic reference value.
| Parameters | Description | Distribution |
|---|
| Moment of inertia | |
| Aerodynamic lift coefficients | |
| Aerodynamic drag coefficients | |
| Lateral force coefficients | |
| Roll moment coefficients | |
| Pitching moment coefficients | |
| Yaw moment coefficients | |
| Damping and cross derivative | |
Table 5.
The operating data and performance of the GNSS/INS system.
Table 5.
The operating data and performance of the GNSS/INS system.
| Index | Roll | Pitch | Yaw |
|---|
| Sampling frequency | 100 Hz |
| Measuring range of rate | −200°/s~+200°/s |
| Measuring range of angle | −180°~+180° | Measuring range of angle | −180°~+180° |
| Measuring accuracy of angle | ≤0.1° | Measuring accuracy of angle | ≤0.1° |
Table 6.
The operating data and performance of the three-axis turntable.
Table 6.
The operating data and performance of the three-axis turntable.
| Index | Roll | Pitch | Yaw |
|---|
| Range of measuring angle | No limit |
| Measuring accuracy of angle | ±0.001° |
| Repeatability accuracy of angle | ±0.0005° |
| Resolution of angle | ±0.0001° |
| Range of rated speed | ±2500°/s | Range of rated speed | ±2500°/s |
| Resolution at rated speed | 0.0001°/s | Resolution at rated speed | 0.0001°/s |
Table 7.
The operating data and performance of the used servo.
Table 7.
The operating data and performance of the used servo.
| Index | Roll |
|---|
| Max. speed without load | 230°/s |
| Rated speed | 150°/s |
| Default travel angle | ±45° |
| Max. travel angle | ±85° |
| Backlash (mechanical) | ≤0.5° |
Table 8.
The comparison of accuracy and smoothness between PID and NN. The better terms are bolded.
Table 8.
The comparison of accuracy and smoothness between PID and NN. The better terms are bolded.
| Controller | | | | | | | | |
|---|
| PID | 0.125 | 0.193 | 0.393 | 2.915 | 9.50 × 10−5 | 4.48 × 10−5 | 0.00 × 10−5 | 1.12 × 10−5 |
| RL | 0.073 | 0.084 | 0.448 | 0.956 | 3.03 × 10−5 | 6.63 × 10−5 | 1.05 × 10−5 | 1.27 × 10−5 |
Table 9.
Parameter perturbation in hardware-in-loop simulation verification. The notation is inherited from
Table 4.
Table 9.
Parameter perturbation in hardware-in-loop simulation verification. The notation is inherited from
Table 4.
| Parameters | Positive | Negative |
|---|
| | |
| | |
| | |
| | |
| | |
| | |
| | |