Heterogeneous Multi-UAV Mission Reallocation Based on Improved Consensus-Based Bundle Algorithm

Abstract

In dynamic complex environments, it is inevitable for UAVs to be damaged due to their confrontational nature. The challenge to minimize the adverse effects of the damage and reallocate the mission is vital for achieving the operational goal. This paper proposes a distributed Multi-UAV mission reallocation method in the case of UAV damage based on the improved consensus-based bundle algorithm (CBBA). Firstly, a dynamic optimization model for Multi-UAV mission reallocation is established based on an improved resource update model. Secondly, a distributed damage inspection method based on the heartbeat hold mechanism is proposed for real-time monitoring of UAV conditions, which could enable the rapid response to UAV damage events. Furthermore, the CBBA is improved by introducing a timeliness parameter to adjust the bidding strategy and optimizing the mission selection strategy based on the time-order priority insertion principle to generate mission reallocation plans quickly. Through numerical examples, the results show that the proposed method can effectively reallocate Multi-UAV missions under damage events and has superior performance compared with original the CBBA, the particle swarm optimization (PSO) algorithm, and the performance impact (PI) algorithm. The proposed method has a faster solving speed, while the obtained solution has higher mission reallocation effectiveness.

1. Introduction

With the rapid development of autonomous and control technology, the Unmanned Aerial Vehicle (UAV) has been widely used in dynamic complex environments. In many complex cases, multiple heterogeneous UAVs need to cooperate with each other to accomplish various missions and achieve the operational goal [1,2]. The complexity of the dynamic environment makes various uncertainties increase [3], while the UAV may also be subject to enemy counterattack during mission execution and will inevitably be damaged during missions, making it difficult to properly execute the mission pre-allocation plan developed before. In order for Multi-UAVs to successfully perform their missions, they need to respond with agility to sudden events and adjust mission plans in real time with feedback mechanisms and dynamic planning capabilities. Therefore, the purpose of Multi-UAV mission reallocation is to use the sharing resource of Multi-UAVs to reasonably adjust the mission allocation plan after all kinds of sudden events, increase their probability of accomplishing the mission, and reduce the loss of mission effectiveness as a result of improving mission effectiveness and avoiding failure of mission objectives due to changing environments.

The Multi-UAV mission reallocation problem can be regarded as a combinatorial optimization problem under complex multi-constraint conditions, which is also an NP-hard problem. The solutions for mission reallocation are mainly classified into two categories: centralized and distributed. Since the dynamic adjustment of Multi-UAVs urgently requires the fast convergence of the reallocation algorithm to meet the real-time demands of dynamic environments, the running time of the algorithm is an important criterion to evaluate the merits of the reallocation methods [4].

Centralized methods are those in which the UAV is controlled by a single or multiple centers and the mission reallocation plan is calculated by the control center. Intelligent algorithms are most widely used among centralized methods, including genetic algorithms [5,6,7,8], particle swarm optimization algorithms [9,10,11], ant colony optimization algorithms [12,13], artificial neural networks [14,15,16], etc. Ref. [17] presents the probabilistic chain-enhanced parallel genetic algorithm (PC-EPGA), which combines probabilistic chains with genetic algorithms to significantly enhance the quality of solutions by taking into account both the quantity of tasks assigned to UAVs and the associated costs of inter-task flights. Considering the impact of multiple uncertain factors such as uncertain mission execution time, target disappearance time, and UAV cruise speed on the mission allocation results, ref. [18] proposed a grey wolf optimization algorithm integrating multiple strategies to enhance the search ability of the algorithm and population diversity. However, these algorithms often suffer from high complexity and computational demands on the central controller, and it often results in local optima when there is a large number of UAVs. Moreover, each UAV must have a communication link with the control center, which makes the central server bear a large communication burden and thus is not efficient in the case of the rapidity demand of solving the reallocation problem.

Compared to centralized methods, distributed methods are more suitable for larger-scale systems in dynamic environments because of their strong fault tolerance and flexibility [19,20,21,22], where each UAV can compute in parallel to give reallocation plans quickly. In ref. [23], a Multi-UAV dynamic mission planning algorithm based on the time window mechanism is proposed under a distributed formation structure to solve the problem of the limited time duration and spatial instability of time-sensitive targets. In ref. [24], a Q-learning-based fast task allocation (FTA) algorithm was proposed to develop a Q-network encoded task allocation rule that not only considers the effect of environment uncertainty but also is capable of handling totally different tasks. In ref. [25], a coupled and distributed planning method was proposed for heterogeneous fixed-wing UAV swarms performing consecutive missions over multiple targets, and the distributed planning framework proved to be highly reliable by effectively avoiding single-point failures. In ref. [26], a distributed decision-making framework based on game theory was proposed with verified stability and robustness of the algorithm, which is adapted to dynamic environments.

Inspired by economic theory, market-based approaches have been used in many distributed methods with promising results for their advantages of high efficiency, robustness, and scalability [27,28]. As a typical market-based approach, auction algorithms have attracted attention from scholars widely and have gradually become a hot topic of mission reallocation algorithm research [29,30,31]. The auction process includes multiple rounds of bidding. UAVs bid on each mission based on value, cost, etc., as objectives, ultimately generating the mission allocation plan that maximizes the objectives. The CBBA proposed in ref. [27] acts as a combined auction algorithm where UAVs bid on bundles rather than individual missions. Unlike traditional auction approaches, this algorithm runs on each UAV individually without an auctioneer, and a consensus mechanism is used to reach consensus on the winning bids rather than situational awareness. It has been proven that CBBA can offer similar solutions to some optimized-based approaches and 50% optimality is guaranteed. Several studies have improved and extended the CBBA by optimizing mission selection strategies [32,33,34] and constraining communication conditions [35]. Ref. [36] proposed an iterative strategy with an improved mission planning framework that reduces the computational complexity, obtains better performance of the planning results, and consumes less computational resources by improving the auction algorithm. Ref. [37] proposed a robustness module (ROB-M algorithm) which can work effectively with the CBBA to improve the performance under simulated uncertain conditions. Ref. [38] presented a novel mission allocation and reallocation algorithm based on potential game theory, which guarantees to improve the global utility with lower complexity. Ref. [39] considered mission assignment under strict time constraints and created the feasible slots for unassigned missions by transferring the assignment to achieve the goal of maximizing the number of missions assigned.

In order to improve the effectiveness of mission reallocation [40,41], reduce the running time [42], and enhance the real-time performance of reallocation [43], there have been various studies on modifying the market-based methods. Ref. [44] modified the criteria for mission inclusion and conflict solution, proposed an extended performance impact algorithm for critical missions, and designed a new mission list adjustment phase to assign critical missions. In ref. [45], an incremental sub-team formation mechanism and a partial releasing mechanism were developed to release the computation and communication burden for new missions and mission information change problems. For the problem with time-sensitive uncertainty, ref. [46] proposes a practical online hierarchical planning algorithm.

However, existing studies still suffer from slow response to UAV damage events by Multi-UAVs. In order to adapt to the rapid changes in the dynamic environment more efficiently, it is necessary to respond to UAV damage events as quickly as possible and to reallocate missions in real time. In ref. [47], the heartbeat signal latency used to detect the loss of a UAV in a highly dynamic environment. Ref. [48] proposed an auto-replacement scheme when a newly inserted UAV or a lost UAV is recovered from failures.

In this paper, a distributed mission reallocation method is designed for rapid response to UAV damage events, including a damage inspection method and improved mission selection strategy in the CBBA. More in detail, this paper makes the following innovations:

• A resource update model is established for heterogeneous UAV resource consumption during mission execution. A dynamic optimization model of Multi-UAV mission reallocation based on the timeliness constraint and mission effectiveness is constructed to provide a real-time reliable database for the solution of Multi-UAV mission reallocation.
• A heartbeat-hold-based UAV damage inspection method under a distributed Multi-UAV control structure is proposed, which can make a fast response to UAV damage events in dynamic environments and improve the timeliness of Multi-UAV mission reallocation.
• A timeliness parameter is introduced to the bidding strategy and the mission selection strategy in the CBBA is optimized based on the time-order priority insertion principle to reduce the consumption of computational resources and generate a mission reallocation plan more quickly.

The rest of this paper is structured as follows. In Section 2, the mission reallocation scenario is described and a dynamic optimization model is developed. In Section 3, a novel distributed mission reallocation frame is designed and a Multi-UAV mission reallocation method based on the improved CBBA is proposed. In Section 4, the performance of the proposed method is illustrated by simulations, and it is compared and analyzed with other reallocation algorithms. Section 5 concludes the work of this paper.

2. Problem Formulation

During Multi-UAV missions, N heterogeneous UAVs ($N_r$, $N_c$, $N_{rc}$ representing the number of reconnaissance, cargo, and reconnaissance-and-cargo-integrated UAVs, respectively, $N=N_r+N_c+N_{rc}$) perform M different types of missions ($M_r$, $M_a$ representing the number of reconnaissance and airdrop missions, respectively, $M=M_r+M_a$) according to a mission pre-allocation plan developed prior to the operation.

Due to the interference of various uncertainties, such as damage by attack, loss of connection or malfunction of the UAV because of bad weather, etc., the mission effectiveness is reduced or the mission cannot be continued, thus affecting the achievement of the objectives of the mission. This paper defines a UAV damage event as follows. We suppose the collection of UAV damage events is ${\mathbf{E}}_{\mathbf{damage}}^{\mathbf{G}}=\left\{E_1^G,E_2^G,\cdots ,E_{N_{damage}}^G\right\}$. $N_{damage}$ is the number of UAV damage events. The properties of each type of damage event are represented as a triplet $\left[m_e,N{R}_e^l,t_e\right]$, where $m_e$ is the serial number of the UAV affected by the event, $N{R}_e^l$ is the loss of the l^th type resource capability value of the UAV due to this damage event, and $t_e$ is the occurrence time of the event.

It is necessary to reallocate unfinished missions in the pre-allocated mission sequence of the damaged UAVs to other capable UAVs in order to minimize losses and ensure successful completion of mission objectives.

A list of key symbols used hereafter is provided in

Table 1. Symbol definitions.

Symbol	Definition
$N_r$	Number of reconnaissance UAVs
$N_c$	Number of cargo UAVs
$N_{rc}$	Number of reconnaissance-and-cargo-integrated UAVs
$M_r$	Number of reconnaissance missions
$M_a$	Number of airdrop missions
${\mathbf{E}}_{\mathbf{damage}}^{\mathbf{G}}$	Collection of UAV damage events, consisting of event $E_e^G$
$N_{damage}$	Number of UAV damage events
$m_e$	Serial number of the UAV affected by the event $E_e^G$
$N{R}_e^l$	Loss of the lth type resource capability of the UAV due to the damage event $E_e^G$
$t_e$	Occurrence time of the event $E_e^G$
$\mathbf{G}$	Collection of Multi-UAV group, consisting of UAV $g_i$
${\mathbf{P}}_i$	Collection of initial resource capacity vector of UAV $g_i$
$R_{il}$	Value of the lth type of resource capacity that $g_i$ has
L	Number of resource types
$v_i$	Cruising speed of $g_i$
$G{P}_i$	Position of $g_i$, represented in 3D coordinates
$\mathbf{T}$	Collection of missions, consisting of mission $T_j$
$d{t}_j$	Mission execution time of $T_j$
$f{t}_j$	Completion time of $T_j$
$s{t}_j$	Start time of $T_j$
$sb{t}_j$	Earliest start time set for $T_j$
$fb{t}_j$	Latest completion time set for $T_j$
$T{P}_j$	Mission execution location of $T_j$, represented in 3D coordinates
${\mathbf{R}}_{\mathbf{j}}$	Collection of resource demand vector of $T_j$
$R_{jl}$	Capacity value of the lth type resource required to perform $T_j$
$T{v}_j$	Mission value of $T_j$
${\phi }_{ij}$	Allocation 0–1 variable
${\epsilon }_{jk}$	Sequence 0–1 variable
${\tilde{R}}_{ijl}$	Value of the lth type of resource that $g_i$ has to perform $T_j$
$Ta(j,l)$	Accessible resource requirement of $T_j$
$T{a}_j$	Static benefit of $T_j$
${\tilde{R}}_{il}$	Actual consumption of the lth type resource by $g_i$ when performing $T_j$
$R_{il}^{renew}(j)$	lth resource capability of $g_i$ after performing $T_j$
${\omega }_l$	lth static resource loss parameter
${\mathit{P}}_i^{renew}(j)$	Collection of updated resource capacity vector of $g_i$ after performing $T_j$
$d{t}_{bef}$	Time for $g_i$ to travel from the previous mission $T_{j^{\prime }}$ location to mission $T_j$ location
$d{t}_{nex}$	Time for $g_i$ to travel from mission $T_j$ location to the next mission $T_{j^{″}}$ location
$Pat{h}_j^{g_i}$	Trajectory cost for $g_i$ to perform $T_j$
$S_{ij}$	Mission effectiveness for $g_i$ performing $T_j$
$\beta$	Discount factor that determines the extent to which the cost of the trajectory affects mission effectiveness
$\chi$	Discount factor that determines the extent to which the timeliness constraint affects mission effectiveness
$S{e}_i$	Single UAV mission effectiveness of $g_i$
$Te(\mathbf{T},\mathbf{G})$	Total mission effectiveness of Multi-UAV G to perform missions T

.

2.1. Mission Reallocation Scenario

(1)

Multi-UAV group $\mathbf{G}=\left\{g_i(R_{il},v_i,G{P}_i)\right\}(i=1,2,\cdots ,N)$. N is the number of UAVs. A single UAV $g_i$ has the following properties.

• Initial resource capacity vector ${\mathbf{P}}_i=\left\{R_{il}\right\}(l=1,2,\cdots ,L)$. $R_{il}$ is the value of the l^th type of resource capacity that $g_i$ has, generally including reconnaissance resources, quantity of material carried, endurance, etc. L is the number of resource types. Different types of UAVs carry different types of resources.
• Cruising speed $v_i$. It is assumed that the UAV maintains the same speed during the mission.
• Coordinates $G{P}_i=(x_{g_i},y_{g_i},z_{g_i})$, indicating the position of the UAV throughout the mission.

(2)

Mission $\mathbf{T}=\left\{T_j(d{t}_j,sb{t}_j,fb{t}_j,T{P}_j,R_{jl},T{v}_j)\right\}\left(j=1,2,\cdots ,M\right)$. M is the number of missions. Every mission $T_j$ has the following properties.

• Mission execution time $d{t}_j=f{t}_j-s{t}_j$, where $f{t}_j$ is the completion time and $s{t}_j$ is the start time of the mission.
• Time window constraint $\left(sb{t}_j,fb{t}_j\right)$, where $sb{t}_j$ is the earliest start time set for the mission $T_j$ and $fb{t}_j$ is the latest completion time. The time window must satisfy $fb{t}_j-sb{t}_j>d{t}_j$.
• 3D coordinates of the mission execution location $T{P}_j=(x_j,y_j,z_j)$, where once the UAV arrives, the mission is considered to be underway.
• Resource demand vector ${\mathbf{R}}_{\mathbf{j}}=\left\{R_{jl}\right\}(l=1,2,\cdots ,L)$. $R_{jl}$ is the capacity value of the lth type resource required to perform the mission.
• Mission value $T{v}_j$. Different types of missions have different values.

(3)

Mission reallocation variables

• Allocation variable ${\phi }_{ij}$: If the mission $T_j$ is allocated to UAV $g_i$, then ${\phi }_{ij}=1$; else ${\phi }_{ij}=0$.
• Sequence variable ${\epsilon }_{jk}$: If mission $T_j$ must be completed before $T_k$ is executed, then ${\epsilon }_{jk}=1$; else ${\epsilon }_{jk}=0$.

2.2. UAV Resource Update Model

The UAVs are heterogeneous with respect to type and resources to meet the variable needs of different missions. Therefore, we define the value of the l^th type of resource that the UAV $g_i$ has to perform the mission $T_j$ as

$${\tilde{R}}_{ijl}={\phi }_{ij}·R_{il}$$

(1)

The demand of the mission $T_j$ for the l^th resource is measured by a variable with a value between 0 and 1 after normalization, defined as the accessible resource requirement of the mission $T_j$, which is expressed as the ratio of the available resources of UAV $g_i$ to the value of resource demand of the mission $T_j$.

$$Ta(j,l)=\{\begin{array}{l}1, {\tilde{R}}_{ijl}\ge R_{jl}\\ {\tilde{R}}_{ijl}/R_{jl}, {\tilde{R}}_{ijl}<R_{jl}\end{array}$$

(2)

The resource requirement of a mission is recorded as 1 when the UAV resource capability is greater than or equal to its demand, namely, the mission resource requirement is fully satisfied. The static benefit of mission $T_j$ is defined as the mean of all types of resource requirements, namely,

$$T{a}_j={\displaystyle \sum _{l}Ta(j,l)/L}$$

(3)

During missions, UAVs perform missions that cause the consumption of their resources; thus, a UAV resource capability update model is required. We define the actual consumption of the l^th type resource by UAV $g_i$ when performing mission $T_j$ as ${\tilde{R}}_{il}$, namely,

$${\tilde{R}}_{il}=\{\begin{array}{l}0, R_{jl}=0\\ R_{jl}, R_{jl}\le R_{il}\\ R_{il}, R_{jl}>R_{il}\end{array}$$

(4)

After UAV $g_i$ performs mission $T_j$, the l^th resource capability is updated to

$$R_{il}^{renew}(j)=R_{il}-{\omega }_l·{\tilde{R}}_{il}$$

(5)

where ${\omega }_l$ is the l^th static resource loss parameter, which is determined only by the l^th resource characteristic regardless of the corresponding UAV and mission.

The l^th resource capacity update model of $g_i$ is as follows.

$$R_{il}^{renew}(j)=\{\begin{array}{l}{R}_{il}, R_{jl}=0\\ R_{il}·(1-{\omega }_l), R_{jl}\le R_{il}\\ 0, R_{jl}>R_{il}\end{array}$$

(6)

The resource capacity vector of $g_i$ after mission $T_j$ is completed is updated to ${\mathit{P}}_i^{renew}(j)=\left\{R_{i1}^{renew}(j),R_{i2}^{renew}(j),\cdots ,R_{iL}^{renew}(j)\right\}$.

2.3. Single UAV Mission Effectiveness Function Based on Timeliness Constraints

Multi-UAVs may be damaged during missions, and once that happens, the damaged UAV will no longer be able to perform subsequent missions, thus creating a need for mission reallocation. Each mission requires an effectiveness function that reflects the benefits of mission reallocation. When Multi-UAVs cooperate to perform a sequence of missions, it is necessary to consider not only the mission effectiveness of all UAVs but also the overall sequence mission execution time. This section will quantify the impact of these factors on mission effectiveness separately and establish a model of mission reallocation effectiveness.

Due to the importance of timeliness in mission reallocation, each mission needs to be completed as early as possible within the desired time limit. Firstly, based on the fact that each mission requires the UAV to arrive at the mission location before starting execution, $d{t}_{bef}$ is defined as the time it takes for the UAV $g_i$ to travel from the previous mission $T_{j^{\prime }}$ location in the mission sequence to mission $T_j$ location.

$$d{t}_{bef}=\sqrt{{\left(x_j-x_{j^{\prime }}\right)}^2+{\left(y_j-y_{j^{\prime }}\right)}^2+{\left(z_j-z_{j^{\prime }}\right)}^2}/v_i$$

(7)

If mission $T_j$ is the first mission in the sequence, then $d{t}_{bef}=0$. Similarly, $d{t}_{nex}$ is the time for $g_i$ to travel from mission $T_j$ location to the next mission location $T_{j^{″}}$ in the mission sequence. If mission $T_j$ is the last mission, then $d{t}_{nex}=0$.

$$d{t}_{nex}=\sqrt{{\left(x_j-x_{j^{″}}\right)}^2+{\left(y_j-y_{j^{″}}\right)}^2+{\left(z_j-z_{j^{″}}\right)}^2}/v_i$$

(8)

If Multi-UAVs have a collaborative relationship on a mission, it is required that all collaborating UAVs arrive at the mission location before execution begins. Thus, the start of the mission cannot be earlier than the latest arrival time of all UAVs allocated to the mission, namely,

$$s{t}_k\ge \underset{j\in \left\{m|{\phi }_{im}=1,m=1,2,\cdots ,M\right\}}{\max }\left(s{t}_j+d{t}_j+d{t}_{bef}\right)$$

(9)

The shorter distance a UAV travels between missions, the faster it can reach the mission execution location, ensuring real-time mission reallocation. $Pat{h}_j^{g_i}$ is defined as the trajectory cost of the UAV $g_i$ to perform mission $T_j$, related to the distance between UAV $g_i$ and mission $T_j$.

$$Pat{h}_j^{g_i}=\sqrt{{\left(x_j-x_{g_i}\right)}^2+{\left(y_j-y_{g_i}\right)}^2+{\left(z_j-z_{g_i}\right)}^2}$$

(10)

To further highlight the importance of real time, a timeliness constraint is introduced to continuously improve the Multi-UAV capability to quickly reallocate missions. Under this constraint, each mission must be executed within the time window:

$$sb{t}_j-s{t}_j\le 0 \& {ft}_j-fb{t}_j\le 0$$

(11)

However, this timeliness constraint makes it possible that reallocation may cause other missions to be forced to delay the start of execution, resulting in reduced individual or even global mission effectiveness. Therefore, the impact on other missions needs to be considered when reallocating each mission. We define the impact of the timeliness constraint on mission effectiveness as the gain from the UAV performing the mission minus the cost of the trajectory, with an exponential function of the time spent traveling to the mission location as the timeliness parameter. Finally, the effectiveness of UAV $g_i$ performing mission $T_j$ is calculated as

$$S_{ij}=\left(T{v}_j·T{a}_j-\beta ·Pat{h}_j^{g_i}\right)·e^{-\chi (d{t}_{bef}+d{t}_{nex})}$$

(12)

where $\beta$, $\chi$ is the discount factor that determines the extent to which the cost of the trajectory and the timeliness constraint affect mission effectiveness, respectively.

For the entire mission execution process of UAV $g_i$, the single UAV mission effectiveness function is defined as follows.

$$S{e}_i={\displaystyle \sum _{j=1}^{\left|T\right|}{S}_{ij}}={\displaystyle \sum _{j=1}^{\left|T\right|}\left(T{v}_j·T{a}_j-\beta ·Pat{h}_j^{g_i}\right)·e^{-\chi (d{t}_{bef}+d{t}_{nex})}}, j\in b_i$$

(13)

2.4. Dynamic Optimization Model for Multi-UAV Mission Reallocation

Based on a comprehensive consideration of the overall mission timeliness and effectiveness, the sum of the mission effectiveness of all UAVs is defined as the total mission effectiveness $Te(T,G)$.

$$Te(\mathbf{T},\mathbf{G})={\displaystyle \sum _{i=1}^{N}S{e}_i}, i=1,2,\cdots ,N$$

(14)

Damage events occurring at time t will inevitably cause a decrease in mission effectiveness. To ensure that the total mission effectiveness is always maintained at a high level, the mission allocation plan needs to be dynamically adjusted. The reallocated mission sequence $T(t)$ is the mission that has not been completed since the trigger time t. With the objective of maximizing the total mission effectiveness, and considering the mission resource constraint, execution order constraint, and time window constraint, a dynamic optimization model for Multi-UAV mission reallocation is established as follows.

$$\max Te\left(\mathbf{T}\left(\mathbf{t}\right),\mathbf{G}\right)$$

(15)

$$\begin{array}{l}s.t.\left\{\begin{array}{}\mathrm{(15a)}& \forall j\in b_i, R_{il}^{renew}(j)\ge R_{jl}, l=1,2,\dots ,L\hfill \mathrm{(15b)}& \forall j\in b_i, {\displaystyle \sum _{j=1}^{\left|T(t)\right|}{\phi }_{ij}·R_{jl}\le R_{il}}\hfill \mathrm{(15c)}& s{t}_k\ge \underset{j\in \left\{m|{\phi }_{im}=1,m=1,2,\cdots ,M\right\}}{\max }\left(s{t}_j+d{t}_j+d{t}_{nex}\right)\hfill \mathrm{(15d)}& sb{t}_j-s{t}_j\le 0 \& f{t}_j-fb{t}_j\le 0\hfill \end{array}\right.\end{array}$$

Equation (15a) indicates that the allocation of a mission must satisfy its corresponding resource requirement constraint. Equation (15b) indicates that all mission requirements cannot exceed the resource capacity of the UAV $g_i$. Equation (15c) indicates the execution order in which the mission start time cannot be earlier than the latest arrival time of all UAVs allocated to the mission. Equation (15d) represents the time window constraint of the mission.

3. Mission Reallocation Based on Improved CBBA

The CBBA is a distributed auction algorithm that provides a reliable and fast solution to the Multi-UAV mission allocation problem [28]. However, as the performance requirements for mission reallocation algorithms in complex environments continue to increase, the rapidity and efficiency of the CBBA need to be further improved.

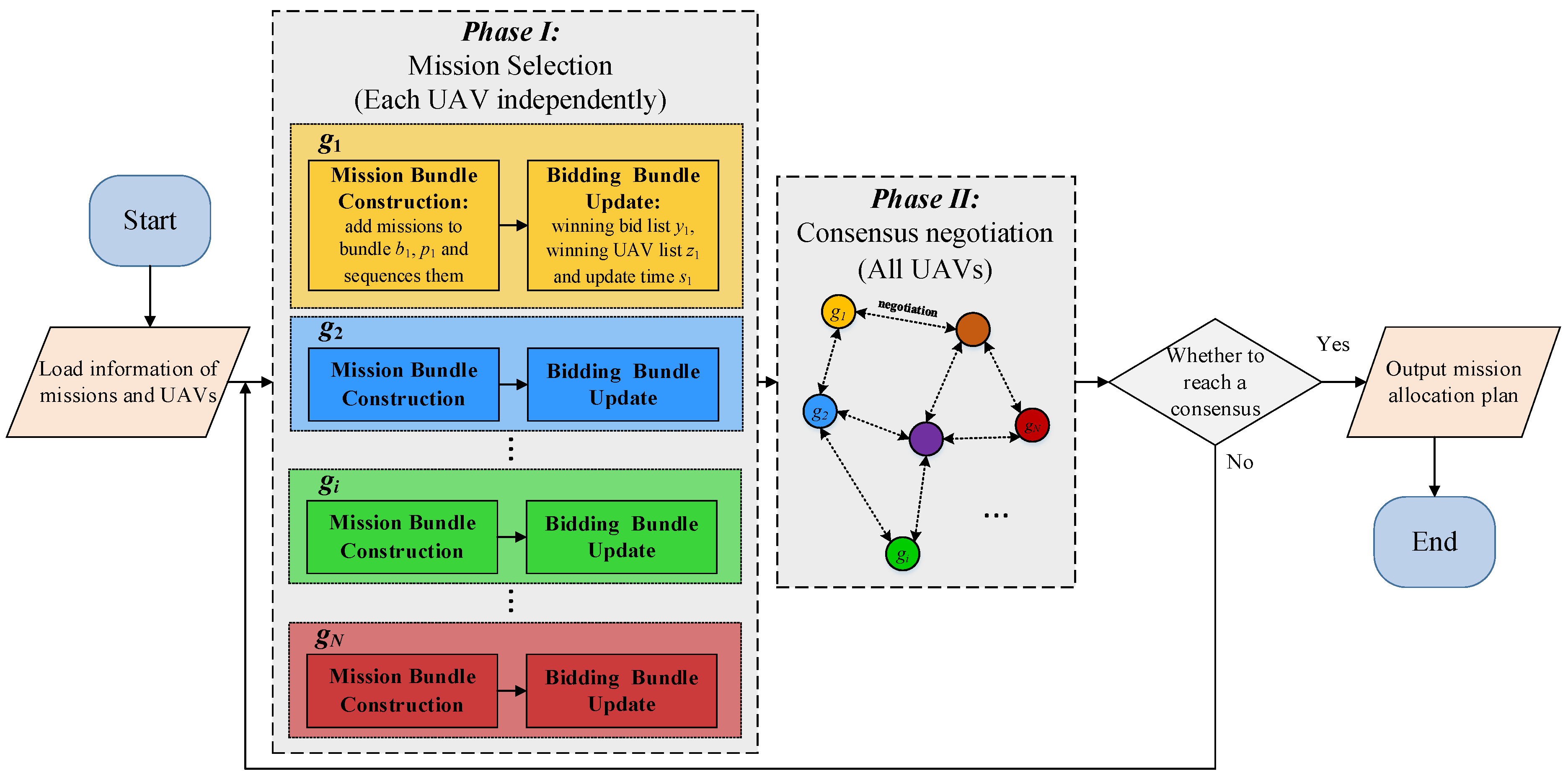
As shown in Figure 1, the CBBA can be divided into two main phases: the mission selection phase and the consensus negotiation phase. Each UAV progresses independently in phase I. First, based on information of the missions and UAVs, each UAV constructs their mission bundle. Then, the bids for the mission selected are determined, and then the bidding bundle is updated. After the mission selection phase for each UAV is completed, phase II is entered. All UAVs engage in a one-to-one consensus negotiation with neighboring UAVs to determine the bidding result for the same mission based on the information in the bidding bundles. Then the mission bundle construction is re-performed and bidding bundle is updated based on the results. The algorithm iterates between these two phases until the bidding bundles reach a consensus for all UAVs.

Phase I: Mission selection

Each UAV constructs its own mission bundle containing all the missions it plans to accomplish. Then, UAVs continuously add missions to their own bundle and sequence them logically. Each UAV mission bundle contains two vectors: $b_i$ and $p_i$. The missions in $b_i$ are sorted in the order they are added into the bundle, while in $p_i$ they are sorted in the order in which the UAVs are scheduled to perform their missions. Each UAV inserts a new mission at all possible locations in the current $p_i$, thus determining the location n that maximizes its bid. Then, all the missions that the UAV can perform are added to the mission bundle in order to determine the $p_i$ that maximizes mission effectiveness. After constructing its own mission bundle, each UAV needs to update the bidding bundle containing the bid information: winning bid list $y_i$, winning UAV list $z_i$, and update time $s_i$. In the CBBA, each UAV needs information about not only whether it is outbid on the mission it selects but who is allocated to each mission as well. This enables better allocation based on more sophisticated conflict-resolution rules.

Phase II: Consensus negotiation

The CBBA performs conflict resolution in this phase to avoid UAVs being allocated to the same mission. When UAV $g_i$ receives a message from another UAV $g_k$, $y_i$, $z_i$, and $s_i$ are used to determine which UAV’s information is the most up to date for each mission in order to generate a conflict-free mission allocation plan.

If a bid is changed by the decision rules above, each UAV checks if any of the updated or reset missions were in their bundle, and if so, these missions are released. Because releasing these missions changes the score of subsequent missions, all of the missions that were added to the bundle after them are released as well, with the winning bid $y_i$ and the winning UAV $z_i$ reset according to Equation (16).

$$y_{i,b_{in}}=0, b_{in}=\varnothing , z_{i,b_{in}}=\varnothing , \forall n\ge n_{i,j}$$

(16)

The allocation conflicts are resolved for each mission in turn, and then the algorithm returns to the first phase and re-adds the remaining missions. The algorithm iterates over these two phases until they reach a consensus and converge to a conflict-free solution.

Nevertheless, the following problems exist when the CBBA is applied directly to mission reallocation in the case of UAV damage.

• Lower mission effectiveness due to poor timeliness

In a distributed structure, if a damaged UAV is not detected in time, it is difficult to evaluate its mission execution, which greatly reduces the timeliness of mission reallocation and mission effectiveness.

• Lower efficiency due to double counting of complete reallocations

The original CBBA is to reallocate all missions after the UAV damage event, which will obtain some duplicated results, thus wasting computational resources and reducing the rapidity of algorithm convergence.

Therefore, a damage inspection method must be designed and the CBBA needs to be improved to enhance the total effectiveness of the Multi-UAVs solving mission reallocation problems.

3.1. Distributed Damage Inspection Method Based on Heartbeat Hold Mechanism

For UAV damage events in dynamic environments, this paper proposes a distributed dynamic damage inspection based on the heartbeat hold mechanism. The UAV sends periodic heartbeat signals within its communication range, and neighboring UAVs update their communication time and continue to send after receiving the signals. If all UAVs do not receive a message from a certain UAV in successive periods, the UAV is considered to have been damaged, which triggers the mission reallocation.

Heartbeat inspection can be divided into push-type (Figure 2) and pull-type (Figure 3) heartbeats according to how signals are sent. The fundamental difference between the two is that the push type is realized by the detected UAV actively pushing heartbeat signals to other UAVs. In contrast, the pull type is where the UAV actively sends an inquiry signal and the other UAVs send a response signal after receiving the heartbeat signal. The push type can reduce the number of signals in the system, which is one half of the pull type in the same case. Although the communication load of the push type is much lower, it is very inflexible and passive, for the relationship between detecting and detected is specified at system initialization, namely, the damage inspection topology of the entire system cannot be dynamically changed. On the contrary, the pull type is active detection, and the detection process can change the detection structure according to the system environment, which has more practicality. Moreover, in large-scale distributed systems, the dynamic applicability of damage inspection is more important than the communication load. Therefore, considering the distributed structure of Multi-UAV mission reallocation, this paper uses pull-type heartbeat inspection.

The UAV sends a heartbeat response signal as soon as the heartbeat signal is received, where the heartbeat inspection interval T_HI and the heartbeat time-out (HTO) are both fixed values. The algorithm procedure is summarized in Algorithm 1.

The heartbeat detector determines whether damage has occurred based on whether the UAV sending the heartbeat signal can receive heartbeat response signals from other UAVs on its side. If the condition information of the UAV is not updated within 3*HTO, the UAV is considered damaged.

Algorithm 1: Heartbeat inspection process
1	The process is performed concurrently for all UAVs.
2	Send heartbeat signal with heartbeat interval THI;
3	if heartbeat response signal received from gi within HTO then
4	UAV gi is in normal condition with its number recorded.
5	Update UAV condition information
6	Update HTO
7	else if (t − si) > 3 × HTO then
8	UAV gi was damaged
9	Tre ← uncompleted missions of gi
10	end if
11	end if

3.2. Mission Selection Strategy Based on the Time-Order Priority Insertion Principle

Based on the mission selection phase of the original CBBA, this paper proposes a mission selection strategy based on the time-order priority insertion principle. Specifically, during the mission selection phase, we add a resource constraint judgment to avoid the waste of computational resources caused by effectiveness calculations of missions that do not satisfy the conditions. Based on the pre-allocation plan, we try to insert the mission to be reallocated according to the time window constraint. Then, according to the bidding strategy adjusted by the timeliness parameter in Equation (12), the mission with high timeliness requirement is inserted in priority to ensure real time while obtaining high mission effectiveness. The specific steps of t^th round mission selection of $g_i$ are as follows and shown in Algorithm 2.

Table 2. Description of the improved CBBA parameters.

Parameter	Description
n	Position of the mission added to the bundle
$b_i$	Mission bundle of UAV $g_i$
$b_{in}$	nth entry of bundle $b_i$
$p_i$	Mission path of UAV $g_i$
$p_i(t)$	Mission path of UAV $g_i$ in the tth bidding round
$y_i$	Winning bid list considered by UAV $g_i$
$y_{i,b_{in}}$	$b_{in}$th in the winning bid list of $g_i$
$z_i$	Winning UAV list considered by UAV $g_i$
$s_i$	Update time for information UAV $g_i$ gets from other UAVs
$n_{i,j}$	Position number of mission $T_j$ in $p_i$
$T_{i\_out}$	Missions released during mission reallocation due to unsatisfied constraints of UAV $g_i$
$|·|$	Length of the mission bundle, namely, the number of missions in the bundle
$S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}$	Single UAV mission effectiveness of the UAV $g_i$ after inserting mission $T_j$ to the nth position of the mission path $p_i$
${\mathbf{T}}^{re}$	Collection of missions to be reallocated
$S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}\otimes \left\{T_{i\_out}\right\}}$	Single UAV mission effectiveness of $g_i$ after $T_j$ inserted into the nth position of path $p_i$ and $T_{i\_out}$ released from path $p_i$.
$c_{ij}$	Bid for $g_i$ to perform $T_j$, namely, the amount of effectiveness increase due to adding mission $T_j$ to the mission bundle $b_i$
$g_{ik}$	Communication 0–1 variable indicates whether there is a direct connection between UAV $g_i$ and $g_k$
$s_{ik}$	Time of the last information of $g_i$ updated from $g_k$.
${\tau }_r$	Information reception time
$N_e$	Number of damaged UAVs

lists the description of the improved CBBA parameters.

Step1: After the mission reallocation is invoked, based on the bundle information of the (t − 1)^th bidding round of UAV $g_i$ and the collection of missions to be reallocated, when mission $T_j$ can satisfy the resource constraints of the UAV, search for a free position that can satisfy the time window constraints of $T_j$, insert it into the mission bundle of $g_i$, and compute the effectiveness of $g_i$ performing mission $T_j$ with Equation (12).

Step2: Calculate the bid for UAV $g_i$ to perform mission $T_j$ with Equation (17) and update the resource capacity vector ${\mathit{P}}_i^{renew}$ of UAV $g_i$.

$$c_{ij}={\max }_{n\le \left|p_i(t-1)\right|+1}S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}-S{e}_i^{p_i(t-1)}$$

(17)

In Equation (17), $c_{ij}$ indicates the amount of effectiveness increase due to adding mission $T_j$ to the mission bundle $b_i$ and $|·|$ indicates the length of the mission bundle. $S{e}_i^{p_i(t-1)}$ denotes the effectiveness obtained by UAV $g_i$ performing the mission according to the mission sequence in $p_i(t-1)$, as shown in Equation (18). When the new mission $T_j$ is inserted in the bundle, $S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}$ represents the effectiveness obtained after inserting the mission into the n^th position of the mission path $p_i$, as shown in Equation (19). If the mission is already included in the path, then it provides no additional improvement in effectiveness.

$$S{e}_i^{p_i(t-1)}={\displaystyle \sum _{j=1}^{\left|p_i\left(t-1\right)\right|}\left(T{v}_j·T{a}_j-\beta ·Pat{h}_j^{g_i}\right)·e^{-\chi (d{t}_{bef}+d{t}_{nex})}}$$

(18)

$$S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}={\displaystyle \sum _{j=1}^{\left|p_i\left(t\right)\right|}\left(T{v}_j·T{a}_j-\beta ·Pat{h}_j^{g_i}\right)·e^{-\chi (d{t}_{bef}+d{t}_{nex})}}$$

(19)

Step3: Determine whether the insertion of mission $T_j$ causes the mission after position n in path $p_i$ to fail to satisfy its resource constraints and cannot be executed. If so, denote the mission in the $p_i$ that does not satisfy the resource constraints as $T_{i\_out}$, and release it from the path $p_i$. The corresponding mission effectiveness is reduced and the bid of UAV $g_i$ for mission $T_j$ is then changed to

$$c_{ij}={\max }_{n\le \left|p_i(t-1)\right|+1}S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}\otimes \left\{T_{i\_out}\right\}}-S{e}_i^{p_i(t-1)}$$

(20)

where $S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}\otimes \left\{T_{i\_out}\right\}}$ denotes the effectiveness obtained after inserting mission $T_j$ into the n^th position of path $p_i$ and releasing mission $T_{i\_out}$ from path $p_i$.

$$S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}\otimes \left\{T_{i\_out}\right\}}=S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}-\left(T{v}_{i\_out}·T{a}_{i\_out}-\beta ·Pat{h}_{i\_out}^{g_i}\right)·e^{-\chi (d{t}_{bef}+d{t}_{nex})}$$

(21)

Then, the resource capacity vector of UAV $g_i$ is updated and mission $T_{i\_out}$ is removed from bundle $b_i$ and path $p_i$, adding to the collection of missions to be reallocated.

Step4: Determine which missions in ${\mathbf{T}}^{re}$ the UAV $g_i$ has obtained by bidding. $y_{ij}(t-1)$ denotes the UAV’s highest bid for mission $T_j$ in the winning bid list received in the (t − 1)^th bidding round. If $c_{ij}>y_{ij}(t-1)$, then the insertion position $n_{i,j}$ of mission $T_j$ in $p_i$ is determined with Equation (22).

$$n_{i,j}=\arg {\max }_{n}S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}$$

(22)

Step5: Update the information of mission bundle of UAV $g_i$. Add the mission $T_j$ at the last position of $b_i$ (Equation (23)) and at the position $n_{i,j}$ of $p_i$ (Equation (24)).

$$b_i(t)=b_i(t-1){\oplus }_{end}\left\{T_j\right\}$$

(23)

$$p_i(t)=p_i(t-1){\oplus }_{n_{i,j}}\left\{T_j\right\}$$

(24)

Step6: Update the information of the bidding bundle of UAV $g_i$ (Equation (25)).

$$y_{ij}(t)=c_{ij}, z_{ij}(t)=i$$

(25)

Algorithm 2: tth round mission selection procedure of gi
Input: Winning UAVs list $z_i(t-1)$, winning bid list $y_i(t-1)$, mission bundle $b_i(t-1)$ and path list $p_i(t-1)$ Output: $z_i(t)$, $y_i(t)$, $b_i(t)$, $p_i(t)$
1	for j = 0 to $\left|{\mathbf{T}}^{re}\right|$ do
2	while$\forall R_{il}^{renew}(n)\ge R_{jl},l=1,2,\dots ,L$
3	if there’s a free position n that can satisfy time window constraints then
4	$c_{ij}={\max }_{n\le \left|p_i(t-1)\right|+1}S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}-S{e}_i^{p_i(t-1)}$
5	update ${\mathit{P}}_i^{renew}$
6	end if
7	end while
8	for r = n to $\left|p_i(t-1)\right|$ do
9	if the mission after n in pi failed to satisfy its resource constraints then
10	$c_{ij}={\max }_{n\le \left|p_i\right|+1}S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}\otimes \left\{T_r^i\right\}}-S{e}_i^{p_i}$
11	update ${\mathit{P}}_i^{renew}$
12	remove Ti_out from bundle bi and path pi
13	${\mathbf{T}}^{re}\leftarrow T_{i\_out}$
14	end if
15	end for
16	if $c_{ij}>y_{ij}(t-1)$ then
17	$n_{i,j}=\arg {\max }_{n}S{e}_i^{p_i{\oplus }_n\left\{T_j\right\}}$
18	$b_i(t)=b_i(t-1){\oplus }_{end}\left\{T_j\right\}$
19	$p_i(t)=p_i(t-1){\oplus }_{n_{i,j}}\left\{T_j\right\}$
20	$y_{ij}(t)=c_{ij}$
21	$z_{ij}(t)=i$
22	end if
23	end for

3.3. Improved Mission Reallocation Method

This section introduces the mission reallocation method based on the improved CBBA, whose specific steps are shown in Figure 4.

Step I: The initial static environment mission pre-allocation plan is given based on the actual information in the mission scenario. Specifically, the list of mission paths for each UAV and the start time of each mission are determined, and all UAVs receive the same list of effectiveness for all missions, winning bid, and winning UAV.

Step II: According to the distributed damage inspection method based on the heartbeat hold mechanism in Section 3.2, no heartbeat response signal is received from the UAV $g_i$, triggering the mission reallocation.

Step III: Each UAV judges its own condition to obtain its current position. If the UAV is performing a mission, the current position is the location of the mission being performed. If the UAV is on its way to the next mission location, the position of the UAV at moment t_e should be calculated. The collection ${\mathbf{T}}^{re}$ of missions to be reallocated is composed of missions of failed UAV $g_i$ that have not been completed at the occurrence time t_e of the UAV damage event. Each UAV independently adds missions from ${\mathbf{T}}^{re}$ according to the mission selection procedure in Section 3.2.

Step IV: Enter the phase of consensus negotiation. Each UAV performs conflict resolution by communicating with neighboring UAVs. The following information is shared simultaneously between neighboring UAVs: winning bid list $y_i$, winning UAV list $z_i$, and update time $s_i$. The update formula for $s_i$ of the UAV $g_i$ is as follows.

$$s_{ik}=\{\begin{array}{l}{\tau }_r, g_{ik}=1\\ {\max }_{m(g_{im}=1)}{s}_{mk}, g_{ik}=0\end{array}$$

(26)

where $g_{ik}=1$ denotes that there is a direct connection between UAV $g_i$ and $g_k$ and vice versa. $s_{ik}$ represents the time of the last information of $g_i$ updated from $g_k$. If the UAV $g_i$ is connected to $g_k$, then $s_{ik}$ is the information reception time τ_r; otherwise, it is the time when the UAV $g_m$, which is adjacent to UAV $g_i$, receives the latest information from the UAV $g_k$ in the communication network.

When the UAV $g_i$ receives a message from another UAV $g_k$, $z_i$ and $s_i$ are used to determine which UAV’s information is the most up to date for each mission. There are three possible actions UAV $g_i$ can take on mission $T_j$:

(1)

Update: $y_{ij}=y_{kj}$, $z_{ij}=z_{kj}$;

(2)

Leave: $y_{ij}=y_{ij}$, $z_{ij}=z_{ij}$;

(3)

Reset: $y_{ij}=0$, $z_{ij}=\varnothing$.

When the receiver UAV $g_i$ communicates with the sender UAV $g_k$ on mission $T_j$, the specific behavior the receiver should perform based on the received information is outlined in

Table 3. Action rules for UAV g_i based on communication with UAV g_k on mission T_j.

Sender gk Think zkj is	Receiver gi Think zij is	Receiver’s Action
k	i	if $y_{kj}>y_{ij}$, update
	k	update
	$m\notin \left\{i,k\right\}$	if $s_{km}>s_{im}$ or $y_{kj}>y_{ij}$, update
	$\varnothing$	update
i	i	leave
	k	reset
	$m\notin \left\{i,k\right\}$	if $s_{km}>s_{im}$, reset
	$\varnothing$	leave
$m\notin \left\{i,k\right\}$	i	if $s_{km}>s_{im}$ and $y_{kj}>y_{ij}$, update
	k	if $s_{km}>s_{im}$, update; else, reset
	m	if $s_{km}>s_{im}$, update
	$n\notin \left\{i,k,m\right\}$	if $s_{km}>s_{im}$ and $s_{kn}>s_{in}$, update
		if $s_{km}>s_{im}$ and $y_{kj}>y_{ij}$, update
		if $s_{km}>s_{in}$ and $s_{im}>s_{km}$, reset
	$\varnothing$	if $s_{km}>s_{im}$, reset
$\varnothing$	i	leave
	k	update
	$m\notin \left\{i,k\right\}$	if $s_{km}>s_{im}$, update
	$\varnothing$	leave

.

The first two columns of the table indicate the UAV that both the sender $g_k$ and receiver $g_i$ believe to be the current winner for a given mission; the third column indicates the action the receiver should take. After receiving the message, the UAV verifies which message is correct according to the rules in the table and takes the appropriate action.

According to Table 3, if a bid is changed by the decision rules, each UAV checks if any of the updated or reset missions which change its winning bid list and winning UAV list are in their bundle, and if so, missions with failed bids will be removed from their mission bundle.

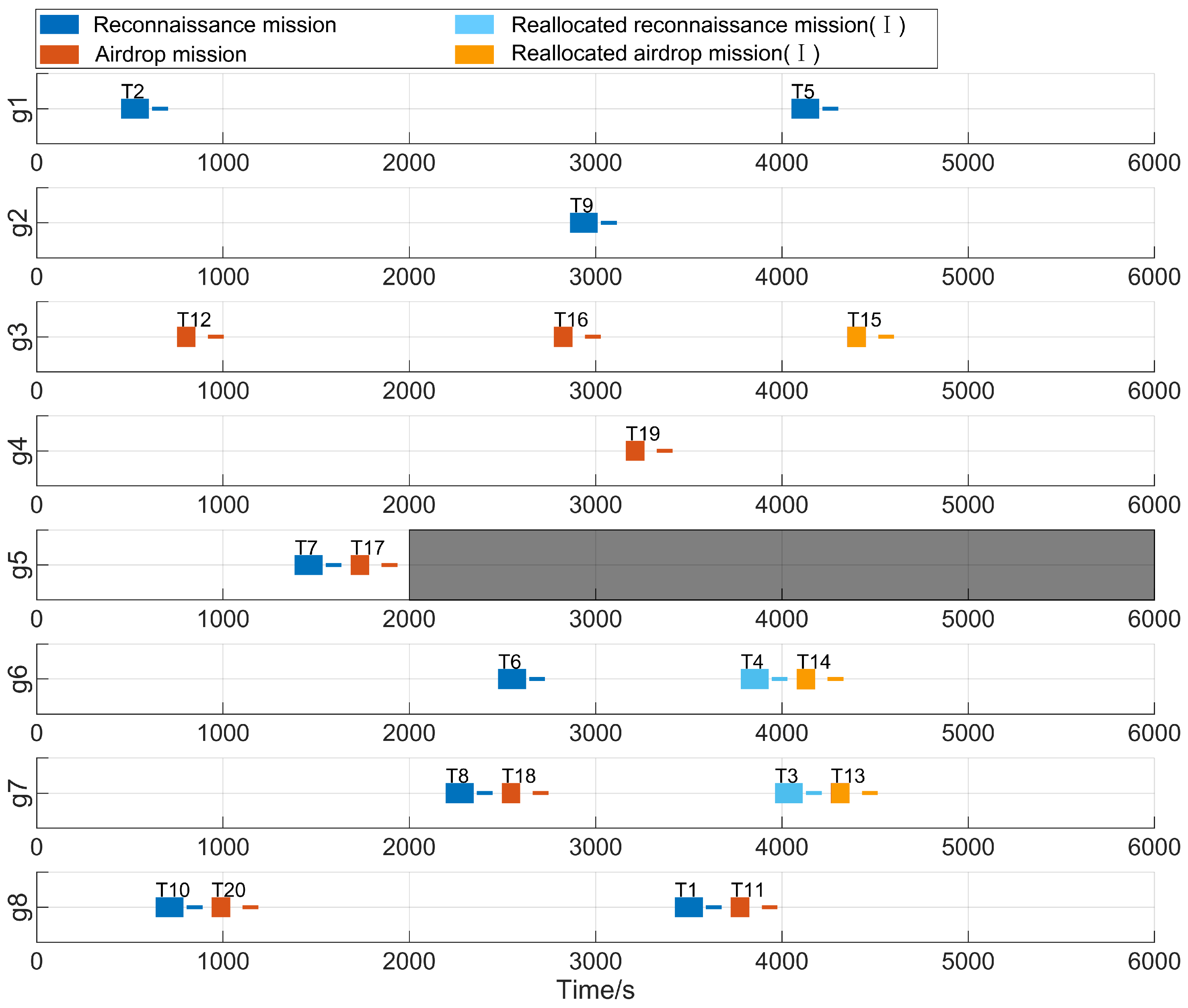
Step V: Repeat step III–IV until all UAVs agree on the three lists, the winning bid list, winning UAV list, and update time. Thus, a conflict-free mission reallocation plan is obtained and the Multi-UAVs can continue to perform the missions according to the order in path $p_i$, quickly responding to UAV damage events and reallocating missions in a dynamic environment.

4. Numerical Simulations and Results

This section presents the simulation results for the proposed method to demonstrate its effectiveness and outstanding performance. The experimental scenario is first introduced and used to illustrate the solving process of proposed method, including the reallocation application for dealing with different numbers of UAV damage events. In addition, the proposed method based on the improved CBBA is conducted to compare with the original CBBA and the PSO and PI algorithms to demonstrate its efficiency.

4.1. Scenario and Simulation Setup

In order to verify the performance of the models and algorithms proposed in this paper, we selected post-earthquake rescue missions in a mountainous area as a simulated experimental scenario. Assume that in this scenario UAVs need to be utilized to conduct a quick reconnaissance of the disaster situation in different areas and then provide emergency rescue supplies in the form of airdrops to the disaster victims, which include medical supplies, daily necessities, and other items.

We assume that these missions randomly take place in a 3D space spanning 10 km × 10 km × 3 km and the UAV takes off from the 2D ground space. The number of multirotor UAVs is N = 8, which are divided into three heterogeneous types: reconnaissance, cargo, and reconnaissance-and-cargo-integrated (R&C-integrated), and their respective initial attributes are shown in

Table 4. UAV attribute parameters.

Type	Reconnaissance	Cargo	R&C Integrated
UAV number	2	2	4
UAV speed	15 m/s	30 m/s	25 m/s
Initial resource capacity Pi	[5 3 0]	[5 0 3]	[5 2 2]
Initial coordinates	10 km × 10 km × 0 km 2D ground

. The initial resource capability vector of a UAV consists of the different types of resources it carries. The resource type is L = 3, including battery limit, reconnaissance resources, and quantity of rescue supplies carried. The number of pre-allocated missions is M = 20, a total of 10 mission locations, evenly divided into two categories of reconnaissance and airdrop. The mission of the same position must be reconnaissance first and then airdrop; mission scenario parameters are shown in

Table 5. Mission scenario parameters.

Type	Reconnaissance	Airdrop
Mission number	$\left\{T_1,T_2,\dots ,T_{10}\right\}$	$\left\{T_{11},T_{12},\dots ,T_{20}\right\}$
Mission value	1000	500
Resource demand Rj	[1 1 0]	[1 0 1]
Execution time	150 s	100 s
Time window length	300 s	300 s
Mission execution location	10 km × 10 km × 3 km 3D space
Mission start time	[0 s, 5000 s]

.

Assuming that each UAV can autonomously identify the type of mission based on the resources they carry. The positions of the UAVs and missions are generated based on the specific parameters in Table 4 and Table 5 to provide a mission pre-allocation plan. Different experimental conditions can be created by varying the number of missions and UAVs, and different seed values are used to change the UAV and mission locations to change the experimental scenarios. Note that the scenario settings described are arbitrarily chosen and are not necessary for the algorithm to work. All methods are conducted on MATLAB R2018b with Intel(R) Core(TM) i9-11900K CPU @3.50 GHz.

4.2. Simulations of Handling Two UAV Damage Events

4.2.1. Simulation of One Damaged UAV

Figure 5 shows the pre-allocated mission schedule for all UAVs. Each row represents one UAV, where $g_1$ and $g_2$ are reconnaissance UAVs, $g_3$ and $g_4$ are cargo UAVs, and the rest are R&C-integrated UAVs. The blue and red colors indicate reconnaissance and airdrop missions, respectively. The dotted line represents the mission time window, denoting that the mission must be completed within the time frame. The rectangle represents the time when the UAV actually performs the mission. As shown in Figure 5, we suppose the time of UAV damage event $E_1^G$ is $t_{e1}=2000s$, and the heartbeat inspection process detects that UAV $g_5$ is damaged. The shaded parts denote the time when the UAV was unable to perform its mission. One hundred simulations of different scenarios were conducted, and Figure 6 shows the mission reallocation results for one of the simulations. Cyan rectangles denote reallocated reconnaissance missions and yellow ones denote reallocated airdrop missions.

At $t_{e1}$, the heartbeat inspection process detects that UAV $g_5$ has been damaged, at which time the missions $T_7$ and $T_{17}$ in the mission path $p_5$ have been completed and are not considered for reallocation. However, missions $T_4$ and $T_{14}$ (shaded part in Figure 5) start later than $t_{e1}$, so they cannot be performed according to the pre-allocation plan. These two missions are released to the reallocation mission collection and start the mission reallocation process. After the calculation by the reallocation method above, missions $T_4$ and $T_{14}$ are reallocated to the UAV $g_6$. Missions $T_3$ and $T_{13}$ in the pre-allocated mission path $p_6$ of UAV $g_6$ are also released to the reallocated mission collection due to resource constraints, as well as mission $T_{13}$ of UAV $g_3$. The final missions involved in the reallocation are ${\mathbf{T}}^{re}=\left\{T_3,T_4,T_{13},T_{14},T_{15}\right\}$, and as shown in Figure 6, all missions are successfully reallocated.

4.2.2. Simulation of Two Damaged UAVs

Based on the simulation in the previous section, we suppose the occurrence time of UAV damage event II is $t_{e2}=4000s$, and the heartbeat inspection process detects that UAV $g_6$ is damaged. One hundred simulations of different scenarios are conducted, and Figure 7 shows the mission reallocation results for one of the simulation results. Purple rectangles denote reallocated airdrop missions for the second time. At $t_{e2}$, the heartbeat inspection process detects that UAV $g_6$ has been damaged, at which time missions $T_6$ and $T_4$ in the mission path $p_6$ have been completed and mission $T_{14}$ needs reallocation. Results in Figure 7 show that mission $T_{14}$ is reallocated to UAV $g_3$. Additionally, in the reallocation process, as mission $T_{14}$ is directly inserted into the mission path, the mission resource requirement exceeds the capacity of UAV $g_3$; the result is that the subsequent mission $T_{15}$ cannot be performed and is released to the reallocation mission collection as well to participate in the mission reallocation process, which finally is reallocated to UAV $g_4$. All missions are successfully reallocated.

Figure 8 shows the algorithm runtime for 100 runs of each case in the same scenario. When the number of damaged UAVs is 1, 2, and 3, the proposed method for three cases takes an average time of 1.9 ms, 4.4 ms, and 5.3 ms, respectively. For these cases, the proposed method is able to handle the sudden events of one and two damaged UAVs faster with more stable solution times. For the case of one damaged UAV, after 100 simulations of different mission scenarios, as shown in Figure 9, the proposed method can efficiently realize mission reallocation, and the average total mission effectiveness is 7435. For the case where two UAVs are damaged successively, as shown in Figure 10, the average total mission effectiveness is 7298. In both cases, comparing the mission reallocation method based on the original CBBA [27] and the PSO [9] and PI [45] algorithms, the proposed method is better in terms of total mission effectiveness, suggesting that the improved method obtains a better real-time mission reallocation plan.

4.3. Simulations of the Mission Reallocation Method to Cope with Dynamic Events

Based on the two UAV damage events in the previous section, this section simulates Multi-UAV mission reallocation in a dynamic environment by varying the length of the time window to represent different degrees of timeliness constraints, as shown in

Table 6. The degree of dynamics corresponding to different time window constraints.

Type of Missions	Mission Execution Time	Time Window
		Weak	Medium	Strong
Reconnaissance	150 s	300 s	250 s	200 s
Airdrop	100 s	300 s	200 s	150 s

. One hundred simulations are conducted for scenarios with different dynamic degrees, and the total mission effectiveness is shown in Figure 11 by comparing the mission reallocation method based on the original CBBA and the PSO and PI algorithms.

As shown in Figure 11, the total mission effectiveness of different methods is affected to different degrees when reallocating missions with different timeliness constraints. Although the mission effectiveness decreases as the mission time window shortens, the PSO and the PI algorithms and the original CBBA show a more pronounced decline in effectiveness compared to the proposed method. The PSO algorithm may fall into local optima in some cases, while the original CBBA and PI algorithm lead to a greater decline in total mission effectiveness because they seek to maximize global mission effectiveness. When the number of damaged UAVs is increased to two, the improved CBBA also has better stability in dealing with the mission reallocation problem with stronger timeliness constraints.

4.4. Comparative Analysis of Mission Reallocation Methods at Different Scales

This section illustrates the performance of the proposed method in terms of runtime and solution quality at different scales of UAVs by comparing it with the original CBBA and the PSO and PI algorithms. The ten settings shown in

Table 7. Scenario settings.

No.	1	2	3	4	5	6	7	8	9	10
N	8	8	12	12	16	16	24	24	40	40
M	20	20	30	30	50	50	80	80	120	120
Ne	1	2	2	3	3	4	5	6	9	10
Ne/N	12.5%	25%	16.7%	25%	18.7%	25%	20.8%	25%	22.5%	25%

are used to further illustrate the advantages of the proposed method for handling UAV damage events of large-scale UAV systems, where $N_e$ denotes the number of damaged UAVs and $N_e/N$ denotes the UAV damage rate. The ratio of the number of reconnaissance, cargo, and reconnaissance-and-cargo-integrated UAVs is N_r:N_c:N_rc = 1:1:2.

Since the UAV and mission locations are randomly placed for each simulation, the solution quality of the three different methods was reflected by the total mission effectiveness after reallocation, and each method is simulated 10 times and averaged, as shown in Figure 12. To show more clearly, the solution qualities of the proposed method are regarded as the benchmarks and the differences between the total effectiveness of each method are also provided. The runtime is the computation time for handling the UAV damage event plus the computation time for the last UAV to obtain the final converged plan, as shown in Figure 13. For a more obvious comparison, the runtimes of the proposed method, the PI algorithm, and the original CBBA are individually displayed.

As shown in Figure 12, the proposed method in this paper, after adding the bidding strategy adjusted by the timeliness parameter, has higher effectiveness and better timeliness than the other two methods in mission reallocation. The PSO algorithm takes more time to converge to the optimal solution in order to seek a conflict-free mission reallocation plan, and is much inferior to the CBBA based on the distributed market mechanism in terms of real-time performance. For the PI algorithm and the original CBBA, which are also distributed algorithms, the proposed method in this paper also has certain superiority with better total mission effectiveness. Furthermore, when the solution scale increases, it can ensure higher total mission effectiveness.

From Figure 13, it can be seen that the improved CBBA proposed in this paper saves some computational resources by adding constraints to the process of mission selection and excluding missions that do not meet the resource constraints in advance. Compared to centralized algorithms such as PSO, the runtime of the improved CBBA is greatly reduced. By introducing the time-order priority insertion principle, the solution speed is also improved compared to the PI algorithm and the original CBBA-based mission reallocation method. Therefore, the proposed method has improved the real-time performance of the CBBA for solving mission reallocation effectively.

5. Conclusions and Future Work

In the dynamic complex environment, UAVs will inevitably be damaged or destroyed; thus, how to deal with damage events as soon as possible is the key to achieving the mission objectives successfully. Thus, this paper proposes a distributed mission reallocation method based on the heartbeat inspection mechanism and improved CBBA. Firstly, a dynamic optimization model for Multi-UAV mission reallocation is established based on a resource update model, timeliness constraints, and mission effectiveness. Secondly, a distributed damage inspection method based on a heartbeat hold mechanism is proposed for real-time monitoring of UAV conditions and rapid response to damage events. Furthermore, the CBBA is improved by introducing a timeliness parameter to adjust the bidding strategy and optimize the mission selection strategy based on the time-order priority insertion principle to generate mission reallocation plans quickly.

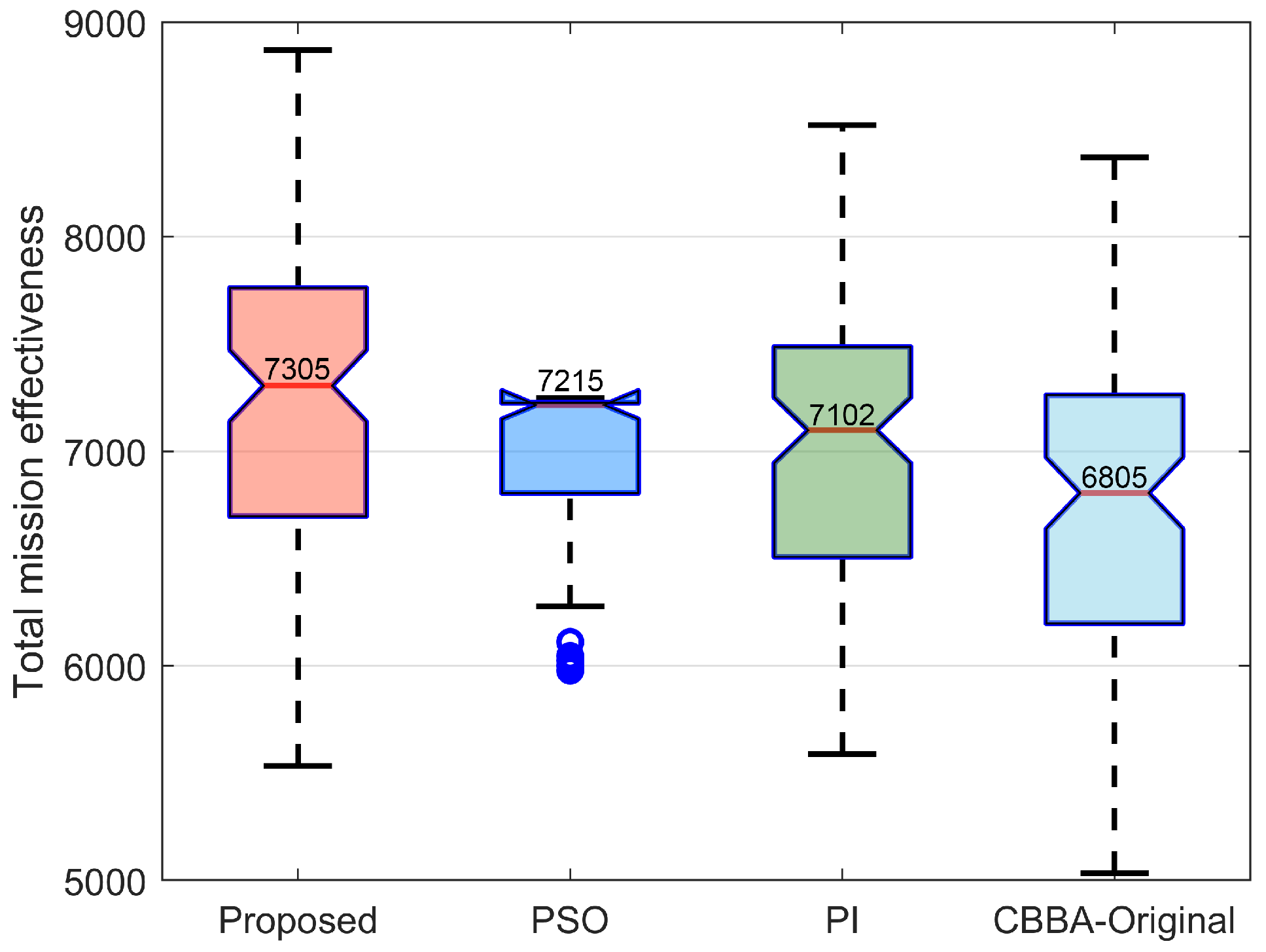
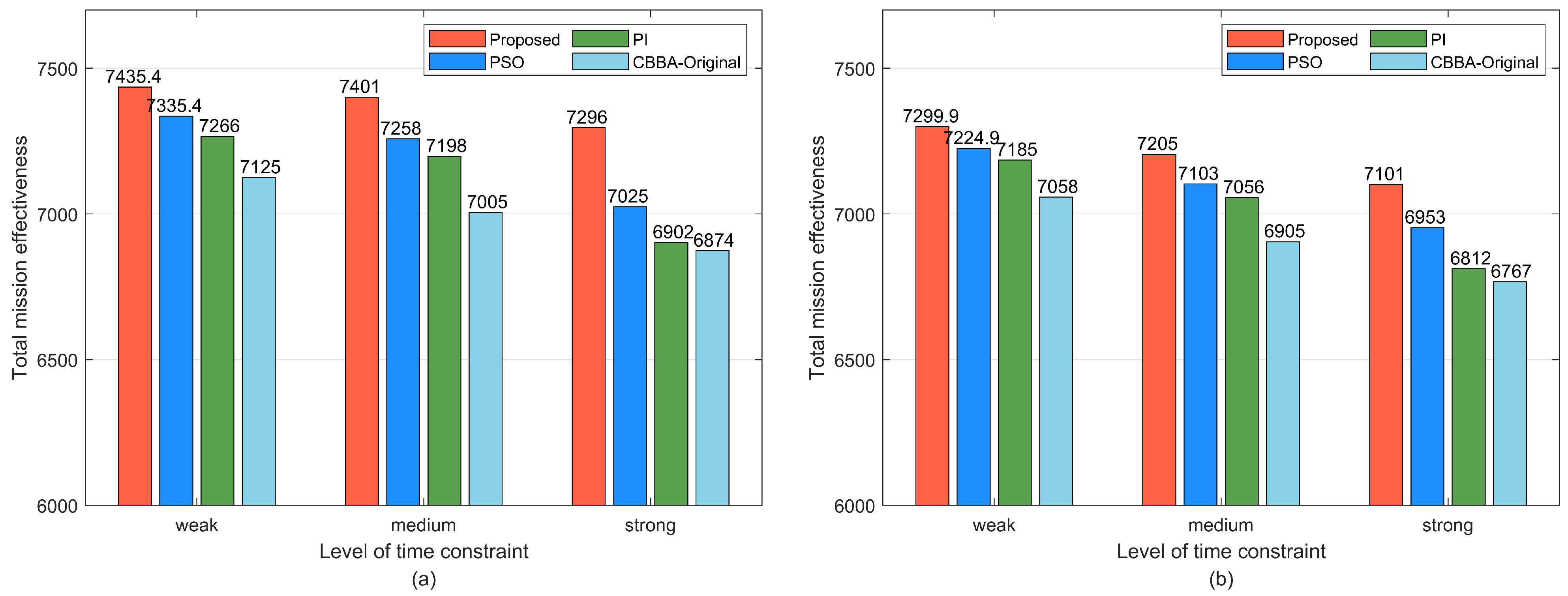
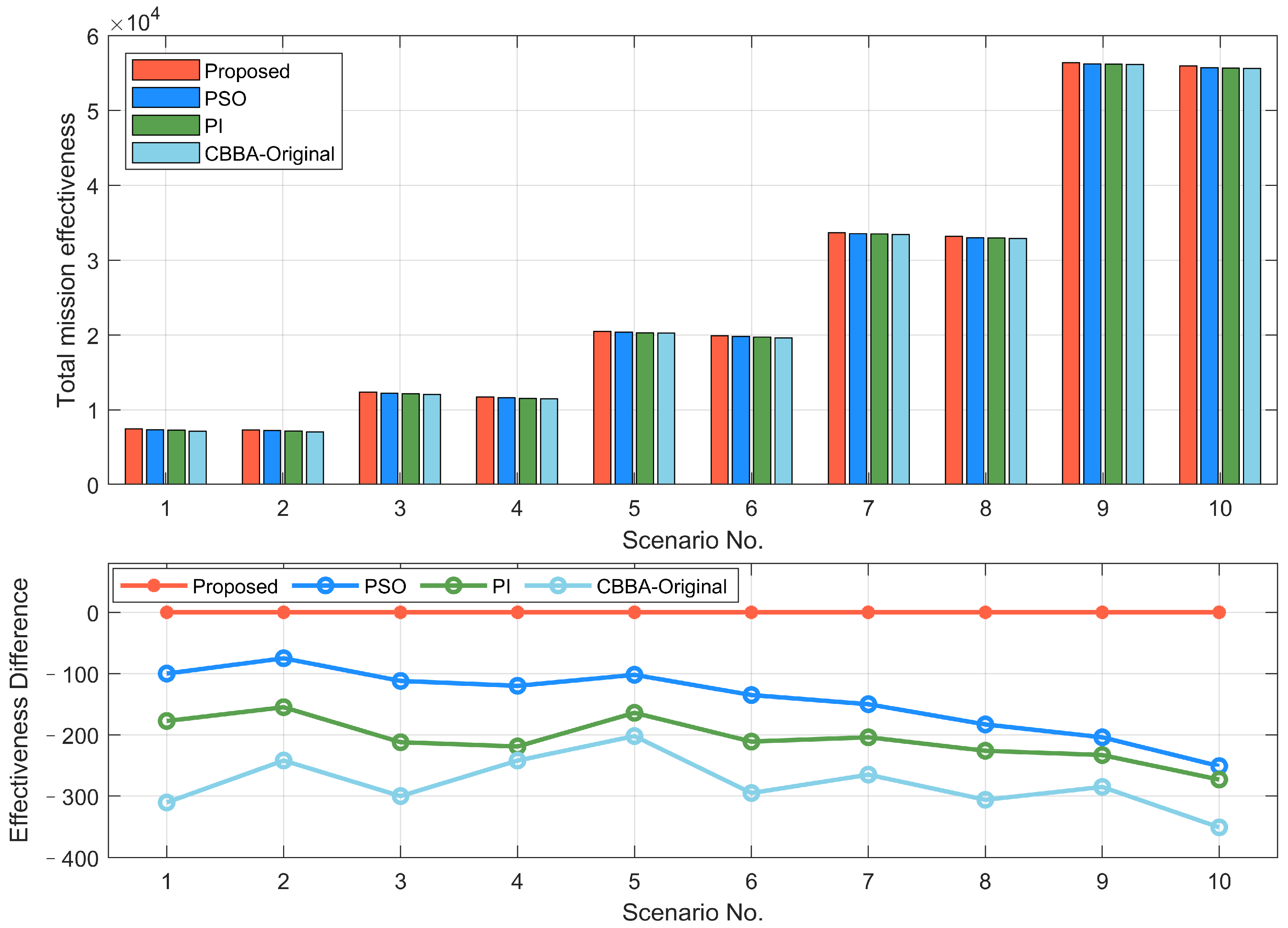
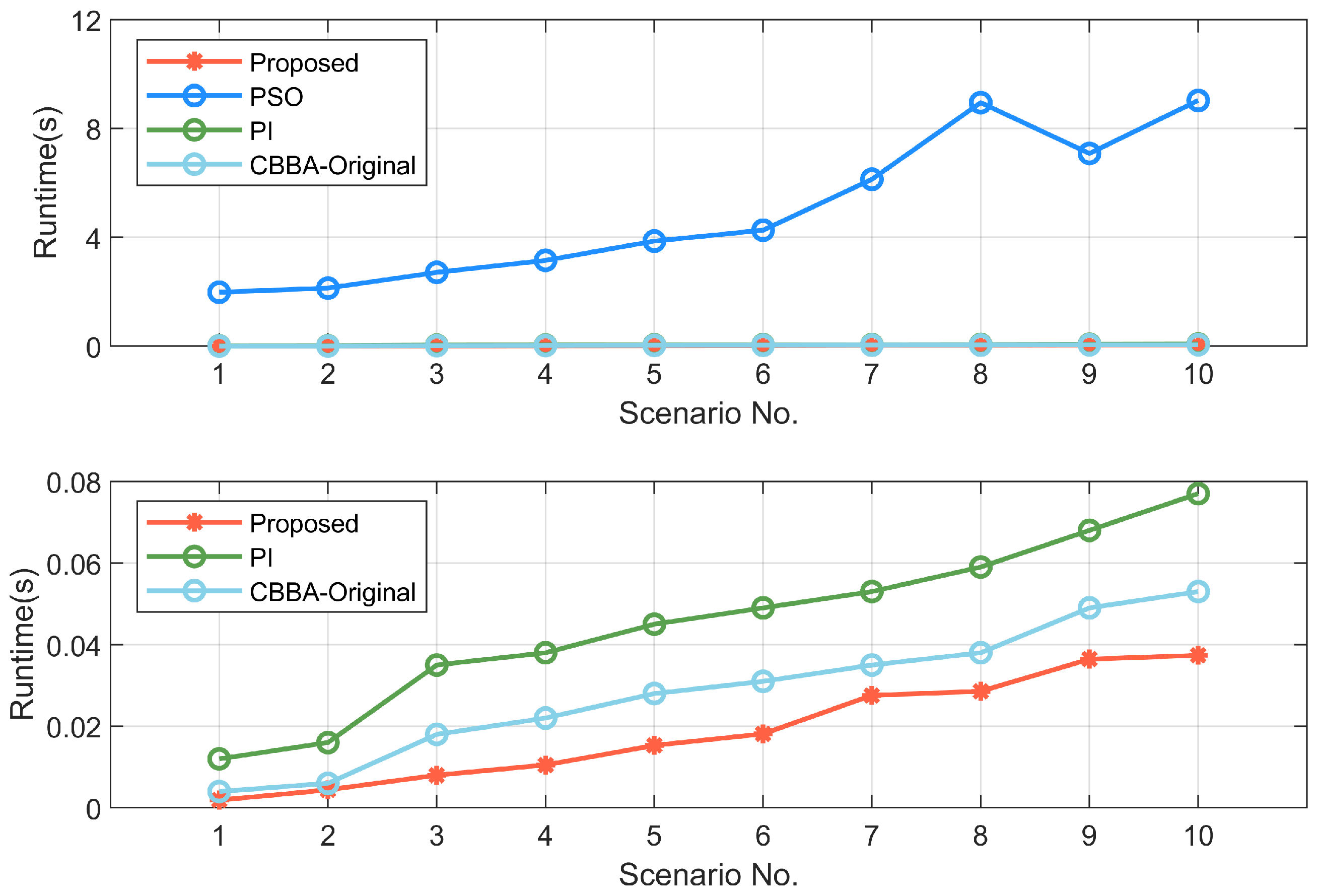
Simulation results show that the method can provide a mission reallocation solution quickly for UAV damage events in the dynamic environment, reducing the runtime of the algorithm and saving computational resources to reduce the burden of distributed communication networks while ensuring higher mission effectiveness.

However, due to the uncertainty of the complex environment, mission requirements, locations, and other parameters may change at any time, and reallocation methods for dynamic missions will be included in our future study. Meanwhile, we will build actual 3D models of agents and design obstacle avoidance strategies to further improve the applicability of the proposed method in more complex scenarios.