Abstract
This article presents a virtual swashplate mechanism for a mini helicopter in classic configuration. The propeller bases are part of a passive mechanism driven by main rotor torque modulaton, this mechanism generates a synchronous and opposite change in the propellers angle of attack, then the thrust vector tilts. This approach proposes to control the 6 degrees of freedom of the aircraft using two rotors. The main rotor controls vertical displacement and uses torque modulation and swing-hinged propellers to generate pitch and roll moments and the horizontal displacement while the yaw moment is controlled by the tail rotor. The dynamic model is obtained using the Newton-Euler approach and robust control algorithms are proposed. Experimental results are presented to show the performance of the proposed virtual swashplate in real-time outdoor hover flights.
1. Introduction
The swashplate is an essential mechanism for classic helicopters that enables them to perform takeoffs and landings in short areas and hover flights. Since its invention, slight modifications have been proposed to reduce its complexity in order to reduce maintenance and repair costs. However, multirotors are less efficient than a classic helicopter but their maintenance and repair are simpler and cheaper. A virtual swashplate approach is an option where a main rotor torque modulation and a lead-lag hinge modification are used to also synchronously increase or decrease the angle of attack of the blades. It is then possible to reduce the number of mechanical parts, their complexity and the number of actuators used to control the mini helicopter. Thus, the use of a classic configuration helicopter does not imply an increase in maintenance or repair costs. The electronic control is an important topic in the development of autonomous missions of the Unmanned Aerial Vehicles (UAVs).
The theoretical analysis of the dynamics of a classic helicopter differs from that of a fixed-wing aircraft due to its hovering capacity. The analysis of a mini helicopter provides the dynamic characteristics necessary for the design of control algorithms to perform stable flights. In [1] the authors presents a simple learning control strategy based on gradient descent that minimizes the cost function defined by the error dynamics of the nonlinear helicopter system for a test bench with two degrees of freedom and compares a Linear-Quadratic Regulators (LQR) and a Proportional-Integral-Derivative (PID) controllers. In [2,3] the authors present a flight system based on a non-linear model and a robust control based on H∞ algorithm for the stabilization of a helicopter in classic configuration showing experimental results in real time outdoor flights. The authors in [4] present the robust stabilization of the nonlinear model of a helicopter in the face of disturbances caused by wind gusts, a nonlinear controller was designed based on a chain of integrators with saturated feedback and its performance is successfully shown in numerical simulations.
Swashplate mechanisms are used in different helicopter as coaxial, tandem, or classical configurations to control maneuvering, the angular moments are resulting from increasing the collective angle of attack or tilting the propellers more to one side than the other. Swashplates are mechanically complex, expensive and fragile, therefore our objective is to design a virtual swashplate control approach that does not require any actuators to stabilize a helicopter’s flight. In such a virtual swashplate approach the rotors can be used to generate thrust and pitch and roll moments, tilting the thrust vector. A UAV applying a virtual swashplate approach is an underactuated system having six degrees of freedom that are controlled with only two actuators. In recent years, important technological advances have been developed around the world on helicopter sensors and actuators.
In [5] the authors propose a novel coaxial helicopter that provides its main actuator the ability to tilt its thrust vector without using servo actuators or control surfaces to perform attitude control maneuvers, reducing the mechanical complexity of the swashplate when flying indoors. The authors in [6] present the technique of cyclic control of the blade pitch in the rotors of a helicopter in tandem configuration without using servomotors to maneuver using a PID control algorithm, also showing tests of indoor flights. In [7] the authors present a theoretical study on the design of a cylindrical mono-rotor using swashplateless torque modulation approach, employing a rotor to control thrust, pitch and roll and anti-torque moments fins for rotor drag compensation. A non-linear model is also proposed using the Euler-Poincare approach and proposing a non-linear control for the control of the proposed vehicle. Virtual cyclic control is not only applicable in the torque modulation, in [8] the authors propose a cyclic control for a rotor composed of two fixed-wing aircraft joined with a rigid rod and uses the control surfaces to coordinate the pitch and roll moments, the performance of this virtual swashplate and its nonlinear control are tested in numerical simulations.
The present manuscript focuses on the hover flight of a mini helicopter with a virtual swashplate depicted in Figure 1 and the experimental results showing the performance of the robust control algorithms during outdoor flights. The main rotor tilts the thrust vector through torque modulation and hinged blades. The tail rotor compensates for the reactive torque of the main rotor. Torque modulation and slanted hinges at the hub of the propellers generate the change in the angle of attack and therefore the inclination of the thrust vector. Sensors like an inertial measurement unit (IMU), Global Positioning System (GPS), and barometer have been used on autopilot to obtain the helicopter attitude and position.

Figure 1.
Mini helicopter with virtual swashplate.
The novelty in this work can be listed as follows:
- (1)
- The virtual swashplate approach is implemented in a classic helicopter platform, which is the most efficient aerodynamically with respect to coaxial or tandem configurations.
- (2)
- An estimated torque of the main rotor and the nonlinear dynamics is developed.
- (3)
- Several outdoor flight tests are carried out to validate the algorithm robust control.
- (4)
- The swing-hinged mechanism has only three pieces reducing the weight and complexity of the main rotor.
- (5)
- The blades used with symmetric airfoil reduce the stress and heating of motor in contrast to cambered blades that have higher drag coefficients due to the changes in angle of attack.
The paper is organized as follows: Section 2 presents the virtual swashplate mechatronics. Section 3 describes the mathematical model. Section 4 is devoted to the control strategies. The experimental results are shown in Section 5. Concluding remarks are presented in the Section 6 and Section 7 sections respectively. Appendix A describes the gyroscopic effect present in the helicopter main rotor.
2. Virtual Swashplate
The mini helicopter in classic configuration prototype used in this work does not have an angular velocity reduction gear, so the propellers and the motor are linked by the same shaft and the torque applied is the same. Then, to produce the pitch and roll moments, the torque modulation changes as a sinusoidal signal with variable amplitude. The amplitude of this signal corresponds to the amplitude of the desired torque. The tail rotor is used to compensate the yaw moment produced by the main rotor. Figure 2 shows the swing-hinged propellers lag due to torque modulation of the main rotor. The propeller bases are passive mechanisms driven by main rotor torque modulation, this mechanism generates a synchronous and opposite change in the blades angle of attack, then the thrust vector tilts.
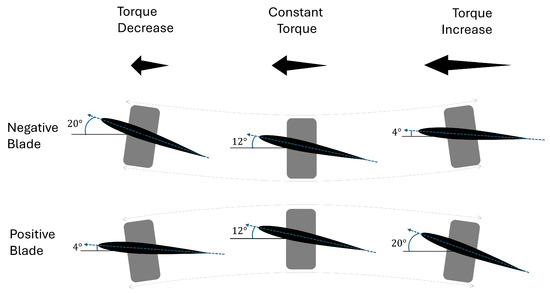
Figure 2.
Lead-lag swing-hinged blades due torque modulation.
2.1. Mechanics
The constant torque means constant angular velocity of the rotor and keeps the angle of inclination of the propeller blades constant at 12 degrees (see Figure 3a). This would be the case of the helicopter in hover under ideal conditions, without roll or pitch control inputs. The main parts of the rotor are the brushless motor, the central hub fixed to the motor shaft, the propeller bases which are attached to the rotor hub by two angled and parallel hinges and the symmetrical airfoil blades, see Figure 3b. Due to the inertia of the blades, they convert the variations in angular velocity into an orderly and synchronous change of the blades angle of attack.
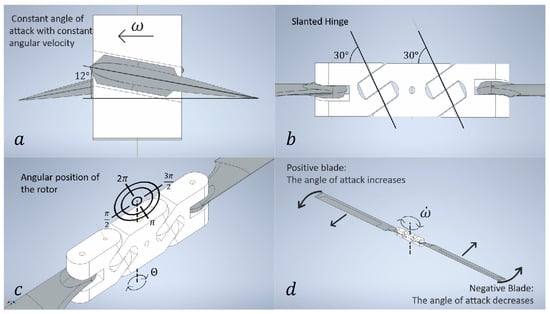
Figure 3.
Swashplate mechanism: propellers hub and bases. (a) shows the constant angle of attack with constant angular velocity. (b) shows the slatend hinge inclination. (c) shows the angular position of the rotor. (d) shows the synchronous change of the angle of attack in the positive propeller and in the negative propeller due to the lag.
The angular position of the main rotor is measured by using a high-resolution Hall effect sensor (Figure 3c) to guarantee the torque modulation in each period even at high revolutions per second. In the same way a high-resolution speed controller is necessary to command the high frequency Pulse-Width Modulation (PWM) signal.
The swing-hinged propellers shown in the Figure 3d react to torque modulation of the main motor. Given a control input at the roll or pitch moment, the angular velocity reference is a sine wave that lags the propellers with respect to the center hub and the propellers angles of attack increase and decrease synchronously due to the inclination of their bases. The torque modulation and the swing-hinged blades generates an inclination in the thrust vector, and it can control the forward-backward and left-right movements with the main rotor.
2.2. Electronics
The mini helicopter electronic system is a set of embedded hardware and software systems that control different parameters involved in the flight such as attitude, position and swashplate virtualization. In the autopilot, the hardware involved in orientation control is the Inertial Measurements Unit (IMU) that includes accelerometers, gyroscopes and magnetometers, while a Global Positioning System (GPS) and barometer are used for position control. A Hall effect sensor to measure the angular position and an external microcontroller to combine the roll, pitch and thrust signals to command the torque modulation in the main rotor are necessary to virtualize the swashplate. The autopilot is compatible with the PX4 firmware and is programmed with algorithms to control attitude and position while the microcontroller processes the control signals to generate a single high frequency output for the main rotor.
Figure 4 shows the Pixhawk Cube Black as an autopilot, it has redundancy in inertial sensors and a frequency of 168 MHz for the fusion and processing of signals and control algorithms. The PWM signals that come out of the autopilot are the yaw moment control that is sent directly to the Electronic Speed Controller (ESC) tail rotor and the thrust, roll, and, pitch moment control signals with a frequency of 50 Hz. The microcontroller receives the control signals of the autopilot and the angular position of the main rotor from the Hall effect sensor through the SPI port at a frequency of 8 kHz. The microcontroller fuses and processes the control and rotor angular position signals at a frequency of 16 MHz to send to the High frequency ESC of the main rotor brushless motor at a frequency of 32 kHz considering that the motor can reach up to 6000 revolutions per minute. The autopilot and the microcontroller are programmed with their own language based on C++. The autopilot firmware does not have a default configuration for a virtual swashplate helicopter and the mixer also needed to be created.
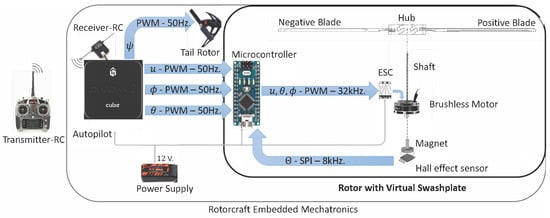
Figure 4.
Virtual swashplate flight system diagram.
The AS5047P is a Hall effect based high resolution angular position sensor for high speed angle measurement (up to 28,000 rpm) over a full 360 degree range. The microcontroller receives the absolute angle position data with 14-bit resolution. This sensor provides the angular position feedback with a constant magnetic field magnet fixed to the motor shaft for cycle control of the virtual swashplate.
The high-performance electronic speed controller processes the PWM signal of nominal input frequency up to 40 kHz whose pulse width varies from 1 ms to 2 ms. Figure 5 shows the pulse width modulation with a sinusoidal reference where many pulses are produced in each rotation cycle of the main rotor to virtually emulate the control of a traditional swashplate.
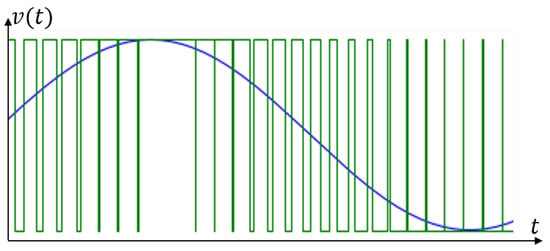
Figure 5.
PWM signal (green line) with sinusoidal reference (blue line).
2.3. Pitch and Roll Control through Torque Modulation and Swing-Hinged Propellers
The angular moments generated with the virtual swashplate approach emulate the cyclic control of a helicopter, substantially decreasing its mechanical complexity. The thrust, pitch and roll control signals are combined to control the thrust vector and the yaw moment is controlled by the tail rotor which compensates for the reactive torque of the main rotor. The following picture illustrates how the angular moments of the helicopter with a virtual swashplate are generated.
As shown in Figure 6, the roll moment for lateral control is activated when the rotor passes through the position then the acceleration of the rotor lags the blades with respect to the center of the rotor increasing the angle of attack of the positive blade up to and decreasing the angle of attack of the negative blade up to synchronously. This control command tilts the thrust vector to the left or right, producing a roll moment and consequently a lateral displacement.
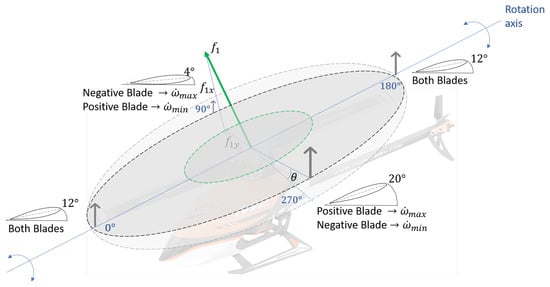
Figure 6.
Roll moment and Lateral displacement.
As shown in Figure 7, the pitch moment for longitudinal control is activated when the rotor passes through the position then the acceleration of the rotor lags the blades with respect to the center of the rotor increasing the angle of attack of the positive blade up to and decreasing the angle of attack of the negative blade up to synchronously. This control command tilts the thrust vector to forward or backward, producing a pitch moment and consequently a longitudinal displacement.
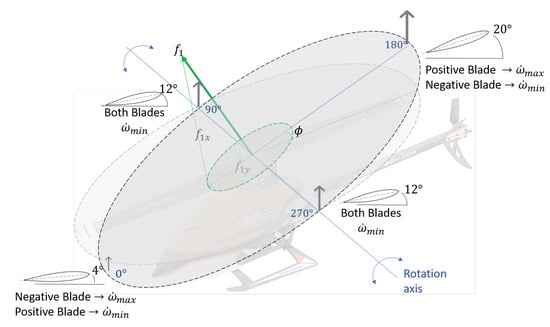
Figure 7.
Pitch moment and Longitudinal displacement.
A hover flight would assume that the speed of the main rotor is constant and that its reactive torque is compensated by the tail rotor in addition to the blades having the same angle of attack at all times and the thrust vector and the vertical axis are collinear as shown in Figure 8.
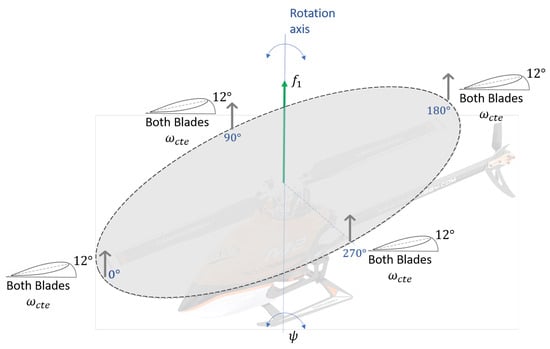
Figure 8.
Yaw moment and vertical displacement.
3. Mathematical Model
From [9] the mini helicopter with virtual swashplate can be modelled as
where m is the mass, g is the acceleration due to the gravity, u is the control input, C is the Coriolis matrix, is the attitude vector, is the control input vector and represents the inertia matrix where
Figure 9 shows the representation of the mini helicopter where for represents the main and tail rotors force where represents a set of propellers aerodynamics constants and represents the angular velocities of the rotors. The tail rotor reactive torque is neglected. The Euler angles rates are get as
where
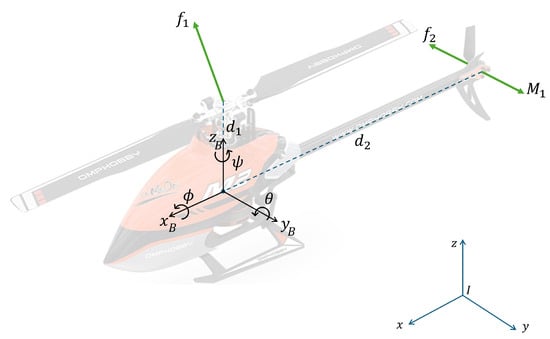
Figure 9.
Mini helicopter diagram.
The rotor torque is defined as
where is torque due to the main rotor, and are the distances from the main rotor and tail rotor to the center of mass, is the angular position of the main rotor and and are the aircraft control inputs.
4. Control Strategies
4.1. Attitude Control
Let us propose the following linear dynamics
The error is defined as
then
In order to estimate the unknown dynamics described in (8) a Levant differentiator is implemented [10]. Building a third order Levant differentiator for each
4.2. Position Control
5. Experimental Results
This section presents the experimental results to validate the proposed attitude and position control strategies for the mini helicopter with virtual swashplate. The controller parameters were adjusted in order to reduce the transitory overpeak until the best performance was obtained. The parameters used are shown in Table 1.

Table 1.
Mini helicopter flight parameters.
The terms of the inertia matrix were estimated using computer-aided design, modeling and analysis software. Although the matrix is not diagonal, the parameters decrease as it move away from the main diagonal to values close to and and it is clear that the main diagonal terms are significantly larger.
A mixer algorithm is designed and implemented in px4 autopilot using classic configuration helicopter and its actuators. This mixer produces four signals, two for the motors and two for the servos. The motor signals are for the main rotor and tail rotor, varying the speed to control vertical displacement and yaw moment, while the servo motors are for the pitch and roll moment signals. The thrust, pitch and roll signals are sending from the autopilot to the external microcontroller at a frequency of 50 Hz to produce the torque modulation signal. Is necessary to obtain the angular position of the main rotor and sent it to Electronic Speed Controller (ESC). The signal from the tail rotor is sent directly to the ESC. Equation (3) shows the mixer design implemented in the external microcontroller.
Figure 10 shows the performance of the control algorithm for the roll, pitch and yaw angles of the helicopter with virtual swashplate. The reference for the roll and pitch angles is zero while the reference for the yaw angle is −1.3 radians.
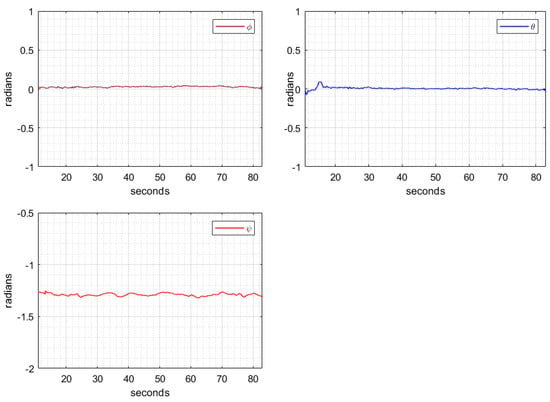
Figure 10.
Angular roll, pitch, and yaw displacements ().
Figure 11 shows the performance of the virtual swashplate helicopter position control algorithm during hover flight. The references for the position are −4.7 m for the x axis, −1.5 m in the y axis and 1.5 m for the z axis.
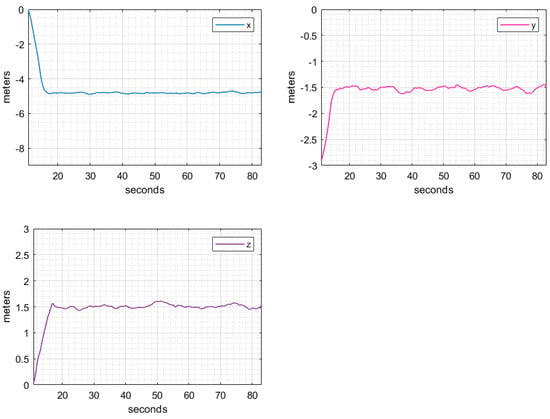
Figure 11.
Lateral, longitudinal, and vertical displacements ().
Figure 12 shows the trajectory of the helicopter with virtual swashplate during hover. The helicopter moves to the reference position during the first 15 s and then maintains its position for one minute with an accuracy of ±0.05 m.
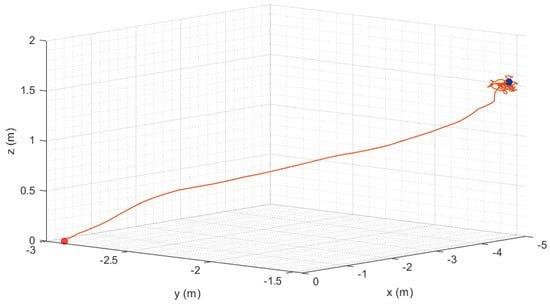
Figure 12.
Threedimensional trajectory in hover flight.
Table 2 presents the mean standard deviations of the position and velocity error during hover flight.

Table 2.
Standard error of the mean.
To prevent accidents related to energy consumption, the following safety actions are implemented: At low battery levels, an acoustic warning at 30% and an emergency landing at 15%. This safety protocol prevents overheating of the main motor and overdegradation due to battery wear.
Figure 13 shows the hover stability for helicopter using virtual swashplate is ensured in outdoor flight. The mini helicopter reaches the position references in a short period of time with some oscillatory behavior around the horizontal reference values. Therefore, the results obtained are satisfactory.

Figure 13.
Mini helicopter with virtual swashplate in outdoor hover flight.
6. Discussion
UAVs using virtual swashplate are found in the literature as torque modulation, swashplateless or servomotorless vehicles and the main examples are mentioned in the Introduction section. The virtual swashplate approach reduces the number of actuators needed, typically from 4 to 2, to control the 6 degrees of freedom. This approach reduces the complexity of the mechanism necessary to tilt the thrust vector.
The classic helicopter UAV is aerodynamically more efficient than other configurations like tandem and coaxial. However, it is necessary to compensate the reactive torque produced by the main rotor (see Appendix A). The virtual swashplate requires an extra microcontroller and a high-resolution angular position sensor, even at the high revolutions per minute that a brushless motor can provide.
Position accuracy can be improved by using a Real-Time Kinematic (RTK) system. However, the size of the helicopter restricts the space available for payloads.
Flight tests showed that aggressive maneuvering increases the drag in the blades and consequently the brushless motor overheated. Implement the virtual swashplate approach in a helicopter with a speed reduction gear to reduce stress and heating of the brushless motor is proposed as future work.
7. Conclusions
The mini helicopter with virtual swashplate demonstrates hover stability and a good performance in attitude and position control in hover flight. The attitude angles follow the reference in a smooth way. The swing-hinged mechanism has been manufactured in strong and light materials to resist the centrifugal force of the propellers at high revolutions per minute.
The sinusoidal reference includes thrust, roll and pitch signals to produces the acceleration and deceleration of the rotor in each cycle. The high frequency torque modulation ensure the attitude and position command control. The positive blade increases the lift force on one hemisphere of the rotating disk and negative blade decreases in the other hemisphere by generating angular momentum. The emulation of the swashplate of a helicopter is obtained by torque modulation and simple swing-hinged mechanics. The control algorithm is designed to compensate the nonlinearities and reactive torque to perform outdoor flights.
Author Contributions
Investigation, J.F.; Investigation, S.S.; Supervision, I.G.-H.; Project administration, Y.R.; data curation, R.L.; conceptualization, E.S. and B.N. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by Department of Research and Multidisciplinary Studies of Research and Advanced Studies Center of the National Polytechnic Institute (CINVESTAV-IPN).
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors are grateful to National Council of Science, Humanities, and, Technology (CONAHCYT) for its support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| UAV | Unmanned Aerial Vehicle |
| LQR | Linear–Quadratic Regulator |
| PID | Proportional Integral Derivative |
| IMU | Inertial Measurement Unit |
| GPS | Global Position System |
| PWM | Pulse-Width Modulation |
| ESC | Electronic Speed Controller |
| RPM | Revolutions Per Minute |
| RTK | Real-Time Kinematic |
Appendix A. Main Rotor Gyroscopic Effect
The pitch and roll control inputs increase the lift force on one hemisphere of the rotor and decrease lift force on the opposite hemisphere. This imbalance effect generates an angular momentum that acts on the helicopter. The helicopter’s rotating blades behave like a gyroscope. Precession is a physical phenomenon of the gyroscopes when the applied force acts to the side of its rotation.
Due to the gyroscopic effect, a pitch angular momentum induces a roll angular momentum, i.e., with a displacement of , as shown in Figure A1. An empirical adjustment is applied so that the behavior of the helicopter is correct.
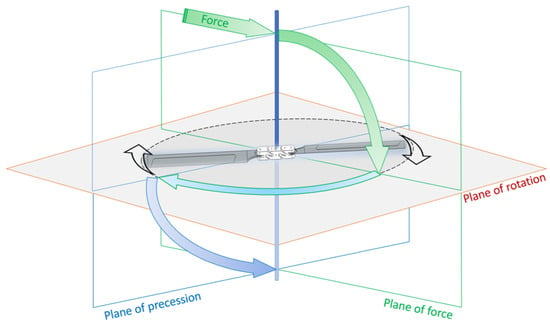
Figure A1.
Gyroscopic effect on the main rotor. The applied force green plane, the rotation red plane and the precession blue plane.
References
- Reyhanoglu, M.; Jafari, M.; Rehan, M. Simple learning-based robust trajectory tracking control of a 2-DOF helicopter system. Electronics 2022, 11, 2075. [Google Scholar] [CrossRef]
- Cai, G.; Chen, B.M.; Dong, X.; Lee, T.H. Design and implementation of a robust and nonlinear flight control system for an unmanned helicopter. Mechatronics 2011, 21, 803–820. [Google Scholar] [CrossRef]
- He, M.; He, J.; Scherer, S. Model-based real-time robust controller for a small helicopter. Mech. Syst. Signal Process. 2021, 146, 107022. [Google Scholar] [CrossRef]
- Kumeresan, A.; Leth, J.; Harbo, A.; Bisgaard, M. Robust helicopter stabilization in the face of wind disturbance. In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010. [Google Scholar]
- Paulos, J.; Caraher, B.; Yim, M. Emulating a fully actuated aerial vehicle using two actuators. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 7011–7016. [Google Scholar]
- Qin, Y.; Chen, N.; Cai, Y.; Xu, W.; Zhang, F. Gemini II: Design, Modeling, and Control of a Compact Yet Efficient Servoless Bi-copter. Ieee/Asme Trans. Mechatronics 2022, 27, 4304–4315. [Google Scholar] [CrossRef]
- Bernardes, E.; Boyer, F.; Viollet, S. Modelling, control and simulation of a single rotor UAV with swashplateless torque modulation. Aerosp. Sci. Technol. 2023, 140, 108433. [Google Scholar] [CrossRef]
- Bautista-Medina, J.A.; Lozano, R.; Osorio-Cordero, A. Modeling and Control of a Single Rotor Composed of Two Fixed Wing Airplanes. Drones 2021, 5, 92. [Google Scholar] [CrossRef]
- Lozano, R. (Ed.) Unmanned Aerial Vehicles: Embedded Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Levant, A.; Livne, M. Globally convergent differentiators with variable gains. Int. J. Control 2018, 91, 1994–2008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).