Abstract
Given the rapid advancements in kinetic pursuit technology, this paper introduces an innovative maneuvering strategy, denoted as LSRC-TD3, which integrates line-of-sight (LOS) angle rate correction with deep reinforcement learning (DRL) for high-speed unmanned aerial vehicle (UAV) pursuit–evasion (PE) game scenarios, with the aim of effectively evading high-speed and high-dynamic pursuers. In the challenging situations of the game, where both speed and maximum available overload are at a disadvantage, the playing field of UAVs is severely compressed, and the difficulty of evasion is significantly increased, placing higher demands on the strategy and timing of maneuvering to change orbit. While considering evasion, trajectory constraint, and energy consumption, we formulated the reward function by combining “terminal” and “process” rewards, as well as “strong” and “weak” incentive guidance to reduce pre-exploration difficulty and accelerate convergence of the game network. Additionally, this paper presents a correction factor for LOS angle rate into the double-delay deterministic gradient strategy (TD3), thereby enhancing the sensitivity of high-speed UAVs to changes in LOS rate, as well as the accuracy of evasion timing, which improves the effectiveness and adaptive capability of the intelligent maneuvering strategy. The Monte Carlo simulation results demonstrate that the proposed method achieves a high level of evasion performance—integrating energy optimization with the requisite miss distance for high-speed UAVs—and accomplishes efficient evasion under highly challenging PE game scenarios.
1. Introduction
The development of technology for kinetic pursuit has improved the guidance performance and robustness of pursuers. This has resulted in increased uncertainty faced by high-speed UAVs during the entire flight cycle [1,2,3]. Due to the long mid-flight period of high-speed UAVs and the limitation of the maximum usable overload, the mid-flight period has become the weakest link in the entire flight period. Consequently, it has become a challenging task to study the evasion and guidance strategies of high-speed UAVs under highly challenging PE game scenarios and to improve their survival probability in the ever-changing airspace [4,5].
Currently, the mid-flight evasion technology of high-speed UAVs can be divided into two main categories: programmed maneuvering strategy and autonomous maneuvering strategy [6]. The programmed maneuvering strategy makes it more challenging for the tracking system to predict the trajectory of high-speed UAVs by complicating the vehicle’s trajectory, such as through the square wave maneuver, sine–cosine maneuver, serpentine maneuver, and triangle wave maneuver [7,8,9]. The programmed maneuvering strategy development is mature, but evasion robustness is poor and cannot be adjusted in real time. If detected, our pursuit threat will increase dramatically. Therefore, high-speed UAVs need to be more intelligent and change their maneuvering strategies according to the situations of PE games. The autonomous maneuvering strategy dynamically generates overload commands in real time through the UAV’s onboard computer, utilizing the relative motion relationships of the parties involved in the PE game. This approach is more flexible than programmed maneuvering and can be adjusted according to the situation of each PE game, increasing the practicality of high-speed UAV evasion and the probability of success.
The conventional theoretical study of autonomous maneuver strategy is based on the differential game, which has been extensively studied both domestically and internationally. Shinar J et al. investigated the optimal evasive maneuvering strategy of a vehicle relative to a proportional guidance pursuer using a linearized model in a two-dimensional plane. The authors found that the number of maneuver switches is related to the proportional guidance coefficients of the pursuer, provided an analytical expression of the specific moments of the maneuver, and analyzed the miss distance changes in different cases [10]. Subsequently, they investigated the optimal three-dimensional evasion using the linear kinematics modeling maneuver method. This method reduces the evasion problem to roll position control, including two aspects: rotating the lift vector into the optimal avoidance plane, and performing a 180° roll maneuver according to the switching function, in order to obtain the optimal effect of evasion [11]. Wang et al. devised a differential game guidance law for the mid-guidance phase of high-speed UAVs that employs reasonable assumptions to yield an analytical solution to the game problem. This approach effectively reduces the UAV’s energy consumption while significantly increasing the energy consumption of the pursuer, offering a significant advantage over traditional maneuvering strategies such as sinusoidal maneuvering. [12]. Guo et al. conducted an investigation of a mid-guidance strategy based on terminal collision angle constraints within the cruise segment, with the objective of satisfying the limitations of control inputs imposed by saturation. To this end, they designed the evasion trajectory to accommodate the specific two-party terminal trajectory angle deviation by maximizing the terminal transverse and longitudinal position deviation and minimizing the control energy as performance indexes, in order to enhance the evasion efficiency [13]. In contrast to the conventional approach, which maximizes the miss distance, Yan et al. established a lower bound of successful escape miss distance; introduced the concept of an evasion window for pursuers with unknown guidance laws; and proposed a minimum energy-consuming evasion strategy that can realize minimum energy-consuming evasion within the evasion window obtained through a differential game [14]. In the event that the dynamics of the pursuer are unknown, Yan employed the gradient descent method to estimate the parameters of the tracker’s dynamics and, furthermore, developed the energy-optimal evasion guidance law algorithm, which considers overload constraints and energy optimization [15].
In recent years, due to the rapid advancement of artificial intelligence technology, decision-making algorithms such as deep reinforcement learning have been extensively applied in manufacturing, control, optimization, and games [16]. Reinforcement learning allows agents to autonomously make decisions within specific environments by interacting with the environment and maximizing cumulative rewards [17]. It is well suited for complex decision-making problems, as it can handle high-dimensional continuous data without relying on precise mathematical models. However, there is currently limited research on high-speed UAV PE game technology based on DRL. Wang et al. [18] introduced an intelligent maneuvering evasion algorithm for UAVs using deep reinforcement learning and imitation learning theory. The authors developed a Generative Adversarial Imitation Learning-Proximal Policies Optimization (GAIL-PPO) intelligent evasion network comprising a discriminative network, actor network, and critic network. These enhance the convergence speed of the network and achieve superior performance compared to expert strategies. Yan et al. [19] modeled the evasion strategy as a deep neural network and employed centralized training with decentralized execution under a reinforcement learning framework to train its parameters. The trained maneuver evasion strategy network enables high-speed UAVs to successfully evade defenses. Additionally, Zhao et al. [20] proposed an intelligent evasive maneuvering strategy that combines optimal control with deep reinforcement learning while introducing meta-learning to improve generalization in unknown scenarios; this approach achieves successful evasion of high-speed UAVs by adjusting longitudinal and lateral maneuvering overload. Gao et al. [21] utilized a two-delay deep deterministic (TD3) gradient strategy to construct a control decision framework based on the actor–critic approach, which enables high-speed UAVs to perform successful evasion.
In general, the majority of the aforementioned literature considers PE game scenarios in which the performance levels of the pursuer and the high-speed UAVs are comparable, or the performance of the pursuer is weaker. However, it largely overlooks the highly challenging situations that arise when the performance of a high-speed UAV is weaker than that of its pursuer, resulting in a head-on confrontation. This head-on pursuit position allows the pursuer to have a more abundant maneuvering capability during its terminal guidance segment, improving its probability of successful pursuit [22]. Meanwhile, when using DRL algorithms to solve the PE problem, the existing literature only considers the process and terminal rewards, but does not address how to utilize the reward function to guide agents and reduce the difficulty of pre-exploration. The design of the reward function also does not comprehensively take into account the evasion, the trajectory constraints, or the energy consumption. Furthermore, the impact of the LOS angle rate on evasion strategy has not been studied in the above literature, despite its status as one of the most critical parameters in the pursuer tracking law. Therefore, it is essential to comprehensively consider the evasion, trajectory constraint, and energy consumption issues of high-speed aircraft in highly competitive scenarios. Moreover, the impact of the LOS angle rate on game strategy should be considered in order to enhance the effectiveness and generalization ability of high-speed UAV evasion strategy during PE games.
In order to address the aforementioned issues, this paper proposes an intelligent evasion strategy that combines LOS angle rate correction and deep reinforcement learning (LSRC-TD3). The primary contributions of this paper are as follows:
- To ensure the rigor and challenge of the research scenarios in this paper, variables that significantly affect the difficulty of the PE game are considered from multiple perspectives. These variables include the pursuer tracking strategy, the PE game parties’ relative motion relationships, and the performance parameters of the vehicle.
- During the design of the reward function, evasion, energy consumption, and subsequent trajectory constraints are considered comprehensively. The intelligent maneuvering strategy minimizes energy consumption during evasion while reserving space for subsequent trajectory constraints, provided that successful evasion is achieved.
- In order to reduce the difficulty of the agent’s preliminary exploration and accelerate the convergence speed of the PE game network, we propose a combination of “terminal” and “process” rewards, as well as “strong” and “weak” incentive guidance forms of reward function.
- This paper presents a novel integration of an intelligent algorithm with LOS angle rate correction, aimed at enhancing the sensitivity of high-speed UAVs to changes in LOS angle rate and improving maneuver timing accuracy. This approach allows the intelligent algorithm to generate a decision online, simultaneously with the correction, thereby improving the effectiveness and generalization ability of the proposed algorithm.
The structure of the paper is as follows: Section 2 presents a three-degrees of freedom mathematical model of high-speed UAVs and pursuers. Section 3 introduces a Markov decision model based on the TD3 algorithm and incorporates a correction term related to the LOS angle rate. In Section 4, the effectiveness and robustness of the proposed intelligent maneuvering strategy (LSRC-TD3), which integrates LOS angle rate correction and DRL, is validated through simulation, and conclusions are drawn in Section 5.
2. Pursuit–Evasion Game Model and Problem Formulation
2.1. The Pursuit–Evasion Game Model
In this paper, the flight of the high-speed UAV during the mid-flight period, the end of the pursuer’s guidance section, and the two sides of the PE game form the head-on scenario. The relative motion relationship is shown in Figure 1, where and represent high-speed UAVs and pursuers, respectively; and denote the speeds of the two opposing sides in the PE game; and are the ballistic deflection angles of the pursuit and evasion sides, respectively; represents the LOS azimuthal angle; and are the overloads of the two opposing sides; and refers to the relative distance between the two sides.
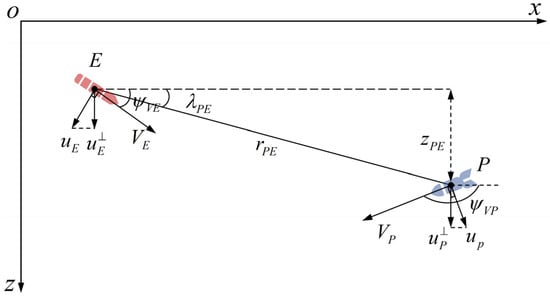
Figure 1.
The PE game scenario.
2.1.1. Three-Degrees of Freedom Model for Both Sides of the Game
By analyzing the forces affecting high-speed UAVs and pursuers in flight, considering their overall dynamics and kinematics, and carrying out coordinate transformation and simplification, three-degrees of freedom dynamics and kinematics models of both the center of mass of the high-speed UAVs and the center of mass of the pursuers were established, as shown below:
where denotes the high-speed UAVs and pursuers; represents the ballistic inclination angles of the high-speed UAVs and pursuers; express the coordinates of the vehicles in the three directions of the ground coordinate system; and is the overload of the vehicles, , .
2.1.2. Relative Motion Model
and can be obtained from the geometrical relations in Figure 1:
and in the above equation are the positions of high-speed UAVs and pursuers in the ground coordinate system, and the derivatives of both sides of the above equation are taken simultaneously to obtain the relative motion equation:
where , , and use the same definitions.
2.1.3. The Guidance Law of the Pursuer
In order to enhance the tracking capability of the pursuer, this paper postulates that the pursuer will adopt the two-dimensional augmented proportional navigation guidance law, which incorporates overload compensation based on the traditional proportional guidance. The lateral overload command expression is as follows:
where is the scaling factor, is the correction factor, and is the actual lateral overload response of the high-speed UAVs.
2.1.4. Autopilot Model
This paper considers the characteristics of the two-party autopilot, assuming that the two-party autopilot model is a first-order inertial element. The relationship between the actual overload of the vehicle and the overload command is expressed as follows:
where is the overload command of the vehicle, is the actual overload response, and is the responsive time constant of first-order dynamic characteristics.
2.2. The Pursuit–Evasion Game Problem
In the PE game problem, if the miss distance of the rendezvous moment between the two sides of the game is greater than the miss distance threshold, it can be concluded that evasion has been successful.
where is the rendezvous moment between the two sides of the PE game and is the miss distance threshold.
Moreover, the usable overloads of high-speed UAVs are constrained by their inherent structural and aerodynamic characteristics.
While the success of evasion is considered, energy consumption is also a focus of this paper. The energy consumption during the evasion of high-speed UAVs is characterized as the integral of the square of its own actual overload.
The pursuit–evasion game problem for high-speed UAVs can now be formulated as Problem 1.
Problem 1.
(Energy-optimized PE game problem): in the given PE game scenario, Figure 1, the pursuer employs the guidance law (5) and utilizes an intelligent algorithm trained to minimize the energy consumption of the game process (9) within the constraints of the maximum available overload (8) and the prerequisite of successful evasion by its side (7).
Assumption 1.
The speeds of both sides are constant during the PE game.
Remark 1.
Due to the high speed characteristics of both sides of the PE game, the game process is relatively short, so the speed losses of both can be ignored, and in addition, because the longitudinal overloads of both sides are relatively small, the speed differential can be ignored, so it is assumed that the speeds of both sides are constant values.
Remark 2.
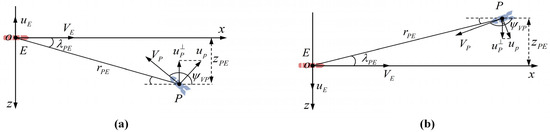
During the training process of the intelligent method, the agent employs a single game strategy to address all observed PE scenarios. If we take the center of mass of the high-speed UAVs as the origin and establish a coordinate system with the direction of the high-speed UAVs’ speed vector as the positive direction of the x-axis, when facing the pursuers from the positive direction of the z-axis, the agent will maneuver to the negative direction of the z-axis first, which will leave space for subsequent energy optimization and trajectory constraints. However, when confronted with a pursuer from the negative direction of the z-axis, the agent adopts the same game strategy to maneuver to the negative direction of the z-axis first, which compresses the subsequent game space and greatly reduces the probability of successful evasion. In this paper, the PE game problem is divided into two categories, as shown in Figure 2, according to the initial positions of the two sides of the game, and the agent is trained for these two positions.

Figure 2.
(a,b)Two initial positions for PE game.
3. Intelligent Maneuvering Strategy
This paper proposes an intelligent maneuvering strategy (LSRC-TD3) that combines LOS angle rate correction and deep reinforcement learning for highly challenging situations, as shown in Figure 3.
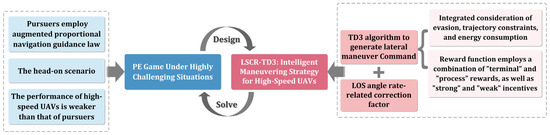
Figure 3.
Block diagram of intelligent maneuvering strategy.
3.1. Markov Decision Model
In order to resolve the pursuit–evasion game problem during the mid-flight of high-speed UAVs by adopting the intelligent method of deep reinforcement learning, it is first necessary to model the problem as a Markov Decision Process (MDP). This involves the construction of a PE game environment, where the agent interacts with the environment through states, actions, and rewards, as shown in Figure 4. A Markov Decision Process is typically defined by a quintuple , where is a finite state space, is a finite action space, is a status transition matrix, is a reward function, and is a discount factor.
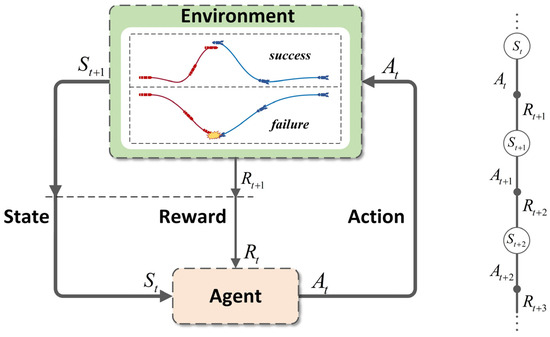
Figure 4.
Markov Decision Process.
3.1.1. State Space
In the PE game scenario, the agent needs to perceive the current situation of the two sides based on the information in the state space, and make corresponding maneuvers. A complicated state space will reduce the efficiency of the agent in extracting and understanding important information and weaken the generalization ability of the intelligent algorithm, while an overly simple state space cannot provide sufficient information for the agent to make optimal decisions. Consequently, a normalized state space, as defined by Equation (10), was devised on the basis of the states and relative motions of the two parties engaged in the PE game.
where , , , , are the normalized relative distances of the game, the LOS azimuth angle, the LOS azimuth angle rate, and the trajectory declination angles of the high-speed UAVs and the pursuers. In addition, and are the relative distances between the two sides of the game at the current moment and the initial moment, respectively.
3.1.2. Action Space
In the scenario explored in this article, it is essential for a high-speed UAV to implement appropriate evasive maneuvers in accordance with its own state and relative position in relation to the pursuer in order to avoid pursuit. To address Problem 1, this paper employs deep reinforcement learning to train high-speed UAVs to generate real-time maneuver commands under varying conditions. In conjunction with the two-dimensional spatial PE game problem, the lateral overload of the high-speed UAV should be selected as the action, with the range of action set to be , taking into account the limitations of the available overload of each UAV.
3.1.3. Reward Function
The reward function plays a pivotal role in guiding the agent to generate appropriate maneuver commands in different scenarios. The efficacy of the training process and the convergence speed of the algorithm are directly proportional to the quality of the reward function. Therefore, identifying an optimal reward function is crucial for effectively utilizing deep reinforcement learning algorithms to address PE game problems. In the context of this paper, the primary focus is on the quantity of miss distance and the evasion energy consumption, which is quantified in the form of the total overload of high-speed UAV maneuvers. Furthermore, in order to consider the subsequent trajectory limitations of high-speed UAVs, it is essential to deviate from the original trajectory as little as possible. In order to address the convergence problem of agent training, the reward function in this paper employs a combination of “terminal” and “process” rewards, as well as “strong” and “weak” incentive guidance, with the objective of inducing faster convergence of agents. The reward function for this problem is designed as follows:
- Miss distance-related reward function:where is the moment of rendezvous between the two sides of the game, is the miss distance, is the miss distance threshold for determining the success of evasion, and , , are the weighting coefficients. When the miss distance is less than , a larger punishment should be given, and the closer the miss distance threshold, the smaller the punishment; when the miss distance is larger than , a larger reward should be given, and on this basis, the larger the miss distance, the larger the reward.
- Energy consumption-related reward function:where is the actual overload of high-speed UAVs and is the weighting factor.
- Line-of-sight angle rate-dependent reward function:where is the rate of the LOS azimuth angle and is the weighting coefficient. When the LOS azimuth angle becomes larger, the lateral distance increases and a weak reward should be given, and vice versa, a weak punishment is given. The main role of this sub-reward function is to guide the agent to increase the LOS azimuth angle to enhance the probability of successful evasion. However, the LOS angle does not determine the success of evasion, so its reward and punishment are small.
- Reward function related to ballistic deflection angle for high-speed UAVs:where is the ballistic deviation angle of the high-speed UAV, is the ballistic deviation angle of the vehicle at the beginning of the game, and is the weighting coefficient. In order to deviate from the original trajectory as little as possible, it is necessary to ensure that the difference between the ballistic declination of the high-speed UAV and the ballistic declination at the initial moment is as small as possible.
Considering evasion, trajectory constraints, and energy consumption, the reward function is as follows:
Remark 3.
In the sub-reward function, the miss distance-related reward function is the terminal reward; , , and are all process rewards. In this paper, the primary consideration indexes are miss distance and energy consumption. Therefore, and are strong rewards, while and are weak incentives. Moreover, the correlation between miss distance and energy consumption is significant. Following successful evasion, the energy consumption of maneuver commands with larger miss distances is also higher. It is, therefore, necessary to consider the relationship between miss distance and energy consumption in depth when setting the weight coefficients. In order to avoid the weight coefficients of energy consumption being too high, the agent adopts a strategy of low energy consumption, but evasion is unsuccessful. It is also necessary to avoid the agent ignoring energy optimization due to the weight coefficients of miss distance being too high.
3.1.4. The Termination Condition
The relative distance between the high-speed UAV and the pursuer is a crucial factor in determining the outcome of the PE game. When this distance begins to increase, it signals that the two sides have intersected, which marks the end of the PE game.
Remark 4.
Terminating training at the instant results in the terminal reward function resembling an impulse signal with a narrow pulse width. This can lead to the agent disregarding the terminal reward associated with miss distance. Delaying the training for a number of steps after the moment before stopping will enhance the sensitivity of the agent and facilitate convergence.
3.2. TD3 Algorithm
TD3 (Twin Delayed Deterministic Policy Gradient) is an online and off-policy deep reinforcement learning algorithm for solving continuous control problems, obtained by Scott Fujimoto et al. [23] by improving on the DDPG (Deep Deterministic Policy Gradient) algorithm; its network architecture and updating process are shown below.
DDPG is more sensitive to changes in parameters such as hyperparameters and adjustments in the correlation structure. Additionally, the trained Q function significantly overestimates the Q-value, which can lead to the strategy being corrupted by exploiting the error between the true Q-value and the estimated Q-value. To address the overestimation problem of DDPG, the TD3 algorithm is improved as follows.
3.2.1. Double Network
Two sets of critic networks are employed, with the smaller of the two being utilized in the calculation of the target value, thereby mitigating the issue of overestimation of the Q function.
where is the target value, is the gain at the current moment, is the discount factor, and are the two critic networks’ estimates of the gain for at the next moment (state, action), and is the parameter of the gain estimation function.
3.2.2. Target Policy Smoothing Regularization
In calculating the target value, a perturbation is introduced into the next state action in order to enhance the accuracy of the value assessment.
where is the added perturbation, which conforms to a normal distribution, and the perturbation is cropped to approximate the original action. This is done to estimate the target value by using the region around the target action, which is beneficial for smoothing the estimate.
3.2.3. Delayed Policy Update
The critic network is updated on multiple occasions prior to the actor network, thereby ensuring a more stable training process for the actor network. The actor network is updated by maximizing the cumulative expected return and, thus, requires the critic network to evaluate it. In the event that the critic network is unstable, the actor network will also oscillate. Consequently, it is possible to update the critic network more frequently than the actor network. This entails waiting for the critic network to become more stable before updating the actor network, thereby ensuring the stability of training.
3.3. TD3 Algorithm Based on LOS Angle Rate Correction
In the PE game scenario of this paper, the pursuer employs the augmented proportional navigation guidance law as described in (5), which is strongly correlated with the LOS angle rates of the two sides of the game. During the training process, although the state space (10) also contains the angle rate of line of sight, it is only one of the observations, and the weight is much smaller than that of the angle rate of line of sight in the guidance law (5) of the pursuing party. The pursuer is more sensitive to changes in the angle rate of line of sight than high-speed UAVs, which increases the probability of failure in some critical states. It is, therefore, necessary to introduce a correction term based on the existing intelligent maneuvering commands that is strongly related to the LOS angle rate, as shown in Equation (19).
where is the maneuver instruction that introduces the correction term for the angle rate of sight, is the lateral maneuver command generated by the agent according to the positions of both sides, is the angle rate of LOS, and is the scaling factor, which is related to the initial positions of both sides of the game and the time of the game.
Remark 5.
The innovations of this paper, in comparison with the existing research on PE games based on traditional and intelligent methods, are as follows:
- In the design of the reward function, evasion, energy consumption, and subsequent trajectory constraints are considered comprehensively, and the relevant sub-reward functions are designed. Evasion, energy consumption, and trajectory constraints are quantified as miss distance-related sub-reward function , overload-related sub-reward function , and trajectory deflection angle-related sub-reward function .
- In order to reduce the difficulty of the agent’s preliminary exploration and accelerate the convergence speed of the PE game network, we propose a combination of “terminal” and “process” rewards, as well as “strong” and “weak” incentive guidance forms of reward function. This is characterized by the fact that is the terminal reward; , , and are process rewards; and are strong rewards; and and are weak incentives.
- In enhancing the sensitivity of high-speed UAVs to changes in LOS angle rate and the accuracy of maneuver timing, this paper combines the intelligent algorithm with LOS angle rate correction for the first time. This integration of the intelligent algorithm with the correction enables the intelligent algorithm to generate the decision online, concurrently with the correction, which further improves the effectiveness and generalization ability of the proposed algorithm.
Remark 6.
At present, the LOS angle rate extraction technology is more mature [24,25]. The objective of this paper is to examine the efficacy of implementing the LOS angle rate correction term to enhance the performance and versatility of the proposed algorithm. Consequently, the acquisition of the LOS angle rate is not discussed in depth in this paper due to space limitations.
Remark 7.
The angle rate of line of sight can be utilized as a relatively weak incentive to guide the agent through the training process. However, there is no hard constraint, so it is not possible to increase the sensitivity of the agent to the angle rate of LOS by increasing the weights of the angle rate of LOS-related sub-reward function and the normalized angle rate of sight during the observation term. In the PE game process, the pursuer is induced to perform a full-overload maneuver by guiding the agent to increase the angle rate of line of sight. It should be noted, however, that the angle rate of LOS does not determine the success of evasion. Consequently, it can only be used as a weak incentive. The angle rate of LOS is only one of the observation items of the agent, but it is the most critical variable in the guiding law of the pursuer. The sensitivity of each side of the PE game to changes in the angle rate of LOS cannot be altered by increasing the weights.
4. Simulation and Analysis
4.1. Initial Positions and Training Parameter Settings for PE Game
According to the previous assumptions, the PE game occurs in the horizontal plane. The two sides of the game constitute the head-on scenario [26,27,28,29]. High-speed UAVs employ an intelligent maneuvering strategy to evade their pursuer. Table 1 presents the performance parameters of both sides and the initial scenario of the PE game.

Table 1.
Initial state of the PE game and performance parameters of both sides.
Remark 8.
In the game scenario presented in this paper, the delay effect of the first-order inertial element has a significant impact on the results of evasion. To validate the efficacy of the proposed method, it is assumed that the first-order time constants of the two sides of the game are identical.
As illustrated in Figure 5, the actor network is tasked with generating maneuver instructions in accordance with the current state parameters of the two sides of the game. Its input is observation, while its output is action. Similarly, the critic network is responsible for calculating the Q-value based on the current state of the system and the maneuver instructions. Its inputs are observation and action, with the output being the Q-value. The specific network structure and specific number are depicted in Figure 6. The relevant parameters in the training of the TD3 algorithm are presented in Table 2 [30,31,32,33].
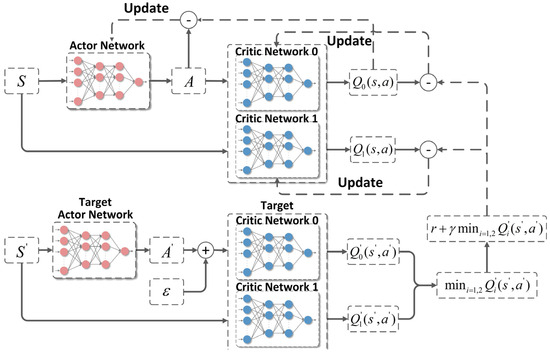
Figure 5.
Network architecture of the TD3 algorithm.
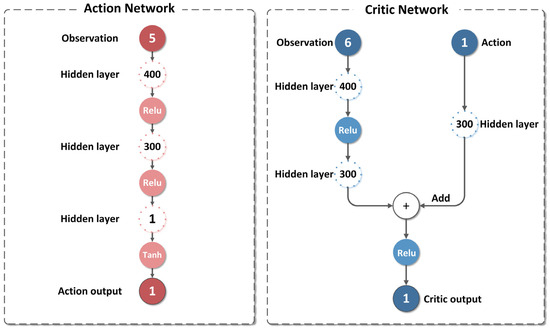
Figure 6.
Specific network structure.

Table 2.
TD3 algorithm training-related parameters.
4.2. Simulation and Result Analysis
A coordinate system is established, with the center of mass of high-speed UAVs as its origin. The average reward and the cumulative reward per round of the TD3 intelligent evasion algorithm based on the training are shown in Figure 7a for the initial game situation with a positive z-axis pursuer, as shown in Figure 2a. For an initial game situation with a negatively oriented z-axis pursuer, as shown in Figure 2b, the training varies the pull-off range of the pursuer’s trajectory deflection angle from the LOS azimuth angle, as well as the weight coefficients and in the miss distance correlation sub-reward function . The average rewards of the training evasion algorithm versus the rewards per round are shown in Figure 7b.
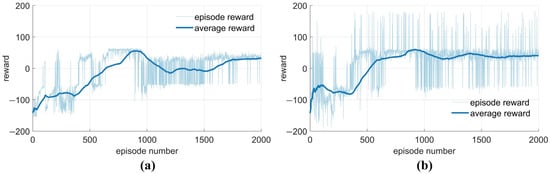
Due to the differences of the weight coefficients and in the miss distance correlation sub-reward function during training, the maximum values of the cumulative rewards in Figure 7a,b are different in each round, but the trends of the average rewards are similar. At the initial stage of exploration, the agent rapidly identifies a maneuvering strategy that yields the highest cumulative reward. This strategy peaks in value at approximately 900 rounds, at which point it resembles bang–bang control, as illustrated in Figure 8c,d. Subsequently, the agent continues to explore the evasion strategy that balances the miss distance and energy consumption. Convergence is observed at approximately 1700 rounds for Figure 7a and at approximately 1400 rounds for Figure 7b. The converged intelligent maneuvering strategy of the agent is illustrated in Figure 8e,f. In this paper, we propose a reward function that combines “terminal” and “process” rewards, as well as “strong reward” and “weak incentive” in the form of guidance. The proposed reward function can effectively reduce the difficulty of pre-exploration and accelerate the convergence speed of the game network.
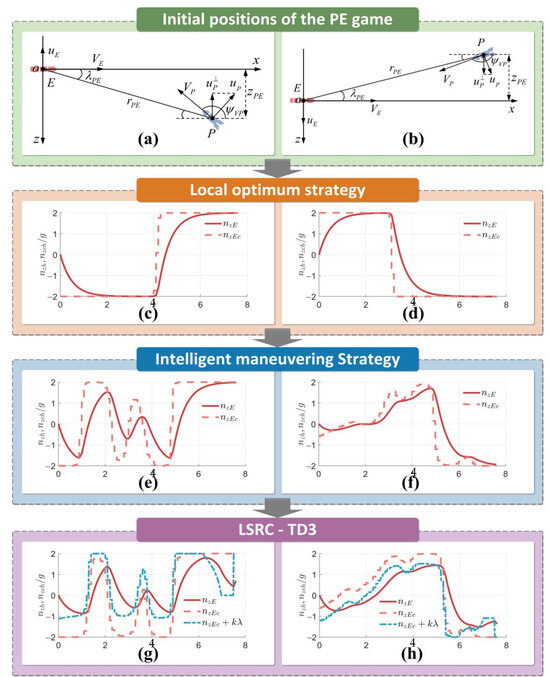
Figure 8.
LSRC-TD3 training flowchart. (a,b) The two initial positions, (c,d) Corresponding locally optimal strategy overload curves for the two initial positions, (e,f) Overload curves of the corresponding intelligent maneuvering strategy for two initial positions, (g,h) Corresponding LSRC-TD3 strategy overload curves for two initial positions.
Following the application of TD3 algorithm training to derive an intelligent maneuvering strategy that integrates evasion, energy consumption, and trajectory constraints, the LSRC-TD3 algorithm is obtained through the introduction of the LOS angle rate correction factor, as expressed in Equation (19). Figure 8g,h illustrate the high-speed UAV overload command and the actual overload subsequent to the introduction of the correction term for the angle rate of sight. A comparison between Figure 8e,f and Figure 8g,h reveals that it can be observed that the correction factor reduces the magnitude of the maneuver command in the initial and intermediate stages of the game, further optimizes energy consumption, and significantly enhances the sensitivity of high-speed UAVs to the angle rate of LOS in the latter stages of the game.
Subsequently, Monte Carlo simulation and single-point simulation will be used to verify the LOS angle rate correction factor’s enhancement of the effectiveness and generalization performance of the intelligent maneuvering strategy.
Figure 9a and Figure 10a,c show 1000 Monte Carlo simulations without the correction factor, using the relative initial distance, the initial trajectory deflection angle, and the initial LOS azimuth angle of the pursuer as the variables. Figure 9b and Figure 10b,d depict 2000 Monte Carlo simulations with the addition of the LOS angle rate correction factor, using the initial trajectory deflection angle and the initial LOS azimuth angle of the pursuer as the variables.
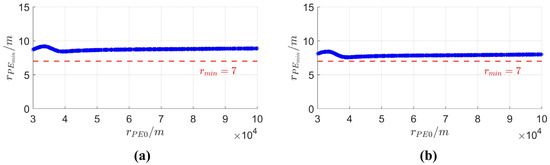
Figure 9.
Monte Carlo simulations with relative initial distance as the variable. (a) No correction factor introduced, (b) introduced correction factor.
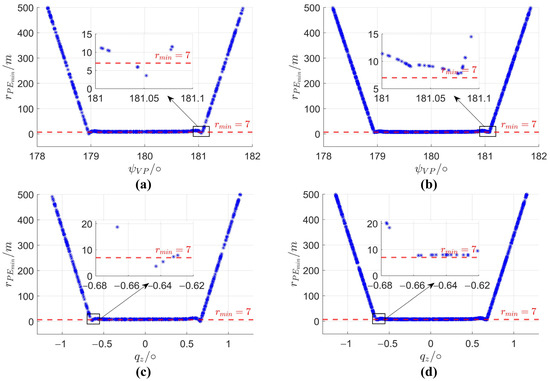
Figure 10.
Monte Carlo simulations with relative initial angle as the variable. (a,b) Monte Carlo simulations of the trajectory deflection angle without and with correction factor, respectively, (c,d) Monte Carlo simulations of the LOS angle without and with correction factor, respectively.
Comparison of Figure 9a,b reveals that the introduction of the correction term brings the miss distance of a high-speed UAV closer to the miss distance threshold while ensuring successful evasion during the PE game. Typically, the miss distance at this stage and the energy consumption due to evasion are strongly correlated. Therefore, integrating the correction term tends to reduce evasion energy consumption further, consistent with the findings in Figure 8e–h.
Figure 10a,c demonstrate that, under the condition of a small initial angular deviation, high-speed UAVs can realize successful evasion by using the intelligent maneuvering strategy without the correction term, and when the initial angle deviation is large, the pursuer is unable to track UAVs effectively due to the limitation of its own available overload; but the different sensitivities to LOS angle rate of the two sides of the game in the critical regions of the two cases mentioned above leads to differences in the accuracy of maneuver timing. There is a pursuit window of about 0.04 degrees on each side, in which we cannot realize successful evasion.
The optimization impact of introducing the LOS rate correction factor into intelligent maneuvering strategies strongly depends on the selection of the scaling factor in Equation (19). This coefficient varies with the initial relative positions and the duration of the PE game. When initial positions are outside the pursuit window, the corrective influence of the factor remains limited throughout the game. Conversely, within the pursuit window, the correction factor more effectively adjusts the overload commands for high-speed UAVs, with its efficacy increasing as the distance between the parties diminishes during the PE game.
Comparing Figure 10a,c with Figure 10b,d, respectively, reveals that the correction factor has minimal impact on miss distance when outside the pursuit window. In contrast, inside the pursuit window, the correction term notably increases the sensitivity of each high-speed UAV to LOS angle rates. This enhancement aids the UAV in precisely determining maneuver timing, enabling successful evasion within the pursuit window, aligning with the intended function of the correction term proposed in this study.
Remark 9.
It is crucial to recognize that the magnitude of the scaling factor in the correction formula may vary depending on factors such as the positions and performances of the PE game participants. This paper does not provide a specific mathematical formula for determining the proportionality coefficient . Therefore, it is essential to conduct a comprehensive analysis when applying it in different scenarios.
In order to further verify the effectiveness, robustness, and generalization ability of the correction factor during the intelligent maneuvering strategy, the initial trajectory deflection angle of the pursuer is selected as 181.020°, 181.052°, and 181.087° for the single-point simulation, in which the initial position of the UAV—with an initial trajectory deflection angle of the pursuer of 181.052°—is located in the pursuit window, and the remaining two positions are located outside the pursuit window.
Figure 11a,b show the overload commands of both sides of the game without and after the correction factor is added, respectively, and Figure 11c,d show the trajectories of the PE game without and after the correction factor is added, respectively. In the absence of the correction factor, high-speed UAVs adopt similar maneuvering strategies in the three initial positions, while the pursuer employs a pursuit strategy that is analogous to bang–bang maneuvering at different times. This is also evident from the PE game trajectories of both sides in Figure 11c, which depicts the three flight trajectories. The three flight trajectories of the high-speed UAVs are almost overlapped, while the pursuer’s flight trajectories are three completely different parabolas. It can be seen that the sensitivity to the initial situation has significant differences, which also reveals the reason why the high-speed UAVs cannot successfully evade within the pursuit window.
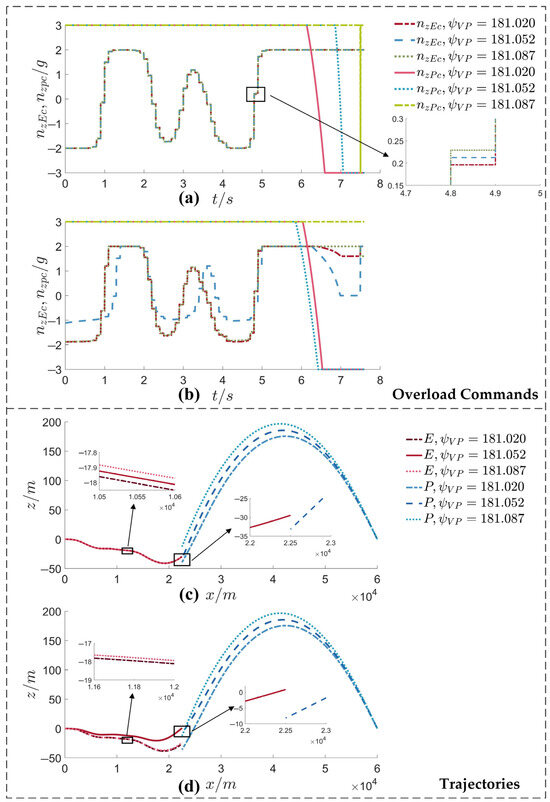
Figure 11.
Overload commands and trajectories of both sides of the PE game. (a,b) Overload commands for the two sides without and with the correction term, respectively, (c,d) Trajectories for the two sides without and with the correction term, respectively.
The incorporation of the correction factor has rendered high-speed UAVs more sensitive to alterations in the angle rate of LOS. This phenomenon is particularly evident in the temporal vicinity of 2 s prior to the moment of rendezvous. Furthermore, as demonstrated by the overload command of the pursuer with an initial ballistic deflection angle of 181.052°, the weight of the correction term is greater and the correction of the overload command is more pronounced when the initial position is within the pursuit window.
Figure 12a,b show the relative distances between the two sides of the PE game for different initial ballistic deflection angles without adding the correction factor and after adding the correction factor, respectively. When the correction term is not added, the miss distance at the rendezvous moment with the initial game positions located in the pursuit window is less than the miss distance threshold of 7 m, and the remaining initial positions all succeed in evasion. After the correction factor has been added, the miss distance at the rendezvous moment with different initial ballistic deflection angles is larger than the miss distance threshold of 7 m. The specific values of the miss distance are shown in Table 3.
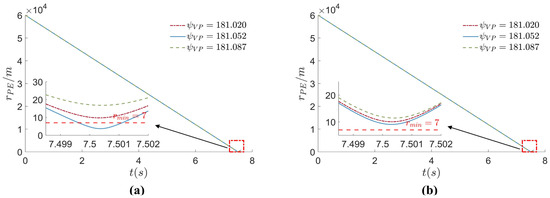
Figure 12.
Relative distances between the two sides of the PE game. (a) No correction factor introduced, (b) introduced correction factor.

Table 3.
Miss distance at the moment of rendezvous.
The preceding simulation results and analysis demonstrate that the intelligent maneuvering strategy integrating LOS angle rate correction is highly effective, robust, and exhibits a strong overall performance. Furthermore, it enhances sensitivity to LOS angle rate while reducing the energy consumption associated with evasion, thereby achieving efficient maneuvering evasion in challenging scenarios.
5. Conclusions
This paper examines the PE game problem of high-speed UAVs in highly challenging situations, and proposes an intelligent maneuvering strategy (LSRC-TD3) combining LOS angle rate correction and deep reinforcement learning by introducing an LOS angle rate correction factor into the double-delay deep deterministic (TD3) gradient strategy. In addition, by comprehensively considering evasion, trajectory constraints, and energy consumption, this paper innovatively proposes a combination of “terminal” and “process” rewards, as well as “strong” and “weak” incentive guidance forms of reward function.
The simulation results demonstrate that the reward function forms proposed by this paper can effectively reduce exploration difficulty during pre-exploration and accelerate convergence of the PE game network. Meanwhile, this paper introduces the LOS angle rate correction factor, which can significantly enhance the sensitivity of high-speed UAVs to changes in the LOS angle rate and the accuracy of the time of maneuver, and dramatically improves the probability of successful evasion near the critical angle. The proposed method has a high degree of validity, robustness, and generalization, ensuring the miss distance required by high-speed UAVs while considering energy optimization and subsequent trajectory constraints, which achieves efficient evasion in a highly challenging PE game situation.
Author Contributions
Conceptualization, all authors; methodology, T.Y., C.L. and M.G.; software, T.Y. and C.L.; validation, T.Y., C.L. and M.G.; formal analysis, T.Y., C.L. and M.G.; resources, Z.J.; writing—original draft preparation, T.Y., C.L. and T.L.; writing—review and editing, C.L., Z.J. and T.L.; supervision, T.Y. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 62176214) and supported by the Fundamental Research Funds for the Central Universities.
Data Availability Statement
All the data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, B.; Gan, Z.; Chen, D.; Sergey Aleksandrovich, D. UAV Maneuvering Target Tracking in Uncertain Environments Based on Deep Reinforcement Learning and Meta-Learning. Remote Sens. 2020, 12, 3789. [Google Scholar] [CrossRef]
- Zhuang, X.; Li, D.; Wang, Y.; Liu, X.; Li, H. Optimization of high-speed fixed-wing UAV penetration strategy based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 148, 189089. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, Y.; Han, T.; Hu, Q. Incremental guidance method for kinetic kill vehicles with target maneuver compensation. Beijing Hangkong Hangtian Daxue Xuebao/J. Beijing Univ. Aeronaut. Astronaut. 2024, 50, 831–838. [Google Scholar]
- Li, Y.; Han, W.; Wang, Y. Deep Reinforcement Learning with Application to Air Confrontation Intelligent Decision-Making of Manned/Unmanned Aerial Vehicle Cooperative System. IEEE Access 2020, 8, 67887–67898. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, T.; Chen, W.; He, T. Optimal maneuver penetration strategy based on power series solution of miss distance. Beijing Hangkong Hangtian Daxue Xuebao/J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 159–169. [Google Scholar]
- Lu, H.; Luo, S.; Zha, X.; Sun, M. Guidance and control method for game maneuver penetration missile. Zhongguo Guanxing Jishu Xuebao/J. Chin. Inert. Technol. 2023, 31, 1262–1272. [Google Scholar]
- Zarchan, P. Proportional Navigation and Weaving Targets. J. Guid. Control Dyn. 1995, 18, 969–974. [Google Scholar] [CrossRef]
- Imado, F.; Uehara, S. High-g barrel roll maneuvers against proportional navigation from optimal control viewpoint. J. Guid. Control Dyn. 1998, 21, 876–881. [Google Scholar] [CrossRef]
- Zhu, G.C. Optimal Guidance Law for Ballistic Missile Midcourse Anti-Penetration. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Shinar, J.; Steinberg, D. Analysis of Optimal Evasive Maneuvers Based on a Linearized Two-Dimensional Kinematic Model. J. Aircr. 1977, 14, 795–802. [Google Scholar] [CrossRef]
- Shinar, J.; Rotsztein, Y.; Bezner, E. Analysis of Three-Dimensional Optimal Evasion with Linearized Kinematics. J. Guid. Control Dyn. 1979, 2, 353–360. [Google Scholar] [CrossRef]
- Wang, Y.; Ning, G.; Wang, X.; Hao, M.; Wang, J. Maneuver penetration strategy of near space vehicle based on differential game. Hangkong Xuebao/Acta Aeronaut. Astronaut. Sin. 2020, 41, 724276. [Google Scholar]
- Guo, H.; Fu, W.X.; Fu, B.; Chen, K.; Yan, J. Penetration Trajectory Programming for Air-Breathing Hypersonic Vehicles During the Cruise Phase. Yuhang Xuebao/J. Astronaut. 2017, 38, 287–295. [Google Scholar]
- Yan, T.; Cai, Y.L. General Evasion Guidance for Air-Breathing Hypersonic Vehicles with Game Theory and Specified Miss Distance. In Proceedings of the 9th IEEE Annual International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (IEEE-CYBER), Suzhou, China, 29 July–2 August 2019; pp. 1125–1130. [Google Scholar]
- Yan, T.; Cai, Y.L.; Xu, B. Evasion guidance for air-breathing hypersonic vehicles against unknown pursuer dynamics. Neural Comput. Appl. 2022, 34, 5213–5224. [Google Scholar] [CrossRef]
- Liu, Q.; Zhai, J.W.; Zhang, Z.Z.; Zhong, S.; Zhou, Q.; Zhang, P.; Xu, J. A Survey on Reinforcement Learning. Chin. J. Comput. 2018, 41, 1–27. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: London, UK, 2018. [Google Scholar]
- Wang, X.F.; Gu, K.R. A penetration strategy combining deep reinforcement learning and imitation learning. J. Astronaut. 2023, 44, 914–925. [Google Scholar]
- Yan, P.; Guo, J.; Zheng, H.; Bai, C. Learning-Based Multi-missile Maneuver Penetration Approach. In Proceedings of the International Conference on Autonomous Unmanned Systems, ICAUS 2022, Xi’an, China, 23–25 September 2022; pp. 3772–3780. [Google Scholar]
- Zhao, S.B.; Zhu, J.W.; Bao, W.M.; Li, X.P.; Sun, H.F. A Multi-Constraint Guidance and Maneuvering Penetration Strategy via Meta Deep Reinforcement Learning. Drones 2023, 7, 626. [Google Scholar] [CrossRef]
- Gao, M.J.; Yan, T.; Li, Q.C.; Fu, W.X.; Zhang, J. Intelligent Pursuit-Evasion Game Based on Deep Reinforcement Learning for Hypersonic Vehicles. Aerospace 2023, 10, 86. [Google Scholar] [CrossRef]
- Zhou, M.P.; Meng, X.Y.; Liu, J.H. Design of optional sliding mode guidance law for head-on interception of maneuvering targets with large angle of fall. Syst. Eng. Electron. 2022, 44, 2886–2893. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Wang, J.; Bai, H.Y.; Chen, Z.X. LOS rate extraction method based on bearings-only tracking. Zhongguo Guanxing Jishu Xuebao/J. Chin. Inert. Technol. 2023, 31, 1254–1261+1272. [Google Scholar]
- Zhang, D.; Song, J.; Zhao, L.; Jiao, T. Line-of-sight Angular Rate Extraction Algorithm Considering Rocket Elastic Deformation. Yuhang Xuebao/J. Astronaut. 2023, 44, 1905–1915. [Google Scholar]
- Sun, C. Development status,challenges and trends of strength technology for hypersonic vehicles. Acta Aeronaut. et Astronaut. Sin. 2022, 43, 527590. [Google Scholar]
- Liu, S.X.; Liu, S.J.; Li, Y.; Yan, B.B.; Yan, J. Current Developments in Foreign Hypersonic Vehicles and Defense Systems. Air Space Def. 2023, 6, 39–51. [Google Scholar]
- Luo, S.; Zha, X.; Lu, H. Overview on penetration technology of high-speed strike weapon. Tactical Missile Technol. 2023, 5, 1–9. [Google Scholar] [CrossRef]
- Guo, H. Penetration Game Strategy for Hypersonic Vehicles. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2018. [Google Scholar]
- Li, K.X.; Wang, Y.; Zhuang, X.; Yin, H.; Liu, X.Y.; Li, H.Y. A Penetration Method for UAV Based on Distributed Reinforcement Learning and Demonstrations. Drones 2023, 7, 232. [Google Scholar] [CrossRef]
- Weiss, M.; Shima, T. Minimum Effort pursuit/evasion guidance with specified miss distance. J. Guid. Control Dyn. 2016, 39, 1069–1079. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Zhuang, X.; Liu, X.; Li, H. A Reinforcement Learning Method Based on an Improved Sampling Mechanism for Unmanned Aerial Vehicle Penetration. Aerospace 2023, 10, 642. [Google Scholar] [CrossRef]
- Wan, K.; Gao, X.; Hu, Z.; Wu, G. Robust motion control for UAV in dynamic uncertain environments using deep reinforcement learning. Remote Sens. 2020, 12, 640. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).